Abstract
Neuroimaging evidence suggests that the aging brain relies on a more distributed set of cortical regions than younger adults in order to maintain successful levels of performance during demanding cognitive tasks. However, it remains unclear how task demands give rise to this age-related expansion in cortical networks. To investigate this issue, functional magnetic resonance imaging was used to measure univariate activity, network connectivity, and cognitive performance in younger and older adults during a working memory (WM) task. Here, individuals performed a WM task in which they held letters online while reordering them alphabetically. WM load was titrated to obtain four individualized difficulty levels with different set sizes. Network integration—defined as the ratio of within-versus between-network connectivity—was linked to individual differences in WM capacity. The study yielded three main findings. First, as task difficulty increased, network integration decreased in younger adults, whereas it increased in older adults. Second, age-related increases in network integration were driven by increases in right hemisphere connectivity to both left and right cortical regions, a finding that helps to reconcile existing theories of compensatory recruitment in aging. Lastly, older adults with higher WM capacity demonstrated higher levels of network integration in the most difficult task condition. These results shed light on the mechanisms of age-related network reorganization by demonstrating that changes in network connectivity may act as an adaptive form of compensation, with older adults recruiting a more distributed cortical network as task demands increase.
1. Introduction
Despite substantial anatomical and functional decline, the aging brain retains a surprising degree of neural plasticity. In functional neuroimaging studies, for example, older adults often activate brain regions not engaged by younger adults during the same tasks (Cabeza and Dennis, 2013; Park and Reuter-Lorenz, 2009). Although over-recruitment in older adults is often interpreted as compensatory (Cabeza et al., 2018), it is unclear if and how the regions over-recruited by older adults are integrated with the network mediating task performance. To investigate this question, the current study assessed the effects of aging on network integration, an established concept of interest in characterizing brain dynamics (Tononi et al., 1994), during a working memory (WM) manipulation task. The study had three main goals.
The first goal of the study was to examine how the effects of age on network integration differ as a function of WM demands. As the number of items maintained in WM (load) increases, brain activity tends to rise monotonically in several regions, including dorsolateral prefrontal cortex (DLPFC) and lateral parietal cortex (LPC, Beauchamp et al., 2001; Braver et al., 1997; Rypma et al., 1999; Veltman et al., 2003). These activations tend to increase more rapidly in older than younger adults up to a certain level of WM demands (Cappell et al., 2010; Low et al., 2009; Schneider-Garces et al., 2010). According to the Compensation-Related Utilization of Neural Circuits hypothesis (CRUNCH, Reuter-Lorenz and Cappell, 2008), due to processing inefficiencies, older adults over-recruit neural resources at lower levels of task difficulty than younger adults. What is unclear from available CRUNCH evidence is whether the accelerated brain recruitment in older adults is limited to the activation of individual regions or whether it involves a reorganization of the underlying task network. Much recent work has focused on mapping functional brain networks in older adults, and a number of these more recent investigations of age-related changes in multivariate network connectivity have shown that PFC regions over-recruited by older adults often show stronger long-range functional connectivity outside of local cortical communities, and these changes are often associated with differences in cognitive performance (Damoiseaux et al., 2016; Geerligs et al., 2014, 2015, 2017). In the current study, therefore, we hypothesized that as task demands increase, the WM network would become more integrated with the rest of the brain and this effect would be greater for older than younger adults (Hypothesis 1).
The second goal of this study was to examine hemispheric differences in network integration for young and older adults. In functional neuroimaging studies, activations are often more bilateral in older adults than younger adults, an effect known as Hemispheric Asymmetry Reduction in Older Adults (HAROLD, Cabeza, 2002). For example, during a verbal WM task that yields left lateralized activations in younger adults, older adults may show additional activity in the right hemisphere (Reuter-Lorenz et al., 2000). As in the case of CRUNCH, most evidence for HAROLD is based on univariate activity in individual regions, and hence, the network mechanisms of age-related hemispheric differences remain uncertain. In the current study, we therefore hypothesized that during the left-lateralized verbal WM task, older adults would show greater demand-related network integration in the right-hemisphere (Hypothesis 2).
The third goal of the study was to investigate if age-related changes in network integration relate to individual differences in WM performance. It has been suggested that more widespread activity in older adults is beneficial for performance (Cabeza and Dennis, 2013; Park and Reuter-Lorenz, 2009), and both CRUNCH and HAROLD effects have been interpreted as compensatory. However, the evidence for compensation has been mostly based on univariate activity and evidence that network changes in older adults contribute to cognitive performance is largely missing (however, see Monge et al., 2018). We hypothesized that age-related WM network integration would be associated with WM ability in older adults (Hypothesis 3).
To test these hypotheses, participants completed a verbal WM manipulation task in which they briefly maintained consonants in memory while mentally rearranging them into alphabetical order. fMRI analyses focused on the effects of WM load on functional connectivity during the delay period, while the WM network was defined as regions activated by the task irrespective of load. Here, network integration was measured as the ratio of within-versus between-network connectivity, while network integration was compared within and between hemispheres, and correlated with WM capacity to test the three stated hypotheses.
2. Materials and methods
2.1. Participants
Forty-four young adults aged 18 to 35 (21 females; mean age 22.8 ± 4.6) and 32 older adults aged 60 to 80 (15 females; mean age 69.1 ± 5.3) participated in the study for monetary compensation and consented to the protocol approved by the Duke Medical School IRB (#Pro00065334). All subjects were self-reported right-handed. Older adults were screened for possible incidence of dementia, as measured by a Mattis Dementia Rating Scale-2 (DRS-2) total scaled score below 8 (Jurica et al., 2001). Qualifying participants were enrolled in a 6-day TMS protocol (Beynel et al., 2019; Beynel et al., in review), but only data from the screening session (Day 1) and MRI session (Day 2) are reported here. Participants had no history of psychiatric or neurological disorders and were not using psychoactive drugs. Participants were excluded because of poor functional imaging quality (excessive movement or falling asleep during data acquisition, n = 3), or due to poor task performance in the scanner (accuracy greater than two standard deviations below the group mean, n = 6). Thus, 37 young adults and 30 older adults were included in the final analysis.
2.2. Experimental design and statistical analyses
2.2.1. Behavioral procedure and task design
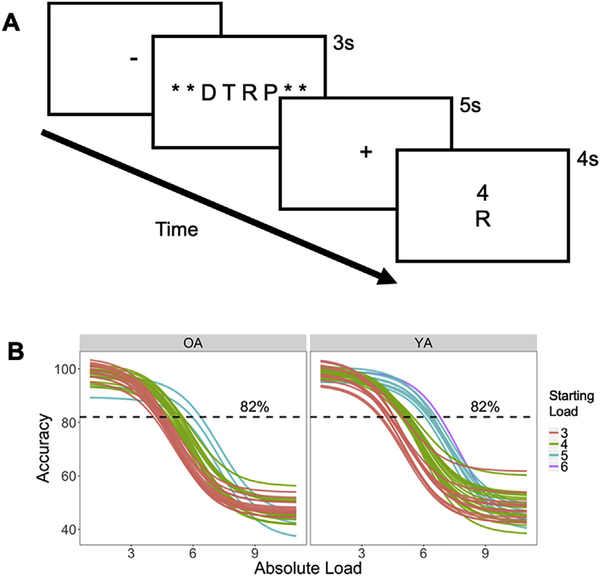
Participants performed a verbal WM manipulation task (Fig. 1A). In this task, an array of 3–9 consonant letters was presented for 3 s followed by a 5-s delay period, during which participants mentally rearranged letters into alphabetical order. Vowels were excluded to prevent chunking. After the delay period, a letter and number were presented together for 4 s and the participants pressed one of three buttons to indicate if the probe letter (1) appeared in the position indicated by the number in the alphabetized list (Valid, 40% of trials), (2) was part of original set but the number did not match the position in the alphabetized list (Invalid, 40% of trials), or (3) was not part of the original set (New, 20% of trials). These three types of trials occurred in random order. During the subject-specific titration on Day 1 (see the following paragraph), the response phase was followed by a 5-s inter-trial interval (ITI). During practice, participants were given feedback during this ITI on their accuracy after each trial, and at the end of each block. Twenty-five trials were included in each of the 6 blocks with a brief, self-paced rest interval between blocks.
Fig. 1.
Task paradigm and individual WM load determination. (A) Illustration of WM manipulation during an array of 3–9 letters was presented, followed by a delay during which participants were asked to rearrange the original array in alphabetical order and subsequently report if a probe number matches the serial position of a probe letter in the alphabetized array. (B) Individually-titrated Difficulty Levels were determined using sigmoid curves fitted to individual performance data from screening visit, based on accuracy.
As part of the overall protocol, subjects participated in up to 6 experimental sessions, but only the first two are relevant to this study. In the first session, participants performed the WM manipulation task outside the scanner in order to identify the range of WM loads producing parametric changes in performance for each participant. The optimal load was identified using 2-down-1-up staircase procedure: when a trial was answered correctly, the load was increased by 1, and when it was answered incorrectly, the load was decreased by 2. New trials were excluded from the analysis and accuracy data, collapsed across Valid and Invalid trials at each load, were then fitted to a sigmoid function with performance threshold criterion set at 82% accuracy. To ensure that the psychometric function was not strongly influenced by noise in loads with a low number of trials, 50% accuracy was used for the largest loads if less than 10 trials were tested. To achieve more stable curve fits, anchors were added by including points for loads of 1 and 2 at 100% accuracy and loads 10 and 11 at 50% accuracy. Four individualized difficulty levels were defined according to the intersection between the sigmoid curve and an 82% accuracy threshold, referred to here as WM capacity (for similar staircase approaches, see Garcia-Perez, 1998). The two loads below this intersection were defined as the Very Easy and Easy levels, and the two loads above were defined as the Medium and Hard levels. Thus, the four Absolute Loads selected for an individual depended on his/her WM ability (e.g., 3–4-5–6 letters in one participant, 4–5-6–7 in another participant) and therefore potentially reduced state-dependency that would be caused by fixed difficulty levels that do not match individual capabilities. Furthermore, given the intensive testing schedule inherent in our 6-session protocol, we excluded participants who could not accurately perform the WM task. Participants for whom this curve-fitting procedure (based on Day 1 data) did not estimate a minimum set size of at least 3 letters were excluded from subsequent imaging and rTMS sessions. As such, for clarity the Very Easy, Easy Medium and Hard conditions are referred to as WM Difficulty Levels. Individual sigmoid curves for all young and older adults, and subsequent determination of their Starting Load (i.e. the Absolute Load value of the Very Easy condition), are shown in Fig. 1B.
In the second session, participants performed the WM manipulation task inside the MRI scanner. Four blocks, each with 30 trials, were performed using the 4 individually-titrated Difficulty Levels. Stimuli were back-projected onto a screen located at the foot of the MRI bed using an LCD projector. Subjects viewed the screen via a mirror system located in the head coil and the start of each run was synchronized with the MRI acquisition computer. Trial-by-trial feedback was not given, but the overall block accuracy was presented at the end of each block. Behavioral responses were recorded with a 4-key fiber-optic response box (Resonance Technology, Inc.). Scanner noise was reduced with ear plugs, and head motion was minimized with foam pads. When necessary, vision was corrected using MRI-compatible lenses that matched the distance prescription used by the participant. The total scan time, including breaks and structural scans, was approximately 1 h 40 min.
2.2.2. MRI scanning and data preprocessing
MRI was performed in a 3-T GE scanner at the at Duke Brain Imaging Analysis Center (BIAC). Structural MRI and diffusion-weighted imaging (DWI) scans were followed by performing 4 fMRI runs of the WM manipulation task. The anatomical MRI was acquired using a 3D T1-weighted echo-planar sequence (matrix = 256 × 256, time repetition (TR) = 7.15 ms, time echo (TE) = 2.7 ms, field of view (FOV) = 256mm2, slices = 196, slice thickness = 1 mm). In the fMRI runs, coplanar functional images were acquired using an inverse spiral sequence (64 × 64 matrix, TR = 2000 ms, TE = 25 ms, FOV = 220mm2, 34 slices, 4mmslice thickness, 280 images). Finally, DWI data were collected using a single-shot echo-planar imaging sequence (TR = 17,000 ms, slices = 76, thickness = 2.0 mm, FOV = 256 × 256 mm2, matrix size 128 × 128, voxel size = 2 mm3, b value = 2000 s/mm2, diffusion-sensitizing directions = 26, total images = 960, total scan time = 7.5 min).
Functional images were preprocessed using image processing tools, including FLIRT and FEAT from the fMRIB Software Library (FSL), in a publicly available pipeline developed by the Duke Brain Imaging and Analysis Center (https://wiki.biac.duke.edu/biac:analysis:resting_pipeline). Images were corrected for slice acquisition timing, motion, and linear trend; motion correction was performed using MCFLIRT, and 6 motion parameters estimated from the step were then regressed out of each functional voxel using standard linear regression. A comparison of mean displacement across all functional runs between younger and older adults revealed no group differences (t66 = 1.21). Nonetheless, motion regressors were used in all univariate models, and included in all subsequent correlational psychophysical interaction (cPPI) analyses (see below) to adjust for any potential confounds due to motion. Images were then temporally smoothed with a high-pass filter using a 190-s cutoff and normalized to the Montreal Neurological Institute (MNI) stereotaxic space. White matter and CSF signals were also removed from the data, using white matter/CSF masks generated by FSL’s FAST and regressed from the functional data using the same method as the motion parameters. Spatial filtering with a Gaussian kernel of full-width half-maximum (FWHM) of 8 mm was applied.
2.2.3. Behavioral analyses
Accuracy and reaction times (RTs) of WM manipulation trials were analyzed for each individually-titrated WM Difficulty Level. RTs were analyzed, only for correct trials (74.6% of total trials), using a linear restricted maximum likelihood model. Accuracy was analyzed using a binomial logistic regression model including all trials. In both models, R (R Core Team, 2012) and lme4 (Bates et al., 2012) were used to perform mixed effects analysis. WM Difficulty Level was entered as a fixed effect, and both model intercepts and by-subject random slopes across WM Difficulty Levels were included as random effects. Gender and each subject’s WM capacity were also included to account for standardizing difficulty levels across subjects and general differences in task ability. No deviations from homoscedasticity or normality were observed. P-values were obtained by likelihood ratio tests of the full model with the variable in question against a null model without the variable in question using an ANOVA to compare the model fits. There was no missing data, but in 1.8% of trials participants failed to respond within the 4-s response window (143 out of 8040 trials); these trials were excluded from all analyses.
2.2.4. fMRI analyses
A parametric approach was used to investigate how activity varied as a function of WM load. First-level voxel time-series analysis was carried out using general linear modeling (GLM); fixed effects models were carried out to examine the effects of load; separate events were modeled for the array presentation (duration: 3 s), delay period (duration: 5 s), and response (duration: subject reaction time), each with an onset at the beginning of the event. Four separate delay-period regressors were used to model each of the WM Difficulty Levels for each subject; correct valid and correct invalid responses were modeled under the same task regressor; despite decreasing accuracy in difficulty conditions, the number of correct trials in each condition was still sufficient for fMRI response estimation (mean trial count = 23, 23, 21, 20 across difficulty levels). Incorrect and non-response trials were modeled identically, but separately, and were not considered in the univariate results below. Subsequent to individual-level models, random-effects analysis was performed on parameter estimates of the delay-period regressors (p < 0.005). Subsequent group-level analyses were performed across the four delay-period regressors in SPM12.
2.2.5. Cortical parcellation
Before functional matrices were constructed, a consistent parcellation scheme was established across all subjects that reflects an accurate summary of full connectome effects (Bellec et al., 2015). Subjects’ T1-weighted images were segmented using SPM12 (www.fil.ion.ucl.ac.uk/spm/software/spm12/), yielding a grey matter (GM) and white matter mask in the T1 native space for each subject. The entire GM was then parcellated into 471 regions of interest (ROIs), each representing a network node by using a subparcellated version of the Harvard-Oxford Atlas (HOA), (Tzourio-Mazoyer et al., 2002), defined originally in MNI space. Subsequent follow-up analyses utilized a parcellation scheme defined by Yeo et al. (2011), also defined in MNI space. The T1-weighted image was then nonlinearly normalized to the ICBM152 template in MNI space using fMRIB’s Non-linear Image Registration Tool (FNIRT, FSL, www.fmrib.ox.ac.uk/fsl/). The inverse transformations were applied to the HOA atlas in the MNI space, resulting in native-T1-space GM parcellations for each subject. Then, functional time series were extracted from the above MNI-normalized functional data for each individual, each ROI, for subsequent functional connectivity analyses.
2.2.6. Functional connectivity
Functional connection matrices representing task-related connection strengths were estimated using a cPPI analysis used previously by our group (Davis et al., 2017) and others (Fornito et al., 2012) to estimate a whole-brain connectivity matrix that describes task-related interactions between brain regions. Briefly, the model relies on the calculation of a PPI regressor for each region (or node), based on the product of that region’s time course and a task regressor of interest, in order to generate a term reflecting the psychophysical interaction between the seed region’s activity and the specified experimental manipulation.
The convolved task regressors from the univariate model described above were used as the psychological regressor, which were originally coded as the four Set-Size-modulated delay regressors (range = 1–4); all regressors are mean-adjusted in FSL; as such, our linear, mean-centered parameterization forms an effective contrast of [−1.5 −0.5 0.5 1.5] across Very Easy, Easy, Medium, and Difficulty item loads (respectively). The correct-trial delay-period regressors were each multiplied with two network time courses for region i and j. As is typical in most working memory paradigms, our delay period interval was of a fixed length (4 s), and therefore not jittered with the array presentation or response periods of the task. In order to address the possibility that this delay period-activity was thus contaminated by these other events, we repeated this partial correlation by including convolved regressors for array and response periods in the z-term. Nonetheless, the inclusion of these regressors had no influence, suggesting that the confound in isolating delay-period activity during fMRI of working memory cannot be solved under the current data design parameters. The partial correlation was then computed, removing the variance z, which includes both the psychological regressor and the time courses for regions i and j, as well as constituent noise regressors including 6 motion parameters and noise regressors coding for the concurrent signal in white matter and CSF during each run. This cPPI analysis resulted in 4 separate output matrices, comprising connectivity delineated by WM load. Task-related connectivity was estimated from the resulting output matrices; negative connections were included in these analyses, as they may inform important, explicit interpretations about how networks may be segregated (Braun et al., 2012). Of note, our inclusion of the motion regressors did not have a significant effect on overall connectivity values; nonetheless, it remains an open question whether such an inclusion in task-related connectivity helps to control for the residual influence of motion not removed in initial preprocessing stages, or instead re-introduces noise into the data (see Lindquist et al., 2019). To facilitate future work, we have made available cPPI connectomes both with and without motion regressors included as controlling random variables.
Lastly, in order to summarize system-wide behavior in the task-related network, a previously reported measure of system segregation was applied with modifications (Chan et al., 2014). This measure is calculated as the difference between the mean magnitudes of between-system correlations from the within-system correlations as a proportion of mean within-system correlation.
where is the mean r-values between nodes of one partition, module, or system (similar to within-module degree or WMD), and is the mean of r-values between nodes of separate partitions (similar to between-module degree or BMD, Davis et al., 2017). Accordingly, values greater than 0 reflect relatively lower between-system correlations in relation to within-system correlations (i.e., stronger integration of systems), and values less than 0 reflect higher between-system correlations relative to within-system correlations (i.e., diminished integration of systems). This measure was then modified by taking 1 – Segregation to reflect system integration, or the inverse effect of segregation. In subsequent connectivity analyses, one older adult participant’s average network integration value was greater than two standard deviations below the mean and was thus excluded from this analysis. All plots were created using R (R Core Team, 2012) and ggplot (Wickham and Wickham, 2007). All connectivity data was visualized using BrainNet Viewer (http://www.nitrc.org/projects/bnv/).
3. Results
3.1. Behavioral results
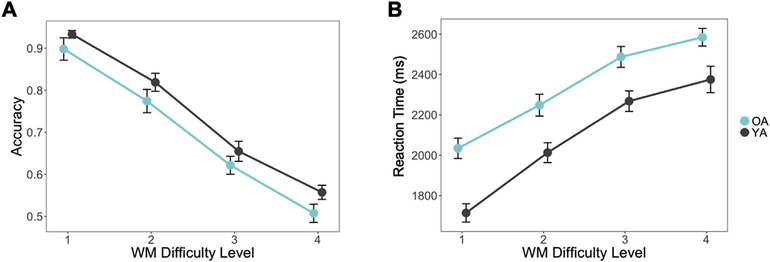
There were no significant group differences between young and older adults in either Starting Load (t66 = 0.46, p = 0.65) or WM capacity values (t66 = 1.26, p = 0.21) (Table 1). This suggests that both age groups were fairly equivalent in baseline performance level. Results from the linear and logistic regression models demonstrated that increasing WM Difficulty Level corresponded to lower accuracy (χ2 = 86.84, p < 2.2e-16) and slower RTs (χ2 = 63.37, p = 1.7e-15). Additionally, while there was no main effect of group on accuracy (i.e., correctly recognizing old probes), older adults demonstrated significantly slower RTs (χ2 = 12.30, p = 4.5e-4). This lack of group difference in accuracy is not surprising given that low performers were screened out of the experiment, and previous studies have demonstrated that titrating for individual performance largely removes age differences in task performance that are typically found (Cappell et al., 2010; Schneider-Garces et al., 2010). Accuracy and response time was further summarized across difficulty level for valid, invalid, or new trials separately to further investigate performance differences across trial type (Fig. S1A; accuracies for the Valid/Invalid Position decision are presented in Table S1B, but not the focus of the current analysis). From these data, we see that older adult subjects correctly recognized both old probes (valid or invalid letter probes, which both constitute “old” trials) with a high degree of accuracy, (all subject means > 80%, even at the highest levels of difficulty). Furthermore, older adult subjects were also correctly identified lure probes (i.e., New trials; all subject means < 18%, even at the highest levels of difficulty). Higher WM capacity significantly predicted lower accuracy (χ2 = 10.98, p = 9.2e-4) but not reaction time. Plots of response accuracy show a linear trend across WM Difficulty Level (Fig. 2A & B) wherein WM load strongly predicts performance, but no group-by-difficulty interactions were found. This titration therefore allows brain measures to be more directly compared both within and across age groups, as these differences would be unrelated to any disparity in task performance.
Table 1.
ANOVA of factors affecting accuracy and RTs.
| Effect | Estimate | Std. Error | χ2 Value | Pr > |t| |
|---|---|---|---|---|
| Accuracy | ||||
| Intercept | 7.76 | 0.66 | ||
| Age Group | −0.05 | 0.54 | 0.01 | 0.92 |
| WM Difficulty Level | −0.99 | 0.10 | 86.84 | <2.2e–16 |
| Age x WM Difficulty | −0.09 | 0.13 | 0.40 | 0.52 |
| WM Capacity | −0.37 | 0.11 | 10.98 | 9.2e–4 |
| RTs | ||||
| Intercept | 1210.63 | 236.10 | ||
| Age Group | 328.68 | 90.98 | 1230 | 4.5c–4 |
| WM Difficulty Level | 231.09 | 22.37 | 6337 | 1.7e–15 |
| Age x WM Difficulty | −34.43 | 34.18 | 1.04 | 0.30 |
| WM Capacity | 37.71 | 39.37 | 0.89 | 0.35 |
Note: χ2 statistics and p-values were obtained by likelihood ratio tests of the full model with the effect in question against the model without the effect in question.
Fig. 2.
Behavioral performance on Valid and Invalid trials in each group across difficulty, with figures representing (A) showing average Accuracy ± standard error and (B) RTs ± standard error. Linear mixed effects models for the effects of Age Group and WM Difficulty were performed on both forms of data. While clear Difficulty effects are present in both measures, Group differences are present for Reaction Time (χ2 = 12.3, p = 4.5e-4), but not for Accuracy (χ2 = 0.01, p = 0.92).
3.2. fMRI results
As described in the introduction section, the study had three main goals: (1) investigate how age effects on WM network integration vary as a function of WM demands; (2) examine hemispheric differences in network integration in young and older adults; and (3) investigate if age-related changes in network integration relate to individual differences in WM performance. Before turning to each of these analyses, the next section describes how the task-related network was identified.
3.2.1. Task-related network identification
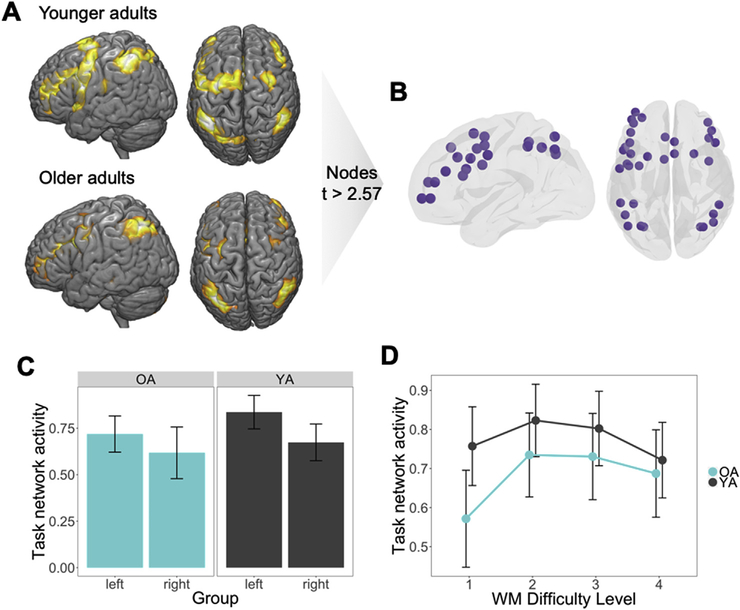
As illustrated by Fig. 3A, when collapsing across WM loads, the network of activated regions consisted of frontal and parietal areas, similar to what is typically found in fMRI studies of WM (Cabeza and Nyberg, 2000). To select ROIs for network analyses, all commonly activated ROIs across young and older adults that had average ROI-level t-value above 2.59, corresponding to a significance of p < 0.005 uncorrected, were included in the task network. This resulted in a 35-node network consisting of bilateral frontoparietal and sensorimotor regions (see Fig. 3B). Next, we address whether age was associated with differences in the symmetry of task-network activation. Splitting the Task network activity by left and right ROIs, we then performed a Age x Hemisphere ANOVA on the univariate activity values to test this hypothesis (Fig. S2); As expected given the verbal nature of the task, average activity within this network was greater in the left hemisphere in young adults (F1,36 = 8.21, p = 0.007), but this hemispheric asymmetry activity was not observed in older adults (F1,29 = 1.09, p = 0.31, Fig. 3C); nonetheless, we found no significant hemisphere-by-age interaction. Average univariate activity in all task-related regions showed a weak inverse-U pattern as a function of WM load, with no significant differences between groups across difficulty level (Fig. 3D). This finding supports previous findings of load effects disappearing when normalized to individual performance (Schneider-Garces et al., 2010), and thus may be a better measure of directly comparing brain differences rather than WM capacity differences in aging. Thus, this task-based network is utilized to more effectively investigate changes in network connectivity, such as how task regions communicate with each other at network and whole-brain levels.
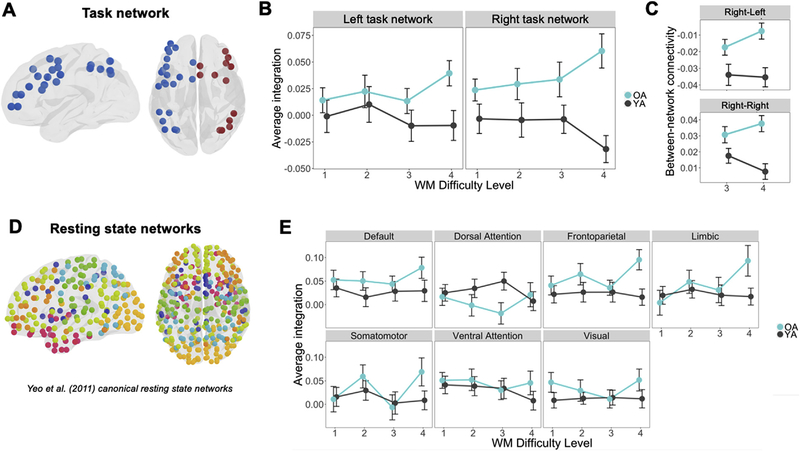
Fig. 3.
Converting univariate information into multivariate topology (p < 0.05 = *, p < 0.01 = **). (A) Thresholded average delay-period maps, averaging responses within each ROI in the HOA471, used to identify regions responsive to the task. (B) Nodes of the network with a t-value greater than 2.57 common to both groups were then assigned to the task network. (C) Average activity was higher in left than right hemisphere task regions, with a significant main effect in younger adults. (D) While task network activity was higher for younger than older adults, univariate activity within the task network did not differ across WM Difficulty Level between age groups.
3.2.2. Network integration and task difficulty
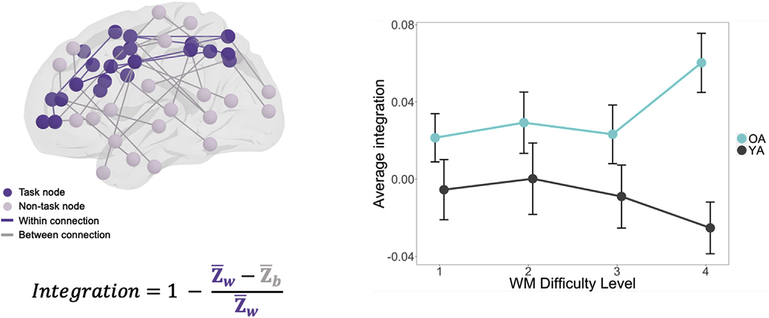
The first goal of the study was to investigate how age effects on WM network integration vary as a function of WM demands. Specifically, we tested the hypothesis that as task demands increase, the WM network becomes more integrated with the rest of the brain and this effect is greater for older than younger adults (Hypothesis 1). In order to test this hypothesis we applied task-related connectivity (as defined by cPPI, see Davis et al., 2017; Fornito et al., 2012), which examines the degree to which the correlation of fMRI timeseries between a pair of cerebral regions may be modulated by the hemodynamic response associated with a cognitive event. As illustrated by Fig. 4, the results were consistent with this hypothesis: as a function of WM Difficulty Level, network integration decreased slightly in young adults, but increased substantially in older adults. When entered into a 2-way group by difficulty ANOVA, there were significant differences in group (F1,64 = 6.19, p = 0.015) and no general Difficulty Level differences. The interaction between group and load was also significant (F1,196 = 5.72, p = 0.018). This effect emerged particularly in the hardest level (Level 4: t65 = −4.21, p = 8.1e-05). This finding is consistent with the univariate activity evidence for the CRUNCH hypothesis (Cappell et al., 2010; Low et al., 2009; Reuter--Lorenz and Cappell, 2008; Schneider-Garces et al., 2010), but it extends this evidence by showing that demand-related over-recruitment in older adults involves changes in network integration.
Fig. 4.
Components of integration value determination and parametric effects of WM Difficulty Level on network integration (±standard error, across WM Difficulty Level; p < 0.05 = *, p < 0.01 = **).
3.2.3. Hemispheric differences in network integration
The second goal of the study was to identify which regions are driving the integration effect by using informed decompositions of the networks examined above. First, we sought to test whether hemispheric differences in network integration in young and older adults help to explain the observed pattern above. This approach is motivated by the common finding that activations are less lateralized in older adults than younger adults. In particular, we tested the hypothesis that during a left-lateralized verbal WM task, older adults show greater demand-related network integration in the right-than the left-hemisphere (Hypothesis 2). To do so, integration measures were calculated separately within the left and right hemispheric components of the task network (Fig. 5A) and entered into a 3-way group by difficulty by hemisphere ANOVA. While the 3-way interaction was not significant, interactions emerged in group by difficulty (F1,456 = 10.06, p = 0.002) and group by hemisphere (F1,456 = 4.26, p = 0.040), with no interaction of difficulty by hemisphere. Thus, the lack of a significant 3-way interaction precludes that “older adults show increased difficulty-related network connectivity in the right, more than the left hemisphere.” Nonetheless, such a conclusion is based on a more explicit comparison of the left and right hemisphere; we therefore performed follow-up tests to characterize the connection profile left and right hemisphere independently. Thus, separate 2-way group by difficulty ANOVAs for each hemisphere were then computed to probe this possibility. Consistent with the Hypothesis 2, the difficulty by age interaction remained significant in the right hemisphere (F1,196 = 3.90, p = 0.048), but not in the left hemisphere (F1,196 = 1.68, p = 0.19; Fig. 5B). This finding suggests that age-related increases in network integration were driven by greater integration of the right hemisphere task nodes. To further investigate this effect, we split the connectivity of right-hemisphere task nodes with other right-hemisphere nodes (right-right) and with left-hemisphere nodes (right-left) focusing on the difference between Difficulty Levels 3 and 4 since these consecutive levels demonstrated the greatest interaction effect. As illustrated by Fig. 5C, both right-right and right-left connections showed greater integration with WM demands in older adults. An age (young vs. old) by difficulty (Level 3 vs Level 4) by connection type (right-right, right-left) ANOVA showed a significant age by difficulty interaction (F1,192 = 5.45, p = 0.02), but no other interactions. These results are consistent with univariate activity evidence for the HAROLD model (Cabeza and Dennis, 2013), but extends this evidence by showing that age-related contralateral recruitment is associated with greater between-network connectivity of the contralateral hemisphere network both within- and across-hemispheres.
Fig. 5.
Network integration of subdivided task and resting-state networks (p < 0.05 = *, p < 0.01 = **). (A) Parcellation of the task network split by hemisphere. (B) Average integration ± standard error of left-hemisphere and right-hemisphere task networks treated separately. (C) Right hemisphere task region between-network connectivity with right and left non-task regions. (D) Data-driven parcellation of modules determined by average resting state data across young and older adults. (E) Average integration ± standard error of each module as defined by resting state.
A potential concern of the hemispheric differences in network integration is that it could be driven by differences in canonical intrinsic networks, such as the default mode network (DMN). A growing body of evidence suggests that older adults show less modular architecture (Betzel et al., 2014), and that relationships between frontal control and DMN regions become less decoupled with age (Spreng and Turner, 2019). To investigate this issue, our second approach was to investigate the alternative hypothesis that the task-based integration was driven by changes in the modularity of resting state networks. Each ROI in the 471-node network was assigned to one of the seven network parcellation schemes defined by Yeo et al. (2011) based on the greatest area of overlap. The regions were thus labeled as Visual, Somatomotor, Dorsal Attention, Ventral Attention, Limbic, Frontoparietal, and Default networks according to this standard atlas (Fig. 5D). In this analysis integration between nodes of each of the seven canonical resting-state modules (or networks) was calculated to determine whether the network integration effects observed in Fig. 5B were present in any specific standard resting-state network (the task network was excluded from this analysis). Integration scores were assessed for each canonical network using a repeated-measures ANOVA for each module. The Limbic network, comprising regions in anterior temporal and orbitofrontal cortex, was the only resting state network to demonstrate a significant group by difficulty interaction after Bonferroni correction (Fig. 5E; F1,196 = 8.25, p = 0.032). There were no other significant interaction effects in any module, and there were no significant group or difficulty level effects in any module. It is noteworthy that while no limbic regions (e.g., hippocampus, inferior/anterior temporal cortex) exhibited greater univariate activity in the present study, sub-threshold activity in these regions may nonetheless be contributing to successful working memory performance. Many regions classified as Limbic in the Yeo atlas comprise loci implicated in multiple investigations of stimulus representation in working memory including age-related changes in anterior temporal connectivity during working memory (Nyberg et al., 2016; Viviano et al., 2019); nonetheless, there is no overlap between task-related working memory regions in the current study (which comprise largely frontoparietal regions), and regions in the Yeo Limbic module, suggesting that individuals in the current study may rely on connectivity-based support from an extended network of medial temporal lobe regions during increasingly difficult working memory conditions.
Lastly, in order to address the possibility that connectivity differences were driven by simple BOLD differences, the relationship between task-network univariate activity and integration in the task-related regions (i.e., nodes) was also investigated across all task difficulty conditions. No significant relationships between BOLD activity within the task network regions and network integration emerged at any level. Even in the most difficult condition, there was no trend between integration and activity in older adults (OA: r30 = 0.00, Fig. S3A). Nonetheless, because the putative task network was defined across all levels of difficulty, we sought to test whether the observed age-related increases in integration may have emerged due to the recruitment of additional regions outside the task network at the highest levels of difficulty. Post hoc tests of older versus younger adults revealed age-related increases in activity in right inferior frontal cortex, right inferior temporal cortex, and inferior parietal cortex (see Supplemental Results, Fig. S1), consistent with other reports (Li et al., 2015; Luo et al., 2016). Activation within these regions was similarly uncorrelated with integration scores in older adults (r30 = −0.02, Fig. S3B). These null results suggest that the observed age-related increases in integration in the task network cannot be attributed to either increases or decreases in univariate activity, and that connectivity information offers new information not revealed by univariate activity differences.
3.2.4. Network integration and individual differences in WM performance
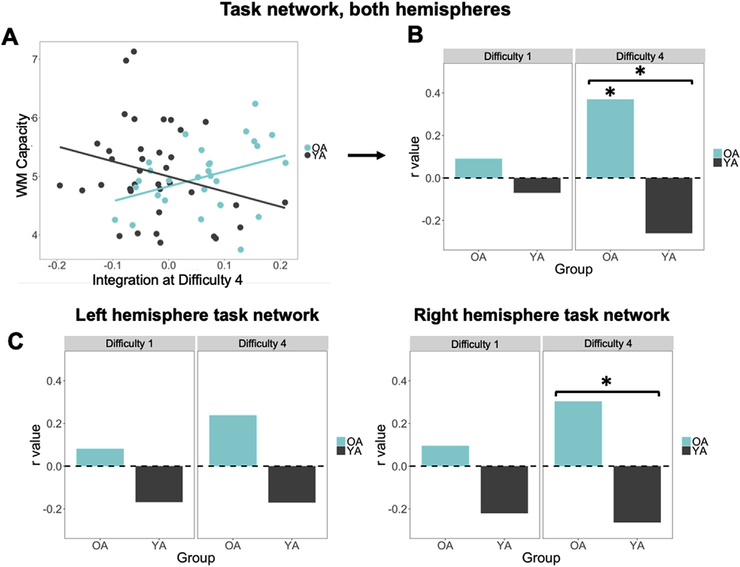
The third goal of the study was to investigate if age-related changes in network integration relate to individual differences in WM performance. Specifically, we tested the hypothesis that age-related WM network integration would be associated with WM ability in older adults (Hypothesis 3). As illustrated by Fig. 6A, the results were consistent with this hypothesis: in older adults, there was a significant correlation between network integration in the most difficult condition and WM capacity (r = 0.37, p = 0.048). In younger adults, in contrast, this relationship was not significant (r = −0.26, p = 0.18); a Fischer r-to-z transform confirmed a significant difference in these relationships (z = 2.54, p = 0.011, two-tailed), providing further support for the idea that older adults rely more on the right hemisphere than their younger counterparts during difficulty working memory processing. The correlation of WM capacity with integration was also examined at the easiest difficulty level to determine whether this effect was specific to the highest difficulty level. Neither correlation was significant (young adults: r = −0.07, p = 0.67; older adults: r = 0.09, p = 0.66; Fig. 6B). A Fisher r-to-z transformation was used to assess the significance of the difference between the brain-behavior correlations in younger and older adults. This difference was also significant only in the highest difficulty level (z = 2.54, p = 0.01), suggesting that network integration serves a different functional purpose in younger versus older adults. Nonetheless, to test for the possibility that individuals with higher WM capacity will also have a numerically higher number of items to maintain and manipulate in the most difficult condition (a natural consequence of our titrating procedure), we tested for any significant relationship between participant accuracies at the highest difficulties, and their WM capacity; we found no relationship between these measures (all |r| < 0.1). Thus, the tendency for older adults with higher WM capacity to integrate more in the difficult task condition implies that this increase in integration is an adaptive benefit to WM. This pattern of correlations also suggests that in younger adults, the segregation of the task network from non-task regions is similarly adaptive, but in the reverse direction; such a pattern of greater segregation associated with positive outcomes for behavior is consistent with other studies finding a link between increase modularity and WM performance in younger populations (Braun et al., 2015; Stanley et al., 2014).
Fig. 6.
Relationship of task-network integration and WM capacity (p < 0.05 = *, p < 0.01 = **). (A) Task-network integration in the most difficult task condition positively correlates with individual WM capacity scores in older adults. (B) r values of these correlations are significant for older adults with a significant difference across group only in the high difficulty level. (C) Split by hemisphere, the difference in correlation values is significant only for the Right hemisphere in the high difficulty level.
To better understand hemispheric influences, the same pattern of brain-behavior relationships was examined when integration scores were split across left and right hemisphere task regions. Only the highest difficulty level was examined in order to reduce the number of comparisons, which is justified by the age by difficulty effect observed above (Fig. 4); correlations with the easiest difficulty level are included for comparison. Of particular interest was whether younger and older adults exhibited qualitatively different brain-behavior relationships, specifically whether the age-related difference in the correlation between network integration and WM capacity was significant. After correcting for the remaining number of correlations compared, the right hemisphere showed a significant difference in correlation values in older, compared to young adults (z = 2.24, p = 0.025), while the left hemisphere did not show a significant difference (z = 1.59, p = 0.11; Fig. 6C). This indicates that older adults may rely more than their younger counterparts on right hemisphere network integration with the rest of the brain, and that the bilateral integration effects associated with WM capacity and age seen above (Fig. 6A) are likely driven by the right hemisphere. This finding is in line with our result above, in the current analysis, that the age-related differences in network integration are largely attributable to the right hemisphere. Thus, an age-related difference in brain-behavior relationships is consistent with the interpretation that integration is good for older and bad for younger adult brains.
Correlations between average integration and accuracy during task performance at the highest difficulty level were also computed in both the bilateral task network and task network split by hemisphere; no significant relationships emerged (|r| < 0.2), suggesting that the relationship of integration with behavior may be driven more strongly by individual differences rather than task-related recruitment of a so-called compensatory mechanism.
4. Discussion
The current study examined how aging affects network integration during the manipulation of information in working memory and how this integration influences individual differences in WM ability. Our analysis focused on the use of task-related whole-brain connectivity, which describes the modulation in the correlation of timeseries between cortical regions in response to a cognitive event. The study yielded three main findings. First, as task difficulty increased, network integration decreased in younger adults but increased in older adults. Second, the increase in network integration due to task demands that was observed in older adults was driven by stronger connectivity in the right hemisphere, which is less activated in younger adults during the WM task. Third, older adults with higher working memory capacity had significantly higher levels of task network integration in the most difficult condition, consistent with a compensation account as articulated in the HAROLD and CRUNCH models. These three findings are discussed in separate sections below.
4.1. Age effects on network integration as a function of task demands
The first finding of the study was that older adults showed a significant increase in network integration as a function of WM demands (load), whereas young adults showed the reverse pattern. To our knowledge, this is the first demonstration of a demand-related increase in task-related network integration in older adults, as well as the first report of a clear age-by-difficulty interaction in network connectivity. The age-related increase in network integration is generally consistent with studies observing load-related increases in PFC activity in older adults (Nagel et al., 2009), but it goes beyond univariate activation findings by showing that the task-related regions over-recruited by older adults are selectively integrated with the broader cortical network. This result also extends findings of age-related increases in bivariate functional connectivity (Daselaar et al., 2006; Dennis et al., 2008; St. Jacques et al., 2009) by showing the effect at the level of whole-brain networks and revealing the global context for these bivariate interactions. Finally, while the current results fit with previous evidence of age-related increases in network integration during rest (Chan et al., 2014, 2017), they also expand this evidence by showing a clear link between network integration and task demands.
In contrast with older adults, integration decreased in younger adults as a function of difficulty. There is not currently a consensus on what the benefits of more widespread network community integration may be, and there is evidence showing task demands can be associated with either increased integration (Braun et al., 2015; Hearne et al., 2017) or decreased integration (Davis et al., 2018; Mattar et al., 2018), depending on task investigated. Furthermore, there is evidence that, depending on the task, greater integration can be associated with better (Braun et al., 2015; Cohen and D’Esposito, 2016) or worse (Cohen and D’Esposito, 2016) performance. In the current study, the task was the same and opposite effects of task demands on integration were seen for older versus younger adults. Given that networks tend to show less functional segregation in older adults (Betzel et al., 2014; Chan et al., 2014; Cohen and D’Esposito, 2016), one possibility is that older adults benefit more from integration than younger adults. Opposing effects of univariate activity on WM performance in older and younger adults have been previously shown (Peira et al., 2016; Rypma and D’Esposito, 2000)., suggesting that younger and older adults recruit task-sensitive regions differently in response to shifting cognitive demands.
The first finding that older adults showed increased network integration is consistent with univariate activity supporting the CRUNCH hypothesis (Cappell et al., 2010; Low et al., 2009; Reuter-Lorenz and Cappell, 2008), while also showing that faster recruitment in older adults at higher task demands is not limited to the activity of individual regions. In univariate fMRI studies, manipulating WM load typically results in an inverted-U fMRI activity pattern, first increasing with task difficulty but then declining at higher levels of difficulty (Cappell et al., 2010; Low et al., 2009; Schneider-Garces et al., 2010; Vidal-Pineiro et al., 2017). In older adults, activity increases faster at lower levels of difficulty, but it also declines faster at higher difficulty levels. These findings are postulated to result from processing inefficiencies in older adults who over-recruit neural resources at lower levels of demands and, as a result, do not have additional resources at high demand levels. In contrast to univariate activity, network integration did not decrease at the highest difficulty level, despite clear limits in working memory capacity at this level (see Fig. 2). This pattern suggests that connectivity may represent a fundamentally different neural signal, one which remains more adaptive in aged participants.
4.2. Hemispheric differences in network integration in young and older adults
The second finding of the study was that increases in demand-related network integration in older adults were driven by connectivity changes in the right hemisphere. This finding fits with evidence for the HAROLD model (Cabeza and Dennis, 2013) showing age-related increases in univariate activity in the hemisphere less activated in younger adults, such as the right hemisphere in the current verbal WM task. Previous results speak in favor of the idea that bilateral activation patterns in the PFC are often associated with higher task demands across the lifespan (Belger and Banich, 1992; Davis and Cabeza, 2015), and therefore suggest a flexible bilateral cortical mechanism by which older adults may maintain youthful levels of performance. The current laterality findings, however, provide new insight by showing the consequence of these changes as expressed across whole-brain networks. Interestingly, right-hemisphere network integration increases in older adults were mediated by both connections within the right hemisphere and by connections between the right and the left hemisphere. The latter observation is consistent with previous results showing greater bivariate connectivity between left and right DLPFC in older than younger adults (Davis et al., 2012). This therefore suggests that the bilateral compensatory pattern may not be limited to strictly contralateral regions of the brain.
A central debate cognitive neuroscience of aging is whether or not age-related increases in recruitment of neural processes outside those recruited by younger adults reflect an adaptive compensation for the deleterious effects of age, or instead reflect more non-specific neural activity that fails to contribute meaningfully to cognition. The more specific question of how best to interpret age-related increases in right-hemisphere BOLD activation in the context of memory-related behaviors has traditionally relied on indirect relationships between activation and performance (Mattay et al., 2006; Suzuki et al., 2018), while nonetheless ignoring how such bilateral neural systems emerge from more traditional unilateral networks. In a consensus opinion article, compensation was defined as a cognition-enhancing over-recruitment of neural resources in response to cognitive demands (Cabeza et al., 2018). Thus, there are two essential criteria for attributing brain responses to compensation: they increase as a function of task demands and are associated with better cognitive performance. In the current results we found that age-related increases in task-related, right hemisphere network connectivity both increased with task difficulty and were significantly related to WM ability. Thus, in the present paradigm the age-related increase was clearly adaptive, given the strong parametric increases in connectivity in response to increasing task demand (Fig. 4) and right hemisphere connectivity in particular was related to successful performance (Fig. 6), fulfilling two of the aforementioned criteria for successful compensation. Having clarified the utility of this approach, it is important for future work to clarify the reasons why such a neural mismatch in neural resources emerges—namely declines in structural brain health. Furthermore, the justification for considering the left and right hemispheres separate in this respect is clear once one considers that this verbal task is left-lateralized (see Davis et al., 2018), and hence increased integration within the right hemisphere is consistent with contralateral recruitment (Davis et al., 2012). However, we found no concomitant increase in bilateral connectivity in OAs, suggesting that the task-related increase in right hemisphere connectivity in response to task difficulty is not reliant on signaling from the contralateral hemisphere. Such observations would not be possible by relying only on BOLD activation of left and right hemispheres. Thus, while this debate is typically formulated in terms of univariate activation, the current manuscript offers support that connectivity modulation in response to task difficulty may be more sensitive to right-hemisphere recruitment (for a generally left-lateralized lexical working memory task) than univariate activity.
When our connectivity patterns were decomposed by their membership to canonical resting state networks, rather than by hemisphere, only the Limbic network showed a significant age by difficulty interaction in network integration (Fig. 5E). Interestingly, the resting state-derived Frontoparietal network did not demonstrate an interaction, suggesting that canonical parcellations may not be as sensitive to such task-related changes in network connectivity. Furthermore, a post hoc test of the correlation comparing between-network connectivity (between the task network and any of the resting state networks defined by the Yeo atlas) and behavioral performance (either WM capacity or performance during the task) failed to identify any significant brain-behavior relationships (all r < 0.4, all N.S. after Bonferroni correction). Despite the popularity of resting state networks, it is unlikely that these partitions are fully representative of task-based networks (Cole et al., 2014; Davis et al., 2016), which could explain lack of integration in all but one of the resting state networks, and a lack of behavioral impact for connectivity in these subnetworks. Thus, while a growing body of evidence from resting state data suggests that older adults show less modular architecture (Betzel et al., 2014), our finding highlights the importance of task specificity in the context of investigating network connectivity, the use of more standardized network labels may obscure effects specific to a unique task-related network.
Notably, task-related connectivity has been assessed previously using similar techniques to describe age-related changes in network organization (Geerligs et al., 2014; Grady et al., 2016). Large-scale descriptions of network organization have largely focused on resting-state connectivity, findings (Betzel et al., 2014; Vij et al., 2018); we and others have cautioned that the inferences available from these “task-free” data is limited (Campbell and Schacter, 2017; Davis et al., 2016; Spreng et al., 2016). Nonetheless, the current data suggest that Task Difficulty is a highly salient modulator of connectivity, specifically within regions activated by the task. Nonetheless, the generalizability of our task-based parcellation scheme rests on the fact that a bilateral frontoparietal activation pattern during working memory comprises one of the most ubiquitous patterns in cognitive neuroscience (Owen et al., 2005). To be sure, the data-driven nature of resting state analysis has afforded the field new capacities to determine highly reliable network definitions based on consistent intra- and inter-subject consistencies in coactivation (Gordon et al., 2017; Power et al., 2011; Yeo et al., 2014), local homogeneity in activation (Gordon et al., 2016), or convergent multimodal information (Glasser et al., 2016). The influence of a parcellation scheme on functional network properties is therefore an underappreciated, but growing domain of study (Romero-Garcia et al., 2012; Zhong et al., 2015). Clearly more systematic work in this domain is needed, and an increase in data-and code-sharing practices will enable this work to proceed.
4.3. Network connectivity and WM capacity
The third main finding of the study was that older adults with higher WM capacity showed significantly higher network integration in the most difficult condition. While the association between higher integration and better behavioral performance has been shown in resting state data (Sala-Llonch et al., 2014), this is, to our knowledge, the first time this relationship is found in task-based functional connectivity. Interestingly, while WM capacity was found to relate to task network integration, no such pattern emerged with overall accuracy or reaction time at any given WM difficulty level. It is possible that the individual titration of difficulty may have obscured such effects, or that this finding reflects a relationship with individual ability rather than successful task performance. The lack of difference in behavioral performance between groups, thus, may be attributed to different patterns of network integration at high difficulty levels being utilized as alternative, and equally successful, processing strategies, resulting in equivalent WM capacity between age groups.
The significant difference in brain-behavior correlations between younger and older adults (Fig. 6E) provides some evidence for this interpretation. Given that network integration in the current study increased with task demand and was driven by the hemisphere less engaged by younger adults, the link between more widespread connectivity and WM performance provides further support for the compensatory interpretation of both CRUNCH and HAROLD (Cabeza and Dennis, 2013; Park and Reuter-Lorenz, 2009). Taken together, these findings point to the possibility that younger and older adults differ fundamentally in their approach to the WM task. The factors driving this age-related reorganization in processing are unknown, but the current study sheds some light on the topology of that reorganization. Working memory tasks, in particular, have been associated with 5Hz theta-band coupling between frontal and parietal regions during the memory retention period (Jensen and Tesche, 2002; Siegel et al., 2009) which increase parametrically with memory load. Empirical findings demonstrate that WM representations can be maintained in the absence of sustained activity during the delay in a distributed set of regions linked by oscillatory activity (LaRocque et al., 2013). The extent to which distributed activation/connectivity and distributed representation drive age-related reorganization has not been studied, but a recent analysis suggests these measures are largely decoupled (Morcom and Henson, 2018). In a recent definition of compensation, the possibility was outlined that functional compensation in older adults reflects not simply the same cognitive process extended to new cortex, but rather the recruitment of additional cognitive processes not utilized in younger adults (Cabeza et al., 2018). Thus, the finding that successful performance in older adults relies on greater integration suggests that this group may rely on a more distributed set of processing cues, or a more flexible cognitive strategy, to perform the same task as younger adults.
5. Conclusions
In sum, this study yielded three main findings. First, as task difficulty increased, younger adults showed decreased network integration, whereas older adults showed increased network integration. Second, age-related increase in network integration was driven by increases in right hemispheric connectivity to both left and right cortical regions. Lastly, older adults with higher working memory capacity demonstrated significantly higher levels of network integration in the most difficult condition. These findings are generally consistent with two popular theories regarding age effects on brain function, CRUNCH and HAROLD, as well as with the compensatory interpretation of these effects, while also extending the evidence for these theories from univariate activity to network architecture.
Supplementary Material
Acknowledgments
This research was funded by grant support from the National Institute of Aging grants U01AG050618 and K01AG053539, and in part by the National Institute of Health Intramural Research program (ZIAMH00295). The authors wish to thank Duy Nguyen, Joyce Wang and Wesley Lim for their assistance with running experimental sessions and data processing, and Mariam Hovhannisyan for helpful comments on the manuscript. This study was based on a study pre-registered on ClinicalTrials.gov (NCT02767323).
Footnotes
Declaration of competing interest
The authors have no competing financial interests.
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2020.116959.
References
- Bates D, Maechler M, Bolker B, Walker S, Christensen RHB, Singmann H, Dai B, Scheipl F, Grothendieck G, 2012. Package ‘lme4’ CRAN. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Beauchamp MS, Petit L, Ellmore TM, Ingeholm J, Haxby JV, 2001. A parametric fMRI study of overt and covert shifts of visuospatial attention. Neuroimage 14, 310–321. [DOI] [PubMed] [Google Scholar]
- Belger A, Banich MT, 1992. Interhemispheric interaction affected by computational complexity. Neuropsychologia 30, 923–929. [DOI] [PubMed] [Google Scholar]
- Bellec P, Benhajali Y, Carbonell F, Dansereau C, Albouy G, Pelland M, Craddock C, Collignon O, Doyon J, Stip E, Orban P, 2015. Impact of the resolution of brain parcels on connectome-wide association studies in fMRI. Neuroimage 123, 212–228. [DOI] [PubMed] [Google Scholar]
- Betzel RF, Byrge L, He Y, Goni J, Zuo XN, Sporns O, 2014. Changes in structural and functional connectivity among resting-state networks across the human lifespan. Neuroimage 102 Pt 2, 345–357. [DOI] [PubMed] [Google Scholar]
- Beynel L, Davis SW, Crowell CA, Hilbig SA, Lim W, Nyguyen D, Peterchev AV, Luber B, Lisanby SH, Cabeza R, Appelbaum LG, in review. Site-specific Effects of Online rTMS during a Working Memory Task in Healthy Older Adults. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beynel L, Davis S, Crowell C, Hilbig S, Lim W, Nguyen D, Palmer H, Brito A, Peterchev A, Luber B, 2019. Online repetitive transcranial magnetic stimulation during working memory in younger and older adults: a randomized within-subject comparison. PloS One 14, e0213707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun U, Plichta MM, Esslinger C, Sauer C, Haddad L, Grimm O, Mier D, Mohnke S, Heinz A, Erk S, Walter H, Seiferth N, Kirsch P, Meyer-Lindenberg A, 2012. Test-retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. Neuroimage 59, 1404–1412. [DOI] [PubMed] [Google Scholar]
- Braun U, Schafer A, Walter H, Erk S, Romanczuk-Seiferth N, Haddad L, Schweiger JI, Grimm O, Heinz A, Tost H, Meyer-Lindenberg A, Bassett DS, 2015. Dynamic reconfiguration of frontal brain networks during executive cognition in humans. Proc. Natl. Acad. Sci. U. S. A. 112, 11678–11683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braver TS, Cohen JD, Nystrom LE, Jonides J, Smith EE, Noll DC, 1997. A parametric study of prefrontal cortex involvement in human working memory. Neuroimage 5, 49–62. [DOI] [PubMed] [Google Scholar]
- Cabeza R, 2002. Hemispheric asymmetry reduction in older adults: the HAROLD model. Psychol. Aging 17, 85–100. [DOI] [PubMed] [Google Scholar]
- Cabeza R, Dennis NA, 2013. Frontal lobes and aging: deterioration and compensation In: Stuss DT, Knight RT (Eds.), Principles of Frontal Lobe Function. Oxford University Press, New York. [Google Scholar]
- Cabeza R, Nyberg L, 2000. Imaging cognition II: an empirical review of 275 PET and fMRI studies. J. Cognit. Neurosci. 12, 1–47. [DOI] [PubMed] [Google Scholar]
- Cabeza R, Albert M, Belleville S, Craik FIM, Duarte A, Grady CL, Lindenberger U, Nyberg L, Park DC, Reuter-Lorenz PA, Rugg MD, Steffener J, Rajah MN, 2018. Maintenance, reserve and compensation: the cognitive neuroscience of healthy ageing. Nat. Rev. Neurosci. 19, 701–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell KL, Schacter DL, 2017. Aging and the resting state: is cognition obsolete? Lang. Cogn. Neurosci. 32, 661–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappell KA, Gmeindl L, Reuter-Lorenz PA, 2010. Age differences in prefontal recruitment during verbal working memory maintenance depend on memory load. Cortex 46, 462–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan MY, Park DC, Savalia NK, Petersen SE, Wig GS, 2014. Decreased segregation of brain systems across the healthy adult lifespan. Proc. Natl. Acad. Sci. U. S. A. 111, E4997–E5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan MY, Alhazmi FH, Park DC, Savalia NK, Wig GS, 2017. Resting-state network topology differentiates task signals across the adult life span. J. Neurosci. 37, 2734–2745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JR, D’Esposito M, 2016. The segregation and integration of distinct brain networks and their relationship to cognition. J. Neurosci. 36, 12083–12094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Bassett DS, Power JD, Braver TS, Petersen SE, 2014. Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux JS, Viviano RP, Yuan P, Raz N, 2016. Differential effect of age on posterior and anterior hippocampal functional connectivity. Neuroimage 133, 468–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daselaar SM, Fleck MS, Dobbins IG, Madden DJ, Cabeza R, 2006. Effects of healthy aging on hippocampal and rhinal memory functions: an event-related fMRI study. Cerebr. Cortex 16, 1771–1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis SW, Cabeza R, 2015. Cross-hemispheric collaboration and segregation associated with task difficulty as revealed by structural and functional connectivity. J. Neurosci. 35, 8191–8200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis SW, Kragel JE, Madden DJ, Cabeza R, 2012. The architecture of cross-hemispheric communication in the aging brain: linking behavior to functional and structural connectivity. Cerebr. Cortex 22, 232–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis SW, Stanley MS, Cabeza R, Moscovitch M, 2016. Resting-state networks do not determine cognitive function networks: a commentary on campbell and schacter . Lang. Cognit. Neurosci 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis SW, Luber B, Murphy DLK, Lisanby SH, Cabeza R, 2017. Frequency-specific neuromodulation of local and distant connectivity in aging and episodic memory function. Hum. Brain Mapp. 32 (6), 669–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis SW, Crowell C, Beynel L, Deng L, Lakhlani D, Hilbig S, Lim W, Nguyen D, Peterchev A, Luber B, Lisanby S, Appelbaum L, Cabeza R, 2018. Complementary topology of maintenance and manipulation brain networks in working memory. Sci. Rep. 8, 17827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennis NA, Hayes SM, Prince SE, Madden DJ, Huettel SA, Cabeza R, 2008. Effects of aging on the neural correlates of successful item and source memory encoding. J. Exp. Psychol. Learn. Mem. Cognit. 34, 791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornito A, Harrison BJ, Zalesky A, Simons JS, 2012. Competitive and cooperative dynamics of large-scale brain functional networks supporting recollection. Proc. Natl. Acad. Sci. U. S. A. 109, 12788–12793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Perez MA, 1998. Forced-choice staircases with fixed step sizes: asymptotic and small-sample properties. Vis. Res. 38, 1861–1881. [DOI] [PubMed] [Google Scholar]
- Geerligs L, Maurits NM, Renken RJ, Lorist MM, 2014. Reduced specificity of functional connectivity in the aging brain during task performance. Hum. Brain Mapp. 35, 319–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geerligs L, Renken RJ, Saliasi E, Maurits NM, Lorist MM, 2015. A brain-wide study of age-related changes in functional connectivity. Cerebr. Cortex 25, 1987–1999. [DOI] [PubMed] [Google Scholar]
- Geerligs L, Tsvetanov KA, Cam C, Henson RN, 2017. Challenges in measuring individual differences in functional connectivity using fMRI: the case of healthy aging. Hum. Brain Mapp. 38, 4125–4156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, Smith SM, Van Essen DC, 2016. A multi-modal parcellation of human cerebral cortex. Nature 536, 171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE, 2016. Generation and evaluation of a cortical area parcellation from resting-state correlations. Cerebr. Cortex 26, 288–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Gilmore AW, Newbold DJ, Greene DJ, Berg JJ, Ortega M, Hoyt-Drazen C, Gratton C, Sun H, Hampton JM, Coalson RS, Nguyen AL, McDermott KB, Shimony JS, Snyder AZ, Schlaggar BL, Petersen SE, Nelson SM, Dosenbach NUF, 2017. Precision functional mapping of individual human brains. Neuron 95, 791–807 e797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grady C, Sarraf S, Saverino C, Campbell K, 2016. Age differences in the functional interactions among the default, frontoparietal control, and dorsal attention networks. Neurobiol. Aging 41, 159–172. [DOI] [PubMed] [Google Scholar]
- Hearne LJ, Cocchi L, Zalesky A, Mattingley JB, 2017. Reconfiguration of brain network architectures between resting-state and complexity-dependent cognitive reasoning. J. Neurosci. 37, 8399–8411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St Jacques PL, Dolcos F, Cabeza R, 2009. Effects of aging on functional connectivity of the amygdala for subsequent memory of negative pictures: a network analysis of functional magnetic resonance imaging data. Psychol. Sci. 20, 74–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen O, Tesche CD, 2002. Frontal theta activity in humans increases with memory load in a working memory task. Eur. J. Neurosci. 15, 1395–1399. [DOI] [PubMed] [Google Scholar]
- Jurica PJ, Leitten CL, Mattis S, 2001. Dementia Rating Scale-2: DRS-2: Professional Manual. Psychological Assessment Resources Inc., Lutz, FL. [Google Scholar]
- LaRocque KF, Smith ME, Carr VA, Witthoft N, Grill-Spector K, Wagner AD, 2013. Global similarity and pattern separation in the human medial temporal lobe predict subsequent memory. J. Neurosci. 33, 5466–5474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li HJ, Hou XH, Liu HH, Yue CL, Lu GM, Zuo XN, 2015. Putting age-related task activation into large-scale brain networks: a meta-analysis of 114 fMRI studies on healthy aging. Neurosci. Biobehav. Rev 57, 156–174. [DOI] [PubMed] [Google Scholar]
- Lindquist MA, Geuter S, Wager TD, Caffo BS, 2019. Modular preprocessing pipelines can reintroduce artifacts into fMRI data. Hum. Brain Mapp. 40, 2358–2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Low KA, Leaver EE, Kramer AF, Fabiani M, Gratton G, 2009. Share or compete? Load-dependent recruitment of prefrontal cortex during dual-task performance. Psychophysiology 46, 1069–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C, Zhang X, Cao X, Gan Y, Li T, Cheng Y, Cao W, Jiang L, Yao D, Li C, 2016. The lateralization of intrinsic networks in the aging brain implicates the effects of cognitive training. Front. Aging Neurosci. 8, 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar MG, Wymbs NF, Bock AS, Aguirre GK, Grafton ST, Bassett DS, 2018. Predicting future learning from baseline network architecture. Neuroimage 172, 107–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattay VS, Fera F, Tessitore A, Hariri AR, Berman KF, Das S, Meyer-Lindenberg A, Goldberg TE, Callicott JH, Weinberger DR, 2006. Neurophysiological correlates of age-related changes in working memory capacity. Neurosci. Lett. 392, 32–37. [DOI] [PubMed] [Google Scholar]
- Monge ZA, Stanley ML, Geib BR, Davis SW, Cabeza R, 2018. Functional networks underlying item and source memory: shared and distinct network components and age-related differences. Neurobiol. Aging 69, 140–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morcom AM, Henson RNA, 2018. Increased prefrontal activity with aging reflects nonspecific neural responses rather than compensation. J. Neurosci. 38, 7303–7313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagel IE, Preuschhof C, Li SC, Nyberg L, Backman L, Lindenberger U, Heekeren HR, 2009. Performance level modulates adult age differences in brain activation during spatial working memory. Proc. Natl. Acad. Sci. U. S. A. 106, 22552–22557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyberg L, Karalija N, Salami A, Andersson M, Wahlin A, Kaboovand N, Kohncke Y, Axelsson J, Rieckmann A, Papenberg G, Garrett DD, Riklund K, Lovden M, Lindenberger U, Backman L, 2016. Dopamine D2 receptor availability is linked to hippocampal-caudate functional connectivity and episodic memory. Proc. Natl. Acad. Sci. U. S. A. 113, 7918–7923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owen AM, McMillan KM, Laird AR, Bullmore E, 2005. N-back working memory paradigm: a meta-analysis of normative functional neuroimaging studies. Hum. Brain Mapp. 25, 46–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park DC, Reuter-Lorenz P, 2009. The adaptive brain: aging and neurocognitive scaffolding. Annu. Rev. Psychol. 60, 173–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peira N, Ziaei M, Persson J, 2016. Age differences in brain systems supporting transient and sustained processes involved in prospective memory and working memory. Neuroimage 125, 745–755. [DOI] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE, 2011. Functional network organization of the human brain. Neuron 72, 665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuter-Lorenz PA, Cappell KA, 2008. Neurocognitive aging and the compensation hypothesis. Curr. Dir. Psychol. Sci. 17, 177–182. [Google Scholar]
- Reuter-Lorenz P, Jonides J, Smith ES, Hartley A, Miller A, Marshuetz C, Koeppe RA, 2000. Age differences in the frontal lateralization of verbal and spatial working memory revealed by PET. J. Cognit. Neurosci. 12, 174–187. [DOI] [PubMed] [Google Scholar]
- Romero-Garcia R, Atienza M, Clemmensen LH, Cantero JL, 2012. Effects of network resolution on topological properties of human neocortex. Neuroimage 59, 3522–3532. [DOI] [PubMed] [Google Scholar]
- Rypma B, D’Esposito M, 2000. Isolating the neural mechanisms of age-related changes in human working memory. Nat. Neurosci. 3, 509. [DOI] [PubMed] [Google Scholar]
- Rypma B, Prabhakaran V, Desmond JE, Glover GH, Gabrieli JD, 1999. Load-dependent roles of frontal brain regions in the maintenance of working memory. Neuroimage 9, 216–226. [DOI] [PubMed] [Google Scholar]
- Sala-Llonch R, Junque C, Arenaza-Urquijo EM, Vidal-Pineiro D, Valls-Pedret C, Palacios EM, Domenech S, Salva A, Bargallo N, Bartres-Faz D, 2014. Changes in whole-brain functional networks and memory performance in aging. Neurobiol. Aging 35, 2193–2202. [DOI] [PubMed] [Google Scholar]
- Schneider-Garces NJ, Gordon BA, Brumback-Peltz CR, Shin E, Lee Y, Sutton BP, Maclin EL, Gratton G, Fabiani M, 2010. Span, CRUNCH, and beyond: working memory capacity and the aging brain. J. Cognit. Neurosci. 22, 655–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel M, Warden MR, Miller EK, 2009. Phase-dependent neuronal coding of objects in short-term memory. Proc. Natl. Acad. Sci. U. S. A. 106, 21341–21346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng RN, Turner GR, 2019. The shifting architecture of cognition and brain function in older adulthood. Perspect. Psychol. Sci. 1745691619827511. [DOI] [PubMed] [Google Scholar]
- Spreng RN, Stevens WD, Viviano JD, Schacter DL, 2016. Attenuated anticorrelation between the default and dorsal attention networks with aging: evidence from task and rest. Neurobiol. Aging 45, 149–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanley ML, Dagenbach D, Lyday RG, Burdette JH, Laurienti PJ, 2014. Changes in global and regional modularity associated with increasing working memory load. Front. Hum. Neurosci. 8, 954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki M, Kawagoe T, Nishiguchi S, Abe N, Otsuka Y, Nakai R, Asano K, Yamada M, Yoshikawa S, Sekiyama K, 2018. Neural correlates of working memory maintenance in advanced aging: evidence from fMRI. Front. Aging Neurosci. 10, 358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G, Sporns O, Edelman GM, 1994. A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. Unit. States Am 91, 5033–5037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M, 2002. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289. [DOI] [PubMed] [Google Scholar]
- Veltman DJ, Rombouts SA, Dolan RJ, 2003. Maintenance versus manipulation in verbal working memory revisited: an fMRI study. Neuroimage 18, 247–256. [DOI] [PubMed] [Google Scholar]
- Vidal-Pineiro D, Sneve MH, Storsve AB, Roe JM, Walhovd KB, Fjell AM, 2017. Neural correlates of durable memories across the adult lifespan: brain activity at encoding and retrieval. Neurobiol. Aging 60, 20–33. [DOI] [PubMed] [Google Scholar]
- Vij SG, Nomi JS, Dajani DR, Uddin LQ, 2018. Evolution of spatial and temporal features of functional brain networks across the lifespan. Neuroimage 173, 498–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viviano RP, Hayes JM, Pruitt PJ, Fernandez ZJ, van Rooden S, van der Grond J, Rombouts S, Damoiseaux JS, 2019. Aberrant memory system connectivity and working memory performance in subjective cognitive decline. Neuroimage 185, 556–564. [DOI] [PubMed] [Google Scholar]
- Wickham H, Wickham MH, 2007. The ggplot package. [Google Scholar]
- Yeo BT, Krienen FM, Eickhoff SB, Yaakub SN, Fox PT, Buckner RL, Asplund CL, Chee MW, 2014. Functional specialization and flexibility in human association cortex. Cerebr. Cortex 88, 212–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Z€ollei L, Polimeni JR, 2011. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 106, 1125–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong S, He Y, Gong G, 2015. Convergence and divergence across construction methods for human brain white matter networks: an assessment based on individual differences. Hum. Brain Mapp. 36, 1995–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.