Abstract
Spinal-driven locomotion was first hypothesized to exist in biological systems in the 1980s. However, only recently has the concept been applied to legged robots. In implementing spinal-driven locomotion in robots to-date, researchers have focused on bending in the spine. In this article, we propose an additional mode of spinal-driven locomotion: axial torsion via helical actuation patterns. To study torsional spinal-driven locomotion, a six-legged robot with unactuated legs is used. This robot is designed to be modular to allow for changes in the physical system, such as material stiffness of the spine and legs, and has actuators that spiral around the central elastomeric spine of the robot. A model is provided to explain torsional spinal-driven locomotion. Three spinal gaits are developed to allow the robot to walk forward, through which we demonstrate that the speed of the robot can be influenced by the stiffness of the spine and legs. We also demonstrate that a single gait can be used to drive the robot forward and turn the robot left and right by adjusting the leg positions or foot friction. The results indicate that the inclusion of helical actuation patterns can assist in movement. The addition of these actuation patterns or active axial torsion to future, more complex robots with active leg control may enhance the energy efficiency of locomotion or enable fast, dynamic maneuvering.
Keywords: Soft robot materials and design, legged robots, biologically-inspired robots
I. Introduction
THE study of locomotion in legged robots is typically focused on the legs. Yet, it is becoming increasingly evident through the observation of animals that the spine plays a large role in legged locomotion as well [1], [2]. Gracovetsky theorized and later demonstrated that the spine is fundamental to locomotion and can itself be used as an engine to propel an animal without requiring motion from the legs [3], [4]. This hypothesis of the spinal engine was later expanded to explain how the spine and legs work in unison for locomotion [5]. Understanding that locomotion goes beyond the legs in biology has influenced how researchers have thought about and designed robots.
Legged robots are slowly transitioning away from their rigidly designed bodies to biologically inspired bodies that incorporate a passive [6]-[8] or an active spine [9]-[12]. These new robots with flexible spines (either through traditional hinges or soft materials) have shown many advantages. First, the use of compliant, passive spines can increase the energy efficiency of a robot [6], [7], which has also been shown for biological systems [13]. Second, the use of active spines can increase the speed [10] and energy efficiency [11], [14] of a robot. While these results are very promising and show the benefits of incorporating spines into robots, the spines are generally designed to bend along one axis [6]-[8], [10], [12] or two axes [9], [11].
While bending is an important part of spinal motion, the current designs for spines in robots neglect axial torsion, which is experienced by biological spines [15]. Although it is known that axial torsion is an important component to human walking and running gaits [3], [16], it is less studied in legged animals. In exploring how axial torsion may affect four-or-more-legged animals, we can consider research on lizards and salamanders. When lizards and salamanders walk, they alternate their feet in such a way that an axial torsion is applied along the spine [17], [18]. Lizards and salamanders have helical muscle patterns that spiral along their body, like many animals [19], that are believed to resist this axial torsion [17], [20]. However, when those same muscles are observed in lizards and salamanders moving at high velocity, those muscles do not appear to function as torsional control [21], [22]. It is unclear if other muscles resist the axial torsion or if, at high velocities, axial torsion may be beneficial to locomotion.
While axial torsion has not been shown as a contributing factor to locomotion in four-or-more-legged vertebrates, it is well known that helical muscle patterns enabling coupled axial torsion and bending that exist along the spine in vertebrate animals are also observed in octopus tentacles and elephant trunks, where they have been shown to be beneficial for other tasks [19], [23], [24]. Additionally, highly coupled actuation patterns, including helical tendons, have been demonstrated to reduce the actuator requirements for robotic continuum arms [25], [26]. Helical tendons have been applied to both continuum arms [26], [27] as well as the legs of a walking robot that was inspired by the octopus [28]. It follows that helical actuation patterns will be beneficial in other robotic applications.
This paper studies the applicability of helical actuation patterns to locomotion of a legged robot. Herein, we test the hypothesis that torsional spinal-driven locomotion is possible through helical actuation patterns alone via a six-legged robot with a soft, elastomeric spine, shown in Fig. 1. The legs on this robot do not actuate, isolating the motion of the robot to the spiralling actuators around the spine. A model is provided to explain the principles of operation for this robot and why it is capable of walking. On the physical system, experiments are conducted with multiple spinal gaits to determine if locomotion is possible. Additionally, we sought out a single spinal gait that is capable of forward motion as well as rotating left and right by altering the leg positions or foot friction. Altering the leg positions or foot friction is used to demonstrate how actuated legs could be used alongside torsional spinal-driven locomotion for fully actuated robots in the future and having a single gait for the spine will simplify the control complexity of such a robot. Finally, stiffnesses of the spine and the legs are changed to understand their correlation to speed of the robot. This work provides insight into how torsional spinal-driven locomotion of spines can be used to augment the design of robots.
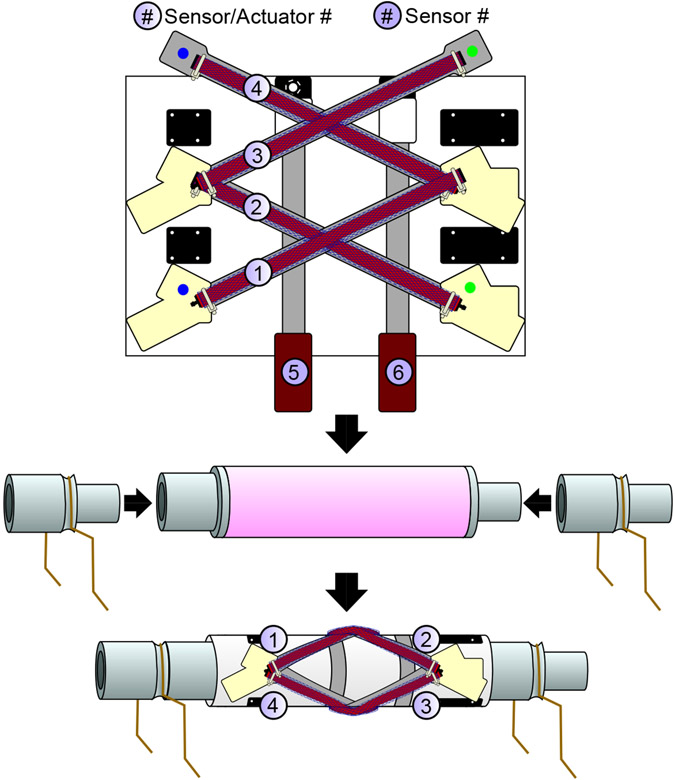
Fig. 1.
(a) The legged robot with actuator elements aligned in a spiral configuration to enable twisting along the spine. (b) The structural robot design where the pink elements are elastomer, the light gray elements are end caps on either end of the elastomer to enable connections between other elements, and the dark gray elements are the leg connectors to which the legs are attached.
II. System Design
In order to explore torsional spinal-driven locomotion, a modular and reconfigurable approach was taken to enable the testing of various design choices. Specifically, we looked at a two-segment, six-legged robot manufactured with a passive elastomeric spine, fabricated from either EcoFlex 00–50 (Shore hardness: 00–50; Smooth-On, Inc.) or Dragon Skin 10 (Shore hardness: 10 A; Smooth-On, Inc.),1 and actuated with robotic skins [29]. Robotic skins allow assembly of different continuum robots by easily swapping the robotic skin, which contains the actuating and sensing components, from structure-to-structure. For this work, a new robotic skin was designed with sensors and actuators arranged such that they spiralled around a cylindrical structure, shown in Fig. 2. While sensors were included on the skin, they were not utilized for this work, although previous works have used sensors in a different skin design for state estimation and closed-loop control [30], [31]. The skins in this work were operated with open-loop control using pressure regulators [32] to control the pressure in each actuator. The pressure regulators were connected to a 138 kPa line and a vacuum line, which quickly deflated the actuators. Additionally, two types of legs were tested: rigid legs fabricated from brass tubing and compliant legs fabricated from copper wire. These legs were also modular, allowing us to change out the legs as needed. Further information on component fabrication is provided in the Supplementary Materials.
Fig. 2.
Basic layout for the twisting skin and how it fits around the cylindrical structures. The skin is shown unwrapped. In the physical skins, the sensor and actuator pairs with the blue and green dots are sewn at the locations on the skin with matching blue and green dots. The actuators and sensors are labeled for reference. This skin is stretched around the cylindrical structure and leg connectors are applied on either side.
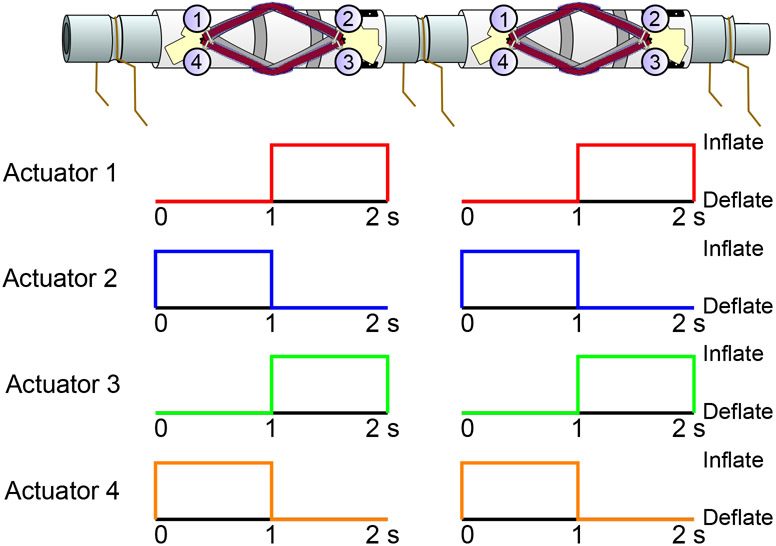
Several robot configurations and spinal gaits were considered: twist (i.e., both skins twist in the same direction), counter-twist (i.e., skins twist in opposite directions), and bend-and-twist. The inflation patterns of the two robotic skins for the twist gait are shown in Fig. 3, with the other gaits shown in the Supplementary Materials. Additionally, the various robot configurations that are used with each gait and discussed in this section are outlined in Table I. All tests occurred with the robot walking on felt fabric to provide friction for the feet.
Fig. 3.
Inflation and deflation patterns for the twist spinal gait. The left and right columns represent the front and back skins of the robot, respectively.
TABLE I.
Summary of Different Conditions Tested With the Spinal Gaits
| Twist | Counter- Twist |
Bend-and- Twist |
||
|---|---|---|---|---|
| Legs | Rigid | ✓ | ✓ | |
| Compliant | ✓ | |||
| Spine Material | Ecoflex 00-50 | ✓ | ✓ | |
| Dragon Skin 10 | ✓* | ✓ | ||
| Fool Friction | Constant | ✓ | ✓ | |
| Varied | ✓ | ✓ | ||
Indicates the Configuration That Explored Rotation.
A. Twist
The twist gait was the most rigorously studied to demonstrate the capabilities of torsional spinal-driven locomotion in this paper and is used in the model described in the following section. This gait involves inflating antagonistic actuator pairs one after the other to twist both segments in the same direction back and forth to achieve forward locomotion (shown in Fig. 3). The twist gait required the rigid legs and was not functional with the compliant legs. It was tested with both the Ecoflex 00–50 and Dragon Skin 10 spine in forward walking. Turning was demonstrated using the Dragon Skin 10 spine in two manners: (1) maintaining foot friction while changing the leg positions, and (2) maintaining the leg positions (such that they match what is shown in Fig. 1 b) while changing the foot friction. To change the leg positions, the legs were bent by hand to bias the robot into rotating in either a clockwise or counter-clockwise direction, effectively turning the robot to the left or right. To change the foot friction, an acrylic sheet was slid under either all the legs on the left or right side of the robot to encourage slipping of those feet and, thus, turning of the robot.
B. Counter-Twist
The counter-twist gait is a slight variation on the twist gait. Rather than having both robotic skins twist in unison, the counter-twist gait has the skins twist in opposite directions (shown in Fig. S2). This gait required the compliant legs and was not functional with the rigid legs. The counter-twist gait used the Ecoflex 00–50 spine and was only demonstrated moving forward. The full cycle of this gait was about 35 % faster than the twist gait.
C. Bend-and-Twist
The final gait tested was a bend-and-twist gait. The bend-and-twist gait differentiates from the other two because it inflates a single actuator on each skin at a time rather than actuating pairs, which changes the system behavior. The bend-and-twist gait causes the robot to essentially pick up a leg and twist it forward in the air to take a step. The leg is then placed on the ground and twisted back to propel itself forward. Since this gait has a very clear direction and stepping pattern unlike the simple twist and counter-twist gaits, the inflation pattern can be reversed to drive the robot backwards (shown in Fig. S3). However, in order to achieve this backwards motion in practice, the foot friction of the middle legs had to be reduced through the use of smooth plastic caps on the bottom of the feet. The bend-and-twist gait was demonstrated with the use of the rigid legs and the Dragon Skin 10 spine.
III. Model
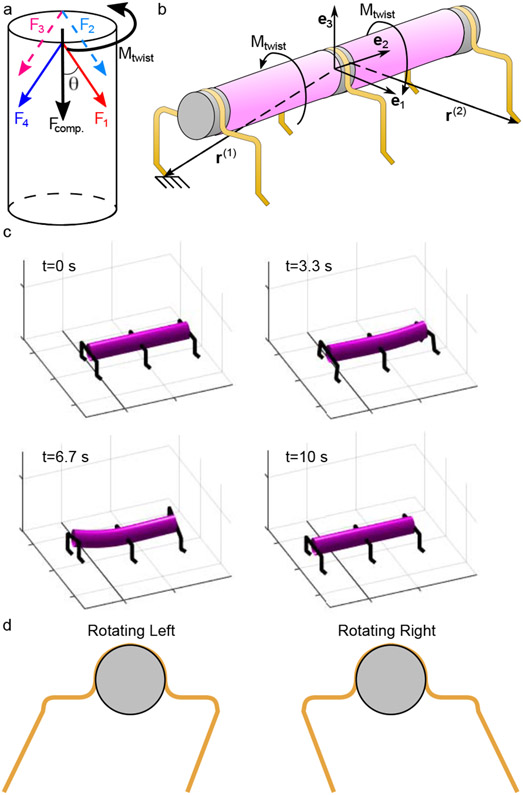
In order to achieve torsional spinal-driven locomotion, the actuators must exert a moment along the spine. The angle, θ, that the actuator is placed on the robotic skin will translate to the angle of the force applied to the cylindrical structure, as shown in Fig. 4a. A single actuator force will result in bending, twisting, and compression of the cylindrical structure. When θ = 0°, the actuator will cause only bending and compression, which was demonstrated in previous works [29]-[31]. When 0° < θ < 90°, the actuator will cause a combination of bending, twisting, and compression. If two ideal actuators work together in opposite directions (such as Actuators 1 and 3 in Fig. 2, which are shown as F1 and F3 in Fig. 4a, respectively), they cause twisting and compression while eliminating the bending in the cylindrical structure. If we let F1 (t) = F3 (t) = F(t), the force and moment experienced by the cylindrical structure can be written as,
| (1a) |
| (1b) |
where Fcomp. is the axial compression force, Mtwist is the moment that causes the cylindrical structure to twist, t is the time, and r is the radius of the cylindrical structure. In this section, we explore how walking is achievable through alternating pairs of actuators (1 & 3 and 2 & 4), such that the skin only causes twisting and compression.
Fig. 4.
(a) Model of cylindrical structure with forces from the actuators. (b) Model of a robot showing an example of how the axis of rotation is defined for both legs when the front, right and rear, left feet remain on the ground. This model also shows how the local coordinate frame, ei, is defined. (c) Example simulation demonstrating a robot walking with θ = 26.5°. (d) Diagram showing how to adjust the legs for rotating as seen by the front of the robot.
A. Theory of Walking
1). Complex, Local Deformation of the Elastomer Sections:
As the robot walks, the torsional and compressive inputs from the robotic skins alongside the forces from the feet result in complex deformations along the spine that shrink the length of the robot along the e2-axis. In this paper, we make several simplications to the spinal deformation in order to explain the principles of motion for this robot. We assume the twisting behavior can be described in terms of an angle and axis homogeneous transformation [33], where the angle is defined by Mtwist and the axis is defined such that a given foot remains on the e1-e3 plane. Additionally, the deformation is defined such that the middle feet also remain on the e1–e3 plane. To simplify the model further, we assume ideal actuators, which enables the use of Eqn. 1 and remove the rigid parts for the model and simulation. Thus, our robot can be described with q(t) = {λ(t), α(X2, t), r(1) (t), r(2) (t)}T, where q is the state of the robot, λ is axial stretch, and α(X2) is the angle of twist where X2 is the point along the length of the robot in the reference configuration, and r(i) is the axis of rotation along the ith segment for i = 1, 2. The deformation of the system can be written as,
| (2a) |
| (2b) |
| (2c) |
| (2d) |
where x = {x1, x2, x3}T is the deformed point given the reference point of X = {X1, X2, X3}T, cα = cos(α), sα = sin(α), and vα = 1 – cos(α), αmax is the maximum angle of twist experienced by a single elastomer section, and L is the length of a single elastomer section. The point P is defined in the reference frame and the definition depends on if the point is on the elastomer sections or the legs. If the point is on the elastomer sections,
| (3) |
where ν is Poisson’s ratio (assumed to be 0.5 for elastomers). To define the position of the feet on the legs, we use
| (4a) |
| (4b) |
| (4c) |
where Pfront refers to the front legs, Pmid refers to the middle legs, Prear refers to the rear legs, the ±d1 term is positive for the left foot and negative for the right foot. The terms d1 = 73.8 mm, d2 = 25.9 mm, d3 = 13.5 mm, and β = 45° are found with Fig. S1.
2). Boundary Conditions:
The walking gait of the robot can be divided into four steps based on which foot is assumed to be immovable due to high friction on the foot and resistance to slide backwards. The feet are assumed to be planted in place in the following order: (1) front, right foot; (2) rear, left foot; (3) front, left foot; and (4) rear, right foot. We assume the feet cannot slide backwards, as they were designed to only slide forwards. This foot pattern results in the front legs pulling the body forward as it twists the body upward and the back feet pushing the body forward as it twists downward. To hold the feet in place, we assume xplanted,1 = Pplanted, 1 and xplanted,3 = Pplanted,3, where xplanted is the deformed location of the planted foot. Using Eqn. 2 a to determine these equations along with ∥r(i)∥ = 1, the solutions for r(i) for i = 1, 2 can be solved for using Newton’s method. An example of how r(i) is defined when the front right foot is planted in the given configuration is shown in Fig. 4b.
3). Solving the Deformation of the Elastomer Sections:
To explain the general mechanics behind how the twisting of the skins assist in locomotion, we simplify the force relationship with the state of the deformation such that it can be written as,
| (5a) |
| (5b) |
where Ka is the axial rigidity and Kt is the torsional rigidity of the elastomer sections.
To determine how far the robot has walked in a given time step (u(t)), we can write,
| (6) |
An example of this model used in a simulation is shown in Fig. 4c. A complete derivation of this model, example simulation, and code for its simulation are provided in the Supplementary Materials.
B. Theory of Rotating
With an understanding of how the robot walks, we can closer analyze what changes can be made to get the robot to rotate, or turn in place. To achieve directional change in the robot, we considered two methods: (1) changing leg position and (2) changing foot friction. If the legs are bent either to the left or right, as shown in Fig. 4d, as the robot twists, it will take larger steps to one side than the other, due to the distance of the foot from the body center-line. This results in the robot effectively pivoting, or rotating, to the left or right. If the legs are held in their initial unbent position, altering the friction under the feet will also enable the robot to rotate. If there is a large enough difference in foot friction between the right and left side of the robot, the side with lower foot friction will allow the feet to slip on that side while the other feet will not slip. This slipping will result in the robot favoring one direction (left or right) over the other and will also result in the robot rotating.
IV. Results & Discussion
In testing the robot, we sought to determine what conditions made torsional spinal-driven locomotion possible and what factors could influence the behavior of the system. For every robot configuration and gait tested, we measured the speed to determine how the choice of gait, legs, spine material, actuator angle, and foot friction may influence the behavior of the robot. Since the robot does not move at a constant velocity, speed was averaged together after a full step cycle was performed (e.g., half the cycle shown in Fig. 3 for the twist gait). For the experimental data, the speed was measured by pixel distance the robot had moved forward over the length of time from the initial position to the measured position. The pixel distance was converted to millimeters through a known pixel-millimeter measurement. Additionally, for the twist gait, we did additional analysis with a simulation using the model provided in Section III.
A. Speed is Influenced by the Spine Stiffness and Actuator Angle
To explore how the spine stiffness affects the speed at which a robot walks, the twist gait was tested on the physical robot with both spine materials (Ecoflex 00–50 and Dragon Skin 10). For both materials, the twist gait successfully drove the robot forward (shown in Fig. 5), but differed in speed. For the stiffer Dragon Skin 10 spine, the robot walked at 1.9±0.2 mm/s with a corresponding simulation speed of 1.8 mm/s. The errors reported for the experimental measurements are the standard deviation over three measurements. For the softer Ecoflex 00–50 spine, the robot walked at 4.1 ±0.1 mm/s with a corresponding simulation speed of 4.0 mm/s. By reducing the stiffness of the spine, an increase of 115 % in the speed was observed. This is due to the increased ability in twisting and deforming the spine given the same actuator outputs.
Fig. 5.
Forward locomotion with the twist gait demonstrated with (a) Dragon Skin 10 and (b) Ecoflex 00–50 spine.
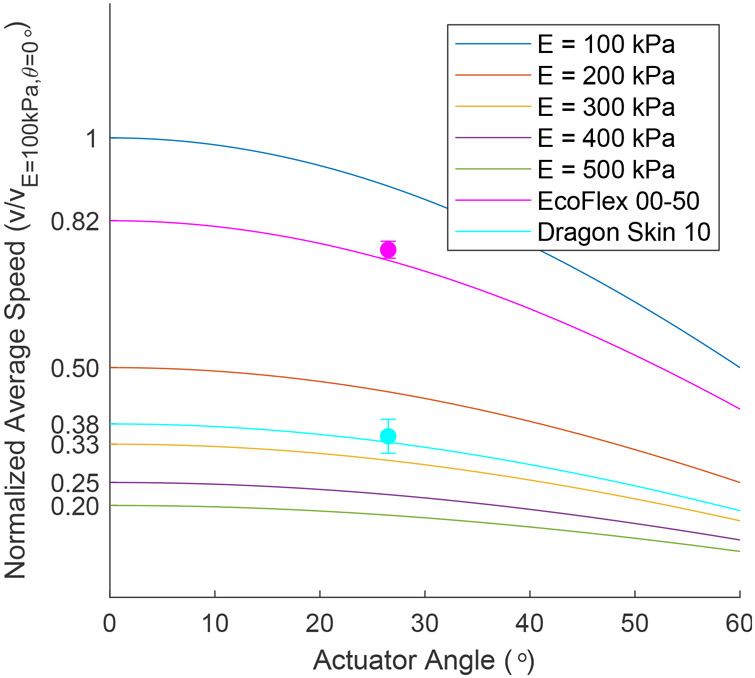
To get a better understanding of how the spine material and the actuator angle affect the speed of the robot, an additional study was done in simulation. The input force into the simulation was chosen such that the corresponding speed of a simulated EcoFlex 00–50 robot matched that of the physical robot. We tested seven different elastic moduli ranging from 100 kPa to 500 kPa, including the elastic moduli of Ecoflex 00–50 (122 kPa - calculated from [34]) and Dragon Skin 10 (256 kPa [30]), along with a range of actuator angles from 0° to 60°. From Fig. 6, we can observe that the material stiffness has a larger influence in the speed of the robot than the actuator angle. However, isolating actuator angle, robots with an actuator angle of θ = 0° were found to be the fastest for each stiffness. This makes sense since all of the work from the actuators would go into shortening the length of the elastomer sections, rather than deforming them out-of-plane. However, purely compressing the segments increases the likelihood that the segment will buckle, which will affect the overall behavior of the system.
Fig. 6.
Simulation of the normalized average walking speed of robots with different elastic moduli as the actuator angle is changed from 0 to 60°. The speed is normalized by the speed of the robot with an elastic modulus of 100 kPa and an actuator angle of 0°. The dots indicate the speed of the robots tested experimentally.
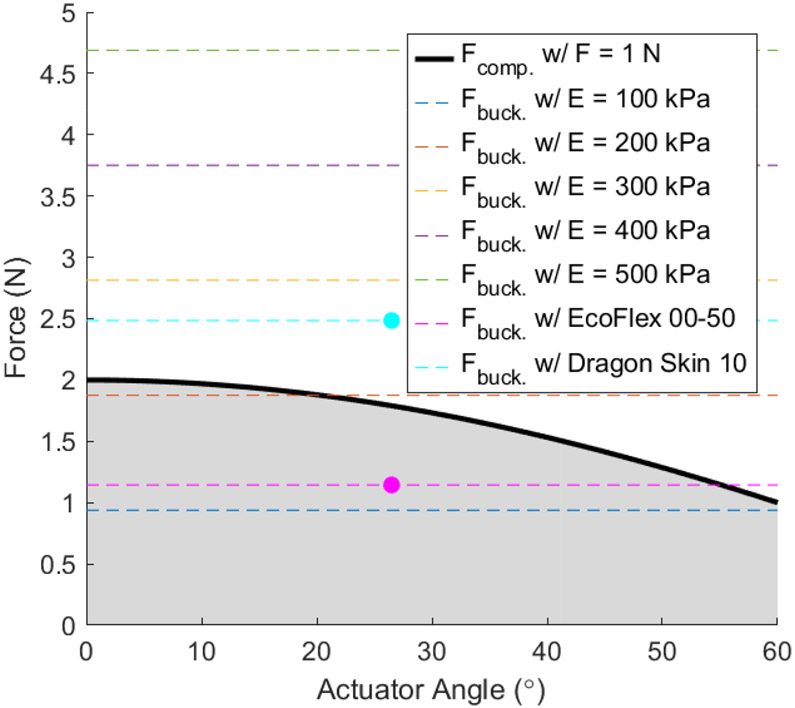
To study buckling in this robot, we used Timoshenko beams under the fixed-free boundary condition [35]. As an example, we looked at the case where the force from the actuators was set to 1 N. Fig. 7 shows that softer segments are more likely to buckle, but as the actuator angle increases, the likelihood of buckling decreases; this is best shown when the elastic modulus is 200 kPa. Fig. 7 shows that our EcoFlex 00–50 robot falls within the buckled region for that material, and we did observe the EcoFlex 00–50 robot buckling during experimental testing, which compromised its overall performance. While the robot was able to walk forward sufficiently well, the EcoFlex 00–50 robot was unable to turn left or right when we changed the leg positions. Additionally, it should be noted that if the actuator angle is set to 0°, the robot will be unable to turn by simply adjusting the leg positions. Turning would require a change in the spinal gait as demonstrated in [29]. A balance needs to be struck between the stiffness of the spine and strength of the actuators to prevent issues due to buckling.
Fig. 7.
Simulation comparing the compression force with each actuator at 1 N to the buckling force of robots with varying stiffnesses. The shaded region highlights the combinations of actuator angle and elastic modulus that would buckle under the applied force, and the two dots indicate where the physical robots fall on the graph.
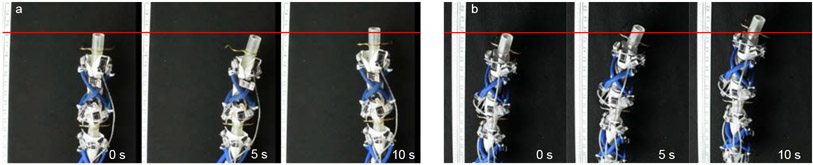
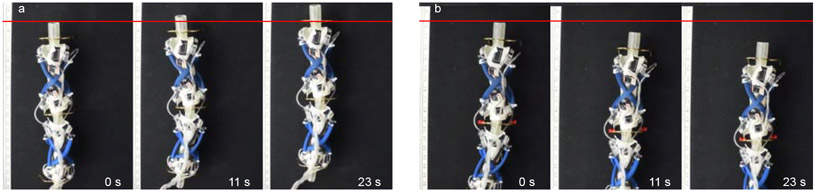
B. Rotation is Possible by Adjusting Leg Positions
The same spinal gait that is able to drive the robot forward can also be used to turn the robot left and right by adjusting the position of the legs. We demonstrate this ability through the use of the twist gait with the Dragon Skin 10 spine (shown in Fig. 8a-b). The robot was able to rotate left at a rate of 1.3±0.1°/s and right at a rate of 1.2±0.1°/s, essentially rotating in either direction at the same rate. This result indicates that a consistent twisting spinal gait can be used to drive a robot with the position of the legs and feet serving as steering for the robot. Therefore, a simple twisting spinal gait is capable of generating a variety of movements when working with the legs, which means that complex gaits are not required to achieve rotating of the robot. Having a single, simple gait lowers the barrier to including this type of locomotion on future robots.
Fig. 8.
Demonstration of the robot turning (a) left and (b) right by adjusting the leg positions and (c) left and (d) right by adjusting foot friction.
C. Rotation is Possible by Adjusting Foot Friction
In addition to rotating by adjusting the leg positions, it is also possible to achieve rotating by adjusting the friction on the right or left legs [36]. Rotating by adjusting foot friction was demonstrated through the use of acrylic sheets and the twist gait with the Dragon Skin 10 spine (shown in Fig. 8c-d). Using the acrylic sheets to alter foot friction, the robot rotated left at 1.5±0.2°/s and right at 0.8±0.2°/s. The large variability in the rotational speeds between rotating left and right is likely due to variability in placing the acrylic sheets under the feet of the robot. Essentially, this demonstration highlights that the ability to rotate is also achievable by changing the foot friction behavior, enabling one side of the robot being more prone to slipping, which facilitates rotating.
D. Compliant Legs Can Increase the Speed of the Robot
In addition to testing torsional spinal-driven locomotion with rigid legs, compliant legs were also tested to see if their energy storage capabilities would enhance walking. To test the compliant legs, the Ecoflex 00–50 spine was used with the counter-twist gait (shown in Fig. 9). While using these legs, the robot drifted to the left. We believe this was due to differences in the legs caused by the manufacturing process rather than the introduced compliance in the legs. With this configuration and spinal gait, the robot walked forward at a speed of 8.7±1.0 mm/s. While the counter-twist gait is run 35 % faster than the twist gait, the increase in speed is 110 % faster, which indicates that this increase in speed is likely due to the compliance in the legs in addition to the faster rate of the gait. The compliant-legged robot appears to have more of a bounce to its gait than its rigid legged counterpart (see Supplementary Video), which helps it move faster. This bouncier gait is more reminiscent of biological systems.
Fig. 9.
Demonstration of walking with compliant legs. The scale bar represents 100 mm.
E. Additional Gaits Allow Bi-Directional Motion Without Changing the Angular Offset of the Foot
While the simplicity of the twist and counter-twist gaits are appealing, they are not the only gaits that enable walking of the robot. An additional gait (bend-and-twist) was found that allowed the robot to walk both forward and backward (albeit with a change in foot friction of the middle feet required) without the need to adjust angle of the feet. This is due to a fundamental change in how the robot is driven. This gait was tested with the Dragon Skin 10 spine (shown in Fig. 10). Using the new gait, the robot was able to walk forward at a speed of 1.4±0.3 mm/s and backward at a speed of 1.9±0.5 mm/s. The speed achieved by the bend-and-twist gait is comparable to that achieved by the twist gait with the same robot configuration.
Fig. 10.
Demonstration of the bend and twist gait moving (a) forward and (b) backward by reversing the gait and altering the friction of the middle feet.
V. Conclusion & Future Work
In this letter, we demonstrated that torsional spinal-driven locomotion is achievable through the use of a helical actuation pattern that is capable of twisting and bending the spinal structure of the robot and provided a theory to explain the achieved locomotion. We believe this is the first demonstration of a robot achieving locomotion through the use of active torsion along the spine. In order to isolate locomotion behavior originating from torsional motion about the spine, this study focused on a robot with unactuated legs. We demonstrated how solely twisting or bending-and-twisting motions of the spine are sufficient for robot locomotion. Additionally, we demonstrated that through changes in leg position or foot friction, a single spinal gait can be used to move the robot forward, or rotate it left or right, which simplifies how torsional spinal-driven locomotion can be incorporated into future systems.
In addition to showing the basic abilities of torsional spinal gaits, we considered how additional changes to the basic robot structure affect system behavior. First, we demonstrated that the speed of the robot is influenced by the spine material. A softer spine will be able to twist further and will, thus, drive the robot further with each step. Second, we demonstrated that the use of compliant legs can further increase the speed of the robot. This increase in speed is likely due to the fact that compliant legs can store energy and then release it as the robot walks forward. Finally, we showed that alternative gaits are possible with the spiralling actuators in the forward and backward driving bend-and-twist gait. While this gait enables the robot to move forward at the same speed as the twist gait, the exact mechanics in which the robot is driven forward differs.
While we believe this work represents a significant contribution to locomotion of legged robots, there are additional areas to continue studying in the future. One such area is in energy efficiency. Animals have actuators distributed throughout their entire body (i.e., muscles) that contribute to locomotion. We believe that a distributed actuator system in robots could increase their overall energy efficiency due to distributed loads throughout the systems, and that this use of torsional spinal gaits will contribute to that efficiency. Alongside the spiralling actuators presented here, actuators that run parallel to the neutral axis of the cylindrical structures could be added to generate pure bending motions on the spine. This would result in a system that more closely mirrors biological systems and could potentially lead to more advantageous gaits. Additionally, the sensors could be used to inform future control strategies of the current state of the spine. We also believe that the twisting ability of the spine is relevant to fast, dynamic maneuvers seen by animals, such as cheetahs when they chase prey, and the inclusion of active twisting in spines will improve the maneuverability of robots.
Supplementary Material
Acknowledgment
The authors would like to thank Prof. Charles M. Krousgrill of Purdue University for the helpful conversations pertaining to the deformation and model of the robot and Gabrielle Branin of Yale University for preliminary testing of the design of the robot.
This work was supported by the National Aeronautics and Space Administration under the Early Career Faculty Program (80NSSC17K0553).The work of J. C. Case was supported by a NASA Space Technology Research Fellowship (NNX15AQ75H) and an NRC Research Associateship award at NIST.
Footnotes
This article has supplementary downloadable material available at http://ieeexplore.ieee.org, provided by the authors.
Certain commercial materials are mentioned in this paper to specify the experiment adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the material is necessarily the best available for the purpose.
Contributor Information
Jennifer C. Case, School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907 USA; School of Engineering & Applied Science, Yale University, New Haven, CT 06520 USA; Intelligent Systems Division, National Institute of Standards and Technology, Gaithersburg, MD 20899 USA.
James Gibert, School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907 USA.
Joran Booth, School of Engineering & Applied Science, Yale University, New Haven, CT 06520 USA.
Vytas SunSpiral, Zymergen, Emeryville, CA 94608 USA.
Rebecca Kramer-Bottiglio, School of Engineering & Applied Science, Yale University, New Haven, CT 06520 USA.
References
- [1].Hildebrand M, “ Motions of the running cheetah and horse,” J. Mammalogy, vol. 40, no. 4, pp. 481–495, November 1959. [Google Scholar]
- [2].Hildebrand M, “How animals run,” Scientific Amer, vol. 2, no. 5, pp. 148–160, 1960. [DOI] [PubMed] [Google Scholar]
- [3].Gracovetsky S, “An hypothesis for the role of the spine in human locomotion: A challenge to current thinking,” J. Biomed. Eng, vol. 7, no. 3, pp. 205–216, July 1985. [DOI] [PubMed] [Google Scholar]
- [4].Gracovetsky S, The Spinal Engine. Vienna, Austria: Springer, 1988. [Google Scholar]
- [5].Gracovetsky SA, “Linking the spinal engine with the legs: A theory of human gait,” in Movement, Stability & Low Back Pain: The Essential Role of the Pelvis. London, U.K.: Churchill Livingstone, 1997, pp. 243–251. [Google Scholar]
- [6].Takuma T, Ikeda M, and Masuda T, “Facilitating multi-modal locomotion in a quadruped robot utilizing passive oscillation of the spine structure,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst, October 2010, pp. 4940–4945. [Google Scholar]
- [7].Kani MHH, Derafshian M, Bidgoly HJ, and Ahmadabadi MN, “Effect of flexible spine on stability of a passive quadruped robot: Experimental results,” in Proc. IEEE Int. Con. Robot. Biomimetics, December 2011, pp. 2793–2798. [Google Scholar]
- [8].Eckert P, SprÃűwitz A, Witte H, and Ijspeert AJ, “Comparing the effect of different spine and leg designs for a small bounding quadruped robot,” in Proc. IEEE Int. Conf. Robot. Automat, May 2015, pp. 3128–3133. [Google Scholar]
- [9].Zhao Q, Sumioka H, and Pfeifer R, “The effect of morphology on the spinal engine driven locomotion in a quadruped robot,” in Proc. 5th Int. Symp. Adaptive Motion Animals Mach. (amam), 2011, pp. 51–52. [Google Scholar]
- [10].Khoramshahi M, SprÃűwitz A, Tuleu A, Ahmadabadi MN, and Ijspeert AJ, “Benefits of an active spine supported bounding locomotion with a small compliant quadruped robot,” in Proc. IEEE Int. Conf. Robot. Automat, May 2013, pp. 3329–3334. [Google Scholar]
- [11].Seok S et al. , “Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot,” IEEE/ASME Trans. Mechatronics, vol. 20, no. 3, pp. 1117–1129, June 2015. [Google Scholar]
- [12].Seibel A and Schiller L, “Systematic engineering design helps creating new soft machines,” Robot. Biomimetics, vol. 5, no. 1, October 2018. [Online]. Available: 10.1186/s40638-018-0088-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Gracovetsky SA and Iacono S, “Energy transfers in the spinal engine,” J. Biomed. Eng, vol. 9, no. 2, pp. 99–114, April 1987. [DOI] [PubMed] [Google Scholar]
- [14].Zhao Q, Nakajima K, Sumioka H, Yu X, and Pfeifer R, “Embodiment enables the spinal engine in quadruped robot locomotion,” in Proc. IEEE/RSJInt. Conf. Intell. Robots Syst, October 2012, pp. 2449–2456. [Google Scholar]
- [15].Smit TH, “ The use of a quadruped as an in vivo model for the study of the spine – Biomechanical considerations,” Eur. Spine J, vol. 11, no. 2, pp. 137–144, April 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Witte H, Fischer MS, Preuschoft H, Voges D, Schilling C, and Ijspeert AJ, “Quadruped locomotion,” in Living Machines: A Handbook of Research in Biomimetics and Biohybrid Systems. London, U.K.: Oxford Univ. Press, 2018, pp. 289–303. [Google Scholar]
- [17].Bennett WO, Simons RS, and Brainerd EL, “Twisting and bending: The functional role of salamander lateral hypaxial musculature during locomotion,” J. Exp. Biol, vol. 204, no. 11, pp. 1979–1989, June 2001. [DOI] [PubMed] [Google Scholar]
- [18].O’Reilly JC, Summers AP, and Ritter DA, “The evolution of the functional role of trunk muscles during locomotion in adult amphibians,” Integrative Comparative Biol, vol. 40, no. 1, pp. 123–135, February 2000. [Google Scholar]
- [19].Wainwright SA, Axis and Circumference, The Cylindrical Shape of Plants and Animals. Cambridge, MA, USA: Harvard Uni. Press, 2014. [Google Scholar]
- [20].Carrier DR, “Action of the hypaxial muscles during walking and swimming in the salamander dicamptodon ensatus,” J. Exp. Biol, vol. 180, no. 1, pp. 75–83, July 1993. [Google Scholar]
- [21].Ritter D, “Epaxial muscle function during locomotion in a lizard (Varanus salvator) and the proposal of a key innovation in the vertebrate axial musculoskeletal system,” J. Exp. Biol, vol. 198, no. 12, pp. 2477–2490, December 1995. [DOI] [PubMed] [Google Scholar]
- [22].Ritter D, “ Axial muscle function during lizard locomotion,” J. Exp. Biol, vol. 199, no. 11, pp. 2499–2510, November 1996. [DOI] [PubMed] [Google Scholar]
- [23].Kier WM and Smith KK, “Tongues, tentacles and trunks: the biomechanics of movement in muscular-hydrostats,” Zoological J. Linnean Soc, vol. 83, no. 4, pp. 307–324, April 1985. [Google Scholar]
- [24].Kier WM, “ The diversity of hydrostatic skeletons,” J. Exp. Biol, vol. 215, no. 8, pp. 1247–1257, April 2012. [DOI] [PubMed] [Google Scholar]
- [25].Case JC, White EL, SunSpiral V, and Kramer-Bottiglio R, “Reducing actuator requirements in continuum robots through optimized cable routing,” Soft Robot, vol. 5, pp. 109–118, February 2018. [DOI] [PubMed] [Google Scholar]
- [26].Starke J, Amanov E, Chikhaoui MT, and Burgner-Kahrs J, “On the merits of helical tendon routing in continuum robots,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst, September 2017, pp. 6470–6476. [Google Scholar]
- [27].Rucker DC and Webster III RJ, “Statics and dynamics of continuum robots with general tendon routing and external loading,” IEEE Trans. Robot, vol. 27, no. 6, pp. 1033–1044, December 2011. [Google Scholar]
- [28].Barreiros J, O’Brien KW, Hong S, Xiao MF, Yang H, and Shepherd RF, “Configurable tendon routing in a 3d-printed soft actuator for improved locomotion in a multi-legged robot,” in Proc. 2nd IEEE Int. Conf. Soft Robot, April 2019, pp. 94–101. [Google Scholar]
- [29].Booth JW et al. , “OmniSkins: Robotic skins that turn inanimate objects into multifunctional robots,” Sci. Robot, vol. 3, no. 22, September 2018, Paper eaat1853. [DOI] [PubMed] [Google Scholar]
- [30].Case JC, Booth J, Shah DS, Yuen MC, and Kramer-Bottiglio R, “State and stiffness estimation using robotic fabrics,” in Proc. IEEE Int. Conf. Soft Robot, April 2018, pp. 522–527. [Google Scholar]
- [31].Case JC, Yuen MC, Jacobs J, and Kramer-Bottiglio R, “Robotic skins that learn to control passive structures,” IEEE Robot. Automat. Lett, vol. 4, no. 3, pp. 2485–2492, July 2019. [Google Scholar]
- [32].Booth JW, Case JC, White EL, Shah DS, and Kramer-Bottiglio R, “An addressable pneumatic regulator for distributed control of soft robots,” in Proc. IEEE Int. Conf. Soft Robot, April 2018, pp. 25–30. [Google Scholar]
- [33].Siciliano B, Sciavicco L, Villani L, and Oriolo G, Robotics: Modelling, Planning and Control. Berlin, Germany: Springer, 2010. [Google Scholar]
- [34].Kulkarni P, “Centrifugal forming and mechanical properties of silicone-based elastomers for soft robotic actuators,” Ph.D. dissertation, Dept. Mech. Aerosp. Eng, Rutgers Univ.-Graduate School-New Brunswick, New Brunswick, NJ, USA, 2015. [Google Scholar]
- [35].Wang C, Wang C, and Reddy J, Exact Solutions for Buckling of Structural Members. Boca Raton, FL, USA: CRC Press, July 2004. [Google Scholar]
- [36].Vikas V, Grover P, and Trimmer B, “Model-free control framework for multi-limb soft robots,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst, September 2015, pp. 1111–1116. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.