Combining Multiple Observational Data Sources to Estimate Causal Effects

Abstract

The era of big data has witnessed an increasing availability of multiple data sources for statistical analyses. We consider estimation of causal effects combining big main data with unmeasured confounders and smaller validation data with supplementary information on these confounders. Under the unconfoundedness assumption with completely observed confounders, the smaller validation data allow for constructing consistent estimators for causal effects, but the big main data can only give error-prone estimators in general. However, by leveraging the information in the big main data in a principled way, we can improve the estimation efficiencies yet preserve the consistencies of the initial estimators based solely on the validation data. Our framework applies to asymptotically normal estimators, including the commonly used regression imputation, weighting, and matching estimators, and does not require a correct specification of the model relating the unmeasured confounders to the observed variables. We also propose appropriate bootstrap procedures, which makes our method straightforward to implement using software routines for existing estimators. Supplementary materials for this article are available online.

1. Introduction

Unmeasured confounding is an important and common problem in observational studies. Many methods have been proposed to deal with unmeasured confounding in causal inference, such as sensitivity analyses (e.g., Rosenbaum and Rubin 1983a), instrumental variable approaches (e.g., Angrist, Imbens, and Rubin 1996). However, sensitivity analyses cannot provide point estimation, and valid instrumental variables are often difficult to find in practice. We consider the setting where external validation data provide additional information on unmeasured confounders. To be more precise, the study includes a large main dataset representing the population of interest with unmeasured confounders and a smaller validation dataset with additional information about these confounders.

Our framework covers two common types of studies. First, we have a large main dataset, and then collect more information on unmeasured confounders for a subset of units, for example, using a two-phase sampling design (Neyman 1938; Cochran 2007; Wang et al. 2009). Second, we have a smaller but carefully designed validation dataset with rich covariates, and then link it to a larger main dataset with fewer covariates. The second type of data is now ubiquitous. In the era of big data, extremely large data have become available for research purposes, such as electronic health records, claims databases, disease data registries, census data, and to name a few (e.g., Imbens and Lancaster 1994; Schneeweiss et al. 2005; Chatterjee et al. 2016). Although these datasets might not contain full confounder information that guarantees consistent causal effect estimation, they can be useful to increase efficiencies of statistical analyses.

In causal inference, Stürmer et al. (2005) proposed a propensity score calibration method when the main data contain the outcome and an error-prone propensity score based on partial confounders, and the validation data supplement a gold standard propensity score based on all confounders. Stürmer et al. (2005) then applied a regression calibration technique to correct for the measurement error from the error-prone propensity score. This approach does not require the validation data to contain the outcome variable. However, this approach relies on the surrogacy property entailing that the outcome variable is conditionally independent of the error-prone propensity score given the gold standard propensity score and treatment. This surrogacy property is difficult to justify in practice, and its violations can lead to substantial biases (Stürmer et al. 2007; Lunt et al. 2012). Under the Bayesian framework, McCandless, Richardson, and Best (2012) specified a full parametric model of the joint distribution for the main and validation data, and treat the gold standard propensity score as a missing variable in the main data. Antonelli, Zigler, and Dominici (2017) combined the ideas of Bayesian model averaging, confounder selection, and missing data imputation into a single framework in this context. Enders et al. (2018) use simulation to show that multiple imputation is more robust than two-phase logistic regression against misspecification of imputation models. Lin and Chen (2014) developed a two-stage calibration method, which summarizes the confounding information through propensity scores and combines the results from the main and validation data. Their two-stage calibration focuses on the regression context with a correctly specified outcome model. Unfortunately, regression parameters, especially in the logistic regression model used by Lin and Chen (2014), may not be the causal parameters of interest in general (Freedman 2008).

In this article, we propose a general framework to estimate causal effects in the setting where the big main data have unmeasured confounders, but the smaller external validation data provide supplementary information on these confounders. Under the assumption of ignorable treatment assignment, causal effects can be identified and estimated from the validation data, using commonly used estimators, such as regression imputation, (augmented) inverse probability weighting (Horvitz and Thompson 1952; Rosenbaum and Rubin 1983b; Robins, Rotnitzky, and Zhao 1994; Bang and Robins 2005; Cao, Tsiatis, and Davidian 2009), and matching (e.g., Rubin 1973; Rosenbaum 1989; Heckman, Ichimura, and Todd 1997; Hirano, Imbens, and Ridder 2003; Hansen 2004; Rubin 2006; Abadie and Imbens 2006; Stuart 2010; Abadie and Imbens 2016). However, these estimators based solely on the validation data may not be efficient. We leverage the correlation between the initial estimator from the validation data and the error-prone estimator from the main data to improve the efficiency over the initial estimator. This idea is similar to the two-stage calibration in Lin and Chen (2014); however, their method focuses only on regression parameters and requires the validation data to be a simple random sample from the main data. Alternatively, the empirical likelihood is also an attractive approach to combine multiple data sources (Chen and Sitter 1999; Qin 2000; Chen, Sitter, and Wu 2002; Chen, Leung, and Qin 2003). However, the empirical likelihood approach needs sophisticated programming, and its computation can be heavy when data become large. Our method is practically simple, because we only need to compute commonly used estimators that can be easily implemented by existing software routines. Moreover, Lin and Chen (2014) and the empirical likelihood approach can only deal with regular and asymptotically linear (RAL) estimators often formulated by moment conditions, but our framework can also deal with non-RAL estimators, such as matching estimators. We also propose a unified bootstrap procedure based on resampling the linear expansions of the estimators, which is simple to implement and works for both RAL and matching estimators.

Furthermore, we relax the assumption that the validation data are a random sample from the study population of interest. We also link the proposed method to existing methods for missing data, viewing the additional confounders as missing values for units outside of the validation data. In contrast to most existing methods in the missing data literature, the proposed method does not need to specify the missing data model relating the unmeasured confounders with the observed variables.

For simplicity of exposition, we use “IID” for “identically and independently distributed,” 1(·) for the indicator function, ${\xi }^{\otimes 2}=\xi {\xi }^{\text{T}}$ for a vector or matrix $\xi$ “plim” for the probability limit of a random sequence, and $A_n\cong B_n$ for two random sequences satisfying $A_n=B_n+o_P(n^{-1/2})$ with n being the generic sample size. We relegate all regularity conditions for asymptotic analyses to the online supplementary material.

2. Basic Setup

2.1. Notation: Causal Effect and Two Data Sources

Following Neyman (1923) and Rubin 1974), we use the potential outcomes framework to define causal effects. Suppose that the treatment is a binary variable A ∈ {0,1}, with 0 and 1 being the labels for control and active treatments, respectively. For each level of treatment a ∈ {0,1}, we assume that there exists a potential outcome Y(a), representing the outcome had the subject, possibly contrary to the fact, been given treatment a. The observed outcome is Y = Y(A) = AY(1) + (1 − A)Y(0). Let a vector of pretreatment covariates be (X, U), where X is observed for all units, but U may not be observed for some units.

Although we can extend our discussion to multiple data sources, for simplicity of exposition, we first consider a study with two data sources. The validation data have observations ${\mathcal{O}}_2=\{(A_j,X_j,U_j,Y_j):j\in {\mathcal{S}}_2\}$ with sample size n₂ = |${\mathcal{S}}_2$|. The main data have observations ${\mathcal{O}}_1=\{(A_i,X_i,Y_i):i\in {\mathcal{S}}_1\backslash {\mathcal{S}}_2\}\cup {\mathcal{O}}_2$ with sample size $n_1=|{\mathcal{S}}_1|$. In our formulation, we consider the case with ${\mathcal{S}}_2$ ⊂ ${\mathcal{S}}_1$, and let $\rho ={\lim }_{n_2\to \infty }{n}_2/n_1\in \text{[0,1]}$. If one has two separate main and validation datasets, the main dataset in our context combines these two datasets. Although the main dataset is larger, that is, n₁ > n₂, it does not contain full information on important covariates U. Under a superpopulation model, we assume that {A_i, X_i, U_i, Y_i(0), Y_i (1) : i ∈ ${\mathcal{S}}_1$} are IID for all i ∈ ${\mathcal{S}}_1$, and therefore the observations in ${\mathcal{O}}_1$ are also IID. The following assumption links the main and validation data.

Assumption 1.

The index set ${\mathcal{S}}_2$ for the validation data of size n₂ is a simple random sample from ${\mathcal{S}}_1$.

Under Assumption 1, {A_j, X_j, U_j, Y_j(0), Y_j(1) : j ∈ ${\mathcal{S}}_2$} and the observations in ${\mathcal{O}}_2$ of the validation data are also IID, respectively. We shall relax Assumption 1 to allow ${\mathcal{S}}_2$ to be a general probability sample from ${\mathcal{S}}_1$ in Section 7. But Assumption 1 makes the presentation simpler.

Example 1.

Two-phase sampling design is an example that results in the observed data structure. In a study, some variables (e.g., A, X, and Y) may be relatively cheaper, while some variables (e.g., U) are more expensive to obtain. A two-phase sampling design (Neyman 1938; Cochran 2007; Wang et al. 2009) can reduce the cost of the study: in the first phase, the easy-to-obtain variables are measured for all units, and in the second phase, additional expensive variables are measured for a selected validation sample.

Example 2.

Another example is highly relevant in the era of big data, where one links small data with full information on (A, X, U, Y) to external big data with only (A, X, Y). Chatterjee et al. (2016) recently consider this scenario for parametric regression analyses.

Without loss of generality, we first consider the average causal effect (ACE)

$$\tau =E\{Y(1)-Y(0)\},$$ (1)

and will discuss extensions to other causal estimands in Section 4.1. Because of the IID assumption, we drop the indices i and j in the expectations in (1) and later equations.

In what follows, we define the conditional means of the outcome as

$${\mu }_a(X,U)=E(Y|A=a,X,U),$$

$${\mu }_a(X)=E(Y|A=a,X),$$

the conditional variances of the outcome as

$${\sigma }_a^2(X,U)=\mathrm{var}(Y|A=a,X,U),$$

$${\sigma }_a^2(X)=\mathrm{var}(Y|A=a,X),$$

the conditional probabilities of the treatment as

$$e(X,U)=P(A=1|X,U),e(X)=P(A=1|X).$$

2.2. Identification and Model Assumptions

A fundamental problem in causal inference is that we can observe at most one potential outcome for a unit. Following Rosenbaum and Rubin (1983b), we make the following assumptions to identify causal effects.

Assumption 2 (Ignorability).

$Y(a)⫫A|(X,U)$ for a = 0 and 1.

Under Assumption 2, the treatment assignment is ignorable in ${\mathcal{O}}_2$ given (X, U). However, the treatment assignment is only “latent” ignorable in ${\mathcal{O}}_1\backslash {\mathcal{O}}_2$ given X and the latent variable U (Frangakis and Rubin 1999; Jin and Rubin 2008).

Moreover, we require adequate overlap between the treatment and control covariate distributions, quantified by the following assumption on the propensity score e(X, U).

Assumption 3 (Overlap).

There exist constants c₁ and c₂ such that with probability 1, $0<c_1\le e(X,U)\le c_2<1$.

Under Assumptions 2 and 3, P{A = 1 | X, U, Y(1)} = P{A = 1 | X, U, Y(0)} = e(X, U), and E{Y(a) | X, U} = E{Y(a) | A = a, X, U} = μ_a(X, U). The ACE τ can then be estimated through regression imputation, inverse probability weighting (IPW), augmented inverse probability weighting (AIPW), or matching. See Rosenbaum (2002), Imbens (2004), and Rubin (2006) for surveys of these estimators.

In practice, the outcome distribution and the propensity score are often unknown and therefore need to be modeled and estimated.

Assumption 4 (Outcome model).

The parametric model ${\mu }_a\left(X,U;{\beta }_a\right)$ is a correct specification for μ_a(X, U),for a = 0, 1; that is, ${\mu }_a(X,U)={\mu }_a\left(X,U;{\beta }_a^{*}\right)$, where ${\beta }_a^{*}$ is the true model parameter, for a = 0, 1.

Assumption 5 (Propensity score model).

The parametric model e(X, U; α) is a correct specification for e(X, U); that is, $e(X,U)=e(X,U;{\alpha }^{*})$, where α^* is the true model parameter.

The consistency of different estimators requires different model assumptions.

3. Methodology and Important Estimators

3.1. Review of Commonly Used Estimators Based on Validation Data

The validation data {(A_j, X_j, U_j, Y_j) : j ∈ ${\mathcal{S}}_2$} contain observations of all confounders (X, U). Therefore, under Assumptions 2 and 3, τ is identifiable and can be estimated by some commonly used estimator solely from the validation data, denoted by ${\widehat{\tau }}_2$. Although the main data do not contain the full confounding information, we leverage the information on the common variables (A, X, Y) as in the main data to improve the efficiency of ${\widehat{\tau }}_2$. Before presenting the general theory, we first review important estimators that are widely used in practice.

Let μ_a(X, U; β_a) be a working model for μ_a(X, U), for a = 0, 1, and e(X, U; α) be a working model for e(X, U). We construct consistent estimators ${\widehat{\beta }}_a(a=0,1)$ and $\widehat{\alpha }$ based on ${\mathcal{O}}_2$, with probability limits ${\beta }_a^{*}(a=0,1)$ and α^*, respectively. Under Assumption 4, ${\mu }_a\left(X,U;{\beta }_a^{*}\right)={\mu }_a(X,U)$, and under Assumption 5, e(X, U; α^*) = e(X, U).

Example 3 (Regression imputation).

The regression imputation estimator is ${\widehat{\tau }}_{\text{reg},2}=n_2^{-1}{\sum }_{j\in {\mathcal{S}}_2}{\widehat{\tau }}_{\text{reg},2,j}$, where

$${\widehat{\tau }}_{\text{reg},2,j}={\mu }_1(X_j,U_j;{\widehat{\beta }}_1)-{\mu }_0(X_j,U_j;{\widehat{\beta }}_0).$$

${\widehat{\tau }}_{\text{reg},2}$ is consistent for τ under Assumption 4.

Example 4 (Inverseprobability weighting).

The IPW estimator is ${\widehat{\tau }}_{\text{IPW},2}=n_2^{-1}{\sum }_{j\in {\mathcal{S}}_2}{\widehat{\tau }}_{\text{IPW},2,j}$, where

$${\widehat{\tau }}_{\text{IPW},2,j}=\frac{A_j{Y}_j}{e(X_j,U_j;\widehat{\alpha })}-\frac{(1-A_j)Y_j}{1-e(X_j,U_j;\widehat{\alpha })}.$$

${\widehat{\tau }}_{\text{IPW},2}$ is consistent for τ under Assumption 5.

The Horvitz-Thompson-type estimator ${\widehat{\tau }}_{\text{IPW},2}$ has large variability, and is often inferior to the Hajek-type estimator (Hájek 1971). We do not present the Hajek-type estimator because we can improve it by the AIPW estimator below. The AIPW estimator employs both the propensity score and the outcome models.

Example 5 (Augmented inverse probability weighting).

Define the residual outcome as $R_j=Y_j-{\mu }_1(X_j,U_j;{\widehat{\beta }}_1)$ for treated units and $R_j=Y_j-{\mu }_0(X_j,U_j;{\widehat{\beta }}_0)$ for control units. The AIPW estimator is ${\widehat{\tau }}_{\text{AIPW},2}=n_2^{-1}{\sum }_{j\in {\mathcal{S}}_2}{\widehat{\tau }}_{\text{AIPW},2,j}$, where

$$\begin{gathered} {\widehat{\tau }}_{\text{AIPW},2,j}=\frac{A_j{R}_j}{e\left(X_j,U_j;\widehat{\alpha }\right)}+{\mu }_1\left(X_j,U_j;{\widehat{\beta }}_1\right) \\ -\frac{\left(1-A_j\right)R_j}{1-e\left(X_j,U_j;\widehat{\alpha }\right)}-{\mu }_0\left(X_j,U_j;{\widehat{\beta }}_0\right). \end{gathered}$$ (2)

${\widehat{\tau }}_{\text{AIPW},2}$ is doubly robust in the sense that it is consistent if either Assumption 4 or 5 holds. Moreover, it is locally efficient if both Assumptions 4 and 5 hold (Bang and Robins 2005; Tsiatis 2006; Cao, Tsiatis, and Davidian 2009).

Matching estimators are also widely used in practice. To fix ideas, we consider matching with replacement with the number of matches fixed at M. Matching estimators hinge on imputing the missing potential outcome for each unit. To be precise, for unit j, the potential outcome under A_j is the observed outcome Y_j; the (counterfactual) potential outcome under 1 − A_j is not observed but can be imputed by the average of the observed outcomes of the nearest M units with 1 − A_j. Let these matched units for unit j be indexed by ${\mathcal{J}}_{d,V,j}$, where the subscripts d and V denote the dataset ${\mathcal{O}}_d$ and the matching variable V (e.g., V = (X, U)), respectively. Without loss of generality, we use the Euclidean distance to determine neighbors; the discussion applies to other distances (Abadie and Imbens 2006). Let $K_{d,V,j}={\sum }_{l\in {\mathcal{S}}_d}1(j\in {\mathcal{J}}_{d,V,l})$ be the number of times that unit j is used as a match based on the matching variable V in ${\mathcal{O}}_d$.

Example 6 (Matching).

Define the imputed potential outcomes as

$$\begin{array}{l}{\widehat{Y}}_j(1)=\{\begin{array}{ll}{M}^{-1}{\sum }_{l\in {\mathcal{J}}_{2,(X,U),j}}{Y}_l\hfill & \text{if}{A}_j=0,\hfill \\ Y_j\hfill & \text{if}{A}_j=1,\hfill \end{array}\\ {\widehat{Y}}_j(0)=\{\begin{array}{ll}{Y}_j\hfill & \text{if}{A}_j=0,\hfill \\ M^{-1}{\sum }_{l\in {\mathcal{J}}_{2,(X,U),j}}{Y}_l\hfill & \text{if}{A}_j=1.\hfill \end{array}\end{array}$$

Then the matching estimator of τ is

$$\begin{gathered} {\widehat{\tau }}_{\text{mat},2}^{(0)}=n_2^{-1}\sum _{j\in {\mathcal{S}}_2}\{{\widehat{Y}}_j(1)-{\widehat{Y}}_j(0)\} \\ =n_2^{-1}\sum _{j\in {\mathcal{S}}_2}(2A_j-1)\left(Y_j-M^{-1}\sum _{l\in {\mathcal{J}}_{2,(X,U),j}}{Y}_l\right). \end{gathered}$$

Abadie and Imbens (2006) obtained the decomposition

$$n_2^{1/2}\left({\widehat{\tau }}_{\text{mat},2}^{(0)}-\tau \right)=B_2+D_2,$$

where

$$\begin{gathered} B_2=n_2^{-1/2}\sum _{j\in {\mathcal{S}}_2}(2A_j-1) \\ \times \left[M^{-1}{\sum }_{l\in {\mathcal{J}}_2,(X,U),j}\left\{{\mu }_{1-A_j}(X_j,U_j)-{\mu }_{1-A_j}(X_l,U_l)\right\}\right], \end{gathered}$$ (3)

$$\begin{gathered} D_2=n_2^{-1/2}\sum _{j\in {\mathcal{S}}_2}[{\mu }_1(X_j,U_j)-{\mu }_0(X_j,U_j)-\tau \\ +(2A_j-1)\{1+M^{-1}{K}_{2,(X,U),j}\}\left\{Y_j-{\mu }_{A_j}(X_j,U_j)\right\}]. \end{gathered}$$

The difference ${\mu }_{1-A_j}(X_j,U_j)-{\mu }_{1-A_j}(X_l,U_l)$ in (3) accounts for the matching discrepancy, and therefore B₂ contributes to the asymptotic bias of the matching estimator. Abadie and Imbens (2006) showed that the matching estimators have nonnegligible biases when the dimension of V is greater than one. Let ${\widehat{\mu }}_a(X,U)$ be an estimator for μ_a(X, U), obtained either parametrically, for example, by a linear regression estimator, or nonparametrically, for a = 0, 1. Abadie and Imbens (2006) proposed a bias-corrected matching estimator

$${\widehat{\tau }}_{\text{mat},2}={\widehat{\tau }}_{\text{mat},2}^{(0)}-n_2^{-1/2}{\widehat{B}}_2,$$

where ${\widehat{B}}_2$ is an estimator for B₂ by replacing μ_a(X, U) with ${\widehat{\mu }}_a(X,U)$.

3.2. A General Strategy

We give a general strategy for efficient estimation of the ACE by utilizing both the main and validation data. In Sections 3.3 and 3.4, we will provide examples to elucidate the proposed strategy with specific estimators.

Although the estimators based on the validation data ${\mathcal{O}}_2$ are consistent for τ under certain regularity conditions, they are inefficient without using the main data ${\mathcal{O}}_1$. However, the main data ${\mathcal{O}}_1$ do not contain important confounders U; if we naively use the estimators in Examples 3–6 with U being empty, then the corresponding estimators can be inconsistent for τ and thus are error-prone in general. Moreover, for robustness consideration, we do not want to impose additional modeling assumptions linking U and (A, X, Y).

Our strategy is straightforward: we apply the same error-prone procedure to both the main and validation data. The key insight is that the difference of the two error-prone estimates is consistent for 0 and can be used to improve efficiency of the initial estimator due to its association with ${\widehat{\tau }}_2$. Let an error-prone estimator of τ from the main data be ${\widehat{\tau }}_{1,\text{ep}}$, which converges to some constant τ_ep, not necessarily the same as τ. Applying the same method to the validation data $\{(A_j,X_j,Y_j):j\in {\mathcal{S}}_2\}$, we can obtain another error-prone estimator ${\widehat{\tau }}_{2,\text{ep}}$. More generally, we can consider τ_ep to be an L-dimensional vector of parameters identifiable based on the joint distribution of (A, X, Y), and ${\widehat{\tau }}_{1,\text{ep}}$ and ${\widehat{\tau }}_{2,\text{ep}}$ to be the corresponding estimators from the main and validation data, respectively. For example, ${\widehat{\tau }}_{d,\text{ep}}$ an contain estimators of τ using different methods based on ${\mathcal{O}}_d$.

We consider a class of estimators satisfying

$$n_2^{1/2}\left(\begin{array}{c}{\widehat{\tau }}_2-\tau \\ {\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}\end{array}\right)\to \mathcal{N}\left\{0_{L+1},\left(\begin{array}{cc}{v}_2& {\mathrm{\Gamma }}^{\text{T}}\\ \mathrm{\Gamma }& V\end{array}\right)\right\},$$ (4)

in distribution, as $n_2\to \infty$, which is general enough to include all the estimators reviewed in Examples 3–6. Heuristically, if (4) holds exactly rather than asymptotically, by the multivariate normal theory, we have the following the conditional distribution

$$\begin{gathered} n_2^{1/2}({\widehat{\tau }}_2-\tau )|n_2^{1/2}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}) \\ ~\mathcal{N}\left\{n_2^{1/2}{\mathrm{\Gamma }}^{\text{T}}{V}^{-1}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}),v_2-{\mathrm{\Gamma }}^{\text{T}}{V}^{-1}\mathrm{\Gamma }\right\}. \end{gathered}$$

Let ${\widehat{v}}_2$, $\widehat{\mathrm{\Gamma }}$ and $\widehat{V}$ be consistent estimators for v₂, $\mathrm{\Gamma }$ and V. We set $n_2^{1/2}({\widehat{\tau }}_2-\tau )$ to equal its estimated conditional mean $n_2^{1/2}{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}})$, leading to an estimating equation for τ:

$$n_2^{1/2}({\widehat{\tau }}_2-\tau )=n_2^{1/2}{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}).$$

Solving this equation for τ, we obtain the estimator

$$\widehat{\tau }={\widehat{\tau }}_2-{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}).$$ (5)

Proposition 1.

Under Assumption 1 and certain regularity conditions, if (4) holds, then $\widehat{\tau }$ is consistent for τ, and

$$n_2^{1/2}(\widehat{\tau }-\tau )\to \mathcal{N}(0,v_2-{\mathrm{\Gamma }}^{\text{T}}{V}^{-1}\mathrm{\Gamma }),$$ (6)

in distribution, as $n_2\to \infty$. Given a nonzero Γ, the asymptotic variance, $v_2-{\mathrm{\Gamma }}^{\text{T}}{V}^{-1}\mathrm{\Gamma }$, is smaller than the asymptotic variance of ${\widehat{\tau }}_2,v_2$.

The consistency of $\widehat{\tau }$ does not require any component in ${\widehat{\tau }}_{1,\text{ep}}$ and ${\widehat{\tau }}_{2,\text{ep}}$ to correctly estimate τ. That is, these estimators can be error prone. The requirement for the error-prone estimators is minimal, as long as they are consistent for the same (finite) parameters. Under Assumption 1, ${\widehat{\tau }}_{1,\text{ep}}-{\widehat{\tau }}_{2,\text{ep}}$ is consistent for a vector of zeros, as $n_2\to \infty$.

We can estimate the asymptotic variance of $\widehat{\tau }$ by

$$\widehat{v}=({\widehat{v}}_2-{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}\widehat{\mathrm{\Gamma }})/n_2.$$ (7)

Remark 1.

We construct the error prone estimators ${\widehat{\tau }}_{1,\text{ep}}$ and ${\widehat{\tau }}_{2,\text{ep}}$ based on ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$, respectively. Another intuitive way is to construct ${\widehat{\tau }}_{1,\text{ep}}$ and ${\widehat{\tau }}_{2,\text{ep}}$ based on ${\mathcal{O}}_1\backslash {\mathcal{O}}_2$ and ${\mathcal{O}}_2$, respectively. In general, we can construct the error prone estimators based on different subsets of ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ as long as their difference converges in probability to zero. We show in the supplementary material that our construction maximizes the variance reduction for ${\widehat{\tau }}_2,{\mathrm{\Gamma }}^{\text{T}}{V}^{-1}\mathrm{\Gamma }$, given the procedure of the error prone estimators.

Remark 2.

We can view (5) as the best consistent estimator of τ among all linear combinations $\{{\widehat{\tau }}_2+{\lambda }^{\text{T}}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}):\lambda \in {ℝ}^L\}$, in the sense that (5) achieves the minimal asymptotic variance among this class of consistent estimators. Similar ideas appeared in design-optimal regression estimation in survey sampling (Deville and Särndal 1992; Fuller 2009), regression analyses (Chen and Chen 2000; Chen 2002; Wang and Wang 2015), improved prediction in high dimensional datasets (Boonstra, Taylor, and Mukherjee 2012), and meta-analysis (Collaboration 2009). In the supplementary material, we show that the proposed estimator in (5) is the best estimator of τ among the class of estimators {$\widehat{\tau }=f({\widehat{\tau }}_2,{\widehat{\tau }}_{1,\text{ep}},{\widehat{\tau }}_{2,\text{ep}}):f(x,y,z)$ is a smooth function of (x, y, z), and $\widehat{\tau }$ is consistent for τ}, in the sense that (5) achieves the minimal asymptotic variance among this class.

Remark 3.

The choice of the error-prone estimators will affect the efficiency of $\widehat{\tau }$. From (6), for a given ${\widehat{\tau }}_2$, to improve the efficiency of $\widehat{\tau }$ with a 1-dimensional error-prone estimator, we would like this estimator to have a small variance V and a large correlation with ${\widehat{\tau }}_2$, Γ. In principle, increasing the dimension of the error-prone estimator would not decrease the asymptotic efficiency gain as shown in the supplementary material. However, it would also increase the complexity of implementation and harm the finite sample properties. To “optimize” the tradeoff, we suggest choosing the error-prone estimator to be the same type as the initial estimator ${\widehat{\tau }}_2$. For example, if ${\widehat{\tau }}_2$ is an AIPW estimator, we can choose ${\widehat{\tau }}_{d,\text{ep}}$ to be an AIPW estimator without using U in a possibly misspecified propensity score model. The simulation in Section 5 confirms that this choice is reasonable.

To close this subsection, we comment on the existing literature and the advantages of our strategy. The proposed estimator $\widehat{\tau }$ in (5) utilizes both the main and validation data and improves the efficiency of the estimator based solely on the validation data. In economics, Imbens and Lancaster (1994) proposed to use the generalized method of moments (Hansen 1982) for using the main data which provide moments of the marginal distribution of some economic variables. In survey sampling, calibration is a standard technique to integrate auxiliary information in estimation or handle nonresponse; see, for example, Chen and Chen (2000), Wu and Sitter (2001), Kott (2006), Chang and Kott (2008), and Kim, Kwon, and Paik (2016). An important issue is how to specify optimal calibration equations; see, for example, Deville and Särndal (1992), Robins, Rotnitzky, and Zhao (1994), Wu and Sitter (2001), and Lumley, Shaw, and Dai (2011). Other researchers developed constrained empirical likelihood methods to calibrate auxiliary information from the main data; see, for example, Chen and Sitter (1999), Qin (2000), Chen, Sitter, and Wu (2002), and Chen, Leung, and Qin (2003).

Compared to these methods, the proposed framework is attractive because it is simple to implement which requires only standard software routines for existing methods, and it can deal with estimators that cannot be derived from moment conditions, for example, matching estimators. Moreover, our framework does not require a correct model specification of the relationship between unmeasured covariates U and measured variables (A, X, Y).

3.3. Regular Asymptotically Linear (RAL) Estimators

We first elucidate the proposed method with RAL estimators.

From the validation data, we consider the case when ${\widehat{\tau }}_2-\tau$ is RAL; that is, it can be asymptotically approximated by a sum of IID random vectors with mean 0:

$${\widehat{\tau }}_2-\tau \cong n_2^{-1}\sum _{j\in {\mathcal{S}}_2}\psi (A_j,X_j,U_j,Y_j),$$ (8)

where $\{\psi (A_j,X_j,U_j,Y_j):j\in {\mathcal{S}}_2\}$ are IID with mean 0. The random vector $\psi (A,X,U,Y)$ is called the influence function of ${\widehat{\tau }}_2$ with $E(\psi )=0$ and $E({\psi }^2)<\infty$ (e.g., Bickel et al. 1993). Regarding regularity conditions, see, for example, Newey (1990).

Let $e(X;\gamma )$ be an error-prone propensity score model for, $e(X)$, and ${\mu }_a(X;{\eta }_a)$ be an error-prone outcome regression model for μ_a(X), for a = 0, 1. The corresponding error-prone estimators of the ACE can be obtained from the main data ${\mathcal{O}}_1$ and the validation data ${\mathcal{O}}_2$. We consider the case when ${\widehat{\tau }}_{d,\text{ep}}$ is RAL:

$${\widehat{\tau }}_{d,\text{ep}}-{\tau }_{\text{ep}}\cong n_d^{-1}\sum _{j\in {\mathcal{S}}_d}\varphi \left(A_j,X_j,Y_j\right),(d=1,2)$$ (9)

where $\{\varphi (A_j,X_j,Y_j):j\in {\mathcal{S}}_d\}$ are IID with mean 0.

Theorem 1.

Under certain regularity conditions, (4) holds for the RAL estimators (8) and (9), where $v_2=\mathrm{var}\{\psi (A,X,U,Y)\}$, $\mathrm{\Gamma }=(1-\rho )\mathrm{cov}\{\psi (A,X,U,Y),\varphi (A,X,Y)\}$, and $V=(1-\rho )\times \mathrm{var}\{\varphi (A,X,Y)\}$.

To derive $\widehat{\mathrm{\Gamma }}$ and $\widehat{V}$ for RAL estimators, let ${\widehat{\varphi }}_d(A,X,Y)$ and $\widehat{\psi }(A,X,U,Y)$ be estimators of $\varphi (A,X,Y)$ and $\psi (A,X,U,Y)$ by replacing E(·) with the empirical measure and unknown parameters with their corresponding estimators. Note that the subscript d in ${\widehat{\varphi }}_d(A,X,Y)$ indicates that it is obtained based on ${\mathcal{O}}_d$. Then, we can estimate Γ and V by

$$\begin{gathered} \widehat{\mathrm{\Gamma }}=\widehat{\mathrm{cov}}({\widehat{\tau }}_2,{\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}) \\ =\left(1-\frac{n_2}{n_1}\right)\frac{1}{n_2}\sum _{j\in {\mathcal{S}}_2}\widehat{\psi }(A_j,X_j,U_j,Y_j){\widehat{\varphi }}_2(A_j,X_j,Y_j), \end{gathered}$$

$$\widehat{V}=\widehat{\mathrm{cov}}({\widehat{\tau }}_{1,\text{ep}}-{\widehat{\tau }}_{2,\text{ep}})=\left(1-\frac{n_2}{n_1}\right)\frac{1}{n_1}\sum _{i\in {\mathcal{S}}_1}{\left\{{\widehat{\varphi }}_1(A_i,X_i,Y_i)\right\}}^{\otimes 2}.$$

Finally, we can obtain the estimator and its variance estimator by (5) and (7), respectively.

The commonly-used RAL estimators include the regression imputation and (augmented) inverse probability weighting estimators. Because the influence functions for ${\widehat{\tau }}_{\text{reg},2}$ and ${\widehat{\tau }}_{\text{IPW},2}$ are standard, we present the details in the supplementary material. Below, we state only the influence function for ${\widehat{\tau }}_{\text{AIPW},2}$.

For the outcome model, let S_a (A, X, U, Y; β_a) be the estimating function for β_a, for example,

$$S_a(A,X,U,Y;{\beta }_a)=\frac{\partial {\mu }_a(X,U;{\beta }_a)}{\partial {\beta }_a}\{Y-{\mu }_a(X,U;{\beta }_a)\},$$

for a = 0, 1, which is a standard choice for the conditional mean model. For the propensity score model, let S(A, X, U; α) be the estimating function for α, for example,

$$S(A,X,U;\alpha )=\frac{A-e(X,U;\alpha )}{e(X,U;\alpha )\{1-e(X,U;\alpha )\}}\frac{\partial e(X,U;\alpha )}{\partial \alpha },$$

which is the score function from the likelihood of a binary response model. Moreover, let

$$\begin{gathered} {\Sigma }_{\alpha \alpha }=E\left\{S^{\otimes 2}(A,X,U;\alpha )\right\} \\ =E\left[\frac{1}{e(X,U;{\alpha }^{*})\{1-e(X,U;{\alpha }^{*})\}}{\left\{\frac{\partial e(X,U;{\alpha }^{*})}{\partial \alpha }\right\}}^{\otimes 2}\right] \end{gathered}$$

be the Fisher information matrix for α in the propensity score model. In addition, let ${\widehat{\beta }}_a(a=0,1)$ and $\widehat{\alpha }$ be the estimators solving the corresponding empirical estimating equations based on ${\mathcal{O}}_2$, with probability limits ${\beta }_a^{*}(a=0,1)$ and α^*, respectively.

Lemma 1 (Augmented inverse probability weighting).

For simplicity, denote $e_j^{*}=e(X_j,U_j;{\alpha }^{*}),{\dot{e}}_j^{*}=\partial e(X_j,U_j;{\alpha }^{*})/\partial {\alpha }^{\text{T}},S_j^{*}=S(A_j,X_j,U_j;{\alpha }^{*}),{\mu }_{aj}^{*}={\mu }_a(X_j,U_j;{\beta }_a^{*}),{\dot{\mu }}_{aj}^{*}=\partial {\mu }_a(X_j,U_j;{\beta }_a^{*})/\partial {\beta }_a^{\text{T}},S_{aj}^{*}=S_a(A_j,X_j,U_j,Y_j;{\beta }_a^{*})$, and ${\dot{S}}_{aj}^{*}=\partial S_a(A_j,X_j,U_j,Y_j;{\beta }_a^{*})/\partial {\beta }_a^{\text{T}}$ for a = 0, 1. Under Assumption 4 or 5, ${\widehat{\tau }}_{\text{AIPW},2}$ has the influence function

$$\begin{gathered} {\psi }_{\text{AIPW}}\left(A_j,X_j,U_j,Y_j\right) \\ =\frac{A_j{Y}_j}{e_j^{*}}+\left(1-\frac{A_j}{e_j^{*}}\right){\mu }_{1j}^{*} \\ -\frac{(1-A_j)Y_j}{1-e_j^{*}}-\left(1-\frac{1-A_j}{1-e_j^{*}}\right){\mu }_{0j}^{*}-\tau +H_{\text{AIPW}}{\Sigma }_{\alpha \alpha }^{-1}{S}_j^{*} \\ +E\left\{\left(1-\frac{1-A}{1-e^{*}}\right){\dot{\mu }}_0^{*}\right\}{\left\{E({\dot{S}}_0^{*})\right\}}^{-1}{S}_{0j}^{*} \end{gathered}$$ (10)

$$-E\left\{\left(1-\frac{A}{e^{*}}\right){\dot{\mu }}_1^{*}\right\}{\left\{E({\dot{S}}_1^{*})\right\}}^{-1}{S}_{1j}^{*},$$ (11)

where

$$H_{\text{AIPW}}=E\left[\left\{\frac{A(Y-{\mu }_1^{*})}{{(e^{*})}^2}-\frac{(1-A)(Y-{\mu }_0^{*})}{{(1-e^{*})}^2}\right\}{\dot{e}}^{*}\right].$$

Lemma 1 follows from standard asymptotic theory, but as far as we know it has not appeared in the literature. Lunceford and Davidian (2004) suggest a formula without (10) and (11) for ${\psi }_{\text{AIPW}}$, which, however, works only when both Assumptions 4 and 5 hold. Otherwise, the resulting variance estimator is not consistent if either Assumption 4 or 5 does not hold, as shown by simulation in Funk et al. (2011). The correction terms in (10) and (11) also make the variance estimator doubly robust in the sense that the variance estimator for ${\widehat{\tau }}_{\text{AIPW},2}$ is consistent if either Assumption 4 or 5 holds, not necessarily both.

For error-prone estimators, we can obtain the influence functions similarly. The subtlety is that both the propensity score and outcome models can be misspecified. For simplicity of the presentation, we defer the exact formulas to the online supplementary material.

3.4. Matching Estimators

We then elucidate the proposed method with non-RAL estimators. An important class of non-RAL estimators for the ACE are the matching estimators. The matching estimators are not regular estimators because the functional forms are not smooth due to the fixed numbers of matches (Abadie and Imbens 2008). Continuing with Example 6, Abadie and Imbens 2006) express the bias-corrected matching estimator ${\widehat{\tau }}_{\text{mat},2}$ in a linear form as

$${\widehat{\tau }}_{\text{mat},2}-\tau \cong n_2^{-1}\sum _{j\in {\mathcal{S}}_2}{\psi }_{\text{mat},j},$$ (12)

where

$$\begin{gathered} {\psi }_{\text{mat},j}={\mu }_1(X_j,U_j)-{\mu }_0(X_j,U_j)-\tau \\ +(2A_j-1)\left\{1+M^{-1}{K}_{2,(X,U),j}\right\}\left\{Y_j-{\mu }_{A_j}(X_j,U_j)\right\}. \end{gathered}$$ (13)

Similarly, ${\widehat{\tau }}_{\text{mat,}d\text{,ep}}$ has a linear form

$${\widehat{\tau }}_{\text{mat},d,\text{ep}}-{\tau }_{\text{ep}}\cong n_d^{-1}\sum _{j\in {\mathcal{S}}_d}{\varphi }_{\text{mat},d,j},$$ (14)

where

$$\begin{gathered} {\varphi }_{\text{mat},d,j}={\mu }_1(X_j)-{\mu }_0(X_j)-{\tau }_{\text{ep}} \\ +(2A_j-1)(1+M^{-1}{K}_{d,X,j})\left\{Y_j-{\mu }_{A_j}(X_j)\right\}. \end{gathered}$$ (15)

Theorem 2.

Under certain regularity conditions, (4) holds for the matching estimators (12) and (14), where

$$\begin{gathered} v_2=\mathrm{var}\{\tau (X,U)\} \\ +\mathrm{plim}\left[n_2^{-1}\sum _{j\in {\mathcal{S}}_2}{\left\{1+M^{-1}{K}_{2,(X,U),j}\right\}}^2{\sigma }_{A_j}^2\left(X_j,U_j\right)\right], \\ \mathrm{\Gamma }=(1-\rho )(\mathrm{cov}\left\{{\mu }_1(X,U)-{\mu }_0(X,U),{\mu }_1(X)-{\mu }_0(X)\right\} \\ +\mathrm{plim}\left[n_2^{-1}\sum _{j\in {\mathcal{S}}_2}\left\{1+M^{-1}{K}_{2,(X,U),j}\right\} \\ \times \left(1+M^{-1}{K}_{2,X,j}\right){\sigma }_{A_j}^2\left(X_j,U_j\right)\right]), \end{gathered}$$

$$\begin{gathered} V=(1-\rho )\left[\mathrm{var}\left\{{\mu }_1(X)-{\mu }_0(X)\right\} \\ +\mathrm{plim}\left\{n_2^{-1}\sum _{j\in {\mathcal{S}}_2}{(1+M^{-1}{K}_{2,X,j})}^2{\sigma }_{A_j}^2(X_j)\right\}\right]. \end{gathered}$$

The existence of the probability limits in Theorem 2 are guaranteed by the regularity conditions specified in the supplementary material (c.f. Abadie and Imbens 2006).

To estimate (v₂, Γ, V) in Theorem 2, we need to estimate the conditional mean and variance functions of the outcome given covariates. Following Abadie and Imbens (2006), we can estimate these functions via matching units with the same treatment level. We will discuss an alternative bootstrap strategy in the next subsection.

3.5. Bootstrap Variance Estimation

The asymptotic results in Theorems 1 and 2 allow for variance estimation of $\widehat{\tau }$. In addition, we also consider the bootstrap for variance estimation, which is simpler to implement and often has better finite sample performances (Otsu and Rai 2016). This is particularly important for matching estimators because the analytic variance formulas involve nonparametric estimation of the conditional variances ${\sigma }_a^2(x,u)\text{and}{\sigma }_a^2(x)$.

There are two approaches for obtaining bootstrap observations: (a) the original observations; and (b) the asymptotic linear terms of the proposed estimator. For RAL estimators, bootstrapping the original observations will yield valid variance estimators (Efron and Tibshirani 1986; Shao and Tu 2012). However, for matching estimators, Abadie and Imbens (2008) showed that due to lack of smoothness in their functional form, the bootstrap based on approach (a) does not apply for variance estimation. This is mainly because the bootstrap based on approach (a) cannot preserve the distribution of the numbers of times that the units are used as matches. As a remedy, Otsu and Rai (2016) proposed to construct the bootstrap counterparts by resampling based on approach (b) for the matching estimator.

To unify the notation, let ${\psi }_j$ indicate $\psi (A_j,X_j,U_j,Y_j)$ for RAL ${\widehat{\tau }}_2$ and ${\psi }_{\text{mat},j}$ for ${\widehat{\tau }}_{\text{mat},2}$ and similar definitions apply to ${\varphi }_{d,j}(d=1,2)$. Let ${\widehat{\psi }}_j$ and ${\widehat{\varphi }}_{d,j}$ be their estimated version by replacing the population quantities by the estimated quantities (d = 1, 2). Following Otsu and Rai (2016), for b = 1,...,B, we construct the bootstrap replicates for the proposed estimators as follows:

Step 1. Sample n₁ units from ${\mathcal{S}}_1$ with replacement as ${\mathcal{S}}_1^{*(b)}$, treating the units with observed U as the bootstrap validation data ${\mathcal{S}}_2^{*(b)}$.

Step 2. Compute the bootstrap replicates of ${\widehat{\tau }}_2-\tau \text{and}{\widehat{\tau }}_{d,\text{ep}}-{\tau }_{\text{ep}}$ as

$$\begin{gathered} {\widehat{\tau }}_2^{(b)}-{\widehat{\tau }}_2=n_2^{-1}\sum _{j\in S_2^{*}(b)}{\widehat{\psi }}_j, \\ {\widehat{\tau }}_{d,\text{ep}}^{(b)}-{\widehat{\tau }}_{d,\text{ep}}=n_d^{-1}\sum _{j\in {\mathcal{S}}_d^{*(b)}}{\widehat{\varphi }}_{d,j},(d=1,2). \end{gathered}$$

Based on the bootstrap replicates, we estimate Γ, V and v₂ by

$$\widehat{\mathrm{\Gamma }}={(B-1)}^{-1}\sum _{b=1}^B({\widehat{\tau }}_2^{(b)}-{\widehat{\tau }}_2)({\widehat{\tau }}_{2,\text{ep}}^{(b)}-{\widehat{\tau }}_{1,\text{ep}}^{(b)}-{\widehat{\tau }}_{2,\text{ep}}+{\widehat{\tau }}_{1,\text{ep}}),$$ (16)

$$\widehat{V}={(B-1)}^{-1}\sum _{b=1}^B{\left({\widehat{\tau }}_{2,\text{ep}}^{(b)}-{\widehat{\tau }}_{1,\text{ep}}^{(b)}-{\widehat{\tau }}_{2,\text{ep}}+{\widehat{\tau }}_{1,\text{ep}}\right)}^{\otimes 2},$$ (17)

$${\widehat{v}}_2={(B-1)}^{-1}\sum _{b=1}^B{({\widehat{\tau }}_2^{(b)}-{\widehat{\tau }}_2)}^2.$$ (18)

Finally, we estimate the asymptotic variance of $\widehat{\tau }$ by (7), that is, $\widehat{v}=({\widehat{v}}_2-{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}\widehat{\mathrm{\Gamma }})/n_2$.

Theorem 3.

Under certain regularity conditions, $(\widehat{\mathrm{\Gamma }},\widehat{V},{\widehat{v}}_2,\widehat{v})$ are consistent for $\{\mathrm{\Gamma },V,\mathrm{var}({\widehat{\tau }}_2),\mathrm{var}(\widehat{\tau })\}$.

Remark 4.

If the ratio of n₂ and n₁ is small, the above bootstrap approach may be unstable, because it is likely that some bootstrap validation data contain only a few or even zero observations. In this case, we use an alternative bootstrap approach, where we sample n₂ units from ${\mathcal{S}}_2$ with replacement as ${\mathcal{S}}_2^{*}$, sample n₁ − n₂ units from ${\mathcal{S}}_1$\${\mathcal{S}}_2$ with replacement, combined with ${\mathcal{S}}_2^{*}$, as ${\mathcal{S}}_1^{*}$, and obtain the proposed estimators based on ${\mathcal{S}}_1^{*}$ and ${\mathcal{S}}_2^{*}$. This approach guarantees that the bootstrap validation data contain n₂ observations.

Remark 5.

It is worthwhile to comment on a computational issue. When the main data have a substantially large size, the computation for the bootstrap can be demanding if we follow Steps 1 and 2 above. In this case, we can use subsampling (Politis, Romano, and Wolf 1999) or the Bag of Little Bootstraps (Kleiner et al. 2014) to reduce the computational burden. More interestingly, when $n_1\to \infty$ and ρ = 0, that is, the validation data contain a small fraction of the main data, Γ and V reduce to $\mathrm{cov}({\widehat{\tau }}_2,{\widehat{\tau }}_{2,\text{ep}})$ and $\mathrm{var}({\widehat{\tau }}_{2,\text{ep}})$, respectively. That is, when the size of the main data is substantially large, we can ignore the uncertainty of ${\widehat{\tau }}_{1,\text{ep}}$ and treat it as a constant, which is a regime recently considered by Chatterjee et al. (2016). In this case, we need only to bootstrap the validation data, which is computationally simpler.

4. Extensions

4.1. Other Causal Estimands

Our strategy extends to a wide class of causal estimands, as long as (4) holds. For example, we can consider the average causal effects over a subset of population (Crump et al. 2006; Li, Morgan, and Zaslavsky 2016), including the average causal effect on the treated.

We can also consider nonlinear causal estimands. For example, for a binary outcome, the log of the causal risk ratio is

$$\log \text{CRR}=\log \frac{P\{Y(1)=1\}}{P\{Y(0)=1\}}=\log \frac{E\{Y(1)\}}{E\{Y(0)\}},$$

and the log of the causal odds ratio is

$$\begin{gathered} \log \mathrm{COR}=\log \frac{P\{Y(1)=1\}/P\{Y(1)=0\}}{P\{Y(0)=1\}/P\{Y(0)=0\}} \\ =\log \frac{E\{Y(1)\}/[1-E\{Y(1)\}]}{E\{Y(0)\}/[1-E\{Y(0)\}]}. \end{gathered}$$

We give a brief discussion for the log CRR as an illustration. The key insight is that under Assumptions 2 and 3, we can estimate E{Y(a)} with commonly-used estimators from ${\mathcal{O}}_2$, denoted by $\widehat{E}\{Y(a)\},\text{for}a=0,1$. We can then obtain an estimator for the log CRR as log $[\widehat{E}\{Y(1)\}/\widehat{E}\{Y(0)\}]$. Similarly, we can obtain error-prone estimators for the log CRR from both ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ using only covariates X. By the Taylor expansion, we can linearize these estimators and establish a similar result as (4), which serves as the basis to construct an improved estimator for the log CRR.

4.2. Design Issue: Optimal Sample Size Allocation

As a design issue, we consider planning a study to obtain the data structure in Example 1 in Section 2 subject to a cost constraint. The goal is to find the optimal design, specifically the sample allocation, that minimizes the variance of the proposed estimator subject to a cost constraint, as in the classical two-phase sampling (Cochran 2007).

Suppose that it costs C₁ to collect (A, X, Y) for each unit, and C₂ to collect U for each unit. Thus, the total cost of the study is

$$C=n_{\text{1}}{C}_{\text{1}}\text{+}{n}_{\text{2}}{C}_{\text{2}}.$$ (19)

The variance of the proposed estimator $\widehat{\tau }$ is of the form

$$n_2^{-1}{v}_2-(n_2^{-1}-n_1^{-1})\gamma ,$$ (20)

for example, for RAL estimators,

$$\begin{gathered} \gamma =\mathrm{cov}{\{\psi (A,X,U,Y),\varphi (A,X,Y)\}}^{\text{T}}{[\mathrm{var}\{\varphi (A,X,Y)\}]}^{-1} \\ \mathrm{cov}\{\psi (A,X,U,Y),\varphi (A,X,Y)\} \end{gathered}$$

is the variance of the projection of $\psi (A,X,U,Y)$ onto the linear space spanned by $\varphi (A,X,Y)$. Minimizing (20) with respect to n₁ and n₂ subject to the constraint (19) yields the optimal $n_1^{*}$ and $n_2^{*}$, which satisfy

$${\rho }^{*}=\frac{n_2^{*}}{n_1^{*}}={\left\{(1-R_{\psi |\varphi }^2)\times \frac{C_1}{C_2}\right\}}^{1/2},$$ (21)

where $R_{\psi |\varphi }^2=\gamma /v_2$ is the squared multiple correlation coefficient of $\psi (A,X,U,Y)\text{on}\varphi (A,X,Y)$, which measures the association between the initial estimator and the error-prone estimator. We derive (21) using the Lagrange multipliers, and relegate the details to the supplementary material. Not surprisingly, (21) shows that the sizes of the validation data and the main data should be inversely proportional to the square-root of the costs. In addition, from (21), a large size n₂ for the validation data is more desirable when the association between the initial estimator and the error-prone estimator is small.

4.3. Multiple Data Sources

We have considered the setting with two data sources, and we can easily extend the theory to the setting with multiple data sources ${\mathcal{O}}_1,\dots ,{\mathcal{O}}_K$, where ${\mathcal{O}}_1,\dots ,{\mathcal{O}}_{K-1}$ contain partial covariate information, and the validation data, ${\mathcal{O}}_K$, contain full information for (A, X, U, Y). For example, for $d=1,\dots ,K-1$, ${\mathcal{O}}_d$ contains variables $\left(A,V_d,Y\right)$ where $V_d⫋(X,U)$. Each dataset ${\mathcal{O}}_d$, indexed by ${\mathcal{S}}_d$, has size n_d for d = 1,...,K. This type of data structure arises from a multi-phase sampling as an extension of Example 1 or multiple sources of “big data” as an extension of Example 2.

Let ${\widehat{\tau }}_K$ be the initial estimator for τ from the validation data ${\mathcal{O}}_K$, and ${\widehat{\tau }}_{d,\text{ep}}$ be the error-prone estimator for τ from ${\mathcal{O}}_d(d=1,\dots ,K-1)$. Let ${\widehat{\tau }}_{d,K,\text{ep}}$ be the estimator obtained by applying the same error-prone estimator for $O_d$ to ${\mathcal{O}}_K$, so that ${\widehat{\tau }}_{d,\text{ep}}-{\widehat{\tau }}_{d,K,\text{ep}}$ is consistent for 0, for $d=1,\dots ,K-1$. Assume that

$$\begin{gathered} n_K^{1/2}\left(\begin{array}{c}{\widehat{\tau }}_K-\tau \\ {\widehat{\tau }}_{1,\text{ep}}-{\widehat{\tau }}_{1,K,\text{ep}}\\ ⋮\\ {\widehat{\tau }}_{K-1,\text{ep}}-{\widehat{\tau }}_{K-1,K,\text{ep}}\end{array}\right) \\ \to \mathcal{N}\left\{\left(\begin{array}{c}0\\ 0_L\end{array}\right),\left(\begin{array}{cc}{v}_K& {\mathrm{\Gamma }}^{\text{T}}\\ \mathrm{\Gamma }& V\end{array}\right)\right\}, \end{gathered}$$

in distribution, as $n_K\to \infty$, where $L=\sum _{d=1}^{K-1}\dim ({\widehat{\tau }}_{d,\text{ep}})$. If Γ and V have consistent estimators $\widehat{\mathrm{\Gamma }}$ and $\widehat{V}$, respectively, then, extending the proposed method in Section 3, we can use

$$\widehat{\tau }={\widehat{\tau }}_K-{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}{\left({\widehat{\tau }}_{1,\text{ep}}^{\text{T}}-{\widehat{\tau }}_{1,K,\text{ep}}^{\text{T}},\dots ,{\widehat{\tau }}_{K-1,\text{ep}}^{\text{T}}-{\widehat{\tau }}_{K-1,K,\text{ep}}^{\text{T}}\right)}^{\text{T}}$$

to estimate τ. The estimator $\widehat{\tau }$ is consistent for τ with the asymptotic variance $v_K-{\mathrm{\Gamma }}^{\text{T}}{V}^{-1}\mathrm{\Gamma }$, which is smaller than the asymptotic variance of ${\widehat{\tau }}_K,v_K$, if Γ is nonzero. Similar to the reasoning in Remark 3, using more data sources will improve the asymptotic estimation efficiency of τ.

5. Simulation

In this section, we conduct a simulation study to evaluate the finite sample performance of the proposed estimators. In our data generating model, the covariates are $X_i~\mathrm{Unif}(0,2)$ and $U_i=0.5+0.5X_i-2\sin (X_i)+2\mathrm{sign}\{\sin (5X_i)\}+{ϵ}_i$, where ${ϵ}_i~\text{Unif}(-0.5,0.5)$. The potential outcomes are $Y_i(0)=-X_i-U_i\text{+}{ϵ}_i(0)$, and $Y_i(1)=-X_i+4U_i+{ϵ}_i(1)$, where ${ϵ}_i(0)~\mathcal{N}(0,1),{ϵ}_i(1)~\mathcal{N}(0,1),\text{and}{ϵ}_i(0)\text{and}{ϵ}_i(1)$ are independent. Therefore, the true value of the ACE is τ = E(5U_i). The treatment indicator A_i follows Bernoulli $({\pi }_i)$ with $\mathrm{logit}({\pi }_i)=1-0.5X_i-0.5U_i$. The main data ${\mathcal{O}}_1$ consist of n₁ units, and the validation data ${\mathcal{O}}_2$ consist of n₂ units randomly selected from the main data.

The initial estimators are the regression imputation, (A)IPW and matching estimators applied solely to the validation data, denoted by ${\widehat{\tau }}_{\text{reg},2},{\widehat{\tau }}_{\text{IPW},2},{\widehat{\tau }}_{\text{AIPW},2},\text{and}{\widehat{\tau }}_{\text{mat},2}$ respectively. To distinguish the estimators constructed based on different error-prone methods, we assign each proposed estimator a name with the form ${\widehat{\tau }}_{\text{method},2\text{\&methods}}$, where “method,2” indicates the initial estimator applied to the validation data ${\mathcal{O}}_2$ and “methods” indicates the error-prone estimator(s) used to improve the efficiency of the initial estimator. For example, ${\widehat{\tau }}_{\text{reg},2\&\text{IPW}}$ indicates the initial estimator is the regression imputation estimator and the error-prone estimator is the IPW estimator. We compare the proposed estimators with the initial estimators in terms of percentages of reduction of mean squared errors, defined as $\{1-\text{MSE}({\widehat{\tau }}_{\text{method},2\&\text{methods}})/\text{MSE}({\widehat{\tau }}_{\text{method},2})\}\times \text{100}\%$. To demonstrate the robustness of the proposed estimator against misspecification of the imputation model, we consider the multiple imputation (MI, Rubin 1987) estimator, denoted by ${\widehat{\tau }}_{\text{mi}}$, which uses a regression model of U given (A, X, Y) for imputation. We implement MI using the “mice” package in R with m = 10.

Based on a point estimate $\widehat{\tau }$ and a variance estimate $\widehat{v}$ obtained by the asymptotic variance formula or the bootstrap method described in Section 3.5, we construct a Wald-type 95% confidence interval $(\widehat{\tau }-z_{0.975}{\widehat{v}}^{1/2},\widehat{\tau }+z_{0.975}{\widehat{v}}^{1/2})$, where $z_{0.975}$ is the 97.5% quantile of the standard normal distribution. We further compare the variance estimators in terms of empirical coverage rates.

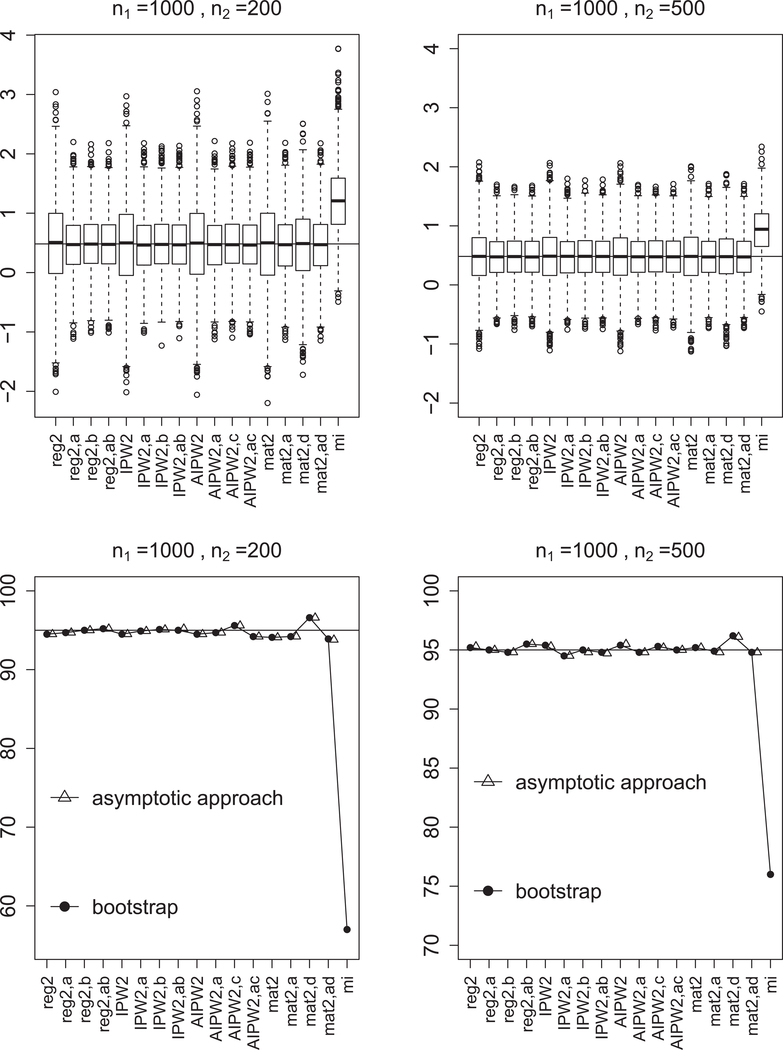
Figure 1 shows the simulation results over 2000 Monte Carlo samples for (n₁, n₂) = (1000,200) and (n₁, n₂) = (1000,500). The multiple imputation estimator is biased due to the misspecification of the imputation model. In all scenarios, the proposed estimators are unbiased and improve the initial estimators. Using the error-prone estimator of the same type of the initial estimator achieves a substantial efficiency gain, and the efficiency gain from incorporating additional error-prone estimator is not significantly important. Because of the practical simplicity, we recommend using the same type of error-prone estimator to improve the efficiency of the initial estimator. Confidence intervals constructed from the asymptotic variance formula and the bootstrap method work well, in the sense that the empirical coverage rate of the confidence intervals is close to the nominal coverage rate. In our settings, the matching estimator has the smallest efficiency gain among all types of estimators.

Figure 1.

Simulation results of point estimates (top panels) and coverage rates (bottom panels): the subscripts “a,” “b,” “c,” and “d” stand for methods “reg,” “IPW,” “AIPW,” and “mat,” respectively, “reg2” is ${\widehat{\tau }}_{\text{reg},2}$ “reg2,method” is ${\widehat{\tau }}_{\text{reg},2\&\text{method}}$, other notation is defined similarly, and “mi” is ${\widehat{\tau }}_{\text{mi}}$

6. Application

We present an analysis to evaluate the effect of chronic obstructive pulmonary disease (COPD) on the development of herpes zoster (HZ). COPD is a chronic inflammatory lung disease that causes obstructed airflow from the lungs, which can cause systematic inflammation and dysregulate a patient’s immune function. The hypothesis is that people with COPD are at increased risk of developing HZ. Yang et al. (2011) find a positive association between COPD and development of HZ; however, they do not control for important counfounders between COPD and HZ, for example, cigarette smoking and alcohol consumption.

We analyze the main data from the 2005 Longitudinal Health Insurance Database (LHID, Yang et al. 2011) and the validation data from the 2005 National Health Interview Survey conducted by the National Health Research Institute and the Bureau of Health Promotion in Taiwan (Lin and Chen 2014). The 2005 LHID consist of 42,430 subjects followed from the date of cohort entry on January 1, 2004 until the development of HZ or December 31, 2006, whichever came first. Among those, there are 8,486 subjects with COPD, denoted by A = 1, and 33,944 subjects without COPD, denoted by A = 0. The outcome Y was the development of HZ during follow up (1, having HZ and 0, not having HZ). The observed prevalence of HZ among COPD and non-COPD subjects are 3.7% and 2.2% in the main data and 2.5% and 0.8% in the validation data.

The confounders X available from the main data were age, sex, diabetes mellitus, hypertension, coronary artery disease, chronic liver disease, autoimmune disease, and cancer. However, important confounders U, including cigarette smoking and alcohol consumption, were not available. The validation data ${\mathcal{O}}_2$ use the same inclusion criteria as in the main study and consist of 1,148 subjects who were comparable to the subjects in the main data. Among those, 244 subjects were diagnosed of COPD, and 904 subjects were not. In addition to all variables available from the main data, cigarette smoking and alcohol consumption were measured. In our formulation, the main data ${\mathcal{O}}_1$ combine the LHID data and the validation data. Table 4 in Lin and Chen (2014) shows summary statistics on demographic characteristics and comorbid disorders for COPD and Non-COPD subjects in the main and validation data. Because the common covariates in the main and validation data are comparable, it is reasonable to assume that the validation sample is a simple random sample from the main data. Moreover, the difference in distributions of alcohol consumption between COPD and non-COPD subjects is not statistical significant in the validation data. But, the COPD subjects tended to have higher cumulative smoking rates than the non-COPD subjects in the validation data.

We obtain the initial estimators applied solely to the validation data and the proposed estimators applied to both data. As suggested by the simulation in Section 5, we use the same type of the error-prone estimator as the initial estimator. Following Stürmer et al. (2005) and Lin and Chen (2014), we use the propensity score to accommodate the high-dimensional confounders. Specifically, we fit logistic regression models for the propensity score e(X, U; α) and the error-prone propensity score $e(X;\gamma )$ based on $\{(A_j,X_j,U_j):j\in {\mathcal{S}}_2\}$ and $\{(A_i,X_i):j\in {\mathcal{S}}_1\}$, respectively. We fit logistic regression models for the outcome mean function μ_a(X, U) based on a linear predictor ${\{1,e(X,U;\widehat{\alpha })\}}^{\text{T}}{\beta }_a$, and for ${\mu }_a(X)$ based on a linear predictor ${\{1,e(X;\widehat{\gamma })\}}^{\text{T}}{\eta }_a$, for a = 0, 1.

We first estimate the ACE τ. Table 1 shows the results for the average COPD effect on the development of HZ. We find no big differences in the point estimates between our proposed estimators and the corresponding initial estimators, but large reductions in the estimated standard errors of the proposed estimators. As a result, all 95% confidence intervals based on the initial estimators include 0, but the 95% confidence intervals based on the proposed estimators do not include 0, except for ${\widehat{\tau }}_{\text{mat}2\text{\&mat}}$. As demonstrated by the simulation in Section 5, the variance reduction by utilizing the main data is the smallest for the matching estimator. From the results, on average, COPD increases the percentage of developing HZ by 1.55%.

Table 1.

Point estimate, bootstrapped standard error and 95%Wald-type confidence interval

	Est	SE	95% CI		Est	SE	95% CI
${\widehat{\tau }}_{\text{reg},2}$	0.0178	0.0112	(−0.0047, 0.0402)	${\widehat{\tau }}_{\text{reg},2\&\text{reg}}$	0.0155	0.0023	(0.0109, 0.0200)
${\widehat{\tau }}_{\text{IPW},2}$	0.0175	0.0111	(−0.0048, 0.0398)	${\widehat{\tau }}_{\text{IPW},2\text{\&IPW}}$	0.0155	0.0024	(0.0108, 0.0202)
${\widehat{\tau }}_{\text{AIPW},2}$	0.0179	0.0111	(−0.0044, 0.0402)	${\widehat{\tau }}_{\text{AIPW},2\&\text{AIPW}}$	0.0156	0.0024	(0.0109, 0.0203)
${\widehat{\tau }}_{\text{mat},2}$	0.0077	0.0092	(−0.0106, 0.021)	${\widehat{\tau }}_{\text{mat},2\&\text{mat}}$	0.0079	0.0053	(−0.0027, 0.0184)

We also estimate the log of the causal risk ratio of HZ with COPD. The initial IPW estimate from the validation data is log ${\widehat{\text{CRR}}}_{\text{IPW},2}=1.10$ (95% confidence interval: 0.02, 2.18). In contrast, the proposed estimate by using the error-prone IPW estimators is log ${\widehat{\text{CRR}}}_{\text{IPW},2\text{\&IPW}}=0.57$ (95% confidence interval: 0.41, 0.72), which is much more accurate than the initial IPW estimate.

7. Relaxing Assumption 1

In previous sections, we invoked Assumption 1 that ${\mathcal{S}}_2$ is a random sample from ${\mathcal{S}}_1$. We now relax this assumption and link our framework to existing methods for missing data. Let I_i be the indicator of selecting unit i into the validation data, that is, I_i = 1 if i ∈ ${\mathcal{S}}_2$ and I_i = 0 if $i\notin {\mathcal{S}}_2$. Alternatively, I_i can be viewed as the missingness indicator of U_i. Under Assumption 1, $I⫫(A,X,U,Y)$; that is, U is missing completely at random. We now relax it to $I⫫U|(A,X,Y)$, that is, U is missing at random. In this case, the selection of ${\mathcal{S}}_2$ from ${\mathcal{S}}_1$ can depend on a probability design, which is common in observational studies, for example, an outcome-dependent two-phase sampling (Breslow, McNeney, and Wellner 2003; Wang et al. 2009).

We assume that each unit in the main data is subjected to an independent Bernoulli trial which determines whether the unit is selected into the validation data. For simplicity, we further assume that the inclusion probability $P(I=1|A,X,U,Y)=P(I=1|A,X,Y)\equiv \pi (A,X,Y)$ is known as in two-phase sampling. Otherwise, we need to fit a model for the missing data indicator I given (A, X, Y). We summarize the above in the following assumption.

Assumption 6.

$\{(I_i,A_i,X_i,U_i,Y_i):i\in {\mathcal{S}}_1\}$ are IID with $I⫫U|(A,X,Y).{\mathcal{S}}_2$ is selected from ${\mathcal{S}}_1$ with a known inclusion probability $\pi (A,X,Y)>0$.

In what follows, we use π for π(A, X, Y) and π_j for π(A_j, X_j, Y_j) for shorthand. Because of Assumption 6, we drop the indices i and j in the expectations, covariances, and variances, which are taken with respect to both the sampling and superpopulation models.

7.1. RAL estimators

For the illustration of RAL estimators, we focus on the AIPW estimator of the ACE τ, because the regression imputation and inverse probability weighting estimators are its special cases. Let $\widehat{\alpha }$ and ${\widehat{\beta }}_a$ solve the weighted estimating equations ${\sum }_{j\in {\mathcal{S}}_2}{\pi }_j^{-1}S(A_j,X_j,U_j;\alpha )=0$ and ${\sum }_{j\in {\mathcal{S}}_2}{\pi }_j^{-1}{S}_a(A_j,X_j,U_j,Y_j;{\beta }_a)=0$, and let ${\alpha }^{*}$ and ${\beta }_a^{*}$ satisfy $E\{S(A,X,U;{\alpha }^{*})\}=0$ and $E\{S_a(A,X,U,Y;{\beta }_a^{*})\}=0$. Under suitable regularity condition, $\widehat{\alpha }\to {\alpha }^{*}$ and ${\widehat{\beta }}_a\to {\beta }_a^{*}$ in probability, for a = 0, 1. Let the initial estimator for τ be the Hajek-type estimator (Hájek 1971):

$${\widehat{\tau }}_2=\frac{{\sum }_{j\in {\mathcal{S}}_2}{\pi }_j^{-1}{\widehat{\tau }}_{\text{AIPW},2,j}}{{\sum }_{j\in {\mathcal{S}}_2}{\pi }_j^{-1}},$$ (22)

where ${\widehat{\tau }}_{\text{AIPW},2,j}$ has the same form as (2). Under regularity conditions, Assumption 4 or 5, and Assumption 6, we show in the supplementary material that

$${\widehat{\tau }}_2-\tau \cong n_1^{-1}\sum _{j\in {\mathcal{S}}_1}{\pi }_j^{-1}{I}_j\psi (A_j,X_j,U_j,Y_j),$$ (23)

where $\psi (A,X,U,Y)$ is given by (11). Because $\{{\pi }_j^{-1}{I}_j\psi (A_j,X_j,U_j,Y_j):j\in {\mathcal{S}}_1\}$ are IID with mean 0, ${\widehat{\tau }}_2$ is consistent for τ.

Similarly, let ${\widehat{\gamma }}_d$ and ${\widehat{\eta }}_{d,a}$ solve the weighted estimating equation ${\sum }_{j\in {\mathcal{S}}_d}{\pi }_j^{-1}S(A_j,X_j;\gamma )=0$ and ${\sum }_{j\in {\mathcal{S}}_d}{\pi }_j^{-1}{S}_a(A_j,X_j,Y_j;{\eta }_a)=0$, and let ${\gamma }^{*}$ and ${\eta }_a^{*}$ satisfy $E\{S(A_j,X_j;{\gamma }^{*})\}=0$ and $E\{S_a(A_j,X_j,Y_j;{\eta }_a^{*})\}=0$. Under suitable regularity condition, ${\widehat{\gamma }}_d\to {\gamma }^{*}\text{and}{\widehat{\eta }}_{d,a}\to {\eta }_a^{*}$ in probability, for a = 0, 1 and d = 1, 2. Let the error-prone estimators be

$${\widehat{\tau }}_{1,\text{ep}}=n_1^{-1}\sum _{i\in {\mathcal{S}}_1}{\widehat{\tau }}_{\text{AIPW},1,\text{ep},i},{\widehat{\tau }}_{2,\text{ep}}=\frac{\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}{\widehat{\tau }}_{\text{AIPW},2,\text{ep},j}}{\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}},$$ (24)

where ${\widehat{\tau }}_{\text{AIPW},d,\text{ep},j}$ has the same form as (S8) in the supplementary material. Following a similar derivation for (23), we have

$$\begin{gathered} {\widehat{\tau }}_{1,\text{ep}}-{\tau }_{\text{ep}}\cong n_1^{-1}\sum _{i\in {\mathcal{S}}_1}\varphi (A_i,X_i,Y_i), \\ {\widehat{\tau }}_{2,\text{ep}}-{\tau }_{\text{ep}}\cong n_1^{-1}\sum _{j\in {\mathcal{S}}_1}{\pi }_j^{-1}{I}_j\varphi (A_j,X_j,Y_j), \end{gathered}$$ (25)

where $\varphi (A,X,Y)$ is given by (S9) in the supplementary material. Because both $\{\varphi (A_i,X_i,Y_i):i\in {\mathcal{S}}_1\}$ and $\{{\pi }_j^{-1}{I}_j\varphi \left(A_j,X_j,Y_j\right):j\in {\mathcal{S}}_1\}$ are IID with mean 0, ${\widehat{\tau }}_{1,\text{ep}}\text{and}{\widehat{\tau }}_{2,\text{ep}}$ are consistent for τ_ep.

Theorem 4.

Under certain regularity conditions, (4) holds for the Hajek-type estimators (22) and (24), where $\rho ={\text{plim}}_{n_2\to \infty }(n_2/n_1),v_2=\rho \times \mathrm{var}\{{\pi }^{-1}I\psi (A,X,U,Y)\},\mathrm{\Gamma }=\rho \times \mathrm{cov}\{{\pi }^{-1}I\psi (A,X,U,Y),({\pi }^{-1}I-1)\varphi (A,X,Y)\}\text{and}V=\rho \times \mathrm{var}\{({\pi }^{-1}I-1)\varphi (A,X,Y)\}$.

Similar to Section 3.3, we can construct a consistent variance estimator for $\widehat{\tau }$ by replacing the variances and covariance in Theorem 4 with their sample analogs.

7.2. Matching Estimators

Recall that ${\mathcal{J}}_{d,V,l}$ is the index set of matches for unit l based on data ${\mathcal{O}}_d$ and the matching variable V, which can be (X, U) or X. Define ${\delta }_{d,V,(j,l)}=1\text{if}j\in {\mathcal{J}}_{d,V,l}\text{and}{\delta }_{d,V,(j,l)}=0$ otherwise. Now, we denote $K_{d,V,j}={\pi }_j{\sum }_{l\in {\mathcal{S}}_d}{\pi }_l^{-1}1\{A_l=1-A_j\}{\delta }_{d,V,(j,l)}$ as the weighted number of times that unit j is used as a match. If π_j is a constant for all j ∈ ${\mathcal{S}}_d$, then $K_{d,V,j}$ reduces to the number of times that unit j is used as a match defined in Section 3.1, which justifies using the same notation as before.

Let the initial matching estimator for τ be the Hajek-type estimator:

$$\begin{gathered} {\widehat{\tau }}_{\text{mat},2}^{(0)}={\left(\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}\right)}^{-1} \\ \times \sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}(2A_j-1)\left(Y_j-M^{-1}\sum _{l\in {\mathcal{J}}_{2,(X,U),j}}{Y}_l\right) \\ ={\left(\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}\right)}^{-1} \\ \times \sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}(2A_j-1)\left\{1+M^{-1}{K}_{2,(X,U),j}\right\}{Y}_j. \end{gathered}$$

Let a bias-corrected matching estimator be

$${\widehat{\tau }}_{\text{mat},2}={\widehat{\tau }}_{\text{mat},2}^{(0)}-n_1^{-1/2}{\widehat{B}}_2,$$ (26)

where

$$\begin{gathered} {\widehat{B}}_2=n_1^{-1/2}\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}(2A_j-1) \\ \times \left[M^{-1}\sum _{l\in {\mathcal{J}}_{2,(X,U),j}}\left\{{\widehat{\mu }}_{1-A_j}(X_j,U_j)-{\widehat{\mu }}_{1-A_j}(X_l,U_l)\right\}\right], \end{gathered}$$

We show in the supplementary material that

$${\widehat{\tau }}_{\text{mat},2}-\tau \cong n_1^{-1}\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}{\psi }_{\text{mat},j},$$ (27)

where ${\psi }_{\text{mat},j}$ is defined in (13) with the new definition of $K_{2,(X,U),j}$.

Similarly, we obtain error-prone matching estimators and express them as

$$\begin{gathered} {\widehat{\tau }}_{\text{mat},1,\text{ep}}-{\tau }_{\text{ep}}\cong n_1^{-1}\sum _{j\in {\mathcal{S}}_1}{\varphi }_{\text{mat},1,j}, \\ {\widehat{\tau }}_{\text{mat},2,\text{ep}}-{\tau }_{\text{ep}}\cong n_1^{-1}\sum _{j\in {\mathcal{S}}_2}{\pi }_j^{-1}{\varphi }_{\text{mat},2,j}, \end{gathered}$$ (28)

where ${\varphi }_{\text{mat},d,j}$ is defined in (15) with the new definition of $K_{d,X,j}$.

From the above decompositions, ${\widehat{\tau }}_{\text{mat},2}$ is consistent for τ, and ${\widehat{\tau }}_{\text{mat},1,\text{ep}}-{\widehat{\tau }}_{\text{mat},2,\text{ep}}$ is consistent for 0.

Theorem 5.

Under certain regularity conditions, (4) holds for the estimators (26) and ${\widehat{\tau }}_{\text{mat},d,\text{ep}}(d=1,2)$, where $\rho ={\text{plim}}_{n_2\to \infty }(n_2/n_1)$,

$$\begin{gathered} v_2=\rho \times (E\left[\frac{1-\pi }{\pi }{\{\tau (X,U)-\tau \}}^2\right] \\ +\mathrm{plim}[n_1^{-1}\sum _{j\in {\mathcal{S}}_1}\frac{1-{\pi }_j}{{\pi }_j}{\left\{1+M^{-1}{K}_{2,(X,U),j}\right\}}^2 \\ {\sigma }_{A_j}^2(X_j,U_j)]), \end{gathered}$$

$$\begin{gathered} \mathrm{\Gamma }=\rho \times E[\frac{1-\pi }{\pi }\left\{{\mu }_1(X,U)-{\mu }_0(X,U)-\tau \right\} \\ \left\{{\mu }_1(X)-{\mu }_0(X)-{\tau }_{ep}\right\}] \\ +\rho \times \mathrm{plim}[n_1^{-1}\sum _{j\in {\mathcal{S}}_1}\frac{1-{\pi }_j}{{\pi }_j}\left\{1+M^{-1}{K}_{2,(X,U),j}\right\} \\ (1+M^{-1}{K}_{2,X,j}){\sigma }_{A_j}^2(X_j,U_j)] \end{gathered}$$

$$\begin{gathered} V=\rho \times E\left[\frac{1-\pi }{\pi }{\left\{{\mu }_1(X)-{\mu }_0(X)-{\tau }_{\text{ep}}\right\}}^2\right] \\ +\rho \times \mathrm{plim}\left[n_1^{-1}\sum _{j\in S_1}\frac{1-{\pi }_j}{{\pi }_j}{(1+M^{-1}{K}_{1,X,j})}^2{\sigma }_{A_j}^2(X_j)\right]. \end{gathered}$$

We can construct variance estimators based on the formulas in Theorem 5. However, this again involves estimating the conditional variances ${\sigma }_0^2(x)$ and ${\sigma }_1^2(x)$. We recommend using the bootstrap variance estimator in the next subsection.

7.3. A Bootstrap Variance Estimation Procedure

The asymptotic linear forms (23), (25), (27), and (28) are useful for the bootstrap variance estimation. For b = 1,...,B, we construct the bootstrap replicates as follows:

Step 1. Sample n₁ units from ${\mathcal{S}}_1$ with replacement as ${\mathcal{S}}_1^{*(b)}$.

Step 2. Compute the bootstrap replicates of ${\widehat{\tau }}_2-\tau$ and ${\widehat{\tau }}_{d,\text{ep}}-{\tau }_{\text{ep}}$ as

$$\begin{gathered} {\widehat{\tau }}_2^{(b)}-{\widehat{\tau }}_2=n_1^{-1}\sum _{i\in {\mathcal{S}}_1^{*(b)}}{\pi }_i^{-1}{I}_i{\widehat{\psi }}_i, \\ {\widehat{\tau }}_{1,\text{ep}}^{(b)}-{\widehat{\tau }}_{1,\text{ep}}=n_1^{-1}\sum _{i\in {\mathcal{S}}_1^{*(b)}}{\widehat{\varphi }}_{1,i}, \\ {\widehat{\tau }}_{2,\text{ep}}^{(b)}-{\widehat{\tau }}_{2,\text{ep}}=n_1^{-1}\sum _{i\in {\mathcal{S}}_1^{*(b)}}{\pi }_i^{-1}{I}_i{\widehat{\varphi }}_{2,i}, \end{gathered}$$

where $({\widehat{\psi }}_i,{\widehat{\varphi }}_{d,i})$ are the estimated versions of $\left({\psi }_i,{\varphi }_i\right)$ from ${\mathcal{O}}_d$ d = 1, 2).

We estimate Γ, V and v₂ by (16)–(18) based on the above bootstrap replicates, and var $(\widehat{\tau })$ by (7), that is, $\widehat{v}={\widehat{v}}_2-{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}\widehat{\mathrm{\Gamma }}$.

Theorem 6.

Under certain regularity conditions, $(\widehat{\mathrm{\Gamma }},\widehat{V},{\widehat{v}}_2,\widehat{v})$ are consistent for $\left\{\mathrm{\Gamma },V,\mathrm{var}({\widehat{\tau }}_2),\mathrm{var}(\widehat{\tau })\right\}$.

For RAL estimators, we can also use the classical nonparametric bootstrap based on resampling the IID observations $\{\left(I_i,A_i,X_i,U_i,Y_i\right):i\in {\mathcal{S}}_1\}$ and repeating the analysis as for the original data. The above bootstrap procedure based on resampling the linear forms are particularly useful for the matching estimator.

7.4. Connection With Missing Data

As a final remark, we express the proposed estimator in a linear form that has appeared in the missing data literature.

Proposition 2.

Under certain regularity conditions and Assumption 6, $\widehat{\tau }$ has an asymptotic linear form

$$\begin{gathered} n_1^{1/2}(\widehat{\tau }-\tau )=n_1^{-1/2}\sum _{i\in {\mathcal{S}}_1}\left\{\frac{I_i}{{\pi }_i}{\psi }_i-\left(\frac{I_i}{{\pi }_i}-1\right)\mathrm{\Gamma }{V}^{-1}{\varphi }_i\right\} \\ \text{+}{o}_P(1) \end{gathered}$$ (29)

where ${\psi }_i$ is $\psi \left(A_i,X_i,U_i,Y_i\right)$ for RAL estimators and ${\psi }_{\text{mat},i}$ for the matching estimator, and a similar definition applies to ${\varphi }_i$. Under Assumption 1, π_i ≡ ρ.

Expression (29) is within a class of estimators in the missing data literature with the form

$$\begin{gathered} n_1^{1/2}(\widehat{\tau }-\tau )=n_1^{-1/2} \\ \sum _{i\in {\mathcal{S}}_1}\left\{\frac{I_i}{{\pi }_i}s\left(A_i,X_i,U_i,Y_i\right)-\left(\frac{I_i}{{\pi }_i}-1\right)\kappa \left(A_i,X_i,Y_i\right)\right\}+o_P(1), \end{gathered}$$ (30)

where π = E(I | A, X, U, Y), s(A, X, U, Y) satisfies E{s(A, X, U, Y)} = 0, and s(A, X, U, Y) and $\kappa (A,X,Y)$ are square integrable. Given $s(A,X,U,Y)$ the optimal choice of $\kappa (A,X,Y)\text{is}{\kappa }_{\text{opt}}(A,X,Y)=E\{s(A,X,U,Y)|A,X,Y\}$, which minimizes the asymptotic variance of (30) (Robins, Rotnitzky, and Zhao 1994; Wang et al. 2009). However, K_opt(A, X, Y) requires a correct specification of the missing data model $f(U|A,X,Y)$. In our approach, instead of specifying the missing data model, we specify the error-prone estimators and utilize an estimator that is consistent for zero to improve the efficiency of the initial estimator. This is more attractive and closer to empirical practice than calculating K_opt(A, X, Y), because practitioners only need to apply their favorite estimators to the main and validation data using existing software. See also Chen and Chen (2000) for a similar discussion in the regression context under Assumption 1.

8. Discussion

Depending on the roles in statistical inference, there are two types of big data: one with large-sample sizes and the other with richer covariates. In our discussion, the main observational data have a larger sample size, and the validation observational data have more covariates. Although some counterexamples exist (Pearl 2009, 2010; Ding and Miratrix 2015; Ding, Vanderweele, and Robins 2017), it is more reliable to draw causal inference from the validation data. The proposed strategy is applicable even the number of covariates is high in the validation data. In this case, we can consider ${\widehat{\tau }}_2$ to be the double machine learning estimators (Chernozhukov et al. 2018) that use flexible machine learning methods for estimating regression and propensity score functions while retain the property in (4). Our framework allows for more efficient estimators of the causal effects by further combining information in the main data, without imposing any parametric models for the partially observed covariates. Coupled with the bootstrap, our estimators require only software implementations of standard estimators, and thus are attractive for practitioners who want to combine multiple observational data sources.

The key insight is to leverage an estimator of zero to improve the efficiency of the initial estimator. If a certain feature is transportable across datasets (Bareinboim and Pearl 2016), we can construct a consistent estimator of zero. We have shown that if the validation data are simple random samples from the main data, the distribution of (A, X, Y) is transportable from the validation data to the main data. We then construct a consistent estimator of zero by taking the difference of the estimators based on (A, X, Y) from the two datasets. In the presence of heterogeneity between two data sources, the transportability of the whole distribution of (A, X, Y) can be stringent. However, if we are willing to assume the conditional distribution of Y given (A, X) is transportable, we can then take the error prone estimators to be the regression coefficients of Y on (A, X) from the two datasets. As suggested by one of the reviewers, if the subgroups of two samples are comparable, we can construct the error prone estimators based on the subgroups. Similarly, this construction of error prone estimators can adapt to different transportability assumptions based on the subject matter knowledge.

In the worst case, the heterogeneity is intrinsic between the two samples, and we cannot construct two error prone estimators with the same probability limit. We can still conduct a sensitivity analysis combining two data. Instead of (4), we assume

$$n_2^{1/2}\left(\begin{array}{c}{\widehat{\tau }}_2-\tau \\ {\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,\text{ep}}-\delta \end{array}\right)\to \mathcal{N}\left\{0_{L+1},\left(\begin{array}{cc}{v}_2& {\mathrm{\Gamma }}^{\text{T}}\\ \mathrm{\Gamma }& V\end{array}\right)\right\},$$ (31)

where δ is the sensitivity parameter, quantifying the systematic difference between ${\widehat{\tau }}_{2,\text{ep}}$ and ${\widehat{\tau }}_{1,\text{ep}}$. The adjusted estimator becomes ${\widehat{\tau }}_{\text{adj}}(\delta )={\widehat{\tau }}_2-{\widehat{\mathrm{\Gamma }}}^{\text{T}}{\widehat{V}}^{-1}({\widehat{\tau }}_{2,\text{ep}}-{\widehat{\tau }}_{1,e\text{p}}-\delta )$. With different values of δ, the estimator ${\widehat{\tau }}_{\text{adj}}(\delta )$ can provide valuable insight on the impact of the heterogeneity of the two data, allowing an investigator to assess the extent to which the heterogeneity may alter causal inferences.