Quantitative T₂ Mapping using Accelerated 3D Stack-of-Spiral Gradient Echo Readout

Abstract

Purpose:

To develop a rapid T₂ mapping protocol using optimized spiral acquisition, accelerated reconstruction, and model fitting.

Materials and Methods:

A T₂-prepared stack-of-spiral gradient echo (GRE) pulse sequence was applied. A model-based approach joined with compressed sensing was compared with the two methods applied separately for accelerated reconstruction and T₂ mapping. A 2-parameter-weighted fitting method was compared with 2- or 3-parameter models for accurate T₂ estimation under the influences of noise and B₁ inhomogeneity. The performance was evaluated using both digital phantoms and healthy volunteers. Mitigating partial voluming with cerebrospinal fluid (CSF) was also tested.

Results:

Simulations demonstrates that the 2-parameter-weighted fitting approach was robust to a large range of B₁ scales and SNR levels. With an in-plane acceleration factor of 5, the model-based compressed sensing-incorporated method yielded around 8% normalized errors compared to references. The T₂ estimation with and without CSF nulling was consistent with literature values.

Conclusion:

This work demonstrated the feasibility of a T₂ quantification technique with 3D high-resolution and whole-brain coverage in 2–3 min. The proposed iterative reconstruction method, which utilized the model consistency, data consistency and spatial sparsity jointly, provided reasonable T₂ estimation. The technique also allowed mitigation of CSF partial volume effect.

1. Introduction

Quantitative relaxometry is a desired MRI tool for longitudinal or cross-sectional characterization of lesion structures [1,2]. Conventional T₂ mapping methods generate and reconstruct T₂ weighted images frame-by-frame followed by voxel-wise fitting. The associated long acquisition time hinders its practical utility, especially for applications that require 3D high spatial resolution and broad volume coverage.

Various rapid imaging techniques have been adapted to T₂ mapping experiments. Parallel imaging exploits the data redundancy generated by multiple receiver coils to recover missing k-space samples [3,4]. With the development of compressed sensing (CS) [5], several constrained reconstruction methods have been developed for acceleration and applied to parameter mapping [6–14]. Block et al. proposed iterative reconstruction using a total variation (TV) constraint on radial acquisition [6]; Lustig et al. applied sparsifying transform of images acquired with incoherent sampling for acceleration [7]. In addition to the undersampling of spatial characteristics, redundancy in the temporal [8] or parametric [9–12] dimensions of image series has been explored as well. Some methods combined the aforementioned constraints [13,14]. Another promising strategy for fast parameter mapping is model-based reconstruction, which incorporated the underlying signal model as prior knowledge in an iterative reconstruction to estimate parameter maps directly from k-space data [15–21]. Advanced reconstruction imposing subspace constraints has also been demonstrated for parameter mapping [22–24].

Majority of these studies applied 2D multi-slice acquisition with Cartesian trajectories [9,10,13,15,18], which achieved up to 5-fold acceleration. 3D acquisition typically uses the smaller slice thickness without gaps and even isotropic resolution, which allows visualization of small lesions in any reformatted orientation. 3D radial trajectory has been adopted for T₁ and/or T₂ estimation with undersampling [25,26]. Spiral trajectory offers the great advantages of high acquisition efficiency [27] and accelerated reconstruction [28], as well as robustness to motion artifacts [29]. 3D T₂ mapping has been performed using pulse sequences based on gradient echo (GRE) steady state conditions [30], multi-echo fast spin echo (FSE) [25], or T₂ magnetization preparation followed by GRE [26,31–37] or FSE [38,39].

During the last decade or so, brain T₂ mapping has largely been applied with advanced 2D acquisitions [9,12–16,18,23,40,41] and few with 3D methods [25,30,37]. In the clinical setting, multi-parametric MRI would be straightforward for corregistration when different magnetization preparation modules are appended with the same acquisition readout. In this work, we chose a T₂-prepared GRE sequence combined with 3D stack-of-spiral acquisition for T₂ mapping with whole-brain coverage and high spatial resolution. Different fitting models, k-space sampling strategies, and reconstruction techniques were evaluated in both numerical simulation and brain scans for optimum performance. Suppression of cerebrospinal fluid (CSF) signal to reduce its partial volume effect was also tested for brain T₂ quantification.

2. Materials and Methods

2.1. Simulation of T₂ Fitting

All numerical simulations were implemented in MATLAB 2019B (Mathworks, Natick, MA, USA). To investigate the effects of various B₁ offsets on the 90⁰/−90⁰ hard pulses used at the beginning and end of the T₂ preparation module (Appendix) as well as different noise levels, numerical simulations were conducted to study the performance of three non-linear T₂-fitting models: 1) classic 2-paramter fitting to a mono-exponential decay; 2) 2-parameter-weighted fitting with each signal intensity as the weighting; and 3) 3-paramter fitting with an additional constant to account for the effect of incorrect B₁ setting.

Typically, the longitudinal magnetization after a T₂ preparation module follows an exponential decay with respect to its duration (TE_prep):

$$y=A_0{e}^{-{\text{TE}}_{\text{prep}}/T_2},$$ (1)

Where A₀ is the longitudinal magnetization prior to the T₂ preparation. This is a 2-parameter model where only two parameters, A and T₂ are fitted, with several TE_prep fixed as a vector ${\overline{\text{TE}}}_{prep}$, and corresponding signal obtained as a vector $\overline{\text{y}}$. The classic 2-parameter fitting makes use of the least-square-fitting with a cost function of:

$$\underset{A_0,T_2}{\min }{\Vert \overline{\text{y}}-A_0{e}^{-\overline{\text{TE}}prep/T_2}\Vert }_2^2$$ (2)

Alternatively the 2-parameter-weighted fitting weights the least-square-fitting with signal intensity for different TE_prep, resulting in a modified cost function:

$$\underset{A_0,T_2}{\min }{\Vert \text{diag}(\overline{\text{y}})\left(\overline{\text{y}}-A_0{e}^{-\overline{\text{TE}}prep/T_2}\right)\Vert }_2^2$$ (3)

where $\text{diag}(\overline{\text{y}})$ reshapes the vector $\overline{\text{y}}$ to a diagonal matrix, which weights obtained signal $\overline{\text{y}}$ differently.

Considering B₁ inhomogeneity (Eq. (A3) in the Appendix), a constant ε is added to the exponential decay to make up a 3-parameter model:

$$\text{y}=A_0{e}^{-{\overline{\text{TE}}}_{prep/T_2}}+\epsilon$$ (4)

Therefore, the cost functions for the 3-parameter fitting model can be formulated as:

$$\underset{A_0,T_2}{\min }{\Vert \overline{\text{y}}-\left(A_0\left(e^{-\overline{\text{TE}}prep/T_2}+\epsilon \right)\right)\Vert }_2^2$$ (5)

For all three fitting models, Levenberg–Marquardt algorithm [42] was used to solve the non-linear least squares problems. The voxel-wise fitting iterations were calculated in a matrix form to avoid the slow for-loops in MATLAB. T₂ values were set from 40 ms to 200 ms in intervals of 10 ms and the T₁ value was set as 1000 ms. Their signal intensities at the end of different TE_prep, [20, 40, 80, 120, 160] ms, with B₁+ = 1.0 and 0.8, were calculated based on Eq. (A3) in the Appendix. With signal-to-noise ratio (SNR) of the data at TE_prep = 20 ms increasing from 10 to 50 in intervals of 5, random noise with normal distribution were added to the signal of various T₂ weighting. For each noise level, the data generation was repeated 10000 times through a Monte Carlo simulation in order to compute the mean and standard deviation (std) of the estimated T₂. The mean values of the error percentages of the fitted parameters with respect to the input values were analyzed as an indicator of accuracy of each fitting approach. The corresponding coefficient of variation values (CoV = std / mean) were measured as an indicator of precision.

2.2. Simulation of k-space Sampling and Reconstruction

To evaluate the performance of different k-space sampling and reconstruction methods used in the in vivo experiments, a 2D digital phantom (192×192) with four T₂ values, [80, 100,150, 200] ms, and a uniform T₁ value (1000 ms) was adopted and the T₂ weighting was attained with five echo times (TEs), [20, 40, 80, 120, 160] ms, respectively.

2.3. k-Space Sampling

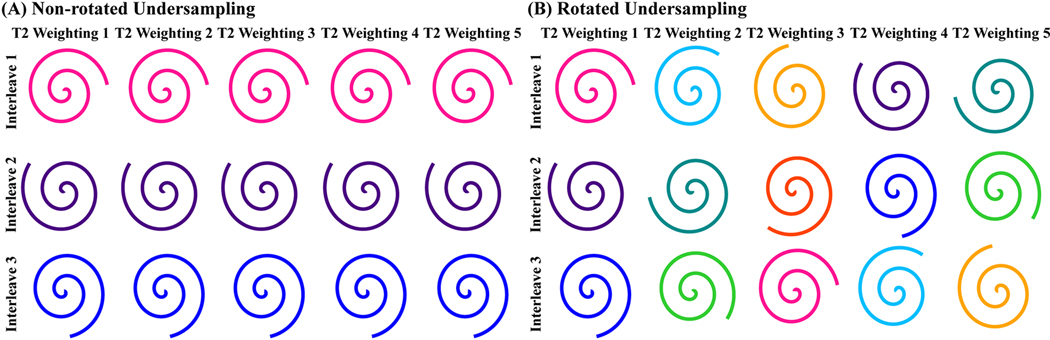
A 2D variable-density spiral trajectory [29,43] was applied to generate k-space data based on the Bloch equation simulation. Specific parameters for the sampling include: the central 15% k-space was fully sampled; the peripheral 15% k-space was sampled with a acceleration factor of 3; the the sampling density reduced linearly between central and peripheral 15% k-space; the readout duration of the spiral trajectory for each phase-encoding interleave was kept 10 ms to mitigate blurring due to off-resonance [44] and the T₂* decay [45] during the k-space sampling and the dwell time of the readout sampling was 4.3 μs; number of interleaves was 8 with acceleration factor of 2; 8 simulated coils were uniformly distributed around the digital phantom. Retrospective undersampling was performed for each TE by selecting a subset of three equally spaced interleaves (total acceleration factor of 5). For k-space with different TE_prep, both non-rotated and rotated undersampling schemes were tested, with the sampled spiral interleaves identical or being rotated with a fixed angle as between adjacent interleaves (360⁰ / 8 = 45⁰) (Figure 1).

Figure 1:

(A) Non-rotated retrospective undersampling scheme: the same interleaves selected for each T₂ preparation; (B) Rotated retrospective undersampling scheme: different interleaves selected for each T₂ preparation.

2.4. Reconstruction

For T₂ estimation, a model-based reconstruction method incorporating CS in spatial domain was applied, which can be formulated as:

$${\text{minimize}}_{\overline{\text{f}}}\parallel \text{E}\overline{\text{f}}-\text{d}{\parallel }_2^2+\lambda \parallel \text{s}(\tilde{\text{s}}(\text{f}))-\overline{\text{f}}{\parallel }_1+\alpha \text{TV}(\overline{\text{f}})$$ (6)

where E is the encoding matrix including the nonuniform Fourier transform and the complex coil sensitivity, $\overline{\text{f}}$ is the image series, d is the k-space data, S is the 2-parameter T₂ decay model (Eq. (1)), $\tilde{\text{S}}$ is the adjoint operator mapping image series to T₂ maps with 2-parameter-weighted fitting model (Eq. (3)), and TV is the in-plane spatial total variation [6]. ||·||₂ stands for the spatial l₂norm. ||·||₁ is the l₁-norm along parameter dimension, which was implemented to eliminate outliers in the T₂ fitting process [17]. Parameter λ balances the data consistency and the model consistency. Parameter α trades sparsity with data consistency, and specifically, if α = 0, the objective function degenerates to model-based reconstruction [17]. Fully sampled central k-space was used to obtain a low-resolution coil sensitivity map. The algorithm was implemented using a projected-gradient approach [46], with a projection designed to apply the model-consistency condition [17]. Data consistency, model consistency and spatial sparsity constraint were combined into a joint constrained problem and iteratively optimized with the maximum iteration number set to 60, which is empirically determined to ensure full convergence. The proposed method was compared with regular SENSE [47], CS SENSE [48] and model-based methods without CS constraint [17]. SENSE and CS SENSE were implemented by non-linear conjugate gradient algorithm [7] and the model-based methods was implemented using the projected-gradient approach described above. All reconstruction and fitting process were implemented in MATLAB 2019B (Mathworks, Natick, MA, USA).

2.5. In vivo Experiments

Experiments were performed on a 3T Philips Ingenia scanner (Philips Medical Systems, Best, The Netherlands) with a 32-channel head-only coil for signal reception. Four healthy volunteers (3 females and 1 male, 44–59 years old) were enrolled after providing informed consent in accordance with the Institutional Review Board guidelines.

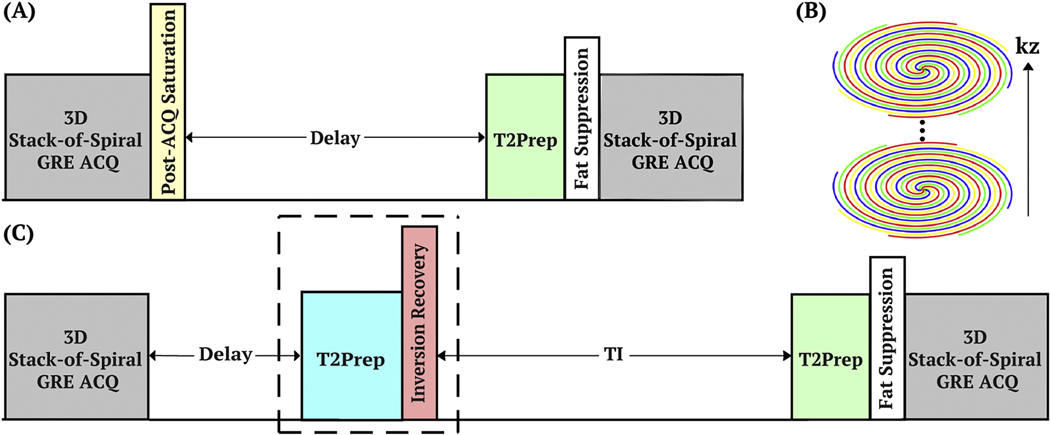
The pulse sequence diagram for T₂ mapping is shown in Figure 2A. A post-acquisition spatially selective saturation pulse train was applied with a fixed delay (1500 ms) to ensure the same longitudinal magnetization before each T₂ preparation module. The non-selective T₂ preparation pulse train starts with a hard pulse excitation (90°_x), followed by a series of composite refocusing pulses (90°_x180°_y90°_x) with an MLEV phase-cycling pattern [49] and then a flip-back pulse (90°_-x). In order to successively generate different T₂ contrasts with TE_prep = [20, 40, 80, 120, 160] ms, the number of refocusing pulses was chosen to be [2, 4, 8, 12, 16], respectively, with a constant inter-echo spacing of τ_CPMG = 10 ms [50]. Immediately following the T₂ preparation, a frequency-selective fat-suppression module was inserted before data acquisition.

Figure 2:

(A) Diagram of the pulse sequence with T₂-prepared gradient echo (GRE) readout for each T₂ weighting. (B) 3D stack-of-spiral trajectory with turbo direction applied along slice direction. (C) Diagram of the pulse sequence with a CSF nulling module (the dashed box) to remove the CSF partial volume effect. Abbreviations: acquisition (ACQ), T₂ preparation (T2Prep).

A GRE sequence, turbo-field-echo (TFE), with a train of low-flip-angle excitation pulses was applied with 3D segmented stack-of-spiral trajectory (Figure 2B) in the axial orientation. In addition to the variable-density spiral trajectory described in the simulation section (acceleration factor of 2), a fully sampled readout with a uniform density spiral trajectory (no acceleration) was acquired for reference. Readout duration of the fully sampled uniform density acquisition was identical to the variable-density case (10 ms) and 16 phase encoding interleaves were required to fill the k-space, indicating a net prospective acceleration factor of 2 (16 / 8) using variable-density spiral trajectory and a net acceleration factor of 5.3 (16 / 3) after retrospective undersampling (approximately 5-fold). Acquisition parameters: TR/TE/flip angle = 15 ms/1.2 ms/12°; the acquisition resolution was 1.2 mm³ isotropic and the reconstructed voxel size was 0.6 mm³ isotropic; field of view (FOV) = 220×220×96 mm³, slice oversampling = 1.25, number of acquired slices = 100; low-high profile order with TFE factor = 25 along the slice direction. Thus, each spiral interleave required four shots for the full encoding of the slice direction, and for the variable-density undersampled and uniform density fully sampled spiral trajectories, 8 and 16 spiral interleaves for in-plane encoding or 32 and 64 shots needed to be interleaved, respectively. With 2000 ms TFE shot interval and five separate T₂ preparations, total scan duration was 5.5 min and 11 min for the two datasets. Note that the undersampled acquisition with acceleration factor of 5 would only take 2.2 min. The reference T₂ map was fitted by the non-linear 2-parameter-weighted T₂ decay model using fully sampled data voxel by voxel. Singular value decomposition (SVD) was used to compress 32 channels to 8 virtual channels to mitigate computational burden in the reconstruction. Retrospective undersampling and reconstruction methods were the same as for simulation. And the 2-paramter-weighted fitting model was applied.

When CSF suppression is desired, an SNR-improved inversion recovery method can be implemented [51]. This CSF-suppression module (the dashed box in Figure 2C) utilized a T₂ preparation module (TE_prep = 300 ms) with double refocused hyperbolic tangent pulses (5.0 ms, tanh/tan, maximum amplitude of 575 Hz and a frequency sweep of 9 kHz). Since CSF has a long T₂ value (~1500 ms [52]), thus would be less affected by the prior T₂ weighting and inverted and nulled by the following inversion pulse with a delay TI = 1100 ms. The brain tissue with relatively short T₂ values were largely saturated after T₂ preparation and thus recovered with a higher longitudinal magnetization than experiencing inversion alone. Only variable-density spiral trajectory was used in the CSF-nulled sequence. With a 3000 ms TFE shot-interval, total scan time was 8 min and the acquisition of undersampling with acceleration factor of 5 would take 3.2 min.

2.6. Data Analysis

Quantitative evaluation was performed on simulation and in vivo experiments. To compare the performance of different reconstruction methods and retrospective undersampling schemes, the relative difference of T₂ maps to the reference values were computed in each voxel. Normalized root-mean-square-error (nRMSE) was calculated over the entire digital phantom for simulation. For in vivo experiments, CSF and nearby tissue were removed by masking areas of T₂ values longer than 200 ms. For results with CSF nulling, the mask was created by thresholding the intensity of the images of TE_prep = 20 ms. The nRMSE values were estimated from the segmented brain tissue as well as manually selected regions of interest (ROIs) of white matter and gray matter. To compare the pulse sequences with and without the CSF nulling module, estimated T₂ values and corresponding differences were reported in ROIs of frontal gray matter (FGM), frontal white matter (FWM), globus pallidus (GPA), occipital gray matter (OGM), occipital white matter (OWM), splenium, and thalamus.

3. Results

3.1. Simulation of T₂ Fitting

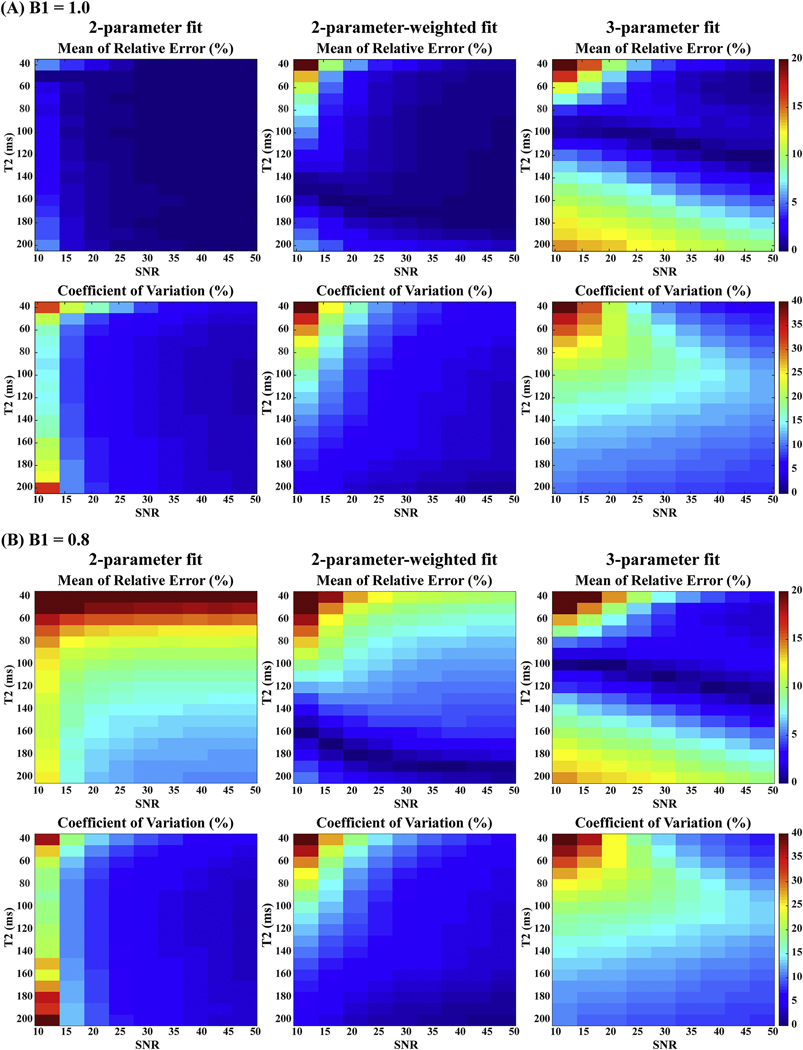
Figure 3 shows the mean of relative errors of estimated T₂ and the corresponding CoV (std / mean) using the prescribed T₂ preparation modules under different noise levels with three T₂ fitting approaches respectively. For each fitting, higher SNR invariably delivered more accurate and precise estimates as expected. When B₁ scale was ideal (B₁+ = 1.0), at the same SNR levels, the 2-parameter or 2-parameter-weighted fitting ensured distinct robustness than fitting with the 3-parameter model. The relative T₂ errors and CoV of the 2-parameter-weighted fitting were slightly higher than the results from the 2-parameter fitting, under 5% and 10% respectively for most cases. 3-parameter fitting was much more sensitive to noise with higher T₂ errors and CoV in most cases. When B₁ scale was with offset (B₁+ = 0.8), 2-parameter fitting was 15–20% overestimated for shorter T₂ values (40–80 ms), which indicated that 2-parameter fitting was most sensitive to B₁ inhomogeneities. In contrast, 2-parameter-weighted fitting reduced these relative errors largely to under 15%. The 3-parameter fitting yielded minimal sensitivity to B₁ inhomogeneities, with relative errors less than 5% when SNR was high, but was much more sensitive to noise. The 2-parameter-weighted fitting was thus chosen for its overall stable performance with various B₁ scales and noise levels.

Figure 3:

Simulation results of T₂ estimation using 2-parameter, 2-parameter-weighted, and 3parameter fitting models: the mean of relative errors (indicating accuracy) and coefficient of variation (indicating precision) of 10000 repetitions as a function of SNR using Monte Carlo simulation with (A) B₁+ = 1.0 and (B) B₁+ = 0.8. Compared to the other two fitting approaches, the 2-parameter-weighted fitting demonstrated a balanced robustness to different B₁ scales and noise levels.

3.2. Simulation of k-space Sampling and Reconstruction

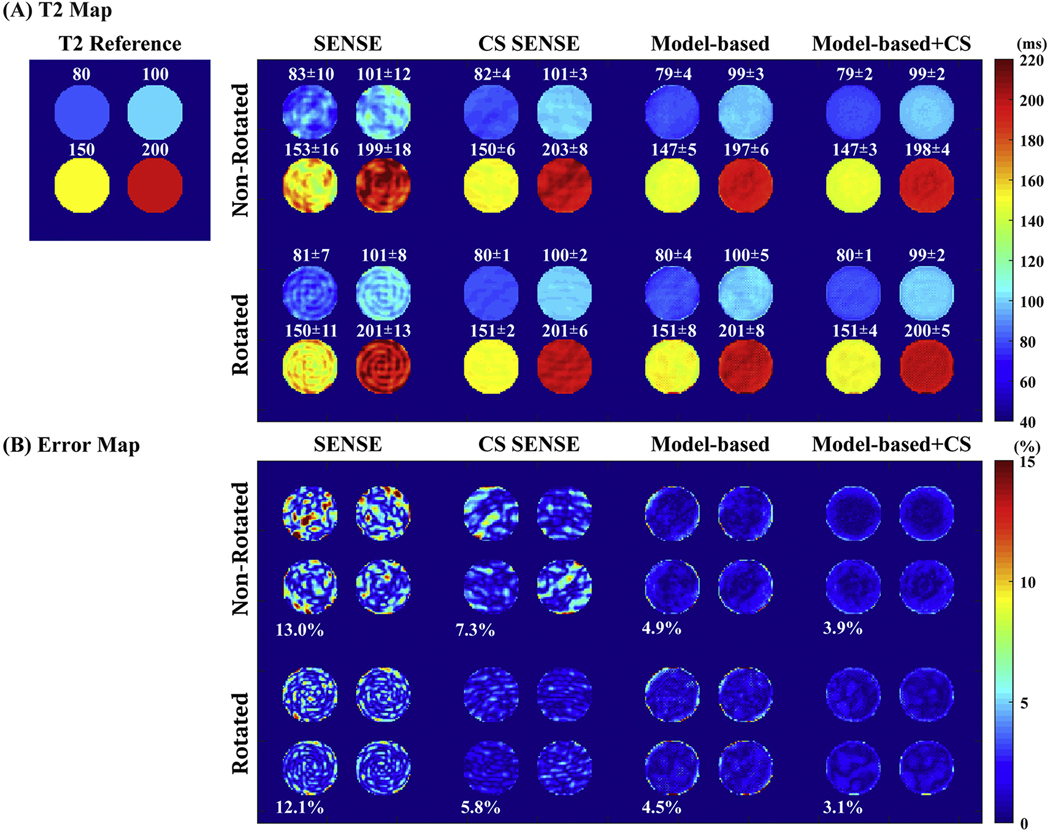
Figure 4A shows the simulation results of T₂ maps obtained by different undersampling schemes and reconstruction methods with 5-fold acceleration. CS SENSE reduced the aliasing artifacts which were apparent in the T₂ maps obtained using SENSE alone. Model-based methods with joint reconstruction provided more accurate T₂ estimation with less artifacts and noises than applying the individual reconstruction followed by 2-parameter-weighted voxel-by-voxel fitting. When incorporating CS, model-based approach further improved the performance with reduced T₂ std by reducing artifacts manifested as stripes. Results derived from rotating k-space trajectories through the T₂ weighting (bottom panel) show slight improvements than the corresponding ones from the non-rotating methods (top panel). These qualitative observations were confirmed by the absolute normalized errors of the estimated T₂ values across the pixels within the digital phantom, as shown in Figure 4B. The nRMSE of SENSE, CS SENSE, model-based, and model-based CS-incorporated were 13.0%, 7.3%, 4.9%, and 3.9% using non-rotated spiral trajectories, slightly higher than 12.1%, 6.8%, 4.1%, and 3.1% using rotated spiral trajectories (P < 0.05 on the corresponding error maps, two-tailed student’s t-test). The nRMSE of model-based methods were all less than 5% with the model-based CS-incorporated delivering the minimal errors. The computation speed to fit a 192×192 T2 map from 5 time points was around 0.07 s and 0.10 s on a 2.3 GHz 4-core CPU with 8 GB memory for 2-parameter and 3-parameter models respectively.

Figure 4:

Simulation results of (A) T₂ maps: (left) T₂ reference map composed of four regions with values of 80 ms, 100 ms. 150 ms and 200 ms, respectively; (right) T₂ maps estimated by different undersampling schemes (non-rotated and rotated trajectories along T₂ weighting dimension) and different reconstruction methods (SENSE, CS SENSE, model-based, and model-based CS-incorporated) with an in-plane acceleration factor of 5. Corresponding mean and std of the T2 values of each region is labeled above the region. (B) The absolute normalized error maps in percentage of different undersampling schemes and different reconstruction methods. The corresponding nRMSE of the T₂ estimation of the entire digital phantom are labeled on left bottom corner of each cell.

3.3. In vivo Experiments

The T₂ maps and corresponding error maps obtained by different sampling and reconstruction methods of one slice from one volunteer are displayed Figure 5. Similar to the simulation result of digital phantom (Figure 4), aliasing artifacts and noises were most notable when using SENSE, and were minimized when applying the model-based CS-incorporated method, for either non-rotated or rotated spiral trajectories. The nRMSE of SENSE, CS SENSE, model-based, and model-based CS-incorporated of brain tissue without CSF partial volume averaged from four volunteers were 16.9%, 11.4%,10.0%, and 8.9% using non-rotated trajectories, vs. 15.9%, 11.2%, 9.6%, and 8.2% using rotated trajectories. The model-based CS-incorporated method generated 47%, 22%, 11% and 48%, 27%, 15% less nRMSE using non-rotated and rotated trajectories than the other three reconstruction approaches, respectively (P < 0.05 on the corresponding error maps, two-tailed student’s t-test). Compared to using non-rotated trajectories, rotating schemes returned slightly improved accuracy, similar to the simulation results.

Figure 5:

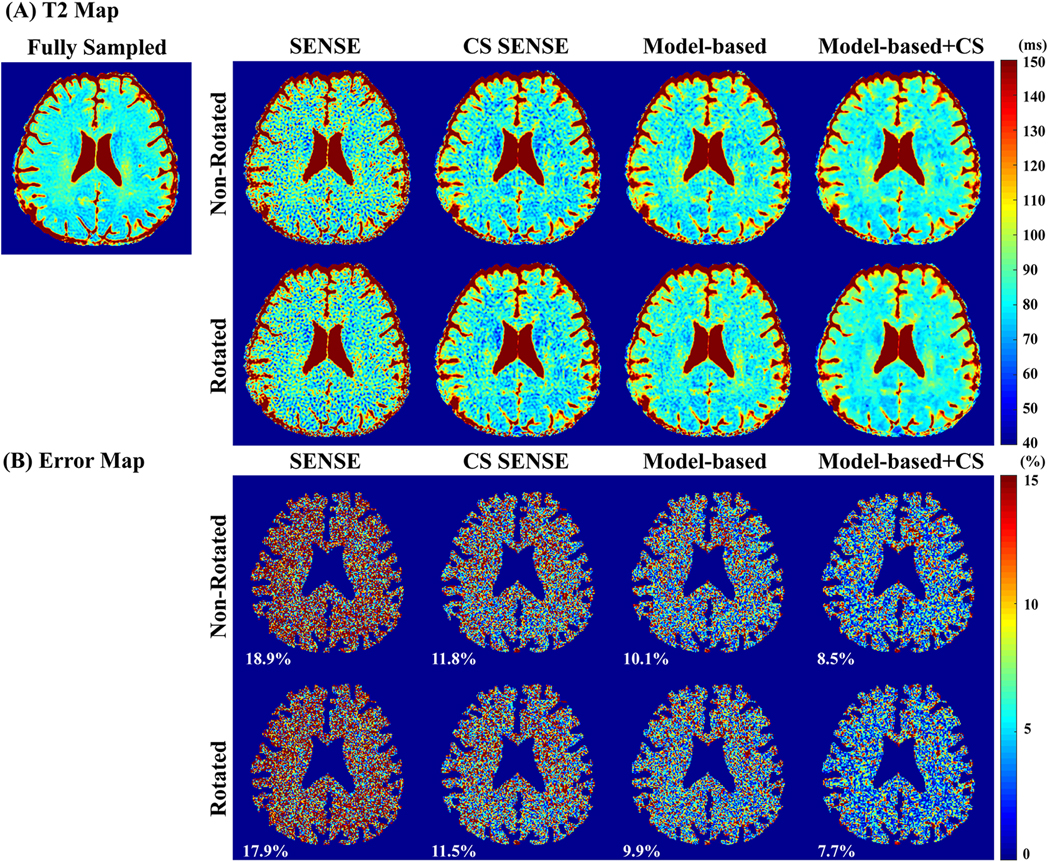
In vivo experiment results of a 44-year-old male: (A) T₂ maps and (B) corresponding normalized error maps estimated by different undersampling and reconstruction methods with an in-plane 5-fold acceleration. Error maps were masked by an eroded mask of T2 maps to exclude CSF. The corresponding nRMSEs of the masked maps were labeled on left bottom corner of each cell in the error maps.

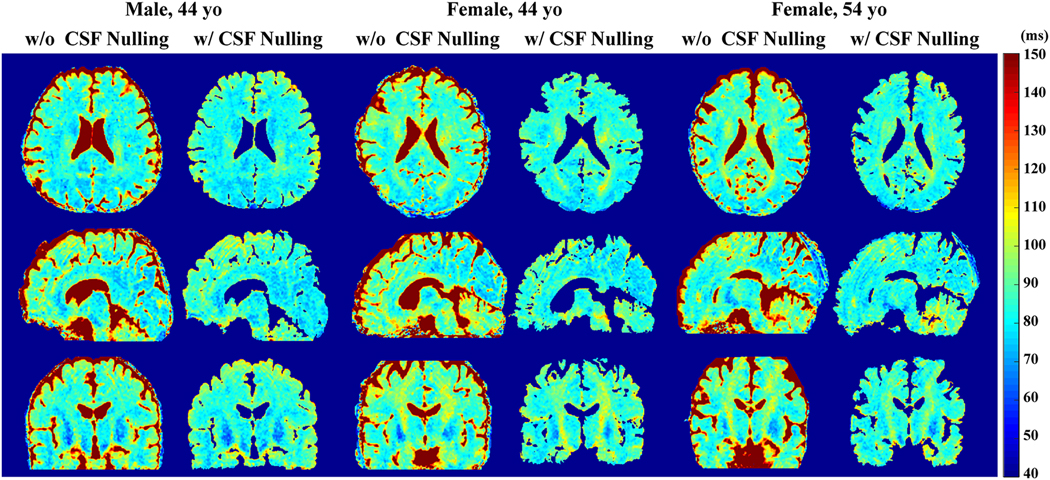
The CSF-nulling sequence (Figure 2C) yielded similar results among different reconstruction techniques (data not shown). The whole-brain T₂ maps with and without the CSF nulling module, estimated by the Model-based CS-incorporated method using rotated spiral trajectories, are exhibited for three healthy volunteers (Figure 6) for comparison, showing largely in agreement. The corresponding whole-brain T₂-weighted images at TE_prep = 80 ms are shown in Figure S2, where the CSF was mostly suppressed with the sequence with the CSF nulling module. The averaged T₂ values of several brain tissues (See Supporting Information Figure S3 for ROI selections) are listed in Table 1. The absolute T₂ values were close to other literature values [19,53,54], with white matter in the range from 70 to 80 ms, and gray matter in the range from 90 to 110 ms. For all ROIs, the estimated T₂ values were found to be slightly shorter by the sequence with CSF nulling. Note that the SNR (mean/std) within these ROIs of the T₂-weighted images at TE_prep = 20 ms were around 10–50 (data not shown) with 5-fold reconstruction, which correspond to the setting in simulation.

Figure 6:

Whole-brain cross-sectional T₂ maps along axial, sagittal and coronal views of three healthy volunteers estimated by pulse sequences with and without CSF nulling, using the rotated spiral trajectories and the model-based CS-incorporated reconstruction method with an in-plane 5-fold acceleration.

Table 1:

The averaged T₂ values (ms, mean±std) within ROIs of typical structures, estimated by pulse sequences with and without CSF nulling, using the rotated spiral trajectories and the model-based CS SENSE incorporated reconstruction method. ROI: FWM = frontal white matter; FGM = frontal gray matter; GPA = globus pallidus; OWM = occipital white matter; OGM = occipital gray matter.

	without CSF nulling	with CSF nulling
FGM	92±5	90±4
FWM	80±2	75±2
GPA	68±7	64±4
OGM	81±3	76±4
OWM	78±3	74±3
Splenium	85±3	81±2
Thalamus	75±3	70±4

4. Discussion

This work demonstrated the feasibility of a rapid (2–3 min with 5-fold in-plane acceleration) T₂ quantification technique with 3D high-resolution (1.2 mm³ isotropic) and whole-brain coverage. The method utilized a T₂-prepared GRE sequence and the model-based CS-incorporated joint reconstruction. The reliability of its T₂ estimation across the brain was achieved with around 8% normalized errors compared to references using fully sampled data.

This work only explored 3D stack-of-spiral trajectory with in-plane variable-density. The acceleration could be further improved with undersampling along slice direction or alternative 3D non-Cartesian trajectories [55,56]. The combination of model-based and CS reconstructions in this study delivered 11–28% less errors than applying them separately. This is expected, as the joint spatial and parametric constraints would improve the performance of the reconstructions.

The non-rotated and rotated undersampling schemes in spiral trajectory along the T₂ weighting dimension were implemented, which were similar to the shifting in Cartesian trajectory [18,57] and golden-angle radial trajectory [8,26]. It was presumed that different undersampling trajectories induced different artifacts which might be compensated and reduced when reconstructing the k-space data along the parametric dimension jointly. However, the improvement by rotated trajectory was not as significant as in Cartesian or radial trajectory. One possible reason was that the 45⁰ angle fixed between interleaves within one T₂ preparation or rotated between T₂ preparations in the acquired spiral trajectories were not the golden angle [58] and thus might not be incoherent for compressed sensing. Further improvements may be achieved by applying golden-angle interleaves along parametric dimension or exploring other trajectories to fulfill incoherent sampling.

In the current implementation, the iterative reconstruction was implemented slice-by-slice, through 2D nonuniform Fast Fourier transform (NUFFT) [59] on CPU and projected-gradient constraint optimization. An optimal implementation is to conduct iteration and 3D NUFFT on GPU. The projected-gradient algorithm converges quickly to obtain a local optimal solution, but there is no guarantee on the convergence of the non-convex problem to a global minimum [16]. Magnetic resonance fingerprinting (MRF) [60–62] and other non-MRF techniques [9,32,63,64] circumvented this problem with dictionary matching reconstruction by generating data with varying sequence parameters and sampling trajectories together.

An essential module of the proposed pulse sequence is T₂ preparation, which is commonly adopted for T₂ weighting with 3D readout. The effect of the imperfect B₁ scales on the prescribed 90° flip down and flip-up hard pulses appends the desired pure T₂ weighting with a complexed T₁ component (Eq. (A3) in the Appendix). This deviation from the simple mono-exponential decay model can cause fitting bias for T₂ prepared approaches, which has been largely overlooked. Although more exact fitting with a 3-parameter model would avert this issue, its accuracy and precision were rather poor with moderate SNR levels (Figure 3). Our simulation results indicated that the 2-parameter-weighted fitting was robust to a wide range of B₁ scales and noise levels. The simulation was performed for T₁ = 1000 ms. According to Eq. (A3) in the Appendix, longer T₁ values, such as of gray matter or at higher field, would induce more bias to 2-parameter fitting model and approximate to the square of cos(B₁⁺ × 90°).

In order to remove the previous T₂ weighting history before each T₂ preparation module, a post-acquisition saturation pulse was applied with a fixed delay in this work. Another strategy is to add sufficient number of dummy pulses after the GRE readout to ensure the same steady state conditions are reached with each T₂ weighting [34]. This could potentially enhance the available signal as it leads to higher longitudinal magnetization before the T₂ preparation.

Routine T₂-weighted FLAIR imaging enhances the conspicuity of brain lesions with long T₂ by suppressing the CSF signal. Similarly, brain T₂ mapping would be more readily translated to the clinic if the fluid signal is removed. In this study, a CSF nulling module (Figure 2C) was applied to mitigate CSF partial volume effect. This method was shown to be effective for T₂ estimation of typical structures in the brain, which provided small differences with the results obtained by the sequence without CSF nulling (Figure 6, Table 1). This method inevitably suffered some loss of SNR efficiency due to the longer recovery time per acquisition, which is also the challenge faced by the 3D FLAIR sequence [65]. Alternatively, CSF partial voluming could be accounted for with additional sampling of the relaxation curves and fitted by a two-compartment three- or even four-parameter model, which would certainly be more SNR demanding and computationally complex.

The proposed protocol was referenced with the same T₂ prepared spiral GRE protocol using fully sampled data. A fully sampled Cartesian spin-echo acquisition would be desired for a more rigorous validation. However, the gold-standard single-echo spin-echo sequence is quite time-consuming even for a 2D scan [32,64] and thus not practical for 3D high-resolution human experiments. Multi-echo spin-echo sequence would be more efficient but its signal is not pure mono-exponential decay as stimulated echoes could be generated from imperfect refocusing [63,66]. The accuracy, precision and reproducibility of our method should be evaluated using system phantoms with known relaxation properties [67,68]. Note that if spatial resolution is lowered than the 1.2 mm³ isotropic chosen for this study, acquisition time would be even faster than 2–3 min, and attained SNR would be higher as well due to the larger voxel size, at the cost of more partial voluming between gray matter and white matter and between normal tissues and lesions. Further investigation among patients with central nervous system disease is needed to explore the clinical value of the proposed technique.

5. Conclusion

In this work, a T₂-prepared 3D stack-of-spiral GRE pulse sequence was introduced for T₂ mapping with high isotropic resolution, whole-brain coverage, and clinical acceptable scan time. A non-linear 2-parameter-weighted fitting approach was implemented to reduce sensitivity to wide B₁ inhomogeneity and high noise level. An iterative model-based reconstruction method, which jointly utilized the model consistency, data consistency, and spatial sparsity, achieved reasonable T₂ estimation with an in-plane acceleration factor of 5. This sequence also allowed flexibility of appending with a CSF nulling module to suppress CSF partial volume effect and thus potentially ameliorate lesion detection.

Appendix:

The T₂ preparation module (Supplementary Material Figure S1) is typically composed of a hard pulse excitation (90°), followed by paired refocusing pulses (180°) and then a flip-back pulse (−90°). The refocusing pulses are robust to B₁ inhomogeneities as they are either composite or adiabatic pulses, so perfect 180° is assumed in the following analytical derivation. In contrast, the flip angles of the hard pulses at the beginning or end of the T₂ preparation module, although prescribed as 90⁰, are proportional to the B₁ scales:

$$\theta =\left(B_1+\right)\cdot {90}^{\circ }$$

Assuming the longitudinal and transverse magnetization before T₂ preparation (point A) are:

$$M_{z,A}=M^0,M_{xy,A}=0$$

where M⁰ is the equilibrium magnetization at fully recovery.

After the first pulse, the magnetizations become:

$$M_{Z,B}=M^{0}cos\theta ,M_{xy,B}=M^{0}sin\theta$$

The formula of T₁ recovery and T₂ decay are:

$$M_Z(t)=M^0+\left(M_Z(0)-M^0\right)e^{-t/T_1}$$ (A.1)

$$M_{xy}(t)=M_{xy}(0)e^{-t/T_2}$$ (A.2)

where M_z(t) and M_xy(t) are the longitudinal and transverse magnetizations at time = t, respectively.

T₂ weighting is set by the duration of the T₂ preparation module (T). The longitudinal magnetizations before each of the following pulses are:

$$M_{z,C}=M^0\left(1+(cos\theta -1)e^{-T/4T_1}\right))$$

$$M_{Z,E}=M^0\left(1-2e^{-T/2T_1}-(cos\theta -1)e^{-3T/4T_1}\right)$$

$$M_{z,G}=M^0\left(1-2e^{-T/4T_1}+2e^{-3T/4T_1}+(cos\theta -1)e^{-T/T_1}\right)$$

And the transverse magnetization before the flip-back pulse is:

$$M_{xy,G}=M^{0}sin\theta e^{-T/T_2}$$

Therefore, the longitudinal magnetization at the end of T₂ preparation is:

$$\begin{gathered} M_{z,H}=M_{z,G}\cos (-\theta )-M_{xy,G}sin(-\theta ) \\ =M^0\left(si{n}^2\theta e^{-T/T_2}+cos\theta \left(1-2e^{-T/4T_1}+2e^{-3T/4T_1}+(cos\theta -1)e^{-T/T_1}\right)\right)) \\ \approx M^0\left(si{n}^2\theta e^{-\frac{T}{T_2}}+co{s}^2\theta \right),whenT\ll T_1 \end{gathered}$$ (A.3)

In addition to the T₂ weighting, the signal after T₂ preparation also has dependence on the B₁ scale and T₁ relaxation. If θ is equal to 90°, it becomes pure T₂ dependent as desired:

$$M_{Z,H}=M^0{e}^{-T/T_2}$$ (A.4)

Note that Eq. (A3) does not deviate significantly if the number of refocusing pulses applied in the T₂ preparation module is more than 2, as done in the current study (simulation analysis results not shown).