Denoising Arterial Spin Labeling Perfusion MRI with Deep Machine Learning

Abstract

Purpose:

Arterial spin labeling (ASL) perfusion MRI is a noninvasive technique for measuring cerebral blood flow (CBF) in a quantitative manner. A technical challenge in ASL MRI is data processing because of the inherently low signal-to-noise-ratio (SNR). Deep learning (DL) is an emerging machine learning technique that can learn a nonlinear transform from acquired data without using any explicit hypothesis. Such a high flexibility may be particularly beneficial for ASL denoising. In this paper, we proposed and validated a DL-based ASL MRI denoising algorithm (DL-ASL).

Methods:

The DL-ASL network was constructed using convolutional neural networks (CNNs) with dilated convolution and wide activation residual blocks to explicitly take the inter-voxel correlations into account, and preserve spatial resolution of input image during model learning.

Results:

DL-ASL substantially improved the quality of ASL CBF in terms of SNR. Based on retrospective analyses, DL-ASL showed a high potential of reducing 75% of the original acquisition time without sacrificing CBF measurement quality.

Conclusion:

DL-ASL achieved improved denoising performance for ASL MRI as compared with current routine methods in terms of higher PSNR, SSIM and Radiologic scores. With the help of DL-ASL, much fewer repetitions may be prescribed in ASL MRI, resulting in a great reduction of the total acquisition time.

Introduction

Arterial spin labeling (ASL) perfusion MRI is a non-invasive technique for measuring cerebral blood flow (CBF) [1] [2]. In ASL, arterial blood water is labeled with radio-frequency (RF) pulses in locations proximal to the tissue of interest. A perfusion-weighted MR image is acquired after the labeled spins reach the imaging place and perfuse into brain tissue. To remove the background MR signal, a control image is also acquired using the same ASL sequence and acquisition timing but with phase modulations to the labeling pulses (by alternating phase of adjacent pulses to be either 0 or 180 degree in the pseudocontinuous ASL) so that arterial spins can approximately stay unaffected. Perfusion signal is subsequently determined by pair-wise subtraction of the spin labeled image (L image) and the spin untagged image (the control image or C image) which is then converted into the quantitative CBF in a unit of ml/100 g/min [3]. Limited by the longitudinal relaxation rate (T1) of blood water, labeling efficiency, and the post-labeling delay, the labeled blood signal is small, resulting in a low SNR [4]. Many pairs of L/C images are often acquired to improve SNR of the mean perfusion map. Because the total scan time is often around 3–6 mins, only 10–50 L/C pairs can be acquired, resulting in a modest SNR improvement by averaging across the limited number of measurements. A number of post-processing methods have been proposed to reduce different types of artifacts in ASL data, including ASL MRI specific motion correction [5], physiological noise correction [6], and spatial noise reduction [7] [8] [9]. Advanced methods have also been published to suppress non-local noise [10], spatio-temporal noise [11] [12] [13] [14], and outliers [15] [16] [17] [18]. These methods are based on either implicit or explicit models about the data, which may not be accurate and may change across subjects.

Deep learning (DL) is a subtype of machine learning (ML) algorithms [19] which has made widespread impact on nearly every research field it has been applied (from image classification [20] [21], video recognition [22] [23] [24], voice recognition/generation [25] [26] [27] [28], medical image processing [29] [30], to AlphaGo [31], AlphaGo Zero [32], etc). The concept of DL can be traced back to early 1980s [33], but only became practical until the advent of fast general-purpose graphics processors in late 2000s [20] [34]. DL is now dominating nearly every field it has reached such as classification, computer vision, auditory processing, information generation, and translational research [21] [29] [30] [35] [36]. Using a hierarchical multiple layers (deep) of “neurons” (the processing units) with a greedy layer-wise training, DL can reliably learn any nonlinear function from the sampled data [35] [37] [6] [19]. In natural image denoising, DL-based denoising has been reported by a few papers [38] [39] [40] [41] [42]. The most popular DL-based denoising approach is based on convolutional neural networks (CNNs) [21]. CNNs learn a hierarchy of features by a series of convolution, feature pooling, and non-linear activation operations, presenting a high flexibility and capability for learning distributions or manifold of images [42]. Encouraged by the outstanding performance as listed above, DL has been introduced into many medical imaging processing fields, including image segmentations [30] [29], image reconstructions [43] [44], image synthesis [45] [46] etc.

The purpose of this study was to test DL for ASL MRI denoising. For the simplicity of description, we dubbed our DL-based ASL denoising method as DL-ASL thereafter. One journal paper [47], one conference paper [48], and a conference abstract [49] have been published in ASL denoising focusing on different scopes of work. Kim et al. [47] published the first paper on this research topic. Their denoising CNNs consist of two parallel pathways to integrate the multi-scale contextual information. As an initial study, the model was trained with a small dataset and the CNN architecture adapted therein was originally designed for image segmentations [50] [51], which may not be optimal for denoising. Ulas et al. [48] trained a deep learning model with a customized loss function based on the Buxton Kinetic model [52] but with a simple CNN architecture. Gong et al. [49] proposed a technique first using multi-lateral guided filter to pre-process input data, generating denoised ASL with different smoothing levels. Then they combined a stack of multi-contrast images as input to train a deep learning network for final CBF denoising. However, the multi-lateral filter is a local filter which cannot incorporate global information for denoising. Generating a stack of multi-contrast image could be time-consuming. While encouraging, these studies were all based on a small sample size and used a standard CNN not specifically optimized for denoising.

By contrast, our paper presents two novelties: first, we incorporated wide activation residual blocks [53] with a Dilated Convolution Neural Network (DilatedNet) [54] to achieve improved denoising performance in term of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity (SSIM) index; second, we evaluated our proposed model given different inputs and references to show that DL-ASL denoising model can be generalized to input with different levels of SNR and yielded images with better quality than other methods.

The rest of this paper is organized as follows. In Section 2, we present our proposed DL-ASL architecture in details. Section 3 demonstrates the experiment of our methods on clinical ASL datasets. Section 4 discusses the main contributions and results of this work. In Section 5, we conclude the paper with several remarks.

2. Materials and Methods

2.1. Problem formulation

Traditional denoising methods often rely on establishing an explicit model for either signal or noise, so the two components can be easily separated from their mixtures. By contrast, DL-based denoising methods learn the denoising model directly from the noise contaminated data. Denote the noisy image by x_i and its reference (noise-free or less noisy version) by y_i, where i=1 …N, N is the total number of training samples. A parametric regression model f_Θ, typically a convolutional neural network (CNN), can be built to learn the mapping f_Θ(x_i) → y_i by minimizing the following loss function:

$$\sum _{\text{i}}\text{L}\left({\text{f}}_{\Theta }\left(x_i\right),{\text{y}}_{\text{i}}\right)$$

, where Θ are the parameters of CNN and are adjusted through the training process.

Assume that the i-th subject’s CBF image x_i is a summation of the latent noise-free CBF image y_i and unknown noise n_i: x_i = y_i + n_i. DL-ASL is to learn an implicit transform which can predict y_i from x_i, so that f_Θ(x_i) → y_i. In DL-ASL, we used mean CBF map obtained without using any explicit denoising as the input and the image denoised with the current state-of-the-art methods (see below) as the reference y_i. To avoid potential overfitting due to the high similarity between x_i and y_i, DL-ASL is configured to learn their difference n_i following the residual learning strategy [41] [42] [53] [54]. Correspondingly, the transform to learn became T(x_i) = y_i − x_i = −n_i. During testing or new image denoising, the output of DL-ASL was added up to the input to generate the final denoised CBF map y_i. Mean Square Error (MSE) and Mean Absolute Error (MAE) are standard loss function used for training. According to [42] [53], MAE is better for image restoration tasks because MSE tends to give over-smoothed results. Thus, to control the training accuracy, MAE between input and reference images was used as our loss function:

$$\text{L}\left(\Theta \right)=\frac{1}{\text{N}}\sum _{\text{i}=1}^{\text{N}}\left|{\text{y}}_{\text{i}}+\text{T}\left({\text{x}}_{\text{i}};\Theta \right)-{\text{x}}_{\text{i}}\right|$$

2.2. Network architecture

Figure 1 illustrates the new CNN structure that was used to build our DL-ASL network. Overall it was a residual learning CNN [55] but with dilated filters [54] replacing the regular non-dilated filters at each layer and with wide activation residual blocks [53] replacing the regular residual blocks [55]. DilatedNet was used due to the capability of extracting both local and global contextual features [54]. Similar to [47], we used two pathways: a local path for extracting the local features and a global path for preserving global data patterns. Wide activation residual blocks are new in the literature but were shown to be able to expand data features and pass more information through the network [53]. As this combination was new, we dubbed it as Dilated Wide Activation Network (DWAN) thereafter.

Figure 1.

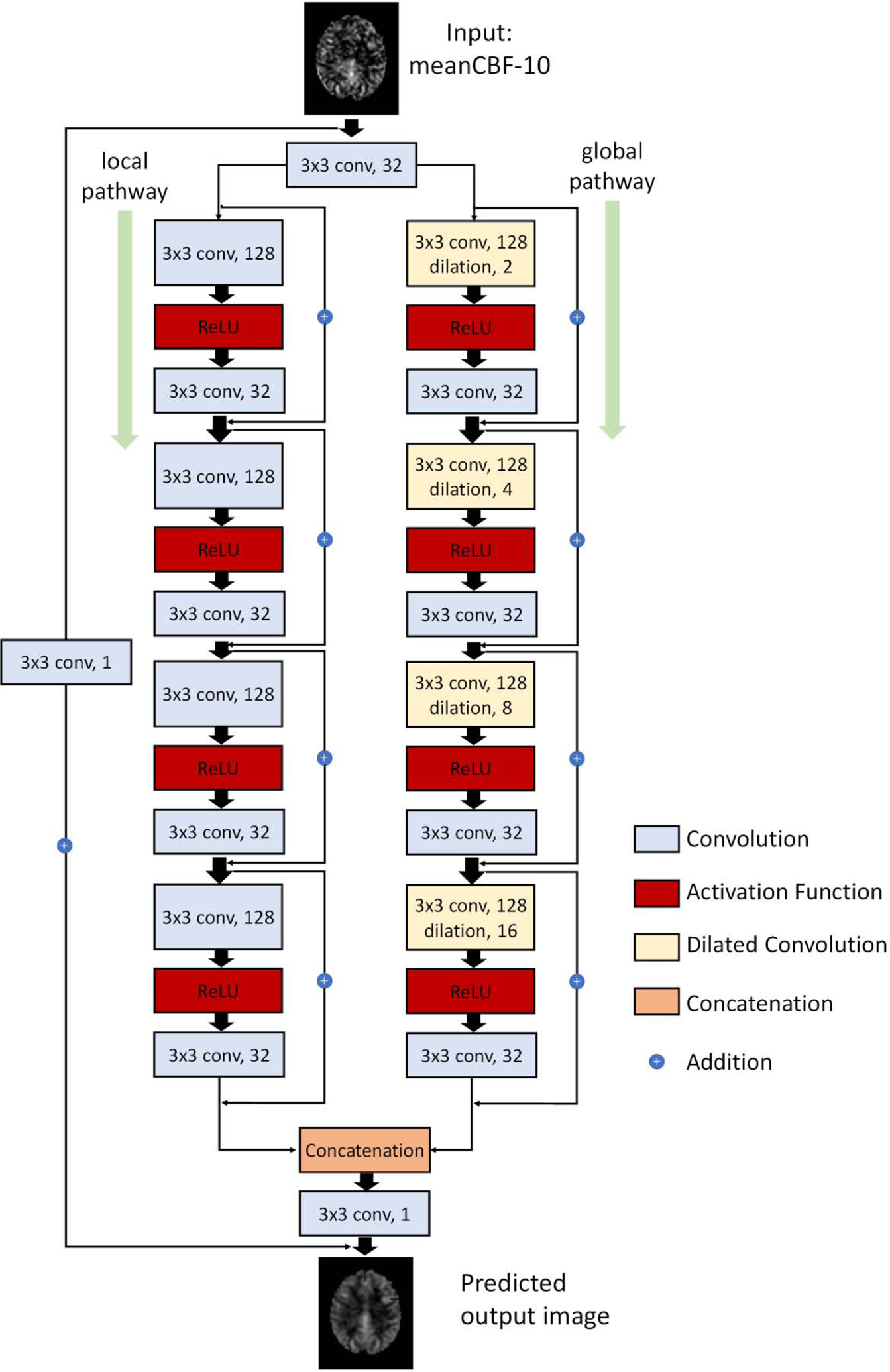
Schematic illustration of the architecture of our proposed DWAN network. The first layer consists of 3×3×32 convolutional filters for the input image. Then the output of first layer were fed to both local pathway and global pathway. Each pathway contains 4 consecutive wide activation residual blocks. Each wide activation residual blocks contain two convolutional layers (3×3×128 and 3×3×32) and one activation function layer. The 3×3×128 convolutional layers in global pathway were dilated convolutional layers with a dilation rate of 2, 4, 8, 16, respectively. The output of local pathway and global pathway were concatenated and fed to another 3×3×1 convolutional filter. The 3×3×1 convolutional layer was attached to the end to get the predicted output image with additional input from the input image with 3×3×1 convolution. (a×b×c indicates the property of convolution. a×b is the kernel size of one filter and c is the number of the filters).

Wide Activation Residual Block:

A regular residual block for low-level vision tasks (e.g., image denoising and image super-resolution) has a convolution layer with a ReLU activation layer, followed by another convolution layer. Each convolution layer has the same number of filters inside a regular residual block. The direct connection from input to output represents the residual learning [55], a key element of modern CNNs for the purpose of improving accuracy and training speed [41] [42] [53] [55]. Since the ReLU layer inside the residual block may cause information loss before being passed to next layer [53], the so-called wide activation residual block uses more filters to extract more features in the layer preceding the ReLU layer, which can subsequently pass more information to the next block [53]. For denoising, this modification would preserve more high resolution information to reduce the blurring effects as supported by the results in image super-resolution [53] and image restoration [56]. In this paper, the number of filters of the convolution layer before the ReLU activation layer was expanded by a factor of 4. After the ReLU activation layer, the following convolution layer shrinks the number of feature maps back to input size.

Residual Learning and Batch Normalization:

DL-ASL was configured to learn the residuals between the input and the reference. The residual learning was implemented through a 3×3 convolution [53] from the input layer to the output layer. Though Kim et al. [47] and Gong et al. [46] used Batch Normalization (BN) [57] layer in their network, recent researches [53] [58] [59] [60] found that BN undermined the accuracy for image super-resolution tasks. We conducted experiments and found out that BN did not improve PSNR and SSIM in our case either. Thus, we discarded BN layers.

2.3. Image Acquisition and Preprocessing

ASL data were pooled from 280 subjects (normal healthy subjects with age from 23–47, 110 females, 170 males) in local database. The data were acquired in a Siemens Trio 3T scanner using a pseudocontinuous ASL sequence [61] [62] (40 control/labeled image pairs with labeling time = 1.5 sec, post-labeling delay = 1.5 sec, FOV=22 cm, matrix=64×64, TR/TE=4000/11ms, 20 slices with a thickness of 5 mm plus 1 mm gap). ASLtbx [63] was used to preprocess ASL images using the following updated procedures: 1) ASL-specific motion correction method was applied to the raw ASL images (C/L images) to correct systematic label/control labeling induced spurious motions [5]; 2) the average of all 40 C/L image pairs was calculated and used as a template for registering the ASL C/L images to the high-resolution T1 image. Registration was performed with SPM12 (Wellcome Department of Imaging Neuroscience, London, UK, http://www.fil.ion.ucl.ac.uk/spm); 3) simple regression was used to regress out residual motions, mean CSF signal and global signal; an isotropic Gaussian kernel with full-width-half-maximum = 3mm was used to smooth ASL C/L images subsequently; 4) adjacent C and L images were subtracted using simple subtraction to generate perfusion-weighted images which were then converted into quantitative CBF using the same method as in [63]. M0 is approximated by the control image in each label/control image pair and M0 calibration is performed at each voxel separately using the value at the corresponding voxel location of the control image. Outlier CBF image timepoints were identified and removed using the priors-guided slice-wise adaptive outlier cleaning algorithm [17] [18]; 5) each subject’s structural MRI was spatially normalized to the Montreal Neurologic Institute (MNI) standard brain using SPM12. The same transform was then applied to the CBF image series; 6) mean CBF maps were calculated from different number of CBF images and were named as meanCBF-n where n indicates the number of CBF images to be averaged. meanCBF-40 was the one calculated from the full ASL scan. The same procedures were repeated after removing the spatial smoothing step and the corresponding mean CBF maps were named by an affix “nsm”.

2.4. Data preparation and model training

To maximally demonstrate the benefit of DL-ASL, we chose meanCBF-10_nsm (mean CBF map of the first 10 ASL C/L pairs without being spatially smoothed during preprocessing) as the input to the DL-ASL models. As there is no groundtruth (GT) to ASL CBF maps, meanCBF-40 -- mean CBF map of the entire 40 C/L image pairs, was used as a surrogate GT (the reference) for training the DL-ASL models. The same model was also trained for projecting the meanCBF-10_nsm to meanCBF-40_nsm and name appended by the suffix ‘nsm’ was added to the name of each model to mark the difference of both input and the reference during model training.

200 subjects’ CBF maps were randomly selected as the training set. 20 subjects’ CBF maps were used as validation samples during training. The remaining 60 subjects were used as the test set. For each subject, we extracted axial slices every 3 slices from slice 36 to slice 60 of 3D CBF maps in the MNI space, resulting a training set containing 200 X 9 = 1800 2D CBF image slices. Each image slice had 91 X 109 pixels.

U-Net [64], a popular CNN structure widely used in medical imaging, was implemented as a comparison to our DWAN-based DL-ASL. Because U-Net has pooling and upsampling layers that requires the image size equal to the power of 2, all the images were resized to 128 × 128 during the training and testing of U-Net, by centering images and padding 0s on each side. U-Net, U-Net with BN (U-Net_BN) [45], DilatedNet and DilatedNet with BN (DilatedNet_BN) [47] were implemented as additional comparisons. To test the denoising capability of DL-ASL for inputs with different noise levels, we applied the same model (trained by meanCBF-10_nsm) to meanCBF-15, 20, 25, 30, 35 and 40 datasets (mean CBF maps obtained from 15, 20, 30, 35, and 40 L/C images).

All networks were implemented using the Keras platform [65]. The network was trained using Adaptive moment estimation (ADAM) algorithm [66] with basic learning rate of 0.001. All the models were trained with batches, each containing 64 training samples. DWAN was trained for 10000 iterations and DWAN_nsm was trained for 5000 iterations. Tensorflow [67] was used as the backend of Keras to train all the models. All experiments were performed on a PC with Intel(R) Core(TM) i7–5820k CPU @3.30GHz and a Nvidia GeForce Titan Xp GPU.

2.5. Effects of different model configurations

An experiment was conducted to assess the performance of DL-ASL containing different number of wide activation residual blocks. A grid search experiment was conducted to find the best combination of expansion rate E and the number of input filter M for each wide activation residual block. Noted that the regular residual block [55] [58] is essentially a special case of wide activation residual block [53] when the expansion rate E is 1. Thus, by setting expansion rate as 1, we also compared the DilatedNet that contains regular residual blocks with DWAN. Furthermore, additional experiments were performed to assess the effects of residual learning and the MAE/MSE loss function used in training.

2.6. Evaluation metrics

We used Peak Signal to Noise Ratio (PSNR), Structural Similarity index (SSIM), Mean Absolute Error (MAE), Lin’s Concordance Correlation Coefficient (CCC) [68] and Radiologic score as our evaluation metrics. PSNR, SSIM, MAE, and CCC were calculated from the denoised CBF maps and the surrogate GT to evaluate performance of different methods. PSNR assess the quality of image denoising quantitatively while SSIM measures the nonlocal structure similarity. MAE and CCC were used to assess the accuracy of predicted CBF values. The Bland-Altman plot and image profiles of CBF map were used to access the fidelity of predicted CBF values qualitatively. CBF image profiles were taken from the 50^th row of the 54^th axial slice. The Bland-Altman plot was drawn using the CBF values in the GM area of one representative subject’s 50^th axial slice. CBF image quality was qualitatively assessed by two radiologists (T.W. and F.Z.). The quality score ranges from 1 to 4 and the value 1/2/3/4 means severe noise/moderate noise that disturbs evaluation/mild noise that not affects evaluation/clear perfusion map, respectively. Randomly selected 10 subjects’ CBF images processed by the 4 different methods: UNet, DilatedNet, DWAN, non-DL method were provided to the two radiologists independently without disclosing which method was used to process which image.

2.6.1. PSNR

PSNR is defined as:

$$\text{PSNR}=20*{\text{log}}_{10}\left(\frac{\text{MAX}}{\sqrt{\text{MSE}}}\right)$$

where MAX is the maximum possible pixel value of the image and MSE is the mean square error between the denoised image (the output of DL-ASL) and the surrogate GT (meanCBF-40_sm). Higher PSNR means less voxel-wise differences.

2.6.2.

The SSIM is defined as

$$\text{SSIM}\left(\text{x},\text{\hspace{0.17em}y}\right)=\frac{\left(2{\mu }_{\text{x}}{\mu }_{\text{y}}+{\text{c}}_1\right)\left(2{\sigma }_{\text{xy}}+{\text{c}}_2\right)}{\left({\mu }_{\text{x}}^2\text{+}{\mu }_{\text{y}}^2+{\text{c}}_1\right)\left({\sigma }_{\text{x}}^2\text{+}{\sigma }_{\text{y}}^2+{\text{c}}_2\right)}$$

where μ_x, μ_y, σ_x, σ_y, and σ_xy are the mean, variance, and covariance of two patches (x, y) at the same location of the output image and the surrogate GT, respectively. c₁ and c₂ are constants used to avoid division by zero. Higher SSIM means more structure similarity. For the networks trained with meanCBF-40_nsm (the mean CBF map calculated from the non-smoothed ASL C/L images), PSNR and SSIM were calculated based on the difference between the network output and the meanCBF-40_sm as our goal of DL-ASL was to provide better quality in relative to the mean CBF map processed with current standard steps.

2.6.3.

The Lin’s CCC is formulated as:

$${\rho }_{\text{c}}=\frac{2{\sigma }_{\text{xy}}}{{\sigma }_{\text{x}}^2+{\sigma }_{\text{y}}^2+{\left({\mu }_{\text{x}}-{\mu }_{\text{y}}\right)}^2}$$

where μ_x, μ_y, σ_x and σ_y are the mean and variance of the output image and the surrogate GT, respectively. σ _xy is the covariance between the output image and the surrogate GT. The CCC accesses the image fidelity to the surrogate GT, in which a value of 1 represents a perfect agreement and a value of 0 represents no agreement.

3. Results

3.1. Results of DL-ASL for projecting meanCBF-10 to meanCBF-40

Figure 2 shows a representative subject’s mean CBF maps produced by different denoising methods. As compared with meanCBF-10_nsm (Fig. 2A, the input to DL-ASL), all DL methods (Fig. 2B–2D) produced much better image quality in terms of improved tissue perfusion signal, suppressed noise (especially in white matter), better perfusion contrast between grey matter and white matter. The DL methods even showed CBF map quality improvement as compared with the surrogate GT (Fig. 2E, meanCBF-40_sm). DWAN_sm (Fig. 2D) showed the best quality as compared against other DL methods. Figure 3 shows the image profile of CBF images processed with different methods. Figure 4 shows the Bland-Altman plots of CBF values in GM area obtained from different processing methods using one representative subject. The plots demonstrate that our proposed method achieved better accuracy in CBF values with smaller bias (green solid line) and variance (difference between dashed grey lines). The linear regression line (solid red) in U-Net_sm and DilatedNet_sm shows a systematic underestimation error while this error is reduced by DWAN_sm as its regression line is closer to the y = 0 line. Note that outlier voxels existed in all the methods due to excessive noises and artifacts from L/C subtractions.

Figure 2.

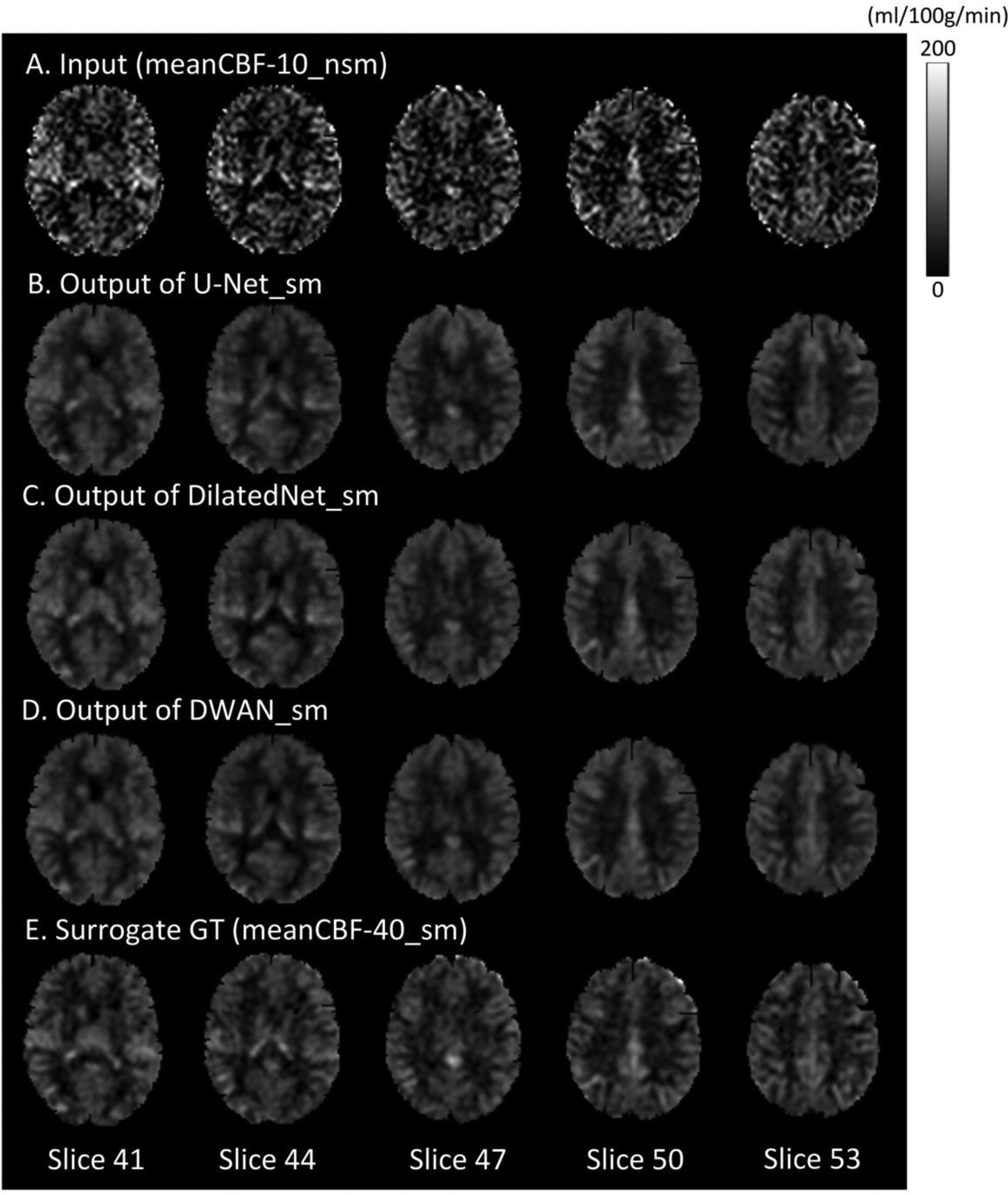
Mean CBF images (only 5 axial slices were shown) from a representative subject with different processing methods. From top to bottom: meanCBF-10_nsm as input, the output of U-Net_sm, the output of DilatedNet_sm, the output of proposed DWAN_sm and the surrogate GT (meanCBF-40_sm) as training reference.

Figure 3.

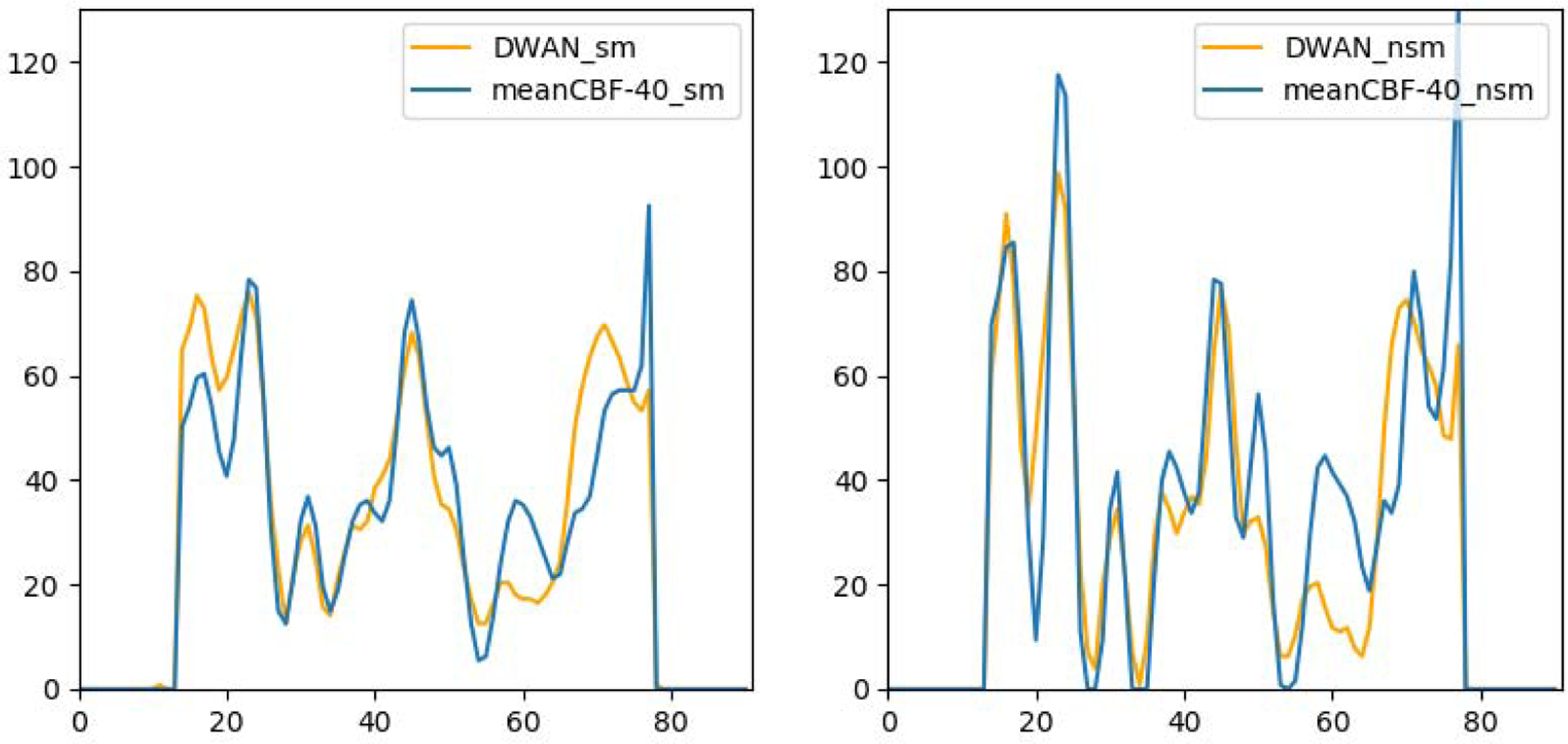
CBF image profiles taken from the 50^th row of the 54^th axial slice from one representative subject.

Figure 4:

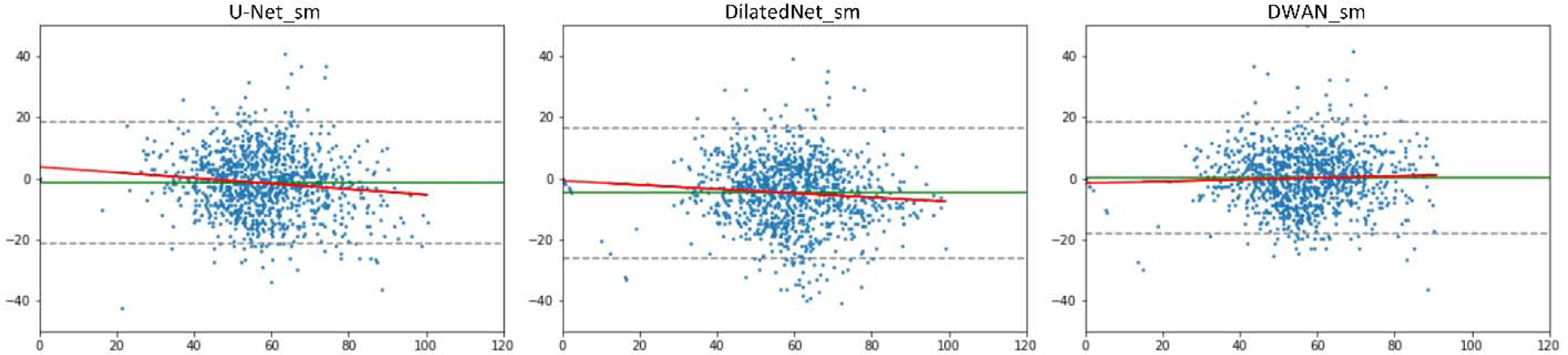
Bland-Altman plots of different methods obtained in the GM area from one representative subject. Y-axis shows the differences between the surrogate GT and compared method in CBF values. X-axis shows the mean CBF values of the two. The unit for x and y axes are in ml/100g/min. Solid green lines indicate mean difference. Dashed gray lines at top and bottom indicates upper and lower margins of 95% limits of agreement. red solid lines are linear regression lines.

Table 1 and 2 list the performance indices of different methods. As compared with other methods, DWAN_sm and DWAN_nsm presented the better performance indices (PSNR and SSIM) (p<0.05). Our experiments also confirmed that adding BN layers did not improve denoising performance as described in [53] [58] [59] [60]. Table 3 list the MAE and CCC of different methods. DWAN_sm and DWAN_nsm has lower MAE and higher CCC than other methods.

Table 1.

The average PSNR and SSIM over 60 test subjects. All the models were trained with meanCBF-40_sm as reference images.

Model	U-Net_sm	U-Net_BN_sm	DilatedNet_sm	DilatedNet_BN_sm	DWAN_sm
PSNR	25.87	25.63	26.18	26.13	26.25
SSIM	0.813	0.806	0.819	0.817	0.822

Table 2.

The average PSNR and SSIM over 60 test subjects. All the models were trained with meanCBF-40_nsm as reference images.

Model	U-Net_nsm	U-Net_BN_nsm	DilatedNet_nsm	DilatedNet_BN_nsm	DWAN_nsm
PSNR	24.53	24.16	24.78	24.60	24.81
SSIM	0.796	0.787	0.802	0.798	0.803

Table 3.

The average MAE and CCC over 60 test subjects.

	U-Net_sm	DilatedNet_sm	DWAN_sm	U-Net_nsm	DilatedNet_nsm	DWAN_nsm
MAE	6.017	5.936	5.926	6.285	6.289	6.281
CCC	0.896	0.898	0.900	0.854	0.857	0.859

Figure 5 shows the radiologic scores of ASL CBF maps processed by different methods. DWAN_sm, DilatedNet_sm, and U-Net_sm had an average score of 3.08, 3.00 and 2.78 by radiologist #1 (Tianyao Wang), and an average score of 2.81, 2.73 and 2.72 by radiologist #2 (Fuqing Zhou), respectively. The surrogate GT (meanCBF-40_sm) had an average score of 2.16 and 2.50 by the two radiologists. As figure 5 shows, DWAN_sm consistently achieves better denoising results than other methods qualitatively. Figure 6 shows the corresponding results when using the meanCBF-40_nsm as the reference during model training. The outputs of DWAN_nsm are less blurring than those of DWAN_sm.

Figure 5.

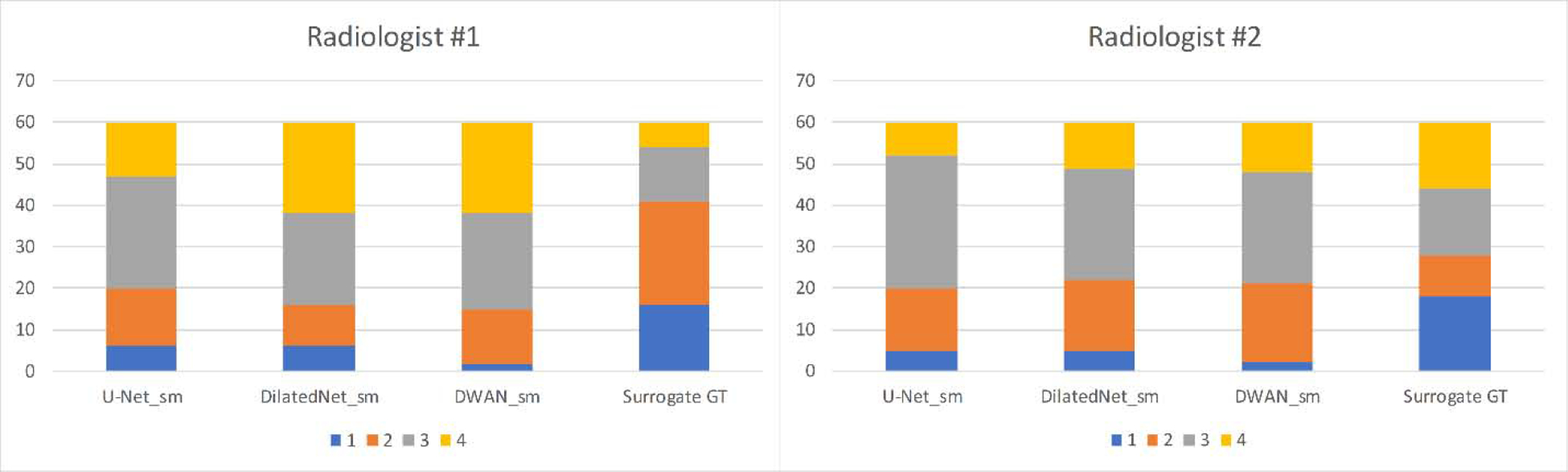
Comparison of Radiologic score between different methods over 60 subjects’ CBF maps. Radiologic scores are displayed with four different colors. Vertical axis indicates the number of subjects of each radiologic score.

Figure 6.

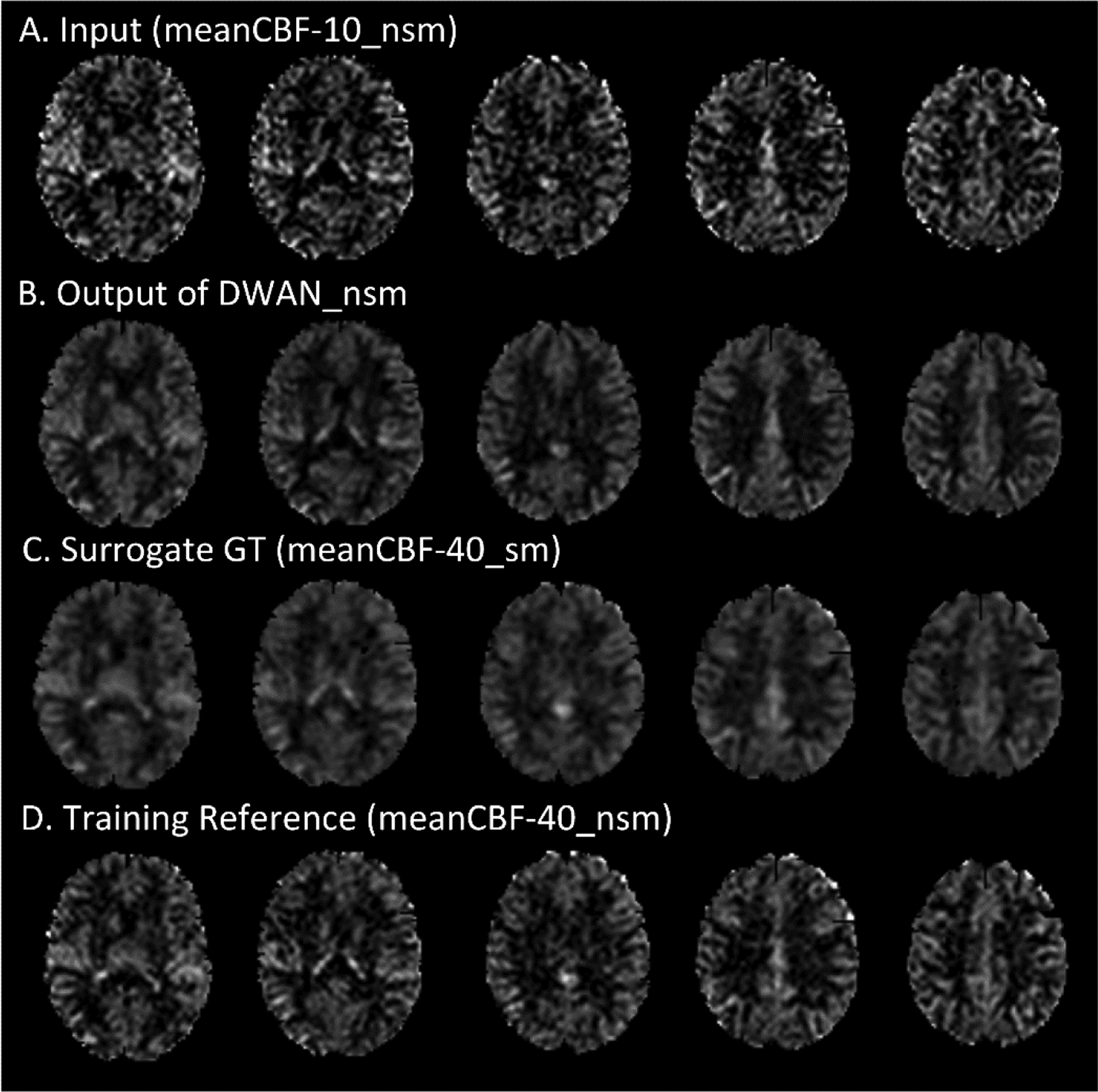
ASL CBF images with meanCBF-10_nsm as input. From top to bottom: the input (meanCBF-10_nsm), the output of DWAN_nsm, the surrogate GT (meanCBF-40_sm) for comparison and the training reference (meanCBF-40_nsm).

3.2. Effects of different noise levels in input data on the model trained with meanCBF-10_nsm

Without any additional training, we directly applied the same model (trained by meanCBF-10_nsm) to different meanCBF-n_nsm (n=10, 15, 20, 25, 30, 35, 40) datasets. Figure 7 shows the quantitative results in terms of PSNR and SSIM. When input is meanCBF-10_nsm to meanCBF-30_nsm, DWAN_sm showed higher PSNR and SSIM than U-Net_sm and DilatedNet_sm. When input is meanCBF-35_nsm or meanCBF-40_nsm, DWAN_nsm had higher PSNR and SSIM than all other models.

Figure 7.

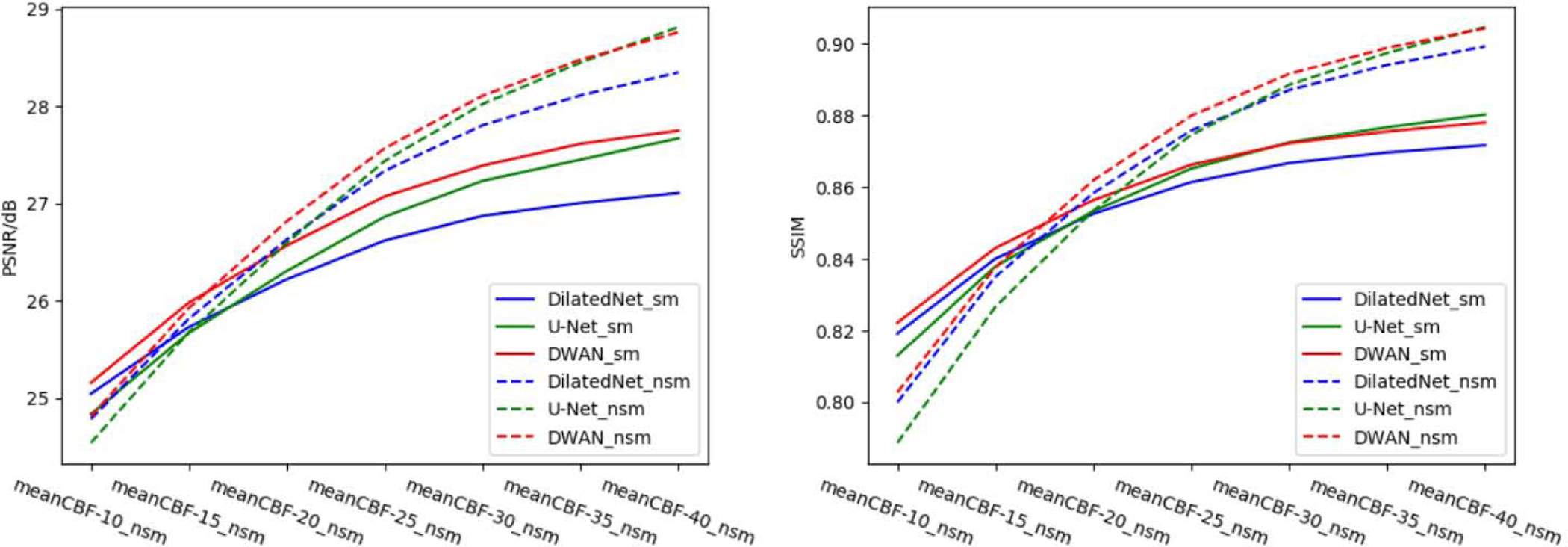
PSNR and SSIM of U-Net_sm, U-Net_nsm, DilatedNet_sm, DilatedNet_nsm, DWAN_sm and DWAN_nsm over different mean CBF test datasets.

Figure 8 shows the output of DWAN_sm and DWAN_nsm when the input was different meanCBF-n_nsm (n = 10, 15, 20, 25 and 30) from one representative subject. When the quality of input image increased, the quality of output image of DWAN_sm and DWAN_nsm increased. Besides, when input was meanCBF-25_nsm or meanCBF-30_nsm, DWAN_nsm produced better results with better grey matter/white matter contrast and image sharpness and less noise. Similar quantitative results were shown in the PSNR and SSIM plot in Figure 7.

Figure 8.

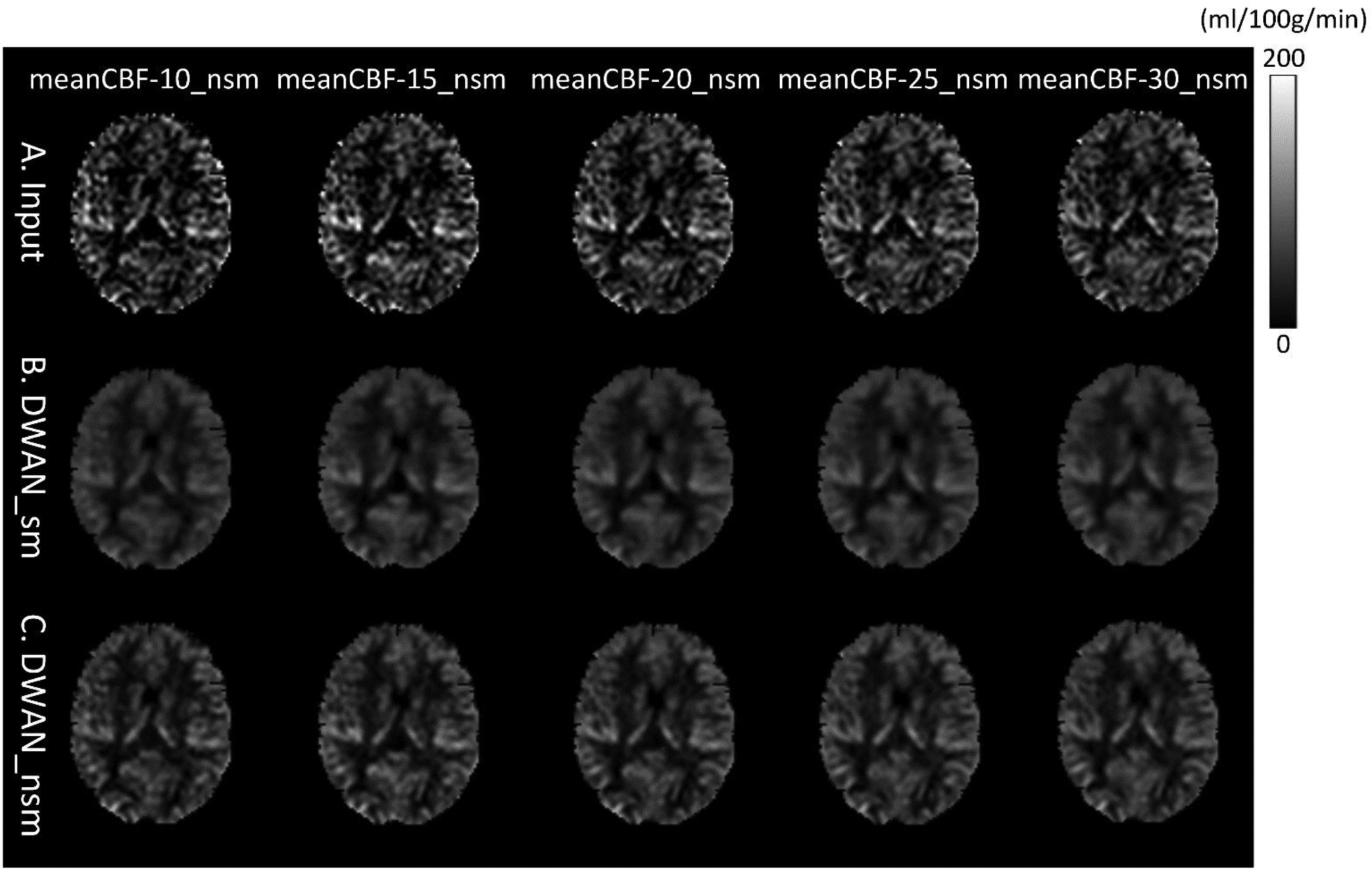
The same slice of a representative subject’s mean CBF images (only 1 axial slice was shown) processed using the same DWAN_sm or DWAN_nsm model trained with the (meanCBF-10_nsm, meanCBF-40_sm) or (meanCBF-10_nsm, meanCBF-40_nsm) image pairs, respectively. A) input images to the model, B) output images of DWAN_sm for the input shown in A, C) output images of DWAN_nsm for the input shown in A. The input to the model is meanCBF-10_nsm, meanCBF-15_nsm, meanCBF-20_nsm, meanCBF-25_nsm and meanCBF-30_nsm from the leftmost column to the rightmost column.

3.3. Effects of model configurations, residual learning, and loss function

Figure 9 shows the performance of DWAN_sm with different number of wide activation residual blocks. In general, DWAN_sm with 4 wide activation residual blocks (DWAN_4) yielded the highest PSNR and SSIM on meanCBF-10_nsm to meanCBF-20_nsm, whereas DWAN_sm with 3 wide activation residual blocks (DWAN_3) yielded better SSIM for meanCBF-30_nsm to meanCBF-40_nsm. Since our goal was to train a model that has the best denoising performance with low SNR input, we chose DWAN_4 in our DL-ASL. Figure 9 also shows that DWAN_sm with residual learning had better PSNR and SSIM performance than without residual learning. Table 4 shows the grid search results of finding the best combination of expansion rate E and the number of input filter M for all wide activation residual blocks. We found that E=4 and M =32 achieved the best denoising performance.

Figure 9.

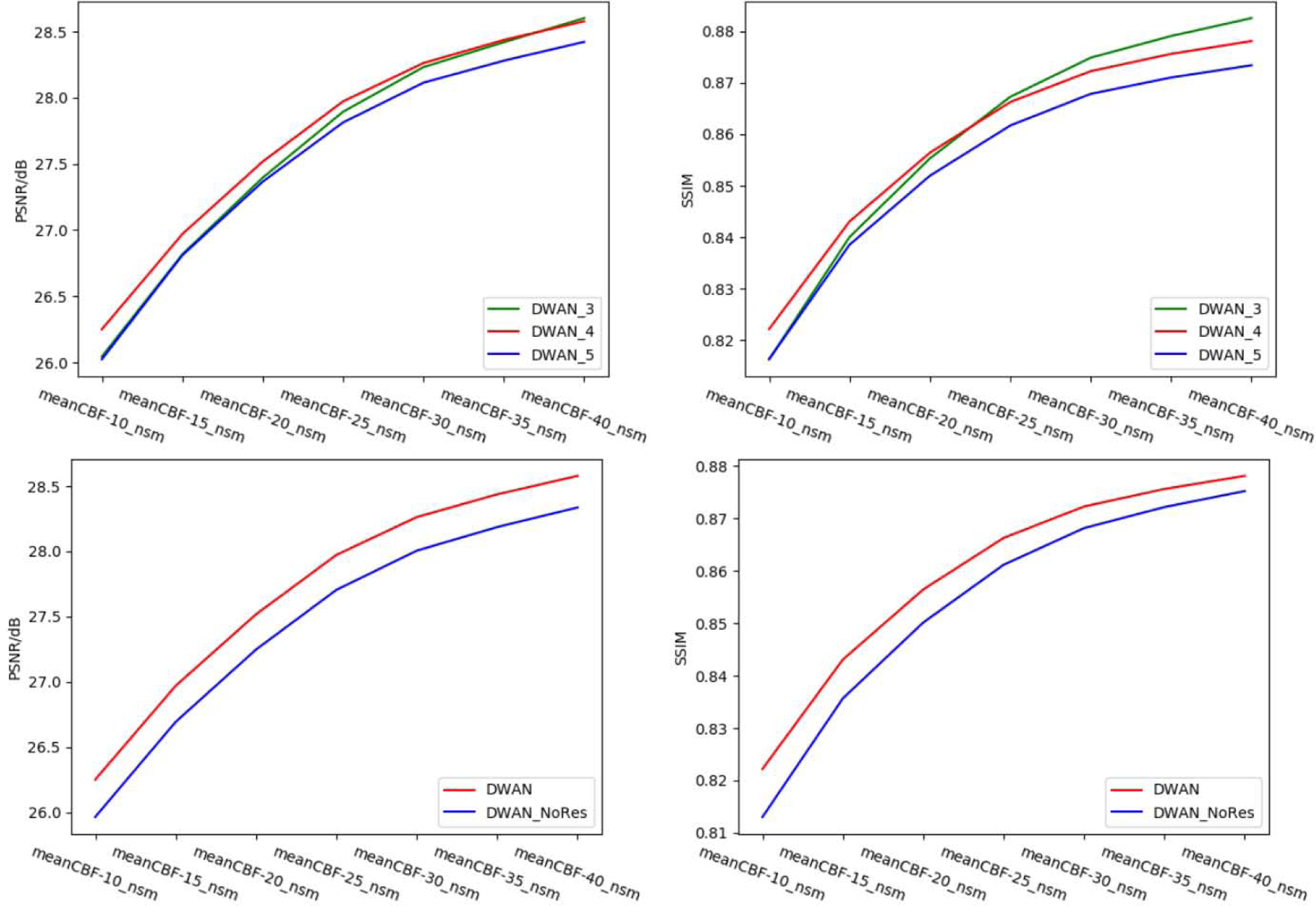
Top: performance of DWAN with different number of wide activation residual blocks. The number in the suffix of the model represents the number of wide activation residual blocks in each pathway. Bottom: performance of DWAN with and without of residual learning. DWAN_NoRes has the same architecture as DWAN except residual learning.

Table 4.

The PSNR of DWAN with different expansion rate E and different number of input filters M. N/A = Not Applicable due to the total number of filters E*M exceeding limitation of GPU memory and causing unstable training of DWAN.

M╲E	1	2	4	6	8
16	26.00	25.83	26.02	25.81	26.11
32	26.07	26.12	26.26	26.12	N/A
64	26.14	26.15	N/A	N/A	N/A
128	25.63	N/A	N/A	N/A	N/A

Figure 10 shows the training loss and validation loss of DWAN_sm. Training loss was the MAE between output images and surrogate GT over the training dataset. Validation loss was the MAE between output images and surrogate GT over the validation dataset (the validation dataset was a small sample of data that was separated from training set, and was used to provide an unbiased evaluation of a model’s performance during training). When the validation loss stopped decreasing and the training loss was still decreasing, the model started to overfit the training dataset, which would make the model performance decrease on test datasets. To avoid the overfitting problem, the early stopping [69] technique was used during training.

Figure 10.

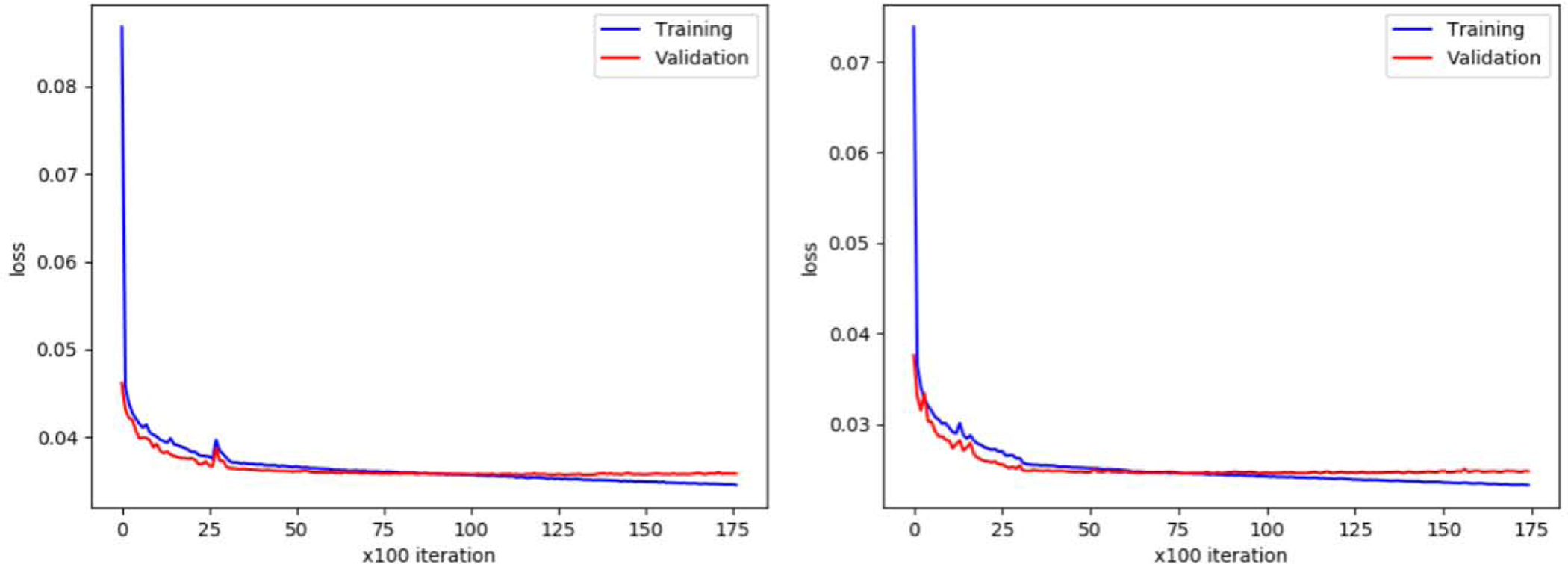
Left, training and validation loss of DWAN_sm. Right, training and validation loss of DWAN_nsm.

4. Discussion

This paper proposed a new CNN architecture, DWAN, and validated it in ASL CBF denoising. Dilated convolutions were combined with wide activation residual blocks to form the basic units of DWAN. Applied to mean CBF maps calculated from different number of L/C image pairs, DWAN demonstrated better denoising performance than other CNNs and the non-DL based approach though all DL-based methods outperformed the traditional approaches. The performance was evidenced by image appearance, quantitative measures (PSNR, SSIM, MAE and CCC) and qualitative measure (radiologic scores). We also demonstrated that the same DWAN model can be used to denoise CBF images with different noise levels without retraining the model.

The decrease of MAE and increase of PSNR, SSIM and CCC of DL-ASL can be explained by two features of the CNN-based DL network. First, the spatially incoherent noise is suppressed by the many hierarchical convolutional filters in CNN. Each filter is learned to have different weights, resulting in suppressing different aspects of noise while retaining the cross-subject and cross-regional perfusion signal features. By using a hierarchical structure, the remaining noise can be further suppressed in the upper level through another series focal convolution processes. Second, DL-ASL is constructed to learn the cross-subject cross-regional perfusion features, making it robust to noise which usually doesn’t have common spatial patterns across subjects and regions [70]. A common concern in denoising is the loss of resolution or equivalently the increase of blurring as typical noise contains a substantial high-frequency band like the random noise. However, DL has been repeatedly shown to be able to increase image resolution in many super-resolution papers [72] [59] [58]. Our group has recently demonstrated this capability of DL in ASL using data acquired with different resolutions [73] [74]. We also showed that DL can achieve higher SNR while increase ASL CBF resolution. But the dataset used in this paper didn’t have high resolution ASL CBF maps and gold standard CBF images, making it difficult to evaluate the potential blurring effects. Nevertheless, the concern of blurring still stands and will need future work to be fully addressed.

We chose the central slices as the training data because of the relatively better SNR they provided than other slices. For 2D ASL MRI without inferior saturation, the inferior slices in 2D ASL often suffer from large flow effects (fresh blood entered the imaging slices) and should be avoided during training because current processing approaches do not have a good way to remove those artifacts, so they will be preserved in the reference image as well as in the model. The superior slices had the lowest SNR due to the long transit time. According to additional experiments, the superior slices can be included in training without affecting the denoising effects especially because of the “learning from noise” capability of DL [71].

Our evaluations converge to a major benefit: with the help of DWAN, we can shorten the acquisition time by 4 times to be 1min 20 sec without losing much CBF image quality as compared with the full-length acquisition, which was 40 C/L pairs in this paper. Shortening acquisition time is highly valuable when subjects or patients have difficulty in keeping still in the scanner.

It is worth to note that DL-ASL was only trained with data from healthy subjects. Both signal and noise might have different distributions in diseased populations, which may cause a less efficient denoising for patients’ data as it may not be able to suppress the extra noise in diseased populations. While that problem is universal to non-deep learning and deep learning-based methods, it might be less severe in DL as the model is trained to learn the signal or noise across many different people and distributed brain regions which themselves present large variability. On the contrary, traditional methods often rely on a pre-determined model which doesn’t change based on the data and then is less adaptive to the data. To have a model full capable of suppressing noise or artifacts for patients, the model must be trained with additional data from patients.

5. Conclusion

In conclusion, we introduced DL into ASL MRI denoising and proposed a new denoising model DWAN. DL-ASL substantially improved the quality of ASL CBF, suggesting a potential of significantly reducing acquisition time. Besides, DL-ASL showed the generalizability to denoising CBFs with different noise levels without model retraining.