Abstract
With many commodity and financial markets reportedly experiencing poor performances during this COVID-19 pandemic, this study intends to examine the effect of the pandemic on the connectedness among the markets. There are several reasons that suggest that apart from the pandemic affecting the performances of the markets, it can also be a driver of their connectedness, coming from the perspective of the global financial cycle channel. Therefore, we first employ the recently developed time-varying parameter vector autoregressions (TVP-VAR) technique to examine the volatility spillover among the commodity and financial assets. We find evidence of strong volatility across the markets, with gold and USD being net receivers of shocks, and others, net transmitters. With this evidence, we proceed to the evaluation of the influence of the COVID-19 pandemic on the connectedness across the markets using both the linear and non-linear (causality-in-quantiles) causality tests. The causality-in-quantiles test outperforms the linear Granger-causality test, and the results show significant causal impacts of the two measures of COVID-19 pandemic (infectious diseases-based equity market volatility and the growth rate of the U.S. COVID-19 reported cases) on the connectedness across the markets, especially at the lower and middle-level quantiles. Overall, these findings prove that the pandemic has been largely responsible for risks transmission across various commodity and financial markets. This is because it has significantly raised investors’ and policy uncertainties and immensely altered global financial cycle which in turn results in global flows of capital, and movements in the prices of assets across different financial markets.
Keywords: COVID-19 pandemic, Financial markets, Commodity markets, Connectedness, Volatility spillover, Causality-in-quantiles test.
1. Introduction
The growing level of global trade integration and the search for alternative investment assets in the face of market risks has seen to the connectedness among global asset markets, particularly since the past few decades. In fact, more than ever before, the recent years have witnessed a high degree of causal relationships among commodity and financial markets, with risks and opportunities in one easily spilling over to others. Commodities are now increasingly being considered as significant components of investment portfolios for both portfolio managers and investors following the vulnerability of common financial markets (especially stock markets) to unfavourable shocks that lead to losses. Choi and Hammoudeh (2010) rightly infer that investors in commodity assets consistently track movements in the prices of commodities and stocks, certainly to make optimal investment choices. Thus, there is substitution mechanism among financial (stocks, and by extension other financial assets including cryptocurrencies, foreign exchanges, etc.) and commodity assets (oil, gold and other precious metals) following the viability of the latter as suitable assets for hedging and safe-haven purposes (Jain and Biswal, 2016).
The literature has revealed different channels through which commodity and financial markets relate. However, these channels largely explain the links among the markets mostly in split, implying that channels that connect all the markets together in one attempt are rare. The foremost seems to be the inflation mechanism which connects the oil market with the metals market. One of the major historic sources of market risks has been traced to inflation (see Rubens et al., 1989) through the business cycle. In the first instance, investors in the economy with high inflation caused by increase in oil price increase their demand for gold in order to serve as hedge against inflation (Jain and Biswal, 2016). On the other hand, due to the relative stability of the value of gold, oil exporting countries increase the proportion of gold in their external reserves portfolios as oil price and revenue increase (see Melvin and Sultan, 1990). As oil price rises due to any external factors, inflation also rises in many countries, and this is consequently followed by hike in the prices of metals. Another prominent channel takes its stand from the unified currency measurement (U.S. dollar) of most globally traded assets. Assuming the dollar appreciates, the purchasing power of other countries other than the U.S. diminishes, thereby reducing their demand for all the assets denominated in this common currency. Hence, their prices jointly fall (see Adekoya and Oliyide, 2020). The interest rate channel explains how investors in stocks become discouraged when interest rate is low. This could make them consider other high interest-yielding assets in order to gain higher returns.
The last but not the least channel which appears to be the most all-encompassing as it brings more markets together is the macroeconomic factors-based channel. This is also the channel through which we derive the objective of this study. It explains that different global markets (oil, metals and financial) are connected via common economic factors, especially global economic events. Although earliest studies have connected the global markets through global economic activity especially for oil and metals markets since the commodities being traded in these markets are important industrial inputs (see Ahmadi et al., 2016; Reboredo, 2010), subsequent studies are now considering the role of global economic and equity market uncertainties that connect commodity and financial markets in entirety (see Albulescu et al., 2019).
Against these highlighted mechanisms, the literature is now increasingly being flooded with studies that examine the relationship among oil, metals, stocks, cryptocurrencies and foreign exchange markets in different dimensions (see Singhal et al., 2019; Jain and Biswal, 2016; Akbar et al., 2019; Bedoui et al., 2019, etc.). However, connectedness among the global markets may not just occur unless it is driven by notable factors, particularly policy uncertainty. The pioneers of this theoretical stand (see Pástor and Veronesi, 2012; Gomes et al., 2012) argue that spillovers in returns and volatilities of financial markets can be driven by policy uncertainty via its influence on investment decisions and personal consumption. The recent study of Albulescu et al. (2019) confirms this by proving that the connectedness between the oil and currency markets is mainly driven by policy-induced uncertainty.
Needless to say, empirical studies on the impact of policy uncertainty on the spillovers across commodity and financial markets are very scarce, as available ones have their focus limited to spillover analysis (see, for instance, Hussain et al., 2019; Malik and Umar, 2019; Jiang and Gu, 2016). What causes the spillover has remained understudied. Worse still, no study has linked such connectedness to the influence of health crisis and the uncertainty induced by such. This serves as the main thrust of this paper. In essence, this paper examines the impact of the current COVID-19 pandemic on the volatility connectedness among oil, gold, and financial (stock, bitcoin and exchange rate) markets.
Notably, the current COVID-19 pandemic has created a dent on the global economy more than what is historically known of past crises, including the Spanish Flu pandemic of 1918 and the latest global financial crisis of 2008. To reveal its impact on global markets, Zhang et al. (2020) reveal that the pandemic has raised the volatility of, and inability to predict, stock markets, while Mhalla (2020) show that it has significant consequences on the global crude oil market. Also, it has resulted in the increased level of market fears and policy uncertainties. For instance, the infectious diseases-based equity market volatility index which measures the extent of investors fear due to the outbreak of notable infectious diseases records the highest value of 112.93 on March 15, 2020 as against the pre-COVID-19 maximum value of 36 on January 29, 2009. Other measures of uncertainties follow similar pattern. This is definitely expected as economic and market uncertainties affect the trio of investors, consumers and corporate organizations. Individual investors and corporate firms could be discouraged from investing in new projects while consumers could be led to imbibing conservative spending habits (see Handley and Limao, 2015; Converse, 2017). Similarly, uncertainties raise investors’ sentiments which make them to want to shift attention from the most adversely affected markets to another for safety. An example is seen during this COVID-19 pandemic when investors began to offer their stocks for sale having been pessimistic of the short-run prospects of the stock markets (Salisu and Vo, 2020). This is probably in favour of other assets, hence the spillover across markets during this period. Lastly, if we rely on the global financial cycle channel, the pandemic has induced significantly high global uncertainty which has altered the global financial cycle by affecting capital flows, global credits and movements in assets prices. The eventual outcome of this is the transmission of risks among international markets.
In short, the gap this study covers is examining how COVID-19 drives the spillover connectedness among oil, gold and various financial markets. This is the first paper, to the best of our knowledge, to explore this. The other contribution is in terms of methodologies which are in two folds following the dual nature of this study's objective. We first employ the time-varying parameter vector autoregressions (TVP-VAR) approach of Antonakakis and Gabauer (2017) to explore the spillover connectedness across the markets unlike the dynamic connectedness methods of Diebold and Yılmaz (2009, 2012, 2014). The superiority of the TVP-VAR is that it avoids the problem of choosing the optimal size of rolling window, as well as the avoidance of the loss of observations during estimation. Secondly, we favour the use of the causality-in-quantiles test suggested by Balcilar et al. (2016) which is an improvement over the test of Jeong et al., 2012 to further evaluate the causal impact of the COVID-19 variable measures on the connectedness across the markets. Since financial and high frequencies series often exhibit nonlinearities, asymmetries, structural shifts and regime changes, linear models can produce spurious results due to functional misspecification and dependence of series.
The remainder of this paper has the following structure: the review of relevant studies is done in Section 2, while the methodologies are developed in Section 3. Section 4 is meant for the discussion of the estimated results. We provide the conclusion in Section 5.
2. Literature review
The linkages among different markets have been extensively analyzed in extant literature. However, the studies are largely in parts, with the important role of oil market in influencing other markets appearing to dominate. Major researchers unravel that stock markets can be influenced directly or indirectly by oil shocks (see Broadstock and Filis, 2014; Arouri et al., 2011a). The direct link relates to oil price shocks influencing the current and future cash flows, while the indirect link relates to the influence oil shocks have on interest rates that is often used to influence future cash flows (see Arouri et al., 2011a; Jones and Kaul, 1996).1 In another way, the exclusive relationship between stock and oil markets has also been recently modelled through financialization2 (see Zhang, 2017, 2018; Peng et al., 2018). Thus, the increased financialization process has also strengthened the inter-connectedness between oil and stock markets (see Mensi et al., 2017).
On the issue of spillover, there has been a high evidence of the presence of spillovers between oil and stock markets. Different studies analyze the spillovers between these markets while noting the level of stock aggregation (see Basher et al., 2018; Zhang, 2017; Maghyereh et al., 2016; Phan et al., 2016., 2016, Bouri, 2015 for aggregate stock market level; Narayan and Sharma, 2011; Tiwari et al., 2018; Hamdi et al., 2019; Arouri et al., 2012; Fang and Egan, 2018 for sectoral/industrial stock level; Antonakakis et al., 2018; Peng et al., 2018; Broadstock et al., 2016 for firm level). For instance, through the use of the generalized VAR-GARCH model, Arouri et al. (2011b) note the existence of return and volatility spillovers between oil and stock markets in the Gulf Cooperation Council (GCC) countries. Awartani and Maghyereh (2013) use the Diebold and Yilmaz (2014) technique to unravel the presence of bi-directional spillovers between oil and stock markets in GCC countries. Although, their findings reveal that there is large transmission form oil markets to equities market, Zhang (2017) shows that a contrast link exists after the global financial crisis of 2008. Basher et al. (2018) utilize a structural VAR model to unravel that the oil market transmits shocks to the stock returns of major oil exporting countries. Relating to the oil and stock markets relationship at the sectoral/industrial level, Fang and Egan (2018), while considering the oil and stock markets nexus for China, show that shocks spillover from oil to stock market differs across sectors. They further suggest that information at the sectoral-level should not be neglected while analyzing the spillovers between these two markets (see also Ma et al., 2019; Broadstock and Filis, 2014; Zhang and Cao, 2013; Degiannakis et al., 2013; Narayan and Sharma, 2011). Through the use of quantile-on-quantile Granger causality test, Peng et al. (2018) analyze the nexus between oil and stock markets at firm level. Their study credits the importance of accounting for stock at firm level. They find that there is extreme risk from oil price shocks to firm returns. However, Mohanty et al. (2010) note that there is no significant relationship between oil and stock prices of oil and gas companies in five Central and Eastern Europe.
Also, oil has been linked with gold (Aguilera and Radetzki, 2017; Reboredo, 2013; Wang and Chueh, 2013; Zhang and Wei, 2010) and industrial metals (see Adekoya and Oliyide, 2020). For example, Wang and Chueh (2013) note that oil and gold nexus follows a mixed relationship in the long run, but only a positive relationship experienced in the short run. They further indicate that both gold and oil have been serving as prime benchmarks in the international market (see also Beckmann and Czudaj, 2013a, 2013b; Zhang and Wei, 2010). Gokmenoglu and Fazlollahi, 2015 disclose that movement in oil price augments inflation and price of gold. Also, a good number of studies have shown that gold price can be explained from the fluctuations in oil prices (Beckmann and Czudaj, 2013a, 2013b; Souček, 2013; Wang and Chueh, 2013; Narayan et al., 2010; Le and Chang, 2012; inter alia). Furthermore, since the advent of the financial crisis of 2008, studies have emanated to determine whether investors can find succor in gold against oil price risks. However, most of these studies are unable to establish evidence in favour of the hedging ability of gold (see Reboredo, 2013; Rehman et al., 2018; Salisu and Adediran, 2020).
In another regards, oil has been connected with currency markets. One can relate the linkages between these markets through the portfolio and wealth channel (see Bénassy-Quéré et al., 2007; Buetzer et al., 2012; Coudert et al., 2008; Ding and Vo, 2012; Fedoseeva, 2018; Volkov and Yuhn, 2016), and the terms of trade channel (see Amano and Van Norden, 1998a, 1998b; Chen and Chen, 2007; Huang and Guo, 2007; Lizardo and Mollick, 2010).3 Beckmann and Czudaj (2013b) and Zhang et al. (2008) document the evidence for risk and return spillovers from US dollar to international oil prices. However, recent studies of Brahmasrene et al. (2014), Uddin et al. (2013), Tiwari et al. (2013a, 2013b), among others, reveal that the relationship is bidirectional. Wang and Wu (2012) through the use of vector error correction and Markov-switching frameworks observe that a unidirectional causality runs from oil prices to US dollar, while the study of Beckmann and Czudaj (2013a) shows a reversal.
After the global financial crisis of 2008, there has been a debate as regards the hedging ability of bitcoin, its diversification importance, safe haven features and characteristics as a currency or a commodity (see Guesmi et al., 2019; Pieters and Vivanco, 2017; Katsiampa, 2017; Cheah and Fry, 2015; Dyhrberg, 2016a, 2016b). For instance, Dyhrberg (2016a) enquire into the nature of the relation between bitcoin, stock index, US/EUR and USD/GBP exchange rates. The study unravels that bitcoin exhibits similar returns with gold and US dollar. This is also corroborated by the findings of Dyhrberg (2016b) which disclose that bitcoin offers hedging and safe haven opportunities just like gold, and can be categorized just as US dollar and gold. However, Baur et al. (2018) establish contrasting results to the findings of Dyhrberg (2016a,b). They prove that bitcoin has extremely different features when compared with gold and US stock.
Following the increasing level of integration among international markets, the recent strand of literature is evaluating the interaction among several markets at a time. For instance, Gajardo et al. (2018) employ the MF-ADCCS to analyze the existence of cross-correlation among gold price, oil market, bitcoin, exchange rates and the DJIA. The results from their study show differences between bitcoin's relationship with stock markets, and its relationship with commodities. Relating to the spillover between bitcoin and other markets, Symitsi and Chalvatzis (2018) indicate that there are significant return spillovers from technology and energy stocks to bitcoin. Through the use of DCC-GARCH models, Guesmi et al. (2019) analyze volatility spillover and conditional cross effects between bitcoin and financial assets. Their findings show that the inclusion of bitcoin among hedging strategies that comprise gold, oil and emerging stocks reduce portfolio risks considerably compared to the one without them. In contrast, Trabelsi (2018) adopts the generalized forecast error variance decomposition methodology of Diebold and Yilmaz (2012) and Barunik and Krehlik, 2018 to analyze the volatility spillover among cryptocurrencies and widely traded assets. The study finds no significant evidence for spillover between cryptocurrencies and other assets classes. On the other hand, Bouri et al. (2018) adopt the VAR-GARCH-in-mean model to explore the return and volatility spillovers among bitcoin, commodities, equities, currencies and bond. Evidence is found for bitcoin being a receiver of more shocks than it transmits to other markets.
2.1. Connection of uncertainty with commodity and financial markets
Very recent years have seen to the increased concern about uncertainty and how it affects economic indicators. This has attracted a handful of studies on the impact of various forms of uncertainty on economic activities and different markets (see Converse, 2017; Rodrik, 1991; Handley and Limao, 2015, etc.). For instance, Pástor and Veronesi (2012) use the political uncertainty to establish a negative influence of uncertainty on stock markets. Corroboratively, studies including You et al. (2017), Liu et al. (2017), Arouri et al. (2016), Arouri and Roubaud (2016), Chang et al. (2015) confirm that uncertainty negatively influences stock market returns, and further contributes to stock market volatility. Apart from stock market performances, other studies have also focused on the commodity and currency markets. Aloui et al., 2016 disclose that policy uncertainty is connected to oil prices during financial stress. However, Reboredo and Uddin (2016) find opposing evidence for causal relationship between policy uncertainty and commodity market. For the currency market, Han et al. (2019), using quantile-on quantile approach, confirm the presence of state-dependent spillover effects of uncertainty.
From the foregoing, it is obviously seen that numerous studies have been conducted on the interactions among commodity and financial markets, at least in part, and the literature is now witnessing increasing consideration of the effect of uncertainty on the performances of these markets. However, how uncertainty drives the connectedness among the commodity and financial markets remains exclusively understudied. Meanwhile, in line with the global financial cycle channel, uncertainty can affect the capital flows, global credits and asset prices, thereby leading to significant risks transmission among international markets. The recent work of Albulescu et al. (2019) seems to be notable in this move as it considers and confirms the impact of the U.S. economic policy uncertainty on the interactions among oil and commodity currencies.
However, Rather than economic policy uncertainty, this study focuses on the role of COVID-19 pandemic, measured through the infectious diseases-based equity market volatility and the growth rate of the U.S. COVID-19 reported cases. Uncertainty seems to loom more in the period of crisis. With the current pandemic, the high nature of market volatility, significant oil price fall and the instability of markets are definitely not palatable for governments, investors and investment analysts. Among major happenings, Baker et al. (2020) indicate that the negative impact COVID 19 is the greatest of all time. There is also evidence on how the pandemic has led to the nosediving of the prices of many stocks in different countries and commodities (see Salisu and Vo, 2020; OECD, 2020). Evidently, most of these fluctuations in the workings of these markets might possibly spill over to the other markets. Thus, what will investors and and portfolio managers do when risks and losses are looming continuously in the face of rising cases of this pandemic? What should investors and analysts do in health pandemic situations? What resultant effect should investors and government expect in the assets, financial and commodities markets during similar health crisis in the future? To the best of our knowledge, these questions are unanswered by previous studies. Therefore, we extend extant literature by looking into how the current COVID-19 pandemic influences the connectedness among oil, bitcoin, gold, US dollar and stock markets.
3. Methodology
3.1. Time-varying parameter vector autoregressions (TVP-VAR)
We take a step towards achieving the first objective of this study by adopting the TVP-VAR methodology of Antonakakis and Gabauer (2017) which extends the extant works of the originally proposed dynamic connectedness by Diebold and Yılmaz (2009, 2012, 2014) .4 Antonakakis et al. (2020) disclose two main merits of this technique. First, it helps to overcome the challenge of arbitrarily choosing the optimal rolling-window size. Second, it circumvents the problem of loss of valuable observations, thus making it suitable for short sample also. By adopting this method therefore, we allow the variance to vary through a Kalman Filter estimation with forgetting factors. To start with, the TVP-VAR model is specified as.
| (1) |
| (2) |
with
where and represent and vectors respectively, depicts all the information available until , and are and dimensional matrices respectively. As regards the error term, is an vector, while is an dimensional vector. The time varying variance-covariance matrices, and , are and dimensional matrices respectively. However, the vectorization of as depicted by is an dimensional vector.
To further calculate the generalized impulse response functions (GIRF) and generalized forecast error variance decompositions (GFEVD) which are pertinent in estimating the dynamic connectedness, as is the case with the approach of Diebold and Yilmaz (2014), we transform the TVP-VAR to its vector moving average (VMA) representation based on the Wold theorem as specified in Eqs. (3), (4), (5), (6):
| (3) |
| (4) |
| (5) |
| (6) |
with.
where , and L are and dimensional matrices.
By taking the limit of Eq. (6) as tends to , we get:
| (7) |
such that it follows directly
| (8) |
| (9) |
where represents an matrix.
The term defines the responses of all variables j to a shock in variable i. Due to the absence of a structural model, the differences between an H-step-ahead forecast are computed, for where variable i is shocked and another where variable i is not shocked. This difference can be regarded to be due to shock in variable i, which is consequently computed by:
| (10) |
| (11) |
| (12) |
where is an selection vector with 1 in the jth position, and zero otherwise. Also, we compute the , which is the pairwise directional connectedness from j to i and further demonstrates the influence variable j has on variable i in terms of its forecast variance share. However, the variance shares are then normalized by summing up all rows to one. This depicts that all variables together explain 100% of variable i's forecast error variance. The GFEVD is calculated as follows:
| (13) |
where and . Also, the numerator term denotes the cumulative effect of a shock in variable i, while the denominator term represents the cumulative effect of all the shocks. Thereafter, we compute the total connectedness index through the use of the GFEVD thus:
| (14) |
The connectedness approach in Eq. (14) generally shows how a shock in one variable spills over to other variables under investigation. However, to further analyze the directional connectedness, the method under consideration divides it into three: total directional connectedness to others; total directional connectedness from others; and net total directional connectedness.
First, the total directional connectedness to others as shown in Eq. (15) analyses a situation where variable i transmits its shocks to all other variables j.
| (15) |
Second, we account for the shocks variable i receives from other variables j in Eq. (16). That is, the directional connectedness from others:
| (16) |
Lastly, we subtract Eq. (16) from (15) to derive the net total directional connectedness. In other words, to obtain the net total directional connectedness, we subtract the total directional connectedness from others from the total directional connectedness to others.
| (17) |
Intuitively, Eq. (17) can be interpreted as the influence variable i has on the analyzed network. Thus, a positive means that variable i influences the network more than itself being influenced, while a negative means that variable i is driven by the network.
Finally, we dissect the net total directional connectedness to further examine the bidirectional relationships by computing the net pairwise directional connectedness (NPDC) as shown in Eq. (18).
| (18) |
If , it implies that variable i is dominated by variable j. However, if , then variable i dominates variable j.
3.2. Causality tests
After the derivation of the total and the net spillovers through the use of the TVP-VAR, we proceed to the second phase of our analyses. Here, we examine the causal effect of the current COVID-19 pandemic (proxied by the equity market volatility due to infectious diseases and the growth rate of the U.S. COVID-19 reported cases) on the connectedness across the oil, gold, bitcoin, stock and USD (measured through the volatility spillover series). To achieve this, we adopt the linear causality test of Granger (1969) and the non-linear causality (causality-in-quantiles) test of Jeong et al., 2012 which was later improved by Balcilar et al. (2016).
Starting with the linear causality test, it analyzes the relationship between two variables at a time, where is the dependent variable and is the independent variable, which in this study are the proxies for the connectedness across the assets and the COVID-19 measures. The VAR model is specified thus:
| (19) |
| (20) |
where and are error terms which are uncorrelated. Granger (1969) shows that Granger-causes if the lagvalues of can predict the current value of .
However, financial and high frequency series have often been fraught with nonlinearity, structural shifts and regime changes. Due to the presence of these undesirable statistical features, there have been a quite number on non-linear causality techniques. Among other options, we adopt the causality-in-quantiles test of Jeong et al., 2012 due to two pertinent reasons. First, its robustness to functional misspecification error and ability to detect general dependence between time series makes the technique unique. Second, the test does not only test for causality in the mean, but also causality that may exist in the tail area of the joint distribution of the series.
In the spirit of Jeong et al., 2012, does not cause in the -quantile with respect to the lag-vector of if:
| (21) |
Thus, is a prima facie cause of in the quantile with relation to if:
| (22) |
where is the quantile of depending on t, and.
Also, assuming , and and denote the conditional distribution function of given and respectively. Based on the assumption , the conditional distribution is absolutely continuous in for almost all . Denoting and will then transform to having with a probability of one.
Thereafter, we test for the null and alternative hypotheses of Eqs. (21), (22) as defined in Eqs. (23), (24).
| (23) |
| (24) |
To consistently test for the null hypothesis as specified in Eq. (23), Jeong et al., 2012 specify the distance measure as follows:
| (25) |
Importantly, the condition of only holds if the null hypothesis as specified in Eq. (23) is true, while holds if the alternative hypothesis is true (Eq. (24)). To proceed, Jeong et al., 2012 note that the feasible kernel-based test statistic for K can be specified thus:
| (26) |
where is the kernel function with bandwidth r, while T, P, are sample size, lag-order and the estimate of the unknown regression error. The regression error is specified below:
| (27) |
Also, we proceed with Jeong et al., 2012 methodology by estimating the parameter of the conditional quantile of given through the non-parametric kernel method as:
| (28) |
where the Nadarya-Watson kernel estimator is given by:
| (29) |
where the kernel function in this case is and r is the bandwidth.
Later, Balcilar et al. (2016) extend the framework of Jeong et al., 2012 by developing a test for the second moment. Therefore, they adopt the nonparametric Granger-quantile-causality approach by Nishiyama et al. (2011). To illustrate the causality in higher order moment, we assume:
| (30) |
where is the white noise process, and and are equal to the unknown functions that fulfill the stationarity condition. Although, this specification does not allow Granger-type causality testing from , however, it could detect the “predictive power” from to when is a general nonlinear function. We further re-formulate Eq. (30) to account for the null and alternative hypotheses for causality in variance in Eqs. (21), (22), respectively:
| (31) |
| (32) |
We obtain the feasible test statistic for the testing of the null hypothesis in Eq. (31), and then replace in Eq. (27) – (29) with (that is, volatility). Unlike the approach of Jeong et al., 2012, we overcome the issue that causality in mean implies causality in variance. More specifically, we can interpret the causality in higher-order moments through the use of the following model:
| (33) |
Thus, we specify the higher order quantile causality as:
| (34) |
| (35) |
We test that Granger-causes in quantile up to the K-th moment by using Eq. (34) to construct the test statistic of Eq. (26) for each k. Although, Nishiyama et al. (2011) note that combining different statistics for each into one statistic for the joint null in Eq. (34) which is mutually correlated appears not to be easy, circumventing this issue requires the adoption of a sequential-testing method described by Nishiyama et al. (2011) with some modifications. We start by testing for the nonparametric Granger-causality in mean (k = 1). Failure to reject the null hypothesis of k = 1 does not translate into non-causality in variance. Therefore, we construct the tests for k = 2. We select the bandwidth by employing least squares validation technique and then employ the Guassian kernels for .
4. Discussion of empirical results
4.1. Preliminary analyses
We begin by briefly indicating the nature and sources of the data used. The data obtained for analysis in this study are the various financial and commodity markets series including dollar exchange rate, prices of gold, crude oil, S&P 500 stock and bitcoin, and the COVID-19 proxies which are the equity market volatility due to infectious diseases index and the U.S. COVID-19 reported cases. Since our focus is on the COVID-19 period, the data are on daily frequency from January 21, 2020 to July 2, 2020 so that enough observations are generated. Prices of bitcoin and the U.S. COVID-19 reported cases are respectively sourced from coinmarketcap.com and the website of the Centres for Disease Control and Prevention (covid.cdc.gov), while the remaining data are obtained from Federal Reserve Economic Database (fred.stlouisfed.org). We provide first-hand information on the descriptive and distribution properties of these series or their transformed values in order to keep up with standard practice in the empirical literature. As observed from Table 1 , only oil and stock report average negative returns during the period of global pandemic among all the assets under consideration. Bitcoin, gold and USD show positive returns with the highest reported for gold (0.122%), suggesting that investors in these three markets are likely to enjoy positive gains. This is unlike the evidence of loss associated with the oil and stock markets. Of course, the reasons for these results are not far-fetched. The global crude oil and stock markets are more flexible and sensitive to shocks from whatever source. This is due to their strong connection with the macroeconomy. For instance, crude oil is a crucial input into production processes (see Adekoya and Adebiyi, 2019) such that significant alteration to industrial and commercial activities affects its demand, thus lowering its price. This is true of most economies of the world during the current COVID-19 pandemic that results into the shut-down of most firms and the paralysis of economic activities. Consequently, price of oil significantly fell following a fall in its demand. Whatever creates fear or uncertainty in investors has the tendency of adversely affecting the performance of the stock markets. The pandemic has raised investors’ sentiments so high that it is regarded as the crisis with the greatest impact on stock markets (see Baker et al., 2020). On the other hand, others report positive average returns due to their nature. Bitcoin is not physically traded as it is an electronic asset whose trade is not easily impaired. Although gold is a physical asset, it has a very high intrinsic value and has enjoyed stability over time as a good store of value (see Adekoya and Oliyide, 2020). This has made it to even be a suitable hedge against oil and stock markets risks during this period.
Table 1.
Descriptive statistics.
| Asset returns |
Health indicators |
||||||
|---|---|---|---|---|---|---|---|
| Bitcoin | Gold | Oil | Stock | USD | COVID | ID-EMV | |
| Mean | 0.047 | 0.122 | −0.330 | −0.039 | 0.0124 | 13.337 | 24.698 |
| Std. Dev. | 6.133 | 1.400 | 12.255 | 3.088 | 0.553 | 23.552 | 16.446 |
| Skewness | −3.907 | −0.369 | −1.341 | −0.584 | −0.150 | 3.385 | 0.462 |
| Kurtosis | 31.908 | 6.341 | 14.435 | 6.484 | 4.317 | 17.599 | 2.770 |
| Jarque-Bera | 4147.268 | 54.146 | 638.012 | 62.445 | 8.434 | 1197.711 | 4.190 |
Value in bold suggests the non-rejection of the null hypothesis of normal distribution.
All the returns series, except USD, are also seen to be highly volatile judging from the values of the standard deviation. Oil is associated with the highest degree of variability, followed by bitcoin and then stock. Concerning their distribution, they are all negatively skewed, coupled with excess kurtosis. It is thus not surprising why the Jarque-Bera test rejects the null hypothesis of normal distribution for all of them.
Turning to the health indicators, the extent to which the COVID-19 pandemic hits financial markets and even the so-called advanced countries is seen in the high mean values of the equity market volatility due to infectious diseases (EMV-ID) and the growth rate of COVID-19 reported cases in the U.S. While the average infectious diseases-based uncertainty in the equity market is 24.698, the reported cases of COVID-19 pandemic grow at a daily average of 13.337%. These measures are also followed by high variability. However, while the growth rate of COVID-19 is far from being normally distributed having shown high skewness and kurtosis estimates, the Jarque-Bera test discloses ID-EMV as being normally distributed as also reflected in its fair skewness and kurtosis values.
These descriptive statistics offer basic insights that are worth pointing out as we proceed in the analysis. The first is that the positive returns of some of the assets and the negative returns of the others may suggest the likelihood of give-and-take nexus among them. In other words, as we would find out in the next section, it is most likely that there is significant volatility spillovers and connectedness among the assets. Secondly, both the asset returns and the health-based factors demonstrate high degree of volatility. This suggests that the latter, especially the infectious diseases-based equity market volatility, may be responsible for any inherent volatility spillovers among the former. It is thus necessary to examine the possibility of the COVID-19 health indicators to cause the connectedness among the assets. Lastly, with the series being largely non-normally distributed, coupled with negative/positive skewness and high kurtosis values, it shows that they are heavily tailed either to the right or left, and have excess kurtosis. What this merely indicates is the likelihood of nonlinearity, structural breaks and regime changes in the series. Hence, applying linear models which are basically known for constant parameter estimation would yield results devoid of originality and reliability for appropriate policy formulation and investment decisions. This therefore informs our proposed causality-in-quantiles test which accounts for all the above highlighted features.
4.2. Spillover results
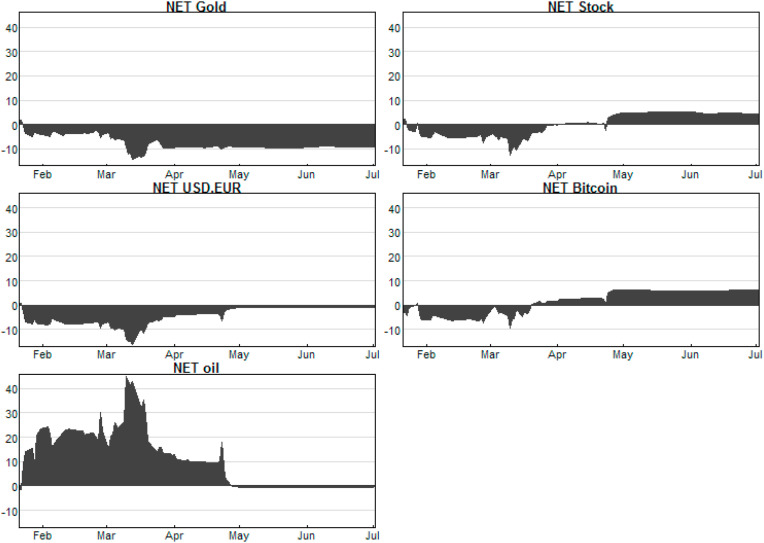
We are more concerned in this study with how the volatility spillovers across the commodity and financial markets are affected by the considered COVID-19 health indicators rather than the individual returns of the assets. Therefore, it becomes necessary to first estimate the volatility spillovers among the assets. The estimates of the spillover analysis are presented in Table 2 . Three things matter in the results, which are the unidirectional spillovers, the total spillover from and to a particular asset, and the net directional spillovers for individual asset. The net directional spillover is obtained by subtracting the total contributions received by an asset from others from the total contributions it gives to others. This makes the asset in question to be a net transmitter of shocks if a positive net spillover value is obtained. Otherwise, it is a net shock receiver. Summarizing the results, it can be seen that there is a very strong spillover effect among the assets with all of them significantly giving and receiving. On average, stock and oil are the highest givers of shocks with values being 65.5% and 63.7% respectively, while gold is the least giver (32.9%). USD and bitcoin also give much with their individual values exceeding 50%. Interestingly, the assets that give less appear to be those that receive more. For instance, gold and USD receive more shocks from others (71.6% and 73.7% respectively), while oil receives the least (10.5%). Since all the assets transmit and receive, it is important to determine whether each of them receives more shocks or gives more, as revealed by the net spillover. Obviously, only gold and USD are net receivers of shocks, implying that they receive more than they transmit. The net spillover results in Table 2 are also consistent with the net spillover graphs in Fig. 2.5 These results strongly align with expectations, and they corroborate the descriptive results in Table 1 where it is shown that gold and USD/EUR have positive returns. Their relative stability during this period seems to be the reason why shocks from other assets move in their direction. Gold particularly stands as a good hedge against the risks from other markets for this time frame. On the other hand, oil and stock appear to be the most adversely affected as evidenced from their negative returns and empirical evidences. Investors in these markets are therefore giving attention to other assets.
Table 2.
Dynamic connectedness results.
| To(i) | Gold | Stock | USD/EUR | Bitcoin | Oil | From(j) |
|---|---|---|---|---|---|---|
| Gold | 28.4 | 16.6 | 15.4 | 18.0 | 21.6 | 71.6 |
| Stock | 8.7 | 35 | 21.9 | 23.4 | 10.9 | 65 |
| USD/EUR | 9.3 | 23.4 | 26.3 | 12.9 | 28.1 | 73.7 |
| Bitcoin | 6.6 | 25 | 13.1 | 52.3 | 3.1 | 47.7 |
| Oil | 8.3 | 0.5 | 1.6 | 0.1 | 89.5 | 10.5 |
| Contribution to others | 32.9 | 65.5 | 51.9 | 54.3 | 63.7 | 268.4 |
| Net directional connectedness | −38.7 | 0.5 | −21.8 | 6.6 | 53.3 | TCI = 53.7% |
Fig. 2.
Total net spillover for each asset.
Interestingly, our net spillover results largely contradict those of Hussain et al. (2019) despite using similar spillover framework. For instance, they establish that stock is neither a transmitter nor a net receiver of shocks, and that oil and gold are respectively net receiver and net transmitter. We can then argue that the current COVID-19 pandemic is responsible for the dynamic change in the connectedness among the financial markets. This is consistent with the total spillover graph in Fig. 1 where it is seen that the overall volatility spillover peaked during the months when the COVID-19 pandemic was really hitting hard on countries of the world, and newspapers reports gathered momentum. This further makes it imperative to examine if the connectedness among the assets is driven by the COVID-19 pandemic health indicators. Meanwhile, Hussain et al. (2019) argue that metals, oil and financial markets are functionally linked via diverse channels. Hence, financial market volatility can sweep into other connected markets via the business cycle (Wang and Chueh, 2013; Kearney and Lombra, 2009). With the current health pandemic having significantly altered business cycle, it is important to examine its effect on the connectedness across the markets. The next section addresses this.
Fig. 1.
Overall spillover.
4.3. Causality tests results
So far, we have observed very strong volatility connectedness across the commodity and financial markets with gold being the highest net receiver and oil the highest net transmitter of shocks. We now focus on the role played by COVID-19 pandemic in the volatility connectedness among these markets. We proxy the COVID-19 pandemic with two indicators, namely equity market volatility due to infectious diseases (ID-EMV) and the growth rate of COVID-19 pandemic reported cases in the U.S. (COVID), and for which distinct results are reported. For robustness, the causality results are in three folds for each category of COVID-19 pandemic indicators: (i) effect of COVID-19 pandemic on the overall spillover; (ii) effect of COVID-19 pandemic on the total net spillover for each asset; and (iii) effect of COVID-19 pandemic on net pair-wise spillover.
We begin with the linear causality test results which are presented in Table 3, Table 4 . When ID-EMV is made as the causal variable, Table 3 shows that the null hypothesis of Granger-non-causality cannot be rejected in a relatively large number of cases. The few exemptions where rejection is found at either 5% or 10% significance levels are the overall spillover, net spillovers for bitcoin, gold and stock, and net pair-wise spillover between stock and gold, bitcoin and stock, and USD and stock. If we turn to Table 4 where COVID is the causal variable, the causal evidence is just about half of the cases, but those with significant estimates are quite different from when ID-EMV is the causal variable, especially for the net pair-wise spillovers. In this regards, spillover connections with oil find more significance (net spillover for oil, net pair-wise spillover between oil and each of gold, stock and USD) unlike in Table 3. In addition, the net spillovers for stock and USD, net pair-wise spillover between bitcoin and USD, and USD and stock are found to be significant.
Table 3.
Linear causality test results: ID-EMV as the causal variable.
| F-stat. | Prob. | |
|---|---|---|
| Panel A:: ID-EMV does not Granger-cause: | ||
| overall spillover | 4.16590** | 0.0182 |
| Panel B:: ID-EMV does not Granger-cause: | ||
| net spillover for bitcoin | 3.46913** | 0.0348 |
| net spillover for gold | 3.35560** | 0.0387 |
| net spillover for oil | 2.00393 | 0.1400 |
| net spillover for stock | 3.51790** | 0.0332 |
| net spillover for USD | 1.28332 | 0.2815 |
| Panel C:: ID-EMV does not Granger-cause: | ||
| net spillover between oil and bitcoin | 1.40920 | 0.2490 |
| net spillover between oil and gold | 0.54799 | 0.5798 |
| net spillover between oil and stock | 2.07973 | 0.1301 |
| net spillover between oil and USD | 1.92577 | 0.1509 |
| net spillover between stock and gold | 2.38676* | 0.0969 |
| net spillover between bitcoin and gold | 2.13728 | 0.1231 |
| net spillover between bitcoin and stock | 3.34563** | 0.0391 |
| net spillover between bitcoin and USD | 0.52012 | 0.5960 |
| net spillover between USD and gold | 3.61543** | 0.0303 |
| net spillover between USD and stock | 1.97756 | 0.1436 |
**and * denote the rejection of the null hypothesis of Granger-non-causality at 5% and 10% significance levels respectively.
Table 4.
Linear causality test results: COVID as the causal variable.
| F-stat. | Prob. | |
|---|---|---|
| Panel A:: COVID does not Granger-cause: | ||
| overall spillover | 0.54183 | 0.5833 |
| Panel B:: COVID does not Granger-cause: | ||
| net spillover for bitcoin | 0.99088 | 0.3747 |
| net spillover for gold | 0.79977 | 0.4522 |
| net spillover for oil | 4.45215** | 0.0140 |
| net spillover for stock | 2.93897* | 0.0573 |
| net spillover for USD | 5.09877*** | 0.0077 |
| Panel C:: COVID does not Granger-cause: | ||
| net spillover between oil and bitcoin | 1.92771 | 0.1506 |
| net spillover between oil and gold | 4.00886** | 0.0210 |
| net spillover between oil and stock | 3.65550** | 0.0292 |
| net spillover between oil and USD | 5.02702** | 0.0082 |
| net spillover between stock and gold | 0.92037 | 0.4016 |
| net spillover between bitcoin and gold | 1.86704 | 0.1597 |
| net spillover between bitcoin and stock | 0.99227 | 0.3742 |
| net spillover between bitcoin and USD | 4.36678** | 0.0151 |
| net spillover between USD and gold | 1.83812 | 0.1642 |
| net spillover between USD and stock | 3.35715** | 0.0386 |
***, ** and * denote the rejection of the null hypothesis of Granger-non-causality at 1%, 5% and 10% significance levels respectively.
We can conclude from the results that, to some extent, the linear causality test reveals just fair evidence of causal relationship between COVID-19 pandemic and the connectedness among the assets. As we pointed out under the statistical description, the series are associated with fat tails, excess kurtosis and non-normality. These undesirable statistical features are first-hand indication of the possibility of nonlinearity, structural breaks and regime changes in the series. It is also known from empirical evidences that financial series often exhibit nonlinear movements and structural shifts along their time paths (see Adekoya and Oliyide, 2020). Against this evidence, linear models become weak in producing reliable results. Hence, we choose to consider causality-in-quantiles test, a nonlinear model, which is flexible and can conveniently account for the aforementioned undesirable statistical issues. To provide formal evidence for the need to use this nonlinear technique, however, we conduct the BDS test which was developed by Brock et al. (1996). The results support the rejection of the null hypothesis of serial dependence of the spillover residual series across all the dimensions regardless of the COVID-19 pandemic indicator used (see Table 5, Table 6 ). The only exemption is the net pair-wise spillover between bitcoin and stock. Overall, the BDS test suggests that the series are nonlinearly related, thus justifying our choice of causality-in-quantiles test.
Table 5.
BDS test results: ID-EMV as the causal variable.
| Spillover series | Dimension |
||||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | |
| Overall spillover | 0.068*** | 0.125*** | 0.165*** | 0.181*** | 0.204*** |
| Net spillover for bitcoin | 0.054*** | 0.118*** | 0.182*** | 0.227*** | 0.250*** |
| Net spillover for gold | 0.081*** | 0.162*** | 0.218*** | 0.249*** | 0.271*** |
| Net spillover for oil | 0.052*** | 0.125*** | 0.184*** | 0.218*** | 0.242*** |
| Net spillover for stock | 0.058*** | 0.131*** | 0.192*** | 0.235*** | 0.257*** |
| Net spillover for USD | 0.053*** | 0.139*** | 0.195*** | 0.223*** | 0.247*** |
| Net spillover between oil and bitcoin | 0.104*** | 0.173*** | 0.212*** | 0.227*** | 0.231*** |
| Net spillover between oil and gold | 0.071*** | 0.141*** | 0.185*** | 0.212*** | 0.219*** |
| Net spillover between oil and stock | 0.080*** | 0.157*** | 0.215*** | 0.248*** | 0.264*** |
| Net spillover between oil and USD | 0.053*** | 0.102*** | 0.146*** | 0.173*** | 0.190*** |
| Net spillover between stock and gold | 0.066*** | 0.128*** | 0.182*** | 0.209*** | 0.221*** |
| Net spillover between bitcoin and gold | 0.067*** | 0.135*** | 0.185*** | 0.230*** | 0.253*** |
| Net spillover between bitcoin and stock | -0.000 | -0.000 | -0.001 | -0.001 | -0.002 |
| Net spillover between bitcoin and USD | 0.053*** | 0.129*** | 0.174*** | 0.199*** | 0.217*** |
| Net spillover between USD and gold | 0.027** | 0.081*** | 0.135*** | 0.172*** | 0.198*** |
| Net spillover between USD and stock | 0.037*** | 0.090*** | 0.128*** | 0.170*** | 0.195*** |
***Denotes the rejection of the null hypothesis of serial dependence, and therefore presence of nonlinearity, at 1% significance level.
Table 6.
BDS test results: COVID as the causal variable.
| Spillover series | Dimension |
||||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | |
| Overall spillover | 0.068*** | 0.131*** | 0.181*** | 0.204*** | 0.226*** |
| Net spillover for bitcoin | 0.067*** | 0.128*** | 0.194*** | 0.238*** | 0.260*** |
| Net spillover for gold | 0.069*** | 0.138*** | 0.196*** | 0.228*** | 0.252*** |
| Net spillover for oil | 0.063*** | 0.136*** | 0.194*** | 0.227*** | 0.249*** |
| Net spillover for stock | 0.059*** | 0.130*** | 0.180*** | 0.206*** | 0.219*** |
| Net spillover for USD | 0.065*** | 0.147*** | 0.197*** | 0.218*** | 0.242*** |
| Net spillover between oil and bitcoin | 0.095*** | 0.165*** | 0.207*** | 0.223*** | 0.227*** |
| Net spillover between oil and gold | 0.076*** | 0.145*** | 0.188*** | 0.211*** | 0.220*** |
| Net spillover between oil and stock | 0.037*** | 0.093*** | 0.149*** | 0.181*** | 0.198*** |
| Net spillover between oil and USD | 0.041*** | 0.098*** | 0.148*** | 0.174*** | 0.190*** |
| Net spillover between stock and gold | 0.066*** | 0.134*** | 0.182*** | 0.207*** | 0.222*** |
| Net spillover between bitcoin and gold | 0.072*** | 0.151*** | 0.211*** | 0.255*** | 0.277*** |
| Net spillover between bitcoin and stock | -0.000 | -0.001 | -0.00 | -0.002 | -0.003 |
| Net spillover between bitcoin and USD | 0.035** | 0.088*** | 0.135*** | 0.172*** | 0.190*** |
| Net spillover between USD and gold | 0.038*** | 0.091*** | 0.141*** | 0.184*** | 0.208*** |
| Net spillover between USD and stock | 0.031** | 0.074*** | 0.104*** | 0.131*** | 0.157*** |
***Denotes the rejection of the null hypothesis of serial dependence, and therefore presence of nonlinearity, at 1% significance level.
The results for the causality-in-quantiles test are presented in Fig. 3, Fig. 4 . Against any reasonable doubt, there are significant improvements in the results when nonlinearity is accounted for compared to those of the linear Granger-causality model. In Fig. 3 which shows the nonlinear effect of ID-EMV on the spillovers (overall, net spillover for each asset and net pair-wise spillover between the assets), it can be seen that only for the net pair-wise spillover between bitcoin and stock can we not reject the null hypothesis of causality from ID-EMV. Others are significant at either or both lower- and middle-level quantiles as their causality curves are above the 5% significant line. The causal impact of ID-EMV is exceptionally profound in some cases, such as for total net spillover for bitcoin, net pair-wise spillover between bitcoin and gold, USD and stock, oil and stock, and oil and USD, following their significance in most of the quantiles.
Fig. 3.
Causality-in-quantiles test result for the effect of ID-EMV on connectedness across oil, gold and financial markets
Fig. 4.
Causality-in-quantiles test result for the effect of COVID on connectedness across oil, gold and financial markets
Considering COVID as the causal variable (see Fig. 4), significance at 5% is mostly found for most of the spillover series at the lower quantiles. Also, COVID ceases to significantly cause overall spillover and net pair-wise spillover between oil and bitcoin. Notwithstanding, similar results as those of ID-EMV are also found. For instance, COVID also causes the net pair-wise spillovers between bitcoin and gold, oil and stock, and oil and USD in most of the quantiles.
Overall, the findings from this study show that the current COVID-19 pandemic has significant causal impact on the spillover connectedness across the commodity and financial assets. The pandemic has serious implications on the interactions across the commodity and financial markets via its alteration of the global business cycle which drives investors’ sentiments and consequently raises risks variance across the markets. Of course, the influence of the pandemic is the reason behind the difference between the volatility spillover results reported in this study and those of Hussain et al. (2019). However, our findings run similar to the evidence provided by the study of Albulescu et al. (2019) which establishes that economic policy uncertainty drives volatility spillover in the oil and commodity currency markets. In addition to this evidence, accounting for nonlinearity in the causal relationship is of utmost importance, as the neglect of such would produce spurious results.
5. Conclusion
This study is motivated by two factors. First, there are theoretical propositions on the connectedness among commodity and financial markets through various channels. This has resulted into the increasing empirical evidences on the connectedness among these markets, although in split forms. Second, the current COVID-19 pandemic has been adjudged as the health crisis of all time with the greatest impact on financial markets, especially the stock markets. Beyond this, it is believed to have significantly altered global business or financial cycle. Meanwhile, changes in the global business or financial cycle are symbolic in the movements in global capital flows and prices of tradable assets across diverse financial markets (see Rey, 2018; Nier et al., 2014) since they induce risks preferences for investors. If the global economy has truly experienced changes in the business cycle during this period, it can then be empirically argued that the COVID-19 pandemic drives the connectedness among the commodity and financial markets.
Thus, the thrust of this paper is to examine the causal effect of the current COVID-19 pandemic on the connectedness among the globally traded commodity and financial assets (oil, gold, stock, bitcoin and dollar-euro exchange rate). To the best of our knowledge, no study has covered this gap in the literature. The analyses are in two folds. We first examine the volatility spillovers among the assets. After this, we determine the causal effect of COVID-19 pandemic (which is proxied by two health indicators namely infectious diseases-induced equity market volatility index and the growth rate of the COVID-19 reported cases in the U.S.) on three categories of spillovers (overall spillover, total net spillover for each asset and net pair-wise spillover between the assets). We find that there is strong volatility spillover among the assets as they are all significant transmitters and receivers of shocks. Moreover, both gold and USD are found to be net receivers of shocks, while others are net transmitters. Further analysis through graphical illustration reveals that overall spillover is higher for about the first four and half months of the pandemic, and these months interestingly coincide with the periods when global panic over the pandemic was at its peak. Based on this evidence, we proceed to the causality analysis with the nonlinear causality test (causality-in-quantiles) proving superior to the linear Granger-causality test. The findings show that COVID-19 has significant causal effect on the connectedness across the assets. Particularly, the effect of the pandemic on the connectedness across the markets is stronger mostly at the lower- and middle-level quantiles, while only in very few cases is insignificance established. These results are robust to the two COVID-19 health indicators used.
Investors and policy makers can draw policy insights from these findings. There is a strong alignment between the findings of this study and the postulation of the global business or financial cycle channel which is in a way driven by the current COVID-19 pandemic that induces investors' sentiments and risks, and further transmits the same across the commodity and financial assets. This is because the pandemic adversely affects global capital flows, credit transactions and financial liquidity. It is thus a very smart investment strategy for investors to closely monitor changes in global business cycle, especially during the period of notable global health crisis, and adjust their investment portfolios accordingly in order to mitigate or circumvent losses. This can even be generalized for the periods of any crisis that affects global capital flow and credit activity which further have the tendency of altering the business cycle and consequently inducing transmission of risks. Also, it is crucial for investors to include assets with relative stability, such as gold, in their investment portfolios so as to advance the performance of their overall adjusted risks. For policy makers, it is important to strengthen their financial markets, especially the stock market, against exposure to risks. The financial markets have for long been used to gauge the performance of the macroeconomy, thus making the overall economy to be at the receiving end of the exposure of the the financial markets to negative shocks. Finally, it would be an interesting empirical adventure for future studies to examine how the pandemic connects spillover among commodity and financial markets’ fears rather than returns.
Footnotes
This direct and indirect relationship has been established by many studies. For instance, the works of Arouri et al., 2011and Basher et al. (2018) note that in the long run, stock prices should equal the summation of discounted values of expected future cash flows at different investment periods. Evidently, oil is one of the major factor inputs in the production of goods and services, thus in a way, its price changes can directly influence firms' future cash flow (Huang et al., 1996; Jones and Kaul, 1996). Also, the discount rate which encompasses the expected inflation and real interest rate is also affected by oil price fluctuations (see Jones and Kaul, 1996).
The work of Zhang (2017) note that studies has increasingly linked oil price changes to stock markets since the 2008 financial crisis. Importantly, the rising number of oil-related financial derivatives has also increased faster the process of financialization in the oil market (See Ji and Zhang, 2019; Ma et al., 2019).
The portfolio channel relates the benefits (that is, wealth transfer) oil exporting countries gain from a rise in the oil price. This channel relates the nominal exchange rate to the current oil prices. The terms of trade channel relate oil prices to fluctuations in real exchange rate through its pertinent effect on the terms of trade.
Methodologically, the clear difference and improvement has also been noted in the works of Gabauer and Gupta (2018), Antonakakis et al., 2018, Antonakakis et al., 2018, etc.
Only the overall spillover and total net spillover graphs are reported due to space consideration.
References
- Adekoya O.B., Adebiyi A.N. Oil price-inflation pass-through in OECD countries: the role of asymmetries, impact of global financial crisis and forecast evaluation. Intl. J. Ener. Sec. Mang. 2019;14:126–147. doi: 10.1108/IJESM.02.2019.0013. [DOI] [Google Scholar]
- Adekoya O.B., Oliyide A.J. The hedging effectiveness of industrial metals against different oil shocks: evidence from the four newly developed oil shocks datasets. Resour. Pol. 2020;69 doi: 10.1016/j.resourpol.2020.101831. [DOI] [Google Scholar]
- Aguilera R., Radetzki M. The synchronized and exceptional price performance of oil and gold: explanations and prospects. Resour. Pol. 2017;54:81–87. [Google Scholar]
- Ahmadi M., Bashiri N., Manera M. How is volatility in commodity markets linked to oil price shocks? Energy Econ. 2016;59:11–23. [Google Scholar]
- Akbar M., Iqbal F., Noor F. Bayesian analysis of dynamic linkages among gold price, stock prices, exchange rate and interest rate in Pakistan. Resour. Pol. 2019;62:154–164. 2019. [Google Scholar]
- Albulescu C.T., Demirer R., Raheem I.D., Tiwari A.K. Does the U.S. economic policy uncertainty connect financial markets? Evidence from oil and commodity currencies. Energy Econ. 2019;83:375–388. [Google Scholar]
- Aloui R., Gupta R., Miller S.M. Uncertainty and crude oil return. Energy Econ. 2016;55:92–100. [Google Scholar]
- Amano R., Van Norden S. Exchange rates and oil prices. Rev. Int. Econ. 1998;6:683–694. [Google Scholar]
- Amano R., Van Norden S. Oil prices and the rise and fall of the US real exchange rate. J. Int. Money Finance. 1998;17:299–316. [Google Scholar]
- Antonakakis N., Cunado J., Filis G., Gabauer D., De Gracia F.P. Oil volatility, oil andgas firms and portfolio diversification. Energy Econ. 2018;70:499–515. [Google Scholar]
- Antonakakis N., Gabauer D. University Library of Munich; Munich: 2017. Refined Measures of Dynamic Connectedness Based on TVP-VAR. Technical Report. [Google Scholar]
- Antonakakis N., Chatziantoniou I., Gabaur D. Redefined measures of dynamic connectedness based on time-varying parameter vector autoregressions. J. Risk Financ. Manag. 2020;13(84) [Google Scholar]
- Arouri M., Roubaud D. On the determinants of stock market dynamics in emerging countries: the role of economic policy uncertainty in China and India. Econ. Bull. 2016;36:760–770. [Google Scholar]
- Arouri M.E.H., Jouini J., Nguyen D.K. Volatility spillovers between oil prices and stock sector returns: implications for portfolio management. J. Int. Money Finance. 2011;30(7):1387–1405. [Google Scholar]
- Arouri M.E.H., Lahiani A., Nguyen D.K. Return and volatility transmission between world oil prices and stock markets of the GCC countries. Econ. Modell. 2011;28(4):1815–1825. [Google Scholar]
- Arouri M.E.H., Jouini J., Nguyen D.K. On the impacts of oil price fluctuations on European equity markets: volatility spillover and hedging effectiveness. Energy Econ. 2012;34(2):611–617. [Google Scholar]
- Antonakakis N., Gabauer D., Gupta R., Plakandaras V. Dynamic connectedness of uncertainty across developed economies: a time-varying approach. Econ. Lett. 2018;166:63–75. [Google Scholar]
- Arouri M., Estay C., Rault C., Roubaud D. Economic policy uncertainty and stock markets: long-run evidence from the US. Finance Res. Lett. 2016;18:136–141. [Google Scholar]
- Awartani B., Maghyereh A.I. Dynamic spillovers between oil and stock markets in the Gulf cooperation Council countries. Energy Econ. 2013;36:28–42. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Terry S.J. 2020. Covid-induced economic uncertainty. NBER Working Paper No. 26983. [Google Scholar]
- Balcilar M., Bekiros S., Gupta R. The role of news-based uncertainty indices in predicting oil markets: a hybrid nonparametric quantile causality method. Empir. Econ. 2016;1–11 doi: 10.1007/s00181-016-1150-0. [DOI] [Google Scholar]
- Barunik J., Krehlik T. Measuring the frequency dynamics of financial connectedness and systemic risk. Journal of Financial Econometrics. 2018;16:271–296. [Google Scholar]
- Basher S.A., Haug A.A., Sadorsky P. The impact of oil-market shocks on stock returns in major oil-exporting countries. J. Int. Money Finance. 2018;86:264–280. [Google Scholar]
- Baur D.G., Hong K., Lee A.D. Bitcoin: medium of exchange or speculative assets? Journal of International Markets, Institutions and Money. 2018;54:177–189. [Google Scholar]
- Beckmann J., Czudaj R. Oil and gold price dynamics in a multivariate cointegration framework. Int. Econ. Econ. Pol. 2013;10:453–468. [Google Scholar]
- Beckmann J., Czudaj R. Oil prices and effective dollar exchange rates. Int. Rev. Econ. Finance. 2013;27:621–636. [Google Scholar]
- Bedoui R., Braiek S., Guesmi K., Chevallier J. On the conditional dependence structure between oil, gold and USD exchange rates: nested copula based GJR-Garch model. Energy Econ. 2019;80:876–889. [Google Scholar]
- Bénassy-Quéré A., Mignon V., Penot A. China and the relationship between the oil price and the dollar. Energy Pol. 2007;35:5795–5805. [Google Scholar]
- Bouri E. Oil volatility shocks and the stock markets of oil-importing MENA economies: a tale from the financial crisis. Energy Econ. 2015;51:590–598. [Google Scholar]
- Bouri E., Das M., Gupta R., Roubaud D. Spillovers between bitcoin and other assets during bear and bull markets. Appl. Econ. 2018;(55):5935–5949. [Google Scholar]
- Brahmasrene T., Huang J.H., Sissoko Y. Crude oil prices and exchange rates: causality, variance decomposition and impulse response. Energy Econ. 2014;44:407–412. [Google Scholar]
- Broadstock D.C., Filis G. Oil price shocks and stock market returns: new evidence from the United States and China. J. Int. Financ. Mark. Inst. Money. 2014;33:417–433. [Google Scholar]
- Broadstock D.C., Fan Y., Ji Q., Zhang D. Shocks and stocks: a bottom-up assessment of the relationship between oil prices, gasoline prices and the returns of Chinese firms. Energy J. 2016;37(1):55–86. [Google Scholar]
- Brock W., Dechert D., Scheinkman J., LeBaron B. A test for independence based on the correlation dimension. Econom. Rev. 1996;15:197–235. [Google Scholar]
- Buetzer S., Habib M.M., Stracca L. 2012. Global Exchange Rate Configurations: Do Oil Shocks Matter? European Central Bank Working. Paper No. 1442. [Google Scholar]
- Chang T., Chen W.Y., Gupta R., Nguyen D.K. Are stock prices related to the political uncertainty index in OECD countries? Evidence from the bootstrap panel causality test. Econ. Syst. 2015;39:288–300. [Google Scholar]
- Cheah E.T., Fry J. Speculative bubbles in bitcoin markets? An empirical investigation into the fundamental value of bitcoin. Econ. Lett. 2015:32–36. [Google Scholar]
- Chen S.-S., Chen H.-C. Oil price and real exchange rates. Energy Econ. 2007;29:390–404. [Google Scholar]
- Choi K., Hammoudeh S. Volatility behavior of oil, industrial commodity and stock markets in a regime-switching environment. Energy Pol. 2010;38(8):4388–4399. [Google Scholar]
- Converse N. Uncertainty, capital flows, and maturity mismatch. J. Int. Money Finance. 2017;88:260–275. [Google Scholar]
- Coudert V., Mignon V., Penot A. Oil price and the dollar. Energy Stud. Rev. 2008;15:45–58. [Google Scholar]
- Degiannakis S., Filis G., Floros C. Oil and stock returns: evidence from European industrial sector indices in a time-varying environment. J. Int. Financ. Mark. Inst. Money. 2013;26:175–191. [Google Scholar]
- Diebold F.X., Yilmaz K. Better to give than to receive: predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012;28:57–66. [Google Scholar]
- Diebold F.X., Yilmaz K. On the network topology of variance decompositions: measuring the connectedness of financial firms. J. Econ. 2014;182(1):119–134. [Google Scholar]
- Diebold F.X., Yılmaz K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009;119:158–171. [Google Scholar]
- Ding L., Vo M. Exchange rates and oil prices: a multivariate stochastic volatility analysis. Q. Rev. Econ. Finance. 2012;52:15–37. [Google Scholar]
- Dyhrberg A.H. Hedging capabilities of bitcoin: is it the virtual gold? Finance Res. Lett. 2016:139–144. [Google Scholar]
- Dyhrberg A.H. Bitcoin, gold and the dollar – a GARCH volatility analysis. Finance Res. Lett. 2016:85–92. [Google Scholar]
- Fang S., Egan P. Measuring contagion effects between crude oil and Chinese stock market sectors. Q. Rev. Econ. Finance. 2018;68:31–38. [Google Scholar]
- Fedoseeva S. Under pressure: dynamic pass-through of oil prices to the RUB/USD exchange rate. International Economics. 2018;156:117–126. [Google Scholar]
- Gabauer D., Gupta R. On the transmission mechanism of country-specific and international economic uncertainty spillovers: evidence from A TVP-VAR Connectedness Decomposition Approach. Econ. Lett. 2018;171:63–71. [Google Scholar]
- Gajardo G., Kristjanpoller W.D., Minutolo M. Does bitcoin exhibit the same asymmetric multifractal cross-correlations with crude oil, gold and DJIA as the Euro, Great British pound and Yen? Chaos, Solit. Fractals. 2018;109:195–205. [Google Scholar]
- Gokmenoglu K.K., Fazlollahi N. The interactions among gold, oil, and stock market: Evidence from S&P 500. Procedia Economics and Finance. 2015;25:478–488. [Google Scholar]
- Gomes F.J., Kotlikoff L.J., Viceira L.M. The excess burden of government indecision. Tax Pol. Econ. 2012;26:125–164. [Google Scholar]
- Granger C.W.J. Investigating causal relations by econometric models and cross spectral methods. Econometrica. 1969;37:424–438. [Google Scholar]
- Guesmi K., Samir S., Ilyes A., Zied F. Portfolio diversification with virtual currency: evidence from bitcoin. Int. Rev. Financ. Anal. 2019;63:431–437. [Google Scholar]
- Hamdi B., Aloui M., Alqahtani F., Tiwari A. Relationship between the oil price volatility and sectoral stock markets in oil-exporting economies: evidence from wavelet nonlinear denoised based quantile and Granger-causality analysis. Energy Econ. 2019;80:536–552. [Google Scholar]
- Han L., Liu Y., Yin L. Uncertainty and currency performance: a quantile-on-quantile approach. N. Am. J. Econ. Finance. 2019;48:702–729. [Google Scholar]
- Handley K., Limao N. Trade and investment under policy uncertainty: theory and firm evidence. Am. Econ. J. Econ. Pol. 2015;7:189–222. [Google Scholar]
- Huang Y., Guo F. The role of oil price shocks on China's real exchange rate. China Econ. Rev. 2007;18:403–416. [Google Scholar]
- Huang R.D., Masulis R.W., Stoll H.R. Energy shocks and financial markets. J. Futures Mark.: Futures, Options, and Other Derivative Products. 1996;16(1):1–27. [Google Scholar]
- Hussain S., Tiwari A.K., Sohag K., Shahbaz M. Connectedness among crude oil prices, stock index and metal prices: an application of network approach in the USA. Resour. Pol. 2019;62:57–65. [Google Scholar]
- Jain, A., Biswal, P.C.,2016 Dynamic linkages among oil price, gold price, exchange rate, and stock market in India. Resour. Pol. 49, 179-185.
- Jeong K., Härdle W.K., Song S. A consistent nonparametric test for causality in quantile. Econom. Theor. 2012;28:861–887. [Google Scholar]
- Ji Q., Zhang D. How much does financial development contribute to renewable energy growth and upgrading of energy structure in China? Energy Pol. 2019;128:114–124. [Google Scholar]
- Jiang J., Gu R. Asymmetric long-run dependence between oil price and US dollar exchange rate- Based on structural oil shocks. Physica A. 2016;456:75–89. [Google Scholar]
- Jones C.M., Kaul G. Oil and the stock markets. J. Finance. 1996;51(2):463–491. [Google Scholar]
- Katsiampa P. Volatility estimation for bitcoin: a comparison of GARCH models. Econ. Lett. 2017;158:3–6. [Google Scholar]
- Kearney A.A., Lombra R.E. Gold and platinum: toward solving the price puzzle. Q. Rev. Econ. Finance. 2009;49(3):884–892. [Google Scholar]
- Le T.-H., Chang Y. Oil price shock and gold returns. Int. Econ. 2012;131:71–103. [Google Scholar]
- Liu Z., Ye Y., Ma F. Can economic policy uncertainty help to forecast the volatility: a multifractal perspective. Physica A. 2017;482:181–188. [Google Scholar]
- Lizardo R.A., Mollick A.V. Oil price fluctuations and U.S. dollar exchange rates. Energy Econ. 2010;32:399–408. [Google Scholar]
- Ma Y., Zhang D., Ji Q., Pan J. Spillovers between oil and stock returns in the US energy sector: does idiosyncratic information matter? Energy Econ. 2019;81:536–544. [Google Scholar]
- Maghyereh A.I., Awartani B., Bouri E. The directional volatility connectedness between crude oil and equity markets: new evidence from implied volatility indexes. Energy Econ. 2016;57:78–93. [Google Scholar]
- Malik F., Umar Z. Dynamic connectedness of oil price shocks and exchange rates. Energy Econ. 2019;84 doi: 10.1016/j.eneco.2019.104501. [DOI] [Google Scholar]
- Melvin M., Sultan J. South African political unrest, oil prices, and the time varying risk premium in the gold futures market. J. Futures Mark. 1990;10:103–111. [Google Scholar]
- Mensi W., Hammoudeh S., Shahzad S.J.H., Shahbaz M. Modeling systemic risk and dependence structure between oil and stock markets using a variational model decomposition-based copula method. J. Bank. Finance. 2017;75:258–279. [Google Scholar]
- Mhalla M. The impact of novel coronavirus (COVID-19) on the global oil and aviation markets. J. Asian Sci. Res. 2020;10(2):96–104. [Google Scholar]
- Mohanty S., Nandha M., Bota G. Oil shocks and stock returns: the case of the Central and Eastern European (CEE) oil and gas sectors. Emerg. Mark. Rev. 2010;11(4):358–372. [Google Scholar]
- Narayan P.K., Sharma S.S. New evidence on oil price and firm returns. J. Bank. Finance. 2011;35(12):3253–3262. [Google Scholar]
- Narayan P.K., Narayan S., Zheng X. Gold and oil futures markets: are markets efficient? Appl. Energy. 2010;87:3299–3303. [Google Scholar]
- Nier E., Sedik T.S., Mondino T. International Monetary Fund; 2014. Gross private capital flows to emerging markets: can the global financial cycle be tamed? IMF Working Papers 14/196. [Google Scholar]
- Nishiyama Y., Hitomi K., Kawasaki Y., Jeong K. A consistent nonparametric Test for nonlinear causality - specification in time series regression. J. Econom. 2011;165:112–127. [Google Scholar]
- OECD . OECD Interim Economic Assessment; 2020. Coronavirus: the world economy at risk. [Google Scholar]
- Pástor L., Veronesi P. Uncertainty about government policy and stock prices. J. Finance. 2012;67:1219–1264. [Google Scholar]
- Peng C., Zhu H., Guo Y., Chen X. Risk spillover of international crude oil to China's firms: evidence from granger causality across quantile. Energy Econ. 2018;72:188–199. [Google Scholar]
- Phan D.H.B., Sharma S.S., Narayan P.K. Intraday volatility interaction between the crude oil and equity markets. J. Int. Financ. Mark. Inst. Money. 2016;40:1–13. [Google Scholar]
- Pieters G., Vivanco S. Financial regulations and price inconsistencies across bitcoin markets. Inf. Econ. Pol. 2017:1–14. [Google Scholar]
- Reboredo J.C. Nonlinear effects of oil shocks on stock returns: a Markov-switching approach. Appl. Econ. 2010;42(29):3735–3744. [Google Scholar]
- Reboredo J.C. Is gold a safe haven or a hedge for the US dollar? Implications for risk management. J. Bank. Finance. 2013;37:2665–2676. [Google Scholar]
- Reboredo J.C., Uddin G.S. Do financial stress and policy uncertainty have an impact on the energy and metals markets? A quantile regression approach. Int. Rev. Econ. Finance. 2016;43:284–298. [Google Scholar]
- Rehman M.U., Shahzad S.J.H., Uddin G.S., Hedstrom A. Precious metal returns and oil shocks: a time varying connectedness approach. Resour. Pol. 2018;58:77–89. [Google Scholar]
- Rey H. NBER Working Paper. 2018. Dilemma not trilemma: the global financial cycle and monetary policy independence; p. 21162. Feb. 2018. [Google Scholar]
- Rodrik D. Policy uncertainty and private investment in developing countries. J. Dev. Econ. 1991;36:229–242. [Google Scholar]
- Rubens J., Bond M., Webb J. The inflation-hedging effectiveness of real estate. J. R. Estate Res. 1989;4(2):45–55. [Google Scholar]
- Salisu A.A., Adediran I. Gold as a hedge against oil shocks: evidence from new datasets for oil shocks. Resour. Pol. 2020;66 doi: 10.1016/j.resourpol.2020.101606. [DOI] [Google Scholar]
- Salisu A.A., Vo X.V. International Review of Financial Analysis. 2020. Predicting stock returns in the presence of COVID-19 pandemic: the role of health news. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singhal S., Choudhary S., Biswal P.C. Return and volatility linkages among international crude oil price, gold price, exchange rate and stock markets: evidence from Mexico. Resour. Pol. 2019;60:255–261. [Google Scholar]
- Souček M. Crude oil, equity and gold futures open interest co-movements. Energy Econ. 2013;40:306–315. [Google Scholar]
- Symitsi E., Chalvatzis K.J. Return, volatility and shock spillovers of bitcoin with energy and technology companies. Econ. Lett. 2018:127–130. [Google Scholar]
- Tiwari A.K., Dar A.B., Bhanja N. Oil price and exchange rates: a wavelet based analysis for India. Econ. Modell. 2013;31:414–422. [Google Scholar]
- Tiwari A.K., Mutascu M.I., Albulescu C.T. The influence of the international oil prices on the real effective exchange rate in Romania in a wavelet transform framework. Energy Econ. 2013;40:714–733. [Google Scholar]
- Tiwari A.K., Jena S.K., Mitra A., Yoon S.M. Impact of oil price risk on sectoral equity markets: implications on portfolio management. Energy Econ. 2018;70:382–395. [Google Scholar]
- Trabelsi N. Are there any volatility spill-over effects among cryptocurrencies and widely traded asset classes? J. Risk Financ. Manag. 2018;11:1–17. [Google Scholar]
- Uddin G.S., Tiwari A.K., Arouri M., Teulon F. On the relationship between oil price and exchange rates: a wavelet analysis. Econ. Modell. 2013;35:502–507. [Google Scholar]
- Volkov N.I., Yuhn K.h. Oil price shocks and exchange rate movements. Global Finance J. 2016;31:18–30. [Google Scholar]
- Wang Y., Chueh Y. Dynamic transmission effects between the interest rate, the US dollar, gold and crude oil prices. Econ. Modell. 2013;30:792–798. [Google Scholar]
- Wang Y., Wu C. 2012. Energy prices and exchange rates of the U.S. dollar: further e. [Google Scholar]
- You W., Guo Y., Zhu H., Tang Y. Oil price shocks, economic policy uncertainty and industry stock returns in China: asymmetric effects with quantile regression. Energy Econ. 2017;68:1–18. [Google Scholar]
- Zhang D. Oil shocks and stock markets revisited: measuring connectedness from a global perspective. Energy Econ. 2017;62:323–333. [Google Scholar]
- Zhang D. Energy finance: background, concept and recent developments. Emerg. Mark. Finance Trade. 2018;54:1687–1692. [Google Scholar]
- Zhang D., Cao H. Sectoral responses of the Chinese stock market to international oil shocks. Emerg. Mark. Finance Trade. 2013;49(6):37–51. [Google Scholar]
- Zhang Y.J., Wei Y.M. The crude oil market and the gold market: evidence for cointegration, causality and price discovery. Resour. Pol. 2010;35:168–177. [Google Scholar]
- Zhang Y.J., Fan Y., Tsai H.T., Wei Y.M. Spillover effect of US dollar exchange rate on oil prices. J. Pol. Model. 2008;30:973–991. [Google Scholar]
- Zhang D., Hu M., Ji Q. Finance Research Letters; 2020. Financial markets under the global pandemic of COVID-19. [DOI] [PMC free article] [PubMed] [Google Scholar]