State-level needs for social distancing and contact tracing to contain COVID-19 in the United States

Abstract

Starting in mid-May 2020, many US states began relaxing social distancing measures that were put in place to mitigate the spread of COVID-19. To evaluate the impact of relaxation of restrictions on COVID-19 dynamics and control, we developed a transmission dynamic model and calibrated it to US state-level COVID-19 cases and deaths. We used this model to evaluate the impact of social distancing, testing and contact tracing on the COVID-19 epidemic in each state. As of July 22, 2020, we found only three states were on track to curtail their epidemic curve. Thirty-nine states and the District of Columbia may have to double their testing and/or tracing rates and/or rolling back reopening by 25%, while eight states require an even greater measure of combined testing, tracing, and distancing. Increased testing and contact tracing capacity is paramount for mitigating the recent large-scale increases in U.S. cases and deaths.

Introduction

The novel coronavirus pandemic (COVID-19) emerged in Wuhan, China in December 2019 and has now reached pandemic status, with spread to more than 210 countries and territories, including the United States (US) ¹. The US reported its first imported case of COVID-19 on January 20, 2020, arriving via an international flight from China ². Since then, the disease has spread rapidly within the US, with every state reporting confirmed cases within three weeks of the first reported community transmission. As of August 1^st, the US has exceeded 4.5 million cases and 150,000 deaths, heterogeneously distributed across all states ¹. So far, states such as New York, New Jersey, and California have borne the highest burden with more than 420,000, 183,000, and 510,000 cases and 32,000, 15,000, and 9,000 deaths, respectively, while Alaska and Hawaii have each reported less than 4000 cases and 25 deaths each ¹.

COVID-19 is caused by a newly described and highly transmissible SARS-like coronavirus (SARS-CoV-2). Severe clinical outcomes have been observed in approximately 20% of symptomatic cases ^3,4. There is no vaccine and no cure or approved pharmaceutical intervention for this disease, making the fight against the pandemic reliant on non-pharmaceutical interventions (NPIs). These NPIs include: case-driven measures, such as testing, contact tracing, and isolation ⁵; personal preventive measures such as hand hygiene, cough etiquette, face mask use, eye protection, physical distancing, and surface cleaning, which aim to reduce the risk of transmission during contact with potentially-infectious individuals ⁶; and social distancing measures to reduce interpersonal contact in the population. In the US, social distancing measures have included policies and guidelines to close schools and workplaces, cancel and restrict mass gatherings and group events, restrict travel, maintain physical separation from others (e.g. keeping six feet distance), and stay-at-home orders ⁷.

NPIs and other responses to COVID-19, especially stay-at-home orders, have varied widely across states, leading to spatial and temporal variation in the timing and implementation of mitigation strategies. This variation in policies and response efforts may have contributed to the observed heterogeneity in COVID-19 morbidity and mortality across states ⁸. Recent studies suggest that statewide social distancing measures have likely contributed to reducing the spread COVID-19 epidemic in the US ^9,10. Understanding the extent to which NPIs, such as social distance, testing, contact tracing, and self-quarantine, influence COVID-19 transmission in a local context is pivotal for predicting and better managing the future course of the epidemic on a state-by-state basis. This in turn will inform how these NPIs should be optimized to mitigate the spread and burden of COVID-19 while awaiting development of pharmaceutical interventions (e.g. therapeutics and vaccines).

After several weeks of statewide stay-at-home orders, most US states began to ease their social distancing requirements in May-June, 2020 ¹¹, while attempting to increase their testing and contact tracing capacities ¹². Mathematical modeling is a unique tool to help answer these important and timely questions. Models can contribute valuable insight for public health decision-makers by providing an evaluation of the effectiveness of ongoing control strategies along with predictions of the potential impact of alternative policy scenarios ¹³.

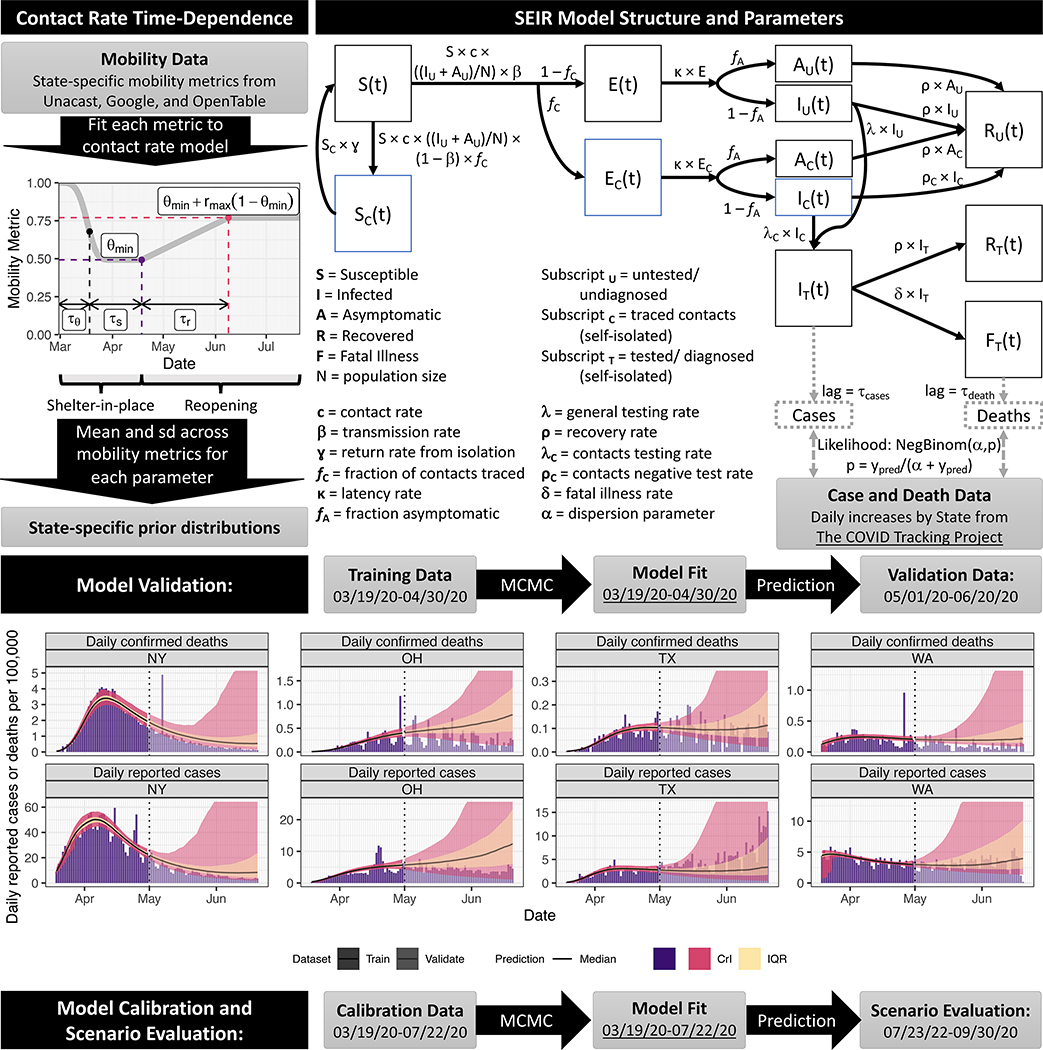
To address these needs, we developed and validated a data-driven transmission dynamic model to evaluate the impact of social distancing, state-reopening, testing, and contact tracing on the state-level dynamics of COVID-19 infections and mortality in the US, shown schematically in Figure 1. Like many other COVID-19 transmission models ^14–17, we used an extended SEIR (susceptible, exposed, infectious, removed) compartmental model. The model divides the population into several disease compartments and tracts movements of individuals between the compartments through different transition rates. The main model compartments include: S, susceptible, E, exposed, A, infectious and asymptomatic, I, infectious and symptomatic, R, recovered, and F, dead. In addition to disease progression stages, our model incorporates social distancing informed by several public sources of mobility data, case identification via testing, isolation of detected cases, and contact tracing. This is a mean-field epidemiological modeling approach that captures the average disease dynamics behavior within a population ^18,19. We used Bayesian inference methods to calibrate and validate our model prediction to state-level daily reported COVID-19 cases and fatality data. Model parameters, prior distributions, and their sources are shown in Table 1. We used the calibrated model to evaluate the transmissibility of COVID-19 in each state from March, 2020 to late July, 2020, to estimate the state-level impact of shelter-in-place and reopening on COVID-19 transmission. Finally, we evaluated the degree to which increasing testing efforts (rate of identification of infected cases) and/or contact tracing could curtail the spread of the diseases and enable greater relaxation of social distancing restrictions while preventing a resurgence of infections and deaths. A detailed description of the model considerations, parameterization, and analysis is provided in Methods.

Figure 1. SEIR model structure, parameter, data sources, and fitting/validation methods.

We used mobility data to constrain the time-dependence of the contact rate. We fitted the model to daily reported cases and confirmed deaths from March 19^th to April 30^th and validated its projections against data from May 1^st to June 20^th. On the model projections, the black solid line is the median, the pink band is the 95% credible interval (CrI) and the orange is the interquartile range (IQR). We show model fitting and validation for four states: New York (NY), Ohio (OH), Texas (TX), and Washington (WA).

Table 1.

Model inputs, parameters and prior distributions for Bayesian analysis.

Symbol	Definition (units)	Calibrated parameter(s)	Prior [Truncation]	Notes
N	Population size	Input (not calibrated)	Constant	40
Ninit	Initial IU on 2020–02-29	Ninit	LogN(1000, 10) [1, 10000]	¶
1/γ	Self-isolation time after contact tracing	Tisolation = 1/γ	LogN(14, 2) [7, 21]	ϯ
1/κ	Latent period (d)	Tlatent = 1/κ	N(4,1) [2,7]	41,42
c0	Baseline contact rate (contacts d−1)	c0	N(13, 5) [7, 20]	43
ρ	Recovery rate (d−1)	Trecover= 1/ρ	LogN(10, 1.5) [5, 30]	42,44
β0	Transmission probability per contact (unitless)	R0 = c0β0/ρ	N(2.9, 0.78) [1.46, 4.5]	45–47
fC	Fraction of contacts traced (unitless)	fC	LogN(0.25, 2) [0.05, 1]	48
fA	Fraction of infected asymptomatic (unitless)	fA	N(0.295,0.275) [0.02, 0.57]	49
T50T	Date of 50% of final testing rate (d)	T50T	U(60, 106) (Mar 1 – Apr 15)	¶
λ	General positive diagnosis rate (d−1)	λ = Ftest Senstest ktest	Derived	45,50,51
Ftest	General test coverage (unitless)	Ftest	Beta(2,2)	45,50,51
Senstest	Test sensitivity (unitless)	Senstest	N(0.7, 0.1) [0.6, 0.95]	52
ktest	General testing rate (d−1)	τtest = 1/ktest	N(7, 3) [2, 12]	53,54
λC	Contacts positive diagnosis rate (d−1)	λC = Senstest ktest,C	Derived
kC,test	Contacts testing rate (d−1)	τC,test = 1/kC,test	N(2, 1) [1, 3]	¶
ρC	Rate of infected contacts testing negative (d−1)	ρC = (1 – Senstest) ktest,C	Derived
δ	Fatal illness rate (d−1)	IFR (infected fatality rate)*	LogN(0.01, 2) [0.001, 0.1]	44,55
θmin	Minimum of θ(t)	θmin	Validation: Beta(2,2) Calibration: State-specific	¶ ƣ
τθ	Weibull scale parameter	τθ	Validation: N(21, 7) [7, 35] Calibration: State-specific	¶ ƣ
nθ	Weibull shape parameter	nθ	Validation: LogN(6, 2) [1,11] Calibration: State-specific	¶ ƣ
η	Hygiene effectiveness relative to social distancing (unitless)	η	Beta(2,4)	¶
τs	Duration of shelter in place (d)	τs	Validation: N(45, 30) [21, 90] Calibration: State-specific	56
τr	Duration of linear increase after shelter-in-place (d)	τr	Validation: N(45, 30) [14, 105] Calibration: State-specific	¶ ƣ
rmax	Maximum relative increase in contacts from shelter-in-place (unitless)	rmax	Validation: N(1, 1) [0, 2] Calibration: State-specific	¶ ƣ
τcase	Lag time for observing confirmed case	τcase	LogN(7, 2) [1, 14]	¶
τdeath	Lag time for observing confirmed death	τdeath	LogN(7, 2) [1, 14]	¶
αpos	Negative Binomial shape parameter for cases likelihood function	αpos	LogU(0.1, 40)	¶
αdeath	Negative Binomial shape parameter for deaths likelihood function	αdeath	LogU(0.1, 40)	¶

LogN(GM, GSD) = lognormal distribution with geometric mean GM and geometric standard deviation GSD

N(M,SD) = normal distribution with mean M and standard deviation SD

U(MIN,MAX) = uniform distribution with minimum MIN and maximum MAX

LogU(MIN, MAX) = log-uniform distribution with minimum MIN and maximum MAX

Beta(a,b) = beta distribution with shape parameters a and b

Time (t) is measured from t=1 corresponds to 2020–01-01.

^¶Assumed, non-informative prior wide enough to have adequate validation coverage.

^ϯStandard contact tracing guidance is to self-isolate for 2 weeks.

^ƣFor calibration to 6/20/20, state-specific priors were derived by fitting to different social distancing data sets, with each parameter’s mean, standard deviation, and range used to define a normal distribution prior.

^*See Methods for relationship between IFR and δ.

Results

Model performance and validation

We used state-level mobility data from Unacast, Google, and OpenTable to calibrate a parametric model of shelter-in-place and reopening (Supplementary Figure 1), and used the results to inform prior distributions for the transmission model (Figure 1). We fit our model to state-level daily cases and deaths data using a Bayesian inference approach (see Methods). Model performance assessment for several representative states is shown in Figure 1, with full results in Supplementary Figures 2 and 3. With respect to validation, the posterior 95% credible interval of our model projections, estimated using data through April 30^th, 2020, covered 84% of the data points from May 1^st through June 20^th, 2020. For seven states (Alaska, Montana, South Dakota, Iowa, Illinois, Michigan, and Minnesota), validation had low coverage (<50%) because of insufficient training data through April 30 to adequately inform sheltering and reopening in those states. This inaccuracy was not unexpected because the length of sheltering and the degree of reopening could not have been known on April 30th, and thus our model predictions were based on generic prior distributions. However, during model calibration to data through July 22nd, these parameters were informed by updated state-specific mobility data. Model performance for fitting all data through July 22^nd is shown in Supplementary Figures 4–6, with posterior parameter distributions shown in Supplementary Figure 7. Good fits with high coverage (>88% for cases; >92% for deaths) were obtained for all states.

Estimations of effective reproduction number

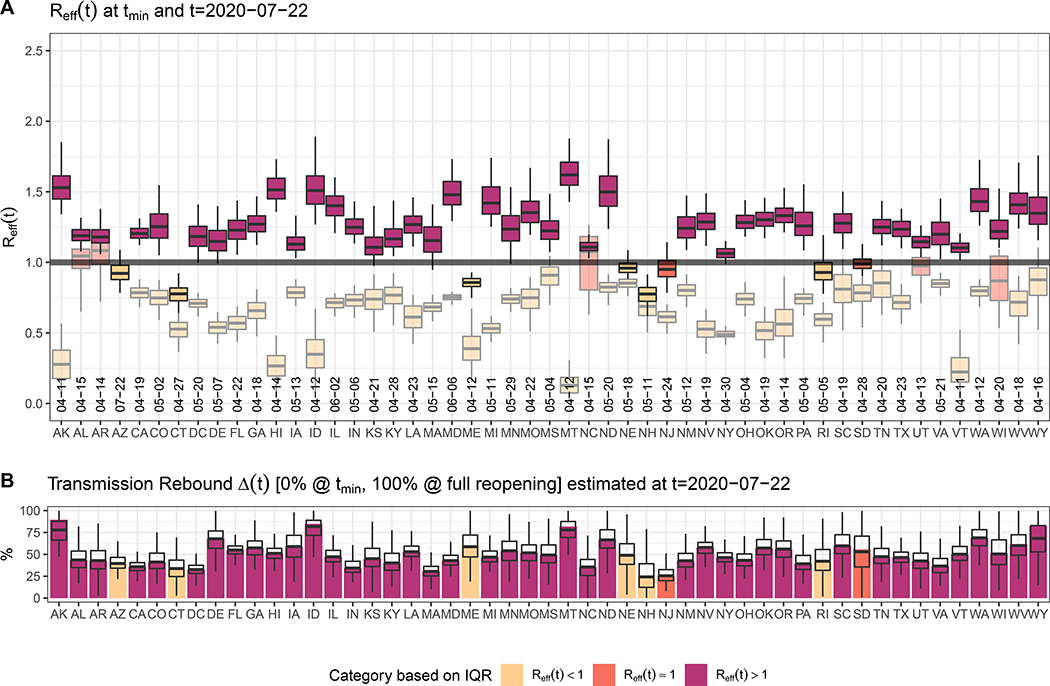
The effective reproduction number, R_eff is the average number of secondary infection cases generated by a single infectious individual during her infectious period ¹⁸. When R_eff > 1 the epidemic curve is increasing, and when R_eff < 1, the epidemic curve is decreasing ¹⁸. Using the posterior distribution of our model parameters we estimated the effective reproduction number R_eff from March 19^th to late July, 2020 and identified the minimum level of transmission achieved in each state (Figure 2A). We found that for all except five states (Alabama, Arkansas, North Carolina, Wisconsin, and Utah), the inter-quartile range for the minimum R_eff value was less than 1 (varying from 0.07 – 0.98) and these values were mainly achieved during the state shelter-in-place (April 11^th to May 29^th, 2020) (Figure 2A). Following states’ relaxations of social distancing measures, disease transmission started to re-increase. By July 22^nd, 2020, 42 states and the District of Columbia had at least a 75% probability that R_eff > 1. Thus, the model predicts that as states are reopening, a majority of states are at risk of continued increases in the scale of the outbreak and require additional mitigation to contain the spread of the disease.

Figure 2. Estimated effective reproduction number R_eff and the level of reopening/rebound in transmission as of July 22^nd, 2020 for all states.

(A) shows estimated R_eff (median, IQR, and 95% CrI) across States. The figure shows the value of R_eff on July 22^nd, 2020, as well as the “minimum” value of R_eff between March 19^th, 2020 and July 22^nd, 2020, in lighter shades of each color. It also includes the date of the minimum R_eff. (B) shows the level of reopening/rebound in disease transmission in each state relative to its minimum value during state shelter-in-place (median, IQR, and 95% CrI).

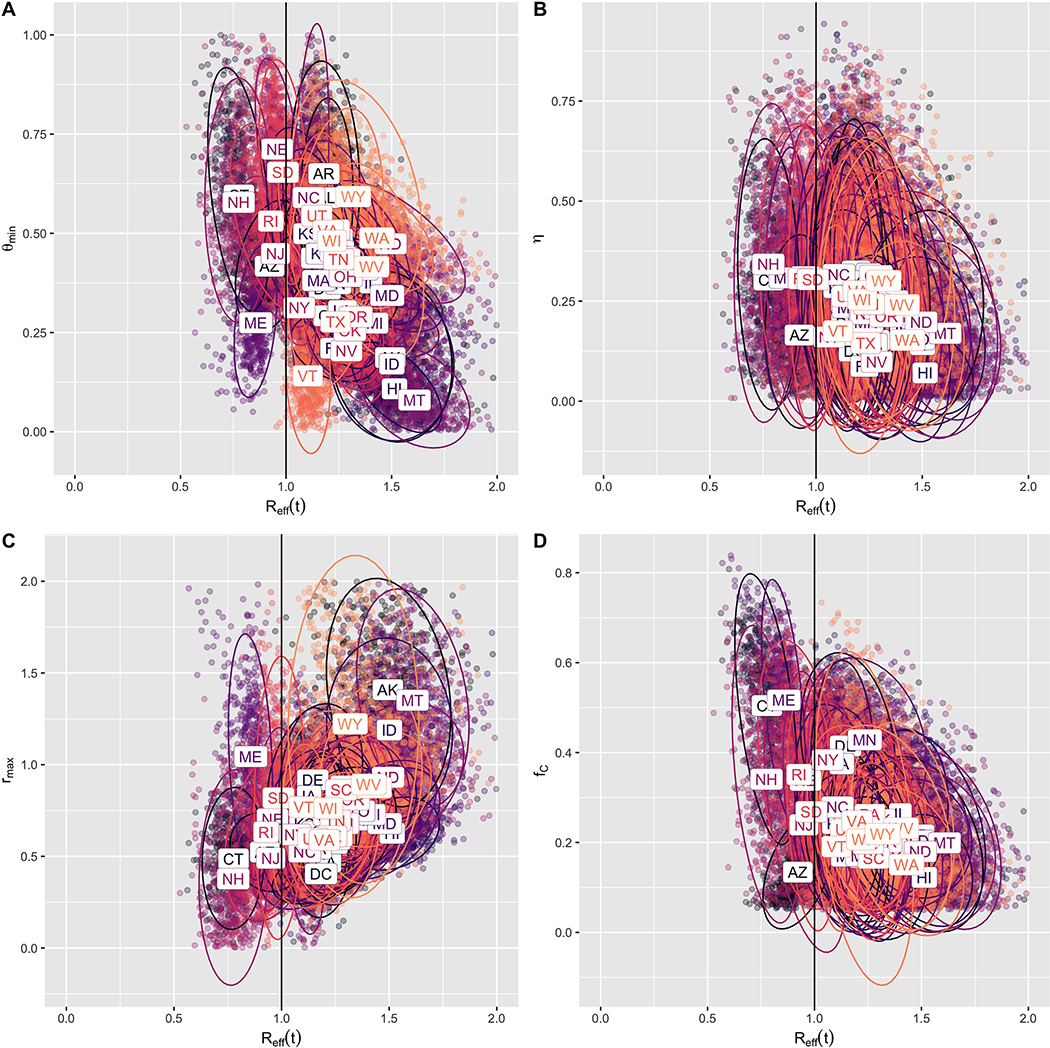
We conducted an analysis of variance to evaluate the contribution of each parameter to the variation in R_eff value (Supplementary Table 1). Across states, we found that the largest drivers of variation in R_eff are the power parameter for relating social distancing to hygiene-associated reduction in transmission, η (ANOVA F values [1 degree of freedom] =2989.166, p values < 2.2e-16, etâ2 >= 5%, lower 95% CI of etâ2 >= 4.5%), degree of mitigation during shelter-in-place, θ_min (ANOVA F values [1 degree of freedom] =5177.354, p values < 2.2e-16, etâ2 >= 8.7%, lower 95% CI of etâ2 >= 8.1%), the maximum relative increase in contact after shelter-in-place orders, r_max (ANOVA F values [1 degree of freedom] =8051.61, p values < 2.2e-16, etâ2 >= 13.5%, lower 95% CI of etâ2 >= 12.8%), and the fraction of contact traced, f_c (ANOVA F values [1 degree of freedom] =13834.053, p values < 2.2e-16, etâ2 >= 23.2%, lower 95% CI of etâ2 >= 22.4%), which together contribute over 50% of variance (Extended Data Figure 1 and Supplementary Table 1). This observation is consistent with mobility data alone being insufficient to account for the combined effect of multiple control measures, and suggest that the degree of adoption of non-mobility-related measures, such as enhanced hygiene practices and contact tracing, play a large role in the extent to which a state may reduce disease transmission.

For each state, we defined Δ as the level of reopening/rebound (Δ = 0% at minimum, 100% at full reopening) in disease transmission relative to its lowest transmission rate observed during shelter-in-place, and estimated the current level of reopening/rebound (Figure 2B). We found that 24 states had an average of 50 – 80% rebound in COVID-19 transmission by July 22nd, 2020, while no state had less than 25% rebound in transmission (Figure 2B).

Impact of testing and contact tracing on easing of social distancing

Bringing and keeping the effective reproduction number, R_eff, below 1 is necessary to curtail the spread of an outbreak. We evaluated the probability of keeping R_eff < 1 for different levels of testing and contact tracing under the July 22^nd, 2020 level of state reopening. We found that in 42 states and the District of Columbia bringing and keeping R_eff < 1 may not be possible without increased contact tracing efforts, as increasing testing and isolation alone would require at least a 3.5 fold increase of coverage to curtail the epidemic curve with a 0.975 probability (Extended Data Figures 2 & 3, and Supplementary Table 2). The challenges are even greater to ensure continued control of the epidemic with full reopening, as testing and isolation alone would be insufficient to curtail the epidemic in 33 states and in all states a 50% to 75% contact tracing coverage would be required to curtail the epidemic curve with a 0.975 probability (Extended Data Figure 4, Supplementary Table 3).

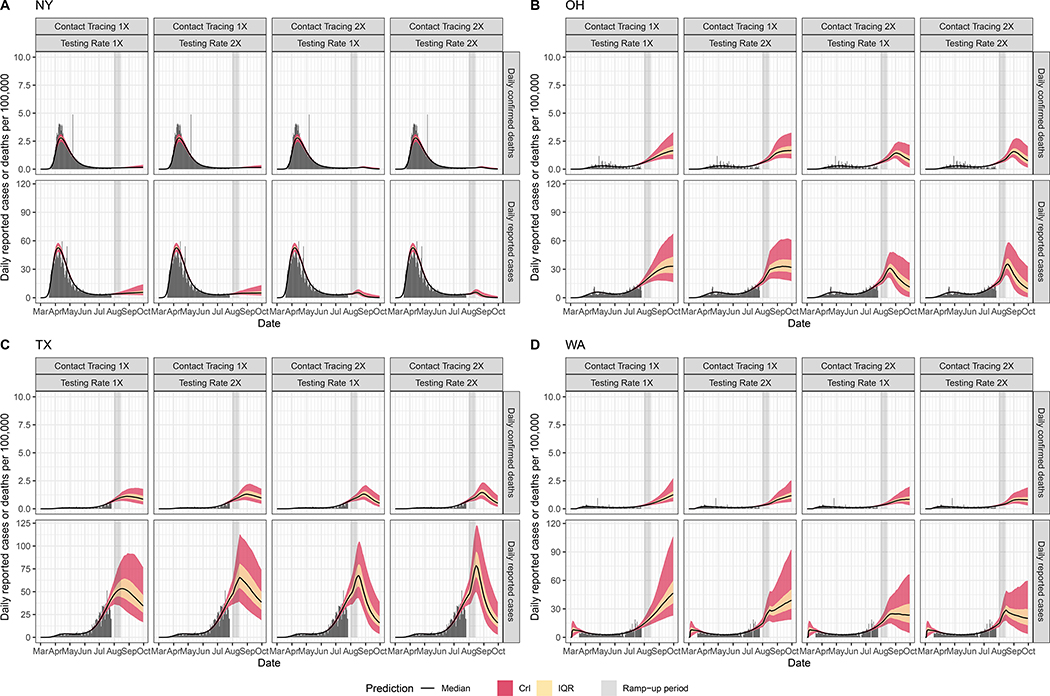
To evaluate the impact of scaling up testing and contact tracing on the epidemic dynamics in each state, we assumed a linear “ramp-up” of either testing and/or contact tracing from August 1^st – 14^th, 2020, after which both parameters remain constant. We then predicted the daily number of reported cases and deaths (Figure 3 and Supplementary Figure 8). We found that under current levels of reopening and control, 40 states would be unable to curtail the spread of the epidemic within the next two months (Supplementary Figure 8). Even with increased testing and contact tracing, these states will still experience between a two-week to two-month increase in reported cases and deaths (Figure 3 and Supplementary Figure 8). For example, Ohio, Texas, and Washington may experience a two-week increase of cases and a one-month increase of deaths even if their current testing and contact tracing rate were doubled within the next two weeks (Figure 3B–D). Moreover, reported cases increase during the two weeks “ramp-up” period (Figure 3). We found that in 27 states and the district of Columbia an additional 25% (50%) relaxation of restrictions without simultaneously increasing contact tracing may exacerbate disease dynamics and results on average in a 25% – 65% (45% – 150%) increase of cases and 22% – 48% (35% – 92%) increase of deaths within the next two months (Supplementary Figure 8).

Figure 3.

Predicted time-course (median, IQR, and 95% CrI) of daily reported cases and deaths under different testing and contact tracing rates (1X and 2X) in New York (A), Ohio (B), Texas (C), and Washington State (D).

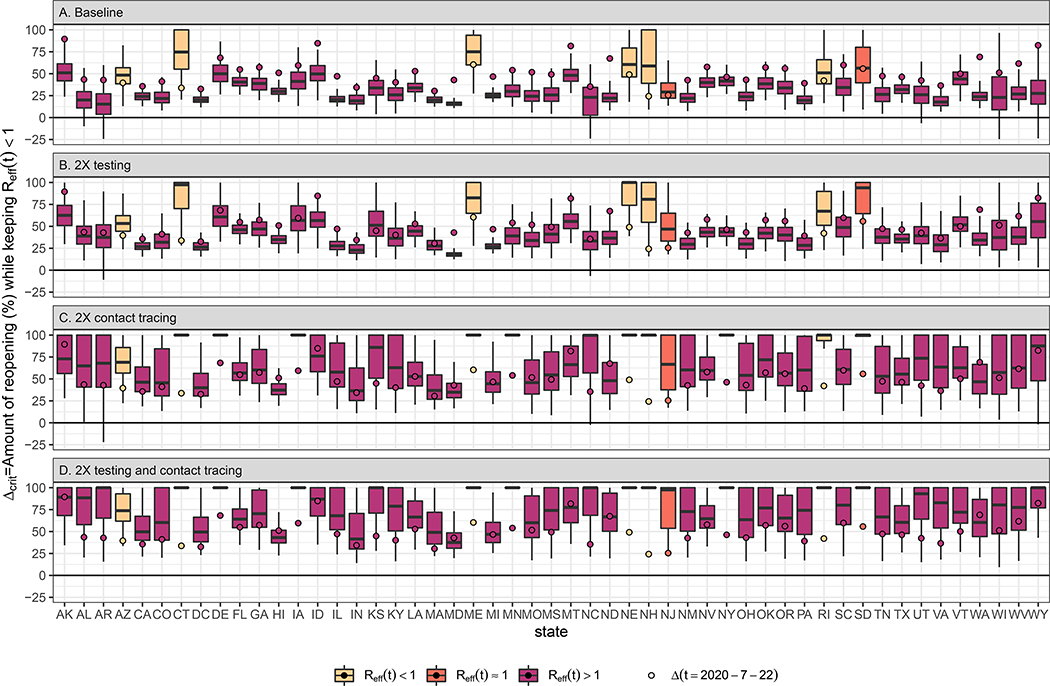
We next evaluated the maximal degree of rebound in transmission (i.e., level of reopening) permitted while keeping R_eff < 1 under different testing and contact tracing scenarios (Figure 4). We found that under the current level of testing and contact tracing rate, 27 states cannot keep their R_eff < 1 (at 75% confidence) even with only 25% reopening/rebound in transmission (Figure 4A). By doubling the current testing rate, eight states could keep their R_eff < 1 (at 75% confidence) even with a 50% level of reopening (Figure 4B). By doubling contact tracing, nine states could remove all mobility restrictions while keeping R_eff < 1 (at 100% confidence) (Figure 4C). By doubling both testing rate and contact tracing, ten states could remove all mobility restrictions while keeping R_eff < 1 (at 100% confidence) (Figure 4D).

Figure 4. Reopening/rebound in transmission Δ_crit permitted (0% = minimum shelter-in-place value, 100% = return to no restrictions) to keep R_eff < 1.

(A) If testing and contact rates are unchanged, (B) testing rate is doubled, (C) contact tracing is doubled, or (D) both testing and contact tracing are doubled. Δ(t) the level of reopening/rebound in transmission on July 22^nd, 2020 is shown by the circle. All boxplots show median, IQR, and 95% CrI.

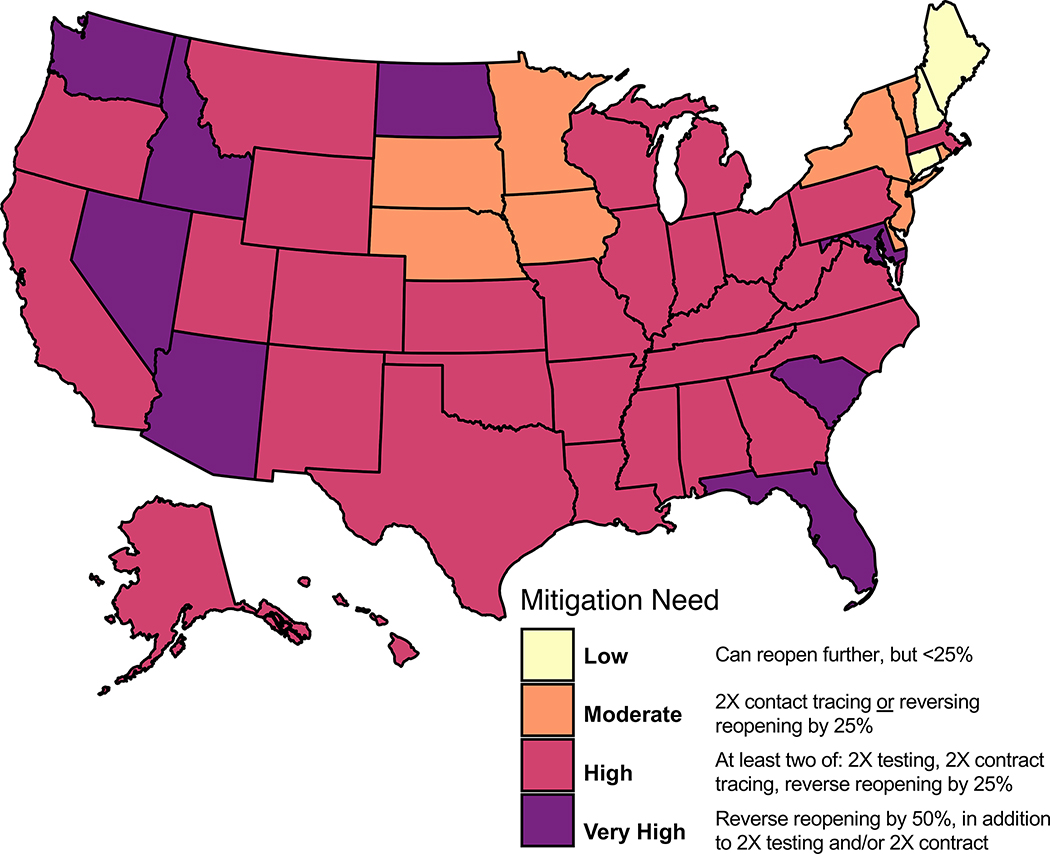
We categorized states by the additional amount of mitigation efforts needed to keep R(t) < 1 with at least 75% confidence (Figure 5 and Supplementary Figure 8). We found that under current control efforts, no states could reduce and keep R(t) < 1 if their current level of reopening was relaxed by an additional 25% (“Very Low” category), and three states (Connecticut, Maine, New Hampshire) could reduce and keep R(t) < 1 without additional reopening (“Low” category). Eight states could reduce and keep R(t) < 1 by doubling their contact tracing rate or implementing additional social distancing restrictions, a 25% reversal of current level of reopening (“Moderate” category), while 30 states and the District of Columbia need a combined intervention of doubling both testing and contact tracing and/or 25% reversal of current reopening to reduce and keep R(t) < 1 (“High” category). For the remaining eight states (Arizona, Florida, Idaho, Maryland, North Dakota, Nevada, South Carolina, and Washington) a 50% reversal of current reopening in addition to increased testing and/or contact tracing are needed in order to to reduce and keep R(t) < 1 (“Very High” Category).

Figure 5. State-specific level of mitigation needed as a July 22^nd, 2020 to curtail the spread of COVID-19.

(keeping R < 1 with at least 75% confidence, equivalent to the upper bound of the Interquartile range (IQR)). Categories based on evaluating scenarios with different combinations of baseline/doubling testing, baseline/doubling contact tracing, and baseline/+25%/−25% in the reopening parameter Δ. Categories are defined as follows: Very Low (no states): Can reopen further by >25% while keeping R(t)<1; Low (3 states): Can reopen further by < 25% with up to 2X increase in testing while keeping R(t)<1; Moderate (9 states): Requires 2X contact tracing or reversal of reopening by 25% to keep R(t)<1; High (30 states and DC): Requires multiple interventions (2X testing, 2X contract tracing, reversal of reopening by 25%) to keep R(t)<1; Very High (8 states): Reverse of reopening by 50%, combined with 2X testing and/or 2X contact tracing with to keep R(t)<1. The U.S. map shapefile is from the “usmap” R package, which is open source under GPL-3.

Discussion

There is a delicate and continuous balance to strike between the use of social distancing measures to mitigate the spread of an emerging and deadly disease such as COVID-19 and the need for re/opening various sectors of activities for the social, economic, mental, and physical well-being of a community. To address this issue, it is imperative to design measurable, data-driven, and flexible milestones for identifying when to make specific transitions with regard to easing or retightening specific social distancing measures. We developed a data-driven SARS-CoV-2 transmission dynamic model not only to make short-term predictions on COVID-19 incidence and mortality in the US, but more importantly to evaluate the impact that relaxing social distancing measures and increasing testing and contact tracing would have on the epidemic in each state.

We showed that in most states, control strategies implemented during their “shelter-in-place” period were sufficient to contain the outbreak, defined as reducing and ultimately maintaining the effective reproduction number below 1 (R_eff < 1). However, for the majority of states, our modelling suggests that “reopening” has proceeded too rapidly and/or without adequate testing and contact tracing to prevent a resurgence of the epidemic. Our model suggests for some states, a substantial fraction of the population may have already been infected such that even without additional intervention, R_eff(t) is declining towards (or below) 1 even as R(t) > 1. The most extreme example is Arizona, where R_eff(t) is estimated to have declined below the previous minimum R_eff value achieved during shelter-in-place. However, accurate estimation of the susceptible fraction of the population is difficult due to uncertain degree of undercounting in the reported case data. Thus, we used R(t) to categorize the mitigation needs in each state and evaluate the level of control effort needed to curtail the spread of the epidemic in each state.

Moreover, even in states with currently decreasing incidence and mortality, such as Maine and New Jersey, additional relaxation of restrictions is likely to “bend the epidemic curve upwards” in the absence of increased testing or tracing. However, our model predicts that a combination of increased testing, increased contact tracing, and/or scaling back reopening will be sufficient for curtailing the spread of COVID-19 in most states. Specifically, doubling of current testing and contact tracing rates would enable the majority of states to either maintain or increase the easing of social distancing restrictions in a “safe” manner in the short term. Scaling back the current level of reopening by 25% in combination with doubling of testing and tracing will be sufficient to control the epidemic in the long term in all but eight “Very High” risk states. The impact of these interventions on the epidemic curve was evaluated by computing their probability of reducing and keeping the reproduction number below one. However, in states with high overdispersion in disease transmission, epidemic with high super-spreadability characteristics, the reproduction number may be subject to large fluctuation as the number of infection cases decreases. This may more likely be the case for states with lower dispersion parameters posterior values such as Arkansas, Connecticut, Idaho, Kansas, Kentucky, Louisiana, Mississippi, New Hampshire, South Carolina, and Wyoming (see Supplementary Figure 7).

Increasing testing and contact tracing rates entails both increasing the number of tests performed per day as well as requiring early identification and effective isolation of COVID-19 infected individuals. This can be accomplished through active case detection via efficient contact tracing strategies. However, it should also be noted that increased testing and contact tracing will lead to a short-term increase in reported cases because a larger fraction of the infected population is being observed, and that several weeks may pass before these rates begin to show a decline. Therefore, it is imperative that policymakers and the public recognize that such a surge is actually a sign that testing and tracing efforts are succeeding, and exercise the patience to wait several weeks before these successes are reflected as declining rates of reported cases.

Other modeling studies have used SEIR-type compartmental models to assess the impact of social distancing, testing and contact tracing to curb the epidemic curve in Italy and the United Kingdom ^14–17. Consistent with our results, these studies have shown that rapid reopening of the economy without adequate testing and contact tracing could lead to a resurgence of the epidemic ^14–17. Specifically, they show that high testing and contact tracing rates may enable to maintain/increase the easing of social distancing restrictions without an increased rate of COVID-19 transmission ¹⁴.

Our study has several limitations due to modelling assumptions and the quality of available data. Like most COVID-19 transmission models ^14–17, we used a compartmental SEIR-type model to model the spread of SARS-CoV-2 because of its simplicity and ability to capture population average dynamics. This modeling approach does not account for heterogeneity in individual-level behavior, overdispersion due to “super-spreaders,” social contact networks, and inherent stochasticity which may play an important role in SARS-CoV-2 transmission dynamics. These factors can be modeled through the use of individual-based models ^20–22. However, individual-based modeling is a more complex modeling framework and may require a substantial amount of individual-level data for model parameterization, calibration, and validation.

To characterize the limitations of using cell phone-based mobility data to infer (prior distributions for) contact rates, we examined the state-to-state variation in mobility data to the corresponding posterior distributions for each mobility-related parameter (see Supplementary Figure 9). Three parameters of particular interest are the minimum relative contact rate θ_min, the duration of the shelter-in-place phase τ_s, and the maximum amount of reopening r_max. For θ_min, none of the r² values were consistently less than 0.2, although the slope and intercept of the regression line for the Unacast Visitation metric were within 15% of 1 and 0, respectively. Similarly, for τ_s, the highest r² value was 0.37, for OpenTable Bookings data, which also had a relatively accurate regression line (again within 15%). For r_max, the highest r² values were for Google retail and recreation (0.49), and Unacast Visitation (0.52) metrics, but the Google data were much more accurate, with a slope close to 1 and intercept close to 0. Overall, these results suggest that cell-phone based mobility data vary substantially in their accuracy (slope and intercept near 1 and 0, respectively) and overall have low precision (no r² more than about 0.5), and supports our use of the range across multiple sources in developing prior distributions, rather than using such data directly for modeling contact rates.

The initiation of social distancing measures, such as stay-at-home orders in the US, for mitigating the spread of COVID-19 has occurred concurrently with increased promotion and application of other NPIs, such as hygiene practices (e.g. hand hygiene, surface cleaning, cough etiquette, and wearing of face mask). These hygiene practices coupled with the avoidance of physical contact whenever possible (keeping six feet apart) could impact the spread of COVID-19 by reducing both the risk of exposure and the risk of transmission of SARS-CoV-2 from infected patients ^23,24. Though our model explicitly accounts for the differential contribution of social distancing (mobility reduction) versus hygiene practices and physical distancing to reducing COVID-19 transmission, we assume that the impact of hygiene practices and physical distancing was a function of social distancing (mobility reduction). While cell phone mobility data may continue to be informative as to contact rates, at least in aggregate, the impact of enhanced hygiene practices is more difficult to measure independently. As several states have eased their social distancing requirements, especially their stay-at-home orders, compliance with hygiene practices would become even more important for reducing individuals’ risk of getting or transmitting the pathogen. However, keeping a high population-level adherence to these measures is required to mitigate the spread of the COVID-19 epidemic ²⁵. As states are reopening various aspects of their economy, data on compliance with enhanced hygiene practices and physical distancing are needed to improve the estimation of these measures’ population-level impact on reducing disease transmission.

Additionally, consistent with previous COVID-19 modeling studies ^26–28, our model uses a simple functional form to model increases in testing rate from early March to June, 2020. This testing rate was estimated through model fitting to daily reported case and mortality data. Particularly in states that have seen a substantial increase in testing capability and efforts during the month of May, our simple time varying assumption may underestimate the current level of testing and contact tracing. However, it should be noted that increased testing capacity does not necessarily lead to increased rate of testing if individuals are unaware, unwilling, or unable to be tested ²⁹. Having contact tracing and date of symptoms onset data would enable us to compute a better estimate of the current testing and contact tracing rate in each state. Our model also assumes that all individuals who test positive to COVID-19 are effectively isolated for the rest of their infectious period and no longer contribute to disease transmission. Though voluntary compliance to COVID-19 self-quarantine recommendations may be high across the US, it is likely not 100%. Therefore, the assumption of effective isolation of all identified cases may cause our model to slightly overestimate the impact of increased testing rate on disease dynamics. However, we anticipate that this assumption would only have a marginal impact on the qualitative nature of our results.

Finally, our model does not explicitly account for age-stratified risk of disease transmission and mortality. This age-stratification is important for designing and evaluating social distancing and testing strategies that are targeted towards the elderly population, which is at higher risk of COVID-19-induced hospitalization and death ³⁰. As reopening the economy becomes an imperative for states across the US, age- or risk-targeted interventions may be a valuable tool to mitigate the burden of the pandemic. Future modeling studies could investigate the effectiveness of age- or risk-targeted non-pharmaceutical and potential pharmaceutical (vaccine or therapeutic) interventions for controlling the spread and burden of COVID-19.

In sum, we use a data-driven mathematical modeling approach to study the impacts of social distancing, testing, and contact tracing on the transmission dynamics of SARS-CoV-2. Our findings emphasize the importance for public health authorities not only to monitor the case and mortality dynamics of SARS-CoV-2 in their state, but also to understand the impact of their existing social distancing measures on SARS-CoV-2 transmission and evaluate the effectiveness of their testing and contact tracing programs for promptly identifying and isolating new cases of COVID-19. As reported case rates are increasing widely across US states because social distancing restrictions have been eased to allow more economic activity to resume, we find that most states need to either significantly scale back reopening or enhance their capacity and scale of testing, case isolation, and contact tracing programs in order to mitigate large-scale increases in COVID-19 cases and deaths.

Methods

Our overall approach is as follows: 1) develop a mathematical model (an SEIR-type compartmental model)^18,19 that incorporates social distancing data, case identification via testing, isolation of detected cases, and contact tracing; 2) assess the model’s predictive performance by training (calibrating) it to reported cases and mortality data from March 19^th to April 30^th, 2020 and validating its predictions against data from May 1^st to June 20^th, 2020; and 3) use the model, trained on data through July 22^nd, 2020, to predict future incidence and mortality. The final stage of our approach predicts future events under a set of scenarios that include increased case detection through expanded testing rate, contact tracing, and relaxation or increase of measures to promote social distancing. All model fitting is performed in a Bayesian framework in order to incorporate available prior information and address multivariate uncertainty in model parameters.

Model formulation

We modified the standard SEIR model to address testing and contact tracing, as well as asymptomatic individuals. A fraction f_A of those exposed (E) to enter the asymptomatic A class (divided into A_U for untested, and A_C for contact traced) instead of the infected I class, which in our model formulation also includes infectious pre-symptomatic individuals. With respect to testing, separate compartments were added for untested, “freely roaming” infected individuals (I_U), tested/isolated cases I_T, fatalities F_T. Upon recovery, untested infected individuals I_U) and all asymptomatic individuals move to the untested recovered compartment I_U, and tested infected individuals move to the tested recovered compartment I_T. In balancing considerations of model fidelity and parameter identifiability, we made the reasonably conservative assumptions that all tested cases are effectively isolated (through self-quarantine or hospitalization) and thus unavailable for transmission, and that all COVID-related deaths are identified/tested.

With respect to contact tracing, the additional compartment S_C represents unexposed contacts, who undergo a period of isolation during which they are not susceptible before returning to S; while E_C, A_C, and I_C represent contacts who were exposed. Again, the reasonably conservative assumption was made that all exposed contacts undergo testing, with an accelerated testing rate compared to the general population. We assume a closed population of constant size N for each state.

The ordinary differential equations governing our model are as follows:

$$\frac{dS}{dt}=-S\cdot c\cdot [\beta +(1-\beta )\cdot f_C]\cdot (I_U+A_U)/N+S_C\cdot \gamma$$

$$\frac{d{S}_C}{dt}=-S_C\cdot \gamma +S\cdot c\cdot (1-\beta )\cdot f_C\cdot (I_U+A_U)/N$$

$$\frac{dE}{dt}=-E\cdot \kappa +S\cdot c\cdot \beta \cdot (1-f_C)\cdot (I_U+A_U)/N$$

$$\frac{d{E}_C}{dt}=-E_C\cdot \kappa +S\cdot c\cdot \beta \cdot f_C\cdot (I_U+A_U)/N$$

$$\frac{d{I}_U}{dt}=-I_U\cdot (\lambda +\rho )+E\cdot \kappa \cdot (1-f_A)$$

$$\frac{d{A}_U}{dt}=-A_U\cdot \rho +E\cdot \kappa \cdot f_A$$

$$\frac{d{I}_C}{dt}=-I_C\cdot ({\lambda }_C+{\rho }_C)+E_C\cdot \kappa \cdot (1-f_A)$$

$$\frac{d{A}_C}{dt}=-A_C\cdot {\rho }_C+E_C\cdot \kappa \cdot f_A$$

$$\frac{d{R}_U}{dt}=(I_U+A_U+A_C)\cdot \rho +I_C\cdot {\rho }_C$$

$$\frac{d{I}_T}{dt}=-I_T\cdot (\rho +\delta )+I_U\cdot \lambda +I_C\cdot {\lambda }_C$$

$$\frac{d{R}_T}{dt}=I_T\cdot \rho$$

$$\frac{d{F}_T}{dt}=I_T\cdot \delta$$

c is the contact rate between individuals, β is the transmission probability per infected contact, f_C is the fraction of contacts identified through contact tracing, 1/γ is the duration of self-isolation after contact tracing, 1/κ is the latent period, f_A is the fraction of exposed who are asymptomatic, λ is the testing rate, δ is the fatality rate, ρ is the recovery rate, λ_C and ρ_C is the testing rate and recovery rate of contact traced individuals, respectively. The testing rates λ and λ_C, the fatality rate δ, and the recovery rate of traced contacts ρ_C are each composites of several underlying parameters. The testing rate defined as

$$\lambda (t)=F_{test,0}\cdot [1-\frac{1}{1+e^{(t-{T50}_T)/{\tau }_T}}]\cdot Sen{s}_{test}\cdot k_{test},$$

where F_test,0 is the current testing coverage (fraction of infected individuals tested), Sens_test is the test sensitivity (true positive rate), and k_test is rate of testing for those tested, with a typical time-to-test equal to 1/k_test. The time-dependence term models the “ramp-up” of testing using a logistic function with a growth rate of 1/τ_T days⁻¹, where T50_T is the time where 50% of the current testing rate is achieved. Similarly, for testing of traced contacts, the same definition is used with the assumption that all identified contacts are tested, F_test,0 = 1 and at a faster assumed testing rate k_C,test:

$${\lambda }_C(t)=[1-\frac{1}{1+e^{(t-{T50}_T)/{\tau }_T}}]\cdot Sen{s}_{test}\cdot k_{C,test},$$

Because all contacts are assumed to be tested, the rate ρ_C at which they enter the “recovered” compartment R_U is simply the rate of false negative test results:

$${\rho }_C(t)=[1-\frac{1}{1+e^{(t-{T50}_T)/{\tau }_T}}]\cdot (1-Sen{s}_{test})\cdot k_{test}$$

The fatality rate is adjusted to maintain consistency with the assumption that all COVID-19 deaths are identified, assuming a constant infected fatality rate (IFR). Specifically, we first calculated the fraction of infected that are tested and positive

$$f_{pos}(t)=f_C\frac{{\lambda }_C(t)}{{\lambda }_C(t)+{\rho }_C(t)}+(1-f_C)\frac{\lambda (t)}{\lambda (t)+\rho }.$$

Then the case fatality rate CFR(t) = IFR/f_pos(t). Because the CFR = δ/(δ + ρ), this implies

$$\delta (t)=\rho \frac{CFR(t)}{1-CFR(t)}=\rho \frac{IFR}{f_{pos}(t)-IFR}.$$

The model is “seeded” N_initial cases on February 29^th, 2020. Because in the early stages of the outbreak, there may be multiple “imported” cases, we only fit to data from March 19^th, 2020 onwards, one week after the U.S. travel ban was put in place ³¹.

Our model is fit to daily case y_c and death y_d data (cumulative data are not used for fitting because of autocorrelation). To adequately fit the case and mortality data, we accounted for two lag times. First, a lag is assumed between leaving the I_U compartment and public reporting of a positive test result, accounting for the time it takes to seek a test, obtaining testing, and have the result reported. No lag is assumed for tests from contact tracing. Second, a lag time is assumed between entering the fatally ill compartment F_T and publicly reported deaths. Additionally, we use a negative binomial likelihood in order to account for the substantial day-to-day overdispersion in reporting results. The corresponding equations are as follows:

$$y_{obs,[c,d]}(t)\sim NegBin[{\alpha }_{[c,d]},p_{[c,d]}(t)]$$

$$p_{[c,d]}(t)=\frac{y_{pred,[c,d]}(t)}{{\alpha }_{[c,d]}+y_{pred,[c,d]}(t)}$$

$$y_{pred,c}(t)=I_U(t-{\tau }_{case})\cdot \lambda (t)+I_C(t)\cdot {\lambda }_C(t)$$

$$y_{pred,d}(t)=I_T(t-{\tau }_{death})\cdot \delta (t)$$

In this parameterization, as the dispersion parameter α → ∞, the likelihood becomes a Poisson distribution with expected value y_pred,[c,d], whereas for small values of α there is substantial inter-individual variability. Case and death data were sourced from The COVID Tracking Project ³².

Finally, we derived the time-dependent reproduction number, R(t) and the effective reproduction number, R_eff(t) of this model, given by

$$R(t)=c\cdot \beta \cdot (1-f_C)(\frac{1-f_A}{\lambda +\rho }+\frac{f_A}{\rho })$$

and

$$R_{eff}(t)=R(t)\cdot \frac{S(t)}{N}$$

R_eff(t) is the average number of secondary infection cases generated by a single infectious individual during her infectious period in partially susceptible population at time t. It is equal to the product of the transmission risk per contact of an infectious individuals with her untraced contacts, c ⋅ β ⋅ (1 − f_C), times her average duration of infection, $(\frac{1-f_A}{\lambda +\rho }+\frac{f_A}{\rho })$, and the portion of contacts that are susceptible $\frac{S(t)}{N}$. This accounts for the relative contribution of asymptomatic, $c\cdot \beta \cdot (1-f_C)\left(\frac{f_A}{\rho }\right)\cdot \frac{S(t)}{N}$, and symptomatic infection, $c\cdot \beta \cdot (1-f_C)\left(\frac{1-f_A}{\lambda +\rho }\right)\cdot \frac{S(t)}{N}$. Using posterior samples for all 50 states and the District of Columbia, we conducted an analysis of variance using a linear model to characterize the contributions to the combined inter- and intra-state variation in R_eff. Specifically, we used a linear model for R_eff with the model parameters R₀, η, θ_min, r_max, f_C, f_A, λ, and ρ as predictors, and evaluated the percentage of variance in R_eff contributed by each parameter.

Incorporating social distancing, enhanced hygiene practices, and reopening

The impact of social distancing, hygiene practices, and reopening were modeled through a time-dependence in the contact rate c and the transmission probability per infected contact β:

$$c(t)=c_0\cdot \left[\theta (t)+(1-{\theta }_{min})\cdot r(t)\right]$$

$$\beta (t)={\beta }_0\cdot \theta (t{)}^{\eta }$$

The θ(t) function parameterized social distancing during the progression to shelter-in-place, and is modeled as a Weibull function

$$\theta (t)={\theta }_{min}+(1-{\theta }_{min})e^{-(t/{\tau }_{\theta }{)}^{n_{\theta }}},$$

which starts a unity and decreases to θ_min, with τ_θ being Weibull scale parameter and n_θ the Weibull shape parameter (Figure 1).

The r(t) function parameterized relative increase in contacts due to reopening after shelter-in-place, with r = 1 corresponding to a return to baseline c = c₀.

$$r(t)=r_{max}\frac{t-{\tau }_{\theta }-{\tau }_s}{{\tau }_r}\left[u(t-t_r)-u(t-t_{rmax})\right]+u(t-t_{rmax})$$

$$u(t)=Heaviside(t)\approx 1-\frac{1}{1+e^{4t}}$$

$$t_r={\tau }_{\theta }+{\tau }_s$$

$$t_{rmax}={\tau }_{\theta }+{\tau }_s+{\tau }_r$$

The term r(t) is 0 before t_r, linear between t_r and t_rmax, and constant at a value of r_max after that, and made continuous by approximating the Heaviside function by a logistic function. The reopening time is defined as τ_s days after τ_θ, and the maximum relative increase in contacts r_max happens τ_r days after that.

We selected the functional form above for c(t) because it was found to be able to represent a wide variety of social distancing data, including cell phone mobility data from Unacast ³³ and Google ³⁴, as well as restaurant booking data from OpenTable ³⁵. We used these different mobility sources to derive state-specific prior distributions because different social distancing datasets had different values for θ_min, τ_θ, n_θ, τ_S, r_max, and τ_R (Figure S1).

With respect to the reduction in transmission probability β, we assumed that during the “shelter-in-place” phase, hygiene-based mitigation paralleled this decline with an effectiveness power η, and that this mitigation continued through re-opening.

Finally, we define an overall “reopening” parameter Δ that measures the “rebound” in disease transmission c ⋅ β relative to its minimum, defined to be 0 during shelter-in-place (i.e., R(t) is at a minimum), and 1 when all restrictions are removed (when R(t) = R₀), which can be derived as:

$$\Delta (t)=\frac{c\cdot \beta /(c_0\cdot {\beta }_0)-{\theta }_{min}^{1+\eta }}{1-{\theta }_{min}^{1+\eta }}.$$

Our model is illustrated in Figure 1, with parameters and prior distributions listed in Table 1.

Scenario evaluation

We used the model to make several inferences about the current and future course of the pandemic in each state. First, we consider the effective reproduction number. Two time points of particular interest are the time of minimum R_eff, reflecting the degree to which shelter-in-place and other interventions were effective in reducing transmission, and the final time of the simulation, July 22^nd, 2020, reflecting the extent to which reopening has increased R_eff. Additional parameters of interest are the current levels of reopening Δ(t), testing λ, and contact tracing f_C.

We then conducted scenario-based prospective predictions using our model’s parameters as estimated through July 22^nd, 2020. We asked the following questions:

1. Assuming current levels of reopening, what increases in general testing λ and/or contact tracing f_C would be necessary to bring R_eff < 1?

2. What amount reopening Δ can maintain R_eff < 1 under four different scenarios: current values of testing and contact tracing, doubling testing, double tracing, and doubling both testing and tracing?

3. What will the rates of new cases and deaths be under different scenarios? Specifically, we evaluate the impact of increases in testing and contact tracing under current levels of reopening, as well as increases or decreases of 25% or 50%.

For (a), we evaluated the posterior probability that R_eff < 1 under scaling transformations λ → λ ⋅ μ_λ and f_C → f_C ⋅ μ_C with scaling factors μ_λ and μ_C:

$$R_{eff}(t)=S(t)\cdot c\cdot \beta \cdot (1-{\mu }_C\cdot f_C)(\frac{1-f_A}{{\mu }_{\lambda }\cdot \lambda +\rho }+\frac{f_A}{\rho })$$

We additionally derived “critical” values of μ_C and μ_λ where R_eff(t) < 1 under the conditions of increased testing only (μ_C = 1), increased contact tracing only (μ_λ = 1), and equal increases in testing and tracing (μ_C = μ_λ). We also performed the same analysis under a full re-opening scenario (i.e., setting S(t) = 1, c = c₀, and β = β₀).

For (b), we re-arranged the equation for R_eff in terms of the reopening parameter Δ

$$R_{eff}(t)=S(t)\cdot c_0\cdot {\beta }_0\cdot (1-{\mu }_C\cdot f_C)(\frac{1-f_A}{{\mu }_{\lambda }\cdot \lambda +\rho }+\frac{f_A}{\rho })\left[\Delta \cdot (1-{\theta }_{min}^{1+\eta })+{\theta }_{min}^{1+\eta }\right]$$

We then fixed the scaling factors at 1 or 2, and solved the above equation for Δ_crit such that R_eff < 1. Values of Δ_crit ≥ Δ(t) indicate the additional degree of reopening possible while maintaining R_eff < 1, while values of Δ_crit < Δ(t) indicate a reduction of reopening is needed. To convert back to testing and contact tracing rates, we multiplied the scaling factors μ_C and μ_λ by the original values of f_C and λ, respectively.

Finally, for (c), we additionally evaluated changes in reopening Δ → Δ + Δ_Δ for Δ_Δ values of +25% (+50%) or −25% (−50%), for a total of 20 scenarios (4 different levels of testing and tracing, and 5 different levels of reopening). We then ran the SEIR model forward in time until September 30th, 2020. For all three intervention parameters μ_C, μ_λ, and Δ_Δ, we assumed a “ramp-up” period of 2 weeks from August 1^st–14^th, 2020.

To summarize the relative need for mitigation in each state, we categorized states based on which scenarios resulted in the IQR of R(t) being < 1 on August 15^th, 2020. The categories were defined as follows:

• Very Low: Can reopen further by >25% while keeping R(t) < 1;

• Low: Can reopen further by < 25% with up to 2X increase in testing while keeping R(t) < 1;

• Moderate: Requires 2X contact tracing or reversal of reopening by 25% to bring and keep R(t) < 1;

• High: Requires multiple interventions (2X testing, 2X contract tracing, reversal of reopening by 25%) to bring and keep R(t) < 1;

• Very High: Combining 2X testing, 2X contact tracing, and reversal of reopening by 50% is needed to bring and keep R(t) < 1.

We use R(t) instead of R_eff(t), to minimize the impact of heterogeneity and uncertainty in the value of S(t)/N on our results. Thus, requiring R(t) < 1 provides greater assurance of state-wide control of the epidemic.

Software and code

Posterior distributions were sampled using Markov chain Monte Carlo simulation performed using MCSim version 6.1.0 using Metropolis within Gibbs sampling ³⁶. For each US state, four chains of 200,000 iterations each were run, with the first 20% of runs discarded, and 500 posterior samples saved for analysis. For each parameter, comparison of interchain and intrachain variability was assessed to determine convergence, with the potential scale reduction factor R ≤ 1.2 considered converged ³⁷. Additional analysis of model outputs was performed in RStudio version 1.2.1335 ³⁸ with R version 3.6.1³⁹.

Data availability statement

The following publicly available datasets are used:

• Mobility data from Unacast were sourced from https://covid19-scoreboard-api.unacastapis.com/api/search/covidstateaggregates_v3.

• Mobility data from Google were sourced from https://www.gstatic.com/covid19/mobility/Global_Mobility_Report.csv.

• Restaurant booking data were sourced from OpenTable https://www.opentable.com/state-of-industry.

• Case and death data were sourced from The COVID Tracking Project (https://covidtracking.com/).

Mobility data are shown in Supplemental Figure 1. Case and death data are shown in Figures 1 and 3, and Supplemental Figures 3–6, 8. All data used are also available in the software and code repository.

Code availability statement

The codes used to generate our results will be available on GitHub prior to publication at https://github.com/wachiuphd/COVID-19-Bayesian-SEIR-US.

Extended Data

Extended Data Fig. 1: Correlations across states between R_eff(t) and (A) θ_min, (B) η, (C) Δ, and (D) f_C.

For each state, 500 posterior samples are shown. Substantial state-to-state heterogeneity is evident in all parameters, with η,θ_min, r_max, and f_C contribute over 50% of the variance in R_eff(t) under a linear model (estimated from ANOVA table [Table S1] using the sum-of-squares relative to the total sum-of-squares). For θ_min, while lower values appear to be associated with greater current values of R_eff(t) in a univariate model (linear model coefficient = −0.54, t statistic = −78.14, p < 2.2e-16, 95% CI = [−0.56,−0.53]), the correlation is positive in the multivariate model (coefficient = 0.11, t statistic = 13.65, p < 2.2e-16, 95% CI = [0.09, 0.13]). The other parameters correlate as expected: higher R_eff(t) is correlated with lower contribution from hygiene practices (smaller η) (coefficient = −0.39, t statistic = −59.7, p < 2.2e-16, 95% CI = [−0.40,−0.38]), more reopening (larger r_max) (coefficient = 0.44, t statistic = 119.0, p < 2.2e-16, 95% CI = [0.43, 0.45]), and lower rates of contact tracing (smaller f_C) (coefficient = −0.90, t statistic = −114.6, p < 2.2e-16, 95% CI = [−0.92, −0.89]).

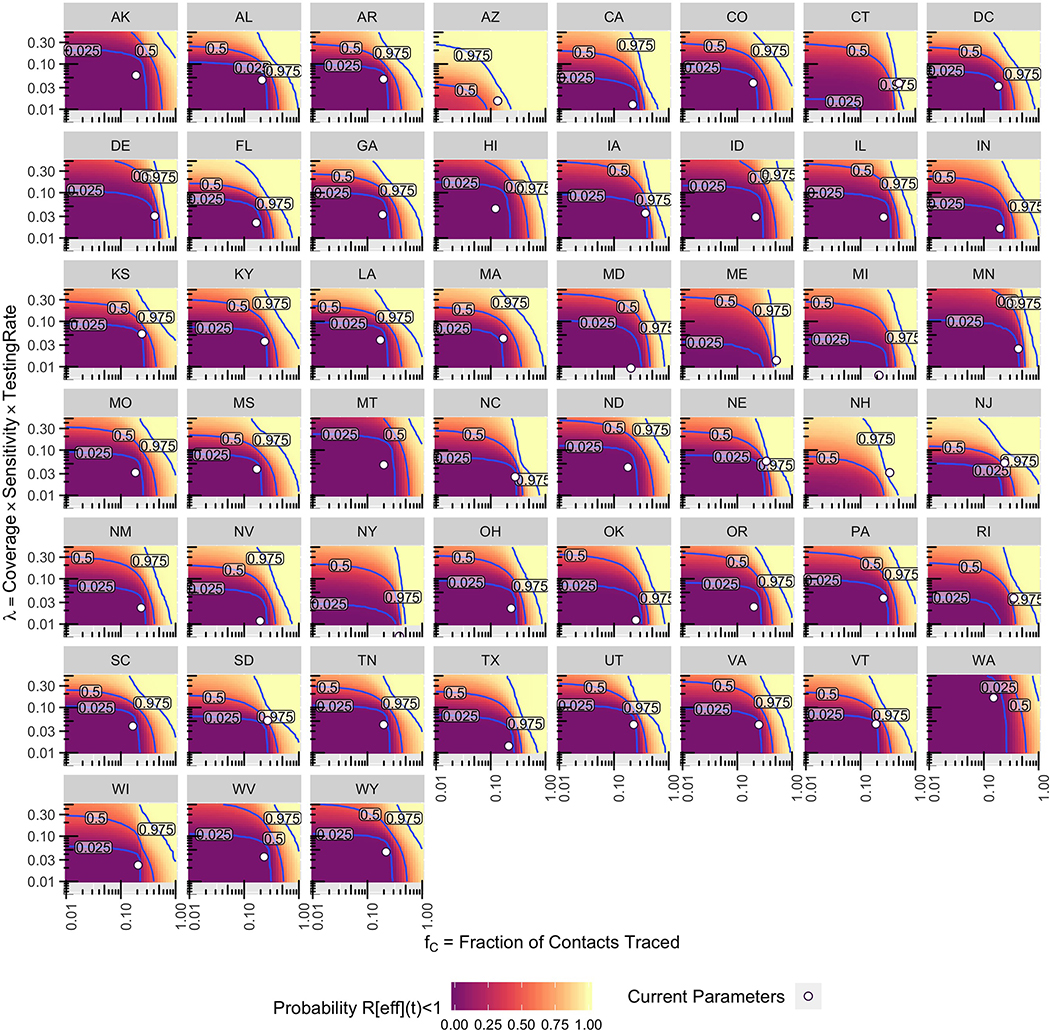
Extended Data Fig. 2: Contour maps for each state of the probability that R_eff(t) at different levels contact tracing f_C and testing λ.

Contours are labelled as by median and 95% Credible interval, and current median estimates of f_C and λ are shown by the circle.

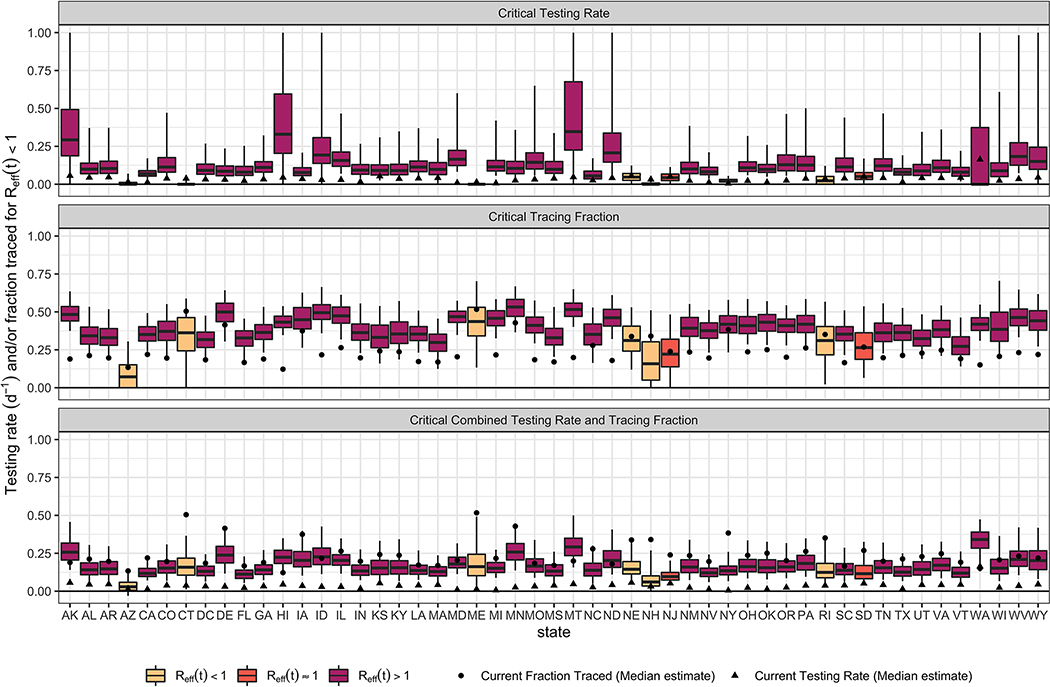
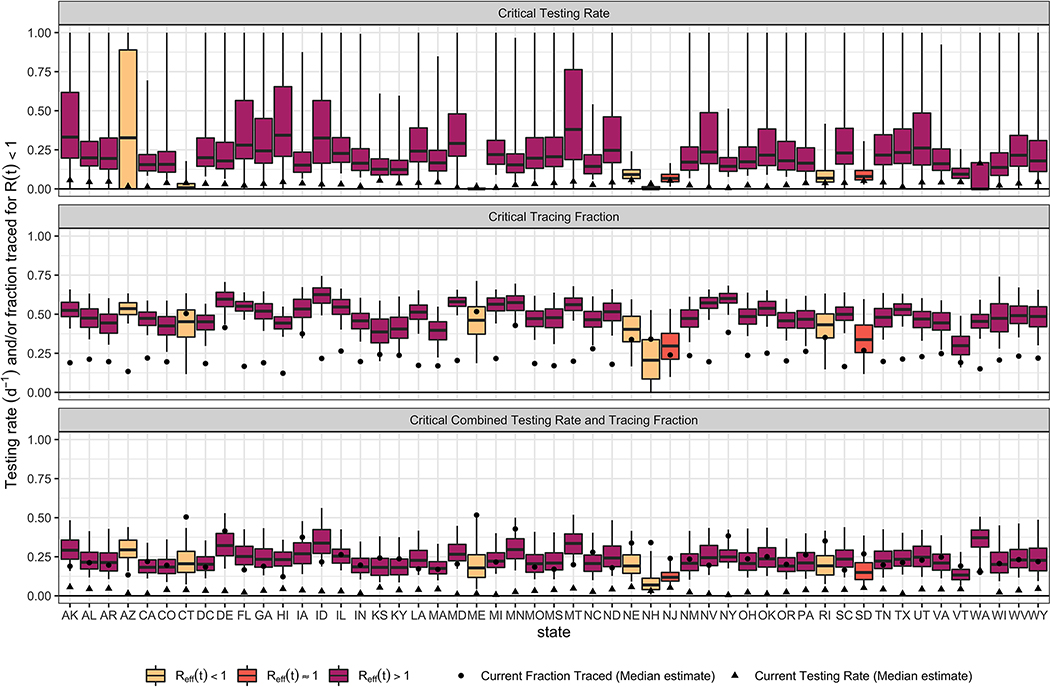
Extended Data Fig. 3: Estimated testing and contact tracing rates needed for R_eff(t) < 1 as of July 22, 2020.

Boxplots (line = median, box = IQR, whiskers = 95% CrI) are filled based on the estimated R_eff(t) on July 22, 2020, as shown in the legend. Top panel is changing testing rate alone, the middle panel is changing contact tracing rate alone, and the bottom panel is changing both to the same value. Also shown are the current median estimates of the testing and contact tracing rates.

Extended Data Fig. 4: Estimated testing and contact tracing rates needed for R(t) < 1 with complete re-opening (i.e., removal of all social distancing and hygiene mitigation).

Boxplots (line = median, box = IQR, whiskers = 95% CrI) are filled based on the estimated R_eff(t) on July 22, 2020, as shown in the legend. Top panel is changing testing rate alone, the middle panel is changing contact tracing rate alone, and the bottom panel is changing both to the same value. Also shown are the current median estimates of the testing and contact tracing rates.