Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 25;9(10):2797–2807. doi: 10.1021/acssynbio.0c00330

Transcription and Translation in Cytomimetic Protocells Perform Most Efficiently at Distinct Macromolecular Crowding Conditions

Mahesh A Vibhute 1, Mark H Schaap 1, Roel J M Maas 1, Frank H T Nelissen 1, Evan Spruijt 1, Hans A Heus 1, Maike M K Hansen 1,*, Wilhelm T S Huck 1,*
PMCID: PMC7573978  PMID: 32976714

Abstract

graphic file with name sb0c00330_0005.jpg

The formation of cytomimetic protocells that capture the physicochemical aspects of living cells is an important goal in bottom-up synthetic biology. Here, we recreated the crowded cytoplasm in liposome-based protocells and studied the kinetics of cell-free gene expression in these crowded containers. We found that diffusion of key components is affected not only by macromolecular crowding but also by enzymatic activity in the protocell. Surprisingly, size-dependent diffusion in crowded conditions yielded two distinct maxima for protein synthesis, reflecting the differential impact of crowding on transcription and translation. Our experimental data show, for the first time, that macromolecular crowding induces a switch from reaction to diffusion control and that this switch depends on the sizes of the macromolecules involved. These results highlight the need to control the physical environment in the design of synthetic cells.

Keywords: Protocells, liposomes, macromolecular crowding, microfluidics, cell free gene expression

Reconstituting living cells from their building blocks is one of the grand challenges in bottom-up synthetic biology.1−3 To this end, much progress has been made in incorporating complex cellular systems such as parts of the bacterial divisome,4−8 the oscillating Min system,9−12 synthetic signaling pathways,13 and cell-free gene expression systems14−16 inside lipid-based vesicles. Cytomimetic protocells provide an ideal platform for improving our capabilities to engineer ever more complex and integrated systems with life-like properties.17−20 However, current protocell models fail to mimic the physicochemical nature of the cytoplasm. The bacterial cytoplasm is a highly crowded and heterogeneous mixture of proteins, nucleic acids, and metabolites. With the intracellular macromolecular concentration ranging between 200 and 300 mg/mL, the cytoplasmic conditions are far from the dilute conditions typically employed in protocell experiments.21,22 Seminal experiments have shown glass-like dynamics in osmotically compressed, or metabolically depleted cells.23,24 Crowded conditions, thus, are bound to have a significant impact on the stability and mobility of macromolecular complexes, influencing all aspects of intracellular chemistry.22,25−27 We, and others, have previously shown that macromolecular crowding can indeed affect essential biochemical processes.28−31 However, previous in vitro studies did not quite recapitulate the bacterial environment, as crowding was typically achieved by the addition of synthetic polymers with large excluded volumes such as polyethylene glycol (PEG) and Ficoll. These polymers do not replicate the electrostatic and hydrophobic interactions that are present between protein surfaces and are thus inaccurate mimics of the crowded cellular environment.25,32−34

We recently reported a microfluidic method to produce and shrink monodisperse liposomes by 2 to 3 orders of magnitude in volume. These shrunk liposomes are stable and capable of efficient protein expression.35 Here, we employ this method to systematically increase crowding, achieving lysate concentrations up to 390 mg/mL. First, we show how the diffusion of biologically relevant molecules inside our liposomal protocells is dramatically affected not only by crowding but also by enzymatic activity. We then studied the effect of cytosolic crowding on gene expression. Surprisingly, gene expression efficiency (i.e., the amount of protein produced from a fixed amount of nutrients in the protocells) shows a highly nonlinear relationship with the degree of macromolecular crowding. From our experimental data, we build a mathematical model to determine the underlying reaction-versus-diffusion kinetics that drive this nonlinear relationship. We find that macromolecular crowding in protocells induces differential effects on transcription and translation kinetics, and show for the first time a switch from reaction-to-diffusion controlled kinetics at distinct macromolecular crowding conditions for transcription and translation. This switch has been theoretically postulated since the early 1990s.22,36−38 Yet, such a switch has thus far only been reported for protein phosphorylation in vitro, and not for more complex cellular processes.39 Together, these results mandate future incorporation of the physical environment in the design of synthetic cells.

Results and Discussion

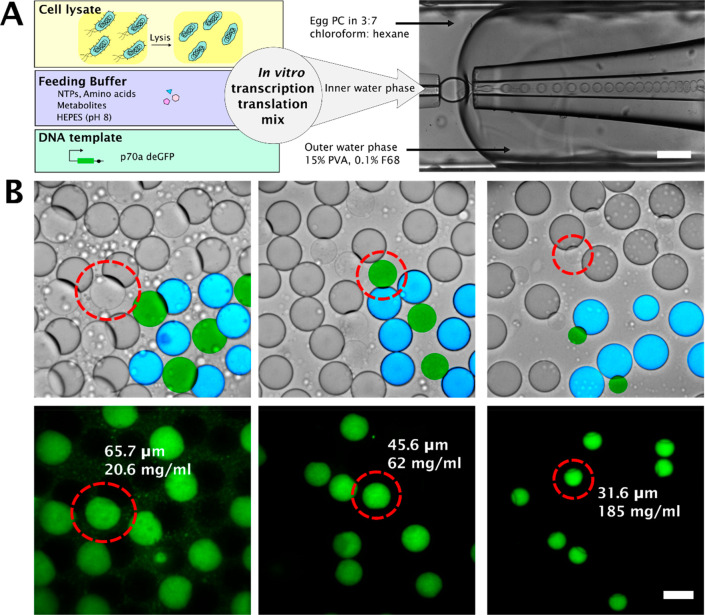
Using our previously reported method35 we prepared liposomes filled with cell lysate, feeding buffer (AAs, NTPs, essential metabolites), salts (Mg-glutamate and K-glutamate) and DNA (linear template) (Figure 1A). These liposomes undergo partial dewetting,35 as can be seen in Figure 1B (In the brightfield images, liposomes are colored green, and oil droplets are colored cyan), allowing us to osmotically shrink the liposomes by tuning the concentration of the hypertonic (sucrose) solution outside the liposomes and the salt concentration inside them. We shrank the liposomes to different extents, achieving lysate concentrations ranging from 14 mg/mL to 390 mg/mL lysate. These shrunk liposomes were stable for at least 18 h. Notably, shrinking leads to not only increased lysate concentrations but also increased concentrations of all other components, the importance of which we will discuss in more detail below.

Figure 1.

Figure 1

Open in a new tab

Schematic overview of the workflow. (A) Transcription-translation machinery is encapsulated in monodisperse double emulsion droplets, which undergo partial dewetting.35 Scale bar 200 μm. (B) Brightfield and fluorescence images of partially dewetted liposomes, crowded to different extent by osmotic shrinkage. A section of brightfield images has been superimposed with false color images to highlight the liposomes (colored green) and the attached oil droplet (colored blue). The diameter and lysate concentration are denoted, alongside the circled liposome. Scale bar 50 μm.

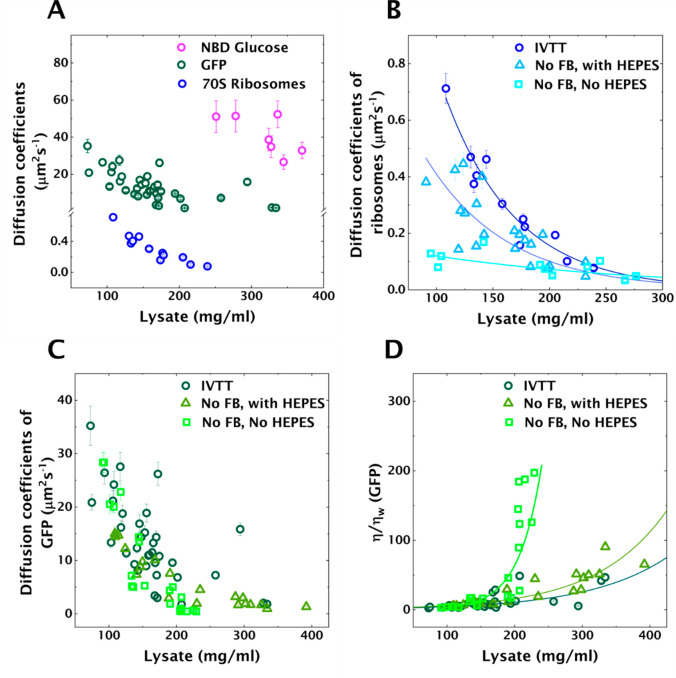
The cytoplasm behaves like a dense, heterogeneous colloid close to its glass transition for large particles (30–40 nm)23 and like a liquid for small molecules such as sugar and metabolites.40 We wished to ascertain whether we can capture this aspect of the cytoplasm inside our protocells, to determine if our system can mimic the crowded nature of the cytoplasm. Therefore, we studied diffusion of relevant biomolecules of three different sizes (0.34 kDa, 27 kDa, and 2.7 MDa) as a function of crowding. We used fluorescence recovery after photobleaching (FRAP) to determine diffusion coefficients of these biomolecules in protocells crowded to different extents (Figure 2A, Tables S1–S3).

Figure 2.

Figure 2

Open in a new tab

Diffusion coefficients as a function of crowding (lysate concentration) determined using FRAP in protocells. The error bars represent standard deviation calculated by estimating the uncertainties in fit parameters (see Methods). (A) Diffusion coefficients of NBDG, GFP and Atto488 labeled 70S ribosomes. (B) Diffusion coefficients of Atto488 labeled 70S ribosomes in crowded protocells in three different conditions (the solid lines are exponential fits): (i) in the presence of IVTT; (ii) metabolically inactive with buffered pH (HEPES at pH 8); (iii) metabolically inactive without buffered pH. (C) Diffusion coefficients of GFP under the same three conditions as B. (D) Effective viscosity determined using GFP diffusion coefficients and Stokes–Einstein equation. The solid lines are exponential fits.

As reported in the literature23,41 enzymatic activity can significantly impact the state of the cytoplasm. To make sure that we approximate the intracellular environment accurately, we conducted diffusion measurements in the presence of cell-free expression of cyan fluorescent protein (deCFP) (see Methods) inside the shrunk liposomes. Notably, the protein being expressed was chosen to be different than the protein used for the diffusion studies to decouple diffusion from enzymatic activity, i.e., gene expression.

We first studied the mobility of small molecules using a fluorescent analogue of glucose: 2-(N-(7-nitrobenz-2-oxa-1,3-diazol-4-yl)amino)-2-deoxyglucose (NBDG). FRAP measurements on NBDG were technically challenging at low lysate concentration due to poor signal and rapid diffusion post/during bleaching. However, NBDG was mobile, giving diffusion coefficients >26 μm2 s–1 even at lysate concentrations exceeding 300 mg/mL, indicating that small molecules diffuse uninhibited, with the effect of crowding being negligible (Table S3). Next, we studied diffusion of green fluorescent protein (GFP) in crowded liposomes. With a molecular weight of about 27 kDa, GFP serves well for approximating diffusion of midsized proteins in the cytoplasm. Diffusion coefficients of GFP decreased from 35 ± 3.6 μm2 s–1 to 1.8 ± 0.1 μm2 s–1 (Table S1A) for increasingly crowded protocells (73–334 mg/mL), reaching similar values reported for in vivo measurements of GFP diffusion in bacterial cytoplasm.40,42 Finally, we studied the properties of some of the largest complexes in lysate, 70S ribosomes. Ribosomes were purified43 and labeled with Atto488 NHS ester dye. The diffusion coefficients of ribosomes decreased significantly from 0.71 ± 0.05 μm2 s–1 at 100 mg/mL to 0.077 ± 0.007 μm2 s–1 at 240 mg/mL lysate concentration (Figure 2A, Table S2A). At a lysate concentration of 250 mg/mL, the ribosomes appeared essentially immobile, with the bleached region not fully recovering fluorescence in 100 s. Calculating the diffusion coefficient at 250 mg/mL based on an exponential fit to the data yielded a value of 0.07 μm2 s–1. This is comparable with in vivo measurements reporting a diffusion coefficient of actively translating ribosomes of 0.04 μm2 s–1 in Escherichia coli (E. coli).44

Above, we studied the change in diffusion as a function of lysate concentration for biomolecules of different sizes. These studies showed that our protocells are indeed able to capture the size-dependent diffusion of biomolecules observed in bacterial cytoplasm. However, the bacterial cytoplasm has been observed to vitrify upon metabolic depletion, thereby undergoing a liquid-like to solid-like transition with respect to particle size.23 In ref (23), Parry et al. compare the cytoplasm to glass-forming liquids near a glass transition, wherein large particles are trapped or caged by neighboring macromolecules. Processes associated with metabolic activities collectively fluidize the cytoplasm. Since our system captures the crowded nature of cytoplasm, we aimed to explore the effect of metabolic (or enzymatic) activity on diffusion. In addition, we note that Parry et al. achieved metabolic depletion in bacterial cells23 by treatment with 2,4-dinitrophenol (DNP). DNP is a proton ionophore that rapidly shuttles protons across the membrane. As a result, the intracellular pH is bound to be affected. Changes in pH will in turn strongly influence protein solubility and drive assembly of proteins, leading to gelation.45−47 Therefore, we also took into consideration the effect of pH in crowded lysates. To that end, we studied diffusion of 70S ribosomes and GFP in three conditions: in the presence of enzymatic activity; in the absence of enzymatic activity but with buffered pH; and in the absence of both enzymatic activity and pH buffer (Tables S1, S2). The presence of enzymatic activity was approximated by in vitro transcription translation (IVTT) (IVTT in Figure 2B,C,D). Diffusion measurements with FRAP were conducted in the presence of deCFP expression as mentioned above (see Methods). As shown in Figure 1A, an IVTT reaction mixture consists of cell lysate, feeding buffer (FB), and DNA template, with the FB consisting of energy elements such as NTPs, amino acids, essential metabolites, and 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) to maintain a pH around 8. To achieve the second condition, i.e., absence of metabolic activity, but with pH buffer, we omitted the FB, but added HEPES to buffer the pH at 8 (No FB, with HEPES in Figure 2B,C,D). Finally, the third condition, i.e. absence of both enzymatic activity and pH buffer, was achieved by omitting both FB and HEPES (No FB, no HEPES in Figure 2B,C,D).

Parry et al. observed that diffusion of particles decreased upon metabolic depletion in a size-dependent manner.23 Diffusion coefficients of ribosomes noticeably decreased upon metabolic depletion (Figure 2B, No FB, with HEPES, Table S2B) ranging from 0.38 ± 0.02 to 0.047 ± 0.003 μm2 s–1 for lysate concentrations 90–230 mg/mL. Moreover, a further decrease in diffusion coefficients was observed in the absence of pH buffer (Figure 2B, No FB, no HEPES, Table S2C). Yet, above a lysate concentration of 200 mg/mL, the difference between these three regimes is no longer apparent. We performed a similar set of experiments with GFP (Figure 2C). Considering the size of GFP molecule (∼3 nm,48 BNID 104396), we wanted to test whether diffusion of GFP would be affected by metabolic depletion, or in the absence of a pH buffer. A decrease in diffusion of GFP by metabolic or buffer depletion was not immediately apparent, especially at low crowding ([lysate] < 200 mg/mL) (Table S1B). However, diffusion coefficients of GFP in the absence of pH buffer were comparatively lower, at lysate concentrations above 200 mg/mL (Table S1C). For a closer examination, we calculated the effective viscosity experienced by GFP molecules using the Stokes–Einstein equation (Figure 2D; see Supporting Information, note on viscosity curves). We observed a slight increase in viscosity upon metabolic depletion, and a dramatic increase in the absence of pH buffer, at a lysate concentration exceeding 200 mg/mL. We hypothesize that this large change originated from a change in pH in the lysate. Using a ratiometric pH indicator dye (SNARF-5F 5-(and-6)-carboxylic acid) we estimated the pH in the absence of HEPES to be around 6.37 (Figure S3).

We performed an additional control experiment wherein we determined diffusion coefficients, and thereby effective viscosity experienced by GFP molecules, in the presence of HEPES buffered to pH 6 (Figure S4). The E. coli proteome is known to be acidic, with the isoelectric point of most of the cytoplasmic proteins being lower than 6.49 Proteins close to their isoelectric points typically have low solubility, as the low net charge results in weakened repulsive interactions. The corresponding increase in the contribution of attractive interactions drives the formation of protein assemblies.46,47 The absence of a pH buffer can thus lead to protein aggregation explaining the observed increase in viscosity.

Our system captures the physicochemical properties of the cytoplasm, by displaying a particle-size dependent decrease in diffusion upon metabolic depletion. Furthermore, we find that coupling metabolic depletion with a reduction in pH further impairs diffusion. The size dependence of these two conditions is also different, since metabolic depletion impacts primarily large particles such as 70S ribosomes, whereas the combined effect of metabolic depletion and lowered pH exerts an influence on small particles like GFP as well.

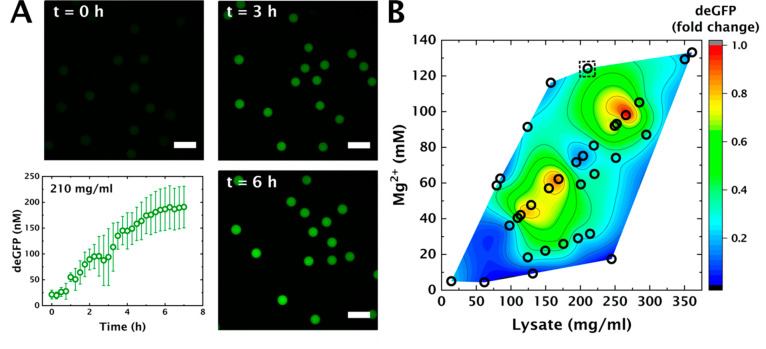
Having established the cytomimetic nature of our protocell interior, we wanted to gain insights into the efficiency of essential biochemical processes in such crowded conditions. Therefore, we proceeded to study gene expression in these protocells. To probe the impact of cytosolic crowding on gene expression efficiency, we studied expression of deGFP50 under control of the endogenous σ70-specific promotor p70a in crowded liposomes. Mg2+ plays a diverse role in gene expression, as it influences tRNA folding51,52 and ribosome assembly,53 and is a cofactor for RNA polymerase.54 We therefore systematically investigated the effect of different combinations of [Mg2+] and [lysate] on protein production in crowded protocells (see Methods and Figures S5–S7 for experimental details). We encapsulated the IVTT reaction mix of varying initial [Mg2+] in liposomes and shrank (crowded) them to different extents. We then determined the total amount of deGFP expressed after 4 h, at room temperature. Interestingly, we observe considerably different yields of deGFP at different levels of macromolecular crowding (Figure 3B), even though the absolute amount of starting material (NTPs, AAs, metabolites, DNA, and cell lysate) was near-identical. We also performed control experiments to verify that the variation we observed in these experiments corresponds to the different amounts of deGFP expressed (Figures S8, S9). The different amounts of deGFP produced in these varying conditions, are plotted in Figure 3B as a function of the final concentrations of magnesium and lysate (Figures S10, S11). Intriguingly, the level of gene expression shows two optimal combinations detected around lysate concentrations of 170 and 260 mg/mL, respectively.

Figure 3.

Figure 3

Open in a new tab

Cell free gene expression in crowded protocells in varying combinations of [lysate] and [Mg2+]. (A) deGFP expression inside shrunk liposomes with lysate concentration at 210 mg/mL. The error bars indicate standard deviation when measuring fluorescence in multiple liposomes (n = 15). Scale bar: 100 μm. (B) Contour plot denoting amount of deGFP produced in shrunk liposomes corresponding to different concentrations of lysate and Mg2+ after 4 h at 21 °C. The dotted square denotes the protein yield corresponding to IVTT denoted in caption A. [Mg2+] was varied by changing the amount of magnesium added in the IVTT mix. The fold change is calculated with respect to the maximum amount of protein produced, corresponding to lysate concentration ∼260 mg/mL.

Notably, the second optimum occurs at a lysate concentration that is similar to the intracellular protein concentration for E. coli (∼0.24 mg/mL, BNID 105938, 108263).48 The corresponding optimal [Mg2+] is around 100 mM, which is far higher than the estimated concentration of free Mg2+ in E. coli (around 1–2 mM).

However, also in E. coli, the total concentration—including bound Mg2+—has been reported as high as 100 mM48 (BNID 115774), and it is therefore likely that most of the Mg2+ is bound to nucleic acids or proteins. Optimal expression at 100 mM Mg2+ in our protocells could also be explained by considering that shrinkage also increases the concentration of NTPs, and increasing [NTP] and [Mg2+] at the same time leads to stable transcription.55 Nevertheless, this does not explain the presence of two maximum expression levels at different degrees of lysate crowding. We must therefore consider that macromolecular crowding not only decreases diffusion but also increases thermodynamic activities and association constants,56,57 with the net effect of crowding on a reaction being the result of these opposing mechanisms. Additionally, transcription and translation are likely impacted at different levels of crowding, due to the differences in size of the reactants involved in each process.58 We thus expect translation to be affected at a comparatively lower volume fraction than transcription, as it involves larger molecular species such as ribosomes.

To better understand the effect of liposome shrinkage and [Mg2+] on transcription and translation kinetics we developed a model that includes three effects: first, the differential effect of macromolecular crowding on diffusion-controlled and reaction-controlled rates;59 second, higher diffusion coefficients for RNA polymerases (size 5–9 nm,48,60 BNID 114467) than ribosomes (size 21 nm,48 BNID 102320); and third, the previously observed effect of [Mg2+] on transcription efficiency55 (increasing [Mg2+] increases transcription efficiency, yet after a certain maximum, further increasing [Mg2+] inhibits transcription).

Specifically, to incorporate the effect of macromolecular crowding on diffusion- and reaction-controlled rates, we used the formula previously derived by Berezhovskii and Szabo.59 We expressed transcription (ktx) and translation (ktl) rate constants as follows:

graphic file with name sb0c00330_m001.jpg 1
graphic file with name sb0c00330_m002.jpg 2

where Dx/l are the diffusion coefficients for RNA polymerase (Dx) and ribosomes (Dl); Rx/l are the respective contact radii; k0x/l are the rate constants in dilute conditions; and Δux/l are the respective finite potential well-depths resulting from the crowder-induced interactions. As described by Berezhovskii and Szabo,59Δux/l is expected to increase and Dx/l decreases as a function of the degree of macromolecular crowding, and the competition between these two effects determines the dependence of the rate constant (ktx and ktl) on macromolecular crowding.

For the crowding-dependent diffusion coefficients (Dx and Dl), we used measured values of GFP and ribosome diffusion respectively (Figure 2A). The GFP diffusion coefficients are an approximation for RNA polymerase, since both GFP and RNA polymerases are in the same size range compared to ribosomes (∼3–9 nm versus 21 nm respectively, BNID 104396, 114467, 102320). For the Rx/l we used the respective radii of RNA polymerase (Rx = 3.5 nm) and ribosomes (Rl = 10.5 nm). For k0x/l we used literature values in dilute conditions (k0l = 1092 nM h–1, k0x = 966 nM h–1),61 corrected for the measured fold reduction in yield when performing cell-free gene expression in bulk versus liposomes (see Model section in Methods).

Next, we incorporated the dependence of macromolecular crowding on the rate constants (eqs 1 and 2) into a set of coarse-grained differential equations representing mRNA and protein production (eqs 3 and 4).

graphic file with name sb0c00330_m003.jpg 3
graphic file with name sb0c00330_m004.jpg 4

Here, ktx and ktl are the aforementioned production rate constants, M is a scaling parameter representing the effect of magnesium on transcription, and Res represents the finite resources of the transcription and translation machinery. Res will deplete over time as follows:

graphic file with name sb0c00330_m005.jpg 5

where kdep is the depletion rate constant, which for simplicity we assume to be the same for transcription and translation machinery. To obtain values for kdep and Res we fit measured GFP expression in shrunk liposomes over time at 250 mg/mL of lysate (Figure 4A). At these high degrees of macromolecular crowding Dl approaches 0 (Figure 2A) and eq 2 reduces to

graphic file with name sb0c00330_m006.jpg 6

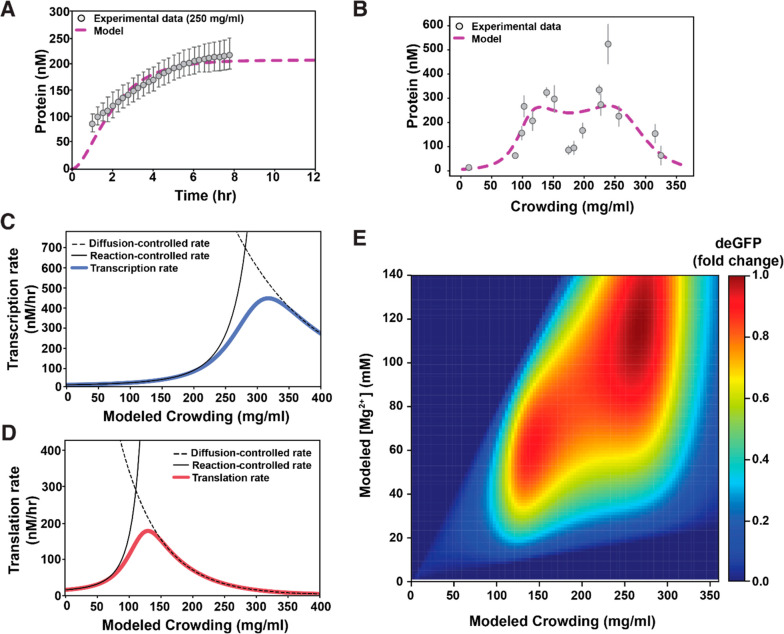
as previously described by Berezhovskii and Szabo.59 We can thus fit our time-lapse data to obtain kdep and initial Res (Root mean square error RMSE = 10.1). We obtained kdep = 0.67 h–1, which is only marginally higher than previously reported depletion rates of 0.05 h–1 and 0.27 h–1 for transcription and translation, respectively.61 Additionally, the fit yielded a starting value for our resources Res = 0.19; this value represents the pool of limiting transcription and translation resources—i.e., polymerases, ribosomes, tRNAs, NTPs, amino acids, or other unknown factors. Notably, obtaining two different Res values for transcription (Restx) and translation (Restl) did not improve the fit (Figure S13A, RMSE = 10.1), so we can assume Restx = Restl. To verify our values, we quantified time-lapse measurements at 210 mg/mL of lysate (Figure 3A) and compared the experimental data to our model predictions under these crowding conditions. Notably, our model at 210 mg/mL (i.e., for slightly increased Dx and Dl compared to 250 mg/mL) accurately predicted the experimental data for these reduced concentrations of macromolecular crowding (Figure S13B), indicating the accuracy of the fitted values for kdep and Res.

Figure 4.

Figure 4

Open in a new tab

Mathematical modeling of gene expression as macromolecular crowding is increased. (A) The model fit to experimental time-lapse data at 250 mg/mL of macromolecular crowding to obtain values for kdep and Res (RMSE = 10.1). The error bars in the experimental data correspond to standard deviation when measuring fluorescence in multiple liposomes (n = 19). (B) The model fit to experimental protein yield at 4 h, for varying concentrations of macromolecular crowding conditions to obtain values for Δux/l. The error bars in the experimental data correspond to standard deviation over liposomes imaged corresponding to each lysate concentration. The number of liposomes corresponding to each lysate concentration ranged between 4 and 23. (C and D) Black dashed lines represent the diffusion-controlled rates calculated from the experimental data in Figure 2A. Black full lines represent the reaction-controlled rates calculated from the experimental data in Figure 4B; blue and red full lines represent the transition from reaction-to-diffusion control for transcription and translation, respectively. (E) Modeled fold change in deGFP produced for different amounts of modeled macromolecular crowding and final [Mg2+] in shrunk liposomes. The fold change is calculated with respect to the maximum amount of protein produced corresponding to ∼260 mg/mL of lysate.

Next, to determine the dependency of Δux/l on macromolecular crowding, we compared the model to experimental data for a range of macromolecular crowding conditions. We varied the values for Δux (Figure S14B) and Δul (Figure S14B) independently, selecting values for Δux/l that best fit our experimental data (i.e., with the lowest RMSE, Figure S14) for the full range of macromolecular crowded conditions (Figure 4B, gray circles versus purple dashed line). As expected, for both transcription and translation Δu increases with increased crowding, and Δul > Δux since the attraction forces are larger for larger macromolecules (Figure S15).59 Once the values for Δux and Δul were obtained that best fit the experimental data (Figure 4B), we could calculate transcription and translation rates for the full range of macromolecular crowding conditions. When comparing the reaction controlled regime (k0eΔu, Figure 4C and D black full line) with the diffusion controlled regime (4πDR, Figure 4C and D black dashed line), we can clearly see two distinct transitions from reaction to diffusion control in the transcription and translation rates—i.e., two distinct lysate concentrations where transcription and translation rates are at their respective maxima. For transcription, this transition occurs at 320 mg/mL (Figure 4C) and for translation this transition occurs at 133 mg/mL (Figure 4D), explaining the two maxima observed in the experimental data. NB: our model provides a rationale for the two maxima observed, but does not show a pronounced local minimum in between; future work will need to study the dependence of transcription and translation rates on crowding in more detail.

Finally, to include the dependency of transcription on Mg2+ into our model, we fit a second-degree polynomial to gene expression yields at varying Mg2+ concentrations in dilute conditions (Figure S16). The polynomial describes previously observed behavior, where the increased ratio of Mg2+ compared to other transcriptional components enhances transcription up to a defined maximum, after which Mg2+ inhibits transcription (see Methods, Figure S12, and Figure S17 for more details).55 When we incorporate this effect of Mg2+ on gene expression and plot final [Mg2+]—accounting for the increased final [Mg2+] due to liposome shrinkage—versus macromolecular crowding, the model accurately describes our experimental findings (Figure 4E). Notably, the two maxima in protein yields are expected to be at different macromolecular crowding conditions than the transitions from reaction to diffusion control observed in transcription and translation rates, because the protein yield is a result of the product of the transcription and translation rates. Taken together, these data show that transcription and translation perform most efficiently under different ideal macromolecular crowding conditions and highlight the necessity to account for these differential effects when designing synthetic cells.

Conclusion

In summary, we demonstrated how shrinking of microfluidically prepared liposomes is a robust method for cytomimetic compartmentalization, with the interior of our protocells closely resembling the cytoplasm, in terms of diffusion of macromolecules as well as metabolism-dependent viscosity. We systematically studied the combined effect of [Mg2+] and macromolecular crowding on the efficiency of gene expression in these protocells. We found that our experimental observations can be explained by transcription and translation having differential transitions from reaction-controlled to diffusion-controlled rates with increasing macromolecular crowding. Our results represent a major advance toward physiologically relevant protocells by accurately capturing the physicochemical properties of the cytoplasm. However, gene expression in these cytomimetic liposomes is still not an accurate representation of gene expression in vivo, which occurs from nucleoid DNA. Considering the size of bacterial genomes and nucleoid-associated proteins, the nucleoid plays a major role in crowding as well as localization of mRNA and proteins.62,63 However, there are very few reports on cell-free gene expression from genomic DNA.64 Future studies will address this gap by implementing cell-free gene expression from isolated nucleoid DNA with endogenous transcription and translation machinery. Further challenges will also include understanding stochastic and spatial aspects of gene expression from nucleoid DNA in crowded environments.

The results reported in this work emphasize the important role the physical environment can play in cells. The crowded environment clearly impacts different biochemical processes to varying extent, depending on the size of the reactants involved. This raises interesting new questions about how crowding affects cells during different parts of their growth cycles as they undergo changes in volume. At a given level of crowding, the efficiency of biochemical processes will be governed by the size of the reactants and the corresponding effect of crowding. Such a regulatory role of crowding also suggests subcompartmentalization observed in eukaryotic cells as an evolutionary strategy, which enables not only spatial separation of different processes but also confinement of these processes at optimal crowding level. The different extent of crowding in the nucleus (170–400 mg/mL65) and the cytoplasm (∼100 mg/mL66) in eukaryotic cells raises a fertile line of inquiry for understanding how these cells form and function. For example, RNA is often involved in the formation of membraneless organelles. The relatively high macromolecular crowding could play a role in lowering the critical concentration of RNA required for phase separation.

Finally, our findings are of special interest for the efforts toward building synthetic cells. As different biological modules are combined for assembling synthetic cells, it will be important to consider the size-dependent diffusion limitation that crowding will impose and how it will affect the output as well as coordination of these different modules.

Methods

Fluorescence Microscopy

Imaging and diffusion measurements with FRAP were conducted on an Olympus Ix81 confocal microscope, equipped with an Andor FRAPPA photobleach module and a Yokogawa CSU-X1 spinning disk. 405 and 488 nm lasers were used to excite the samples. Images were recorded with an Andor iXon3 EM-CCD camera. Images were acquired at room temperature. A previously established protocol was used for FRAP measurements.28 Briefly, a thin strip in the middle of the liposome was bleached, and the recovery of fluorescence intensity was recorded. The experimental recovery was fitted to predicted recovery based on a 1D diffusion problem for fluorophore concentration along the bleached strip. Uncertainties in the fit parameters were estimated by calculating the change in log likelihood for a range of parameter values around their fitted values and determining the curvature of the resulting plot. The standard deviation was taken as the point at which the log likelihood changed by one unit. A custom-made routine in MATLAB was used for image analysis and data fitting.

For FRAP measurements, we approximated metabolically active cytoplasm by performing diffusion measurements in the presence of IVTT with p70a deCFP. We chose CFP to avoid interference with FRAP measurements (at 488 nm for NBDG and Atto488 labeled 70S ribosomes, and at 405 nm with GFP). The concentration of NBDG, GFP, and Atto-488 labeled 70S ribosomes used were 200 μM, 10 μM, and 0.21 μM respectively.

Microfluidics

Fabrication of microfluidic devices for making monodisperse double emulsion droplets was based on the procedure outlined by Deng et al.67 and Utada et al.68 Two cylindrical glass capillaries of inner diameter 300 μm and outer diameter 1 mm (Hilgenberg) were tapered using a capillary puller (PN-31, Narishige). The tapered ends were then polished with sandpaper to achieve orifice sizes of 60–80 μm and 100–120 μm for the inner and outer phase capillary, respectively. The inner phase capillary was treated with trimethylsilyl chloride (Sigma-Aldrich) to render its surface hydrophobic. This is especially important for encapsulation of protein-rich mixtures. The capillaries were then arranged in a coaxial manner inside a square capillary of inner diameter 1 mm (Vitrocom). Fluids flow through the gaps between the cylindrical and square capillaries. Dispensing needles were fixed at the junctions as inlets. The junctions were then sealed with a two-component epoxy glue (Bison). Monodisperse double emulsion droplets were generated by coaxial flow, as shown in Figure 1A. The outer water phase, inner water phase, and middle oil phase consisted of an aqueous solution with 15 wt % poly(vinyl alcohol) and 0.1% F-68 solution, IVTT reaction mix, and a mixture of chloroform and hexane (40:60, v/v) containing 5–8 mg/mL l-α-phosphatidylcholine (egg PC), respectively. The double emulsion droplets were collected on a glass slide inside a silicone isolation chamber (SecureSeal, diameter 13 mm, height 0.12 mm). For osmotic shrinkage, 5 μL hypertonic sucrose solution were added. The chamber was then sealed with a coverslip for further observation. Additional details about accuracy, and experimental procedure of microfluidic encapsulation and osmotic shrinkage, are included in the Supporting Information (Figures S2, S5–S7).

IVTT

An IVTT reaction mix consists, primarily of three components: Cell lysate, feeding buffer, and DNA template. Cell lysate and feeding buffer were prepared according to a protocol optimized by Sun et al.69 and Caschera et al.70

Cell Lysate

BL21 Rosetta2 cells were grown in 2xYT medium, supplemented with 0.22 mM sodium phosphate monobasic and 40 mM sodium phosphate dibasic. The cells were grown until they reached OD600 of 1.7 and then harvested by centrifugation. The pellet was washed with S30A buffer (14 mM Mg-glutamate, 60 mM K-glutamate, 50 mM Tris, 2 mM DTT, pH 8.2 set with acetic acid). They were then resuspended in S30A buffer of volume equal to 0.75 times the pellet weight. The suspension was then passed through a cell press at a pressure of 16 000 lb. The resulting extract was then spun down, and the supernatant was incubated at 37 °C for 1 h. It was then dialyzed in S30B buffer (14 mM Mg-glutamate, 150 mM K-glutamate, 1 mM DTT, pH 8.2 set with 2 M Tris) and spun down. The supernatant was then aliquoted, flash frozen with liquid nitrogen, and stored at −80 °C. The protein content of lysate was determined using a Pierce BCA assay (Figure S1).

Feeding Buffer

The feeding buffer amounted to following composition in the IVTT reaction mix: 50 mM HEPES (pH 8), 1.5 mM ATP and GTP, 0.9 mM CTP and UTP, 1.5 mM each amino acid, except leucine (1.25 mM), 30 mM 3-PGA, 0.26 mM CoA, 0.33 mM NAD, 0.068 mM folinic acid, 0.75 mM cAMP, 0.2 mg/mL tRNA, and 1 mM spermidine. The components were mixed, aliquoted, flash frozen with liquid nitrogen, and stored at −80 °C.

We also added E. coli pyrophosphatase (final concentration 1U) (New England Biolabs) to the reaction mix to avoid precipitation of Mg2+ with inorganic phosphate and keep it freely available in the solution. GamS was also added to a final concentration of 1 μM, to prevent degradation of linear DNA templates.

DNA Templates

DNA templates, corresponding to p70a deCFP and p70a deGFP sequences, were obtained from Arbor Biosciences. PCR was performed using Phusion High-Fidelity DNA Polymerase (New England Biolabs), in a thermocycler using the manufacturers protocol. The PCR products were purified using QIAGEN PCR purification kits, and their concentration were determined with a NanoDrop ND-1000 UV–vis spectrophotometer. The concentration of linear DNA templates in IVTT was 7 nM.

Model

Estimation of k0x/l

Control experiments were performed to establish the expression activity of lysate in unshrunk liposomes compared to bulk, using 7 nM of p70a deGFP linear DNA template. These experiments yielded 14.5 nM and 1497.6 nM deGFP in unshrunk liposomes and in bulk, respectively. Thus, for the final k0x/l we used literature values in dilute conditions (k0l = 1092 nM h–1, k0x = 966 nM h–1).61 This was corrected for the measured 103 fold-reduction in yield when performing cell-free gene expression in bulk versus liposomes:

graphic file with name sb0c00330_m007.jpg
graphic file with name sb0c00330_m008.jpg

Inference of Reaction-Controlled Rates

To find approximations for Δux and Δul we used the inverse of the diffusion coefficient from Figure 2A multiplied by a scaling parameter (Figure S14A and B). We varied these parameters to find an optimal fit with the lowest RMSE (Figure S14C and D). Values that best fit experimental data were as follows:

graphic file with name sb0c00330_m009.jpg
graphic file with name sb0c00330_m010.jpg

for transcription and translation respectively, where Cr is the concentration of macromolecular crowding.

Effect of Mg2+ on Transcription (M)

Experimental gene expression yields at varying [Mg2+] in dilute conditions (Figure S17) were fit with a polynomial function.

graphic file with name sb0c00330_m011.jpg S1

M is thus the fold change in protein yield caused by [Mg2+] (in mM), which has previously been shown to affect transcription55 (Figure S17), so we make M (and as a result transcription) (eq 3 main text) depend on the starting concentration of Mg2+, eq S1 (Figure S18). Notably, in Figure 4E we plot the final [Mg2+] after shrinkage to match the experimental data in Figure 3B.

Acknowledgments

We thank Oliver Maguire and Aleksandr Pogodaev for helpful discussions. Aafke Jonker is thanked for providing purified 70S ribosomes. This work was supported by The Netherlands Organization for Scientific Research (NWO, TOPPUNT Grant 718.014.001, and through the “BaSyC – Building a Synthetic Cell” Gravitation grant (024.003.019) of the Ministry of Education, Culture and Science.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssynbio.0c00330.

  • Supplementary tables S1–S3, extended methods descriptions, calibration curves, control experiments, details of model construction, and Figures S1–S18 (PDF)

The authors declare no competing financial interest.

Supplementary Material

sb0c00330_si_001.pdf (1.8MB, pdf)

References

  1. Jia H.; Schwille P. (2019) Bottom-up synthetic biology: reconstitution in space and time. Curr. Opin. Biotechnol. 60, 179–187. 10.1016/j.copbio.2019.05.008. [DOI] [PubMed] [Google Scholar]
  2. Noireaux V.; Libchaber A. (2004) A vesicle bioreactor as a step toward an artificial cell assembly. Proc. Natl. Acad. Sci. U. S. A. 101, 17669–17674. 10.1073/pnas.0408236101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Garenne D.; Noireaux V. (2019) Cell-free transcription–translation: engineering biology from the nanometer to the millimeter scale. Curr. Opin. Biotechnol. 58, 19–27. 10.1016/j.copbio.2018.10.007. [DOI] [PubMed] [Google Scholar]
  4. Osawa M.; Anderson D. E.; Erickson H. P. (2008) Reconstitution of contractile FtsZ rings in liposomes. Science 320, 792–4. 10.1126/science.1154520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cabré E. J.; Sánchez-Gorostiaga A.; Carrara P.; Ropero N.; Casanova M.; Palacios P.; Stano P.; Jiménez M.; Rivas G.; Vicente M. (2013) Bacterial division proteins FtsZ and ZipA induce vesicle shrinkage and cell membrane invagination. J. Biol. Chem. 288, 26625–26634. 10.1074/jbc.M113.491688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Jiménez M.; Martos A.; Cabré E. J.; Raso A.; Rivas G. (2013) Giant vesicles: a powerful tool to reconstruct bacterial division assemblies in cell-like compartments. Environ. Microbiol. 15, 3158–3168. 10.1111/1462-2920.12214. [DOI] [PubMed] [Google Scholar]
  7. Rivas G.; Vogel S. K.; Schwille P. (2014) Reconstitution of cytoskeletal protein assemblies for large-scale membrane transformation. Curr. Opin. Chem. Biol. 22, 18–26. 10.1016/j.cbpa.2014.07.018. [DOI] [PubMed] [Google Scholar]
  8. Garenne D.; Libchaber A.; Noireaux V. (2020) Membrane molecular crowding enhances MreB polymerization to shape synthetic cells from spheres to rods. Proc. Natl. Acad. Sci. U. S. A. 117, 1902–1909. 10.1073/pnas.1914656117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kohyama S.; Yoshinaga N.; Yanagisawa M.; Fujiwara K.; Doi N. (2019) Cell-sized confinement controls generation and stability of a protein wave for spatiotemporal regulation in cells. eLife 8, e44591. 10.7554/eLife.44591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Godino E.; López J. N.; Foschepoth D.; Cleij C.; Doerr A.; Castellà C. F.; Danelon C. (2019) De novo synthesized Min proteins drive oscillatory liposome deformation and regulate FtsA-FtsZ cytoskeletal patterns. Nat. Commun. 10, 4969. 10.1038/s41467-019-12932-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Litschel T.; Ramm B.; Maas R.; Heymann M.; Schwille P. (2018) Beating Vesicles: Encapsulated Protein Oscillations Cause Dynamic Membrane Deformations. Angew. Chem., Int. Ed. 57, 16286–16290. 10.1002/anie.201808750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Loose M.; Fischer-Friedrich E.; Ries J.; Kruse K.; Schwille P. (2008) Spatial regulators for bacterial cell division self-organize into surface waves in vitro. Science 320, 789–92. 10.1126/science.1154413. [DOI] [PubMed] [Google Scholar]
  13. Hindley J. W.; Zheleva D. G.; Elani Y.; Charalambous K.; Barter L. M. C.; Booth P. J.; Bevan C. L.; Law R. V.; Ces O. (2019) Building a synthetic mechanosensitive signaling pathway in compartmentalized artificial cells. Proc. Natl. Acad. Sci. U. S. A. 116, 16711–16716. 10.1073/pnas.1903500116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. van Nies P.; Westerlaken I.; Blanken D.; Salas M.; Mencía M.; Danelon C. (2018) Self-replication of DNA by its encoded proteins in liposome-based synthetic cells. Nat. Commun. 9, 1583. 10.1038/s41467-018-03926-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Garamella J.; Marshall R.; Rustad M.; Noireaux V. (2016) The All E. coli TX-TL Toolbox 2.0: A Platform for Cell-Free Synthetic Biology. ACS Synth. Biol. 5, 344–355. 10.1021/acssynbio.5b00296. [DOI] [PubMed] [Google Scholar]
  16. Karig D. K.; Jung S.-Y.; Srijanto B.; Collier C. P.; Simpson M. L. (2013) Probing Cell-Free Gene Expression Noise in Femtoliter Volumes. ACS Synth. Biol. 2, 497–505. 10.1021/sb400028c. [DOI] [PubMed] [Google Scholar]
  17. Su W.-C.; Gettel D. L.; Chabanon M.; Rangamani P.; Parikh A. N. (2018) Pulsatile Gating of Giant Vesicles Containing Macromolecular Crowding Agents Induced by Colligative Nonideality. J. Am. Chem. Soc. 140, 691–699. 10.1021/jacs.7b10192. [DOI] [PubMed] [Google Scholar]
  18. Dreher Y., Spatz J. P., and Göpfrich K.. Protein-free division of giant unilamellar vesicles controlled by enzymatic activity. bioRxiv 2019, 2019.12.30.881557. [Google Scholar]
  19. Libicher K.; Hornberger R.; Heymann M.; Mutschler H. (2020) In vitro self-replication and multicistronic expression of large synthetic genomes. Nat. Commun. 11, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Deng N.-N.; Huck W. T. S. (2017) Microfluidic Formation of Monodisperse Coacervate Organelles in Liposomes. Angew. Chem. 129, 9868–9872. 10.1002/ange.201703145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zimmerman S. B.; Trach S. O. (1991) Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J. Mol. Biol. 222, 599–620. 10.1016/0022-2836(91)90499-V. [DOI] [PubMed] [Google Scholar]
  22. Ellis R. J. (2001) Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 11, 114–119. 10.1016/S0959-440X(00)00172-X. [DOI] [PubMed] [Google Scholar]
  23. Parry B. R.; Surovtsev I. V.; Cabeen M. T.; O’Hern C. S.; Dufresne E. R.; Jacobs-Wagner C. (2014) The Bacterial Cytoplasm Has Glass-like Properties and Is Fluidized by Metabolic Activity. Cell 156, 183–194. 10.1016/j.cell.2013.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zhou E. H.; Trepat X.; Park C. Y.; Lenormand G.; Oliver M. N.; Mijailovich S. M.; Hardin C.; Weitz D. A.; Butler J. P.; Fredberg J. J. (2009) Universal behavior of the osmotically compressed cell and its analogy to the colloidal glass transition. Proc. Natl. Acad. Sci. U. S. A. 106, 10632–10637. 10.1073/pnas.0901462106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Rivas G.; Minton A. P. (2016) Macromolecular Crowding In Vitro, In Vivo, and In Between. Trends Biochem. Sci. 41, 970–981. 10.1016/j.tibs.2016.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Minton A. P. (1981) Excluded volume as a determinant of macromolecular structure and reactivity. Biopolymers 20, 2093–2120. 10.1002/bip.1981.360201006. [DOI] [Google Scholar]
  27. Zimmerman S. B.; Harrison B. (1987) Macromolecular crowding increases binding of DNA polymerase to DNA: an adaptive effect. Proc. Natl. Acad. Sci. U. S. A. 84, 1871–5. 10.1073/pnas.84.7.1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sokolova E.; Spruijt E.; Hansen M. M. K.; Dubuc E.; Groen J.; Chokkalingam V.; Piruska A.; Heus H. A.; Huck W. T. S. (2013) Enhanced transcription rates in membrane-free protocells formed by coacervation of cell lysate. Proc. Natl. Acad. Sci. U. S. A. 110, 11692–7. 10.1073/pnas.1222321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hansen M. M. K.; Meijer L. H. H.; Spruijt E.; Maas R. J. M.; Rosquelles M. V.; Groen J.; Heus H. A.; Huck W. T. S. (2016) Macromolecular crowding creates heterogeneous environments of gene expression in picolitre droplets. Nat. Nanotechnol. 11, 191–197. 10.1038/nnano.2015.243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hansen M. M. K.; Paffenholz S.; Foschepoth D.; Heus H. A.; Thiele J.; Huck W. T. S. (2016) Cell-Like Nanostructured Environments Alter Diffusion and Reaction Kinetics in Cell-Free Gene Expression. ChemBioChem 17, 228–232. 10.1002/cbic.201500560. [DOI] [PubMed] [Google Scholar]
  31. Norred S. E.; Caveney P. M.; Chauhan G.; Collier L. K.; Collier C. P.; Abel S. M.; Simpson M. L. (2018) Macromolecular Crowding Induces Spatial Correlations That Control Gene Expression Bursting Patterns. ACS Synth. Biol. 7, 1251–1258. 10.1021/acssynbio.8b00139. [DOI] [PubMed] [Google Scholar]
  32. Sarkar M.; Li C.; Pielak G. J. (2013) Soft interactions and crowding. Biophys. Rev. 5, 187–194. 10.1007/s12551-013-0104-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Guseman A. J.; Speer S. L.; Perez Goncalves G. M.; Pielak G. J. (2018) Surface Charge Modulates Protein–Protein Interactions in Physiologically Relevant Environments. Biochemistry 57, 1681–1684. 10.1021/acs.biochem.8b00061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tyrrell J.; Weeks K. M.; Pielak G. J. (2015) Challenge of Mimicking the Influences of the Cellular Environment on RNA Structure by PEG-Induced Macromolecular Crowding. Biochemistry 54, 6447–6453. 10.1021/acs.biochem.5b00767. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Deng N.-N.; Vibhute M. A.; Zheng L.; Zhao H.; Yelleswarapu M.; Huck W. T. S. (2018) Macromolecularly Crowded Protocells from Reversibly Shrinking Monodisperse Liposomes. J. Am. Chem. Soc. 140, 7399–7402. 10.1021/jacs.8b03123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Minton A. P.; Colclasure G. C.; Parker J. C. (1992) Model for the role of macromolecular crowding in regulation of cellular volume. Proc. Natl. Acad. Sci. U. S. A. 89, 10504–6. 10.1073/pnas.89.21.10504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Minton A. P. (1990) Holobiochemistry: The effect of local environment upon the equilibria and rates of biochemical reactions. Int. J. Biochem. 22, 1063–1067. 10.1016/0020-711X(90)90102-9. [DOI] [PubMed] [Google Scholar]
  38. Zimmerman S. B.; Minton A. P. (1993) Macromolecular Crowding: Biochemical, Biophysical, and Physiological Consequences. Annu. Rev. Biophys. Biomol. Struct. 22, 27–65. 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
  39. Aoki K.; Takahashi K.; Kaizu K.; Matsuda M. (2013) A quantitative model of ERK MAP kinase phosphorylation in crowded media. Sci. Rep. 3, 1–8. 10.1038/srep01541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mika J. T.; Van Den Bogaart G.; Veenhoff L.; Krasnikov V.; Poolman B. (2010) Molecular sieving properties of the cytoplasm of Escherichia coli and consequences of osmotic stress. Mol. Microbiol. 77, 200–207. 10.1111/j.1365-2958.2010.07201.x. [DOI] [PubMed] [Google Scholar]
  41. Nishizawa K.; Fujiwara K.; Ikenaga M.; Nakajo N.; Yanagisawa M.; Mizuno D. (2017) Universal glass-forming behavior of in vitro and living cytoplasm. Sci. Rep. 7, 1–12. 10.1038/s41598-017-14883-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Konopka M. C.; Sochacki K. A.; Bratton B. P.; Shkel I. A.; Record M. T.; Weisshaar J. C. (2009) Cytoplasmic protein mobility in osmotically stressed Escherichia coli. J. Bacteriol. 191, 231–7. 10.1128/JB.00536-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Blanchard S. C.; Kim H. D.; Gonzalez R. L.; Puglisi J. D.; Chu S. (2004) tRNA dynamics on the ribosome during translation. Proc. Natl. Acad. Sci. U. S. A. 101, 12893–8. 10.1073/pnas.0403884101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Bakshi S.; Siryaporn A.; Goulian M.; Weisshaar J. C. (2012) Superresolution imaging of ribosomes and RNA polymerase in live Escherichia coli cells. Mol. Microbiol. 85, 21–38. 10.1111/j.1365-2958.2012.08081.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Petrovska I.; Nüske E.; Munder M. C.; Kulasegaran G.; Malinovska L.; Kroschwald S.; Richter D.; Fahmy K.; Gibson K.; Verbavatz J. M.; Alberti S. (2014) Filament formation by metabolic enzymes is a specific adaptation to an advanced state of cellular starvation. eLife 3, e02409. 10.7554/eLife.02409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Renard D.; Lefebvre J. (1992) Gelation of globular proteins: effect of pH and ionic strength on the critical concentration for gel formation. A simple model and its application to β-lactoglobulin heat-induced gelation. Int. J. Biol. Macromol. 14, 287–291. 10.1016/S0141-8130(05)80042-X. [DOI] [PubMed] [Google Scholar]
  47. Munder M. C.; Midtvedt D.; Franzmann T.; Nüske E.; Otto O.; Herbig M.; Ulbricht E.; Mü Ller P.; Taubenberger A.; Maharana S.; Malinovska L.; Richter D.; Guck J.; Zaburdaev V.; Alberti S. (2016) A pH-driven transition of the cytoplasm from a fluid-to a solid-like state promotes entry into dormancy. eLife 5, e09347. 10.7554/eLife.09347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Milo R.; Jorgensen P.; Moran U.; Weber G.; Springer M. (2010) BioNumbers--the database of key numbers in molecular and cell biology. Nucleic Acids Res. 38, D750–3. 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Schavemaker P. E.; Śmigiel W. M.; Poolman B. (2017) Ribosome surface properties may impose limits on the nature of the cytoplasmic proteome. eLife 6, e30084. 10.7554/eLife.30084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Shin J.; Noireaux V. (2010) Efficient cell-free expression with the endogenous E. Coli RNA polymerase and sigma factor 70. J. Biol. Eng. 4, 8. 10.1186/1754-1611-4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Stein A.; Crothers D. M. (1976) Conformational changes of transfer RNA. The role of magnesium(II). Biochemistry 15, 160–168. 10.1021/bi00646a025. [DOI] [PubMed] [Google Scholar]
  52. Lindahl T.; Adams A.; Fresco J. R. (1966) Renaturation of transfer ribonucleic acids through site binding of magnesium. Proc. Natl. Acad. Sci. U. S. A. 55, 941–8. 10.1073/pnas.55.4.941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zitomer R. S.; Flaks J. G. (1972) Magnesium dependence and equilibrium of the Escherichia coli ribosomal subunit association. J. Mol. Biol. 71, 263–279. 10.1016/0022-2836(72)90350-6. [DOI] [PubMed] [Google Scholar]
  54. Nelson D. L., Cox M. M., and Lehninger A. L. (2017) Lehninger principles of biochemistry, 7th ed., W.H. Freeman & Company, New York. [Google Scholar]
  55. Li Z.; Lau C.; Lu J. (2016) Effect of the Concentration Difference between Magnesium Ions and Total Ribonucleotide Triphosphates in Governing the Specificity of T7 RNA Polymerase-Based Rolling Circle Transcription for Quantitative Detection. Anal. Chem. 88, 6078–6083. 10.1021/acs.analchem.6b01460. [DOI] [PubMed] [Google Scholar]
  56. Ellis R. J. (2001) Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 26, 597–604. 10.1016/S0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
  57. Groen J.; Foschepoth D.; te Brinke E.; Boersma A. J.; Imamura H.; Rivas G.; Heus H. A.; Huck W. T. S. (2015) Associative Interactions in Crowded Solutions of Biopolymers Counteract Depletion Effects. J. Am. Chem. Soc. 137, 13041–13048. 10.1021/jacs.5b07898. [DOI] [PubMed] [Google Scholar]
  58. Gomez D.; Klumpp S. (2015) Biochemical reactions in crowded environments: revisiting the effects of volume exclusion with simulations. Front. Phys. 3, 45. 10.3389/fphy.2015.00045. [DOI] [Google Scholar]
  59. Berezhkovskii A. M.; Szabo A. (2016) Theory of Crowding Effects on Bimolecular Reaction Rates. J. Phys. Chem. B 120, 5998–6002. 10.1021/acs.jpcb.6b01892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Milo R., and Phillips R. (2015) Cell biology by the numbers, 1st ed., Garland Science, New York. [Google Scholar]
  61. Stögbauer T.; Windhager L.; Zimmer R.; Rädler J. O. (2012) Experiment and mathematical modeling of gene expression dynamics in a cell-free system. Integr. Biol. 4, 494. 10.1039/c2ib00102k. [DOI] [PubMed] [Google Scholar]
  62. Tabaka M.; Kalwarczyk T.; Holyst R. (2014) Quantitative influence of macromolecular crowding on gene regulation kinetics. Nucleic Acids Res. 42, 727–738. 10.1093/nar/gkt907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Matsuda H.; Putzel G. G.; Backman V.; Szleifer I. (2014) Macromolecular Crowding as a Regulator of Gene Transcription. Biophys. J. 106, 1801–1810. 10.1016/j.bpj.2014.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Fujiwara K.; Sawamura T.; Niwa T.; Deyama T.; Nomura S. M.; Taguchi H.; Doi N. (2017) In vitro transcription–translation using bacterial genome as a template to reconstitute intracellular profile. Nucleic Acids Res. 45, 11449–11458. 10.1093/nar/gkx776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Nolin F.; Michel J.; Wortham L.; Tchelidze P.; Balossier G.; Banchet V.; Bobichon H.; Lalun N.; Terryn C.; Ploton D. (2013) Changes to cellular water and element content induced by nucleolar stress: Investigation by a cryo-correlative nano-imaging approach. Cell. Mol. Life Sci. 70, 2383–2394. 10.1007/s00018-013-1267-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Kühn T.; Ihalainen T. O.; Hyväluoma J.; Dross N.; Willman S. F.; Langowski J.; Vihinen-Ranta M.; Timonen J. (2011) Protein diffusion in mammalian cell cytoplasm. PLoS One 6, e22962. 10.1371/journal.pone.0022962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Deng N.-N.; Yelleswarapu M.; Huck W. T. S. (2016) Monodisperse Uni- and Multicompartment Liposomes. J. Am. Chem. Soc. 138, 7584–7591. 10.1021/jacs.6b02107. [DOI] [PubMed] [Google Scholar]
  68. Utada A. S.; Lorenceau E.; Link D. R.; Kaplan P. D.; Stone H. A.; Weitz D. A. (2005) Monodisperse double emulsions generated from a microcapillary device. Science 308, 537–41. 10.1126/science.1109164. [DOI] [PubMed] [Google Scholar]
  69. Sun Z. Z.; Hayes C. A.; Shin J.; Caschera F.; Murray R. M.; Noireaux V. (2013) Protocols for Implementing an Escherichia coli Based TX-TL Cell-Free Expression System for Synthetic Biology. J. Visualized Exp. e50762. 10.3791/50762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Caschera F.; Noireaux V. (2014) Synthesis of 2.3 mg/mL of protein with an all Escherichia coli cell-free transcription–translation system. Biochimie 99, 162–168. 10.1016/j.biochi.2013.11.025. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

sb0c00330_si_001.pdf (1.8MB, pdf)

Articles from ACS Synthetic Biology are provided here courtesy of American Chemical Society

RESOURCES