Abstract
Background Investment in pandemic preparedness is a long-term gamble, with the return on investment coming at an unknown point in the future. Many countries have chosen to stockpile key resources, and the number of pandemic economic evaluations has risen sharply since 2009. We assess the importance of uncertainty in time-to-pandemic (and associated discounting) in pandemic economic evaluation, a factor frequently neglected in the literature to-date.
Methods We use a probability tree model and Monte Carlo parameter sampling to consider the cost effectiveness of antiviral stockpiling in Cambodia under parameter uncertainty. Mean elasticity and mutual information (MI) are used to assess the importance of time-to-pandemic compared with other parameters. We also consider the sensitivity to choice of sampling distribution used to model time-to-pandemic uncertainty.
Results Time-to-pandemic and discount rate are the primary drivers of sensitivity and uncertainty in pandemic cost effectiveness models. Base case cost effectiveness of antiviral stockpiling ranged between is US$112 and US$3599 per DALY averted using historical pandemic intervals for time-to-pandemic. The mean elasticities for time-to-pandemic and discount rate were greater than all other parameters. Similarly, the MI scores for time to pandemic and discount rate were greater than other parameters. Time-to-pandemic and discount rate were key drivers of uncertainty in cost-effectiveness results regardless of time-to-pandemic sampling distribution choice.
Conclusions Time-to-pandemic assumptions can “substantially” affect cost-effectiveness results and, in our model, is a greater contributor to uncertainty in cost-effectiveness results than any other parameter. We strongly recommend that cost-effectiveness models include probabilistic analysis of time-to-pandemic uncertainty.
Keywords: Pandemic, modelling, cost effectiveness, economic evaluation, uncertainty, discounting
KEY MESSAGES.
Pandemic preparedness requires investment now for benefits later, and it is standard economic practice to discount future benefits.
We find that time-to-pandemic and discount rate uncertainty are the greatest drivers of uncertainty in cost-effectiveness results.
Published pandemic preparedness economic evaluations frequently omit or do not adequately deal with time-to-pandemic and discount rate uncertainty.
Introduction
Pandemic influenza events have occurred repeatedly throughout history (Potter 2001). The recent re-emergence of highly pathogenic avian influenza H5N1 in 2003 and the less fatal but more transmissible H1N1 swine influenza strain of 2009 have pushed pandemic influenza up the public health policy agenda. As a consequence funds earmarked for pandemic influenza preparedness have risen markedly over the past decade (United Nations System Influenza Coordinator 2010).
Correspondingly, the number of economic evaluation or cost-effectiveness studies of pandemic influenza investment options has also increased. A recent systematic review by Pérez Velasco et al. (2012) indicates that there have been 44 such studies to date.
Methodology for the economic evaluation of pandemic preparedness investments, and public health interventions generally, draws on methods developed for health technology assessment. Methodological challenges raised by the more complex decision context of public health investment including pandemic influenza preparedness are still being identified and addressed (Weatherly et al. 2009; Drake et al. 2012).
Modelling pandemic uncertainty
Uncertainty is a characteristic feature of a pandemic. There is a risk that an as yet unknown highly pathogenic and highly transmissible pathogen will emerge and cause substantial mortality and morbidity worldwide. We do not, and perhaps cannot, know when this will happen, how virulent or how infectious a novel pathogen will be.
In general, healthcare economic evaluations make an implicit assumption of consistency in health burden. An analysis based on a clinical trial, for example, is only relevant to policy making if the evaluation context remains reasonably consistent over time. In contrast to this, a pandemic is a one-off event and although there may be similarities to previous pandemics it will nevertheless be fundamentally and unpredictably different. A key challenge for pandemic influenza health economists is to model prospectively; considering how future pandemic events could present differently from past events.
Sensitivity and uncertainty analysis are separate but related approaches for assessing the influence of input model parameters on the outcome result. These terms are sometimes used interchangeably but we use the concept of ‘sensitivity’ to refer to the degree of change in model output for a given change in a model input parameter. In contrast, ‘uncertainty’ has Bayesian connotations and has been defined as ‘any deviation from the unachievable ideal of completely deterministic knowledge of the relevant system’ (Walker et al. 2003). We consider attributable model uncertainty in terms of the total imprecision in the model output due to imprecision in one or more parameter inputs (O’Hagan and Luce 2003; Cooper et al. 2004; Duintjer Tebbens et al. 2008).
Pandemic economic evaluations often consider a single base case pandemic scenario, then explore a small number of variations from this base case using univariate sensitivity analysis (e.g. Eynard et al. 2004; Halder et al. 2011). Pandemic ‘uncertainty’ is usually not given special attention and the parameters included in a sensitivity analysis vary between studies with pandemic attack rate, mortality rate and particularly time-to-pandemic, all omitted in different studies to-date.
A more robust approach than a simple deterministic sensitivity analysis is to simulate a large number of scenarios, drawing new parameter results for each scenario according to predefined probability distributions. This method is known as ‘Monte Carlo’ sampling, and in health economics is increasingly used in probabilistic sensitivity analysis. However, Monte Carlo sampling (or its stratified version, Latin Hypercube Sampling) can also be used for uncertainty analysis or even replace the deterministic base case scenario. Many pandemic economic evaluations do take a probabilistic approach, including the first published study of this kind (Meltzer et al. 1999). However, many subsequent studies present a single base-case scenario despite the choice of pandemic characteristics being somewhat arbitrary.
Time-to-pandemic—does it affect decision making?
To a policy maker or public health planner, whether a pandemic occurs in 5 or 50 years makes a big difference in terms of investment choices and resource allocation. In all sectors, including health, the length of time before gains or losses are likely to occur is weighed in the decision making process. In economics, discounting is the practice of adjusting the value of future gains or losses to reflect their present day equivalent. This is applied to costs and, in many cases, to health impact and in theory reflects the time preferences of the population.
When undertaking cost-effectiveness analysis of pandemic influenza investment options, there are four general ways to handle pandemic timing:
Retrospective—fixed time analysis.
Prospective—fixed time analysis.
Prospective—deterministic sensitivity analysis.
Prospective—probabilistic sensitivity or uncertainty analysis.
Interestingly only a minority of pandemic economic evaluations to date include a sensitivity analysis of time-to-pandemic. Within the pandemic economic evaluations included in the review by Pérez Velasco et al. (2012), we identify four studies that include pandemic timing in a univariate sensitivity analysis (Meltzer et al. 1999; Siddiqui et al. 2008; Lee et al. 2009; Newall et al. 2010), and a further three that model uncertainty in pandemic timing probabilistically (Balicer et al. 2005; Lugnér and Postma 2009a,b; Carrasco et al. 2011). Siddiqui and Edmunds (2008) found that pandemic timing is the second largest source of parameter uncertainty after mortality rate, while Meltzer et al. (1999) find the results and implications for policy ‘depend most [our emphasis] on the assumed probability of the pandemic’, although they do not include this in the probabilistic analysis.
To date, all probabilistic models assume a Poisson stochastic process (a sequence of discrete events where the times between successive events are independent and exponentially distributed), expressed in some studies as a constant annual probability of a pandemic. The implicit assumption is that emergence of a pandemic event has a constant year on year probability driven by random mutation or re-assortment, which eventually produces an influenza strain that results in effective human-to-human transmission and thus has pandemic potential (Webster 1997). While viral mutation will be important, there are a range of socio-economic, environmental and ecological factors which may influence the emergence of a future pandemic (Jones et al. 2008). The probability of a pandemic event that arises from these complex factors may not be well characterized by Poisson stochasticity.
Pandemic preparedness measures such as stockpiling of antiviral therapies or personal protective equipment require an upfront investment for an unknown benefit at an unknown point in the future. The aim of this study is to establish whether uncertainty in when a pandemic will next occur (henceforth ‘time-to-pandemic’) is important when evaluating whether pandemic preparedness activities are an efficient use of scarce resources. Is calculation of a cost-effectiveness ratio sensitive to changes in assumptions of time-to-pandemic? Is time-to-pandemic an important driver of total model uncertainty?
Methods
We explore the importance of this uncertainty when using standard cost-effectiveness methods to evaluate investment in health system pandemic preparedness. We consider a case study of antiviral stockpiling in Cambodia, a low-income country with many pressing demands on healthcare resources considered a hotspot for emerging infectious diseases (Coker et al. 2011). The comparison is ‘no stockpile’, and the evaluation perspective is from the medical provider. Health impact is measured in disability adjusted life years (DALYs), and costs are the cost of the antiviral stockpile. Health gains resulting from the stockpile occur at a certain point in the future in the event of a pandemic and are therefore discounted, whereas the investment cost occurs in the present and so is not. This analysis is intended as a stylized decision scenario and is not intended as a cost-effectiveness analysis of antiviral stockpiling in Cambodia.
Pandemic Model
To analyse the impact of time-to-pandemic on model output, we use a simple pandemic event model to generate an incremental cost-effectiveness ratio (ICER) for an antiviral stockpile. For a population 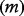 a proportion
a proportion  is hospitalized due to the pandemic virus during the course of the pandemic. Of these a further proportion
is hospitalized due to the pandemic virus during the course of the pandemic. Of these a further proportion 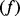 dies from the pandemic disease. A quantity
dies from the pandemic disease. A quantity 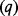 of antivirals are stockpiled at cost
of antivirals are stockpiled at cost 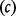 ; for simplicity the cost of stockpile replenishment is not included. Receiving an antiviral when hospitalized due to pandemic influenza reduces the risk of fatality by a proportion
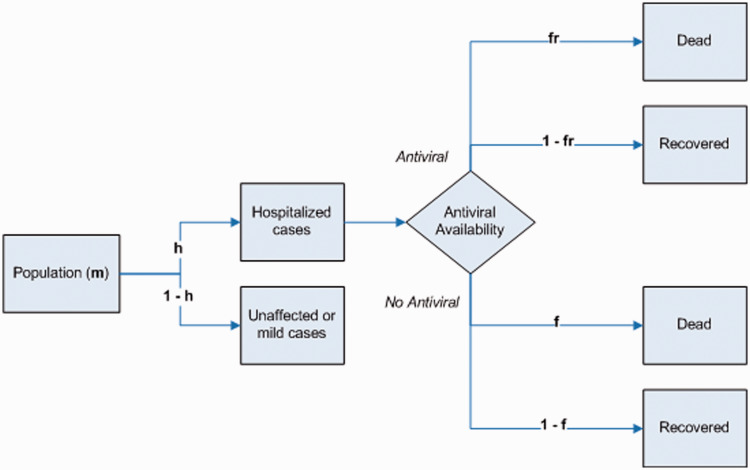
; for simplicity the cost of stockpile replenishment is not included. Receiving an antiviral when hospitalized due to pandemic influenza reduces the risk of fatality by a proportion 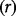 . We define a parameter set which is broadly representative of the Cambodian context. The model structure is outlined as a probability tree in Figure 1, and all parameters are detailed in Table 1. The model was coded in the statistical software package ‘R’, version 2.15.2.
. We define a parameter set which is broadly representative of the Cambodian context. The model structure is outlined as a probability tree in Figure 1, and all parameters are detailed in Table 1. The model was coded in the statistical software package ‘R’, version 2.15.2.
Figure 1.
Simple probability tree for pandemic event outcomes under limited antiviral availability.
Table 1.
Parameter details and justification for cost-effectiveness analysis of antiviral stockpiling in Cambodia
| Parameter | Notation | Value or sampling distribution | Uncertainty justificationa |
|---|---|---|---|
| Pandemic characteristics | |||
| Hospitalization proportion | h | Uniform (0.001–0.05) | Assumed between 0.1% and 5% of the population would be hospitalized at some point during the course of a pandemic. |
| Case fatality proportion | f | Uniform (0.10–0.70) | Lower: WHO severe pandemic threshold is 2% case fatality; however, this refers to the proportion of all cases which die. This is the case fatality proportion for hospitalized patients which we would expect to be higher. We assume a lower bound of 10% and upper bound of 70% case fatality. |
| Time-to-pandemic (years) | t | Uniform | All fitted to data in Table 2 using fitdistrplus package in R using maximum likelihood method. |
| Gamma | |||
| Normal | |||
| Poisson | |||
| Population characteristics | |||
| Population | m | 14 305 183 | World Bank 2012 |
| Discount rate | d | Uniform (0–0.15) | Lower: logical limit |
| Upper: limit of plausibility | |||
| Intervention characteristics | |||
| Population covered by intervention | q | 1 million | Assumed |
| Cost of intervention (US$) | c | Uniform (3–15 million) | The estimated range considers possible reduction in price on patent expiry. Upper bound defined as current wholesale price from the manufacturer. Lower bound set to 20% of this. |
| Fatality risk reduction ratio | r | Uniform (0.02–0.8) | Lower: 2% efficacy is close to ineffective—recent reviews have challenged evidence on Olestamivir effectiveness (ref Jefferson, BMJ communications) |
| Upper: limit of plausibility | |||
aFor all parameters assigned sampling distributions apart from time-to-pandemic the aim of the distribution is to estimate or overestimate parameter uncertainty.
The net health impact 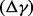 in terms of DALYs is calculated by subtracting total deaths in a baseline scenario from total deaths in an intervention scenario and converting to DALYs using a conservative assumption of an average 30 DALYs lost per death. Pandemic costs and consequences are adjusted to present day value using the discount factor (1 + discount rate)
in terms of DALYs is calculated by subtracting total deaths in a baseline scenario from total deaths in an intervention scenario and converting to DALYs using a conservative assumption of an average 30 DALYs lost per death. Pandemic costs and consequences are adjusted to present day value using the discount factor (1 + discount rate) 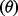 and time-to-pandemic
and time-to-pandemic 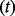 .
.
The discounted health impact  is given by:
is given by:
| (1) |
The ICER 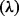 is then given by:
is then given by:
| (2) |
This highlights that the ICER is proportional to the discount factor to the power of ‘time-to-pandemic’, clarifying the interaction between discount rate and pandemic timing. The presence of a power law helps to explain the extent to which uncertainty in discount rate and time-to-pandemic affects the ICER.
There is some debate as to whether health outcomes should be discounted (Severens and Milne 2004; Bos et al. 2005). This debate centres on whether the measure of health utility already incorporates a valuation of time. It seems reasonable that long duration illnesses such as HIV/AIDS do contain consideration of the value of future years. For pandemic or epidemic events where the disease duration is short but when the case occurs is uncertain, it seems likely that some form of discounting is needed to reflect time preferences. That is, given the choice, an individual would prefer to contract a highly pathogenic influenza in 10 years rather than next year.
The cost-effectiveness analysis considers the cost per DALY averted for scaling up the antiviral stockpile by 1 million courses. Potentially serving 7% of the 14.3 million total population a stockpile of 1 million courses is a substantial increase on the 75 000 courses currently retained (data supplied by Ministry of Health, Cambodia).
Time-to-pandemic parameter sensitivity and uncertainty analysis
To gather data on time-to-pandemic, we considered major pandemics in the last 300 years and calculated the inter-pandemic period. Information on possible earlier pandemic event years was not included as the veracity of some pandemic dates is disputed (Potter 2001) (pandemic dates and intervals are presented in Table 2). Using the historical pandemic interval data we carry out a univariate sensitivity analysis to assess whether observed differences in the number of years between pandemics can substantially affect cost-effectiveness results.
Table 2.
Historical pandemics and the cost per death averted for a stockpile of 1 million courses adjusting outcomes according to historical pandemic intervals
| Pandemic | Strain | Pandemic year | Pandemic intervala (years) | Cost per DALY averted (US$) |
|---|---|---|---|---|
| Swine Flu | H1N1 | 2009 | 41 | 978 |
| Hong Kong Flu | H3N2 | 1968 | 11 | 112 |
| Asian Flu | H2N2 | 1957 | 39 | 846 |
| Spanish Flu | H1N1 | 1918 | 29 | 410 |
| Russian Flu | Unknown | 1889 | 59 | 3599 |
| Unknown | 1830 | 49 | 1745 | |
| Unknown | 1781 | 52 | 2169 | |
| Unknown | 1729 | – | ||
| Mean | 30 | 1409 |
aYears since previous pandemic.
However, univariate analysis is limited because it does not account for interaction between the values of other model parameters. Sensitivity to time-to-pandemic may be different given a different set of other input parameter values. We therefore use multivariate Monte Carlo simulation to sample parameter values from uniform distributions of six model parameters (time-to-pandemic, case fatality proportion, hospitalization proportion, discount rate, intervention cost and intervention effectiveness), repeating 20 000 times to produce results from a wide range of parameter combinations. Parameter ‘importance’ is assessed using elasticity and mutual information (MI) measures (described below).
The purpose of this study is to determine whether uncertainty in the number of years before a pandemic occurs (time-to-pandemic) is important in cost-effectiveness analysis. For this reason, the analysis is designed as a ‘challenge’ model using large estimates of uncertainty in other model parameters to present the greatest challenge to the importance of time-to-pandemic. In most cases, little data exists to fit sampling distributions of the model parameters so in general uniform distributions have been used with ranges at logical or plausible limits. If pandemic timing uncertainty is shown to be important compared with large estimates of uncertainty in other pandemic characteristics then we can conclude that pandemic timing uncertainty is important to cost-effectiveness analysis of pandemic influenza preparedness.
Measuring parameter importance
We use two measures to determine the importance of uncertainty in the time to the pandemic to the overall uncertainty in ICER: mean elasticity and MI. Although the potential value of the MI measure in health economics has been reported (Coyle et al. 2003), it is not commonly seen in the health economics literature. Similarly, while elasticity is a concept commonly used in economics it is rarely found in healthcare economic evaluation. We describe both measures fully here for completeness.
Mean elasticity
The elasticity of a parameter describes the extent to which an output changes given an incremental change in an input parameter. This is frequently used in economics to describe effect of demand given a change in price. Using elasticity to measure parameter importance is a logical step from routine sensitivity analysis of economic evaluation, which commonly presents a change in ICER given fixed univariate changes in an input parameter. Standard univariate sensitivity analysis is useful in quantifying the impact of possible parameter changes on cost effectiveness. To compare the sensitivity of the ICER to each parameter on equal basis, we normalize the univariate sensitivity analysis, producing a point elasticity for each Monte Carlo simulation. We take the mean of the point elasticities and report the mean parameter elasticity as a unit-less measure of parameter importance.
The ICER is a function of the parameters listed in Table 1. In a general mathematical formulation if we denote the ICER by 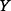 and the model parameters by
and the model parameters by 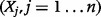 where
where  is the total number of parameters, then the ICER can be represented as a non-linear function
is the total number of parameters, then the ICER can be represented as a non-linear function 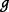 of the
of the  parameters:
parameters:
| (3) |
The normalized local elasticity measure is defined as:
| (4) |
where the symbol  denotes partial differentiation, and the elasticity is evaluated at
denotes partial differentiation, and the elasticity is evaluated at 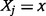 .
. 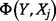 is the proportional change in
is the proportional change in 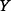 due to a small proportional change in
due to a small proportional change in 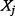 . The mean elasticity measure
. The mean elasticity measure 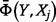 is more appropriate to assess parameter sensitivity under uncertainty (where there is not a high degree of confidence in the expected value). This is given by Coyle et al. (2003):
is more appropriate to assess parameter sensitivity under uncertainty (where there is not a high degree of confidence in the expected value). This is given by Coyle et al. (2003):
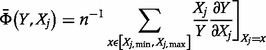 |
(5) |
where  is the number of point-wise evaluations carried out within the range
is the number of point-wise evaluations carried out within the range 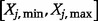 , and the symbol
, and the symbol  means ‘element of’.
means ‘element of’.
Mutual information
MI analysis is based on information and entropy theory (Fraser and Swinney 1986; Veyrat-Charvillon and Standaert 2009; Batina et al. 2011), the origins of which lie in estimating the entropy of thermodynamic systems. Its use has been advocated in the health economics literature (Coyle et al. 2003).
The entropy 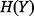 of an uncertain variable
of an uncertain variable 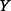 (such as the ICER) is defined in continuous space by the following integral equation:
(such as the ICER) is defined in continuous space by the following integral equation:
| (6) |
where 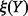 is the probability density function of
is the probability density function of 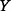 and
and 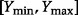 is the range of
is the range of 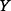 (i.e.
(i.e. 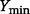 and
and 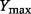 are the lower and upper bounds of
are the lower and upper bounds of 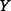 , respectively).
, respectively).
The MI between the ICER  and a variable on which it depends
and a variable on which it depends 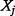 (e.g. case fatality proportion or time-to-pandemic) is defined by the following double integral equation:
(e.g. case fatality proportion or time-to-pandemic) is defined by the following double integral equation:
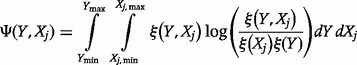 |
(7) |
where the double integration is carried over the range of ICER and the range of parameter 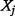 ,
, 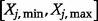 and
and 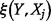 is the joint probability density function of
is the joint probability density function of 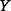 and
and 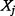 .
.
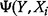 ) is the MI and can be interpreted as the amount of uncertainty that is reduced in
) is the MI and can be interpreted as the amount of uncertainty that is reduced in 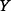 if the uncertainty in
if the uncertainty in 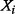 is removed (e.g. because of new information acquired on
is removed (e.g. because of new information acquired on 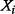 ) or alternatively the amount of information that
) or alternatively the amount of information that 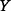 and
and 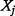 share. In practice, discrete rather than continuous analysis is carried out. The counterpart equations to (6) and (7) in discrete space are:
share. In practice, discrete rather than continuous analysis is carried out. The counterpart equations to (6) and (7) in discrete space are:
| (8) |
and
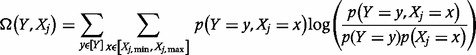 |
(9) |
where 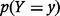 denotes the probability that
denotes the probability that 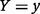 , and
, and 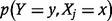 denotes joint probability that
denotes joint probability that 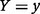 and
and 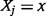 . From Equation (9), it can be shown mathematically (Dragomir and Goh 1996) that
. From Equation (9), it can be shown mathematically (Dragomir and Goh 1996) that 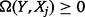 ,
, 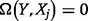 if
if  is independent of
is independent of  and that
and that 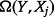 attains its maximum when
attains its maximum when 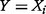 (i.e.
(i.e. 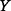 and
and 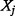 are the same) or when
are the same) or when 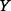 is a deterministic function of
is a deterministic function of  . This fits exactly with the interpretation given above of MI. In one extreme, if the ICER is independent of a parameter then reducing the uncertainty of that parameter would not have any effect on the uncertainty of the ICER. At the other extreme, if the ICER depends on one parameter only, then reducing the uncertainty in the ICER is maximized by reducing the uncertainty of the parameter to its minimum. We used the R package ‘entropy’ for MI calculations (Hausser and Strimmer 2009).
. This fits exactly with the interpretation given above of MI. In one extreme, if the ICER is independent of a parameter then reducing the uncertainty of that parameter would not have any effect on the uncertainty of the ICER. At the other extreme, if the ICER depends on one parameter only, then reducing the uncertainty in the ICER is maximized by reducing the uncertainty of the parameter to its minimum. We used the R package ‘entropy’ for MI calculations (Hausser and Strimmer 2009).
Time-to-pandemic sampling distribution choice
In the parameter uncertainty analysis outlined above a uniform distribution is used to model time-to-pandemic uncertainty (mean 40 years, range 14–66 years). We relax this assumption in a secondary analysis of uncertainty by also running analyses with normal, Poisson and gamma distributions. All distributions are fitted to the data on pandemic interval in Table 2, using the fitdistrplus package within R (Delignette-Muller et al. 2012). The normal distribution is truncated at 0 to prevent sampling of negative values. We use the MI to assess whether time-to-pandemic uncertainty remains important irrespective of sampling distribution choice.
The World Health Organization recommends using a cost-effectiveness threshold of 1–3 times the national Gross Domestic Product (GDP) per capita (World Health Organization 2012); however, there are many limitations to using this rule including situations when funds originate from international organizations (Drake 2013). Nevertheless, we include an illustrative calculation of the proportion of simulations found to be ‘cost effective’ at a threshold of US$900 per DALY averted, the GDP per capita in Cambodia (World Bank 2012).
Results
Base case cost-effectiveness analysis
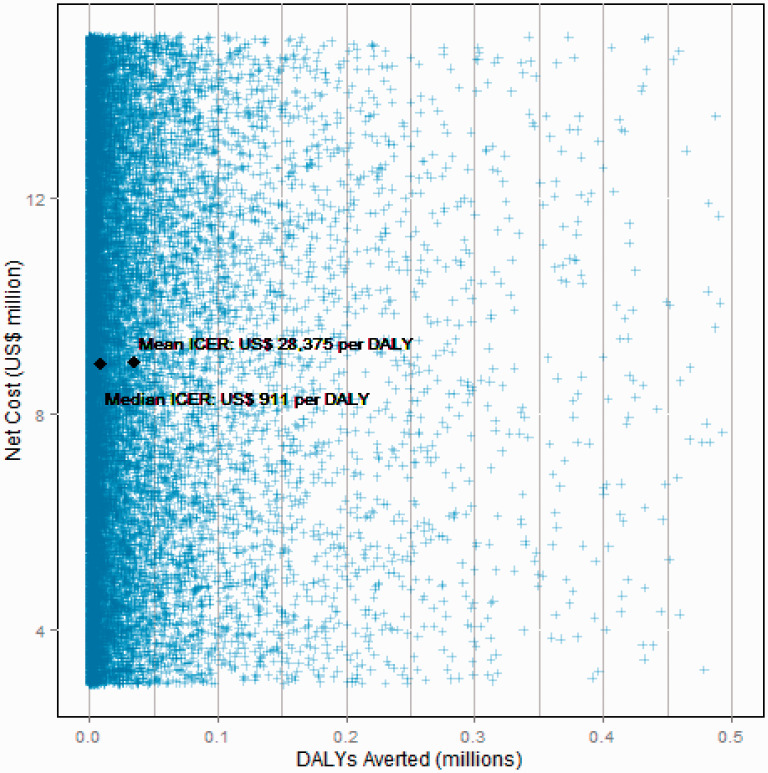
The mean cost of the 1 million course stockpile is US$9 million (median also US$9m) with mean 831 000 DALYs averted (median: 235 000 DALYs averted), and a mean ICER of US$28 375 per DALY averted (median: US$911 per DALY averted). Note that the mean and median ICER is calculated per Monte Carlo simulation not from the mean and median costs and DALYs averted. Figure 2 shows the spread of simulation results on the cost-effectiveness plane. Costs range uniformly between US$3 and 15 million while deaths averted are highly skewed with a small number of pandemic scenarios producing a high death toll.
Figure 2.
Cost and DALYs averted of antiviral stockpiling.
Time-to-pandemic parameter sensitivity and uncertainty analysis
Univariate analysis of change in ICER adjusting for timing according to pandemic intervals from historical data is presented in Table 2; the range is US$112 to US$3599 per DALY averted.
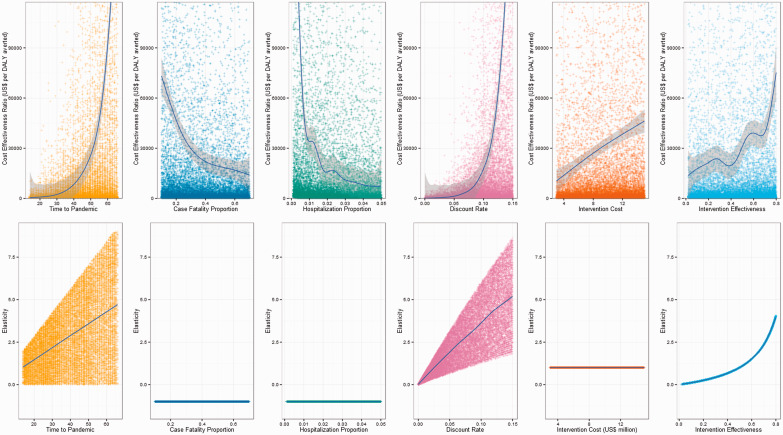
In the probabilistic analysis, parameter sensitivity and uncertainty are assessed by calculation of elasticity and MI, respectively (Table 3). Using both measures, the most ‘important’ parameters identified are discount rate and time-to-pandemic. These have an elasticity slightly greater than two, indicating that, on average, an increase in discount rate or time-to-pandemic causes a greater than proportional increase in the ICER. All other parameters have a mean elasticity magnitude of 1 indicating that a change in the parameter causes a roughly proportional increase or decrease (for negative elasticities) in the ICER; that is an doubling of the parameter value causes the ICER to double or halve, respectively. Similarly, MI scores for discount rate and time-to-pandemic are two to three times larger than the other parameters, indicating a greater contribution to total uncertainty in the ICER result.
Table 3.
Parameter importance in pandemic stockpiling cost-effectiveness model
| Parameter | Measure of importance |
||
|---|---|---|---|
| univariate mean elasticity | Probabilistic mean elasticity | MI | |
| Time-to-pandemic | 2.91 | 2.87 | 0.019 |
| Case fatality proportion | −1.00 | −1.00 | 0.011 |
| Hospitalization proportion | −1.00 | −1.00 | 0.015 |
| Discount rate | 2.74 | 2.74 | 0.022 |
| Intervention cost | 1.00 | 1.00 | 0.009 |
| Intervention effectiveness | 1.04 | 1.04 | 0.010 |
Figure 3 presents how ICER and elasticity vary with each parameter. The first row of Figure 3 shows how change in input parameter (x-axis) affects the ICER result (y-axis). Each point represents a model simulation and skewness in the distribution of simulations reflects the relationship between the parameter and the ICER. A loess mean regression line with 95% confidence interval is overlaid using the R package ‘ggplot’ (Wickham 2009). The second row of Figure 3 also plots change in input parameter (x-axis) but this time against elasticity, outlining whether parameter point elasticity is dependent on the value of the parameter being measured or on other parameters. Elasticity is measured for each Monte Carlo simulation, and each simulation probabilistically samples from six model parameters, so each elasticity measurement corresponds to a new model parameter set describing a new pandemic scenario. For the hospitalization proportion and the case fatality proportion elasticity is constant at −1 irrespective of their value at measurement or the value of other parameters. Similarly, intervention cost has a constant elasticity of 1. Elasticity for intervention effectiveness increases at greater parameter values but is independent of other model parameter values. The elasticity for discount rate and time-to-pandemic is dependent not only on their own parameter value but also on the value of the other parameter. That is, there is an interaction between discount rate and time-to-pandemic when assessing elasticity.
Figure 3.
Variation in ICER and parameter elasticity by parameter value.
Time-to-pandemic sampling distribution choice
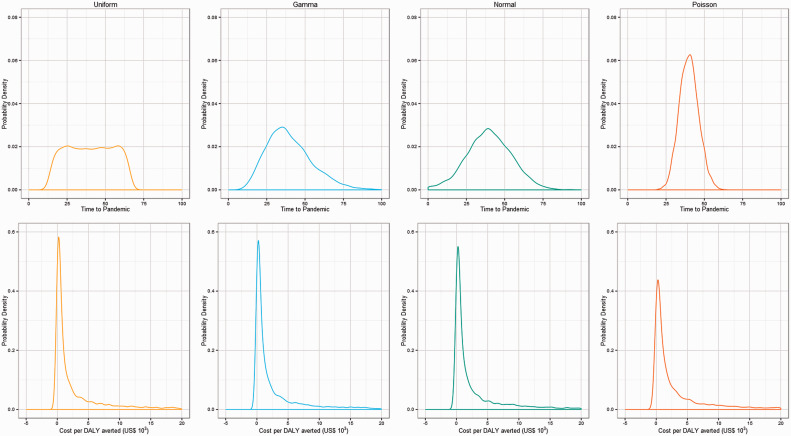
The uniform sampling distribution for time-to-pandemic is replaced with gamma, normal and Poisson distributions, repeating 20 000 Monte Carlo simulations for each distribution type. Mean ICERs for Uniform, Gamma, Normal and Poisson distributions are US$28 375, US$78 809, US$33 006, US$10 199 per DALY averted, respectively (Table 4). The proportion of simulations cost effective at a willingness-to-pay of US$900 per DALY averted does not differ substantially with different time-to-pandemic sampling distributions and the contribution of time-to-pandemic to uncertainty in the ICER remains high compared with other model parameters as measured by the MI. This can be seen in Figure 4 which presents the prior (time-to-pandemic) and posterior (ICER) probability density curves. The shape of the posterior or ICER probability density curve is consistent irrespective of the prior or time-to-pandemic distribution choice.
Table 4.
Cost effectiveness and MI of pandemic stockpiling using different sampling distributions for time-to-pandemic
| Distribution type | Mean ICER (US$) | Proportion cost effective (%) | MI |
|||||
|---|---|---|---|---|---|---|---|---|
| Time-to- pandemic | Case fatality proportion | Hospitalization proportion | Discount rate | Intervention cost | Intervention effectiveness | |||
| Uniform | 28 375 | 49.5 | 0.036 | 0.017 | 0.023 | 0.040 | 0.017 | 0.018 |
| Gamma | 78 809 | 48.8 | 0.016 | 0.007 | 0.007 | 0.009 | 0.007 | 0.007 |
| Normal | 33 006 | 48.5 | 0.049 | 0.021 | 0.026 | 0.043 | 0.021 | 0.020 |
| Poisson | 10 199 | 44.9 | 0.026 | 0.024 | 0.043 | 0.060 | 0.020 | 0.020 |
Figure 4.
Prior for uniform, gamma, normal and Poisson time-to-pandemic sampling distributions and corresponding ICER output distribution.
Discussion
The results of this analysis demonstrate that uncertainty in time-to-pandemic is important in pandemic cost-effectiveness models. Both univariate and multivariate measures of elasticity found that in our model the ICER was most sensitive to changes in time-to-pandemic and discount rate. Similarly, MI analysis found that time-to-pandemic and discount rate were the principle drivers of uncertainty in the model results. Uncertainty in pandemic hospitalization rate was also important, as would be expected. While time-to-pandemic is important the choice of sampling distribution was less so, with similar contributions to uncertainty resulting from uniform, gamma, normal and Poisson distributions.
Pandemic cost-effectiveness models should either take a probabilistic (Bayesian) modelling approach to incorporate uncertainty in time-to-pandemic and other pandemic parameters into the base case analysis or conduct a full probabilistic sensitivity analysis around a fixed base case scenario. The large amount of pandemic uncertainty in the model, which cannot easily be reduced, may mean that reducing uncertainty in other parameters, such as treatment effectiveness, offers minimal improvement to the usefulness of pandemic cost-effectiveness models.
One additional aspect of the relationship between time-to-pandemic and cost effectiveness is that if year-on-year no pandemic occurs then the expected time to pandemic decreases and the expected cost effectiveness of investment rises. Ironically there may be an inverse relationship between cost effectiveness and likelihood of investment in pandemic preparedness measures, i.e. decision makers are more likely to act on pandemic preparedness immediately following a pandemic and interest wanes with time.
The consequence of discounting future health losses leads to a greater emphasis on the short term. Should standard rate of time preference be applied to events with potentially catastrophic impact? Are population time preferences in line with individual preferences? Individual preferences can betray the public good as seen in individual vs social demand curves for vaccine uptake (Fine and Clarkson 1986). If we take a long run perspective, individuals come and go, and so they have a clear time-preference, but the population remains. In effect the problem becomes philosophical; relating to the current generation’s responsibility to future generations. This problem is mirrored in other population level challenges such as climate change, national debt accumulation or risk of redundant antibiotics resulting from widespread antibiotic usage. This analysis points towards the heavy impact that time-preferences of individuals has on these decision contexts. Further work is needed to (re)establish norms for discounting in these contexts. Central to this will be the question of whether time preferences are different when individuals make decisions as a community, whether time preferences differ with very high impact events and whether discount rates are indeed constant for long time-spans.
This study has several limitations. The model is a simple decision tree and does not include more sophisticated model structures recommended in pandemic preparedness cost-effectiveness analysis (Lugnér and Postma 2009a,b; Drake et al. 2012). However, this is not likely to be a significant problem as these approaches aim to more accurately assess the effectiveness of pandemic preparedness of interventions and therefore would be unlikely to lead to a lower estimate of the importance of time-to-pandemic. The model also only considers antiviral stockpiling as a pandemic preparedness measure. Other pandemic preparedness options may not require upfront investment, such as social distancing measures in response to a pandemic and therefore time-to-pandemic would not be an issue.
Conclusion
Pandemic preparedness requires upfront investment and the benefits of this investment are only realized during the course of the next pandemic, an unknown number of years after the investment. We find that in the economic evaluation of pandemic preparedness investments the uncertainty in time-to-pandemic is a dominant factor in model uncertainty. Mathematical models to assess the cost effectiveness of pandemic preparedness options should include probabilistic sensitivity or uncertainty analysis of time-to-pandemic. At the same time, steps should be taken to carefully consider the most appropriate approach to discounting the impact of future catastrophic events such as pandemics.
Supplementary Material
Acknowledgements
The authors would like to thank Korbinian Strimmer for advice on calculating MI using the R ‘entropy’ package and Yoel Lubell for comments on the study aims and methods.
Funding
The work was supported by the German Federal Ministry for Economic Cooperation and Development (BMZ) as part of Deutsche Gesellschaft für Internationale Zusammenarbeit’s (GIZ) German Pandemic Preparedness Initiative.
Ethics Statement
Ethical approval for the wider project has been granted by the Ministry of Health in Cambodia and the London School of Hygiene and Tropical Medicine. No empirical data was collected for this study.
Original Publication Statement
This manuscript has not been published in whole or in part elsewhere.
Conflict of interest
None declared.
References
- Balicer RD, Huerta M, Davidovitch N, Grotto I. Cost-benefit of stockpiling drugs for influenza pandemic. Emerging Infectious Diseases. 2005;11:1280–2. doi: 10.3201/eid1108.041156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batina L, Gierlichs B, Prouff E, et al. Mutual information analysis: a comprehensive study. Journal of Cryptology. 2011;24:269–91. [Google Scholar]
- Bos JM, Postma MJ, Annemans L. Discounting health effects in pharmacoeconomic evaluations: current controversies. PharmacoEconomics. 2005;23:639–49. doi: 10.2165/00019053-200523070-00001. [DOI] [PubMed] [Google Scholar]
- Carrasco LR, Lee VJ, Chen MI, et al. Strategies for antiviral stockpiling for future influenza pandemics: a global epidemic-economic perspective. Journal of the Royal Society Interface. 2011;8:1307–13. doi: 10.1098/rsif.2010.0715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coker RJ, Hunter BM, Rudge JW, Liverani M, Hanvoravongchai P. Emerging infectious diseases in southeast Asia: regional challenges to control. Lancet. 2011;377:599–609. doi: 10.1016/S0140-6736(10)62004-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper NJ, Sutton AJ, Abrams KR, Turner D, Wailoo A. Comprehensive decision analytical modelling in economic evaluation: a Bayesian approach. Health Economics. 2004;13:203–26. doi: 10.1002/hec.804. [DOI] [PubMed] [Google Scholar]
- Coyle D, Buxton MJ, O’Brien BJ. Measures of importance for economic analysis based on decision modeling. Journal of Clinical Epidemiology. 2003;56:989–97. doi: 10.1016/s0895-4356(03)00176-8. [DOI] [PubMed] [Google Scholar]
- Delignette-Muller ML, Pouillot R, Denis JB, Dutang C. fitdistrplus: to fit a parametric distribution to non-censored or censored data. 2012 http://cran.r-project.org/web/packages/fitdistrplus/citation.html. [Google Scholar]
- Dragomir SS, Goh CJ. A counterpart of Jensen’s discrete inequality for differentiable convex mappings and applications in information theory. Mathematical and Computer Modelling. 1996;24:1–11. [Google Scholar]
- Drake T. Priority setting in global health: towards a minimum DALY value. Health Economics. 2013 doi: 10.1002/hec.2925. (early view online), doi: 10.1002/hec.2925. [DOI] [PubMed] [Google Scholar]
- Drake T, Chalabi Z, Coker R. Cost-effectiveness analysis of pandemic influenza preparedness: what’s missing? Bulletin of the World Health Organization. 2012;90:940–1. doi: 10.2471/BLT.12.109025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duintjer Tebbens RJ, Thompson KM, Hunink MGM, et al. Uncertainty and sensitivity analyses of a dynamic economic evaluation model for vaccination programs. Medical Decision Making. 2008;28:182–200. doi: 10.1177/0272989X07311752. [DOI] [PubMed] [Google Scholar]
- Eynard FP, Piercy J, Mueller DA, Miles A, Matter HC. Influenza pandemic planning in Switzerland—an economic perspective. International Congress Series. 2004;1263:247–51. [Google Scholar]
- Fine PEM, Clarkson JA. Individual versus public priorities in the determination of optimal vaccination policies. American Journal of Epidemiology. 1986;124:1012–20. doi: 10.1093/oxfordjournals.aje.a114471. [DOI] [PubMed] [Google Scholar]
- Fraser AM, Swinney HL. Independent coordinates for strange attractors from mutual information. Physical Review. 1986;33:1136–40. doi: 10.1103/physreva.33.1134. [DOI] [PubMed] [Google Scholar]
- Halder N, Kelso JK, Milne GJ. Cost-effective strategies for mitigating a future influenza pandemic with H1N1 2009 characteristics. PLoS One. 2011;6:e22087. doi: 10.1371/journal.pone.0022087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hausser J, Strimmer K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. Journal of Machine Learning Research. 2009;10:1469–84. [Google Scholar]
- Jones K, Patel NG, Levy MA, et al. Global trends in emerging infectious diseases. Nature. 2008;451:990–3. doi: 10.1038/nature06536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee VJ, Tok MY, Chow VT, et al. Economic analysis of pandemic influenza vaccination strategies in Singapore. PLoS One. 2009;4:e7108. doi: 10.1371/journal.pone.0007108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lugnér AK, Postma MJ. Investment decisions in influenza pandemic contingency planning: cost-effectiveness of stockpiling antiviral drugs. The European Journal of Public Health. 2009a;19:516–20. doi: 10.1093/eurpub/ckp119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lugnér AK, Postma MJ. Mitigation of pandemic influenza: review of cost-effectiveness studies. Expert Review of Pharmacoeconomics and Outcomes Research. 2009b;9:547–58. doi: 10.1586/erp.09.56. [DOI] [PubMed] [Google Scholar]
- Meltzer MI, Cox NJ, Fukuda K. The economic impact of pandemic influenza in the United States: priorities for intervention. Emerging Infectious Diseases. 1999;5:659–71. doi: 10.3201/eid0505.990507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newall AT, Wood JG, Oudin N, MacIntyre CR. Cost-effectiveness of pharmaceutical-based pandemic influenza mitigation strategies. Emerging Infectious Diseases. 2010;16:224–30. doi: 10.3201/eid1602.090571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Hagan A, Luce B. A Primer on Bayesian Statistics in Health Economics and Outcomes Research. Seattle, United States of America: MEDTAP International; 2003. [Google Scholar]
- Pérez Velasco R, Praditsitthikorn N, Wichmann K, et al. Systematic review of economic evaluations of preparedness strategies and interventions against influenza pandemics. PLoS One. 2012;7:e30333. doi: 10.1371/journal.pone.0030333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potter CW. A history of influenza. Journal of Applied Micrbiology. 2001;91:572–9. doi: 10.1046/j.1365-2672.2001.01492.x. [DOI] [PubMed] [Google Scholar]
- Severens JL, Milne RJ. Discounting health outcomes in economic evaluation: the ongoing debate. Value in Health. 2004;7:397–401. doi: 10.1111/j.1524-4733.2004.74002.x. [DOI] [PubMed] [Google Scholar]
- Siddiqui MR, Edmunds WJ. Cost-effectiveness of antiviral stockpiling and near-patient testing for potential influenza pandemic. Emerging Infectious Diseases. 2008;14:267–74. doi: 10.3201/eid1402.070478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- United Nations System Influenza Coordinator (UNSIC) Animal and Pandemic Influenza: A Framework for Sustaining Momentum. Global Progress Report. New York, USA: UNSIC; 2010. [Google Scholar]
- Veyrat-Charvillon N, Standaert F-X. Mutual information analysis: how, when and why? In: Clavier C, Gaj K, editors. Cryptographic Hardware and Embedded Systems—CHES 2009. Notes in Computer Science. Springer Berlin Heidelberg; 2009. pp. 429–43. http://link.springer.com/chapter/10.1007/978-3-642-04138-9_30, accessed 25 January 2013. [Google Scholar]
- Walker W, Harremoës P, Rotmans J. Defining uncertainty: a conceptual basis for uncertainty management in model-based decision support. Integrated Assessment. 2003;4:5–17. [Google Scholar]
- Weatherly H, Drummond M, Claxton K, et al. Methods for assessing the cost-effectiveness of public health interventions: key challenges and recommendations. Health Policy. 2009;93:85–92. doi: 10.1016/j.healthpol.2009.07.012. [DOI] [PubMed] [Google Scholar]
- Webster RG. Predictions for future human influenza pandemics. The Journal of Infectious Diseases. 1997;176:S14–9. doi: 10.1086/514168. [DOI] [PubMed] [Google Scholar]
- Wickham H. ggplot2: Elegant Graphics for Data Analysis. New York: Springer; 2009. [Google Scholar]
- World Bank. 2012 World Development Indicators. http://data.worldbank.org/indicator/NY.GDP.PCAP.CD, accessed 22 January 2013. [Google Scholar]
- World Health Organization. Cost-effectiveness Thresholds. 2012. http://www.who.int/choice/costs/CER_thresholds/en/index.html, accessed 21 November 2012. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.