Is spread of COVID-19 a chaotic epidemic?

Highlights

• •Analysis suggests that COVID-19 shows chaotic behavior, like previous epidemics.
• •Spread of COVID-19 varies between countries unpredictably.
• •Variation in spread of COVID-19 is highly sensitive to physical factors.
• •Policymakers need to consider unpredictability as they respond to the pandemic.

Abstract

The COVID-19 epidemic challenges humanity in 2020. It has already taken an enormous number of human lives and had a substantial negative economic impact. Traditional compartmental epidemiological models demonstrated limited ability to predict the scale and dynamics of COVID-19 epidemic in different countries. In order to gain a deeper understanding of its behavior, we turn to chaotic dynamics, which proved fruitful in analyzing previous diseases such as measles. We hypothesize that the unpredictability of the pandemic could be a fundamental property if the disease spread is a chaotic dynamical system. Our mathematical examination of COVID-19 epidemic data in different countries reveals similarity of this dynamic to the chaotic behavior of many dynamics systems, such as logistic maps. We conclude that the data does suggest that the COVID-19 epidemic demonstrates chaotic behavior, which should be taken into account by public policy makers. Furthermore, the scale and behavior of the epidemic may be essentially unpredictable due to the properties of chaotic systems, rather than due to the limited data available for model parameterization.

1. Introduction

1.1. Background

The developing COVID-19 pandemic challenges humanity in 2020. According to aggregated worldwide data posted at the international Worldometer.info website, more than 15 million were infected by COVID-19 and more than 600,000 people died in relation to this disease (as of July 20, 2020). The pandemic has already caused a huge economic loss due to national lock-downs, travel restrictions, and global distractions of trade and manufacturing chains. As the pandemic developed around the globe, severe border control and travel limitations were implemented that led to unprecedented national isolation. Different countries, while being isolated, implemented various strategies to limit epidemic spread: many countries implemented extended national-level lock-downs including closure of businesses, schools and stay-at-home orders (for example France, Italy, Germany, Austria, Hungary, South Korea, and more), some introduced practically no such lock-down measures (for example, Sweden, Belarus, and Brazil). Many countries implemented only regional lock-downs (for example, China and the USA). The overall challenge for the development of scientifically-based COVID-19 containment strategy is the apparent unpredictability of this pandemic [5].

Traditional compartmental epidemiological models demonstrated quite limited ability to predict the scale and dynamics of this epidemic in different countries [5], [11], [25]. This apparent unpredictability of the COVID-19 pandemic creates an additional challenge for governments around the globe, who need more accurate predictions to develop a reasonable containment strategies [9], [16]. This limitation of traditional modeling approaches can be partially explained by the novelty of the virus and limited relevant epidemiological data necessary for model parameterization [28] as well as statistical problems in model calibration [25]. In particular, until recently, we did not know the rate and mechanisms of the transmission of COVID-19 virus as well as its biology and ability to survive and spread outside host organisms [11], [19]. A previous study [4] demonstrated that the coronavirus raw data in China’s first two months of the disease suggest chaotic growth, similar to other epidemics like H1N1 and measles.

1.2. History

Mathematical chaos theory originated from studying deterministic systems represented as differential equations where initial conditions dictate their behavior. In these systems sensitivity to the initial conditions was so large that the systems were practically unpredictable. This was originally studied by Poincaré in the 1880s in relation to the three-body problem in astronomy, an example of which is the Earth-Moon-Sun celestial system [23]. As Poincaré critically stated, “it may happen that small differences in the initial conditions produce very great ones in the final phenomena” [23]. In physical systems described by differential equations, systems which experience this effect are described as having “high sensitivity” to initial conditions. One example which demonstrates this concept is a bowling ball; imagine a very small spin on the ball at the beginning of its roll. This small spin in combination with the oiled bowling lane could cause it to move wildly off-course, making it “highly-sensitive” to initial conditions. Due to the effect Poincaré found, “measurements made on the state of a system at a given time may not allow us to predict the future situation” [3]. These systems are now termed “chaotic.” Unpredictability due to highly-sensitive reliance on initial conditions inspired the term “deterministic chaos.” After Poincaré’s studies, the deterministic chaotic behavior was discovered in numerous dynamical systems and confirmed experimentally [2], [6], [15], [20].

The spread and “fade out” cycle of epidemic diseases often exhibits deterministic chaos. Qualitative analysis of that deterministic chaos can offer more information than a “multifactorial stochastic paradigm of causation” [21]. In the late 80s, scientists noticed that measles outbreaks exhibited deterministic behavior. By studying this they hoped to quantify conditions for the maintenance of [an] infection in human populations” [7]. In 1991, Grenfell published his study of the chaotic measles outbreaks in the paper “Chance and Chaos in Measles Dynamics.” That study found that certain parameters in the chaotic disease system created deterministic behavior. For example, applying his model to the city of Copenhagen and mapping with Poincaré’s methods produced drastic results: one example is that doubling the immigration rate into the city could completely eliminate the fade-out of measles [7]. Similar findings in relation to COVID-19 could have wide-ranging societal implications.

1.3. Criteria for chaos

In this work, we consider the COVID-19 epidemic within the framework of complex dynamic systems [14]. This framework is broadly applied in modern ecology, social and medical sciences [2], [6], [13], [20], [21]. In particular, the COVID-19 pandemic can be considered as a complex phenomena developing simultaneously at multiple temporal and spatial scales varying from individual level to the global scale. Within this framework, particular disease dynamics patterns result from major self-organisation mechanisms within the system. The chaotic behavior is a common phenomenon in complex systems, and we hypothesise that the unpredictability of the epidemic scope in different countries is a fundamental property of this dynamic system which demonstrates chaotic behavior. In order to examine this hypothesis we have analysed COVID-19 epidemic data from different countries. In particular, we examine if the COVID-19 epidemic demonstrates a chaotic regime based on the analysis of observed data. We do not aim to derive or validate a correct dynamical system model. Instead we consider epidemiological data collected in different isolated countries as an independent observations of the same dynamical system. In order to evaluate whether or not the spread of coronavirus is chaotic, we employ the following criteria, derived from Poincaré’s definition of chaos [4], [23]:

• 1.Large number of solutions - to what extent does the behavior of the virus vary between countries? Are there different shapes of curves for the data? This criterion was established from Poincaré’s definition of chaos [23]. In the study, we find extremely high variation between countries, even when normalizing by patient-zero date and total population of each country.
• 2.Sensitive - does the growth of the virus experience large regions of activity? Are there real reasons for regions of activity, specifically changes in the physical system? This criterion has precedent in the aforementioned University of Florida / Wuhan University paper [4]. Later in the study, we present multiple examples of high regions of sensitivity in the spread of COVID-19, as revealed by the derivatives of the system.
• 3.Numerically unpredictable - Can the behavior of the system change unexpectedly from one point to another? This criterion was also introduced in the University of Florida / Wuhan University paper [4]. We found numerous examples of sets of countries which exemplified unpredictability by behaving similarly and then suddenly diverging, which we discuss later in the paper.
• 4.Deterministic - What causes activity in the system? Is the system random, or is it determined by some factors of the physical system, as required in order to be chaotic? This is a qualitative criterion derived from Poincaré’s definition of chaos [23]. We present cases where real-world changes such as mandated lockdowns had a profound impact on the spread of the disease, suggesting deterministic behavior.

The study concluded that the spread of COVID-19 exhibits the major qualitative characteristics of chaotic systems. Most countries show a roughly logistic growth curve, but activity in the second derivative revealed great variability in system behavior. When examined under the context that infectious epidemics in the past have exhibited chaotic behavior, the study concluded that the spread of COVID-19 suggests that the epidemic is a chaotic system.

2. Materials and methods

Johns Hopkins University has continuously collected data on the coronavirus epidemic from various sources such as the World Health Organization, including daily cases per country, which is the data source used for this study [10]. The data is organized by country and cumulative cases by date. A sample with the first five days of one country is shown in Table 1 .

Table 1.

Sample of the COVID-19 spread data used for this study.

Country	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	...
USA	1 case	1	2	2	5
...

We considered the data from the beginning of the global data set, January 22nd, 2020, to May 30th, 2020. Each data-point tells the number of confirmed COVID-19 cases in that country by that day. In the example shown in Table 1, the United States had five confirmed cases by January 26th, 2020. With almost 35,000 data-points corresponding to 267 countries or territories, the study required a dynamic analysis tool instead of analyzing static charts. In order to investigate deeper, a web-based interface was designed and developed to allow for close inspection of the data through interactive charts. The evolution of the COVID-19 epidemic was mapped over time, in terms of total number of confirmed cases per country per day. Data was adjusted to account for country population and date of first-confirmed-case in order to accurately compare the spread behavior between countries. The raw data was extracted as an CSV file and analysed using original JavaScript software [12], the graphing utility Plotly [22] was employed to generate all the graphs.

3. Results and discussion

3.1. Cases per capita

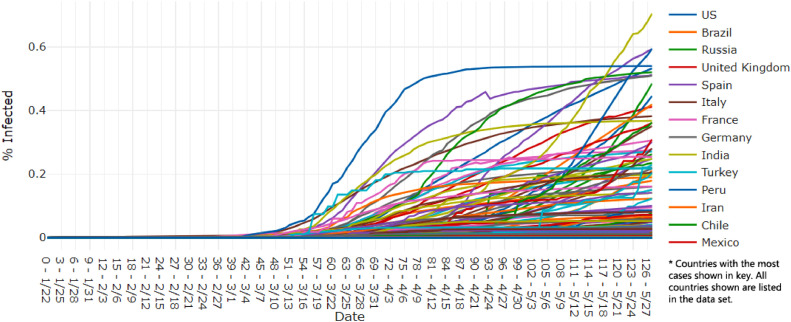
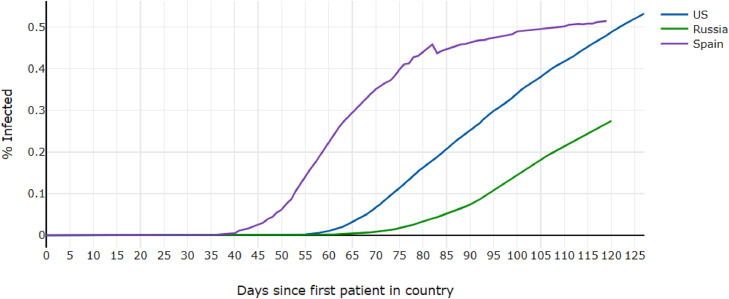
Fig. 1 demonstrates the raw data as percentages of each country’s population. Since the data only pertains to the total number of confirmed cases, not accounting for decreases like recovery and death, the total number of cases in every country/region increases or remains constant at all times. Highlighted in Fig. 2 , almost all regions show 1 of 3 possible parts of the beginning of a logistic graph: a curved ramp-up (Russia), or a curved ramp-up into roughly a line (US), or an upward curve into a line which curves toward horizontal (Spain), which is a logistic curve. This is sensible for an infectious disease with a maximum number of infections, that maximum being the population of each country.

Fig. 1.

COVID-19 Cases per Country per Capita Some countries hidden from legend. Key countries highlighted in other figures.

Fig. 2.

COVID-19 Cases per Capita in the US, Russia, and Spain.

So far, these patterns don’t directly suggest chaos: it still seems possible there might be some parameters which control the shape of the curves predictably, potentially population density, weather patterns, etc.

3.2. Cases per capita with shifted dates

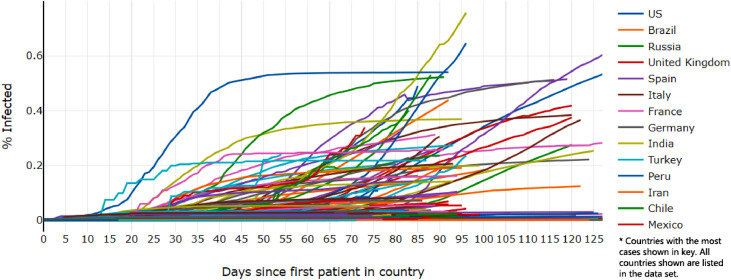
Fig. 3 demonstrates the case data shifted to show the percent of the population that had been infected as a function of the number of days since the first case in each country, instead of the absolute date.

Fig. 3.

COVID-19 cases per country per capita, shifted to date of first infection in each country Some countries hidden from legend. Key countries highlighted in other figures.

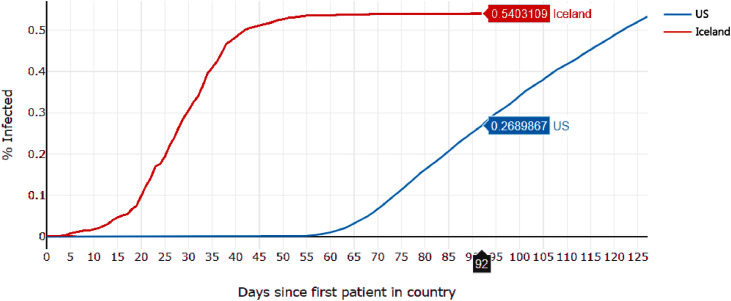
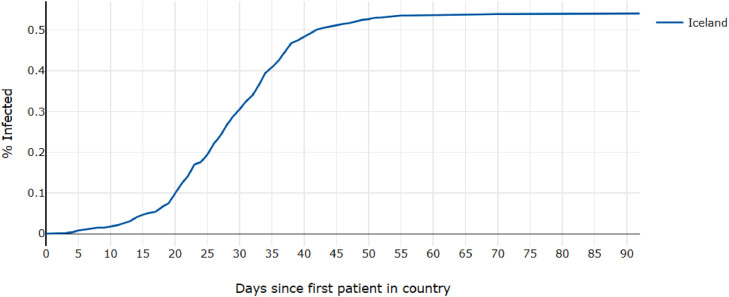
This graph is more revealing about the relative behavior of the epidemic in each country. It is clear the virus ran its course faster in some countries, where the growth seems to have flattened in fewer days. For example, only 55 days after the first case in Iceland, the country had almost completely stopped the spread. Meanwhile, the US at 130 days in was still seeing almost linear positive spread (Fig. 4 ).

Fig. 4.

COVID-19 cases per country per capita, shifted to date of first infection in each country; Comparison of Iceland and the US.

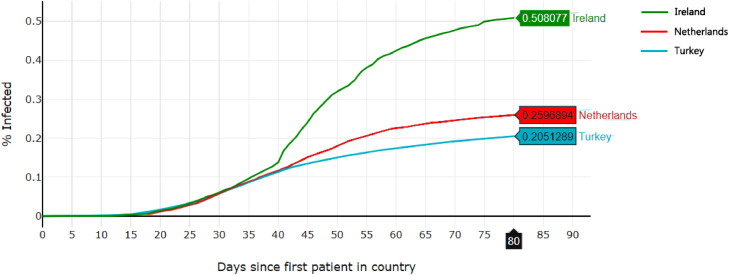
These differences confirm that there are a large number of potential solutions or equilibrium and varying behavior between countries over time. Another key observation from this graph is that countries which seemed to follow similar growth curves can very rapidly diverge. For example, as shown in Fig. 5 , in the first 40 days of the epidemic in Ireland, the Netherlands, and Turkey, the percentage of the population that was infected grew almost identically in each country. However, between days 40 and 42, the three countries’ curves diverged greatly, to such an extent that by day 60, Ireland had almost three times the infected population percentage as Turkey, and Turkey and the Netherlands are 25% apart as well.

Fig. 5.

COVID-19 cases per country per capita, shifted to date of first infection in each country, Comparison of Ireland, Netherlands, and Turkey.

This example exhibits unpredictability because, by Poincaré’s definition, the behavior following day 40 cannot be predicted by the state at day 40, since there are clearly multiple possible behaviors. This is one example confirming unpredictability in the spread of COVID-19. It is also important to note that these three countries are not alone in displaying unpredictability after formerly-similar spread of COVID-19. Another example is Kuwait, France, and Sweden, shown in Fig. 6 .

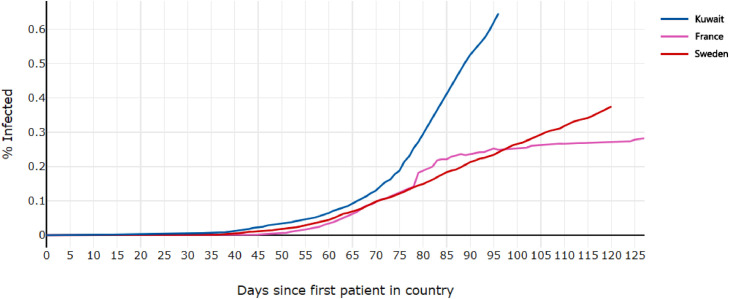
Fig. 6.

COVID-19 cases per country per capita, shifted to date of first infection in each country, Comparison of Kuwait, France, and Sweden.

Until approximately day 70, the infected percentage in all three countries had grew with similar shaped curves. However, within days after that point, the infected percentage in Kuwait spiked drastically, while it entered linear growth in France and Sweden. By 10 days later, even France and Sweden diverged, with Sweden’s infected percent still growing linearly while the spread slowed down in France. By Poincaré’s definition of unpredictability, knowing the spread behavior in Sweden from day 60 to 120 would not provide any accurate prediction of the behavior in Kuwait or France, suggesting a chaotic nature.Yet another example of unpredictability is Cabo Verde and New Zealand, shown in Fig. 7 .

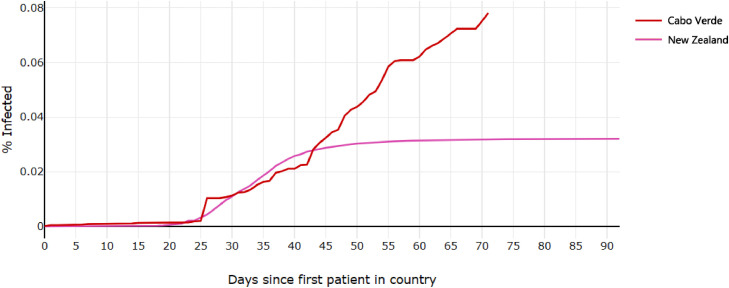
Fig. 7.

COVID-19 cases per country per capita, shifted to date of first infection in each country, Comparison of Cabo Verde and New Zealand.

In Cabo Verde and New Zealand, the disease spread almost identically until day 25, at which point it continued to grow similarly in each country until day 40, and then the behaviors sharply diverge: cases grow steeply linearly in Cabo Verde, but level off almost entirely in New Zealand. This example further demonstrate that spread of COVID-19 is unpredictable, because at any given point there are multiple possible behaviors in the time following that point. The observation of unpredictability fulfills one of Poincaré’s key criteria for choatic systems.

3.3. Derivative of cases per capita, with shifted dates

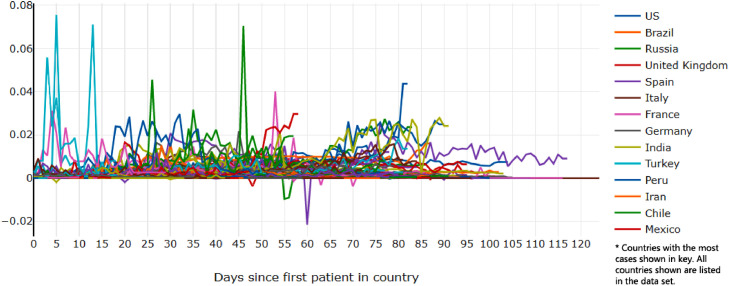
We looked at the rate of spread of COVID-19, the derivative of the number of cases, adjusted similarly to Fig. 3. This data, shown in Fig. 8 shows the spread rate as a function of the number of days since the first patient. Negative derivatives represent decreasing numbers of cases, which shows corrections to data, since the data set does not account for real decreases in active cases (by recovery or death).

Fig. 8.

First derivative of daily COVID-19 cases per country per capita, with shifted dates. Some countries hidden from legend. Key countries highlighted in other figures.

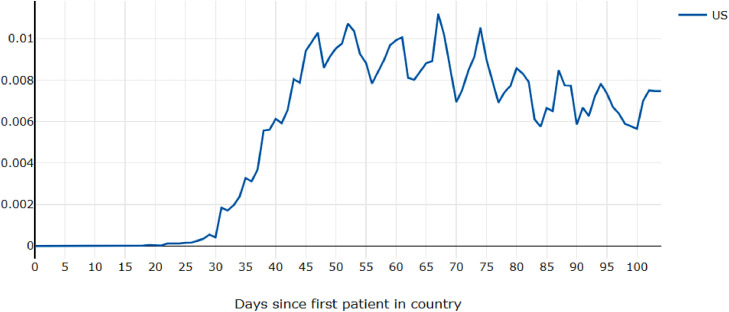
While the raw data shows mostly similar shaped, roughly logistic trajectories with some small bumps and jumps, the daily rate of growth shows a lot of variation in behavior. For example, in the US from day 92 to day 99, just one week, the daily growth rate decreases by 30% and increases back to almost the same starting point (shown in Fig. 9 ).

Fig. 9.

First derivative of daily COVID-19 cases per country per capita, shifted, First derivative in the US.

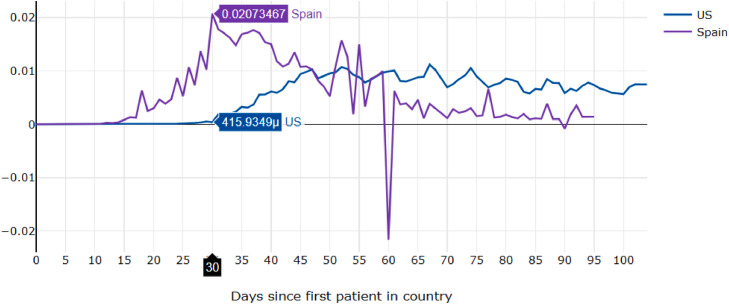
We also see drastically different behavior between different regions, unlike the roughly logistic graphs of the Raw Data. One example is the comparison of the spread rates of the US and Spain. By their respective day 30s, the spread rate in Spain started to decline, while the US spread rate was just starting to increase, as shown in Fig. 10 .

Fig. 10.

First derivative of daily COVID-19 cases per country per capita, shifted, First derivative in the US and Spain.

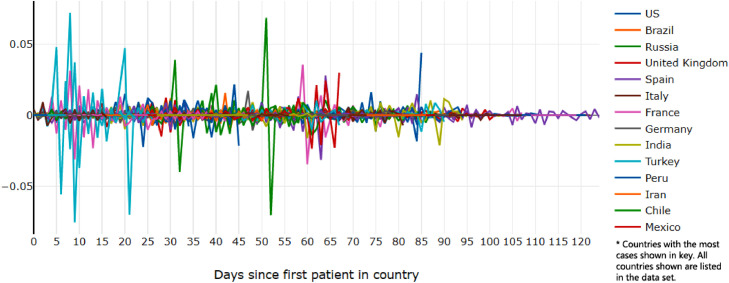
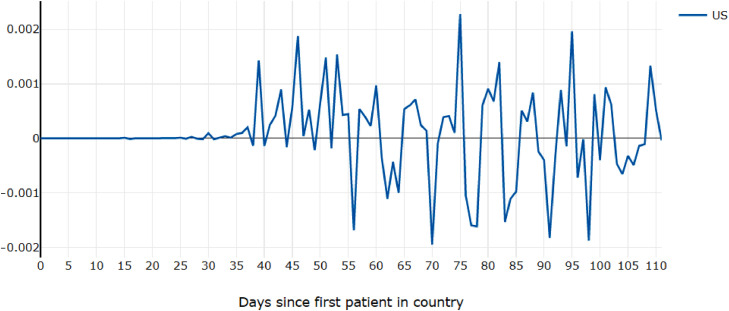
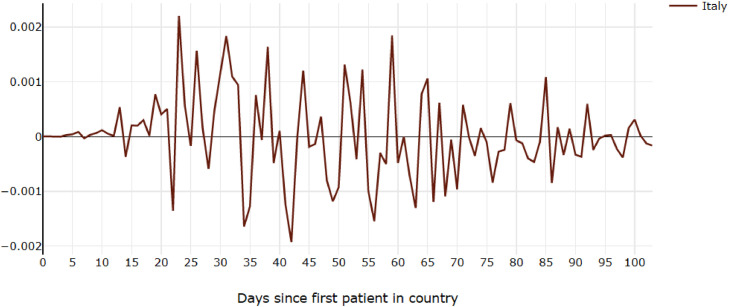
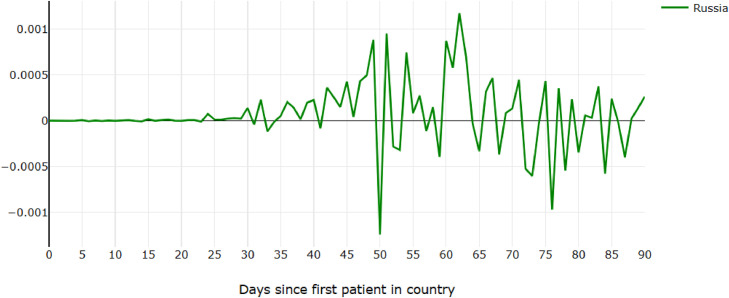
The amount of unpredictable variation within a country and different possible models for each country suggest chaos. However, most countries still follow a very rough pattern of increasing and then leveling-off and decreasing spread rates. The second derivative helps to measure this sensitivity (Fig. 11 ) because its behavior shows activity in the system [4]. The rate of change of the spread rate in each region fluctuates greatly. The US (Fig. 12 ) seems to oscillate between roughly two values, Spain and Italy (Fig. 13 ) appear to exhibit a single heart-beat-like pulse surrounded by ramp-up and ramp-down, and Russia (Fig. 14 ) and Germany show clusters of high activity.

Fig. 11.

Second derivative of daily COVID-19 cases per country per capita, with shifted dates. Some countries hidden from legend. Key countries highlighted in other figures.

Fig. 12.

Second derivative of daily COVID-19 cases per country per capita, with shifted dates, Oscillating second derivative of COVID cases in the US.

Fig. 13.

Second derivative of daily COVID-19 cases per country per capita, with shifted dates, Spike pulse of second derivative of daily COVID-19 cases in Italy.

Fig. 14.

Second derivative of daily COVID-19 cases per country per capita, with shifted dates, Two clusters of activity in second derivative of daily COVID-19 cases in Russia.

In summary, the results reveal the following:

• 1.Large number of solutions - While most countries have a roughly logistic curve of COVID-19 growth, there is a huge amount of variation in: the time it takes to reach the same point in that logistic curve, the highest percent of the population which the logistic curve reaches, and the degree of curvature of the logistic model.
• 2.Sensitive - the second derivative shows clusters, spikes, and oscillations, revealing that the system is highly sensitive due to the high amount of activity in the system instead of steady or constant behavior.
• 3.Numerically unpredictable - while the raw data shows roughly predictable shapes, the extreme variation first and second derivatives of different countries reveal a high amount of variability, making the growth of the system unpredictable. Furthermore, there are examples of growth curves appearing identical and then suddenly diverging. We may predict that spread in the US will level off logistically, but we cannot tell when that will occur based on the US data or other countries’ curves.

One important question remaining is what causes the activity: is the system random, or is it determined by some factors of the physical system, as required in order to be chaotic? Qualitative investigation is required to answer that, and even then we cannot definitively determine the factors contributing to every change in every country. However, we investigated some of the countries and found good examples suggesting the system is deterministic.

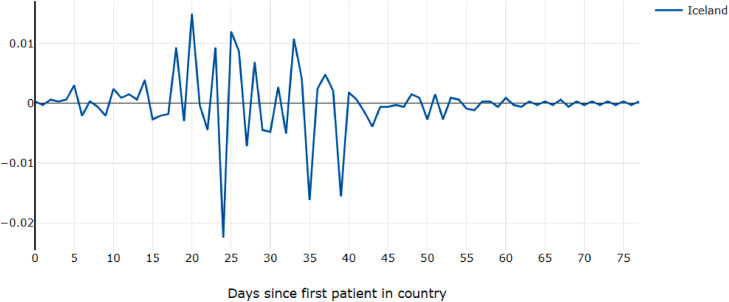
New cases take up to 14 days to show symptoms and therefore be reported [18]. In Iceland, lockdown was initiated on March 24th [29], day 25 when shifted. Exactly two weeks after that change, there are few new cases reported (Fig. 15 ) and almost all activity shown by the second derivative ceases (Fig. 16 ).

Fig. 15.

Daily confirmed cases in Iceland shifted to start-date.

Fig. 16.

Second derivative of daily confirmed cases in Iceland shifted to start-date.

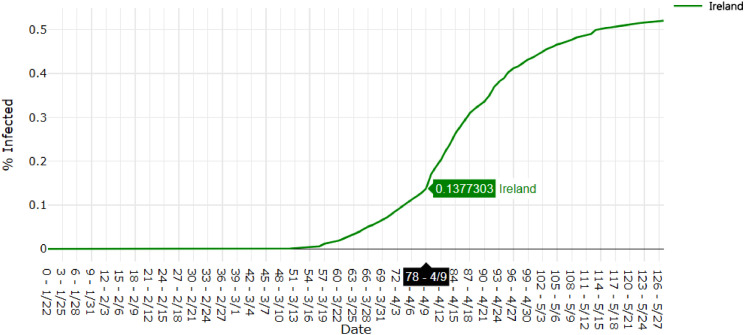
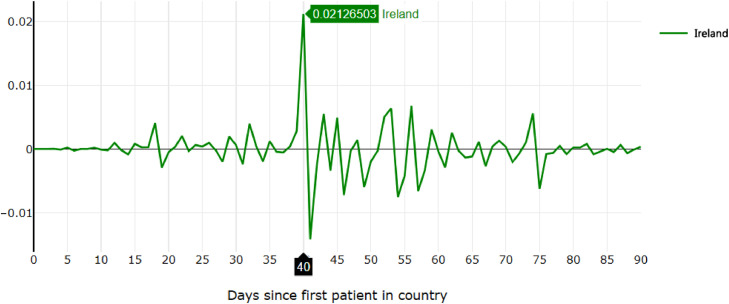
In Ireland, there was an extremely sharp increase in the number of cases reported per day around April 9th, day 78 of the data overall and day 40 in Ireland’s shifted scale (Figs. 17 , 18 ).

Fig. 17.

Daily confirmed cases per capita in Ireland.

Fig. 18.

Second derivative of daily confirmed cases in Ireland shifted to start-date.

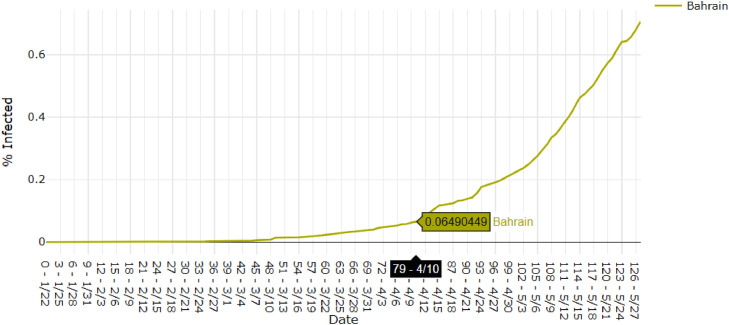
This is also the day with the sharpest increase in testing in Ireland [8], which would explain the jump in the data and higher activity following that day. In Bahrain, re-opening efforts began on April 9th [1], which is the likely cause of a the immediately following spikes in number of cases (Fig. 19 ).

Fig. 19.

Daily confirmed cases per capita in Bahrain.

These examples suggest that real changes in the physical conditions of the system are causing changes in the spread of the virus. The outcome, amount and rate of spread, is determined by these real factors. This suggests the behavior of the system is deterministic, not random, a key qualifier for a chaotic system.

3.4. General discussion: Deterministic chaos and COVID-19

Complex natural systems often demonstrate chaotic behavior. However, rigorous proof of chaos from empirical data or experimental observations alone is a substantial challenge. In this work, rather than attempt a rigorous mathematical proof, we investigate the hypothesis that the COVID-19 pandemic exhibits chaotic behavior by mapping the disease over time from available epidemiological data. Our results suggest that the COVID-19 epidemic exhibits deterministic chaos.

The overall predictions of the SIR model demonstrate a typical sigmoidal curve. This functional response is characterised by an exponential growth stage, inflection point and slow-down growth phase towards a horizontal asymptote. The first wave of COVID-19 pandemics in different countries demonstrates similar behavior (Fig. 3). Empirical sigmoidal models such as the logistic curve are also broadly employed for modeling of COVID-19 and other epidemics [24], [26], [27]. The discrete counterpart of the logistic curve is a well-known Logistic Map model that demonstrates a chaotic behavior [17]. Our examination of the epidemic dynamics in different countries reveals amazing similarity to the chaotic behavior known in this and many other dynamics systems. We conclude that the scale of the epidemic is essentially unpredictable due to fundamental properties rather than due to the limited data available for model parameterization. We find that the chaotic behavior in the spread of COVID-19 suggests that it is a deterministic chaotic system, which should be taken into account by public policy makers.

4. Conclusion

Through use of an interactive data map, it was shown that the spread of COVID-19 exhibits the major characteristics of chaotic systems, namely, determinism, high sensitivity, large number of equilibria, and unpredictability. When examined under the context that infectious epidemics in the past have exhibited chaotic behavior, we conclude that spread of COVID-19 is likely a chaotic system. We may be able to gain some insights into its behavior, such as the common logistic pattern, but we cannot assume that it will follow a logistic path in any one country and we cannot numerically predict the behavior of a particular logistic curve.

CRediT authorship contribution statement

Andrew Jones: Conceptualization, Methodology, Software, Investigation, Formal analysis, Data curation, Writing - original draft, Writing - review & editing, Visualization. Nikolay Strigul: Supervision, Investigation, Writing - review & editing, Project administration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.