Meta-analysis of several epidemic characteristics of COVID-19

Abstract

As the COVID-19 pandemic has strongly disrupted people’s daily work and life, a great amount of scientific research has been conducted to understand the key characteristics of this new epidemic. In this manuscript, we focus on four crucial epidemic metrics with regard to the COVID-19, namely the basic reproduction number, the incubation period, the serial interval and the epidemic doubling time. We collect relevant studies based on the COVID-19 data in China and conduct a meta-analysis to obtain pooled estimates on the four metrics. From the summary results, we conclude that the COVID-19 has stronger transmissibility than SARS, implying that stringent public health strategies are necessary.

1. Introduction

Coronavirus disease (COVID-19) is an infectious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), a newly discovered coronavirus, which leads to respiratory illness and can be transmitted from person to person. Ever since December 2019, when the first case of COVID-19 in Wuhan, P, R, China (or mainland China) was reported, the novel coronavirus has hit most of the countries in the world, with the United States (U.S.) being the one having the largest number of confirmed cases (Worldometer, 2020). On March 11, 2020, the World Health Organization (WHO) declared COVID-19 a global pandemic. As of May 9, 2020, the WHO has reported a total of 3,855,788 confirmed cases all over the world and the total number of deaths has reached 265,862 (https://covid19.who.int/).

The COVID-19 pandemic has significant negative impacts on both the global health and the economy. In the U.S., for example, the unemployment rate has jumped up to 14,7% in April, 2020, reaching the highest rate and the largest monthly increase since January 1948 (U.S. Bureau of Labor Statistics, https://www.bls.gov/bls/newsrels.htm). Continuous efforts have been made by every country in the world to slow the spread of the disease and mitigate the associated negative impacts on various aspects of the society.

So far, a great amount of scientific research has been conducted on COVID-19, ranging from ongoing clinical trials that evaluate potential treatments to statistical analyses on the characteristics of this infectious disease. With more and more COVID-19 data and studies available, it is vitally important to aggregate the information and pool the statistical findings. Hence, here we conduct a meta-analysis based on published studies of the COVID-19 outbreak in mainland China.

Our meta-analysis that accounts for between-study heterogeneity concentrates on four common epidemic metrics that characterize the transmission of the COVID-19:

1. Basic reproduction number: Often referred to as R₀, the basic reproduction number measures the contagiousness or transmissibility of infectious agents and is interpreted as the expected number of infections caused directly by one case in a completely susceptible population,

2. Incubation period·. This metric is defined as the number of days between when an individual was actually infected and when this person starts to show symptoms. Understanding the incubation period of the COVID-19 is crucial as it provides guidelines on deciding a reasonable length of the quarantine period.

3. Serial interval : Defined as the time between the start of symptoms in the primary patient (infector) and onset of symptoms in the patient being infected by the infector (the infectee), the serial interval is critical in the calculation of R₀.

4. Epidemic doubling time: This metric measures the period of time needed for the total number of cases in the epidemic to double, and is an important factor that reflects the speed at which the COVID-19 is spreading.

The rest of this manuscript is organized as follows. We first provide details on the data collection process in Section 2. Then in Section 3, we introduce the key ingredients for a meta-analysis, where the modeling and estimation methods are outlined. Section 4 lists a detailed summary for the four epidemic metrics as given above. Statistical results from the meta-analysis are reported in Section 5, and sensitivity analysis is given in Section 6. Concluding remarks are then disclosed in Section 7.

2. Study selection

We conduct a comprehensive literature screening for the articles published in scientific journals (including early versions) or preprint platforms, e.g., medRxiv and bioRxiv. The key words of our searching are COVID-19 (SARS-CoV-2 or 2019-nCOV), the epidemic characteristics of interest (basic reproduction number, incubation period, serial interval and epidemic doubling time), and China, where the selection criteria is relaxed for regional labels. Specifically, we include the studies in the whole country of China, China except for Hubei province (where the city of Wuhan is located), a list of provinces and municipalities, a collection of cities or even a specific region, in order to increase the sample size and the potential statistical power. The variability and heterogeneity across the selected studies are accounted when adopting appropriate methodologies in the meta-analysis.

In addition, we only include studies reporting unambiguous estimates and the associated 95% confidence intervals or standard deviations. If the standard deviation of an estimator is given, we calculate a 95% confidence interval under the assumption of normal approximation provided that the fitted model is valid. This selection criterion is needed to ensure the consistency of analysis results. Besides, we do not include the articles, where the inference about the individual metrics are made based upon aggregate statistics. The inclusion of these studies in meta-analysis usually cause ecological bias (also known as aggregation bias or ecological fallacy in the literature).

Some studies included here provide more than one estimates that are obtained from various methods or models. For those studies, we select one estimate and its associated confidence interval in our analysis. We illustrate our choices and the corresponding reasons in details in Section 5.

3. Meta-analysis

Meta-analysis is a statistical procedure aiming to combine scientific results from multiple comparable studies or trials. It is one of the most popular analytical tools in the statistical analysis, which derives a pooled estimate by aggregating relevant information, thus increasing the statistical power. In particular, when comparing different studies addressing the same question, the crux is to measure the standardized difference across various results, i.e. the effect size. Meta-analysis is a useful tool for estimating a pooled effect size by combining multiple studies, and potentially improves the precision of estimation.

In general, there are two methods to pool effect sizes from multiple studies: the fixed-effects model (FEM) and the random-effects model (REM), A FEM assumes all included studies come from the same population, whereas a REM is constructed under the assumption that data are collected from different populations. Although we restrict our data search to mainland China only, there may still exist potential variations in the populations across the studies. Hence, we choose the REM in our analysis.

Let Y_k be the estimator in the k-th study, for k = 1,2,…,K, where K is the total number of collected studies. A REM assumes a normal-normal hierarchical model:

$$Y_k\mid {\theta }_k~\mathcal{N}\left({\theta }_k,s_k^2\right),$$

$${\theta }_k~\mathcal{N}\left(\mu ,{\tau }^2\right).$$

Here θ_k is the parameter of interest, and $s_k^2$ is the variance of Y_k. The hyper-parameters μ and τ² correspond to the mean effect and the across-study variance that reflects heterogeneity of the population, respectively.

The inference for REM is conducted sequentially as follows: we first estimate the heterogeneity variance τ² (denoted as ${\widehat{\tau }}^2$); then given ${\widehat{\tau }}^2$, we obtain an estimate of the effect μ. There are a variety of estimation methods for τ²; see Veroniki et al. (2016) for a concise survey. We adopt the Hartung-Knapp-Sidik-Jonkman (HKSJ) method (Hartung and Knapp, 2001; Sidik and Jonkman, 2002), which is shown to be more robust when the number of studies is small and there is a substantial heterogeneity in the population.

Given ${\widehat{\tau }}^2$, the conditional maximum likelihood estimator of the effect μ becomes

$$\widehat{\mu }=\frac{{\sum }_k{w}_k{y}_k}{{\sum }_k{w}_k},$$

where the weights are specified as

$$w_k=\frac{1}{s_k^2+{\widehat{\tau }}^2},k=1,2,\dots ,K.$$

The weight w_k can be interpreted as the inverse of the variance of the estimate of the k-th study. Then we use the normal approximation to construct confidence intervals, where the standard deviation of $\widehat{\mu }$ is given by

$${\widehat{\sigma }}_{\mu }=\sqrt{\frac{1}{{\sum }_k{w}_k}}.$$

Later in Section 5, we also provide prediction intervals, which are equally significant components in a meta-analysis. In the presence of a substantial heterogeneity index, prediction intervals are recommended to be reported alongside with confidence intervals as they not only quantitatively provide a range for the effect size of a new study, but also measure the uncertainty of the estimate in a way that acknowledges the heterogeneity.

4. Epidemic characteristics

In this section, we briefly introduce the epidemic characteristics that are investigated in this manuscript.

Basic reproduction number

In epidemiology, the basic reproduction number, denoted R₀, is the expected number of cases caused by one case in a completely susceptible population. It is a critical metric to describe the contagiousness or transmissibility of infectious diseases (Delamater et al., 2019). The estimation of R₀ is primarily based on compartmental models, where the susceptible-infectious-recovered (SIR) model and its extensions are the most commonly used. A variety of methods have been developed to estimate R₀, such as maximum likelihood methods and Bayesian approaches; we refer the interested readers to Dietz (1993) for a concise survey and to Nikbakht et al. (2019) for a practical comparison of the methods. For the users of statistical software R, the package R0 includes most standard methods for the estimation of R₀.

Since the outbreak of COVID-19, R₀ has been one of the most critical metrics receiving substantial interest in the community, as it provides a basic benchmark (with threshold 1) to define a pandemic. Besides, R₀ helps indicate the potential severity of an epidemic outbreak. It is evident that R₀ is closely related to the fraction of a susceptible population who will eventually be infected (Holme and Masuda, 2015). Furthermore, R₀ is an indispensable component when estimating the effective reproduction numbers (denoted as R_t), which are often used to assess the effectiveness of the intervention procedure to mitigate the spread of an epidemic.

Incubation period

The second characteristic we investigate here is the incubation period. The incubation period of an epidemic is the period from the time of the contact of a transmission source (susceptible or confirmed infector) and the time of symptom onset. The incubation period provides important information during an outbreak, as it helps to determine when the infected individuals who are symptomatic are most likely to spread the disease, and signal necessary public health activities such as monitoring, surveillance and intervention.

From a statistical perspective, the incubation period is a crucial factor to model the current and future trends of an epidemic, as well as evaluate intervention strategies. One of the biggest challenges of estimating the incubation period is that data are often coarsely observed, in addition to several other issues such as censoring and selection bias. The estimation of incubation period is generally based on the methods developed in Reich et al. (2009) and the extensions.

Serial interval

The serial interval is defined as the time duration between the onset of symptoms in the primary patient and the onset of symptoms in the secondary patient who receives the disease from that primary one (Lipsitch et al., 2003). It is the sum of the latent period and the duration of infectiousness. Being another crucial factor for constructing epidemiological models, the serial interval is one of the fundamentals for computing and estimating R₀; see Fine (2003) for a summary of the importance of serial interval in epidemiological studies.

The estimation of serial interval is based on the generation time distribution, which is closely related to the infection rate of a epidemic. Standard estimation procedures are given in Diekmann et al. (2013, Chapter 13). In practice, the R package R0 collects functions that can be used to estimate serial intervals via maximum likelihood methods (White et al., 2009), and the estimation of serial interval in the package EpiEstim is based on the method developed in Cori et al. (2013).

Epidemic doubling time

The epidemic doubling time, (or simply doubling time) is another important index in epidemic studies, as it measures the length of the period during which the number of confirmed cases is doubled. It is evident that the doubling time is inversely related to another epidemic parameters of interest: case-fatality rate. Hence, learning doubling time helps epidemiologists not only understand the transmissiblity of an infectious disease but also evaluate its severity. In the course of pathology, the doubling time is useful for analyzing the growth rate of the virus. Doubling time can also be used to assess the effectiveness of public health interventions and protocols, as an increase in the doubling time usually indicates a slowdown in epidemic transmission.

The estimation of the epidemic doubling time is generally model based, where exponential growth models are the most frequently adopted (Galvani et al., 2003; Du et al., 2020b). In this manuscript, we conduct a meta-analysis on the doubling time to study the growth rate of COVID-19.

5. Results

In this section, we apply the methods introduced in Section 3 to estimate the epidemic characteristics of interest listed in Section 4. The analysis is primarily done in R, where several standard packages for meta-analysis are utilized; for instance, meta, metafor, dmetar among others.

Basic reproduction number

Relevant studies used for our meta-analysis are summarized in Table 2, where a total of 12 research articles are included. Note that the number of collected studies is not large, so we depict a funnel plot in Figure 1 to see whether there is any bias owing to the small sample size. In a funnel plot, a significantly asymmetry pattern indicates the existence of the publication bias. A more rigorous method is to exploit the Egger’s test (Egger et al., 1997), for which a small p-value suggests rejecting the null hypothesis (i.e., some bias caused by the small sample size does exist). Recently, an alternative approach has been proposed by Lin and Chu (2018), but is not considered in the present article. The p-value of the Egger’s test here is 0.47, showing that no further procedure is needed for correcting the effect size for the present meta-analysis.

Using the estimation procedure demonstrated in Section 3, we see that the estimate of R₀ is 3.19 with a 95% confidence interval [2.63,3.74] and a 95% prediction interval [1.28,5.09]. The associated forest plot is presented in Figure 2. The index of heterogeneity, I², which ranges from 0 to 1, is used to quantify the dispersion of effect sizes. Here we have I² = 97%, indicating a substantial heterogeneity in the population. Hence, the REM is indeed more appropriate than the FEM for our meta-analysis.

With high heterogeneity in the underlying population, prediction intervals that incorporate heterogeneity are more informative than confidence intervals that focus only on summary estimates. We hence report both of the confidence interval and the prediction interval when inferring R₀.

Based on the results from our meta-analysis, we conclude that the basic reproduction number (R₀) of COVID-19 appears to be greater than that of SARS (point estimate around 3), as reported by WHO in “Consensus document on the epidemiology of severe acute respiratory syndrome (SARS)”. However, it is not as large as an average-based estimate (3.28) for COVID-19 reported in Liu et al. (2020b). Compared with the results from other two meta-analyses on COVID-19, our estimate is slightly greater than 3.15 reported in He et al. (2020a), and moderately greater than 3.05 reported in Dong et al. (2020). Nonetheless, we do not observe statistically significant difference in either case, but the high value of R₀ alerts the community that COVID-19 is a highly contagious disease.

Incubation period

Analogous to the previous part, we give the funnel plot in Figure 3, from which a (roughly) symmetric pattern is observed. This is consistent with the p-value (0.84) from the Egger’s test. Hence, again, publication bias is not present here.

The estimate of the mean of the incubation period of COVID-19 based on our meta-analysis is 5.34 (days), with a 95% confidence interval [4.29, 6.40] and a 95% prediction interval [1.97, 8.73]; see Figure 4. Our result is greater than the median (4 with interquartile range (IQR) from 2 to 7) of the incubation period estimated by, Guan et al. (2020), which is not included in our meta-analysis as no 95% confidence interval is provided therein. One possible reason is that the study period of Guan et al. (2020) is between December 11, 2019 and January 29, 2020, which is considered as a relatively early stage of the COVID-19 outbreak in mainland China. Besides, our estimate is larger than that (5.08) from another meta-analysis in He et al. (2020a).

Serial interval

For this part, we collect 10 studies to proceed along our meta-analysis. Albeit the funnel plot in Figure 5 displaying an asymmetric pattern, the p-value from the 0.26, suggesting that it is not required to implement a correction procedure. The estimate of the serial interval is 5.40 with a 95% confidence interval [4.53, 6.26] and a 95% prediction interval [2.89, 7.90].

The estimate of the serial interval of COVID-19 based on our meta-analysis is close to that of SARS (5–6 days according to WHO’s report in “Consensus document on the epidemiology of severe acute respiratory syndrome (SARS)”), A shorter serial interval of COVID-19, together with a shorter mean incubation period, suggests higher possibility that a transmission is completed before the onset of symptoms. Therefore, reducing the source of transmission (by hospitalizing infected individuals or implementing “stay-at-home” protocols to susceptible individuals) and reasonably extending the quarantine period are extensively helpful to slow the progression of COVID-19.

Epidemic doubling time

The number of the collected studies for epidemic doubling time is 8 (less than 10), As a small sample size is likely to cause bias in a meta-analysis (Lin, 2018), the visualization of the funnel plot in Figure 7 exhibits asymmetry.

We consider the trim-and-fill procedure (Duval and Richard, 2000) based on the motivation of reducing the bias owing to a small sample size, and the estimation results before and after implementing the trim-and-fill procedure are given in Figure 8. The estimate without correction is 4.86 (with a 95% confidence interval [3.26,6.45]), which is larger than the trimmed estimate of value 3.48 (with a 95% confidence interval [1.60,5.35]). Hence, even though the p-value of the Egger’s test is not significant, a remedy is still necessary, as an extensively small sample size usually jeopardizes the statistical power of the Egger’s test. In contrast, when we apply the trim-and-fill procedure to the previous three epidemic metrics, no significant difference has been detected.

Although there seems to be no official report on the epidemic doubling time of SARS from WHO or CDC, we find that an estimate of the doubling time of SARS from a published article (Galvani et al., 2003) is 16.3 through a literature search. The estimate of the doubling time of SARS is three times more than that of COVID-19 based on our analysis, suggesting that COVID-19 is a more contagious disease.

6. Sensitivity analysis

Meta-analysis and sensitivity analysis usually go hand in hand. While the meta-analysis focuses on the summary of a systematic review of relevant studies, the sensitivity analysis is used to assess the robustness of the results from the meta-analysis. In practice, the sensitivity analysis is a repeat of the meta-analysis, substituting alternative studies or the results from unclear studies. In other words, the goal of sensitivity analysis is to explore the impact of the meta-analysis by including or excluding studies in the meta-analysis based on some criteria as in Higgins et al. (2019, Section 9.7). In this section, we present a couple of sensitivity analyses for the basic reproduction number R₀. Analogous studies can be carried out for other epidemic characteristics mutatis mutandis. For the sake of brevity, we present the details on the sensitivity analysis of R₀ only in this section.

In the first sensitivity analysis, we only include the published articles (a total number of 7 left) in the new analysis, by leaving out preprints that have not yet been through the peer review process. The new estimate of R₀ is 2.85 with a 95% confidence interval [2.09,3.60]. Having observed a large value of heterogeneity index (I² = 89%), we accordingly report a 95% prediction interval [0.58,5.11] as well.

Now instead of leaving out ambiguous results, we expand the scope of our study to the East Asia. We add several studies from Japan, Korea and the Diamond Princess Cruise, which are listed in Table 6. The estimate of R₀ for this analysis is 2.82 with a 95% confidence interval [2.35,3.28] and a prediction interval [0.93,4.71].

7. Concluding remarks

In this meta-analysis, we study a collection of recent studies on the COVID-19 pandemic, focusing mainly on four epidemic characteristics: R₀ or the basic reproduction number, the incubation period, the serial interval, and the doubling time of the epidemic. We summarize our numerical findings in Table 1 and include corresponding comparisons with SARS, which is also a viral respiratory illness caused by a coronavirus in 2003. From Table 1, we see that compared to SARS, the COVID-19 has a larger R₀, a longer incubation period and much shorter doubling time, thus suggesting this novel coronavirus be more contagious and stringent public health strategies be necessary.

Table 1:

Summary of our numerical findings with respect to R₀ or the basic reproduction number, the incubation period, the serial interval and the doubling time of the epidemic.

Metric	Est.	95% CI	95% PI	≥ or ≤ SARS (Est.)
Basic Eep. Num.	3.19	[2.63, 3.74]	[1.28, 5.09]	≥ (3)
Incub. Period	5.34	[4.29, 6.40]	[1.97, 8.72]	≥ (3 ~ 5)
Serial Int.	5.40	[4.53, 6.26]	[2.89, 7.90]	≈ (5 ~ 6)
Epi. Doub. Time	3.48	[1.60, 5.35]	[−2.78, 9.74]	≤ (16:3)

The numerical results also provide insights on further studies. For example, with pooled estimates of R₀ and the doubling time available, we can then compare them with the effective reproduction number (or R_t) or the doubling time after the nationwide lockdown protocol has been implemented in China to see the effectiveness of the public health strategies. The estimates of the incubation period and the serial interval reassure the necessity of reinforcing a 14-dav quarantine period to prevent the spread of the disease.

It is also worthwhile noting the potential limitations of the current meta-analysis. To ensure the accuracy of the estimates collected, we do not include publications that report estimates with a 90% confidence interval or estimates with quartiles. This may lead to some loss of precision or publication bias for our estimates in meta-analysis. Meanwhile, the study on the COVID-19 may not be only restricted to the four characteristics listed in the manuscript. Other metrics, e.g., the case-to fatality rate and the testing capacity, and factors, e.g., significant clusters and patients’ underlying chronic medical conditions, are also of great importance in the future endeavors to mitigate the negative impacts of the COVID-19 pandemic.

Appendix

In the appendix, we give the details about the studies that are collected for this meta-analysis as well as the graphic representations of the analysis results. Specifically for the collected studies (in Tables 2 to 5), we present the point estimates of the epidemiological metrics and their associated 95% confidence intervals (in terms of lower bounds (L.B.) and upper bounds (U.B.)). Besides, we provide some additional information about these studies, such as sample size and study period. Note that in some of the studies, the authors stated that they obtained the data from publicly available online sources (such as the Chinese Center for Disease Control and Prevention) without specifying the exact number of sample size, which are marked as “na” in the summary tables.

Basic reproduction number

We list the sources that are utilized for estimating R₀ via meta-analysis in Table 2, In Sun et al, (2020); Zhu and Chen (2020), multiple estimates of R₀ and associated confidence intervals were reported. We selected the most appropriate one based on the proposed models, estimation time and some other decisive factors. Specifically, we considered the study period before January 23, 2020 (if available), the date that the lockdown of the city of Wuhan was officially announced by Chinese government.

Table 2:

Estimates and confidence intervals of R₀ for COVID-19 in China in the literature

	basis reproduction number			additional information
Source	Estimate	95% L.B.	95% U.B.	Size	Study period
Cao et al. (2020)	4.08	3.37	4.77	618	12.16.2019–1.25.2020
Kucharski et al. (2020)	2.35	1.15	4.77	na	12.1.2019–2.11.2020
Li et al. (2020a)	2.20	1.40	3.90	425	12.29.2019–1.22.2020
Liu et al. (2020a)	2.90	2.32	3.63	164	12.26.2019–1.23.2020
Imai et al. (2020)	2.60	1.50	3.50	4000	12.2.2019–1.18.2020
Read et al. (2020)	3.11	2.39	4.13	na	1.1.2020–1.22.2020
Sanche et al. (2020)	5.70	3.80	8.90	140	1.15.2020–1.30.2020
Shen et al. (2020)	4.71	4.50	4.92	na	12.12.2019–1.22.2020
Sun et al. (2020)	2.94	2.38	3.50	na	1.23.2020–2.10.2020
Tian et al. (2020)	3.15	3.04	3.26	3156	1.23.2020–2.19.2020
Wu et al. (2020a)	2.68	2.47	2.86	5993	12.31.2019–1.28.2020
Zhu and Chen (2020)	2.69	2.61	2.77	na	12.1.2019–1.23.2020

Incubation period

We list the sources that are utilized for estimating incubation period via meta-analysis in Table 3, In Linton et al, (2020), the authors adopted a variety of distributions for modeling the probability density function of incubation period, leading to slightly different results. We picked the confidence interval under the assumption of log-normal, referring to the best-fit model therein.

Serial interval

We list the sources that are utilized for estimating incubation period via meta-analysis in Table 4, In Li et al, (2020b), serial interval estimates of different generations were given, where the estimate for the first generation was chosen for the present analysis.

Figure 1:

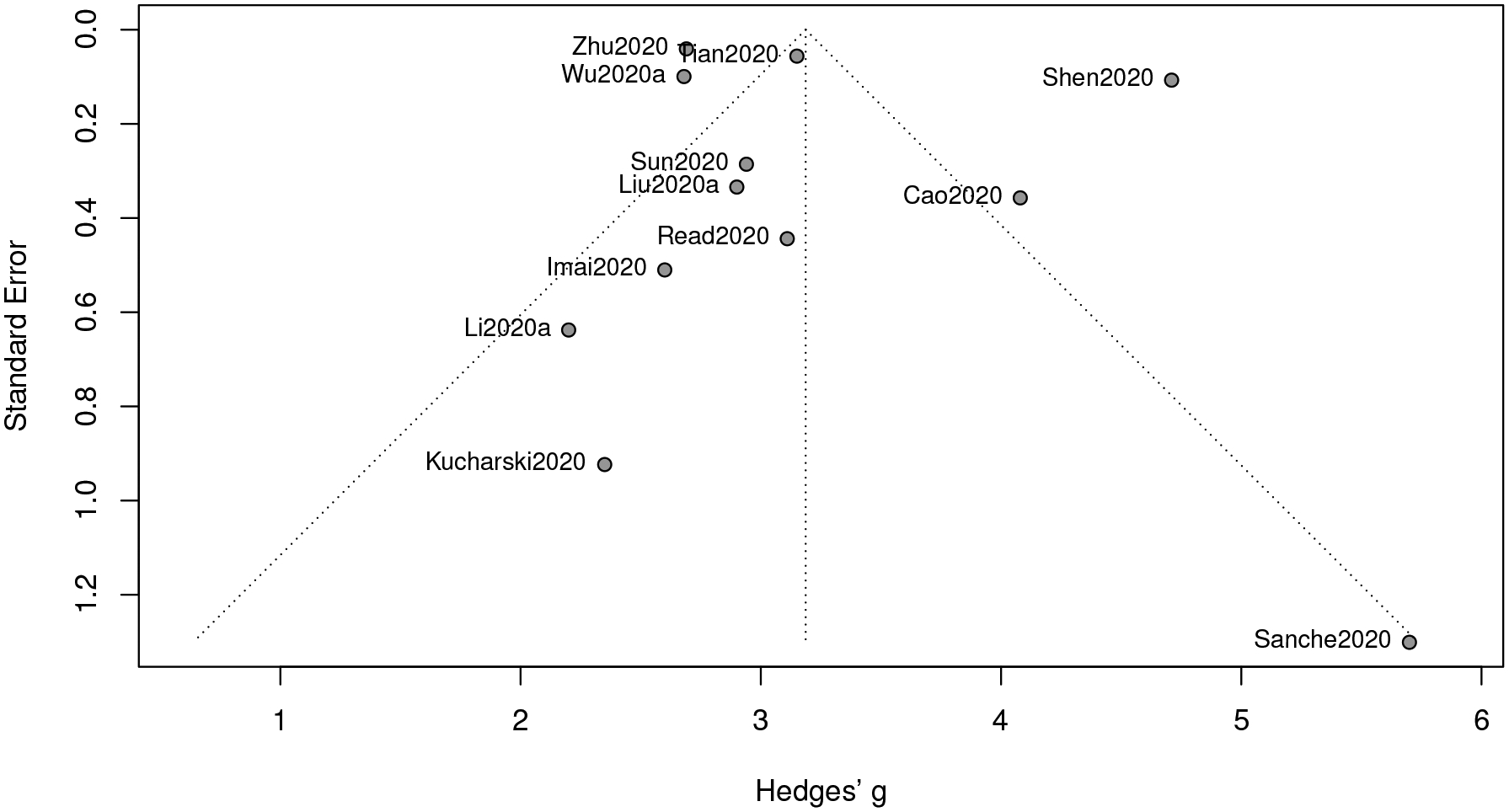
Funnel plot of meta-analysis for R₀

Epidemic doubling time

We list the sources that are utilized for estimating epidemic doubling time via meta-analysis in Table 5, In Lau et al, (2020), the authors reported two estimates of epidemic doubling time and associated confidence intervals, respectively before and after the implementation of lockdown in mainland China; we adopted the latter in the analysis. In Muniz-Rodriguez et al, (2020), the authors estimated epidemic doubling times for 31 provinces and municipalities in mainland China; we picked the one for “mainland China (except for Hubei province)” in our study.

Sensitivity analysis

We list the sources that are utilized for estimating basic reproduction number in sensitivity analysis in Table 6, The additional studies include recent research in Japan, South Korea and Diamond Princess Cruise.

Figure 2:

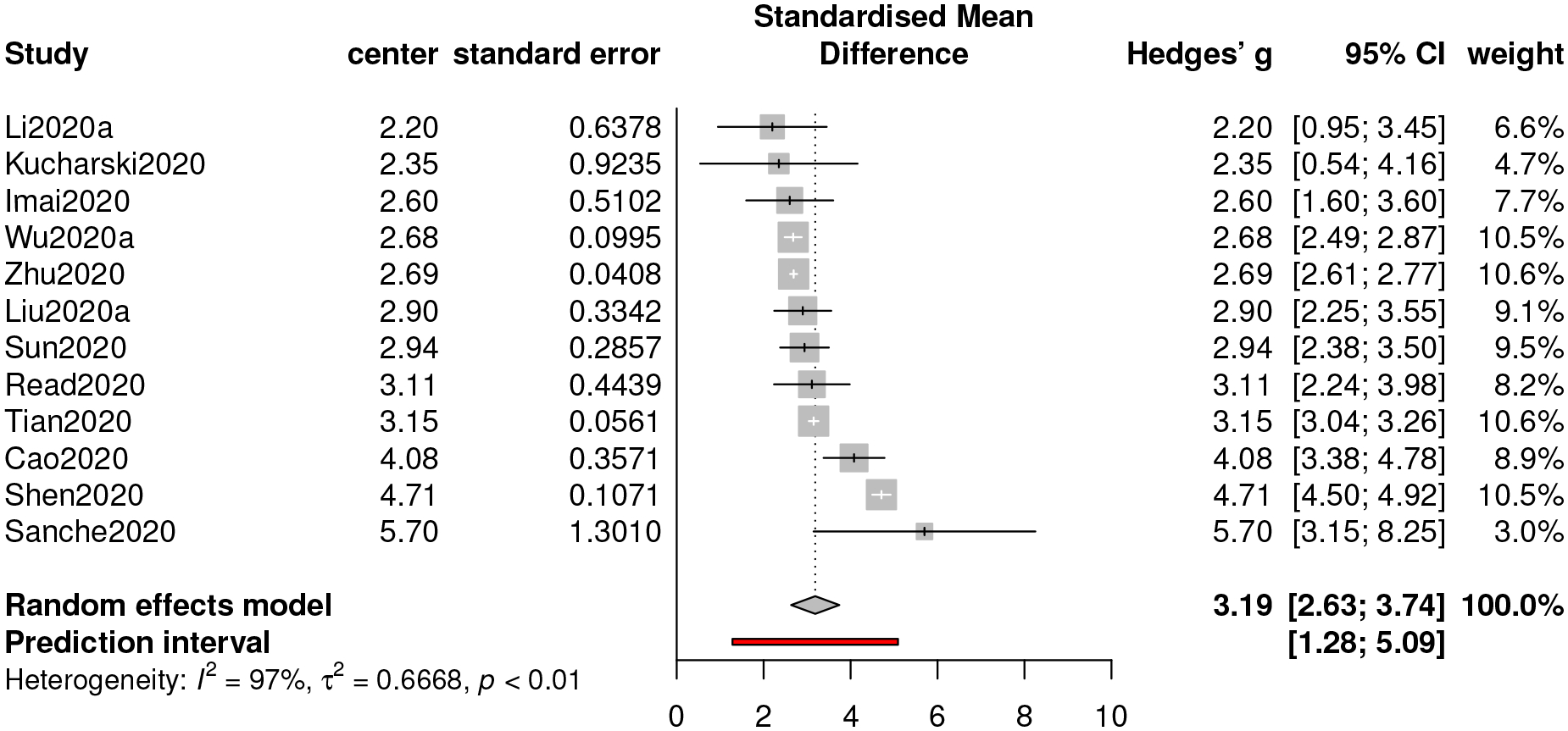
Forest plot of meta-analysis for R₀

Table 3:

Estimates and confidence intervals of incubation period of COVID-19 in China in the literature

	incubation period			additional information
Source	Estimate	95% L.B.	95% U.B.	Size	Study period
Backer et al. (2020)	6.40	5.70	7.70	88	1.21.2020–1.28.2020
He et al. (2020b)	2.30	0.80	3.00	94	1.21.2020–2.14.2020
Lauer et al. (2020)	5.10	4.50	5.80	181	1.4.2020–2.24.2020
Leung (2020)	6.90	5.50	8.30	152	1.20.2020–2.7.2020
Li et al. (2020a)	5.20	4.10	7.00	425	12.29.2019–1.22.2020
Linton et al. (2020)	5.00	4.40	5.60	276	1.1.2020–1.31.2020
Liu et al. (2020a)	4.80	2.20	9.40	164	12.26.2019–1.23.2020
Men et al. (2020)	5.84	2.91	8.75	59	12.29.2019–2.5.2020
Qin et al. (2020)	8.13	7.37	8.91	1922	1.19.2020–2.15.2020
Sanche et al. (2020)	4.20	3.50	5.10	140	1.15.2020–1.30.2020
Xia et al. (2020)	4.90	4.40	5.40	106	1.3.2020 – 1.25.2020

Figure 3:

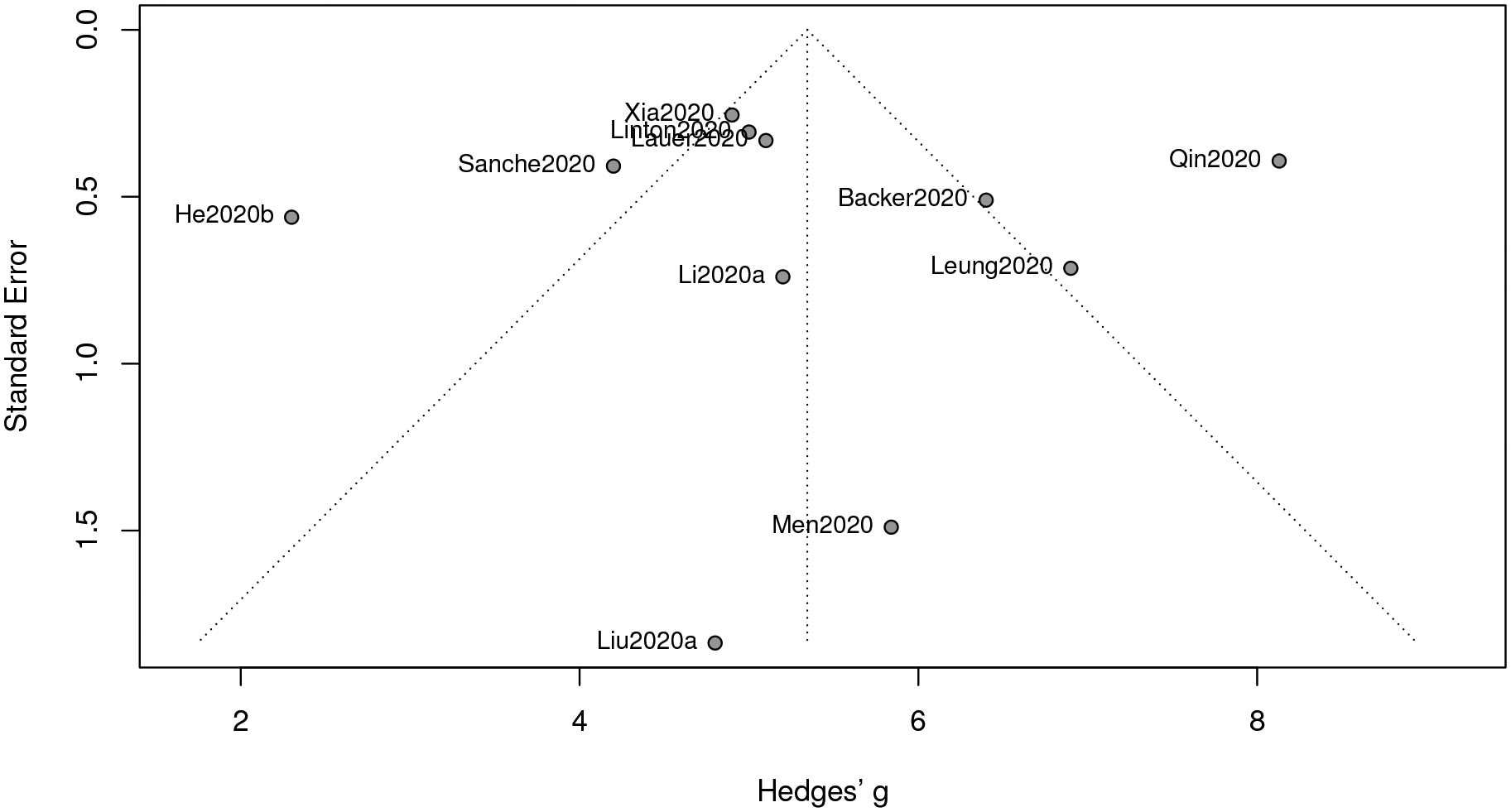
Funnel plot of meta-analysis for incubation period

Figure 4:

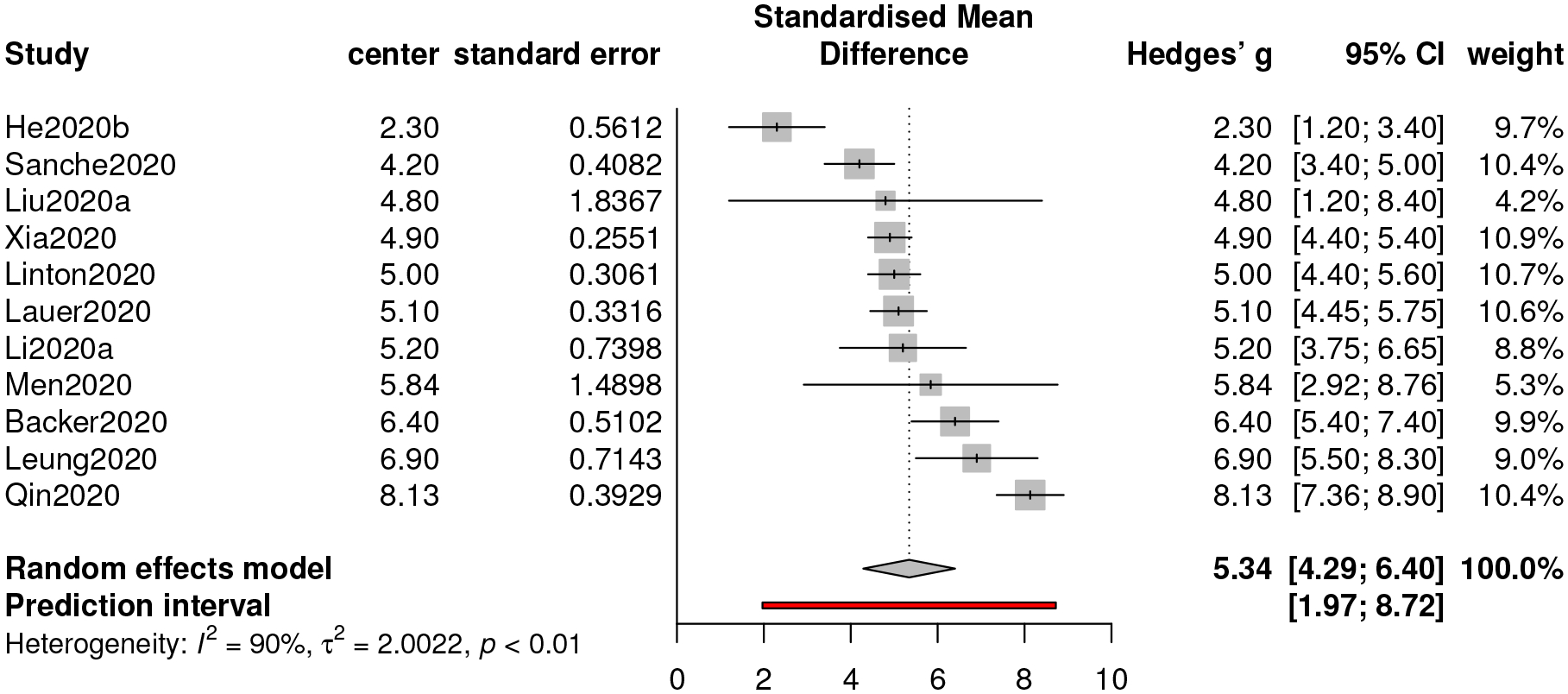
Forest plot of meta-analysis for incubation period

Table 4:

Estimates and confidence intervals of serial interval of COVID-19 in China in the literature

	serial interval			additional info.
Source	Estimate	95% L.B.	95% U.B.	Size	Study period
Bi et al. (2020)	6.30	5.20	7.60	391	1.14.2020–2.12.2020
Du et al. (2020a)	3.96	3.53	4.39	486	1.21.2020–2.8.2020
Du et al. (2020c)	5.29	4.72	5.86	339	1.20.2020–2.19.2020
He et al. (2020b)	5.20	4.10	6.40	94	1.21.2020–2.14.2020
Li et al. (2020a)	7.50	5.30	19.00	425	12.29.2019–1.22.2020
Li et al. (2020b)	6.27	5.62	6.98	337	1.21.2020–2.29.2020
Shao et al. (2020)	4.40	2.90	6.70	21	1.16.2020–2.15.2020
Tindale et al. (2020)	4.22	3.43	5.01	135	1.21.2020–2.22.2020
Wu et al. (2020b)	7.50	5.80	8.10	43	12.20.2019–2.10.2020
Zhang et al. (2020a)	5.10	1.30	11.60	35	1.19.2020–2.17.2020

Figure 5:

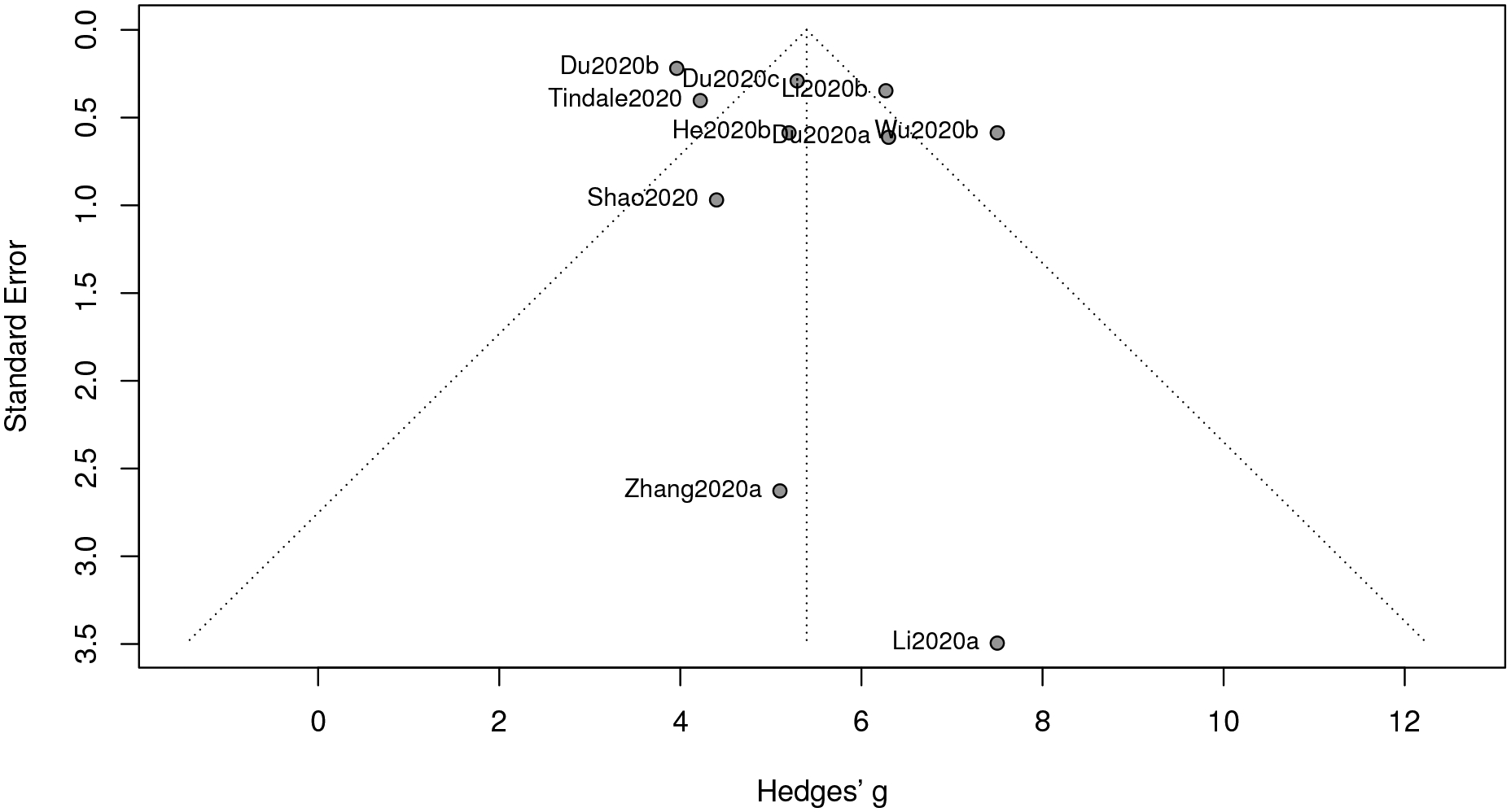
Funnel plot of meta-analysis for serial interval

Figure 6:

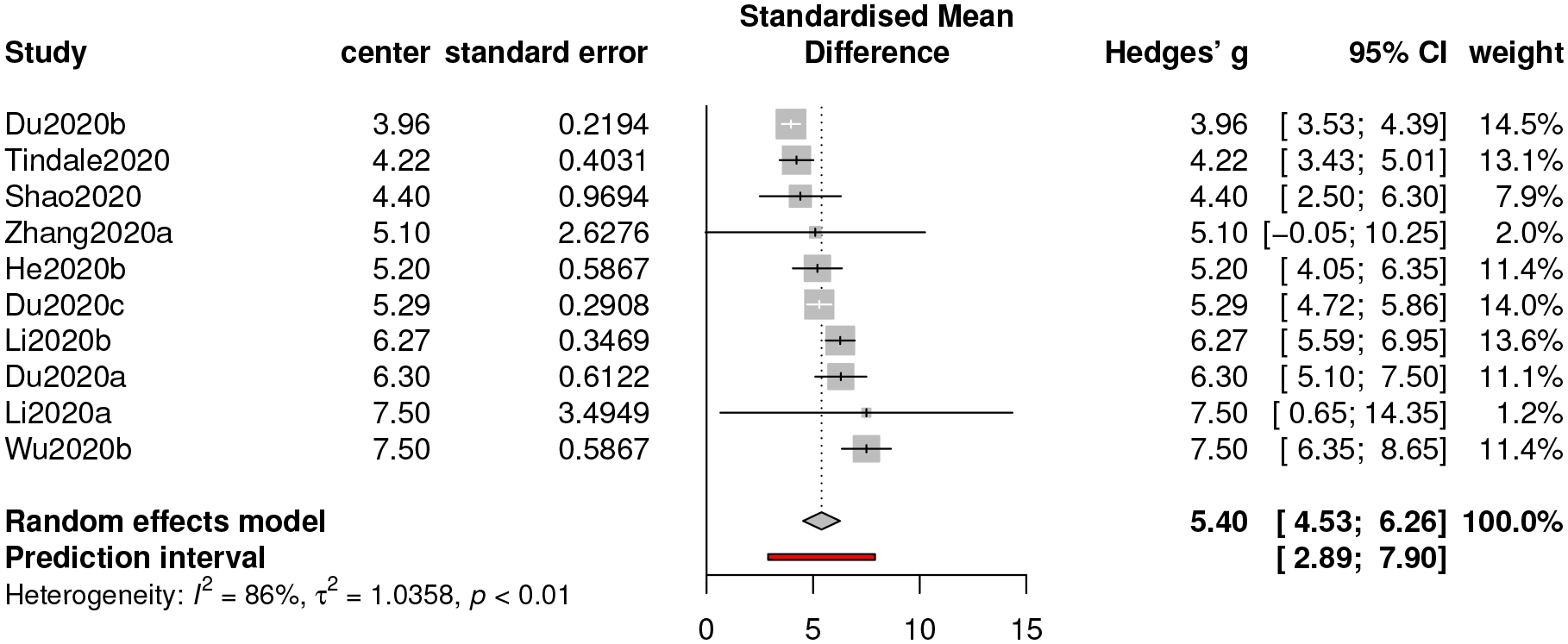
Forest plot of meta-analysis for serial interval

Table 5:

Estimates and confidence intervals of epidemic doubling time of COVID-19 in China in the literature

	epidemic doubling time			additional information
Source	Estimate	95% L.B.	95% U.B.	Size	Study period
Du et al. (2020b)	7.31	6.26	9.66	425	12.3.2019–1.24.2020
Kraemer et al. (2020)	4.00	3.60	5.00	554	1.1.2020–1.31.2020
Lau et al. (2020)	4.00	3.50	4.30	na	1.20.2020–2.13–2020
Li et al. (2020a)	7.10	3.00	20.50	425	12.29.2019–1.22.2020
Muniz-Rodriguez et al. (2020)	1.80	1.50	2.30	na	1.20.2020–2.19.2020
Volz et al. (2020)	6.60	4.00	12.70	53	12.8.2019–2.3.2020
Wu et al. (2020a)	6.40	5.80	7.10	5993	12.31.2019–1.28.2020
Wu et al. (2020b)	5.20	4.60	6.10	43	12.20.2019–2.10.2020

Table 6:

Additional estimates and confidence intervals of basic reproduction number of COVID-19 for sensitivity analysis

		R0
Source	region	estimate	95% L.B.	95% U.B.
Kuniya (2020)	Japan	2.60	2.40	2.80
Sugishita et al. (2020)	Japan	1.99	1.89	2.09
Shim et al. (2020)	South Korea	1.50	1.40	1.60
Zhang et al. (2020b)	Diamond Princess Cruise	2.28	2.06	2.52
Zhao et al. (2020)	Diamond Princess Cruise	2.20	2.10	2.40

Figure 7:

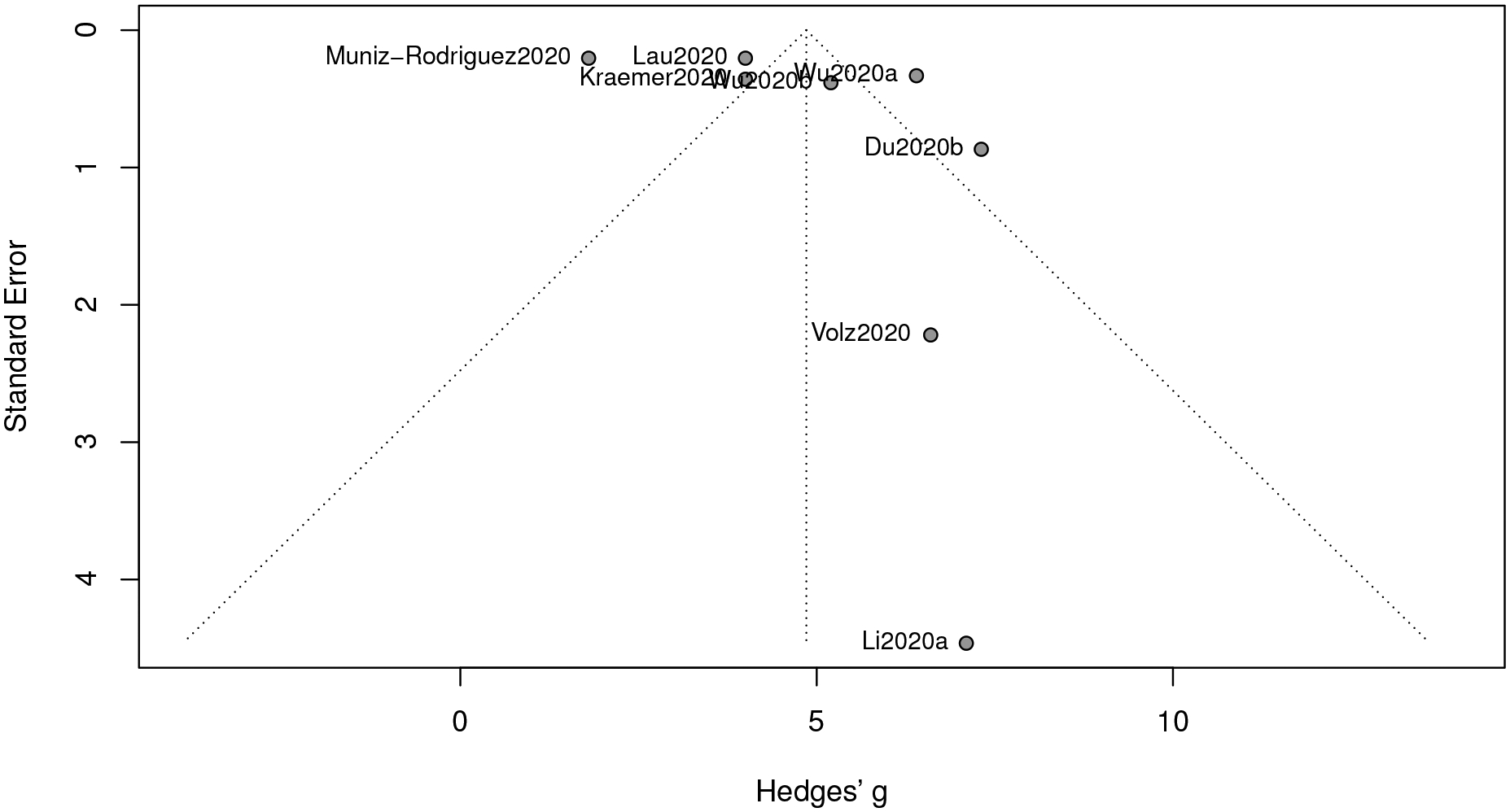
Funnel plot of meta-analysis for epidemic doubling time

Figure 8:

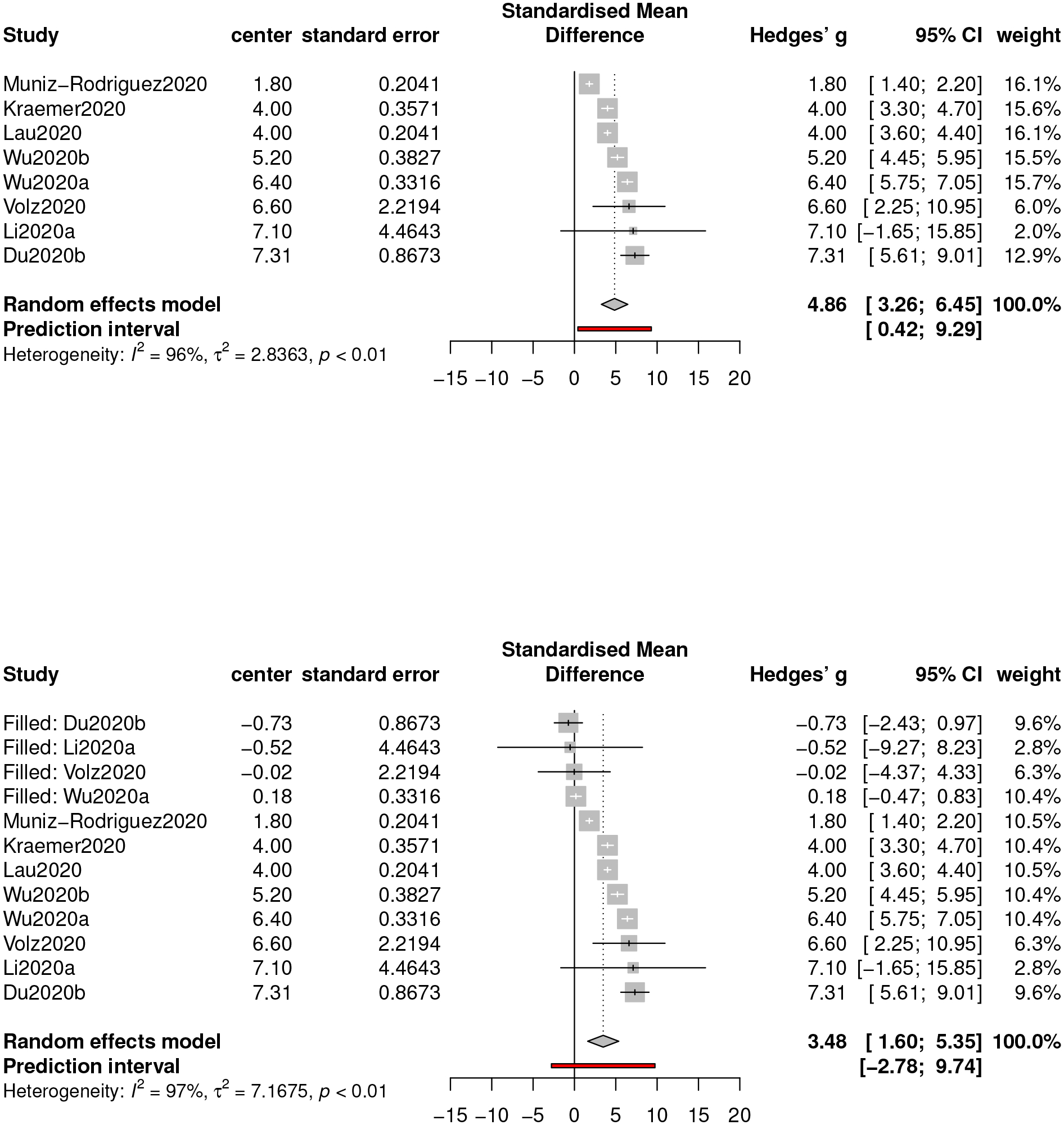
Forest plots of meta-analysis for epidemic doubling time before (top) and after (bottom) implementing the trim-and-fill procedure