Environmental fluctuations can promote evolutionary rescue in high-extinction-risk scenarios

Abstract

Substantial environmental change can force a population onto a path towards extinction, but under some conditions, adaptation by natural selection can rescue the population and allow it to persist. This process, known as evolutionary rescue, is believed to be less likely to occur with greater magnitudes of random environmental fluctuations because environmental variation decreases expected population size, increases variance in population size and increases evolutionary lag. However, previous studies of evolutionary rescue in fluctuating environments have only considered scenarios in which evolutionary rescue was likely to occur. We extend these studies to assess how baseline extinction risk (which we manipulated via changes in the initial population size, degree of environmental change or mutation rate) influences the effects of environmental variation on evolutionary rescue following an abrupt environmental change. Using a combination of analytical models and stochastic simulations, we show that autocorrelated environmental variation hinders evolutionary rescue in low-extinction-risk scenarios but facilitates rescue in high-risk scenarios. In these high-risk cases, the chance of a run of good years counteracts the otherwise negative effects of environmental variation on evolutionary demography. These findings can inform the development of effective conservation practices that consider evolutionary responses to abrupt environmental changes.

1. Introduction

Abrupt environmental change can expose populations to conditions beyond their ecological persistence limits. Following such change, a race is started between demographic extinction and adaptive evolution [1]. If adaptation occurs fast enough, it can save the population from extirpation, a process known as ‘evolutionary rescue' [2,3]. Understanding the determinants of evolutionary rescue can aid the development of conservation practices designed to protect species from extinction [3–6], and inform other areas of applied ecology, such as invasion biology. One well-recognized factor in determining the probability of evolutionary rescue is the magnitude (or rate) of environmental change [2,3,7], but there is growing evidence that we must also consider how temporal variation in environmental conditions affects the likelihood of evolutionary rescue [8–11].

Rarely are biotic or abiotic conditions static through time. The abundances of predators, prey and competitors often vary greatly from year to year or among seasons (e.g. [12,13]). Temperature and precipitation rates change over time, and there is even temporal variation in the quantity of pollutants humans release into the environment (e.g. [14,15]). Environmental fluctuations can increase the probability of a population going extinct because increasing variance in the environment lowers long-run population growth rates [16]. Environmental variation is often positively autocorrelated [17]. Greater temporal autocorrelation can either increase or decrease the probability of extinction, with the outcome depending on the form of density dependence and spatial structure in the population [18,19].

Despite its prominent role in the theory of extinction, studies of evolutionary rescue have not typically accounted for environmental fluctuations. The few evolutionary rescue studies that have explicitly considered environmental variation have incorporated it as fluctuations in an environmental stressor (modelled as fluctuations in the optimal phenotype of a quantitative trait) and have generally concluded that greater magnitudes of such fluctuations decrease the probability of rescue [8,9,11]. This occurs because fluctuations in the optimal phenotype decrease expected population size, increase variance in population size and increase the lag of the mean phenotype of the population behind the environmental optimum (evolutionary lag load) [11,20–22]. The degree of autocorrelation has opposing effects on evolutionary rescue; populations are more able to evolutionarily track autocorrelated changes in the optimal phenotype, thus reducing the lag load [20–22], but autocorrelation also increases the variance in population trajectories, which increases the probability of extinction due to a run of bad years [11].

Previous studies of evolutionary rescue in temporally fluctuating environments have primarily focused on scenarios in which evolutionary rescue was likely to occur [11]. However, natural populations lie on a spectrum of extinction risk. For instance, smaller populations are typically more prone to extinction even in benign environments [16,23] and are less likely to be saved by adaptation following an environmental change [1,24,25]. Likewise, evolutionary rescue is less likely with greater magnitudes [24,26] and greater rates of environmental change [27–29]. In this study, we assess how baseline extinction risk—defined as the probability of a population going extinct following an initial abrupt environmental change without environmental fluctuations—modulates the effects of temporal environmental variation on evolutionary rescue.

To accomplish this, we developed two sets of models: polygenic models and monogenic models. We manipulate baseline extinction risk by changing the initial population size, degree of environmental change or mutation rate. The polygenic models assume that fitness is determined by a polygenic quantitative trait (an assumption used in previous studies [8,10,11]). For these models, we present results of both population-level and individual-based simulations. The population-level simulations provide a more analytically tractable understanding of dynamics of the system but require some simplifying assumptions (i.e. no demographic stochasticity). Our individual-based simulations relax many of the assumptions of the population-level models (and permit extinction via demographic stochasticity), but at the cost of analytic tractability. Our monogenic models assume fitness is determined by a single gene locus of major effect. This assumption may match some biological systems of important societal concern (e.g. the evolution of pesticide resistance [30]). For these monogenic models, we present results of simulations with demographic stochasticity, as well as an analytical model which (with simplifying assumptions) provides insights into the patterns produced by the simulations. We conclude with a discussion of how our results may apply to issues ranging from conservation biology to the control of drug-resistant pathogens.

2. Methods

Throughout, we vary the ‘baseline extinction risk', which we define as the probability of a population going extinct following an abrupt environmental change without environmental fluctuations. This baseline extinction risk is influenced by intrinsic properties of the population (e.g. initial population size and mutation rate) and by the degree of environmental change. We explore how baseline extinction risk influences the effect of random environmental fluctuations on the probability of local extinction (i.e. the realized extinction risk).

(a). Polygenic model

Our first model describes the evolution of an ecologically important quantitative trait in a closed population with discrete generations. At the start of each generation, all individuals are juveniles. The juveniles then undergo viability selection and all surviving individuals mature into adults and reproduce with random mating. At the end of each generation, after reproduction, all adults die. Trait z of an individual determines its probability of surviving from birth to adulthood (viability), and the relationship between trait value and survival is V(z) = exp [ −(z − θ_t)²/(2ω²)], where θ_t is the optimal trait value in generation t and ω² is inversely related to the strength of stabilizing selection. The model assumes that z is a polygenic trait (phenotype), given by the sum of an additive-genetic component g and a normally distributed environmental component with mean zero and variance E (which can include developmental noise and non-additive-genetic components of the phenotype). At the start of generation t, the phenotype is assumed to be normally distributed across the population with mean ${\overline{z}}_t$ and phenotypic variance P (which is the sum of the additive-genetic variance G and environmental variance E). As in previous models of the evolution of a polygenic trait in response to an environmental change (e.g. [1,11]), we assumed that G and P are constant. In essence, this assumes that random mating, recombination and mutation replenish genotypic and phenotypic variation every generation (this assumption is relaxed in our individual-based simulations below). Given these assumptions, averaging viability over the trait distribution gives the mean viability of the population in generation t, which is

$${\overline{V}}_t=V_{max}\exp \left[\frac{-{({\overline{z}}_t-{\theta }_t)}^2}{2({\omega }^2+P)}\right],$$

where V_max = ω/[ω² + P]^1/2 is the average viability of a perfectly adapted population (${\overline{z}}_t={\theta }_t$). The recursions for the mean phenotype and population size are, respectively [1,8],

$${\overline{z}}_{t+1}={\overline{z}}_t-\left(\frac{G}{{\omega }^2+P}\right)({\overline{z}}_t-{\theta }_t)$$ 2.1a

and

$$N_{t+1}=N_t{\overline{V}}_t{F}_t,$$ 2.1b

where F_t is the mean number of offspring produced by each adult in generation t. Note that equation (2.1a) is consistent with the response to selection in [31]. Also note that there is no density dependence in this model.

We incorporated temporal environmental variation into this model by varying the optimal phenotype θ_t. This simulates variation in the environmental stressor to which the population is adapting. Autocorrelated random sequences of θ_t were generated from a temporally uncorrelated zero-mean, unit-variance Gaussian random sequence η_t using the equation

$${\theta }_{t+1}={\mu }_{\theta }+\rho [{\theta }_t-{\mu }_{\theta }]+{\sigma }_{\theta }\sqrt{1-{\rho }^2}{\eta }_t,$$ 2.2

where μ_θ and σ_θ are, respectively, the mean and standard deviation of the optimal phenotype and ρ is the correlation coefficient between values for consecutive generations (see electronic supplementary material for more details). For results presented in the main text, the mean population fecundity F_t­ was fixed at the value μ_F, but we also ran additional simulations in which we varied fecundity instead of the optimal phenotype. Because the results of both methods were qualitatively similar, we focus on variation in the optimal phenotype in the main text (methods and results for variation in fecundity are available in the electronic supplementary material).

Using the above recursions, we simulated population dynamics for 1000 generations following a sudden change in the optimal phenotype (simulating a sudden environmental change). The simulations were initiated with a population size of N* and an initial mean phenotype of 0. We assumed that the environment was constant before the environmental change and therefore initial conditions were unaffected by the σ_θ. At the beginning of the simulations (t = 1), the mean optimal phenotype abruptly changed from 0 to μ_θ (thus, θ₁ = μ_θ). We chose to keep the initial degree of environmental change μ_θ the same for all levels of environmental variation rather than to have the initial degree of environment change be a random value with a mean μ_θ because the effects of the initial degree of environmental change are well known [1,24] and we were focused on the effects of variation afterwards (the statistical properties of this assumption can be found in the electronic supplementary material).

We evaluated the models for a range of degrees of environmental change (μ_θ). The population's initial mean genotype was zero, so a larger μ_θ meant a more maladapted initial population and thus a greater baseline extinction risk. A limitation of these types of population-level models is that they ignore demographic stochasticity and, as long as heritability is not zero, the population size never reaches (nor asymptotically approaches) zero. Therefore, following previous studies (e.g. [1,10,11]), we heuristically defined a critical population size N_c below which rapid extinction is expected due to demographic or genetic factors not explicitly included in the model (e.g. Allee effects, demographic stochasticity, mutational meltdown [32]). Results are presented in terms of the probability of persistence, which is the proportion of 1000 runs of the model in which the population size did not drop below this critical value. In the main text, we only present results for a limited range of parameters, but sensitivity analyses for certain parameters are available in the electronic supplementary material (electronic supplementary material, figure A1).

To check the robustness of the assumptions of our population-level models, we also developed individual-based simulations. These simulations allowed us to more directly evaluate extinction probabilities, because they included demographic stochasticity and hence population sizes could go to zero. Furthermore, these simulations do not require assumptions about the genotypic and phenotypic distributions, which instead arise from simulating mating, segregation, mutation, and selection (in effect, G and P are allowed to evolve). These models are related to those originally developed by Bürger & Lynch [8] and later expanded on by others (e.g. [33]). The full methods for our individual-based simulations are described in the appendix, and the C++ source code with accompanying documentation is available in the Dryad Digital Repository [34]. Briefly, populations had discrete generations and individuals were assumed to be diploid and hermaphroditic. The probability that a given individual survived to adulthood was determined by its phenotype, which was the sum of allelic values at 10 freely recombining, additive loci plus a random environmental component drawn from a normal distribution with a mean of zero and unit variance. As in the population-level models, we varied the optimal phenotype over time using equation (2.2), after allowing the initial population to equilibrate in an environment with a constant optimal phenotype of 0.

(b). Monogenic model

This model assumes that fitness is determined by a single diallelic haploid locus in a species with fully clonal reproduction. Unlike in the polygenic models in which selection could act on standing genetic variation in the population, in our monogenic model, adaptation can only occur via novel mutations. The model begins with an initially monomorphic maladapted (non-mutant) population. With a low probability u for each newborn, a mutation arises that produces an adapted individual (a mutant). We assumed that there was only one possible mutation and no back mutation. There is also no density dependence and generations are discrete.

We assumed that the mean per capita number of births, F_t, is the same for both non-mutants and mutants, and varies over time as given by the following equations

$$f_{t+1}={\mu }_f+\rho [f_t-{\mu }_f]+{\sigma }_f\sqrt{1-{\rho }^2}{\eta }_t$$ 2.3a

and

$$F_t=\exp (f_t),$$ 2.3b

where μ_f, σ_f, and ρ are, respectively, the mean, standard deviation, and autocorrelation coefficient of a random sequence that determined fecundity and η_t is a temporally uncorrelated zero-mean, unit-variance Gaussian random sequence (equation (2.3a) is analogous to equation (2.2)). The fecundity was set by exponentiating f_t to preclude negative values. Therefore, the geometric mean population fecundity is μ_F = exp [μ_f]. The number of offspring of each individual was assumed to have a Poisson distribution with mean F_t. Mutation affects the probability that an offspring dies before adulthood; non-mutants have a probability V of surviving to adulthood, while mutants have a higher probability v (both constant). Survival of each offspring is independent of all others. Parameters were chosen so that the geometric mean of the number of surviving offspring of a non-mutant was less than 1, while that of a mutant was greater than 1, so that the population could persist if the mutation established but would otherwise go extinct.

With these assumptions, the effect of the magnitude and autocorrelation of the variation in fecundity on the probability of evolutionary rescue can be found. We used two approaches. The first was direct simulation of this scenario, which in principle is similar to the individual-based simulations mentioned above (it includes demographic stochasticity and the possibility of extinction), except that it was much simpler because there are only two types of individuals (mutants and non-mutants). Therefore, at each step, mutants and non-mutants could each be handled as a group using the appropriate random number generator given our assumptions above: Poisson for the total number of offspring produced by each type given F_t and the number of adults of that type, binomial for number of survivors of each type given the survival rate and number of offspring of that type, and for the number of mutants given the mutation rate and the number of offspring of non-mutants.

In order to understand the patterns produced by direct simulation, we examined this system with a second approach by analytical exploration of a stochastic model. Evolutionary rescue requires that before the initial population goes extinct, at least one mutant is produced that gives rise to a lineage that persists (is not lost to demographic stochasticity). We therefore examined mutant production, and then the probability of persistence of the lineage of a mutant. Below, we summarize these analytical methods while derivations of the model can be found in the electronic supplementary material.

We first found expressions for the expected total number of non-mutant births from the initial generation until no non-mutants remained. The product of this number and the mutation rate is the expected total number of mutants that arise before the non-mutants go extinct. A branching process was then used to calculate the probability that the lineage of a mutant persists. Both were calculated as a function of the amount of variation for different degrees of non-mutant maladaptation, with and without autocorrelation in F_t (the equations usually required numerical solution). These results therefore provide insight into whether mutant production or mutant lineage persistence is more sensitive to variation.

3. Results

(a). Polygenic model

In the absence of environmental fluctuations, our population-level polygenic model behaves deterministically and is equivalent to the model of Gomulkiewicz & Holt [1]. Recall that this model ignores demographic stochasticity and assumes that the population goes extinct if it drops below a critical population size N_c. The time to reach N_c is given by the first root t of

$$t\ln [{\mu }_F{V}_{max}]-\frac{{\mu }_{\theta }^2}{2({\omega }^2+P)}\left(\frac{1-k^{2t}}{1-k^2}\right)=\ln \left[\frac{N_c}{N^{\ast }}\right]$$ 3.1

where k = 1 − [G/(ω² + P)] [1]. If no root exists, the population never goes below the critical population size N_c. For these population-level polygenic simulations, we considered any change in parameter values that decreases the time given by equation (3.1) as an increase in baseline extinction risk (e.g. caused by increased degree of environmental change or decreased initial population size; electronic supplementary material, figure A2A,B). More broadly, if, given the parameters, there were no roots t to equation (3.1), we classified that scenario (joint characteristics of the population and environmental change) as ‘low extinction risk' and if there were roots, we classified the scenario as ‘high extinction risk', corresponding to the expected persistence or extinction of that population with an environment that undergoes the given change but is constant thereafter (electronic supplementary material, figure A2C).

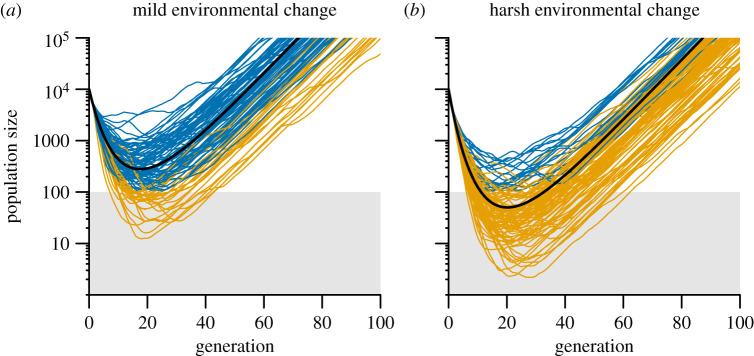
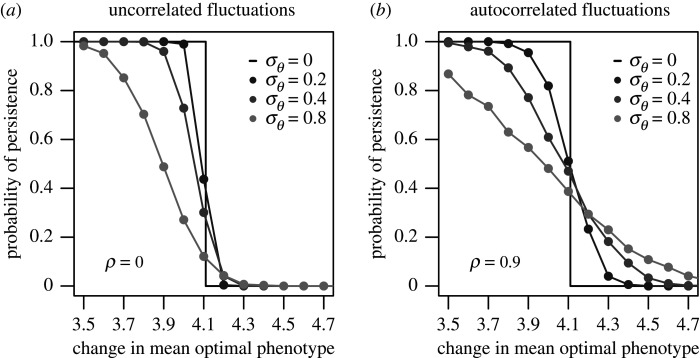
Our population-level polygenic simulations showed that the effect of variation in the optimal phenotype on population persistence depended on both the degree of environmental change and autocorrelation. In response to mild environmental changes (low μ_θ), to which populations never went extinct in a non-fluctuating environment, variation in the optimal phenotype decreased the probability of evolutionary rescue (see sample population trajectories in figure 1a). This occurs because greater variation (especially with autocorrelation) increases the chance that runs of bad years will occur (high θ_t), which can cause the population to crash towards extinction. Conversely, in response to harsh environmental changes (high μ_θ), to which populations went extinct in a non-fluctuating environment, variation in the optimal phenotype promoted evolutionary rescue, because variation now increases the chances of a run of good years (low θ_t), which can sometimes slow the population's decline towards extinction and thus give it more time to adapt (see sample population trajectories in figure 1b). In general, the effects of environmental variation on evolutionary rescue were more prominent with greater degrees of variation (figure 2), but the positive effects seen with harsh changes disappeared at very high levels of variation (σ_θ > 1.5 for parameters in figure 2) because populations could not evolutionarily track extreme fluctuations in the optimal phenotype (electronic supplementary material, figure A3).

Figure 1.

Examples of the evolutionary rescue process following a mild environmental change (a; μ_θ = 3.8) and a harsh environmental change (b; μ_θ = 4.3) in the population-level polygenic model. Black lines denote population trajectories for non-fluctuating environments (σ_θ = 0). Grey lines (coloured online) show individual runs of the simulation with a fluctuating optimal phenotype (σ_θ = 0.6) with positive autocorrelation (ρ = 0.9). Shaded area represents the heuristically defined extinction zone. Populations that entered this zone (shown in light orange online) were assumed to go extinct because of demographic or genetic processes not included in the model. Runs of the simulation that never entered this extinction zone are shown in dark blue online. Parameter values were N* = 10 000, N_c = 100, μ_F = 1.2, ω² = 10, P = 1,G = 0.5. (Online version in colour.)

Figure 2.

The probability of persistence in the population-level polygenic model for different magnitudes of environmental change μ_θ. Each point represents the proportion of 1000 runs of the simulation in which the population persisted until the end of the simulation (N_t > N_c for all t). Lighter shades of grey indicate greater degrees of variation in the optimal phenotype (σ_θ). (a) shows results for uncorrelated (ρ = 0) fluctuations in the optimal phenotype and (b) shows results for autocorrelated (ρ = 0.9) fluctuations in the optimal phenotype. Other parameter values were μ_F = 1.2, N* = 10 000, N_c = 100, ω² = 10, p = 1, G = 0.5. (Estimated values have a binomial distribution, which using 1000 runs have a maximum standard deviation of 0.016 around the true value.)

The positive effects of environmental variation seen with harsh changes in the optimal phenotype were minor when fluctuations were temporally uncorrelated (figure 2a) because the fluctuations were too rapid for the populations to respond demographically or evolutionarily (electronic supplementary material, figure A4A,B). When fluctuations in the optimal phenotype were more positively autocorrelated, however, the benefits of environmental variation became more prominent (figure 2; electronic supplementary material, figure A5) because populations could demographically and evolutionarily respond to the slower fluctuations (electronic supplementary material, figure A4C,D). However, the positive effects of increased degrees of autocorrelation disappeared at very high degrees of autocorrelation (ρ > 0.98 for parameters in figure 2) because fluctuations were too slow to be demographically meaningful (electronic supplementary material, figure A5). We note that this loss of benefits at very high degrees of autocorrelation was dependent on our assumptions about how fluctuations were implemented into the model (see electronic supplementary material).

The optimal phenotypes found in the generations immediately following the step change in the environment were crucial for determining whether or not populations would go extinct. Given the parameter values in figure 1b, the mean optimal phenotype of the first 20 generations predicted whether or not a population would go extinct with 96% accuracy (McFadden's R² = 0.781), while the mean optimal phenotype of generations 21–40 and 41–60 only predicted the outcome with 82% (McFadden's R² = 0.081) and 80% (McFadden's R² = 0.003) accuracy, respectively (electronic supplementary material, figure A6; statistical methods for prediction are provided in the electronic supplementary material). Note that 80% of the populations went extinct, and thus models could attain this accuracy by simply always predicting extinction. Variation in the optimal phenotype long after the step change is rather inconsequential, because after the 50th generation almost all populations have either gone below the critical population size and been ruled extinct, or adapted and reached a sufficient population size, such that a run of good or bad years no longer affects the outcome of the rescue process (electronic supplementary material, figures A4 and A7). Therefore, for a given mean optimal phenotype over the course of the simulation, adaptation should be favoured when the mild years occur soon after the step change and the harsh years occur later (electronic supplementary material, figures A6 and A8).

For most results, our individual-based simulations showed the same qualitative patterns as the population-level models, although in the individual-based simulations, the effects of variation were generally dampened (electronic supplementary material, figure A9). One key difference between the results of the two models, however, was that in the individual-based simulations, there was no benefit of uncorrelated fluctuations following a harsh environmental change (electronic supplementary material, figure A9C). One explanation for the decreased benefits of environmental variation in the individual-based simulations could be that in these simulations, populations were regulated at a fixed number of mating individuals K, which could have minimized the demographic benefits obtained in runs of good years as well as allowed the extinction of even well-adapted populations. However, only a small fraction of the populations that went extinct ever obtained more than K adults in the population (electronic supplementary material, figure A10). Therefore, density regulation cannot fully explain the difference between the population-level and individual-based results. The differences between simulations also do not seem to be explained by differences in genetic variation between treatments in the individual-based simulations (electronic supplementary material, figure A11). The differences between the simulation results may also be partially explained by the additional sources of stochasticity in individual-based simulations such as demographic stochasticity and stochasticity in the non-genetic proportion of the phenotype.

The results above quantified baseline extinction risk by the magnitude of environmental change (μ_θ). However, results were qualitatively similar if we instead used initial population size as a metric for baseline extinction risk. That is, variation in the optimal phenotype was beneficial with small initial population sizes but detrimental with large initial population sizes (electronic supplementary material, figure A12).

(b). Monogenic model

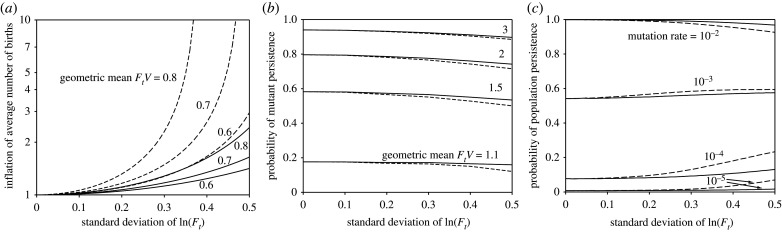
In the monogenic model, variation in fecundity increases the average cumulative number of births before extinction and therefore the expected number of mutations, especially if the variation is autocorrelated (figure 3a). Gonzalez & Holt [35] observed a similar pattern for a source–sink scenario; our model shows that this inflationary effect of temporal variation arises even in the absence of immigration. Conversely, variation in fecundity has little effect on the probability of a mutant's lineage surviving once it arises (figure 3b), only causing a small drop with increasing variation (albeit greater with autocorrelation). We believe this is because survival or extinction is mostly determined by fitness in the first few generations after the mutation occurs [36], during which the lineage usually either goes extinct or grows, making extinction much less likely. Therefore, there is insufficient time for anything other than a very short run of good or bad years to have an effect, which mutes the effect of autocorrelation. Because (given the parameters used in figure 3a and b) the positive effect of inflation in the number of mutants is generally larger than the negative effect on the survival of each mutant lineage, the combined effect should be an increase in population persistence with increased variation, so long as the expected number of mutants is low. In this case, the probability of persistence increases if the expected number of mutant lineages that persist (which is the product of values from figure 3a and b and the mutation rate) increases. However, if this product is large, most populations are expected to persist, and extinctions only occur when populations experience conditions much worse than average, which cannot be predicted based on averages (environmental variation, especially with autocorrelation, increases not only the mean but the variance, so the probability of a low value can increase even as the mean value increases).

Figure 3.

Effect of variation in fecundity on evolutionary rescue in the monogenic model. (a) Analytical calculation of the expected number of births to non-mutants before extinction for different degrees of variation in fecundity, relative to the expected number of births with no variation. See supplementary material for derivation. (b) Using a branching process, analytic predictions of the probability of persistence of the lineage of an adult mutant with given geometric mean fitness for different degrees of variation in fecundity, averaged over 10 000 fecundity time series for each parameter set. (See supplementary material for derivation and details.) (c) Probability of population persistence from simulations with 1 000 000 realizations for each parameter set (at intervals of 0.01 on the abscissa). Initial population size was 100, the geometric mean F_t = 4, V = 0.2, v = 0.5. In all panels, solid lines show results of uncorrelated fluctuations and dashed lines show autocorrelated fluctuations with ρ = 0.5.

In this model, mutation rate can be used as a proxy for baseline extinction risk because mutations give rise to locally adapted individuals (i.e. populations with a low mutation rate have a high baseline extinction risk and populations with a high mutation rate have a low baseline extinction risk; also, the effect of mutation rate and initial population size on expected number of mutations is through their product, so varying the initial population size should give very similar results). Our simulations showed that, for sufficiently low mutation rates, increased variation in fecundity increased the probability of adaptation (figure 3c), as expected based on the results of our analytical model (figure 3a,b). However, similar to what was seen in our polygenic model, for populations with low baseline extinction risk (high mutation rates), variation in fecundity decreased the probability of adaptation. Once again, this is because of the possibility of a run of bad years, which if it occurs early could cause the population to plummet so that, even with a relatively high mutation rate, few mutants are likely. Both these positive and negative effects of variation are amplified with increased autocorrelation (figure 3).

4. Discussion

Although there has been a substantial amount of work on the relationship between environmental variation and extinction [37], until recently studies of evolutionary rescue have largely ignored environmental noise, typically assuming either a single abrupt environmental change or a linearly changing environment. Evolutionary rescue studies that have explicitly considered variation with environmental change have shown that such variation can have significant negative effects on the probability of rescue [8,9,11]. Our models expand on this work and demonstrate that, following an abrupt environmental change, the effect of environmental variation on evolutionary rescue depends on the population's baseline extinction risk (which is influenced by the magnitude of environmental change, initial population size or beneficial mutation rate). In low-extinction-risk scenarios, environmental variation increases the chance of extinction (e.g. figure 1a). Conversely, in high-extinction-risk scenarios, environmental variation decreases the probability of extinction (e.g. figure 1b), because without variation, the population will almost certainly go extinct, and environmental variation provides the chance for a run of good years, which can grant the population time to adapt and persist. This qualitative pattern emerges from both our polygenic and monogenic models.

Parenthetically, we note that this effect in some respects echoes ideas in behavioural ecology, where investigators have shown that foragers may prefer ‘safe' (constant food supply) environments over ‘risky' (variable food supply) ones, provided they have a positive energy budget, but when they have a negative energy budget, they may actually prefer the variable environment (e.g. [38]).

We have also identified a critical period immediately following the sudden environmental change when environmental variation is most consequential. Intervention strategies should target this critical period in order to most effectively facilitate or impede evolutionary rescue.

(a). Importance of autocorrelation

A key finding of our models is that autocorrelation in environmental conditions can have significant effects on evolutionary rescue. Increased autocorrelation increases the variance in population trajectories because it increases the probability of long runs of either particularly mild or harsh years [11,39]. Therefore, populations in low-extinction-risk scenarios are more likely to go extinct because of a run of harsh years, whereas high-extinction-risk populations are more likely to adapt because of a run of mild years. When environmental variation is incorporated via fluctuations in the phenotypic optimum, increased autocorrelation allows the population mean phenotype to more closely track the optimum, thus reducing lag load [20–22]. For low-extinction-risk scenarios, these contrasting effects of autocorrelation (increased variance in population trajectories but decreased evolutionary lag) lead to relatively minor effects of autocorrelation on the probability of rescue [11]. However, for high-extinction-risk scenarios, the benefits of autocorrelation are two-fold (an increased chance of a run of good years and decreased evolutionary lag) and thus increased autocorrelation significantly increases the probability of evolutionary rescue (figure 2).

Human-induced climate change may involve not only changes in mean conditions but also changes in the temporal correlation structure of environments [40]. Our models suggest that these changes may affect the probability of evolutionary rescue because the likelihood of rescue depends on the degree of autocorrelation. However, to fully understand these anthropogenic impacts, future studies should more directly investigate how temporal changes in correlation structure affect the rescue process (e.g. [10]).

(b). Fluctuating phenotypic optimum versus fluctuating fecundity

Previous studies have incorporated environmental variation as fluctuations in the optimal phenotype of a polygenic quantitative trait [8,10,11,39]. This is applicable to many situations, but variation could also affect many other ecological parameters. For example, imagine an insect population that has been exposed to a novel pesticide. Variation in pesticide exposure might generate variation in the optimal phenotype (e.g. variation in the optimal levels of detoxifying metabolic pathways). Alternatively, pesticide exposure could remain temporally constant, but birth rates could vary because of fluctuations in temperature or food availability (factors to which the insect cannot adapt in this example). We found that both types of variation had similar effects on the probability of evolutionary rescue. This suggests that changes in extinction probabilities with respect to the extent of environmental variation are mainly due to variations in population trajectories and not because of changes in the evolutionary lag load. We may have seen greater differences between the two type of variation if we instead had analysed a linearly changing environment, where evolutionary lag is known to be a major cause of extinction [8,41–43].

(c). Assumptions and caveats

We have focused on an abrupt environmental change, which may be representative of pollution, habitat loss, movement of a population into a new habitat, or the introduction of non-native enemies, but other forms of environmental change (e.g. climate change) occur more gradually and are typically modelled as a linearly changing environment. The benefit of environmental variation that we see in high-extinction-risk scenarios might not exist in a linearly changing environment because there is no longer a critical period during which environmental conditions are more consequential. Indeed, Bürger & Lynch [8] found that with a linear environmental change, the mean time to extinction decreased with larger fluctuations in the optimal phenotype. However, with other forms of gradual change such as a decelerating rate of environmental change, which more accurately matches future climate models [44], there is once again a critical period [6] and therefore environmental variation may be beneficial in high-extinction-risk scenarios.

Most of our models ignored density-dependent regulation. Our models should be a reasonable approximation of evolutionary rescue dynamics if there is weak density dependence, but given strong density dependence that acts even at small population sizes the rescue process might differ [45]. In addition, in models without density dependence, once a population is locally adapted (e.g. mean absolute fitness is greater than 1), the population size can grow without bound. Therefore, most of our results only pertain to extinction over relatively short time-scales due to maladaptation following environmental change and do not pertain to the long-term extinction risk in a population following adaptation. Following adaptation, environmental variation should increase the probability of extinction in a finite population, and the expected time to extinction is known to scale with carrying capacity [16,46,47].

Our polygenic and monogenic models produced qualitatively similar results, suggesting that our conclusions should be robust to assumptions about the genetic basis of fitness. We have only evaluated two rather simple genetic systems, however, and additional studies are necessary in order to fully understand how genetic architecture and the fitness landscape interact with environmental variation to influence evolutionary rescue (e.g. [48,49]).

Our models also do not consider phenotypic plasticity within or across generations, both of which can help species survive in novel environments and thus facilitate evolutionary rescue [50–53]. However, Ashander et al. [10] showed that evolving plasticity only facilitates evolutionary rescue when fluctuations in the optimal phenotype are sufficiently predictable and that plastic responses in fact may be detrimental when fluctuations are unpredictable. Incorporating plasticity into our model could potentially add an additional benefit of positive autocorrelation, which adds short-term predictability to the environment.

(d). Applications

Evolutionary rescue theory is relevant to a wide range of medical, agricultural and conservation issues [54]. We briefly highlight some scenarios for which our results are potentially useful. However, we should note that in our models, environmental fluctuations are random in timing, direction and magnitude, while intervention strategies can in principle influence all of these factors. Therefore, the suggestions below merely provide hypotheses, which we hope could be expanded on and tested with more system-specific models and experiments.

Our results suggest that conservation managers should aim to space out the use of limited funds in order to facilitate long-term stable conditions for populations that are a priori reasonably likely to recover. By contrast, for high-extinction-risk populations, managers should prioritize intervention as soon after the environmental change as possible, thus replicating the scenarios that led to the rescue of these populations in our models (i.e. a chance run of good years early on). However, the effects of environmental variation that we have explored in this study are relatively minor compared with the importance of the magnitude of environmental change or initial population size. Therefore, managers should first prioritize mitigating these first-order factors of extinction risk before considering the more subtle effects of environmental variation.

Our conclusions could be used to inform strategies for more efficient use of pesticides to limit the evolution of resistance. If resistance readily evolves in the pest species, then applying occasional large pulses of pesticides, thus creating high environmental variation, may minimize the probability of resistance evolving and thus facilitate elimination of the pest. Alternatively, if the evolution of resistance seems unlikely, the most effective strategy may be to apply a steady stream of pesticides to steadily push the target pest towards extirpation.

Finally, our results might shed light on the development of medical treatments that could minimize the evolution of drug resistance (i.e. reducing the likelihood that a targeted pathogen will adapt to our attempts to control or eliminate it). Recent studies show that pulsed treatment schedules may sometimes reduce the probability of resistance evolving during both antibiotic and cancer treatments [55,56]. Our models suggest that the optimal treatment regime might be context-dependent; pulsed treatments might be best in situations where resistance almost always emerges, while steady, consistent treatment might be optimal when the evolution of resistance is relatively uncommon.

5. Conclusion

Extinction risk modulates the effect of environmental variation on evolutionary rescue. Temporal variation is harmful in low-extinction-risk scenarios but beneficial in high-risk-scenarios, particularly when such variation is positively autocorrelated. This presents a more nuanced view of the eco-evolutionary response of populations to an abrupt environment change, one that requires an understanding of not only the magnitude of the change, but also the level of variation afterwards and its autocorrelation. We must continue to incorporate more complexity and realism into the study of evolutionary rescue if we hope to develop effective conservation policies, agricultural practices and medical treatments that account for the outcomes of eco-evolutionary dynamics in changing environments.

Data accessibility

Full C++ source code and accompanying documentation for our polygenetic individual-based simulations is available in the Dryad Digital Repository: https://doi.org/10.5061/dryad.4xgxd2568 [34].

Authors' contributions

All authors participated in the conceptualization and design of this study. J.H.P. constructed the polygenic models and wrote the first draft of the manuscript. M.B. constructed the monogenic models and contributed to the writing of the manuscript. A.G. and R.D.H. contributed to the design and interpretation of models and edited the manuscript. R.D.H. led the collaboration.

Competing interests

We declare we have no competing interests.

Funding

Financial support from the National Science Foundation (R.D.H.; DEB 1923495).