Toward understanding of evolutionary constraints: experimental and theoretical approaches

Abstract

Although organisms have diversified remarkably through evolution, they do not exhibit unlimited variability. During evolution, the phenotypic changes do not occur at random; instead, they are directional and restricted by the constraints imposed on them. Despite the perceived importance of characterizing the unevenness of these changes, studies on evolutionary constraints have been primarily qualitative in nature. In this review, we focus on the recent studies of evolutionary constraints, which are based on the quantification of high-dimensional phenotypic and genotypic data. Furthermore, we present a theoretical analysis that enables us to predict evolutionary constraints on the basis of phenotypic fluctuation, modeled on the fluctuation–response relationship in statistical physics. The review lays emphasis on the tight interactions between experimental and theoretical analyses in evolutionary biology that will contribute to a better understanding of evolutionary constraints.

Introduction

Although organisms have undergone remarkable diversification during evolution, it has not occurred in entirely random directions. Previous studies have shown unevenness and directionality in the evolutionary changes and phenotypic variations (Arnold 1992; Smith et al. 1985). For example, all vertebrates have a maximum of two pairs of limbs, and all insects have the same basic body plan (Urry et al. 2016). These limits of diversity have often been attributed to the limited potential for diversification or constraints on the production of variable phenotypes; however, the exact mechanism remains largely unclear.

The theoretical approach, which is based on the concept of statistical physics, contributed significantly toward formulating the constraints, leading to tight collaborations between theoretical and experimental studies (Kaneko and Furusawa 2018; Sato et al. 2003). Technological innovations also enabled the quantitative analyses of high-dimensional phenotypic and genotypic data, allowing scientists to experimentally test the theoretical frameworks. The present review highlights the contribution of quantitative and theoretical analyses of evolutionary dynamics toward the understanding of its constraints. The three topics are presented below, including studies on bacterial evolution, animal development, and the fluctuation–response relationship in evolution. Here, we discuss a variety of biological targets since the purpose of this review article is to offer a general concept and theoretical framework toward the understanding of evolutionary constraints.

Analysis of evolutionary constraints in bacterial laboratory evolution

Laboratory evolution of bacterial cells is a powerful method for understanding the nature of evolutionary dynamics (Conrad et al. 2011; Elena and Lenski 2003). Technological advances, such as high-throughput sequencing, have enabled us to quantify the phenotypic and genetic changes occurring during their adaptive evolution. In these experiments, bacterial cells are exposed to environmental stresses, which cause a partial or complete inhibition of cell growth, resulting in a selective advantage for strains resistant to the corresponding stress. An interesting phenomenon observed here is that the evolutionary adaptation to a specific environment is frequently accompanied by fitness changes in other environments. For instance, in the phenomenon of cross-resistance, the acquisition of resistance to one antibiotic is often accompanied by resistance to other antibiotics as well. On the other hand, it can also cause increased sensitivity to other drugs, known as collateral sensitivity (Lázár et al. 2013; Munck et al. 2014; Suzuki et al. 2014). The interplay between mechanisms of stress resistance could constrain possible phenotypic changes during adaptive evolution. In the following section, we discuss the results of our previous study (Suzuki et al. 2014) on the laboratory evolution of Escherichia coli under antibiotics to propose a possible approach to the study of evolutionary constraints.

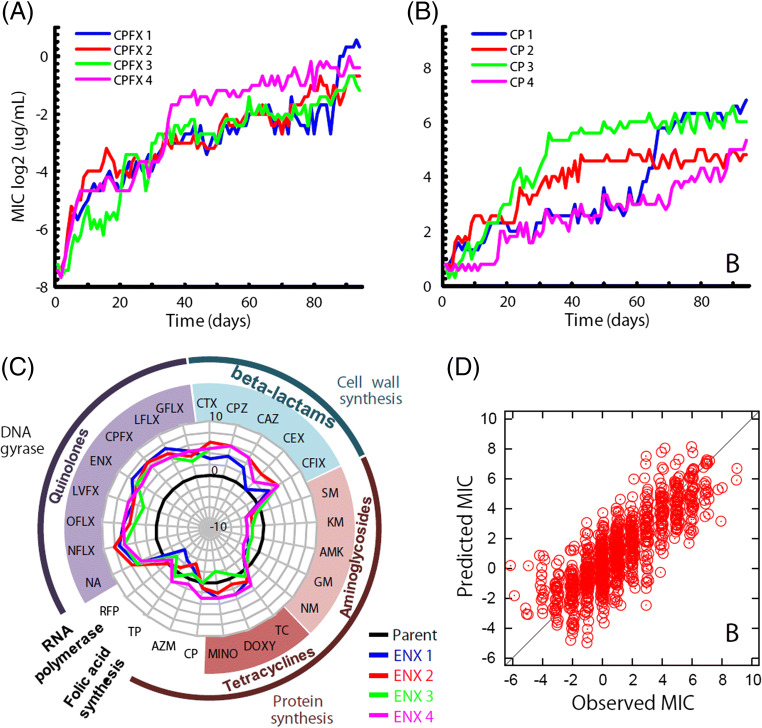
In our study, the laboratory evolution of E. coli cells on the addition of 10 antibiotics with different action mechanisms was investigated. The range of antibiotics included those that disrupt bacterial cell wall synthesis, protein synthesis, folic acid biosynthesis, and DNA replication. After 90 days of experimental evolution in the presence of each of these antibiotics, we obtained 40 resistant strains (4 independently evolved strains for 10 antibiotics), which showed significant increases in minimum inhibitory concentrations (MICs; Fig. 1a, b). For each drug-resistant strain, transcriptome and genome resequencing analyses were performed to identify fixed mutations and changes in gene expression. We also studied the effect of acquisition of resistance to one drug on the resistance and susceptibility to other drugs (Fig. 1c, for example). The results demonstrated that cross-resistance and collateral sensitivity are ubiquitous in antibiotic resistance evolution. For instance, the acquisition of resistance to enoxacin, a DNA replication inhibitor, is accompanied by collateral sensitivity to aminoglycosides, which are protein synthesis inhibitors, and vice versa. The newly acquired sensitivity to aminoglycosides could possibly be due to the changes in proton-motive force across the cell membrane (Lázár et al. 2013; Suzuki et al. 2014). It was also demonstrated that E. coli cells cannot acquire resistance to both aminoglycosides and various other antibiotics simultaneously (Munck et al. 2014; Suzuki et al. 2017). These results demonstrated the constraint placed by the network of cross-resistance and collateral sensitivity on the possible course of drug-resistance evolution in E. coli.

Fig. 1.

Laboratory evolution of E. coli under antibiotics. a, b The time courses of the increase in MIC for enoxacin (ENX) and Cefixime (CFIX) in 90-day laboratory evolution, respectively. Four parallel series of experiments were performed. c Changes in MICs for other antibiotics in ENX-resistant strains, respectively. The radial axis depicts the log2-transformed relative MIC to the parent strain. The thick black line indicates MICs of the parent strain, and the colored thick lines indicate relative MICs of four parallel-evolved ENX resistant strains. d Comparisons between observed and predicted MICs calculated by using expression levels of 8 genes. See reference Suzuki et al. (2014)) for details

Constraints represented by the network of cross-resistance and collateral sensitivity probably represent a low-dimensional nature of possible phenotypic changes. To check the dimensionality of phenotypic changes, we analyzed the transcriptome data of the drug-resistant strains. It showed that the level of resistance can be quantitatively predicted based on the expression levels of a small number of genes (e.g., 8 genes), using a simple linear model (Fig. 1d). The results suggest that, even though the expression profile is governed by complex interactions of thousands of genes, the changes in the expression profile during evolution are constrained by low-dimensional dynamics, which results in predictable antibiotic resistance. It should be noted that recent theoretical studies have demonstrated that phenotypic changes during adaptive evolution can be constrained by low-dimensional dynamics, which is consistent with the observed low dimensionality in the adaptive evolution of E. coli (Furusawa and Kaneko 2018; Kaneko and Furusawa 2018).

To further analyze the evolutionary constraint in bacterial adaptive evolution, we utilized an automated system developed in-house to perform a high-throughput laboratory evolution of E. coli under 95 stress environments (Maeda et al. 2020). Again, significant collateral resistance and sensitivity were found to be ubiquitous during the evolution. By applying interpretable machine learning techniques to transcriptome and resistance profile data, the emergence of low-dimensional phenotypic states in the evolved strains was observed, indicating the presence of evolutionary constraints. These findings bridge the gap between genotypic, gene expression, and drug resistance spaces and lead to a better understanding of the constraints for antibiotic resistance evolution.

The developmental hourglass model: pleiotropic constraint behind animal body plan

The basic anatomical pattern of animals, or body plans, show striking conservation during evolution and are often considered as a typical example of phylogenetic inertia (Shanahan 2011). Because of its conservativeness, the body plan is one of the criteria for defining the largest phylogenetic category or phylum. The vertebrate body plan, for example, includes the heart, liver, notochord, gonad, kidney, anus, eye, ear, and dorsal nerve cord; the set of these anatomical traits remained conserved for more than 550 million years of evolution (Onai et al. 2014). There is no clear consensus on the evolutionary mechanism behind this body plan conservation. However, a promising hypothesis would be to attribute it to the conservation of the basic body plan during mid-embryonic development, also known as the developmental hourglass model (Duboule 1994; Fig. 2). This model predicts that mid-embryonic organogenesis stages represent the period of highest conservation and that the phylotypic period is the source of the basic body plan at a phylum level. This hypothesis has been supported in a variety of animal groups, including vertebrates, arthropods, nematodes, and annelids (Hu et al. 2017; Irie and Kuratani 2011; Irie and Sehara-Fujisawa 2007; Kalinka et al. 2010; Wang et al. 2013; Xu et al. 2016; Zalts and Yanai 2017); however, it leads to another question regarding the mechanism of conservation of body plan–defining mid-embryonic phase, the answer to which remains unclear. A possible clue would be that the mid-embryonic phase has always been the target of conservation through vertebrate evolution (persistent conservation (Irie and Kuratani 2014)), despite the fact that vertebrates have diversified into various environmental niches, such as ocean and land (Hu et al. 2017). This implies that the changes in environmental factors were not strong enough to diversify the mid-embryonic phase of vertebrates, which, in turn, points to the possible contribution of intrinsic factors within the organisms. The fragility hypothesis of the mid-embryonic phase is consistent with this idea; due to inter-modular complex signaling networks between organ primordia, even subtle noise or perturbation leads to embryonic lethality and thus ends up in evolutionary conservation (Galis and Metz 2001; Raff 1996). However, the results of our previous study, which quantitatively measured the survival rates of vertebrate embryos under various perturbations, including UV irradiation, transcription, and translation inhibitors, showed that the early stages showed the highest rate of lethal phenotypes compared to the mid-embryonic phase, and it was inconsistent with the fragility hypothesis (Uchida et al. 2018). Another intrinsic factor behind the mid-embryonic conservation would be developmental constraints (Raff 1996). In this regard, Zalts et al. reported that during the conserved mid-embryonic phase in nematodes, the variations in gene expression were the smallest when under the near-absence of positive selection and proposed this as an evidence of developmental constraints (Zalts and Yanai 2017). This does not provide an actual mechanism of the constraints; however, it is possible that robustness of the mid-embryonic system contributes to the conservation through fluctuation–response relationship (Furusawa & Kaneko, 2006; 2015; 2018), which we will introduce in the next section. By performing a detailed analyses of conserved gene expression profiles of mid-embryonic stages in 8 chordate species, we also found a possible contribution of constraints for the mid-embryonic conservation (Hu et al. 2017). In brief, the conserved mid-embryonic phase was enriched with genes expressed in a variety of biological processes. These pleiotropically expressed genes showed higher lethality when mutated, and their products were predicted to have higher protein–protein interactions. Furthermore, pleiotropically expressed genes tended to show conserved expression levels between Xenopus frogs. These results indicate that different biological processes are “chained” or held together by sharing the same genetic system, and this could have led to evolutionary conservation through pleiotropic constraint (Galis 1999). Meanwhile, a major caveat of these constraint-related ideas is that they fail to offer an explanation on the actual mechanism that leads to evolutionary conservation. Pleiotropic constraint, for example, may explain the conservation effect on the gene body itself since mutations in the coding sequence would result in catastrophic effects on all the biological processes that utilize the gene. However, it does not provide an actual mechanism of how the expression levels of pleiotropic genes become conserved, as the modularity of gene regulatory elements may allow independent changes in the expression levels of different developmental processes (Hu et al. 2017). Furthermore, gene recruitment of existing genes or gene co-option is known to contribute to evolutionary novel traits (Carrol et al. 2005; Seki et al. 2017). Hence, pleiotropic expression or gene-recruitment may not always end up in constraint, it may have a double-edged effect toward evolutionary diversification. Altogether, further experimental studies are needed to test the presence of a constraint and to shed light on its mechanism. Based on previous studies, it would be worth studying the robustness of mid-embryonic stages in light of the fluctuation–response relationship.

Fig. 2.

Potential mechanism behind animal body plan conservation. In accordance with the prediction of the developmental hourglass model (Duboule 1994), body plan establishing, mid-embryonic stages (bottle-neck part of the hourglass) were persistently conserved through the vertebrate evolution. The nested hourglasses represent evolutionary diversity in the different evolutionary scales, implying that environmental factors are not powerful enough to diversify the mid-embryonic period. This conserved period was significantly enriched with genes having pleiotropic expressions (left, dark circles represent genes with temporarily and spatially pleiotropic expressions), suggesting that pleiotropic constraint contributed to the body plan conservation (Raff 1996)

Evolutionary fluctuation–response relationship

Several experimental studies, including those presented above, suggest the existence of constraints in adaptive evolution. The next challenge is understanding the detailed mechanisms of the constraints and the prediction of future evolution. The integration of experimental and theoretical approaches can play a significant role in this. Here, we briefly present a theoretical approach to sense and predict the evolutionary constraint, which is based on the relationship between phenotypic fluctuation and evolutionary response (Kaneko and Furusawa 2006, 2018; Sato et al. 2003)

Consider a system that can be characterized by parameter “a,” representing a genotype and phenotype X. Next, we evaluate the change in X by changing the parameter value from a to a+Δa. Here, the proposed fluctuation–response relationship is given by

$$\frac{{〈X〉}_{a+∆a}-{〈X〉}_a}{∆a}\propto 〈{\left(\mathit{\delta X}\right)}^2〉$$

where 〈X〉_a and 〈(δX)²〉 = 〈(X − 〈X〉)²〉_a are the average and variance of the phenotype for a given system parameterized by a, respectively. The relationship presented above was derived by assuming that the distribution P(X; a) is regarded as a Gaussian distribution, and the effect of the changing a on the phenotype is represented by bilinear coupling between X and a (for details of the derivation, see Sato et al. (2003))). For example, for the gene expression level of x, we used X = log x as the phenotype since the distribution of the expression level of x over an isogenic cell population is rather close to a log-normal distribution (Furusawa et al. 2005), and thus the distribution of log x approximately follows a Gaussian distribution. When parameter a can be regarded as characterizing the environmental condition and ∆a represents the environmental change, the above relationship implies that the proportionality between the response of the average phenotype to the environmental change is proportional to V_ip = 〈(δX)²〉, the variance of the phenotypic distribution under a given fixed environmental condition. That is, the responsiveness to environmental change is proportional to the fluctuation in phenotype.

On the other hand, if a represents the parameter that corresponds to the genotype and ∆a indicates the change of genotype by mutations, the relationship implies that the evolutionary rate, that is, the change in the average phenotype per generation, is proportional to V_ip, the phenotypic fluctuation in the isogenic population. In standard population genetics, the phenotypic variance due to genetic variation is represented by genetic variance V_g. In fact, the fundamental theorem of natural selection proposed by Fisher shows that the evolutionary rate is proportional to V_g (Fisher 1930). Thus, by assuming that the fundamental theorem and above relationship between fluctuation and response are true, it can be inferred that V_g and V_ip should proportionally change in evolutionary dynamics.

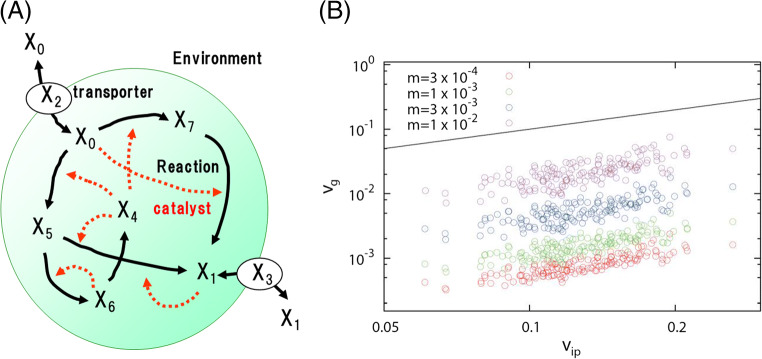
The relationship between the response to parameter change (environmental or genetic perturbation) and phenotypic fluctuation was examined by using the numerical simulation of a replicating cell model with a network of stochastic catalytic reactions (Fig. 3; Furusawa and Kaneko 2015). We confirmed that the above relationship is generally held in the cell model after the evolution has proceeded to achieve robust replicating dynamics. This relationship was also observed in the evolution of the gene-regulatory network model with on-off switching expression dynamics (Kaneko 2007). There is further experimental evidence for the above fluctuation–response relationship, including an artificial selection experiment of signal intensity of fluorescent proteins in E. coli (Sato et al. 2003), laboratory evolution of D. melanogaster (Stearns et al. 1995), and expression noise and mutational variance in yeast (Landry et al. 2007; Lehner and Kaneko 2011).

Fig. 3.

Evolutionary fluctuation-response relationship in replicating cell model. a Schematic representation of the replicating cell model. A cell has an intracellular catalytic reaction network, by which the amount of each chemical changes over time in a stochastic manner. The nutrient chemicals are transported into the cell with the aid of other chemical components (transporter). The cell will divide into two daughter cells when the total amount of chemicals in the cell exceeds a given threshold. b Relationship between V_ip and V_g. V_ip and V_gwere calculated based on the simulation results of randomly generated networks with various mutation rates m (the number of randomly replaced reaction paths divided by the total number of paths). The solid line is the y = x for the reference. Reproduced from (Furusawa and Kaneko 2015)

The mechanism for the emergence of the fluctuation–response relationship can be explained by the evolution of robustness to noise (Kaneko and Furusawa 2018). In general, complicated functions in biological systems, such as cell replication and development of multicellular organisms, are perturbed by stochastic noise as gene expression noise ubiquitous in the systems, which might result in non-fit states. Thus, to achieve a fitted state, evolutionary dynamics prefer robustness to stochastic noise, resulting in global attraction to the fitted state. Furthermore, genetic changes could also cause perturbations in such biological functions. Here, it can be expected that after the evolution of robustness to noise, the fitted state becomes less influenced by the perturbation due to genetic changes. Hence, through the course of evolution, the dynamics become more robust to noise, which results in the robustness of genetic changes. This is an intuitive explanation for the positive correlation between phenotypic noise and response to genetic mutations.

The fluctuation–response relationship provided a novel approach to analyze evolutionary constraints. This relationship means that a phenotype with higher variability in evolutionary dynamics tends to have larger fluctuations before evolution (Kaneko and Furusawa 2018). Thus, based on this relationship, we can predict the evolvability by measuring phenotypic fluctuations without directly analyzing evolutionary dynamics. This approach enables us to quantitatively assess the constraints and in long-term evolution by analyzing short-term phenotypic fluctuations.

Conclusion

In this review, we present recent studies on evolutionary constraints using both experimental and theoretical approaches. The analysis of large-scale phenotypic and genotypic data enables us to quantitatively assess the evolutionary constraints. Furthermore, the theoretical analysis presented above provides clues on the analyses of evolutionary constraints in long-term evolution, based on experimentally observable phenotypic fluctuations and environmental responses. Nonetheless, experimental evidence for the theoretical predictions is limited. Thus, to evaluate the universality of theoretical prediction and to elucidate the nature of evolutionary constraints, we need to further analyze various evolving systems from molecules, cells, and, finally, the complex anatomical traits or ecological level evolution. We believe that the integration of experimental and theoretical approaches will contribute to establishing a new theoretical framework to deal with evolutionary constraints.

Funding information

This work was supported by the Japan Society for the Promotion of Science (JSPS) [grant number 15H05746 (to CF)] and the Ministry of Education, Culture, Sports, Science and Technology (MEXT) [grant numbers 17H06389 (to CF) and 17H06387 (to NI)].