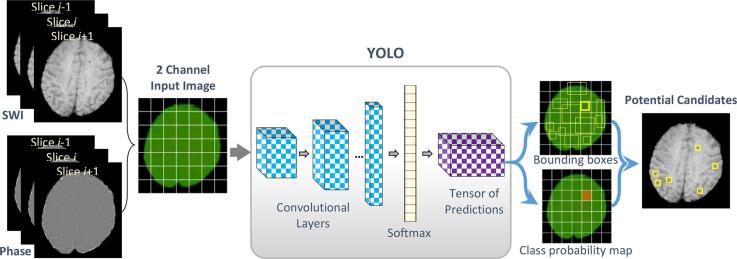
Graphical abstract
Keywords: Cerebral microbleeds, Computer-aided detection, Deep learning, CNNs, YOLO, Susceptibility-weighted imaging
Highlights
-
•
A new two-stage deep learning approach for efficient microbleeds detection is proposed.
-
•
1st stage detects potential microbleeds candidates, while 2nd stage reduces false positives.
-
•
A sensitivity of 93.62% is achieved via 1st stage using high in-plane resolution data.
-
•
The average number of false positives per subject is reduced to 1.42 in the 2nd stage.
-
•
A validation of using low in-plane resolution data is performed as well.
Abstract
Cerebral Microbleeds (CMBs) are small chronic brain hemorrhages, which have been considered as diagnostic indicators for different cerebrovascular diseases including stroke, dysfunction, dementia, and cognitive impairment. However, automated detection and identification of CMBs in Magnetic Resonance (MR) images is a very challenging task due to their wide distribution throughout the brain, small sizes, and the high degree of visual similarity between CMBs and CMB mimics such as calcifications, irons, and veins. In this paper, we propose a fully automated two-stage integrated deep learning approach for efficient CMBs detection, which combines a regional-based You Only Look Once (YOLO) stage for potential CMBs candidate detection and three-dimensional convolutional neural networks (3D-CNN) stage for false positives reduction. Both stages are conducted using the 3D contextual information of microbleeds from the MR susceptibility-weighted imaging (SWI) and phase images. However, we average the adjacent slices of SWI and complement the phase images independently and utilize them as a two-channel input for the regional-based YOLO method. This enables YOLO to learn more reliable and representative hierarchal features and hence achieve better detection performance. The proposed work was independently trained and evaluated using high and low in-plane resolution data, which contained 72 subjects with 188 CMBs and 107 subjects with 572 CMBs, respectively. The results in the first stage show that the proposed regional-based YOLO efficiently detected the CMBs with an overall sensitivity of 93.62% and 78.85% and an average number of false positives per subject () of 52.18 and 155.50 throughout the five-folds cross-validation for both the high and low in-plane resolution data, respectively. These findings outperformed results by previously utilized techniques such as 3D fast radial symmetry transform, producing fewer and lower computational cost. The 3D-CNN based second stage further improved the detection performance by reducing the to 1.42 and 1.89 for the high and low in-plane resolution data, respectively. The outcomes of this work might provide useful guidelines towards applying deep learning algorithms for automatic CMBs detection.
1. Introduction
Cerebral Microbleeds (CMBs) are small foci of chronic brain hemorrhages that are generated by structural malformation of the small blood vessels and the deposits of blood products. CMBs have a high prevalence in several populations, including healthy elderlies (Martinez-Ramirez et al., 2014). It is observed that CMBs may cause a high risk of future intracranial hemorrhage and can be a biomarker for cerebral amyloid angiopathy and cerebral small-vessel diseases. Besides, the presence of microbleeds could increase the possible clinical implications of ischemic stroke, traumatic brain injury, and Alzheimer’s diseases. Indeed, direct pathological observations have also revealed that CMBs bring about damage to the surrounding brain tissue, which cause dysfunction, dementia, and cognitive impairment (Koennecke, 2006, Charidimou et al., 2013). Therefore, accurate differentiation of CMBs from different suspicious regions (i.e., CMB mimics) such as calcifications, irons, and veins is important for proper diagnosis and appropriate treatment.
Currently, Computed Tomography (CT) and Magnetic Resonance (MR) imaging technologies are the most reliable screening modalities used for CMBs or hemorrhages identification. In clinical practice, MR imaging specifically with the modern advances of using gradient-echo (GRE) and susceptibility-weighted imaging (SWI) is usually preferred over CT imaging due to the ionization radiation effect by CT scanner (Chen et al., 2014). According to the theory of brain tissue magnetic susceptibility, MR imaging could assist in differentiating between paramagnetic hemorrhages and diamagnetic calcifications. Thence, the paramagnetic blood products (i.e., CMBs) are highly sensitive to screening in SWI, producing small spherical regions with hypointensities (Chen et al., 2014). Although SWI improves the identification of CMBs, visual inspection by neuroradiologists is still time-consuming, fault-prone, laborious, and subjective. Actually, a tradeoff between true positive detection rates (TPR) and number of false positives (FPs) has been recognized during the CMBs identification process. Therefore, a need of the second reader either via other expert or automated computer-aided detection (CAD) is demanded for further improving the efficiency of microbleeds detection assessment. However, automated detection of CMBs is a challenging task due to the large variation among the CMBs locations in the brain, their small sizes, and the presence of CMB mimics such as calcifications (Charidimou and Werring, 2011, Charidimou et al., 2013).
The past decade has witnessed numerous investigations and attempts to solving this challenging task. Early studies have applied low-level hand-crafted features to differentiate between CMBs and CMB mimics, including size, geometrical information, and voxel intensity. A semi-automated detection method based on the statistical thresholding technique and support vector machine (SVM) is proposed to distinguish the true CMBs from hypointensities within SWI image (Barnes et al., 2011). Authors in (Bian et al., 2013) developed a semi-automated detection method that employed a two-dimensional fast radial symmetry transform (2D-FRST) algorithm on minimum intensity projected SWI to detect putative CMBs. Furthermore, the work in (Kuijf et al., 2012) applied a 3D version of FRST on 7.0 T MR images to derive 3D contextual information of microbleeds for further enhancement of detection performance. Their method achieved a sensitivity of 71.2%, while the FPs were censored manually. In fact, these studies required a user-intervention that manually eliminate the false positives.
The main shortcoming of the aforementioned conventional methods is associated with the limitations of utilizing the engineering features (i.e., designed or hand-crafted features). Recently, supervised deep learning convolutional neural networks (CNNs) have gained a lot of attention in various medical imaging applications, including brain, breast, lung, and skin cancers detection (Al-masni et al., 2018b), classification (Al-Antari et al., 2018, Masood et al., 2018), segmentation (Al-Masni et al., 2018a, Zhao et al., 2018, Chen et al., 2018) as well as in the detection of CMBs. This is due to the capability of CNNs in learning and extracting robust and effective hierarchy features, which lead to significant improvement of detection performance. In fact, most of the recent works on automatic detection of CMBs were accomplished in a two-cascaded framework; detection stage for potential candidate revelation and classification or discrimination stage for FPs reduction (Dou et al., 2016, Chen et al., 2019, Wang et al., 2019). A two-stage CNN for automatic detection of CMBs is proposed using SWI images (Dou et al., 2016). They exploited the 3D fully convolutional network (3D-FCN) followed by 3D-CNN as screening stage and discrimination stage, respectively. Their cascaded network achieved a sensitivity or TPR of 93.16%, a precision of 44.31%, and an average number of FPs per subject () of 2.74. More recently, Liu et al. developed a 3D-FRST for candidate detection stage using SWI images and 3D deep learning residual network (3D-ResNet) for the FPs reduction stage using both SWI and phase images (Liu et al., 2019). This framework obtained a sensitivity of 95.80%, a precision of 70.90%, and an of 1.6. Similar work was proposed by Chen et al., which integrated 2D-FRST (Bian et al., 2013) and 3D-ResNet using 7.0 T SWI images (Chen et al., 2019). The detection performance of CMBs was improved over using only the 2D-FRST and achieved a sensitivity, precision, and of 94.69%, 71.98%, and 11.58, respectively. In 2019, Wang et al. employed the 2D densely connected neural network (2D-DenseNet) for detection of the CMBs (Wang et al., 2019). They dispensed the candidate detection stage by using a sliding window over the entire MR image and achieved higher performance with overall sensitivity of 97.78% and classification accuracy of 97.71%. Similarly, Hong et al. adapted the 2D-ResNet-50 for distinguishing the 2D CMBs patches retrieved by the sliding window from the non-CMBs, achieving a sensitivity of 95.71% and an accuracy of 97.46% (Hong et al., 2019). However, utilizing a 2D sliding window strategy over the whole 3D MR volume per subject requires high computational burden and large execution time. For example, if we consider the detection of lesions from a data with a size of 512 × 448 × 72 voxels (as the case of this study), over 16 million 2D patches have to be extracted in a pixel-wise manner. It is of note that all the above studies have utilized high-resolution images with an in-plane resolution of about 0.45 × 0.45 . Although this high-resolution data is preferred for more accurate CMBs detection either by expert physicians or computer-aided detection algorithms, it is not practically used in routine clinical exams due to lengthened scan time.
In this paper, we present a new two-stage integrated deep learning approach for automatic CMBs detection. In the first stage, a regional-based CNN method based on You Only Look Once (YOLO) is proposed for detecting potential CMBs candidates. Then, a 3D-CNN is designed for distinguishing the true CMBs from challenging mimics and hence reducing the FPs. Both stages are conducted using the 3D contextual information from the MR SWI and phase images. It is noteworthy that the proposed deep learning regional-based YOLO method (i.e., candidate detection stage) outperforms the commonly utilized FRST strategy and achieves superior detection performance in terms of sensitivity and with a lower computational cost. This is due to that YOLO directly learns the spatial contextual features of input MR images during the training process.
The contributions of this paper are summarized as follows: 1) we develop a completely integrated deep learning method for efficient CMBs identification throughout a combination of the regional-based YOLO utilized for CMBs candidate detection and 3D-CNN used for FPs reduction. 2) For the first time, we address using low in-plane resolution MR data besides the high-resolution images with in-plane resolution of 0.80 × 0.80 mm and 0.50 × 0.50 mm, respectively, which makes the proposed work more applicable for practical clinical usage. 3) For the first stage, we average the adjacent slices of SWI and complement phase images independently and utilize them as a two-channel input for regional-based YOLO method. These settings enable YOLO to learn more reliable and representative hierarchal features and hence achieve better detection performance compared to the using of only one-channel image. In the same context, the input of 3D-CNN stage is small 3D patches including both original SWI and phase images. 4) We make the utilized dataset along with the ground-truth labels available for researchers for further improvement and investigations through this link: https://github.com/Yonsei-MILab/Cerebral-Microbleeds-Detection.
The rest of this paper proceeds as follows. Section 2 explains in detail the proposed deep learning two-stage approach. Experimental results of both stages are drawn in Section 3. Discussion of the findings and comparison against the recent studies are presented in Section 4. Finally, we present the conclusions in Section 5.
2. Materials and methods
2.1. Proposed deep learning architecture
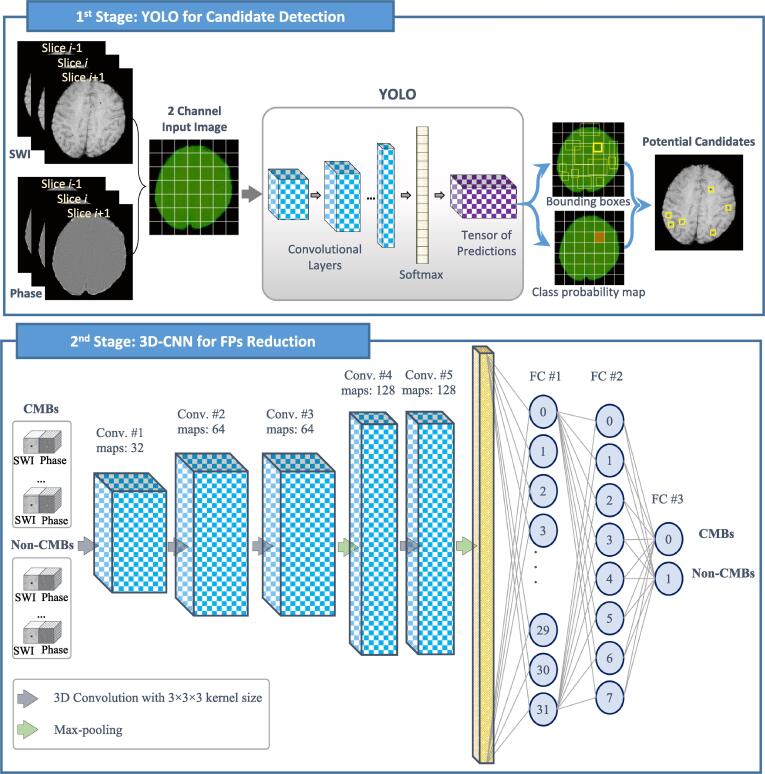
The proposed deep learning two-stage approach for CMBs detection integrates a regional-based YOLO for potential candidate detection and a 3D-CNN for discrimination of actual CMBs from putative false positives. The locations information of suspicious regions that may include microbleeds is first determined via the regional-based YOLO, which provides multiple bounding boxes associated with confidence scores for all sub-regions of input MR images. Then, all these predicted candidates, which represent CMBs and CMB mimics, are cropped in small 3D patches and passed into the 3D-CNN stage to reduce the FPs. An overview diagram of the proposed work is illustrated in Fig. 1.
Fig. 1.
Overview diagram of the proposed two-stage deep learning approach.
2.1.1. First stage: regional-based YOLO for candidates detection
You Only Look Once (YOLO) is one of the recent regional deep learning CNN techniques that originated for object detection in the images. It is able to simultaneously detect the locations of objects in the input images and classify them into different categories. Unlike the conventional R-CNN (Girshick et al., 2014) and Fast-RCNN (Girshick, 2015) that applied classification network to several proposal regions within an image and hence required expensive computational cost and also be hard to optimize, YOLO proceeds both detection and classification tasks utilizing a single convolutional network as a regression problem, which provides bounding boxes’ coordinates along with their class predictions. Thus, YOLO is able to encode the global contextual information via looking into the entire input image only once. In fact, the regional-based YOLO technique has achieved successes in computer vision tasks and widely utilized in medical applications such as lung nodules (Sindhu et al., 2018), breast abnormalities (Al-Masni et al., 2018b, Al-Masni et al., 2017), and lymphocytes detection (Rijthoven et al., 2018). The following paragraphs summarize the principal concepts of YOLO, however, more technical details exist in the original papers (Redmon et al., 2016, Redmon and Farhadi, 2017).
The input composite MR image is divided into non-overlapped grid cells, where in this work. For each microbleed presented on the input image, only one grid cell is responsible to detect it. In the end, each grid cell is represented by bounding boxes known as anchors associated with five components: . The () represent the center location coordinates of CMB in the MR image, while the reflects the probability of the presence of microbleeds within a certain and from the center location. In other words, could be defined as an intersection over union (IOU) between the predicted boxes by YOLO and the ground-truth labels by neuroradiologists. Consider, if there are no microbleeds in a particular grid cell, then, the scores of the bounding boxes of that cell should be zero. The () coordinates, and are normalized relative to the size of the MR image to [0, 1].
In this paper, we employed YOLOv2 for more accurate detection of CMBs from brain images (Redmon and Farhadi, 2017). This version of YOLO adds a variety of ideas to the initial YOLO for better detection results and faster performance, including batch normalization, fine-tuning with high-resolution network, using anchor boxes, multi-scale training, and pass-through layer concatenation. The configuration of the utilized regional-based YOLO consists of 23 convolutional layers with kernel sizes of and various feature maps; and five max-pooling layers with sizes of and strides of two. Convolutional layer with a kernel size of is placed between every two sequential convolutional layers with a kernel size of . This operation is inspired by GoogleNet (Inception) model (Szegedy et al., 2015) and known as the bottleneck layer. It fastens the computations through feature maps reduction. The sub-sampling layers shrink the input MR brain image by a factor of 32 () from into pixels. Further, each convolutional layer is followed by batch normalization and leaky activation function except the last convolutional layer, which is followed by a linear activation function. By taking the advantages of residual networks (He et al., 2016), the presented regional-based YOLO adds a pass-through layer that concatenates the higher resolution features from early layers with the low-resolution features. The number of features of the last convolutional layer should be computed as follows:
| (1) |
where and refer to the number of anchors and classes, respectively. In our case, we have chosen to retrieve most possible bounding boxes associated to different aspect ratios that may contain microbleeds. Since we have trained this stage using only one class (i.e., CMBs), we set . Thus, the last convolutional layer has a number of features equals to 30. Finally, a multimodal logistic regression layer, softmax classifier, is placed at the top of the network to produce a tensor of predictions, containing the detected bounding boxes information and the predicted class. During training, regional-based YOLO optimizes the network by minimizing the loss function computed as a relation with the ground-truth and predicted bounding boxes. The designed loss function is computed as an aggregation of four parts related to the coordinates (), and , scores, and classification loss of the detected bounding boxes and ground-truth. This work is conducted using a batch size of 64, learning rate and decay of 0.0005, and a momentum of 0.9. The complete configuration with source code is available online here (Redmon and Farhadi).
In this paper, we input a composite image consisting of MR SWI and the complement of phase images as a two-channel input image to the regional-based YOLO. In order to address the 3D contextual information of microbleeds, we independently average the adjacent slices of both channels. Different combinations of input format to the candidate detection stage have been investigated in Section 3.1.1. Moreover, we inspect training the proposed regional-based YOLO using high in-plane resolution (HR) and low in-plane resolution (LR) data. This investigation provides a glimmer of hope towards the possibility of using the LR data practically for CMBs detection in actual clinical settings. Related to this, more details exist in Section 3.1.2.
At the end of this stage, we receive the locations of the detected bounding boxes from those having high confidence score and then, we deliver all these locations, including CMBs and non-CMBs, with an integrating of both 3D small patches from SWI and phase images to the 3D-CNN discrimination stage for further reduction of FPs.
2.1.2. Second Stage: 3D-CNN for FPs reduction
As an integration with the potential candidate detection stage, the second stage is designed to robustly reveal the positive samples (i.e., CMBs) from a large number of negative samples (i.e., CMB mimics) as a classification task. The input to this stage is 3D cropped regions around the center position of the detected bounding boxes associated with higher confidence scores via regional-based YOLO. As successfully applied in (Liu et al., 2019), we exploit training the proposed 3D-CNN using both SWI and phase images with sizes of voxels for each. Thus, the 3D-CNN stage is able to learn richer contextual spatial representations of CMBs from 3D training samples with sizes of voxels. The input size is chosen to be large enough to include the microbleeds and limit the computational workload.
The structure of the proposed 3D-CNN contains five convolutional layers with kernel sizes of and two max-pooling layers with sizes of and strides of two. To increase the stability of the network and speed up the learning process, each convolutional layer is appended by batch normalization and rectified linear unit (ReLU) activation function. Then, the extracted features from these convolutional layers are flattened and passed into three fully-connected (FC) layers. The number of units or neurons of the last FC layer is assigned to the number of classes in our task, which represents the CMBs and Non-CMBs. Additionally, one dropout layer is utilized after the first FC layer to regularize and prevent networks from overfitting. This network is trained using learning rate, batch size, and number of epochs equals to 0.001, 50, and 200. Structural details are presented in Fig. 1. It is noteworthy that to avoid the overfitting that may occur during training the high imbalanced training samples at this stage, a non-complicated network should be utilized besides the using of dropout, weighted-class, and data augmentation strategies. Hence, we implemented a non-complicated 3D-CNN to accomplish the second stage instead of adapting the well-known ResNet or DenseNet. As overall, the proposed 3D-CNN contains five convolutional layers and three FC layers with 1,355,450 trainable parameters.
2.2. Dataset
2.2.1. Original dataset
To evaluate the proposed two-stage deep learning approach for CMBs detection, we have collected a set of MR brain volumes at Gachon University Gil Medical Center. Human data acquisition was performed in accordance with the relevant regulations and guidelines. Written informed consent was obtained from all participants and the study was approved by Institutional Review Board of Gachon University Gil Medical Center.The dataset used in this work existed of two in-plane resolutions; high-resolution (HR) with 0.50 × 0.50 and low-resolution (LR) with 0.80 × 0.80 . Data was acquired using 3.0 T Verio and Skyra Siemens MRI scanners (Siemens Healthineers, Germany). For HR data, a total of 72 subjects including 188 microbleeds were collected with the following imaging parameters: repetition time (TR) of 27 ms, echo time (TE) of 20 ms, flip angle (FA) of 15°, pixel bandwidth (BW) of 120 Hz/pixel, image matrix size of 512 × 448 × 72 voxels, slice thickness of 2 mm, field of view (FOV) of 256 × 224, and scan time of 4.45 min. In addition, a total of 107 subjects including 572 microbleeds were acquired for LR data with the following parameters: TR of 40, TE of 13.7, FA of 15°, BW of 120 Hz/pixel, image matrix size of 288 × 252 × 72 voxels, slice thickness of 2 mm, FOV of 201 × 229 , and scan time of 1.62 min.
To properly train and test the proposed deep learning detection framework, the dataset was split, on the subject-level instead of image-level that contains microbleeds, into five-folds. Table 1 summarizes the distribution of the utilized dataset throughout five-folds. This division is utilized for the generation of the training, validation, and testing sets as described in Section 2.4. It is of note that this division was applied on both the candidate detection stage via regional-based YOLO and the FPs reduction stage via 3D-CNN.
Table 1.
Distribution of dataset throughout five-folds.
| Fold |
HR Data |
LR Data |
Total |
|||
|---|---|---|---|---|---|---|
| Subjects | CMBs | Subjects | CMBs | Subjects | CMBs | |
| Fold 1 | 14 | 36 | 21 | 143 | 35 | 179 |
| Fold 2 | 14 | 28 | 21 | 101 | 35 | 129 |
| Fold 3 | 14 | 40 | 21 | 68 | 35 | 108 |
| Fold 4 | 14 | 36 | 21 | 134 | 35 | 170 |
| Fold 5 | 16 | 48 | 23 | 126 | 39 | 174 |
| Total | 72 | 188 | 107 | 572 | 179 | 760 |
2.2.2. Ground-truth labeling
Expert neuroradiologist with 24 years of experience and a neurologist with 15 years of experience reviewed the images together, where the gold standard was obtained based on the consensus of all the raters. The gold standard labeling of CMBs was performed by expert neuroradiologists using both the pre-processed SWI and phase images. This process was accomplished using our in-house software developed by Matlab 2019a (MathWorks Inc., Natick, MA, USA). The neuroradiologists were able to simultaneously examine the axial plane of the SWI and phase brain images of the same subject. Once the microbleeds were assigned, the locations information with the slice numbers were derived. This manual annotation was performed by determining the central position of microbleeds in MR image. Then, we adjusted a small bounding box around each labeled microbleeds with a size of 20 × 20 pixels as a requirement of the first stage YOLO detector. The labeling was performed according to the criteria proposed by (Greenberg et al., 2009). CMB were defined as =<10 mm in diameter and was discriminated from calcification using phase images.
2.3. Pre-Processing and augmentation
Image pre-processing is a prerequisite step in most MR applications. In this work, data normalization, brain region extraction, and SWI generation were applied. In order to increase the consistency among the input intensities, all input slices of each subject were normalized in range 0 to 1 as follows:
| (2) |
where , , , and refer to the original, normalized, minimum, and maximum pixel intensities. Moreover, we applied the fast, robust, and automated brain extraction tool (BET) on the MR magnitude images to segment the head into brain and non-brain (Smith, 2002). The generated binary mask of brain tissue via BET is then applied to the MR SWI and phase images. This process enables computer-aided detection algorithms to avoid getting more incorrect candidates of CMBs located outer the brain tissue region (i.e., over the skull region). Fig. 2 shows some examples of the segmented brain tissue on both HR and LR MR SWI images. For SWI generation, magnitude and unwrapped phase images are required. The process starts by generating a phase mask from the unwrapped phase image, which linearly scales negative phase values (i.e., amplitudes) between zero and unity. Then, the final SWI is produced by multiplying the original magnitude image few times with the corresponding phase mask (Haacke et al., 2004). Furthermore, for the input of the regional-based YOLO stage, HR images were resized into 448 × 448 pixels by eliminating 64 zero rows from the top and bottom of the HR data, while the LR images were scaled into 448 × 448 pixels using bilinear interpolation. Regarding the 3D-CNN stage, the input of 16 × 16 × 16 voxels from each SWI and phase images was captured from the original data.
Fig. 2.
Examples of brain tissue extraction via BET on both high and low in-plane resolution data appeared on first and second rows, respectively. Every sample is extracted from a different subject. White contours indicate the boundaries of brain mask generated by BET, while small green boxes refer to the locations of microbleeds assigned by radiologists. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
For appropriate training of deep learning networks and overcoming the issue of insufficient training data, we applied the augmentation process to enlarge the training samples in both proposed stages. This process included rotation operation of input images that contains CMBs four times with angles of 0°, 90°, 180°, and 270°. In addition, we applied horizontal and vertical flipping to the rotated images with angles of 0° and 270°. Thus, a total of eight 2D images were generated for each training data in the regional-based YOLO stage. These augmentation processes were also applied to the 3D input data of the 3D-CNN stage and repeated three times along with the three directions (i.e., axial, sagittal, and coronal). Therefore, 24 3D samples were generated for each training data in the 3D-CNN stage.
2.4. Training and testing
In this study, the proposed deep learning two-stage approach proceeded using a k-fold cross-validation (k = 5) to increase the reliability and effectiveness of the proposed work and reduce the bias error. To this end, our data was randomly split into five subsets based on the subject-level with almost equal number of subjects as presented in Table 1. Then, we consider one subset as a testing set, while the remaining four subsets were utilized as training and validation sets. This process is repeated k times to involve all subsets as testing. For each k-fold, the proposed networks of the candidate detection stage and FPs reduction stage should be trained, validated, and tested using separate sets. The training set is utilized to train the networks with different hyper-parameters. However, the network optimization and final model evaluation were independently performed using the validation and testing sets, respectively. Since the proposed work is kind of supervised learning which only requires the ground-truth labeling at the training time, it can be considered as a fully automated approach. However, at testing time, the input data is only passed into networks to obtain predictions without the need of ground-truth. Nevertheless, we utilized the ground-truth of testing data for overall performance evaluation.
The system implementation was performed on a personal computer equipped with a GPU of NVIDIA GeForce GTX 1080 Ti. The regional-based YOLO stage was conducted using C++ programming language on the Darknet framework, while the 3D-CNN stage was implemented with Python programming language using Keras and Tensorflow backend.
2.5. Evaluation metrics
To quantitatively evaluate the capability of the proposed deep learning two-stage approach for CMBs detection, we computed the following evaluation indices. Sensitivity, also known as the true positive rate (TPR), computes the ratio of CMBs that are correctly detected. Precision, also known as the positive predictive value (PPV), indicates the proportion of the accurately detected CMBs from all cases that detected as CMBs (i.e., from all positive detected cases). F1-score is utilized since it is preferred when dealing with imbalanced data. It is defined as a harmonic mean between PPV and TPR. We also used the average number of false positives per subjects (). All these metrics could be defined mathematically as follows.
| (3) |
| (4) |
| (5) |
| (6) |
where TP and FN are the actual positive cases named as true positive and false negative; FP and TN are the actual negative cases defined as false positive and true negative, respectively. N refers to the number of subjects in the testing set. The detection performance of the first stage YOLO detector was computed as the overlap between the automatically resulted bounding boxes via YOLO and the manually ground-truth annotation boxes with intersection over union (IOU) of greater than 80%. Since the size of boxes would affect the metrics, we determined all the ground-truth boxes by 20 × 20 pixels. Thus, when YOLO was trained using this size information, it produced a similar box size.
3. Experimental results
3.1. Experimental setup
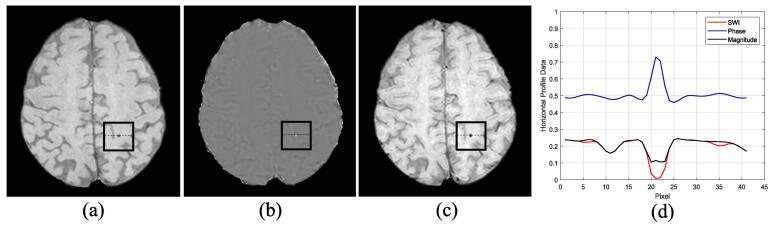
Several attempts and investigations for selecting proper input along with training the regional-based YOLO network using different resolution data were tested. All the experiments in the following subsections were evaluated using the first fold test on the CMBs candidate detection stage with a confidence score equals to 0.01. The reason of performing the experiments using only the first fold test is to check how efficient are the designed experiments. After the verification of different setups, the best scenario was utilized to test and analyze the results over all the five folds. All the obtained results throughout these experiments were achieved with tuned deep learning hyper-parameters such as learning rate, batch size, and number of epochs. All these hyper-parameters have been fixed for all k-folds. In this experiment, we generated different input combinations from the original magnitude, high-pass filtered phase and SWI images as shown in Fig. 3 (a), (b), and (c), respectively. The use of different images was motivated by the fact that clinical radiologists also use these various images when diagnosing CMB (e.g. to differentiate between CMB and calcification).
Fig. 3.
Criteria of selecting proper input data throughout various combinations of (a) magnitude, (b) phase, and (c) SWI images. (d) Horizontal profile lines of the original magnitude, phase, and SWI images generated from black boxes.
3.1.1. Experiments on proper composite input data
In this section, all experiments were trained and tested using the HR data.
3.1.1.1. One-Channel: SWI image
We first examined the performance of the regional-based YOLO using an MR input image containing only single channel of the HR SWI image. The input image can be represented as follows.
| (7) |
where is the channel number of input image and refers to the slice number that involved microbleeds. SWI images are known to display blood products such as microbleeds with high sensitivity when screening. Fig. 3 (d) shows the line profile of the SWI, phase and magnitude images over a CMB which partially explains performance of the different combinations. Thus, training network using SWI images provided good CMBs detection sensitivity of 91.67% and of 23.57 as presented in Table 2.
Table 2.
Performance of regional-based YOLO on different HR inputs throughout first fold test.
| Number of Channels | Input Image | Complement* | Averaging of Adjacent Slices | Sensitivity (%) | |
|---|---|---|---|---|---|
| One-Channel | SWI | × | × | 91.67 | 23.57 |
| Two-Channels | SWI and Phase | × | × | 97.22 | 275.50 |
| Three-Channels | SWI, Phase, and Magnitude | × | × | 88.89 | 69.50 |
| Two-Channels | SWI and Phase | ✓ | × | 94.44 | 56.44 |
| Two-Channels | SWI and Phase | ✓ | ✓ | 100.00 | 53.71 |
Complement is applied to the phase image.
3.1.1.2. Two-Channels: SWI and phase images
Here, we investigated the significance of using phase image besides the SWI. The input image has two channels, including SWI and phase images as follows.
| (8) |
The detection performance using this input composite image (i.e., SWI and Phase) was improved in term of sensitivity to 97.22% compared to the case of using only one-channel of SWI. However, the overall was declined generating more false positives of 275.50 as shown in Table 2. This is due to that the overall visualization of microbleeds can be portrayed as being blurred when the input integrates the low intensities from SWI (red line in Fig. 3 (d)) and high intensities from phase image (blue line in Fig. 3 (d)) in regions containing microbleeds. If the input image consists of multi-channel, the filter at the first convolutional layer should have the same number of channels. Then, convolution is performed as a pixel-wise dot product for all channels producing a single channel output. This aggregation could be the reason behind extracting insufficient features in the case of using SWI and phase images. More specifically, the contrast the composite input of SWI and phase at the microbleeds regions is deteriorated due to that the convolution process on an image of two-channels with opposite intensities (i.e., hypointensity on SWI and hyperintensity on phase image) may accumulate them, leading to obtain a larger number of FPs. Another explanation could be due to that the optimization algorithm gets stuck in some local minimum.
3.1.1.3. Three-Channels: SWI, Phase, and magnitude images
Here, three-channels input image is composed as follows.
| (9) |
As presented in Table 2, the detection performance of the regional-based YOLO decreased with a sensitivity of 88.89%. Even though this composite input enhanced the measure with 69.50 FPs per subject compared to the 275.50 FPs that were generated in the previous trial. As shown in Fig. 3 (d), the information generated from the magnitude image is not beneficial since similar and clearer data could be exploited from SWI images. The tradeoff between sensitivity and motivates to think of generating more effective composite input without the need of adding the magnitude information.
3.1.1.4. Two-Channels: SWI and complement phase images
To overcome the problem of 3.1.1.2 due to the integration of hypointensities from SWI and hyperintensities from phase images in the microbleeds locations, here usage of the complement phase image along with the original SWI image is described in the following expression.
| (10) |
It is of note that both SWI and phase images were normalized in the range of 0 to 1. This composite input enables the candidate detection network to be trained more effectively since it becomes more intelligible. The detection performance was improved in terms of sensitivity and with 94.44% and 56.44, respectively.
3.1.1.5. Two-Channels: Average of adjacent slices of SWI and complement phase images
Finally, we examined using 3D contextual information by averaging the adjacent slices of SWI and complement phase images as follows.
| (11) |
This combination input enables using addition details of microbleeds from adjacent slices. The results given in Table 2 shows the detection of CMBs was achieved with a sensitivity of 100% and of 53.71 cases. Because of this increased sensitivity, the following studies were implemented using this input channels.
3.1.2. Experiments on different In-Plane resolutions
3.1.2.1. HR data
In this section, we trained and tested the effect of training the proposed regional-based YOLO using only the HR data (i.e., 0.5 × 0.5 ). As presented in Table 3, the detection performance shows that using the HR data plays a critical role in obtaining higher true positive cases with a sensitivity of 100% as well as fewer number of false positives with a of 53.71 cases throughout the first fold test.
Table 3.
Performance of regional-based YOLO on various in-plane resolution throughout the first fold test.
| In-Plane Resolution | Sensitivity (%) | |
|---|---|---|
| High-Resolution (HR) | 100.00 | 53.71 |
| Low-Resolution (LR) | 83.22 | 683.0 |
| Combinations of HR and LR | 91.62 | 479.17 |
3.1.2.2. LR data
Here, we investigated the impact of training and testing the candidate detection stage using only the LR data (i.e., 0.80 × 0.80 ). As expected, the regional-based YOLO network encounters difficulty to learn more representative features of microbleeds from the LR data, which causes a drop of the detection performance, achieving a sensitivity of 83.22%. Moreover, the number of false positives was dramatically increased to 683 candidates per subject (Table 3). This decline of performance is due to that most of the CMBs in the LR data are not clearly appeared and also considered as challenging cases for radiologists.
3.1.2.3. Combination of HR and LR data
In this experiment, we trained and tested the proposed detection stage using a dataset contains both HR and LR data. When training the proposed candidate detection stage using the combination of high and low in-resolution data, the overall detection performance of the regional-based YOLO throughout the first fold test achieves a sensitivity of 91.62% and a of 479.17 as shown in Table 3. These results are extremely close to the weighted average performance of HR and LR cases. Accordingly, training the deep learning networks using these combinations of different in-plane resolutions affects directly the overall performance and specifically on the case of using HR data, which leads to generating a high number of false positives. Therefore, this type of heterogeneous training using different in-plane resolution data is not preferred.
3.2. Performance of CMBs detection via regional-based YOLO (1st Stage)
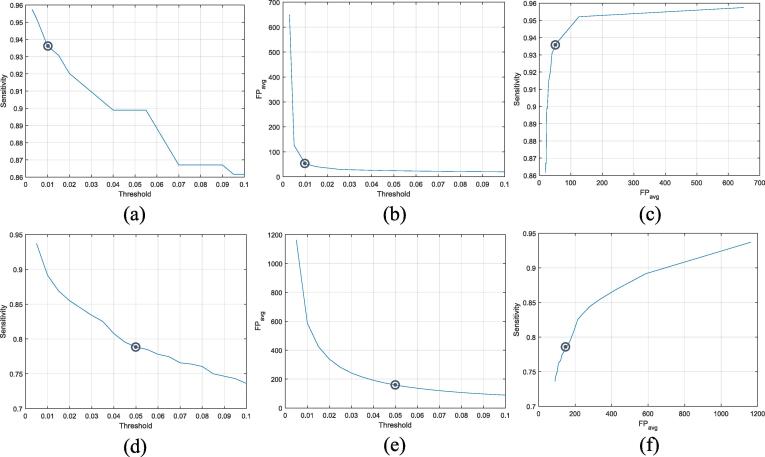
This section analyzes the performance of CMBs candidate detection via the proposed regional-based YOLO technique. As aforementioned, the potential candidates of microbleeds generated by YOLO are associated with confidence scores. However, determining proper threshold of the confidence score is a critical issue since it directly affects the detection performance. The higher the confidence, the lower detection sensitivity of microbleeds and the lower number of potential candidates. The effectiveness of the confidence score threshold on both sensitivity and throughout all five-folds test is presented in Fig. 4 (a), (b), and (c) for the HR data and Fig. 4 (d), (e), and (f) for the LR data. Larger number of bounding boxes candidates are generated in the case of applying small confidence score. As a result, different threshold values of 0.01 and 0.05 have been carefully chosen for the HR and LR data, respectively. These threshold values provide reasonable tradeoff between false positive candidates and detectable CMBs. Even though applying a single threshold could achieve good performance and provide generalization throughout all the five-folds, selecting the threshold based on looking at its effect on the performance in the test set may cause overfitting. It is true that with these thresholds we achieved not very high sensitivity but at the same time not too many . This is because we have a limited size of labeled data, including only 188 CMBs in the case of HR data. Then, if we lower the threshold, a large number of FPs will be generated causing very high imbalanced training samples (i.e., CMBs vs Non-CMBs), leading to cause overfitting problem during the network training.
Fig. 4.
Impact of the confidence score threshold on the detection performance of the proposed regional-based YOLO throughout all five-folds test. (a) and (d) Sensitivity versus threshold. (b) and (e) versus threshold. (c) and (f) Sensitivity versus . The top row is for the HR data, while the second row is for the LR data.
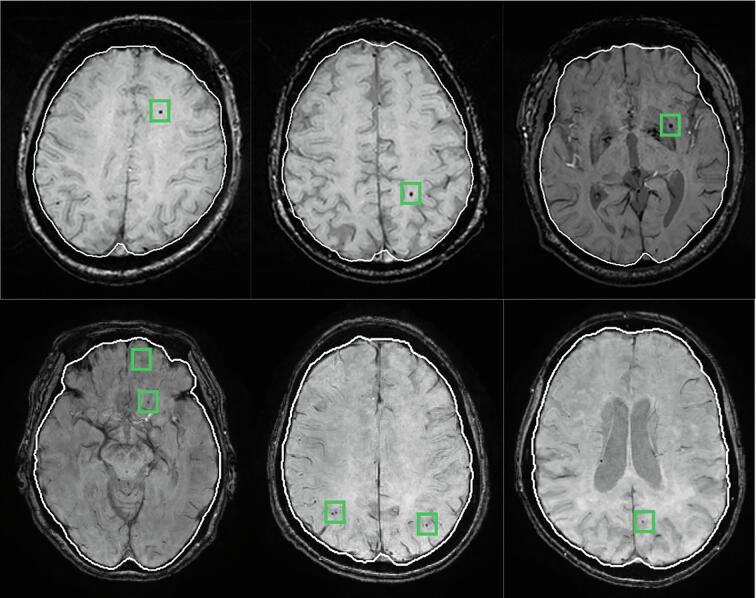
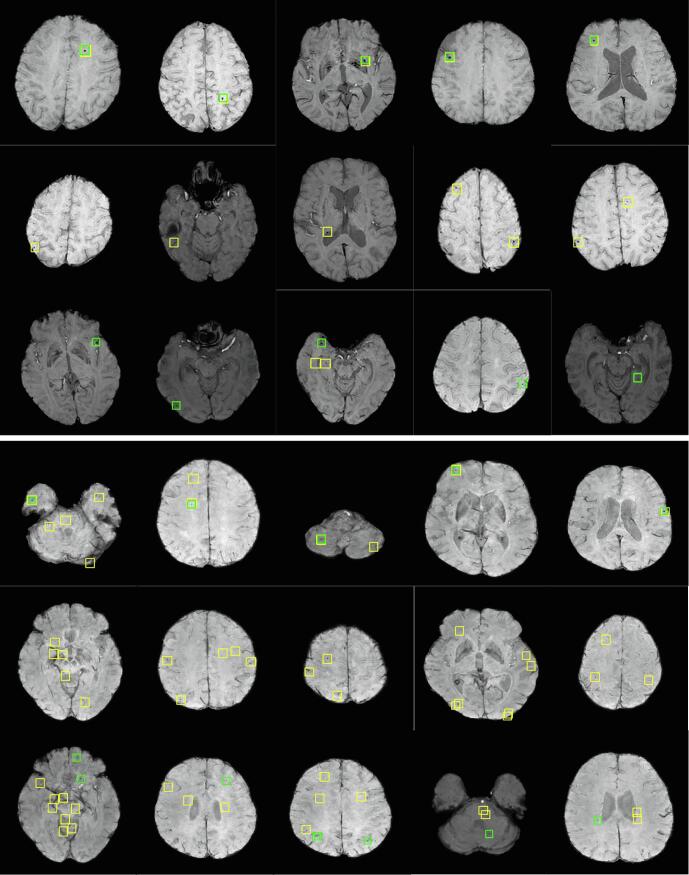
For quantitative assessment, we present the overall candidate detection performance of the proposed regional-based YOLO technique throughout all five-folds test in Table 4. For HR data, the proposed candidate detection network achieves overall sensitivity and of 93.62% and 52.18, respectively. It accurately detects 176 out of 188 microbleeds, while it only loses 12 microbleeds. However, for LR data, the overall detection performance was decreased with sensitivity and of 78.85% and 155.5, respectively. The true positives of 451 out of 472 and false negatives of 121 microbleeds were derived. Fig. 5 shows some examples of the true positives, false positives, and false negatives that are generated by the regional-based YOLO for both resolutions. It is obvious from these examples that the number of false positive candidates (i.e., CMBs mimics) in the LR data is bigger compared to the false positives in the HR data.
Table 4.
Overall candidate detection performance via the regional-based YOLO throughout all five-folds test for both HR and LR data.
| Fold Test |
High in-plane Resolution |
Low in-plane Resolution |
||||||
|---|---|---|---|---|---|---|---|---|
| TPs | FNs | Sensitivity (%) | TPs | FNs | Sensitivity (%) | |||
| 1st Fold* | 36 | 0 | 100.00 | 53.71 | 99 | 44 | 69.23 | 157.00 |
| 2nd Fold | 27 | 1 | 96.43 | 41.14 | 89 | 12 | 88.12 | 171.00 |
| 3rd Fold | 34 | 6 | 85.00 | 64.35 | 45 | 23 | 66.18 | 133.29 |
| 4th Fold | 34 | 2 | 94.44 | 51.07 | 104 | 30 | 77.61 | 148.67 |
| 5th Fold | 45 | 3 | 93.75 | 50.80 | 114 | 12 | 90.48 | 182.35 |
| Total | 176 | 12 | 93.62 | 52.18 | 451 | 121 | 78.85 | 155.50 |
Since the first fold test is utilized in the experimental setup, the results of this fold test may get biased.
Fig. 5.
Examples of the detected suspicious regions by the proposed regional-based YOLO (yellow boxes) for HR (top three rows) and LR (bottom three rows), however, first, second, and third rows in each indicate the TPs, FPs, and FNs cases, respectively. Green boxes refer to labeled ground-truth microbleeds by radiologists. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.3. Performance of FPs reduction via 3D-CNN (2nd Stage)
The main aim of the 3D-CNN stage is to reduce the large number of false positive candidates that were generated through the candidate detection stage and further single out CMBs from the challenging ones. It is of note that the inputs to this stage represent all the generated potential candidates from the regional-based YOLO technique. Thus, the false negatives cases cannot be included in the FPs reduction stage. The proposed FPs reduction stage via the 3D-CNN is conducted as a classification task, in which the proposed network learns robust features from the combined 3D SWI and phase patches and further distinguishes them into CMBs and non-CMBs. Since the number of true CMBs and non-CMBs candidates are not equal, we have applied the weighted-class strategy during training of our 3D-CNN classifier in order to address the imbalanced issue of training data.
For the quantitative results of the proposed 3D-CNN, Table 5 and Table 6 present the classification performance throughout all five-folds test for high and low in-plane resolutions, respectively. It is shown that the proposed network has the capability to differentiate between CMBs and non-CMBs candidates with high classification achievement. We obtain overall sensitivity of 94.32% and 91.80% and a precision of 61.94% and 67.21% for the high and low in-plane resolutions, respectively. The disparity of results between the high and low in-plane resolutions is due to the variations of the number of input data and their image quality. Regarding the average number of false positives per subject (), we achieved promising results with 1.42 for the HR and 1.89 for the LR data.
Table 5.
Evaluation performance of the FPs reduction stage via the proposed 3D-CNN for the HR data.
| Fold Test | TPs | FNs | Sensitivity (%) | Precision (%) | F1-score (%) | |
|---|---|---|---|---|---|---|
| 1st Fold | 34 | 2 | 94.44 | 75.56 | 83.95 | 0.79 |
| 2nd Fold | 27 | 0 | 100.00 | 52.94 | 69.23 | 1.71 |
| 3rd Fold | 31 | 3 | 91.18 | 91.18 | 91.18 | 0.21 |
| 4th Fold | 32 | 2 | 94.12 | 47.06 | 62.75 | 2.57 |
| 5th Fold | 42 | 3 | 93.33 | 60.00 | 73.04 | 1.75 |
| Total | 166 | 10 | 94.32 | 61.94 | 74.77 | 1.42 |
Table 6.
Evaluation performance of the FPs reduction stage via the proposed 3D-CNN for the LR data.
| Fold Test | TPs | FNs | Sensitivity (%) | Precision (%) | F1-score (%) | |
|---|---|---|---|---|---|---|
| 1st Fold | 91 | 8 | 91.92 | 73.98 | 81.98 | 1.52 |
| 2nd Fold | 82 | 7 | 92.13 | 77.36 | 84.10 | 1.14 |
| 3rd Fold | 41 | 4 | 91.11 | 51.90 | 66.13 | 1.81 |
| 4th Fold | 93 | 11 | 89.42 | 64.14 | 74.70 | 2.48 |
| 5th Fold | 107 | 7 | 93.86 | 65.64 | 77.26 | 2.43 |
| Total | 414 | 37 | 91.80 | 67.21 | 77.60 | 1.89 |
3.4. Further testing on normal healthy subjects
In this section, we performed further analysis by testing our proposed deep learning two-stage networks using normal healthy subjects. To this end, we have collected additional 22 MR brain volumes from the same medical healthcare center in which fourteen subjects represent HR data, while the rest are in the LR settings. It is of note that we utilized these data as further testing using the best network’s weights of the regional-based YOLO and 3D-CNN stages independently for both HR and LR data. In other words, for the candidate detection stage via regional-based YOLO, we tested the HR and LR normal healthy subjects using the final trained network weights of the first and fifth folds, respectively, since they resulted in the highest sensitivities as reported in Table 6. Similarly, we tested the FPs reduction stage via 3D-CNN using the final weights from the second and fifth folds for HR and LR data, respectively (see Table 5 and Table 6). The results of this testing are presented in Table 7. It is shown that the proposed two-stage networks could only retrieve of 0.50 and 2.14 for both HR and LR data, respectively. Superior performances were achieved for both HR and LR data in term of specificity. All the provided scans of healthy subjects were checked by neuroradiologists and also all the were confirmed as Non-CMBs. As we are dealing with healthy subjects (i.e., only negative samples), it is impossible to compute other measurements such as sensitivity and precision, which are directly in relation to the true positive samples (i.e., microbleeds). Hence, we present the specificity which is a true negative rate. Fig. 6 (a) and (b) illustrate some CMBs candidates, which are generated by the regional-based YOLO for HR and LR data, respectively. The second row in this figure shows some remaining candidates (i.e., falsely detected as microbleeds) after the FPs reduction stage via 3D-CNN.
Table 7.
Performances of the proposed two-stage networks on normal healthy subjects.
| Data |
Candidate Detection Stage via Regional-based YOLO |
FPs Reduction Stage via 3D-CNN |
|
|---|---|---|---|
| Specificity (%) | |||
| HR (14 Subjects) | 54.29 | 99.08 | 0.50 |
| LR (8 Subjects) | 202.25 | 98.15 | 2.14 |
Fig. 6.
Examples of some CMBs candidates via the regional-based YOLO for normal healthy subjects: (a) for HR data and (b) for LR data. The second row indicates the remaining FPs after the FPs reduction via 3D-CNN.
4. Discussion
Many investigations and efforts have been conducted in recent years for automatic detection of intracranial diseases such as hemorrhage and calcification. For example, the reliable differentiation between cerebral microbleeds from calcifications is crucial for accurate diagnosis and hence appropriate treatment. Currently, generating the SWI from the MR magnitude and phase images is essential for better visualization of cerebral veins without the need for applying the contrast agents. This is due to that SWI is highly sensitive to the local tissue susceptibility and paramagnetic blood products such as microbleeds. In this study, we developed a new two cascaded deep learning approach for CMBs detection from the 3D-MR images. The first candidate detection stage is performed using the regional-based YOLO technique, which generates potential CMBs candidates. The second stage via 3D-CNN is developed as an integration with the potential candidate detection stage, where its main role is to rigorously differentiate between true positive candidates (i.e., CMBs) and negative candidates (i.e., CMB mimics). In fact, a two-stage process is usually inevitable to fulfill the challenging task of automated CMBs detection from MR brain images. This is due to that CMBs have small sizes, a high degree of visual similarity with other CMB mimics, as well as their wide distribution throughout the brain. Our proposed framework was trained using 3D contextual spatial information from both SWI and phase images. The proper choice of the input data is critical and may lead the proposed network to provide superior detection performance. As presented in section 3.1.1, we investigated five different combinations of inputs. We found that the information from both SWI and phase images facilitated the regional-based YOLO network to learn appropriate representations of microbleeds. However, the information from the magnitude images did not add further details. Similar results have been presented in the work of Liu et al. (Liu et al., 2019). Also, using the complement of phase besides the original SWI images enable the detection network to obtain better detection of CMBs. Moreover, the detection stage via the regional-based YOLO achieved superior detection performance of CMBs and less number of FPs when it was trained using SWI and complement phase images with additional details of microbleeds from the adjacent slices as shown in Table 2. It is noteworthy that we applied the brain extraction tool (BET) as a preprocessing step to all input images. This process enables our proposed deep learning regional-based YOLO to only detect potential candidates of CMBs from the brain tissue region and further avoid getting more incorrect candidates existed over the skull region.
Regarding the in-plane resolution data, it is of note that most of the recent previous works on CMBs detection were performed using HR data of approximately 0.45 × 0.45 . In this paper, we performed further analyses to show the effect of training the proposed deep learning regional-based YOLO using different in-plane resolutions; HR with 0.50 × 0.50 and LR with 0.80 × 0.80 as explained in section 3.1.2. The results in Table 3 show how the detection stage could provide higher achievements on microbleeds detection when the network was trained with HR data compared to LR data. Besides, the effect of training the detection stage network using the combined data from both HR and LR data is also evaluated. In this case, the proposed deep learning regional-based YOLO learned features from both in-plane resolutions (i.e., good representations from HR and plain features from LR), leading to obtaining moderate detection sensitivity and a large number of . To preserve higher detection performance while keeping not too many FPs per subject, it is better to train the deep learning network separately using the same in-plane resolution data every time.
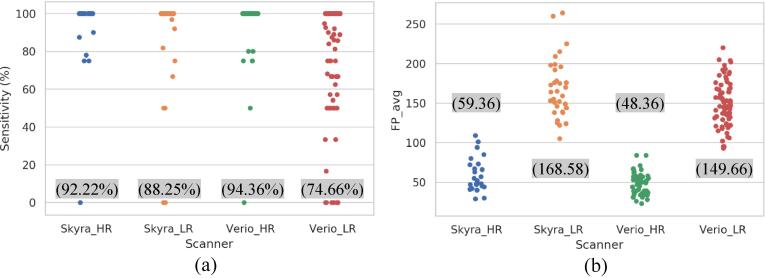
In this paper, we collected our data from two different scanners (i.e., 3.0 T Verio and Skyra Siemens MRI). We analyzed the performance of the YOLO detector throughout all test folds by visualizing the performance distribution per subject for each scanner. This analysis provides an intuitive overview of the results in terms of sensitivity and . Fig. 7 shows how the performances of different scanners that have similar in-plane resolution are very close to each other, which could reflect minimal differences in their noise characteristics. Moreover, we performed the generalization study between scanners for both LR and HR data. In this investigation, we trained the 3D-CNN using candidates from Verio scanner (i.e., 47 subjects for HR and 74 subjects for LR), while we tested the network using the Skyra data (i.e., 25 subjects for HR and 33 subjects for LR). This investigation provides general observation on how the deep learning methods could be generalized when they are tested on different data acquired from other scanners. The generalization performances of the 3D-CNN for both HR and LR are presented in Table 8. As expected, the results show that performance is inferior due to the reduced amount of training data. However, the results show a potential ability for generalization.
Fig. 7.
Distribution performances per subject for the YOLO detector throughout all fold tests for each scanner and in-plane resolution in terms of (a) sensitivity and (b) . The highlighted measurements in the parenthesis represent the overall average performances per scanner within a particular in-plane resolution in terms of (a) sensitivity and (b) The number of data collected using Skyra is 25 HR and 33 LR scans, while 47 HR and 74 LR scans were collected using Verio scanner.
Table 8.
Generalization performances of 3D-CNN on both HR and LR data that are trained using data from Verio scanner and tested on data from Skyra scanner.
| Data | TPs | FNs | Sensitivity (%) | Precision (%) | F1-Score (%) | |
|---|---|---|---|---|---|---|
| HR | 44 | 18 | 70.97 | 51.16 | 59.46 | 1.68 |
| LR | 148 | 24 | 86.05 | 64.35 | 73.63 | 2.48 |
In spite of that splitting the data based on scanner type, in which training and testing are performed using different sets from different scanners, could provide a generalization performance, this kind of splitting will reduce the amount of training data and may cause an overfitting problem on the built network, leading to provide untrusted detection system. Due to this, in this paper we merged all data with the same in-plane resolution from both scanners to generate a bigger amount of training data. The identified imaging parameters that were utilized in this study for data acquisition could be heterogeneous with other scanners. Despite this, we think that acquiring MRI data with a comparable spatial resolution is sufficient to test and validate our proposed work on microbleeds detection.
The limited size of labeled training data is a major obstacle that encounters the deep learning approaches in biomedical clinical applications. To address this issue, we have augmented the training data eight times in the CMBs candidate detection stage via YOLO using different rotation and flipping operations. For the FPs reduction stage via 3D-CNN, the input 3D patches were also enlarged 24 times where the augmentation process was repeated three times along with the three views (i.e., axial, sagittal, and coronal). Further, we have utilized 5-folds cross-validation throughout the proposed deep learning two-stage approach. This scheme increases the reliability of the proposed framework since all the MR brain images for all subjects were evaluated and tested. In contrast, the previous studies on the CMBs detection did not utilize this procedure, however, they allocated a fixed small portion of their data as a test set, while the remaining data was utilized for training. The only limitation of applying the k-fold cross-validation strategy is that it requires to train and evaluate the proposed network k times. Hence, in this work, we have trained the proposed two-stage approach five times to fulfill the tasks of CMBs candidate detection and FPs reduction separately for both HR and LR data.
Furthermore, we present a comparison with the latest relevant works in the literature as reported in Table 9. As presented, most of the previous works adapted the fast radial symmetry transform (FRST) as a candidate detection stage. The FRST is a method that uses the local radial symmetry to single out spherical regions existed in the brain images. It is observed that our proposed deep learning regional-based YOLO outperforms the most commonly utilized FRST method on the detection of the CMBs and achieves high sensitivity and a limited number of false positives per subject. Since the utilized datasets among all previous methods are not the same, we provide direct comparison through implementing the 3D version of FRST and applied it to our dataset. Here, we also implemented 3D-FRST to check its ability on detecting CMB potential candidates against the proposed YOLO detector. The 3D-FRST is more sensitive, but at the cost of generating a lot of FPs per subject. The proposed regional-based YOLO generates a limited number of of 155.5 and 52.18 compared to a large number of candidates generated by 3D-FRST with of 946.1 and 497.4 for LR and HR data, respectively. Then, for the second stage, we trained and tested the 3D-CNN on the CMB candidates generated by the 3D-FRST method. Similar to what we performed on the candidates via YOLO, we evaluated this investigation using five-folds cross-validation separately for HR and LR data. Since the 3D-FRST method generates very high imbalanced training samples (i.e., CMBs against Non-CMBs) even after augmenting the CMB samples, this could affect the overall performance. The results show that the 3D-CNN does not only affect the , but it also reduces the overall sensitivity. Table 9 shows the overall performances of 3D-CNN on the candidates generated by 3D-FRST for both HR and LR data. Based on this results, larger number of candidates that includes larger FPs has greater possibility to be classified falsely as CMBs compared to lower number of candidates. Our proposed YOLO proved its effectiveness and feasibility compared to others with lower computation cost. It only requires 0.69 s to process one subject and generate potential candidates. It is 13.4 and 47.9 times faster than the 3D-FRST when it was applied to LR and HR data, respectively. The difference of the processing speed for the 3D-FRST (i.e., 9.24 s for LR and 33.03 s for HR) is due to that LR and HR data have different input sizes. However, both data resolutions were resized into a same size as a requirement for the YOLO structure. Hence, similar processing time per subject of 0.69 s for YOLO was recorded for both LR and HR data. In addition, the quite high performances in terms of sensitivity and precision achieved by (Wang et al., 2019, Hong et al., 2019) could be due to the very huge number of the utilized microbleeds compared to other studies. (Wang et al., 2019) extracted 68,847 CMBs and over 56 million Non-CMBs from 20 patients, while (Hong et al., 2019) extracted 4287 CMBs from 10 subjects. In the FPs reduction stage, the execution time per subject was computed as a multiplication of the processing time of each 3D input patch via the 3D-CNN by the total number of false positives per subject (i.e., 155.5 in case of LR and 52.18 in case of HR). Finally, the proposed FPs reduction stage via the 3D-CNN was able to robustly reduce the FPs from 155.5 to 1.89 per subject for LR data and from 52.18 to 1.42 for HR data. The practical benefits of the proposed approach compared to the previous works are as follows. It requires lower computation time, deals with low in-plane resolution data which can be used in routine clinical exams, and works well with smaller dataset. Also, we make the dataset and code available for further investigations and developments.
Table 9.
Comparison between the proposed deep learning two-stage approach against the latest studies in the literature on CMBs Detection.
| Reference | Method | Data Subjects /CMBs | In-plane resolution() | Performance |
||||
|---|---|---|---|---|---|---|---|---|
| Sen.*(%) | Prec.*(%) | Test Time/subject(sec) | Overall Sen. (%) | |||||
| (Dou et al., 2016) | 1st stage: 3D-FCN | 3.0 T320/1149 | 0.45 × 0.45 | 98.29 | 282.8 | 64.35 | 91.45♦ | |
| 2nd stage: 3D-CNN | 93.16 | 2.74 | 44.31 | |||||
| (Liu et al., 2019) | 1st stage: 3D-FRST | 1.5 T and 3.0 T220/1641 | 0.45 × 0.57and 0.50 × 0.50 | 99.40 | 276.8 | 39 | 95.24♦ | |
| 2nd stage: 3D-ResNet | 95.80 | 1.60 | 70.90 | 9 | ||||
| (Chen et al., 2019) | 1st stage: 2D-FRST | 7.0 T73/2835 | 0.50 × 0.50 | 86.50 | 231.88 | |||
| 2nd stage: 3D-ResNet | 94.69 | 11.58 | 71.98 | |||||
| (Kuijf et al., 2012) | 3D-FRST | 7.0 T18/66 | 0.35 × 0.35 | 71.20 | 17.17 | 13.20 | 900 | 71.20 |
| (Wang et al., 2019) | 2D-DenseNet | 20/68847 | 97.78 | 11.8♦ | 97.65 | 97.78 | ||
| (Hong et al., 2019) | 2D-ResNet-50 | 10/4287 | 95.71 | 3.4♦ | 99.18♦ | 95.71 | ||
| Proposed Work | Implemented 3D-FRST | 3.0 T107/572 | LR 0.80 × 0.80 | 80.06 | 946.1 | 9.24 | 62.59 | |
| 3D-CNN on 3D-FRST candidates | 78.17 | 4.69 | 41.63 | 0.961 | ||||
| 1st stage: YOLO | 78.85 | 155.5 | 0.69 | 72.78 | ||||
| 2nd stage: 3D-CNN | 91.80 | 1.89 | 67.21 | 0.159 | ||||
| Implemented 3D-FRST | 3.0 T72/188 | HR 0.50 × 0.50 | 97.34 | 497.4 | 33.03 | 81.38 | ||
| 3D-CNN on 3D-FRST candidates | 83.61 | 3.74 | 36.26 | 0.505 | ||||
| 1st stage: YOLO | 93.62 | 52.18 | 0.69 | 88.30 | ||||
| 2nd stage: 3D-CNN | 94.32 | 1.42 | 61.94 | 0.053 | ||||
Sen. and Prec. refer to the sensitivity and precision indices, respectively.
These values are not provided in the related articles, but were computed from other results.
The main limitation of this study and most of the deep learning methods in the field of medical image analysis is the limited size of labeled training and testing data. This is due to that manual labeling process of microbleeds by expert radiologists is laborious, time-consuming, and subjective. In addition, the task of CMBs detection from brain MR images was proceeded in this work using two-stage deep learning architectures through different software environments. This could decrease the possibility of adapting the proposed work practically during the routine clinical exams. Thus, it may be interesting to tackle this issue via developing a single end-to-end deep learning object detection network, which can learn robust contextual features from the CMBs and CMB mimics altogether during the training stage. Further, understanding the domain shift between high and low in-plane resolution by adapting the transfer learning and generating more training samples via the generative adversarial network could improve the efficiency and feasibility of CMBs detection. Also, it may be interesting in the future work to differentiate between microbleeds and calcifications within a single network.
5. Conclusion
In this work, we presented a new two-stage integrated deep learning approach for efficient CMBs detection. The detection stage via the regional-based YOLO endeavors to deny the background regions and simultaneously retrieve potential microbleeds candidates. Subsequently, the 3D-CNN stage is developed to reduce the FPs and single out the accurate microbleeds. We found that training the networks using 3D contextual information by averaging the adjacent slices of the SWI and complement phase images could improve the detection performance. This finding matches with the clinicians who utilized the SWI image as a preferred clinical way of CMBs detection and phase images for further confirmation of challenging cases. Further, it is preferred to train and evaluate the network using the same data in-plane resolution, since using heterogeneous training led the network to decrease its detection capability.
CRediT authorship contribution statement
Mohammed A. Al-masni: Conceptualization, Methodology, Software, Writing - original draft, Visualization. Woo-Ram Kim: Data curation, Investigation. Eung Yeop Kim: Data curation, Investigation. Young Noh: Conceptualization, Data curation, Investigation. Dong-Hyun Kim: Conceptualization, Writing - review & editing, Supervision.
Acknowledgments
This research was supported by the Brain Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (2018M3C7A1056884) and (NRF-2019R1A2C1090635). This research was also supported by a grant of the Korea Healthcare Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (HI14C1135).
Contributor Information
Mohammed A. Al-masni, Email: m.almasani@yonsei.ac.kr.
Young Noh, Email: ynoh@gachon.ac.kr.
Dong-Hyun Kim, Email: donghyunkim@yonsei.ac.kr.
References
- Al-Antari M.A., Al-Masni M.A., Choi M.T., Han S.M., Kim T.S. A fully integrated computer-aided diagnosis system for digital X-ray mammograms via deep learning detection, segmentation, and classification. Int. J. Med. Inf. 2018;117:44–54. doi: 10.1016/j.ijmedinf.2018.06.003. [DOI] [PubMed] [Google Scholar]
- Al-Masni M.A., Al-Antari M.A., Choi M.T., Han S.M., Kim T.S. Skin lesion segmentation in dermoscopy images via deep full resolution convolutional networks. Comput. Methods Programs Biomed. 2018;162:221–231. doi: 10.1016/j.cmpb.2018.05.027. [DOI] [PubMed] [Google Scholar]
- Al-Masni M.A., Al-Antari M.A., Park J.M., Gi G., Kim T.Y., Rivera P., Valarezo E., Choi M.T., Han S.M., Kim T.S. Simultaneous detection and classification of breast masses in digital mammograms via a deep learning YOLO-based CAD system. Comput. Methods Programs Biomed. 2018;157:85–94. doi: 10.1016/j.cmpb.2018.01.017. [DOI] [PubMed] [Google Scholar]
- Al-Masni, M. A., Al-Antari, M. A., Park, J. M., Gi, G., Kim, T. Y., Rivera, P., Valarezo, E., Han, S. M. & Kim, T. S. 2017. Detection and classification of the breast abnormalities in digital mammograms via regional Convolutional Neural Network. 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2017/10/25 ed. Jeju, Republic of Korea. [DOI] [PubMed]
- Barnes S.R.S., Haacke E.M., Ayaz M., Boikov A.S., Kirsch W., Kido D. Semiautomated detection of cerebral microbleeds in magnetic resonance images. Magn. Reson. Imaging. 2011;29:844–852. doi: 10.1016/j.mri.2011.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian W., Hess C.P., Chang S.M., Nelson S.J., Lupo J.M. Computer-aided detection of radiation-induced cerebral microbleeds on susceptibility-weighted MR images. Neuroimage-Clinical. 2013;2:282–290. doi: 10.1016/j.nicl.2013.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charidimou A., Krishnan A., Werring D.J., Jager H.R. Cerebral microbleeds: a guide to detection and clinical relevance in different disease settings. Neuroradiology. 2013;55:655–674. doi: 10.1007/s00234-013-1175-4. [DOI] [PubMed] [Google Scholar]
- Charidimou A., Werring D.J. Cerebral microbleeds: detection, mechanisms and clinical challenges. Fut. Neurol. 2011;6:587–611. [Google Scholar]
- Chen H., Dou Q., Yu L.Q., Qin J., Heng P.A. VoxResNet: Deep voxelwise residual networks for brain segmentation from 3D MR images. Neuroimage. 2018;170:446–455. doi: 10.1016/j.neuroimage.2017.04.041. [DOI] [PubMed] [Google Scholar]
- Chen W., Zhu W., Kovanlikaya I., Kovanlikaya A., Liu T., Wang S., Salustri C., Wang Y. Intracranial Calcifications and Hemorrhages: Characterization with Quantitative Susceptibility Mapping. Radiology. 2014;270:496–505. doi: 10.1148/radiol.13122640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, Y. C., Villanueva-Meyer, J. E., Morrison, M. A. & Lupo, J. M. 2019. Toward Automatic Detection of Radiation-Induced Cerebral Microbleeds Using a 3D Deep Residual Network (vol 32, pg 766, 2019). J. Dig. Imag., 32, 898-898. [DOI] [PMC free article] [PubMed]
- Dou Q., Chen H., Yu L.Q., Zhao L., Qin J., Wang D.F., Mok V.C.T., Shi L., Heng P.A. Automatic Detection of Cerebral Microbleeds From MR Images via 3D Convolutional Neural Networks. IEEE Trans. Med. Imaging. 2016;35:1182–1195. doi: 10.1109/TMI.2016.2528129. [DOI] [PubMed] [Google Scholar]
- Girshick, R. 2015. Fast R-CNN. IEEE International Conference on Computer Vision (ICCV). Washington, USA.
- Girshick, R., Donahue, J., Darrell, T. & Malik, J. 2014. Rich feature hierarchies for accurate object detection and semantic segmentation. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Columbus, OH, USA.
- Greenberg S.M., Vernooij M.W., Cordonnier C., Viswanathan A., Salman R.-A.-S., Warach S., Launer L.J., Buchem M.A.V., Breteler M.M.B. Cerebral Microbleeds: A Field Guide to their Detection and Interpretation. Lancet Neurol. 2009;8:165–174. doi: 10.1016/S1474-4422(09)70013-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke E.M., Xu Y.B., Cheng Y.C.N., Reichenbach J.R. Susceptibility weighted imaging (SWI) Magn. Reson. Med. 2004;52:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- He, K., Zhang, X., Ren, S. & Sun, J. 2016. Deep Residual Learning for Image Recognition. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA: IEEE.
- Hong J., Cheng H., Zhang Y.D., Liu J. Detecting cerebral microbleeds with transfer learning. Mach. Vis. Appl. 2019;30:1123–1133. [Google Scholar]
- Koennecke H.C. Cerebral microbleeds on MRI - Prevalence, associations, and potential clinical implications. Neurology. 2006;66:165–171. doi: 10.1212/01.wnl.0000194266.55694.1e. [DOI] [PubMed] [Google Scholar]
- Kuijf H.J., De Bresser J., Geerlings M.I., Conijn M.M.A., Viergever M.A., Biessels G.J., Vincken K.L. Efficient detection of cerebral microbleeds on 7.0 T MR images using the radial symmetry transform. Neuroimage. 2012;59:2266–2273. doi: 10.1016/j.neuroimage.2011.09.061. [DOI] [PubMed] [Google Scholar]
- Liu S.F., Utriainen D., Chai C., Chen Y.S., Wang L., Sethi S.K., Xia S., Haacke E.M. Cerebral microbleed detection using Susceptibility Weighted Imaging and deep learning. Neuroimage. 2019;198:271–282. doi: 10.1016/j.neuroimage.2019.05.046. [DOI] [PubMed] [Google Scholar]
- Martinez-Ramirez S., Greenberg S.M., Viswanathan A. Cerebral microbleeds: overview and implications in cognitive impairment. Alzheim. Res. Therapy. 2014;6 doi: 10.1186/alzrt263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masood A., Sheng B., Li P., Hou X.H., Wei X.E., Qin J., Feng D.G. Computer-Assisted Decision Support System in Pulmonary Cancer detection and stage classification on CT images. J. Biomed. Inform. 2018;79:117–128. doi: 10.1016/j.jbi.2018.01.005. [DOI] [PubMed] [Google Scholar]
- Redmon, J., Divvala, S., Girshick, R. & Farhadi, A. 2016. You Only Look Once: Unified, Real-Time Object Detection. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA.
- Redmon, J. & Farhadi, A. 2017. YOLO9000: Better, Faster, Stronger. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI, USA.
- Rijthoven, M. V., Swiderska-Chadaj, Z., Seeliger, K., Laak, J. V. D. & Ciompi, F. 2018. You Only Look on Lymphocytes Once. 1st Conference on Medical Imaging with Deep Learning. Amsterdam, The Netherlands.
- Sindhu, R. S., George, J., Skaria, S. & Varun, V. V. 2018. Using YOLO based deep learning network for real time detection and localization of lung nodules from low dose CT scans. Medical Imaging 2018: Computer-Aided Diagnosis. Texas, United States.
- Smith S.M. Fast robust automated brain extraction. Hum. Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V. & Rabinovich, A. 2015. Going deeper with convolutions. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA, IEEE.
- Wang S.H., Tang C.S., Sun J.D., Zhang Y.D. Cerebral Micro-Bleeding Detection Based on Densely Connected Neural Network. Front. Neurosci. 2019;13 doi: 10.3389/fnins.2019.00422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X.M., Wu Y.H., Song G.D., Li Z.Y., Zhang Y.Z., Fan Y. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation. Med. Image Anal. 2018;43:98–111. doi: 10.1016/j.media.2017.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]