Abstract
In the last decades, antibodies have emerged as one of the most important and successful classes of biopharmaceuticals. The highest variability and diversity of an antibody is concentrated on six hypervariable loops, also known as complementarity determining regions (CDRs) shaping the antigen-binding site, the paratope. Whereas it was assumed that certain sequences can only adopt a limited set of backbone conformations, in this study we present a kinetic classification of several paratope states in solution. Using molecular dynamics simulations in combination with experimental structural information we capture the involved conformational transitions between different canonical clusters and additional dominant solution structures occurring in the micro-to-millisecond timescale. Furthermore, we observe a strong correlation of CDR loop movements. Another important aspect when characterizing different paratope states is the relative VH/VL orientation and the influence of the distinct CDR loop states on the VH/VL interface. Conformational rearrangements of the CDR loops do not only have an effect on the relative VH/VL orientations, but also influence in some cases the elbow-angle dynamics and shift the respective distributions. Thus, our results show that antibodies exist as several interconverting paratope states, each contributing to the antibody’s properties.
Subject terms: Biophysics, Computational biophysics, Computational biology and bioinformatics, Computational models, Protein structure predictions
Fernández-Quintero et al. employ molecular dynamics simulations in combination with experimental structural information to demonstrate that antibodies exist as several interconverting paratope states. They propose that dynamic conformational transitions on the micro-to-millisecond timescale are responsible for antibody allostery in contrast to the long believed paradigm of static canonical structures determining binding properties and specificity of antibodies.
Introduction
Antibodies have become one of the fastest-growing class of biopharmaceuticals and are key players as therapeutic agents because of their ability to bind a variety of targets1–4. Therefore, the importance to characterize and engineer the structure of antibodies to improve specificity, stability, and suitability as biotherapeutics increased substantially. The antibody binding site consists of six hypervariable loops, each three on the variable domains of the heavy (VH) and the light chain (VL), that shape the antigen-binding site, the paratope5–7. Five of the six CDR loops, except for the CDR-H3 loop, have been classified into canonical clusters, assuming that depending on the length and sequence, antibody CDR loops can only adopt a limited number of backbone conformations8–11. The highest diversity in length, sequence, and structure can be observed for the CDR-H3 loop9,12. Due to its ability to adopt various distinct conformations during the V(D)J recombination and somatic hyper-mutation, the CDR-H3 loop structure prediction still remains challenging13–19. Together with the CDR-H3 loop, the CDR-L3 loop is located in the center of the paratope and contributes to antigen recognition. The diversity of the CDR-L3 loop is comparable to the CDR-H3 loop, however without the contribution of a D gene, the variability is lower20,21. With the exponential rise of antibody structures the number of antibody databases and sequence-based classification servers increased substantially1,22. Numerous studies tried to classify antibody CDR loops based on their sequence and structure and to correlate them with their locus to improve fast antibody structure prediction and design22–26. Recent studies using molecular dynamics simulations extended the model of static canonical clusters to a characterization of the CDR-L3 and CDR-H3 loops as ensembles in solution by showing that for a given CDR-L3/CDR-H3 loop sequence several conformations should be considered. Besides capturing several conformational transitions between different canonical clusters, other probable CDR-L3 loop structures in solution were identified that are not apparent from X-ray analysis most likely due to crystal packing effects27,28. Another crucial aspect in antibody structure design is the relative orientation of the two variable domains VH/VL, which influences the shape of the paratope and plays an important role in understanding antigen-specificity29,30. The variability in the relative orientation of the VH and VL domains is an additional structural feature of antibodies, which increases the effective size of the antibody repertoire. This is in line with the concept of conformational diversity that the same antibody can adopt various conformations, which influences the binding properties31–33. To characterize and understand favorable orientations of the VH and VL domains, where essential solution structure recognizing different antigens, the considerable binding site flexibility in the low nanosecond timescale should be considered30. It has been shown that conformational rearrangements of the binding site might not only have an effect on the relative VH and VL orientations but also on the elbow-angle34,35.
In this study, we analyze the conformational diversity of all CDR loops to identify transition probabilities between distinct paratope rearrangements and kinetically characterize the CDR loop ensembles in solution. Additionally, we investigate correlated movements between different CDR loops and show the influence of distinct paratope states on the relative VH and VL orientations and on the elbow-angle dynamics. The set of antibodies investigated in this study are chosen based on strong experimental information (the availability of highly resolved crystal structures, affinity, specificity). Additionally, we preferred an assignment to different canonical clusters, to investigate the effect of affinity maturation, multispecificity, different light chain types on the CDR loop ensemble, the relative interdomain orientations, and the elbow-angle dynamics.
Results
Anti-polyhydroxybutyrate antibody
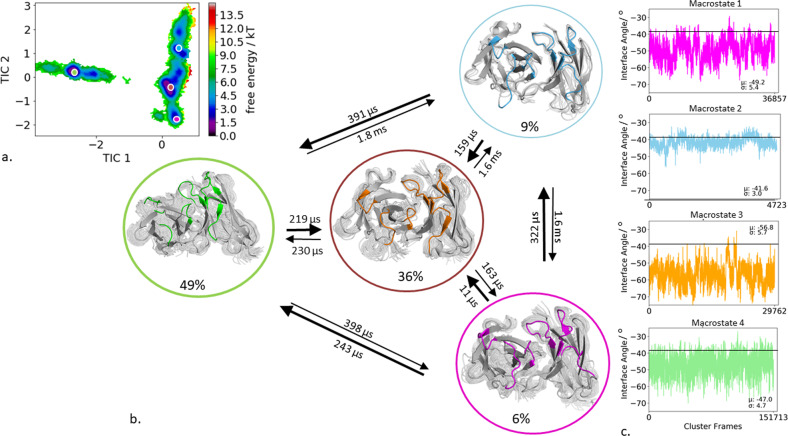
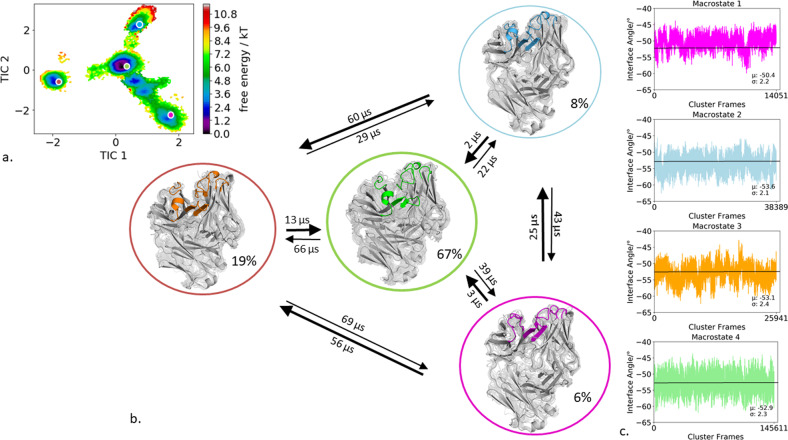
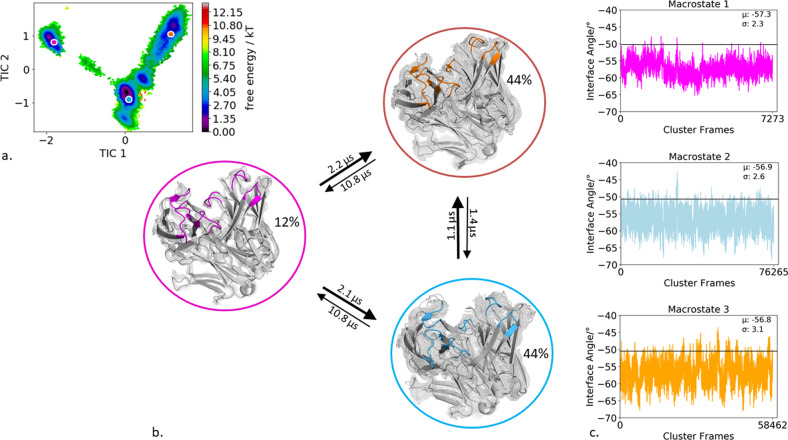
The first antibody studied is the human anti-polyhydroxybutyrate antibody variable fragment (PDB accession code: 2D7T), which binds with high affinity to the biodegradable polymer film. As described in the “methods” section we clustered the obtained 200 ns bias-exchange metadynamics simulation and used the resulting 254 cluster representatives as starting structures for each 100 ns molecular dynamics simulations. This approach does not only allow us to generate a broad ensemble of CDR loop conformations but also to characterize the paratope states in solution kinetically. Figure 1a shows the resulting tICA free energy surface of the 25.4 µs of trajectories of all CDR loops combined to identify kinetically relevant paratope states. The state probabilities, transition kinetics, and the respective macrostate ensembles are shown in Fig. 1b. We obtained four macrostates with CDR binding loop transition timescales up to the millisecond timescale. Additionally, these four macrostate ensembles were then used to calculate the respective interface angle distributions to investigate if CDR loop rearrangements change the relative VH and VL orientation (Fig. 1c). We clearly see that different paratope loop states shift the relative interdomain orientation distributions. The combined free energy surface of all CDR loops reveals a strong macrostate separation in the tIC1, which describes conformational changes of the CDR-H3, the CDR-H1, the CDR-H2, and CDR-L2 loops. Additionally, all four macrostates are further separated by the tIC2 which describes conformational transitions in the CDR-H3, CDR-H1, and CDR-L2 loops.
Fig. 1. Paratope states of the anti-polyhydroxybutyrate antibody Fv including the results of the Markov-state model and shows the relative VH–VL interface distributions for the respective macrostates.
a Combined free energy landscape of all CDR loops with the respective four macrostate representatives. b Markov-state model, transition kinetics, and state probabilities of different paratope states for the anti-polyhydroxybutyrate antibody. c Relative VH–VL interface dynamics of the macrostate ensembles, color-coded according to the Markov-state model in (b). The horizontal line depicts the interface orientation of the crystal structure.
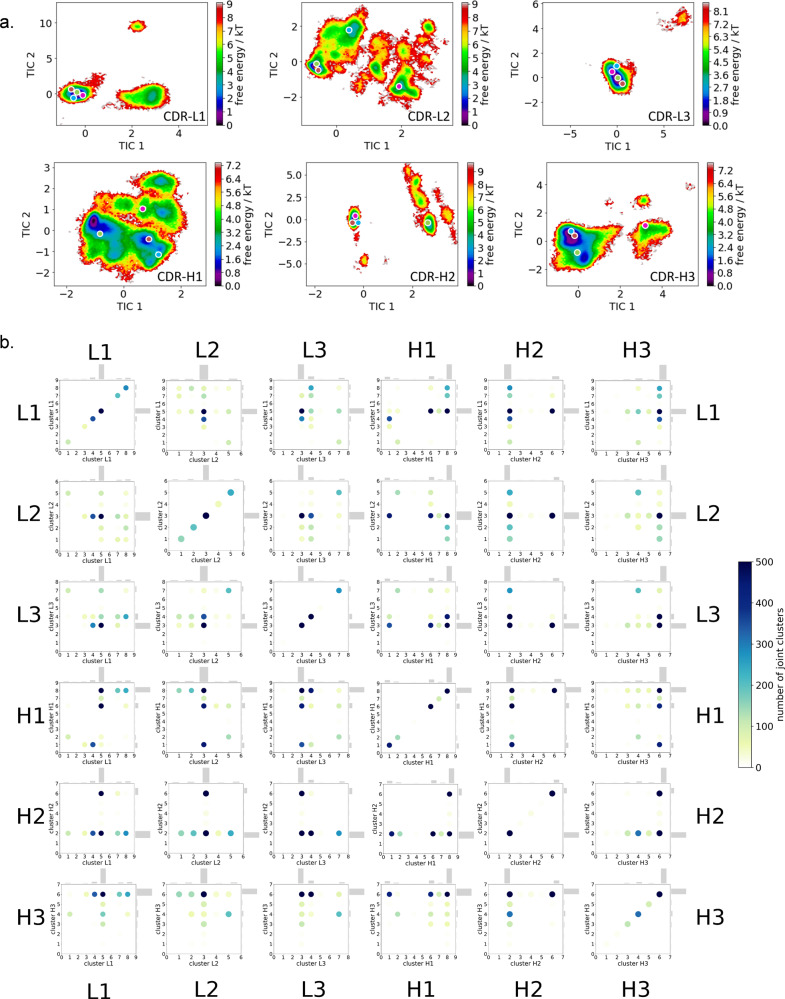
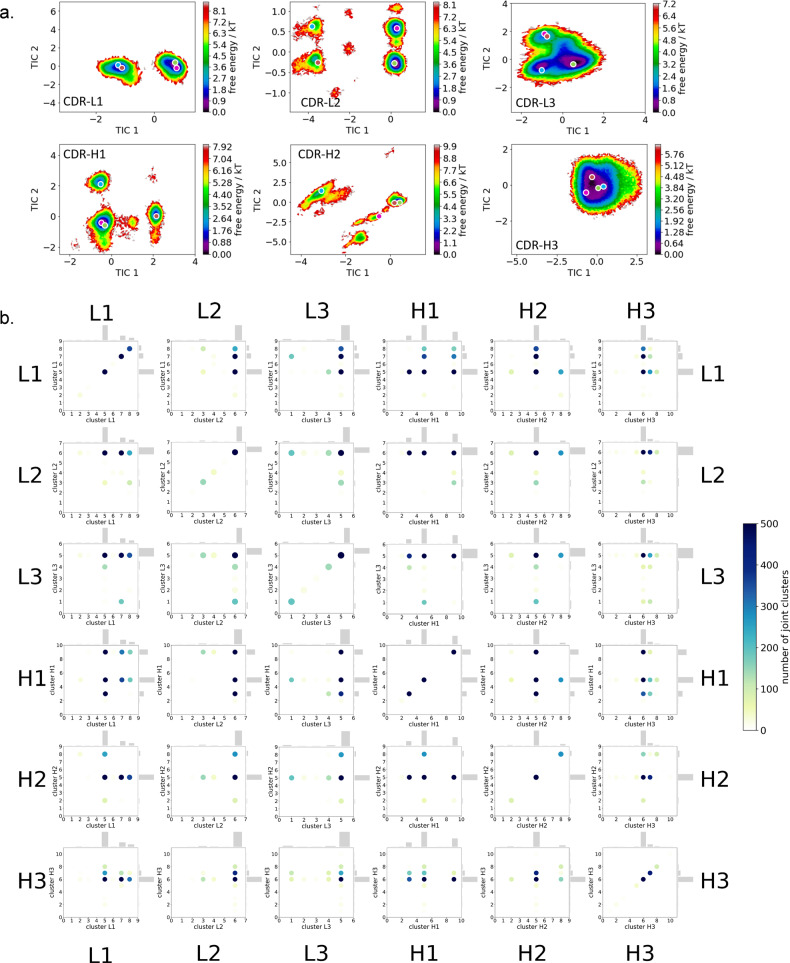
The free energy landscapes of the individual CDR loops are shown in Fig. 2a, including the projections of the paratope macrostate representatives of Fig. 1b to investigate correlated loop movements and to identify the involved loop rearrangements occurring within the four paratope states.
Fig. 2. Free energy surfaces and loop correlations for all individual CDR loops, showing which loops contribute to conformational rearrangements in the different paratope states.
a Free energy surfaces of all individual CDR loops of the anti-polyhydroxybutyrate antibody including the projections of macrostates of Fig. 1b). b Visualization of simultaneous occurrence of CDR loop conformations for all CDR loops.
Besides classifying the states kinetically, the individual CDR loops are clustered geometrically and the resulting cluster populations are plotted against each other to visualize and describe the simultaneous occurrence of distinct loop conformations (Fig. 2b). Figure 2b illustrates a matrix including all individual CDR loops and displays which loop conformations occur at the same time and therefore might be correlated. Strong correlations and multiple simultaneous occurring CDR loop conformations can be observed between the CDR-L1, CDR-L2, CDR-L3, CDR-H1, and CDR-H3 loops. A weaker correlation can be observed for the CDR-H2 loop. It only adopts two main conformations, which is limiting for the correlations with other CDR loops.
Specific murine antigen-binding fragment binding to IL-18
The second antibody studied, is the specific murine antigen-binding fragment (Fab) in complex with a the unique cytokine human IL-18, a proinflammatory cytokine that participates in the regulation of innate and acquired immunity (PDB accession code: 2VXT)36. Clustering of the bias-exchange simulation resulted in 174 cluster representatives, which were used as starting structures for each 100 ns of molecular dynamics simulations. Figure 3a illustrates the tICA free energy landscape of all CDR loops of the obtained 17.4 µs of trajectories. The Markov-state model in Fig. 3b reveals three macrostates, corresponding to three paratope states, including the state probabilities, transition timescales, and the respective macrostate ensembles. By using the macrostate representatives to analyze the influence of CDR loop states on the relative interdomain orientation we observe nearly no shifts in the distributions for the interface angle for different paratope states (Fig. 3c). Slightly bigger shifts upon conformational changes in the paratope can be observed for the elbow-angle. For the obtained three macrostates the elbow-angle distributions are not only shifted but reveal differences in distributions (Supplementary Fig. S1). To identify correlated loop movements, the free energy surfaces of the individual CDR loop states with the projected macrostate representatives of the overall paratope states are displayed in Fig. 4a.
Fig. 3. Paratope states of the specific IL-18 antibody including the results of the Markov-state model and shows the relative VH–VL interface distributions for the respective macrostates.
a Combined free energy landscape of all CDR loops with the respective three macrostate representatives. b Markov-state model, transition kinetics, and state probabilities of different paratope states for the specific IL-18 antibody. c Relative VH–VL interface dynamics of the macrostate ensembles, color-coded according to the Markov-state model in (b). The horizontal line depicts the interface orientation of the crystal structure.
Fig. 4. Free energy surfaces and loop correlations for all individual CDR loops, showing which loops contribute to conformational rearrangements in the different paratope states.
a Free energy surfaces of all individual CDR loops of the IL-18 antibody including the projections of macrostates of Fig. 3b). b Visualization of simultaneous occurrence of CDR loop conformations for all CDR loops. We observe strong correlations between the different CDR loop conformations.
Additionally, to the kinetic classification of the states, the individual CDR loops are clustered and the resulting cluster populations are plotted against each other to visualize and describe the simultaneous occurrence of distinct loop configurations (Fig. 4b). In this case, the CDR-H1 loop reveals strong correlated loop configurations with all other CDR loops.
T-cell receptor-like Fab-Hyb3 in complex with the MAGE-A1-derived peptide
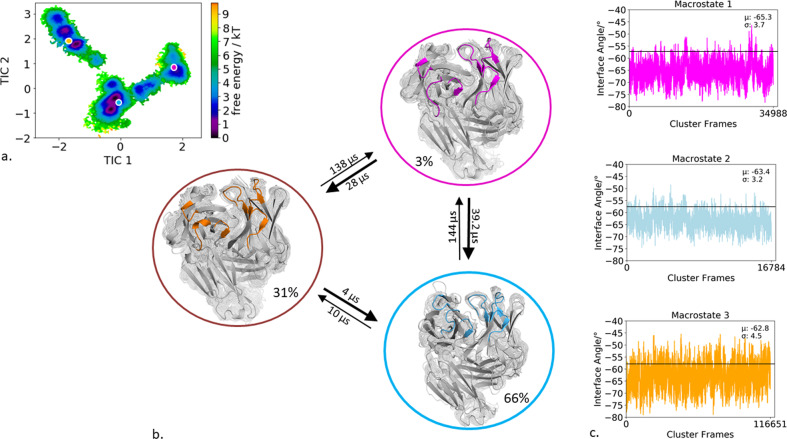
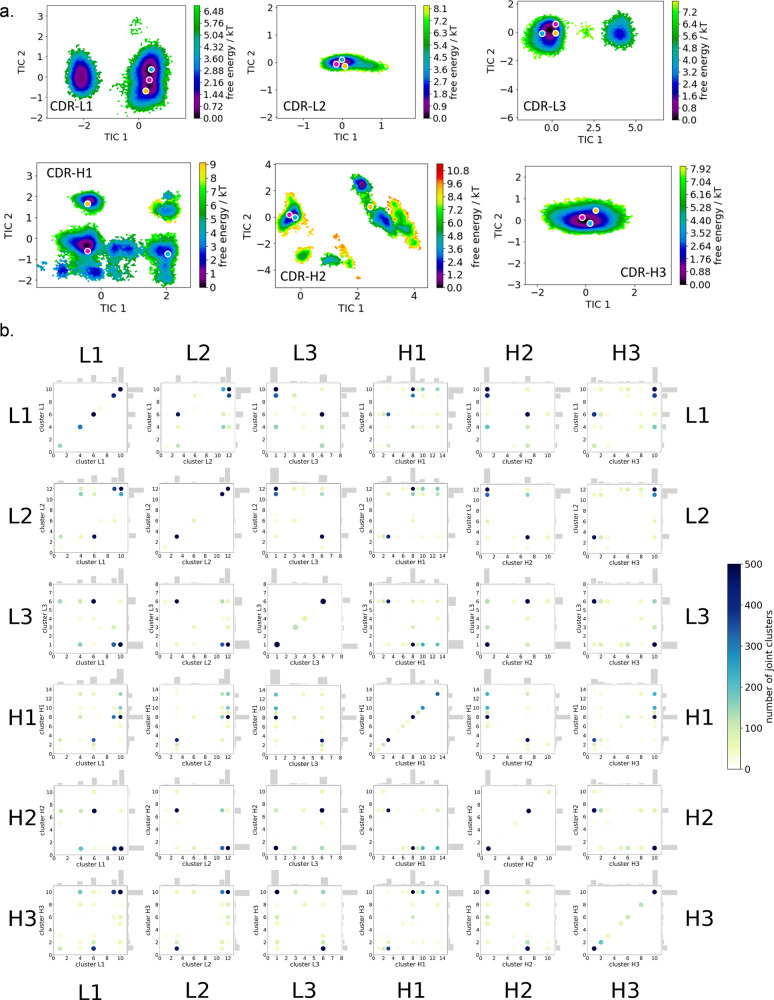
Another antibody fragment studied is the matured Fab-Hyb3 with T-cell receptor-like binding specificity, in complex with the melanoma antigen-encoding gene (MAGE)-A1-derived peptide (PDB accession code: 1W72)37. The free energy landscape and kinetic characterization of all CDR loops of the obtained 22.6 µs of trajectories are illustrated in Fig. 5a, b. The four macrostate ensembles were then used to investigate the role of the CDR loop binding interface on the relative VH and VL orientations. We observe small shifts in the VH and VL interdomain distributions upon conformational rearrangements in the paratope (Fig. 5c). In line with the small shift in the interface angle distributions also the elbow-angle distributions reveal a small shift upon conformational changes in the CDR loops (Supplementary Fig. S2). In line with the previous examples also in this case we observe strong correlations between the CDR loops and illustrate the simultaneous occurrence of specific CDR loop configurations in Fig. 6.
Fig. 5. Paratope states of the matured Fab-Hyb3 including the results of the Markov-state model and shows the relative VH–VL interface distributions for the respective macrostates.
a Combined free energy landscape of all CDR loops with the respective four macrostate representatives. b Markov-state model, transition kinetics, and state probabilities of different paratope states for the matured Fab-Hyb3. c Relative VH–VL interface dynamics of the macrostate ensembles, color-coded according to the Markov-state model in (b). The horizontal line depicts the interface orientation of the crystal structure.
Fig. 6. Free energy surfaces and loop correlations for all individual CDR loops, showing which loops contribute to conformational rearrangements in the different paratope states.
a Free energy surfaces of all individual CDR loops of the Fab-Hyb3 including the projections of macrostates of Fig. 5b). b Visualization of simultaneous occurrence of CDR loop conformations for all CDR loops. We observe strong correlations between the different CDR loop conformations.
Characterizing multispecificty of an SPE7 antibody
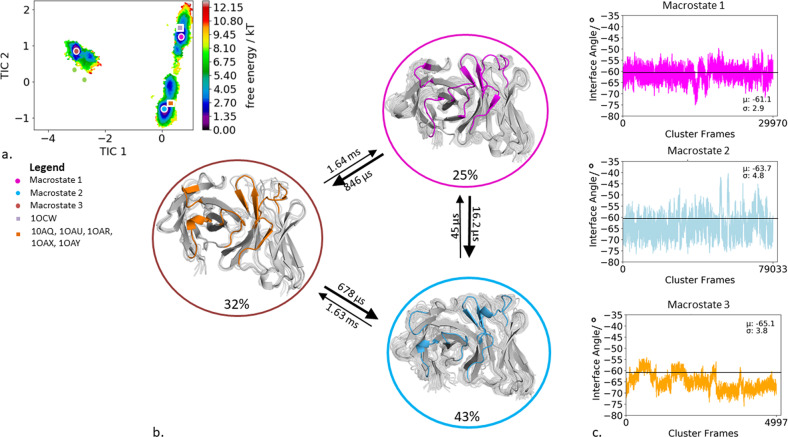
The fourth antibody fragment investigated is part of a study characterizing multispecificity by conformational diversity, where the same SPE7 antibody can adopt various conformations and recognize different antigens (PDB accession code: 1OAQ)38. The free energy landscape of all CDR binding loops of 11.4 µs of trajectories reveals three accessible macrostates, in which all available crystal structures binding to different antigens are present (Fig. 7a). The available crystal structures reveal the greatest differences in the heavy chain, in particular the CDR-H3 loop (Cα-RMSD of 5.38 Å between the 1OCW and 1OAX, Cα-RMSD of 4.81 Å between the 1OCW and 1OAQ). The structure with the PDB accession code 1OCW, crystallized without antigen, shows the greatest structural difference, due to strong crystal packing effects in the CDR-H3, CDR-L3, and CDR-H1 loop28. While all other available structures lie in the same dominant minimum in solution, the 1OCW lies in a separate local side minimum. The three macrostate ensembles are again used to investigate if different CDR loop conformations reveal different relative VH and VL interdomain distributions (Fig. 7b). In line with the previous results, we observe shifted relative VH and VL interdomain distributions upon conformational changes in the binding interface. A substantial shift in the VH and VL interdomain distribution can be observed between the macrostates, in which the 1OCW and all the other available crystal structures are present (Fig. 7c). Also, for this antibody we observe a strong correlation and dependency of loop conformations for all CDR loops (Supplementary Fig. S5).
Fig. 7. Paratope states of the SPE7 antibody including the results of the Markov-state model and shows the relative VH − VL interface distributions for the respective macrostates.
a Combined free energy landscape of all CDR loops with the respective three macrostate representatives. b Markov-state model, transition kinetics, and state probabilities of different paratope states for the SPE7 antibody. c Relative VH–VL interface dynamics of the macrostate ensembles, color-coded according to the Markov-state model in (b). The horizontal line depicts the interface orientation of the crystal structure.
Affinity maturation of an anti-lysozyme binding Fab
Another key aspect when characterizing different states of the complete binding interface is the affinity maturation process and its effect on the CDR loops. The binding site of polyreactive antibodies, which can bind with low affinity to various distinct antigens, has been shown to be substantially more flexible compared to matured antibodies39,40. To investigate the effect of affinity maturation on the accessible binding site states, the relative interdomain orientation and the elbow-angle, we chose the affinity maturation pair D44.1 (naïve) and the F10.6.6 (matured) anti-lysozyme binding Fab41,42. Both Fabs originate from the same germline rearrangement and are therefore related in sequence and structure. The D44.1 Fab differs from the matured F10.6.6 in twenty mutations, seven of them located in the CDR loops and four being directly in the VH–VL interface. As starting structures for 200 ns bias-exchange simulations we used the Fabs with the PDB accession codes: 1MLC (naïve) and 1P2C (matured). By clustering the 200 ns bias-exchange simulations we already observe a substantial rigidification upon affinity maturation reflected in the number of resulting CDR binding site clusters. By using the same distance cut-off criterion of 1.2 Å as described in the “Methods” section the naïve antibody resulted in 301 cluster representatives while the matured antibody revealed only 141 clusters. The resulting 30.1 and 14.1 µs of trajectories were then used to construct a Markov-state model of the complete binding interface to test if the rigidification does not only occur in the CDR loops but also in the relative VH and VL interdomain distributions.
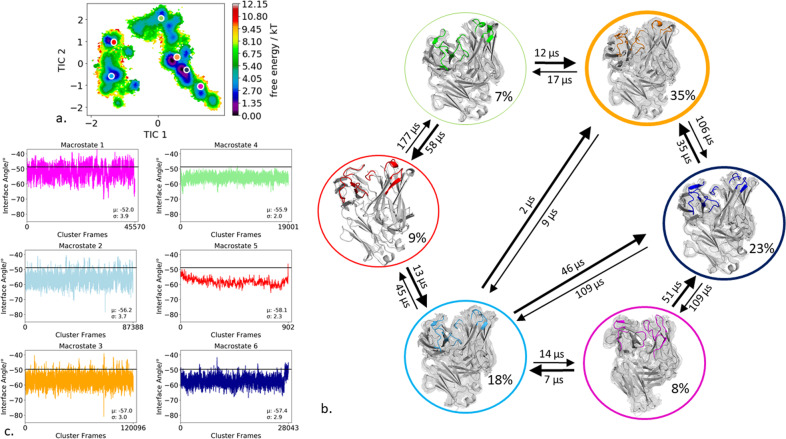
Figure 8a shows the resulting free energy surface of the 30.1 µs of trajectories of the naïve antibody CDR binding interface. We obtained six macrostates with transition kinetics between the resulting six paratope states in the microsecond timescale (Fig. 8b). The VH and VL interdomain distributions of the six respective macrostate ensembles are shifted for the different CDR loop states, confirming a strong correlation of CDR loop rearrangements with the relative domain orientations (Fig. 8c). The relative interdomain orientations of the individual paratope macrostates for the D44.1 antibody fragment were computed by using the torsion-based interface angle definition and also by calculating the HL angle with ABangle (Supplementary Fig. 22). The relative interdomain distributions for the individual macrostates show the same trend and depict the same shifts upon conformational changes in the CDR loops independent of the applied method. The elbow-angle distributions for each macrostate ensemble are visualized in Supplementary Fig. S3 and reveal in this case an extremely low dependency on the distinct CDR loop states and the relative interdomain orientations. Very similar variations up to 55° for the elbow-angle distributions, as in the examples before, can be observed for the D44.1 antibody (Supplementary Fig. S3). The individual free energy surfaces of the CDR loops with the projected six macrostate representatives are shown in Supplementary Fig. S6a, while Supplementary Fig. S6b shows and visualizes the simultaneous occurrence of distinct loop configurations. Loop correlations can be observed between all CDR loops.
Fig. 8. Paratope states of the naive D44.1 antibody including the results of the Markov-state model and shows the relative VH–VL interface distributions for the respective macrostates.
a Combined free energy landscape of all CDR loops with the respective six macrostate representatives. b Markov-state model, transition kinetics, and state probabilities of different paratope states for the naïve D44.1 antibody. c Relative VH–VL interface dynamics of the macrostate ensembles, color-coded according to the Markov-state model in (b). The horizontal line depicts the interface orientation of the crystal structure.
The free energy surface of CDR binding loops of the matured F10.6.6 antibody (14.1 µs of trajectories) is illustrated in Fig. 9a. The Markov-state model in Fig. 9b reveals three macrostates with conformational transitions between different CDR binding site states in the micro-to millisecond timescales. Again, by analyzing the respective ensemble of each macrostate to identify the role of conformational changes in the paratope on the interface angle, we observe nearly no difference in the relative interdomain orientations between the different paratope states (Fig. 9c). Also, in the elbow-angle distributions nearly no shifts can be observed for different CDR loop states (Supplementary Fig. S4). However, upon affinity maturation the elbow angle substantially rigidifies compared to the naïve antibody D44.1 antibody and only reveals variations up to 40°. Supplementary Fig. S7a, S7b shows again the free energy landscapes of the individual CDR loops and visualize the simultaneous occurrence of loop conformations. We observe a strong correlation and dependency of loop conformations for the frames (in particular for macrostate 2) in Supplementary Fig. S7a for the CDR-L1, CDR-L2, CDR-H1, CDR-H2, and CDR-H3 loop conformations.
Fig. 9. Paratope states of the matured F10.6.6 antibody including the results of the Markov-state model and shows the relative VH–VL interface distributions for the respective macrostates.
a Combined free energy landscape of all CDR loops with the respective three macrostate representatives. b Markov-state model, transition kinetics, and state probabilities of different paratope states for the matured F10.6.6 antibody. c Relative VH–VL interface dynamics of the macrostate ensembles, color-coded according to the Markov-state model in (b). The horizontal line depicts the interface orientation of the crystal structure.
To visualize the conformational diversity of each CDR loop individually we included 2D-rmsd plots, residual b-factors and ensemble pictures for each macrostate in the supporting information (Supplementary Figs. S10–S20).
Discussion
Antibody CDR loops are flexible and can adopt various distinct conformations31–33,38. Studies revealed that the high conformational diversity of the CDR loops can be captured by kinetically characterizing the loops as ensembles in solution. For all CDR loops conformational transitions between canonical clusters and additional dominant solution structures have been observed18,27,28. Additionally, these conformational transitions between different CDR loop states occur in the micro-to-millisecond timescale18,27,28,43, while the relative VH and VL interdomain dynamics can be captured in the 0.1–10 ns timescale44,45.
Our results are in line with previous studies; however, we observe that the slow components of these relative VH and VL interdomain dynamics, slower than 10 ns, might be strongly correlated with the CDR loop rearrangements occurring in the micro-to millisecond timescale. Our results reveal that certain CDR loop conformations favor specific interface angle distributions, fluctuating in the 0.1–10 ns timescale. Similar fast dynamics as for the relative VH and VL interdomain dynamics can be seen for the elbow angle, which exhibits the majority of movements in the low nanosecond timescale. It has already been shown that the elbow-angle has high flexibility and that antigen-binding or even single point-mutations can strongly influence the elbow-angle35,36,46. In all examples, we observe broader variations in the elbow-angle compared to the relative VH and VL interdomain dynamics. This is line with the idea that conformational CDR loop rearrangements, which are involved in the antigen-binding process, induce shifts or changes in the elbow-angle distributions. Thus, also in this case the transitions between different CDR loop binding interface states, which strongly influence the relative VH and VL interdomain dynamics, might also correlate with the slower dynamics of the elbow-angle movements. Our results clearly show that conformational rearrangements in the CDR loop backbone occur in the micro-to-millisecond timescale, while the interdomain and elbow-angle dynamics can be captured in the low nanosecond timescale. Side-chain flexibility (vibrations and side-chain rotation) occurs on a substantially faster timescale (in the low nanosecond timescale), compared to conformational changes in the backbone (in the microsecond timescale)47–50. Thus, for all our macrostates possible side-chain conformations and their dynamics should be represented comprehensively in our simulations.
Especially interesting is the effect of affinity maturation on the resulting CDR binding loop states and the resulting changes in the distributions of the relative VH and VL interdomain dynamics and the elbow angle. The results of the naïve and matured antibody in Figs. 8b and 9b, respectively, indicate that not only the paratope rigidifies upon affinity maturation, but also the relative VH and VL interdomain dynamics and the elbow-angle exhibit less flexibility (Figs. 8c, 9c, Supplementary Figs. S3, S4). The direct comparison of the conformational spaces between the naïve and the matured Fab in the same coordinate system is shown in Supplementary Fig. S8 and a substantial decrease in conformational space is evident. The D44.1 antibody fragment was crystallized with and without antigen (PDB accession codes: 1MLC, 1MLB, respectively). We observe that the X-ray structure of the D44.1 antibody crystallized without antigen lies in a local side minimum due to crystal packing effects, while the bound structure belongs to the dominant minimum in solution28. Also the relative interdomain orientation VH–VL differs 2° between the two available X-ray structures and both interface orientations are present within the obtained ensemble in solution. For the naïve D44.1 antibody, conformational rearrangements of the paratope result in substantial shifts of the relative interface orientation. The sampled canonical clusters for the individual CDR loops, for both the naïve and the matured antibody fragment, are depicted in Supplementary Tables S4 and S5. The results clearly reveal that various canonical cluster representatives lie within the same minimum in solution and that we clearly see transitions between different canonical structures. A substantial rigidification upon maturation of the binding interface loops can be observed, which is in line with the smaller variability of the VH and VL interdomain dynamics and the reduced elbow-angle flexibility. Smaller conformational changes in binding site loops also induce less effect on the interface angle and the elbow-angle distributions. In line with these observations, also the matured Fab-Hyb3 exhibits only small shifts in the relative VH and VL interdomain angles and elbow-angle distributions for the different paratope macrostates in solution. Supplementary Table S3 illustrates the sampled canonical clusters and to shows which macrostate in solution they belong to. Again, various canonical clusters belong to the same kinetic minimum in solution. Especially interesting is that the Fab-Hyb3 consists of a lambda light chain and is the representative canonical cluster median of the L1-11-3 cluster, containing only lambda chain structures. The other CDR-L1 loop canonical clusters are not present within the obtained ensemble in solution, indicating that the kappa CDR-L1 loop conformations might not be energetically favorable when starting from a lambda light chain CDR-L1 conformation. Besides sampling various canonical clusters for all CDR loops, we also observe a strong correlation between different CDR loop conformational rearrangements (Fig. 6).
In agreement with previous findings for highly specific antibody fragments, the IL-18 specific Fab shows only small shifts in the relative interdomain angle distributions upon conformational changes in the CDR loop states between the three different macrostates (Fig. 3, Fig. 4). Additionally, Fig. 4 displays the correlation between different CDR loops, in particular, the CDR-H1 loop appears to strongly influence the CDR-H3, CDR-H2, CDR-L3, and CDR-L2 loop and thereby consequently reduces the combinatorics of possible binding site conformations. Furthermore, we identified for each individual loop that various canonical clusters are sampled within our CDR loop ensemble in solution and the assignments to the respective macrostates are shown in Supplementary Table S2. The substantial shifts in the elbow-angle distributions can be interpreted as allosteric effect induced by conformational changes in the CDR loops, which is in line with previously shown results, discussing substantial changes in the elbow-angle upon antigen binding34,35. Another example, where the different CDR loop conformational states strongly influence the resulting relative VH and VL interdomain dynamics is the human anti-polyhydroxybutyrate antibody variable fragment. The obtained four paratope states show substantial differences in the interface angle distributions upon differences in the CDR loop conformations, following the idea of certain CDR loop states favoring certain VH and VL interdomain orientations (Fig. 1). Furthermore, the free energy landscape in Fig. 1a shows a strong state separation in the first tIC component, dominated by correlated structural rearrangements in the CDR-H3, CDR-H1, CDR-L1, and CDR-L2 loops. Supplementary Table S1 summarizes the individual CDR loops which canonical clusters are sampled and even belong to the same macrostate in solution. Within macrostate 4, which is the highest populated paratope state, a high number of the available canonical cluster representatives for all CDR loops are present, this especially is true for the CDR-L3 loop. Various canonical clusters are present within the obtained ensembles in solution and again belong to the same kinetic minimum and thus should be combined.
Multispecificity of antibodies has been discussed to be mediated by conformational diversity. Conformational diversity follows the concept that one single sequence can adopt multiple structures and functions. Thus the functional diversity of the limited repertoire of antibody sequences is increased and the evolution of new proteins and functions is facilitated31–33.
The variable fragment of SPE7 was crystallized with four different antigens and without antigens. In the absence of the antigen, substantial conformational rearrangements due to crystal packing effects, especially in the CDR-H3, CDR-H1, and CDR-L3 loops can be observed. While five of the six structures belong to the same kinetic dominant minimum in solution, the 1OCW, crystallized without antigen, differing substantially from all other structures, lies in a side minimum in solution. We obtained three macrostates and again observe shifts in the interface angle distributions upon changes in the binding site CDR loop conformations. Furthermore, Supplementary Table S6 summarizes the canonical cluster representatives present within the obtained macrostate ensembles in solution and again for certain CDR loops various canonical cluster representatives belong to the same kinetic minimum and thus should be combined. For the highest populated canonical cluster of the CDR-L3 loop with a loop length of nine, five of the six available canonical clusters belong to the same kinetic minimum. Our results are in strong agreement with previous studies, showing that the CDR-L3 loop can adopt various conformations in solution, in which the majority of canonical clusters are present and even belong to the same kinetic minimum27. Recent studies discussed the hidden role of the DE loops in antibodies, which are usually considered as framework region. This fourth solvent-exposed loop, the so-called DE loop, adjacent to CDR1 and CDR2 loops, also shows, similar as the CDR loops, a high variability in sequence and structure and is involved in some antibody-antigen interactions; however, even if no direct contact with the antigen is present, it can modulate the behavior of the CDR loops51. The DE loop located on the heavy chain is called H4 loop, while the DE loop of the light chain is known as L4 loop. The crucial role of the H4 binding site loop for molecular recognition and in the antigen-binding process has recently been discussed for T-cell receptors52. The free energy surfaces and conformational diversity of both the L4 and the H4 loops are illustrated in Supplementary Fig. S9. We clearly see that both the L4 and H4 loops are correlated with the CDR loops, indicating their prominent role in antigen-binding and their influence on the binding site loop conformations.
For antibody structure design our results imply, that all CDR loops can adopt different conformations in solution, which are not only strongly correlated with each other, but can also shift the relative VH–VL interdomain distributions. Conformational changes in the paratope are mainly dominated by CDR-L2, CDR-H1, and CDR-H3 loop rearrangements, which directly influence the relative interdomain orientations and in some cases even the elbow-angle (Fig. 10). Conformational changes in the antibody binding site can induce changes in the elbow-angle, indicating an allosteric effect. The CDR-H2 loop conformation has been discussed to be determined by the heavy chain framework residue 7153. In two studied antibody fragments residue 71 is an arginine resulting in a stabilization of the CDR-H2 and CDR-H1 loop, as salt bridges and hydrogen bond interactions are formed. While the salt bridges and hydrogen bond interactions with the CDR-H2 loop occur in up to 90% of the frames, interactions with the CDR-H1 loop occur only in certain macrostates, indicating that residue H71 plays an important role in stabilizing and favoring specific CDR-H1 loop conformational states in solution. Besides interactions with residue H71, both the CDR-H1 and CDR-H2 loops are strongly influenced by rearrangements of the paratope. The CDR-H3 loop is not influenced by different paratope states in the example of the specific IL-18 binding antibody. Apart from the high specificity of this antibody, the CDR-H3 loop is rather short, containing only four residues. Both aspects together might explain this low flexibility and the small contributions to conformational rearrangements of the paratope. However, it has already been shown, that a less specific or naïve antibody of the same short CDR-H3 loop length, can reveal a high flexibility, possibly influencing the other CDR loop conformations18. In line with these observations, the multispecific SPE7 antibody contains a nine residue long CDR-H3 loop, which substantially contributes together with the CDR-H1 and CDR-L2 loops to rearrangements of the CDR loop binding interface. The CDR loop length might influence the resulting flexibility, but as can be seen in the affinity maturation pair, the CDR loops of the same length rigidify substantially upon affinity maturation, indicating that the conformational diversity of a loop and the influence on the other binding CDR loops is governed by their sequence composition and not necessarily by their length. Upon affinity maturation and for highly specific antibodies we observe smaller conformational changes in the CDR loops and consequently also smaller shifts in the relative VH–VL orientation, compared to naïve or multispecific antibodies. Additionally, we sample conformational transitions between different canonical clusters for all CDR loops and identify additional dominant solution structures, which are not apparent from X-ray structures most likely due to crystal packing effects. We also observe that various canonical conformations belong to the same kinetic minimum in solution and thus might be combined.
Fig. 10. Overview and summary of all investigated antibody fragments with their respective PDB codes, visualizing which of the CDR loops is influenced by different paratope states.
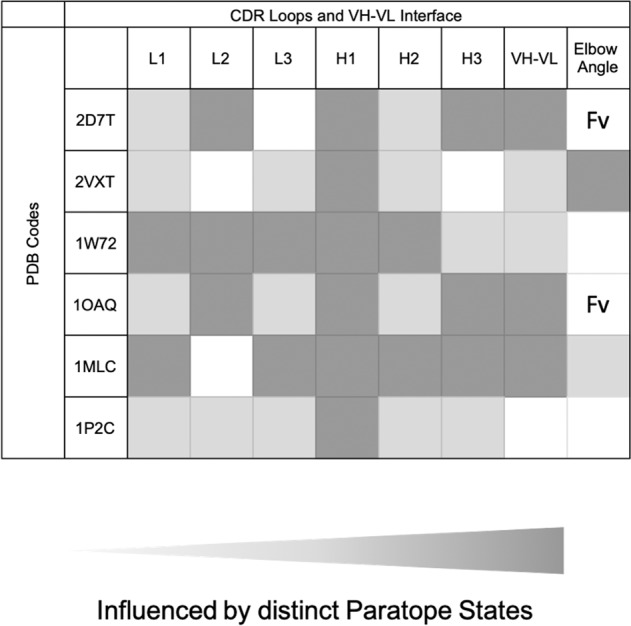
As we observe a strong dependency of the CDR loop conformations on the relative VH–VL domain orientation we also included the influence of different paratope states on the relative interface distributions. The strength of the influence of different paratope states on the individual CDR loops, the VH–VL domain orientation and the elbow-angle correlates with the intensity of the different shades of gray.
In conclusion, antibody paratopes are flexible and exist in several different conformations. We characterize kinetically accessible paratope states and observe correlated binding interface loop rearrangements for several antibody fragments. Besides kinetic characterization of the paratope into different correlated CDR loop states, we also present a strong dependence of the CDR loop conformations on the relative interdomain orientation. In the studied Fab cases we also see an influence of the different paratope states, including CDR loop movements and changes in the relative interdomain orientation, on the obtained elbow-angle distributions. We show that antibody CDR loop conformations are strongly correlated, reducing the combinatorics of possible states of the complete binding interface and shifting the relative VH and VL orientation and the elbow-angle distributions. These findings have broad implications in the field of antibody design and in the development of biotherapeutics as they provide a new paradigm in the understanding of CDR binding loop states, antibody-antigen recognition, relative VH and VL interface angles and elbow-angle distributions and their respective dynamics.
Methods
Structure preparation
Experimental structure information was available for all considered antibody fragments. We deleted the co-crystallized antigen in all complex crystal structures. The starting structures for simulations were prepared in MOE (Molecular Operating Environment, Chemical Computing Group, version 2018.01) using the Protonate3D tool54,55. To neutralize the charges we used the uniform background charge56–58. Using the tleap tool of the AmberTools1856,57 package, the crystal structures were soaked with cubic water boxes of TIP3P water molecules with a minimum wall distance of 10 Å to the protein59. The box size in MD simulations can influence the resulting dynamics if sampling is insufficient60,61. For all crystal structures parameters of the AMBER force field 14SB were used62. The antibody fragments were carefully equilibrated using a multistep equilibration protocol63.
Metadynamics simulations
To enhance the sampling of the conformational space well-tempered bias-exchange metadynamics64–66 simulations were performed in GROMACS67,68 with the PLUMED 2 implementation69. As enhanced sampling technique, we chose metadynamics as it allows to focus the enhanced sampling on predefined collective variables (CV). The sampling is accelerated by a history-dependent bias potential, which is constructed in the space of the CVs64,66,70. As collective variables, we used a well-established protocol, boosting a linear combination of sine and cosine of the ψ torsion angles of all CDR loops calculated with functions MATHEVAL and COMBINE implemented in PLUMED 218,27,43,52,69,71. As discussed previously the ψ torsion angle captures conformational transitions comprehensively72. The underlying method presented in this paper has been validated in various studies against a large number of experimental results. The simulations were performed at 300 K in an NpT ensemble using the GPU implementation of the pmemd module47 to be as close to the experimental conditions as possible and to obtain the correct density distributions of both protein and water. We used a Gaussian height of 10.0 kcal/mol. Gaussian deposition occurred every 1000 steps and a bias factor of 10 was used. 200 ns of bias-exchange metadynamics simulations were performed for each available antibody fragment crystal structure. The resulting trajectories were clustered in cpptraj57,73 by using the average linkage hierarchical clustering algorithm with a distance cut-off criterion of 1.2 Å resulting in a large number of clusters. The cluster representatives for the antibody fragments were equilibrated and simulated for 100 ns using the AMBER1874 simulation package.
Molecular dynamics simulations
Molecular dynamics simulations were performed in an NpT ensemble using pmemd.cuda47. Bonds involving hydrogen atoms were restrained by applying the SHAKE algorithm75, allowing a time step of 2.0 fs. Atmospheric pressure (1 bar) of the system was set by weak coupling to an external bath using the Berendsen algorithm76. The Langevin thermostat77 was used to maintain the temperature during simulations at 300 K.
With the obtained trajectories we performed a time-lagged independent component analysis (tICA) using the python library PyEMMA 2 employing a lag time of 10 ns78. Thermodynamics and kinetics were calculated with a Markov-state model79 by using PyEMMA 2, which uses the k-means clustering algorithm80 to define microstates and the PCCA + clustering algorithm81 to coarse grain the microstates to macrostates. Markov-state models are network models which provide valuable insights for conformational states and transition probabilities between them, as it is possible to accurately identify the boundaries between two states79. The states are defined based on kinetic criteria, which allow us to identify the boundaries between free energy wells. Basically, MSMs coarse-grain the system’s dynamics, which reflect the free energy surface and ultimately determine the system’s structure and dynamics. Thus, MSMs provide important insights and enhance the understanding of states and transition probabilities, which can make a quantitative connection with experiment79,82.
The sampling efficiency and the reliability of the Markov-state model (e.g., defining optimal feature mappings) can be evaluated with the Chapman–Kolmogorov test46,83, by using the variational approach for Markov processes84 and by taking into account the fraction of states used, as the network states must be fully connected to calculate probabilities of transitions and the relative equilibrium probabilities. To build the Markov-state model we used the backbone torsions of the respective CDR loop, defined 150 microstates using the k-means clustering algorithm and applied a lag time of 10 ns.
The median canonical structure information for each CDR loop, provided in the tables in the supplementary material, was extracted from the PyIgClassify database22 and compared to the obtained CDR loop ensembles in solution. We then used the respective macrostate ensembles to investigate correlations between the different paratope states and the relative VH and VL orientations and the elbow angles.
Relative VH and VL orientations and elbow-angle calculations
For the relative VH and VL orientations, described in this study, we defined a torsion angle between the center of mass (COM) of the CDR loops of the light chain, the COM of the VL domain, the COM of the VH domain and the COM of the CDR loops of the heavy chain. Additionally, we also performed calculations using the well-established program ABangle85,86 to calculate the dependence of the relative VH–VL orientations on the CDR loop conformations. The results of the ABangle are shown in Supplementary Table S8. A comparison of the ABangle results with our defined torsion angle to characterize the antibody interface is illustrated in Supplementary Fig. 22.
As measure for the elbow-angle we calculated a torsion angle between the COM of variable domain, a defined vector between the COMs of the switch regions and the COM of the constant region. We also included the results (Supplementary Table S7) for the elbow-angle calculations by using the measure presented by Stanfield et al. in the supporting information87.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Supplementary information
Acknowledgements
This work was supported by the Austrian Science Fund (FWF) via the grants P30565, P30402 and DOC30 P31434.
Author contributions
M.F.Q., N.D.B., K.R.L. conceived the study. M.F.Q., N.D.B., B.F.M., K.B.K., and F.W. performed research under the supervision of A.B., G.G., and K.R.L. M.F.Q. drafted the manuscript. All authors critically reviewed the manuscript.
Data availability
All data generated or analyzed during this study are included in this published article (and its supplementary information files).
Code availability
The code generated used in the current study is available from the corresponding author on reasonable request.
Competing interests
A.B. and G.G. are Roche employees; Roche has an interest in developing antibody-based therapeutics.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary information is available for this paper at 10.1038/s42003-020-01319-z.
References
- 1.Kaplon H, Reichert JM. Antibodies to watch in 2019. mAbs. 2019;11:219–238. doi: 10.1080/19420862.2018.1556465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Reichert JM. Antibodies to watch in 2017. mAbs. 2016;9:167–181. doi: 10.1080/19420862.2016.1269580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chames P, Van Regenmortel M, Weiss E, Baty D. Therapeutic antibodies: successes, limitations and hopes for the future. Br. J. Pharm. 2009;157:220–233. doi: 10.1111/j.1476-5381.2009.00190.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kaplon H, Muralidharan M, Schneider Z, Reichert JM. Antibodies to watch in 2020. mAbs. 2020;12:1703531. doi: 10.1080/19420862.2019.1703531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nguyen MN, Pradhan MR, Verma C, Zhong P. The interfacial character of antibody paratopes: analysis of antibody–antigen structures. Bioinformatics. 2017;33:2971–2976. doi: 10.1093/bioinformatics/btx389. [DOI] [PubMed] [Google Scholar]
- 6.Davies DR, Chacko S. Antibody structure. Acc. Chem. Res. 1993;26:421–427. doi: 10.1021/ar00032a005. [DOI] [Google Scholar]
- 7.Wong, W. K., Leem, J., Deane, C. M. Comparative analysis of the CDR loops of antigen receptors. bioRxiv10.1101/709840 (2019). [DOI] [PMC free article] [PubMed]
- 8.Al-Lazikani B, Lesk AM, Chothia C. Standard conformations for the canonical structures of immunoglobulins11Edited by I. A. Wilson. J. Mol. Biol. 1997;273:927–948. doi: 10.1006/jmbi.1997.1354. [DOI] [PubMed] [Google Scholar]
- 9.Chothia C, et al. Conformations of immunoglobulin hypervariable regions. Nature. 1989;342:877–883. doi: 10.1038/342877a0. [DOI] [PubMed] [Google Scholar]
- 10.North B, Lehmann A, Dunbrack RL, Jr, New A. Clustering of antibody CDR loop conformations. J. Mol. Biol. 2011;406:228–256. doi: 10.1016/j.jmb.2010.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Martin ACR, Thornton JM. Structural families in loops of homologous proteins: automatic classification, modelling and application to antibodies. J. Mol. Biol. 1996;263:800–815. doi: 10.1006/jmbi.1996.0617. [DOI] [PubMed] [Google Scholar]
- 12.Regep C, Georges G, Shi J, Popovic B, Deane CM. The H3 loop of antibodies shows unique structural characteristics. Proteins. 2017;85:1311–1318. doi: 10.1002/prot.25291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burkovitz A, Sela-Culang I, Ofran Y. Large-scale analysis of somatic hypermutations in antibodies reveals which structural regions, positions and amino acids are modified to improve affinity. FEBS J. 2014;281:306–319. doi: 10.1111/febs.12597. [DOI] [PubMed] [Google Scholar]
- 14.Davenport TM, et al. Somatic hypermutation-induced changes in the structure and dynamics of HIV-1 broadly neutralizing antibodies. Structure. 2016;24:1346–1357. doi: 10.1016/j.str.2016.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Clark LA, Ganesan S, Papp S, van Vlijmen HWT. Trends in antibody sequence changes during the somatic hypermutation process. J. Immunol. 2006;177:333. doi: 10.4049/jimmunol.177.1.333. [DOI] [PubMed] [Google Scholar]
- 16.Bassing CH, Swat W, Alt FW. The mechanism and regulation of chromosomal V(D)J recombination. Cell. 2002;109:S45–S55. doi: 10.1016/S0092-8674(02)00675-X. [DOI] [PubMed] [Google Scholar]
- 17.French D, Laskov R, Scharff M. The role of somatic hypermutation in the generation of antibody diversity. Science. 1989;244:1152. doi: 10.1126/science.2658060. [DOI] [PubMed] [Google Scholar]
- 18.Fernández-Quintero ML, et al. Characterizing the diversity of the CDR-H3 loop conformational ensembles in relationship to antibody binding properties. Front. Immunol. 2019;9:3065. doi: 10.3389/fimmu.2018.03065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Marks C, et al. Sphinx: merging knowledge-based and ab initio approaches to improve protein loop prediction. Bioinformatics. 2017;33:1346–1353. doi: 10.1093/bioinformatics/btw823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuroda D, Shirai H, Kobori M, Nakamura H. Systematic classification of CDR-L3 in antibodies: Implications of the light chain subtypes and the VL–VH interface. Proteins: Struct., Funct., Bioinform. 2009;75:139–146. doi: 10.1002/prot.22230. [DOI] [PubMed] [Google Scholar]
- 21.Townsend CL, et al. Significant differences in physicochemical properties of human immunoglobulin kappa and lambda CDR3 Regions. Front Immunol. 2016;7:388–388. doi: 10.3389/fimmu.2016.00388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Adolf-Bryfogle J, Xu Q, North B, Lehmann A, Dunbrack RL. PyIgClassify: a database of antibody CDR structural classifications. Nucleic Acids Res. 2015;43:D432–D438. doi: 10.1093/nar/gku1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Marcatili P, Rosi A, Tramontano A. PIGS: automatic prediction of antibody structures. Bioinformatics. 2008;24:1953–1954. doi: 10.1093/bioinformatics/btn341. [DOI] [PubMed] [Google Scholar]
- 24.Weitzner BD, et al. Modeling and docking of antibody structures with Rosetta. Nat. Protoc. 2017;12:401. doi: 10.1038/nprot.2016.180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kuroda D, Shirai H, Jacobson MP, Nakamura H. Computer-aided antibody design. Protein Eng., Des. Selection. 2012;25:507–522. doi: 10.1093/protein/gzs024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nowak J, et al. Length-independent structural similarities enrich the antibody CDR canonical class model. mAbs. 2016;8:751–760. doi: 10.1080/19420862.2016.1158370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fernández-Quintero ML, Math BF, Loeffler JR, Liedl KR. Transitions of CDR-L3 loop canonical cluster conformations on the micro-to-millisecond timescale. Front. Immunol. 2019;10:2652. doi: 10.3389/fimmu.2019.02652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fernández-Quintero ML, Kraml J, Georges G, Liedl KR. CDR-H3 loop ensemble in solution – conformational selection upon antibody binding. mAbs. 2019;11:1077–1088. doi: 10.1080/19420862.2019.1618676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Abhinandan KR, Martin ACR. Analysis and prediction of VH/VL packing in antibodies. Protein Eng. Des. Selection. 2010;23:689–697. doi: 10.1093/protein/gzq043. [DOI] [PubMed] [Google Scholar]
- 30.Banfield MJ, King DJ, Mountain A, Brady RL. VL:VH domain rotations in engineered antibodies: crystal structures of the Fab fragments from two murine antitumor antibodies and their engineered human constructs. Proteins: Struct. Funct., Bioinforma. 1997;29:161–171. doi: 10.1002/(SICI)1097-0134(199710)29:2<161::AID-PROT4>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 31.James LC, Tawfik DS. Conformational diversity and protein evolution—a 60-year-old hypothesis revisited. Trends Biochem. Sci. 2003;28:361–368. doi: 10.1016/S0968-0004(03)00135-X. [DOI] [PubMed] [Google Scholar]
- 32.Pauling L. A theory of the structure and process of formation of antibodies*. J. Am. Chem. Soc. 1940;62:2643–2657. doi: 10.1021/ja01867a018. [DOI] [Google Scholar]
- 33.Foote J, Milstein C. Conformational isomerism and the diversity of antibodies. Proc. Natl Acad. Sci. USA. 1994;91:10370–10374. doi: 10.1073/pnas.91.22.10370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sotriffer CA, Rode BM, Varga JM, Liedl KR. Elbow flexibility and ligand-induced domain rearrangements in antibody Fab NC6.8: large effects of a small hapten. Biophys. J. 2000;79:614–628. doi: 10.1016/S0006-3495(00)76320-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sotriffer CA, Liedl KR, Linthicum DS, Rode BM, Varga JM. Ligand-induced domain movement in an antibody fab: molecular dynamics studies confirm the unique domain movement observed experimentally for fab NC6.8 upon complexation and reveal its segmental flexibility11Edited by I. Wilson. J. Mol. Biol. 1998;278:301–306. doi: 10.1006/jmbi.1998.1684. [DOI] [PubMed] [Google Scholar]
- 36.Argiriadi MA, Xiang T, Wu C, Ghayur T, Borhani DW. Unusual water-mediated antigenic recognition of the proinflammatory cytokine interleukin-18. J. Biol. Chem. 2009;284:24478–24489. doi: 10.1074/jbc.M109.023887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hülsmeyer M, et al. A major histocompatibility complex·peptide-restricted antibody and T cell receptor molecules recognize their target by distinct binding modes: crystal structure of human leukocyte antigen (HLA)-A1·MAGE-A1 in complex with FAB-HYB3. J. Biol. Chem. 2005;280:2972–2980. doi: 10.1074/jbc.M411323200. [DOI] [PubMed] [Google Scholar]
- 38.James LC, Roversi P, Tawfik DS. Antibody multispecificity mediated by conformational diversity. Science. 2003;299:1362–1367. doi: 10.1126/science.1079731. [DOI] [PubMed] [Google Scholar]
- 39.Zhou Z-H, Tzioufas AG, Notkins AL. Properties and function of polyreactive antibodies and polyreactive antigen-binding B cells. J. Autoimmun. 2007;29:219–228. doi: 10.1016/j.jaut.2007.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gunti S, Notkins AL. Polyreactive antibodies: function and quantification. J. Infect. Dis. 2015;212:42–46. doi: 10.1093/infdis/jiu512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Braden BC, et al. Three-dimensional structures of the free and the antigen-complexed Fab from monoclonal anti-lysozyme antibody D44.1. J. Mol. Biol. 1994;243:767–781. doi: 10.1016/0022-2836(94)90046-9. [DOI] [PubMed] [Google Scholar]
- 42.Cauerhff A, Goldbaum FA, Braden BC. Structural mechanism for affinity maturation of an anti-lysozyme antibody. Proc. Natl Acad. Sci. USA. 2004;101:3539. doi: 10.1073/pnas.0400060101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fernández-Quintero, M. L., Heiss, M. C., Liedl, K. R. Antibody humanization—the Influence of the antibody framework on the CDR-H3 loop ensemble in solution. Protein Engineering, Design and Selection10.1093/protein/gzaa004 (2020). [DOI] [PMC free article] [PubMed]
- 44.Fernández-Quintero, M. L. et al. VH-VL interdomain dynamics observed by computer simulations and NMR. Proteins: Struct. Funct. Bioinform.10.1002/prot.25872 (2020). [DOI] [PMC free article] [PubMed]
- 45.Niederfellner G, et al. Epitope characterization and crystal structure of GA101 provide insights into the molecular basis for type I/II distinction of CD20 antibodies. Blood. 2011;118:358–367. doi: 10.1182/blood-2010-09-305847. [DOI] [PubMed] [Google Scholar]
- 46.Karush J. On the Chapman–Kolmogorov Equation. Ann. Math. Stat. 1961;32:1333–1337. doi: 10.1214/aoms/1177704871. [DOI] [Google Scholar]
- 47.Salomon-Ferrer R, Götz AW, Poole D, Le Grand S, Walker RC. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput. 2013;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- 48.Fuchs JE, et al. Independent metrics for protein backbone and side-chain flexibility: time scales and effects of ligand binding. J. Chem. Theory Comput. 2015;11:851–860. doi: 10.1021/ct500633u. [DOI] [PubMed] [Google Scholar]
- 49.Boehr DD, Dyson HJ, Wright PE. An NMR perspective on enzyme dynamics. Chem. Rev. 2006;106:3055–3079. doi: 10.1021/cr050312q. [DOI] [PubMed] [Google Scholar]
- 50.Henzler-Wildman K, Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 51. Kelow, S. P., Adolf-Bryfogle, J., Dunbrack, R. L. Hiding in plain sight: structure and sequence analysis reveals the importance of the antibody DE loop for antibody-antigen binding. bioRxiv10.1101/2020.02.12.946350 (2020). [DOI] [PMC free article] [PubMed]
- 52.Fernández-Quintero ML, Seidler CA, Liedl KR. T-Cell receptor variable β domains rigidify during affinity maturation. Sci. Rep. 2020;10:4472. doi: 10.1038/s41598-020-61433-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tramontano A, Chothia C, Lesk AM. Framework residue 71 is a major determinant of the position and conformation of the second hypervariable region in the VH domains of immunoglobulins. J. Mol. Biol. 1990;215:175–182. doi: 10.1016/S0022-2836(05)80102-0. [DOI] [PubMed] [Google Scholar]
- 54.Labute P. Protonate3D: assignment of ionization states and hydrogen coordinates to macromolecular structures. Proteins. 2009;75:187–205. doi: 10.1002/prot.22234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chemical Computing Group (CCG), 1010 Sherbrooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7 (2020).
- 56.Case DA, et al. AMBER 2016. San Francisco: University of California; 2016. [Google Scholar]
- 57.Roe DR, Cheatham TE. PTRAJ and CPPTRAJ: software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- 58.Hub JS, de Groot BL, Grubmüller H, Groenhof G. Quantifying artifacts in ewald simulations of inhomogeneous systems with a net charge. J. Chem. Theory Comput. 2014;10:381–390. doi: 10.1021/ct400626b. [DOI] [PubMed] [Google Scholar]
- 59.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- 60.Gapsys, V., de Groot, B. L. Comment on “Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size.” bioRxiv10.1101/563064 (2019). [DOI] [PMC free article] [PubMed]
- 61.El Hage K, Hédin F, Gupta PK, Meuwly M, Karplus M. Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size. eLife. 2018;7:e35560. doi: 10.7554/eLife.35560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Maier JA, et al. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015;11:3696–3713. doi: 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wallnoefer HG, Liedl KR, Fox T. A challenging system: free energy prediction for factor Xa. J. Comput. Chem. 2011;32:1743–1752. doi: 10.1002/jcc.21758. [DOI] [PubMed] [Google Scholar]
- 64.Barducci A, Bussi G, Parrinello M. Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett. 2008;100:020603. doi: 10.1103/PhysRevLett.100.020603. [DOI] [PubMed] [Google Scholar]
- 65.Biswas, M., Lickert, B. Stock, G. Metadynamics Enhanced Markov Modeling of Protein Dynamics. 10.1021/acs.jpcb.7b11800 (2018). [DOI] [PubMed]
- 66.Barducci A, Bonomi M, Parrinello M. Metadynamics. WIREs Comput Mol. Sci. 2011;1:826–843. doi: 10.1002/wcms.31. [DOI] [Google Scholar]
- 67.Abraham MJ, et al. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. doi: 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- 68.Pronk S, et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Tribello GA, Bonomi M, Branduardi D, Camilloni C, Bussi G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014;185:604–613. doi: 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
- 70.Ilott AJ, Palucha S, Hodgkinson P, Wilson MR. Well-tempered metadynamics as a tool for characterizing multi-component, crystalline molecular machines. J. Phys. Chem. B. 2013;117:12286–12295. doi: 10.1021/jp4045995. [DOI] [PubMed] [Google Scholar]
- 71.Fernández-Quintero, M. L., Pomarici, N. D., Seidler, C. A., Loeffler, J. R. & Liedl, K. R. T-cell receptor CDR3 loop confor mations in solution shift the relative VH-VL domain distributions. Front. Immunol., 10.3389/fimmu.2020.01440 (2020). [DOI] [PMC free article] [PubMed]
- 72.Ramachandran GN, Ramakrishnan C, Sasisekharan V. Stereochemistry of polypeptide chain configurations. J. Mol. Biol. 1963;7:95–99. doi: 10.1016/S0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- 73.Shao J, Tanner SW, Thompson N, Cheatham TE. Clustering molecular dynamics trajectories: 1. Characterizing the performance of different clustering algorithms. J. Chem. Theory Comput. 2007;3:2312–2334. doi: 10.1021/ct700119m. [DOI] [PubMed] [Google Scholar]
- 74.Case DA, et al. AMBER 2020. San Francisco: University of California; 2020. [Google Scholar]
- 75.Miyamoto S, Kollman PA. Settle: an analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Computat. Chem. 1992;13:952–962. doi: 10.1002/jcc.540130805. [DOI] [Google Scholar]
- 76.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. doi: 10.1063/1.448118. [DOI] [Google Scholar]
- 77.Adelman SA, Doll JD. Generalized Langevin equation approach for atom/solid-surface scattering: general formulation for classical scattering off harmonic solids. J. Chem. Phys. 1976;64:2375–2388. doi: 10.1063/1.432526. [DOI] [Google Scholar]
- 78.Scherer MK, et al. PyEMMA 2: a software package for estimation, validation, and analysis of Markov models. J. Chem. Theory Comput. 2015;11:5525–5542. doi: 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- 79.Chodera JD, Noé F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014;25:135–144. doi: 10.1016/j.sbi.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Likas A, Vlassis N, Verbeek JJ. The global k-means clustering algorithm. Pattern Recognit. 2003;36:451–461. doi: 10.1016/S0031-3203(02)00060-2. [DOI] [Google Scholar]
- 81.Röblitz S, Weber M. Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification. Adv. Data Anal. Classification. 2013;7:147–179. doi: 10.1007/s11634-013-0134-6. [DOI] [Google Scholar]
- 82.Bowman, G. R., Pande, V., Noé, F. (eds) An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation (Springer, 2014).
- 83.Miroshin RN. Special solutions of the Chapman–Kolmogorov equation for multidimensional-state Markov processes with continuous time. Vestn. St. Petersburg Univ.: Math. 2016;49:122–129. doi: 10.3103/S1063454116020114. [DOI] [Google Scholar]
- 84.Wu, H. & Noé, F. Variational Approach for Learning Markov Processes from Time Series Data10.1007/s00332-019-09567-y (2017).
- 85.Dunbar J, Fuchs A, Shi J, Deane CM. ABangle: characterising the VH–VL orientation in antibodies. Protein Eng., Des. Selection. 2013;26:611–620. doi: 10.1093/protein/gzt020. [DOI] [PubMed] [Google Scholar]
- 86.Bujotzek A, et al. VH-VL orientation prediction for antibody humanization candidate selection: acase study. mAbs. 2016;8:288–305. doi: 10.1080/19420862.2015.1117720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Stanfield RL, Zemla A, Wilson IA, Rupp B. Antibody elbow angles are influenced by their light chain class. J. Mol. Biol. 2006;357:1566–1574. doi: 10.1016/j.jmb.2006.01.023. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated or analyzed during this study are included in this published article (and its supplementary information files).
The code generated used in the current study is available from the corresponding author on reasonable request.