A Semi-supervised Joint Network for Simultaneous Left Ventricular Motion Tracking and Segmentation in 4D Echocardiography

Abstract

This work presents a novel deep learning method to combine segmentation and motion tracking in 4D echocardiography. The network iteratively trains a motion branch and a segmentation branch. The motion branch is initially trained entirely unsupervised and learns to roughly map the displacements between a source and a target frame. The estimated displacement maps are then used to generate pseudo-ground truth labels to train the segmentation branch. The labels predicted by the trained segmentation branch are fed back into the motion branch and act as landmarks to help retrain the branch to produce smoother displacement estimations. These smoothed out displacements are then used to obtain smoother pseudo-labels to retrain the segmentation branch. Additionally, a biomechanically-inspired incompressibility constraint is implemented in order to encourage more realistic cardiac motion. The proposed method is evaluated against other approaches using synthetic and in-vivo canine studies. Both the segmentation and motion tracking results of our model perform favorably against competing methods.

1. Introduction

Echocardiography is a non-invasive and cost-efficient tool that allows clinicians to visually evaluate the left ventricular (LV) wall and detect any motion or structural abnormalities in order to evaluate cardiovascular health and diagnose cardiovascular diseases (CVD). However, qualitative assessment is prone to inter-observer variability and cannot completely characterize the severity of the abnormality. As a result, many efforts have been made to develop objective, quantitative methods for assessing cardiovascular health through the use of echocardiography.

Motion tracking and segmentation both play crucial roles in the detection and quantification of myocardial dysfunction and can help in the diagnosis of CVD. Traditionally, however, these tasks are treated uniquely and solved as separate steps. Often times, motion tracking algorithms will use segmentations as an anatomical guide to sample points and regions of interest used to generate displacement fields [8,11,12,17]. If initial segmentations are poorly done, errors in the segmentation will propagate and lead to inaccurate displacement fields, which can further propagate to inaccurate clinical measurements. This is problematic as the task of segmentation is nontrivial, especially in echocardiography where the low signal-to-noise ratio (SNR) inherent in ultrasound results in poorly delineated LV borders. Additionally, there is limited ground truth segmentations available for clinical images due to the impracticality of having an expert manually annotate complete volumetric echocardiographic sequences. Often, only the end-diastolic or end-systolic frames are segmented. This makes it difficult to train and implement automatic segmentation models that rely on supervised learning techniques [15,23].

Recent works in the computer vision and magnetic resonance (MR) image processing fields suggests that the tasks of motion tracking and segmentation are closely related and information used to complete one task may complement and improve the overall performance of the other. In particular, Tsai et al. proposed ObjectFlow, an algorithm that iteratively optimizes segmentation and optical flow in a multi-scale framework until both tasks reach convergence [21]. Building on this, Chen et al. proposed SegFlow, a deep learning approach that combines segmentation and optical flow in an end-to-end unified network that simultaneously trains both tasks. The net exploits the commonality of these two tasks through bi-directional feature sharing [4]. However, these approaches have practical limitations. ObjectFlow is optimized online and, therefore, is computationally intensive and time-consuming [21]. SegFlow is trained in a supervised manner and requires ground truth segmentation and flow fields [4]. Qin et al. successfully implements the idea of combining motion and segmentation on 2D cardiac MR sequences by developing a dual Siamese style recurrent spatial transformer network and fully convolutional segmentation network to simultaneously estimate motion and generate segmentation masks. Features are shared between both branches [13,14]. However, this work is limited to MR images, which have higher SNR than echocardiographic images and, therefore, more clearly delineated LV walls which makes it challenging to directly apply to echocardiography. Furthermore, similar works in echocardiography are limited to 2D images [1,20]. Because of this, out of plane motion cannot be accurately captured, which provides valuable clinical information for cardiac deformation analysis.

This paper proposes a 4D (3D+t) semi-supervised joint network to simultaneously track LV motion while segmenting the LV wall. The network is trained in an iterative manner where results from one branch influences and regularizes the other. Displacement fields are further regularized by a biomechanically-inspired incompressibility constraint that enforces realistic cardiac motion behavior. The proposed model is different from other models in that it expands the network to 4D in order to capture out of plane motion. Furthermore, it addresses the issue of limited ground truth in clinical datasets by employing a training framework that only requires a single segmented frame per sequence and no ground truth displacement fields. To the knowledge of the authors, this work is the first to successfully combine segmentation and motion tracking simultaneously on volumetric echocardiographic sequences.

2. Method

The architecture of the proposed model is illustrated in Fig. 1. The objective is to simultaneously generate displacement fields and LV masks in 4D echocardiography by taking advantage of the complementary nature between the tasks of segmentation and motion tracking with the assistance of a biomechanical incompressibility constraint.

Fig. 1.

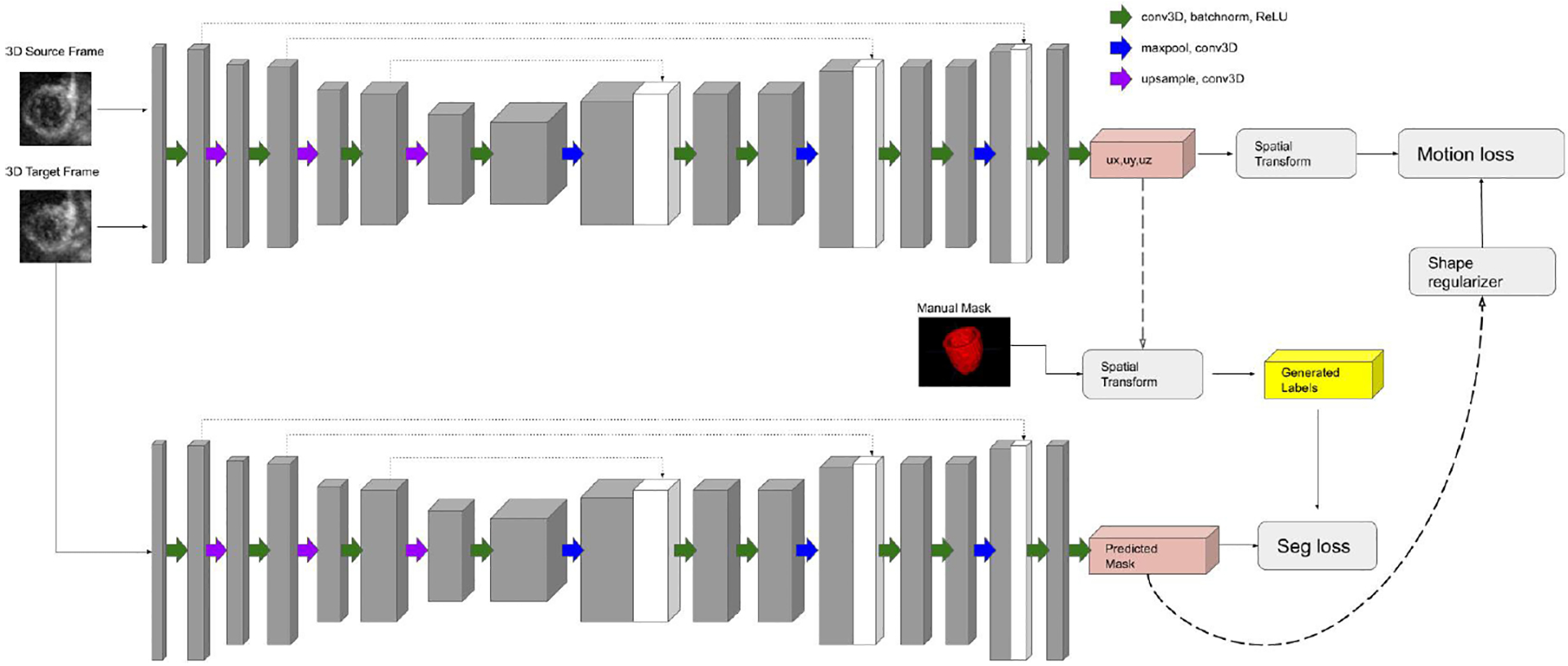
Architecture of our proposed joint network: The motion branch (top) and the segmentation branch (bottom).

2.1. Motion Network (Unsupervised)

Large amounts of ground truth clinical data is often difficult to obtain. A 3D U-Net inspired architecture is designed to input an image pair. This pair is comprised of two volumetric images (a source frame and a target frame, stacked as a 2 channel single input) from a single sequence. The network consists of a downsampling analysis path followed by an upsampling synthesis path with skip connections that concatenate features learned in the analysis path with features learned in the synthesis path [23]. The output of the network is a 3 channel volumetric displacement map, corresponding to displacements in the x-y-z directions. In order for the network to train without the usage of ground truth, a VoxelMorph inspired training framework is implemented [3]. The output x-y-z displacement field is used to transform the input source frame via trilinear interpolation. Network weights are trained by minimizing the mean square difference between the transformed source frame and the target frame, effectively encoding the displacement field between the two frames. The loss function can be described as follows:

$$L_{\mathit{\text{motion}}}={\lambda }_{\mathit{\text{motion}}}\frac{1}{N}\sum _{i=1}^N{\left(I_{i,t}-F\left(I_{i,s},U_i\right)\right)}^2$$ (1)

where I_i,s and I_i,t are the source and target images, respectively of the i-th image pair, U_i is the predicted displacement field that maps the source and target images, F = (I_i,s, U_i)) is a spatial transforming operator that morphs I_i,s to I_i,t using U_i, and λ_motion is a weighting term.

2.2. Segmentation Network (Weakly-supervised)

The segmentation branch of the proposed model follows generally the same 3D U-Net inspired architecture as the motion branch [23]. The primary difference being that the input of the segmentation branch is a single volumetric image (the same target frame used to generate the displacement field of the motion network), and the output is a single volmetric segmented LV mask. The displacement field generated by the motion network is used to transform a manually segmented source frame (corresponding to the inputted target frame) in a similar Voxelmorph-inspired framework as the motion branch [6]. This transformed segmentation acts as a pseudo-ground truth label for training the segmentation branch. The network seeks to optimize a combined binary cross entropy and dice score between the propagated source segmentation and the predicted target segmentation. The loss function can be described as follows:

$$L_{\mathit{\text{dice}}}=\frac{1}{N}\sum _{i=1}^N\left(1-\frac{\left|M_{i,t}\cap F\left(Y_{i,s},U_i\right)\right|}{\left|M_{i,t}\right|+\left|F\left(Y_{i,s},U_i\right)\right|}\right)$$ (2)

$$L_{\mathit{\text{bce}}}=\frac{1}{N}\sum _{i=1}^N(-y_i(\mathit{\text{log}}\left(p_i\right)+\left(1-y_i\right)\left(\mathit{\text{log}}\left(1-p_i\right)\right)$$ (3)

$$L_{\mathit{\text{seg}}}={\lambda }_{\mathit{\text{dice}}}{L}_{\mathit{\text{dice}}}+{\lambda }_{\mathit{\text{bce}}}{L}_{\mathit{\text{bce}}}$$ (4)

where Y_i,s is the manually segmented mask of the source image, M_i,t is the predicted mask of the target image, y is a binary indicator for if a voxel is correctly labeled, and p is the predicted probability a voxel is part of the LV segmentation, and λ_dice and λ_bce are weighting terms. All other terms are as previously defined.

2.3. Combining Networks (Joint Learning)

Each network is optimized separately with their respective loss functions. An iterative training framework is designed such that the results and training of one network can positively influence the other in order to create a connection between the two branches. Initially, the motion tracking network is trained in a completely unsupervised manner, as described in Sect. 2.1. This generates a rough 3D displacement field that effectively maps the source frame to the target frame. Using this displacement field, the corresponding source frame segmentation is propagated to obtain a rough target frame segmentation. These rough target frame segmentations are used to retrain the motion tracking branch and act as an additional shape regularization term to guide the network to produce smoother displacement estimations. This regularization term is added to L_motion and can be described as follows:

$$L_{\mathit{\text{shape}}}={\lambda }_{\mathit{\text{shape}}}\frac{1}{N}\sum _{i=1}^N{\left(G_{i,t}-F\left(Y_{i,s},U_i\right)\right)}^2$$ (5)

where G_i,t is the pseudo-ground truth label and λ_shape is a weighting term. All other terms are as previously defined.

These shape regularized displacement estimations are used to generate new, smoother pseudo-ground truth labels, which are then used to retrain the segmentation network to produce more accurate segmentations.

2.4. Incompressibility Constraint

To ensure spatial smoothness and encourage more realistic cardiac motion patterns, flow incompressibility is enforced by penalizing divergence as seen in [9,12,18]. In real cardiac motion, tissue trajectories cannot collapse to a single point nor can a single point generate multiple tissue trajectories. To discourage this unrealistic behavior, sources or sinks in the motion field are penalized. This term is added to L_motion can be described as follows:

$$L_{\mathit{\text{inc}}}={\lambda }_{\mathit{\text{inc}}}\frac{1}{N}\sum _{i=1}^N\Vert \nabla U_i\Vert$$ (6)

where λ_inc is a weighting term. All other terms are as previously defined.

3. Experiments and Results

The general framework is qualitatively evaluated on a synthetic dataset with ground truth displacement fields and segmentations and the joint model is quantitatively evaluated on an in-vivo canine dataset with implanted sonomicrometer crystals for motion detection [19] and manual segmentations. Images are resampled and resized to [64 × 64 × 64] for computational purposes. Experiments and processing were performed using MATLAB and Python. The network was built using PyTorch and trained on a GTX 1080 Ti GPU in batch sizes of 1 for 200 epochs with a learning rate of 1e-4 using Adam optimizer. Online data augmentation included random rotations, flips, and shears. Model hyperparameters were fine-tuned to each dataset.

3.1. Evaluation Using Synthetic Data

An open access dataset, 3D Strain Assessment in Ultrasound (STRAUS) [2], was used. The dataset contained 8 different volumetric sequences with different physiological conditions: 2 left anterior descending artery (LAD) occlusions in the proximal and distal arteries, 1 left circumflex artery occlusion, 1 right circumflex artery occlusion, 2 left bundle branch blocks, a sychronous sequence, and a normal (healthy) sequence. 1 sequence is left out for each testing and validation and 6 sequences are used for training. In total, the model is trained on 204 pairs, validated on 32 pairs, and tested on 32 pairs.

As a proof-of-concept, the effect of a shape regularization term on unsupervised motion tracking and the feasibility of training a segmentation network in a weakly-supervised manner using propagated pseudo-ground truth labels is qualitatively evaluated. For the motion tracking branch, the performance of the network after implementing the shape regularization term using ground truth segmentations is compared to the network trained in a completely unsupervised manner. For the segmentation branch, the network is trained on weak labels generated by propagating an initial manual label using motion fields generated via a shape-tracking algorithm (which originally tracked ground truth labels) and an unsupervised motion network. Figures 2, 3 show improved results after including the shape regularization term and feasible segmentation predictions when trained in a weakly-supervised manner.

Fig. 2.

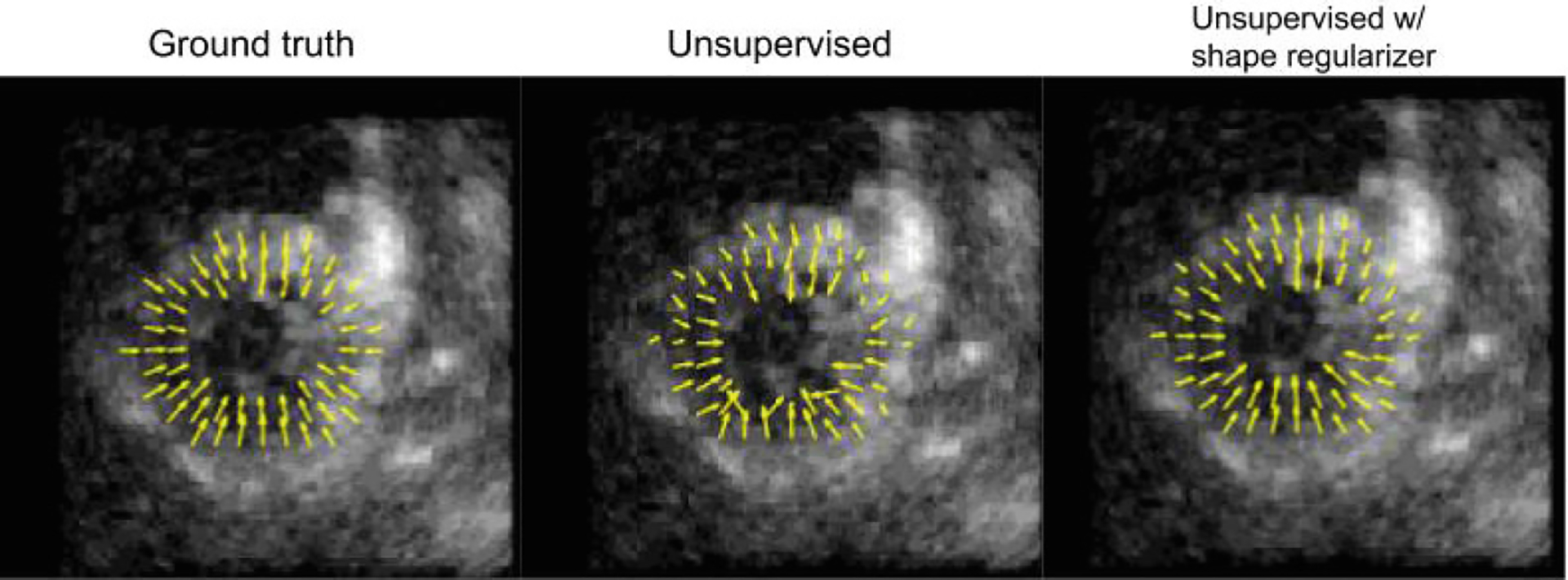
A short-axis view of the displacement vectors for a normal (healthy) synthetic sequence using different methods

Fig. 3.

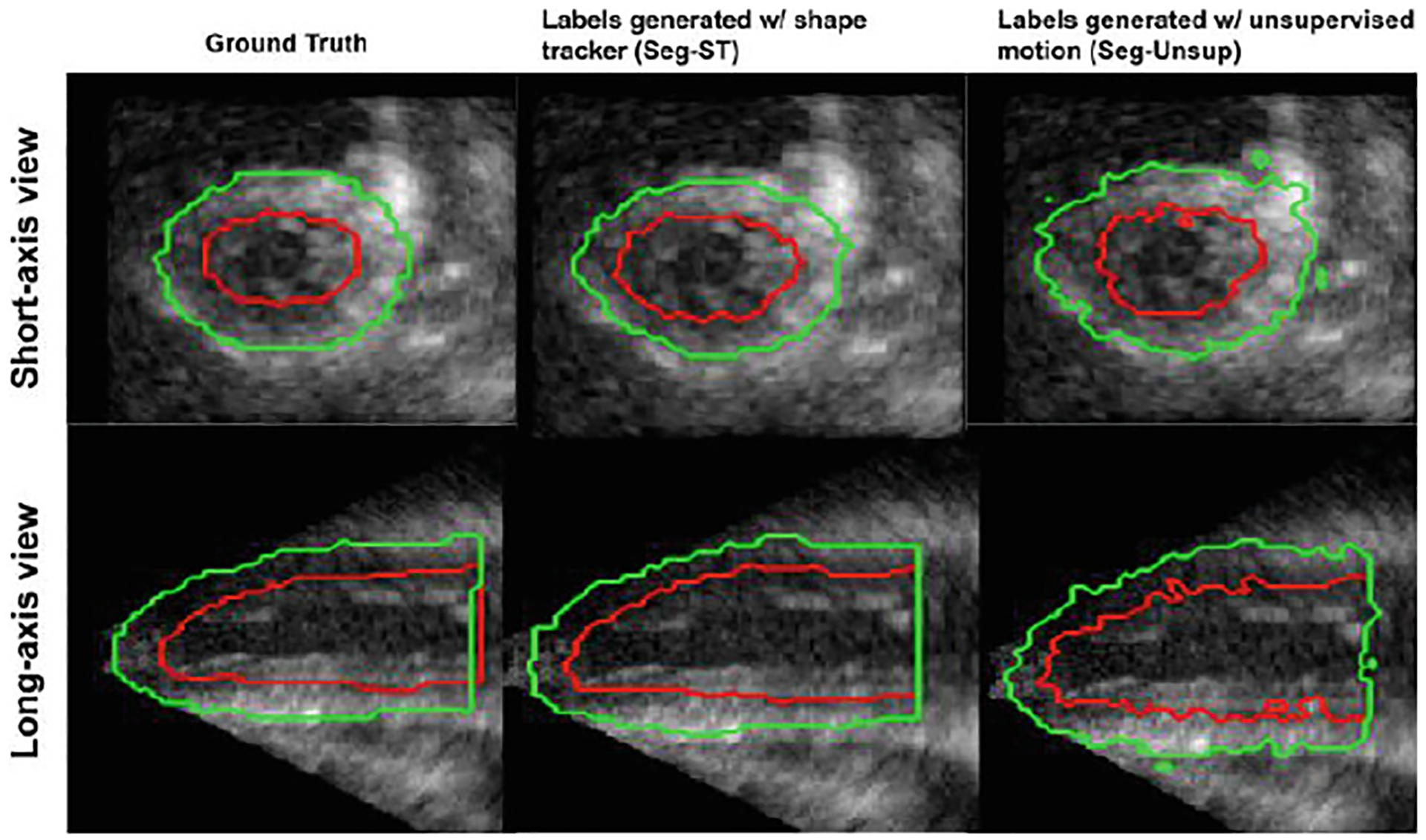
Epicardium (green) and endocardium (red) segmentations for a normal (healthy) synthetic sequence using different methods

3.2. Evaluation Using Animal Study

In vivo animal studies were done on 8 anesthetized open-chest canines, and images were captured using a Philips iE33 scanner and a X7–2 probe. Each study was conducted under five physiological conditions: baseline, mild LAD stenosis, moderate LAD stenosis, mild LAD stenosis with low-dose dobutamine (5μg/kg/min), and moderate LAD stenosis with low-dose dobumatine. 1 full study is used each for testing and validation and 6 studies are used for training. In total, the model is trained on 745 pairs, validated on 133 pairs, and tested on 126 pairs. All procedures were approved under Institutional Animal Care and Use Committee policies.

Each task of the joint model is evaluated separately. The displacement predictions are compared against displacements derived from an implanted array of sonomicrometers as previously reported [19]. It is important to note that dense displacement fields from the sonomicrometer crystals are generated through RBF based interpolation [5] and cannot be considered absolute ground truth, but act as a useful validation metric. The root mean squared error (RMSE) of the displacement fields generated by the joint model are compared against a non-rigid registration algorithm with b-spline parameterization (NRR) [16], and Lucas-Kanade optical flow (LK) algorithm [10], a shape-tracking algorithm (ST) [12], and the unsupervised single motion tracking branch without (Usup) and with (Usup+Shape) manually segmented shape regularization. According to Table 1 and Fig. 4, the joint model performs comparably to Unsup+Shape and favorably against all other methods in all metrics. For segmentation results, label predictions are evaluated against manually traced segmentations [22]. The Dice score and Hausdorff distance (HD) of the predicted endocardium and epicardium borders of the joint model are compared to a dictionary learning-based dynamic appearance model (DAM) [7], and weakly supervised versions of the joint model using crystal derived displacements (Seg-CD), nonrigid registration (Seg-NRR), optical flow (Seg-LK), and unsupervised motion (Seg-Unsup) to generate pseudo-ground truth labels. According to Table 2 and Fig. 5, the joint model performs comparably to Seg-CD and favorably against all other methods in all metrics.

Table 1.

Root mean squared error (RMSE) in the x-y-z direction. Lower RMSE means better performance

Method	Ux (mm)	Uy (mm)	Uz (mm)
NRR	0.95± 0.38	1.06± 0.34	0.62±0.17
LK	0.85 ± 0.37	0.91 ± 0.38	0.58 ± 0.17
ST	0.81 ± 0.32	0.72 ± 0.40	0.63 ± 0.21
Unsup+Shape	0.80 ± 0.33	0.70 ± 0.33	0.60 ± 0.18
Unsup	1.07 ± 0.42	1.31 ± 0.41	0.74 ± 0.17
Proposed model	0.79 ± 0.33	0.70 ± 0.36	0.62 ± 0.20

Fig. 4.

A short-axis view of the displacement vectors for a normal (healthy) in vivo sequence using different methods: A) crystal derived displacement, B) nonrigid registration (NRR), C) Lucas-Kanade Optical Flow (LK), D) Shape Tracking (ST), E) Unsupervised w/ shape regularizer (Unsup+Shape), F) Unsupervised G) Proposed Model

Table 2.

Dice and Hausdorff Distance (HD) for the endo- and epi- cardium. Higher Dice score and lower HD means better performance

Methods	Endocardium		Epicardium
	Dice	HD (mm)	Dice	HD (mm)
DAM	0.81±0.05	3.02±0.29	0.92±0.04	3.12±0.24
Seg-CD	0.84±0.07	2.63±0.20	0.96±0.01	2.75±0.08
Seg-NRR	0.80±0.08	2.80±0.28	0.88±0.06	3.22±0.43
Seg-LK	0.83±0.05	2.79±0.24	0.93±0.03	3.16±0.31
Seg-Unsup	0.84±0.06	2.91±0.26	0.94±0.02	3.11±0.16
Proposed model	0.88±0.04	2.70±0.17	0.95±0.02	2.97±0.19

Fig. 5.

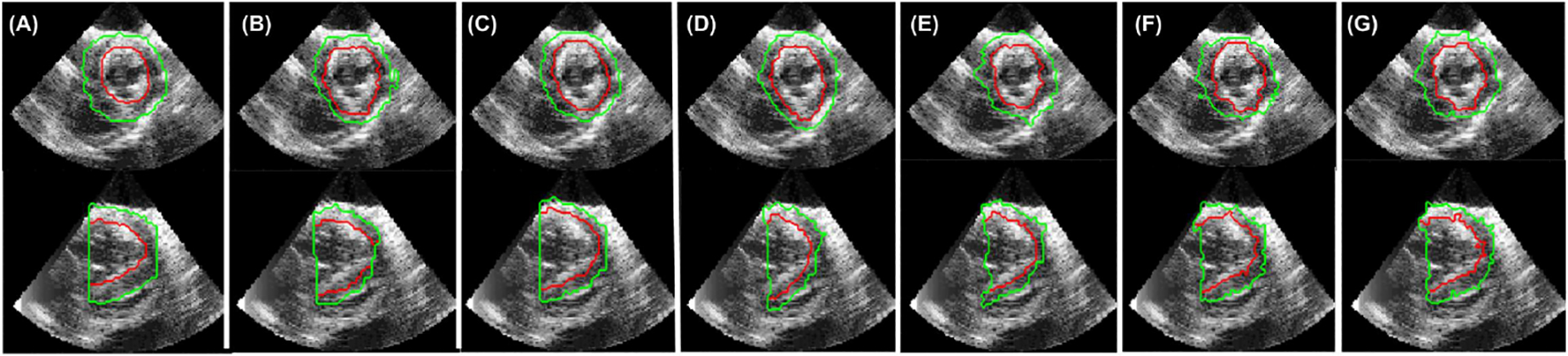
Epicardium (green) and endocardium (red) segmentations for a normal (healthy) in vivo sequence using different methods: A) manual, B) dynamic appearance model (DAM), C) trained with crystal-generated labels (Seg-CD) (LK), D) nonrigid registration-generated labels (Seg-NRR), E) Lucas-Kanade generated labels (Seg-LK), F) Unsupervised motion generated labels (Seg-Unsup) G) Proposed Model

4. Conclusions

This paper proposes a novel joint learning network for simultaneous LV segmentation and motion tracking in 4D echocardiography. Motion tracking and segmentation branches are trained iteratively such that the results of one branch positively influences the other. Motion is trained in an unsupervised manner and the resulting displacement fields are used to create pseudo-ground truth labels by propagating a single manually segmented time frame. Predicted labels are then used as landmarks to smooth the displacement fields. An incompressibility constraint is added to enforce spatially realistic LV motion patterns. Experimental results show our proposed model performs favorably against competing methods. Future work includes further validation on larger datasets and exploring temporal regularization.