Novel Mechanistic PBPK Model to Predict Renal Clearance in Varying Stages of CKD by Incorporating Tubular Adaptation and Dynamic Passive Reabsorption

Abstract

Chronic kidney disease (CKD) has significant effects on renal clearance (CL_r) of drugs. Physiologically‐based pharmacokinetic (PBPK) models have been used to predict CKD effects on transporter‐mediated renal active secretion and CL_r for hydrophilic nonpermeable compounds. However, no studies have shown systematic PBPK modeling of renal passive reabsorption or CL_r for hydrophobic permeable drugs in CKD. The goal of this study was to expand our previously developed and verified mechanistic kidney model to develop a universal model to predict changes in CL_r in CKD for permeable and nonpermeable drugs that accounts for the dramatic nonlinear effect of CKD on renal passive reabsorption of permeable drugs. The developed model incorporates physiologically‐based tubular changes of reduced water reabsorption/increased tubular flow rate per remaining functional nephron in CKD. The final adaptive kidney model successfully (absolute fold error (AFE) all < 2) predicted renal passive reabsorption and CL_r for 20 permeable and nonpermeable test compounds across the stages of CKD. In contrast, use of proportional glomerular filtration rate reduction approach without addressing tubular adaptation processes in CKD to predict CL_r generated unacceptable CL_r predictions (AFE = 2.61–7.35) for permeable compounds in severe CKD. Finally, the adaptive kidney model accurately predicted CL_r of para‐amino‐hippuric acid and memantine, two secreted compounds, in CKD, suggesting successful integration of active secretion into the model, along with passive reabsorption. In conclusion, the developed adaptive kidney model enables mechanistic predictions of in vivo CL_r through CKD progression without any empirical scaling factors and can be used for CL_r predictions prior to assessment of drug disposition in renal impairment.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Physiologically‐based pharmacokinetic (PBPK) modeling has been used to simulate the effect of chronic kidney disease (CKD) on renal clearance (CL_r) for hydrophilic nonpermeable drugs with active secretion, but not for hydrophobic permeable drugs with passive reabsorption. The overall confidence and consistency in PBPK modeling of CKD is low.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study quantifies the impact of CKD on tubular flow rate, subsequent passive reabsorption, and resulting CL_r using a novel adaptive kidney model.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ A novel physiologically‐based mechanistic adaptive kidney model was developed to capture the effect of CKD on tubular flow rate, allowing accurate prediction of passive reabsorption and CL_r throughout CKD progression using in vitro data without scaling factors. We successfully verified the adaptive model and showed that proportional glomerular filtration rate scaling approach is inadequate for predicting CL_r in CKD.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ Our adaptive model enables successful CL_r prediction of secreted, nonsecreted, permeable, and nonpermeable drugs and metabolites at all CKD stages, facilitating dosing regimen optimization and trial design prior to renal impairment studies.

Chronic kidney disease (CKD) is a progressive illness that is pathologically heterogeneous ¹ and systemic. ² It is mainly characterized by declining functional nephron mass and glomerular filtration rate (GFR). ³ As such, GFR is a critical index for CKD diagnosis, progression, and classification. ⁴ Clinically, patients with severe (stage 4, GFR ~ 15–29 mL/min) and end‐stage (stage 5, GFR < 15 mL/min) CKD are at high risk for comorbidities, polypharmacy, and adverse drug reactions, ⁵ , ⁶ , ⁷ , ⁸ necessitating careful medication management due to dramatically altered pharmacokinetics (PK) because of CKD. As a result, clinical characterization of drug disposition in patients with CKD is critically important. However, predicting the disease effects on drug PK and estimating the optimal dosing regimen is challenging and often unreliable prior to dedicated renal impairment studies due to several factors. For instance, renal clearance (CL_r) may decrease more than proportionally with GFR in CKD stages 4 and 5 for highly renally secreted drugs, ⁹ , ¹⁰ due to inhibition of renal transporters by uremic solutes. CL_r can also decrease less than proportionally with GFR in CKD stages 4 and 5 for highly renally reabsorbed drugs due to tubular adaptation/compensation processes. ¹¹ , ¹² , ¹³ Nonetheless, the most commonly accepted approach to predict CL_r in patients with CKD is to follow the Intact Nephron Hypothesis ¹⁴ and assume all renal drug handling pathways and CL_r decrease proportionally with filtration. Although this assumption is supported by clinical data for predominantly filtered drugs without significant secretion or reabsorption, ¹⁵ , ¹⁶ such proportional GFR scaling approach is inadequate to capture active secretion or passive reabsorption in severe CKD due to the complex disease effects on renal drug handling.

Physiologically‐based pharmacokinetic (PBPK) models that capture disease‐specific characteristics can potentially predict CKD effects on drug PKs more accurately than proportional GFR based scaling. Yet, use of PBPK models in predicting drug disposition in renal impairment scenarios is currently considered a low‐confidence application, ¹⁷ , ¹⁸ suggesting that current PBPK models do not fully capture the physiological changes observed in CKD. PBPK modeling has been used to specifically predict the CKD effect on renal active secretion, ¹⁹ , ²⁰ , ²¹ but the test drugs used for model verification all lack significant permeability and hence passive reabsorption. At present, no PBPK model can quantitatively predict the alterations in renal passive reabsorption or CL_r for highly reabsorbed drugs in CKD, let alone systematically capture the diverse effects of CKD on renal elimination.

Physiologically, patients with CKD show reduced water reabsorption/increased tubular flow rates per remaining functional nephron ¹² , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ as an adaptation mechanism. This is to compensate for the reduced number of functional nephrons and reduced GFR, to maintain critical homeostasis, such as extracellular fluid volume and plasma sodium concentration. ²⁴ , ²⁵ , ²⁸ , ²⁹ , ³⁰ We hypothesized that such physiological adaptation in renal tubular water reabsorption and tubular flow rate will dramatically decrease the drug concentration gradient between intratubular filtrate and peritubular blood, leading to reduced passive reabsorption and higher CL_r than expected from residual GFR alone. Indeed, this hypothesis is supported by observed data for various permeable drugs, such as pefloxacin, metronidazole, and minocycline. ¹¹ , ¹² , ¹³ For these drugs, the observed CL_r in patients with CKD was reduced to 30–37% of healthy when residual GFR was only 4–9% of healthy, ¹¹ , ¹² , ¹³ demonstrating an over 7‐fold disproportionality between the change in CL_r and GFR.

To simulate the effect of CKD on tubular passive reabsorption, we expanded our previously developed and verified mechanistic kidney model ³¹ to incorporate the physiologically‐based tubular changes of reduced water reabsorption/increased tubular flow rate per remaining functional nephron across varying CKD stages. The developed adaptive kidney model enables prediction of changes in passive reabsorption and CL_r from in vitro drug permeability data in different CKD stages. The model was globally verified across the progression of CKD from healthy to end‐stage CKD using a set of 20 test compounds with differing properties without any compound‐specific empirical scaling.

METHODS

Development and sensitivity analyses of proportional and adaptive kidney model for CKD

Two distinct CKD models were built using MATLAB and Simulink platform (R2018a; MathWorks, Natick, MA) to predict CL_r in patients with different stages of CKD. Both models were established based on our previously published and verified physiologically‐based mechanistic kidney model ³¹ for healthy humans, but with modified system parameters to reflect physiological changes in CKD. The first model, the proportional model, was built assuming all functions of the nephron, all pathways of renal drug handling, and therefore the values of CL_r decline proportionately with GFR. The second model, the adaptive model, was built by accounting for the tubular adaptation of reduced water reabsorption/increased water excretion per remaining functional nephron, as observed in many patients with CKD. ¹² , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ In both models, all of the volume (n = 33), surface area (n = 22), peritubular renal blood flow (n = 12), basolateral uptake clearance (n = 3), and apical efflux clearance (n = 3) parameters were reduced proportionally with GFR by multiplying the baseline parameters in healthy subjects by the fraction of GFR remaining (ratio of GFR_i in a specific CKD stage_i over 120 mL/min, the healthy GFR). The major distinction between the proportional model and the adaptive model is the parameterization of renal tubular flow rate (TFR) in patients with CKD. In the proportional model, all TFR parameters were decreased proportionally with GFR like other model parameters. In contrast, the adaptive model incorporates the physiologically‐based adaptation of tubular water reabsorption in patients with CKD to parameterize TFR, and therefore TFR decreases less than proportionally in relation to GFR. Quantitatively, a set of tubular subsegment‐specific adaptation factors (AF_i) was calculated based on reported mean urine formation of 0.62 mL/min (62% of healthy urine flow) in patients with CKD (n = 216) with a mean GFR of 10 mL/min (8.3% of healthy GFR). ²⁷ Physiologically and mathematically, the magnitude of adaptation of TFR in patients with CKD must be different in different tubular subsegments. The inflow of the first subsegment of the proximal tubule must equal GFR and as such must decline proportionally with GFR. Similarly, the outflow of the last subsegment of the collecting duct must match the observed urine flow in patients with CKD and hence decline much less than GFR. For example, at a GFR of 10 mL/min, the observed urine flow is 7.5‐fold higher than what would be expected from the change in GFR. ²⁷ Based on these boundaries, the tubular subsegment‐specific AF (AF_i) for each TFR was calculated after optimization (details shown in Supplementary Material) using Eq. 1:

$${\text{Adaptation Factor}}_i({\text{AF}}_i)=min+\frac{max‐min}{1+{10}^{n\left({\text{Log}}_{10}{\text{TFR}}_{i,H}‐1\right)}}$$ (1)

where min and max represent the minimum and maximum adaptation capacities of 0 and 0.57, n is analogous to Hill coefficient (set as 1.80). TFR_i,H represents the renal tubular flow rate entering each tubular subsegment (including bladder) in healthy (H) subjects (GFR = 120 mL/min) where i ranges from 1 to 12.

The calculated AF_i was incorporated into the subsegment‐specific TFR at a given GFR (GFR_j), using Eq. 2 defined scalar:

$${\text{Scalar}}_{\mathit{ij}}=1‐\left(1‐\frac{{\text{GFR}}_j}{120}\right)\times \left(1‐{\text{AF}}_i\right)$$ (2)

where GFR_j represents the specific GFR value (mL/min) of patients with CKD (j ranges from 5 to 120 mL/min), GFR_j/120 represents the remaining renal function in patients with CKD, and AF_i is as defined by Eq. 1. The TFR_{ij ,CKD} for each tubular subsegment (i ranges from 1 to 12) at different CKD stages (j ranges from 5 mL/min to 120 mL/min) was calculated using Eq. 3:

$${\text{TFR}}_{ij,\text{CKD}}={\text{TFR}}_{i,H}\times {\text{Scalar}}_{\mathit{ij}}$$ (3)

where TFR_i,H represents renal tubular flow rate entering each tubular subsegment (including bladder) in healthy subjects and the Scalar_ij is defined by Eq. 2. The full set of calculated AF values and representative TFR values are shown in Table 1 and Table S1 and the model file is included as Supplementary Material. Each GFR input value results in a different set of TFR values for all 12 subsegments, producing a unique CKD stage‐specific kidney model that describes the diseased renal tubular system at that level of renal impairment.

Table 1.

Representative renal TFR for the proportional and adaptive models at different stages of CKD

Model subsegment	Healthy (stage 1) GFR = 120 mL/min	Adaptation factor	Mild stage CKD (stage 2) GFR = 80 mL/min		Moderate stage CKD (stage 3) GFR = 40 mL/min		Severe stage CKD (stage 4) GFR = 20 mL/min		End‐stage CKD (stage 5) GFR = 5 mL/min
	TFR		TFRP	TFRA	TFRP	TFRA	TFRP	TFRA	TFRP	TFRA
Proximal tubule1	120	0	80.00	80.00	40.00	40.00	20.00	20.00	5.00	5.00
Proximal tubule2	94	0.0099	62.67	62.98	31.33	31.96	15.67	16.44	3.92	4.81
Proximal tubule3	68	0.018	45.33	45.73	22.67	23.46	11.33	12.33	2.83	3.98
Loop of HenleD	43	0.038	28.67	29.22	14.33	15.44	7.17	8.55	1.79	3.38
Loop of HenleA	24	0.098	16.00	16.78	8.00	9.56	4.00	5.95	1.00	3.25
Distal tubule	24	0.098	16.00	16.78	8.00	9.56	4.00	5.95	1.00	3.25
Collecting duct1	11	0.26	7.33	8.29	3.67	5.58	1.83	4.22	0.46	3.21
Collecting duct2	9	0.31	6.00	6.94	3.00	4.87	1.50	3.84	0.38	3.07
Collecting duct3	7	0.37	4.67	5.54	2.33	4.08	1.17	3.35	0.29	2.80
Collecting duct4	5	0.44	3.33	4.07	1.67	3.14	0.83	2.68	0.21	2.33
Collecting duct5	3	0.51	2.00	2.51	1.00	2.02	0.50	1.78	0.13	1.60
Bladder (urine)	1	0.56	0.67	0.85	0.33	0.71	0.17	0.63	0.04	0.58

The tubular subsegment‐dependent adaptation factors (AF_i) were calculated according to Eq. 1 and implemented for the adaptive model. The renal TFRs were calculated using either proportional model (TFR_P) by direct scaling to GFR, as described in Methods, or using the adaptive model (TFR_A) according to Eqs. 2 and 3. The renal TFR (mL/min) shown here indicates the inflow rate of entering each renal subsegment, which equals the outflow rate exiting from the previous renal subsegment. The inflow rate of the first proximal tubule subsegment always equals the GFR. The outflow rate of the last subsegment of collecting duct always equals the inflow rate of bladder and the urine formation rate (as no reabsorption occurs within bladder). All flows are presented in mL/min.

CKD, chronic kidney disease; GFR, glomerular filtration rate; TFR, tubular flow rate.

To ensure model integrity and evaluate sensitivities of CL_r to drug properties and physiological parameters, five sets of local sensitivity analyses were conducted to evaluate the impact of drug permeability (P _app = 1–100 × 10^‐6 cm/s), plasma unbound fraction (f _u,p = 0.1–1), peritubular renal blood flow (300–1,000 mL/min), unbound intrinsic basolateral uptake transport clearance (CL_uptake = 10–3,000 mL/min), and unbound intrinsic apical efflux transport clearance (CL_efflux = 10–3,000 mL/min) on simulated CL_r using both proportional and adaptive models across varying levels of renal impairment.

Prediction of CL_r for 20 test compounds in varying CKD stages using proportional and adaptive kidney models

To assess the performance of the proportional and adaptive models in predicting CL_r with declining GFR, the CL_r of 20 test compounds were simulated and compared with observed values. The 20 test compounds included three parent‐metabolite pairs, six nonpermeable drugs, six highly permeable drugs, all of which lacked significant secretion (CL_r < 1.25 × f _u,pGFR, Table S2 ) and two renally secreted compounds. All the permeable nonsecreted drugs are highly renally reabsorbed (1‐CL_r/(f _u,p × GFR) ~ 72% to 97%). The collected pK_a values, in vitro permeability data, f _u,p, and observed CL_r values in healthy subjects and patients with CKD stages 4 and 5 are summarized in Table S2 . Overall, the 20 test compounds had a wide range of pK_a values (2.9–11.5), in vitro permeabilities (0.1–120 × 10^‐6 cm/s), f _u,p (0.05–1), and CL_r (0.42–599 mL/min in healthy subjects and 0.19–76.4 mL/min in patients with CKD stages 4 and 5), providing a robust dataset to verify the adaptive model and to differentiate the performance of the adaptive and proportional models.

The CL_r of all 20 test compounds were simulated as described before ³¹ using both proportional and adaptive models with GFR input value decreasing from 120 mL/min to 5 mL/min with a decrement of 1 mL/min. Permeability and f _u,p were compound‐specific input parameters and uptake/efflux transport clearances were set as 0 for all test compounds except para‐aminohippuric acid (PAH) and memantine for which previously published transport clearance values ³¹ were used. The simulated CL_r using both proportional and adaptive models were compared with the observed values at different CKD stages. To quantitatively evaluate the performance of proportional and adaptive models, absolute fold‐error (AFE; Eq. 4) between the simulated and observed mean CL_r in patients with severe/end‐stage (i.e., stages 4 and 5) CKD along with a twofold acceptance criterion was used.

$$\text{AFE}={10}^{\left|{\log }_{10}\frac{\text{Simulated Mean}}{\text{Observed Mean}}\right|}$$ (4)

RESULTS

Development of proportional and adaptive kidney models for CKD

To predict CL_r of drugs in patients with CKD, the proportional and adaptive models were developed and tested. In the proportional model, all TFR are reduced proportionally with GFR (Figure 1 ) resulting in a predicted urine flow that is reduced by the same percentage as GFR. For GFR of 10 mL/min (92% decrease from 120 mL/min), the proportional model predicts a urine flow of 0.083 mL/min, which is 87% lower than the observed urine flow of 0.6 mL/min. ²⁷ In contrast, in the adaptive model, the TFR values are reduced (Eq. 3) by scalars (Eq. 2) defined by the remaining GFR and the adaptation factors (Eq. 1), resulting in a urine flow of 0.6 mL/min (Figure 1 ) when GFR = 10 mL/min, matching the observed data.²⁷ This suggests that the adaptive model successfully captures the physiologic changes in renal tubules of remaining functional nephrons in patients with CKD. Table 1 summarizes the representative TFR values predicted using both adaptive and proportional models at GFRs of 80, 40, 20, and 5 mL/min. At mild CKD (GFR = 80 mL/min), the difference of TFR values between proportional and adaptive models was small, with a maximum of 28% difference in the final urine flow. However, the difference in urine flow between proportional and adaptive models increased with declining GFR reaching an ~ 200% difference in moderate CKD (GFR = 40 mL/min), ~ 400% difference in severe CKD (GFR = 20 mL/min), and ~ 1,400% difference in end‐stage CKD (GFR = 5 mL/min).

Figure 1.

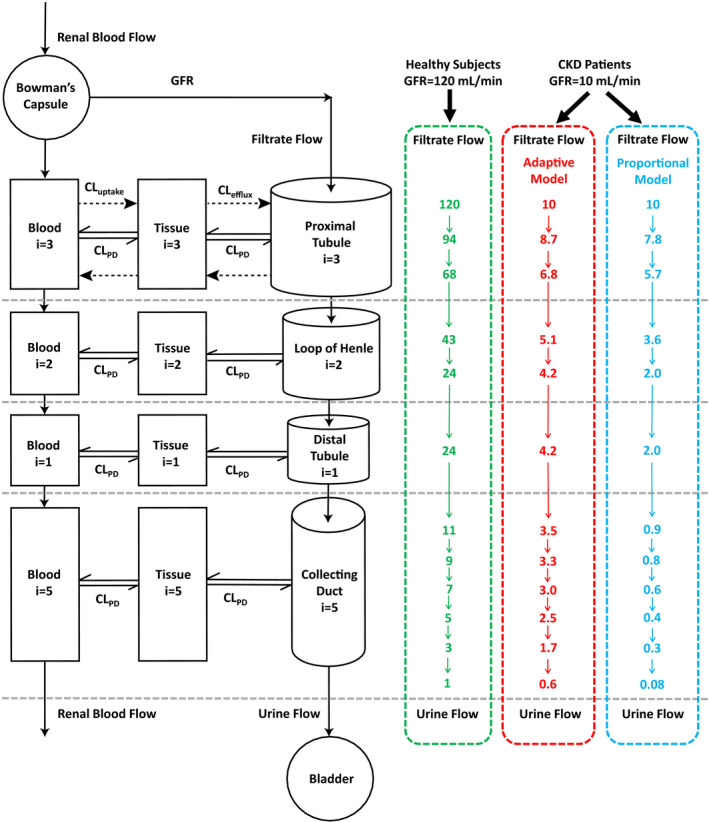
Schematic presentation of the mechanistic kidney model structure, together with the corresponding renal tubular flow rate (TFR; in mL/min) for each individual tubular subsegment (a total of 12) of the model. Three sets of physiologically‐based TFR shown here are for healthy subjects (glomerular filtration rate (GFR) 120 mL/min, in green) and for the representative patients with chronic kidney disease (CKD) who have residual GFR of 10 mL/min using the adaptive model (in red) and the proportional model (in blue). The dynamic physiologically‐based mechanistic kidney model shown here is parameterized by 33 volume parameters, 22 surface area parameters, 12 peritubular renal blood flow parameters, 12 renal TFR parameters, 3 basolateral uptake clearance parameters, and 3 apical efflux clearance parameters to fully capture the disposition of drugs/metabolites between renal tubules, cells, and vasculature. CL, clearance.

Sensitivity analyses of proportional model and novel adaptive kidney model for CKD

To further test which drug‐specific or system‐specific parameters impact the CL_r predictions across varying levels of renal impairment, sensitivity analyses were conducted to examine the effects of P _app, f _u,p, and peritubular renal blood flow. For the proportional model, the fold‐decrease in CL_r with decreasing GFR was unaffected by P _app (Figure 2a ), whereas for the adaptive model the fold‐decrease in CL_r with decreasing GFR was highly sensitive to P _app (Figure 2b ). Using the adaptive model, when GFR decreased by 96% to 5 mL/min, the simulated CL_r for drugs with low permeability (e.g., 1 × 10^‐6cm/s) also decreased by 96%, whereas the simulated CL_r for drugs with high permeability (e.g., 100 × 10^‐6cm/s) only decreased by 32%, resulting in considerable difference in the predicted effect of CKD on CL_r (Figure 2b ). Overall, the adaptive model predicts dramatically different effects of CKD on CL_r than the proportional model for drugs with moderate to high permeability (> 10 × 10^‐6cm/s) in severe/end‐stage CKD (GFR < 30 mL/min; Figure 2c ). As expected, f _u,p correlated negatively with simulated CL_r (Figure 2d ,e), and had no impact on the difference in simulated CL_r between proportional and adaptive models (Figure 2f ). Further, peritubular renal blood flow had no effect on simulated CL_r regardless of CKD stage in both proportional and adaptive models for nonsecreted drugs (Figure 2g–i ).

Figure 2.

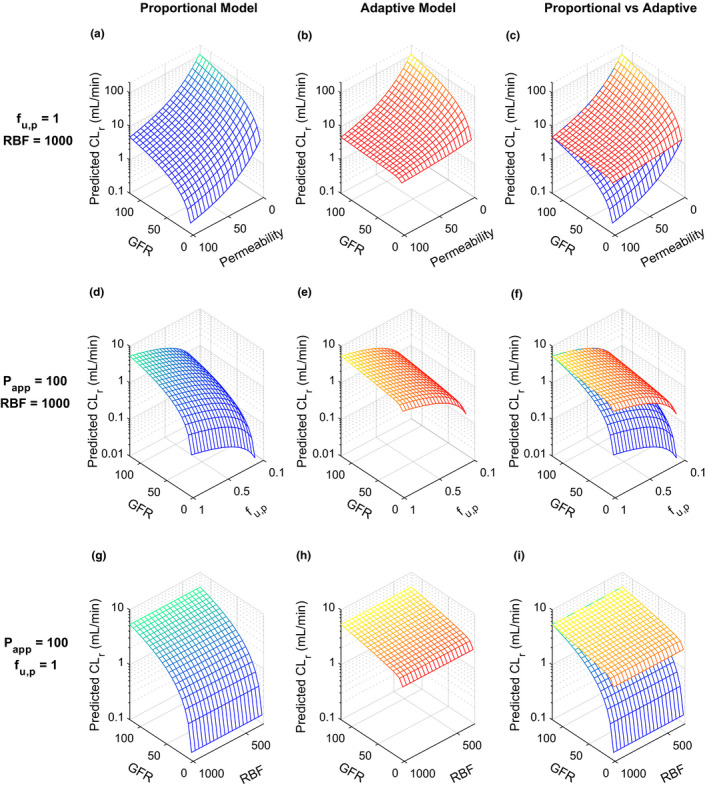
Sensitivity analyses of simulated renal clearance (CL_r, in mL/min) at multiple stages of chronic kidney disease (CKD) reflected as varying glomerular filtration rate (GFR, in mL/min) using proportional model (shown in blue‐green) vs. adaptive model (shown in yellow‐red). Three sets of sensitivity analyses were conducted, (1) CL_r of neutral drugs with varying permeability values (P _app = 1–100 × 10^‐6 cm/s, all values shown are in 10^‐6 cm/s) but a constant plasma unbound fraction (f _u,p = 1) and peritubular renal blood flow (RBF = 1,000 mL/min, the average of healthy human subjects) were simulated using proportional model (a), adaptive model (b), and both models (c) across a wide range of GFR values from 5 mL/min to 120 mL/min, (2) renal clearances of highly permeable neutral drugs (P _app = 100 × 10^‐6 cm/s) with varying f _u,p (0.1–1) but a constant peritubular RBF (1,000 mL/min) were simulated using the proportional model (d), the adaptive model (e), and both models (f) across a range of GFR from 5 mL/min to 120 mL/min, (3) CL_r of a highly permeable neutral drugs (P _app = 100 × 10^‐6 cm/s) with varying peritubular RBF (300–1,000 mL/min) but a constant f _u,p (1) were simulated using proportional model (g), adaptive model (h), and both models (i) across a range of GFR from 5 mL/min to 120 mL/min. In panel a (proportional model), the decrease in CL_r between GFR of 120 mL/min and GFR of 5 mL/min is 24‐fold for all permeability values. In contrast, in panel b (adaptive model), the CL_r decreases by 22‐fold for a drug with a permeability of 1 between GFR of 120 mL/min and GFR of 5 mL/min, whereas the CL_r decreases by 1.5‐fold for a drug with a permeability of 100 between GFR of 120 mL/min and GFR of 5 mL/min, demonstrating a high sensitivity of the CL_r reduction to drug permeability.

Prediction of CL_r for nonsecreted compounds in varying CKD stages and verification of the adaptive kidney model

To verify the adaptive model for different CKD stages, the CL_r of 18 nonsecreted compounds at different CKD stages (GFR 120 mL/min to 5 mL/min) were predicted and compared with observed CL_r. First, the CL_r of all compounds were simulated in healthy subjects (GFR = 120 mL/min) based on reported f _u,p and in vitro permeability (experimentally determined or optimized in healthy subjects) and all predicted CL_r values were within twofold of the observed (Table S2 ), confirming satisfactory baseline simulation in healthy subjects and appropriate model parameterization. In healthy subjects, the adaptation was 0, therefore, both adaptive and proportional models resulted in identical simulation results when GFR input was 120 mL/min (Figures 3 , 4 , 5 and Figure S1 ).

Figure 3.

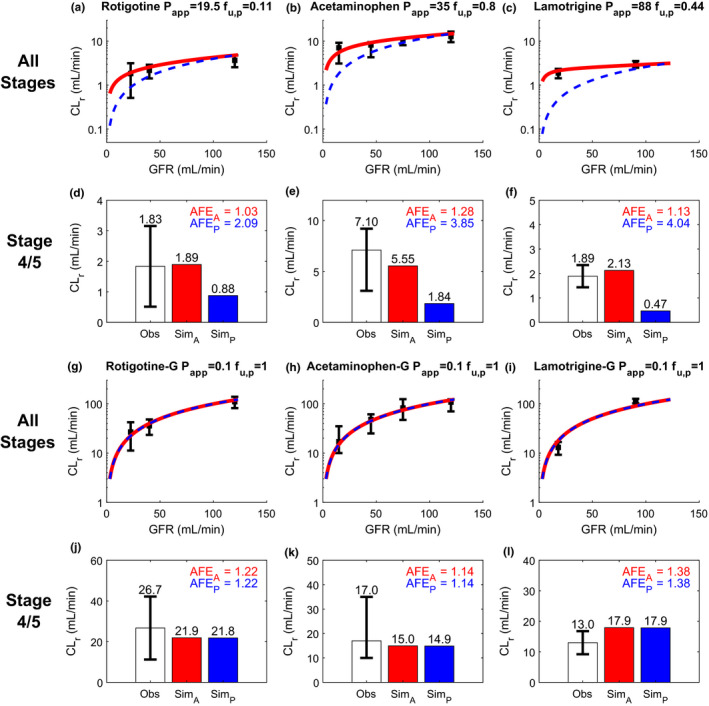
Simulation (Sim) and verification of renal clearance (CL_r) of three drugs and their corresponding glucuronide metabolites at multiple stages of chronic kidney disease (CKD) reflected by varying glomerular filtration rate (GFR). Observed (Obs) CL_r data are shown as black solid squares depicting the group mean value with error bar showing the 95% confidence interval. The simulated CL_r of different test compounds at varying stages of CKD are shown with red curves for the adaptive model and blue dashed curves for the proportional model (a–c, g–i). The performance of the adaptive and proportional models was evaluated at CKD stages 4 and 5 where GFR ≤ 30 mL/min using calculated absolute fold‐error (AFE)_A (shown in red) and AFE_P (shown in blue), respectively (d–f, j–l). The experimentally determined apparent permeability (P _app), plasma unbound fraction (f _u,p), and observed CL_r data of rotigotine a, d, acetaminophen b, e, and lamotrigine c, f were collected from literature and summarized in Table S2 . The P _app and f _u,p values of all glucuronide metabolites g–l were assumed to be 0.1 × 10^‐6 cm/s and 1, respectively, based on their physicochemical properties. The observed CL_r data of all metabolites were from the same subjects in the same studies of their respective parent drugs (Table S2 ). The simulation results are shown on linear scale in Figure S1 .

Figure 4.

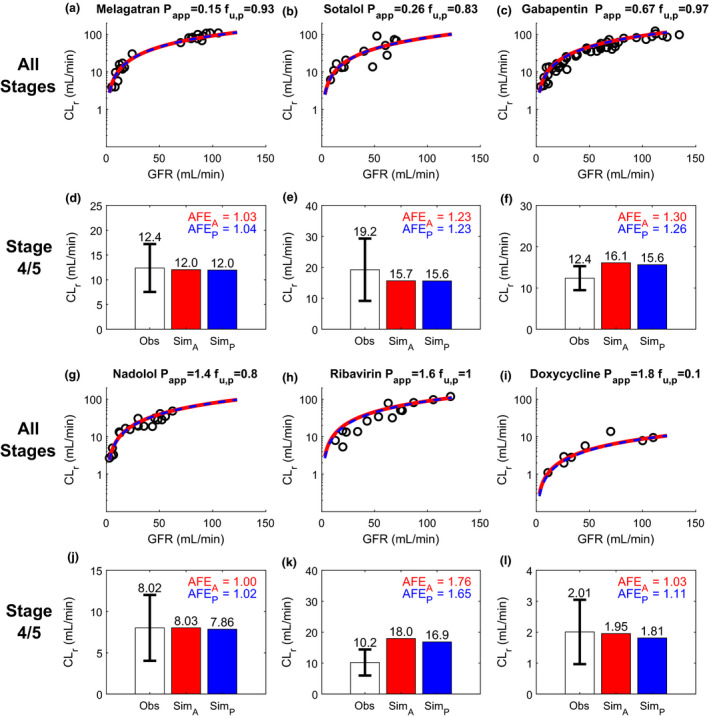
Simulation (Sim) and verification of renal clearance (CL_r) of six nonpermeable compounds at multiple stages of chronic kidney disease (CKD) reflected by varying glomerular filtration rate (GFR). Observed (Obs) CL_r data of the test compounds are shown as black open circles and are from individual subjects in the reported studies. The simulated CL_r of different test compounds at varying stages of CKD are shown with red curves for the adaptive model and blue dashed curves for the proportional model (a–c, g–i). The performance of the adaptive model and proportional model was evaluated at CKD stages 4 and 5 (GFR ≤ 30 mL/min) using calculated absolute fold‐error (AFE)_A (shown in red) and AFE_P (shown in blue), respectively (d–f, j–l). The experimentally determined apparent permeability (P _app), plasma unbound fraction (f _u,p), and observed CL_r data of melagatran a, d, sotalol b, e, gabapentin c, f, nadolol g, j, ribavirin h, k, and doxycycline i, l were collected from literature and summarized in Table S2 . The simulation results are shown on linear scale in Figure S1 .

Figure 5.

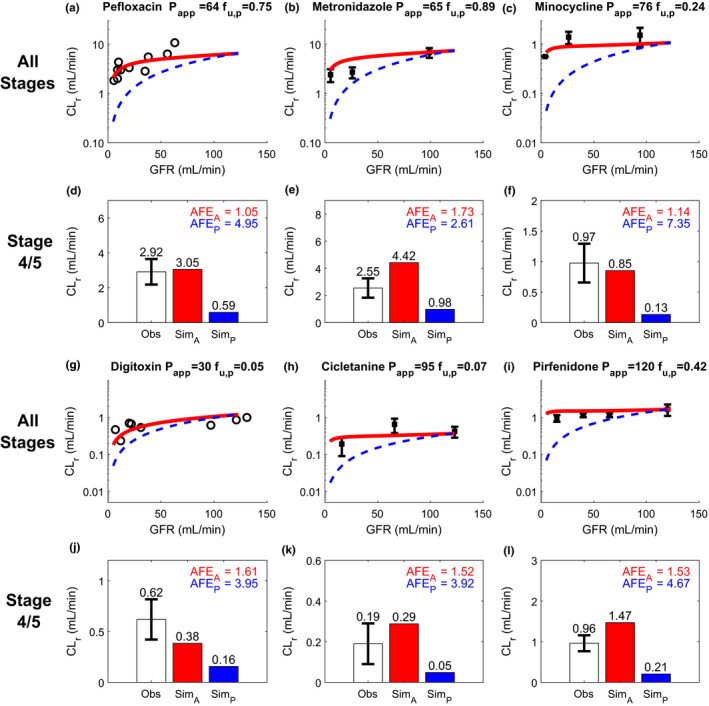
Simulation (Sim) and verification of renal drug clearance (CL_r) of six permeable and highly renally reabsorbed compounds at multiple stages of chronic kidney disease (CKD) reflected by varying glomerular filtration rate (GFR). Observed (Obs) CL_r data of the test compounds are from individual subjects when available and are shown as black open circles. If only group mean data were available, data are shown as black solid squares with 95% confidence interval as the error bar. The simulated CL_r of different test compounds at varying stages of CKD are shown with red curves for the adaptive model and blue dashed curves for the proportional model (a–c, g–i). The performance of adaptive and proportional model was evaluated at CKD stages 4 and 5 (GFR ≤ 30 mL/min) using calculated absolute fold‐error (AFE)_A (shown in red) and AFE_P (shown in blue), respectively (d–f, j–l). The plasma unbound fraction (f _u,p) and observed CL_r data of pefloxacin a, d, metronidazole b, e, and minocycline c, f, digitoxin g, j, cicletanine h, k, and pirfenidone I, l were collected from literature and summarized in Table S2 . The apparent permeability (P _app) values of pefloxacin, metronidazole, and minocycline were experimentally determined, whereas the P _app values of other drugs were optimized using the f _u,p and observed CL_r in healthy subjects, assuming no active secretion. The same optimized P _app values were used for extrapolated simulations at varying stages of CKD. The simulation results in linear plot are shown in the Figure S1 .

To evaluate the performance of adaptive and proportional models with decreasing GFR (advancing CKD), three pairs of permeable drugs and their respective nonpermeable glucuronide metabolites studied concomitantly were used as the first test set. For all three permeable drugs, the adaptive model successfully predicted the CL_r across the entire range of GFRs considered (Figure 3a–c ) whereas the proportional model only predicted the CL_r acceptably in mild CKD where physiological changes are not drastic. In stages 4 and 5 CKD (Figure 3d–f ), the calculated AFE_A ranged from 1.03 to 1.28 using adaptive model whereas the calculated AFE_P were all > 2 using the proportional model. This suggests successful verification of the adaptive model in predicting CL_r at all stages of CKD, and inadequate performance of proportional model for severe/end‐stage of CKD. For the nonpermeable glucuronide metabolites measured in the same studies, both adaptive and proportional models successfully predicted the CL_r (Figure 3g–i ) across varying levels of renal impairment, including CKD stages 4 and 5 (AFE 1.14–1.38, all < 2; Figure 3j– l).

For further verification, the adaptive and proportional models were evaluated using six nonpermeable drugs that are predominantly filtered without significant reabsorption or secretion (Figure 4 ) and six permeable drugs that are significantly renally reabsorbed (Figure 5 ). Both adaptive and proportional models successfully predicted the CL_r for all 6 nonpermeable drugs across varying levels of renal impairment, including CKD stages 4 and 5 (Figure 4a–c ,g–i), with calculated AFE_A of 1.00–1.76 (adaptive model) and AFE_P of 1.02–1.65, (proportional model; Figure 4d–f ,j–l). In addition, the ratio between AFE_A and AFE_P for individual drugs was within the 0.8 to 1.25 range for all nonpermeable test drugs, suggesting an equivalent performance between adaptive and proportional models for CL_r prediction for nonpermeable and nonsecreted compounds. In contrast, the performance of the adaptive model was considerably better than the proportional model (Figure 5 ) for advanced CKD stages for permeable compounds that undergo significant renal reabsorption (83–97%; Table S2 ). The adaptive model successfully (AFE_A = 1.05–1.73, all < 2) predicted the CL_r across varying levels of renal impairment, including stages 4 and 5 CKD (Figure 5 ), suggesting high confidence in the use of the adaptive model to predict CL_r in patients with CKD. In contrast, discrepancy between the proportional model‐simulated CL_r and observed CL_r was pronounced as the GFR decreased (Figure 5 ). At stages 4 and 5 CKD, the proportional model dramatically underpredicted the CL_r (AFE_P = 2.61–7.35, all > 2) with 83% of drugs having AFE_P > 3 (Figure 5 ). This demonstrates alarming inappropriateness of applying proportional model (or proportional GFR scaling of CL_r) in patients with CKD for drugs with medium‐to‐high permeability.

Prediction of CL_r for secreted compounds in varying stages of CKD

To test whether the adaptive model could incorporate tubular secretion and predict impact of CKD on the CL_r of secreted drugs, two sets of local sensitivity analyses were first conducted for uptake and efflux transport clearance after incorporating these processes, as previously described. ³¹ The simulated CL_r showed a strong positive association with CL_uptake at all stages of CKD, with gradually lessened sensitivity as increasing CL_uptake surpassed 1,000 mL/min, the average renal blood flow in healthy humans (Figure 6a ). Conversely, the simulated CL_r showed weak sensitivity with CL_efflux at all stages of CKD, suggesting that apical efflux is not the rate‐determining step for CL_r (Figure 6b ). The adaptive model was then used to predict CL_r of two secreted compounds, PAH and memantine, across a range of GFRs (5–120 mL/min) and compared with the observed data. Overall, the simulation results for PAH and memantine agreed with the observed CL_r for all stages of CKD (Figure 5 ) with high accuracy (AFE = 1.10–1.12, CKD stages 4/5). This suggests that the adaptive model can be used to predict CL_r of secreted compounds as well as in varying stages of CKD in addition to nonsecreted drugs. Sensitivity analyses and CL_r predictions for PAH and memantine in CKD were also done using the proportional model and are shown in Figure S2 and Figure S3 .

Figure 6.

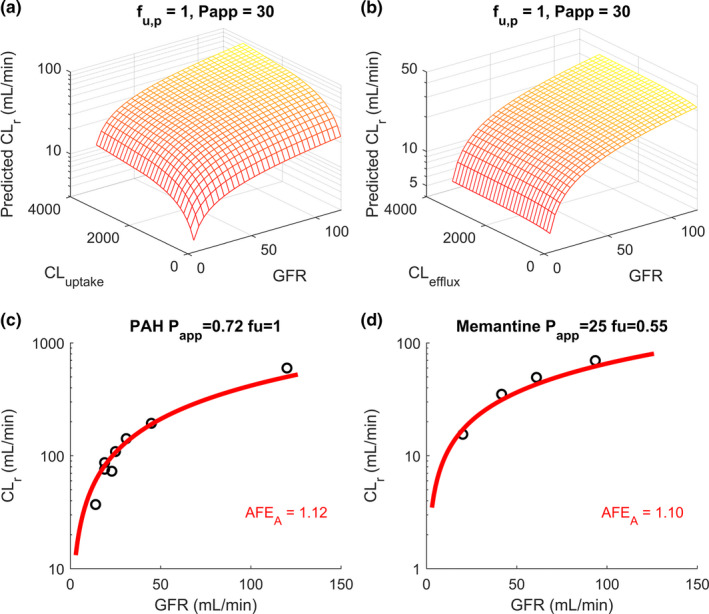
Sensitivity analyses of simulated renal clearance (CL_r in mL/min) at multiple stages of chronic kidney disease (CKD) reflected by varying glomerular filtration rates (GFR in mL/min) using adaptive model (shown in yellow‐red). (a) The sensitivity analyses of adaptive model‐simulated CL_r of neutral unbound permeable drugs (f _u,p = 1, P _app = 30 × 10^‐6 cm/s) with a constant unbound intrinsic apical efflux transport clearance (CL_efflux = 150 mL/min) and different unbound intrinsic basolateral uptake transport clearances (CL_uptake = 10–3,000 mL/min) across a range of GFRs (5–120 mL/min). (b) The sensitivity analyses of adaptive model‐simulated CL_r of neutral unbound permeable drugs (f _u,p = 1, P _app = 30 × 10^‐6 cm/s) with a constant unbound intrinsic basolateral uptake transport clearance (CL_uptake = 150 mL/min) and different unbound intrinsic apical efflux transport clearances (CL_efflux = 10–3,000 mL/min) across a range of GFRs (5–120 mL/min). The sensitivity analyses using proportional model and the comparison between the two models are shown in the Figure S2 . (c, d) The simulations of CL_r of para‐amino‐hippuric (PAH) and memantine in red curves, respectively, using adaptive model, at multiple stages of CKD, and comparison to the observed data (Table S2 ) shown in black open circles with calculated absolute folderror (AFE)_A shown in the insets. The simulation results for PAH and memantine using proportional model are shown in Figure S3 .

DISCUSSION

PBPK modeling has been proposed as a promising tool to predict drug disposition in complicated and unknown scenarios, including patients with renal impairment, ³² , ³³ , ³⁴ , ³⁵ , ³⁶ due to its mechanistic capability of integrating multiple complex interactions. Indeed, progress has been made in PBPK modeling of CKD effects on drug disposition, with special attention focused on altered hepatic metabolism ³⁵ , ³⁷ , ³⁸ , ³⁹ and renal active secretion. ¹⁹ , ²⁰ , ²¹ In contrast, the effect of CKD on renal passive reabsorption has not been considered in existing CKD models. This study is the first to systematically explore the observed effects of CKD on highly renally reabsorbed drugs, and to investigate the adaptive physiological changes in CKD, to establish a PBPK modeling framework to predict CL_r through CKD progression. We expanded our previously developed and verified mechanistic kidney model ³¹ to incorporate the physiologically‐based tubular changes of reduced water reabsorption/increased TFR per remaining functional nephron across varying CKD stages. Incorporation of the adaptive changes in water reabsorption is necessary to address the significant discrepancy in urine flow between the proportional model‐derived urine flow of 0.083 mL/min and the observed mean urine flow of 0.6 mL/min in patients with CKD with GFR = 10 mL/min. ²⁷ Our final physiologically‐based adaptive model developed here is consistent with the observed urine flow in patients with CKD (i.e., urine flow = 0.6 mL/min when GFR = 10 mL/min), and successfully predicted CL_r of a wide variety of compounds at different stages of CKD using f _u,p and in vitro permeability without any optimization or empirical scaling.

Using 20 test compounds representing different degrees of permeability and extent of passive renal reabsorption, our analyses unequivocally show that passive reabsorption and hence renal clearance may not decrease proportionally with GFR in CKD (Figures 3 , 4 , 5 ) due to the adaptation in tubular water reabsorption. Instead, the permeable and renally reabsorbed drugs had much lower (by 261–735%) reduction of CL_r than the reduction of GFR (Figure 5 ), whereas nonpermeable and predominantly filtered drugs did not show such disproportionality (Figure 4 ). Our model, which considers physiologically‐based tubular surface area and dynamic tubular flow, allows prediction of the extent of passive reabsorption based on P _app, conferring appropriate model sensitivity to P _app that reflects the observed CL_r in humans. Further, only the adaptive model shown here that accounts for the tubular flow adaptation (decreased water reabsorption/increased TFR per remaining functional nephron) due to CKD allowed simulation of the decrease in drug concentration gradient between intratubular filtrate and peritubular blood, and subsequently reduced passive reabsorption and higher CL_r than expected from residual GFR alone. The proportional model or the empirical GFR scaling approach that assumes all renal handling pathways are reduced proportionally (linearly) with GFR was shown to be inappropriate for drugs with moderate‐to‐high permeability (Figure 5 ) and thus only applicable to low permeability, non‐reabsorbed drugs (Figure 4 ).

Over the recent decade, PBPK modeling has been used to model CKD effects on renal elimination, primarily for highly secreted drugs that do not have significant permeability or passive reabsorption. ¹⁹ , ²⁰ , ²¹ , ⁴⁰ , ⁴¹ Although these models recovered the drug disposition in CKD, inconsistent scaling factors, such as relative activity factor (scalars ranging from 0.28 ⁴¹ to 3 ⁴⁰ ) and proximal tubular cells per gram of kidney (scalars up to 15) ¹⁹ have been applied, to allow the model to recover the observed data in healthy subjects and patients with CKD. This suggests low confidence on both in vitro‐to‐in vivo extrapolation of renal transport and understanding of CKD effect on renal drug handling. This is concerning as many renally secreted drugs, such as amphetamines, also have considerable permeability and reabsorption. ⁴² For such drugs, the practice of empirically optimizing active secretion using data from healthy subjects and extrapolating to patients with CKD may result in erroneous parameter optimization and misleading prediction of unstudied scenarios, as recently demonstrated in the context of full‐body PBPK modeling. ⁴³ As such, the adaptive system model shown here was entirely developed based on physiologic knowledge independent of drug molecules, and was collectively verified against 20 test compounds with different permeabilities throughout CKD stages without any optimization or empirical scaling for any of the test compounds. Our work demonstrates successful simulations of CL_r in CKD for a wide variety of drugs, establishing confidence on disease effect on renal passive reabsorption and laying a foundation for incorporating the impact of CKD on renal active secretion.

It is well‐established that transporter‐mediated renal active secretion is reduced in CKD due to declined number of functional nephrons and accumulating uremic solutes that may inhibit OAT1/3 activity. ⁹ In this study, we used the developed and verified adaptive model to simulate CL_r for the two secreted test compounds, PAH and memantine, and showed successful CL_r prediction (AFE = 1.10–1.12; Figure 6 ) in varying stages of CKD. We demonstrated that our adaptive model can effectively incorporate specific transporter (OAT1/3 and OCT2) mediated renal secretion into CL_r prediction. Based on the simulation results, the novel adaptive model together with proportional decline in transporter‐mediated secretion clearance adequately captures the changes in CL_r with progression of CKD for PAH and memantine. Uremic solutes have been shown to inhibit OAT1/3‐mediated renal uptake ⁹ but this is unlikely to impact CL_r prediction for PAH and memantine, as CL_r (and the vectorial secretion) of PAH is renal plasma flow limited and memantine is a substrate of OCT2, which is less affected by uremic solutes. ⁴⁴ Further studies on OAT1/3 and OCT2 activity and expression in CKD and clinical data on secreted drugs that have moderate‐to‐high permeability in CKD are warranted for future model refinement.

The approach described in this study also has several assumptions and limitations. Disease effect on the f _u,p was assumed to be insignificant, as the plasma albumin concentration is only 7% lower in mild and 16% lower in severe CKD than in healthy subjects, ³² and alterations in f _u,p due to uremic solute displacement likely only apply to acidic ⁴⁵ compounds with a reported median (n = 16) increase ³³ of 35% in f _u,p in severe CKD. For the 20 test compounds included here, only 3 are highly protein bound (Table S2 ) and digitoxin is the only acid, although the f _u,p of digitoxin is unchanged in patients with CKD. ⁴⁶ As illustrated by the sensitivity analyses (Figure 2 ), the small changes in f _u,p in CKD cannot explain the dramatic (mean = 458% (261–735%)) discrepancy between the observed CL_r and the expected CL_r from the proportional model for permeable drugs (Figure 5 ). Yet, the modeling framework established here could readily incorporate changes in f _u,p during CKD if observed/expected. Another challenge for model verification is the paucity of data on GFR, urine flow, and CL_r measurements for individual subjects in CKD studies. It would be ideal to compare simulated and observed CL_r for each individual subject with known GFR and urine flow. However, most clinical studies only report group mean CL_r and eGFR for each CKD stage. Future work is needed to expand the current model to include sex differences and age‐dependent changes in CL_r in pediatric subjects, which are currently not incorporated in the model. The model can be further refined as more detailed clinical data are collected for physiological changes in patients with varying degrees of CKD.

Funding

This work was supported by National Institutes of Health grant P01 DA032507. W.H. was supported by Warren G. Magnuson Scholarship and William E. Bradley Fellowship from the University of Washington, Seattle, WA.

Conflict of Interest

Both authors declared no competing interests for this work.

Author Contributions

W.H. and N.I. designed the research, performed the research, analyzed data, and wrote the manuscript.

Supporting information

Supplementary Material

Supplementary Material