Is apparent instability a guiding feature in visual search?

Abstract

Humans are quick to notice if an object is unstable. Does that assessment require attention or can instability serve as a preattentive feature that can guide the deployment of attention? This paper describes a series of visual search experiments, designed to address this question. Experiment 1 shows that less stable images among more stable images are found more efficiently than more stable among less stable; a search asymmetry that supports guidance by instability. Experiment 2 shows efficient search but no search asymmetry when the orientation of the objects is removed as a confound. Experiment 3 independently varies the orientation cues and perceived stability and finds a clear main effect of apparent stability. Experiment 4 shows converging evidence for a role of stability using different stimuli that lack an orientation cue. However, here both search for stable and unstable targets is inefficient. Experiment 5 is a control for Experiment 4, showing that the stability effect in Experiment 4 is not simple side-effects of the geometry of the stimuli. On balance, the data support a role for instability in the guidance of attention in visual search. (184 words)

Asymmetry in Search for Apparent Instability

The human visual system has remarkable abilities to represent and infer the state of the outside world. In this paper, we are interested in the ability to determine whether an object is stable or unstable. Will the object fall over in the near future? There are various cues to stability relative to gravity. Physics tells us that an object will fall over if it is tilted at an angle that places the gravity vector, pointing down from the center of mass (COM) outside of the base supporting the object (See Figure 1 for an example). Human observers are quite accurate at estimating the “critical angle” of an object – that angle of tilt at which an object will is as likely to fall over or return back to a stable, upright position (Cholewiak, Fleming, & Singh, 2013; Samuel & Kerzel, 2011).

Figure 1:

If this was a snapshot in time, which objects would fall over in the next moments? It is easy to make the decision and you will notice that more of the upper row of objects look unstable than the lower.

The ability to detect the apparent instability develops quite early. For example, Baillargeon, Needham, and DeVos (1992) found that 6.5 month-old infants were able to infer the impact of gravity based on the proportion of the contact area between a box’s bottom and a platform’s corner. Additionally, even 3 month-old infants understood that a box should fall if it was pushed beyond a platform without any support (Baillargeon & Hanko-Summers, 1990).

Recent studies on the perceived effects of stability also showed that adult human observers are very good at detecting instability, even when the visual stimulus is presented for a very brief period. For example, in a change detection task, Firestone and Scholl (2016) briefly presented an apparently stable tower of blocks. A change in one of the tower’s blocks could either influence the tower’s stability or not. The observers were better able to detect a change that altered the tower’s stability than a change that did not alter overall stability. This suggests that perceived stability might grab attention automatically (Firestone and Scholl, 2016; 2017).

Does the assessment of instability require attention? One could imagine that it would be useful to be able to look out at the kitchen and rapidly notice the cup that was about to fall or too look out over the playground and be able to process all the children in parallel so as to note the one who was about to crash off the climbing structure. If instability behaves like a “preattentive feature” (Wolfe & Utochkin, 2018) that can automatically guide attention (Wolfe & Horowitz, 2017), that should be detectable in visual search experiments. An unstable object might “pop-out” of an array of stable objects the way that a red item pops out from a field of green items (Egeth, Jonides, & Wall, 1972; Treisman, 1986).

It is typically easier to find the presence of a feature among distractors that lack that feature than it is to detect the absence of a feature. Thus, it is easier to find a moving target among stationary distractors than a stationary target among moving distractors (Dick, Ullman, & Sagi, 1987). This bias toward detecting the presence and not the absence of something is a major source of what Anne Treisman called “search asymmetries” (Treisman, & Gormican, 1988; Treisman, & Souther, 1985). In a visual search asymmetry, it is easier to find A among B than B among A. Sometimes this is due to the structure of the task, not the nature of the stimuli (Rosenholtz, 2001). In other cases, asymmetries arise because it is harder for attention to leave one type of stimulus than another (e.g., Becker & Rheem, 2020; Horstmann, Becker, Bergmann, & Burghaus, 2010; Zhang & Onyper, 2020). However, there are cases where a search for A among B is very efficient while B among A is an inefficient search. Motion, noted above, may be the clearest example (Royden, Wolfe, & Klempen, 2001) and in those cases, Treisman’s argument that search asymmetry is one marker of a preattentive feature seems reasonable.

Returning to visual stability, one might imagine that it would be less valuable to know that one stimulus was stable in a field of unstable items. If all the wine glasses are about to fall over, how useful is it to know that one of them will remain standing? If stability is the merely absence of instability, then one would predict that stable among unstable would be a less efficient search than unstable among stable. Of course, these appeals to real-world examples are far from definitive. If, in some action movie, you were leaping from rock to rock amidst a river of lava, it might be very useful to rapidly find the stable items. To assess the status of stability or instability as preattentive features in visual search, we conducted a series of five experiments. Experiment 1 shows a search asymmetry based on apparent instability. In Experiment 2, we use vertical stimuli that do not rely on tilt to produce instability, the results showed an efficient search but no search asymmetry. In Experiment 3, independently manipulated orientation and apparent stability to show a clear effect of the stability factor. Experiment 4 uses stimuli where the apparent stability is not based on orientation. Apparent stability has a clear effect, though, arguably, not a preattentive effect. Finally, Experiment 5 is a control that demonstrates that the results of Experiment 4 are not due to some geometric factors unrelated to stability.

General Methods

Participants

The sample size was determined by the data set from Wolfe, Palmer, and Horpwitz (2010), in which the standard deviation (SD) of slopes is about 0.3 of the mean slope and SD of RTs is about 0.4 of the mean RT. To detect a 2X increase in slope and/or a 100 msec main effect of RT, G*Power 3.1 toolbox (Faul, Erdfeler, Lang, & Buchner, 2007) shows that 11 observers were required to achieve power (1 − β) = .8 with Type I error (α) = .01. Therefore, 12 observers (Os) were recruited in each experiment, Except for Experiment 3 where only recruited 10 Os based on experimental design (counterbalancing, see Methods of Experiment 3). In total, 58 Os (36 Females; 22 Males) were tested.

All observers were between the age of 18 and 52 (mean = 29, SD = 10). Each observer passed Ishihara’s Tests for Color-Blindness and had 20/25 corrected vision or better. They were naïve to the purpose of the experiment and gave IRB-approved, informed consent before participating in the experiment.

Apparatus

Unless stated otherwise (as in Experiment 3 and 5), all other experiments were conducted on an Apple 24″ iMac, model A1225 (EMC2211) with resolution = 1920 × 1200 pixels and 60Hz refresh rate. Stimuli were presented at a refresh rate of 60 Hz from a distance of approximately 60 cm. All experiments were written in MATLAB 7.10.0 (MathWorks, Natick, USA) using Psychophysics Toolbox 3.0 (Brainard, 1997; Pelli, 1997).

Stimuli

We chose some stimuli because they could vary in their perceived stability. These included vases (Experiments 1, 2 and 3; Cholewiak, Fleming, & Singh, 2015) and schematic human figures (Experiment 4). Control stimuli varied in orientation by not in perceived stability: bugs (Experiment 2) and geometric shapes (Experiment 5). For experiments 1–3, 12, 18 or 24 items (each item, approximately 5° × 5°) were randomly placed on an invisible 5 × 5 array of cells. Each cell was 6° × 6°, thus the array subtended 30° × 30°. For Experiments 4–5, 6, 9 or 12 items (each item, approximately 5.8° × 5.8°) were randomly presented on an invisible 4 × 4 array of cells. Each cell was 7° × 7° and the array subtended 28° × 28°. The item was randomly jittered within the cell in order to disrupt the apparent regularity of the display.

Procedure

All these visual search experiments followed a similar, standard procedure. In each block of each experiment, observers (Os) were asked to search for the presence of a specific target item in a series of visual search arrays. Each trial started with a fixation for 300ms, followed by the onset of the visual search array with a beep sound (100ms). Os were asked to respond as “accurately and quickly as possible” whether a target was “present” or “absent”. Target present and absent responses were made via computer keypress. After the response, a feedback message was presented on top of the display. It could be “HIT” (for answering “present” when the target was present), “MISS” (answering “absent” when the target was present), “FA” (False Alarm - answering “present” when the target was absent), and “TNEG” (True Negative - answering “absent” when the target was absent). In addition, a feedback frame was placed surrounding the target position if the target had been present. Targets were present on 50% of trials. To keep the set size constant, the target was replaced by one of the distractors on target absent trials.

In each block, Os completed 30 practice trials prior to the experimental trials. The number of experimental trials varied across experiments and details are reported in each experiment section. The sequence of blocks was determined with a Latin square procedure across Os.

Experiment 1: Center of Mass

The purpose of Experiment 1 is intended to determine if there is a visual search asymmetry for apparent instability. That is, is it easier to find a more unstable object among less unstable objects than a less unstable object among more unstable objects? In the first experiment, we manipulated the tilted angle of vases with either 0 ° or 20 ° to generate the appearance of a stable or an unstable object, respectively. Stimuli are taken from Cholewiak et al. (2013). Figure 2 shows sample search arrays with a search for unstable on the left and stable on the right. The same objects could be inverted to create less stable objects with higher COMs.

Figure 2:

Search for unstable among stable (left) and stable among unstable (right). Note that, in this case, unstable items would not necessarily fall over. But, under the influence of gravity, they would move in the next, hypothetical frame.

Method

Two vases with different COM (relatively-low or high) were used as visual stimuli. Each vase was either upright (0 °) or tilted (20 °). Each was placed on a virtual “desk” surface. The tilted vase always has a greater overall width than the upright vase (It fills a wider bounding box, if one measures the horizontal distance from lower left to upper right of the object). To thwart a strategy of just looking for a target that extends to the right of the desk edge, the position of the vase was shifted randomly from the edge. Os were asked to search for an upright target among tilted distractors or vice versa.

Four types of target/distractors (T/D) pairs were generated by crossing the COM of the object (low or high) and Stability (Stable: 0 °/20 ° T/D pairs or Unstable: 20 °/0 ° T/D pairs). The four types of pairs were tested in different blocks. In each block, the search arrays were comprised of 12, 18, or 24 objects, and each set size contained 50% target present and target absent conditions. In each block, there were 60 trials for each combination of three set sizes X target presence/absence. Thus, there were 60×6 = 360 trials in each block and 1440 trials in total across four blocks.

Results

The key result for Experiment 1 is shown in Figure 3. It is obvious, looking at the RT x Set size functions, that there is a substantial search asymmetry. Search for the unstable target is faster and more efficient for both versions of the vase stimuli.

Figure 3:

RT x Set Size functions for Experiment 1: Error bars, where visible, are +/− 1 between-subjects SEM

Accuracy.

One Observer was excluded for further analysis due to low hit rate (M = 73.2 %) and high FA rate (M = 34.9 %). Other analyses were performed for the remaining 11 Os. For those Os, mean sensitivity was reasonably high in both Low COM (mean hit rate = 90.1% and mean FA rate = 1.30%) and High COM (mean hit rate = 85.7% and mean FA rate = 1.07%) conditions.

Hit and FA were converted to d′ and the d′ data were submitted to a 2 (COM) × 2 (Stability) × 3 (Set Size) repeated measures analyses of variance (ANOVA). There was a significant main effect of COM, Stability, and Set Size (see Table 1). The sensitivity was better for low COM condition (M = 3.65, SD = .64) than for high COM condition (M = 3.43, SD = .64) and for unstable target (M = 3.84, SD = .48) than for stable target (M = 3.23, SD = .65). As is typical, sensitivity decreased as set size increased. The sensitivity was better for set size 12 (M = 3.64, SD = 0.65) than for set size 24 (M = 3.41, SD = 0.67). The intermediate set size 18 (M = 3.57, SD = 0.61) did not differ from either 12 or 24 (Tukey’s HSD = .18, α = .05). There were no other significant interactions. The only important conclusion to draw from the error data is that errors were higher for conditions where RTs were higher. Thus, there is no evidence for a speed-accuracy tradeoff in this experiment.

Table 1:

ANOVA Results for the d′ inExperiment 1.

		D-prime
Factor	df	F	p	ηp2
COM	1,10	10.10	.010	.50
Stability (S)	1,10	17.52	.002	.64
Set Size (SS)	2,20	5.52	.012	.36
COM × S	1,10	0.03	.859	.00
COM × SS	2,20	1.59	.238	.14
S × SS	2,20	0.00	.998	.00
COM × S × SS	2,20	0.21	.810	.02

Reaction Times.

RT outliers were eliminated if they were more than two standard deviations from the mean calculated for each subject individually. This manipulation reduces the variance, but it does not alter the overall pattern of the data. Correct RTs were averaged across the factor of Set Size and were submitted into a 2 (Target Presence) × 2 (COM) × 2 (Stability) repeated measures ANOVA.

There were significant main effects of Target Presence and Stability, the target present (M = 1252 ms, SD = 511ms) was detected faster than target absent (M = 2143ms, SD = 878ms) and the unstable target (M = 1170 ms, SD = 434 ms) was detected faster than stable target (M = 2226 ms, SD = 827 ms). Moreover, there was an interaction between Target Presence and Stability, and the simple main effect of Stability showed significant differences in both target present (unstable: M = 848 ms, SD = 129 ms; stable: M = 1657 ms, SD = 421 ms) and target absent (unstable: M = 1493 ms, SD = 389 ms; stable: M = 2794 ms, SD = 739 ms) conditions. There was no significant main effect of COM, nor were there interactions.

Search slopes.

To assess search efficiency, we calculated the slopes of the functions for correct RTs × set size. These RT X Set Size functions for the different conditions are shown in Figure 3. All slopes were significantly greater than zero with one-sample t-tests (all t’s > 10.4, all p’s < .01). The slopes were entered into a 2 (Target Presence) × 2 (COM) × 2 (Stability) repeated measures ANOVA.

There were significant main effects of Target Presence and Stability. Search was far more efficient for target present (M = 21.6 ms/item, SD = 20.6 ms/item) than for target absent (M = 43.1 ms/item, SD = 30.6 ms/item) and search was far more efficient for unstable target (M = 17.4 ms/item, SD =16.9 ms/item) than for stable target (M = 47.3 ms/item, SD = 29.3 ms/item). Interestingly, there was an interaction between COM × Stability, and the simple main effect of Stability showed significant differences in both Low COM (unstable: M = 13.7 ms/item, SD = 14.1 ms/item; stable: M = 50.2 ms/item, SD = 28.5 ms/item) and High COM (unstable: M = 21.1 ms/item, SD = 18.6 ms/item; stable: M = 44.4 ms/item, SD = 29.8 ms/item) conditions. There was no significant main effect of COM, nor were there interactions.

Discussion

Experiment 1 clearly demonstrated that searching the tilted vase among vertical vases was more efficient than the vertical vase among tilted vases. This result is consistent with a search asymmetry based on apparent instability. However, the manipulation of the COM of the vases did not modulate the effects in Experiment 1. This result could be due to a ceiling effect. The tilted vases may have been salient enough even in the low COM condition to hide any effects of COM. Alternatively, this search might have nothing to do with stability at all. The search for tilted among vertical is more efficient than vertical among tilted even when the stimuli are simple line segments (Foster & Ward, 1991; Treisman & Gormican, 1988). In the next experiment, we chose to seek converging evidence using stable vs unstable stimuli where relative stability was not based on object orientation.

Experiment 2 – Stable and less stable upright objects

As noted, the results of Experiment 1 are consistent with known findings from orientation search. Search for tilted among vertical is more efficient than search for vertical among tilted (Carrasco, McLean, Katz, & Frieder, 1998; Rosenholtz, 2001; Foster & Ward, 1991). In Experiment 2, we separated apparent stability from object orientation. In this experiment, we compared two types of vases (Figure 4), each type of vases could be presented in a stable or unstable view. The vases would both be stable, as presented. However, it should be intuitively obvious that a slight push would knock over the less stable version, with its higher center of mass. The more stable vase would require more of push to knock it over. Importantly, unlike Experiments 1, both unstable objects and stable vases were presented in a vertical orientation, thus eliminating any effect of object orientation. If instability is a guiding feature, we would expect the search for unstable among stable to be relatively efficient. If stability is coded as the absence of stability, we might also expect to find a search asymmetry with the search for instability being faster and more efficient than search for stability.

Figure 4:

Stimuli that vary in stability without varying in orientation for Experiment 2.

Method

There were two types of T/D pairs as shown in Figure 4. On any given trial, the positions of every vase were randomly shifted on virtual surfaces so that no specific position would be diagnostic. Visual search arrays consisted of either a stable target among unstable distractors or an unstable target among stable distractors. Two types of (T/D) pairs were tested: stable among unstable vases and unstable among stable vases. Each pair was tested in a separate block. Os were asked to search for a stable target among unstable distractors or vice versa. In each block, the search arrays were comprised of 12, 18, or 24 objects, and each set size contained both target present and target absent trials. The order of the above combinations of set size and target presence was pseudorandomized to keep an equal number of 60 trials in each condition. Therefore, there were 360 trials in each block and 720 trials in total.

Results

The mean RT results for correct target present and absent trials are shown in Figure 5. It is clear that, although the searches are quite efficient (all target present slopes < 10 msec/item), there is little or no evidence for a search asymmetry.

Figure 5:

RT x set size functions for correct target-present and target-absent trials for the Vase stimuli. Error bars are +/− 1 between-subjects SEM

Accuracy.

The mean sensitivity was high (mean d′ = 3.23, mean hit rate = 89.2% and mean FA rate = 4.82%). The d′ was submitted into a 2 (Stability) × 2 (Set Size) repeated measures ANOVA.

The main effect of Set Size was marginally significant (F(2, 22) = 3.43, p = .051, η_p ² = .237). However, three pairwise comparison (i.e., 12 vs. 18, 18 vs. 24, and 12 vs. 24) did not show significant differences among set size 12 (M = 3.38, SD = 0.85), set size 18 (M = 3.16, SD = 0.89), and set size 24 (M = 3.15, SD = 0.89) with Tukey’s HSD = .297, α = .05. There was no main effect of Stability (F(1, 11) = 1.32, p = .274, η_p ² = 0.107) , nor was there a Stability × Set Size interaction (F(2, 22) = 1.55, p = .235, η_p ² = 0.123).

Reaction Times.

All correct RTs across Set Size were averaged and were submitted to a 2 (Target Presence) × 2 (Stability) repeated measures ANOVA.

There was a significant main effect of Target Presence (F(1, 11) = 40.97, p < .001, η_p ² = .79), the target present (M = 939 ms, SD = 217 ms) was detected faster than target absent (M = 1375 ms, SD = 408 ms). However, there were no main effects of Stability (F(1, 11) = 0.09, p = .773, η_p ² = .01), nor was there an Target Presence × Stability interaction (F(1, 11) = 0.07, p = .804, η_p ² = .01),

Search slopes.

All slopes of correct RTs × set size were different from zero (all t(11) > 2.41, all p < .035). The slopes were submitted into a 2 (Target Presence) × 2 (Stability) repeated measures ANOVA.

There was no main effect of Target Presence (F(1, 11) = 1.70, p = .220, η_p ² = 0.13), neither was there a main effect of Stability (F(1, 11) = 0.04, p = .850, η_p ² < .005), nor an Target Presence × Stability interaction (F(1, 11) = 0.11, p = .747, η_p ² = .10).

Discussion

Like the results of Experiment 1, the results of Experiment 2 are ambiguous. On the one hand, the slopes of the RT x set size functions are relatively shallow. Search for an upright vase among inverted (or vice versa) is markedly easier than a classically inefficient search for something like a 2 among 5s (Wolfe, Horowitz, & Palmer, 2010) or for an arbitrary realistic object (Vickery, King, & Jiang, 2005). This would argue that some feature, potentially stability/instability, is acting to guide search. This apparent guidance is not particularly strong. A search like red among green would be more efficient, but these slopes are comparable to slopes for other “feature” searches; see, for instance, searches for a ‘Q’ among Os or a cube with unique lighting in Figure 12 of Zhang, Huang, Yigit-Elliott, & Rosenholtz, (2015). On the other hand, there is no search asymmetry. If it were instability that attracted attention, then the absence of instability, like the absence of motion (Dick, et al., 1987) might have been expected to be a less efficient search.

Figure 12:

RT x set size functions for Experiment 5. Error bars show between-subjects +/− 1 SEM

Perhaps the relatively efficient search in this experiment is based on shape. If we think of the vases as having a rough “T” or triangular shape, search for such shapes among distractors rotated 180 deg can be quite efficient (Wolfe, Klempen, & Shulman (1999). Indeed, Shen, Wan, Mu, & Spence (2015) report that downward pointing triangles were faster to find among upward than vice versa. This asymmetry held for pizza slices (!) and, thus, is probably not related to instability.

Experiments 1 and 2 provide evidence that could point to a role for stability but that could also be explained as by-products of search for orientation or shape. There is a certain chicken-and-egg difficulty to this argument. It could be that the asymmetries in the search for orientation, for example, are, themselves, rooted in signals for stability. In Experiment 3, we parametrically manipulated orientation with two different objects in an effort to disentangle these factors.

Experiment 3. Tilted Vases and Oriented Bugs

In Experiment 3, we use two sets of object types, tilted vases and tilted bugs, to disentangle the stability account from orientation account: The vases are the same as in Experiment 1. In Experiment 3, we use a range of stimulus pairs to determine if the less stable item is easier to find than the more stable item even when both are tilted. A vase, if tilted enough, will fall over. In contrast, the oriented bugs in Figure 6 are clearly oriented, but they should appear to be equally stable in any orientation. They are simply bugs on a ground plane or, perhaps, on a wall. In any case, a tilted bug is not a bug who is about to fall over. Thus, comparing bug and vase searches for the same orientation pairs allows us to disentangle simple orientation effects from a possible instability effect.

Figure 6:

These “Bug” stimuli for Experiment 3 are intended to be oriented but not to give an impression of greater or lesser stability as a function of orientation.

Method

Experiment 3 was run on an Apple 13″ MacBook Pro with resolution = 1440 × 900 pixels and 60Hz refresh rate. A bottom-heavy vase and a bug were selected as the visual stimuli. These visual stimuli were tilted at different angles to generate five target/distractor (T/D) pairs: 0°/20°, 20°/40°, 35°/55°, 50°/70°, and 70°/90°. The target/distractor pairs were reversed to generate another five T/D pairs (i.e., 20°/0°, 40°/20°, 55°/35°,70°/50°, and 90°/70°). The vases and bugs were tested in two sessions and were counterbalanced across Os. Within each session, The T/D pairs with less tilted targets (i.e., 0°/20°, 20°/40°, 35°/55°, 50°/70°, and 70°/90°) and with more tilted targets (i.e., 20°/0°, 40°/20°, 55°/35°, 70°/50°, and 90°/70°) were tested in separate blocks. The sequences of ten blocks were controlled by a Latin square. Ten Os were need to fill that design and were tested in this experiment.

In each block, search arrays contained 12, 18, or 24 objects. Targets were present on 50% of trials. The order of the combinations of set size and target presence was pseudorandomized to produce an equal number of 30 trials in each condition. Therefore, there were 180 trials in each block, and 3600 trials in total (vases/bugs × 10 blocks).

Result

RTs x T/D pair functions are shown in Figure 7. The figure plots RT as a function of TD pair for each set size. The spread between the triplet of data points for each TD pair corresponds to the slope of the RT x set size function which is given as the number adjacent to each triplet. Clearly, the results show distinct results depending on the object type. Looking first at the bug data (bottom row), the pattern of results is obviously symmetric around 45 degrees. The classic search asymmetries are present, 20 deg among 0 deg (vertical) is faster and more efficient than 0 among 20 deg. Similarly, 70 deg among 90 deg (horizontal) is faster and more efficient than 90 among 70 deg. Interestingly, 20/40 and 50/70 pairs are also seem somewhat asymmetric, suggesting that it might be easier to find “more tilted” among “less tilted”.

Figure 7:

RTs x T/D pair functions for the vases (top panels) and bugs (bottom panels) in Experiment 3. Target-present and target-absent are plotted in left panels and right panels, respectively. Blue and red symbols denote pairs where the more tilted/more unstable item is the target, green and purple symbols denote pairs where the less tilted/unstable item is the target. Error bars, where visible, show +/− 1 between-subjects SEM. Numbers on the associated with the data points are the slopes of the average RT x set size functions, and the stars indicate that the slopes were significantly higher than zero.

The vase data (top row) are dramatically different. The functions are not symmetrical around 45 degrees. There are strong asymmetries at all orientations with the more tilted vase always found more quickly and efficiently (if you consider a 90deg horizontal vase not to be ‘tilted’ but to be resting on its side. The vase that will fall over first is found first. These results seem to be clear evidence that there is a factor, other than simple orientation at work here.

Accuracy.

The mean sensitivity was high (mean d′ = 3.83, mean hit rate = 94.23% and mean FA rate = 4.77%). The d′ values were submitted to a 2 (Object Types) × 5 (T/D Angles) × 2 (Stability) × 2 (Set Size) repeated measures ANOVA.

As can be seen in the ANOVA results in Table 3, main effects showed that d′ values were significantly higher for bug stimuli (M = 3.84, SD = 0.36) than for vase stimuli (M = 3.68, SD = 0.42), for more tilted target (M = 3.82, SD = 0.38) than for less tilted target (M = 3.70, SD = 0.40). There was a significant main effect of T/D Angles. 0°/20° pairs have marginally better sensitivity than 35°/55°, and there were no other significant differences among 20°/40° pairs, 50°/70° pairs and 70°/90° pairs (Tukey’s HSD = 0.14, α = .05). There was also a significant main effect of Set Size, the set size 12 (M = 3.86, SD = 0.36) has better sensitivity than set size 18 (M = 3.74, SD = 0.39) and set size 24 (M = 3.67, SD = 0.42), but latter two set sizes did not show significant difference (Tukey’s HSD = 0.11, α = .05). The four-way interactions was not significant. Since the main purpose of sensitivity analyses was testing speed-accuracy tradeoffs, we focused on a significant three-way interactions among Object Types, T/D Angles, and Stability, which were corresponding factors in the RTs/slopes analyses (see below). There were significantly simple T/D Angles × Stability interactions in both vases and bugs conditions. In the vases condition, the sensitivity was significantly better for more tilted target than for less tilted target in the 0°/20°and 20°/40°, but significantly reverse patterns were found in 50°/70°, and 70°/90°. On the other hand, in the bugs condition, the sensitivity was significantly better for more tilted target than for less tilted target in the 20°/40°and 35°/55° (see Table 4 [top rows] for the mean and SD of the d′ in each T/D pairs).

Table 3:

ANOVA Results for the d′ inExperiment 3.

		D-prime
Factor	df	F	p	ηp2
Object Types (O)	1,9	9.23	.014	.51
T/D Angles (A)	4,36	3.94	.009	.30
Stability (S)	1,9	48.69	.000	.84
Set size (SS)	2,18	11.74	.001	.57
O × A	4,36	0.82	.521	.08
O × S	1,9	15.37	.004	.63
O × SS	2,18	3.50	.052	.28
A × S	4,36	18.26	.000	.67
A × SS	8,72	1.03	.450	.10
S × SS	2,18	0.37	.698	.04
O × A × S	4,36	6.50	.001	.42
A × S[Vases]	4,72	20.96	.000	.54
A × S[Bugs]	4,72	5.34	.001	.23
O × A × SS	8,72	1.54	.158	.15
O × S × SS	2,18	7.90	.003	.47
A × S × SS	8,72	1.90	.073	.17
O × A × S × SS	8,72	1.96	.064	.18

Table 4:

Mean (SD) for the d′ (top), RTs (middle), and search slopes (bottom) in each T/D pairs inExperiment 3.

	Vases					Bugs
	0°/20°	20°/40°	35°/55°	50°/70°	70°/90°	0°/20°	20°/40°	35°/55°	50°/70°	70°/90°
D-prime
More tiled	3.83(0.38)	3.85(0.34)	3.64(0.42)	3.60(0.41)	3.46(0.37)	3.99(0.24)	4.09(0.19)	3.92(0.32)	3.81(0.29)	3.96(0.33)
Less tilted	3.63(0.36)	3.31(0.34)	3.64(0.40)	3.78(0.36)	4.02(0.25)	3.88(0.31)	3.54(0.43)	3.59(0.36)	3.75(0.35)	3.84(0.37)
F-test(1,90)	5.70*	37.81***	0.01	4.10*	40.98***	1.79	40.52***	14.42***	0.34	2.09
RTs (ms)
More tiled	595(82)	643(87)	690(97)	768(132)	1008(167)	580(66)	710(106)	748(95)	846(109)	1064(178)
Less tilted	1169(234)	1200(243)	1130(272)	1042(218)	617(115)	1077(184)	884(142)	745(126)	685(120)	586(59)
F-test(1,90)	198.7***	187.48***	116.84***	45.42***	92.43***	148.95***	18.37***	0.005	15.79***	138.05***
Slopes (ms/item)
More tiled	1.6(2.5)	−0.8(3.2)	−1.3(2.3)	0.6(5.0)	8.8(6.4)	2.4(2.7)	4–1(5.5)	3.5(3.8)	5.3(4.2)	12.9(4.8)
Less tilted	12.9(5.6)	11.1(7.3)	7.4(5.8)	4.4(7.2)	−0.1(3.2)	14.2(6.8)	2.1(4.6)	2.9(3.3)	2.6(3.2)	1.9(3.2)
F-test(1,90)	23***	60.60***	32.78***	6.22*	34.19***	60.39***	1.82	0.17	3.18	53.06***

Note:

^*indicates p < .05.

^**indicates p < .01.

^***indicates p < .001.

Overall, the sensitivity data follow the RT data, faster RTs are associated with higher sensitivity. There is no evidence for speed-accuracy tradeoffs except for the 50°/70° pairs in the condition of the vases¹ (see below).

Reaction Times.

The correct RTs of Set Size were averaged and were submitted into a 2 (Object Types) × 2 (Target Presence) × 5 (T/D Angles) × 2 (Stability) repeated measures ANOVA. The averaged RTs were shown in Figure 7. Outlier RTs more than 2SD from the individual observer means were removed from the analysis. The results were consistent when using raw correct RTs.

As can be seen in Table 5, main effects showed RTs were significantly faster for bugs stimuli (M = 793 ms, SD = 208 ms) than for vase stimuli (M = 886 ms, SD = 294 ms), for target present (M = 745 ms, SD = 187 ms) than for target absent (M = 934 ms, SD = 285 ms). There was also a main effect of T/D Angles, 70°/90° pairs has faster RTs than 20°/40° pairs, and there was no other significant difference among 0°/20° pairs, 35°/55° pairs and 50°/70° pairs (Tukey’s HSD = 37 ms, α = .05). The four-way interactions was not significant. Based on the main purpose of this experiment, we focused on a significantly three-way interactions among Object Types, T/D Angles, and Stability. There were significantly simple interactions between T/D Angles and Stability in both vase stimuli and bug stimuli. In the vases condition, the more tilted target has faster RTs than less tilted target in 0°/20° pairs, 20°/40° pairs, 35°/55° pairs, and 50°/70° pairs, but reverse pattern was found in 70°/90° pairs. In the bugs condition, the more tilted target has faster RTs than less tilted target in 0°/20° pairs and 20°/40° pairs, but the less tilted target has faster RTs than more tilted target in 50°/70° pairs and 70°/90° pairs. The more tilted target showed similar RTs to the less tilted target in 35°/55° pairs (see Table 4 [middle rows] for the mean and SD of the RTs in each T/D pairs).

Table 5:

ANOVA Results for the RTs and search slopes inExperiment 3.

		RTs			Slopes
Factor	df	F	p	ηp2	F	p	ηp2
Object Types (0)	1,9	13.18	.006	.59	0.74	.412	.08
Target Presence(P)	1,9	85.37	.000	.90	1.68	.229	.16
T/D Angles (A)	4,36	3.67	.013	.29	14.84	.000	.62
Stability (S)	1,9	49.54	.000	.85	12.33	.007	.58
O × P	1,9	9.20	.014	.51	0.36	.561	.04
O × A	4,36	9.80	.000	.52	4.64	.004	.34
O × S	1,9	54.83	.000	.86	24.26	.001	.73
P × A	4,36	2.48	.062	.22	3.95	.009	.30
P × S	1,9	4.76	.057	.35	4.45	.064	.33
A × S	4,36	187.90	.000	.95	64.02	.000	.88
O × P × A	4,36	2.24	.084	.20	1.45	.238	.14
O × P × S	1,9	4.81	.056	.35	2.27	.169	.20
O × A × S	4,36	27.25	.000	.75	8.91	.000	.50
A × S[Vases]	4,72	151.68	.000	.89	38.95	.000	.68
A × S[Bugs]	4,72	126.28	.000	.88	35.76	.000	.67
P × A × S	4,36	39.44	.000	.81	6.70	.000	.43
O × P × A × S	4,36	1.61	.193	.15	1.78	.154	.17

Search slopes.

The overall slopes of correct RTs × set size were relatively shallow, but most of the slopes were significantly higher than zero (ts >1.98, ps < .04). Please see Figure 7 for details.

As can be seen in Table 5 and Figure 7, there was a main effect of T/D Pairs. There was a main effect of Stability showed that search for the more tilted target (M = 3.7 ms/item, SD = 6.0) was more efficient than search for the less tilted target (M = 5.9 ms/item, SD = 7.2). Parallel to the RTs analyses, we focused on significant three-way interactions among Object Types, T/D Angles, and Stability: In the vases condition, the search slopes were similar to the finding of RTs. Search for the more tilted target was more efficient than search for the less tilted target in 0°/20° pairs, 20°/40° pairs, 35°/55° pairs, and 50°/70° pairs, but reverse pattern was found in 70°/90° pairs. In the bugs condition, search for the more tilted target was more efficient than search for the less tilted target in 0°/20° pairs and reverse pattern was found in 70°/90° pairs. The search efficient was similar between more tilted target and less tilted target in 20°/40° pairs, 35°/55° pairs and for 50°/70° pairs (see Table 4 (bottom rows) for the mean and SD of the search slopes in each T/D pairs).

Search Asymmetries

For the Bug conditions, the mean RT asymmetries between pairs (0/20 vs 20/0, etc) are significant for all pairs except 35/55 vs 55/35 for both present and absent trials (paired t-tests, all t(9) > 3.6, all p<0.006, before correction for multiple comparison). For the slopes, the 0/20 vs 20/0 and 70/90 vs 90/70 conditions are different for target present and absent trials (all t(9) > 5.4, all p < 0.0004). The 50/70 vs 70/50 comparison is significant for target-present trials (t(9)=3.6, p=0.0055).

For the Vase conditions, the mean RT asymmetries between all pairs are significant for all pairs for both present and absent trials (paired t-tests, all t(9) > 4.7, all p<0.0012, before correction for multiple comparison). For the slopes, all target absent pairs are significantly different (all t(9) > 5.5, all p < 0.0004). For target present trials, 20/0 (t(9)=5.9, p=0.0002) and 40/20 (t(9)=6.1, p=0.0002) pairs are different. The 70/90 pair is marginal (t(9)=3.1, p=0.0.118) given concerns about multiple comparison. The 35/55 and 50/70 pairs are not significant.

Discussion

Experiment 3 produces an interesting pattern of results that seems to argue in favor of a role for instability in the guidance of visual search. It is obvious that the results varied as a function of Object Types. In the bugs condition, visual stimuli were designed to remove relative stability as a distinction between targets and distractors. The results showed a symmetrical search around 45° as well as the typical search asymmetries along the vertical (0°) and horizontal (90°) axis. The search asymmetries for 20°/40° (both steep) and 50°/70° (both shallow) are weaker but present.

The vase stimuli produce a different pattern of results. One way to think about this is to propose that the vase that is going to crash to the ground first is easier to find. It is easier to find 20 among 0 than vice versa, because a vertical item is not going to crash at all. Perhaps it is easier to find 55 among 35 because the 55 deg vase is a bit close to disaster. The pattern seems to reverse for the 70/90 pair but that could be because a 90 deg vases not going to crash. It is already resting on its side. We are not proposing a sophisticated physics engine at work here. For instance, there is not particular evidence that search efficiency depends on the relation of the center of mass to the footprint of the vase. However, some factor is at work on the vase stimuli that is not at work with the bugs and the relationship of the object to gravity seems like a good candidate.

The results of Experiment 3 are quite compelling but they still involve an interaction with orientation search. In the remaining experiments, we seek evidence for an instability effect that is not tied to search for a target of a specific orientation.

Experiment 4. Falling Man

In an effort to produce a strong sense of instability that was not confounded with orientation, we used the human figures shown in Figure 8. These silhouettes appear to either be leaning forward or falling backward. The main axis of the man was always tilted 45° or 315° from a ground. The man leaning forward is a relatively stable figure since both of his feet are on the ground. The man falling backward man is an unstable figure since his one leg is on the ground while the other is in the air (and he certainly looks as if he is headed for a fall). Since both stable and unstable figures are tilted either 45° or 315°, orientation is not a cue to stability. As in the previous experiment, the question was whether the more unstable figure (i.e., falling backward man) is more salient and, thus, easier to find than the more stable figure (i.e., leaning forward man).

Figure 8.

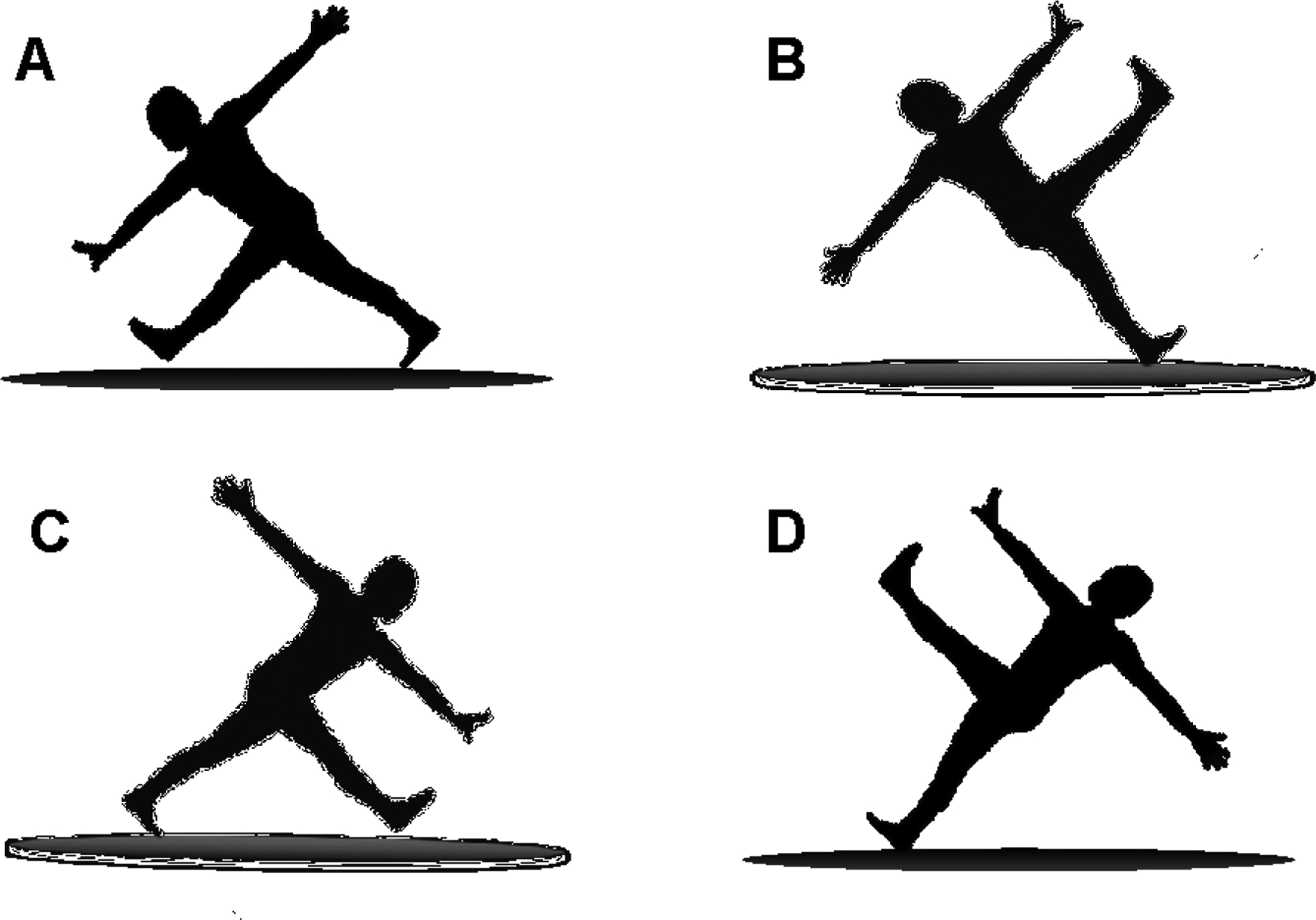
Visual stimuli in Experiment 4. Left and right column show leaning forward man and falling backward man, which were more and less stable, respectively.

Method

There are two versions of the experiment. Referring to Figure 8, in the Same Orientation condition, Os searched for A among B or vice versa (or, equivalently, C among D). In this condition, all items on a trial had the same main-axis orientation. In the Different Orientation condition, the T/D pairs were A among D or vice versa (and B among C). In this case, all the figures in a trial were facing the same way (i.e. A & D face left) but the targets have a main-axis orientation 90° different from the distractors. This provides an orientation cue that could make the search much easier, though, given the orthogonal orientation of the arms and one leg, it is not obvious that a search like A among D would be a “pop-out” search.

For each condition, Os were tested on one block of unstable targets among stable distractors and on another block of stable targets among unstable distractors. Thus, there were four different blocks. The sequence of blocks pseudorandomized by a Latin square procedure across participants. Set sizes were 6, 9, or 12 objects. A target was present on 50% of trials. The set size and target presence were pseudo-randomized to produce an equal number of 50 trials in each of the six combinations of set size and target presence. Therefore, there were 300 trials in each block and 1200 trials in total.

Results

Figure 9 shows the RT x set size functions for both conditions of Experiment 4 with statistical results summarized in Tables 6 and 7. Two points are of interest. First, with these stimuli, search is quite inefficient, even in the Different Orientation condition, when orientation should be a good cue to target presence. Second, search for unstable among stable appears to be somewhat easier than search for stable among unstable.

Figure 9:

RT x set size functions for Experiment 5. Error bars, where visible, represent +/− 1 between-subjects SEM.

Table 6:

ANOVA Results for the d′ inExperiment 4.

		D-prime
Factor	df	F	p	ηp2
Orientation(O)	1,11	7.59	.019	.41
Stability (S)	1,11	3.76	.079	.25
Set Size (SS)	2,22	28.62	.000	.72
O × S	1,11	0.60	.455	.05
O × SS	2,22	0.28	.760	.02
S × SS	2,22	1.23	.314	.10
O × S × SS	2,22	3.76	.039	.25
S × SS[same]	2,44	0.43	.614	.02
S × SS [different]	2,44	3.74	.032	.15

Table 7:

ANOVA Results for the RTs and search slopes inExperiment 4.

		RTs			Slopes
Factor	df	F	p	ηp2	F	p	ηp2
Target Presence (P)	1,11	61.64	.000	.85	18.52	.001	.63
Orienation(O)	1,11	30.08	.000	.73	16.55	.002	.60
Stability (S)	1,11	28.17	.000	.72	4.44	.059	.29
P × O	1,11	1.00	.340	.08	0.07	.800	.01
P × S	1,11	0.76	.402	.06	0.25	.629	.02
O × S	1,11	0.07	.795	.01	0.04	.855	.00
P × S × O	1,11	0.10	.753	.01	1.02	.334	.08

Accuracy.

The mean sensitivity was high in both T/D pairs with same orientation (mean d′ = 3.02, mean hit rate = 82.6% and mean FA rate = 3.2%) and T/D pairs with different orientation (mean d′ = 3.28, mean hit rate = 89.0% and mean FA rate = 4.0 %) conditions.

The d′ values were submitted to a 2 (Orientation) × 2 (Stability) × 2 (Set Size) repeated measures ANOVA. As can be seen in table 6, main effects showed that d′ were significantly higher for the T/D pairs with different orientation (M = 3.28, SD = 0.86) than for the same orientation counterparts (M = 3.02, SD = 0.76). There was a significant main effect of Set Size. The d′ was higher for set size 6 (M = 3.44, SD = 0.73) than for set size 9 (M = 3.15, SD = 0.78), which has higher d′ than for set size 12 (M = 2.87, SD = 0.85), Tukey’s HSD = .247, α = .01. The main effect of Stability was marginally significant, d′ was marginally higher for more tilted target (M = 3.29 SD = 0.84) than for less tilted target (M = 3.01, SD = 0.78). There was a three-way interactions among Orientation × Stability × Set Size. The interaction between Stability and Set Size only occurred in the different orientation of T/D pairs, which showed that the unstable targets condition has higher sensitivity than the stable targets condition when different orientation of T/D pairs presented on set size 9 (F(1, 66) = 7.45, p = .008, η_p ² = .101) and set size 12 display (F(1, 66) = 3.90, p = .05, η_p ² = .056 ). There were no other interaction effects. In general, the error effects were similar to the RT effects, arguing against the importance of any speed-accuracy tradeoff.

Reaction Times.

The correct RTs were submitted into a 2 (Target Presence) × 2 (Orientation) × 2 (Stability) repeated measures ANOVAs.

As can be seen in table 7, there are main effects of target presence, T/D Pair, and stability showing that RTs were significantly faster for target present (M = 1246 ms, SD = 300 ms) than for target absent (M = 1708 ms, SD = 479 ms), significantly faster for T/D pairs with different orientation ( M = 1353 ms, SD = 456 ms) than for T/D pairs with same orientation (M = 1601 ms, SD = 433 ms), and significantly faster for unstable targets (M = 1319 ms, SD = 378 ms) than for stable targets (M = 1636 ms, SD = 483 ms). There were no other significant interactions.

Search slopes.

All slopes of correct RTs × set size were significantly higher than zero (all t(11) > 2.81, all p < .018). The slopes were submitted into a 2 (Target Presence) × 2 (Orientation) × 2 (Stability) repeated measures ANOVA. RTs as a function of Set Size in different conditions were shown in Figure 10.

Figure 10.

visual stimuli in Experiment 5. Left and right column show figures with a downward breach and upward breach, respectively.

As can be seen in the Slopes columns of Table 7, the is the usual main effect of target presence: more efficient search for target present (M = 40.4 ms/item, SD = 29.8 ms/item) than for target absent (M = 71.6 ms/item, SD = 43.7 ms/item). The main effect of T/D pairs shows that pairs with different orientation (M = 46.4 ms/item, SD = 39.6 ms/item) are more efficient than for the T/D pairs with same orientation (M = 65.6 ms/item, SD = 39.1 ms/item), but note that none of these slopes is particularly efficient. Finally, there was a marginally significant main effect of Stability, unstable targets (M = 48.3 ms/item, SD = 37.9 ms/item) were found more efficiently than stable targets (63.7 ms/item, SD = 41.6 ms/item). There were no other significant interactions.

Discussion

What does Experiment four say about the status of stability as a guiding feature in visual search? The main effect of stability argues for the role of stability in search efficiency. However, this is undercut but the inefficiency of these searches overall. If stability was a strong guiding feature, one would expect slopes to be near zero. Instead, they are very steep. When slopes are steep, an alternative interpretation of search asymmetry attributes the asymmetry to “distractor rejection” (Treisman, & Souther, 1985; Horstmann, & Becker, 2019). Imagine that Os are serially attending to item after item, looking for a target, and suppose that unstable items hold attention for a little longer than stable items. In such a case, the search for stable targets will be less efficient than search for unstable targets, because the more compelling unstable distractors slow the search for the stable target. This would show a role for stability, but not necessarily a preattentive role for stability. This account of a stability search asymmetry would not work well for Experiment 3, where many of the slopes are very shallow.

It is interesting that the Different Orientation condition was not more efficient than it was. Search for a left oblique target among right oblique distractors, with target and distractors separated by 90°, might be expected to be efficient (e.g. Figure 8 of Wolfe et al, 1992). Apparently, the orientations of the arms and legs sufficiently mask the main axis orientation to disrupt the efficient guidance of the search. In that context, it is interesting that some effect of stability survives, even with stimuli that are too ‘noisy’ for good orientation guidance. Note that the leaning forward man has two limbs pointing down and only one pointing up (We will consider the other leg to be an extension of the main axis of the figure). In contrast, the man falling backward two limbs pointing up and one pointing down. Perhaps this distinction is important to the search task. Indeed, a ‘dead elephant’ asymmetry experiment (Wolfe, 2001) found that search was more efficient for some ‘dead’ inverted animals with legs pointing upward among ‘live’ upright animals with downward legs than for ‘live’ among ‘dead’. Based on this observation, we conducted a last experiment using visual stimuli that preserved similar geometric shape as the man figure but minimized any perceived effect of gravity.

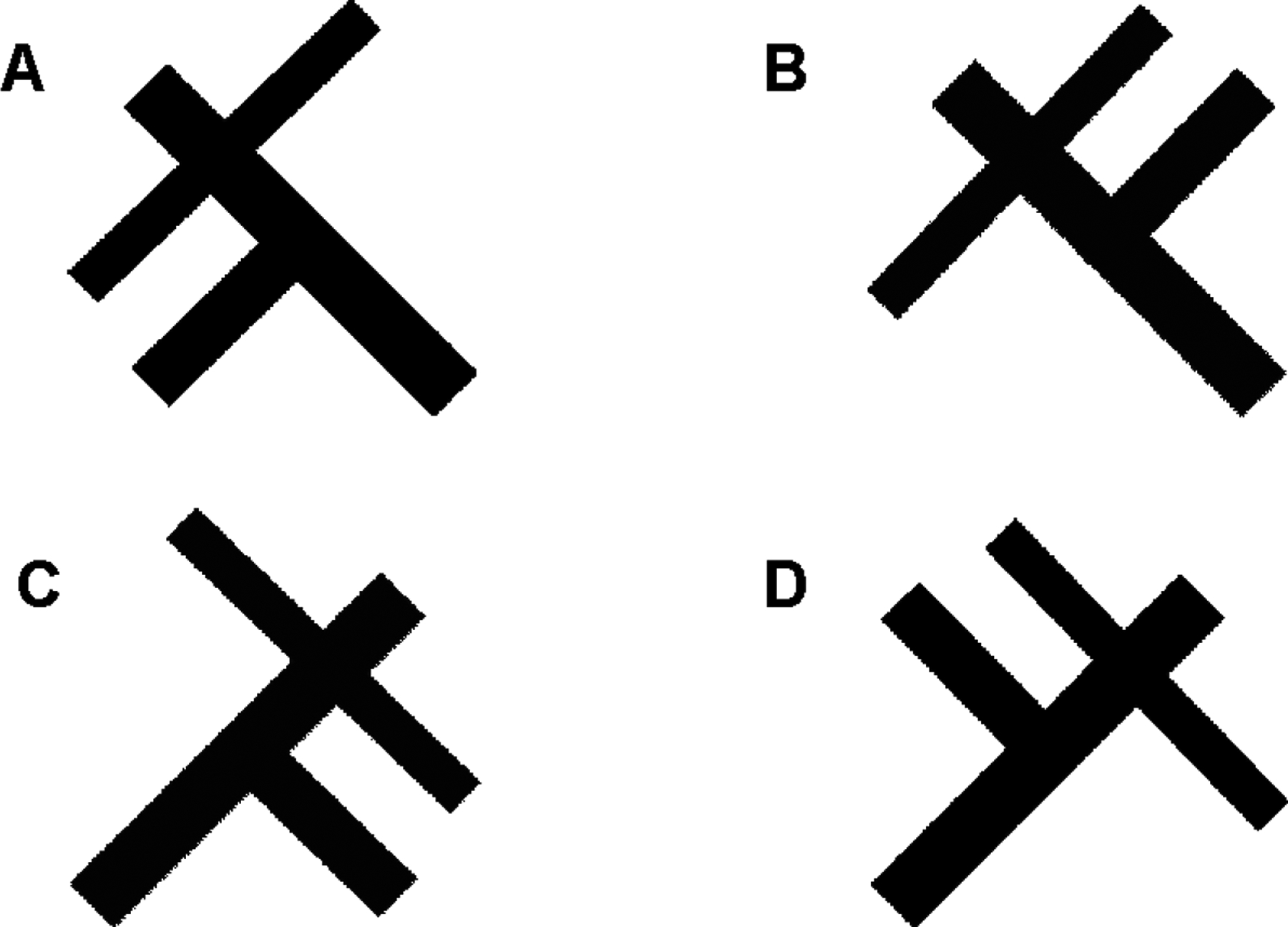
Experiment 5 – Same geometry, different meaning

As noted, Experiment 5 is a control experiment. It is intended to test whether the results of Experiment 4 were related to the perceived effects of gravity or driven by aspects of the geometry of the falling man stimuli. The stimuli used in this experiment have three major differences from the falling man stimuli, all intended to minimize the role of perceived stability or instability while keeping other basic visual properties similar to those of the previous experiment. First, we adopted a figure with the same basic geometric shape as the falling man but without the human-like contours (see Figure 10). The goal was that naïve Os would not notice that these shapes had anything human about them. We assessed this with a questionnaire, administered after the experiment (see below). Of course, when you, the reader, look at Figure 10, you will see falling bodies, but you have been primed by the stimuli of Experiment Four. None of the Os in Experiment Five had experience with the stimuli of Experiment Four. Second, we eliminated any indication that the stimuli were “standing” on the “ground” to reduce visual reference to up and down and the potential effects of gravity. Where the falling men of Experiment Four had a schematic surface below them, the figures of Experiment Five did not. Third, by rotating the plane of the actual monitor, we presented the visual stimuli on a physically horizontal display. The Os were looking down as if searching for objects on top of a desk (see Figure 11). The question was whether a figure with two limbs pointing up like the man falling backward was still easier to find than a figure with two limbs pointing down like the man leaning forward. We did not describe these features as “limbs” when showing them to the Os. These figures should have little or nothing to do with the perception of instability or of a tendency to fall over.

Figure 11:

Sample search trial for Experiment 5. The stimuli placed on a horizontal surface to discourage interpretations having to do with stability.

Method

Experiment 5 was run on a 64-bit Avatar gaming PC running Windows 8. Stimuli were presented on a 55″ TV (Sony XBR55) with resolution = 3840 × 2160 and 29 Hz refresh rate. Screen, multitouch, and PC assembly were performed by Mesa Mundi Inc., Sharon, Massachusetts. During the experiment, the display was rotated 90° from vertical to make it horizontally (see Figure 11). Os were asked to stand in front of the horizontal display. To keep the viewing distance and visual angle of stimuli consistently across Os, the height of the horizontal display was adjusted according to the body length of the Os individually before the experiment. The design was the same as Experiment Four but the visual stimuli were changed to the geometric shapes of Figure 10. Thus, looking at Figure 10, in the Same Orientation condition, Os searched for item A among B or vice versa (or, equivalently, C among D). In this condition, all items on a trial had the same main-axis orientation. In the Different Orientation condition, the T/D pairs were A among D or vice versa (and B among C).

To assess the effectiveness of our stimulus manipulations, we asked the participants three questions after the experiment:

1. Did you use any strategy to find the target? Please describe it.

2. Did the stimuli look like anything to you, other than an abstract shape?

3. During the experiment, did you notice that some of the shapes looked like a falling man (maybe slipping on the ice)?

Results

Questionnaire.

Q1. Did you use any strategy to find the target?

The answers can be grouped into three types. Six Os reported that they searched for a unique one from global trends, four Os assumed that they were searching specific objects (e.g., person, letter “F”, school desk, shape, etc.) and two Os searched the local direction/orientation (e.g., pointing upwards).

Q2. Did the stimuli look like anything to you, other than an abstract shape?

Two Os did not feel that the stimuli resembled anything in particular, six Os reported that the stimuli looked like a letter “F”, and the remainder said that the stimuli looked like some specific objects (e.g., fork, icon, cross, chair, stick figure, hummingbird, slipping person, etc.).

Q3. During the experiment, did you notice that some of the shapes looked like a falling man?

Three of the Os said “yes”, and nine OS said “no”.

The mean RT x set size results for correct trials are shown in Figure 12. We will refer to “stable” and “unstable” targets and distractors to keep the same terms as in Experiment 4. Unstable are those stimuli with two segments pointing up. Comparisons with the results of Experiment 4 suggest that the Experiment 5 task is somewhat more difficult and less efficient. The main patterns of the data are similar with some evidence that the unstable targets are a bit easier to find than stable. Here, however, there does not appear to be evidence for asymmetry in slopes.

Accuracy.

Even though these were the hardest searches in the experiments reported in this paper, the mean sensitivity remained high for T/D pairs with the same orientation (mean d′ = 3.06, mean hit rate = 84.76% and mean FA rate = 4.25%) and for T/D pairs with different orientation (mean d′ = 3.22, mean hit rate = 88.63% and mean FA rate = 4.65%) conditions.

The d′ values were submitted into a 2 (Orientation) × 2 (Stability) × 2 (Set Size) repeated measures ANOVA. There was a significant main effect of Set Size (F(2, 22) = 14.9, p < .001, η_p ² = .575). Set size 12 (M = 2.87, SD = 0.87) produced worse sensitivity than set size 6 (M = 3.34, SD =0.87) and set size 9 (M = 3.21, SD = 0.81), Tukey’s HSD = .264, α = .05. There were no other significant effects (all F < 2.64, all p >.13).

Reaction Times.

The correct RTs were entered into a 2 (Target Presence) × 2 (Orientation) × 2 (Stability) repeated measures ANOVA.

Table 8 shows the ANOVA results for RTs and slopes. The key result is that there is no significant effect of stability on with either RT or slope. There is a main effect of target presence and of T/D Pair; RTs were significantly faster for target present (M = 1408 ms, SD = 319 ms) than for target absent (M = 1839 ms, SD = 485 ms), for the T/D pairs with different orientation (M = 1529 ms, SD = 466 ms) than for the T/D pairs with same orientation (M = 1717, SD = 442 ms). There was also a significant interaction between Target Presence and Orientation. T/D pairs with different orientation have faster RTs than for T/D pairs with same orientation in both target present (different: M = 1343 ms, SD = 325 ms vs. same: M = 1473 ms, SD = 299 ms ) and target absent (different: M = 1716 ms, SD = 509 ms vs. same: M = 1962 ms, SD = 425 ms) conditions. There were no other significant interactions either.

Table 8:

ANOVA Results for the RTs and search slopes inExperiment 5.

		RTs			Slopes
Factor	df	F	p	ηp2	F	p	ηp2
Target Presence (P)	1,11	56.32	.000	.84	19.45	.001	.64
Orienation(O)	1,11	14.60	.003	.57	8.01	.016	.42
Stability (S)	1,11	2.51	.148	.19	0.36	.558	.03
P × O	1,11	16.06	.002	.59	6.67	.026	.38
O [Target Present]	1,22	6.46	.019	.23	0.76	.394	.03
O [Target Absent]	1,22	22.97	.000	.51	14.41	.001	.40
P × S	1,11	0.09	.765	.01	0.33	.576	.03
O × S	1,11	0.03	.874	.00	0.02	.890	.00
P× S × O	1,11	0.39	.547	.03	1.02	.334	.08

Search slopes.

All slopes of correct RTs × set size were significantly higher than zero (all t(11) > 4.93, ps < .001). The slopes of correct RTs × Set Size were submitted into a 2 (Target Presence) × 2 (Orientation) × 2 (Breach Direction) repeated measures ANOVA. RTs as a function of Set Size in different conditions were shown in Figure 12.

As can be seen in Table 8, main effects show that there are more efficient RT x set size functions for target present (M = 59.2 ms/item, SD = 31.5 ms/item) than for target absent (M = 106.7 ms/item, SD = 55.8 ms/item), for the T/D pairs with different orientations (M = 75.3 ms/item, SD =52.1 ms/item) than for the T/D pairs with same orientation (M = 90.6 ms/item, SD = 49.0 ms/item). There was also a significant interaction between Target Presence and Orientation. The simple main effect of orientation only occurred in target absent (different: M = 94.3 ms/item, SD = 61.3 ms/item vs. same: M = 119.2 ms/item, SD = 46.5 ms/item ) but not in target present condition. As noted above, there was no significant main effect of stability, nor were there interactions with stability.

Discussion

The Current experiment aimed to test whether the effects of the stability manipulation on RTs and slopes in Experiment 4 would survive if the perception of instability was minimized. Experiment 4 showed that was easier to find a man falling backward man than it is to find a man leaning forward. Both RTs and slopes (while marginal significant) showed a search asymmetry. However, there is no sign of a search asymmetry in Experiment 5, Slopes for stable and unstable targets were similar. We would conclude from this that Stability played some role in the falling man search in Experiment 4 because part of that effect went away when the cues to instability were reduced. This argument has the usual limitations of an argument from a null result. Moreover, three of our Os reported some explicit awareness of the falling man possibilities in Experiment 5 stimuli. This leaves open the possibility that, despite our efforts, the abstract stimuli of Experiment 5 might have invoked something of the stability/instability attribute that we were trying to eliminate.

General Discussion

To state the obvious, gravity exerts an influence on all terrestrial objects. It is not surprising, therefore, to find that it has an influence on visual perception (Clément & Eckardt, 2005; Wolfe & Held, 1982) and visual attention (Võ & Henderson, 2009). Most previous studies of perceived stability focused on how properties of single objects change their apparent stability (Cholewiak, et al. 2013; Firestone, & Keil, 2016; Firestone and Scholl, 2016; 2017). Visual search studies, like the current experiments, see for evidence that a feature can be processed among multiple objects at the same time. For instance, Marendaz, Stivalet, Barraclough, & Walkowiac (1993) showed that gravity could modulate orientation search tasks. Here, we have provided evidence for the preattentive processing of gravity on the apparent stability of objects. To briefly summarize, in Experiment 1, we established a basic search asymmetry. Search for an unstable (tilted) target among stable (upright) distractors was more efficient than search for a stable target among unstable distractors. However, a similar result would be predicted if simple lines of 0° & 20° were used. The explanation of this classic search asymmetry could be rooted in effects of gravity or it could a function of orientation processing. In Experiment 2, we used stable and unstable vases. We did not find a search asymmetry using these top-heavy and bottom-heavy vertical objects. However, the RT x set size slopes were quite efficient (~8 msec/item for target-present slopes). This suggests that something was guiding search. An unguided search would be expected to be markedly less efficient (Wolfe & Horowitz, 2004; 2017). Since the targets and distractors different in their apparent stability, these results could support a preattentive role for stability, though we cannot rule out the possibility that this was an efficient search for an oriented object (Wolfe, et al., 1999). Experiment 3 provides more compelling evidence for a distinctive role of stability. In Experiment 3, observers always looked for a target among homogeneous distractors, oriented either +/− 20 deg from the target orientation. One set of searches used vases as stimuli. The other set used bugs. The critical difference between these stimuli is that a tilted vase will fall over (or right itself). A tilted bug need do no such thing. The two types of stimuli produce very different patterns of results. The bug data are symmetric around 45 deg with standard search asymmetries when target (or distractors) are vertical or horizontal. The vase data show a very different pattern of search asymmetries. For example, it is easier to find a 55 deg target among 35 deg distractors than vice versa. The 55/35 and 35/55 conditions are identical in bug search. It is clear that a factor beyond simple orientation is shaping the vase results. It is plausible to propose that the rule is that it is easier to find the more tilted object, especially if one recognizes that a 90deg tilted vase is not “tilted” but rather is stably resting on its side. The efficiency of the searches for the larger tilt suggests that whatever is guiding search is an available preattentively. It is possible that something other than a gravitational / stability account might explain this result, but these data look like good support for a preattentive instability signal.

In Experiment 4, we tried one other way to produce search stimuli that varied instability but not in orientation. The results showed that it was easier to find a silhouette of a man falling backward among more apparently stable men, leaning forward than it was to search for leaning forward among falling backward. However, in this case, all the searches were decidedly inefficient. The search asymmetry shown in these data is probably better attributed to an effect of distractor rejection (Treisman & Souther, 1985; Horstmann & Becker, 2019) than to a preattentive preference for finding the presence, rather than the absence of a basic feature. Experiment 4 is probably best seen as evidence for an attentive role for stability. In Experiment 5, we used the same geometric arrangement of elements but minimized any cues to leaning or falling. Here the asymmetry went away.

Some preattentive features, like color and motion, are extremely robust. Essentially any experiment in which such a feature has the chance to guide attention will show evidence for that guidance. Other attributes, such as numerosity (Treisman & Gormican, 1988) or looming (Franconeri, Hollingworth, & Simons, 2005; Skarratt, Cole, & Gellatly, 2009) appear to guide attention in search but the effects are more fragile and the results of the experiments can be ambiguous. Moreover, it is possible to question the whole idea of preattentive features (For example, see Kristjansson, 2015; Kristjánsson, 2016; Wolfe, 2016). Still, if we are working within a framework that endorses the notion of preattentive feature, then stability seems to fall into the category features for which there is evidence but not unequivocal evidence. The evidence, presented here, certainly argues for a role for stability in the guidance of attention. It could be argued that no one experiment is definitive, but it is hard to find a more convincing hypothesis to account for the set of results.

One could think of preattentive instability processing as a form of motion processing; something like representational momentum (Freyd & Finke, 1984; Hubbard, 2014). The percept of instability may show an ability to infer the motion (falling motion) that would be seen in the next frame. A titled object will move. A more tilted object would probably be moving more rapidly. Our results do not produce the simple and powerful search asymmetry that would be produced by the presence or absence of real motion (Dick, et al., 1987; Royden et al., 2001) but instability may be considered to be near relation of that basic guiding feature. We conclude that instability should be provisionally accepted as an attribute that can guide visual attention.

Table 2:

ANOVA Results for the RTs and search slopes inExperiment 1.

		RTs			Slopes
Factor	df	F	p	ηp2	F	p	ηp2
Target Presence (P)	1,10	76.83	.000	.88	18.72	.002	.65
COM	1,10	1.09	.322	.10	0.23	.639	.02
Stability (S)	1,10	76.18	.000	.88	27.76	.000	.74
P × COM	1,10	0.31	.592	.03	2.20	.173	.18
P × S	1,10	27.33	.000	.73	3.04	.112	.23
S[Target Present]	1,20	38.96	.000	.66	n/a
S[Target Absent]	1,20	100.58	.000	.83	n/a
COM × S	1,10	0.04	.849	.00	8.48	.016	.46
S [Low COM]	1,20	n/a			35.68	.000	.64
S [High COM]	1,20	n/a			14.54	.001	.42
P × S × COM	1,10	0.55	.477	.05	0.36	.560	.03

Note: n/a refers to the “not applicable” when the given interaction was not significant.