Population Pharmacokinetics of Cycloserine and Pharmacokinetic/Pharmacodynamic Target Attainment in Multidrug-Resistant Tuberculosis Patients Dosed with Terizidone

Cycloserine is a WHO group B drug for the treatment of multidrug-resistant tuberculosis (TB). Pharmacokinetic/pharmacodynamic data for cycloserine when dosed as terizidone are sparse. The aim of this analysis was to describe the population pharmacokinetics of cycloserine when administered as terizidone and predict the doses of terizidone attaining cycloserine exposures associated with efficacy. The plasma cycloserine level was measured 2 to 6 weeks after treatment initiation in patients hospitalized for second-line tuberculosis treatment.

ABSTRACT

Cycloserine is a WHO group B drug for the treatment of multidrug-resistant tuberculosis (TB). Pharmacokinetic/pharmacodynamic data for cycloserine when dosed as terizidone are sparse. The aim of this analysis was to describe the population pharmacokinetics of cycloserine when administered as terizidone and predict the doses of terizidone attaining cycloserine exposures associated with efficacy. The plasma cycloserine level was measured 2 to 6 weeks after treatment initiation in patients hospitalized for second-line tuberculosis treatment. The pretreatment MICs of cycloserine were determined for the clinical isolates. We enrolled 132 participants with rifampicin-resistant TB; 79 were HIV positive. The median pretreatment MIC was 16 mg/liter. A one-compartment disposition model with two clearance pathways, nonrenal (0.35 liters/h) and renal (0.43 liters/h), described cycloserine pharmacokinetics well. Nonrenal clearance and the volume of distribution were allometrically scaled using fat-free mass. Smoking increased nonrenal clearance by 41%. Simulations showed that with daily doses of terizidone (750 mg and 1,000 mg for patients weighing ≤45 kg and >45 kg, respectively), the probability of maintaining the plasma cycloserine concentration above the MIC for more than 30% of the dosing interval (30% T_>MIC) (which is associated with a 1.0-log₁₀-CFU/ml kill in vitro) exceeded 90% at MIC values of ≤16 mg/liter, but the proportion of patients achieving 100% T_>MIC (which is associated with the prevention of resistance) was more than 90% only at MICs of ≤8 mg/liter. Based on a target derived in vitro, the WHO-recommended doses of terizidone are effective for cycloserine MICs of ≤8 mg/liter, and higher doses are required to prevent the development of resistance.

INTRODUCTION

Terizidone, a structural analogue of cycloserine, is a key group B antituberculosis drug recommended by WHO for the treatment of multidrug-resistant tuberculosis (MDR-TB) at a daily dose of 15 to 20 mg/kg of body weight up to a maximum of 1,000 mg of terizidone (1). Cycloserine commonly causes neuropsychiatric toxicity (2–4), which is concentration related (5).

Terizidone is formed when two molecules of cycloserine are linked by one molecule of terephthalaldehyde (6). Terizidone hydrolyzes in vivo to form cycloserine and terephthalaldehyde. Little is known about the mechanism of biotransformation, but terizidone is thought to hydrolyze in the gastrointestinal tract (7). Cycloserine is partially metabolized, and approximately 60 to 70% is reported to be excreted via the kidneys (8). Cycloserine interferes with peptidoglycan formation and bacterial cell wall synthesis by inhibiting two enzymes, alanine racemase and d-alanine ligase (9, 10). It is generally bacteriostatic against Mycobacterium tuberculosis but can be bactericidal with sufficient exposures (11). The critical concentration, clinical breakpoint, and epidemiological cutoff (ECOFF) for cycloserine have not been defined, due to the insufficiency of existing data (12). Tentative ECOFFs of 32 and 64 mg/liter have been proposed and applied in some studies (11, 13). Importantly, terizidone and cycloserine do not share cross-resistance with companion antituberculosis drugs (14, 15).

Data regarding the pharmacodynamic (PD) indices associated with cycloserine efficacy in humans are lacking. However, in hollow-fiber systems, cycloserine’s efficacy is largely driven by the percentage of the time during the dosing interval that the concentration is above the MIC (T_>MIC). A target value for T_>MIC of ≥30% has been proposed, as it is associated with a 1.0-log₁₀-CFU/ml kill, while a T_>MIC of ≥64% is linked to 80% of maximal kill (11). The complete suppression of acquired drug resistance is achieved with a T_>MIC of 100% (11).

We describe the population pharmacokinetics (PK) of cycloserine dosed as terizidone and the distribution of MICs in patients on second-line tuberculosis treatment. The final population pharmacokinetic model was used to simulate drug exposures in virtual patients and to evaluate the probability of target attainment (PTA) for a range of terizidone doses at each MIC level.

RESULTS

Baseline characteristics.

Table 1 shows the characteristics at recruitment of the 132 participants included in the study. Sixty percent of the participants were HIV positive at the time of recruitment. Twenty participants had two pharmacokinetic sampling visits, receiving whole tablets on the first visit and crushed terizidone on the second visit (16). Eight participants were included in the extended sampling schedule and provided samples at 12, 24, and 26 h postdose.

TABLE 1.

Patient characteristics at recruitment

Characteristica	Value
No. of patients	132
No. (%) of female patients	54 (40.9)
Median (range):
Wt (kg)	47.0 (32.0–84.0)
FFM (kg)	40.7 (23.5–58.9)
BMI (kg · m2)	17.0 (11.2–32.4)
Ht (m)	1.66 (1.43–1.85)
Age (yr)	35.7 (18.8–68.9)
No. (%) of patients with the following HIV infection status:
Positive	79 (59.8)
Negative	51 (38.6)
Unknown	2 (1.60)
No. (%) of patients with the following smoking status:
Current smoker	59 (44.7)
Previous smoker	47 (35.6)
Never smoked	26 (19.7)
Median (range):
ALT concn (U/liter)	11.5 (5.0–83.0)
Serum creatinine concn (μmol/liter)	59 (29–214)
Creatinine clearance (ml/min)	97.3 (19.4–196)
No. (%) of patients who received crushed terizidone	20 (15.2)

^aBMI, body mass index; ALT, alanine aminotransferase.

Pharmacokinetic model.

The enrolled participants contributed to 155 pharmacokinetic profiles with a total of 927 plasma concentrations, of which 5 (0.54%) predose concentration measurements were below the lower limit of quantification (LLOQ). A one-compartment disposition model with first-order absorption (with a delay described by a chain of transit compartments) and elimination best described the pharmacokinetics of cycloserine. The model could separate two clearance pathways, nonrenal and renal, with the latter being modulated by creatinine clearance and accounting, on average, for 55% of the total elimination. Table 2 shows the parameter estimates of the final model and the associated 95% empirical bootstrap confidence intervals. Allometric scaling was included on the nonrenal pathway and the volume of distribution using fat-free mass (FFM) and resulted in a 52-point drop in the objective function value (OFV). The typical values for nonrenal and renal clearance are reported for an individual with an FFM of 40.7 kg and a creatinine clearance of 100 ml/min. The model estimated that cycloserine reached the systemic circulation faster when it was crushed than when it was not crushed (a 9-point drop in the OFV, 1 degree of freedom [df]). The estimated mean transit time on the pharmacokinetic visits where crushed terizidone was administered was small, and we fixed the value to 0.001 h to allow for a larger transfer rate constant between consecutive transit compartments. The effect of tablet crushing on bioavailability was evaluated (as a fixed effect) but was not supported. The model detected a 41% increase in nonrenal clearance among current smokers (a 15-point drop in the OFV, 1 df, P < 0.001). Between-subject variability (BSV) was supported on clearance, and between-occasion variability (BOV) was included on the absorption rate constant, the mean transit time, and relative bioavailability. Clearance was also allowed to vary between the two pharmacokinetic visits. Figure 1 shows a visual predictive check stratified by current smoking status, showing that the model provides a suitable fit to the data. Figure 2a shows the distribution of the model-derived estimate of the 24-h area under the concentration-time curve (AUC_0–24), with the median being 587 mg · h/liter (range, 175 to 1,451 mg · h/liter, excluding one individual with an AUC_0–24 of 1,975 mg · h/liter). The median AUC_0–24 was 419 mg · h/liter (range, 175 to 1,451 mg · h/liter) in participants who received 500 mg of terizidone daily (n = 23, 17%) and 615 mg · h/liter (range, 215 to 1,421 mg · h/liter) in those who received 750 mg daily (n = 107, 82%). Two participants with reduced creatinine clearance received the 250-mg dose of terizidone on the pharmacokinetic sampling day.

TABLE 2.

Population parameter estimates of cycloserine pharmacokinetics

Parameter	Estimate (95% CIa )
Nonrenal clearance (liter/h)b	0.346 (0.203, 0.516)
Renal clearance (liter/h)c	0.43 (0.298, 0.558)
Volume of distribution (liter)b	23.2 (21.8, 24.6)
Absorption rate constant (h−1)	0.832 (0.677, 1.07)
Mean transit time (h)	0.785 (0.434, 1.1)
Mean transit time for crushed tablet (h)	0.001, fixed
No. of transit compartments	4, fixed
Bioavailability (%)	100, fixed
Change in nonrenal clearance due to smoking (%)	+41.1 (6.21, 94.5)
Between-subject variability (%) for clearanced	32.7 (0.327, 39.3)
Between-visit variability (%) for clearanced,e	18.0 (5.45, 31.9)
Between-occasion variability (%) for:
Absorption rate constant	50.7 (33.9, 63.9)
Bioavailability	14.9 (9.55, 18.5)
Mean transit time	67.9 (35.8, 101)
Residual unexplained variability
Proportional error (%)	8.93 (7.67, 9.96)
Additive error (mg/liter)	1.58 (1.18, 1.95)

^aCI, confidence interval, obtained from a nonparametric bootstrap (n = 500).

^bEstimates reported for an individual with a fat-free mass of 40.7 kg.

^cEstimate reported for an individual with a creatinine clearance of 100 ml/min.

^dEstimated jointly for nonrenal and renal pathways.

^eClearance was allowed to vary by visit and not by dose.

FIG 1.

Visual predictive check for final cycloserine model stratified by smoking status. Open circles represent the observed concentrations. The middle continuous line is the 50th percentile of the observed data, and the upper and lower dashed lines are the 97.5th and 2.5th percentiles of the observed data, respectively. The shaded regions represent the 95% confidence interval of the 2.5th, 50th, and 97.5th percentiles.

FIG 2.

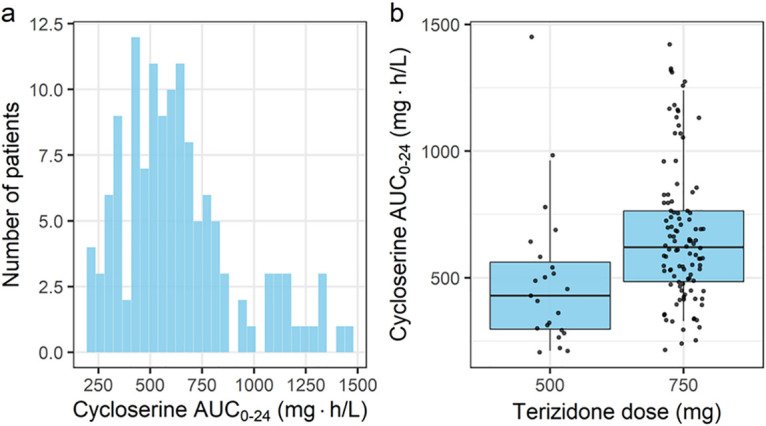
Overall distribution of post hoc estimates of the cycloserine AUC_0–24 (a) and the distribution of the cycloserine AUC_0–24 stratified by terizidone dose (b). The whiskers in panel b represent the 10th and 90th percentiles, and the dots are the observed AUC_0–24.

Distribution of MICs.

Figure 3 shows the distribution of the MICs of cycloserine before treatment initiation for isolates from the 103 participants for whom pretreatment MICs were available. The median MIC was 16 mg/liter. Using the sensitivity threshold of 16 mg/liter, 17% of the M. tuberculosis isolates were resistant to cycloserine.

FIG 3.

Distribution of individual MICs of cycloserine before the start of tuberculosis treatment.

Monte Carlo simulations.

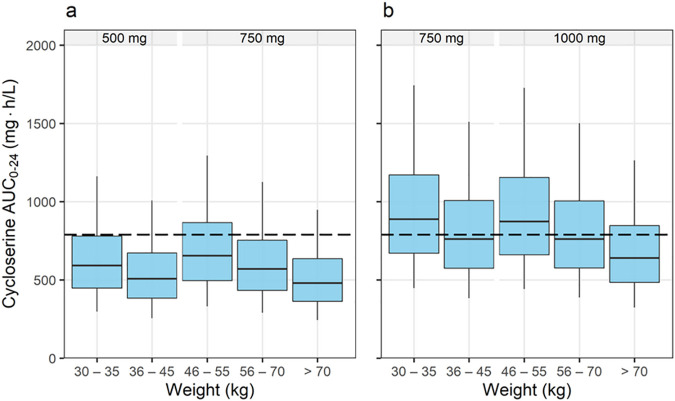
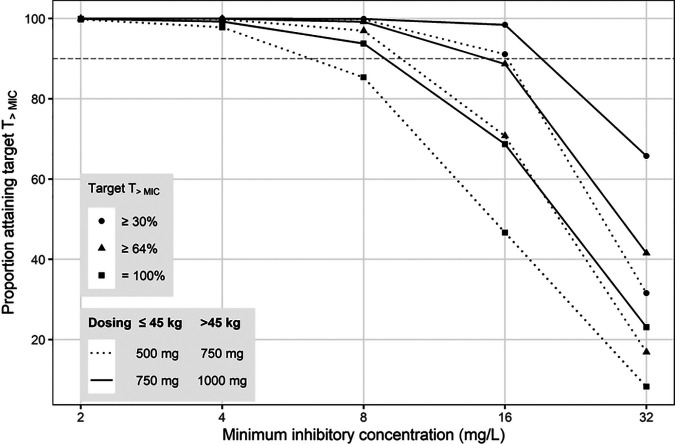
Figure 4a and b show the simulated AUC_0–24 for cycloserine achieved when virtual patients received doses of terizidone within the WHO-recommended dose range from 500 mg to 1,000 mg (1). Our results show that the median AUC_0–24 for terizidone doses of 750 mg (for those weighing ≤45 kg) and 1,000 mg (for those weighing >45 kg) were closer to the AUC_0–24 of 789.5 mg · h/liter reported for a 750-mg daily dose of cycloserine (17). The probabilities of attaining T_>MIC values of ≥30%, ≥64%, and 100% are presented in Fig. 5. The proportion of virtual patients attaining a T_>MIC of ≥30% was at least 90% for MIC values of ≤16 mg/liter. However, the proportion of patients achieving T_>MIC values of ≥64% and 100% was more than 90% only with MICs of ≤8 mg/liter. Doses of 500 mg (for those weighing ≤45 kg) and 750 mg (for those weighing >45 kg) were effective at suppressing the emergence of resistance only in isolates for which MIC values were ≤4 mg/liter. The cumulative fractions of response (CFR) for the dosing strategy shown in Fig. 4a (dotted lines in Fig. 5) were computed to be 93% and 79% for targets of T_>MIC values of ≥30% and ≥64%, respectively. For the dosing strategy shown in Fig. 4b (solid lines in Fig. 5), the computed CFR were 99% (T_>MIC ≥ 30%) and 91% (T_>MIC ≥ 64%). Simulated concentration-time profiles for individuals with a selected weight within each weight band are presented in Fig. S1 in the supplemental material. Patients with poor renal function achieved a maximum concentration in plasma (C_max) between 30 and 40% higher than the C_max for those with a normal creatinine clearance.

FIG 4.

Simulated cycloserine AUC_0–24. (a) Exposures achieved using the WHO-recommended doses of terizidone; (b) exposures achieved when 250 mg is added to the recommended dose. The dashed line represents the cycloserine AUC_0–24 corresponding to a cycloserine dose of 750 mg, recommended by Alghamdi et al. (17) and associated with a PTA of >90% at a MIC of ≤16 mg/liter, using a target of a T_>MIC of 30%.

FIG 5.

Probability of attainment of the T_>MIC values for simulated dosing schedules. Circles represent the probability of a T_>MIC of ≥30% at each MIC level, and the triangles represents the probability of a T_>MIC of ≥64%. The dashed horizontal line represents the 90% probability of reaching the target.

DISCUSSION

We developed a population pharmacokinetic model for cycloserine dosed as terizidone in hospitalized patients treated for rifampicin-resistant TB. Our model detected the effects of renal function, body size, smoking, and tablet crushing on the pharmacokinetic parameters. Monte Carlo simulations were performed to evaluate cycloserine exposure across the weight bands defined in the current WHO dosing guidelines. We also calculated the probability of attaining T_>MIC values of at least 30%, 64%, and 100% when using the WHO recommended doses of terizidone.

The clearance and volume of distribution parameters were scaled allometrically using fat-free mass, consistent with other studies on the pharmacokinetics of antituberculosis drugs (18–21). The relationship between clearance and body size is nonlinear, and failure to adjust for the nonlinearity when giving the same milligram-per-kilogram dose across patients with a range of weights results in lower systemic drug exposures in patients with a low weight and relatively high exposures in patients weighing more. The doses defined in the current WHO guidelines were based on the principle of allometric scaling, and as expected, the simulated cycloserine AUC_0–24 was balanced across the weight bands (1). When using terizidone doses of 500 mg (weight ≤ 45 kg) and 750 mg (weight > 45 kg), the simulated steady-state median AUC_0–24 was lower in all the weight bands than the AUC_0–24 (789.5 mg · h/liter) reported for a 750-mg dose of cycloserine (17). We show that terizidone doses of 750 mg (weight ≤ 45 kg) and 1,000 mg (weight > 45 kg) achieve exposures comparable to those reported for cycloserine doses of 750 mg for patients with a median weight of 58 kg (interquartile range, 51 to 67 kg).

In our cohort, nonrenal clearance was 41% higher among current smokers than among nonsmokers. Polycyclic aromatic hydrocarbons associated with cigarette smoking are potent inducers of cytochrome P450 isoenzymes 1A1, 1A2, and, possibly, 2E1 (22–24). Little is known about the metabolism of cycloserine; our findings suggest that these enzymes may have a role in metabolizing cycloserine. However, the effect of smoking on overall clearance was modest (15%), since the renal pathway contributes a larger proportion of total clearance than other pathways. The proportion of renal clearance estimated from our model (55%) is close to the 60 to 70% previously reported (8).

Our analysis assumes that all administered terizidone is broken down and absorbed as cycloserine, since terizidone was not detected by our assay method. While part of the dose of terizidone could potentially be absorbed before hydrolysis, our model-estimated disposition parameters are in keeping with those from a previous report on cycloserine population pharmacokinetics (17), thus corroborating the validity of our assumption. Our concentration range was also in agreement with the concentrations in the study of Alghamdi et al. (17), and the observed C_max in our cohort was within the expected range of 20 to 35 mg/liter (25). The 500-mg dose of cycloserine is comparable to a 750-mg dose of terizidone (taken by most patients in our study), assuming that all the terizidone is converted to cycloserine.

A longer delay in absorption and a lower rate of absorption were observed in our study compared with the values observed in the study by Alghamdi et al. (17), in which the study participants were dosed with cycloserine tablets. The delayed absorption of terizidone may provide an advantage over the use of cycloserine, which is usually dosed twice daily (4, 26). In our study, maximum concentrations were reached after about 5 h, which is consistent with a previous report on terizidone and cycloserine pharmacokinetics (27). Finally, confirming the findings of our previous study employing noncompartmental analysis (16), we found that capsule crushing was associated with a minimal delay (i.e., a reduced mean transit time), which is reassuring, since tablet crushing is commonly done, especially for children (28).

T_>MIC is the efficacy driver for cycloserine defined in a hollow-fiber system model for tuberculosis infection. Proposed target T_>MIC values of ≥30% and ≥64% were associated with, respectively, bactericidal activity and 80% of maximal kill in a PK/PD analysis evaluating target attainment of selected doses in the hollow-fiber system model (11). In both hollow-fiber system models and patients (11, 17), an assumption was that at each MIC, all patients receive the same dose of cycloserine. In the present study, we assessed PTA for weight-adjusted daily dosing schedules. Our results show that the WHO-recommended doses of 500 mg and 750 mg for patients weighing ≤45 kg and >45 kg, respectively, are not sufficient for M. tuberculosis strains, considering the tentative ECOFF of 32 mg/liter. Drug susceptibility testing for cycloserine is not often performed, and using our pretreatment MIC distribution, the dosing schedule mentioned above is likely to be less effective in about 17% of the patients. There is an urgent need for data defining the relationship between cycloserine exposure and toxicity. One patient experienced seizures classified as grade 3 or higher; no patients experienced symptoms of psychosis or depression of grade 3 or higher. Lower grades of toxicity were reported for seizures (2%) and symptoms of psychosis (7%) and depression (14%).

The limitations of the study include the fact that the nonrandomization of participants into the extended sampling schedule could have biased the clearance estimates. However, the bias may be small, considering that only 6% of the participants were on this sampling schedule. We assumed that cycloserine is not protein bound, and if evidence showing protein binding emerges, the probability of target attainment presented in this report overestimates the true probability. Furthermore, there is a need for clinical studies to validate the targets derived in hollow-fiber models and assess the risks and benefits of higher doses of terizidone evaluated in our study.

In conclusion, we developed a population pharmacokinetic model for cycloserine in participants dosed with terizidone and determined the effect of participant characteristics on pharmacokinetic parameters. We also determined the PTA for a range of doses and propose that doses of 750 mg for patients weighing ≤45 kg and 1,000 mg for patients weighing >45 kg are needed to achieve predefined exposure targets for bactericidal effect and maximal bacterial kill.

MATERIALS AND METHODS

Patient recruitment.

We recruited patients with rifampicin-resistant TB (rifampicin-monoresistant TB and MDR-TB) aged ≥18 years at the Brooklyn Chest and DP Marais TB hospitals in Cape Town, South Africa. Patients initiated on a standard second-line TB regimen within the past 28 days were eligible for recruitment. We excluded critically ill patients from the study. Most patients were hospitalized for a minimum of 3 months, and they all received daily therapy as inpatients under supervision. The standard second-line TB treatment at the time of the study consisted of terizidone, moxifloxacin, kanamycin, pyrazinamide, and ethionamide and/or isoniazid, depending on the katG and inhA mutations identified in the pretreatment sputum culture, indicating high- and low-level resistance to isoniazid, respectively (29). Ethambutol was included in patients who were unlikely to be resistant to ethambutol and in those who did not have exposure to ethambutol within the month prior to second-line TB treatment initiation. Patients received weight-adjusted once-daily doses of terizidone: those with a weight of <33 kg received 15 to 20 mg/kg, while those weighing 33 to 50 kg and >50 kg received 500 mg and 750 mg, respectively. Participants were routinely dosed with whole-capsule formulations of terizidone. If dosing by a crushed formulation was indicated, terizidone capsules were carefully opened and mixed together with the other crushed antituberculosis drugs in approximately 200 ml of water (16).

Pharmacokinetic sampling.

Participants underwent pharmacokinetic blood sampling at between 2 weeks and 6 weeks post-treatment initiation. On the PK sampling day, blood was drawn immediately before and at 2, 4, 6, 8, and 10 h after the dose. Extra blood samples were collected from a subset of the patients at 12, 24, and 26 h. Some patients had two pharmacokinetic sampling days, spaced approximately 2 weeks apart.

Drug quantification.

Within 30 min of blood sampling, plasma was extracted immediately after centrifugation and stored at −80°C until analysis. Cycloserine plasma concentrations were quantified in the Division of Clinical Pharmacology of the University of Cape Town, Cape Town, South Africa, using a liquid chromatography-tandem mass spectrometry assay, as previously described (30).

MICs.

Sputum samples were collected before the start of treatment for MIC determination. Following decontamination of sputum specimens, M. tuberculosis bacilli were cultured in MGIT medium and growth was monitored in a Bactec 960 instrument. The MICs were determined using a commercially available Sensititre MycoTB plate (Trek Diagnostics, Cleveland, OH, USA), following the manufacturer’s instructions. The MIC test range was from 2 to 32 mg/liter. Sensitivity to cycloserine was defined as an MIC of ≤16 mg/liter; isolates with an MIC of >16 mg/liter were considered to be resistant (31). The distribution of MICs was used to calculate the cumulative fraction of response (CFR) for selected dosing schedules (32).

Data analysis.

Concentration-time data were interpreted using nonlinear mixed-effects modeling in NONMEM (version 7.4.3) software (33) and the algorithm first-order conditional estimation with eta-epsilon interaction (FOCE-I). Perl-Speaks NONMEM (PsN) software (version 4.8.8) was used for automation of the methods implemented in the model development and evaluation phases (34), Pirana (version 2.9.8) was used to document the model development process (35), and R (version 3.5.3) and RStudio (version 1.1.463) were used for data management and generating the graphical output (36, 37).

In our model, the dose of terizidone was converted to the equivalent dose of cycloserine by assuming two molecules of cycloserine for each molecule of terizidone (6) and adjusting for the molecular weight (302.28 g/mol and 102.09 g/mol for terizidone and cycloserine, respectively). For example, a 750-mg dose of terizidone was converted to a 506-mg dose of cycloserine. We considered one- and two-compartment models to describe the disposition of cycloserine and evaluated the presence of a delay in drug absorption by including a lag time or transit compartment absorption model.

BSV and BOV were assumed to follow a lognormal distribution, with the data from each dose treated as a separate occasion. To improve model stability, BSV was included on disposition parameters, while BOV was evaluated on absorption parameters. A subset of participants had two pharmacokinetic profiles on separate visits, and this was accounted for in the model by assessing the inclusion of between-visit variability (BVV) on the disposition parameters. An occasion was defined as one dosing interval (all concentration measurements after a dose were assigned to the same occasion), while a visit was defined as a set of consecutive occasions or dosing intervals with pharmacokinetic data. Allometric scaling was included in the initial phases of model development to describe the effect of body size on disposition parameters testing total body weight or FFM as the body size descriptor (38). As recommended, the allometric exponents were fixed to 0.75 and 1 for the clearance and volume of distribution parameters, respectively. All samples with concentrations below the limit of quantitation (BLQ) were handled by the M6 method (39); i.e., concentrations reported as BLQ were replaced with half the LLOQ, except for consecutive BLQ values in a series, for which the trailing BLQ values were ignored. Residual unexplained variability was described using an error model with an additive and proportional component. The effect of physiologically plausible covariates, including tablet crushing and renal function (estimated using the Cockcroft and Gault formula [40]), on the pharmacokinetic parameters was evaluated using graphical techniques and the stepwise covariate modeling approach (41), implemented in PsN software.

Model building was guided by changes in OFV for nested models, which were approximately chi-square distributed; inspection of diagnostic plots; and physiological plausibility. The precision of the parameter estimates of the final model was evaluated using a nonparametric bootstrap method with replacement (n = 500).

Monte Carlo simulations.

The final pharmacokinetic model was used to perform Monte Carlo simulations to evaluate the probability of attaining T_>MIC values of ≥30% and ≥64% under the new WHO-recommended dosing guidelines for drug-resistant tuberculosis (1). Demographic data for the TB patients (n = 1,225) obtained from pharmacokinetic studies conducted in West Africa and South Africa were used to generate a population of virtual patients for the Monte Carlo simulations. First, we took the weight measurement for each of the 1,225 patients and simulated 10 new weight values by assuming a normal distribution centered around each observed weight and a standard deviation of 1 kg. This was done to ensure a uniform distribution of weight in the range of the observed weight measurements of TB patients. Second, we developed a regression model to predict height from the weight and height data for the 1,225 patients, which was done separately for males and females for the purpose of computing FFM. Third, we calculated the height of the virtual patients using the regression model and the simulated weight values. Creatinine clearance was derived from the simulated weight measurement by applying a regression model developed using the creatinine clearance and weight values observed in our study cohort. To determine the T_>MIC for each virtual patient, we created a data set with possible observation time points (separated by 5 min) at steady state using the finedata utility program in NONMEM software. For each dose level (500, 750, and 1,000 mg) of terizidone, a total of 1,000 data sets were simulated and the T_>MIC for cycloserine within a 24-h dosing interval was computed for each patient. The proportion of virtual patients achieving the target T_>MIC values of ≥30%, ≥64%, and 100% was computed separately (11). PTA was calculated by taking into account the effect of body size by applying weight-adjusted dosing. We considered the weight bands currently recommended for the dosing of second-line antituberculosis drugs (30 to 35 kg, 36 to 45 kg, 46 to 55 kg, 56 to 70 kg, and >70 kg) (1). To ensure an equal number of patients in each weight band, we randomly sampled (without replacement) 300 virtual patients per weight band in each simulated data set.

Ethics.

Ethics approval for the study was granted by the Human Research Ethics Committee of the University of Cape Town, Cape Town, South Africa (approval number 106/2016). All patients provided written informed consent before participant recruitment.