Abstract
How effective are restrictions on mobility in limiting COVID-19 spread? Using zip code data across five U.S. cities, we estimate that total cases per capita decrease by 19% for every ten percentage point fall in mobility. Addressing endogeneity concerns, we instrument for travel by residential teleworkable and essential shares and find a 25% decline in cases per capita. Using panel data for NYC with week and zip code fixed effects, we estimate a decline of 30%. We find substantial spatial and temporal heterogeneity; east coast cities have stronger effects, with the largest for NYC in the pandemic’s early stages.
Keywords: COVID-19, Mobility, Contagion, Telework, Essential workers, Public transportation
1. Introduction
A central challenge in evaluating lock-downs and other restrictions on mobility in response to COVID-19 is estimating their effectiveness in limiting the disease’s spread. This estimation is challenging for several reasons. Mobility restrictions are introduced as a response to disease outbreaks, individuals make mobility decisions based on the threat of infection, and the relationship between transmission and mobility depends on the composition of susceptible, infected and recovered agents.
To address these challenges, we combine weekly data on COVID-19 cases by zip code in New York City (NYC) and cross-sectional data for four other U.S. cities, information on mobility from SafeGraph cellular phone data and subway turnstile data for NYC, and exogenous variation in mobility from the ability to work remotely and designation as an essential worker in state shutdown orders. We interpret “mobility” broadly, in the sense of workers leaving home, or passing through a subway turnstile, which exposes them to contact while travelling and at their destination.1 In our preferred instrumental variables specification, we estimate that a ten percentage point decrease in mobility leads to a 30% fall in COVID-19 cases per capita. We find substantial heterogeneity across both space and over time, with stronger effects for NYC, Boston and Philadelphia than for Atlanta and Chicago, and the largest estimated coefficients for NYC in the early stages of the pandemic.
The hypothesis that movement spreads COVID-19 inspired the stay-at-home orders adopted across the world in 2020. While any contagious disease can be propagated through human interaction, the actual link between mobility and contagion is mediated by the nature of the disease and traveler behavior. The social benefits of regulations limiting mobility depend on the empirical magnitude of the link between mobility and disease. The link between mobility and contagion could be minimal if infections occurred mostly through intimate contact, as with sexually transmitted infections, or large if transit hubs enabled super-spreading events.
We focus on the relationship between the logarithm of the COVID-19 cases per capita, and the decline in mobility, relative to February 2020 or the same date one year earlier.2 We cannot determine if the disease spread through travel itself or through interactions at a final destination. We lack individual-specific COVID-19 tests, and consequently measure the number of cases by zip code.
One potential concern is that neighborhood specific COVID-19 rate may not capture the true prevalence of the disease, because of differences in testing rates. To address this, we control for demographic variables that might predict testing rates, and for zip code fixed effects in our panel specifications. Although levels of testing in the United States were low throughout our time period, another concern is that testing could mechanically increase mobility, as people travel to get tested. We address this concern using our instrumental variables for mobility. As an additional specification check, we also replicate our cross-sectional case results with COVID-19 death rates in NYC. Unfortunately, the NYC zip code death data begins the week of May 18–24, 2020, and so cannot be used in our panel specifications.
Our primary mobility data source is the SafeGraph cellphone location data, which is available at the census blockgroup level nationwide. We aggregate travel data to the zip code to conform with our COVID-19 case data. For NYC, we supplement this data with public transit turnstile data provided by the Metropolitan Transit Authority (MTA). For panel analysis, we aggregate the daily case and turnstile data to the week level so that it is compatible with the weekly Safegraph data. As the impact of mobility on infection could change both with the level of infection in the population of travelers and the level of precaution, we test whether that impact changes over time in NYC. We split our sample into an early period that ends on April 26, and a later period, to test whether the impact of mobility on contagion was higher when cases were increasing or after the wave of infection peaked.
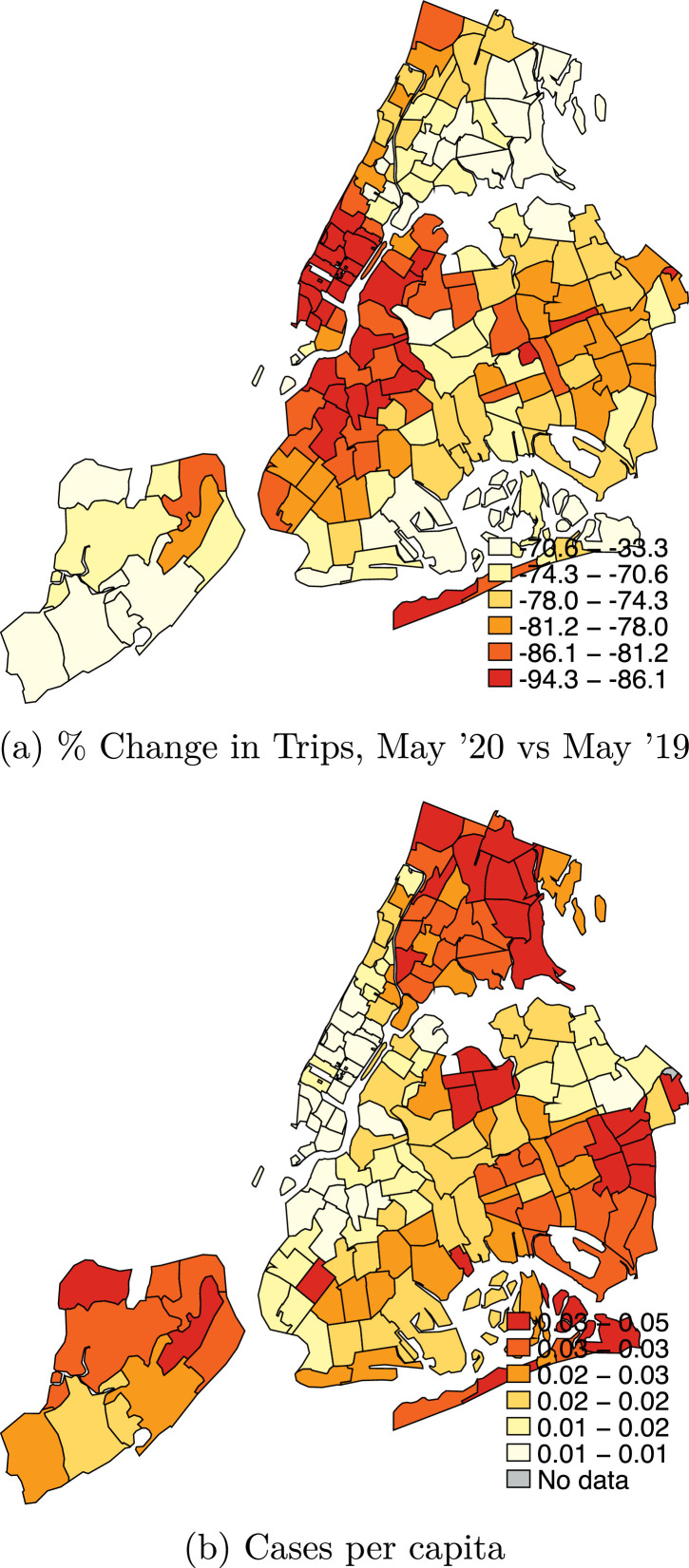
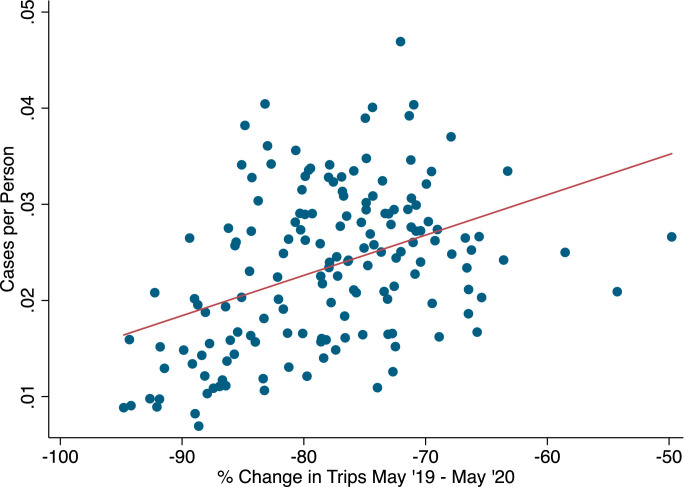
Fig. 1 shows two maps of NYC that illustrate our core findings. The upper map shows the change in cell phone-measured mobility. The lower map shows the total COVID-19 cases per capita as of June 1, 2020. In the parts of NYC where mobility fell, case rates have been low. In the areas of New York where mobility remained higher, COVID-19 cases per capita are higher. Appendix Fig. A1 shows the correlation of 0.41 between change in the number of trips and the number of COVID-19 cases per capita.
Fig. 1.
Mobility Change and COVID-19 Cases per capita in NYC. Source: Cases per capita from NYC Health Department, available at https://www1.nyc.gov/site/doh/covid/covid-19-data.page. % Change in trips from SafeGraph Weekly Patterns Data, using visitors traveling from home. % Change in trips calculated between May 13–19, 2019 and May 4–10, 2020.
Fig. A1.
Correlation between Travel Change and COVID-19 Cases per Capita in NYC. Source: Cases per capita from NYC Health Department, available at https://www1.nyc.gov/site/doh/covid/covid-19-data.page. % Change in trips from SafeGraph Weekly Patterns Data, using visitors traveling from home. % Change in trips calculated between May 13–19, 2019 and May 4–10, 2020.
Exploring the cross-sectional relationship across five major U.S. cities, we estimate a quasi-elasticity of cases with respect to mobility of approximately two, with a 10 percentage point decline in travel leading to a 10(0.019 100) = 19% decline in total cases per capita. We estimate a similar elasticity of deaths with respect to mobility.3 Yet there are many reasons to be skeptical about this estimate. First, zip codes differ along many dimensions, such as income and race, which may influence the spread and measurement of COVID-19. Second, mobility may decline with the level of infection, which could bias downwards the estimated link between cases and mobility. Third, the connection between mobility and disease can differ across cities, both due to different initial infection rates and because travel may take different forms. Finally, improvements in testing might lead to higher case counts, and mobility could respond to testing improvements.
We take two strategies to address omitted neighborhood characteristics. First, we control for racial composition, income and age, which reduce the measured connection between mobility and disease prevalence, so that a 10 percentage point decline in trips is associated with a 7% decline in case rates across the five cities. In NYC, the coefficient is somewhat larger, such that a 10 percentage point decline in trips implies a 10% decline in cases per capita.
Second, we look at results over time within NYC zip codes controlling for neighborhood fixed effects. We follow the medical literature (Lauer et al. 2020) and estimate a model with a two-week gap between new cases and mobility. The average onset time is closer to 1 week, but this two-week gap should capture over 97.5% of cases. Controlling for week and zip code fixed effects, the link between COVID-19 prevalence and mobility disappears when using our SafeGraph mobility measure, and falls by 79% relative to the cross-sectional results when using the turnstile measure.
If movement falls more in places with more disease, then these fixed effect estimates underestimate the true link between contagion and mobility. Consequently, our preferred specifications follow an instrumental variables strategy that uses employment by industry in a given zip code to predict changes in mobility. We consider two instruments. First, following Bartik et al. (2020)), we focus on the share of residents working in essential industries, according to state shutdown essential worker designations. As this first instrument could be be sensitive to workers in especially risky occupations, such as health care and police officers, we exclude workers in the NAICS sector 62 (“Health Care and Social Assistance”) and in NAICS sector 92 (“Public Administation”) in constructing this instrument. Second, we use the share of residents employed in industries where they can work remotely, according to Dingel and Neiman (2020), also excluding NAICS sectors 62 and 92. Bartik et al. (2020) confirm that Dingel and Neiman (2020)’s predictions about remote work during the pandemic have largely born out across industries. Locations with more essential workers have more travel, whereas locations with more teleworkable residents have less travel. In our NYC panel specifications, we allow the instruments to have different impacts week-by-week.
Across almost every specification, the measured link between mobility and disease is larger in these instrumental variable specifications, suggesting reverse causality biased the ordinary least squares estimates downwards. In our multi-city IV specification with demographic controls, we estimate that a 10 percentage point drop in travel implies a 0.25 log point (25%) drop in per capita COVID-19 prevalence. This represents 4.25 fewer cases per 1000 inhabitants, from a sample mean of 17 per 1000.
City-specific estimates produce higher coefficients in New York, Boston and Philadelphia and lower coefficients in Atlanta and Chicago. Mobility seems to spread COVID-19 in the northeastern cities, but not the others. This difference likely reflects the initial infection rate rather than the nature of mobility, since public transportation is also used in Chicago.
Zip codes across cities may still have significant unobserved heterogeneity driving disease spread, motivating our preferred panel research design, which can compare zip codes with large changes in exogenous mobility against those with small changes over the evolution of the pandemic. Moving from the cross-sectional analysis to our NYC-Safegraph data panel, we estimate an instrumental variables coefficient of 0.03 with zip code fixed effects. This translates to our headline finding that a 10 percentage point decline in mobility implies a 30% decline in new cases per capita two weeks later (10(0.03 log points)). Using turnstile data, we estimate a larger coefficient of 0.049 with zip code fixed effects. While the turnstile results support the view that cases rise with mobility, at least over this period in NYC, it does not provide a clean estimate of the impact of public transportation use on the spread of COVID-19 hypothesized by Harris (2020), because our instruments are not public transit specific.
Our paper is related to the broader emerging body of research on COVID-19 in economics. First, a macroeconomics literature has used Susceptible-Infected-Recovered (SIR) models to simulate the impact of policies such as lock-downs on disease burden and economic outcomes, including Acemoglu et al. (2020), Alvarez et al. (2020), Atkeson (2020) and Fernández-Villaverde and Jones (2020). Second, others have analyzed the spatial diffusion of COVID-19, including Antràs et al. (2020), Argente et al. (2020), Birge et al. (2020), Fajgelbaum et al. (2020), Bisin and Moro (2020) and Cuñat and Zymek (2020). A third line of work has examined how agents’ behavioral responses (e.g. social distancing) likely effect the dynamics of COVID-19, including Fenichel et al. (2011), Alfaro et al. (2020), Farboodi et al. (2020), and Toxveard (2020). Fourth, a more microeconometric literature has examined locations’ observable characteristics within cities and across U.S. counties that correlate with COVID-19 incidence, including Almagro and Orane-Hutchinson (2020), Couture et al. (2020) and Desmet and Wacziarg (2020). Finally, other research has compared the spatial diffusion and economic impact of COVID-19 to previous pandemics such as the 1918 influenza, as in Barro et al. (2020) and Correia et al. (2020).
Section 2 discusses our data sources and Section 3 introduces our empirical strategies. Section 4 discusses the results found using the cross-section of zip codes in five cities. Section 5 discusses our panel results. Both Sections 4 and 5 include results using instrumental variables. Section 6 concludes.
2. Data
We build a weekly panel of zip codes for NYC, and take a cross-sectional snapshot of four other US cities: Atlanta, GA, Boston, MA, Chicago, IL and Philadelphia, PA. All of these cities provide new case counts by zip code. Counts of daily new cases and cumulative cases come from each city’s (or county’s) department of public health. We have daily case data for NYC from April 4, 2020 through June 7, 2020. Because this misses much of the run-up in cases, we set cumulative and new cases to 0 in 2020w11, and assume cases double weekly until 2020w14, for which we have data. We use snapshots of cumulative cases for the remaining cities. Atlanta has data as of June 2, 2020; Boston as of May 24, 2020; Chicago and Philadelphia as of June 6, 2020.
SafeGraph released publicly available data for cell phone trips between December 31st, 2018 – present. We pull weekly data for our five cities. The data tracks the number of visitors to a point of interest (POI) in a given week. Every POI observation contains information on its census blockgroup, as well as the number of visitors by their home blockgroup. We construct an origin-destination (OD) matrix from these observed trips, assuming travel from home, by counting how many visitors travel from each origin blockgroup to each POI blockgroup. The data only shows OD pairs with at least 4 visitors, so it undercounts pairs with low travel volume. Finally, we aggregate the blockgroup level OD matrices to zip codes in line with our COVID-19 case data. When using SafeGraph data, our measure of mobility, is the percent change in the number of trips away from one’s home zip code.
Our second mobility datasource comes from the Metropolitan Transit Authority’s turnstile data. Turnstile entries are recorded every few hours, for each unique turnstile. We map each subway turnstile to a zip code, and count the entries each week by zip code. When using MTA data, our measure of mobility, is the percent change in the number of subway entries in zip code .
Our instruments use Dingel and Neiman (2020)’s teleworkability shares by 2-digit NAICS and definitions of essential industries (4-digit NAICS) from Delaware and Minnesota, in combination with zip code level employment data from the American Community Survey (ACS). Details for instrument construction follow in Section 3.1.
To analyse how mobility interacts with demographics, we collect demographic data at the zip level on share African American, median age, and median income from the American Community Survey. To identify zip code level shares of teleworkable and essential workers, we use zip code level employment by industry from the ACS, which identifies the industries in which residents work, the details of which are listed in Table A2.
Finally, for NYC, we have data on where police officers lived as of 2016, via a Freedom of Information Law request by Bell (2020). We use this data to control for the police employment in our panel analysis.
Appendix Table A1 lists the summary statistics for each of our research designs. The first panel lists statistics for zip codes in all 5 cities in our cross-sectional analysis; the middle panel lists statistics for the zip codes in our NYC SafeGraph panel; the bottom panel lists statistics for the zip codes in our NYC turnstile panel. Notably, all three panels show large drops in mobility, between 63% and 71% for the average zip code.
3. Research design
In order to estimate the relationship between mobility the spread of COVID-19, we implement the following:
| (1) |
| (2) |
Eq. (1) regresses log total cases per capita in zip code on the in mobility, measured by SafeGraph trips leaving residential zip code . Eq. (2) regresses log daily new cases in zip code in week on in mobility, measured by SafeGraph trips leaving residential zip code or by the number of turnstile turns in residential zip code two weeks prior. Eq. (1) includes city fixed effects, and Eq. (2) includes zip and week fixed effects to capture persistent differences across zip codes and city-level variation in response to COVID-19. In all cross-sectional analysis, we control for the log of healthcare employment, adding the log of police employment in panel analysis, as we only have police data for NYC. Healthcare workers and police officers were disproportionately exposed to COVID-19 during this time period, and were more likely to continue going to work. These controls ensure that our estimate of the impact of mobility is less likely to reflect the impact of working in a hospital, or responding to an emergency. Even with these controls, our estimates should always be interpreted as the combined impact of exposure during travel and exposure at destination.
While can be interpreted as the change in total cases, since there were no COVID-19 cases before our sample, the same cannot be said for mobility. Because we are limited to a cross-sectional panel, the only way to capture time-varying mobility is to take the difference pre- and post-COVID-19. We use a specification in which we regress the log of our cases variable on the left-hand side on the percentage point reduction in trips on the right-hand side, which implies that the coefficient has an interpretation as a quasi-elasticity: is the % decrease in total (new) cases per capita for each percentage point drop in trips.
Because residents are likely to reduce trips in response to increases in cases of COVID-19, in both equations is likely biased downwards. Additionally, trips and cases may be measured with error, further attenuating . To address these concerns, we build instruments using pre-period information on one’s proclivity to travel during the pandemic.
3.1. Building the instrument
We construct two instruments to address these concerns of bias and measurement error. Both instruments use the American Community Survey’s zip code level data on residents’ employment by industry. We know the share of private-sector employment in the industry classifications listed in Appendix Table A2.
For our first instrument, we use data on essential industries from Minnesota and Delaware. These states designated a subset of the 4-digit NAICS codes as essential, allowing these industries to remain open. Within each 2-digit NAICS grouping in Appendix Table A2, we calculate the national share of employment designated as essential. Using the ACS zip level data, we know employment by 2-digit NAICS grouping. Using the national essential share in combination with the zip code employment composition, we construct for a zip code as the employment-weighted average essential share. For example, consider a zip code with 100 residents working in two industries: 40 in NAICS 42, and 60 in NAICS 31–33. If 50% of the national employment in NAICS 42 is designated as essential, and 30% of NAICS 31–33 is designated essential, we construct .
Because this first instrument could be be sensitive to workers in especially risky occupations such as health care and police officers, we exclude workers in the NAICS sectors 62 (“Healthcare and Social Assistance”) and 92 (“Public Administration”) in constructing this instrument.
For our second instrument, we use Dingel and Neiman (2020)’s definition of teleworkable industries. They provide a list of 2-digit NAICS industry codes, along with the share of that industry that can reliably telecommute. Since the ACS data combines many of Dingel & Neiman’s NAICS codes, we take simple averages across the sub-categories that we combine. As with we take the employment-weighted average telecommuting share across industries within a zip to construct . The second instrument also excludes NAICS sectors 62 and 92.
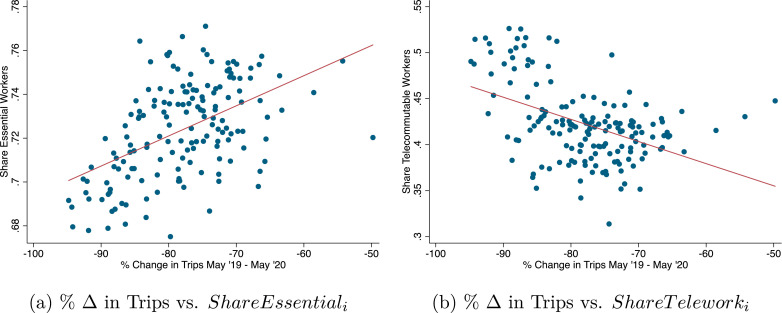
The relevance criterion requires that the share of teleworking or essential workers is correlated with the change in travel within a given zip code. Appendix Fig. A2 shows that trips dropped more in zip codes with lower shares of essential workers or in those with higher shares of workers who could reliably telecommute. The exclusion restriction requires that the share of essential workers or telecommuters in 2018 does not impact COVID-19 cases except through taking trips from home.
Fig. A2.
A visual first stage Travel Change and Instruments in NYC.Source: % Change in trips from SafeGraph Weekly Patterns Data, using visitors traveling from home. % Change in trips calculated between May 13–19, 2019 and May 4–10, 2020. Share Essential workers calculated from DE and MN 4-digit NAICS essential industries. Share Telework created at the zip level using data from Dingel and Neiman (2020) weighted by local neighborhood employment composition.
3.2. Multicity IV
For the cross-sectional, multiple city specification, we track the log of cumulative COVID-19 cases per capita by zip code as of the dates in Section 2 and regress it on the in travel, in percentage points, between May 2019 and May 2020. We instrument for mobility with both instruments, in the first stage shown in Eq. (1.1). This provides variation in using the pre-COVID-19 employment mix, allowing us to estimate the second stage, Eq. (1.2), without concern of behavioral responses such as staying home. We also include city fixed effects and control for the log of employment in healthcare.
| (1.1) |
| (1.2) |
3.3. Panel design
To use the panel data in NYC, we begin by considering Eq. (2). can be interpreted as the % increase in new cases per capita in one’s home zip code associated with an additional 1 percentage point increase in trips originating in the same zip code two weeks prior.4 Once we instrument for trips, the design changes to Eqs. (2.1) and (2.2):
| (2.1) |
| (2.2) |
The first stage regresses trip change (relative to travel in 2020w9) two weeks ago on the instrument, which we interact with a week dummy to introduce temporal variation. We include zip code fixed effects to control for time-invariant characteristics. Week fixed effects control for city-level changes in virus awareness, shut-down, orders, etc. that would impact all locations. Finally, we control for the log of residents working in healthcare or as police officers.
4. Cross-sectional results
Table 1 shows our results using a cross-section of zip codes in Atlanta, Boston, Chicago, New York, and Philadelphia. Our core specification regresses the logarithm of cases per capita identified as of our city-specific snapshot dates in Section 2, on the percent change in trips between the week of May 13–19, 2019 and May 4–10, 2020. Table 2 shows the city-specifc results.
Table 1.
Multiple city demographics.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| OLS | OLS | OLS | OLS | OLS | IV | IV | |
| 0.019 | 0.015 | 0.019 | 0.008 | 0.007 | 0.051 | 0.025 | |
| (0.002) | (0.002) | (0.002) | (0.002) | (0.002) | (0.005) | (0.009) | |
| 0.573 | 0.142 | 0.134 | |||||
| (0.073) | (0.081) | (0.086) | |||||
| 0.780 | 0.289 | 0.131 | |||||
| (0.215) | (0.232) | (0.302) | |||||
| 0.623 | 0.627 | 0.378 | |||||
| (0.053) | (0.072) | (0.137) | |||||
| R-Sq. | 0.531 | 0.571 | 0.549 | 0.648 | 0.652 | ||
| Root MSE | 0.626 | 0.469 | |||||
| Obs. | 448 | 448 | 448 | 448 | 448 | 448 | 448 |
| F-Stat. | 83.82 | 81.12 | |||||
| Fixed Effects | |||||||
| CBSA | X | X | X | X | X | X | X |
Notes: The dependent variable is total cases per capita in zip code . All columns control for log of healthcare employment. Columns (1)–(5) implement versions of Eq. (1), each column adding additional demographics. Columns (6)–(7) implement versions of Eq. (1.2), . Eq. (1.1) available upon request. Specifications (6) and (7) include both the teleworking and essential share instruments. Robust standard errors included in parentheses. Significance:
Table 2.
Multiple city results.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| ln(NYC | ln() NYC | ln() Atlanta | ln() Boston | ln() Chicago | ln() Philadelphia | |
| Panel A: OLS | ||||||
| 0.019 | 0.023 | 0.003 | 0.051 | 0.019 | 0.012 | |
| (0.006) | (0.004) | (0.019) | (0.011) | (0.003) | (0.003) | |
| r-sq. | 0.125 | 0.224 | 0.018 | 0.521 | 0.171 | 0.251 |
| obs. | 159 | 159 | 22 | 19 | 206 | 42 |
| Panel B: OLS With Demographics | ||||||
| 0.004 | 0.010 | 0.001 | 0.034 | 0.005 | 0.008 | |
| (0.005) | (0.003) | (0.013) | (0.016) | (0.003) | (0.005) | |
| R-Sq. | 0.484 | 0.437 | 0.567 | 0.569 | 0.514 | 0.465 |
| Obs. | 159 | 159 | 22 | 19 | 206 | 42 |
| Panel C: IV With Demographics | ||||||
| 0.029 | 0.068 | 0.010 | 0.066 | 0.010 | 0.016 | |
| (0.015) | (0.020) | (0.029) | (0.034) | (0.012) | (0.009) | |
| Root MSE | 0.420 | 0.487 | 0.537 | 0.422 | 0.482 | 0.222 |
| Obs. | 159 | 159 | 22 | 19 | 206 | 42 |
| F-Stat. | 32.170 | 22.199 | 4.040 | 5.648 | 38.891 | 5.091 |
| Controls for Panels B & C | ||||||
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
Notes: The dependent variable is total cases, or total deaths, per capita in zip code . All columns control for log of healthcare employment. Panels A and B show versions of OLS Eqs. (1) for separate cities’ cases, as well as NYC’s deaths. Panel C shows results from Eq. (1.2), adding additional demographic controls, : . Panel C uses both the telework and essential share instuments. Robust standard errors in parentheses. Significance:
Table 1 column (1) shows the ordinary least squares coefficient is 0.019, implying that for every ten percentage points that travel fell between May of 2019 and 2020, the number of cases per capita fell by 0.19 log points (19%). This specification includes metropolitan area fixed effects and controls for the number of residents employed in the health care sector. The average zip code reported 17 cases per 1000 people, so a 10 percentage point reduction in travel would lower this to 13.8 per 1,000.
In regressions (2)–(4) we include our three primary controls separately, and in the fifth regression, we include all three together. These controls will be used in other specifications throughout this paper, but we only directly report the coefficients here. In the specifications including the controls separately, each control is significant. Column (2) shows that a 1 percentage point increase in percent African-American is associated with a 0.57 log point increase in the COVID-19 case rate; this gap between African-American and white case rates is a widely known fact (Yancy 2020).
The coefficient on age in column (3) is strongly negative. This is in line with older people taking protective steps to avoid contagion such as staying home, because they face higher mortality risk. Column (4) documents the stark relationship between income and COVID-19 cases; we estimate an elasticity of the case rate with respect to income of 0.62. This coefficient is stable when we include all three variables together, but the other variables either flip sign or lose significance and magnitude. In this cross-sectional specification income, rather than race or age, is the larger determinant of COVID-19 case rates.
One natural explanation for why income reduces COVID-19 rates is that richer people are better able to adjust their lives to avoid contagion. Reduced mobility is one margin of that adjustment, and richer areas have dramatically less mobility as of May 2020 in these cities. A 0.1 log point increase in the median income of the zip code is associated with a 1.2 percent drop in trips relative to May of last year. Yet despite controlling for the fall in trips, income remains an important explanatory variable, suggesting our trips variable captures only one dimension of protective behavior.
The coefficient on mobility remains stable when controlling for race or age, but the estimate halves when we include income, either on its own or as one of three control variables. In column (5), a 10 percentage point reduction in mobility is associated with a 0.07 log point reduction in cases per capita.
Because this coefficient may be biased downwards as mobility falls more where COVID-19 cases spike, we now use our two instruments for mobility, as in Eqs. (1.1) and (1.2). The coefficient on mobility becomes much larger, both with and without controls, in regressions (6) and (7). The coefficient on income shrinks accordingly, as workers in teleworkable industries have on average higher incomes.5
The coefficient in regression (7) implies that as mobility drops by 10 percentage points, cases per capita drop by 0.25 log points (25%). The average zip code saw 17 cases per 1000 people, so a 10 percentage point drop in mobility would drop the case rate to 12.8 per 1000. This yields 1 fewer case per 1000 than implied by the OLS analysis, for the same drop in travel. We take this as evidence supporting the view that cases have been much lower in places where workers could switch to remote working, but we are cautious about interpreting the coefficient as a causal estimate on trips alone. Workers in essential industries or industries that cannot be done remotely face risks from many places, especially infections in the workplaces. We therefore interpret this as suggestive evidence that remaining at home reduces COVID-19 exposure, but not that we can identify COVID-19 infection rates from an act of mobility.
In Table 2, we report results for all five cities in our sample. We also include the results for NYC death rates in the first column. Panel A shows the ordinary least squares coefficient with no controls. Panel B shows the ordinary least squares coefficient with demographcis controls. Panel C shows the instrumental variables coefficient with controls.
In Panel A column (1), we show the 0.019 coefficient when the logarithm of death rates are regressed on mobility across NYC zip codes. This coefficient becomes insignificant and negative in the first column of Panel B, which adds controls. Death rates are strongly associated with age at the zip code level and with the share of the population that is African-American. In Panel C, we find that after instrumenting for mobility, the coefficient rises to 0.029, a 53% increase from Panel A. While the ordinary least squares coefficient on mobility does not survive controls, the instrumental variables coefficient is robust, reflecting the fact that deaths were much higher in those parts of New York where residents could not switch to remote work, or where essential workers live.
In the second column, we show our results for COVID-19 cases in NYC. The estimate in Panel A is 0.023, which is close to the deaths coefficient in the first column and the coefficient for all cities together in Table 1. When we control for demographics in Panel B, the coefficient falls considerably but remains significant. In contrast, the instrumental variables coefficient in panel C is three times the size of the OLS coefficient from panel A. This may be due to downward bias in the ordinary least squares coefficients as mobility shrank in response to local outbreaks of COVID-19, the reason we seek an instrument, or because the instrument is correlated with the error term.
Column (5) shows results for Chicago, the other city in our sample with more than 50 zip codes. The Chicago coefficient is comparable to the coefficient in NYC when we have no other controls. With controls, the coefficient for Chicago becomes small and statistically insignificant. The instrumental variables strategy does not change that fact for Chicago. These results suggest that mobility was less harmful in Chicago than it was in New York.
The other three cities have small samples of zip codes and we are wary of inferring much from their results. Philadelphia shows a coefficient of 0.012 with uncontrolled ordinary least squares and 0.016 with the instrumental variables results with controls. The ordinary least squares results with controls produce a considerably smaller coefficient. The Boston mobility coefficients are large and significant in all three specification. The Atlanta results are small and insignificant in all three specifications, possibly suggesting that mobility was not strongly associated with the spread of COVID-19 in Atlanta during this time period.
We believe that the results for the east coast cities tell a consistent story. In Boston, New York and Philadelphia, the coefficients in Panels A and C are statistically significant and sizable in magnitude. Mobility appears to have been reliably correlated with the spread of the pandemic in those cities. In Atlanta and Chicago, the correlation between COVID-19 and mobility is weak or non-existent. This pattern of results is consistent with the idea that the impact of mobility is related to the initial infection rate, which is likely to have been higher on the east coast.6 It could also be that the east coast is more connected or shared transport is more prevalent there.
5. NYC panel results
We now turn to our panel results looking within NYC over time. We match the number of new COVID cases with mobility using the Safegraph data in Table 3 . In Table 4 , we repeat those specifications using the MTA turnstile data. In both tables, the Panel A shows results for the entire sample. Panel B shows results splitting the sample in two halves: the first half of the sample as new cases were growing, and the second half of the sample, when new cases were falling.
Table 3.
NYC panel results: safegraph trips.
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| ln() OLS | ln() IV | ln() IV | ln() IV | ln() IV | |
| Panel A: Full Sample | |||||
| 0.002 | 0.061 | 0.044 | 0.046 | 0.030 | |
| (0.002) | (0.004) | (0.007) | (0.006) | (0.007) | |
| Root MSE | 0.382 | 0.625 | 0.554 | 0.525 | 0.413 |
| Observations | 2045 | 2045 | 2045 | 2045 | 2045 |
| First Stage F-Stat. | 156.820 | 100.222 | 66.096 | 17.374 | |
| Panel B: Split Sample (2020w11 – 2020w17 vs. 2020w18 – 2020w23) | |||||
| 0.000 | 0.066 | 0.047 | 0.050 | 0.034 | |
| (0.002) | (0.006) | (0.007) | (0.007) | (0.007) | |
| 0.004 | 0.059 | 0.042 | 0.043 | 0.026 | |
| (0.002) | (0.005) | (0.007) | (0.007) | (0.008) | |
| Root MSE | 0.381 | 0.636 | 0.555 | 0.527 | 0.415 |
| Observations | 2045 | 2045 | 2045 | 2045 | 2045 |
| First Stage F-Stat. | 149.913 | 85.900 | 55.961 | 10.712 | |
| Controls | |||||
| X | X | ||||
| X | X | ||||
| X | X | ||||
| Fixed Effects | |||||
| X | X | ||||
| X | |||||
| X | X | X | X | X | |
Notes: NYC panel results using SafeGraph trips from home. Dependent variable is log of new cases per capita in zip code in week . All columns control for log of healthcare employment and the log of police employment. Panels A shows results for the full panel, reporting from Eq. (1) in the first column, with versions of Eq. (2.2) in columns (2)–(6): . Panel B splits the time period in half, and interacts the coefficient of interest with the two time periods, decomposing into . Columns (2)–(5) use both the telework and essential share instuments. Robust standard errors in parentheses. Significance:
Table 4.
NYC panel results: MTA turnstile trips.
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| ln() OLS | ln() IV | ln() IV | ln() IV | ln() IV | |
| Panel A: Full Sample | |||||
| 0.004 | 0.061 | 0.060 | 0.053 | 0.049 | |
| (0.002) | (0.006) | (0.009) | (0.009) | (0.012) | |
| Root MSE | 0.412 | 0.811 | 0.795 | 0.713 | 0.527 |
| Observations | 1399 | 1399 | 1399 | 1399 | 1399 |
| First Stage F-Stat. | 67.193 | 42.098 | 20.108 | 15.208 | |
| Panel B: Split Sample (2020w11 – 2020w17 vs. 2020w18 – 2020w23) | |||||
| 0.005 | 0.052 | 0.065 | 0.057 | 0.055 | |
| (0.002) | (0.006) | (0.010) | (0.010) | (0.014) | |
| 0.004 | 0.101 | 0.120 | 0.108 | 0.094 | |
| (0.002) | (0.019) | (0.025) | (0.024) | (0.022) | |
| Root MSE | 0.412 | 1.011 | 1.165 | 1.038 | 0.703 |
| Observations | 1399 | 1399 | 1399 | 1399 | 1399 |
| First Stage F-Stat. | 1452.498 | 42.318 | 22.966 | 10.243 | 9.535 |
| Controls | |||||
| X | X | ||||
| X | X | ||||
| X | X | ||||
| Fixed Effects | |||||
| X | X | ||||
| X | |||||
| X | X | X | X | X | |
Notes: NYC panel results using MTA turnstile trips in a given residential zip code. Dependent variable is log of new cases per capita in zip code in week . All columns control for log of healthcare employment and the log of police employment. Panels A shows results for the full panel, reporting from Eq. (1) in the first column, with versions of Eq. (2.2) in columns (2)-(6): . Panel B splits the time period in half, and interacts the coefficient of interest with the two time periods, decomposing into . Columns (2)–(5) use both the telework and essential share instuments.Robust standard errors in parentheses. Significance:
Table 3 column (1) shows our ordinary least squares coefficient, with zip code and week fixed effects. Panel A shows that over the entire time period, there is no correlation between mobility and COVID-19 cases within zip code. This reflects the fact that the zip codes with the large drops in mobility did not necessarily experience fewer cases. Panel B shows that there is next to no relationship during the first period. This coefficient drops during the second period, showing a significant negative coefficient on mobility. As we find it difficult to imagine how reduced mobility could have increased the spread of COVID-19, we interpret this to mean that mobility shut down in places where COVID-19 cases were errupting.
Those fears of reverse causality inspire the remaining regressions. Table 3 column (2) shows results with our two instruments and no other controls. The effect is striking. If this coefficient were correct, then a 10 percentage point drop in trips implies a 0.61 log point decrease in COVID-19 cases per capita. Panel B shows that the effect is stronger in the first half of the sample than in the second half of the sample. This specification is comparable to the cross-sectional results above with no other controls. In both cases, the correlation between our instruments and the demographic variables seems to be biasing the coefficient upwards.
Column (3) includes our three demographic controls. As expected, the coefficient drops and is in line with our previous results, and is significant at the 1% level. A ten percentage point fall in trips is associated with a 0.44 log point decline in cases per capita. The estimated coefficient is again higher in the first half of the sample.
Column (4) includes fixed effects for the five boroughs of NYC. The coefficient are slightly larger than in column (3) which does not include these borough controls. Controlling for borough causes the (unreported) point estimate for income to fall, because boroughs are strongly correlated with income and appear to have an independent impact on cases. As the estimate for income falls, the estimate for mobility rises.
The fifth column shows our preffered results including zip code fixed effects. These effects absorb all of the unobserved variation across the city, and causes the coefficient to drop by a third, with a 10 percentage point decline in travel implying a 0.3 log point (30%) decline in new cases per capita two weeks later.
Breaking the sample into halves, the coefficients are significant and positive across both the rise in daily new cases, as well as when daily new cases declined; however, they are uniformly higher as new cases rose. One interpretation of these results is that the mobility drove COVID-19 contagion through the end of April. After residents spent significant time traveling only for absolute necessity, mobility’s impact on contagion declined.
In Table 4, we turn to our results using NYC turnstile data. It is tempting to view this as providing an independent measure of the impact of public transportation trips, as opposed to all types of mobility. That view is tenable with the ordinary least squares results, if those results are not biased by reverse causality. It is not tenable with our instrumental variable results, because we use the same instruments used for Safegraph mobility. We believe that using the same instruments for different variables is reasonable, as both variables are imperfect attempts to measure mobility.
Column (1) shows our ordinary least squares results with zip code fixed effects. The coefficient is positive and statistically significant, but modest in magnitude over the entire sample, 1st and 2nd halves. A ten percentage point fall in public transit trips is associated with 0.04 log points fewer (4%) COVID-19 cases per capita.
Columns (2)–(4) show instrumental variables results without zip code fixed effects that closely parallel those found in columns (2)–(4) of Table 3. Across the entire time period, the coefficient with no controls in column (2) is about 0.06, and the coefficients in (3) and (4) are similar. In contrast to the SafeGraph analysis, the results are stronger in the second half of our time period than in the first half of our time period. Additionally, they are uniformly stronger than those using the Safegraph data. It could be that the turnstiles data captures a riskier form of mobility, perhaps due to trip duration or shared mode, or that the zip codes with subway stations have more exposure to COVID-19 as more people pass through them.
In column (5) we show results with zip code fixed effects. The coefficient for the overall period is 0.049 and significant at the 1% level. This implies a quite large impact of reducing trips. A 10 percentage point reduction in trips is associated with a 0.49 log point fall in new COVID-19 cases per capita two weeks later.
6. Conclusion
Research is at an early stage on the progress of COVID-19 across America. Yet we already have plausible sources of variation in the behavior of different parts of the population. Some industries comfortably worked from home. Others could not and have braved exposure to COVID-19 to earn a living. In this paper, we used variation in that industrial mix to estimate the impact that mobility had on COVID-19 case rates.
Our estimates were not uniform. The measured effects of mobility were larger in New York, Boston and Philadelphia. They were smaller in Atlanta and Chicago. Moving around New York appears to have been riskier in March and early April than in May. Nonetheless, our estimates paint a consistent picture that mobility led to more COVID-19 exposure. Moreover, almost all estimates imply an elasticity greater than two, so that a 10 percentage point drop in trips lead to a 0.2 log point or more reduction in COVID-19 cases per capita.
We do not claim these large effects would hold in different settings or when people wear masks and gloves while traveling. We hope these results may help future cost-benefit analyses around lockdown policies, but no policy implications follow directly from them. They simply remind us that people whose jobs required them to leave their homes were more likely to get COVID-19, and – at least in NYC – they were more likely to die.
CRediT authorship contribution statement
Edward L. Glaeser: Conceptualization, Methodology, Formal analysis. Caitlin Gorback: Conceptualization, Methodology, Formal analysis. Stephen J. Redding: Conceptualization, Methodology, Formal analysis.
Acknowledgments
We thank Sam Patterson and Andrei Freund for excellent research assistance. Any errors, opinions and omissions are our own. The U.S. Department of Transportation funded this project through an inter-agency agreement with the National Science Foundation (grant 1559013) to the NBER Project on Transportation in the 21st Century. The views expressed herein are those of the authors and do not necessarily reflect the views of the National Bureau of Economic Research.
Footnotes
For the SafeGraph data, “mobility” is the number of trips outside of one’s residential zip code. For the MTA data, “mobility” is the number of turnstile entries in each zip code.
The relationship is governed by a quasi-elasticity, which is in log points. A 1 percentage point increase in implies a (100)% increase in cases per capita.
All analysis of COVID-19 deaths is limited to NYC.
We use the approximation of ln(x+1) when cases or new cases equals 0. Results are robust to using inverse hyperbolic sine.
See for example the American Time Use Survey, as discussed in https://siepr.stanford.edu/research/publications/how-working-home-works-out.
In the conventional SIR model, the rate of new infections depends on the product of the fractions of infected and susceptibles (Kermack and McKendrick 1927).
Appendix A. Appendix Tables and Figures
Table A1.
Summary statistics.
| Variable | Mean | St.Dev. |
|---|---|---|
| Panel A: All 5 Cities | ||
| 758 | 710 | |
| 2682 | 3110 | |
| 803 | 1119 | |
| % | -70 | 13 |
| 0.49 | 0.05 | |
| 0.49 | 0.05 | |
| 41,387 | 22,083 | |
| 37 | 5 | |
| 87,026 | 43,312 | |
| 24 | 28 | |
| Observations | 448 | |
| Panel B: NYC SafeGraph Panel | ||
| 69 | 108 | |
| 63 | 26 | |
| 0.42 | 0.04 | |
| 0.72 | 0.02 | |
| 51,887 | 24,919 | |
| 38 | 5 | |
| 82,318 | 46,052 | |
| 24 | 25 | |
| Observations | 2045 | |
| Panel C: NYC Turnstile Panel | ||
| 74 | 113 | |
| 71 | 26 | |
| 0.51 | 0.05 | |
| 0.50 | 0.05 | |
| 54,828 | 25,561 | |
| 36 | 4 | |
| 87,855 | 57,939 | |
| 21 | 22 | |
| Observations | 1399 | |
Notes: Case data from specific cities’ or counties’ health departments as in Section 2. Trips pre- and during COVID-19 from SafeGraph. Share telecommute and share essential as in Sections 2 and 3.1. Population, age, income and share African American from 2018 ACS data. Panel A uses cross-sectional data for all zips in the 5 cities. Panel B uses all zip codes in NYC from 2020w11 - 2020w23. Panel C uses all zip codes with subway turnstiles in NYC from 2020w11 - 2020w23.
Table A2.
Industries and codes available in zip level ACS employment data.
| ACS Indsutry Description | Associated NAICS Codes |
|---|---|
| Agriculture, forestry, fishing and hunting, and mining | 11, 21 |
| Transportation and warehousing, and utilities | 22, 48–49 |
| Construction | 23 |
| Manufacturing | 31–33 |
| Wholesale trade | 42 |
| Retail trade | 44–45 |
| Information | 51 |
| Finance and insurance, | 52, 53 |
| and real estate and rental and leasing | |
| Professional, scientific, and management | 54, 55, 56 |
| and administrative and waste management services | |
| Educational services, and health care and social assistance | 61, 62 |
| Arts, entertainment, and recreation, | 71, 72 |
| and accommodation and food services | |
| Other services (except public administration) | 81 |
| Public Administration | 92 |
Notes: This tables shows the mapping between industry titles available in the zip code level data from the ACS on residents’ employment by industry, and their asocciated NAICS codes. NAICS codes 62 and 92 not used in constructing zip code level instruments.
Table A3.
NYC cases by borough.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| ln() NYC | ln() The Bronx | ln() Brooklyn | ln() Manhattan | ln() Queens | ln() Staten Island | |
| Panel A: OLS | ||||||
| 0.010 | 0.001 | 0.015 | 0.007 | 0.004 | 0.008 | |
| (0.003) | (0.005) | (0.008) | (0.010) | (0.006) | (0.004) | |
| R-Sq. | 0.437 | 0.645 | 0.544 | 0.624 | 0.262 | 0.892 |
| Obs. | 159 | 20 | 34 | 32 | 48 | 10 |
| Panel B: Reduced form IV | ||||||
| 7.542 | 0.711 | 2.125 | 3.075 | 7.132 | 4.462 | |
| (0.883) | (1.968) | (2.212) | (2.054) | (2.640) | (5.153) | |
| 7.660 | 1.024 | 9.305 | 3.478 | 5.345 | 3.188 | |
| (0.859) | (2.813) | (1.806) | (2.021) | (2.945) | (5.446) | |
| R-Sq. | 0.629 | 0.704 | 0.770 | 0.673 | 0.370 | 0.826 |
| Obs. | 159 | 20 | 34 | 32 | 48 | 10 |
| Panel C: IV | ||||||
| 0.068 | 0.007 | 0.058 | 0.135 | 0.081 | 0.006 | |
| (0.020) | (0.008) | (0.025) | (0.156) | (0.062) | (0.011) | |
| Root MSE | 0.487 | 0.079 | 0.288 | 0.577 | 0.551 | 0.088 |
| Obs. | 159 | 20 | 34 | 32 | 48 | 10 |
| F-Stat. | 22.199 | 10.058 | 4.028 | 2.613 | 1.607 | 1.754 |
| Controls | ||||||
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
Notes: This table is analogous to Table 2 in the main text, but compares cases across boroughs in NYC instead of different cities. All columns control for log of healthcare employment. Panels A shows results from Eq. (1). Panel B shows the reduced form IV regression results from . Panel C shows results from Eq. (1.2), adding additional demographic controls, : . Robust standard errors in parentheses. Significance:
Table A4.
NYC deaths by borough.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| ln() NYC | ln() The Bronx | ln() Brooklyn | ln() Manhattan | ln() Queens | ln() Staten Island | |
| Panel A: OLS | ||||||
| 0.004 | 0.012 | 0.002 | 0.001 | 0.001 | 0.023 | |
| (0.005) | (0.016) | (0.010) | (0.015) | (0.010) | (0.013) | |
| R-Sq. | 0.484 | 0.416 | 0.700 | 0.648 | 0.271 | 0.845 |
| Obs. | 159 | 20 | 34 | 32 | 48 | 10 |
| Panel B: Reduced form IV | ||||||
| 2.741 | 1.700 | 0.222 | 2.130 | 4.240 | 11.645 | |
| (1.299) | (6.164) | (1.438) | (2.816) | (4.061) | (21.270) | |
| 3.254 | 6.217 | 6.798 | 5.509 | 4.303 | 18.423 | |
| (1.249) | (7.827) | (2.122) | (2.741) | (4.838) | (16.230) | |
| R-Sq. | 0.504 | 0.456 | 0.795 | 0.706 | 0.291 | 0.850 |
| Obs. | 159 | 20 | 34 | 32 | 48 | 10 |
| Panel C: IV | ||||||
| 0.029 | 0.030 | 0.039 | 0.230 | 0.045 | 0.030 | |
| (0.015) | (0.030) | (0.023) | (0.242) | (0.047) | (0.044) | |
| Root MSE | 0.420 | 0.254 | 0.303 | 0.933 | 0.453 | 0.334 |
| Obs. | 159 | 20 | 34 | 32 | 48 | 10 |
| F-Stat. | 32.170 | 2.332 | 6.696 | 2.941 | 2.377 | 1.310 |
| Controls | ||||||
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
Notes: This table is analogous to Table 2 in the main text, but compares deaths across boroughs in NYC instead of different cities. All columns control for log of healthcare employment. Panels A shows results from Eq. (1). Panel B shows the reduced form IV regression results from . Panel C shows results from Eq. (1.2), adding additional demographic controls, : . Robust standard errors in parentheses. Significance:
References
- Acemoglu D., Chernozhukov V., Werning I., Whinston M.D. Working Paper 27102. National Bureau of Economic Research; 2020. Optimal targeted lockdowns in a multi-group SIR model. [Google Scholar]
- Alfaro L., Faia E., Lamersdorf N., Saidi F. Working Paper 27134. National Bureau of Economic Research; 2020. Social interactions in pandemics: fear, altruism, and reciprocity. [Google Scholar]
- Almagro M., Orane-Hutchinson A. Working Paper. New York University; 2020. The determinants of the differential exposure to COVID-19 in New York City and their evolution over time. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez F., Argente D., Lippi F. Working Paper 26981. National Bureau of Economic Research; 2020. A simple planning problem for COVID-19 lockdown. [Google Scholar]
- Antràs P., Redding S., Rossi-Hansberg E. Working Paper 27840. National Bureau of Economic Research; 2020. Globalization and pandemics. [Google Scholar]
- Argente D.O., Hsieh C.-T., Lee M. Working Paper 27220. National Bureau of Economic Research; 2020. The cost of privacy: welfare effect of the disclosure of COVID-19 cases. [DOI] [Google Scholar]
- Atkeson A. Working Paper 26867. National Bureau of Economic Research; 2020. What will be the economic impact of COVID-19 in the US? Rough estimates of disease scenarios. [Google Scholar]
- Barro R.J., Ursúa J.F., Weng J. Working Paper. 2020. The coronavirus and the great influenza pandemic: lessons from the “Spanish flu” for the coronavirus’s potential effects on mortality and economics activity. [Google Scholar]
- Bartik A.W., Bertrand M., Cullen Z.B., Glaeser E.L., Luca M., Stanton C.T. Working Paper 26989. National Bureau of Economic Research; 2020. How are small businesses adjusting to COVID-19? Early evidence from a survey. [DOI] [Google Scholar]
- Bell, A., 2020. Your neighborhood NYPD officer isn’t likely to be your neighbor. https://github.com/Bellspringsteen/other.nyc/tree/master/NYCGOV/NYPD/NypdOfficersHomeZip/data.
- Birge J.R., Candogan O., Feng Y. Working Paper 2020-57. Becker Friedman Institute; 2020. Controlling epidemic spread: reducing economic losses with targeted closures. [Google Scholar]
- Bisin A., Moro A. MPRA Paper 101059. University Library of Munich, Germany; 2020. Learning epidemiology by doing: the empirical implications of a spatial SIR model with behavioral responses. [Google Scholar]
- Correia S., Luck S., Verner E. Working Paper 3561560. National Bureau of Economic Research; 2020. Pandemics depress the economy, public health interventions do not: evidence from the 1918 flu. [DOI] [Google Scholar]
- Couture V., Dingel J.I., Green A., Handbury J., Williams K.R. Working Paper. University of Chicago Booth School of Business; 2020. Measuring movement and social contact with smartphone data: a real-time application to COVID-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuñat A., Zymek R. CESifo Working Paper Series 8295. CESifo; 2020. The (structural) gravity of epidemics. [Google Scholar]
- Desmet K., Wacziarg R. Working Paper 27329. National Bureau of Economic Research; 2020. Understanding spatial variation in COVID-19 across the United States. [DOI] [Google Scholar]
- Dingel J.I., Neiman B. Working Paper 26948. National Bureau of Economic Research; 2020. How many jobs can be done at home? [DOI] [Google Scholar]
- Fajgelbaum P., Khandelwal A., Kim W., Mantovani C., Schaal E. Working Paper 27441. National Bureau of Economic Research; 2020. Optimal lockdown in a commuting network. [DOI] [Google Scholar]
- Farboodi M., Jarosch G., Shimer R. Working Paper 27059. National Bureau of Economic Research; 2020. Internal and external effects of social distancing in a pandemic. [DOI] [Google Scholar]
- Fenichel E., Castillo-Chávez C., Ceddia G., Chowell G., Parra P., Hickling G., Holloway G., Horan R., Morin B., Perrings C., Springborn M., Velazquez L., Villalobos C. Adaptive human behavior in epidemiological models. Proc. Natl. Acad. Sci. USA. 2011;108:6306–6311. doi: 10.1073/pnas.1011250108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Villaverde J., Jones C. Working Paper 27128. National Bureau of Economic Research; 2020. Estimating and simulating a SIRD model of COVID-19 for many countries, states, and cities. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris J.E. Working Paper 27021. National Bureau of Economic Research; 2020. The subways seeded the massive coronavirus epidemic in New York City. [DOI] [Google Scholar]
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics, part I. Proc. R. Soc. Lond. Ser. A. 1927;115(772):700–721. [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of Coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 2020;179(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toxveard F. Working Paper 2020-08. Cambridge Working Papers in Economics, Insitute for New Economic Thinking; 2020. Equilibrium social distancing. [Google Scholar]
- Yancy C.W. COVID-19 and African Americans. JAMA. 2020;323(19):1891–1892. doi: 10.1001/jama.2020.6548. [DOI] [PubMed] [Google Scholar]