A potential treatment for COVID-19 based on modal characteristics and dynamic responses analysis of 2019-nCoV

Abstract

The 2019-nCoV is ravaging the world, taking lots of lives, and it is emergent to find a solution to deal with this novel pneumonia. This paper provides a potential treatment for COVID-19 utilizing resonance to destroy the infection ability of 2019-nCoV. Firstly, the geometry size of 2019-nCoV is scaled up by 10,000 times. The additional mass is used to represent the effect of the fluid around a spike protein. The finite element analysis (FEA) is used to study the modal characteristics of the tuned 2019-nCoV model and mistuned 2019-nCoV model in blood, respectively. Based on FEA, the lumped parameter mechanical model of 2019-nCoV is established. Then, the dynamic responses of mistuned 2019-nCoV are investigated through harmonic response and dynamical analysis. Finally, a potential method utilizing 360° sweep excitation to cure COVID-19 is put forward.

Introduction

A novel coronavirus (2019-nCoV) was identified as the causative virus linked with a cluster of cases of pneumonia detected in Wuhan city by Chinese authorities on 7 January [1]. Due to the discovery of 2019-nCoV, the virus has been diagnosed quickly [2, 3]. From December 2019, coronavirus disease 2019 (COVID-19) has been ravaging the world and killed more than 181 thousand people [4]. Medical scientists around the world are exerting themselves to develop vaccines, but vaccine researches are time-consuming, and vaccines can lose efficiency when ribonucleic acid (RNA) for this virus mutates. This paper tries to provide a potential method based on vibration to damage the infectivity of 2019-nCoV and cure COVID-19, and it will not fail if the virus mutates. 2019-nCoV is a kind of coronavirus, which consists of virus sphere and spike proteins on the sphere surface. When 2019-nCoV infect humans, they enter cells of humans by binding their spike proteins to receptors on the cell membrane, and then copy viruses in the cell. It is theoretically feasible to disable the 2019-nCoV by destroying the spike protein structures through resonance, and then it is easy for the immune system to eliminate these viruses and recover. This paper combines finite element analysis (FEA) and theoretical methods to study the modal characteristics and dynamic responses of 2019-nCoV in the blood, and put forward a potential treatment for COVID-19 based on vibration.

Modal characteristics of 2019-nCoV

Model of 2019-nCoV

The geometry size of 2019-nCoV is about 200 nm, and for the convenience of FEA, the geometry size is scaled up by 10,000 times to 2 mm. All other parameters of length dimension are magnified 10,000 times, so that we can get the accurate result by scaling down length dimension of results by 10,000 times.

Generally, it is necessary to utilize the nonlocal elasticity theory to consider the size effect of nano-materials. However, based on studies given by Peddieson et al. [5], for a cantilever under concentrated force, its bending behavior utilizing the nonlocal elasticity theory is identical to the local result. In this paper, spike proteins structure on the novel coronavirus sphere surface is a cantilever structure. Therefore, it is reasonable to apply traditional mechanical methods to conduct the analysis.

The 3D 2019-nCoV model is built in Solidworks software as shown in Fig. 1 with protein material, which is input to ANSYS Workbench to do modal analysis. In the process of analyzing the modal characteristic of structures in the fluid, the additional mass is used to represent the effect of the fluid around the structure. According to fluid mechanics by Mao and Wu [6, 7], the additional mass of the blood per unit length around a spike protein can be calculated as follows

$$m_{\text{bp}}={\rho }_{\text{b}}\frac{R^2+r^2}{R^2-r^2}\pi r^2,$$ 1

where ${\rho }_{\text{b}}$ is the density of the blood, $R$ is the equivalent radius of the environment, and $r$ is the radius of the spike protein. Since $R$ is infinite compared to $r$, $m_{\text{bp}}$ is simplified as $m_{\text{bp}}={\rho }_{\text{b}}\pi r^2$. The parameters are set as ${\rho }_{\text{b}}=1030{\text{kg/m}}^3,r=2\text{nm},l_1=20\text{nm}$. The additional mass of the blood around a spike protein is $m_{\text{b}}=m_{\text{bp}}{l}_1={\rho }_{\text{b}}\pi r^2{l}_1=2.6\times {10}^{-22}\text{kg}$ in the real situation, while in the modal analysis it is added to the spike protein by an equivalent point mass $2.6\times {10}^{-10}\text{kg}$. Because of the relatively heavy mass of the sphere body compared to spike proteins, its modes are rigid body motion, which the sphere of COVID-19 model is fixed in modal analysis.

Fig. 1.

3D model of 2019-nCoV

Modal characteristics of tuned 2019-nCoV model

A tuned 2019-nCoV model indicates that every spike protein is identical. The frequencies of the tuned 2019-nCoV model are shown in Table 1. The first 200 frequencies are very close to each other, and they are all first-order bending vibrations. Figure 2 is one of the corresponding mode shapes. These frequencies are supposed to be identical according to the vibration theory, and the discrepancies are caused by the intrinsic error of finite element analysis (FEA).

Table 1.

Natural frequencies of the tuned COVID-19 model

Mode	Frequency (Hz)	Mode	Frequency (Hz)
1	198,340,000	11	199,080,000
2	198,500,000	12	199,300,000
3	198,530,000	13	199,330,000
4	198,720,000	14	199,340,000
5	198,730,000	15	199,430,000
6	199,000,000	16	199,440,000
7	199,000,000	17	199,450,000
8	199,010,000	18	199,470,000
9	199,050,000	19	199,550,000
10	199,060,000	20	199,560,000

Fig. 2.

Mode shape of the tuned 2019-nCoV model

Modal characteristics of mistuned 2019-nCoV model

In the realistic situation under the electron microscope, the number of spike proteins varies from different novel coronavirus. Even though the number of spike proteins in the same kind of novel coronavirus varies, it is hard to detect the exact number currently. In this paper, the 2019-nCoV model is built based on estimation. In order to achieve mistuning, the circle of spike proteins picked to lengthen could be chosen randomly in principle. But for the sake of analysis, the circle of 30 spike proteins in our model is selected. A mistuned 2019-nCoV model is obtained by lengthening one chosen circle, which has 30 spike proteins. At the same time, keeps the other circles unchanged. The frequencies of the mistuned 2019-nCoV model are shown in Table 2. The first 60 frequencies are very close to each other, and they are all first-order bending vibration of the lengthened spike proteins. From 61st frequency, they are the first-order bending vibration of unchanged spike proteins. Figure 3a, b is one of the corresponding mode shapes, respectively. The discrepancies of the first 60 frequencies are caused by the intrinsic error of FEA.

Table 2.

Natural frequencies of the mistuned COVID-19 model

Mode	Frequency (Hz)	Mode	Frequency (Hz)
1	125,320,000	61	200,290,000
2	125,570,000	62	202,570,000
3	126,220,000	63	203,380,000
4	126,290,000	64	203,830,000
5	126,540,000	65	204,100,000
6	126,830,000	66	204,530,000
7	127,050,000	67	208,010,000
8	127,570,000	68	208,770,000
9	127,770,000	69	208,980,000
10	127,930,000	70	209,870,000

Fig. 3.

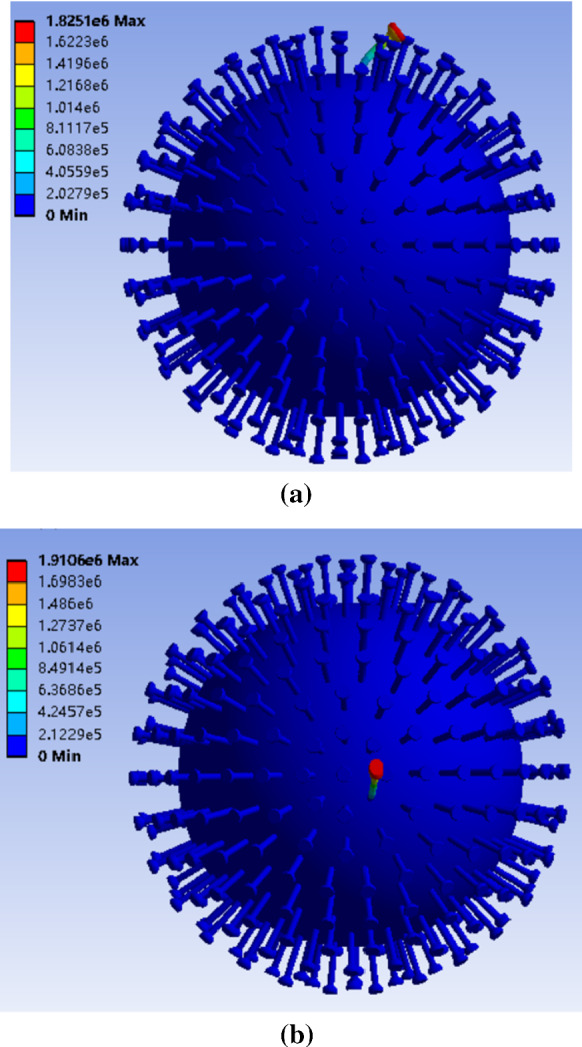
Mode shape of the mistuned 2019-nCoV model. a From the first-order mode to 60th mode; b from 61st mode to 70th mode

The spike proteins in realistic 2019-nCoV are different from each other in geometry, so the frequencies of the realistic 2019-nCoV model are a range of frequencies close to each other, and every frequency corresponds to the first-order bending vibration of one spike protein.

Lumped parameter mechanical model of 2019-nCoV

Choosing the vibration form

According to the mode shape of single spike protein as shown in Fig. 4, the first-order bending mode shape is employed as the vibration form of spike proteins. Based on studies given by Weaver and Timoshenko et al. [8], the Rayleigh method is utilized to calculate the first-order frequency to check this choice

$$f=\frac{p^2}{2\pi }=\frac{1}{2\pi }\frac{{\int }_0^{l}EI{Y}^{″2}\text{d}x}{{\int }_0^l\rho A{Y}^2\text{d}x}=197,900,000\text{Hz},$$ 2

where $p$ is circular frequency, $\rho$ is the density, $E$ is the Young’s Modulus, $I$ is the bending moment, $Y$ is the first-order mode function, $A$ is the area of cross section, and $l$ is the length. Compared with the FEA result, which is 198,340,000 Hz, the relative error is 0.22%. This indicates a reasonable choice.

Fig. 4.

Mode shape of single spike protein

Lumped parameter mechanical model of tuned 2019-nCoV

Based on the first-order bending vibration form, the lumped mechanical model is established as illustrated in Fig. 5. According to the equivalent frequency principle, spike proteins are simplified as mass-spring structures. Each spike protein is identical in geometry except for its location. Based on studies given by Beer et al. [9], the equivalent bending stiffness is calculated as $k_{\text{eq}}=\frac{3EI}{l^3}=1.41\times {10}^{-3}\text{m/N}$, and the equivalent mass $m_{\text{eq}}$ is calculated as $m_{\text{eq}}=9.14\times {10}^{-22}\text{kg}$ by the following Eq. (3)

$$\begin{array}{cc}\hfill T& =T_1+T_2+T_{\text{f}}={\int }_0^{l_1}\frac{\rho A}{2}{\left(\frac{Y(x)}{Y(l_1)}v\right)}^2\text{d}x\hfill \\ \hfill & +{\int }_{l_1}^{l_2}\frac{\rho A_2(x)}{2}{\left(\frac{Y(x)}{Y(l_1)}v\right)}^2\text{d}x\hfill \\ \hfill & +\frac{m_{\text{b}}}{2}{\left(\frac{Y(x_{\text{b}})}{Y(l_1)}v\right)}^2=\frac{m_{\text{eq}}}{2}{v}^2,\hfill \\ \hfill \end{array}$$ 3a

$$\begin{array}{cc}\hfill m_{\text{eq}}& ={\int }_0^{l_1}\rho A{\left(\frac{Y(x)}{Y(l_1)}\right)}^2\text{d}x\hfill \\ \hfill & +{\int }_{l_1}^{l_2}\rho A_2(x){\left(\frac{Y(x)}{Y(l_1)}\right)}^2\text{d}x\hfill \\ \hfill & +m_{\text{b}}{\left(\frac{Y(x_{\text{b}})}{Y(l_1)}\right)}^2,\hfill \\ \hfill \end{array}$$ 3b

where $T$ represents the kinetic energy, $A_2(x)=\pi ·{(5\times {10}^{-9}·x+1\times {10}^{-9})}^2$ is the area of cross section of the end part in a spike protein, $v$ is the velocity at the location $x=l_1$ of the equivalent mass, $x_{\text{b}}=l_1+l_2/2$ indicates the location of the additional mass of the blood around a spike protein.

Fig. 5.

Mechanical model of 2019-nCoV

Verification of lumped parameter mechanical model of tuned 2019-nCoV

According to studies given by Weaver et al. [8], the forced vibration theory of multiple degrees of freedom system is used to yield the natural frequency, which the natural frequency is calculated as $f=\frac{1}{2\pi }\sqrt{\frac{k_{\text{eq}}}{m_{\text{eq}}}}=1.977\times {10}^8\text{Hz}$. Comparing with Eq. (2), the relative error is 0.33%, which validates the accuracy of the model.

Lumped parameter mechanical model of mistuned 2019-nCoV

The lumped parameter mechanical model of mistuned 2019-nCoV is roughly the same with tuned 2019-nCoV. But, there are small differences on equivalent stiffness and mass.

Dynamic response analysis of mistuned 2019-nCoV

Harmonic response of mistuned 2019-nCoV

The harmonic response is conducted after the modal analysis of the mistuned 2019-nCoV model, and acceleration excitation is set as $1{\text{mm/s}}^2$, as shown in Fig. 6. The result of the harmonic response is shown in Fig. 7, where one of the lengthened spike proteins has the largest amplitude. The FEA amplitude–frequency curves of a lengthened spike protein and an unchanged spike protein, whose $\theta$ is $\pi /8$, are illustrated in Figs. 8 and 9, respectively. These results accord with the modal characteristics.

Fig. 6.

Acceleration excitation in the process of harmonic response analysis

Fig. 7.

Harmonic response analysis result

Fig. 8.

The FEA amplitude–frequency curve of a lengthened spike protein

Fig. 9.

The FEA amplitude–frequency curve of an unchanged spike protein

Steady-state dynamic responses of mistuned 2019-nCoV

The excitation $Fsin\omega t$ is imposed on the end of spike proteins of the mistuned 2019-nCoV model. There are totally 32 circles, and each circle consists of spike proteins, which have the same angle $\theta$ between their displacements and excitation. The viscosity of blood is considered as viscous damping. According to studies given by Weaver et al. [8], the vibration theory of multitude degrees of freedom model and the forced vibration equation of lumped parameter model are utilized to obtain the following equation

$$\begin{array}{cc}& m_{\text{eq}i}{\ddot{x}}_i+r_{\text{eq}i}{\dot{x}}_i+k_{\text{eq}i}{x}_i\hfill \\ \hfill & =Fsin\omega t\left|cos{\theta }_i\right|,i=1,\dots ,32,\hfill \\ \hfill \end{array}$$ 4

and the steady-state response as follows

$$x_i=\frac{F}{k_{\text{eq}i}}\frac{\left|cos{\theta }_i\right|}{\sqrt{{\left(1-{\lambda }_i^2\right)}^2+{\left(r_{\text{eq}i}\omega /k_{\text{eq}i}\right)}^2}}sin(\omega t-{\phi }_i),$$ 5

where ${\theta }_i=\frac{(i-1)\pi }{16}$, ${\phi }_i={tan}^{-1}{r}_{\text{eq}i}\omega /k_{\text{eq}}(1-{\lambda }_i^2)$, ${\theta }_i$ is the angle between excitation and displacement, ${\lambda }_i=\frac{\omega }{p_i}$, $p=\sqrt{k_{\text{eq}i}/m_{\text{eq}i}}$.

It is easy to find that the vibration amplitude increases with $\left|cos{\theta }_i\right|$. The spike proteins, whose displacements parallel with the excitation direction, have the biggest vibration amplitude. When $5\pi /16\le {\theta }_i\le 11\pi /16$ and $21\pi /16\le {\theta }_i\le 27\pi /16$, $\left|cos{\theta }_i\right|\le 0.56$, and these vibration amplitudes are relatively small, which it can somehow achieve response concentration.

Amplitude–frequency curves

According to studies given by Weaver et al. [8], the relationship between amplitude and frequency of the lumped parameter model is obtained as follows

$$B_i=\frac{F}{k_{\text{eq}i}}\frac{cos{\theta }_i}{\sqrt{{\left(1-{\left(2\pi f/\sqrt{k_{\text{eq}i}/m_{\text{eq}i}}\right)}^2\right)}^2+{\left(2\pi f{r}_{\text{eq}i}/k_{\text{eq}i}\right)}^2}}.$$ 6

The amplitude–frequency curves of the spike proteins are analyzed in harmonic response, as shown in Fig. 10, where $B_{1\text{max}}=3.56\times {10}^{-12}\text{m}$, $B_{2\text{max}}=7.01\times {10}^{-13}\text{m}$. Compared with the FEA results in Figs. 8 and 9, relative errors are 5.10% and 7.83%, respectively.

Fig. 10.

The amplitude–frequency curve

A potential treatment for COVID-19

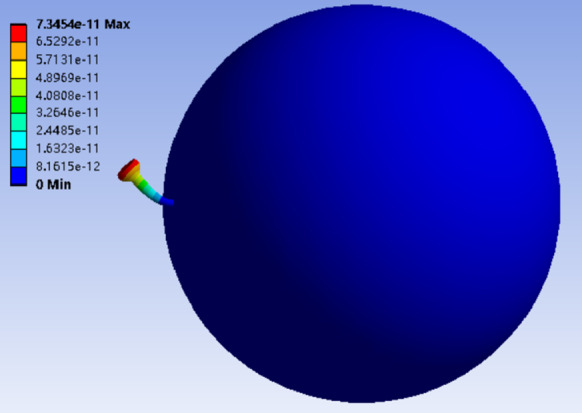
The spike proteins of a realistic 2019-nCoV are usually different from each other in geometry, and every spike protein has a different frequency, which there is small discrepancies. Therefore, it would be possible to utilize an ultrasonic vibration exciter to 360° sweep, whose frequency range is set as the first-order bending vibration frequencies 1.9 × 10⁸ Hz to 2.0 × 10⁸ Hz in order to excite every spike protein of 2019-nCoV to resonate. 360° rotating sweep excitation could evoke resonance of spike proteins in turn and vibration concentration. Given a proper excitation amplitude, it could destroy the spike protein structures and disable the infectivity of 2019-nCoV. Effects of ultrasonic resonance destruction of viral proteins are discussed further. Since the bending strength of the spike protein is unknown, for the reliability of the analysis, it is set as the same as the bending strength of common steels, which is 300 MPa. If the stress in the spike protein is bigger than 300 MPa, it would crack at the base and lose its ability to invade human cells. Then, the required destruction excitation amplitude is analyzed by FEA, as shown in Fig. 11, which is calculated as 1.041 × 10⁻⁵ mm and the equivalent acceleration is 4.164 m/s². Based on studies given by Glaister [10], this acceleration is safe for human body. Based on studies given by Randall et al. [11], it is known that the range of resonant frequencies of standing human bodies was found to be from 9 to 16 Hz. Since the resonant frequencies of human bodies are below 20 Hz, the vibration energy would hardly be absorbed by human body and it would not cause much harm and discomfort to patients. Therefore, it is efficient and safe to utilize an ultrasonic vibration exciter to conduct 360^o rotating sweep excitation to human body if the vibration frequencies are set as 1.9 × 10⁸ Hz to 2.0 × 10⁸ Hz and the amplitude is set as larger than 1.041 × 10⁻⁵ mm.

Fig. 11.

The destruction analysis of spike proteins

Conclusions

In this paper, the modal characteristics and dynamic responses of 2019-nCoV in the blood are investigated by FEA and theoretical analysis. A possible treatment for COVID-19 based on vibration is put forward. Several findings are listed below.

1. The frequencies of the tuned 2019-nCoV model are very close to each other, and they are all first-order bending vibrations. The frequencies of the realistic mistuned 2019-nCoV model are a range of frequencies close to each other, and every frequency corresponds to the first-order bending vibration of one spike protein.

2. The first-order bending vibration is adopted as the vibration form, and the established lumped parameter mechanical model of 2019-nCoV is in good agreement with the FEA model.

3. The harmonic responses and dynamic responses of the mistuned COVID-19 model accord well. When applying an excitation on the 2019-nCoV model, the vibration amplitude increases with $\left|cos{\theta }_i\right|$, and it can somehow achieve response concentration.

4. In order to help cure the COVID-19, a potential method utilizing 360^o sweep excitation to destroy the spike protein structures is put forward. When an ultrasonic vibration exciter is applied 360° rotating sweep excitation to human body, the vibration frequencies is set as 1.9 × 10⁸ Hz to 2.0 × 10⁸ Hz and the amplitude is selected as larger than 1.041 × 10⁻⁵ mm, it is efficient and safe to disable the 2019-nCoV from infecting human cells, which maybe help cure COVID-19.

Compliance with ethical standards

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.