Local axonal conduction shapes the spatiotemporal properties of neural sequences

SUMMARY

Sequential activation of neurons has been observed during various behavioral and cognitive processes, but the underlying circuit mechanisms remain poorly understood. Here we investigate premotor sequences in HVC (proper name) of the adult zebra finch forebrain that are central to the performance of the temporally precise courtship song. We use high-density silicon probes to measure song-related population activity, and we compare these observations with predictions from a range of network models. Our results support a circuit architecture in which heterogeneous delays between sequentially active neurons shape the spatiotemporal patterns of HVC premotor neuron activity. We gauge the impact of several delay sources, and we find the primary contributor to be slow conduction through axonal collaterals within HVC, which typically adds between 1 and 7.5 ms for each link within the sequence. Thus, local axonal ‘delay lines’ can play an important role in determining the dynamical repertoire of neural circuits.

Graphical Abstract

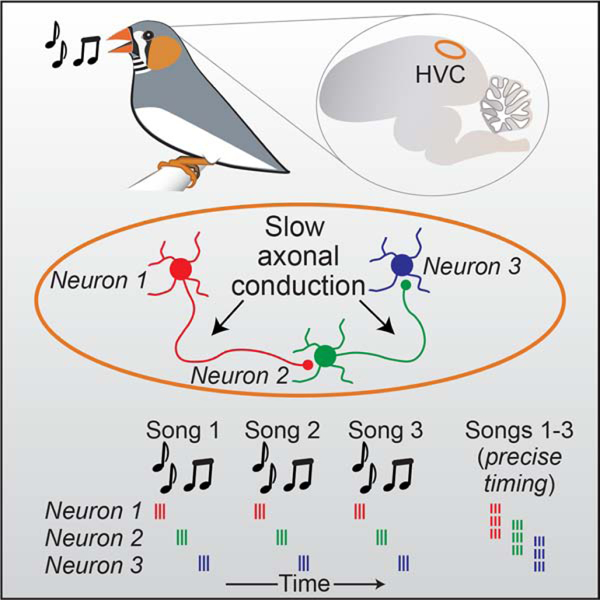
Etoc:

By recording and modeling sequential activity in neurons involved in motor control during the complex behavior of singing in zebra finch, Egger et al., determine that local ultraslow axonal conduction between sequentially active neurons generates network delays that underlie the pattern of network activity within the circuit.

INTRODUCTION

Sequential neural activity in local brain areas is thought to play a critical role in behaviors such as motor control (Luczak et al., 2015; Mauk and Buonomano, 2004; Peters et al., 2014; Prut et al., 1998), navigation (Foster and Wilson, 2007; Pastalkova et al., 2008), and decision-making (Mello et al., 2015; Schmitt et al., 2017). A variety of mechanisms have been proposed to underlie the generation of neural sequences (Diesmann et al., 1999; Fiete et al., 2010; Goldman, 2009; Hahnloser et al., 2002; Kleinfeld and Sompolinsky, 1988; Laje and Buonomano, 2013; Rajan et al., 2016), but experimental tests of these network models have been stymied by the scarcity of data sets that relate behavior, network function and circuit structure. The zebra finch song system is ideally suited for studying the mechanistic basis of neural sequence generation. Each adult male zebra finch produces a courtship song that is nearly identical from one rendition to the next (Glaze and Troyer, 2006), consisting of ~3–7 discrete vocal elements known as ‘syllables’. Many lines of evidence have suggested that neural activity controlling the moment-to-moment timing of song production is primarily mediated by a single brain region, called HVC (proper name) (Hahnloser et al., 2002; Long and Fee, 2008; Nottebohm et al., 1976; Vu et al., 1994). A population of HVC_(RA) projection neurons sends these premotor commands to a primary motor cortical site (i.e., the robust nucleus of the arcopallium, or RA) which in turn drives motoneurons (Wild, 1993) controlling the millisecond-resolution timing of muscle commands that directly impact behavioral output (Adam and Elemans, 2020).

The HVC premotor sequence is composed of roughly 20,000 HVC_(RA) neurons, each producing high-frequency bursts of action potentials (~4–5 spikes/burst, ~5–10 ms duration) at a single moment during the song (Hahnloser et al., 2002; Kozhevnikov and Fee, 2007). At a population level, different HVC_(RA) neurons are often active at different moments of the song, whose length typically ranges from ~0.5–1.0 seconds. Several models have been proposed to explain HVC sequence generation (Cannon et al., 2015; Galvis et al., 2018; Gibb et al., 2009; Hamaguchi et al., 2016; Jin et al., 2007; Long et al., 2010; Pehlevan et al., 2018). A feature at the heart of many of these models is local connectivity between HVC_(RA) neurons capable of propagating activity from earlier to later steps in the song sequence. Previous work had demonstrated the existence of these interconnections (Kornfeld et al., 2017; Kosche et al., 2015; Mooney and Prather, 2005). However, the size of HVC_(RA)-HVC_(RA) synapses appears to be somewhat restricted (Kornfeld et al., 2017), leading to unitary postsynaptic potentials of approximately 2 mV (Mooney and Prather, 2005), considerably smaller than the depolarization observed during a song-related burst (~10–15 mV) (Long et al., 2010), suggesting that multiple convergent presynaptic inputs are required. The exact identity of these presynaptic partners (i.e., specific timing, spatial location) remains unknown, due in part to the technical difficulties in measuring synaptic connectivity between sequentially active neurons during behavior.

As an alternative means of addressing the mechanisms of song-related sequence generation, we leverage detailed measurements of circuit, synaptic and biophysical properties of zebra finch HVC neurons (Benezra et al., 2018; Kornfeld et al., 2017; Kosche et al., 2015; Long et al., 2010; Mooney and Prather, 2005) to develop network models of HVC_(RA) sequence generation where the only free parameter is the connectivity of presynaptic partners. These models predict millisecond-timescale differences in HVC population activity that had eluded existing experimental measurements. Specifically, previous electrophysiological studies had been restricted to measuring responses from individual projection neurons (Hahnloser et al., 2002; Long et al., 2010) or occasionally pairs (Lynch et al., 2016), forcing investigators to retrospectively construct an inferred sequence by relating each measured time point to the produced song. Such an approach can address questions of representation within HVC (Amador et al., 2013; Lynch et al., 2016), but it does not allow for the direct observation of neural sequences that unfold during singing.

We overcome these obstacles by using high-density silicon probes to measure song-related sequential activity of up to 70 simultaneously recorded projection neurons and find that our data strongly favor a network configuration in which axonal conduction delays between sequentially active cells help to distribute the timing of premotor bursts throughout the duration of the song. We then use fluorescence imaging during singing to demonstrate the impact of these delays on the spatial patterns of activated neurons within HVC. To explore the universality of this mechanism, we estimated the distribution of axonal conduction delays in rodent layer 4 (L4) neocortical neurons and found them to be consistent with those we describe in the songbird. Hence, axonal conduction delays may play a key role in shaping network activity across a range of local brain circuits.

RESULTS

Measurement and modeling of network sequences in HVC

We first sought to determine the fine temporal structure of song-related sequences within HVC using high-density silicon probes (Figure 1A), which we used to monitor the spiking activity of 291 HVC projection neurons in 5 birds during song production. We simultaneously recorded between 45 and 70 projection neurons over observation periods lasting 1 to 4.5 hours. We used antidromic responses and other electrophysiological features (see Methods, Figure S1) to distinguish HVC_(RA) neurons (n = 83) from those projecting to the basal ganglia (HVC_(X) neurons, n = 208). We observed stable sequences (11 to 20 HVC_(RA) burst events per bird) that could be clearly visualized in single trials (Figures 1B and 1C).

Figure 1. Measuring and modeling HVC premotor sequences.

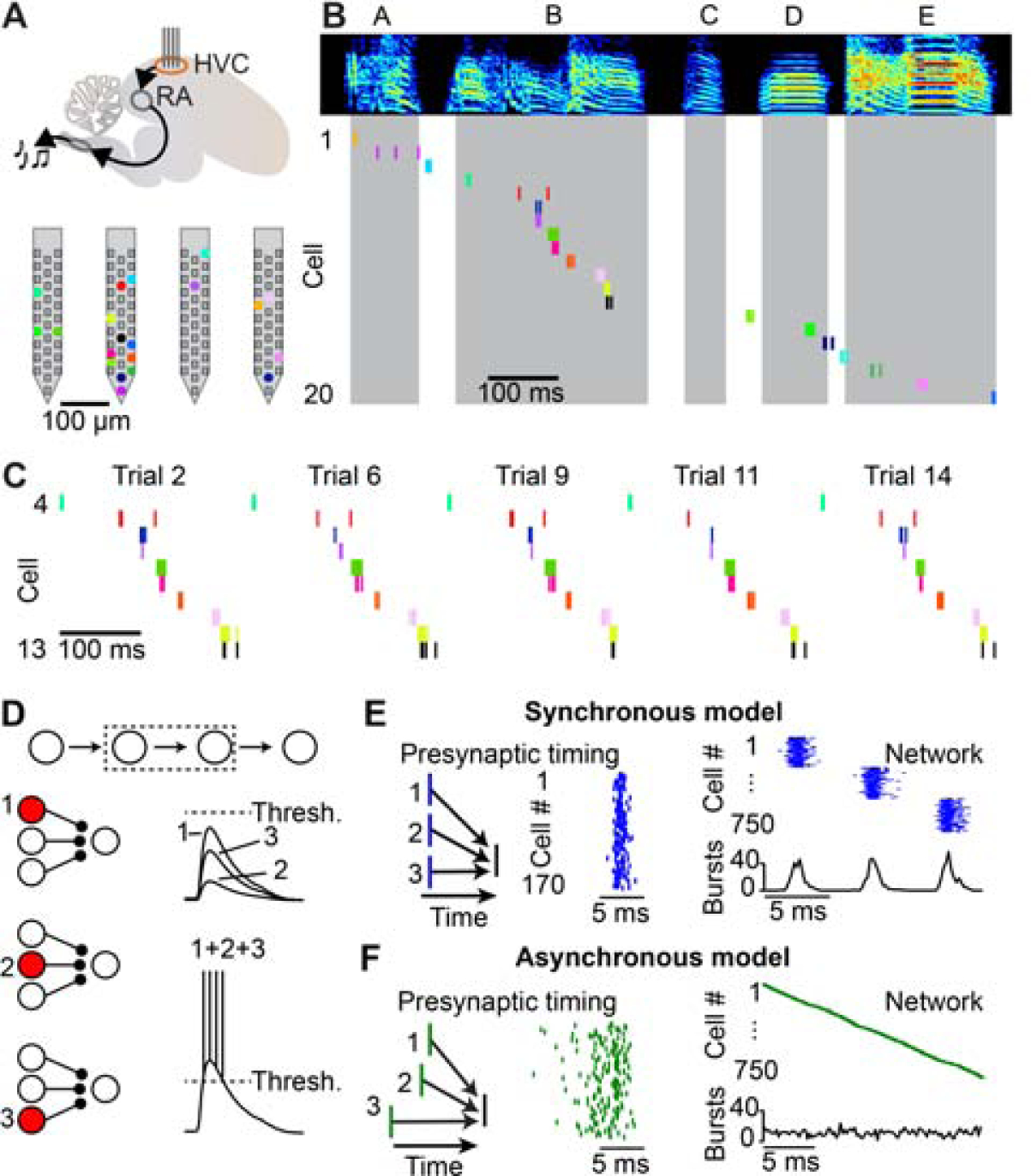
(A) Top: Schematic of a high-density silicon probe placed within HVC of the song production pathway in the zebra finch. Bottom: Location of simultaneously recorded HVC_(RA) neurons (colored dots) on a four-shank silicon probe. (B) Spectrogram of a song motif (letters: individual syllables) and spike raster plots of 20 simultaneously recorded HVC_(RA) neurons. Shaded regions represent syllable times. (C) Raster plot of HVC_(RA) neurons active during syllable B for five example song trials. (D) Inputs from individual presynaptic HVC_(RA) neurons are not likely to be strong enough to drive burst spiking in a postsynaptic neuron; convergence of multiple synaptic inputs is required. (E, F) Left: Presynaptic neurons could be active synchronously (E) or asynchronously (F), as shown in a simplified schematic. Center: Spike timing of 170 presynaptic neurons in two biologically detailed models of the HVC_(RA) network. Right: Simulated network activity of 750 HVC_(RA) neurons. See also Figures S1 and S2.

Previous manipulations of HVC activity during singing support the idea that song-related sequences are sustained by local circuitry (Long and Fee, 2008; Vu et al., 1994). As discussed above, most network models (Galvis et al., 2017; Long et al., 2010; Pehlevan et al., 2018) suggest a functionally feedforward architecture in which connected chains of neurons generate reliable sequential activity, and it is likely that convergent inputs from multiple presynaptic partner neurons are required to drive burst spiking during singing (Figure 1D). There are two categorically different means of accomplishing this arrangement. In the first, each HVC_(RA) neuron is driven by a synchronously active presynaptic population (Figure 1E). In the second, presynaptic populations are active at a range of different times which are accompanied by matching delays that enable simultaneous integration at the postsynaptic neuron (Figure 1F).

To examine whether these connectivity schemes could result in measurable differences in the population activity of HVC_(RA) neurons, we constructed two network models (see Methods; Figure S2) constrained by previous experimental observations (Benezra et al., 2018; Kornfeld et al., 2017; Kosche et al., 2015; Long et al., 2010; Mooney and Prather, 2005) and differing only in the degree of synchrony of presynaptic neurons. Resultant population activity patterns from these two arrangements were categorically distinct: Sequences in the ‘synchronous model’ (Figure 1E) consisted of a series of co-active groups of neurons, while network activity in the ‘asynchronous model’ (Figure 1F) was smoothly evolving in time. Since HVC determines motor timing within the zebra finch song production pathway, each model suggests qualitatively different ‘population clock’ dynamics (Buonomano and Karmarkar, 2002; Paton and Buonomano, 2018) – either with discrete ‘ticks’ at a ~6–7 ms timescale (synchronous model) or with a higher resolution, continuous timing signal throughout the behavior (asynchronous model).

Using population recordings to estimate HVC network structure

To distinguish between synchronous and asynchronous network activity, our measurements must be significantly more precise than the relevant timescales of our model predictions (i.e., the interburst interval of the synchronous model). One existing source of temporal jitter is behavioral variability. Consistent with previous reports (Glaze and Troyer, 2006), the duration of zebra finch songs in our data set varied by 1.8 ± 0.4% across renditions (Figure 2A, n = 5 birds, 12 to 47 song motif renditions per bird). These variations were accompanied by correlated differences in spike timing, where activity of neurons later in the sequence was shifted in proportion to the change in overall song duration (Figures 2B and 2C). To compensate for this source of variability, we aligned neural sequences across different trials to each other using linear transformations (see Methods). After alignment, burst onset times were extremely precise (Figures 2D and 2E; HVC_(RA): 0.64 ± 0.29 ms; HVC_(X): 0.72 ± 0.46 ms; median ± median absolute deviation). Therefore, our electrophysiological measurements of HVC projection neuron activity have the temporal precision to distinguish between the two models presented above (Figures 1E and 1F).

Figure 2. Estimating HVC network activity with submillisecond precision.

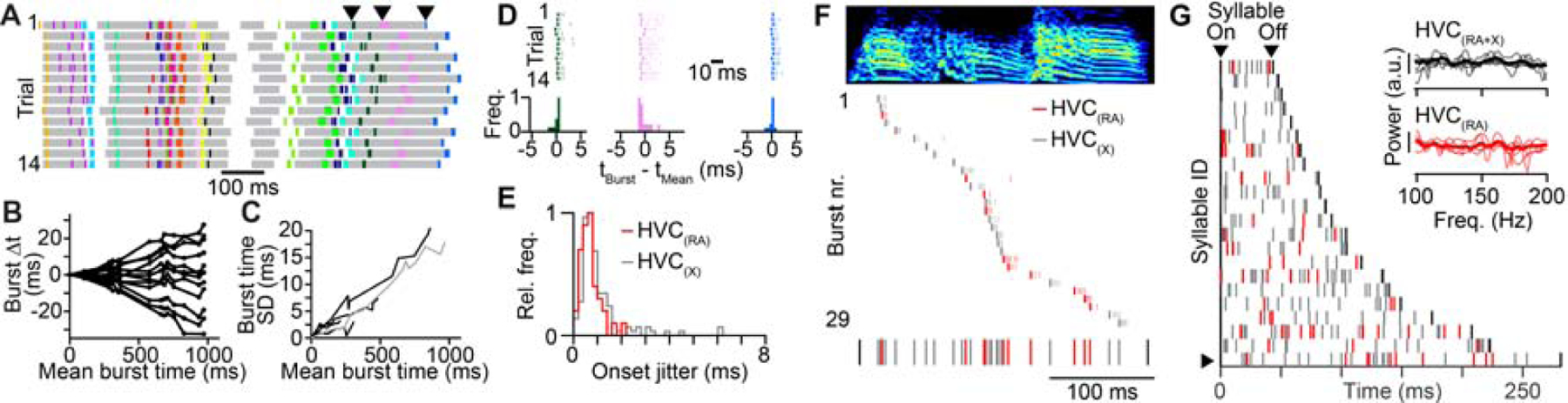
(A) Spike raster plots of HVC_(RA) neurons from one bird. Each row represents a single rendition with the timing of syllables indicated with gray shading during different song repetitions. (B) Difference between burst times in individual song motifs and the mean burst times for the spiking patterns shown in (A). Burst times in the same song motif are connected by lines. (C) Standard deviation (SD) of burst times of HVC_(RA) neurons as a function of burst time during song in five birds. The gray line represents the bird analyzed in Panel (C). (D) Top: Burst times of the three neurons (indicated in (A) with arrowheads) after removing trial-to-trial variation in overall sequence speed. Bottom: Histograms of aligned burst onset times. (E) Histogram of burst onset jitter (root mean squared error) for 39 HVC_(RA) and 216 HVC_(X) bursts recorded in five birds. (F) Top: 10 HVC_(RA) and 19 HVC_(X) burst events occurring during a single syllable, sorted according to burst onset time (bold). Bottom: All burst onset times occurring during this syllable (black: syllable onset/offset). (G) All burst onset times included in this data set (282 bursts – 66 HVC _(RA) and 216 HVC_(X), 22 syllables, 5 birds). Each row shows all bursts occurring during individual syllables. The row with the arrowhead is featured in (F). Inset: Power spectra of burst onset times for all projection neurons (top) and for HVC_(RA) neurons only (bottom). Thin lines: power spectra of individual birds (n=5), thick lines: average across birds.

Our next step was to leverage the submillisecond timing precision of our recordings to test specific predictions concerning the relative timing of song-related burst firing: In the synchronous model (Figure 1E), network activity should be periodic (i.e., occurring only in specific time steps), while the asynchronous model (Figure 1F) predicts continuous coverage of activity throughout the song. We examined cases in which multiple projection neurons were recorded during individual syllables, consisting of 66 HVC_(RA) and 216 HVC_(X) total bursts. Burst events within syllables did not exhibit any obvious regularity (Figures 2F and 2G), which would have been indicative of the synchronous model. To detect the presence of any such periodic structure in population activity, we used a Fourier analysis to analyze burst onset times for all HVC projection neurons as well as for HVC_(RA) neurons, considered separately (Figure 2G).

We formally tested existing network models by comparing the relative timing of HVC projection neuron bursts (Figure 2) with predictions generated from the proposed synchronous and asynchronous circuit configurations (Figures 1E and 1F, 3A and 3B). Importantly, we set the number of simulated burst times to match our observations (i.e., 282 total HVC projection neuron bursts in 22 syllables and 66 HVC_(RA) bursts in 15 syllables) to ensure that our data set would be sufficient to distinguish between these models. The synchronous model predicted a peak in the power spectrum at ~170 Hz (Figures 3C and Figure S3), corresponding to a ~6 ms interval between time steps (e.g., Figure 1E). In contrast, the power spectrum predicted by the asynchronous model, which generates a uniform coverage of bursts throughout the song (e.g., Figure 1F), was flat within this frequency range (Figure 3D). When we compared these simulations with measured burst times, we found that our data set was strongly aligned with the predictions of the asynchronous model (synchronous model: p < 10⁻⁴ for HVC projection neurons and HVC_(RA) only, asynchronous model: p = 0.90 for HVC projection neurons and p = 0.52 for HVC_(RA) neurons, bootstrap, see Methods).

Figure 3. Comparison of network model predictions to recorded data.

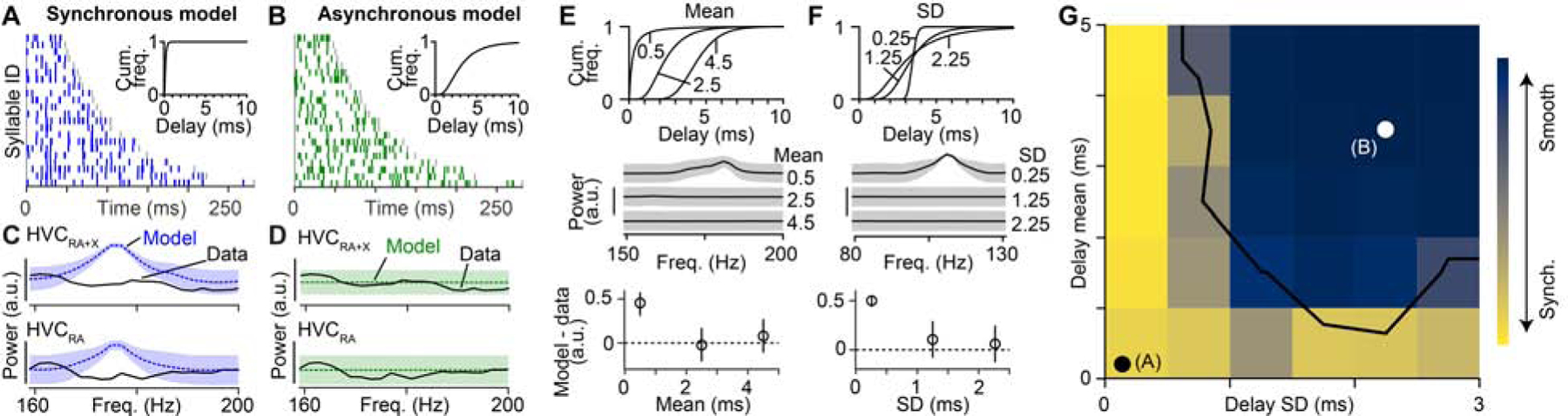
(A, B) Simulated burst onset times for the synchronous (A) and asynchronous (B) models. Insets indicate the distributions of delays used. (C, D) Power spectra used to measure the presence of periodic activity patterns in synchronous (C) and asynchronous (D) models and in the experimental data (from Figure 2G). Shaded area: ± 3 SD. (E, F) Top: Three distributions of delays when varying the mean delay (SD fixed at 1.25 ms) (E) or the delay SD (mean fixed at 3.5 ms) (F). Center: Power spectra of burst onset times for network models with above delay distributions. Bottom: Difference in peak power in the frequency band from 75–200 Hz for the models based on the delay distributions and the observed HVC_(RA) burst times (dashed line). Error bars: 2.5th and 97.5th percentiles. (G) Two-dimensional parameter grid of network synchrony with different mean and SD values for delay distributions. Each grid point is colored according to the peak power of the burst onset times (i.e., smooth sequences in dark blue; synchronous sequences in yellow). White/black dots: Locations of the two models in (A, B). Black line: Models to the left and below this line display sequences with synchronously active groups of neurons that are inconsistent with song-related activity of HVC_(RA) neurons (p < 0.05, bootstrap, see Methods). See also Figures S2, S3 and S4.

The synchronous and asynchronous models represent only two specific network configurations out of a large range of possibilities. To systematically explore the relationship between burst transmission delays and circuit dynamics, we varied both the mean (Figure 3E) and standard deviation (SD; Figure 3F) of our delay distribution over an order of magnitude. We then generated a network model for each case and simulated a family of burst times to compare with observed data, now restricting our analysis to measured sequences of HVC_(RA) neurons (Figures 1G, 3A and 3B). When the delay distribution was narrow or the mean delay was very short, simulated HVC sequences were composed of bursts in discrete time steps. However, delay distributions exceeding a minimum mean and SD, led to smooth simulated network sequences, as observed in HVC during song (Figure 2G). This effect was robust to the presence of recurrent (i.e., non-feedforward) connections (Figures S4A and S4B) as well as the precise shape of the delay distribution (Figure S4C). Thus, our simulations support the hypothesis that delays could provide a robust mechanism for the formation of smooth sequences, as observed within HVC during song.

Biophysical origin of HVC circuit delays

What neural processes can create such delays? For instance, the time between the arrival of a spike at the axon terminal to the start of the postsynaptic potential is typically exceptionally short (~150 μs (Sabatini and Regehr, 1996), and therefore unlikely to explain the smooth network sequences we observe. On the other hand, delays related to postsynaptic integration and axonal conduction velocity have the potential to be significant. Here we consider each of these parameters as they apply to HVC network function.

Postsynaptic integration can generate heterogeneous delays in two primary ways. First, synaptic inputs are spatially summated from separate regions of the dendritic arbor allowing for the possibility that distal and proximal inputs can arrive at the soma at different times. Such spatial summation is unlikely to affect HVC_(RA) neurons, however; their dendrites are short (< 100 μm) and radiate from the somata equally in all directions, leading to a spherical shape of the dendritic tree (Benezra et al., 2018) and therefore limiting delay variability. Second, neuronal time constants, which affect the timescale over which synaptic inputs could be summated, can differ greatly within specific cell classes, potentially influencing network function (Giocomo and Hasselmo, 2008). To directly address this feature in HVC, we reanalyzed a published data set of intracellular recordings performed during singing (Long et al., 2010; Vallentin and Long, 2015). We found that temporal summation – defined as the time course of the depolarization immediately preceding a burst – was highly consistent across neurons (2.3 ± 0.4 ms, n = 11; Figure 4A–C). We modified our network models to explicitly reflect different degrees of temporal summation in HVC_(RA) neurons by parametrically varying their passive integrative properties (see Methods). These simulations suggest that differences in temporal summation across neurons cannot account for the smooth network sequences observed (Figure 4D), further excluding a postsynaptic mechanism as a significant source of network delay.

Figure 4. Heterogeneity of membrane potential rise times is insufficient to explain HVC network dynamics.

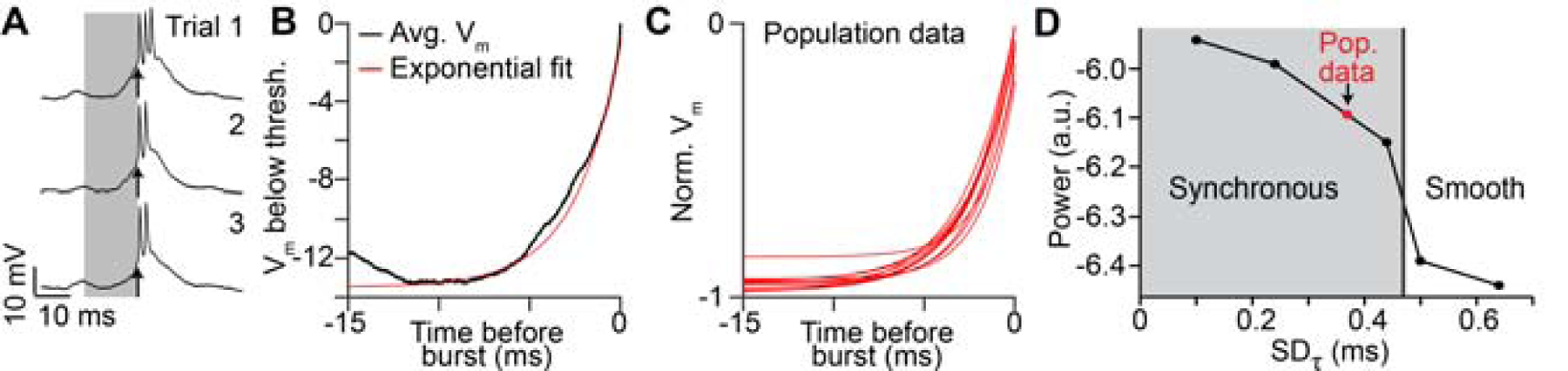
(A) Membrane potential of an HVC_(RA) neuron recorded intracellularly during three song trials. Arrow: Burst onset time. (B) Average membrane potential (in black) preceding burst onsets (shaded region in (A)) with exponential fit (τ = 2.5 ms). (C) Exponential fits to the membrane potential preceding bursts in 11 intracellularly recorded HVC_(RA) neurons. (D) Power spectral analysis for models with varying levels of heterogeneity in membrane potential rise times before burst onsets. Models to the left of the vertical line produce network sequences with synchronous groups of neurons that are incompatible with HVC population recordings (p < 0.05, bootstrap, see Methods).

We then explored the alternative possibility that local connections between HVC_(RA) neurons could exhibit delays related to the time required for an action potential to travel from its initiation site near the neuronal soma to axon terminals (i.e., axonal conduction delays). In previous work (Benezra et al., 2018), we had found that HVC_(RA) neurons often send extensive axonal collaterals throughout HVC, and we used 22 complete reconstructions to estimate the distance from the soma to each of the synaptic sites along the axon, a log-normal distribution ranging from 0.19 to 1.34 mm (5^th to 95^th percentiles). To convert these pathlength measurements into axonal delays, we needed to measure the conduction velocity of local HVC_(RA) axon collaterals, which are thin and difficult to record. However, we could estimate these values using in vivo whole-cell recordings (n = 40 HVC_(RA) neurons) to measure conduction velocity in antidromically activated HVC→RA projection axons (Figures 5A and S5A, see Methods), a path distance of 2.8 ± 0.2 mm (n = 4 neurons, e.g., Figure 5B). We then corrected for differences in axon diameter (descending axon: 446 ± 135 nm, local collaterals: 167 ± 73 nm) using cable theory (Rushton, 1951) (See Methods, Figures 5C and 5D, Figures S5B–D). Assuming homogeneous biophysical properties (i.e., channel density) across the axon, we arrived at a final estimated conduction velocity of 0.187 ± 0.035 mm/ms, corresponding to conduction delays ranging from 1 to 7.5 ms (5^th and 95^th percentiles, Figure 5E). Our network model demonstrates that these values are sufficient to enable HVC to generate smooth sequences (Figure 5F). Taken together, we find that axonal conduction delays contribute significantly to network dynamics within HVC.

Figure 5. Local HVC_(RA) axonal conduction delays support smooth sequences.

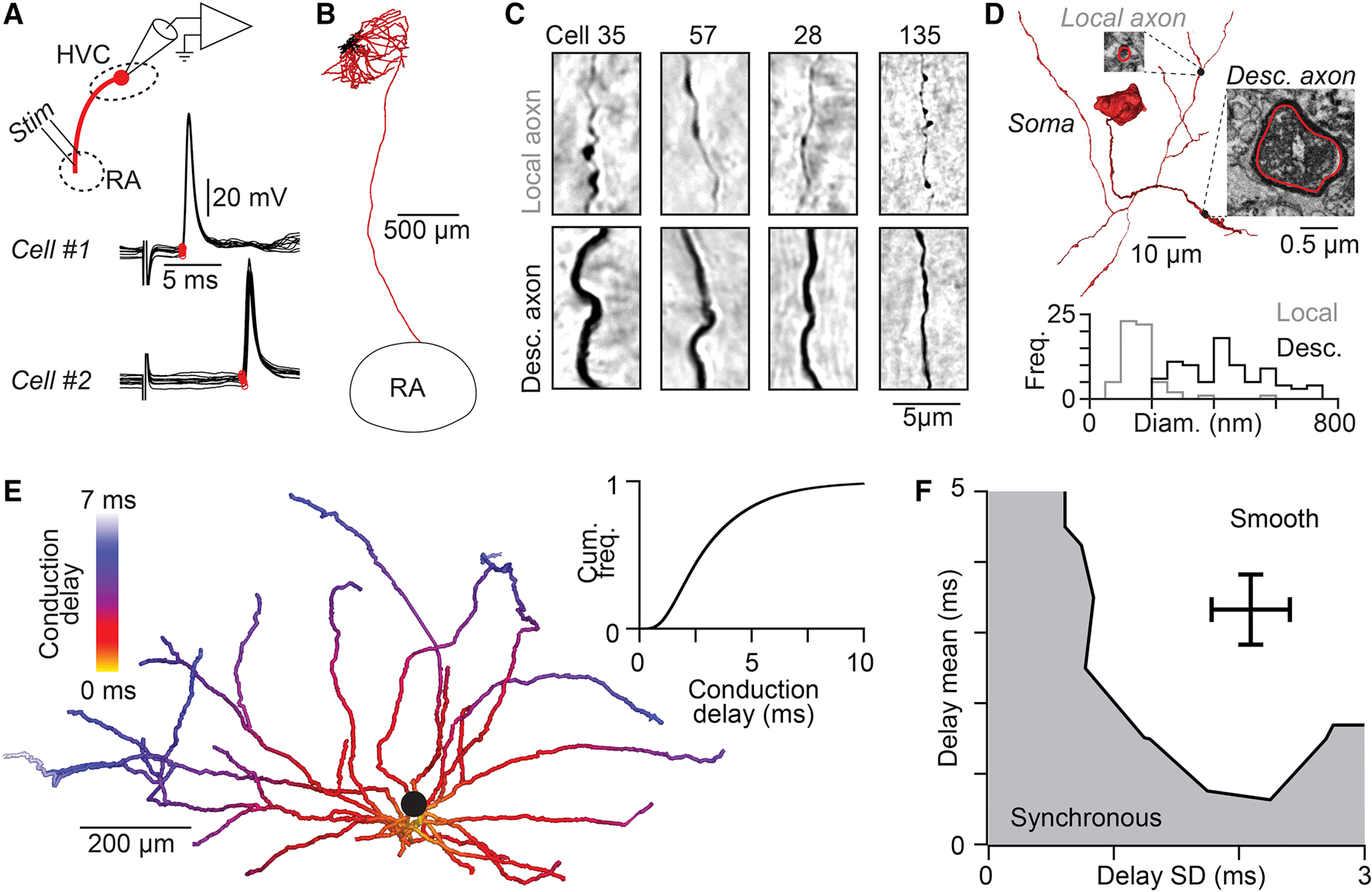
(A) Antidromic responses (10 trials per neuron) following RA stimulation measured with in vivo whole-cell recordings from two HVC_(RA) neurons allows precise measurement of conduction times along the descending axon. Stimulus artifact removed for visualization. (B) Example reconstruction of an HVC_(RA) projection neuron (axons: red, dendrites: black). (C) Light micrographs of local (top row) and descending (bottom row) axons from five HVC_(RA) neurons labeled with neurobiotin. (D) Top: 3D reconstruction of the soma and proximal axons of a retrogradely labeled HVC_(RA) neuron from a serial block-face EM image stack. Insets: EM micrographs of labeled axons. Bottom: Distribution of unmyelineated local and descending HVC_(RA) axon diameters. (E) Estimate of the distribution of conduction delays along thin unmyelinated local axon collaterals of an HVC_(RA) neuron (population inset). (F) The distribution of conduction delays along HVC_(RA) neuron axons falls within the range that generate continuous sequences in our network model (see Figure 3G). See also Figure S5.

Axonal conduction delays can explain song-related spatial activity patterns within HVC

We have demonstrated that axonal conduction delays may have the capacity to significantly impact the temporal structure of the HVC network, potentially leading to continuous burst events throughout song. We next asked whether the impact of axonal delays can be detected in the spatial properties of HVC circuit dynamics. Because synapses located closer to the soma are activated after shorter delays than those further away (i.e., Figure 5E), we reasoned that the spatial distribution of the synapses responsible for driving the next step of the HVC sequence can provide an independent test of the range of delays underlying HVC network dynamics. To investigate this, we generated ‘spatial models’ for a variety of delay distributions, varying the mean and SD values as in the above analysis (i.e., Figure 3G). For each model, we placed ‘virtual synapses’ at specific locations onto 22 morphologically reconstructed HVC _(RA) axon collaterals (Benezra et al., 2018) corresponding to the selected delay distributions given our estimate of conduction velocity. For instance, in cases in which the conduction delays were long but exhibited a low variance, synapses were clustered on distal axons (Figure 6A). We also considered cases in which the means of the conduction delays were low, across different variance conditions (Figures 6B and 6C). We compare these possibilities against a scenario in which the mean and variance were both relatively high (Figure 6D), as we estimate for HVC delays. Because of the differential placement of synapses within the axonal field, each model should result in a different prediction concerning the spatiotemporal pattern of activity (Graber et al., 2013; Markowitz et al., 2015; Peh et al., 2015) in HVC during singing (i.e., the location of postsynaptic neurons that represent the next step within the sequence).

Figure 6. Spatial organization of HVC projection neuron activity during singing is consistent with network dynamics controlled by axonal delays.

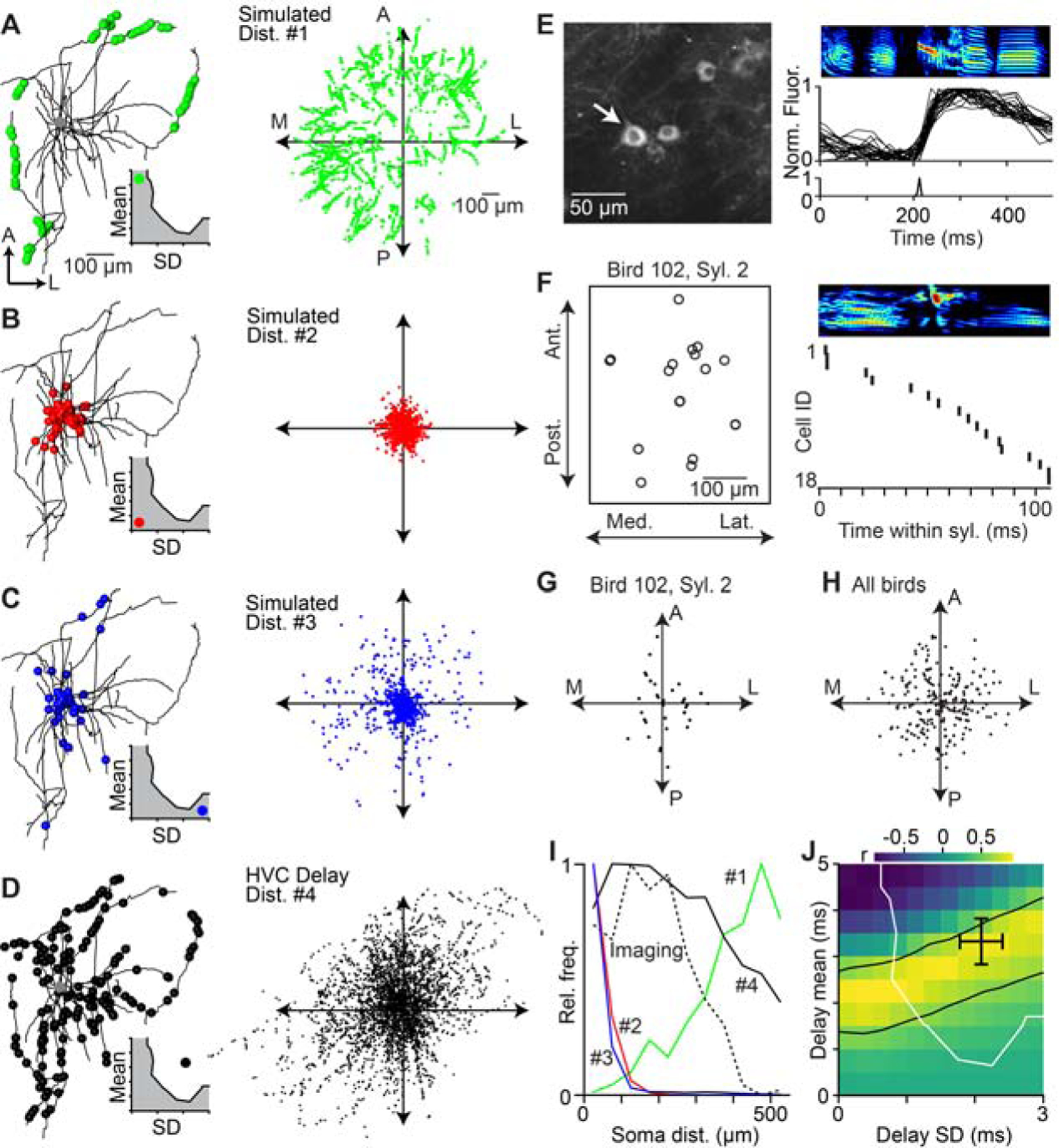
(A–D) Left: Locations of virtual active synapses along the local axonal collaterals of an HVC_(RA) neuron for a given delay distribution (inset; mean ± SD, a: 4.5 ± 0.25 ms; b: 0.5 ± 0.25 ms; c: 0.5 ± 2.75 ms; d: 3.3 ± 2.1 ms). Right: Distribution of virtual active synapses relative to the soma based on the local axonal collaterals of 22 HVC(RA) neurons. (E) 2-photon calcium imaging of song-related bursting activity in HVC. Left: Example image of GCaMP6s-labeled somata. Right: Spectrogram of song motif (top), aligned normalized fluorescence traces of the neuron highlighted in left panel (center), and estimated burst onset time (bottom). (F) Left: Soma locations of 18 neurons active within the same syllable, projected onto the horizontal plane. Right: Estimated burst onset times of the same neurons within the syllable. (G, H) Relative soma locations of sequentially active neurons in (F) (i.e., burst onset times within 20 ms of each other). Each dot is the relative soma location of a postsynaptic neuron and all presynaptic neurons are aligned at the origin. (G) Relative soma locations of putatively connected neurons in 9 birds (H). (I) Radial distribution of neurons in (H) (dashed line) and radial distribution of active synapses predicted by the four simulated distributions in A–D (solid lines). (J) Correlation between the radial distribution of sequentially active neurons (H) and simulated locations of active synapses for delay distributions covering the entire delay parameter space of network models (see Fig. 3G). The region between the black lines contains delay distributions that are significantly correlated with the measured distribution of sequentially active neurons (r ≥ 0.603, two-sided t-test: d.o.f. = 9, t ≥ 2.268, p ≤ 0.05). Black cross: estimated delays of HVC_(RA) neurons (see Fig. 5F). Delay distributions to the right and above of the white line result in smooth sequences, as observed in HVC_(RA) neuron population activity. See also Figure S6.

To examine these song-related spatial patterns, we performed 2-photon imaging of GCaMP6-expressing projection neurons during singing. We combined new observations with a previously published data set (Katlowitz et al., 2018; Picardo et al., 2016), totaling 182 putative HVC_(RA) neurons (Figure 6E, see Methods). Using established techniques (Picardo et al., 2016; Pnevmatikakis et al., 2016), we precisely estimated burst onset times with a temporal resolution of ~10 ms and related these values to the spatial position for each neuron (Figure 6F). We then determined the relative locations and burst time differences of all neuron pairs (n = 5,842 pairs). We excluded all cases with a difference in burst times greater than 20 ms (n = 5,582 pairs, 95.5%) and therefore unlikely to be driven by monosynaptic connections. In the remaining 260 cases, sequentially active neuron pairs were found over a wide range of relative locations (178 ± 102 μm, mean ± SD), from immediately adjacent (~10 μm) to much longer distances (~500 μm, or approximately one third of the maximum extent of HVC) (Figure 6G and 6H). These functional data were most similar to the simulation based on our estimates of local HVC conduction values (Figure 6I). We extended our analysis to consider a wider range of delay distributions and found a family of solutions whose predicted spatial patterns correlated significantly (r > 0.6, p < 0.05, two-sided t-test) with our imaging data (Figure 6J). Importantly, these independently observed solutions overlapped both with the estimated axonal delays (Figure 5F) and the range of models in which HVC forms smooth sequences (Figure 3G), consistent with asynchronous functional connectivity between HVC_(RA) neurons based on local axonal delays.

Delay distributions are conserved from songbird to mammalian neocortex

We have demonstrated the impact of local axonal delays on the timing and structure of network activity within HVC of the zebra finch. Given the extraordinarily slow axonal conduction velocity in HVC compared with known values measured in a variety of different circuits (Figure 7A), it remains unclear whether such delays will play a role within those networks or whether this solution is simply a specialization within zebra finch HVC. We began to examine this issue by analyzing the local collaterals of 14 spiny neurons in Layer 4 of rat somatosensory cortex (Figure 7B) (Narayanan et al., 2015). When we measured the pathlength from the soma to different locations along the axon, we found that the entire size of the axonal field was considerably larger than that of HVC_(RA) neurons (Figure 7C). Surprisingly, when we estimated conduction delays – accounting for both the discrepancies in conduction velocity and pathlength – we find that the range of these values is identical in both cell classes (L4: 3.4 ± 2.3 ms, HVC_(RA): 3.3 ± 2.1 ms, Figure 7D). Therefore, conduction delays could potentially play an important computational role within a broad range of neural circuits.

Figure 7. Conduction delays of neocortical axonal arbors.

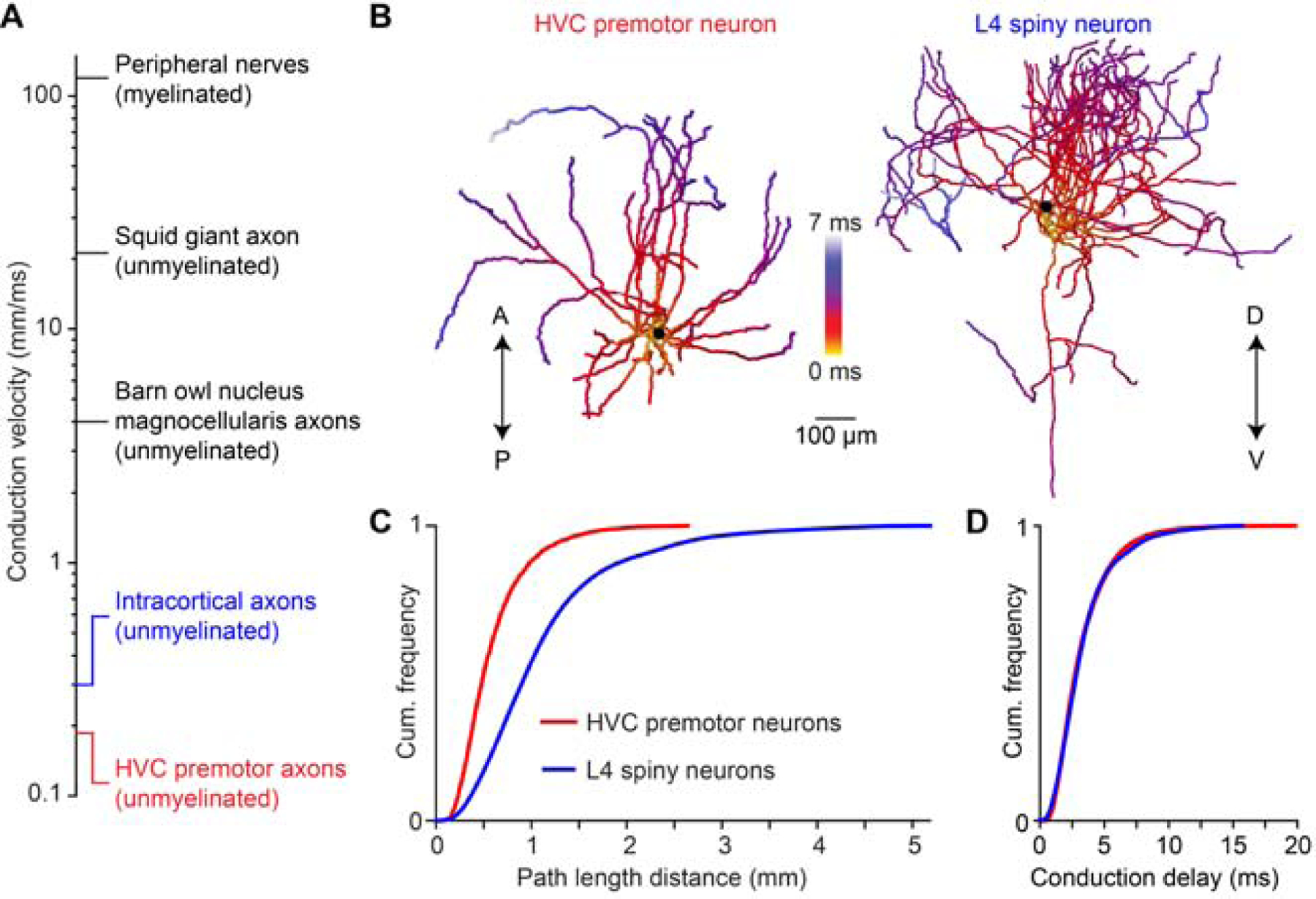
(A) Axonal conduction velocity measurements from the peripheral to the central nervous system. Peripheral nerves: (Hursh, 1939); squid giant axon: (Hodgkin and Huxley, 1952); nucleus magnocellularis axons: (Carr and Konishi, 1990); intracortical axons: (Hirsch and Gilbert, 1991; Shu et al., 2007). (B) Example reconstructions of an HVC premotor neuron axon and a L4 spiny neuron axon from rat somatosensory cortex. A/P: anterior/posterior; D/V: dorsal/ventral. (C, D) Distributions of axonal pathlengths (C) and resulting conduction delays (D) for 22 HVC premotor neuron axons and 14 L4 spiny neuron axons (Narayanan et al., 2015).

DISCUSSION

Using a combination of modeling and experimental approaches, we investigated how local excitatory circuits can give rise to convergent synaptic input underlying sequential activity in the zebra finch song system. We used silicon probes to enable single-trial electrophysiological measurements of song-related sequences within HVC, observations that support a central role for slow and heterogeneous delays in HVC network dynamics. We further demonstrate that these delays are likely due to conduction properties of HVC axon collaterals, and we show that this circuit feature may influence the spatiotemporal patterns of HVC activity observed during singing. Taken together, we have shown that axonal conduction velocity can lead to a continuous distribution of premotor bursts, which facilitates the placement of descending motor commands at any time point during the song. Furthermore, we estimate that conduction delays are significantly larger than those afforded by other biophysical parameters. Approximately half of the total elapsed time of the HVC sequence could be attributed to local axonal conduction, a comparatively inflexible process that may underlie the behavioral stereotypy inherent in the adult zebra finch song (Lombardino and Nottebohm, 2000) by rendering the circuit less sensitive to perturbations (Hamaguchi et al., 2016; Swadlow et al., 1981).

Previous models of premotor sequence generation have suggested that HVC feedforward networks (Galvis et al., 2017; Long et al., 2010; Pehlevan et al., 2018) could be based on a synfire chain architecture (Abeles, 1991; Amari, 1972; Diesmann et al., 1999). In our study, we find that the synchronous model – which is functionally equivalent to the synfire chain configuration – makes predictions about network timing that are inconsistent with our observations. Sufficiently heterogeneous delays change the regime of these feedforward networks to smoothly evolving dynamics. The asynchronous HVC model, strongly supported by our data, has fundamental similarities with previously described ‘polychronous’ networks, which are capable of generating almost arbitrary neural sequences in the presence of a suitable range of delays (Izhikevich, 2006). A salient feature of polychronous networks is the potential to self-organize such connectivity patterns through spike timing-dependent plasticity mechanisms (Gerstner et al., 1996; Izhikevich, 2006), and future work will determine the relevance of axonal delays for assembly of HVC circuits during song learning (Fiete et al., 2010; Jun and Jin, 2007; Okubo et al., 2015).

A potential limitation of our model is its exclusive focus on local excitatory connectivity within HVC (Kornfeld et al., 2017; Long et al., 2010). The role of other circuit elements, such as local inhibitory interneurons, in controlling song-related HVC_(RA) neuron activity also remains to be explored (Gibb et al., 2009; Jin et al., 2007; Kosche et al., 2015; Markowitz et al., 2015; Yildiz and Kiebel, 2011). Furthermore, in addition to local synapses within HVC, premotor neurons also receive excitatory connections from other brain regions (Akutagawa and Konishi, 2010; Nottebohm et al., 1982), and future studies will elucidate how these external inputs contribute to song-related activity in HVC. For example, inputs from the thalamic nucleus Uvaeformis may be instrumental in initiating (Andalman et al., 2011; Danish et al., 2017; Galvis et al., 2018) or maintaining (Hamaguchi et al., 2016) HVC sequential activity.

The idea that axons contribute to information processing in neural circuits has long been explored for long-range connections between different brain areas (Carr and Konishi, 1988; Innocenti et al., 1994; Salami et al., 2003; Sugihara et al., 1993). For instance, in the brainstem of the barn owl, axons carrying sound information from both ears form precisely tuned and spatially organized ‘delay lines’ (Jeffress, 1948) necessary for detecting minute interaural time differences (Carr and Konishi, 1988). In contrast, the role of axonal delays within local microcircuits is often disregarded (Budd et al., 2010), possibly because of the technical challenges involved in obtaining reliable estimates of conduction velocity in local circuits or because of a tenuous relationship between brain activity and behavior. In this study, we find that spatiotemporal patterns within HVC appear to be strongly influence by ‘local delay lines’. We do not yet know whether this specialization is unique to circuits in which a high degree of temporal precision is required or whether it can be more broadly found in other networks, including those capable of more flexibility (Cohen et al., 2020; Fujimoto et al., 2011). Although we find that conduction delays along intracortical axons in a rodent neocortical area are likely to be comparable to those reported here in zebra finch HVC, the extent to which these collaterals may support persistent activity (Sachidhanandam et al., 2013) or some other aspect of processing (Wilson et al., 2011) within this region so far remains unexplored. Further work in other circuits can establish whether this delay distribution represents a universal scaling law (Buzsaki and Mizuseki, 2014; Liewald et al., 2014; Miller, 1996) across different species, brain regions, cell types, etc., or whether these local delays are specially tuned for the requirements of each unique case. Overall, our results suggest that in addition to defining the static architecture of neural networks (Denk et al., 2012; Plaza et al., 2014; Seung, 2012), functional properties of axons within local circuits can also strongly influence neural activity patterns.

STAR METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Michael Long (mlong@med.nyu.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The data sets generated during this study are available upon request from the Lead Contact. Source code and documentation required for setting up and running simulations of the network models can be downloaded from: https://psu.box.com/s/55gh5tjgpvcxikel4wjfkzxdwyc0s7x4.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

We used adult (>90 days posthatch) male zebra finches (Taeniopygia guttata) that were obtained from an outside breeder and maintained in a temperature- and humidity-controlled environment with a 12/12 hr light/dark schedule. All animal maintenance and experimental procedures were performed according to the guidelines established by the Institutional Animal Care and Use Committee at the New York University Langone Medical Center.

METHOD DETAILS

Surgeries

Surgical procedures for retrograde labeling of HVC_(RA) neurons, viral injections, chronic cranial window implantation for 2-photon imaging, intracellular microelectrode recordings, and in vivo whole-cell recordings have previously been described in detail (Kornfeld et al., 2017; Long et al., 2010; Picardo et al., 2016). For extracellular recordings, high-density silicon probes (128 channels; Diagnostic Biochips) were mounted to a microdrive (NeuroNexus), and a stainless steel ground wire (0.001”, California Fine Wires) was soldered to the reference of the headstage, which was held in place by a custom 3D printed enclosure (Formlabs). A craniotomy (~ 1 mm length x 100 μm width) was made over HVC (2.3 mm lateral / 0.25 mm anterior of the bifurcation of the sagittal sinus). Silicon probes were implanted at a depth of ~500–800 μm in HVC. Silicon elastomer (Kwik Cast, WPI) was applied to the craniotomy and dental acrylic was used to secure the microdrive and the enclosure for the headstage in place. For antidromic activation of HVC_(RA) neurons, a bipolar stimulation electrode was implanted into RA.

Silicon probe recordings of HVC activity during song

Neural activity of freely moving birds was recorded using an electrically assisted commutator (Doric Lenses) and the RHD USB Interface Board or RHD Recording Controller (Intan Technologies). Vocalizations were recorded using an omnidirectional microphone (Audio-Technica) and a preamplifier (Presonus). Antidromic stimulation was applied using biphasic current pulses of 20 μs duration and amplitudes between 20–500 μA. To help characterize cell types (Figure S1), we also reanalyzed a previously reported data set of identified HVC neurons (Lynch et al., 2016; Okubo et al., 2015).

Identification of HVC projection neurons in silicon probe recordings

Spike detection and clustering was performed using KiloSort software (Pachitariu et al., 2016) and manual post-processing (merging/splitting of clusters) was performed using phy (Rossant et al., 2016). Spike times of all clusters were aligned to onsets and offsets of song motifs. Reliable burst events across motifs that are characteristic of HVC projection neuron activity (Hahnloser et al., 2002; Kozhevnikov and Fee, 2007) were readily apparent. Clusters lacking these events were not considered any further. The remaining clusters often exhibited more than one burst event and non-zero spontaneous spiking activity (defined as spiking in 5-minute windows before and after each song bout). To determine whether multiple bursts and/or spontaneous activity (if present) in one cluster were likely to originate from the same or multiple, erroneously combined units, we compared the waveforms and amplitude distribution of spontaneous spikes to those of the first spike from each bursting event across multiple channels. Specifically, we only considered bursts and/or spontaneous activity to originate from different units if they differed in both waveform and amplitude distribution. Here, amplitude similarity between the first spikes in bursts and/or spontaneous activity was measured by determining the amplitude (i.e., difference between maximum and minimum of the spike waveform) on each electrode, normalizing these values to the maximum amplitude across channels and computing the mean amplitude distribution for all first spikes in a burst/spontaneous spikes. We then determined the 8 electrodes with the largest mean amplitudes and computed the inner product of the normalized amplitude distribution on these electrodes for all pairwise combinations of first spikes of the same burst event/spontaneous spikes (i.e., generating a null distribution for each burst event/spontaneous activity). We next repeated the calculation of this inner product between all pairwise combinations of first spikes of different burst events/spontaneous spikes and determined whether these distributions were different from the null distributions. After identifying bursting units in this way, we computed their spontaneous activity. Single-bursting units were classified as HVC_(RA) neurons if their spontaneous activity was less than the lowest spontaneous firing rates of HVC_(X) neurons (antidromically identified previously (Lynch et al., 2016; Okubo et al., 2015) (Figures S1B and S1C).

Alignment of neural sequences

First, we determined a reference song motif to which neural sequences in all other motifs were aligned. We chose the motif with a duration closest to the mean motif duration (motif m). For alignment of sequences in individual syllables, we first determined during which (if any) syllable individual bursts occurred. Sequences in individual syllables were aligned independently of sequences in other syllables in the following way: For each motif n, we created a vector t_n of all burst onset times throughout the motif. We then fitted an affine transformation $t_n^{\text{'}}=a_{nm}{t}_n+b_{nm}$ minimizing the squared difference between aligned burst times in trial n and the reference trial $m{\left(t_n^{\text{'}}-t_m\right)}^T\left(t_n^{\text{'}}-t_m\right)$. Burst timing jitter was defined as the root mean squared error of aligned burst times across motifs. Sequences of HVC_(RA) and HVC_(X) bursts were aligned separately. We only performed this alignment for syllables which contained at least three bursts.

Histological procedures

For serial block-face electron microscopic (SBEM) imaging, perfusion and histology was performed as described in detail previously (Kornfeld et al., 2017). For transmission electron-microscopic imaging, the protocol used for SBEM imaging was slightly modified as follows. After the bird was transcardially perfused, the brain was removed from the skull and post-fixed overnight (Kornfeld et al., 2017). The brain was then cut into 100 μm thick slices using a vibratome (Leica VT1000S). Residual peroxidase activity was suppressed by soaking the sample in 3% H₂O₂ for 20 min before labeling the sample with an avidin-peroxidase complex and DAB. A slice containing clearly visible stained fibers from HVC to RA was unmounted by immersing the microscope slide into PB. After washing with PB, the samples were post fixed in 1% OsO₄ for 2 hours, block stained with 1% uranyl acetate for 1 hour, dehydrated in ethanol and embedded in EMbed 812 (Electron Microscopy Sciences, Hatfield, PA). Semi-thin sections were cut at 1 μm and stained with 1% toluidine blue to find the previously identified area of interest containing fibers from HVC to RA. In each sample, 20 serial ultrathin sections with 100 nm thickness were cut, mounted on slot copper grids, and stained with uranyl acetate and lead citrate.

Transmission-electron microscope imaging

Stained grids were examined under a Philips CM-12 electron microscope (FEI; Eindhoven, The Netherlands) and photographed with a Gatan (4k x 2.7k) digital camera (Gatan, Inc., Pleasanton, CA). Samples were imaged at a series of increasing magnifications (i.e., ranging from 3,400x to 66,000x magnification) to allow identification of fiber tracts and ultimately individual fibers within these tracts. Diameter measurements of unmyelinated projection axons were made on images with a magnification of at least 40,000x.

Axon diameter measurements

All light micrographs used for illustration of local and descending axons were captured using a Zeiss AxioObserver Inverted. We acquired images of descending HVC_(RA) neuron axons from ultrathin sections using a transmission electron microscope (see above). Unmyelinated descending axons were identified based on dark DAB labeling in EM micrographs. Myelinated axons were identified morphologically by presence of multiple, closely wrapped membrane layers (i.e., myelin sheaths; Figures S5B and S5C). Diameters were measured along the shortest axis of the circumference of each axon (i.e., axons are roughly cylindrical, and this corresponds to the diameter of the cylinder irrespective of sectioning angle) (Figure S5D). Diameters of local HVC_(RA) neuron collaterals were measured using a previously reported data set acquired using serial block-face EM (Kornfeld et al., 2017) with a voxel size of 11 × 11 × 29 nm³ containing HVC_(RA) neurons labeled by injection of a tracer (BDA-dextran) into RA. Diameters of randomly selected locations along labeled local axon collaterals were measured by determining the image plane that was closest to the orthogonal plane defined by the axon and measuring the axon diameter in that plane.

Estimating axonal conduction delays

Conduction delays along local HVC_(RA) neuron axons were obtained by measuring the pathlength from the soma to points along the axon spaced at the mean inter-bouton interval of HVC_(RA) neuron axons (10.5 μm) (Kornfeld et al., 2017). Combining these measurements from 22 reconstructions of premotor neuron axons reported previously (Benezra et al., 2018) resulted in an average distribution of pathlengths. We then converted these pathlengths into a conduction delay distribution by multiplying each pathlength distance with the conduction velocity of long-range axons. A log-normal distribution described the shape of the conduction delay distribution well (least-squares fit R² = 0.9988). We therefore used mean and standard deviation of a log-normal distribution to parameterize the conduction delays for the network models (Figures 1E and F, Figure 3).

Conduction delays along L4 spiny neuron axons were estimated in the same way. We measured the distribution of pathlength distances of 14 complete reconstructions of the intracortical axonal arbor of L4 neurons labeled in vivo (Narayanan et al., 2015) and multiplied pathlengths by a conduction velocity of 0.3 mm/ms (Hirsch and Gilbert, 1991; Shu et al., 2007) to obtain the conduction delay distribution.

The conduction time along long-range axons from HVC to RA was measured from whole-cell membrane potential recordings of HVC_(RA) neurons as the difference between the onset time of antidromic stimulation in RA and action potential onset. The action potential onset was defined by calculating the second derivative of the membrane potential between 0–20 ms after stimulation and determining the first upward threshold crossing, where the threshold was set as the minimum of either 3 standard deviations of the second derivative or 400 mV/ms². To determine the threshold between groups of conduction delays, we used k-means clustering with two groups. The pathlength of the long-range axon of HVC_(RA) neurons was measured from the soma to the first bifurcation of the axon as it entered RA. The average conduction velocity of unmyelinated descending axons was calculated by dividing the average descending pathlength by the average conduction time of the second mode of the conduction time distribution (Figure S5A). We then used a simple biophysical model relating the diameter of unmyelinated axons to conduction velocity (Hodgkin and Huxley, 1952; Rushton, 1951):

$$u=c\sqrt{d}$$

Here, u is the conduction velocity, d the axon diameter, and c a constant. We determined c using the average conduction velocity and average diameter of putative unmyelinated descending axons and assumed that this constant is the same for unmyelinated local axons of HVC_(RA) neurons (i.e., that the basic biophysical properties underlying action potential propagation are the same). We then calculated a distribution of conduction velocities given the observed distribution of diameters of local axonal projections. To estimate the distribution of conduction times to synapses onto other HVC_(RA) neurons, we used a Monte Carlo simulation approach. We stepped through all possible synapse locations along the set of reconstructed axon morphologies of HVC_(RA) neurons. For each possible location, we calculated the distribution of conduction times to that location given the pathlength to the soma and the estimated distribution of local conduction velocities. We then randomly selected one of the possible conduction times and assigned it as a synapse onto other HVC_(RA) neurons based on EM measurements of premotor synapse density for each location relative to the soma (Kornfeld et al., 2017). We ran 100 Monte Carlo simulations to obtain a robust estimate of the resulting conduction time distribution to other HVC_(RA) neurons.

Simulating synapse locations along axons

Synapse locations along HVC_(RA) neuron axons for a given delay mean and SD were simulated as follows. Points along the reconstructed axon were grouped according to their pathlength distance to the soma into 50 μm bins. If successive points in the reconstruction had an interval of more than 1 μm, additional points were inserted at 0.5 μm intervals using linear interpolation (i.e., leaving the pathlength unchanged). Next, the log-normal delay distribution with given mean and SD was converted to a pathlength distribution by multiplication with the axonal conduction velocity of local HVC_(RA) neuron axons (i.e., 0.187 mm/ms). For each neuron, we generated N_Syn * L_Neuron / L_Avg samples from this log-normal distribution. Here, N_Syn = 170 is the average number of synapses made by each HVC_(RA) neuron onto other premotor neurons (Kornfeld et al., 2017), L_Neuron is the total axonal pathlength of this specific premotor neuron and L_Avg is the average axonal pathlength across all 22 premotor neurons (Benezra et al., 2018). Samples beyond the maximum pathlength distance of an axon to the soma were repeated. A histogram of these pathlength samples with a bin width of 50 μm was computed. For each 50 μm bin, points along the reconstruction in the corresponding pathlength bin were randomly sampled until the number of elements in this bin of the histogram was reached and a synapse was placed at the location of the sampled points along the reconstruction. For comparison with calcium imaging data, simulated synapse locations were aligned by centering each reconstruction at the soma location, projecting onto the horizontal plane, and measuring their distance to the origin (Figure 6I).

Sensitivity analysis of detection of localized activity patterns

Our ability to detect spatially localized patterns of sequentially active neurons (Figures 6A–C) can be compromised by the presence of unconnected neurons that are active at a similar time by chance. To obtain an estimate of the fraction of active neurons that have to be connected in order to detect spatially localized patterns, we simulated the expected spatial distribution of a combination of connected and unconnected neurons. For each localized pattern of connected neurons (Figures S6A–C, top), we computed the spatial distribution of sequentially active neurons as described above. We refer to this distribution as ‘100% connected’ (Figures S6A–C, bottom). Next, we determined the possible locations of unconnected neurons by analyzing all pairs of sequentially active neurons that have a burst time difference of more than 20 ms (we refer to this distribution as ‘unconnected’). We then simulated the spatial distribution expected in the presence of X% connected and (100 – X)% unconnected neurons by sampling from these ‘100% connected’ and ‘unconnected’ distributions in the respective proportions and generating a combined distribution (Figures S6A–C, bottom). We used a two-sided two-sample KS-test to test whether this combined distribution was significantly different from the observed distribution (p-values in Figures S6A–C, bottom).

Estimating postsynaptic integration times

We reexamined two previously reported data sets (Long et al., 2010; Vallentin and Long, 2015) of intracellular recordings of HVC_(RA) neurons during singing. For each neuron, we aligned burst onsets in different song motifs (defined as the peak of the 2^nd derivative of the membrane potential) and calculated the mean membrane potential (Figure 4). We then fitted an exponential function a * exp(b * t) + c to the membrane potential in the time windows [−10, −5] ms and [−2, − 0.1] ms before burst onset (Figures 4B and 4C) and defined the rise time as τ_Rise = 1 / b. To determine the rise time in model HVC_(RA) neurons, we simulated 50 trials in each network model, recorded the membrane potential at the soma in 1,000 randomly selected model neurons and determined burst onset times, average membrane potential and rise time for each neuron as described for intracellular recordings.

Frequency analysis of burst onset times

For each bird in the electrophysiology data set, we determined all syllable lengths and number of bursts occurring during each syllable. In our modeling effort (see Figures 3A and 3B), we simulated possible burst times by sampling random numbers distributed in time according to the burst density of the model, while preserving the distribution of syllable lengths from the experimental data sets and the number of bursts observed during each syllable. For each syllable, we then defined the power spectral density P_s of the burst times as the absolute magnitude squared of the discrete Fourier transform evaluated at frequencies f between 1 and 200 Hz, in increments of 2 Hz:

$$P_s\left(f\right)={\left|\sum _{j=1}^n\exp \left(2\pi if{t}_j\right)\right|}^2$$

Here, n is the number of bursts in the syllable, and t_j the burst onset time of the j^th burst. We then calculated the mean power spectrum across all syllables. In order to obtain a reliable estimate of the predicted power spectrum of each model and its uncertainty, we repeated this procedure 10,000 times. We determined the mean power (P_mean) in a window (± 4 Hz) around the peak in the power spectrum between 75–200 Hz for each bootstrap simulation and P_mean of the observed burst times. We calculated the percentile of the observed P_mean relative to the distribution of simulated P_mean values and defined this as the p-value of the model power spectrum. We visually inspected all power spectra to ensure that the frequency corresponding to the intervals in synchronous network models – and not sub- or higher harmonics – was selected.

Neuron and synapse models

HVC_(RA) neurons were modeled as a two-compartment model with a dendritic and somatic compartment (Long et al., 2010). Current injection at the soma triggers sodium channel-dependent action potentials, while current injection (and synaptic input) to the dendrite compartment triggers an all-or-none calcium spike, which in turn triggers a high-frequency burst of four action potentials at the soma. Ion channels were modeled using the Hodgkin-Huxley formalism. All model parameters are identical to our previous work (Long et al., 2010), except for the following adjustments made to match the rise time prior to burst onset with intracellular recordings during singing: R_c = 130 MΩ, G_s,L = 0.05 mS/cm², τ_c = 15 ms. Conductance-based excitatory synapses were modeled according to ‘kick-and-decay’ dynamics. Upon synaptic release, the synaptic conductance was increased by G_syn, followed by an exponential decay with time constant τ_syn = 5 ms. The weight G_syn of individual synapses was drawn from a uniform distribution [0, G_max], with G_max set to 0.05 mS/cm², a value that leads to a unitary EPSP of ~4 mV at the soma (i.e., the average EPSP amplitude is 2 mV) (Mooney and Prather, 2005).

Network assembly

The feedforward HVC network model was assembled in an iterative process. The algorithm was designed to enforce synchrony of the synaptic inputs to the postsynaptic neurons. The timing of presynaptic bursts must be such that the spikes arrive at the postsynaptic neuron within a narrow time window (discussed below), considering the different burst transmission delays (Figure 3). The number of connections that each neuron can receive was limited to 170, based on previous ultrastructural observations (Kornfeld et al., 2017).

Each iteration consisted of three steps (Figure S2A): (i) simulation of network dynamics to determine the burst onset times of all neurons in the network at the current iteration; (ii) adding feedforward connections constrained by a given delay distribution between ‘source neurons’ (i.e., presynaptic neurons) and ‘target neurons’ (i.e., potential postsynaptic targets which do not form outgoing connections in the current iteration); (iii) adding additional neurons into the network. As a result, the feedforward network grows and the corresponding population sequence in duration during this iterative process (Figure S2B). In step (i) of each iteration, network dynamics were simulated by activating a set of 200 predefined ‘starter neurons’ and recording burst onset times of all active neurons in the network. In step (ii), new feedforward synaptic connections between ‘source’ and ‘target neurons’ were added. First, N _new neurons were moved from the set of ‘target neurons’ in the previous iteration to the set of ‘source neurons’. Specifically, these were the ‘target neurons’ whose simulated burst onset times were within a 2 ms window from the earliest simulated burst onset time of all ‘target neurons’ (Figure S2C). We then generated a ‘synaptic pool’ (i.e., a set of delays δ) of size N_out * N_new (N_out = 170) by sampling from the given distribution of delays. We iterated over all ‘target neurons’ ordered according to the number of synaptic inputs, starting with the smallest number. For each ‘target neuron’, we randomly selected a ‘source neuron’ that fulfilled the synchrony requirement | t_target – τ_int – δ – t _source | ≤ τ_sync using a suitable delay δ from the ‘synaptic pool’ (Figure S2C; i.e., requiring that all synaptic inputs to the ‘target neuron’ arrive within a synchronous time window 2*τ_sync (here: time window of 1 ms). t_source is the burst onset time of the ‘source neuron’, τ_int is the average integration time constant of HVC_(RA) neurons from onset of the synaptic inputs to burst threshold (~5 ms) (Long et al., 2010), and t_target is the burst onset time of the ‘target neuron’. If there were multiple δ allowing a connection between the ‘source neuron’ and the ‘target neuron’, the one minimizing the quantity | t_target – τ_int – δ – t _source | was selected (i.e., only one synapse was placed between a pair of ‘source’ and ‘target neurons’). After placement, this synaptic connection was removed from the ‘synaptic pool’. If the number of synaptic inputs to the ‘target neuron’ reached 170 or no connection from the ‘source neurons’ could be made given the delays in the ‘synaptic pool’, it was not considered as a ‘target neuron’ anymore. In step (iii), neurons were added to the network in order to increase the network from the set of starter neurons to its final size. This step was taken in case there were no more ‘target neurons’ before the ‘synaptic pool’ was exhausted. In this case, the set of ‘target neurons’ was restored to its state at the beginning of the iteration. A new ‘target neuron’ (i.e., without any existing incoming or outgoing synaptic connections) was added to the network by placing a synaptic connection with a randomly selected delay δ from the ‘synaptic pool’ originating from one of the N_new ‘source neurons’ added to the network in this iteration. The putative burst onset time of the new ‘target neuron’ was defined as: t _new = t_source + δ + τ_int. All other synaptic connections placed in this iteration were removed from the network; the associated delays were moved back into the ‘synaptic pool’; and steps (ii) and (iii) were repeated until the ‘synaptic pool’ was empty. Then, the next iteration was started, and this process repeated until all 20,000 HVC_(RA) neurons were incorporated into the network. To investigate the effect of the statistics of delays on sequence generation, we used different delay distributions during network assembly. The delay distributions in the completely assembled networks matched the target distributions (Figure S2D).

To generate network models using postsynaptic delays (Figure 4), we set all delays δ equal to zero and the synchronous time window during which inputs could arrive to individual neurons (2*τ_sync) to 8 ms. Integration times of postsynaptic neurons were controlled by varying the membrane capacitance of the dendritic compartment. Heterogeneity in the population was created by drawing the membrane capacitance for individual neurons from a log-normal distribution truncated below at 1 μF/cm². Parameters of the log-normal distribution were determined such that at a minimum standard deviation the mean membrane potential rise times matched intracellular recordings. Then the SD of the log-normal distribution was increased while keeping the other parameters fixed (Figure 4D).

To generate network models with different degrees of feedforward (FF) and recurrent synaptic connections, we used a network model with delays similar to those observed in HVC (Figure 5F). A fraction of synapses from each neuron was randomly selected to remain as FF synapses and the remaining synapses were connected to other randomly selected neurons in the network model.

Simulations

During simulations, HVC_(RA) neurons received additional independent white noise input currents to their somatic and dendritic compartments with zero mean and amplitudes A_soma = 0.1nA and A_dendrite = 0.2nA, leading to fluctuations of the somatic membrane potential with a standard deviation of 4.2 mV (Long et al., 2010). To account for the white noise currents, the HVC_(RA) neuron models were treated as a system of stochastic differential equations and solved using the AN3D1 weak 3^rd order method (Debrabant, 2010). The simulation time step was set to 0.01 ms.

Each simulation was started by activating the set of 200 ‘starter neurons’ using an excitatory conductance kick with amplitude 300 nS exponential decay with time constant 5 ms (i.e., simulating synchronous synaptic input). This input was delivered to the ‘starter neurons’ either synchronously, uniformly distributed over a 7 ms window, or randomly within a 10 ms window. In order to minimize transient effects of this activation procedure, the first 50 ms of simulated activity were discarded. Network activity patterns after this transient period were qualitatively similar between the different activation procedures. To generate burst densities, we ran 50 simulations, recorded the burst onset time of each neuron (i.e., the time where the membrane potential at the soma crosses 0 mV for the first time during a burst) and calculated the average number of bursts in 0.75 ms bins.

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical details of experiments can be found in figure legends and the Results section, including the statistical tests used, exact value of n and what n represents (e.g., number of animals, number of cells, etc.). Values are reported as mean ± SD unless mentioned otherwise, and values are plotted as mean with error bars representing SD unless mentioned otherwise. Significance was defined at a level of 0.05. Normal distribution of data was not assumed. No data were excluded from analysis. Statistical calculations were performed using MATLAB R2016a.

Supplementary Material

2. Figure S2 (related to Figure 1 and Figure 3). Network model of HVC_(RA) neurons.

(A) Algorithm for feedforward network assembly. (B) During each iteration, neurons are added to the network such that they are active at the end of the current network sequence. (C) Step (i): In each iteration, the sets of source and target neurons are updated according to simulated burst onset times in the current state of the network. Step (ii): Illustration of synapse placement based on synchronous activation of synapses at the postsynaptic neuron. Step (iii): Illustration of placement of synapses onto neurons newly added into the network. (C). Top: Observed delay distribution and log-normal fit. Center, bottom: Mean and SD of the delay distributions in assembled networks match the parameters of the input log-normal distributions. Dashed: identity line.

1. Figure S1 (related to Figure 1). Identification of projection neurons in high-density silicon probe recordings. Related to Figure 1.

(A) Top: Waveforms of an HVC_(RA) neuron in response to antidromic stimulation. Bottom: Distribution of antidromic spike latencies of the same neuron. (B) Distribution of spontaneous firing rates of 206 antidromically identified basal ganglia projecting [HVC_(X)] neurons recorded using single electrodes from previously published data sets. (C) Distribution of spontaneous firing rates of 211 single-bursting units from 5 birds recorded from our silicon probe data set. The dashed line separates putative HVC_(RA) (n = 89) and HVC_(X) neurons (n = 112). (D, E). Distribution of spontaneous firing rates of double (n = 65) and ≥3-bursting (n = 25) units. (F) Burst onset times of all putative HVC_(RA) single-bursting units. Colors correspond to Figure 1B.

3. Figure S3 (related to Figure 3). Power spectra of individual birds.

A comparison of the predicted power spectra in the synchronous model (in blue) and the power spectra from HVC projection neurons recorded from each bird (in black).

4. Figure S4 (related to Figure 3). Robustness of network model design.

(A) Top: Network model including feedforward (FF, arriving synchronously with other synaptic inputs at postsynaptic neurons) and recurrent (Rec., connecting independently and randomly to other neurons in the network) connections. Bottom: Jitter of burst onset times in network sequences with different fraction of FF synapses. Fraction of recurrent synapses: 100% - fraction of FF synapses. Our network model operates with low jitter in the presence of up to 65% recurrent connections, but networks with FF fraction of less than 35% could not sustain sequences. Shaded region represents jitter observed in HVC ensembles during singing (see Figure 2). (B) Left: Simulated membrane potential of an example neuron from the network with FF fraction of 35%. Recurrent excitatory connections can give rise to the repeatable subthreshold events observed during singing. (C) A uniform delay distribution (mean: 3.5 ms, SD: 1.75 ms) can give rise to smooth network sequences.

6. Figure S6 (related to Figure 6). Detecting localized patterns in the presence of background activity.

(A–C) Top: Simulated distributions of sequentially active postsynaptic neurons predicted by different delay distributions that result in synchronous sequences (see Figure 6A–C). Bottom: Comparison of the simulated distribution of sequentially active neurons in the presence of different amounts of connected neurons (see Methods) with the observed distribution (see Figure 6I).

5. Figure S5 (related to Figure 5). Axonal conduction delay and diameter measurements along myelinated and unmyelinated HVC_(RA) long-range axons.

(A) Conduction delay measurements along the HVC→RA projection axon for 40 neurons. Group membership was defined based on k-means clustering with two groups (group I: fast, putatively myelinated axons; group II: slow, putatively unmyelinated axons). (B) Identification of myelinated (orange) and unmyelinated (blue) axons in the HVC→RA fiber tract using transmission electron microscopy. (C) DAB stain enters the axons at nodes of Ranvier (blue), but not at myelinated parts of the axon (orange), leaving myelinated segments unlabeled. (D) Diameters of labeled axons in EM images.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
AAV9.Syn.GCaMP6s.WPRE.SV40	Chen et al. Nature 2013	Addgene #100843
AAV9.CamKII0.4.Cre.SV40	James M. Wilson	Addgene #105558
AAV9.CAG.Flex.GCaMP6f.WPRE.SV40	Chen et al. Nature 2013	Addgene #100835
AAV9.CAG.Flex.GCaMP6s.WPRE.SV40	Chen et al. Nature 2013	Addgene #100842
Chemicals, Peptides, and Recombinant Proteins
Biotinylated dextran (3,000 MW)	Invitrogen	D7135
Hydrogen peroxide solution (3%)	Sigma-Aldrich	CAS: 7722–84-1
DAB (3,3’-Diaminobenzidine)	Sigma-Aldrich	CAS: 91–95-2
Osmium tetroxide solution (2%)	Sigma-Aldrich	CAS: 20816–12-0
Uranyl Acetate	Electron Microscopy Sciences	RT 22400
EMbed-812	Electron Microscopy Sciences	RT 14120
Toluidine Blue	Electron Microscopy Sciences	RT 22050
Lead Citrate	Electron Microscopy Sciences	RT 22410
Critical Commercial Assays
Vectastain ABC Kit	Vector Laboratories	PK-4000
Experimental Models: Organisms/Strains
Zebra finch (Taeniopygia guttata)	Magnolia Bird Farm, Anaheim, CA	N/A
Software and Algorithms
ImageJ	NIH	https://imagej.nih.gov/ij
Matlab	MathWorks	https://www.mathworks.com/products/matlab.html
Markov Chain Monte Carlo deconvolution	Picardo et al., Neuron 2016	https://www.sciencedirect.com/science/article/pii/S0896627316001094?via%3Dihub
RPvdsEx	Tucker-Davis Technologies	http://www.tdt.com/rpvdsex.html
ScanImage	Vidrio Technologies	ScanImage 4.2 (2015)
KiloSort spike sorting software	Pachitariu et al., biorxiv 2016	https://github.com/cortex-lab/KiloSort
HVC network model	This paper	https://psu.box.com/s/55gh5tjgpvcxikel4wjfkzxdwyc0s7x4
Other
Intracellular recording amplifier	Molecular Devices	Axoclamp 700-B
Digital acquisition board	Molecular Devices	Digidata 1550
High-density silicon probe (with integrated headstage)	Diagnostic Biochips	128–5 integrated
Chronic microdrive	Neuronexus	dDrive-xL
Assisted Fiber-optic & Electric Rotary Joint	Doric Lenses	AHRJ-OE_FC_AD_12_HARW
Omnetics cable adapter	Doric Lenses	ADAPTER_HO12
Acquisition board	Intan Technologies	RHD Recording Controller (512 channels)
Stimulus generator	A-M Systems	Model 2100
Omnidirectional microphone	Audio-Technica	AT803
Audio amplifier	Presonus	Studio Channel
Digital signal processor	Tucker-Davis Technologies	RX8
Resonant scanner	Thorlabs	N/A
Movable Objective Microscope	Sutter Instrument Company	N/A
16x water immersion objective	Nikon	MRP-07220
Transmission electron microscope	FEI	Philips CM-12
Digital camera for electron microscopy (4k x 2.7k)	Gatan Inc.	N/A
Brightfield microscope	Zeiss	AxioObserver Inverted

HIGHLIGHTS.

• Simultaneous recording of sequentially active premotor neurons during singing

• Models suggest that network delays impact song-related population activity

• Ultraslow axonal conduction within HVC generates substantial network delays

• Local axonal delays shape spatial patterns of activity within a neural circuit