Abstract
A deep learning MR parameter mapping framework which combines accelerated radial data acquisition with a multi-scale residual network (MS-ResNet) for image reconstruction is proposed. The proposed supervised learning strategy uses input image patches from multi-contrast images with radial undersampling artifacts and target image patches from artifact-free multi-contrast images. Subspace filtering is used during pre-processing to denoise input patches. For each anatomy and relaxation parameter, an individual network is trained. in vivo T1 mapping results are obtained on brain and abdomen datasets and in vivo T2 mapping results are obtained on brain and knee datasets. Quantitative results for the T2 mapping of the knee show that MS-ResNet trained using either fully sampled or undersampled data outperforms conventional model-based compressed sensing methods. This is significant because obtaining fully sampled training data is not possible in many applications. in vivo brain and abdomen results for T1 mapping and in vivo brain results for T2 mapping demonstrate that MS-ResNet yields contrast-weighted images and parameter maps that are comparable to those achieved by model-based iterative methods while offering two orders of magnitude reduction in reconstruction times. The proposed approach enables recovery of high-quality contrast-weighted images and parameter maps from highly accelerated radial data acquisitions. The rapid image reconstructions enabled by the proposed approach makes it a good candidate for routine clinical use.
Keywords: Multi-contrast imaging, T1 mapping, T2 mapping, MR parameter mapping, deep learning, convolutional neural networks, image reconstruction
1. Introduction
Parameter mapping methods in MRI measure tissue specific parameters such as T1, T2, and proton density. These tissue parameters are useful for detection and characterization of a variety of pathologies such as Alzheimer disease [1], multiple sclerosis [2], and liver cirrhosis [3]. Conventional parameter mapping requires the acquisition of several images with different contrast weighting, which are subsequently used to estimate the parameter(s) of interest. However, the long data acquisition times required by these methods have limited their clinical use. With growing interest in quantitative MRI, many techniques have been proposed to accelerate data acquisition for MR parameter mapping [4–19]. These techniques combine accelerated data acquisition methods with constrained reconstruction techniques, which exploit the dependencies along both the spatial and contrast dimensions in multi-contrast images. While these techniques significantly reduce data acquisition times and yield high quality parameter maps, they are computationally intensive and require long reconstruction times due to their iterative nature.
Recently, deep learning (DL) based methods have emerged as state-of-the-art for many image processing and computer vision tasks such as image classification [20], semantic segmentation [21], and image super-resolution [22]. DL methods have been proposed for medical image reconstruction problems as well[23–32]: Wang et al. [23] explored a convolutional neural network (CNN) for accelerating MRI. Han et al. [24, 25] trained a U-Net on CT data and fine-tuned it using MR data for radial MR image reconstruction based on the similarity of the sampling patterns between radial MRI and parallel-beam CT imaging. Knoll and Hammernik et al. [26, 27] proposed a variational network that is embedded in an unrolled gradient descent method and demonstrated improved performance over conventional reconstruction models. Schlemper et al. [28] demonstrated that a deep cascade of convolutional neural networks outperforms compressed sensing approaches for MR cardiac cine reconstruction. More recently, Cai et al. [29] developed a deep neural network for T2 mapping using overlapping-echo detachment planar imaging. Liu et al. [30] demonstrated feasibility of direct reconstruction of T2 maps in the knee joint using deep convolutional neural networks. A common characteristic of these DL-based image reconstruction techniques is that they require reconstruction times that are up to several orders of magnitude faster than the constrained reconstruction methods, which makes them excellent candidates for clinical deployment. On the other hand, these techniques necessitate access to clean reference images for supervised learning. This is a challenging requirement for many accelerated MRI applications where such fully sampled data may be difficult to obtain, particularly in large quantities necessary for supervised training of the networks.
In this work, we present an MR parameter mapping framework that combines accelerated radial data acquisition with a deep neural network reconstruction for T1 and T2 mapping applications. The proposed approach offers several advantages: First, unlike many DL-based medical image reconstruction methods, the proposed technique uses images reconstructed from undersampled data using (slow but accurate) constrained reconstructions as reference during supervised training. This eliminates the need for fully sampled training data, which cannot be obtained in many applications. We demonstrate that the network supervised with undersampled constrained reconstructions generates contrast-weighted images and parameter maps that are comparable to those produced by the network supervised with fully sampled data. Second, although the proposed network is trained using constrained reconstructions, we demonstrate that the network yields superior parameter mapping performance than these constrained reconstructions. Third, the proposed multi-scale residual network (MS-ResNet) requires two orders of magnitude less computation time in comparison to constrained reconstruction methods. We also show that our lightweight network can be trained using a limited amount of undersampled data. The proposed work eliminates the need for fully-sampled reference images or the need for large amount of undersampled data and, thus, enables many MR parameter mapping applications, especially for anatomies where fully sampled data are difficult to acquire. The proposed approach is evaluated in several in vivo T1 and T2 mapping applications.
2. Methods
2.1. Multi-contrast image acquisition and reconstruction
In a parameter mapping experiment, multi-contrast multi-coil k-space data are acquired at N contrasts with Nk measurements at each contrast using Nc coils. These multi-contrast images are denoted by the matrix , where the nth row of matrix represents the contrast-weighted image , 1 ≤ n ≤ N consisting of Np spatial pixels. The relationship between the acquired k-space data k and the contrast-weighted images can be modeled discretely as
| (1) |
where represents the spatial encoding operator consisting of Fourier and coil sensitivity encoding [5, 8, 13], and n denotes the k-space noise vector. The first step in many MR parameter mapping experiments is to estimate the contrast-weighted images from the acquired k-space data k :
| (2) |
where represents the Hermitian adjoint operator of the combined Fourier and coil sensitivity encoding. The direct reconstruction generally suffers from undersampling artifacts when k-space data k is highly undersampled. One way to improve reconstruction quality in parameter mapping is to use a subspace constraint to leverage the contrast (temporal) correlation. This constraint restricts the relaxation signals to a low-dimensional subspace. Using this constraint, the multi-contrast images M can be approximated in the form
| (3) |
where represents the K -dimensional (K ≪ N) subspace basis that could be estimated either from training data [6, 9] or from a suitable signal model [5, 8, 13] and represents the subspace coefficients. This low-dimensional subspace projection improves the quality of direct reconstruction by explicitly confining the multi-contrast images to this low-dimensional subspace, i.e.
| (4) |
where denotes the subspace filtered estimate of the multi-contrast images and Csf denotes the corresponding subspace coefficients. Note the subspace filtering computation reduces to a pixel-wise matrix multiplication in the order of the number of contrasts and adds only a marginal computational load to the entire processing chain.
Although this subspace filtering approach reduces undersampling artifacts, severe undersampling artifacts often remain in the reconstructed images at high acceleration factors used in practical parameter mapping applications. Over the past decade, iterative reconstruction algorithms that combine spatial and contrast dimension constraints to improve the quality of the multi-contrast images and the resulting parameter maps have been proposed [4–15, 19, 34, 35]. One of these recent approaches, referred to as non-local rank 3D (NLR3D) [16, 17], exploits the self-similarity of multi-contrast images in both space and contrast dimensions to yield state-of-the-art reconstruction performance at the expense of high computational complexity.
2.2. Network training and testing framework
Our framework uses supervised learning where the deep neural network is trained using input and target data pairs to create artifact-free multi-contrast images given input images with undersampling artifacts. The proposed training procedure is illustrated in Figure 1(a). The first step in training is to estimate coil sensitivity maps from the radial k-space data using ESPIRiT [36]. These coil sensitivity maps were used for the reconstruction of input and target images. The input images at each contrast were reconstructed using Nonuniform Fast Fourier Transform (NUFFT) [37] followed by coil sensitivity weighted summation as represented in Eq. 2. The resulting images exhibited severe streaking artifacts due to undersampling. Next, subspace filtering described in Eq. 4 was applied to improve network training performance (see Supplementary Material Fig. 3) since it greatly reduces streaking and noise in the input images (see Supplementary Material Fig. 4) while only adding marginal computation time. Subspace bases used in subspace filtering were pre-estimated from training signals using singular value decomposition. For T2 experiments, multi-contrast signal curves were obtained using the slice resolved extended phase graph model over the range of T2 values of interest (20–300 ms) and the range of expected B1 values (0.5–1.4) as described in [38]. Similarly, Bloch simulations were used to generate training signal curves with T1 values ranging from 100 ms to 3000 ms and T2 values ranging from 10 ms to 300 ms for T1 experiments as described in [19]. We always retained 4 principal components across all the experiments [17–19, 39]. In summary, given the subspace basis FK (K = 4) and the undersampled k-space data k, the input image Mi to the network was obtained using (combining Eq. 2 and Eq. 4)
| (5) |
As discussed earlier, multi-contrast images reconstructed from fully sampled k-space data are difficult to obtain in parameter mapping applications. Therefore, the target image Mt was obtained via a subspace constrained compressed sensing method, as a surrogate, using the same undersampled k-space data and estimated coil sensitivity maps. As comparison, the network using fully sampled reference images as label was also evaluated. The input and target image pair Mi and Mt have complex values. Training networks with complex valued input and weights is non-trivial and an active area of research [40–44] and T1/T2 applications were found to be insensitive to image phase in our experiments. Thus, we have opted to take the magnitudes of the input and target images. To reduce training data requirements, patch-scale training was employed for data augmentation. For data normalization, we subtract the mean and divide by the standard deviation of all the training image magnitudes at each contrast (see Supplementary Material Fig. S5).
Figure 1:

Network reconstruction pipeline. (a) The proposed training strategy involves creation of input and target patches from training data. For input data, undersampled k-space data at each TE is processed using NUFFT followed by coil sensitivity weighted combine and subspace filtering using pre-estimated subspace basis. For target data, the radial k-space data is processed using a model-based CS reconstruction. Patches are extracted from the resulting magnitude images and used for supervised learning. In addition, estimated subspace basis and statistics of training data are used during pre-processing and post-processing. (b) For testing/deployment, undersampled k-space data at each contrast is processed using NUFFT and the coil images are combined using coil sensitivity weighted combination. Note that during the testing phase patch extraction is unnecessary since the convolutional kernels can be applied to images.
Figure 3:

Representative TE images and T2 maps of a test subject at (a) R = 12 and (b) R = 16. Reference images on the right were obtained using fully sampled k-space data. The fully sampled k-space data were retrospectively undersampled and reconstructed by the other methods for comparison. The bounding box on the reference image indicates the enlarged muscle region.
Figure 4:
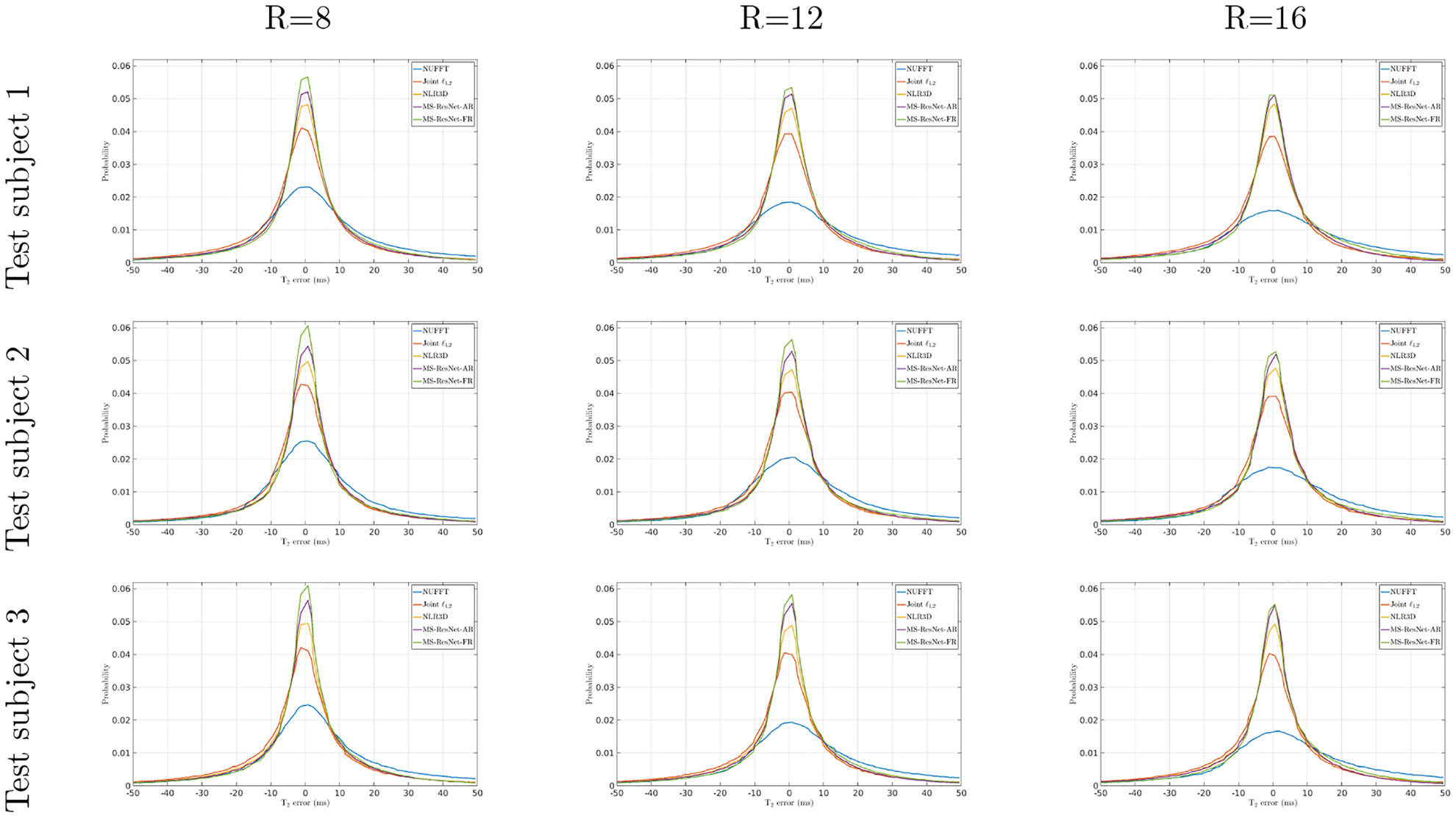
The T2 error histograms of NUFFT, Joint , NRL3D, and the proposed MS-ResNets (MS-ResNet-AR and MS-ResNet-FR) for the retrospectively undersampled (R=8, 12, and 16) knee data of test subject 1, 2, and 3.
The testing/deployment procedure is illustrated in Figure 1(b). Input images with undersampling artifacts were obtained in the same manner as was done during the training phase (Eq. 5). It should be noted that our MS-ResNet trained in patch scale could work in image scale during inference time since MS-ResNet does not contain fully connected layers that are restricted to have fixed input size. The convolutional or pooling layers that process inputs in a sliding window manner can cope with varying input sizes [45]. The output multi-contrast images were fitted in a pixel-by-pixel manner to the corresponding signal models [38, 46] to obtain the parameter maps.
2.3. Data acquisition
To validate the proposed DL-based parameter mapping approach, in vivo T1 and T2 mapping experiments were conducted on different anatomies. All data were acquired on a 3T MRI scanner (Skyra, Siemens Healthcare, Erlangen, Germany) in compliance with the human research subject guidelines and the institutional review board.
For T2 mapping of the knee, fully sampled data were acquired from 12 healthy subjects using a 2D radial turbo spin echo (RADTSE) pulse sequence [47] in the sagittal plane with sequence parameters: TR = 3000 ms, TE = 11 ms, echo train length (ETL) = 8, in plane resolution = 0.50 mm × 0.50 mm, slice thickness = 3 mm, 20 slices, and 512 lines/TE with 320 readout points/line.
For T2 mapping of the brain, undersampled data (R = 31.4) were acquired in the axial plane from 5 healthy subjects using a 2D RADTSE pulse sequence with sequence parameters: TR = 3800 ms, TE = 10.1 ms, echo train length (ETL) = 16, in plane resolution = 0.69 mm × 0.69 mm, slice thickness = 3 mm, 40 slices, and 16 lines/TE with 320 readout points/line. In these acquisitions, a 16-channel head coil and bit-reversed view ordering [47] were used. To evaluate the sensitivity of our proposed approach to variable undersampling patterns, a 6 th subject was scanned first with bit-reversed view ordering and then with “pseudo― golden angle view ordering [48] at the same undersampling rate. To evaluate the robustness of the proposed method to changes in coil sensitivity maps, a 7 th subject was imaged using the 16-channel head coil and a 32-channel head coil during two scan sessions.
For T1 mapping of the brain, undersampled data (R = 31.4) were acquired in the axial plane from 11 healthy subjects using a 2D IR-radSSFP pulse sequence [19] with sequence parameters: TR = 4.92 ms, TE = 2.4 ms, 32 inversion times (TI), in plane resolution = 0.69 mm × 0.69 mm, slice thickness = 3 mm, 40 slices, and 16 lines/TI with 320 readout points/line.
For T1 mapping of the abdomen, undersampled data (R = 37.7) were acquired in the axial plane from 8 healthy subjects using a 2D IR-radSSFP pulse sequence with sequence parameters TR = 4.40 ms, TE = 2.15 ms, 32 inversion time (TI), in plane resolution = 0.83 mm × 0.83 mm, slice thickness = 3 mm, 10 slices, and 16 lines/TI with 384 readout points/line. For this application, an additional dataset was acquired with the same sequence parameters on a subject with pathology for evaluating the generalization ability of MS-ResNet.
2.4. Network Implementation
The network was implemented in PyTorch [49] with CUDA backend and CUDNN support and trained on a NVIDIA GeForce GTX 1080 Ti graphics card. Depending on the training data size, the network training took about 35 hours on average. All model-based reconstructions were implemented in MATLAB and processed on an Intel Xeon CPU E5–2630 v4 @ 2.20GHz, with GPU support for NUFFT operations.
For each anatomy and relaxation parameter, an individual network was trained. In each experiment, one healthy subject was randomly selected for validation and at least 4 subjects (see Supplementary Material Fig. S6) were randomly selected for training. The remaining healthy subjects were used for testing. Patches of size 32 × 32 were randomly extracted on the fly during training. Patch pairs were further augmented 8 times by flipping and/or rotating. The networks were initialized randomly and trained with loss, using ADAM optimization [50] with standard parameters (β1 = 0.9, β2 = 0.999, and ε = 10−8). The learning rate was initialized to 10−4 and halved every 2 × 105 iterations. Each network was trained with a mini-batch size of 4 for 100 epochs. The model with lowest validation loss was selected for testing. During inference, a geometric self-ensemble strategy was used [51, 52]. The input images were flipped and/or rotated in the same manner as the training phase augmentation. The 8 transformed input images, including the original, were processed using the trained network followed by corresponding inverse transforms. The transformed outputs were averaged to obtain the self-ensemble result. T2 maps were calculated from the resulting TE images using the VARPRO [53] approach whereas T1 maps were calculated from the resulting TI images using the reduced dimension non-linear least squares approach [46].
2.5. Experimental setup
Reconstruction time of MS-ResNet was analyzed and compared to iterative CS methods. We used a popular MR image reconstruction package, Gadgetron [54]. The package provides a GPU implementation of the nonlinear conjugate gradient (NLCG) algorithm with Total Variation (TV) regularization for dynamic image reconstruction. Timing comparison were performed on a workstation with an NVIDIA GeForce GTX 1080 Ti GPU using CUDA 10.1 library. We used a default gridding kernel width of 5.5 and ran the NLCG algorithm for 100 iterations. Running time was obtained by averaging five runs of multi-slice reconstructions.
A quantitative analysis of the network performance was conducted using the in vivo T2 knee data. The reference images were obtained by applying NUFFT to fully sampled k-space at each echo time followed by coil sensitivity weighted summation. The fully sampled k-space data was retrospectively undersampled 8, 12, and 16 times to obtain the undersampled k-space data. At each acceleration, MS-ResNet was separately trained using the fully sampled references (FR) or using the NLR3D [16, 17] references reconstructed from the accelerated data (AR). We refer to these two networks as MS-ResNet-FR and MS-ResNet-AR, respectively. In addition, the proposed MS-ResNet approach was compared to NLR3D as well as another compressed sensing approach, Joint [9]. T2 maps were evaluated using Normalized Mean Square Error (NMSE), ROI analysis, and T2 error histogram. The NMSE metric was computed as the ratio of mean squared error to mean squared reference image. Muscle and cartilage ROIs of a knee slice were manually segmented using the first TE image and reference T2 map. The T2 error histogram of a subject is accumulated on the foreground pixels of all the sagittal slices. To quantify the error spread, Cauchy distributions were fitted to the long-tailed T2 error data to obtain the maximum likelihood estimate for the scale parameter γ of a Cauchy distribution. The full width at half maximum (FWHM) of the T2 error histogram is then computed as 2γ. In addition, area under the curve (AUC) of the T2 error histogram within [−5, 5] ms interval was computed per test subject. These two metrics (FWHM and AUC) were also calculated on a per slice basis for all slices in the test cohort and a statistical analysis was performed to compare them for MS-ResNet-FR and MS-ResNet-AR, as described in the Supplementary Material - Statistical Analysis.
The performance of our MS-ResNet was also evaluated for T2 and T1 mapping of the brain and T1 mapping of the abdomen qualitatively, where fully sampled data is not available. An ROI analysis was performed to compare MS-ResNet and NLR3D reconstructions on T2 /T1 brain and T1 abdomen datasets. The generalization ability to pathology of the proposed approach was evaluated using the network trained with data from healthy subjects only in T1 mapping of the abdomen. In T2 mapping of the brain, the sensitivity to variable sampling patterns was evaluated by testing the network using data acquired with a radial sampling trajectory different than the one used during training. Similarly, the robustness to changes in sensitivity maps was also evaluated by testing the network using data acquired with a different head coil than the one used to obtain the training data.
3. Results
3.1. Reconstruction time comparison
Table 1 presents the reconstruction time of the Gadgetron NLCG algorithm and MS-ResNet for four sets of data with various sizes. These k-space data differ in number of readouts, number of views per contrast, number of coils, and number of contrasts. From small size data, such as T2 knee, to large size data, such as T1 abdomen, the reconstruction time of NLCG increases considerably, whereas MS-ResNet runs roughly two orders of magnitude faster than NLCG despite the datasets. Note that the Gadgetron NLCG implementation only includes the TV constraint. Iterative methods with complex priors, e.g. NLR3D, have significantly higher computational requirements. In our MATLAB implementations of NLR3D and Joint , we observed that NLR3D is typically 6–10 times slower than Joint .
Table 1:
Reconstruction time analysis of MS-ResNet and Gadgetron nonlinear conjugate gradient (NLCG) algorithm. Non-uniform Fast Fourier transform (NUFFT) is the major computation for non-Cartesian k-space data reconstruction using NLCG. Oversampling ratio is a critical factor of NUFFT that can be used to trade accuracy for computational time reductions as shown in the table.
| Time (ms/slice) | |||||
|---|---|---|---|---|---|
| Data | Dimensionsa | Gadgetron NLCG | MS-ResNet | ||
| os = 1.2 | os = 2.0 | os = 1.2 | os = 2.0 | ||
| T2 knee | 320,512,15,8 | 6601.4 | 9212.5 | 82.3 | 95.3 |
| T2 brain | 320,256,16,16 | 9697.2 | 14438.3 | 102.2 | 125.7 |
| T1 brain | 320,512,16,32 | 18740.0 | 25914.0 | 158.8 | 194.3 |
| T1 abdomen | 384,512,20,32 | 29181.8 | 73756.3 | 265.7 | 486.4 |
From left to right, the values denote number of readout points, number of total radial lines, number of coils, and number of contrasts.
3.2. Evaluation of knee reconstruction
Figure 2 shows representative TE images (top) and T2 maps (bottom) reconstructed using different methods at R = 8. A muscle region illustrated by the rectangular box is enlarged for closer inspection. Conventional NUFFT generates images with streaking artifacts and noise amplification due to undersampling. Joint suppresses the artifacts and noise but blurs the reconstructions as a result of the local spatial sparsity constraint in this highly accelerated dataset. NLR3D yields a substantially improved reconstruction in comparison to the Joint approach, but the non-ideal patch matching at this high acceleration rate leads to an over-smoothed region within the muscle ROI. In contrast, the two MS-ResNets trained using either NLR3D or fully sampled reference images retain the fine structures and textures. However, the MS-ResNet trained using fully sampled reference images presents better image sharpness and better image contrast to noise. Figure 5 shows the reconstructed TE images (top) and T2 maps (bottom) at (a) R = 12 and (b) R = 16. At these higher acceleration rates, constrained methods cannot fully remove the streaking artifacts as indicated by the yellow arrows on the TE images. These remaining streaks result in artifacts in the T2 maps as indicated by the yellow arrows. In contrast, the proposed MS-ResNets can still suppress streaking artifacts and resolve many of the finer structures in the muscle region, whereas these structures are either corrupted by residual noise or overly smoothed by the constrained reconstruction methods as pointed to by the red arrows on the TE images and T2 maps. Figure 1 shows the T2 error histograms (from −50 ms to 50 ms) of different reconstruction methods for three healthy test subjects at varying acceleration rates. Observing the peak probability of these histograms, MS-ResNet-FR performed the best followed by MS-ResNet-AR, NLR3D, Joint , and NUFFT. Table 3 quantifies the reconstruction performances using AUC [−5,5] and FWHM. These two metrics show that MS-ResNet-AR performed slightly worse than MS-ResNet-FR at most acceleration rates, but was superior to (larger AUC [−5,5] and smaller FWHM) the CS approaches and the conventional NUFFT approach. It is interesting to note that the performance gap between MS-ResNet-AR and MS-ResNet-FR decreases as the acceleration factor increases. This is consistent with the statistical analysis (e.g. the p-values of the Kruskal-Wallis test) shown in Supplementary Material Table S2.
Figure 2:
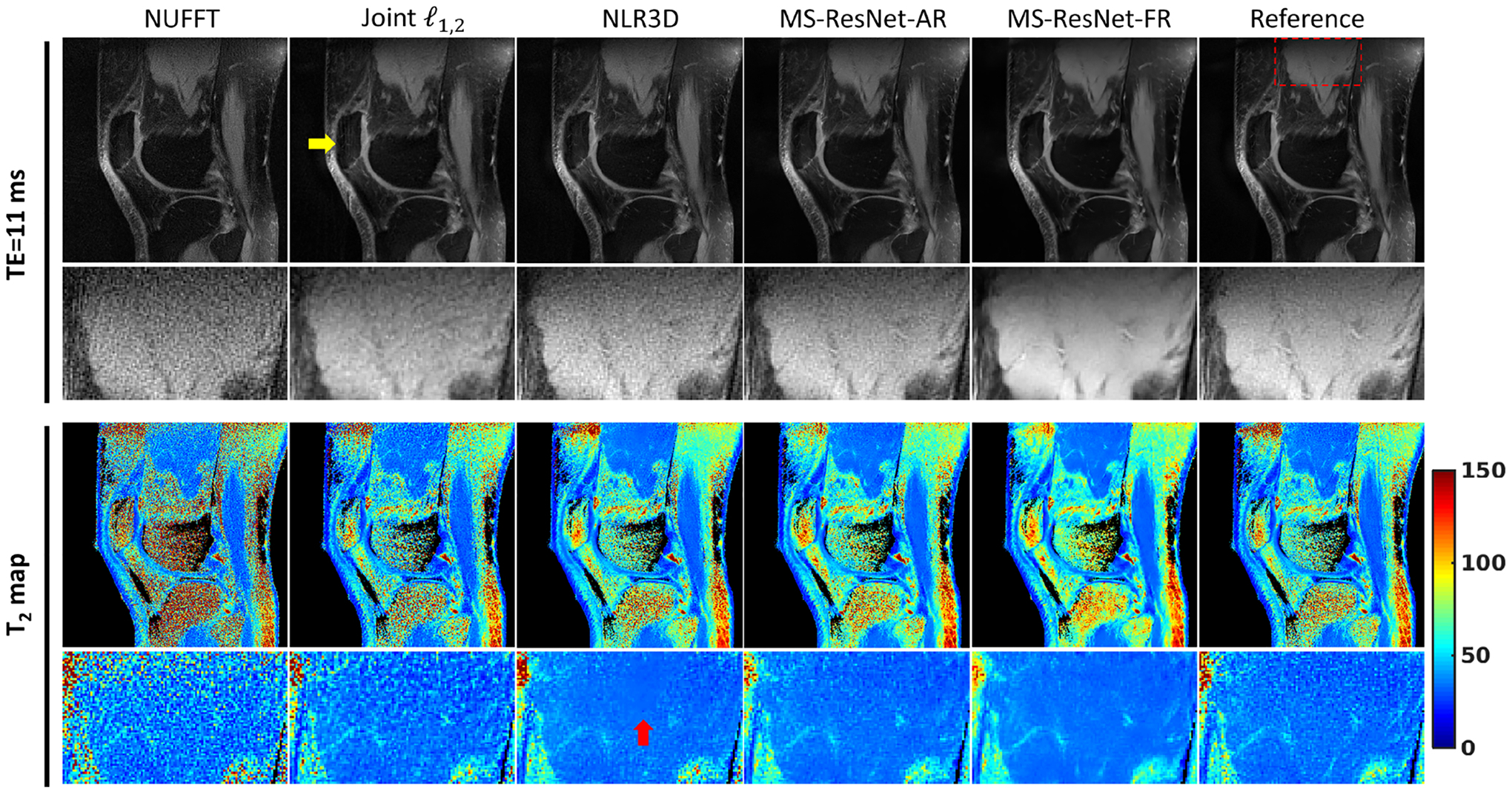
Representative TE images and T2 maps of a test subject. Reference images on the right were obtained using fully sampled k-space data. The fully sampled k-space data were retrospectively undersampled (R=8) and reconstructed by the other methods for comparison. The bounding box on the reference image indicates the enlarged muscle region.
Figure 5:

T2 mapping and (b) T1 mapping comparison on the brain data of a healthy subject. NUFFT, MS-ResNet, and NLR3D constitute the input, output, and target images, respectively, of the proposed network. Early-contrast images, late-contrast images, and parameter maps reconstructed by the three methods are presented.
Table 3:
ROI mean and standard deviation of parameter values of NLR3D and MS-ResNet methods for three parameter mapping applications are compared.
| Data | ROI | NLR3D (ms) | MS-ResNet (ms) | Parameter Map |
|---|---|---|---|---|
| T2 brain | 1 | 74.1 ±1.6 | 74.5 ±1.0 | |
| 2 | 71.1 ±1.3 | 70.5 ±1.3 | ||
| 3 | 66.9 ±1.3 | 65.4 ± 0.9 | ||
| 4 | 158.7 ± 29.4 | 154.9 ± 27.6 | ||
| 5 | 117.6 ± 34.4 | 116.1 ± 32.4 | ||
| 6 | 98.5 ± 29.3 | 93.3 ± 26.7 | ||
| T1 brain | 1 | 889 ± 44 | 877 ± 33 | |
| 2 | 852 ± 53 | 856 ± 37 | ||
| 3 | 869 ± 52 | 850 ± 35 | ||
| 4 | 1575±306 | 1550±293 | ||
| 5 | 2168 ± 571 | 2282 ± 563 | ||
| 6 | 2072 ± 480 | 2053±464 | ||
| T1 abdomen | 1 | 692 ± 58 | 690 ± 50 | |
| 2 | 741± 76 | 738 ± 54 | ||
| 3 | 1470±243 | 1467±255 | ||
| 4 | 1261 ±197 | 1286±200 | ||
| 5 | 1236±76 | 1240 ±89 | ||
| 6 | 1201±110 | 1239 ±104 |
3.3. Evaluation of brain and abdomen reconstruction
Figure 5(a) illustrates MS-ResNet T2 mapping results on the brain of a healthy test subject. Input TE images and T2 maps are heavily corrupted by undersampling artifacts and noise. MS-ResNet removes these undersampling artifacts and suppresses the noise. Figure 5(b) shows MS-ResNet T1 mapping performance on the brain of a healthy test subject. Although the input images are heavily corrupted by noise and undersampling artifacts, MS-ResNet outputs TI images and generates T1 maps comparable to NLR3D. Results of T1 mapping experiments in the abdomen are shown in Figure 7 for (a) a healthy volunteer and (b) a subject with liver lesions. Due to the extremely high acceleration rate (R = 37.7), input images reconstructed with NUFFT are dominated by streaking artifacts and noise. MS-ResNet is able to process these images to yield high quality TI images and T1 maps. In Fig. 6(a), T1 maps from MS-ResNet reveal sharp delineation of the structures of the kidneys. In Fig. 6(b), a lesion within the liver is clearly depicted in the MS-ResNet T1 map. It is worth emphasizing that although MS-ResNet was trained using only data from healthy subjects, it is able to yield high quality TE images and T2 maps on subjects with pathology as illustrated in this case. Table 3 provides the results of an ROI analysis, which compares MS-ResNet and NLR3D reconstructions on T2 and T1 brain, and T1 abdomen datasets. The largest mean T2 deviation between MS-ResNet and NLR3D was 5.2 ms or 5.4% (ROI 6). The largest mean T1 deviation between MS-ResNet and NLR3D was 38 ms or (ROI 6 in T1 abdomen).
Figure 7:
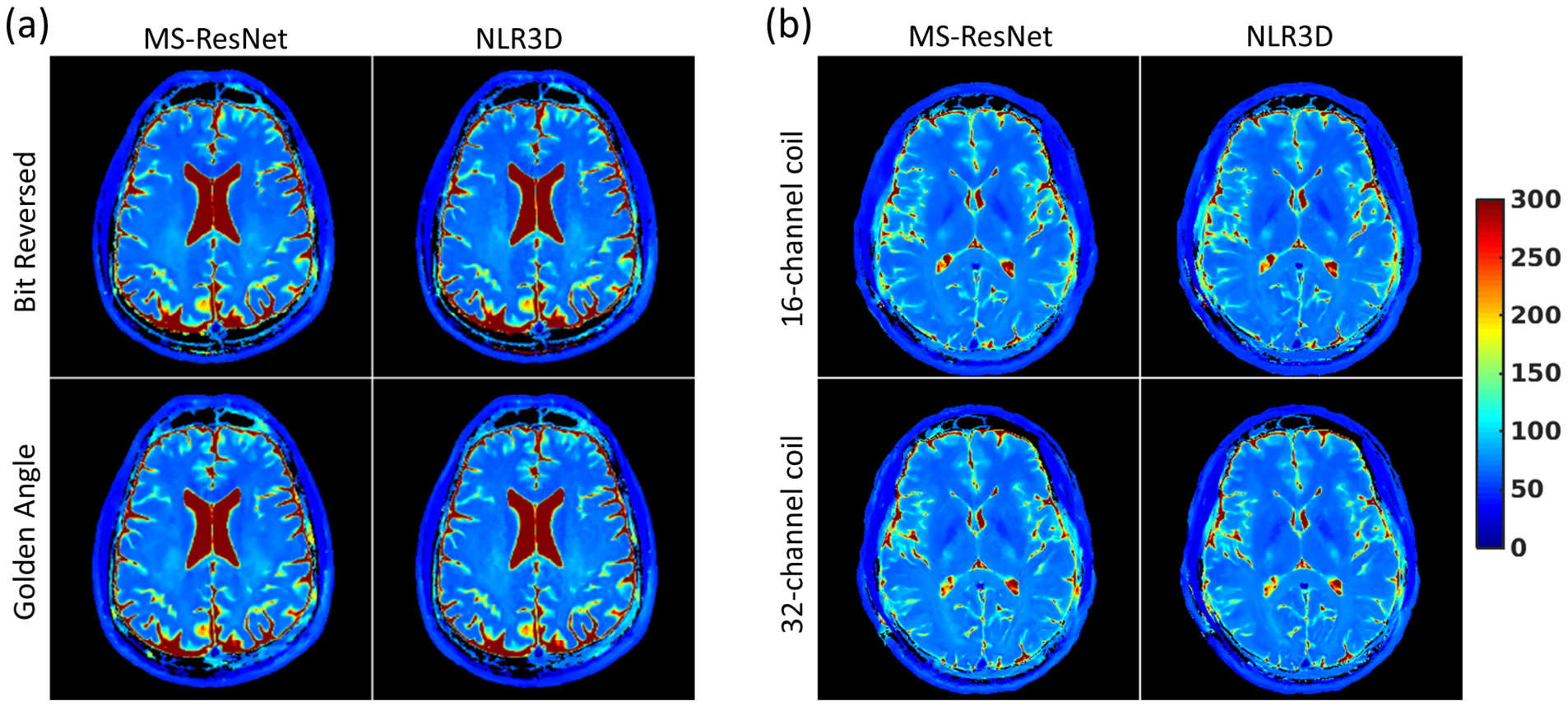
The generalization of proposed approach to (a) variable undersampling patterns and (b) varying sensitivity maps on T2 mapping of the brain. (a) T2 maps were reconstructed from data acquired with bit reversed and golden angle view ordering (at the same undersampling rate) respectively, using the same network trained on the data acquired with bit reversed view ordering only. The resulting T2 maps together with the T2 maps obtained using NLR3D method are shown. (b) T2 map were reconstructed from data acquired with a 16-channel coil and a 32-channel coil respectively, using the same network trained on the data acquired with the 16-channel coil only. The resulting T2 maps together with the T2 maps obtained using NLR3D method are shown.
Figure 6:

T1 mapping comparison on the abdomen data (R=37.7) of a (a) healthy subject (b) a subject with a liver lesion. NUFFT, MS-ResNet, and NLR3D constitute the input, output, and target images, respectively, of the proposed network. Early TI images, late TI images, and T1 maps reconstructed by the three methods are presented.
3.4. Evaluation of network generalization
Figure 7(a) shows the reconstructed T2 maps from data acquired with bit-reversed view ordering and pseudo golden angle view ordering, respectively. Although MS-ResNet was trained only using data acquired with bit-reversed view ordering, Fig. 7(a) illustrates that MS-ResNet is relatively insensitive to the view ordering in radial acquisitions. Figure 7(b) shows the reconstructed T2 maps from data acquired with a 16-channel head coil and a 32-channel head coil, respectively. It can be observed that although MS-ResNet was trained only using data acquired with the 16-channel head coil, MS-ResNet reconstruction of the 32-channel data is comparable to the T2 map obtained using the 16-channel data.
4. Discussion
In this study, we presented a DL-based MR parameter mapping approach which does not require fully sampled data for training. The proposed approach yields high quality contrast-weighted images and accurate parameter maps using training images obtained from accelerated acquisitions. It is interesting to observe that the proposed MS-ResNet supervised with NLR3D reconstructions outperforms NLR3D itself. There are inherent similarities as well as significant differences between the model-based CS techniques such as NLR3D and the proposed DL-based reconstruction: NLR3D identifies similar patches around a given patch using block matching and enforces low-rankness on the 3D (spatial and temporal) patch group. An important parameter in NLR3D is the search window size, which defines the region where similar patches are found. If the search window size is too small, the number of similar patches will be limited, limiting the ability of NLR3D to exploit non-local low-rank constraints. However, increasing the search window size beyond a limit does not necessarily improve performance, although it leads to a significant increase in the complexity of the block matching step. MS-ResNet is trained using patches which are analogous to the search window in NLR3D. Rather than explicitly enforcing a low-rank representation of patches within the search window, MS-ResNet learns complex nonlinear features that provide a compact representation of the patch data through training. Overall, NLR3D can be seen as a more traditional approach where the compact representations (i.e. low-rankness of patches) are predetermined through expert guidance, whereas MS-ResNet learns its representations directly from the training dataset. Importantly, while NLR3D only considers non-local low-rankness within the image of a single data, MS-ResNet is able to learn compact representations across the entire training data.
A major advantage of the proposed approach over the model-based CS techniques is its computational time. Long reconstruction times required by CS methods impede their widespread adoption in the clinic. The proposed approach eliminates this barrier by shifting the major computational burden to an off-line training phase. Another important advantage of the proposed approach is that it utilizes lightweight network architecture and patch scale training and can yield good performance even with small amount of training data (see the Supplementary Material for details). This is particularly useful in applications where large training data sets are difficult to obtain. It should be noted that image scale training may lead to enhanced performance compared to patch scale training in some applications but requires larger training sets. We have demonstrated that the use of images reconstructed with model-based CS techniques as labels enables the use of CNN-based image reconstruction methods in applications where fully sampled reference images are difficult to obtain.
There is growing interest in using DL methods for MR parameter mapping. Recently, the use of DL for T2 mapping in overlapping-echo detachment planar imaging was proposed by Cai et al. [29]. The authors used the ResNet architecture from He et al. [55] to learn the mapping between the overlapping echo images and T2 maps using simulated training data. In comparison, we proposed a novel multi-scale ResNet architecture, which aims to increase the receptive field of the network through multi-scale processing. This larger receptive field can be effective in eliminating the globally distributed streaking artifacts which occur due to radial undersampling. We have also chosen to exclude batch normalization layers from our network. The original ResNet architecture with batch normalization layers was proposed for high-level computer vision tasks such as image classification or object detection. Recent works [51, 56] suggest that batch normalization of features may restrict the flexibility of the networks and/or decrease the network performance in image reconstruction or estimation problems. Our MS-ResNet is also significantly deeper than the network used by Cai et al. [29] (32 ResBlocks vs. 4 ResBlocks). This is relevant because the performance gains between conventional CNNs and ResNet architectures are particularly significant in deeper networks [55]. In addition, we have trained our network directly using in vivo data instead of simulated training data, eliminating the need to simulate imperfections that may occur during in vivo imaging. Finally, our network was designed to work with data obtained from RADTSE [47] and IR-radSSFP [19] sequences which yield significantly higher resolution (T2 mapping: 0.50 mm × 0.50 mm knee/0.69 mm × 0.69 mm brain, T1 mapping: 0.83 mm × 0.83 mm abdomen/0.69 mm × 0.69 mm brain) in comparison to the resolution (1.72 mm × 1.72 mm) of the OLED imaging used by Cai et al. [29].
It is also worth noting that Liu et al. [30] developed a direct CNN mapping from the undersampled images to T2 parameter maps with model-augmented data consistency for accelerated T2 mapping of the knee. The authors acquired non-accelerated knee data for supervised training using a Cartesian multi-echo spin echo T2 mapping sequence. In contrast, we used highly efficient and motion robust radial sequences in both T1 mapping and T2 mapping, which allow for much higher acceleration rates (up to R = 37.7 vs. up to R = 8.0). In addition, we use constrained reconstructions as reference for network training, which eliminates the need for fully-sampled reference data. Our approach enables supervised learning in applications where a fully-sampled reference is difficult to acquire in vivo.
This study has several limitations which may present opportunities for future research. While deciding on the architecture of MS-ResNet (see Supplementary Material Fig. S2), we have made empirical choices on architectural parameters such as the number of layers, number of filters per layer, and filter sizes. Although these parameter values yield good results as shown in this study, they may not be optimal. We have also shown that the MS-ResNet trained using data from healthy subjects is able to provide high quality contrast-weighted images and parameter maps on subjects with pathology. Although this example illustrates the network’s ability to generalize, we are not strictly restricted to training the network using data from healthy subjects. This limitation is due to the relatively small number of subjects recruited for this proof of concept study. A larger study with both healthy subjects and subjects with disease would be beneficial to further evaluate the proposed technique in a clinical setting.
In future work, architectural refinement such as replacement of the ResNet blocks with DenseNet [57] blocks, which have been shown to have compelling advantages over earlier DNN architectures, may further improve the performance of the network. The proposed approach was designed to work with magnitude data. However, since MRI data is in general complex valued, changes to the network architecture and training procedure to enable the network to work with complex valued data may yield enhanced performance. This is an active area of research [40–44]. We have chosen loss over loss for network training as loss is more prone to losing high resolution textures of images [51, 58]. Recent works [59–63] suggest that use of adversarial loss functions can further improve preservation of high frequency details. Incorporation of these loss functions into the proposed framework may result in further improvements in image quality. Our proposed network produces multi-contrast images which are then used to fit to the corresponding signal models to produce the parameter maps. Liu et al. [30] recently evaluated the performance of such two-step fitting vs. direct parameter mapping approaches. Their study found that the two methods perform similarly except when the SNR is low, in which case, the two-step approach may amplify noise. Thus, an extension of the proposed method to direct parameter mapping warrants further investigation and may yield improved reconstruction performance in low SNR applications.
5. Conclusion
Magnetic resonance parameter mapping enables quantification of tissue relaxation parameters. However, conventional parameter mapping approaches require long data acquisition times. Although accelerated data acquisition methods were proposed in parameter mapping applications, many of these methods require constrained reconstruction techniques which are computationally intensive, and, thus, impractical for routine clinical use. In this work, we presented an MR parameter mapping framework, which combines accelerated radial data acquisition with a multi-scale ResNet reconstruction. The performance of the proposed approach was evaluated on T1 and T2 mapping applications. The results suggest that the proposed DL-based approach yields more accurate parameter maps than model-based CS approaches using undersampled acquisitions. The proposed framework can potentially enable deep learning driven image reconstruction for parameter mapping applications, where fully sampled training data is unavailable.
Supplementary Material
Table 2:
The full width at half maximum (FWHM) and area under the curve within [−5,5] ms (AUC [−5,5]) of the T2 error histogram shown in Figure 1 for three test subjects. Smaller FWHM and larger AUC [−5,5] are better. “MS-ResNet-AR” and “MS-ResNet-FR” represent the proposed MS-ResNet trained using accelerated reference and fully sampled reference, respectively.
| Test Subject 1 | Test Subject 2 | TestSubject3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R = 8 | R = 12 | R = 16 | R = 8 | R = 12 | R = 16 | R = 8 | R = 12 | R = 16 | |
| FWHM (ms) | |||||||||
| NUFFT | 30.71 | 39.01 | 46.06 | 27.17 | 34.06 | 40.34 | 30.21 | 38.87 | 46.24 |
| Joint | 17.46 | 18.14 | 18.42 | 16.34 | 17.24 | 17.86 | 17.59 | 18.29 | 18.52 |
| NLR3D | 15.39 | 15.71 | 15.43 | 14.71 | 15.46 | 15.56 | 15.72 | 16.14 | 15.83 |
| MS-ResNet-AR | 14.21 | 14.46 | 14.57 | 13.62 | 14.21 | 14.59 | 14.04 | 14.32 | 14.38 |
| MS-ResNet-FR | 13.34 | 14.13 | 14.86 | 12.76 | 13.69 | 14.49 | 13.10 | 13.91 | 14.48 |
| aAUC[−5,5] | |||||||||
| NUFFT | 0.212 | 0.167 | 0.142 | 0.219 | 0.180 | 0.158 | 0.217 | 0.173 | 0.151 |
| Joint | 0.344 | 0.326 | 0.314 | 0.343 | 0.333 | 0.328 | 0.341 | 0.329 | 0.331 |
| NLR3D | 0.385 | 0.370 | 0.366 | 0.378 | 0.371 | 0.372 | 0.381 | 0.371 | 0.380 |
| MS-ResNet-AR | 0.409 | 0.395 | 0.382 | 0.401 | 0.398 | 0.392 | 0.413 | 0.406 | 0.408 |
| MS-ResNet-FR | 0.431 | 0.405 | 0.381 | 0.429 | 0.417 | 0.401 | 0.436 | 0.417 | 0.409 |
AUC [−5,5] denotes the normalized area under the curve within the interval [−5,5] ms.
ACKNOWLEDGEMENT
The authors would like to acknowledge support from NIH (grant R01CA245920), the Arizona Biomedical Research Commission (grant ADHS14-082996), and the Technology and Research Initiative Fund (TRIF) Improving Health Initiative.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Bartzokis G, Sultzer D, Cummings J, Holt LE, Hance DB, Henderson VW, et al. In Vivo Evaluation of Brain Iron in Alzheimer Disease Using Magnetic Resonance Imaging. Archives of General Psychiatry 2000;57:47. doi: 10.1001/archpsyc.57.1.47. [DOI] [PubMed] [Google Scholar]
- [2].Larsson HBW, Frederiksen J, Petersen J, Nordenbo A, Zeeberg I, Henriksen O, et al. Assessment of demyelination, edema, and gliosis byin vivo determination of T1 and T2 in the brain of patients with acute attack of multiple sclerosis. Magnetic Resonance in Medicine 1989;11:337–348. doi: 10.1002/mrm.1910110308. [DOI] [PubMed] [Google Scholar]
- [3].Kim KA, Park MS, Kim IS, Kiefer B, Chung WS, Kim MJ, et al. Quantitative evaluation of liver cirrhosis using T1 relaxation time with 3 Tesla MRI before and after oxygen inhalation. Journal of Magnetic Resonance Imaging 2012;36:405–410. doi: 10.1002/jmri.23620. [DOI] [PubMed] [Google Scholar]
- [4].Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magnetic Resonance in Medicine 2010;64(4): 1114–1120. doi: 10.1002/mrm.22483. [DOI] [PubMed] [Google Scholar]
- [5].Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magnetic Resonance in Medicine 2011;67(5): 1355–1366. doi: 10.1002/mrm.23128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis. Magnetic Resonance in Medicine 2011;66(3): 706–716. doi: 10.1002/mrm.22826. [DOI] [PubMed] [Google Scholar]
- [7].Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension: Accelerating MR Parameter Mapping. Magnetic Resonance in Medicine 2013;70(5): 1263–1273. doi: 10.1002/mrm.24577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Huang C, Bilgin A, Barr T, Altbach MI. T2 Relaxometry from Highly Undersampled Data with Indirect Echo Compensation. Magnetic Resonance in Medicine 2013;70(4): 1026–1037. doi: 10.1002/mrm.24540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magnetic Resonance in Medicine 2014;74(2): 489–498. doi: 10.1002/mrm.25421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Peng X, Liu X, Zheng H, Liang D. Exploiting parameter sparsity in model-based reconstruction to accelerate proton density and T2 mapping. Medical Engineering & Physics 2014;36(11): 1428–1435. doi: 10.1016/j.medengphy.2014.06.002. [DOI] [PubMed] [Google Scholar]
- [11].Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint: Locally Low Rank Parameter Mapping. Magnetic Resonance in Medicine 2015;73(2): 655–661. doi: 10.1002/mrm.25161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Zhou Y, Shi C, Ren F, Lyu J, Liang D, Ying L. Accelerating MR parameter mapping using nonlinear manifold learning and supervised pre-imaging In: 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). Brooklyn, NY, USA:IEEE; ISBN 978-1-4799-2374-8;2015, p. 897–900. doi: 10.1109/ISBI.2015.7164015. [DOI] [Google Scholar]
- [13].Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, et al. T2shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magnetic Resonance in Medicine 2016;77(1): 180–195. doi: 10.1002/mrm.26102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Peng X, Ying L, Liu Y, Yuan J, Liu X, Liang D. Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA): Accelerated T2 Mapping with MORASA. Magnetic Resonance in Medicine 2016;76(6): 1865–1878. doi: 10.1002/mrm.26083. [DOI] [PubMed] [Google Scholar]
- [15].Roeloffs V, Wang X, Sumpf TJ, Untenberger M, Voit D, Frahm J. Model-based reconstruction for T1 mapping using single-shot inversion-recovery radial FLASH. International Journal of Imaging Systems and Technology 2016;26(4): 254–263. doi: 10.1002/ima.22196. [DOI] [Google Scholar]
- [16].Mandava S, Keerthivasan MB, Martin DR, Altbach MI, Bilgin A. Higher-order subspace denoising for improved multi-contrast imaging and parameter mapping In: Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM). Paris, France;2018,. [Google Scholar]
- [17].Mandava S. Constrained Magnetic Resonance and Computed Tomographic Imaging: Models and Applications. The University of Arizona;2018. [Google Scholar]
- [18].Mandava S, Keerthivasan MB, Li Z, Martin DR, Altbach MI, Bilgin A. Accelerated MR parameter mapping with a union of local subspaces constraint. Magnetic Resonance in Medicine 2018; doi: 10.1002/mrm.27344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Li Z, Bilgin A, Johnson K, Galons JP, Vedantham S, Martin DR, et al. Rapid High-Resolution T1 Mapping Using a Highly Accelerated Radial Steady-state Free-precession Technique: radSSFP Technique for T1 Mapping. Journal of Magnetic Resonance Imaging 2018; doi: 10.1002/jmri.26170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks In: Advances in neural information processing systems. 2012, p. 1097–1105. doi: 10.1145/3065386. [DOI] [Google Scholar]
- [21].Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation In: International Conference on Medical image computing and computer-assisted intervention. Springer;2015, p. 234–241. doi: 10.1007/978-3-319-24574-4\_28. [DOI] [Google Scholar]
- [22].Dong C, Loy CC, He K, Tang X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence 2016;38(2): 295–307. doi: 10.1109/tpami.2015.2439281. [DOI] [PubMed] [Google Scholar]
- [23].Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, et al. Accelerating magnetic resonance imaging via deep learning In: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). IEEE;2016, p. 514–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Han YS, Yoo J, Ye JC. Deep Residual Learning for Compressed Sensing CT Reconstruction via Persistent Homology Analysis. arXiv:161106391 [cs] 2016;. [Google Scholar]
- [25].Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection-reconstruction MR. Magnetic Resonance in Medicine 2018;80(3): 1189–1205. doi: 10.1002/mrm.27106. [DOI] [PubMed] [Google Scholar]
- [26].Knoll F, Hammernik K, Garwood E, Hirschmann A, Rybak L, Bruno M, et al. Accelerated Knee Imaging Using a Deep Learning Based Reconstruction In: Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM). Honolulu, HI, USA;2017,. [Google Scholar]
- [27].Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine 2017; doi: 10.1002/mrm.26977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Transactions on Medical Imaging 2018;37(2): 491–503. doi: 10.1109/tmi.2017.2760978. [DOI] [PubMed] [Google Scholar]
- [29].Cai C, Wang C, Zeng Y, Cai S, Liang D, Wu Y, et al. Single-shot T2 mapping using overlapping-echo detachment planar imaging and a deep convolutional neural network. Magnetic Resonance in Medicine 2018; doi: 10.1002/mrm.27205. [DOI] [PubMed] [Google Scholar]
- [30].Liu F, Feng L, Kijowski R. MANTIS: Model-Augmented Neural neTwork with Incoherent k - space Sampling for efficient MR parameter mapping. Magnetic Resonance in Medicine 2019; doi: 10.1002/mrm.27707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zeng W, Peng J, Wang S, Liu Q. A comparative study of CNN-based super-resolution methods in mri reconstruction and its beyond. Signal Processing: Image Communication 2020;81:115701. [Google Scholar]
- [32].Wang S, Ke Z, Cheng H, Jia S, Ying L, Zheng H, et al. Dimension: Dynamic MR imaging with both k-space and spatial prior knowledge obtained via multi-supervised network training. NMR in Biomedicine 2019;: e4131. [DOI] [PubMed] [Google Scholar]
- [33].Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine 1999;42(5): 952–962. doi:. [DOI] [PubMed] [Google Scholar]
- [34].Zhao B, Lam F, Liang ZP. Model-Based MR Parameter Mapping With Sparsity Constraints: Parameter Estimation and Performance Bounds. IEEE Transactions on Medical Imaging 2014;33(9): 1832–1844. doi: 10.1109/TMI.2014.2322815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, et al. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magnetic Resonance in Medicine 2018;79(2): 730–740. doi: 10.1002/mrm.26726. [DOI] [PubMed] [Google Scholar]
- [36].Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magnetic Resonance in Medicine 2013;71(3): 990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Fessler JA, Sutton BP. Nonuniform fast fourier transforms using min-max interpolation. IEEE Transactions on Signal Processing 2003;51(2): 560–574. doi: 10.1109/tsp.2002.807005. [DOI] [Google Scholar]
- [38].Lebel RM, Wilman AH. Transverse relaxometry with stimulated echo compensation. Magnetic Resonance in Medicine 2010;64(4): 1005–1014. doi: 10.1002/mrm.22487. [DOI] [PubMed] [Google Scholar]
- [39].Keerthivasan MB, Saranathan M, Johnson K, Fu Z, Weinkauf CC, Martin DR, et al. An efficient 3D stack-of-stars turbo spin echo pulse sequence for simultaneous T2-weighted imaging and T2 mapping. Magnetic Resonance in Medicine 2019;82(1): 326–341. doi: 10.1002/mrm.27737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Wang S, Cheng H, Ying L, Xiao T, Ke Z, Zheng H, et al. DeepcomplexMRI: Exploiting deep residual network for fast parallel MR imaging with complex convolution. Magnetic Resonance Imaging 2020;68:136–147. [DOI] [PubMed] [Google Scholar]
- [41].Guberman N. On Complex Valued Convolutional Neural Networks. arXiv:160209046 [cs] 2016;. [Google Scholar]
- [42].Hirose A. Complex-valued neural networks: The merits and their origins In: 2009 International Joint Conference on Neural Networks. Atlanta, Ga, USA:IEEE; ISBN 978-1-4244-3548-7;2009, p. 1237–1244. doi: 10.1109/IJCNN.2009.5178754. [DOI] [Google Scholar]
- [43].Virtue P, Yu SX, Lustig M. Better than real: Complex-valued neural nets for MRI fingerprinting In: 2017 IEEE International Conference on Image Processing (ICIP). Beijing:IEEE; ISBN 978-1-5090-2175-8;2017, p. 3953–3957. doi: 10.1109/ICIP.2017.8297024. [DOI] [Google Scholar]
- [44].Trabelsi C, Bilaniuk O, Zhang Y, Serdyuk D, Subramanian S, Santos JF, et al. Deep Complex Networks In: International Conference on Learning Representations. 2018,. [Google Scholar]
- [45].He K, Zhang X, Ren S, Sun J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence 2015;37(9): 1904–1916. doi: 10.1109/TPAMI.2015.2389824. [DOI] [PubMed] [Google Scholar]
- [46].Barral JK, Gudmundson E, Stikov N, Etezadi-Amoli M, Stoica P, Nishimura DG. A robust methodology for in vivo T1 mapping. Magnetic Resonance in Medicine 2010;64(4): 1057–1067. doi: 10.1002/mrm.22497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Altbach MI, Outwater EK, Trouard TP, Krupinski EA, Theilmann RJ, Stopeck AT, et al. Radial fast spin-echo method for T2-weighted imaging and T2 mapping of the liver. Journal of Magnetic Resonance Imaging 2002;16(2): 179–189. doi: 10.1002/jmri.10142. [DOI] [PubMed] [Google Scholar]
- [48].Natsuaki Y, Keerthivasan MB, Bilgin A, Bolster BD, Johnson KJ, Bi X, et al. Flexible and Efficient 2D Radial TSE T2 Mapping with Tiered Echo Sharing and with “Pseudo” Golden Angle Ratio Reordering In: Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM). Honolulu, HI;2017,. [Google Scholar]
- [49].Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, et al. Automatic differentiation in PyTorch In: NIPS-W. 2017,. [Google Scholar]
- [50].Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. arXiv:14126980 [cs] 2014;. [Google Scholar]
- [51].Lim B, Son S, Kim H, Nah S, Lee KM. Enhanced Deep Residual Networks for Single Image Super-Resolution. IEEE;2017. doi: 10.1109/cvprw.2017.151. [DOI] [Google Scholar]
- [52].Timofte R, Rothe R, Gool LV. Seven Ways to Improve Example-Based Single Image Super Resolution In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA:IEEE; ISBN 978-1-4673-8851-1;2016, p. 1865–1873. doi: 10.1109/CVPR.2016.206. [DOI] [Google Scholar]
- [53].Golub G, Pereyra V. Separable nonlinear least squares: the variable projection method and its applications. Inverse Problems 2003;19(2): R1–R26. doi: 10.1088/0266-5611/19/2/201. [DOI] [Google Scholar]
- [54].Hansen MS, Sørensen TS. Gadgetron: An open source framework for medical image reconstruction: Gadgetron. Magnetic Resonance in Medicine 2013;69(6): 1768–1776. doi: 10.1002/mrm.24389. [DOI] [PubMed] [Google Scholar]
- [55].He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA:IEEE; ISBN 9781467388511;2016, p. 770–778. doi: 10.1109/CVPR.2016.90. [DOI] [Google Scholar]
- [56].Nah S, Kim TH, Lee KM. Deep Multi-scale Convolutional Neural Network for Dynamic Scene Deblurring. IEEE;2017. doi: 10.1109/cvpr.2017.35. [DOI] [Google Scholar]
- [57].Huang G, Liu Z, Maaten L.v.d., Weinberger KQ Densely Connected Convolutional Networks In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI:IEEE; ISBN 978-1-5386-0457-1;2017, p. 2261–2269. doi: 10.1109/CVPR.2017.243. [DOI] [Google Scholar]
- [58].Ledig C, Theis L, Huszar F, Caballero J, Cunningham A, Acosta A, et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI:IEEE; ISBN 978-1-5386-0457-1;2017, p. 105–114. doi: 10.1109/CVPR.2017.19. [DOI] [Google Scholar]
- [59].Shi W, Caballero J, Huszár F, Totz J, Aitken AP, Bishop R, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016, p. 1874–1883. doi: 10.1109/cvpr.2016.207. [DOI] [Google Scholar]
- [60].Yu X, Porikli F. Ultra-Resolving Face Images by Discriminative Generative Networks In: Computer Vision – ECCV 2016. Springer International Publishing;2016, p. 318–333. doi: 10.1007/978-3-319-46454-1_20. [DOI] [Google Scholar]
- [61].Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Xing L, et al. Deep Generative Adversarial Neural Networks for Compressive Sensing MRI. IEEE Transactions on Medical Imaging 2019;38:167–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Yang G, Yu S, Dong H, Slabaugh G, Dragotti PL, Ye X, et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Transactions on Medical Imaging 2018;37(6): 1310–1321. doi: 10.1109/TMI.2017.2785879. [DOI] [PubMed] [Google Scholar]
- [63].Ceccaldi P, Biswas S, Chandarana H, Wang H, Das I, Fenchel M, et al. Improved Wasserstein GAN based Methods for pseudo-CT Synthesis from MR DIXON Images: Application to MR only Radiotherapy In: ISMRM Workshop on Machine Learning Part II. Washington, D.C.;2018,. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


