Abstract
Regional tissue mechanics play a fundamental role in the patient-specific function and remodeling of the cardiovascular system. Nevertheless, regional in vivo assessments of aortic kinematics remain lacking due to the challenge of imaging the thin aortic wall. Herein, we present a novel application of displacement encoding with stimulated echoes (DENSE) magnetic resonance imaging (MRI) to quantify the regional displacement and circumferential Green strain of the thoracic and abdominal aorta. Two-dimensional (2D) spiral cine DENSE and steady-state free procession (SSFP) cine images were acquired at 3T at either the infrarenal abdominal aorta (IAA), descending thoracic aorta (DTA), or distal aortic arch (DAA) in a pilot study of six healthy volunteers (22–59 y.o., 4 females). DENSE data were processed with multiple custom noise reduction techniques including time-smoothing, displacement vector smoothing, sectorized spatial smoothing, and reference point averaging to calculate circumferential Green strain across 16 equispaced sectors around the aorta. Each volunteer was scanned twice to evaluate interstudy repeatability. Circumferential Green strain was heterogeneously distributed in all volunteers and locations. The mean spatial heterogeneity index (standard deviation of all sector values divided by the mean strain) was 0.37 in the IAA, 0.28 in the DTA, and 0.59 in the DAA. Mean (homogenized) peak strain by DENSE for each cross section was consistent with the homogenized linearized strain estimated from SSFP cine. The mean difference in peak strain across all sectors following repeat imaging was −0.1±2.3%, with a mean absolute difference of 1.7%. Aortic cine DENSE MRI is a viable noninvasive technique for quantifying heterogeneous regional aortic wall strain and has significant potential to improve patient-specific clinical assessments of numerous aortopathies, as well as to provide the lacking spatiotemporal data required to refine patient-specific computational models of aortic growth and remodeling.
1. Introduction
Clinical imaging of the cardiovascular system generally assesses two basic but interrelated features: structure and function. Basic structural features were the first to be surveyed, but the advent of increasingly sophisticated time-resolved imaging techniques has allowed functional parameterization of cardiovascular fluid and solid mechanics, yielding unique patient-specific metrics for clinical diagnosis and risk assessment. While characterization of blood flow via Doppler ultrasound (US), phase contrast magnetic resonance imaging (PC-MRI), or other techniques has found many useful cardiac and aortic applications, in vivo quantification of the soft tissue kinematics (e.g., displacement and strain) has focused predominately on the myocardium due to the prevalence of heart disease. Nevertheless, aortopathies such as aneurysms and dissections have recently accounted for over 10,000 deaths and three billion dollars in healthcare costs per year [1,2], and thus, deserve increased attention.
Techniques for quantifying regional myocardial strain by MRI have rapidly advanced and now include magnetization-tagged imaging, tissue velocity phase mapping, and displacement encoding with stimulated echoes (DENSE) [3]; however, application of these techniques to quantifying aortic kinematics has been lacking due to the technical challenge of imaging the aortic wall (an order of magnitude thinner than the ventricular wall). Currently, noninvasive estimations of aortic kinematics are largely restricted to homogenized values of circumferential strain via US, cine computed tomography (CT), or cine MRI by quantifying the change in aortic circumference during the cardiac cycle. Regional variations of circumferential aortic strain are more difficult to assess and require additional techniques (e.g., feature-tracking in CT [4], speckle-tracking in 4D US [5], velocity-mapping in PC-MRI [6], or optical flow from cine MRI [7]). Such reports are few, and except for the MRI optical flow approach, have focused either on large regions (e.g., differences in the anterior, posterior, and lateral walls [4]) or simply quantified indices of overall circumferential heterogeneity without specifically reporting regional values [5,6]. In addition, most prior studies have focused on stretch or linearized strain, as opposed to Green strain, which is a more appropriate metric for large deformations in soft tissues (being exact within continuum theory and independent of rigid body motion [8]).
Thus, there remains a need for a reliable noninvasive technique for quantifying patient-specific regional Green strain of the aortic wall in vivo. These data could be immediately useful for direct clinical correlation to aortic diagnoses and prognoses, such as detecting early changes in aortic function (e.g., due to matrix-associated genetic diseases [9] or significant abnormalities in flow [10]) or predicting the risk of expansion in aneurysms and dissections [11,12]. In addition, spatially resolved kinematic mapping could provide novel in vivo patient-specific data that have been lacking to study and understand the local mechanobiological processes that govern aortic remodeling in response to regionally heterogeneous mechanics and to improve the computational modeling of aortic aging and disease [13].
Herein, we present detailed methods on a novel technique to regionally resolve the Green strain of the aortic wall in vivo using two-dimensional (2D) spiral cine DENSE MRI. Pilot data from six healthy controls, including interstudy and interobserver repeatability and comparisons to regional and homogenized linearized strain, are presented for three distinct axial locations along the aorta that are of clinical interest as frequent sites of dissections and/or aneurysms: the infrarenal abdominal aorta (IAA), descending thoracic aorta (DTA), and distal aortic arch (DAA).
2. Methods
2.1. Study Design and Magnetic Resonance Imaging Sequences.
Following approval by the Institutional Review Board at Emory University, six volunteers without history of aortopathy were recruited to undergo noncontrast magnetic resonance scanning of either the IAA (near the level of the retroperitoneal portion of the duodenum), mid-DTA (at the level of the mitral valve), or DAA (distal to the left subclavian artery) (Fig. 1(a)). After identifying the location of interest, 2D steady-state free procession (SSFP) cine and spiral cine DENSE images were acquired at a selected plane normal to the local longitudinal axis of the aorta. For evaluating interstudy repeatability, each patient was removed from the scanner following the first acquisition, and the study was repeated, including manual reselection of the location of interest.
Fig. 1.
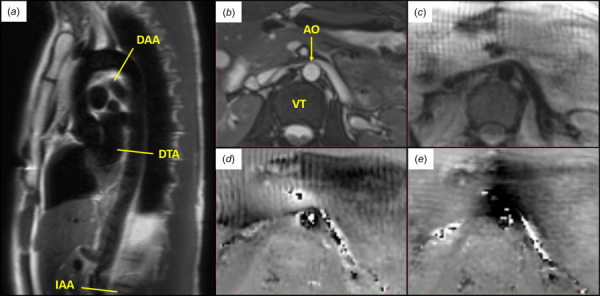
(a) Axial locations along the aorta analyzed by DENSE MRI. (IAA, DTA, and DAA) (b–e) Illustrative example of images acquired at peak systole in the infrarenal abdominal aorta of a healthy 23 year old female: (b) SSFP cine, (c) DENSE magnitude, (d) DENSE x-phase encoding, and (e) DENSE y-phase encoding. (AO—aorta and VT—vertebra)
In order to identify an adequate cross-sectional plane and to provide a general assessment of aortic motion, cardiac-gated 2D SSFP cine imaging was conducted during a single breath-hold using the following parameters: voxel size 1.3 × 1.3 × 6 mm, TR 41.64 ms, TE 1.52 ms, flip angle 37 deg, and geneRalized autocalibrating partial parallel acquisition acceleration factor 3. In the same plane, navigator and ECG-gated 2D cine DENSE images (magnitude, x-encoded (readout direction) phase, and y-encoded (phase direction) phase [14]; Fig. 1) were acquired with spiral k-space sampling and fat suppression using the following parameters: four signal averages, voxel size 1.3 × 1.3 × 8 mm, TR 16 ms, TE 1.21 ms, in-plane displacement encoding frequency = 0.17–0.25 cyc/mm, 18 spiral interleaves, and 2 leaves per heartbeat. For DENSE, the phase data of each voxel in each primary direction directly encode the displacement of the voxels at each acquisition time in reference to the configuration at the time of tagging initiated by the ECG trigger (i.e., R-wave). In order to capture the motion through local systole, 18 temporal acquisitions were acquired every 32 ms beginning immediately after the trigger. All imaging was performed on a 3T Siemens Prisma platform using an 18-channel body matrix in combination with the table-mounted spine coil array.
2.2. Postprocessing
2.2.1. Calculation of Tracked Positions and Displacement.
The analysis was performed offline using custom code in matlab (MathWorks, Natick, MA). For DENSE, the luminal boundary of the aorta at each timepoint was manually segmented using the magnitude and phase images as guides. The outer adventitial boundary was segmented to allow a wall thickness of two voxels (the minimum required for a calculation of 2D Green strain). After using these boundaries as a mask for the aortic wall, tracked positions of each voxel within the mask at reference time were calculated through all 18 temporal images, similar to the previous reports [15]. Briefly, after phase-unwrapping, the displacement vector in the primary direction for each voxel in the mask at time , relative to the configuration at the time of DENSE tagging, was calculated by
| (1) |
where is the unwrapped i-phase imaging value for the voxel at time t. Comparison of displacements for each voxel with its immediate neighbors allowed refinement of the initial segmentation by eliminating voxels with significantly different displacements from the mask. Since the time of DENSE tagging immediately precedes and occurs before local systole in the aorta, the displacement from tagging to is negligible. Thus, is chosen as the reference configuration for convenience. To track the motion of the tissue represented by each reference voxel in through all n timesteps, the three closest back-projected displacement vectors from each voxel in were identified and used to interpolate a forward displacement vector and position for each voxel into each time .
Due to the noise in the displacement data (best observed in the incremental displacement plot in Fig. 2(b)), two displacement-based noise reduction techniques were implemented. First, a piecewise time-smoothing algorithm was developed to create a linear fit for the x and y positions of each tracked voxel from to (the beginning of local systole at the aortic segment of interest) and a fifth-order polynomial fitting from to (the final recorded timepoint) (Fig. 2(a)). A single value of was defined uniquely for each dataset as the timepoint preceding the first increase in mean total incremental displacement for all tracked voxels. Note that =1 was assumed for any dataset where the mean displacement between and was greater than 0.5 pixels. Second, a local spatial smoothing of displacement vectors was performed for each voxel at each time point by averaging the displacement of all voxels included within the aortic wall mask within a specified number of voxel spaces () around the voxel of interest. In order to minimize the amount of spatial smoothing, the integer value of was determined for each dataset from the IAA and DTA as the smallest value for which the calculated circumferential Green strain () for each regional sector of the aortic wall (as described later) monotonically decreased between its peak value and . For the DAA, which exhibited greater heterogeneity in strain patterns, was determined as the smallest value for which > −0.03 in each sector for all times.
Fig. 2.
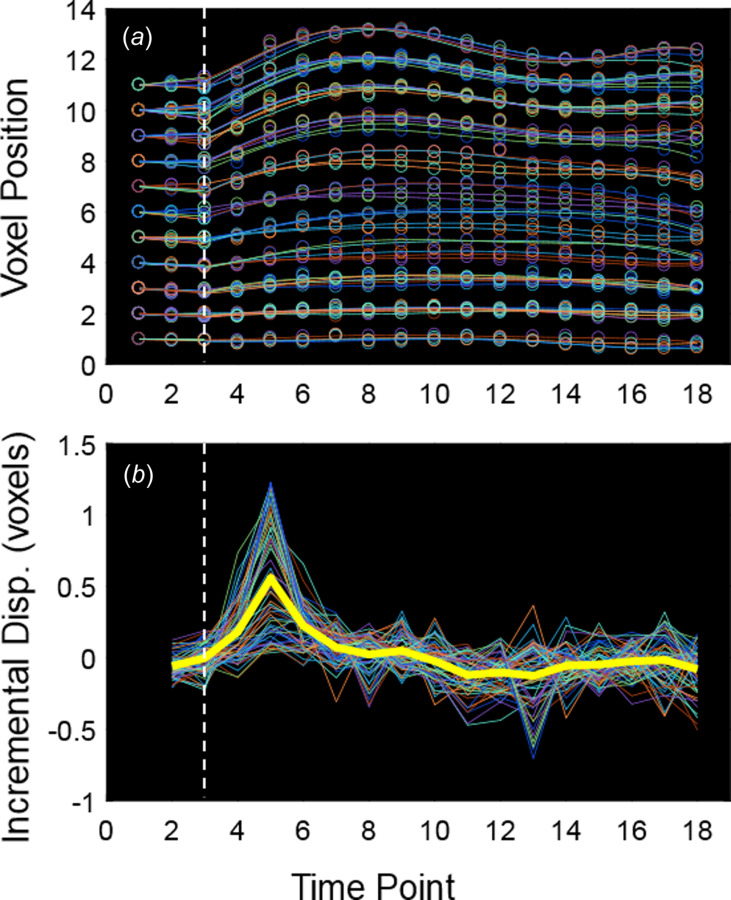
(a) Tracked voxel positions in the y-direction (open circles) and piecewise time-smoothing (lines) for each voxel in the mask over time. (b) Incremental displacement (i.e., displacement since the previous timepoint) in the y-direction for each voxel in the mask over time before time-smoothing. Note the high degree of noise. The thick yellow line represents mean values, and the vertical dashed line identifies .
2.2.2. Calculation of Regional Green Strain.
Given the position and displacement of each voxel of the masked aortic wall through time, Green strain was calculated using a quadrilateral finite element interpolation described by Humphrey [8]. Briefly, the vertices of each finite element were defined using the tracked reference voxels in , where the initial reference position of each vertex was transformed into a normalized coordinate system according to
| (2) |
where are the normalized coordinates (1,1), (1,−1), (−1,−1), and (−1,1), and describes the normalized position of any point within the quadrilateral defined by vertices ( = 1–4) that are ordered to preserve the same connectivity as in the xy-space. Similarly, the normalized displacement was calculated by
| (3) |
where represents the displacement at time t for each vertex. Finally, the Green strain was calculated as a function of the referential displacement gradient, , by
| (4) |
and was transformed from the xy-coordinates () into radial–circumferential coordinates (), such that , where
| (5) |
and is the angle of the position vector of the point of interest with respect to the x-axis after centering the aortic mask to the origin of the xy-plane.
Theoretically, this approach could produce mean strain values between each set of four neighboring voxels; however, due to relatively high noise in the displacement data, a sector-based method was implemented. Eight equispaced sectors were defined using eight spokes radiating from the calculated center of the aortic wall mask in the reference configuration at beginning in the positive y-direction, which yields an approximately 1 cm arc-length per sector around the circumference of the average adult aorta. The innermost and outermost voxels nearest to each spoke were identified, and a sector-wide quadrilateral was formed. A single value of circumferential Green strain () was interpolated along the inner wall at the midpoint of each sector in order to minimize the influence of potential peri-adventitial tissue included in the mask. Since the orientation of the eight sectors is arbitrary, a half-sector rotation (22.5 deg) was applied to the spokes, and the calculation was repeated. The two overlapping 8-sector maps were then combined into a single 16-sector map using a 1:2:1 weighting ratio to generate a unique strain value every 22.5 deg around the aortic circumference (approximately 0.5 cm arc-length per sector) (see Fig. 3(c)).
Fig. 3.
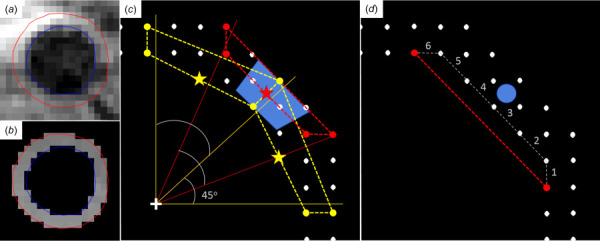
(a) Segmentation of the aortic wall at peak strain from a DENSE magnitude image (blue—luminal border, red—adventitial border). (b) DENSE y-phase image after applying mask and unwrapping the phase data. (c) Diagram of the calculation of Green strain using overlapping sectors from one quadrant of the aortic wall. Dots represent voxels within the mask in the reference configuration at . The reported Green strain for the sector in blue (representing a 22.5 deg arc of the aortic wall) is the weighted average (1:2:1) of the Green strains interpolated at the inner midpoint (stars) of the three overlapping quadrilateral elements defined by vertices representing the closest voxels to each radial spoke emanating from the center of the lumen (+). (d) Diagram of the calculation of circumferential linearized strain along the inner (luminal) row of voxels. Linearized strain is calculated as the relative change in length of the line segment between two voxels separated by voxel spaces (here, = 6) in . A single value of strain is reported at the midpoint of the wall (blue dot) between the two voxels used in the calculation.
To further reduce the effect of noise on the calculation of Green strain without increasing spatial smoothing, a novel reference point averaging was developed. Physiology dictates that minimal displacement occurs in the aorta before time (i.e., in late local diastole before the systolic pulse arrives at the aortic location of interest; see Fig. 2(a)), the calculation of Green strain for all was repeated using each as an independent reference configuration. These independent Green strain measurements were averaged by sector, and the resulting strain data for were time-smoothed with a fifth-order polynomial. For this study, the analysis focused on peak strain, which was defined at the timepoint with the largest mean circumferential strain for the entire cross section for the IAA and DTA, or at the mean timepoint at which the four highest sector strain values that peak before occur for the DAA (due to some sectors peaking significantly past local systole in the aortic arch).
2.2.3. Calculation of Regional Linearized Strain and Homogenized Strain.
The majority of previous reports of aortic kinematics have reported linearized strain; therefore, for comparison and to serve as an internal check for the calculation of circumferential Green strain, linearized strain around the luminal row of masked voxels was calculated for each dataset using the smoothed displacement data. To reduce noise and approximate the overall degree of spatial smoothing used for the calculation of Green strain, the regional linearized strain was calculated between pairs of voxels separated by voxel spaces (Fig. 3(d)), where
| (6) |
and is the total number of voxels in the luminal row. Thus, the linearized strain for each pair of voxels is calculated as , where is the length of the line segment between voxel number and voxel number at the reference time, and is the length between the same voxels at the time of peak strain. Reference point averaging using the same in the calculation of Green strain was also utilized. The regional linearized strain was reported at the midposition circumferentially along the aortic wall between each pair of voxels used in the calculation. Since the displacement vector smoothing allows nonluminal voxels to have some influence on the displacement of the luminal voxels from which the linearized strain is calculated (recall the initial segmentation of the aortic wall is two voxels thick), one dataset from each axial location was resegmented with only a single row of voxels, and the smoothed displacement and linearized strain were recalculated for comparison.
Peak homogenized strain for each dataset was calculated from the SSFP cine images as the difference in aortic circumference from its maximum to its minimum () during the cardiac cycle divided by the circumference at its minimum. The circumference of the aorta was determined on matlab by manually marking greater than 15 points along the aortic wall on the SSFP cine image using function “impoly,” smoothing the set of points with a spline, and summing the distance between 100 interpolated points along the spline. The homogenized strain was directly compared to the mean circumferential Green strain and mean linearized strain for each aortic cross section by averaging all sector values from the regional analysis.
2.2.4. Repeatability Tests and Statistics.
Basic statistics were performed using Microsoft Excel and matlab. Interstudy repeatability of the calculation of peak circumferential Green strain for each dataset was evaluated using the mean difference of strain values across all sectors from the second scan compared to the first (where a mean difference of zero would indicate no bias and the standard deviation of the mean difference indicates a relative degree of error). A single sample t-test was used to evaluate the significance of the mean difference (compared to zero and assuming sector independence), with p < 0.05 representing statistical significance. The mean of the absolute value of the differences was also calculated to express the average magnitude of difference between the scans. Regional heterogeneity of peak circumferential strain within a single dataset was quantified using the spatial heterogeneity index [16] (standard deviation divided by the mean of all sector strain values) and the normalized maximum, minimum, and range (difference between maximum and minimum), where the normalization is performed by dividing by the mean strain value for the given dataset. Sensitivity of the calculated strain to each of the main noise-reduction techniques (sectorization, time-smoothing, reference point-averaging, and displacement vector smoothing) was explored by individually altering or removing each technique and comparing the mean difference, normalized mean difference, and mean normalized peak difference in the resulting circumferential Green strain. Statistical significance was evaluated similar to the interstudy tests. Finally, interobserver repeatability was performed to evaluate the difference in strain calculation due to user variability in manual segmentation. The second observer was trained using half of the data (the second scan for each patient), and then independently segmented each first scan while blinded to the other observer's segmentation and results. Comparison of results was performed similar to the interstudy tests.
3. Results
All six volunteers successfully completed the DENSE imaging protocol and no datasets were excluded. The initial position-based time-smoothing reduced the noise in the displacement data. The effect of spatially smoothing the displacement vectors is illustrated in the displacement vector map and plots of circumferential Green strain by sector over time in Fig. 4. Before smoothing, note the abrupt transition of orientation of the vectors in the right anterolateral region (marked by the asterisk in Fig. 4(a)), which is likely artefactual since it was not present in the repeat study. Following smoothing, the abrupt transition is dampened (Fig. 4(c)), and the abnormally high maximum regional circumferential Green strain (Fig. 4(b)) is reduced (Fig. 4(d)). Note also that the abnormal diastolic increase in circumferential Green strain (arrow in Fig. 4(b)) has been pushed from before to near . The abnormal increase in strain beyond persists due to reduced signal-to-noise ratio as magnetization is lost with repetitive sampling. As expected, the mean displacement of the entire mask (center yellow vector in Figs. 4(a) and 4(c)) was not affected by the smoothing; however, a slight decrease in mean circumferential Green strain was generally noted for each increase in .
Fig. 4.
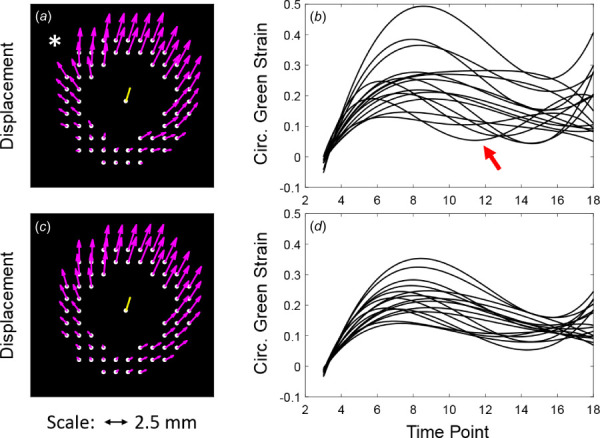
Displacement vector map (at peak strain) and plots of circumferential Green strain versus time for all sectors before (a–b) and after (c–d) spatial smoothing of the displacement vectors. Asterisk* notes focal artifact of the displacement field before smoothing that results in an abnormally high circumferential strain. Red arrow notes artifactual increase in circumferential strain before in (b). Both artifacts improve following smoothing with .
After postprocessing, plots of peak circumferential Green strain versus sector position around the aorta following repeat imaging in each volunteer are shown in Fig. 5, along with the results if all noise-reduction techniques are off. Due to the importance of mechanical tethering of the aorta to the neighboring vertebrae and for normalization when comparing multiple studies, numbering of sectors was assigned by the unique location of the vertebra in each dataset such that the aortic region overlying the vertebra (in the transverse IAA or DTA planes), or nearest to the anterior tip of the vertebra (in the oblique DAA planes), represented the division between Sectors 1 and 16, with the numbers progressing counterclockwise. As a convenient “clinical” visualization of the data, ribbon heatmaps of the circumferential Green strain that highlight regional heterogeneities are shown in Fig. 6, where the diameter of each circular plot represents the mean diameter of the mask at for each dataset.
Fig. 5.
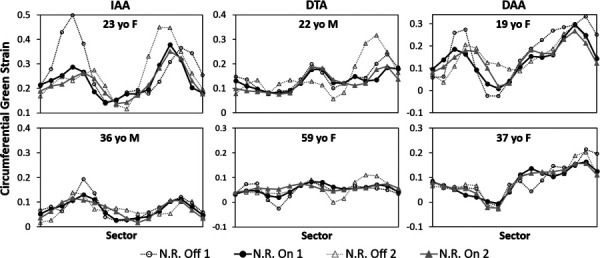
Circumferential Green strain versus sector position at the time of peak strain following repeat imaging in each volunteer when the postprocessing noise-reduction (N.R.) is either off or on. The sectors are numbered counterclockwise around the aorta with the division between Sectors 1 and 16 representing the aorta–vertebral interface. (IAA, DTA, and DAA)
Fig. 6.
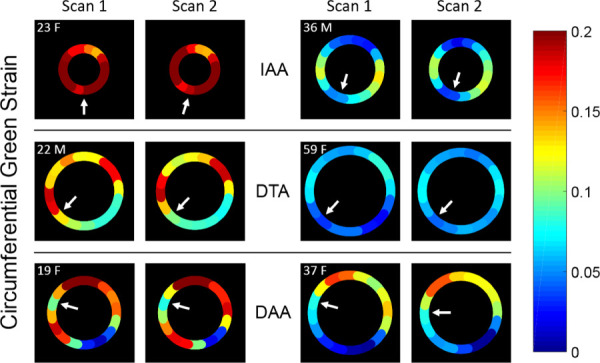
Ribbon heatmaps of circumferential Green strain of the aortic wall at the time of peak strain mapped onto the unadjusted reference configuration at for both scans in each volunteer. Small arrows identify Sector 1 for each scan (near the vertebra). (IAA, DTA, and DAA)
Table 1 records the mean difference (and standard deviation) between the repeated DENSE scans in peak circumferential Green strain across all sectors for each patient, as well as the mean absolute difference in strain. Overall, the mean difference across all sectors for all aortic locations was −0.1 ± 2.3% (p = 0.78), with a mean absolute difference of 1.7%. Table 1 also records metrics for evaluating patient-specific heterogeneities and intervolunteer differences in circumferential strain.
Table 1.
Mean differences in peak circumferential Green strain across all sectors for the interstudy repeatability study in each volunteer by location, and mean (homogenized) circumferential Green strain and metrics of heterogeneity. Values represent means of both scans in each volunteer at the time of peak strain. Normalization is performed by dividing the value of interest by the mean circumferential strain. Range represents the difference from the maximum to the minimum value.
| Location | Volunteer | Mean interstudy diff. in circ. strain ( ± SD) | Mean abs. Diff. | Mean circ. green strain ( ± SD) | Het. index | Norm. maximum | Norm. minimum | Norm. range |
|---|---|---|---|---|---|---|---|---|
| IAA | 23 F | −0.005 ± 0.029 | 0.024 | 0.23 ± 0.06 | 0.28 | 1.61 | 0.62 | 1.00 |
| 36 M | −0.001 ± 0.016 | 0.014 | 0.07 ± 0.03 | 0.46 | 1.72 | 0.31 | 1.41 | |
| Mean | −0.003 ± 0.023 | 0.019 | 0.15 ± 0.05 | 0.37 | 1.67 | 0.46 | 1.21 | |
| DTA | 22 M | −0.005 ± 0.021 | 0.015 | 0.13 ± 0.04 | 0.29 | 1.47 | 0.62 | 0.85 |
| 59 F | 0.004 ± 0.017 | 0.013 | 0.06 ± 0.01 | 0.26 | 1.43 | 0.55 | 0.88 | |
| Mean | −0.001 ± 0.019 | 0.014 | 0.09 ± 0.03 | 0.28 | 1.45 | 0.58 | 0.87 | |
| DAA | 19 F | 0.004 ± 0.035 | 0.027 | 0.14 ± 0.07 | 0.52 | 1.99 | 0.09 | 1.89 |
| 37 F | 0.000 ± 0.015 | 0.011 | 0.08 ± 0.05 | 0.67 | 1.95 | −0.18 | 2.13 | |
| Mean | 0.002 ± 0.027 | 0.019 | 0.11 ± 0.06 | 0.59 | 1.97 | −0.04 | 2.01 | |
| ALL | Mean | −0.001 ± 0.023 | 0.017 | 0.12 ± 0.05 | 0.41 | 1.7 | 0.33 | 1.36 |
Figure 7 compares sector plots of the circumferential Green strain and the linearized strain along the inner row of voxels from the same two-voxel thick segmentation for the repeated study in each volunteer at the time of peak strain. Plots of circumferential Green strain and the linearized strain from a separate single-row segmentation for three of the volunteers showed qualitatively similar results (Supplemental Figure 1 is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). Figure 8 shows the comparison of the mean (homogenized) values of peak circumferential strain using all three DENSE analyses to the peak homogenized circumferential strain calculated from estimating circumference change on the SSFP cine images.
Fig. 7.
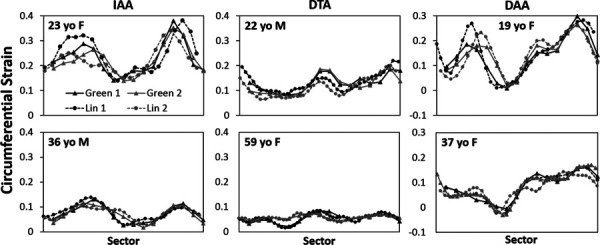
Plots of circumferential Green strain (solid lines) from the two-voxel thick segmentation compared to linearized strain (dashed lines) from the inner row of the two-voxel thick segmentation across all sectors at the time of peak strain for each repeated scan
Fig. 8.
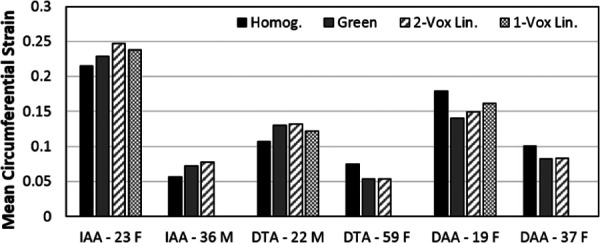
Comparison of peak homogenized circumferential strain estimated from SSFP cine images to mean peak circumferential Green strain, mean peak linearized strain from the two-voxel thick segmentation (2-Vox Lin.), and mean peak linearized strain from the single-voxel thick segmentation (1-Vox Lin.) calculated from cine DENSE imaging
Results of the interobserver repeatability study are shown in Fig. 9, which demonstrate qualitative similarity, including consistency of the location of maximum strain (within one sector) for both observers. The overall mean difference of circumferential strain was small (−0.01±0.04) but reached statistical significance (p = 0.03); however, the normalized mean difference was insignificant (p = 0.99), as expected due to the normalization. Table 2 summarizes absolute and normalized quantitative results of the interobserver study, as well as the sensitivity studies where the number of sectors around the circumference of the aorta was varied (8, 16, or 32) or specific noise-reduction techniques were turned off. A complete table, including comparisons by aortic location, may be found in Supplemental Table 1 which is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection.
Fig. 9.
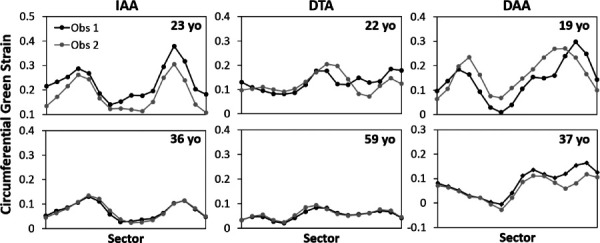
Interobserver comparisons of peak circumferential Green strain across all sectors
Table 2.
Quantitative differences of circumferential Green strain averaged across all sectors and volunteers when varying the number of sectors, turning off noise-reduction techniques, or using different observers. Normalization was performed by dividing each sector strain by the mean strain of the volunteer for the given observer using 16 sectors with all noise-reduction techniques on.
| Variation | Total sectors | Obs. | Mean diff. ± S.D. | P | Norm. mean diff. ± S.D. | P | Mean norm. peak diff. ± S.D. | P | Mean norm. abs. diff. |
|---|---|---|---|---|---|---|---|---|---|
| All smoothing on | 8 | 1 | 0.002±0.031 | 0.63 | 0.015±0.262 | 0.69 | −0.386±0.087 | 0.0001 | 0.217 |
| All smoothing on | 16 | 1 | 0 | — | 0 | — | 0 | — | 0 |
| All smoothing on | 32 | 1 | 0.000±0.025 | 0.91 | 0.006±0.197 | 0.78 | 0.365±0.216 | 0.009 | 0.154 |
| All smoothing off | 16 | 1 | 0.016±0.048 | 0.002 | 0.099±0.360 | 0.008 | 0.440±0.315 | 0.02 | 0.275 |
| Time-smoothing off | 16 | 1 | 0.000±0.011 | 0.66 | −0.014±0.103 | 0.18 | −0.026±0.140 | 0.66 | 0.074 |
| Ref. point avg. off | 16 | 1 | −0.004±0.013 | 0.002 | −0.037±0.124 | 0.005 | −0.065±0.116 | 0.23 | 0.096 |
| Disp. vector Sm. Off | 16 | 1 | 0.018±0.048 | 0.0003 | 0.123±0.308 | 0.0002 | 0.446±0.256 | 0.008 | 0.258 |
| All smoothing on | 16 | 2 | −0.008±0.038 | 0.03 | 0.000±0.236 | 0.99 | −0.018±0.237 | 0.86 | 0.174 |
4. Discussion
Cardiovascular medicine is increasingly moving toward patient-specific diagnosis, prognosis, and treatment; however, a reliable noninvasive method for assessing regional aortic wall strain has been lacking. The results of this pilot study suggest that spiral cine DENSE MRI can provide these important kinematic data regionally and repeatably. Furthermore, by providing regional maps of circumferential Green strain at multiple aortic locations, the results add to the increasing evidence that aortic strain is patient-specific, spatially heterogeneous, and dependent on aortic location.
4.1. Resolution and Noise-Reduction.
The previous cardiac DENSE sequences designed to quantify myocardial strain have operated on in-plane resolutions of approximately 3 × 3 mm [14]. Since 2D Green strain calculations require at least a two-voxel thickness, the resolution for aortic DENSE must be closer to 1 × 1 mm, given a 2 mm thick aortic wall; however, reductions in resolution also decrease signal-to-noise ratio, creating a practical constraint. Using a 3T magnetic field strength, anisotropic voxels with a large through plane dimension, and increasing the number of averages helps offset this limitation at the time of the scan. In addition, postprocessing techniques provide significant additional noise-reduction that have the added benefit of not increasing scan times. Ultimately, these techniques allowed a voxel resolution of 1.3 × 1.3 × 8 mm to provide reasonable strain results with a respiratory-gated scan time of approximately 10 min.
The incorporation of multiple noise-reduction techniques that operate over both time and space minimized the degree of smoothing otherwise required from any single technique alone. Time-smoothing was adequate in qualitatively removing noise for visualizing displacement. However, while the piecewise time-smoothing fits the peak displacement well (e.g., at in Fig. 2(a)), it could overestimate the displacement at timepoint + 1 and underestimate it at timepoint + 2. Since the analysis herein focuses on peak strain, this error is insignificant, but future investigations into strain rates may require further refinement of the time-smoothing to accurately characterize the rapid displacement in early local systole. Displacement vector smoothing provided a robust but flexible spatial smoothing that improved reproducibility by reducing the magnitude of extrema in strain induced by noise or minor unwrapping artifacts when processing the DENSE data (see Fig. 4). By adjusting the value of to control the degree of smoothing depending on the noise in each dataset, spatial smoothing could be minimized in order to preserve the recognition of potential spatial heterogeneities in strain.
Compared to displacement, calculations of strain are more sensitive to noise due to its dependence on not just displacement, but the displacement gradient. To address this challenge, a sector-based analysis was introduced to reduce the relative contribution from fixed noise by increasing the dimensions of the finite element over which the deformation was calculated. Thus, there is some sacrifice of spatial resolution for added accuracy and reproducibility. This finite sectorization also gives the added benefit of a more manageable statistical comparison of discrete aortic regions when making interstudy comparisons. Reference point averaging further reduces random noise without sacrificing spatial resolution but with the tradeoff of any error induced by ignoring the minimal motion of the aortic wall before the onset of local systole (note that the displacement is minimal before the dotted vertical line at in Fig. 2). This averaging serves to minimize noise-induced or segmentation-induced errors in a single reference state that would be transmitted to all strain calculations in future timepoints—noting that discrimination of the aortic lumen and wall is most difficult in the earliest timepoints before the high signal in the blood pool is lost during local systole. Notably, the mean total displacement of all voxels from to for each dataset in this study was less than one-third of the in-plane voxel dimension (∼0.4 mm).
The interstudy repeatability results (Fig. 5) demonstrate the necessity and effectiveness of the noise-reduction techniques in improving repeatability. Sensitivity results summarized in Table 2 suggest that the displacement vector smoothing has the largest effect on the calculated strain. When this smoothing is off, the normalized mean strain increases by 12% (p < 0.001), with a highest recorded difference of 113%. Using displacement vector smoothing, normalized peak strains are significantly lowered by 45% (p < 0.01); however, without the smoothing, these peaks may be artificially high and unrepeatable (see Figs. 4 and 5). Notably, time-smoothing had comparatively little effect on calculating peak strain, though this smoothing may have more effect in future analyses of nonpeak strain or strain rate. Reference point averaging demonstrated a moderate but significant effect of increasing the normalized mean strain by 4% (p < 0.01), though this effect was twice as high in the infrarenal aorta where more time lapses between the R-wave trigger and local systole (i.e., the IAA may still be contracting slightly on average in local late diastole). Finally, while using less (8) or more (32) sectors for the strain analysis did not significantly affect the mean strain, the use of 8 sectors was found to significantly reduce the peak strain by 39% (p < 0.001), while the use of 32 sectors significantly increased the peak strain by 37% (p < 0.01). In addition, the use of 32 sectors generally increased the number of local minima/maxima in strain suggestive of increased noise (Supplemental Figure 2 is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection).
4.2. Repeatability and Comparisons of Circumferential Strain.
Following the initial development of this technique, two primary questions required addressing. The first was whether the implementation of the multiple noise-reduction techniques resulted in a reasonable and repeatable calculation of circumferential strain. For this initial stage of development, a preclinical interstudy repeatability test was performed to ensure that a consistent strain measurement could be achieved by DENSE under ideal conditions (i.e., immediate re-imaging on the same 3T system by a single nonblinded observer experienced in DENSE segmentation and analysis). The results in Fig. 5 and Table 1 suggest that regional patient-specific circumferential Green strain can be repeatably measured with excellent agreement under these controlled conditions (a mean absolute difference across all sectors of <2% for all aortic locations). It is observed that there are regions where the repeated measurements appear slightly “out of phase” spatially by one sector (e.g., in Fig. 5 around sectors 1–8 in the 23 y.o. IAA and 19 y.o. DAA). These results may arise from slight differences in delineation of the sector positions between studies due to patient positioning, manual selection of the imaging planes, and manual segmentation. The overall regional distribution of heterogeneities does not appear to be qualitatively affected; however, it is noted that the manual segmentation can affect the magnitude of strain, particularly with respect to the segmentation of the reference voxels before . Reducing the diameter of the reference segmentation increases the magnitude of strain at future timepoints by increasing the calculated displacement (and vice versa). This effect is likely responsible for some of the difference in mean strain calculated in the interobserver study (e.g., in the 23 y.o. IAA in Fig. 9). Thus, proper segmentation of the aortic wall is key for accurate and repeatable measures of strain. Notably, normalization of the strain data may improve interobserver repeatability by ameliorating any fixed bias in mean strain. Due to the practical constraint that manual segmentation is the costliest processing step in terms of time and labor, future refinements of aortic cine DENSE should seek to automate the segmentation. Alternatively, future studies may consider using DENSE to calculate regional normalized strain but using the mean homogenized strain from higher-resolution cine SSFP imaging to convert the normalized strain to absolute strain.
The close agreement of both the mean peak circumferential Green strain and linearized strain by aortic DENSE with the homogenized strain from SSFP cine demonstrates that the DENSE technique can recover an appropriate global circumferential strain for the aortic cross section of interest (Fig. 8). This does not confirm the actual regionally heterogeneous distribution of strain measured by DENSE, but it does suggest its reasonableness. Notably, the global circumferential strains reported in Table 1 and Fig. 8 are consistent with the previous reports of homogenized circumferential strain in the healthy aorta by US and CT: 12.3 ± 1.4% [17] and 15.3 ± 1.2% [18] in the abdominal aorta, 8.1 ± 3.3% [19] in the distal DTA, and 7.9 ± 2.4% [19] in the DAA. Nevertheless, the novelty of aortic DENSE is its ability to quantify regional aortic wall strain; hence, there are few prior studies to confirm the unique patterns of heterogeneity observed. In the only prior study of DENSE in the aorta, Haraldsson et al. [20] reported gross heterogeneities in stretch in the ascending aorta, but failed to calculate strain or regionally map the distribution of stretch. Two prior studies using 4D ultrasound also provide support for the finding that aortic kinematics are heterogeneous. First in Ref. [5], healthy infrarenal aorta is reported to have a normalized maximum linearized strain value of 1.56–2.54 (using standard versus custom postprocessing), which is similar to the mean value of 1.67 for the normalized maximum circumferential Green strain of the two IAAs in this study. In addition, Derwich et al. [16] reported a spatial heterogeneity index of approximately 0.5 for normal infrarenal aortas, which is similar to the mean value of 0.37 in this study. Using an optical flow approach and cine MRI, Satriano et al. [7] mapped heterogeneities in Green strain over 9 abdominal aortic aneurysms, but did not report regional comparisons or include healthy aortas with which we compare to this study. Finally, Draney et al. [6] suggested circumferential heterogeneity in the strain of the DTA using cine PC-MRI, though this technique produced a much larger standard deviation at peak strain of approximately ±11% strain (compared to ±3% in this study in the DTA). Unlike this DENSE study, the ultrasound and PC-MRI studies did not formally report regional strain values. Technical validation of the calculation of Green strain by aortic cine DENSE is currently underway and will require testing of a cyclically deformable organic or polymeric phantom in vitro, in which strain can be confirmed by analytic or experimental methods; nevertheless, the reasonableness of gross measures of mean strain and indices of heterogeneity with the few available previous studies is promising.
4.3. Partial Volume Effects and Peri-Adventitial Tethering.
The second primary concern was whether the relatively large in-plane voxel dimension (compared to the aortic wall thickness) that was required for adequate signal created significant errors in the strain calculation due to partial volume effects from the lumen or peri-adventitial tissue. In general, the de-phasing of luminal blood following local systole as tagged blood is removed from the imaging plane may reduce its influence on the calculated displacement of the aortic wall while simultaneously aiding in the segmentation of the luminal boundary. However, the adventitial boundary is more difficult to segment due to the potential for similarities in both signal magnitude and phase (i.e., displacement) of peri-aortic tissue. Assigning a two-voxel wall thickness after segmenting the luminal boundary ensures inclusion of the wall with the minimum amount of peri-adventitial tissue that still allows the calculation of 2D Green strain. Of greatest concern is the errant inclusion within the mask of surrounding structures with significantly different material properties than the aortic wall, most notably the vertebral body. The aorta abuts and is likely tethered to the vertebrae along its posterior wall in the IAA, medio-posterior wall in the DTA, and medial wall in the DAA. The results in this pilot study demonstrated relatively low displacement and low to moderate normalized circumferential strain along the aorta–vertebral interface (sectors 1 and 16) in all axial locations. Interestingly, circumferential strains immediately adjacent to the interface tended to be elevated (e.g., in the lateral walls of IAAs and superior walls of DAAs; Fig. 6). Such results would be consistent with the inability of the pressurized aorta to displace the vertebrae, as well as the potential for local tethering both to inhibit strain at the aorta–vertebral interface and to induce elevated strain in adjacent regions as the aorta expands away from a point of fixation. They also illustrate that regionally lower strain does not have to imply stiffer local material properties of the aortic wall itself since strain is dependent on both the inherent properties of the wall as well as the local boundary conditions.
While these results are consistent with anatomy, one must note that inclusion of part of the vertebra within the mask of the aortic wall could also erroneously reduce the calculated displacement of the overlying aorta. This was the primary motivation of interpolating the Green strain along the inner boundary of each finite element. To further investigate this concern, the linearized strain of only the inner row of the two-voxel aortic mask was calculated and found to be qualitatively similar to the heterogeneous circumferential Green strain (Fig. 7). However, one must note that the displacement vector smoothing applied over the two-voxel mask allows signal from the outer layer of voxels to influence the luminal layer of voxels. To eliminate this effect, a single row of voxels must be segmented independently; however, such a segmentation is challenging given the relative size of the voxel dimensions and the aortic wall thickness (i.e., the primary signal from the aortic wall may often overlap two voxels). Thus, while the two-voxel segmentation will almost always include the majority of the signal from the aortic wall, a single voxel segmentation will likely exclude portions of the wall in at least some regions. Indeed, a single voxel segmentation of just the inner row of voxels from the two-voxel mask yielded much less similar results. However, a single-voxel thick mask using a mixture of inner and outer row voxels could be created that yielded a linearized strain that qualitatively replicated the circumferential Green strain (Supplemental Figure 1 is available under the “Supplemental Data” tab for this paper on the ASME Digital Collection). Independently creating and replicating such a single-voxel mask is challenging, though, due to the greater difficulty in deciding which single voxels to include given the partial volume effects and the potentially increased sensitivity of the resulting strain calculations to the inclusion or exclusion of particular voxels. These factors suggest a potential benefit of the two-voxel segmentation and Green strain calculation over a single voxel segmentation and linearized strain.
While there have been no prior high-resolution regional maps of heterogeneities in aortic Green strain in healthy aortas, three of the aforementioned studies offer support for the finding of low strain along the aorta–vertebral interface. Tierney et al. [4] reported that the posterior wall (next to the vertebra) was the most common region of minimal linearized strain in the “neck” of abdominal aortic aneurysms. In addition, while the aforementioned US study by Karatolios et al. [5] and cine PC-MRI study by Draney et al. [6] did not report regional strain values, each included a single figure demonstrating either low linearized strain or low displacement along the expected aorta–vertebral interface. Thus, the results in this study are consistent with the best available literature on regional aortic kinematics. Ultimately, future in vitro and in situ studies that mimic or retain the surrounding aortic structures may be required to verify the kinematic effects of aortic tethering to the vertebrae.
4.4. Clinical Potential, Future Work, and Limitations.
While this proof-of-concept pilot study was not powered to draw clinical conclusions regarding regional aortic strain, some observations are noteworthy and should be considered in future studies. First, the circumferential strain of the aortic wall in all axial locations was both patient-specific and spatially heterogeneous, even in these relatively healthy volunteers. Second, the pattern of heterogeneity suggests consistency based on location (Fig. 6). The IAA demonstrated elevated circumferential strain in the right lateral and left postero-lateral walls and reduced strain in the posterior and anterior walls. The DTA showed elevated strain in the lateral and anterolateral walls. The DAA showed more variability but a consistently high strain in the superior wall (top of the plot in this oblique plane) and low strain in the left inferolateral region corresponding to the lateral connection of the aorta to the left pulmonary artery. These findings are important considering that the majority of computational aortic mechanical models assume material homogeneity and almost all neglect the effect of peri-aortic structures and tethering. The novel ability of aortic cine DENSE to quantify patient-specific regional aortic strain thus creates new opportunities for assessing and understanding the evolution of patient-specific mechanical parameters that can improve the fidelity of future models. This may include inverse methods to calculate regional material properties (noting the limitation of in vivo deformations to describe the material properties below diastolic loading pressures), novel patient-specific inputs for growth and remodeling models that use strain or stress-dependent constitutive laws to evolve the constituents and geometry of the aortic wall [21–23], assistance in assigning patient-specific peri-aortic boundary conditions, and new insights into the correlation of in vivo cyclical strain and mechanobiologically driven aortic remodeling. Furthermore, patient-specific quantification of regional strain opens the possibility of directly correlating regional heterogeneities in aortic strain with a myriad of pathological processes involving focal and diffuse aortic remodeling (e.g., age-associated aortic stiffening, early detection of functional aortic changes due to genetic and structural anomalies such as Marfan's Syndrome or bicuspid aortic valve, or risk assessment in aortic aneurysms and dissections).
In addition to the aforementioned discussion of the constraints on resolution and partial volume effects, a number of limitations regarding this initial development of 2D aortic cine DENSE should be noted. First, the 2D sequence only acquires in-plane strains, and hence, was limited to portions of the aorta with relatively low longitudinal strain (which excludes the ascending aorta [17]); thus, a future three-dimensional implementation of this novel DENSE post-processing should be pursued. Second, the current work focuses solely on the circumferential strain, even though Green strain has the potential to include both radial strain and in-plane shear strain. Such metrics may prove useful; however, their values are muddled during the smoothing process that prioritized the calculation of circumferential strain (particularly during the displacement vector smoothing). Future refinements will seek to recover and identify useful patterns in these other metrics of strain, as well as the nonpeak strains and strain rates that were not explored in this initial study. Finally, while the results of the interobserver repeatability study were qualitatively reasonable, we reiterate the limitation of manual segmentation of the boundaries of the aortic wall and the limited nature of the early ideal test of interstudy repeatability. The two-voxel mask and Green strain analysis likely reduce some of the sensitivity to user-specific variation in segmentation; however, future clinical application would benefit from an automated and strictly repeatable algorithm for segmentation.
5. Conclusions
Aortic cine DENSE MRI is a viable technique for quantifying patient-specific regional circumferential Green strain in vivo in the infrarenal abdominal aorta, descending thoracic aorta, and distal aortic arch. The results of this pilot study demonstrate reasonable initial interstudy repeatability and reveal patient-specific and location-specific heterogeneous distributions of strain that are consistent with the limited previous reports using other modalities. As an MRI technique, cine DENSE offers the added benefit of easy incorporation with other clinical anatomic and functional scans, a lack of radiation, and no restrictions due to inadequate sonographic windows. Initial interobserver repeatability is fair and could be improved by comparison of normalized strain values and/or development of automated segmentation. While technical validation will require future in situ and in silico studies, the calculation of Green strain was consistent with linearized strain from two-voxel and one-voxel thick segmentations, and the mean circumferential strain by DENSE replicated the currently available clinical metric of homogenized strain by SSFP cine. We suggest, therefore, that the ability of aortic cine DENSE to quantify regional aortic kinematics in vivo has significant potential to advance both the understanding and modeling of the key influence of tissue mechanics on aortic remodeling and to apply that knowledge to improve patient-specific diagnoses and clinical interventions.
Supplementary Material
Supplementary Figures
Contributor Information
John S. Wilson, Department of Radiology and Imaging Sciences, , Emory University School of Medicine, , Atlanta, GA 30322 , e-mail: john.s.wilson@emory.edu.
Xiaodong Zhong, Magnetic Resonance R&D Collaborations, Siemens Healthcare, , Atlanta, GA 30322;; Department of Radiology and Imaging Sciences, Emory University School of Medicine, , Atlanta, GA 30322
Jackson Hair, Department of Biomedical Engineering, Emory University and Georgia , Institute of Technology, , Atlanta, GA 30322.
W. Robert Taylor, Department of Biomedical Engineering, Emory University and Georgia , Institute of Technology, , Atlanta, GA 30322; Division of Cardiology, Department of Medicine, , Emory University School of Medicine, , Atlanta, GA 30322; Division of Cardiology, Department of Medicine, , Atlanta VA Medical Center, , Decatur, GA 30033
John N. Oshinski, Department of Radiology and Imaging Sciences, Emory University School of Medicine, , Atlanta, GA 30322; Department of Biomedical Engineering, Emory University and Georgia , Institute of Technology, , Atlanta, GA 30322
Funding Data
NIH-NHLBI Institutional Training (Grant No. T32HL007745 (JSW/WRT)).
Emory University Department of Radiology and Imaging Sciences (JSW/JO).
Shared Instrumentation Grant (S10) (Grant No. 1S10OD016413-01).
Disclosures
Xiaodong Zhong is an employee of Siemens Healthcare, and John Oshinski receives research funding from Siemens Healthcare.
References
- [1]. Kochanek, K. D. , Xu, J. , Murphy, S. L. , Miniño, A. M. , and Kung, H. C. , 2011, “ Deaths: Final Data for 2009,” Natl. Vital Stat. Rep., 60(3), pp. 1–116. [PubMed] [Google Scholar]
- [2].Agency for Healthcare Research and Quality, 2006, Hospital Cost and Utilization Project: Nationwide Inpatient Sample Data Set, Agency for Healthcare Research and Quality, Rockville, MD. [Google Scholar]
- [3]. Chitiboi, T. , and Axel, L. , 2017, “ Magnetic Resonance Imaging of Myocardial Strain: A Review of Current Approaches,” J. Magn. Reson. Imaging, 46(5), pp. 1236–1280. 10.1002/jmri.25718 [DOI] [PubMed] [Google Scholar]
- [4]. Tierney, Á. , Callanan, A. , and McGloughlin, T. M. , 2012, “ Use of Regional Mechanical Properties of Abdominal Aortic Aneurysms to Advance Finite Element Modeling of Rupture Risk,” J. Endovasc. Ther., 19(1), pp. 100–114. 10.1583/11-3456.1 [DOI] [PubMed] [Google Scholar]
- [5]. Karatolios, K. , Wittek, A. , Nwe, T. H. , Bihari, P. , Shelke, A. , Josef, D. , Schmitz-Rixen, T. , Geks, J. , Maisch, B. , Blase, C. , Moosdorf, R. , and Vogt, S. , 2013, “ Method for Aortic Wall Strain Measurement With Three-Dimensional Ultrasound Speckle Tracking and Fitted Finite Element Analysis,” Ann. Thorac. Surg., 96(5), pp. 1664–1671. 10.1016/j.athoracsur.2013.06.037 [DOI] [PubMed] [Google Scholar]
- [6]. Draney, M. T. , Herfkens, R. J. , Hughes, T. J. , Pelc, N. J. , Wedding, K. L. , Zarins, C. K. , and Taylor, C. A. , 2002, “ Quantification of Vessel Wall Cyclic Strain Using Cine Phase Contrast Magnetic Resonance Imaging,” Ann. Biomed. Eng., 30(8), pp. 1033–1045. 10.1114/1.1513566 [DOI] [PubMed] [Google Scholar]
- [7]. Satriano, A. , Rivolo, S. , Martufi, G. , Finol, E. A. , and Di Martino, E. S. , 2015, “ In Vivo Strain Assessment of the Abdominal Aortic Aneurysm,” J. Biomech., 48(2), pp. 354–360. 10.1016/j.jbiomech.2014.11.016 [DOI] [PubMed] [Google Scholar]
- [8]. Humphrey, J. D. , 2002, Cardiovascular Solid Mechanics: Cells, Tissues, and Organs, Springer, New York, pp. 172–174. [Google Scholar]
- [9]. Akazawa, Y. , Motoki, N. , Tada, A. , Yamazaki, S. , Hachiya, A. , Matsuzaki, S. , Kamiya, M. , Nakamura, T. , Kosho, T. , and Inaba, Y. , 2016, “ Decreased Aortic Elasticity in Children With Marfan Syndrome or Loeys-Dietz Syndrome,” Circ. J., 80(11), pp. 2369–2375. 10.1253/circj.CJ-16-0739 [DOI] [PubMed] [Google Scholar]
- [10]. Moaref, A. , Khavanin, M. , and Shekarforoush, S. , 2014, “ Aortic Distensibility in Bicuspid Aortic Valve Patients With Normal Aortic Diameter,” Ther. Adv. Cardiovasc. Dis., 8(4), pp. 128–132. 10.1177/1753944714531062 [DOI] [PubMed] [Google Scholar]
- [11]. Hoegh, A. , and Lindholt, J. S. , 2009, “ Basic Science Review. Vascular Distensibility as a Predictive Tool in the Management of Small Asymptomatic Abdominal Aortic Aneurysms,” Vasc. Endovasc. Surg., 43(4), pp. 333–338. 10.1177/1538574409336019 [DOI] [PubMed] [Google Scholar]
- [12]. Molacek, J. , Baxa, J. , Houdek, K. , Treska, V. , and Ferda, J. , 2011, “ Assessment of Abdominal Aortic Aneurysm Wall Distensibility With Electrocardiography-Gated Computed Tomography,” Ann. Vasc. Surg., 25(8), pp. 1036–1042. 10.1016/j.avsg.2011.05.034 [DOI] [PubMed] [Google Scholar]
- [13]. Wilson, J. S. , Baek, S. , and Humphrey, J. D. , 2012, “ Importance of Initial Aortic Properties on the Evolving Regional Anisotropy, Stiffness and Wall Thickness of Human Abdominal Aortic Aneurysms,” J. R. Soc. Interface, 9(74), pp. 2047–2058. 10.1098/rsif.2012.0097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Zhong, X. , Spottiswoode, B. S. , Meyer, C. H. , Kramer, C. M. , and Epstein, F. H. , 2010, “ Imaging Three-Dimensional Myocardial Mechanics Using Navigator-Gated Volumetric Spiral Cine DENSE MRI,” Magn. Reson. Med., 64(4), pp. 1089–1097. 10.1002/mrm.22503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Spottiswoode, B. S. , Zhong, X. , Hess, A. T. , Kramer, C. M. , Meintjes, E. M. , Mayosi, B. M. , and Epstein, F. H. , 2007, “ Tracking Myocardial Motion From Cine DENSE Images Using Spatiotemporal Phase Unwrapping and Temporal Fitting,” IEEE Trans. Med. Imaging, 26(1), pp. 15–30. 10.1109/TMI.2006.884215 [DOI] [PubMed] [Google Scholar]
- [16]. Derwich, W. , Wittek, A. , Pfister, K. , Nelson, K. , Bereiter-Hahn, J. , Fritzen, C. P. , Blase, C. , and Schmitz-Rixen, T. , 2016, “ High Resolution Strain Analysis Comparing Aorta and Abdominal Aortic Aneurysm With Real Time Three Dimensional Speckle Tracking Ultrasound,” Eur. J. Vasc. Endovasc. Surg., 51(2), pp. 187–193. 10.1016/j.ejvs.2015.07.042 [DOI] [PubMed] [Google Scholar]
- [17]. Wittek, A. , Karatolios, K. , Fritzen, C. P. , Bereiter-Hahn, J. , Schieffer, B. , Moosdorf, R. , Vogt, S. , and Blase, C. , 2016, “ Cyclic Three-Dimensional Wall Motion of the Human Ascending and Abdominal Aorta Characterized by Time-Resolved Three-Dimensional Ultrasound Speckle Tracking,” Biomech. Model Mechanobiol., 15(5), pp. 1375–1388. 10.1007/s10237-016-0769-2 [DOI] [PubMed] [Google Scholar]
- [18]. Astrand, H. , Stalhand, J. , Karlsson, J. , Karlsson, M. , Sonesson, B. , and Länne, T. , 2011, “ In Vivo Estimation of the Contribution of Elastin and Collagen to the Mechanical Properties in the Human Abdominal Aorta: Effect of Age and Sex,” J. Appl. Physiol., 110(1), pp. 176–187. (1985) 10.1152/japplphysiol.00579.2010 [DOI] [PubMed] [Google Scholar]
- [19]. Morrison, T. M. , Choi, G. , Zarins, C. K. , and Taylor, C. A. , 2009, “ Circumferential and Longitudinal Cyclic Strain of the Human Thoracic Aorta: Age-Related Changes,” J. Vasc. Surg., 49(4), pp. 1029–1036. 10.1016/j.jvs.2008.11.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Haraldsson, H. , Hope, M. , Acevedo-Bolton, G. , Tseng, E. , Zhong, X. , Epstein, F. H. , Ge, L. , and Saloner, D. , 2014, “ Feasibility of Asymmetric Stretch Assessment in the Ascending Aortic Wall With DENSE Cardiovascular Magnetic Resonance,” J. Cardiovasc. Magn. Reson., 16(1), p. 6. 10.1186/1532-429X-16-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Grytsan, A. , Watton, P. N. , and Holzapfel, G. A. , 2015, “ A Thick-Walled Fluid-Solid-Growth Model of Abdominal Aortic Aneurysm Evolution: Application to a Patient-Specific Geometry,” ASME J. Biomech. Eng., 137(3), p. 031008. 10.1115/1.4029279 [DOI] [PubMed] [Google Scholar]
- [22]. Farsad, M. , Zeinali-Davarani, S. , Choi, J. , and Baek, S. , 2015, “ Computational Growth and Remodeling of Abdominal Aortic Aneurysms Constrained by the Spine,” ASME J. Biomech. Eng., 137(9), (epub). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Wilson, J. S. , Baek, S. , and Humphrey, J. D. , 2013, “ Parametric Study of Effects of Collagen Turnover on the Natural History of Abdominal Aortic Aneurysms,” Proc. Math. Phys. Eng. Sci., 469(2150), p. 2150. 10.1098/rspa.2012.0556 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures


