Abstract
Pulmonary hypertension (PH) is a degenerative disease characterized by progressively increased right ventricular (RV) afterload that leads to ultimate functional decline. Recent observational studies have documented a decrease in left ventricular (LV) torsion during ejection, with preserved LV ejection fraction (EF) in pediatric and adult PH patients. The objective of this study was to develop a computational model of the biventricular heart and use it to evaluate changes in LV torsion mechanics in response to mechanical, structural, and hemodynamic changes in the RV free wall. The heart model revealed that LV torsion and apical rotation were decreased when increasing RV mechanical rigidity and during re-orientation of RV myocardial fibers, both of which have been demonstrated in PH. Furthermore, structural changes to the RV appear to have a notable impact on RV EF, but little influence on LV EF. Finally, RV pressure overload exponentially increased LV myocardial stress. The computational results found in this study are consistent with clinical observations in adult and pediatric PH patients, which reveal a decrease in LV torsion with preserved LV EF. Furthermore, discovered causes of decreased LV torsion are consistent with RV structural adaptations seen in PH rodent studies, which might also explain suspected stress-induced changes in LV myocardial gene and protein expression.
1. Introduction
During the progression of pulmonary hypertension (PH), the right ventricle (RV) undergoes a structural and morphological transformation [1], which ultimately leads to functional failure [2]. While most ongoing research has been focused on characterizing the RV's morphological, biomechanical, and metabolic changes [2,3], few studies have considered how these changes impact left ventricular (LV) function and contractile mechanics. Several observational imaging studies in children have shown that children with PH reveal significantly decreased LV strain and strain-rate during systole, compared with healthy controls [4–6]. However, the underlying mechanism for this observation is unclear and it is impossible to decipher from clinical imaging studies. The implications of this finding, however, are important for moderating RV functional decline, given that earlier animal studies have shown that the RV relies on mechanical energy transfer from the LV for contractile assistance [7,8].
We propose two possible underlying mechanisms for the observed decrease in LV torsion and torsion rate in PH: (1) the physical burden of biomechanical, geometric, and structural changes in the RV are disrupting normal LV mechanics during systole; and (2) changes in LV myocardial wall stress are altering contractile protein expression (switch from alpha to beta myosin heavy chain isoforms) in the LV. In fact, these two mechanisms are not mutually exclusive, and are likely to have a concurrent effect on LV contractile mechanics. To this end, we also propose that a computational model of the biventricular heart is the ideal modality for exposing the underlying mechanism of decreased LV torsion during PH. It allows us to compare LV contractile mechanics and myocardial stress between different scenarios of RV systolic function, with the power to consider the functional impact of changing a single variable (e.g., increased RV pressure overload or longitudinal RV fiber re-orientation during PH).
The objective of this study was to: (1) develop a computational model of the biventricular heart, which reveals physiological LV contractile mechanics; and (2) use the model to investigate possible biomechanical mechanisms for decreased LV torsion in children with PH. The overall hypothesis of the second objective is that RV remodeling commonly seen in RV pressure afterload pathology creates a mechanical burden on the LV during systole, which interferes with normal LV contractile mechanics and increases myocardial wall stress.
2. Methods
A biventricular finite element computational model (see Fig. 1) was developed to understand the biomechanical mechanistic sequence between RV pressure overload, seen in children with PH, and decreased LV systolic rotation and torsion.
Fig. 1.
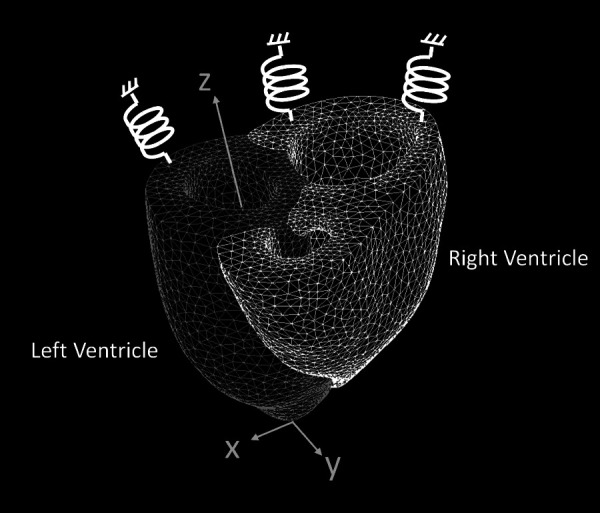
Finite element model of the heart, with the left (darker mesh) and right (lighter mesh) ventricles meshed as separate, but connected, bodies. Each node on the base is connected to a virtual six-degrees-of-freedom spring element that is fixed on the other end.
2.1. Reconstructing the Three-Dimensional Finite Element Model of the Heart.
The model was reconstructed from short-axis cine stack magnetic resonance imaging (MRI) of a healthy male pediatric subject (age = 10 years old), at end systole using ScanIP (Simplewear, Los Angeles, CA). Figure 1 shows a finite element mesh (also developed using ScanIP) of the heart model, with the LV (darker mesh) and RV (lighter mesh) discretized as separate bodies. The interventricular septum was considered part of the LV body. The final model had 13,691 linear tetrahedral elements (7538 nodes), which is substantially more than previously used in converged finite element analysis (FEA) models of the heart [9–11]. Our own mesh convergence study, comparing the 13,691 element model to a 191,724 element model, revealed a 2.1% difference in LV ejection fraction (EF); a 4.4% difference in RV EF; a 1.6% difference in temporally maximum second Piola–Kirchhoff stress throughout the duration of contraction, and a 9.6% difference in spatially maximum second Piola–Kirchhoff stress at end ejection (located 1.6 mm apart).
2.2. Modeling Fiber Orientation.
Fiber orientation within the myocardium was incorporated by computing a local coordinate system for each element, which was done with an in-house code written in matlab (using the built-in partial differential equation (PDE) solver). The local coordinate system consisted of and orthogonal vectors (see Fig. 2(a)). On the epi-and-endocardial surfaces, the orientation of the A–B plane was determined by the surface normal vector (). First, is determined on all endocardial and epicardial surface nodes by , where a = 1 and −1 on the endocardium and epicardium, respectively. Then, on each surface node is computed using . The orientation of the A–B plane within the myocardium was solved using the Poisson equation (, where is any scalar component of a vector) at the interior mesh nodes, and interpolated at the element centroid coordinate.
Fig. 2.
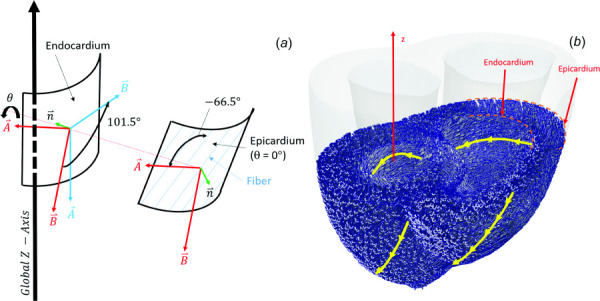
(a) Computation of fiber orientation within the local coordinate system, as it rotates across the myocardium according to Eq. (1). Red vectors represent local coordinate system before rotation (no rotation at the epicardium), and blue vectors represent the local coordinate system after rotation. Fibers are orientated −66.5 deg from the axis; (b) Representation of fiber orientation superimposed on the heart model. Yellow lines show fiber orientation along the epi/endocardium walls.
Once each element had been assigned a local A–B plane coordinate system (with normal, ), each coordinate system was rotated by some angle about . The amount of rotation was determined by Eq. (1), which was chosen to fit the nonlinear fiber angle variation along the thickness of the myocardium [12]. The boundary value problem in Eq. (1) was assigned a rotation angle of 0 at the endocardium and 101.5 deg at the epicardium [12], with the fibers orientated −66.5 deg from the vector within the A–B plane (see Fig. 2(a)). This technique resulted in a fiber orientation vector computed at the centroid of each element (see Fig. 2(b))
| (1) |
This approach is built on a previous technique for modeling fiber orientation in the human heart that was proposed by Wong and Kuhl [13]. However, it overcomes occasional zero-magnitude vectors that arise by linearly interpolating vectors that change direction across the myocardium.
2.3. Constitutive Parameters of the Heart (and Modeling Systolic Contraction).
The myriad of bi-axial mechanical studies on myocardial tissue appear to present varying results. In this study, we fit to mechanical properties of the dog RV to both ventricles in the baseline simulation (Sim 1) [14]. The myocardium of both ventricles has been shown to have similar mechanical properties in humans [15].
We represented ventricular mechanics using the Mooney–Rivlin (M–R) model with an added orthotropic term (last term of Eq. (2)), which accounts for the local fiber orientation vector (. Fiber orientation was computed using the technique outlined in Sec. 2.2. This has been done in multiple previous studies [9,16,17], and fits well to equal-biaxial tension data [14]. are invariants (computed using Eqs. (3)–(5)), which are a function of the Cauchy–Green deformation tensor, or stretch ratios ( along the direction, (i = 1, 2,3).
| (2) |
| (3) |
| (4) |
| (5) |
Equation (2) is divided into four terms, which are governed by six material constants: . The first two terms () describe the curvature of the stress–strain relationship [18]. The material constants C1 and C2 can be considered as the stiffness of the isotropic component, having units N/m2 (or Pa). The third term, with constants D1 and D2, is commonly added for modeling biological material [19], which can reveal exponential rises in the stress–strain curve as various structural proteins become engaged. The constant: D1 has units of stiffens (N/m2), while D2 is unitless and governs the rate of exponential rise in the stress–stretch curve. The last terms (with constants ) are added to the strain energy density function to include the aforementioned orthotropic effect. The units of are N/m2, which governs the stiffness along the fiber direction. is unitless and describes the nonlinearity of the stress–strain curve along the fibers.
The resulting six M–R constants used to characterize passive myocardial tissue were found by fitting Eq. (2) to the bi-axial data presented in Ref. [14] (fitting done using constrained minimization). These data are shown in Fig. 3(a), which presents Cauchy stress along the fiber () and sheet () axis directions [21] measured in a passive dog heart [14]. The fiber axis explains the mechanical properties along the organization of myocytes and collagen fibers. The sheet axis is perpendicular to the fiber axis (i.e., cross-fiber axis), but within the plane of the fibers. The normal axis is orthogonal to the fiber and sheet axis. Fitting to this data revealed the following passive mechanical properties: C1 = 0.0 Pa; C2 = 361.38 Pa; D1 = 130.67 Pa; D2 = 2.77. The orthotropic term in Eq. (2) was excluded during the passive pre-inflation phase (see Sec. 2.4). This was done by setting K1 = 0.0 Pa and K2 = 2.31, which also served as the initial condition of the ejection phase (see Fig. 3(a)).
Fig. 3.
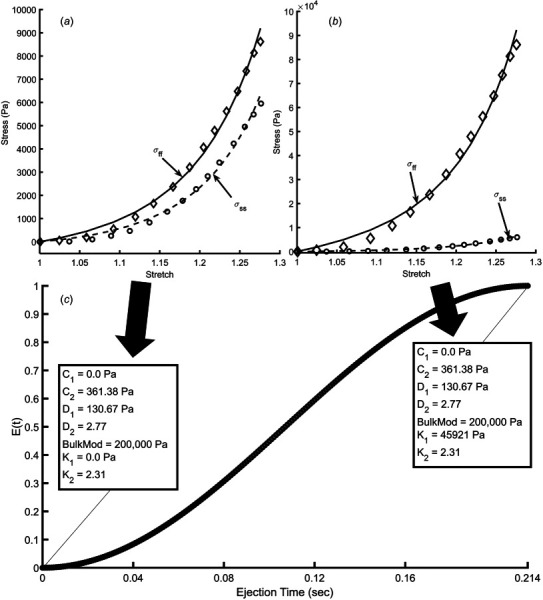
(a) Stress versus stretch curves along the fiber (ff) and sheet (ss) axis. Data are extracted from Ref. [14], obtained from passive RV myocardial tissue during an equal-biaxial mechanical testing experiment. (b) Stress versus stretch data computed to obtain Mooney–Rivlin (M–R) material constants at peak contraction. These data were created from data in (a), but modified by multiplying stress along the fiber direction tenfold at each stretch measurement. (c) Waveform describing the time variation in tissue stiffness during contraction (extracted from the elastance function in Ref. [20]), E(t). Values in boxes show M–R material constants at end diastole and end ejection.
2.4. Simulation Conditions (Modeling Systole).
The finite element model solves for nodal displacement for a prescribed endocardial inflation pressure and tissue mechanical properties (using the ADINA R&D Inc., Watertown, MA). To address the specific study questions, we considered interventricular mechanics during simulated ventricular ejection with a duration of 0.214 s (from beginning-ejection at end-diastole to end-ejection at end-systole), based on pressure waveforms computed using a zero-dimensional (0D) model of the entire cardiovascular system (explained in Sec. 2.4.1) [22,23]. Zero-dimensional models have been shown to simulate physiologically realistic ventricular pressures [24], and the waveforms developed in this study used input parameters from Ref. [23].
2.4.1. Applied Pressure Conditions.
Each simulation reported consisted of two phases: (1) pre-inflation of both ventricles and (2) ejection.
Phase 1: Pre-inflation—because the heart geometry was reconstructed from images at end-systole (just after ejection), a spatially uniform pressure was applied to the RV and LV endocardium to pre-inflate the ventricles to end diastolic volume (EDV). The RV and LV were pre-inflated to 18.33 mmHg (RV EDV = 84.77 mL) and 77.92 mmHg (LV EDV = 50.10 mL), respectively. These pre-inflation pressures were chosen to match the initial pressure at the ejection phase, which were dictated by the aforementioned 0D model.
Phase 2: Ejection—the duration of the ejection phase was simulated for 0.124 s, which was chosen to match the duration of ejection in the 0D model. RV and LV pressure versus time computed in the 0D model during ejection were applied as the spatially uniform pressure boundary conditions on the RV and LV endocardium during the FEA simulation. Fig. 4(a) shows how pressure applied to the RV endocardium varied in time during ejection for normal and hypertensive simulations (all simulations performed are described in Sec. 2.4.4). Fig. 4(b) shows the pressure applied to the LV endocardium during ejection for all simulations reported. Again, this waveform was taken from the 0D model simulated with normal impedance in the systemic circulation [23].
Fig. 4.
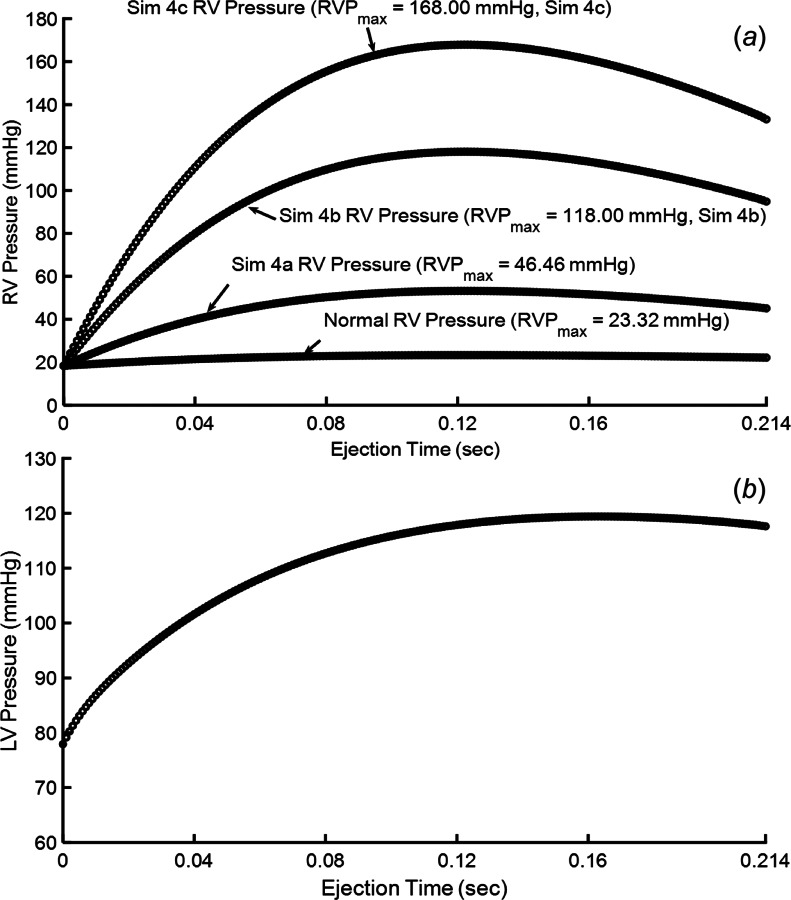
(a) Pressure waveforms applied to the RV endocardial surface under different simulations conditions and (b) pressure waveform applied to the LV endocardium in all reported simulations
2.4.2. Simulating Tissue Contraction.
The transition from a fully passive myocardium to active contraction was simulated by increasing tissue stiffness along the fiber direction, which mostly impacts the orthotropic terms of the M–R equation (Eq. (2)). Gradually increasing stiffness during the duration of the ejection phase was achieved by prescribing the tissue an artificial instantaneous time-varying function, E(t) that governs changes in the Mooney–Rivlin parameters (described in Sec. 2.3, see Figs. 3(a)–3(c)). Therefore, E of 0 and 1 correspond to completely passive and active myocardial tissue, respectively. The E (and therefore stiffness along the fiber directions) variable was assumed to increase in a nonlinear fashion (see Fig. 3(c)), based on the way that a typical time-varying ventricular elastance function behaves during contraction [25]. At peak contraction (E = 1), stress along the fiber direction ()—at a given stretch—is considered to undergo a tenfold increase, which results in the following orthotropic M–R constants: K1 = 45,921 Pa; K2 = 2.31. We settled on a tenfold increase in stress along the fiber direction, between passive and fully active tissue, because it returned the ventricle to end-systolic volume (±5% error) at the end of the 0.214 s ejection phase.
2.4.3. Fixed Boundary.
Finite element nodes on the top surface were restricted from moving in the z-direction and fixed to virtual six-degrees-of-freedom spring elements (see Fig. 1), that were fixed on one end, with a stiffness matrix: , where k = 10 N/m and is the identity matrix.
2.4.4. Simulations Executed.
The biventricular finite element model was simulated for a variety of biomechanical scenarios:
-
(1)
Normal LV and RV contraction (Sim1)—this modeling scenario was considered as the baseline, which simulated normal contraction for both ventricles. All other simulations were compared to this scenario.
-
(2)
Normal LV contraction while RV is passive (Sim2)—this scenario simulated normal LV contraction, but the RV free wall was kept completely passive for the entire duration of ejection.
-
(3)
Normal LV contraction with increased RV contractility (Sim 3)—this scenario simulated normal LV contraction. The RV M–R orthotropic parameter was set to K1 = 50513.1 Pa at peak construction (E = 1), which amounts to a 10% increase in RV contractility.
-
(4)Normal LV contraction with increased RV pressure overload (Sim 4a-c)—this scenario simulated normal physiological pressure applied to the LV epicardium, but with three RV pressure overload scenarios of progressively increasing severity (see Fig. 4(a)):
-
aRVPmax = 46.46 mmHg
-
bRVPmax = 118.00 mmHg
-
cRVPmax = 168.00 mmHg.
-
a
-
(5)
Normal LV contraction with increased RV stiffness (Sim 5)—Hill et al. [3] showed that—under RV pressure overload conditions—the RV free-wall undergoes stiffening along the fiber and sheet axis. This was simulated by extracting Mooney–Rivlin coefficients from a stress–stretch curve given in Ref. [14], but where every stress measurement in Ref. [14] was doubled at every data-point of stretch. Fitting to this reconstructed curve, the RV free-wall constants from the isotropic part of the Mooney–Rivlin equation were increased to . The orthotropic constants () were not changed and varied during systolic contraction as shown in Fig. 3(c). This simulation was executed with RVPmax = 46.46 mmHg waveform (see Fig. 4(a)).
-
(6)
Normal LV contraction with RV myo-fiber re-orientation (Sim 6)—Rodent studies have shown that the RV free-wall myofibers become more longitudinally orientated in response to pressure overload [3]. In this simulation, the LV contraction and structure were identical to Sim1, but the RV endocardial fibers were orientated to −86.5 deg (rotating fibers at the epicardium to −178.0 deg).
Some studies have suggested interventricular electro-mechanical dyssynchrony during the progression of PH. This was not considered in this modeling study because the onset of contraction occurs simultaneously in both PH and control subjects, but the RV continues contracting roughly 100 ms after the LV has completed in PH patients [26], which could possibly contribute to diastolic recoil [27] but was not considered to be a probable contributor to decreased LV torsion in systole.
2.5. Measurements of Ventricular Volume and Left Ventricular Twist
2.5.1. Measuring Volume.
Instantaneous LV cavity volume was measured by creating a three-dimensional convex hull, using the “convhull” function in matlab (Mathworks, Natick, MA), to the nodes on the endocardial surface. The convex hull reconstruction was qualitatively inspected to confirm that vertices used for the convex hull properly enclose the volume. Furthermore, to numerically validate this approach, the volume of a mesh of the fluid cavity at the initial condition was compared against the volume computed using the convex hull approach (error < 1%).
2.5.2. Measuring Torsion.
Apex rotation (deg) was measured using the displacement of all finite element nodes located between z = 28–30 mm from the apex (z = 0 mm, where z is the location along the z-axis). Base rotation considered the displacement of all nodes located between z = 73–75 mm from the apex. First, translation between undeformed and deformed coordinates is removed by recentering both datasets to align the centroids. The optimal rotation about the z-axis between undeformed and deformed coordinates is then found based on the least-squares solution of the rotation matrix, which is based on single value decomposition [28]. Ventricular torsion (deg/cm) was found as the difference between apex and base rotation, divided by the length of the ventricle [29].
3. Results
Qualitative comparisons between simulated LV rotation (and twist) during ejection and patient-measured contractile mechanics show similar trends [30]. At the beginning of ejection, the apex and base rotate in the clockwise and counter-clockwise direction, respectively. However, the apex is rotating counter-clockwise during most of ejection and reverses just before the end of ejection.
3.1. The Impact of Right Ventricular–Left Ventricular Geometry and Structure on Left Ventricular Torsion
3.1.1. Normal Simulated Right Ventricular/Left Ventricular Systolic Function (Sim1).
Under normal simulation conditions, resulting RV and LV ejection fraction () was 37.89% and 50.84%, respectively (Fig. 5(a)). These values are higher in healthy children, but this discrepancy is suitable for the current study because they are used to compare against other simulated scenarios. Maximum LV apex rotation was 16.05 deg in the counter-clockwise direction, while the base slightly rotated in the clockwise direction (Fig. 5(b)).
Fig. 5.
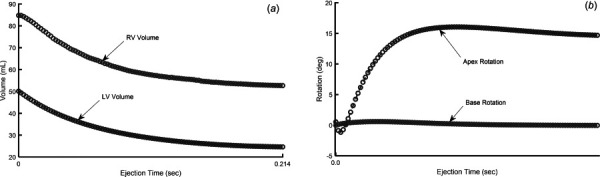
(a) Simulated changes in RV and LV volume during normal systolic contraction and (b) simulated apex and base rotation during normal systolic contraction
3.1.2. What Happens to Left Ventricular Torsion if the Right Ventricular is Not Contracting (Sim2)?.
A completely passive RV is not something one would expect in a clinical scenario. However, in this study, we performed a passive RV simulation to assess how RV contraction would influence LV contraction. As expected, a passive RV resulted in an EF of 4.08%, while the LV maintained a 49.22% EF (compared with 50.84% during Sim1). Notably, a noncontracting RV caused LV apical rotation to decrease by 30%, relative to Sim1 (see Figs. 6(a)–6(b)).
Fig. 6.
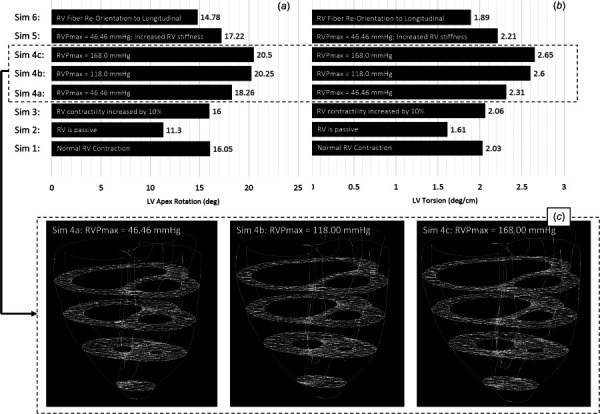
Left ventricular apex rotation (a) and LV twisting (b) at end ejection for eight simulated conditions. (c) Evidence of progressively worse septal flattening for Sim 4a-c, which still revealed progressively increasing LV apex rotation.
3.1.3. What Happens to Left Ventricular Torsion if Right Ventricular Contractility Is Increased (Sim 3)?.
Increasing RV contractility by 10% increased RV EF to 38.34%, without a significant change to LV EF (= 50.89%). Furthermore, increasing RV contractility did not reveal a significant change (<1.0%) in maximum LV apical rotation or LV twist (see Figs. 6(a) and 6(b)).
3.1.4. What Happens to Left Ventricular Torsion if Right Ventricular Pressure is Increased (Sim 4a-c)?.
Three simulations of gradually increasing RV pressure were conducted: (a) RVPmax = 46.46 mmHg, RVPmax/LVPmax = 0.39; (b) RVPmax = 118.0 mmHg, RVPmax/LVPmax = 0.99; (c) RVPmax = 168.0 mmHg, RVPmax/LVPmax = 1.41. Increasing RV pressure, and thus causing the interventricular septum to intrude into the LV cavity (see Fig. 6(c)) revealed an increase in apex rotation and LV twisting (see Figs. 6(a) and 6(b)). Simulations also revealed a linear relationship between increasing RV pressure and decreasing LV EF (R2 = 0.98, P2-tailed < 0.05—normal distribution of data was visually confirmed).
3.1.5. What Happens to Left Ventricular Torsion if Right Ventricular Stiffness Is Increased?.
The simulation increasing RV stiffness was done under hypertensive conditions (Sim 4a, RVPmax = 46.46 mmHg). Increasing RV stiffness causes RV EF to decrease to 21.8%, compared to 30.53% found in Sim 4a, but changes in the LV EF (= 50.46%) were negligible. Furthermore, LV apex rotation and twist were decreased by 5.7% and 4.3%, respectively, relative to Sim4a (see Figs. 6(a) and 6(b)).
3.1.6. What Happens to Left Ventricular Torsion if Right Ventricular Fiber Orientation Is Changed?.
A simulation re-orientating RV free-wall fiber orientation by 20 deg [3] (to near longitudinal) revealed a 7.9% decrease in LV apex rotation and 6.9% decrease in LV torsion, relative to Sim1. This also caused a 1.5% decrease to RV EF and a 1.7% increase to LV EF, relative to Sim1.
3.2. The Impact of Right Ventricular Remodeling on Left Ventricular Myocardial Stress.
In general, the location of maximum myocardial principal stress (P1) appears near the endocardium, and is heterogeneously distributed on the endocardial surface (see Figs. 7(a) and 7(b)). The second Piola–Kirchhoff stress appears gradually decreased across the thickness of the LV free wall to the epicardium. Under normal conditions (Sim 1), the LV myocardium appears to be under substantially higher mechanical stress than the RV. A simulation with a passive RV (Sim 2) or increased RV contractility (Sim 3) had little influence on changes in spatial LV stress distribution or maximum stress (<1.0%). Pressure overload in the RV, however, has a dramatic impact on RV and LV mechanical stress. Figure 7(c) shows that maximum temporal/spatial LV stress is exponentially increased with increasing RVPmax (R2 = 0.99, P2-tailed < 0.05). Although, the relationship is only slightly exponential and almost linear.
Fig. 7.
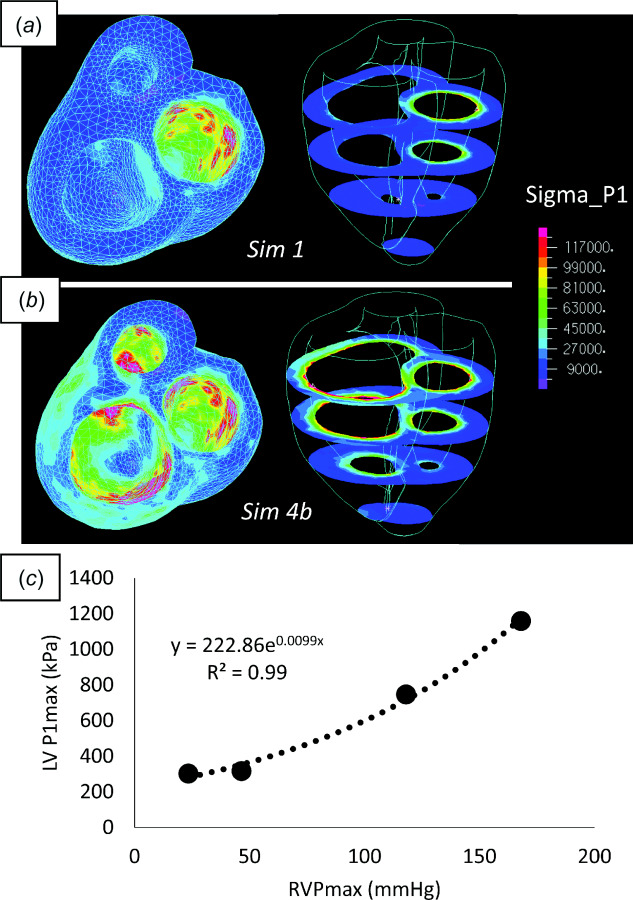
(a) Stress distribution under normal RV/LV ejection. (b) Stress distribution under severely hypertensive RV, with normal LV, ejection. Each plot shows a heat map of the first principal component of stress (P1) superimposed on the endocardial surface viewing the ventricle from the base (left) and at four planes cut along the short axis of the heart (right). (c) Exponential (although near-linear) correlation between maximum RV pressure and the temporal/spatial maximum of P1.
Finally, changing RV fiber orientation (Sim 6) had no impact on LV endocardial stress distribution or maximum stress (< 1.0%).
4. Discussion
4.1. Structure and Contractile Mechanics of the Left Ventricular.
The structure of the heart includes a complex network of fibers. LV myocardial fibers gradually transition from a left-handed helix on the epicardium to a right-handed helix on the endocardium [30,31]. During contraction, fibers on the epicardium generate a higher moment about the longitudinal axis than those on the endocardium, and therefore dominate the overall direction of rotation through this mechanical advantage [32].
Before beginning the discussion on physiological and pathological LV rotational mechanics, it is important to consider how this is measured. There are three primary clinical methods for measuring LV rotation/torsion: (1) speckle tracking echocardiography; (2) MRI with tissue tagging; (3) and cine MRI with feature tracking. While tagged MRI is considered the clinical reference standard [33], the majority of clinical studies rely on speckle tracking echocardiography because it is easy to acquire, portable, and relatively inexpensive. Unfortunately, quantitative agreement between tagged MRI and speckle tracking echocardiography is poor [33], and qualitative comparison of the apical rotation versus time measured using the three methods reveals concerning discrepancies (tagged MRI—[34]; feature tracking MRI—[29]; and speckle tracking echocardiography—[35].
Based on speckle tracking echocardiography in healthy children, early systolic contraction (≈ 20% of systolic time, and mostly in the isovolumic contraction phase) reveals a brief clockwise rotation of the apex ( ≈ 0.1 deg), which is followed by a rapid counter-clockwise rotation to a maximum of ≈ −13.9 deg that occurs just prior to the end of ejection [36]. The base rotates in the counter-clockwise direction to ≈ −3.4 deg in early systole, and reverses to ≈ 5.0 deg in the clockwise direction by the end of ejection. As a result, the global LV torsion during ejection follows a similar waveform to that of apical rotation, and reaches a peak value of ≈ 2.9 deg/cm [36].
Speckle tracking studies comparing children with PH and controls did not find a significant difference in LV torsion and torsion rate between the two groups [37]. However, the PH population in this study was etiologically heterogeneous. Furthermore, some controls were assessed when undergoing evaluation for murmurs, chest pains, palpitations, and syncope. An ongoing tagged MRI study comparing controls (N = 17) and group 1 PH (pulmonary arterial hypertension, N = 19) children at our institution is revealing a significantly decreased LV torsion and torsion rate in PH, and that a decrease in LV torsion rate is highly correlated with multiple metrics of decreased RV function [4,6,38]. Furthermore, a speckle tracking echocardiography study in adults also showed that PH patients revealed a significantly decreased LV torsion, compared with controls [5].
Therefore, given these recent observational studies showing decreased LV torsion in PH (and generally RV pressure afterload pathology), the following discussion offers some mechanistic explanation for these findings.
4.2. The Impact of Right Ventricular Geometry, Structure, and Hemodynamics on Left Ventricular Systolic Function/Torsion.
There is an overwhelming amount of evidence to suggest drastic RV remodeling in response to pressure overload [2,3,39–42], which is commonly attributed to ultimate RV functional decline [43]. However, there has not been a lot of research focusing on the impact of (and on) the LV. Extrapolating volume from two-dimensional echocardiography, Burkett et al. [27] found children with PH had a lower LV EF compared to controls. Our own studies, computing LV volume from MRI, showed no statistical difference between PH and control (CTL) children [6] even though torsion/torsion rate is decreased. Echocardiographic comparison between CTL and PH adults also showed no statistical difference in LV EF [5], although the observed reduced LV systolic strain was associated with early mortality [44]. These observations on changing LV systolic function—in response to RV pressure overload—are consistent with our findings in this computational study. Our simulations show that a passive RV directly interferes with normal LV rotation, but not ejection fraction. In fact, most simulated structural changes to the RV resulted in notable changes to LV rotation and negligible changes to EF.
Simulating a 10% increase in RV contractility did not have a notable impact on LV EF or rotation. Increasing RV contractility is a normal adaptive response to rising pulmonary arterial impedance [45]. In our previous imaging study, comparing LV torsion between PH and CTL children, we found a significant correlation between decreasing LV torsion and decreasing RV contractility [38]. While a correlation could not allude to a possible mechanism, we speculated decreasing LV rotation/torsion was impacting RV contractility, but we could not rule out the possibility that RV contractility was impacting LV torsion. This was based on previous studies by Damiano et al., which showed LV contraction can generate 80% of the pressure and flow in a passive RV, but not the other way around [8]. This modeling study suggests that RV contractility has little impact on the LV, but additional work is needed to definitively identify the LV as the mechanistic culprit.
Computational models of interventricular mechanics have shown that interventricular pressure gradients can have a major impact on ventricular pump mechanics and septal dynamics [42]. Imaging studies in children with PH showed a direct correlation between interventricular septal flatting and decreased LV torsion [38]. Given these findings, we suspected that increasing RV pressure in our simulation—and therefore inflicting septal flattening—would reveal a mechanical burden on the LV and decrease rotation/torsion. Surprisingly, simulation results revealed the complete opposite phenomenon. As the RV endocardium was subjected to incrementally higher maximum pressure during simulated ejection, there was a concurrent increase in septal flattening and LV rotation. From a purely biomechanical perspective, this would suggest that septal flattening—due to increased RV ejection pressure—does not present a mechanical burden on LV twisting mechanics and could possibly even provide some mechanical assistance. Therefore, the aforementioned correlation observed between septal flattening and decreased LV torsion in PH children could either be a result of some biomechanical factor that concurrently influences both observations or possibly some factor that is not biomechanical (discussed in Sec. 4.3).
Increased RV myocardial stiffness has been observed in experimental models of PH and pulmonary artery banding [3,46]. This is due to a concurrent increase in fibrosis and myofibril-mediated stiffening [46,47]. In this computational study, simulating RV myocardial stiffening was done under elevated RV ejection pressure and should be compared to Sim 4a. To this end, we show that increasing RV stiffness can have a negative impact on both RV systolic function and LV rotation mechanics. It is worth noting that our simulated increase in stiffness occurs without a simultaneous change in thickness or other morphological changes. This can be seen as both a limitation (discussed in Sec. 4.6) and an opportunity to evaluate the impact of only RV stiffening, which is not possible clinically or under experimental conditions.
In addition to changes to RV stiffening, RV structural adaptation also includes myo-and collagen fiber re-orientation along the longitudinal axis [3]. Under normal conditions, the shortening of the RV during contraction is greater longitudinally, relative to radial shortening [47], but the efficacy of further longitudinal fiber re-orientation on RV contractility has not been investigated. In our computational study, this re-orientation actually caused a slight decrease in RV EF and a notable decrease in LV rotation. Future studies will need to investigate if this decrease in LV rotation further exacerbates declining RV function, given the influence of LV contraction of RV pressure generation [8].
4.3. The Impact of Left Ventricular Myocardial Stress on Gene Expression (Speculated Discussion).
Right ventricular pressure overload simulations (Sim 4a–c) resulted in a notable increase in LV myocardial stress, which has been supported by other computational studies of PH [11]. It is critical to note that the absolute values of myocardial stress being reported should not be considered as actual physiological stress acting on the tissue. The purpose of these simulations was to evaluate the relative increase/decrease in stress under different biomechanical scenarios and assess general trends.
Gene expression in cardiomyocytes is known to be sensitive to mechanical stress and pressure [48]. Previous studies have shown that the RV of rats with pressure overload becomes hypertrophic, fibrotic, and undergoes changes in fiber orientation [3]. Furthermore, some studies have also shown changes in contractile protein expression (a shift from alpha to beta Myosin Heavy Chain isoforms [49]), which are responsible for slower and less powerful contraction [50]. This could rightfully lead researchers to speculate two possible scenarios of progression to RV dysfunction: (1) contractile protein expression becomes largely beta dependent in both ventricles, which disrupts RV contractile function and LV–RV mechanical energy transfer; and/or (2) contractile protein expression becomes largely beta dependent in the RV, but the changes in LV mechanics are simply a result of the mechanical burden of the stiffer RV, which inevitably disrupt LV–RV mechanical energy transfer. The current study does not settle this debate, but rather suggests that the observed decrease in LV torsion/torsion rate could be a result of simultaneous (or possibly sequential) changes in interventricular biomechanics and LV myocardial stress. However, it cannot be ruled out that increased LV myocardial stress could be driving changes in LV fiber orientation and gene/protein expression, as has been observed in the hypertensive RV [3,49,51].
4.4. The Clinical/Research Impact of Decreased Left Ventricular Torsion and Future Work.
The current study suggests that physicians treating PH patients might need to direct some clinical prognostic focus to the LV, but look beyond the EF. Because RV stiffness and fiber orientation cause a decrease in LV systolic torsion, which can be measured by a myriad of imaging modalities [33,52,53], LV torsion mechanics are a potential surrogate of RV structure/function/hemodynamics. Furthermore, because the RV is relying on LV mechanical energy transfer during systole [8,54], redirecting clinical focus to preserving or improving proper LV contractile mechanics (e.g., increased torsion-rate) could serve to improve RV systolic function, which will need to be investigated in future work.
Left ventricular systolic twisting is also believed to have a large impact on recoil [55], which is decreased in children with PH [27]. Future computational and clinical studies will need to investigate the impact of decreased LV systolic rotation on diastolic function.
4.5. Study Limitations
-
(1)
The current study only considered the geometry reconstructed from a single healthy subject. This geometry is used to simulate both healthy and hypertensive conditions, but the RV is known to undergo wall thickening and morphological remodeling in response to pressure overload [56]. Performing a simulation that would account for increased RV wall thickness would undoubtedly lower peak RV myocardial stress and could impact LV systolic mechanics. Future studies will perform simulations across a range of geometries from normotensive and hypertensive patients.
-
(2)
The short-axis image set available did not provide enough longitudinal resolution to cut the heart model further anterior. The model had to be fixed at nodes on the cut plane at the base, which could interfere with computed myocardial torsion mechanics.
-
(3)
Myocardium mechanical properties were obtained from equal-biaxial mechanical testing data, while neglecting shear stress data and biaxial data at different stretch ratios. This could have had an impact on absolute stress and displacement values in our simulation.
In fact, many of the input parameters (e.g., the stiffness of springs attached to the base) were chosen through trial and error, to achieve ventricular ejection in accordance with physiological norms. These limitations could influence the computed value for torsion, but this study was more focused on relative comparisons of torsion between multiple scenarios. Therefore, while these input parameters could have a significant impact on a resulting computed value (e.g., displacement, stress), they are not as likely to have a large impact when comparing changes in displacement and stress between two comparable simulations.
-
(4)
In simulations 4a–c, the 3 RV pressure waveforms applied to the endocardium were intended to simulate pressure overloaded conditions and recreate septal flattening. However, while the waveforms in Fig 4(a) simulate incrementally increasing maximum systolic pressure, all simulations started at the same initial-ejection pressure, which occurs at the end of the isovolumetric contraction phase. This is physiologically inaccurate because RV initial-ejection pressure is known to increase with PH severity [57], but this was not included in our simulations because we wanted to compare all scenarios starting at the same EDV and residual stress.
-
(5)
Simulating RV stiffening, which is a common phenotype of RV remodeling during PH, presented two primary difficulties: (a) we wanted to start all compared modeling scenarios at the same EDV and end-diastolic pressure (EDP), so the M–R material constants during the pre-inflation phase and at initial condition of the ejection phase were for a normal RV; and (b) simulating a stiffer RV under normotensive conditions required a small Δt due to a rapid contraction, so this scenario was simulated under hypertensive conditions.
5. Conclusion
Multiple recent observational studies have noted a decrease in LV contractile torsion/torsion rate in the adult and pediatric PH, which is present across multiple etiological PH groups. The objective of this study was to investigate some potential mechanisms for this phenomenon, using a finite element computational model of the biventricular heart.
We found that changes in RV free-wall stiffness and fiber orientation, both of which have been documented in mice after pulmonary arterial banding, can lead to a reduction in systolic LV torsion. To our surprise, RV pressure overload, and subsequent interventricular septal flattening, did not have the same impact on LV torsion. However, it did lead to a large increase in LV myocardial stress.
We postulate that the observed decrease in LV torsion/torsion rate in PH patients is driven by changes in RV stiffness and fiber re-orientation. Furthermore, an increase in LV myocardial stress could also be leading to structural and gene/protein expression changes that interrupt interventricular mechanical energy transfer between the two ventricles, which could be an important mechanism in the progressive decline of RV function during PH.
Acknowledgment
NIH NHLBI K25 HL133481, NIH NHLBI K23HL135352, NIH RO1 HL 114753, NIH/NCATS Colorado CTSA Grant Number UL1 TR002535, Actelion ENTELLIGENCE Young Investigator Award, American Thoracic Society Robyn J. Barst Young Investigator Award, Children's Hospital Colorado CCTSI Maternal and Child Award, Children's Hospital Colorado Research Scholar Award, Jayden DeLuca Foundation, Children's Hospital Co Research Scholar Award.
Contributor Information
Vitaly O. Kheyfets, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: vitaly.kheyfets@ucdenver.edu.
Uyen Truong, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: Uyen.Truong@childrenscolorado.org.
Dunbar Ivy, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: Dunbar.Ivy@childrenscolorado.org.
Robin Shandas, University of Colorado Anschutz Medical Campus, , Children's Hospital Colorado, , Aurora, CO 80045 , e-mail: robin.shandas@ucdenver.edu.
References
- [1]. Chin, K. M. , Kim, N. H. , and Rubin, L. J. , 2005, “ The Right Ventricle in Pulmonary Hypertension,” Coron. Artery Dis., 16(1), pp. 13–18. 10.1097/00019501-200502000-00003 [DOI] [PubMed] [Google Scholar]
- [2]. van de Veerdonk, M. C. , Bogaard, H. J. , and Voelkel, N. F. , 2016, “ The Right Ventricle and Pulmonary Hypertension,” Heart Failure Rev., 21(3), pp. 259–271. 10.1007/s10741-016-9526-y [DOI] [PubMed] [Google Scholar]
- [3]. Hill, M. R. , Simon, M. A. , Valdez-Jasso, D. , Zhang, W. , Champion, H. C. , and Sacks, M. S. , 2014, “ Structural and Mechanical Adaptations of Right Ventricle Free Wall Myocardium to Pressure Overload,” Ann. Biomed. Eng., 42(12), pp. 2451–2465. 10.1007/s10439-014-1096-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Dufva, M. J. , Truong, U. , Shandas, R. , and Kheyfets, V. O. , 2016, “ Left Ventricular Torsion Rates by CMR Correlate With Invasively-Derived Hemodynamic Data in Pediatric Pulmonary Hypertension,” J. Cardiovasc. Magn. Reson., 18(Suppl 1), p. 4. 10.1186/1532-429X-18-S1-P4 [DOI] [Google Scholar]
- [5]. Puwanant, S. , Park, M. , Popovic, Z. B. , Tang, W. H. , Farha, S. , George, D. , Sharp, J. , Puntawangkoon, J. , Loyd, J. E. , Erzurum, S. C. , and Thomas, J. D. , 2010, “ Ventricular Geometry, Strain, and Rotational Mechanics in Pulmonary Hypertension,” Circulation, 121(2), pp. 259–266. 10.1161/CIRCULATIONAHA.108.844340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Kheyfets, V. O. , Dufva, M. , Ivy, D. , Shandas, R. , and Truong, U. , 2017, “ Decreasing LV Torsion Rate Causes Inter-Ventricular Mechanical De-Coupling and Thereby Disrupts RV Function in Pediatric Pulmonary Hypertension,” American Heart Association Scientific Sessions, Circulation, Anaheim, CA. [Google Scholar]
- [7]. Hoffman, D. , Sisto, D. , Frater, R. W. , and Nikolic, S. D. , 1994, “ Left-to-Right Ventricular Interaction With a Noncontracting Right Ventricle,” J. Thorac. Cardiovasc. Surg., 107(6), pp. 1496–1502.https://www.jtcvs.org/article/S0022-5223(12)70150-2/pdf [PubMed] [Google Scholar]
- [8]. Damiano, R. J., Jr. , La Follette, P., Jr. , Cox, J. L. , Lowe, J. E. , and Santamore, W. P. , 1991, “ Significant Left Ventricular Contribution to Right Ventricular Systolic Function,” Am. J. Physiol., 261(5), pp. H1514–H1524. 10.1152/ajpheart.1991.261.5.H1514 [DOI] [PubMed] [Google Scholar]
- [9]. Tang, D. , Yang, C. , Geva, T. , and Del Nido, P. J. , 2010, “ Image-Based Patient-Specific Ventricle Models With Fluid-Structure Interaction for Cardiac Function Assessment and Surgical Design Optimization,” Prog. Pediatr. Cardiol., 30(1–2), pp. 51–62. 10.1016/j.ppedcard.2010.09.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Genet, M. , lee, L. C. , Kuhl, E. , and Guccione, J. , 2014, “ Abaqus/Standard-Based Quantification of Human Cardiac Mechanical Properties,” SIMULIA Community Conference, Providence, RI, May 20–24.https://www.researchgate.net/publication/301872735_AbaqusStandard-based_quantification_of_human_cardiac_mechanical_properties
- [11]. Xi, C. , Latnie, C. , Zhao, X. , Tan, J. L. , Wall, S. T. , Genet, M. , Zhong, L. , and Lee, L. C. , 2016, “ Patient-Specific Computational Analysis of Ventricular Mechanics in Pulmonary Arterial Hypertension,” ASME J. Biomech. Eng., 138(11), p. 111001. 10.1115/1.4034559 [DOI] [PubMed] [Google Scholar]
- [12]. Papadacci, C. , Finel, V. , Provost, J. , Villemain, O. , Bruneval, P. , Gennisson, J. L. , Tanter, M. , Fink, M. , and Pernot, M. , 2017, “ Imaging the Dynamics of Cardiac Fiber Orientation In Vivo Using 3D Ultrasound Backscatter Tensor Imaging,” Sci. Rep., 7(1), p. 830. 10.1038/s41598-017-00946-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Wong, J. , and Kuhl, E. , 2014, “ Generating Fibre Orientation Maps in Human Heart Models Using Poisson Interpolation,” Comput. Methods Biomech. Biomed. Eng., 17(11), pp. 1217–1226. 10.1080/10255842.2012.739167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Sacks, M. S. , and Chuong, C. J. , 1993, “ Biaxial Mechanical Properties of Passive Right Ventricular Free Wall Myocardium,” ASME J. Biomech. Eng., 115(2), pp. 202–205. 10.1115/1.2894122 [DOI] [PubMed] [Google Scholar]
- [15]. Blair, C. A. , Guglin, M. E. , Stromberg, A. , and Campbell, K. S. , “ Myocardium From the Left and Right Ventricles of Human Hearts Have Similar Mechanical Properties,” Biophys. J., 110(3), p. 296a. 10.1016/j.bpj.2015.11.1596 [DOI] [Google Scholar]
- [16]. Yang, C. , Tang, D. , Haber, I. , Geva, T. , and Del Nido, P. J. , 2007, “ In Vivo MRI-Based 3D FSI RV/LV Models for Human Right Ventricle and Patch Design for Potential Computer-Aided Surgery Optimization,” Comput. Struct., 85(11–14), pp. 988–997. 10.1016/j.compstruc.2006.11.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Tang, D. , Yang, C. , Geva, T. , Gaudette, G. , and Del Nido, P. J. , 2011, “ Multi-Physics MRI-Based Two-Layer Fluid-Structure Interaction Anisotropic Models of Human Right and Left Ventricles With Different Patch Materials: Cardiac Function Assessment and Mechanical Stress Analysis,” Comput. Struct., 89(11–12), pp. 1059–1068. 10.1016/j.compstruc.2010.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Kumar, N. , and Rao, V. V. , 2016, “ Hyperelastic Mooney-Rivlin Model: Determination and Physical Interpretation of Material Constants,” MIT Int. J. Mech. Eng., 6(1), pp. 43–46.https://www.mitpublications.org/yellow_images/75618-me-book.43-46.pdf [Google Scholar]
- [19].ADINA R&D, Inc., 2015, Theory and Modeling Guide, ADINA R&D, Inc., Watertown, MA. [Google Scholar]
- [20]. Mukkamala, R. , 2000, “ A Forward Model-Based Analysis of Cardiovascular System Identification Methods,” Ph.D thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA. [Google Scholar]
- [21]. Holzapfel, G. A. , and Ogden, R. W. , 2009, “ Constitutive Modelling of Passive Myocardium: A Structurally Based Framework for Material Characterization,” Philos. Trans. A Math. Phys. Eng. Sci., 367(1902), pp. 3445–3475. 10.1098/rsta.2009.0091 [DOI] [PubMed] [Google Scholar]
- [22]. Heldt, T. , Mukkamala, R. , Moody, G. B. , and Mark, R. G. , 2010, “ CVSim: An Open-Source Cardiovascular Simulator for Teaching and Research,” Open Pacing Electrophysiol. Ther. J., 3, pp. 45–54. 10.2174/1876536X01003010001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Heldt, T. , Shim, E. B. , Kamm, R. D. , and Mark, R. G. , 2002, “ Computational Modeling of Cardiovascular Response to Orthostatic Stress,” J. Appl. Physiol., 92(3), pp. 1239–1254. 10.1152/japplphysiol.00241.2001 [DOI] [PubMed] [Google Scholar]
- [24]. Kheyfets, V. O. , Dunning, J. , Truong, U. , Ivy, D. , Hunter, K. , and Shandas, R. , 2016, “ A Zero-Dimensional Model and Protocol for Simulating Patient-Specific Pulmonary Hemodynamics From Limited Clinical Data,” ASME J. Biomech. Eng., 138(12), p. 121001. 10.1115/1.4034830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Suga, H. , Sagawa, K. , and Shoukas, A. A. , 1973, “ Load Independence of the Instantaneous Pressure-Volume Ratio of the Canine Left Ventricle and Effects of Epinephrine and Heart Rate on the Ratio,” Circ. Res., 32(3), pp. 314–322. 10.1161/01.RES.32.3.314 [DOI] [PubMed] [Google Scholar]
- [26]. Beyar, R. , 2008, “ Heart Inefficiency in Pulmonary Hypertension: A Double Jeopardy,” J. Am. Coll. Cardiol., 51(7), pp. 758–759. 10.1016/j.jacc.2007.11.033 [DOI] [PubMed] [Google Scholar]
- [27]. Burkett, D. A. , Slorach, C. , Patel, S. S. , Redington, A. N. , Ivy, D. D. , Mertens, L. , Younoszai, A. K. , and Friedberg, M. K. , 2016, “ Impact of Pulmonary Hemodynamics and Ventricular Interdependence on Left Ventricular Diastolic Function in Children With Pulmonary Hypertension,” Circ. Cardiovasc. Imaging, 9(9), pp. 1–11. 10.1161/CIRCIMAGING.116.004612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Arun, K. S. , Huang, T. S. , and Blostein, S. D. , 1987, “ Least-Squares Fitting of Two 3-D Point Sets,” IEEE Trans. Pattern Anal. Mach. Intell., PAMI-9(5), pp. 698–700. 10.1109/TPAMI.1987.4767965 [DOI] [PubMed] [Google Scholar]
- [29]. Kowallick, J. T. , Lamata, P. , Hussain, S. T. , Kutty, S. , Steinmetz, M. , Sohns, J. M. , Fasshauer, M. , Staab, W. , Unterberg-Buchwald, C. , Bigalke, B. , Lotz, J. , Hasenfuss, G. , and Schuster, A. , 2014, “ Quantification of Left Ventricular Torsion and Diastolic Recoil Using Cardiovascular Magnetic Resonance Myocardial Feature Tracking,” PLoS One, 9(10), p. e109164. 10.1371/journal.pone.0109164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Sengupta, P. P. , Tajik, A. J. , Chandrasekaran, K. , and Khandheria, B. K. , 2008, “ Twist Mechanics of the Left Ventricle: Principles and Application,” JACC Cardiovasc. Imaging, 1(3), pp. 366–376. 10.1016/j.jcmg.2008.02.006 [DOI] [PubMed] [Google Scholar]
- [31]. Nakatani, S. , 2011, “ Left Ventricular Rotation and Twist: Why Should We Learn?,” J. Cardiovasc. Ultrasound, 19(1), pp. 1–6. 10.4250/jcu.2011.19.1.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Taber, L. A. , Yang, M. , and Podszus, W. W. , 1996, “ Mechanics of Ventricular Torsion,” J. Biomech., 29(6), pp. 745–752. 10.1016/0021-9290(95)00129-8 [DOI] [PubMed] [Google Scholar]
- [33]. Edvardsen, T. , Gerber, B. L. , Garot, J. , Bluemke, D. A. , Lima, J. A. C. , and Smiseth, O. A. , 2002, “ Quantitative Assessment of Intrinsic Regional Myocardial Deformation by Doppler Strain Rate Echocardiography in Humans—Validation Against Three-Dimensional Tagged Magnetic Resonance Imaging,” Circulation, 106(1), pp. 50–56. 10.1161/01.CIR.0000019907.77526.75 [DOI] [PubMed] [Google Scholar]
- [34]. Carreras, F. , Garcia-Barnes, J. , Gil, D. , Pujadas, S. , Li, C. H. , Suarez-Arias, R. , Leta, R. , Alomar, X. , Ballester, M. , and Pons-Llado, G. , 2012, “ Left Ventricular Torsion and Longitudinal Shortening: Two Fundamental Components of Myocardial Mechanics Assessed by Tagged Cine-MRI in Normal Subjects,” Int. J. Cardiovasc. Imaging, 28(2), pp. 273–284. 10.1007/s10554-011-9813-6 [DOI] [PubMed] [Google Scholar]
- [35]. Esch, B. T. , Scott, J. M. , Warburton, D. E. , Thompson, R. , Taylor, D. , Cheng Baron, J. , Paterson, I. , and Haykowsky, M. J. , 2009, “ Left Ventricular Torsion and Untwisting During Exercise in Heart Transplant Recipients,” J. Physiol., 587(10), pp. 2375–2386. 10.1113/jphysiol.2009.170100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Kim, H. J. , Yoon, J. H. , Lee, E. J. , Oh, J. H. , Lee, J. Y. , Lee, S. J. , and Han, J. W. , 2015, “ Normal Left Ventricular Torsion Mechanics in Healthy Children: Age Related Changes of Torsion Parameters are Closely Related to Changes in Heart Rate,” Korean Circ. J., 45(2), pp. 131–140. 10.4070/kcj.2015.45.2.131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Burkett, D. A. , Slorach, C. , Patel, S. S. , Redington, A. N. , Ivy, D. D. , Mertens, L. , Younoszai, A. K. , and Friedberg, M. K. , 2015, “ Left Ventricular Myocardial Function in Children With Pulmonary Hypertension: Relation to Right Ventricular Performance and Hemodynamics,” Circ. Cardiovasc. Imaging, 8(8), p. e003260. 10.1161/CIRCIMAGING.115.003260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Dufva, M. , Truong, U. , Tiwari, P. , Ivy, D. , Shandas, R. , and Kheyfets, V. , 2018, “ Left Ventricular Torsion Rate and the Relation to Right Ventricular Function in Pediatric Pulmonary Arterial Hypertension,” Pulm. Circ., 8(8), pp. 1–10. 10.1177/2045894018791352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Cavasin, M. A. , Demos-Davies, K. M. , Schuetze, K. B. , Blakeslee, W. W. , Stratton, M. S. , Tuder, R. M. , and McKinsey, T. A. , 2014, “ Reversal of Severe Angioproliferative Pulmonary Arterial Hypertension and Right Ventricular Hypertrophy by Combined Phosphodiesterase-5 and Endothelin Receptor Inhibition,” J. Transl. Med., 12, p. 314. 10.1186/s12967-014-0314-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. van Wolferen, S. A. , Marcus, J. T. , Boonstra, A. , Marques, K. M. , Bronzwaer, J. G. , Spreeuwenberg, M. D. , Postmus, P. E. , and Vonk-Noordegraaf, A. , 2007, “ Prognostic Value of Right Ventricular Mass, Volume, and Function in Idiopathic Pulmonary Arterial Hypertension,” Eur. Heart J., 28(10), pp. 1250–1257. 10.1093/eurheartj/ehl477 [DOI] [PubMed] [Google Scholar]
- [41]. Aguero, J. , Ishikawa, K. , Hadri, L. , Santos-Gallego, C. , Fish, K. , Hammoudi, N. , Chaanine, A. , Torquato, S. , Naim, C. , Ibanez, B. , Pereda, D. , Garcia-Alvarez, A. , Fuster, V. , Sengupta, P. P. , Leopold, J. A. , and Hajjar, R. J. , 2014, “ Characterization of Right Ventricular Remodeling and Failure in a Chronic Pulmonary Hypertension Model,” Am. J. Physiol. Heart Circ. Physiol., 307(8), pp. H1204–H1215. 10.1152/ajpheart.00246.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42]. Lumens, J. , Delhaas, T. , Kirn, B. , and Arts, T. , 2009, “ Three-Wall Segment (TriSeg) Model Describing Mechanics and Hemodynamics of Ventricular Interaction,” Ann. Biomed. Eng., 37(11), pp. 2234–2255. 10.1007/s10439-009-9774-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Naeije, R. , and Manes, A. , 2014, “ The Right Ventricle in Pulmonary Arterial Hypertension,” Eur. Respir. Rev., 23(134), pp. 476–487. 10.1183/09059180.00007414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Hardegree, E. L. , Sachdev, A. , Fenstad, E. R. , Villarraga, H. R. , Frantz, R. P. , McGoon, M. D. , Oh, J. K. , Ammash, N. M. , Connolly, H. M. , Eidem, B. W. , Pellikka, P. A. , and Kane, G. C. , 2013, “ Impaired Left Ventricular Mechanics in Pulmonary Arterial Hypertension: Identification of a Cohort at High Risk,” Circ. Heart Fail, 6(4), pp. 748–755. 10.1161/CIRCHEARTFAILURE.112.000098 [DOI] [PubMed] [Google Scholar]
- [45]. Bellofiore, A. , and Chesler, N. C. , 2013, “ Methods for Measuring Right Ventricular Function and Hemodynamic Coupling With the Pulmonary Vasculature,” Ann. Biomed. Eng., 41(7), pp. 1384–1398. 10.1007/s10439-013-0752-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Rain, S. , Andersen, S. , Najafi, A. , Gammelgaard Schultz, J. , da Silva Goncalves Bos, D. , Handoko, M. L. , Bogaard, H. J. , Vonk-Noordegraaf, A. , Andersen, A. , van der Velden, J. , Ottenheijm, C. A. , and de Man, F. S. , 2016, “ Right Ventricular Myocardial Stiffness in Experimental Pulmonary Arterial Hypertension: Relative Contribution of Fibrosis and Myofibril Stiffness,” Circ. Heart Fail, 9(7), p. e002636. 10.1161/CIRCHEARTFAILURE.115.002636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47]. Haddad, F. , Hunt, S. A. , Rosenthal, D. N. , and Murphy, D. J. , 2008, “ Right Ventricular Function in Cardiovascular Disease—Part I: Anatomy, Physiology, Aging, and Functional Assessment of the Right Ventricle,” Circulation, 117(11), pp. 1436–1448. 10.1161/CIRCULATIONAHA.107.653576 [DOI] [PubMed] [Google Scholar]
- [48]. Friehs, I. , Cowan, D. B. , Choi, Y. H. , Black, K. M. , Barnett, R. , Bhasin, M. K. , Daly, C. , Dillon, S. J. , Libermann, T. A. , McGowan, F. X. , del Nido, P. J. , Levitsky, S. , and McCully, J. D. , 2013, “ Pressure-Overload Hypertrophy of the Developing Heart Reveals Activation of Divergent Gene and Protein Pathways in the Left and Right Ventricular Myocardium,” Am. J. Physiol. Heart Circ. Physiol., 304(5), pp. H697–H708. 10.1152/ajpheart.00802.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Lowes, B. D. , Minobe, W. , Abraham, W. T. , Rizeq, M. N. , Bohlmeyer, T. J. , Quaife, R. A. , Roden, R. L. , Dutcher, D. L. , Robertson, A. D. , Voelkel, N. F. , Badesch, D. B. , Groves, B. M. , Gilbert, E. M. , and Bristow, M. R. , 1997, “ Changes in Gene Expression in the Intact Human Heart: Downregulation of Alpha-Myosin Heavy Chain in Hypertrophied, Failing Ventricular Myocardium,” J. Clin. Invest., 100(9), pp. 2315–2324. 10.1172/JCI119770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Herron, T. J. , and McDonald, K. S. , 2002, “ Small Amounts of Alpha-Myosin Heavy Chain Isoform Expression Significantly Increase Power Output of Rat Cardiac Myocyte Fragments,” Circ. Res., 90(11), pp. 1150–1152. 10.1161/01.RES.0000022879.57270.11 [DOI] [PubMed] [Google Scholar]
- [51]. Kheyfets, V. O. , Dunning, J. , Truong, U. , Ivy, D. D. , Hunter, K. A. , and Shandas, R. , 2015, “ Assessment of N-Terminal Prohormone B-Type Natriuretic Peptide as a Measure of Vascular and Ventricular Function in Pediatric Pulmonary Arterial Hypertension,” Pulm. Circ., 5(4), pp. 658–666. 10.1086/683697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Haber, I. , Metaxas, D. N. , and Axel, L. , 2000, “ Three-Dimensional Motion Reconstruction and Analysis of the Right Ventricle Using Tagged MRI,” Med. Image Anal., 4(4), pp. 335–355. 10.1016/S1361-8415(00)00028-1 [DOI] [PubMed] [Google Scholar]
- [53]. Chuang, J. S. , Zemljic-Harpf, A. , Ross, R. S. , Frank, L. R. , McCulloch, A. D. , and Omens, J. H. , 2010, “ Determination of Three-Dimensional Ventricular Strain Distributions in Gene-Targeted Mice Using Tagged MRI,” Magn. Reson. Med., 64(5), pp. 1281–1288. 10.1002/mrm.22547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54]. Feneley, M. P. , Gavaghan, T. P. , Baron, D. W. , Branson, J. A. , Roy, P. R. , and Morgan, J. J. , 1985, “ Contribution of Left Ventricular Contraction to the Generation of Right Ventricular Systolic Pressure in the Human Heart,” Circulation, 71(3), pp. 473–480. 10.1161/01.CIR.71.3.473 [DOI] [PubMed] [Google Scholar]
- [55]. Drury, C. T. , Bredin, S. S. , Phillips, A. A. , and Warburton, D. E. , 2012, “ Left Ventricular Twisting Mechanics and Exercise in Healthy Individuals: A Systematic Review,” Open Access J. Sports Med., 2012(3), pp. 89–106. 10.2147/OAJSM.S32851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. Vonk-Noordegraaf, A. , Haddad, F. , Chin, K. M. , Forfia, P. R. , Kawut, S. M. , Lumens, J. , Naeije, R. , Newman, J. , Oudiz, R. J. , Provencher, S. , Torbicki, A. , Voelkel, N. F. , and Hassoun, P. M. , 2013, “ Right Heart Adaptation to Pulmonary Arterial Hypertension: Physiology and Pathobiology,” J. Am. Coll. Cardiol., 62(25), pp. D22–D33. 10.1016/j.jacc.2013.10.027 [DOI] [PubMed] [Google Scholar]
- [57]. Murch, S. D. , La Gerche, A. , Roberts, T. J. , Prior, D. L. , MacIsaac, A. I. , and Burns, A. T. , 2015, “ Abnormal Right Ventricular Relaxation in Pulmonary Hypertension,” Pulm. Circ., 5(2), pp. 370–375. 10.1086/681268 [DOI] [PMC free article] [PubMed] [Google Scholar]


