Implications of the ammonia distribution on Jupiter from 1 to 100 bars as measured by the Juno microwave radiometer

Abstract

The latitude-altitude map of ammonia mixing ratio shows an ammonia-rich zone at 0–5°N, with mixing ratios of 320–340 ppm, extending from 40–60 bars up to the ammonia cloud base at 0.7 bars. Ammonia-poor air occupies a belt from 5–20°N. We argue that downdrafts as well as updrafts are needed in the 0–5°N zone to balance the upward ammonia flux. Outside the 0–20°N region, the belt-zone signature is weaker. At latitudes out to ±40°, there is an ammonia-rich layer from cloud base down to 2 bars which we argue is caused by falling precipitation. Below, there is an ammonia-poor layer with a minimum at 6 bars. Unanswered questions include how the ammonia-poor layer is maintained, why the belt-zone structure is barely evident in the ammonia distribution outside 0–20°N, and how the internal heat is transported through the ammonia-poor layer to the ammonia cloud base.

1. Introduction

Juno’s microwave radiometer (MWR) probes Jupiter’s atmosphere down to pressures of a few hundred bars by measuring thermal radiation at wavelengths from 1–50 cm [Bolton et al., 2017; Janssen et al., 2017]. Variations in brightness temperature are interpreted as variations in ammonia rather than variations in physical temperature, because otherwise the winds would be an order of magnitude larger than those observed. Thus the MWR measures the distribution of ammonia below the weather layer, which is the part of the atmosphere influenced by clouds and precipitation. Thermochemical models [Atreya and Wong, 2005] put the ammonia cloud base at about 0.7 bars and the water cloud base in the 4–9 bar range depending on the water abundance. Models of evaporating rain [Seifert, 2008] extend the pressure range by a factor up to 1.5. The tops of the ammonia clouds are at pressures of a few hundred mbar. The total thickness of the weather layer is less than 0.2% the radius of the planet.

Absorption of sunlight and emission of infrared take place mostly in the weather layer [Sromovsky et al., 1998]. The absorbed sunlight falls off nearly as the cosine of latitude. The emitted infrared is essentially uniform on a global scale, although it varies slightly on the scale of the belts and zones—the half-dozen cloud bands and associated jet streams in each hemisphere that circle the planet at constant latitude [Pirraglia et al., 1981; Conrath et al., 1981; Gierasch et al., 1986; Ingersoll, 1990]. The total radiated power is 1.7 times the absorbed sunlight, and is greater than unity due to the internal heat left over from Jupiter’s formation. The global distributions of winds, heat fluxes, temperature gradients, and chemical species below the weather layer are largely unknown.

The Galileo probe carried instruments to measure temperature, pressure, composition, clouds, radiant flux, lightning, and energetic particles [Young, 2003], but it did so only at one place on the planet and only down to a pressure of 22 bars. The MWR scans pole-to-pole at six wavelengths with a footprint size at the equator of 0.5° in latitude. At microwave frequencies, ammonia vapor is the main opacity source, and the results reported here are based on the molar (or volume) mixing ratio of ammonia in ppm as a function of latitude and altitude. The MWR also measures the global water abundance, which will be the subject of a later paper.

Figure S1, in the Supplementary Online Material, shows the MWR data from two separate orbits, August 27, 2016 and December 11, 2016. This is Fig. 2 of Bolton et al. [2017] and is reproduced with permission. The data are north-south scans of brightness temperature in the six channels of the MWR at latitudes between ±40°. The channels cover different wavelengths and are sensitive to different pressure levels in the atmosphere [Janssen et al., 2017]. Channels 1–6 cover wavelengths of 50.0, 24.0, 11.55, 5.75, 3.0, and 1.37 cm, respectively. Their contribution functions in Jupiter’s atmosphere have maximum values at approximate pressure levels of 240, 30, 9, 3, 1.5, and 0.7 bars, respectively. The exact levels depend on the local ammonia abundance, since ammonia is the chief source of microwave opacity. The average measured brightness temperatures in the six channels are 850, 460, 330, 250, 190, and 150 K, respectively. Although the scans were taken 90° apart in longitude and 106 days apart in time, they are almost identical. This illustrates the steadiness and axisymmetry of Jupiter’s atmosphere and the high stability of the instrument. The scans show the nadir brightness temperatures, as if the spacecraft were looking straight down at the planet. The off-nadir data are still being analyzed. They are important for determining the water abundance and for measuring the atmosphere poleward of ±40°.

The top part of Figure 1, which is Fig. 3 of Bolton et al. [2017], shows the atmosphere in cross section with the molar mixing ratio of ammonia in parts per million (ppm). It was derived by inversion of the radiance data in Figure S1 [Li et al., 2017]. The estimated deep ammonia abundance is 362 ± 33 ppm, and the error of the individual vertical profiles is ± 50 ppm [Li et al., 2017, Figure 3]. The middle part of Figure 1 shows the mean zonal wind profile $\overline{\text{u}}\left(\text{y}\right)$, positive eastward, measured by tracking clouds at the top of the weather layer [Salyk et al., 2006]. The shaded bands are latitudes where the zonal wind profile is cyclonic. The shaded bands are the belts, and the light bands are the zones. Belts and zones have distinct properties, and the linkage to the deep ammonia distribution is considered in detail in this paper. The lower part of Figure 1 is proportional to the eddy momentum flux, which is derived from the residual winds after the zonal means have been subtracted off [Salyk et al., 2006].

Figure 1.

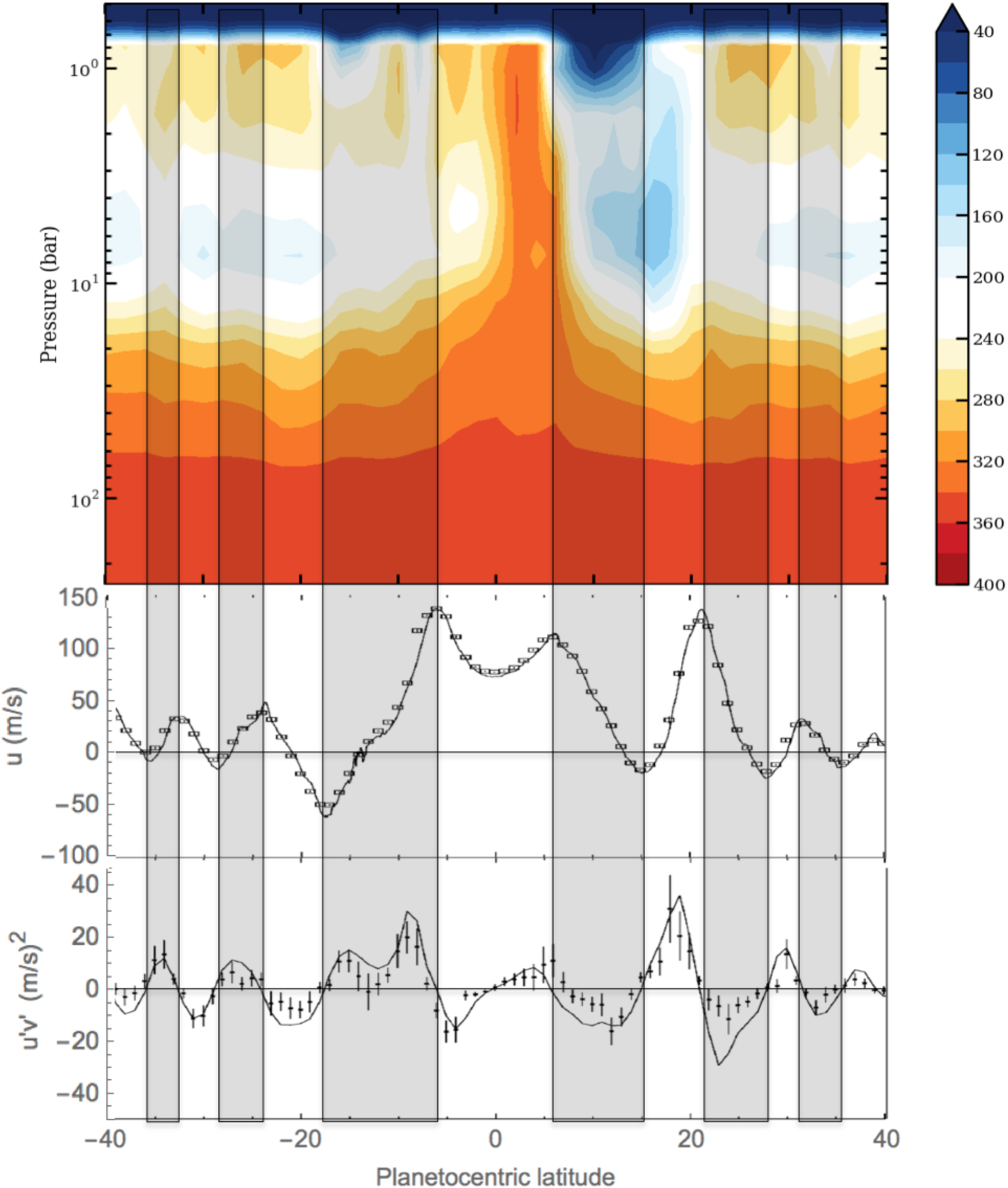
Top: molar mixing ratio of ammonia in parts per million with color code at right [Bolton et al., 2017; Janssen et al., 2017; Li et al., 2017]. Middle: zonal wind profile $\overline{\text{u}}\left(\text{y}\right)$, where y is the northward coordinate [Salyk et al., 2006]. Bottom: eddy velocity covariance $\overline{\text{u}\prime \text{v}\prime }$ (points, units m² s⁻²) and velocity gradient $\text{d}\overline{\text{u}}/\text{dy}$ (smooth curve, units 10⁻⁶ s⁻¹), from Salyk et al. [2006]. The gray bands are where the zonal winds are cyclonic ($\text{d}\overline{\text{u}}/\text{dy<0}$ in the north and $\text{d}\overline{\text{u}}/\text{dy>0}$ in the south). The white bands are anticyclonic.

These early MWR data reveal unexpected features that are related to the dynamics of Jupiter’s atmosphere below the visible clouds. At present the MWR analysis only includes ammonia, and one does not yet know the water abundance, the winds, or the temperatures except down to 22 bars at the Galileo probe site. Our purpose here is to pose the questions raised by the early MWR data and offer a few possible answers in the hope of stimulating further work on the dynamics of Jupiter’s atmosphere. Sections 2, 3, and 4 cover ammonia, belts and zones, and the angular momentum budget, respectively. In each section we summarize earlier measurements and we describe how the MWR data fit in. Section 5 summarizes our conclusions and reviews the unanswered questions.

2. Ammonia

Figure 1 looks like a meridional cross section of Earth’s troposphere with ammonia mixing ratio in place of relative humidity [Peixoto and Oort, 1996, Figure 4]. As on Earth, there appears to be a band of ammonia-rich air rising in the tropics and a band of ammonia-poor air sinking in the subtropics–a Hadley circulation. On Jupiter these bands are the northern half of the Equatorial Zone (EZ) from 0–5°N and the North Equatorial Belt (NEB) at 5–20°N, respectively. These figures suggest a net upward transport of water, which could not be in steady state. However on Earth, the water budget between high and low altitudes is closed by rain falling back to the surface. Similar arguments apply to Earth’s stratospheric methane, which is a tracer of the Brewer-Dobson circulation [Plumb, 2002, Figure 1]. Methane-rich air rises in the tropics, and methane-poor air sinks at higher latitudes, which suggests a net upward transport of methane. However, the budget is closed by chemical reactions in the stratosphere that oxidize methane to CO₂ and water.

On Jupiter, there is no “rain,” and there are no chemical reactions to close the ammonia budget. We calculate, using formulas in Seifert [2008], that solid spheres of ammonia with diameters 1 mm and 5 mm would evaporate completely before they reach pressures of 1 bar and 1.5 bar, respectively. These depths are probably an overestimate, because the falling particles are likely to be ammonia snowflakes rather than solid spheres. Below these levels, ammonia vapor is a conserved tracer. If air simply went up in the EZ and down in the NEB, there would be a net upward transport of ammonia. So from about 1.5 bars to 40–60 bars or deeper [Li et al., 2017] there must be an additional downward transport of ammonia in the vapor phase beside that in the NEB.

What are the constraints on this downward transport? The budget of the main constituents (H₂ + He) in the equatorial column requires ${\dot{\text{m}}}_{\text{up}}={\dot{\text{m}}}_{\text{dn}}+{\dot{\text{m}}}_{\text{po}}$, where ${\dot{\text{m}}}_{\text{up}}$ is the rate at which moles of the main constituents are going up in the EZ, ${\dot{\text{m}}}_{\text{po}}$ is the part that continues poleward into the NEB, and ${\dot{\text{m}}}_{\text{dn}}$ is the part that goes back down in the EZ. The units are moles time⁻¹. All quantities are positive, so ${\dot{\text{m}}}_{\text{up}}/{\dot{\text{m}}}_{\text{dn}}>1$. The corresponding ammonia mixing ratios are r_up, r_po, and r_dn. The ammonia budget requires ${\text{r}}_{\text{up}}{\dot{\text{m}}}_{\text{up}}={\text{r}}_{\text{po}}{\dot{\text{m}}}_{\text{po}}+{\text{r}}_{\text{dn}}{\dot{\text{m}}}_{\text{dn}}$. Eliminating ${\dot{\text{m}}}_{\text{po}}$ gives $\left({\text{r}}_{\text{dn}}-{\text{r}}_{\text{po}}\right)/\left({\text{r}}_{\text{up}}-{\text{r}}_{\text{po}}\right)={\dot{\text{m}}}_{\text{up}}/{\dot{\text{m}}}_{\text{dn}}>1$. The possibilities are either r_po > r_up > r_dn or else r_dn > r_up > r_po. We reject the first because Figure 1 shows that r_po < r_up: the air outside the EZ has a lower mixing ratio than the air inside. The second possibility says that on average, the downdrafts have a higher mixing ratio than the updrafts. This conclusion is independent of the respective areas of the updrafts and downdrafts.

To escape detection in Figure 1, the downdrafts either are at latitudes greater than ±40° or are embedded in the EZ and invisible to the MWR. The first possibility would require a giant Hadley cell transporting ammonia from the equator to the regions poleward of ±40°, which seems unlikely. The second possibility requires downdrafts that are denser than the average for fluid parcels in the EZ. Evaporating precipitation might densify the air in two ways, by cooling and by mass loading [Guillot, 1995; Li and Ingersoll, 2015]. Since ammonia has a higher molecular mass than the main constituents, and the ammonia-rich air has been cooled by evaporation, parcels of air below the cloud base would be denser than air in the updrafts, and would sink. If the effect of cooling were greater than that of mass loading, the downdrafts would be nearly invisible in Figure 1. Or the downdrafts might be below the resolution of the MWR. The columns could be 100’s of km wide and not show up in the figure. This is possible because of the 300-fold vertical exaggeration in Figure 1. For example, the 30-bar level is 150 km below cloud base, and the same distance in the figure covers 36° of latitude, or 45,000 km. The EZ itself is 6000 km wide.

Earth-based observations at radio wavelengths established that ammonia is depleted in the belts and enriched in the zones and that the atmosphere is generally depleted in ammonia down at least to the 6-bar pressure level, which is close to the base of the water cloud [de Pater et al., 1986; 2001; 2016]. Efforts to understand the data invoked horizontal mass transfer between belts and zones [Ingersoll et al., 2000] and downdrafts whose mixing ratio of ammonia exceeds that in the updrafts [Showman and de Pater, 2005], with results similar to ours above. What’s new is that the depleted layer extends down at least to 40–60 bars, much deeper than the water cloud base, and that there is only one belt and one zone that penetrate through this layer (Figure 1).

Sources and sinks of ammonia vapor are: ammonia ice clouds, clouds of ammonium hydrosulfide (NH₄SH), and clouds of liquid water/ammonia solution. However the amount of ammonia sequestered by the latter two cloud types is limited [Showman and de Pater, 2005]. The sulfur/nitrogen (S/N) abundance ratio measured by the probe is in the range 0.11 to 0.13, which represents the fraction of ammonia that can be removed by NH₄SH clouds. The fraction of ammonia that can be removed by water clouds is computed by taking the solar O/N ratio of 7.2 [Asplund et al., 2009] for the cloud as a whole, assuming all the water is liquid and all the ammonia is vapor with partial pressure and temperature appropriate to the base of the water cloud, and using the solubility of ammonia (http://www.engineeringtoolbox.com/gases-solubility-water-d_1148.html) to compute the fraction of ammonia in solution. The result is 0.03, so neither process will have a large impact on the ammonia vapor abundance. We consider it unlikely that multiple rainstorms would remove a larger fraction of the ammonia, because bringing water up to its lifting condensation level for successive storms would also bring up ammonia, leaving the removed fraction at 0.03. Since the sources and sinks of the vapor are small below the 1.5-bar level, ammonia vapor is a conserved tracer at deeper levels.

In inverting the brightness temperature data in Figure S1 one assumes that the horizontal variations are due to horizontal variations of opacity, i.e., ammonia, rather than horizontal variations of temperature. The rationale for this assumption is that real temperature variations T(y, P), i.e., temperature variations at constant pressure, would lead to impossibly large wind speeds. Winds are connected to temperatures by the thermal wind equation

$$f\frac{\partial \overline{\text{u}}}{\partial \text{logP}}=\text{R}{\left(\frac{\partial \text{T}}{\partial \text{y}}\right)}_{\text{P}}$$ (1)

Here f = 2Ωsinϕ is the Coriolis parameter, Ω is the planetary rotation rate, ϕ is latitude, $\overline{\text{u}}$ is the mean eastward velocity, R is the gas constant for the hydrogen-helium atmosphere, and y is the northward coordinate measured from the equator [Holton and Hakim, 2013]. This equation is valid for steady flows whose horizontal dimension is much greater than the vertical dimension. At the equator f is equal to βy, where β = 2Ω/a and a is the radius of the planet. We fit the brightness temperatures in Figure S1 to a Gaussian T(y, P) = ΔT exp (−y²/y₀²), where ΔT = − 40 K and y₀ = 5000 km, about 4° of latitude. Left and right sides of equation (1) vanish at the equator, so we use L’Hôpital’s rule to obtain

$$\frac{\partial \overline{\text{u}}}{\partial \text{logP}}=-\frac{2\text{R}\Delta \text{T}}{\beta {\text{y}}_0^2}\approx 2350\text{ m }{\text{s}}^{-1}$$ (2)

Distributed over log P = 2.3, about one order of magnitude in P, the velocity at the top minus that at the bottom in Figure 1 would be −5,400 m s⁻¹, which is impossibly large and of the wrong sign (westward). Thus the brightness temperature differences must be almost entirely due to ammonia variations.

Ammonia variations can also have a significant effect on the density, because of the high molecular mass of ammonia relative to the hydrogen-helium mixture. In equation (2) a value of ΔT that gives a realistic wind speed, e.g., 110 m s⁻¹ instead of 5400 m s⁻¹ (Figure 1), is 0.8 K. At constant pressure, density is inversely proportional to T/m, so one must compare the fractional changes in T/m due to variation of ammonia to those due to ΔT. Assume a horizontal variation of ammonia mixing ratio from Figure 1 of 150 ppm. Let the molecular mass of H₂ + He be 0.0023 kg mol⁻¹. Then Δm/m ≈ 0.0011, which is more than half of ΔT/T ≈ 0.8/400 = 0.002. If water were varying with ammonia, maintaining the solar O/N ratio, it would increase the effect on density by a factor of 7.7.

We have no explanation for the hemispheric asymmetry in Figures 1 and S1. The season was near northern winter solstice, but Jupiter’s obliquity is only 3°. Instruments on Juno and Earth, which are mainly sensitive to the color and height of the clouds, show the South Equatorial Belt (SEB) looking as prominent as the NEB [Orton et al, 2017]. The puzzle is that the SEB looks less prominent than the NEB when viewed by an instrument sensitive to the ammonia vapor abundance below the clouds.

3. Belts and Zones

Early authors postulated that the winds would decay with depth below the clouds [Hess and Panofsky, 1951; Ingersoll and Cuzzi, 1969; Barcilon and Gierasch, 1970]. The thermal wind equation [Holton and Hakim, 2013] then implies warm air under the anticyclonic zones and cold air under the cyclonic belts. The early authors postulated that the air is rising under the zones, because they are warm, and this agrees with Voyager infrared data [Gierasch et al., 1986]. Specifically, the uniform high clouds of the zones, their high ammonia abundance, and their low para-fraction, which is the thermodynamically favored state of the H₂ molecule at depth, all imply net upwelling. However, above the clouds, the Voyagers observed low temperatures in the zones, which implies winds decaying with height—anticyclones becoming more cyclonic with altitude. Gierasch et al. [1986] interpreted the low temperatures as a sign of upwelling in a stable troposphere, where low potential temperature air is advected from below. Decay of the winds could be forced by wave drag, with the associated vertical advection of potential temperature balanced by radiation [Gierasch et al., 1986]. These inferences about upwelling and downwelling are separate from the updrafts and downdrafts described in section 2, which could be of much smaller scale.

Voyager infrared data seem to imply net upwelling in the zones and net downwelling in the belts, but lightning data from the Galileo orbiter [Little et al., 1999] and the Cassini flyby [Porco et al., 2003; Dyudina et al., 2004] suggest the opposite, at least according to one set of assumptions. The problem is that lightning occurs in the belts, and that contradicts the inference from Voyager of downwelling in the belts if one assumes that lightning requires upwelling of water-laden air. Perhaps the upwelling is in the belts at 1–6 bars (in the water cloud), but it shifts over to the zones and upwells above the 1-bar level [Ingersoll et al., 2000; Showman and de Pater, 2005]. An alternate assumption is that the cyclonic vorticity of the belts triggers moist convection without net upwelling [Little et al., 1999; Li et al., 2006; Showman, 2007; Thomson and McIntyre, 2016]. The idea is that cyclonic vorticity implies low pressure in the weather layer, which implies an upward bulge of denser, lower-layer air, assuming the atmosphere is in isostatic equilibrium. Therefore a sufficiently strong cyclone has moist convection because lower-layer air has been lifted to its lifting condensation level. According to this assumption, there could be net downwelling in the belts and still have moist convection and lightning. Triggered convection and release of a finite amount of convective available potential energy (CAPE) is consistent with the violent, episodic nature of lightning on Jupiter, as pointed out by Showman and de Pater [2005].

The ammonia-poor layer at 3–15 bars, which covers all latitudes outside the equator at least to ±40°, is a mystery. It is sandwiched between two ammonia-rich layers, one at 0.7–2 bars and the other deeper than 40–60 bars. Evaporating precipitation could account for the ammonia-rich layer at 0.7–2 bars. The mixing ratio has its minimum value of 180–200 ppm near the 6-bar level. That air has to come from the ammonia cloud, because it is the only significant source of ammonia-poor air. There could be small-scale downdrafts, unresolved in Figure 1, that bring ammonia-poor air down to the 5–15 bar layer, but the only resolved pathway from the clouds goes through the ammonia-poor downdraft at 5–20°N. From there, the ammonia-poor air could spread poleward either by advection or by diffusion. Spreading by diffusion raises the question of what maintains the ammonia-poor layer at higher latitudes, since it is bounded above and below by ammonia-rich air. Spreading by advection would create upwelling and downwelling at higher latitudes, and that could keep the ammonia-rich air from diffusing in. But that raises the question of how the return flow gets back to the equator. We do not claim to have solved the mystery.

There are latitude variations in the ammonia-rich layer from 0.7 to 2 bars, but the correlation with belts and zones is weak. The exceptions almost outnumber the rules, as noted by Orton et al. [2017]. However at 40–60 bars, the belts seem to have slightly higher mixing ratios than the zones, as evidenced by the little peaks and troughs in the contour lines. This would imply upwelling in the belts, with high-ammonia air advected upward from below, which is opposite to the Voyager observation of upwelling in the zones. Such a correlation might make sense if there were a solid boundary underneath. Friction with the boundary would produce an Ekman layer [Holton and Hakim, 2013], leading to horizontal convergence and upwelling at places where the overlying flow is cyclonic, as it is in the belts. Whether interior processes can mimic a solid lower boundary is a difficult subject. We touch on it briefly at the end of section 4.

The existence of an ammonia-poor layer centered at 6 bars and extending out to ±40° raises the question of how the internal heat reaches the surface at higher latitudes. One might think that the answer involves water and moist convection [Showman and de Pater, 2005], but the layer from 40–60 bars is below the base of the water cloud and below the level where raindrops evaporate, which is less than 10–12 bars [Seifert, 2008]. Even with moist convection, there would still be the question of how the internal heat gets from 40–60 bars to the base of the water cloud. A radiative zone near the water cloud base is a possibility, but it requires a water abundance that is more than 10 times the solar value, and that seems unlikely [Leconte et al., 2017]. A radiative zone could exist between the 1200 and 2900 K levels, but it is not likely to extend into the range covered in Figure 1 [Guillot et al., 1994]. Conveying the heat from 40–60 bars at mid latitude to the base of the ammonia cloud remains a mystery.

4. Angular Momentum: Implications for Upwelling and Downwelling

The angular momentum budget provides further information about upwelling and downwelling. We define $\overline{\text{M}}$ as the zonally averaged angular momentum per unit mass about the planetary axis of rotation. On a thin spherical shell, the expression for $\overline{\text{M}}$ is

$$\overline{\text{M}}=\overline{\text{u}}a\text{cos}\varphi +\Omega a^2{\text{cos}}^2\varphi$$ (3)

We express conservation of $\overline{\text{M}}$ using the primitive equations for the Eulerian mean flow in spherical coordinates [Andrews et al., 1987, section 3.5]. The equation for $\text{D}\overline{\text{M}}/\text{Dt}$ is

$$\frac{\text{D}\overline{\text{M}}}{\text{Dt}}\equiv a\text{cos}\varphi \left[{\overline{\text{u}}}_{\text{t}}+{\overline{\text{w}}}^{*}{\overline{\text{u}}}_{\text{z}}-\mathit{f}{\overline{\text{v}}}^{*}\right]+{\overline{\text{v}}}^{*}{(\overline{\text{u}}\text{cos}\varphi )}_{\varphi }={\rho }_0^{-1}\nabla \cdot F+\overline{\text{X}}a\text{cos}\varphi$$ (4)

The primitive equations are an approximate system valid for atmospheric features that are thin relative to the planetary dimensions. Subscripts are derivatives, and overbars are zonal means. ${\overline{\text{v}}}^{*}$ and ${\overline{\text{w}}}^{*}$ are the transformed Eulerian mean (TEM) velocities to the north and vertical directions, respectively. They are different from the Eulerian mean velocities because they describe tracer transport, and the Eulerian means do not. The vector F = (0, F^(ϕ), F^(z)) is known as the Eliassen-Palm flux [Andrews et al., 1987] and has components

$$\begin{gathered} {\text{F}}^{\left(\varphi \right)}={\rho }_{0}a\text{cos}\varphi \left({\overline{\text{u}}}_{\text{z}}\overline{\text{v}\prime \theta \prime }/{\overline{\theta }}_{\text{z}}-\overline{\text{u}\prime \text{v}\prime }\right) \\ {\text{F}}^{\left(\text{z}\right)}={\rho }_{0}a\text{cos}\varphi \left\{\left[{f-a\text{cos}\varphi )}^{-1}{\left(\overline{\text{u}}\text{cos}\varphi \right)}_{\varphi }\right]\overline{\text{v}\prime \theta \prime }/{\overline{\theta }}_{\text{z}}-\overline{\text{u}\prime \text{v}\prime }\right\} \end{gathered}$$ (5)

Here u’,v’,w’, and θ’ are departures from the zonal means—the eddies, where θ is potential temperature. Although the zonal means of the eddy quantities are zero, the means of their products are generally non-zero. The effect of eddies on tracer transport is entirely contained in the divergence of F. The quantity $\overline{\text{X}}$ is the zonal mean friction force per unit mass. It stands for the effect of unresolved turbulent motions. Without friction and without eddies, equation (4) gives $\text{D}\overline{\text{M}}/\text{Dt=0}$, saying that rings of air moving meridionally and/or vertically conserve their angular momentum. For example, a ring of air at rest relative to the planet at the equator would develop an eastward supersonic wind of 1560 m s⁻¹ if it were moved to 20° latitude. Eddies and friction allow meridional transport without such high winds.

The terms $\overline{\text{u}\prime \text{v}\prime }$ and $\overline{\text{u}\prime \text{w}\prime }$ are proportional to the northward and upward eddy fluxes of angular momentum, respectively, and $\overline{\text{v}\prime \theta \prime }$ is proportional to the northward eddy heat flux. For Jupiter, only the $\overline{\text{u}\prime \text{v}\prime }$ term has been measured. Values are shown in Figure 1. To see its effect on upwelling and downwelling, we assume $\overline{\text{v}\prime \theta \prime }=\overline{\text{X}}=0$ and we use a combination of equations (4) and (5) that is approximately valid for steady flow away from the equator. The Coriolis term $-f{\overline{\text{v}}}^{*}$ dominates on the left in (4), and the two eddy flux terms in (5) become minus the divergence with respect to y and z, respectively. The result is

$$-f{\overline{\text{v}}}^{*}=-{\left(\overline{\text{u}\prime \text{v}\prime }\right)}_{\text{y}}-{\rho }_0^{-1}{\left({\rho }_0\overline{\text{u}\prime \text{w}\prime }\right)}_{\text{z}}$$ (6)

Looking at Figure 1 it is clear that the belts have a local minimum of $\overline{\text{u}\prime \text{v}\prime }$ in the northern hemisphere, where f > 0. Neglecting the last term in equation (6), this implies that ${\overline{\text{v}}}^{\text{*}}$ is negative on the equatorward sides of the belts and positive on the poleward sides. The two ${\overline{\text{v}}}^{\text{*}}$ currents diverging in the middle would imply upwelling. Conversely, the zones have a local maximum of $\overline{\text{u}\prime \text{v}\prime }$ in the north, which implies downwelling. These relations are reversed in the southern hemisphere, but f is also reversed, so again the implication is downwelling in the zones and upwelling in the belts.

The above result is opposite to the tracer transport observations, so one has to consider the other eddy terms. According to (6), if the vertical eddy momentum flux $\overline{\text{u}\prime \text{w}\prime }$ were converging positive momentum from below on the poleward sides of the belts and converging negative momentum on the equatorward sides, it would offset the effects of the $\overline{\text{u}\prime \text{v}\prime }$ term. Since the belts have westward winds on their poleward sides, the vertical eddy momentum flux would have a braking effect on the zonal winds. In contrast, the horizontal eddy momentum flux $\overline{\text{u}\prime \text{v}\prime }$ (Figure 1) has an accelerating effect.

Using the data in Figure 1, we can estimate what ${\overline{\text{v}}}^{*}$ would be if $\overline{\text{u}\prime \text{v}\prime }$ were the only flux term on the right of (6). From 5°S to 5°N, ${\left(\overline{\text{u}\prime \text{v}\prime }\right)}_{\text{y}}$ is about 2 × 10⁻⁶ m s⁻², which gives ${\overline{\text{v}}}^{\text{*}}=\pm 0.065\text{\hspace{0.17em}m\hspace{0.17em}}{\text{s}}^{-1}$ if we evaluate f at ±5°N. This speed is below the limit of measurement according to Figure 4 of Salyk et al. [2006]. At this speed it would take a parcel 3 Earth years to go from latitude 0° to latitude ±5°. Recall, however, that this estimate does not include the other eddy flux terms, which have not been measured.

A more fundamental approach to the TEM system uses the concept of potential vorticity mixing [Plumb, 2002; Dritschel and McIntyre, 2008]. For large-scale, slowly varying, thin-layer flows away from the equator, the quasi-geostrophic equations apply and the steady-state equation analogous to (6) becomes [Andrews et al., 1987]

$$-f{\overline{\text{v}}}^{*}=-{\left(\overline{\text{u}\prime \text{v}\prime }\right)}_{\text{y}}+{\rho }_0^{-1}{\left({\rho }_0\mathit{f}\overline{\text{v}\prime \theta \prime }/{\overline{\theta }}_{\text{z}}\right)}_{\text{z}}=\overline{\text{v}\prime \text{q}\prime }$$ (7)

The advantage of this form is that q’ is the eddy part of q, the potential vorticity (PV), and PV is a conserved quantity. As with other tracers, one might expect it to diffuse down its own mean gradient. Thus

$$\overline{\text{v}\prime \text{q}\prime }=-K_e{\overline{\text{q}}}_{\text{y}}=-f{\overline{\text{v}}}^{*}\text{\hspace{1em} where \hspace{1em}}{\overline{\text{q}}}_{\text{y}}=\beta -{\overline{\text{u}}}_{\text{yy}}-{\rho }_0^{-1}{\left({\rho }_0{f}^2{\overline{\text{u}}}_{\text{z}}/{\text{N}}^2\right)}_{\text{z}}$$ (8)

Here ${\overline{\text{q}}}_{\text{y}}$ is the zonal mean PV gradient [Andrews et al., 1987], K_e is the eddy diffusivity, β = ∂f /∂y, and ${\text{N}}^2=\text{g}{\overline{\theta }}_{\text{z}}/\overline{\theta }$ is the buoyancy frequency squared.

Theory and modeling support the idea of a PV staircase--broad bands of constant PV (with ${\overline{\text{q}}}_{\text{y}}=0$) centered on the westward jets separated by sharp gradient regions (with ${\overline{\text{q}}}_{\text{y}}>0$) centered on the eastward jets [Marcus, 1993; Dritschel and McIntyre, 2008]. The gradient regions are regarded as barriers to mixing, where $\overline{\text{v}\prime \text{q}\prime }={\overline{\text{v}}}^{\text{*}}=0$, according to (7) and (8). However, observations indicate that ${\overline{\text{u}}}_{\text{yy}}$ exceeds β at the centers of the westward jets [Ingersoll and Cuzzi, 1969; Ingersoll et al., 1981; Limaye et al., 1986; Li et al., 2004; Read et al., 2006]. Thus, according to (8), ${\overline{\text{q}}}_{\text{y}}$ might be negative and ${\overline{\text{v}}}^{*}$ might be toward the equator at the centers of the westward jets, since β is everywhere positive and f changes sign at the equator. This would imply horizontal divergence and upwelling on the poleward sides of the westward jets -- the zones, and horizontal convergence and downwelling on their equatorward sides -- the belts, in agreement with the Voyager observations. We caution that this is a speculative line of reasoning, because the terms involving vertical derivatives in (7) and (8) have not been measured. Also, having bands where ${\overline{\text{q}}}_{\text{y}}$ is negative goes against the theoretical idea of a PV staircase, and diabatic heating and friction could outweigh the effects of downgradient PV mixing.

The above discussion uses the primitive equations, which are valid for thin atmospheric layers. There are also published models of fully 3D thermal convection between rotating spherical shells whose spacing is a significant fraction of the outer radius [e.g., Roberts, 1968; Busse, 1970; Glatzmaier et al., 2009; Christensen, 2002; Aurnou et al., 2008; Kaspi et al., 2009; Heimpel et al., 2016]. The 3D models have positive $\overline{\text{v}\prime \text{w}\prime }$ below the surface at the equator and are successful in producing an eastward zonal jet there. Vertical eddy transport of zonal momentum, converging in the weather layer, could balance the northward eddy transport that is diverging in the EZ according to Figure 1. Some of the 3D models produce multiple zonal jets at mid-latitudes as well.

The 3D models suggest that the zonal jets and the belt-zone boundaries might be cylinders centered on the planet’s rotation axis, whereas Figure 1 depicts the belt-zone boundaries as vertical lines. However, Figure 1 exaggerates the vertical scale by a factor of 300, so cylinders would appear almost vertical in the figure. For example, cylinders intersecting the lower boundary at latitudes of 10°, 20°, and 40° would intersect the 1-bar level at latitudes of 11.5°, 20.8°, and 40.3°, respectively. In this respect the thin-layer models are compatible with the 3D models. However, properly connecting the weather layer dynamics to the interior dynamics is an ongoing challenge that is beyond the scope of this paper.

5. Summary and Conclusions

The MWR data present a challenge to the traditional picture of Jupiter’s atmosphere below the weather layer. Except for the EZ at 0–5°N and the NEB from 5–20°N, the belts and zones show up weakly in the MWR map. The MWR data reveal a gap between the deep reservoir of ammonia, where the mixing ratio is greater than 320 ppm, and the water cloud including the sub-cloud region where precipitation is evaporating. Some questions are: How does the internal heat get through the gap? If there is dry convection within the gap, why doesn’t it mix ammonia up into the water cloud? And why is there an ammonia minimum at ~6 bars? Meridional exchange appears weak on Jupiter, and it seems unlikely that the equatorial Hadley cell is supplying heat to higher latitudes. Water is the most important unknown. We don’t know if the ammonia-poor layer is wet or dry, or if the EZ and NEB are wet or dry. Treatment of moist convection, tracer transport, small-scale eddies, and coupling to the fluid interior are difficult problems, and it is unlikely that a picture like Figure 1 will pop spontaneously out of a general circulation model. For now, conceptual models seem called for while the MWR collects more data.

Key points:

• The altitude-latitude map of Jupiter’s ammonia reveals unexpected evidence of large-scale circulation down at least to the 50-bar level.

• A narrow equatorial band is the only region where ammonia-rich air from below the 50-bar level can reach the ammonia cloud at 0.7 bars.

• At higher latitudes the ammonia-rich air appears to be blocked by a layer of ammonia-poor air between 3 and 15 bars.