Abstract
The complex formation of actinium (Ac3+) and californium (Cf3+) ions with macropa (a promising ligand for medical applications, e.g., in targeted α therapy) has been studied by means of density functional theory (DFT) calculations. This work is focused on the structural and bonding properties, the latter on the basis of charge transfer data and topological properties of the electron density distribution. The effect of water solvent on the energetics has been investigated using the SMD model. A comparative analysis with the related properties of two representative lanthanide (La, Lu) complexes has been performed.
Introduction
The actinides (An) are best known for their applications in nuclear weapons and for energy production. However, their radioactivity can make them a very useful tool in nuclear medicine too. Their α-emitting isotopes 225Ac1−4 and 227Th5−8 are at an advanced level of clinical tests for the treatment of a range of cancers by means of targeted α therapy (TAT). Convincing results have been obtained for the treatment of metastatic castration-resistant prostate cancer,9−11 acute myeloid leukemia,12,13 neuroendocrine tumors,14 and tumors expressing mesothelin.15 The α-emitting radioisotope of uranium (230U) is also a promising candidate for TAT based on its short half-life of 20.83 days.16 For this actinide, however, an important issue is to find suitable chelating agents for stable binding of UO22+ under in vivo conditions.17,18 In addition, 252Cf is also considered for the treatment of cancer. The slow spontaneous fission of this radioisotope provides neutron radiation suitable for brachytherapy or internal radiation therapy.19,20
The radioisotopes are generally administered in a chelated form. The chelators for these ions are conjugated to a biological targeting vector (antibody or peptide), which transports them to the desired location in vivo. For such applications, the chelator ligands must possess two important properties:21 (i) they should rapidly complex the metal ion under mild pH and temperature conditions and (ii) they should form highly stable complexes. The latter requirement is of paramount importance to prevent the redistribution of these toxic metal ions throughout the patient.
The design of suitable chelating agents for f-block elements is hampered by the electrostatic nature of their bonding interactions. Their low charge density results mostly in long and weak metal-donor bonds with the consequence of the low stability of these complexes. Hitherto, only a few promising chelators are available for lanthanides (Ln) and actinides. The most widely used chelator for lanthanides is the tetraazamacrocycle 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid (DOTA) forming stable complexes with the small-size Ln ions.22,23 A disadvantage of DOTA for larger ions (e.g., light An) is that the stability decreases with the size significantly. Nevertheless, for the time being, DOTA is the ligand of choice for linking of 225Ac to biomolecules and has been successfully applied in several clinical tests.24 In the meantime, search for improved chelators for An is ongoing.
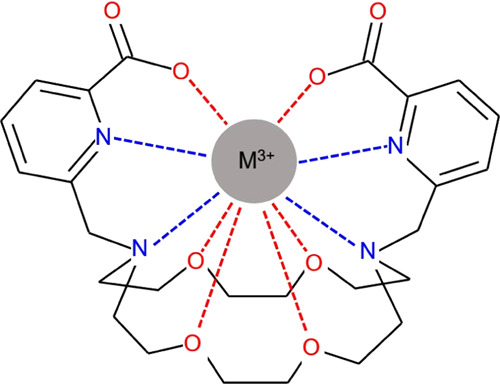
Macrocycles based on the 1,7,10,16-tetraoxa-4,13-diazacyclooctadecane (D18C6) core show a thermodynamic preference for large over small metal ions.25−32 Recently, a D18C6-based macrocycle possessing two picolinate arms (N,N′-bis[(6-carboxy-2-pyridil)methyl]-4,13-diaza-18-crown-6, macropa, Figure 1) has been shown to form rapidly a stable complex with 225Ac3+, the largest 3+ ion in the Periodic Table.33 Macropa was also found to selectively bind large lanthanide,34 alkaline earth,35,36 and p-block35 metal ions over their smaller analogues. The selectivity for the large An and Ln ions was found to be superior to related diaza[18]crown-625,28 and diaza[15]crown-5 derivatives.37,38 This rare reverse size selectivity of macropa makes it a distinguished candidate for medical applications, where efficient chelators for large metal ions are highly needed. The clinical tests of Ac(macropa) derivatives are in progress with promising results: recently, a single dose of 225Ac-RPS-074, an 225Ac(macropa) bifunctional construct designed against prostate cancer, induced complete tumor ablation in mice.39
Figure 1.
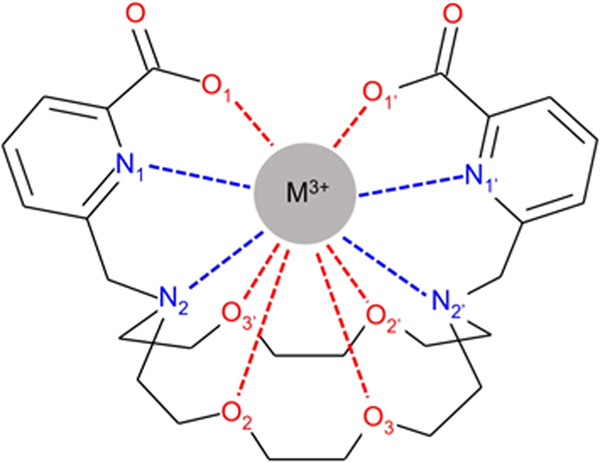
M(L)+ complex with the numbering of selected atoms. In C2 symmetry, the Xn and Xn′ atoms are equivalent.
The present theoretical study aims to uncover the bonding of macropa (H2L) with f elements. The reverse stability trend along the Ln series in aqueous solution (La > Lu) has been detected by potentiometric measurements34 and interpreted on the basis of density functional theory (DFT) calculations.40 The usually observed trend in the stability of gas-phase Ln complexes is the increase from La to Lu due to the increasing charge density of the metal ion in this order. (The latter being the result of the decreasing size of Ln3+ ions due to the Ln contraction.) In aqueous solutions, however, the hydration energy can introduce significant effects. It was shown in ref (40) that the balance between the increasing binding energies in the Ln(L)+ complexes and the variation of the hydration energies across the lanthanide row was dominated by the increasing hydration energies of the Ln3+ ions, being therefore responsible for the reversed trend in the stability constants of these complexes in aqueous solution.
The importance of actinides in TAT calls for detailed information on the physicochemical properties of their complexes with the macropa ligand. There can be differences compared to lanthanides not only because of the size but also in the bonding due to the chemically more active 5f subshell. In the present study, macropa complexes with Ac3+, Cf3+, La3+, and Lu3+ will be compared on the basis of DFT calculations. The properties in focus are the relative stabilities of these ionic M(L)+ complexes, the effect of water solvation, and the characters of the main bonding interactions. The extra H2O solvent molecule coordinating to La in the crystal structure of La(macropa),33 similar to dimethylformamide (DMF) with Ba(macropa)36 and in related complexes,29,32,41,42 is not considered in the present comparative study. These small solvent molecules are supposed to fill the 11th coordination site of large M ions and accordingly, they were not observed with small metal ions, such as Lu3+.33 It should be noted, however, that the water molecule of La(HL)(H2O)2+ has not yet been confirmed in aqueous solution. These 11-coordinate complexes have a different structure in which one of the ligand picolinate arms is protonated, changing in this way the bonding properties of this COO group. While the overall thermodynamic stability of the complexes should be increased by the additional coordination, the macropa–M interaction is likely weakened with respect to 10-coordinate M(macropa) because of the changed COO–M bonding and the steric effects of the additional ligand molecule.
Computational Details
The computations were performed with the Gaussian09 suit of programs43 using the hybrid metageneralized TPSSh exchange–correlation functional44 in conjunction with quasi-relativistic pseudopotentials of the Stuttgart–Cologne group. The selection of the TPSSh functional was based on its good performance for the geometries and stability properties of Ln complexes40,45,46 and accurate 17O Aiso values of coordinated water molecules in various Gd complexes.47 For H, N, C, and O, the standard 6-31G(dp) basis set was used. For the lanthanides and actinides, both the large-core and small-core quasi-relativistic pseudopotentials, LCPPs and SCPPs, respectively, were probed. The 4f-in-core LCPPs48,49 for La and Lu (ECP46MWB and ECP60MWB, respectively) were coupled with a [7s6p5d]/[5s4p3d] valence basis set treating the 5s5p5d6s electrons.48 The 4f-in-valence SCPPs (ECP28MWB)50 had a segmented valance basis set with a contraction scheme of [14s13p10d8f6g]/[10s8p5d4f3g] treating the 4th, 5th, and 6th shells.51 For Ac and Cf, the primary basis was the 5f-in-valence SCPPs (ECP60MWB)52 in conjunction with valence basis sets having a contraction scheme of [14s13p10d8f6g]/[10s9p5d4f3g].53,54 This choice was rationalized by the larger importance of the 5f electrons in the interactions of actinides compared to the intact 4f subshell in lanthanides. However, calculations with SCPPs can be considerably difficult due to SCF convergence problems. In the present study, SCF convergence failed for four conformers of Cf(L)+ and in basis set superposition error (BSSE) calculations for the Cf and Ac complexes. No such problems occurred with the 5f-in-core LCPPs55 (ECP78MWB and ECP87MWB for Ac and Cf, respectively) used in conjunction with a [7s6p5d2f1g]/[6s5p4d2f1g] valence basis set.55 The application of the f and g polarization functions with the latter LCPPs (in contrast to their neglect in the recent literature on Ln(L)+ complexes34,40,45,56) is in accordance with the mentioned larger importance of the 5f electrons in the interactions of actinides. The LCPP calculations provided data very close to the SCPP ones for Ac(L)+, however, with small deviations for Cf(L)+.
The ground state of the computed complexes was verified utilizing the STABLE keyword of the Gaussian09 code. Due to their closed-shell nature, spin-restricted calculations were performed for the Ac, La, and Lu complexes as well as for Cf(L)+ with LCPP. With SCPP, the sextet ground state of open-shell Cf(L)+ was treated using the spin-unrestricted formalism. BSSE was evaluated using the counterpoise method.57 The solvent effects were taken into account using the polarizable continuum model (PCM)58,59 with radii and nonelectrostatic terms for Truhlar and co-workers’ SMD solvation model.60 For the La3+ and Lu3+ ions, the PCM radii (1.874 and 1.659 Å, respectively) from ref (40) were used. The respective PCM radii for Ac3+ and Cf3+ were optimized in the present study to achieve an agreement with the hydration free energies in the literature.61 No scaling factor (α = 1.0) was used for the PCM radii.
The atomic charges and charge transfer (CT) properties were calculated according to natural bond orbital (NBO) theory62 utilizing the NBO 6.0 code.63 The topological analysis of the electron density distribution according to the “quantum theory of atoms in molecules” (QTAIM)64 was performed by means of the AIMAll software.65 These bonding models are widely used for the assessment of bonding trends in organometallic complexes of f elements.66−78
Results and Discussion
The stability of metal complexes in solution is determined by the following two main factors: (i) the binding energy of the ligand to the metal ions and (ii) the hydration energies of the complexes and free metal ions. In the following sections, these two factors are analyzed in detail: in the Structure and Bonding section, the conformational properties, energetics, and bonding in the gas-phase structures, while in the Energetics in Aqueous Solution section, the energies of hydration using the gas-phase reference structures.
Structure and Bonding
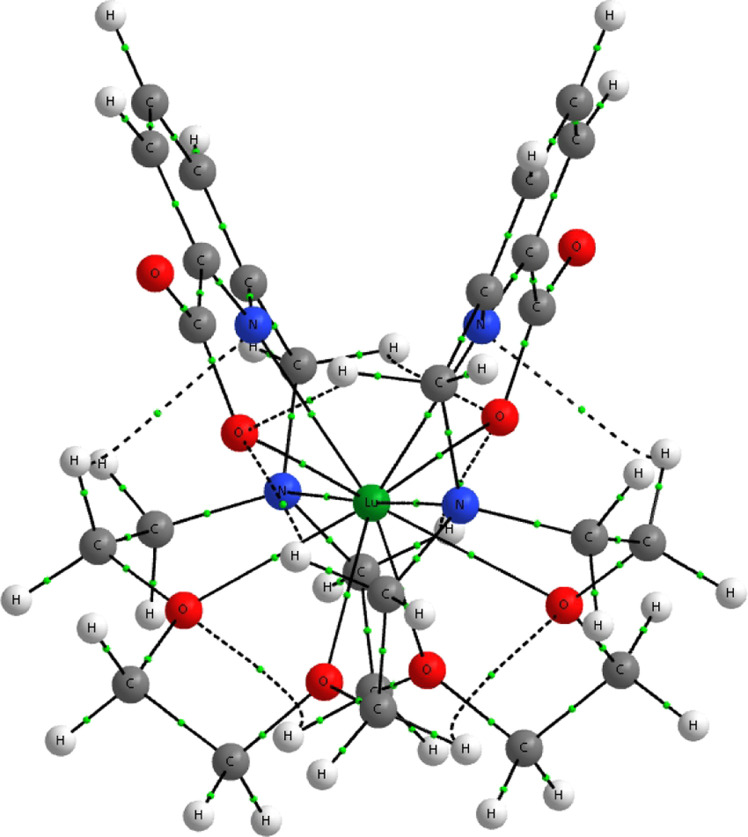
The complex formed by macropa with metals is presented in Figure 1. In the shown syn conformation of the ligand side arms, the metal ion is able to bind to all of the 10 donor atoms. The chiral complex can form 16 possible conformations (eight enantiomeric pairs of diastereoisomers) with C2 symmetry. In a nonchiral environment, enantiomers possess the same physiochemical properties, hence the study of the eight diastereoisomeric forms is sufficient. The conventional nomenclature is X(yyy)(yyy), where X = Δ or Λ (absolute configurations of the picoline pendant arms) and y = δ or λ (absolute configurations of the six five-membered chelate rings formed in the complex).79,80 To keep consistency with the literature, the present article deals with the eight Δ(yyy)(yyy) conformers. As the La(L)+ and Lu(L)+ complexes are well described in the literature,34,40 only two of their relevant Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) conformers are included in the present comparative analysis.
The relative Gibbs free energies are presented in Figure 2, from which the solvation data are discussed in the Energetics in Aqueous Solution section. The effect of BSSE (where available) on the relative energies was a few kJ/mol; these data are given in Table S1 of the Supporting Information.
Figure 2.
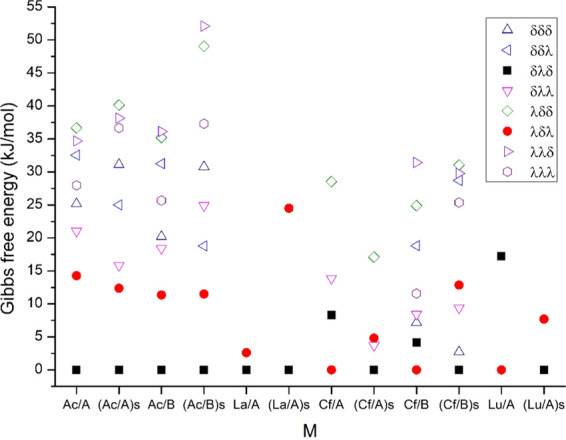
Relative Gibbs free energies of the eight M(L)+ conformers in the gaseous phase and aqueous solution. At the x axis, the notations A, B, and s refer to SCPP and LCPP basis sets and aqueous solution, respectively. The conformers Δ(yyy)(yyy) are abbreviated by the yyy terms.
The ionic radii of the four f elements decrease in the order Ac3+ > La3+ > Cf3+ > Lu3+ (the experimental 6-coordinate ionic radii being 1.12, 1.032, 0.95, and 0.861 Å, respectively).81 In agreement with expectations based on related literature,30,34 the present calculations predicted the preference of the Δ(δλδ)(δλδ) conformer for the large Ac3+ ion (similar to that for La3+) and the preference of the Δ(λδλ)(λδλ) one for the smaller Cf3+ ion (similar to that for Lu3+)30,34 in the gaseous phase. Calculations with SCPPs and LCPPs agreed with these relative stabilities. Regarding the other conformers, the energy differences predicted by the two pseudopotentials are quite similar for Ac(L)+, while the agreement (by SCPP) is somewhat worse for the four obtained conformers of Cf(L)+, referring to the role of the 5f electrons in the latter complex.
The energetic preference of the Δ(δλδ)(δλδ) conformer is well pronounced for Ac(L)+ (with the largest M3+ radius) and similarly the preference of the Δ(λδλ)(λδλ) conformers for Lu(L)+ (with the smallest ionic radius). For La(L)+ and Cf(L)+ (with ionic radii in between), the gas-phase energy differences between the two conformers are smaller.
The metal–ligand interactions are analyzed in the two most significant conformers Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) on the basis of molecular geometries and properties from the NBO62 and QTAIM64 bonding models. The analysis is based on the gas-phase reference geometries obtained with SCPP (taking into account the effect of f valance orbitals in Ac, La, and Cf). Geometry optimizations with LCPP including BSSE indicated marginal effects of BSSE for the main interatomic distances (in general a few thousandths of Å).
The metal–ligand bond distances are presented in Figure 3. Most of them agree within a few hundredths to 0.1 Å with the X-ray crystal structure data33 of La(HL)(H2O)2+ and Lu(L)+ (cf. Table S2), whose experimental structures are less symmetric and the La complex contains an additional H2O ligand. The changes induced by H2O in the latter structure may mainly be responsible for the experimental La–O1 distances being longer by ca. 0.2 Å than the computed ones.
Figure 3.
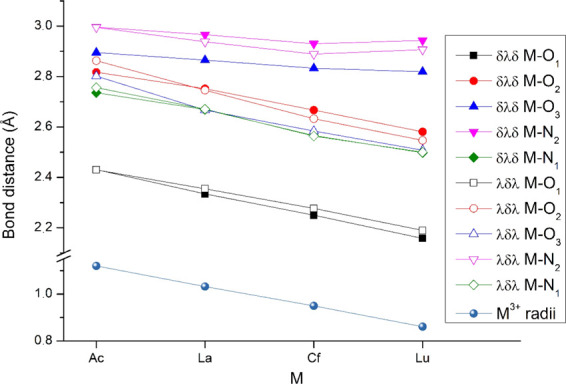
Selected bond distances of the Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) conformers computed at the TPSSh/SCPP level.
For most of the presented computed bond distances, good correlation can be observed with the depicted M3+ ionic radii. Exceptions are the M–N2 bonds of both conformers and the M–O3 bond of the Δ(δλδ)(δλδ) conformer, which shorten only marginally. These are the longest coordinative bonds, i.e., the weakest ones; it is therefore reasonable that they accommodate to a less extent the change of the metal ion size. Most presented coordinative bonds have very close values in the two conformers, except for the M–O3 one. This bond is considerably shorter in the Δ(λδλ)(λδλ) conformer, its length being comparable to the other M–O coordinative bonds.
From the 10 coordinative bonds, the strongest bonding with M3+ is created by the anionic carboxylate oxygens (O1). These bonds are by 0.3–0.7 Å shorter than the bonds with the neutral (though polarized) O and N atoms. The second shortest coordinative bond is the one with the pyridine N1. Hence, the leading role in the complex formation may be played by these M–O1 and M–N1 interactions.
The analogous Ac–O and Ac–N distances in the two Ac(L)+ conformers are very close, suggesting bonding interactions of similar strength in contrast to the other three f elements, where larger differences can be observed. Based on its size, the Ac3+ ion may fit (nearly) equally into the cavity of the two L2– conformers. The energetic preference of the Δ(δλδ)(δλδ) conformer may mainly be due to the smaller strain in this ligand geometry (cf. Figure S1 in the Supporting Information).
Further inspection of Figure 3 aimed to find correlations with the relative stabilities of the Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) conformers of the other complexes. The relative stability does not seem to be determined by the (strongest) M–O1 interaction, whose bond length is slightly shorter in all of these Δ(δλδ)(δλδ) conformers. A similar conclusion can be drawn for the strain energies of the L2– ligand, which are consistently larger by 20–30 kJ/mol in the Δ(λδλ)(λδλ) conformer (cf. Figure S1). The most prominent correlation with the increasing relative stability of the Δ(λδλ)(λδλ) conformer is the significant strengthening of the M–O3 interaction in the latter conformer, as indicated by this bond distance (cf. Figure 3). The M–O2 and M–N2 bond distances also become shorter from Ac to Lu, but the changes are rather small.
Table 1 compiles selected results from the NBO62,63 and QTAIM64 analyses. The natural atomic charges (from NBO) of the metals are between +1.7 and +2.0, in agreement with a major ionic character of the metal–ligand bonding. At the same time, they indicate a considerable CT (1.0–1.3e) to M3+, too. The transferred amount of electrons is represented by the population of lowest unoccupied atomic orbitals (LUAOs) of M3+. These valence s, d, and f orbitals, being empty in the ion, serve as the acceptor orbitals in the L2– → M3+ charge transfer. Altogether, the largest electron transfers occur in La(L)+ and Cf(L)+, while the strongest ionic bonding appears in Ac(L)+. As the atomic charges of the donor O and N atoms indicate, the ionic interaction is particularly strong with O1, its charge being close to the formal charge of the carboxylate anion.
Table 1. Dissociation Gibbs Free Energies and Selected QTAIM and NBO Data for the Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) Conformers of the M(L)+ Complexes.
| a | Ac(L)+ |
La(L)+ |
Cf(L)+ |
Lu(L)+ |
||||
|---|---|---|---|---|---|---|---|---|
| propertya | δλδ | λδλ | δλδ | λδλ | δλδ | λδλ | δλδ | λδλ |
| qM | +2.00 | +2.00 | +1.74 | +1.68 | +1.79 | +1.72 | +1.91 | +1.85 |
| qO1 | –0.91 | –0.91 | –0.82 | –0.81 | –0.84 | –0.83 | –0.88 | –0.87 |
| ∑LUAO | 1.00 | 1.00 | 1.26 | 1.32 | 1.21 | 1.28 | 1.09 | 1.15 |
| pop(6s/7s) | 0.14 | 0.14 | 0.16 | 0.17 | 0.20 | 0.21 | 0.19 | 0.20 |
| pop(5d/6d) | 0.49 | 0.50 | 0.91 | 0.95 | 0.81 | 0.88 | 0.88 | 0.94 |
| pop(4f/5f)b | 0.23 | 0.22 | 0.18 | 0.19 | 0.11 | 0.10 | 0.0 | 0.0 |
| ECT (L → M) | 1667 | 1671 | 3551 | 3969 | 3020 | 3447 | 2709 | 3068 |
| ECT (M → L) | 26 | 30 | ||||||
| ΔM | 1.15 | 1.15 | 1.18 | 1.22 | 1.27 | 1.33 | 0.98 | 1.03 |
| ∑DI | 1.04 | 1.04 | 1.07 | 1.10 | 1.14 | 1.20 | 0.89 | 0.93 |
| ΔGdiss | 3966 | 3951 | 4104 | 4001 | 4323 | 4332 | 4451 | 4468 |
Selected natural atomic charges, q (e); sum of populations of the lowest unoccupied atomic orbitals of M3+, ∑LUAO (e); valence orbital populations of M, pop (e); second-order perturbation energies, ECT (kJ/mol); difference between the integrated electron density and localization index of the atomic basin of M, Δ(M) (e); sum of the delocalization indices between M and L, ∑DI (e); and Gibbs free energies of dissociation without BSSE correction, ΔGdiss (kJ/mol). The conformers Δ(yyy)(yyy) are abbreviated by the yyy terms.
Number of excess electrons with respect to the M3+ ground state.
The populations from the natural atomic orbital (NAO) scheme give information on the distribution of the transferred charge between the M valence (s, d, f) orbitals. In agreement with the expectations, the main CT acceptor orbitals are the valence d orbitals of M, with populations around 0.5e in Ac and around 0.9e in the other metals. Populations of the valence s and excess electrons on the f orbitals are between 20 and 30% of those of the valence d orbitals. While the Ac 5f orbitals are somewhat more involved in CT than the 7s, in Cf the trend is turned over due to the energetic stabilization of the 5f orbitals in the latter An.
The energy gain from CT can be assessed on the basis of the second-order perturbation energies from the NBO analysis. In agreement with the M valence orbital populations, the weakest CT occurs in Ac(L)+, the CT energy being ca. half of those in the other three complexes. Among the latter three, the strongest interaction occurs in La(L)+ while the weakest in Lu(L)+. M → L back-donation was observed only in Cf(L)+, even this one being marginal. Decomposition of the CT energies to donor–acceptor atom pairs is given in Figure 4. Most pronounced is the CT from O1, while the CT energies from the other donors are close and partly overlap. The relative strengths of CTs in terms of the different metals agree qualitatively with the amount of transferred electrons (cf. Table 1).
Figure 4.
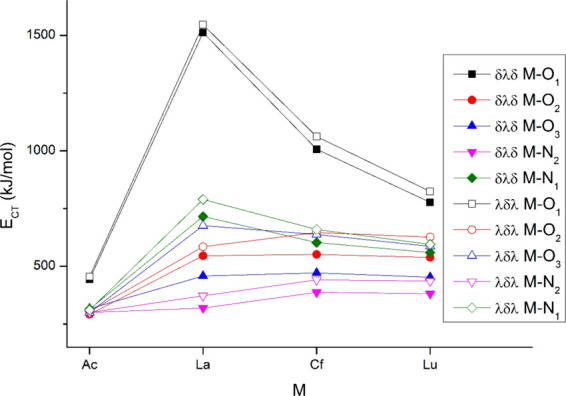
Main second-order perturbation energies from NBO analysis of the Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) conformers.
The above shown main CT features are also reflected in the integral QTAIM parameters. In this model, the total transferred electrons from L2– to M3+ are described by the amount of unlocalized electrons on M (denoted as ΔM in Table 1, obtained as the difference of the integrated electron density and localization index of the atomic basin of M). The basically different QTAIM and NBO models agree in the amount of the transferred electrons of ca. 1e in the complexes and in the trends within the Ln and An rows being Ac < Cf and La > Lu. However, deviation between QTAIM and NBO can be observed when comparing the two f element rows: the NBO model predicts a larger difference between the LUAO populations of Ln and An than that obtained in the ΔM values. Thus, from the four metals, QTAIM predicted the largest amount of transferred electrons in Cf(L)+, while NBO in La(L)+. This disagreement between the two models can also be seen in Figures 4 and 5.
Figure 5.
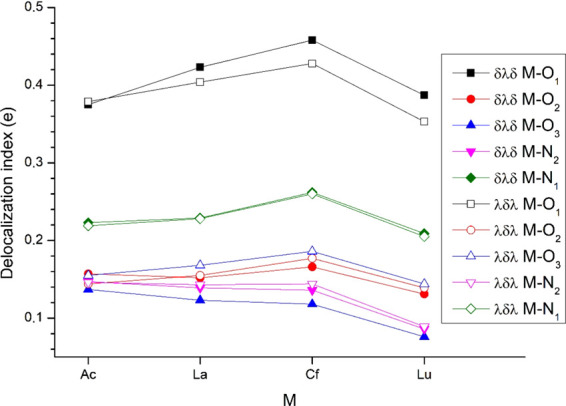
Delocalization indices from QTAIM analysis between selected atom pairs of the Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) conformers.
Another important property from the QTAIM analysis is the delocalization index (DI). This integral parameter quantifies the average number of electrons shared between two atoms connected by a bond path, i.e., forming the covalent bond.72 The sum of the delocalization indices around each M is given in Table 1, while the DI data between the M–O/N atom pairs are presented in Figure 5. In agreement with the second-order perturbation energies from NBO analysis (Figure 4), the M3+ ions form the most extensive electron-sharing interactions with O1 (ca. 0.4e). Considerably weaker (but still pronounced) are the interactions with N1 (ca. 0.23e), while the interactions with the other donors have somewhat smaller DIs.
Bond critical points (BCPs) were located for all of the above 10 coordinative bonds (Figure 6). In addition, a few weak O···H and N···H hydrogen bonds were found in both conformers, contributing to the overall stability of the complexes.
Figure 6.
Bond critical points from QTAIM analysis of the Δ(λδλ)(λδλ) conformer of Lu(L)+.
Both the small electron density (ρ) and the positive Laplacian of the electron density (▽2ρ) values (given in Figures S2 and S3 in the Supporting Information) refer to predominant ionic interactions between M and the heteroatoms in all complexes. Variations of these topological parameters of the BCPs are more or less consistent with those of the delocalization indices. The two significant differences include the increase of the latter Lu–O1 values (while this DI decreased) and the relatively smaller M–N1 ▽2ρ values for all complexes.
The overall stabilities of the gas-phase complexes, expressed by the Gibbs free energies of dissociation to M3+ + L2– (Table 1), are determined by an interplay of covalent (CT by spatial orbital overlap and energy-degeneracy-driven covalency,68,82−86 the latter difficult to estimate quantitatively) and ionic interactions as well as the strain energy of L2– in the complex. The lowest stability of the Ac(L)+ molecule is in agreement with the rather weak CT interactions, which seemingly could not efficiently be compensated by the stronger ionic interactions and the weakest ligand strain in this complex. The promoting effect of short bond distances appears in the largest dissociation energy of Lu(L)+ in spite of the weak CT and largest strain of the ligand but compensated effectively by the strong ionic interactions (cf. qM in Table 1). The latter factor may mainly be responsible for the larger stability of the Cf(L)+ molecule with respect to La(L)+.
Regarding the two analyzed conformers, both the QTAIM and NBO results indicate a somewhat stronger CT in the Δ(λδλ)(λδλ) conformers compared to Δ(δλδ)(δλδ). The bond distances in Figure 3 are inconsistent in this respect, but most of them are shorter in the Δ(λδλ)(λδλ) conformers. Another characteristic feature is the negligible difference between the bonding parameters of the two Ac(L)+ conformers in spite of their distinct energy difference. The very close bonding parameters are in accordance with the nearly identical Ac–O and Ac–N distances in the two conformers (vide supra).
Energetics in Aqueous Solution
One of the main issues regarding the medical application of metal complexes is the stability in aqueous solution. The stability of Ln(macropa) complexes is well explored. Stability constants have been obtained by potentiometric titration for the whole Ln series (except for the radioactive Pm).34 They revealed a gradually decreasing stability from Ce ≈ La to Lu in contrast to complexes with popular ligands such as ethylenediaminetetraacetic acid (EDTA4–) and derivatives87,88 and the macrocyclic 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid (DOTA4–) and derivatives.23,89
The relative stabilities of the M(L)+ complexes can be evaluated from the Gibbs free energies of the following exchange reaction (applicable for both gas phase and solution)
| 1 |
The experimental stability trend for Ln(macropa) complexes in aqueous solution has been reproduced by Regueiro-Figueroa et al. using DFT calculations.40 They revealed that the hydration energies of the Ln3+ ions have a crucial role in the delicate equilibrium of (1). While the calculated gas-phase Gibbs free energies indicated a preference of Lu(L)+ by 372 kJ/mol with respect to La(L)+, the calculated stability order was reversed in aqueous solution. The calculated hydration energies of the Ln(L)+ complexes proved to be nearly the same for the whole Ln series.40 On the other hand, the (experimental) hydration energy of the Lu3+ ion is higher by 419 kJ/mol than that of La3+.90,91 This larger stabilization of the Lu3+ ion in water shifted the equilibrium in (1) to the La(L)+ + Lu3+ side, facilitating in this way the thermodynamic preference of the La(L)+ complex in aqueous solution. The obtained Gibbs free energy of −46.5 kJ/mol for the Lu → La exchange reaction was in good agreement with the experimental value of −38.5 kJ/mol.40
For the reproduction of the above experimental stability trend in aqueous solution, a crucial factor was the use of appropriate ionic radii in the hydration energy calculations of both the Ln3+ ions and their complexes. Calculations using the crystal81 or experimental solution Ln3+ ionic radii (evaluated from the ion–water distances from extended X-ray absorption fine structure data92) in conjunction with the PCM/SMD model resulted in large deviations from the experimental hydration free energies. Regueiro-Figueroa et al. developed a parametrized set of Ln3+ radii for SMD calculations40 by fitting to the experimental hydration free energy values.90,91 This set was adapted to the TPSSh/LCPP theoretical level but comparable results were obtained with other DFT functionals, MP2, and the all-electron second-order Douglas–Kroll–Hess (DKH2) method too. Somewhat larger deviations were noted for the SCPP pseudopotentials.40
In the present study, the calculated Gibbs free energy of the Lu → La exchange reaction 1 was successfully reproduced (−46.2 kJ/mol) by calculations on the Δ(δλδ)(δλδ) conformers at the (same) TPSSh/LCPP level using the PCM radii from ref (40). It should be noted, however, that the Δ(δλδ)(δλδ) conformer used in ref (40) (and similarly in ref (56)) is not the most stable one in aqueous solution for Lu(L)+. According to nuclear magnetic resonance (NMR) measurements, the smaller late Ln(macropa) complexes likely have a different conformation in solution than La(macropa). Moreover, the paramagnetic 1H NMR shifts measured for Yb(macropa) indicated the preference of the Δ(λδλ)(λδλ) conformation in water.34 The previously mentioned DFT studies included only the Δ(δλδ)(δλδ) conformers and did not consider the Δ(λδλ)(λδλ) forms.40,56 Calculations in this work at the TPSSh/LCPP + SMD level predicted a preference of the Δ(δλδ)(δλδ) conformer of La(L)+ over the Δ(λδλ)(λδλ) conformer of Lu(L)+ by 54.4 kJ/mol. Hence, for the more likely Δ(λδλ)(λδλ) conformer, the applied DFT level40 produces a somewhat larger deviation from the experimental value of 38.5 kJ/mol. At the TPSSh/SCPP + SMD level, the preference of La(L)+ is even larger, 63.3 kJ/mol.
Another noteworthy issue is the prediction of the energetic order of the two conformers of Lu(L)+ in solution by the applied DFT + SMD model. As can be seen in Figure 2, in aqueous solution, the computed Δ(δλδ)(δλδ) conformer became superior to the Δ(λδλ)(λδλ) one, in contrast to available experimental information on Ln(macropa) complexes (vide supra).34 Altogether, while recognizing the merits of this complex theoretical model (consisting of the TPSSh functional, SMD solvation model, and PCM radii for Ln3+) on reproducing the experimental stability trend of Ln(L)+ complexes in aqueous solution, the reliability of the predicted energy values is still restricted. In the view of the shown performance of the DFT calculations, (only) a qualitative assessment is reasonable for the thermodynamic properties of the present An(L)+ complexes.
For the Ac3+ and Cf3+ ions, no experimental hydration energies are available. They were calculated on the basis of the ionic model by Bratsch and Lagowski61,93−95 and by David.96 The ΔGhyd0 values from the two different model calculations differ considerably. From the two literature sources, the one by Bratsch and Lagowski56,85 was chosen here because their ΔGhyd results for Ln3+ ions93,95 (after correction for the new standard Gibbs free hydration energy of proton91) achieved excellent agreement40 with the experimental data.90,97 The literature hydration energies of Ac3+ and Cf3+ were also corrected here for the new ΔGhyd0 of H+ according to (2)40,45 and then used as a reference for the development of the PCM radii of these ions.
| 2 |
The PCM radii of hydrated Ac3+ and Cf3+ were obtained here by SMD calculations, applying a correction on the calculated ΔG0 values for the concentration change between the gas and liquid phase (7.83 kJ/mol under standard conditions).40 The thus obtained PCM radii for Ac3+ and Cf3+ were 1.933 and 1.747 Å, respectively, with both the LCPPs and SCPPs. They are depicted together with the ones of La3+ and Lu3+ from ref (40) and available crystal ionic radii81 in Figure S4, where an approximately linear relationship can be recognized. The above PCM radii were used in the SMD calculations of the Ac(L)+ and Cf(L)+ complexes.
The calculated relative stabilities (ΔG0) of the studied M(L)+ conformers in water are given in Figure 2. The relative stabilities of the Ac(L)+ complexes show only small variations in the gaseous and aqueous phases; the preferred stability of the Δ(δλδ)(δλδ) conformer was computed to be ca. 13 kJ/mol with respect to Δ(λδλ)(λδλ). In contrast, for the La, Cf, and Lu complexes, a considerable stabilization of the Δ(δλδ)(δλδ) conformer with respect to Δ(λδλ)(λδλ) was predicted by the theoretical model upon solvation. Similarly, a larger stability of the Δ(δλδ)(δλδ) conformer in aqueous solution with respect to the Δ(λδλ)(λδλ) conformer has been recently obtained at the same theoretical level for Ln(CHX-L)+ complexes, where CHX-L is a slightly modified rigid analogue of macropa.56 In the view of the abovementioned NMR results on Ln(macropa) complexes,34 the predicted stabilizations of the Δ(δλδ)(δλδ) conformers are likely overestimated. Accordingly, here, the predicted preference of the Δ(δλδ)(δλδ) conformer of Cf(L)+ is ambiguous.
From the point of view of medical application, the main question is the stability of the Ac(L)+ and Cf(L)+ complexes in aqueous solution. In Table 2, the computed ΔGaq0 data of the exchange reaction 1 are presented using the Δ(δλδ)(δλδ) conformer of La(L)+ as reference. Because of the lack of BSSE corrections for Ac(L)+ and Cf(L)+ with SCPP, data with both pseudopotentials, furthermore with and without BSSE correction, are presented. According to the available data, correction for BSSE can stabilize the complexes with respect to La(L)+ by 4–15 kJ/mol.
Table 2. Relative Stabilities of M(L)+ Complexes in Aqueous Solution in Terms of ΔGaq0 (kJ/mol) of the Exchange Reaction 1a.
| method | conformerb | Ac(L)+ | La(L)+ | Cf(L)+ | Lu(L)+c |
|---|---|---|---|---|---|
| LCPP + BSSE | δλδ | 8.4 | 0.0 | 43.6 | 46.2 |
| λδλ | 21.1 | 28.3 | 51.9 | 54.4 | |
| SCPP + BSSE | δλδ | 0.0 | 58.0 | ||
| λδλ | 22.7 | 63.3 | |||
| LCPP | δλδ | 13.9 | 0.0 | 52.3 | 56.2 |
| λδλ | 25.4 | 30.7 | 65.1 | 69.9 | |
| SCPP | δλδ | 26.2 | 0.0 | 34.8 | 69.7 |
| λδλ | 38.6 | 24.5 | 39.6 | 77.4 |
Reference is the Δ(δλδ)(δλδ) conformer of La(L)+.
The conformers Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) are denoted by δλδ and λδλ, respectively.
The experimental value is 38.5 kJ/mol.40
The data predict Ac(L)+ and Cf(L)+ relative stabilities between La(L)+ and Lu(L)+ in aqueous solution (cf. Table 2). In agreement with the expectation, the stability of Ac(L)+ is close to that of La(L)+. The computed high thermodynamic stability of Ac(L)+ extends the experimental observations on the outstanding kinetic stability of Ac(macropa), according to which the complex did not release Ac3+ in vivo and 98% of it remained intact against excess La3+ over 7–8 days.33
The LCPP and SCPP results show larger differences for Cf(L)+: the former theoretical level predicted stability close to Lu(L)+ while the latter a considerably higher one in between La(L)+ and Lu(L)+. The source of this difference is the considerably smaller hydration energy of the Cf(L)+ complex calculated with SCPP.
Conclusions
In the present study, the complex formation of four f elements (La and Lu with 4f valence subshell and Ac and Cf with 5f valence subshell) with the 18-membered macrocycle macropa ligand was compared. While all four metals have isotopes with potential radiotherapeutic applications, the greatest interest presently is in finding a suitable chelator ligand for Ac. The bonding interactions in the complexes were analyzed on the basis of characteristic geometrical parameters, topological properties of the electron density distribution, natural atomic charges, and properties of CT interactions based on the NBO model.
For the gaseous phase, the DFT computations predicted very weak charge-transfer interactions in Ac(L)+, which could not efficiently be compensated by the stronger ionic interactions and the weakest strain of L in this complex, resulting in the lowest stability of Ac(L)+ from the four complexes. The largest dissociation energy was obtained for Lu(L)+, in which the strong (short distance) ionic interactions could compensate effectively for the weak CT and largest strain of the L ligand. The strong ionic interactions (due again to the relatively short bond distances) could be suggested to be responsible for the larger stability of the Cf(L)+ molecule with respect to La(L)+, in spite of the strongest computed CT interactions in the latter complex.
The present results demonstrated the strong effect of water solvent on the thermodynamic equilibria of metal complexes. As a major effect, the large differences in the hydration energies of the M3+ ions play a crucial role in the ion exchange reactions of these M(L)+ complexes. Altogether, the computations predicted comparable stability of Ac(L)+ and Cf(L)+ complexes to those of the Ln(L)+ ones in aqueous solution, in agreement with experimental observations on Ac(L)+. The stability of Ac(L)+ was predicted to be somewhat lower than that of La(L)+, while the stability of the smaller Cf(L)+ was even lower but still higher than that of Lu(L)+. These stabilities support a potential medical application of these actinides.
Acknowledgments
The author thanks Dr. A. Morgenstern for advice.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c02873.
Relative Gibbs free energies of the eight M(L)+ complexes in the gaseous phase and aqueous solution; selected bond distances and topological properties of the Δ(δλδ)(δλδ) and Δ(λδλ)(λδλ) conformers; figures on the strain energy of the ligand, electron density distribution, and Laplacian of the electron density distribution at selected bond critical points; PCM radii; Cartesian coordinates of the Ac(L)+ and Cf(L)+ conformers optimized at the TPSSh/SCPP level (PDF)
The author declares no competing financial interest.
Supplementary Material
References
- Geerlings M. W.; Kaspersen F. M.; Apostolidis C.; Van Der Hout R. The feasibility of 225Ac as a source of α-particles in radioimmunotherapy. Nucl. Med. Commun. 1993, 14, 121–125. 10.1097/00006231-199302000-00009. [DOI] [PubMed] [Google Scholar]
- Miederer M.; Scheinberg D. A.; McDevitt M. R. Realizing the potential of the Actinium-225 radionuclide generator in targeted alpha particle therapy applications. Adv. Drug Delivery Rev. 2008, 60, 1371–1382. 10.1016/j.addr.2008.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiele N. A.; Wilson J. J. Actinium-225 for targeted α therapy: Coordination chemistry and current chelation approaches. Cancer Biother. Radiopharm. 2018, 33, 336–348. 10.1089/cbr.2018.2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgenstern A.; Apostolidis C.; Kratochwil C.; Sathekge M.; Krolicki L.; Bruchertseifer F. An overview of targeted alpha therapy with 225Actinium and 213Bismuth. Curr. Radiopharm. 2018, 11, 200–208. 10.2174/1874471011666180502104524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henriksen G.; Bruland Ø. S.; Larsen R. H. Thorium and Actinium Polyphosphonate Compounds As Bone-seeking Alpha Particle-emitting Agents. Anticancer Res. 2004, 24, 101–105. [PubMed] [Google Scholar]
- Dahle J.; Borrebæk J.; Jonasdottir T. J.; Hjelmerud A. K.; Melhus K. B.; Bruland Ø. S.; Press O. W.; Larsen R. H. Targeted cancer therapy with a novel low-dose rate α-emitting radioimmunoconjugate. Blood 2007, 110, 2049–2056. 10.1182/blood-2007-01-066803. [DOI] [PubMed] [Google Scholar]
- Dahle J.; Larsen R. H. Targeted alpha-particle therapy with 227Th-labeled antibodies. Curr. Radiopharm. 2008, 1, 209–214. 10.2174/1874471010801030209. [DOI] [Google Scholar]
- Abbas N.; Heyerdahl H.; Bruland Ø. S.; Borrebæk J.; Nesland J.; Dahle J. Experimental α-particle radioimmunotherapy of breast cancer using 227Th-labeled p-benzyl-DOTA-trastuzumab. EJNMMI Res. 2011, 1, 18 10.1186/2191-219X-1-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kratochwil C.; Bruchertseifer F.; Giesel F. L.; Weis M.; Verburg F. A.; Mottaghy F.; Kopka K.; Apostolidis C.; Haberkorn U.; Morgenstern A. 225Ac-PSMA-617 for PSMA-targeted a-radiation therapy of metastatic castration-resistant prostate cancer. J. Nucl. Med. 2016, 57, 1941–1944. 10.2967/jnumed.116.178673. [DOI] [PubMed] [Google Scholar]
- Kratochwil C.; Bruchertseifer F.; Rathke H.; Bronzel M.; Apostolidis C.; Weichert W.; Haberkorn U.; Giesel F. L.; Morgenstern A. Targeted α-therapy of metastatic castration-resistant prostate cancer with 225Ac-PSMA-617: Dosimetry estimate and empiric dose finding. J. Nucl. Med. 2017, 58, 1624–1631. 10.2967/jnumed.117.191395. [DOI] [PubMed] [Google Scholar]
- Hammer S.; Hagemann U. B.; Zitzmann-Kolbe S.; Larsen A.; Ellingsen C.; Geraudie S.; Grant D.; Indrevoll B.; Smeets R.; von Ahsen O.; et al. Preclinical Efficacy of a PSMA-Targeted Thorium-227 Conjugate (PSMA-TTC), a Targeted Alpha Therapy for Prostate Cancer. Clin. Cancer Res. 2020, 26, 1985–1996. 10.1158/1078-0432.CCR-19-2268. [DOI] [PubMed] [Google Scholar]
- Jurcic J. G.; Rosenblat T. L.; McDevitt M. R.; Pandit-Taskar N.; Carrasquillo J. A.; Chanel S. M.; Zikaras K.; Frattini M. G.; Maslak P. M.; Cicic D.; et al. Targeted Alpha-Particle Nano-Generator Actinium-225 (225Ac)-Lintuzumab (Anti-CD33) in Acute Myeloid Leukemia (AML). Clin. Lymphoma, Myeloma Leuk. 2013, 13, S379–S380. 10.1016/j.clml.2013.07.088. [DOI] [Google Scholar]
- Jurcic J. G.; Ravandi F.; Pagel J. M.; Park J. H.; Smith B. D.; Douer D.; Levy M. Y.; Estey E.; Kantarjian H. M.; Earle D.; et al. Phase I trial of α-particle therapy with actinium-225 (225Ac)-lintuzumab (anti-CD33) and low-dose cytarabine (LDAC) in older patients with untreated acute myeloid leukemia (AML.). J. Clin. Oncol. 2015, 33, 7050. 10.1200/jco.2015.33.15_suppl.7050. [DOI] [Google Scholar]
- Kratochwil C.; Bruchertseifer F.; Giesel F.; Apostolidis C.; Haberkorn U.; Morgenstern A. Ac-225-DOTATOC - an Empiric Dose Finding for Alpha Particle Emitter Based Radionuclide Therapy of Neuroendocrine Tumors. J. Nucl. Med. 2015, 56, 1232. [Google Scholar]
- Hagemann U. B.; Ellingsen C.; Schuhmacher J.; Kristian A.; Mobergslien A.; Cruciani V.; Wickstroem K.; Schatz C. A.; Kneip C.; Golfier S.; et al. Mesothelin-Targeted Thorium-227 Conjugate (MSLN-TTC): Preclinical Evaluation of a New Targeted Alpha Therapy for Mesothelin-Positive Cancers. Clin. Cancer Res. 2019, 25, 4723–4734. 10.1158/1078-0432.CCR-18-3476. [DOI] [PubMed] [Google Scholar]
- Morgenstern A.; Apostolidis C.; Bruchertseifer F.; Capote R.; Gouder T.; Simonelli F.; Sin M.; Abbas K. Cross-sections of the reaction 232Th(p,3n)230Pa for production of 230U for targeted alpha therapy. Appl. Radiat. Isot. 2008, 66, 1275–1280. 10.1016/j.apradiso.2008.02.066. [DOI] [PubMed] [Google Scholar]
- Montavon G.; Apostolidis C.; Bruchertseifer F.; Repinc U.; Morgenstern A. Spectroscopic study of the interaction of U(VI) with transferrin and albumin for speciation of U(VI) under blood serum conditions. J. Inorg. Biochem. 2009, 103, 1609–1616. 10.1016/j.jinorgbio.2009.08.010. [DOI] [PubMed] [Google Scholar]
- Montavon G.; Repinc U.; Apostolidis C.; Bruchertseifer F.; Abbas K.; Morgenstern A. Investigation of para-sulfonatocalix[n]arenes [n = 6, 8] as potential chelates for 230U. Dalton Trans. 2010, 39, 1366–1374. 10.1039/B918426K. [DOI] [PubMed] [Google Scholar]
- Schlea C. S.; Stoddard D. H. Californium Isotopes Proposed for Intracavity and Interstitial Radiation Therapy with Neutrons. Nature 1965, 206, 1058–1059. 10.1038/2061058a0. [DOI] [PubMed] [Google Scholar]
- Wang C.-K. C.Progress in Californium-252 Neutron Brachytherapy. In Brachytherapy; Kishi K., Ed.; InTech: Rijeka, Croatia, 2012; pp 33–58. [Google Scholar]
- Price E. W.; Orvig C. Matching chelators to radiometals for radiopharmaceuticals. Chem. Soc. Rev. 2014, 43, 260–290. 10.1039/C3CS60304K. [DOI] [PubMed] [Google Scholar]
- Cacheris W. P.; Nickle S. K.; Sherry A. D. Thermodynamic study of lanthanide complexes of 1,4,7-triazacyclononane-N,N’,N″-triacetic acid and 1,4,7,10-tetraazacyclododecane-N,N′,N″,N‴-tetraacetic acid. Inorg. Chem. 1987, 26, 958–960. 10.1021/ic00253a038. [DOI] [Google Scholar]
- Clarke E. T.; Martell A. E. Stabilities of trivalent metal ion complexes of the tetraacetate derivatives of 12-, 13- and 14-membered tetraazamacrocycles. Inorg. Chim. Acta 1991, 190, 37–46. 10.1016/S0020-1693(00)80229-7. [DOI] [Google Scholar]
- Morgenstern A.; Apostolidis C.; Bruchertseifer F. Supply and Clinical Application of Actinium-225 and Bismuth-213. Semin. Nucl. Med. 2020, 50, 119–123. 10.1053/j.semnuclmed.2020.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. A.; Rowland M. E. Metal complex formation with 1,10-diaza-4,7,13,16-tetraoxacyclooctadecane-N,N’-diacetic acid. An approach to potential lanthanide ion selective reagents. Inorg. Chem. 1983, 22, 3866–3869. 10.1021/ic00168a010. [DOI] [Google Scholar]
- Damu K. V.; Shaikjee M. S.; Michael J. P.; Howard A. S.; Hancock R. D. Control of metal ion selectivity in ligands containing neutral oxygen and pyridyl groups. Inorg. Chem. 1986, 25, 3879–3883. 10.1021/ic00242a010. [DOI] [Google Scholar]
- Hancock R. D.; Bhavan R.; Wade P. W.; Boeyens J. C. A.; Dobson S. M. Ligand design for complexation in aqueous solution. 1. Neutral oxygen donor bearing groups as a means of controlling size-based selectivity for metal ions. Inorg. Chem. 1989, 28, 187–194. 10.1021/ic00301a007. [DOI] [Google Scholar]
- Brücher E.; Györi B.; Emri J.; Solymosi P.; Sztanyik L. B.; Varga L. 1,10-Diaza-4,7,13,16-tetraoxacyclooctadecane-1,10-bis(malonate), a ligand with high Sr2+/Ca2+ and Pb2+/Zn2+ selectivities in aqueous solution. J. Chem. Soc., Chem. Commun. 1993, 574–575. 10.1039/C39930000574. [DOI] [Google Scholar]
- Zhang X. X.; Bordunov A. V.; Bradshaw J. S.; Dalley N. K.; Kou X.; Izatt R. M. A New Highly Selective Macrocycle for K+ and Ba2+: Effect of Formation of a Pseudo Second Macroring through Complexation. J. Am. Chem. Soc. 1995, 117, 11507–11511. 10.1021/ja00151a014. [DOI] [Google Scholar]
- Su N.; Bradshaw J. S.; Zhang X. X.; Song H.; Savage P. B.; Xue G.; Krakowiak K. E.; Izatt R. M. Syntheses and Metal Ion Complexation of Novel 8-Hydroxyquinoline-Containing Diaza-18-Crown-6 Ligands and Analogues. J. Org. Chem. 1999, 64, 8855–8861. 10.1021/jo991081o. [DOI] [PubMed] [Google Scholar]
- Jensen M. P.; Chiarizia R.; Shkrob I. A.; Ulicki J. S.; Spindler B. D.; Murphy D. J.; Hossain M.; Roca-Sabio A.; Platas-Iglesias C.; de Blas A.; et al. Aqueous Complexes for Efficient Size-based Separation of Americium from Curium. Inorg. Chem. 2014, 53, 6003–6012. 10.1021/ic500244p. [DOI] [PubMed] [Google Scholar]
- Regueiro-Figueroa M.; Barriada J. L.; Pallier A.; Esteban-Gómez D.; de Blas A.; Rodríguez-Blas T.; Tóth É.; Platas-Iglesias C. Stabilizing Divalent Europium in Aqueous Solution Using Size-Discrimination and Electrostatic Effects. Inorg. Chem. 2015, 54, 4940–4952. 10.1021/acs.inorgchem.5b00548. [DOI] [PubMed] [Google Scholar]
- Thiele N. A.; Brown V.; Kelly J. M.; Amor-Coarasa A.; Jermilova U.; MacMillan S. N.; Nikolopoulou A.; Ponnala S.; Ramogida C. F.; Robertson A. K. H.; et al. An Eighteen-Membered Macrocyclic Ligand for Actinium-225 Targeted Alpha Therapy. Angew. Chem., Int. Ed. 2017, 56, 14712–14717. 10.1002/anie.201709532. [DOI] [PubMed] [Google Scholar]
- Roca-Sabio A.; Mato-Iglesias M.; Esteban-Gómez D.; Tóth É.; de Blas A.; Platas-Iglesias C.; Rodríguez-Blas T. Macrocyclic Receptor Exhibiting Unprecedented Selectivity for Light Lanthanides. J. Am. Chem. Soc. 2009, 131, 3331–3341. 10.1021/ja808534w. [DOI] [PubMed] [Google Scholar]
- Ferreirós-Martínez R.; Esteban-Gómez D.; Tóth E.; de Blas A.; Platas-Iglesias C.; Rodríguez-Blas T. Macrocyclic receptor showing extremely high Sr(II)/Ca(II) and Pb(II)/Ca(II) selectivities with potential application in chelation treatment of metal intoxication. Inorg. Chem. 2011, 50, 3772–3784. 10.1021/ic200182e. [DOI] [PubMed] [Google Scholar]
- Thiele N. A.; MacMillan S. N.; Wilson J. J. Rapid Dissolution of BaSO4 by Macropa, an 18-Membered Macrocycle with High Affinity for Ba2+. J. Am. Chem. Soc. 2018, 140, 17071–17078. 10.1021/jacs.8b08704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roca-Sabio A.; Mato-Iglesias M.; Esteban-Gómez D.; de Blas A.; Rodríguez-Blas T.; Platas-Iglesias C. The effect of ring size variation on the structure and stability of lanthanide(III) complexes with crown ethers containing picolinate pendants. Dalton Trans. 2011, 40, 384–392. 10.1039/C0DT00746C. [DOI] [PubMed] [Google Scholar]
- Chang C. A.; Ochaya V. O. Potential Lanthanide Ion Selective Reagents. 3.1,2 Metal Complex Formation with l,7-Diaza-4,10,13-trioxacyclopentadecane-N,N/-diacetic Acid. Inorg. Chem. 1986, 25, 355–358. 10.1021/ic00223a025. [DOI] [Google Scholar]
- Kelly J. M.; Amor-Coarasa A.; Ponnala S.; Nikolopoulou A.; Williams C.; Thiele N. A.; Schyler D.; Wilson J. J.; DiMagno S. G.; Babich J. W. A Single Dose of 225Ac-RPS-074 Induces a Complete Tumor Response in a LNCaP Xenograft Model. J. Nucl. Med. 2019, 60, 649–655. 10.2967/jnumed.118.219592. [DOI] [PubMed] [Google Scholar]
- Regueiro-Figueroa M.; Esteban-Gómez D.; de Blas A.; Rodríguez-Blas T.; Platas-Iglesias C. Understanding Stability Trends along the Lanthanide Series. Chem. – Eur. J. 2014, 20, 3974–3981. 10.1002/chem.201304469. [DOI] [PubMed] [Google Scholar]
- Bhavan R.; Hancock R. D.; Wade P. W.; Boeyens J. C. A.; Dobson S. M. Crystallographic study of the barium(II) complex of a lariat ether with long pendent arms. Inorg. Chim. Acta 1990, 171, 235–238. 10.1016/S0020-1693(00)80438-7. [DOI] [Google Scholar]
- Hancock R. D.; Siddons C. J.; Oscarson K. A.; Reibenspies J. M. The structure of the 11-coordinate barium complex of the pendant-donor macrocycle 1,4,7,10-tetrakis(carbamoylmethyl)–1,4,7,10-tetraazacyclododecane: an analysis of the coordination numbers of barium(II) in its complexes. Inorg. Chim. Acta 2004, 357, 723–727. 10.1016/j.ica.2003.06.016. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2010.
- Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids (TPSSTPSS). Phys. Rev. Lett. 2003, 91, 146401 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
- Roca-Sabio A.; Regueiro-Figueroa M.; Esteban-Gómez D.; de Blas A.; Rodríguez-Blas T.; Platas-Iglesias C. Density functional dependence of molecular geometries in lanthanide(III) complexes relevant to bioanalytical and biomedical applications. Comput. Theor. Chem. 2012, 999, 93–104. 10.1016/j.comptc.2012.08.020. [DOI] [Google Scholar]
- Huang P.-W. Understanding the Stability Trend Along Light Lanthanide Complexes with an Ehtylenediamine-Type Ligand: A Quantum Chemical Study. ChemistrySelect 2019, 4, 12368–12374. 10.1002/slct.201902887. [DOI] [Google Scholar]
- Esteban-Gómez D.; de Blas A.; Rodríguez-Blas T.; Helm L.; Platas-Iglesias C. Hyperfine coupling constants on inner-sphere water molecules of Gd III-based MRI contrast agents. ChemPhysChem 2012, 13, 3640–3650. 10.1002/cphc.201200417. [DOI] [PubMed] [Google Scholar]
- Dolg M.; Stoll H.; Savin A.; Preuss H. Energy-adjusted pseudopotentials for the rare earth elements. Theor. Chim. Acta 1989, 75, 173–194. 10.1007/BF00528565. [DOI] [Google Scholar]
- Dolg M.; Stoll H.; Preuss H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 1993, 85, 441–450. 10.1007/BF01112983. [DOI] [Google Scholar]
- Cao X.; Dolg M. Valence basis sets for relativistic energy-consistent small-core lanthanide pseudopotentials. J. Chem. Phys. 2001, 115, 7348–7355. 10.1063/1.1406535. [DOI] [Google Scholar]
- Cao X.; Dolg M. Segmented contraction scheme for small-core lanthanide pseudopotential basis sets. J. Mol. Struct.: THEOCHEM 2002, 581, 139–147. 10.1016/S0166-1280(01)00751-5. [DOI] [Google Scholar]
- Küchle W.; Dolg M.; Stoll H.; Preuss H. Energy-Adjusted Pseudopotentials for the Actinides. Parameter Sets and Test Calculations for Thorium and Thorium Monoxide. J. Chem. Phys. 1994, 100, 7535–7542. 10.1063/1.466847. [DOI] [Google Scholar]
- Cao X.; Dolg M.; Stoll H. Valence basis sets for relativistic energy-consistent small-core actinide pseudopotentials. J. Chem. Phys. 2003, 118, 487–496. 10.1063/1.1521431. [DOI] [Google Scholar]
- Cao X.; Dolg M. Segmented contraction scheme for small-core actinide pseudopotential basis sets. J. Mol. Struct.: THEOCHEM 2004, 673, 203–209. 10.1016/j.theochem.2003.12.015. [DOI] [Google Scholar]
- Moritz A.; Cao X.; Dolg M. Quasirelativistic energy-consistent 5f-in-core pseudopotentials for trivalent actinide elements. Theor. Chem. Acc. 2007, 117, 473–481. 10.1007/s00214-006-0180-7. [DOI] [Google Scholar]
- Thiele N. A.; Woods J. J.; Wilson J. J. Implementing f-Block Metal Ions in Medicine: Tuning the Size Selectivity of Expanded Macrocycles. Inorg. Chem. 2019, 58, 10483–10500. 10.1021/acs.inorgchem.9b01277. [DOI] [PubMed] [Google Scholar]
- Boys S. F.; Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. 10.1080/00268977000101561. [DOI] [Google Scholar]
- Tomasi J.; Mennucci B.; Cammi R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- Scalmani G.; Frisch M. J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110 10.1063/1.3359469. [DOI] [PubMed] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Choppin G. R.; Jensen M. P.. Actinides in Solution: Complexation and Kinetics. In The Chemistry of the Actinide and Transactinide Elements; Morss L. R.; Edelstein N. M.; Fuger J., Eds.; Springer: Dordrecht, 2006; Vol. 4, pp 2539–2540. [Google Scholar]
- Reed A. E.; Curtiss L. A.; Weinhold F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. 10.1021/cr00088a005. [DOI] [Google Scholar]
- Glendening E. D.; Landis C. R.; Weinhold F. NBO 6.0: Natural Bond Orbital Analysis Program. J. Comput. Chem. 2013, 34, 1429–1437. 10.1002/jcc.23266. [DOI] [PubMed] [Google Scholar]
- Bader R. F. W.Atoms in Molecules. A Quantum Theory; Oxford University Press: Oxford, 1990. [Google Scholar]
- Keith T. A.AIMAll (Version 17.11.14); TK Gristmill Software: Overland Park, 2017.
- Hayton T. W.; Kaltsoyannis N.. Organometallic Actinide Complexes with Novel Oxidation States and Ligand Types. In Experimental and Theoretical Approaches to Actinide Chemistry; Gibson J. K.; de Jong W. A., Eds.; John Wiley & Sons, Inc.: Hoboken, New Jersey, 2018; pp 181–236. [Google Scholar]
- Kaltsoyannis N. Transuranic Computational Chemistry. Chem. – Eur. J. 2018, 24, 2815–2825. 10.1002/chem.201704445. [DOI] [PubMed] [Google Scholar]
- Kerridge A. Quantification of f-element covalency through analysis of the electron density: insights from simulation. Chem. Commun. 2017, 53, 6685–6695. 10.1039/C7CC00962C. [DOI] [PubMed] [Google Scholar]
- Dognon J.-P. Theoretical insights into the chemical bonding in actinide complexes. Coord. Chem. Rev. 2014, 266–267, 110–122. 10.1016/j.ccr.2013.11.018. [DOI] [Google Scholar]
- Jones M. B.; Gaunt A. J.; Gordon J. C.; Kaltsoyannis N.; Neu M. P.; Scott B. L. Uncovering f-element bonding differences and electronic structure in a series of 1:3 and 1:4 complexes with a diselenophosphinate ligand. Chem. Sci. 2013, 4, 1189–1203. 10.1039/c2sc21806b. [DOI] [Google Scholar]
- Schnaars D. D.; Gaunt A. J.; Hayton T. W.; Jones M. B.; Kirker I.; Kaltsoyannis N.; May I.; Reilly S. D.; Scott B. L.; Wu G. Bonding trends traversing the tetravalent actinide series: Synthesis, structural, and computational analysis of AnIV(Aracnac)4 complexes (An = Th, U, Np, Pu; Aracnac = ArNC(Ph)CHC(Ph)O; Ar = 3,5-tBu2C6H3). Inorg. Chem. 2012, 51, 8557–8566. 10.1021/ic301109f. [DOI] [PubMed] [Google Scholar]
- Kerridge A. Oxidation state and covalency in f-element metallocenes (M = Ce, Th, Pu): A combined CASSCF and topological study. Dalton Trans. 2013, 42, 16428–16436. 10.1039/c3dt52279b. [DOI] [PubMed] [Google Scholar]
- Kerridge A. f-Orbital covalency in the actinocenes (An = Th–Cm): multiconfigurational studies and topological analysis. RSC Adv. 2014, 4, 12078–12086. 10.1039/C3RA47088A. [DOI] [Google Scholar]
- Huang Q. R.; Kingham J. R.; Kaltsoyannis N. The strength of actinide-element bonds from the quantum theory of atoms-in-molecules. Dalton Trans. 2015, 44, 2554–2566. 10.1039/C4DT02323D. [DOI] [PubMed] [Google Scholar]
- Banik N. L.; Vallet V.; Réal F.; Belmecheri R. M.; Schimmelpfennig B.; Rothe J.; Marsac R.; Lindqvist-Reis P.; Walther C.; Denecke M. A.; et al. First structural characterization of Pa(iv) in aqueous solution and quantum chemical investigations of the tetravalent actinides up to Bk(iv): the evidence of a curium break. Dalton Trans. 2016, 45, 453–457. 10.1039/C5DT03560K. [DOI] [PubMed] [Google Scholar]
- Kaltsoyannis N. Covalency hinders AnO2(H2O)+ → AnO(OH)2+ isomerisation (An = Pa–Pu). Dalton Trans. 2016, 45, 3158–3162. 10.1039/C5DT04317D. [DOI] [PubMed] [Google Scholar]
- Wu Q. Y.; Cheng Z. P.; Lan J. H.; Wang C. Z.; Chai Z. F.; Gibson J. K.; Shi W. Q. Insight into the nature of M-C bonding in the lanthanide/actinide-biscarbene complexes: A theoretical perspective. Dalton Trans. 2018, 47, 12718–12725. 10.1039/C8DT02702A. [DOI] [PubMed] [Google Scholar]
- Kovács A.; Apostolidis C.; Walter O. Comparative study of complexes of rare earths and actinides with 2,6-bis(1,2,4-triazin-3-yl)pyridine. Inorganics 2019, 7, 26 10.3390/inorganics7030026. [DOI] [Google Scholar]
- Corey E. J.; Bailar J. C. The Stereochemistry of Complex Inorganic Compounds. XXII. Stereospecific Effects in Complex Ions. J. Am. Chem. Soc. 1959, 81, 2620–2629. 10.1021/ja01520a006. [DOI] [Google Scholar]
- Beattie J. K. Conformational Analysis of Tris(ethylenediamine) Complexes. Acc. Chem. Res. 1971, 4, 253–259. 10.1021/ar50043a004. [DOI] [Google Scholar]
- Shannon R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. 1976, A32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
- Kelley M. P.; Su J.; Urban M.; Luckey M.; Batista E. R.; Yang P.; Shafer J. C. On the Origin of Covalent Bonding in Heavy Actinides. J. Am. Chem. Soc. 2017, 139, 9901–9908. 10.1021/jacs.7b03251. [DOI] [PubMed] [Google Scholar]
- Su J.; Batista E. R.; Boland K. S.; Bone S. E.; Bradley J. A.; Cary S. K.; Clark D. L.; Conradson S. D.; Ditter A. S.; Kaltsoyannis N.; et al. Energy-Degeneracy-Driven Covalency in Actinide Bonding. J. Am. Chem. Soc. 2018, 140, 17977–17984. 10.1021/jacs.8b09436. [DOI] [PubMed] [Google Scholar]
- Albrecht-Schmitt T. E.; Hobart D. E.; Páez-Hernández D.; Celis-Barros C. Theoretical examination of covalency in berkelium(IV) carbonate complexes. Int. J. Quantum Chem. 2020, 120, e26254 10.1002/qua.26254. [DOI] [Google Scholar]
- Chandrasekar A.; Ghanty T. K. Uncovering Heavy Actinide Covalency: Implications for Minor Actinide Partitioning. Inorg. Chem. 2019, 58, 3744–3753. 10.1021/acs.inorgchem.8b03358. [DOI] [PubMed] [Google Scholar]
- Kelley M. P.; Deblonde G. J. P.; Su J.; Booth C. H.; Abergel R. J.; Batista E. R.; Yang P. Bond Covalency and Oxidation State of Actinide Ions Complexed with Therapeutic Chelating Agent 3,4,3-LI(1,2-HOPO). Inorg. Chem. 2018, 57, 5352–5363. 10.1021/acs.inorgchem.8b00345. [DOI] [PubMed] [Google Scholar]
- Lacoste R. G.; Christoffers G. V.; Martell A. E. New Multidentate Ligands. II. Amino Acids Containing α-Pyridyl Groups. J. Am. Chem. Soc. 1965, 87, 2385–2388. 10.1021/ja01089a015. [DOI] [Google Scholar]
- Tei L.; Baranyai Z.; Brücher E.; Cassino C.; Demicheli F.; Masciocchi N.; Giovenzana G. B.; Botta M. Dramatic increase of selectivity for heavy lanthanide(III) cations by tuning the flexibility of polydentate chelators. Inorg. Chem. 2010, 49, 616–625. 10.1021/ic901848p. [DOI] [PubMed] [Google Scholar]
- Loncin M. F.; Desreux J. F.; Merciny E. Coordination of Lanthanides by Two Polyamino Polycarboxylic Macrocycles: Formation of Highly Stable Lanthanide Complexes. Inorg. Chem. 1986, 25, 2646–2648. 10.1021/ic00235a031. [DOI] [Google Scholar]
- Guillaumont R.; David F. Fonctions thermodynamiques d’hydration et d’oxydo-reduction des ions M3+ des lanthanides. Radiochem. Radioanal. Lett. 1974, 17, 25–39. [Google Scholar]
- Cosentino U.; Villa A.; Pitea D.; Moro G.; Barone V. Extension of computational chemistry to the study of lanthanide(III) ions in aqueous solution: Implementation and validation of a continuum solvent approach. J. Phys. Chem. B 2000, 104, 8001–8007. 10.1021/jp994022n. [DOI] [Google Scholar]
- D’Angelo P.; Zitolo A.; Migliorati V.; Chillemi G.; Duvail M.; Vitorge P.; Abadie S.; Spezia R. Revised ionic radii of lanthanoid(III) ions in aqueous solution. Inorg. Chem. 2011, 50, 4572–4579. 10.1021/ic200260r. [DOI] [PubMed] [Google Scholar]
- Bratsch S. G.; Lagowski J. J. Lanthanide thermodynamic predictions. 7. Thermodynamics of 2+, 3+, and 4+ aquo ions and standard electrode potentials at 298.15 K. J. Phys. Chem. A. 1985, 89, 3317–3319. 10.1021/j100261a031. [DOI] [Google Scholar]
- Bratsch S. G.; Lagowski J. J. Actinide Thermodynamic Predictions. 3. Thermodynamlcs of Compounds and Aquo Ions of the 2+, 3+, and 4+ Oxidation States and Standard Electrode Potentials at 298.15 K. J. Phys. Chem. B. 1986, 90, 307–312. 10.1021/j100274a021. [DOI] [Google Scholar]
- Bratsch S. G.; Lagowski J. J. Lanthanide thermodynamic predictions. 6. Thermodynamics of gas-phase ions and revised enthalpy equations for solids at 298.15 K. J. Phys. Chem. C. 1985, 89, 3310–3316. 10.1021/j100261a030. [DOI] [Google Scholar]
- David F. H. About low oxidation states, hydration and covalence properties of f elements. Radiochim. Acta 2008, 96, 135–144. 10.1524/ract.2008.1470. [DOI] [Google Scholar]
- Morss L. R. Thermochemical properties of yttrium, lanthanum, and the lanthanide elements and ions. Chem. Rev. 1976, 76, 827–841. 10.1021/cr60304a007. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.