Complex Chemical Data Classification and Discrimination Using Locality Preserving Partial Least Squares Discriminant Analysis

Abstract

Partial least squares discriminant analysis (PLS-DA) is a well-known technique for feature extraction and discriminant analysis in chemometrics. Despite its popularity, it has been observed that PLS-DA does not automatically lead to extraction of relevant features. Feature learning and extraction depends on how well the discriminant subspace is captured. In this paper, discriminant subspace learning of chemical data is discussed from the perspective of PLS-DA and a recent extension of PLS-DA, which is known as the locality preserving partial least squares discriminant analysis (LPPLS-DA). The objective is twofold: (a) to introduce the LPPLS-DA algorithm to the chemometrics community and (b) to demonstrate the superior discrimination capabilities of LPPLS-DA and how it can be a powerful alternative to PLS-DA. Four chemical data sets are used: three spectroscopic data sets and one that contains compositional data. Comparative performances are measured based on discrimination and classification of these data sets. To compare the classification performances, the data samples are projected onto the PLS-DA and LPPLS-DA subspaces, and classification of the projected samples into one of the different groups (classes) is done using the nearest-neighbor classifier. We also compare the two techniques in data visualization (discrimination) task. The ability of LPPLS-DA to group samples from the same class while at the same time maximizing the between-class separation is clearly shown in our results. In comparison with PLS-DA, separation of data in the projected LPPLS-DA subspace is more well defined.

Introduction

With the recent advances in technology, there has been an explosion in the amount of chemical data generated using advanced chemical analysis equipment. These types of data sets possess characteristics such as high dimensionality and small sample size, which make classification and discrimination tasks quite challenging. The effectiveness and efficiency of classification algorithms drop rapidly as the dimensionality increases, and this is referred to as the “curse of dimensionality”.¹ A lot of techniques have been proposed in the past to reduce the dimensionality of the data by either selecting the most representative features from the original ones (feature selection) or by creating new features as linear combinations of the original features (feature extraction). These techniques include principal component analysis (PCA)^2,3 and partial least squares discriminant analysis (PLS-DA)^2,4,5 to mention a few.

PLS-DA is a well-known technique for feature extraction and discriminant analysis in the context of chemometrics.⁶⁻¹⁰ This method is based on the PLS algorithm, which was first introduced for regression task.^11,12 PLS-DA is a supervised algorithm that combines feature extraction and discriminant analysis into one algorithm and is well applicable for high-dimensional data. Theoretically, PLS-DA finds a transformation of the high-dimensional data into a lower-dimensional subspace in which data samples of different classes are mapped far apart. The transformation is readily computed using the nonlinear iterative partial least squares (NIPALS) algorithm.^11,13

The PLS-DA modeling strategy involves two main procedures: (1) PLS-DA component construction (i.e., dimension reduction) and (2) prediction model construction (i.e., discriminant analysis). The output of the PLS-DA algorithms is the X-score (PLS-DA scores), which represents the original data X in a lower-dimensional subspace, and the predicted class membership matrix (Y_pred), which estimates the class membership of the samples. Both the PLS-DA scores and the predicted class membership matrix have been widely used as input variables for the classification method. For example,² compare PCA and PLS-DA in reducing the dimension of face data sets. The authors then used two classification methods, linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA), to construct prediction models using the extracted PCA and PLS-DA scores. Similarly,¹⁴ compare the performance of PCA and PLS-DA in dimensional reduction of microarray gene expression data. Logistic discrimination and QDA were then used to construct prediction models using the extracted PCA and PLS-DA scores. On the other hand,¹⁵ both the PLS-DA scores and the predicted class membership matrix (Y_pred) were used as inputs in an artificial neural network to classify commercial brands of orange juice.

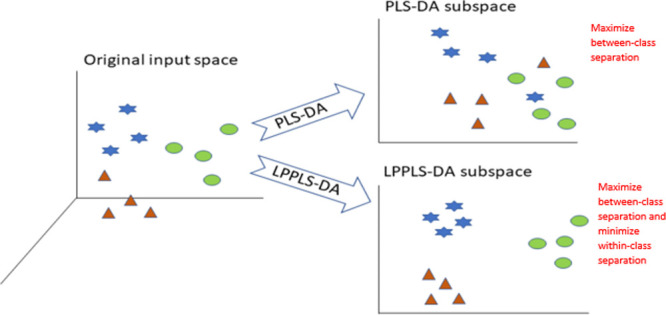
Several studies indicate the need to refine the PLS-DA modeling practice strategies especially in complex data sets such as multiclass, colossal, and imbalanced data sets.^5,16,17 Some recent studies^16,18 have also pointed out that when classification is the goal and dimension reduction is needed, PLS-DA should not be preferred over other traditional methods as it has no significant advantages over them and is a technique full of dangers. Another major drawback of the PLS-DA method is its lack of ability to preserve the local structure of data. PLS-DA sees only the global Euclidean structure of data. It fails to preserve the local distances of data points if the data points lie on a manifold hidden in the high-dimensional Euclidean space. Recently, a locality preserving partial least squares discriminant analysis (LPPLS-DA)¹⁹ method, which can effectively preserve the local manifold structures of data points, is proposed in the context of face recognition. LPPLS-DA has demonstrated great success and outperforms the conventional PLS-DA method.

In this work, we illustrate the practical utility of LPPLS-DA in chemical data analysis. The LPPLS-DA algorithm seeks to find a projection that preserves the local distances among data points and maximize class separation at the same time. Because LPPLS-DA is able to project the data points into two or more dimensions while preserving the local manifold structure of data points, the method can therefore be used for visualization and discrimination of complex high-dimensional data. This is an important advantage of LPPLS-DA that is absent in the conventional PLS-DA method. In addressing the effect of locality preservation of data points, it is only meaningful to look from the perspective of the X-scores because the Laplacian matrix that represents local manifold structure is derived from data samples in X. Thus, practical comparisons between PLS-DA and LPPLS-DA are done using the PLS-DA scores and the associated LPPLS-DA scores (i.e., representations of data X in a lower dimensional space). The K-nearest-neighbor (K-NN) classifier is then used to construct classification models based on the extracted PLS-DA and LPPLS-DA scores.

The overall aim of the paper is two-fold: (a) to introduce the LPPLS-DA algorithm to the chemometrics community and (b) to show that discrimination using the conventional PLS-DA algorithm is not always warranted and the LPPLS-DA algorithm can be used as a powerful alternative.

Results and Discussion

Overview of Experiments

The performances of LPPLS-DA and PLS-DA methods are compared in two ways:

• 1.Visualization: The PLS-DA scores and the LPPLS-DA scores in the low-dimensional subspace are plotted in order to evaluate the discriminant capability of the methods. Between-class separability of each methods is evaluated based on how well the two methods separate the different classes in the data. The ability to preserve local distances and within-class multimodality is evaluated based on how well the two methods grouped samples belonging to the same class.
• 2.Classification: The data sets are randomly partitioned into training and test sets. The K-NN classifier (with K = 2) is used to construct classification models based on the PLS-DA and LPPLS-DA scores extracted from the training set. The performance of the classification model is then evaluated using the corresponding PLS-DA and LPPLS-DA scores extracted from the test set. The results are presented using confusion matrices. Plots of average classification accuracies as functions of the reduced dimensionality are also presented.

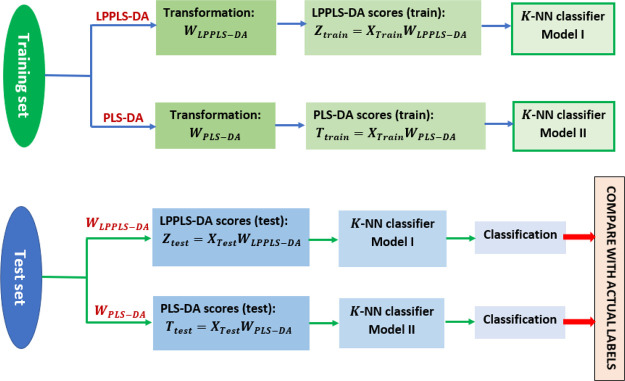
The overall data processing method is depicted in Figure 1.

Figure 1.

Flow chart of the experimental design.

Data Sets

Four publicly available chemical data sets are used in the experiments, which include three spectroscopic data sets and one that contains compositional data. Detailed information on the data sets is provided below as well as in Table 1.

• 1.The Coffee data set²⁰ contains 56 samples belonging to two different species: arabica and robusta species with 29 and 27 samples, respectively. The data was obtained by Fourier transform infrared spectroscopy with diffuse reflectance sampling, where each spectrum contains 286 variables in the range of 810–1910 cm^–1.
• 2.The Pacific cod data set²¹ comes from a study of relative abundance of 47 fatty acids in Pacific cod sampled at two sites, Graves Harbor (site A) and Islas Bay (site B), in the Gulf of Alaska in 2011 and 2013. The data contains fatty acid profiles for 48 fishes with mean fatty acid proportions ranging from about 0.02 to 30%. As well, this data set contains balanced classes with 12 samples per class.
• 3.The ink data set^21,22 contains infrared spectra of eight brands of pen ink obtained using Spectrum 400 (PerkinElmer) equipment with a universal attenuated total reflectance accessory in the range of 4000–650 cm^–1. The goal is to classify blue ink pens by brand. The data set contains balanced classes with 60 samples per class.
• 4.The wood data set²³ consists of near-infrared reflectance spectra from 108 samples of wood obtained from four different species of Brazilian trees: Crabwood (Carapa guianensis Aubl.), Cedar (Cedrela odorata L.), Curupixa (Micropholis melinoniana pierre), and Mahogany (Swietenia macrophylla King). A total of 26, 28, 29, and 25 samples belonging to the Crabwood, Cedar, Curupixa, and Mahogany species, respectively, were collected. The samples were then measured on a handheld spectrometer, Phazir RX (Polychromix), and four replicate spectra were obtained for each sample, resulting in a total of 432 spectra. As a result, the data has imbalanced classes.

Table 1. Summary of Data Sets Used in the Experiments.

data sets	no. of samples	no. of features	no. of classes
coffee	56	286	2
Pacific cod	48	47	4
ink	480	3351	8
wood	432	100	4

Data Visualization

The PLS-DA and LPPLS-DA methods are applied on all four data sets to extract the PLS-DA scores and the LPPLS-DA scores, respectively. Figure 2 shows the scores for two-dimensional embedding of the coffee and Pacific cod data sets, and Figure 3 shows the scores for three-dimensional embedding of the wood and ink data sets.

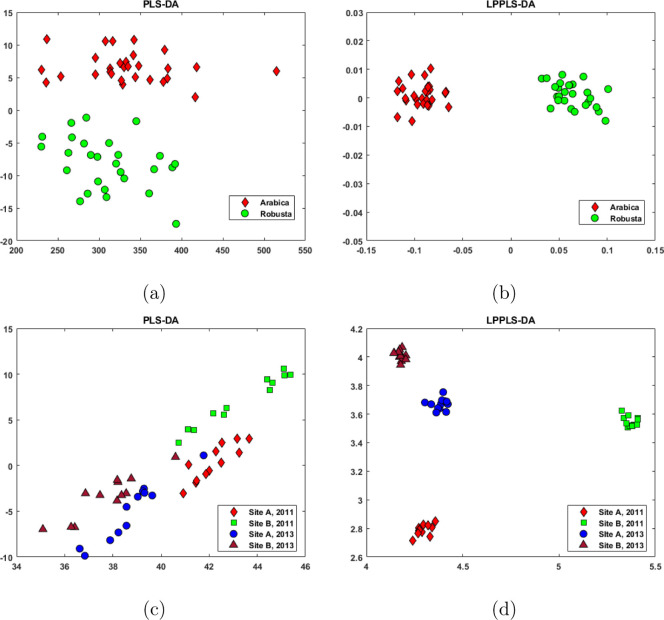
Figure 2.

Visualization of the coffee and Pacific cod data sets: (a) PLS-DA scores for coffee data, (b) LPPLS-DA scores for coffee data, (c) PLS-DA scores for Pacific cod data, and (d) LPPLS-DA scores for Pacific cod data.

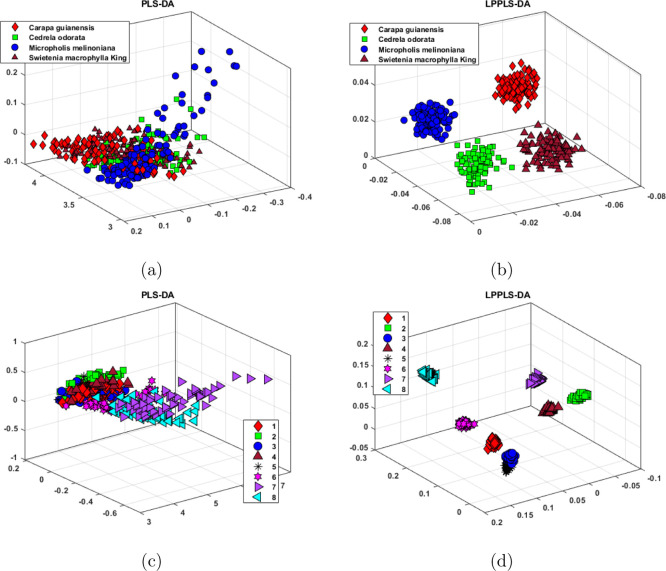
Figure 3.

Visualization of the wood and ink data sets: (a) PLS-DA scores for wood data, (b) LPPLS-DA scores for wood data, (c) PLS-DA scores for ink data, and (d) LPPLS-DA scores for ink data.

From the projection of the coffee data set onto the two-dimensional PLS-DA embedding (Figure 2a), it is seen that PLS-DA is able to separate samples belonging to the robusta species from those belonging to the arabica species. Likewise, successful separation is also observed in the two-dimensional LPPLS-DA embedding (Figure 2b). However, the projected samples are much better clustered in the LPPLS-DA embedding compared to the projection in the PLS-DA embedding. This is clearly the result of preservation of local structures by the minimization of within-class separation, which is attributed to LPPLS-DA. Without locality preservation, we can see that samples belonging to both arabica and robusta species are not well grouped in the PLS-DA subspace. Conversely, with locality preservation, the samples belonging to the two species are well grouped and appear compact in the LPPLS-DA subspace. The Pacific cod data set is made up of samples from four different classes. In Figure 2c, it is observed that PLS-DA fails to find a two-dimensional projection that clearly separates the different classes in the data. There is no clear line of separation between the four different classes in the PLS-DA subspace. On the other hand, with the application of LPPLS-DA, all four classes of the data set are clearly defined to form well-grouped clusters (see Figure 2d). Again, the locality preserving feature helps LPPLS-DA to find a two-dimensional subspace in which the four different classes in the data are well separated from each other.

Results in Figure 3 depict the projection onto three-dimensional PLS-DA and LPPLS-DA embeddings of two multiclass data: the ink data set and the wood data set. PLS-DA performs poorly on both data sets. As shown in Figure 3a,c, not only that PLS-DA fails to find a good separation of the different classes in the data, the projected samples appear to be without any form of discrimination. On the contrary, the projected samples in the three-dimensional LPPLS-DA embedding in Figure 3b,d are well discriminated with clearly defined clusters. The locality preserving feature in LPPLS-DA has successfully overridden the difficulties experienced by PLS-DA in multiclass discrimination. Based on the experimental results above, it can be concluded that LPPLS-DA does provide a more superior discriminant ability compared to PLS-DA in the visualization of complex chemical data. Our results also highlight the need for locality preservation in dimensional reduction and discrimination of multiclass data.

Classification

We perform our experiments by repeated random splitting of the data sets into training and test sets. The training sets are used to extract PLS-DA and LPPLS-DA scores, which are used to train the K-NN classifier. The corresponding PLS-DA and LPPLS-DA scores extracted from the test sets are then used to assess the performance of the classification models generated from the respective methods. We repeat this approach 10 times and report the average classification accuracies.

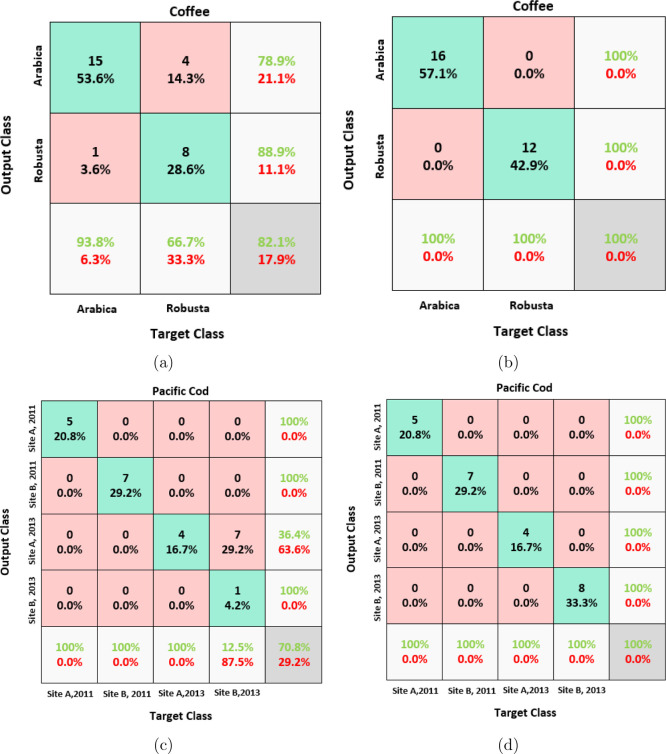
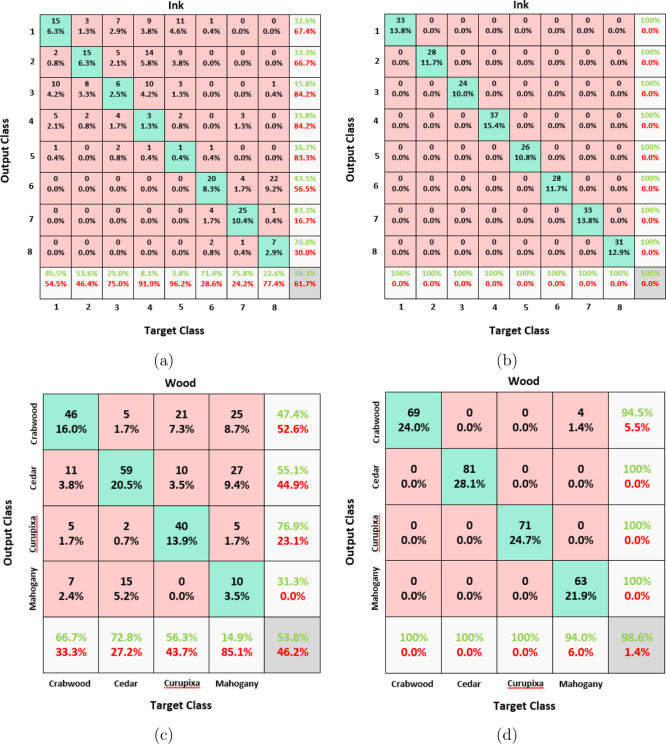
The same four data sets from Table 1 are used to evaluate the performances of both PLS-DA and LPPLS-DA. The first task is to classify unknown samples using a small number of features. For training, half of each data sets are randomly chosen, and the remaining halves are used as test sets. We extracted three features using both PLS-DA and LPPLS-DA on the Pacific cod, ink, and wood data sets, and for the coffee data set, we extracted two features using both methods. The misclassification rates for each method on the four data sets are reported in the form of confusion matrices (see Figures 4 and 5). As expected, LPPLS-DA works well and consistently outperforms PLS-DA on all the data sets. Using only two extracted features on the coffee data set and three extracted features on the Pacific cod and the ink data sets, the LPPLS-DA method was able to correctly classify all the test samples from these data sets with 100% accuracy. Only four samples from the wood data set belonging to the mahogany (S. macrophylla King) species were wrongly classified as Crabwood (C. guianensis) by the LPPLS-DA method. Conversely, a lot of samples from all the four data sets are misclassified by the PLS-DA method. For example, a total of 5, 7, 133, and 148 test samples from the coffee, Pacific cod, wood, and ink data sets, respectively, were wrongly classified by the PLS-DA method. In all the test cases, the LPPLS-DA method is significantly better than the PLS-DA method. The results of this experiment suggest that locality preservation of data samples is an important issue to be considered in chemical data analysis.

Figure 4.

Confusion matrices: (a) PLS-DA results on coffee data, (b) LPPLS-DA results on coffee data, (c) PLS-DA results on Pacific cod data, and (d) LPPLS-DA results on Pacific cod data.

Figure 5.

Confusion matrices: (a) PLS-DA results on ink data, (b) LPPLS-DA results on ink data, (c) PLS-DA results on wood data, and (d) LPPLS-DA results on wood data.

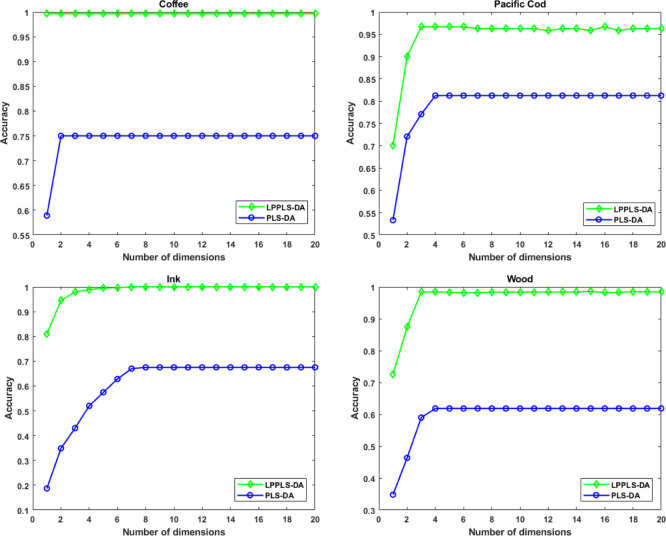
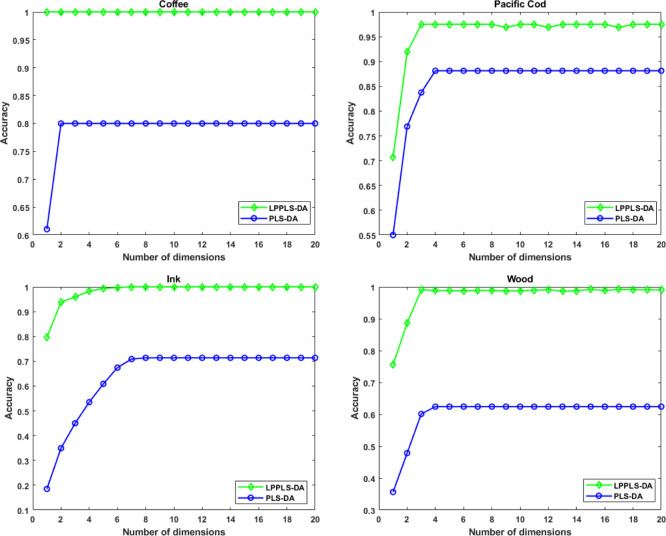
Next, we compare the performance of LPPLS-DA to that of PLS-DA with respect to data partitioning (training and testing sets) and the number of reduced dimensions. Two sets of experiments are done. In the first experiment, each data set is randomly partitioned into training and test sets, where half of the sample is used for training, and the remaining half is used for testing. PLS-DA and LPPLS-DA scores are extracted using the training sets and these are used to train a K-NN classifier. The corresponding PLS-DA and LPPLS-DA scores extracted from the test sets are then used to assess the performance of the classification models generated from the respective methods. We do this repeatedly for 10 random splits of the data sets. In the second experiment, we randomly choose two-thirds of each data sets for training and the remaining third is used for testing. Training and testing of classification models are conducted in the same way as before. Again, we repeat this procedure for 10 random splits of the data sets. The classification results for both experiments are averaged over the 10 random splits and the average classification accuracies are reported. Figures 6 and 7 show the average classification accuracies by the K-NN classifier as a function of reduced dimensionality. The best average classification accuracies, standard deviation, and the corresponding reduced dimensionality (in brackets) obtained using PLS-DA and LPPLS-DA are also reported in Tables 2 and 3. From Figures 6 and 7, we can clearly see that LPPLS-DA is far more effective compared to the PLS-DA method. It gives the highest classification accuracies on all four data sets. We also observe that the performance of LPPLS-DA is not significantly affected by the size of the training sets. Using both half and two-third of the data samples as training sets, LPPLS-DA produced similar results and, in all cases, better than the results produced using PLS-DA. With only the first few extracted features, the LPPLS-DA method is able to give best classification accuracies on the test samples that are far better than PLS-DA. This suggests that, as a dimensional reduction technique, the LPPLS-DA method is far more efficient than the PLS-DA method.

Figure 6.

Average classification accuracies by a K-NN classifier as a function of the reduced dimension. Half of each data set is used as training sets and the remaining half is used as test sets.

Figure 7.

Average classification accuracies by a K-NN classifier as a function of the reduced dimension. Two-thirds of each data set is used as training sets and the remaining one-third is used as test sets.

Table 2. Best Average Accuracy (in Percent), Standard Deviation, and Corresponding Dimensionality (in Brackets) Obtained on the Different Data Sets over 10 Random Splits^a.

data sets	PLS-DA	LPPLS-DA
coffee	75.00 ± 8.42(2)	99.64 ± 1.13(1)
Pacific cod	81.25 ± 10.25(4)	96.67 ± 4.30(3)
ink	67.54 ± 2.62(8)	100.00 ± 0.00(7)
wood	61.85 ± 4.00(4)	98.61 ± 0.82(15)

^aFor each data set, half of the data samples are used for training and the remaining halves are used for testing.

Table 3. Best Average Accuracy (in Percent), Standard Deviation, and Corresponding Dimensionality (in Brackets) Obtained on the Different Data Sets over 10 Random Splits^a.

data sets	PLS-DA	LPPLS-DA
coffee	80.00 ± 8.52(2)	100.00 ± 0.00(1)
Pacific cod	88.12 ± 8.04(4)	97.50 ± 4.37(3)
ink	71.37 ± 3.06(8)	100.00 ± 0.00(7)
wood	62.43 ± 5.01(4)	99.24 ± 0.51(15)

^aFor each data set, two-thirds of the data samples are used for training and the remaining one-third is used for testing.

Conclusions

The purpose of this work is not to develop a new discrimination tool but rather to introduce the LPPLS-DA method to the chemometrics community and to illustrate the superior performance of LPPLS-DA over PLS-DA in chemical data analysis. In the context of chemometrics, it is generally believed that PLS-DA extracts features capable of discriminating the different classes in a high-dimensional data. However, the experimental results presented here demonstrate that this is not always the case.

Our experimental results suggest that LPPLS-DA can be used as a powerful alternative to PLS-DA. LPPLS-DA utilizes the same idea in Laplacian eigenmaps to preserve local manifold structures of data points. Preservation of local nonlinear manifold allows the method to capture intrinsic nonlinear structures in the data, which cannot be captured by a linear technique such as PLS-DA. As a result, LPPLS-DA shows far more superior discriminating power compared to PLS-DA.

In summary, the LPPLS-DA algorithm is an effective method for dimensional reduction and discrimination of chemical data. The experimental results indicate that LPPLS-DA is a good choice for practical classification of complex chemical data. The method performs especially well for high-dimensional, multiclass, balanced, and imbalanced data sets.

Methods

Partial Least Squares Discriminant Analysis

Although detailed discussion about the PLS-DA method is abundant in the literature, we give a brief explanation of the algorithm focusing on major issues that lead to the formulation of the LPPLS-DA algorithm. The PLS-DA method originates from the PLS method,^11,12 which was proposed for regression task. PLS models the linear relationship between sets of observed variables by means of latent vectors (score vectors/components), given the two sets of observed variables X = [x₁, ..., x_n] ∈ R^m and Y = [y₁, ..., y_n] ∈ R^N, where both X and Y are mean-centered. PLS decomposes X and Y into the following form

1

where the n × d matrices T and U represent the score matrices of the d extracted components, P and Q are the m × d and N × d loading matrices of X and Y, respectively, and the n × m matrix E and the n × N matrix F correspond to the residual matrices of X and Y, respectively. The decomposition (eq 1) is commonly determined using the NIPALS algorithm, which finds weight vectors (transformation vectors) w and c such that

2

where cov(t,u) = t^Tu/n is the sample covariance between the extracted score vectors t and u. When the aim of the analysis is discrimination, not regression, the matrix Y encodes the class membership of the observed variables in X, and this approach is generally referred to as PLS-DA. Let X = [X⁽¹⁾, ..., X^(C)], where X⁽ⁱ⁾ (for i = 1, ..., C) denotes the set of data points belonging to the ith class. Then, the class membership matrix Y can be define as

where n_i (for i = 1, ..., C) represents the number of samples in the ith class, ∑_i=1^cn_i = n (total number of samples), and 0_ni and 1_ni are the n_i × 1 vectors of zeros and ones, respectively. In PLS-DA, the components (scores) are constructed such that the covariance between the class membership matrix Y and a linear combination of the observed variables in X is maximized. Thus, PLS-DA finds a transformation vector w* that satisfies the following objective function

3

Equivalently, the optimization problem in 3 can be formulated as an eigenvalue problem

4

where S̃_b = X^TYY^TX, and it is a slightly altered version of the usual between-class scatter matrix from LDA

5

where μ denotes the total sample mean vector, μ^(c) denotes the cth class mean vector, and n_c denotes the number of samples in the cth class (for a detailed derivation of S̃_b, we refer the readers to our previous work in ref (19)). Based on 4, the PLS-DA scores are then calculated as T = XW, where W is an m × d matrix whose columns are made up of the first d dominant eigenvectors of S̃_b.

Mathematically, the PLS-DA method aims to find a projection that maximizes between-class separation on the global Euclidean scale. Unlike linear methods such as LDA, PLS-DA embedding does not take into consideration within-class structures. Several techniques have been introduced to tackle the issue of local structure and within-class structure preservation.²⁴⁻²⁷ Taking advantage of such techniques, Aminu and Ahmad¹⁹ proposed a modification of PLS-DA so that the local manifold structures of data points are taken into consideration. The authors also show that preserving local manifold structures is equivalent to minimizing within-class separation and thereby preserving within-class multimodality.

Locality Preserving Partial Least Squares Discriminant Analysis

LPPLS-DA¹⁹ searches for directions that best discriminate among classes. More formally, given a high-dimensional data, LPPLS-DA finds a projection of the data into a lower-dimensional subspace such that the local manifold structure of data points is preserved and between-class separation is maximized at the same time. Mathematically, we define two objectives:

• 1.Maximizing between-class separation which is based on the same criterion as in PLS-DA (eq 3) which is

6

• 2.Preserving the local manifold structure of data points which is given by²⁵

7

where z_i represents an embedding of the data point x_i into a lower-dimensional subspace and S_ij is the weight of the edge of a graph joining nodes i and j, where the ith node corresponds to the data point x_i. One way of achieving both objectives is to maximize the ratio

8

where the numerator and the denominator are derived from (eqs 6 and 7), respectively. Interested readers are referred to ref (19) for detailed derivation of (eq 8).

Maximizing the numerator in (eq 8) is an attempt to maximize between-class separation after dimension reduction while minimizing the denominator is an attempt to ensure that if x_i and x_j are close in the original space, then z_i and z_j are also close in the lower-dimensional subspace. The transformation vector w that maximizes the objective function (eq 8) is given by the eigenvector associated with the largest eigenvalue of the following generalized eigenvalue problem

9

when a multidimensional projection is assumed (d > 1, where d is the number of projection directions), we consider a projection matrix W whose columns are the eigenvectors of (eq 9) associated with the first d largest eigenvalues λ₁ ≥ λ₂ ≥ ... ≥ λ_d.

In ref (19), the weights S_ij in (eq 7) are defined in such a way that LPPLS-DA becomes identical to the LDA method.²⁸ Using this approach, the LPPLS-DA method can extract at most C transformation vectors, where C is the number of classes in the data. In contrast to ref (19), in this paper, we define the weights S_ij as

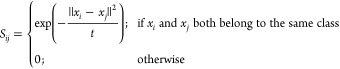10

where t is a user-specified parameter (in our experiments earlier, we set t = 10 for the ink and Pacific cod data sets, and t = 2 and t = 100 for the wood and coffee data sets, respectively). Using this definition of the weights, we can obtain more than C transformation vectors as the solutions to (eq 9). To obtain a stable solution of the eigenvalue problem in (eq 9), the matrix X^TLX is required to be nonsingular. However, in many cases in chemical data analysis, the number of features is larger than the number of samples. Thus, X^TLX is singular. To deal with the complication of having a singular matrix X^TLX, we adopt the idea of regularization, that is, we add a constant value to the diagonal elements of X^TLX as X^TLX + αI, for some α > 0. The matrix X^TLX + αI is nonsingular and the transformation vectors can effectively be extracted as the eigenvectors associated with the largest eigenvalues of the following generalized eigenvalue problem

11

Let w₁, w₂, ..., w_d be the solutions to (eq 11) associated with the first d largest eigenvalues. Then, the final embedding is obtained by

12

where W = [w₁, w₂, ..., w_d] is the transformation matrix whose columns are the eigenvectors from (eq 11) and Z is the matrix containing the transformed data points in the lower dimensional subspace or what we referred to in the previous sections as the LPPLS-DA scores.

Computational Implementations

Our results are computed using MATLAB R2019b, and all our experiments are performed on an Intel core i7 3.20 GHz windows 10 machine with 8 GB memory.

The authors declare no competing financial interest.