Intersystem Crossing and Triplet Dynamics in an Iron(II) N-Heterocyclic Carbene Photosensitizer

Abstract

The electronic excited states of the iron(II) complex [Fe^II(tpy)(pyz-NHC)]²⁺ [tpy = 2,2′:6′,2″-terpyridine; pyz-NHC = 1,1′-bis(2,6-diisopropylphenyl)pyrazinyldiimidazolium-2,2′-diylidene] and their relaxation pathways have been theoretically investigated. To this purpose, trajectory surface-hopping simulations within a linear vibronic coupling model including a 244-dimensional potential energy surface (PES) with 20 singlet and 20 triplet coupled states have been used. The simulations show that, after excitation to the lowest-energy absorption band of predominant metal-to-ligand charge-transfer character involving the tpy ligand, almost 80% of the population undergoes intersystem crossing to the triplet manifold in about 50 fs, while the remaining 20% decays through internal conversion to the electronic ground state in about 300 fs. The population transferred to the triplet states is found to deactivate into two different regions of the PESs, one where the static dipole moment is small and shows increased metal-centered character and another with a large static dipole moment, where the electron density is transferred from the tpy to pyz-NHC ligand. Coherent oscillations of 400 fs are observed between these two sets of triplet populations, until the mixture equilibrates to a ratio of 60:40. Finally, the importance of selecting suitable normal modes is highlighted—a choice that can be far from straightforward in transition-metal complexes with hundreds of degrees of freedom.

Short abstract

Trajectory surface-hopping simulations with a linear vibronic coupling model reveal the competition of major intersystem crossing versus minor internal conversion dynamics in an iron(II) N-heterocyclic carbene dye. The triplet population bifurcates into two regions of the potential energy surfaces, characterized by small and large static dipole moments due to different electronic character and showing coherent oscillations of 400 fs until both triplet populations coexist in a mixture of 60:40.

Introduction

A major challenge pressing modern society is to satisfy the continually increasing global energy demand.¹ This can be met by harvesting the energy reaching the Earth in the form of sunlight if this energy can be efficiently captured at a large scale. Currently, the solar cell technologies most widely employed for this purpose are based on crystalline silicon semiconductors,² which, despite possessing the highest energy conversion efficiency, are still expensive. Low-cost alternatives are dye-sensitized solar cells,³ which often use organic or organometallic dyes attached to nanoporous metal oxides to absorb sunlight.⁴ Efficient organometallic dyes are complexes consisting of rare metals, such as ruthenium, but those render large-scale application costly. Thus, many efforts are directed to find more sustainable and Earth-abundant—and thus cheaper—alternatives such as iron-based⁵ or other 3d metal-based^6,7 complexes.

Unfortunately, simple substitution of the central atom by iron in already efficient ruthenium-based organometallic solar-cell dyes does not work. Upon light absorption, these dyes need to access sufficiently long-lived charge-transfer (CT) excited states in order to efficiently harness solar energy and transform it into electric energy. This is possible in ruthenium(II) polypyridyl compounds, such as the archetypal [Ru^II(bpy)₃]²⁺, because, upon excitation, metal-to-ligand CT (MLCT) states with lifetimes of up to microseconds are populated.⁸ In contrast, in the counterpart iron(II) complex [Fe^II(bpy)₃]²⁺, the excited-state population in the MLCT manifold is rapidly quenched to metal-centered (MC) excited states within a 100 fs time scale.⁹ Such deactivation is not possible in the ruthenium compounds because the larger ligand-field splitting in these complexes increases the energy of their MC states, in turn making them inaccessible during the excited-state dynamics.

Different routes are followed to find iron complexes suitable for solar-cell applications. Copious effort has been invested in designing new ligands that enable longer lifetimes of MLCT states after absorption. One promising strategy is to employ N-heterocyclic carbene (NHC) ligands.¹⁰ Their large σ-donor strength can provide increased ligand-field splittings, which destabilizes the MC states and, thus, leads to longer MLCT lifetimes. This effort culminated in a hexa-NHC iron(II) complex with a triplet MLCT (³MLCT) lifetime of τ = 528 ± 34 ps.¹¹ An alternative route that is less explored as of today involves the use of iron(III) complexes. For such systems, a record lifetime of τ = 1.96 ± 0.04 ns was observed¹² after light absorption leads to the population of ligand-to-metal CT (LMCT) states.

Despite the progress made so far, the rational design of suitable Earth-abundant dyes is still far from straightforward. Small changes in the molecular structure can have pronounced effects on what happens after the complexes absorb light. Thus, in recent years, iron complexes have been the target of numerous time-resolved spectroscopic studies aimed at characterizing the processes occurring after photoexcitation.^11,13−26 Many of these studies include quantum-chemical calculations to aid in the interpretation of experimental observations. Most often the scope is limited to computing electronic states at the Franck–Condon (FC) geometry or selected points in the potential energy surface (PES). Calculation of the explicit excited-state dynamics is much more rare²⁷⁻³⁰ and has been limited to include only a small set of active nuclear degrees of freedom—out of the typically hundreds of different nuclear vibrations that might be involved in the excited-state dynamics of such transition-metal complexes.

In this work, we push the limit of current studies by investigating the photodynamics of [Fe^II(tpy)(pyz-NHC)]²⁺ [tpy = 2,2′:6′,2″-terpyridine; pyz-NHC = 1,1′-bis(2,6-diisopropylphenyl)pyrazinyldiimidazolium-2,2′-diylidene; Figure 1] in acetonitrile (MeCN) using trajectory surface-hopping (SH) dynamics simulations based on a linear vibronic coupling (LVC) Hamiltonian in high dimensionality. Standard pyridyl-NHC ligands allow a combination of the π-deficient pyridine with the σ-donating properties of NHCs.¹⁰ Using pyrazine instead of pyridine increases the π deficiency with lower π* energy levels, which should allow for longer-lived photochemically active MLCT states.³¹ Therefore, the combination of a pyrazine-NHC ligand with a polypyridyl ligand like tpy aims at achieving a long MLCT lifetime with increased absorption in the visible range.²² Thus, [Fe^II(tpy)(pyz-NHC)]²⁺ is an interesting Earth-abundant transition-metal-based photosensitizer with the potential to exhibit stable MLCT states. Moreover, it is a suitable candidate to establish the applicability of vibronic models in high dimensionality for these types of iron(II) complexes, opening up the study of other iron-based photosensitizers with long MLCT lifetimes.

Figure 1.

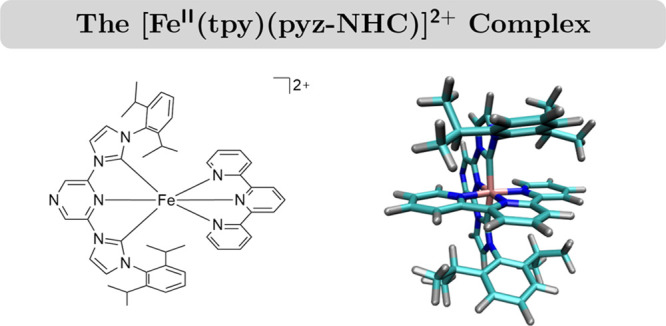
Schematic and ball–stick views on the ground-state equilibrium structure of the [Fe^II(tpy)(pyz-NHC)]²⁺ complex.

The rest of this work is structured as follows. First, we introduce the methods and computational details. Next, we analyze the absorption spectrum of [Fe^II(tpy)(pyz-NHC)]²⁺ and introduce the characterization of the electronic states composing the experimental spectrum. We then describe the theoretical procedure employed to select the nuclear degrees of freedom included in the excited-state study before we discuss in detail the time evolution of the electronic states during simulation of the dynamics. Finally, this manuscript concludes with a summary and outlook.

Methods

Synthesis

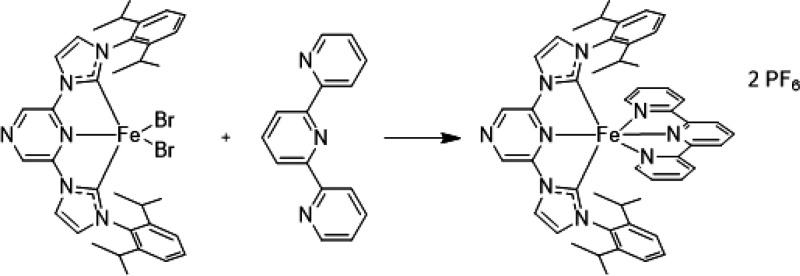
The complex [Fe^II(tpy)(pyz-NHC)]²⁺ was synthesized according to Scheme 1. To a solution of [Fe^II(pyz-NHC)]Br₂²² was added 2,2′:6′,2″-terpyridine (tpy; 101 mg, 0.432 mmol). After the mixture was stirred overnight, the solvent was removed by distillation. The residue was dissolved in water (20 mL) and filtered. KPF₆ (4 equiv) dissolved in a minimum of water was slowly added to the filtrate. The raw product precipitated as a violet powder. After drying in a vacuum, [Fe^II(tpy)(pyz-NHC)](PF₆)₂ was crystallized by diffusion of diethyl ether into a methanol solution (193 mg, 40–64%). The analytical data are given in section S1. Crystals suitable for single-crystal structure determination could be obtained. The crystal structure of [Fe^II(tpy)(pyz-NHC)](PF₆)₂ is deposited as CCDC 2017341 in The Cambridge Crystallographic Data Centre database. More details about the crystal structure are given in section S1. Optical absorption and UV/vis spectra were recorded with a Varian Cary 50 spectrometer and IR spectra with a Bruker Vertex 70 spectrometer in MeCN.

Scheme 1. Synthesis of the Complex [Fe^II(tpy)(pyz-NHC)]²⁺.

Trajectory SH Simulations

To the best of our knowledge, previous dynamical studies on iron complexes²⁷⁻³⁰ were based on wavepacket propagations using the multiconfiguration time-dependent Hartree (MCTDH) method.³² Because the MCTDH method requires precomputation of the PES and scales steeply with the number of nuclear degrees of freedom in the dynamics, these studies were limited to a few (four or five) active normal modes obtained from a spin-vibronic Hamiltonian.³³ An alternative to low-dimensional quantum dynamics is the use of trajectory SH methods.³⁴ In SH, the PESs are computed on-the-fly, i.e., requiring only electronic structure calculations at the present geometry of the molecule. Although such a procedure renders possible the simulation of the early femtosecond (fs) dynamics of transition-metal complexes,^35,36 it is computationally very demanding. The recent implementation of a LVC model within SH³⁷ has made the dynamical simulations of molecules with hundreds of degrees of freedom much more computationally feasible.^38,39

Here, we employ SH dynamics simulations coupled with an LVC model within the SHARC approach.^40,41 Trajectories were set up using initial coordinates and momenta from a Wigner distribution of the ground-state PES.^42,43 A total of 200 initial excited states were selected stochastically within an energy range of 0.5 eV around the maximum of the lowest-energy absorption band (2.55–3.05 eV) based on their oscillator strength.⁴⁴ Thus, trajectories were started in the S₄ (1), S₅ (6), S₆ (15), S₇ (23), S₈ (49), S₉ (42), S₁₀ (43), S₁₁ (13), S₁₂ (7), and S₁₃ (1). Then, the 200 trajectories were propagated for 2 ps using a nuclear time step of 0.5 fs and an electronic time step of 0.02 fs within the local diabatization method.⁴⁵ An energy-based decoherence correction with a constant of C = 0.1 atomic units (au) was used.⁴⁶ During the surface hops, the kinetic energy was adjusted by rescaling the velocity vectors. SH probabilities were approximated using the wave-function overlaps as described in ref (47). The solvent effects of MeCN were included using a continuum model (see below).

The final dynamical results were obtained using a reduced LVC model, where 80 normal modes were excluded from the full LVC model, as described in more detail in the Normal Modes in the LVC Model section. From the 200 trajectories propagated in this manner, four trajectories were excluded from the statistical analysis because they exhibited artificial intersystem crossing (ISC) from the singlet ground state to the triplet manifold. A total of 20 singlet and 20 triplet states were included in the simulations. No quintet states were considered because experimental studies on iron(II) complex deactivation suggest that quintet states only play a role if the complex solely possesses polypyridyl ligands.^{14,20,48−53} As soon as of one of the ligands is replaced by an NHC-decorated moiety^{11,15,19,20,24,54} or the pyridine units are not directly connected,²⁵ only singlet and triplet states are responsible for the photodynamics. This also excludes the most problematic cases of ⁵MC states, which exhibit large displacements of the iron–ligands bonds, that are more challenging to describe in an LVC model.

LVC Model

In an LVC model, the PESs are approximated in terms of the ground-state PES V₀ and first-order (linear) vibronic coupling terms W on the basis of mass-frequency-scaled normal-mode coordinates Q

1

The ground-state PES is approximated as harmonic oscillators with frequencies ω_i, i.e.,

2

The coupling terms read

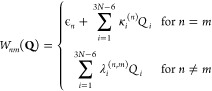3

where ϵ_n are the vertical excitation energies at the FC geometry, while κ_i⁽ⁿ⁾ and λ_i are the intrastate and interstate coupling elements for the normal-mode coordinate Q_i. The coupling elements were obtained numerically from time-dependent density functional theory (TDDFT) and calculations (see below) on geometries displaced by ±0.05 units from the ground-state equilibrium geometry for each normal mode. Note that, as long as there is no S₁/S₀ conical intersection this close to the ground-state equilibrium geometry, the LVC dynamics based on TDDFT is able to describe an S₁/S₀ internal conversion (IC). The intrastate coupling κ_i⁽ⁿ⁾ values were then obtained as numerical gradients, while the interstate coupling λ_i values were obtained from the change in the wave-function overlaps. The spin–orbit couplings (SOCs) in the LVC model potential were approximated by the SOCs obtained at the ground-state equilibrium geometry.

The absorption spectrum and density of states (DOS) were calculated for a Wigner distribution of 1000 geometries using the LVC model potential. Note that the conformational and momentum space that is sampled for the LVC model is the same as that in the TDDFT calculations because the Wigner sampling in both cases uses the same set of normal modes. The resulting absorption spectrum and DOS differ, though, because the excited-state PESs in the LVC model are only approximations of the reference TDDFT ones.

Electronic Structure Calculations

The ground-state geometry of [Fe^II(tpy)(pyz-NHC)]²⁺ in MeCN was optimized using DFT with the range-separated LC-BLYP functional⁵⁵ and 6-31G* basis set.^56,57 The range-separation parameter of the LC-BLYP functional was optimally tuned following the procedure described in refs (58) and (59), resulting in values of α = 0.0 (percentage of exact exchange in the short range) and ω_RS = 0.14 bohr^–1 (long-range separation parameter). Solvent effects for MeCN were described using the conductor-like polarization continuum model (C-PCM). The Cartesian coordinates of the optimized geometry are reported in Table S3. A frequency calculation displayed two imaginary frequencies of 15 cm^–1 corresponding to the torsion of the diisopropylphenyl groups of the pyz-NHC ligand. These modes were excluded in all subsequent calculations. For the self-consistent-field (SCF) calculations, the resolution-of-identity approximation (RIJCOSX), the tight SCF convergence criteria (TightSCF), and the Grid4 integration grid were used. The excited-state calculations were conducted using TDDFT in the Tamm–Dancoff approximation (TDA).⁶⁰ To account for scalar relativistic effects, the zeroth-order regular approximation⁶¹ was used, while SOCs were calculated using the mean-field/effective potential approach,⁶² as implemented in ORCA. All calculations were performed using the ORCA4.1 program package.⁶³

Initially, we considered 30 singlet and 30 triplet excited states to parametrize the LVC potentials. However, SHARC calculations showed artificially large couplings in the LVC Hamiltonian with some of the higher excited singlet and triplet states, and thus the number of states was reduced to 20 singlet and 20 triplet states. On the basis of their DOS (Figure S5), this number of states covers the energy range of up to 3.5 eV, which should be sufficient to describe the excited-state dynamics started in the excitation energy range between 2.55 and 3.05 eV.

The absorption spectrum was calculated using an ensemble of 200 molecular geometries generated by a Wigner distribution,^42,43 for which the resulting stick spectra were then convoluted using a Lorentzian with a full width at half-maximum of 0.05 eV.

The solvent effects of MeCN in the SHARC simulations were also included using the C-PCM. In particular, the solvent effects are evaluated in the parametrization of the LVC model potentials. Thus, the slow component of the C-PCM describing reorganization of the solvent molecules after excitation is not updated during the dynamics, which may lead to a worse description of the solvent effects for extended simulation times.

Quantitative Wave-Function Analysis

Electronically excited states are often described in terms of the canonical orbitals that characterize the most important configurations in the excited-state wave functions. In cases with large numbers of configurations, this description becomes very tedious and often misleading. Instead, a more comprehensible and quantitative analysis of the wave functions involved in the excitations can be obtained by analyzing the one-particle transition-density matrix.⁶⁴ For electronic structure methods including only single excitations such as TDDFT in the TDA, the one-particle transition-density matrix contains the full information of the excited-state wave functions. A singular-value decomposition of the transition-density matrix provides a set of hole and electron natural transition orbitals that give a very compact representation of the excited-state wave function—particularly in cases where a single pair of hole and electron natural transition orbitals represents ∼99% of the character of the excitation. This orbital representation is convenient for analysis of the electronic structure at a single geometry. For multiple geometries, it is not possible to compute meaningful averaged orbitals in a straightforward manner. In these cases, it is possible to partition the molecule into several fragments and compute the contributions of the hole and electron parts of the fragments to the full transition-density matrix. The fragments can comprise several atoms, e.g., a ligand, or correspond to individual atoms; importantly, their representation is invariant to the displacement of the nuclei. This procedure provides an easily understandable illustration of the charge flow that occurs during the dynamics in the different electronic states. Here, analysis of the transition-density matrix has been performed using a locally modified version of the TheoDORE program package.⁶⁵

Results and Discussion

Absorption Spectrum and Initial Excited States

We begin our discussion by analyzing the absorption spectrum of [Fe^II(tpy)(pyz-NHC)]²⁺ in MeCN. One goal is to identify the character of the excited states initially populated after photoexcitation. Another is to determine the quality of the level of theory employed in the dynamics simulations.

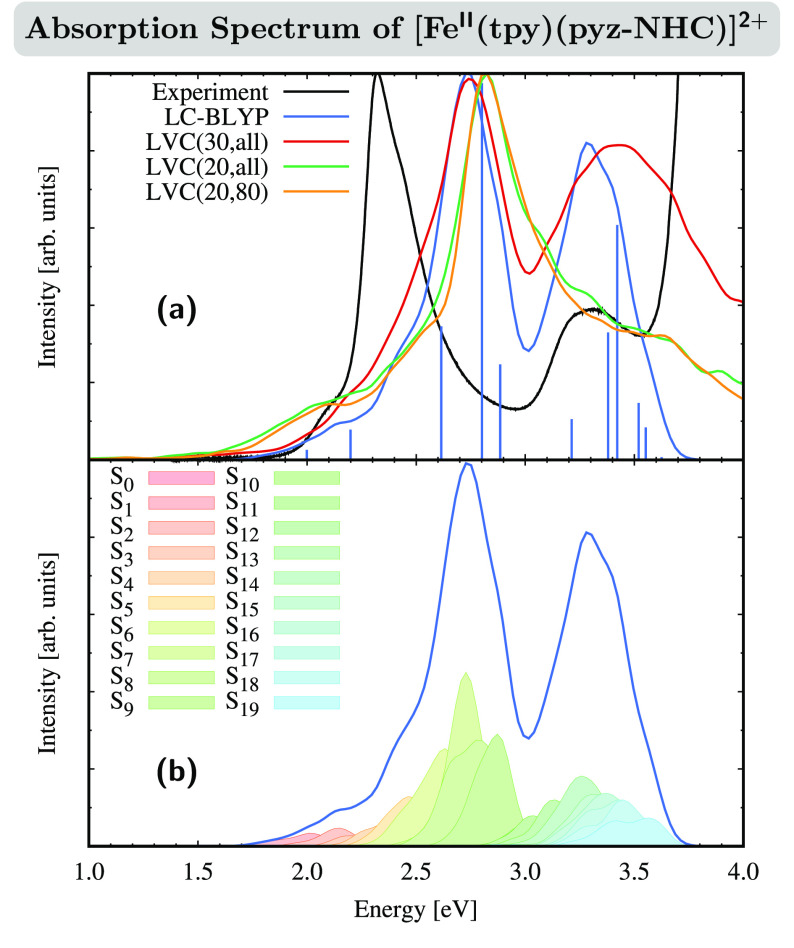
Figure 2a shows the experimental absorption spectrum (see also Figure S3) compared with different simulations. The measured absorption spectrum (black line) exhibits two maxima around 2.31 and 3.30 eV, which are predicted by LC-BLYP (blue line) at 2.71 and 3.30 eV. Thus, the lowest-energy band is blue-shifted by 0.4 eV in the calculations, while the second-energy band coincides in the experiment and theory. This error disparity is due to the differential electron correlation⁶⁶ with which a method is able to describe different electronic excited states. The blue sticks below the blue convoluted line resulting from the Wigner ensemble correspond to the individual excitations calculated from the equilibrium geometry only (see also Table S4). As can be seen, there are three excited states with notable oscillator strength close to the first absorption maximum: S₆, S₇, and S₉. Out of these three states, the S₇ state possesses by far the largest oscillator strength; i.e., loosely speaking, it will contribute the majority to the intensity of the first absorption maximum. This peak is found at slightly higher energies than the absorption maximum of the Wigner averaged LC-BLYP spectrum, which is due to the typical red shift introduced by vibrational motion.^67,68 Under the second absorption band, there are five states with notable oscillator strengths: S₁₂, S₁₄, S₁₅, S₁₆, and S₁₇. Again, the absorption band maximum is red-shifted compared to the brightest of these states (S₁₄ and S₁₅).

Figure 2.

(a) Experimental and simulated absorption spectrum of [Fe^II(tpy)(pyz-NHC)]²⁺ in MeCN. The absorption spectrum was computed at the LC-BLYP/6-31G* level of theory, including all of the 324 vibrational normal modes in the LVC model for 30 singlet and triplet states [LVC(30,all)] and for 20 singlet and triplet states [LVC(20,all)] and using a reduced LVC model for 20 singlet and triplet states where 80 modes were excluded [LVC(20,80)]. The stick spectrum was computed at the LC-BYLP/6-31G* level of theory. (b) Individual state contributions to the LC-BLYP/6-31G* absorption spectrum.

We now proceed to investigate how the LVC model is able to reproduce the reference LC-BYLP spectrum discussed above. First, we consider 30 singlet and 30 triplet states and all of the vibrational degrees of freedom [LVC(30,all), red line]. In this case, both the band shape and location of the maximum of the first absorption band are very similar to those of the reference LC-BLYP, while the second absorption band is blue-shifted by ca. 0.1 eV and appears to be broader in the LVC model than in the reference. In general, given the approximations involved, we consider that the LVC(30,all) description is in reasonable agreement with the reference LC-BLYP description.

Reducing the number of states in the LVC model to 20 singlet and 20 triplet states [LVC(20,all), green line] affects the first absorption band only slightly (a blue shift of ca. 0.1 eV and broader shape) but has a considerable effect on the second absorption band, which does not appear with a distinct maximum anymore. Instead, the second peak merges with the higher-energy part of the first absorption band, resulting in a progression of several shoulders. This worse description of the high-energy tail of the spectrum is a natural consequence of reducing the number of states in the LVC model. While the LVC model uses the same singlet and triplet states obtained at the FC geometry for all geometries sampled in the calculation of the absorption spectrum, a “conventional” TDDFT spectrum always includes the lowest singlet and triplet excited states at each geometry. For geometries further away from the FC geometry, inversion of the excited-state order may take place for the higher excited states in the TDDFT spectrum, introducing some new states that are not included in the definition of the LVC Hamiltonian. Therefore, the LVC model contains states at higher energies than the LC-BLYP spectrum and, thus, will describe the higher-energy part of the spectrum worse. However, because we are interested in the nuclear dynamics after excitation of the lowest absorption band of [Fe^II(tpy)(pyz-NHC)]²⁺, the smaller LVC(20,all) is still satisfactory for the lowest-energy band. For completeness, we mention here that after removal of several vibrational normal modes from this model, in particular 80 (see the discussion later), the description of the first band [LVC(20,80), orange line] is unaffected.

In order to characterize the nature of the states behind each absorption band, Figure 2b displays the different contributions of the individual excited states to the intensity of the LC-BLYP reference absorption spectrum. As can be seen, the first absorption band is composed of contributions from states S₄–S₉, emphasizing the important effect of sampling⁶⁷ around the equilibrium geometry; i.e., its composition is more diverse than one may expect simply considering the excited states at the FC geometry (recall blue sticks in Figure 2a). The larger number of states contributing to the absorption band is due to two factors. First, states that are dark at the FC geometry can mix with bright states when the molecule is displaced from the FC geometry, allowing these states to acquire a notable oscillator strength on their own. This results in unexpected changes of the electronic character of the bright states in the absorption spectrum compared to the bright states at the FC geometry.^69,70 Second, the energetic ordering of the states can change when moving away from the FC geometry because of vibrational motion. For example, parts of the contribution of the S₈ state to the absorption spectrum shown in Figure 2b can arise from geometries, where the S₇ state, which is bright at the FC geometry, has moved to higher energies than the S₈ state at the FC geometry, thus becoming the new S₈ state and, not surprisingly, then contributing to the absorption intensity.

For these reasons, it is useful to introduce an alternative classification of the electronic excited states, not based on the energetic order but on the character of the wave functions involved in the transitions. While such a characterization is often approximately performed by simple inspection of the orbitals involved in the leading configurations of the excited-state configuration interaction vector, this task can be tedious for a large number of states.⁷¹ Alternatives include dipole moments⁷² or transition dipole moments⁷³ or quantitative analysis of the transition-density matrix,⁷⁴ as it will be done in this work.

To this aim, [Fe^II(tpy)(pyz-NHC)]²⁺ is divided into three fragments (Figure 3a), the iron metal center (M), the tpy ligand (ligand L1), and the pyz-NHC ligand (ligand L2). By employment of the CT numbers,⁷¹ all excited-state configurations can then be assigned to one of the nine different excitation types depicted in Figure 3b. They comprise local excitations—centered at either the metal atom (MC) or one of the two ligands (L1C and L2C)—metal-to-ligand charge-transfer excitations (ML1CT and ML2CT), ligand-to-metal charge-transfer excitations (L1MCT and L2MCT), and interligand excitations (L1L2CT and L2L1CT).

Figure 3.

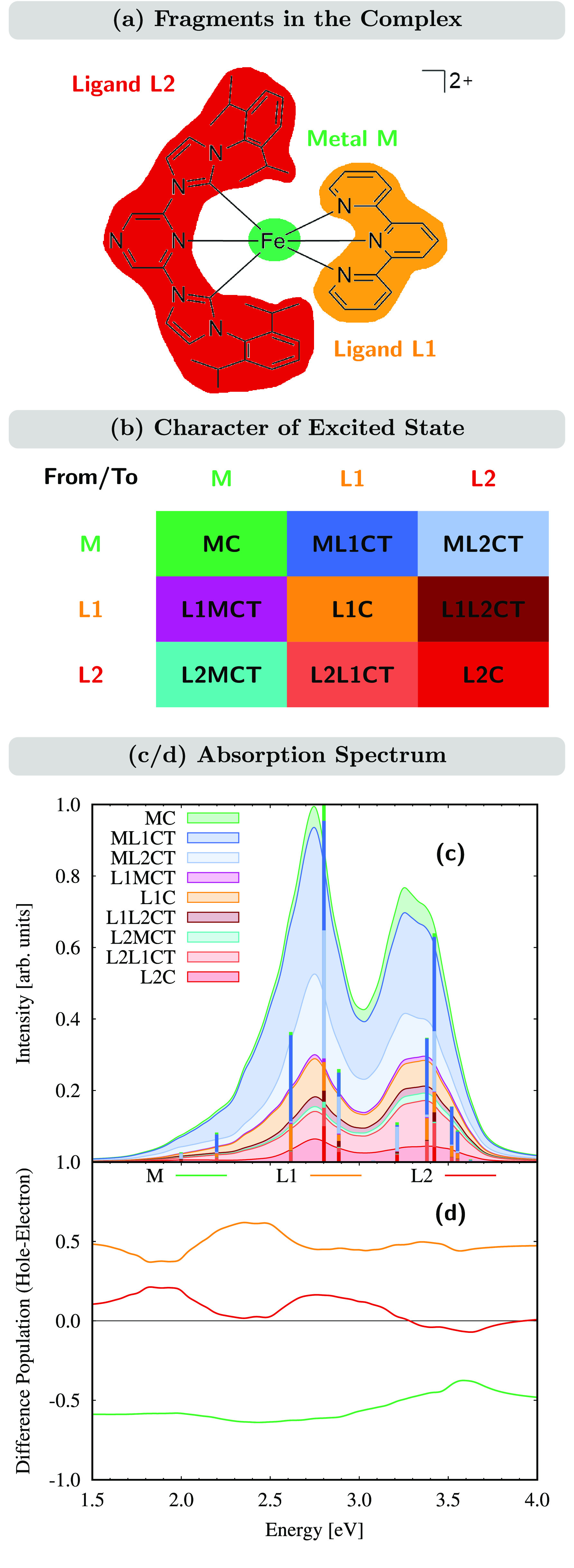
(a) Fragment partition of [Fe^II(tpy)(pyz-NHC)]²⁺. (b) Classification of excited states according to the fragmentation of part a. (c) LC-BLYP/6-31G* absorption spectrum decomposed into different excited states. Stacked curves represent the full spectrum, while stacked lines represent the composition of the FC excited states. Stacking contributions are ordered as given in the legend. (d) Hole/electron difference populations on each fragment as a function of the excitation energy, accumulated for all of the states belonging to the absorption spectrum. The color code corresponds to part a.

Figure 3c shows the composition of the LC-BLYP absorption spectrum in terms of the excitations defined above, together with the position of the excited states at the FC geometry. As can be seen, the excited states of the first absorption band maximum at 2.71 eV are mainly of MLCT character with 41% and 23% contributions from ML1CT and ML2CT, respectively. Additional sizable contributions are given by the ligand-centered L1C and L2C excitations (10% vs 6%) as well as the interligand L2L1CT excitations (8%).

Analysis of the transition density also allows one to quantitatively describe the charge flow that takes place upon population of the excited states in the absorption spectrum. Following irradiation, one electron is promoted from its position in the ground-state electron distribution to a new one, leaving a hole in the ground-state electron density. The positions of the hole and electron after excitation can be spread over the whole molecule; their difference then shows the charge flow in the molecule upon photoexcitation. Figure 3d shows this difference between population of the hole and that of the electron for the three fragments along the excited states involved in the absorption spectrum. Accordingly, upon excitation to the first absorption band at 2.71 eV, the equivalent of 0.61 electrons is removed from the metal center and transferred to ligand L1 (0.46 equiv) and ligand L2 (0.15 equiv). Overall, throughout the energy range of 1–4 eV, excitation leads to similar charge flows, where most of the charge that is removed from the metal center is transferred to the tpy ligand L1. Notably, for the energy range of 2.2–2.5 eV and energies above 3.2 eV, the charge flow toward the pyz-NHC ligand (L2) upon excitation is nearly zero despite large ML2CT character, i.e., due to the additional L2L1CT character that drains the received charge flow.

Normal Modes in the LVC Model

From the discussion above, we concluded that LVC(20,all) should be a reasonable choice to undertake the study of excited-state dynamics launched from the lower-energy absorption band. This model, however, exhibits an additional problem that becomes apparent upon analysis of the DOS. Figure 4 shows the absorption spectra and singlet and triplet DOS, where the same characterization of the states done for the reference LC-BLYP spectrum is performed for the spectrum obtained with a LVC model(s).

Figure 4.

Analysis of the excitation character of the electronic excited state of [Fe^II(tpy)(pyz-NHC)]²⁺ in MeCN. (a, d, and g) Analysis of the excited states computed at the LC-BLYP/6-31G* level of theory. (b, e, and h) Analysis of the excited states obtained in the full LVC model [LVC(20,all)]. (c, f, and h) Analysis of the excited states obtained in the reduced LVC model [LVC(20,80)]. Upper panel (a–c): Excited-state character weighted by the oscillator strength. Middle panel (d–f): Excited-state character in the singlet DOS. The gray state at zero energy corresponds to the ground state S₀. Lower panel (g–i): Excited-state character in the triplet DOS. The stacking order in the curves follows the order in the legend.

The following observations can be made. First, we note again the similar composition of the first absorption band in the LC-BLYP spectrum (a) and LVC spectrum (b), with leading contributions of ML1CT and ML2CT excitations of 41% and 22% for LC-BLYP and 51% and 16% for LVC, respectively. Second, the singlet DOS for both LC-BLYP and LVC of the first absorption band also looks very similar (Figure 4d,e). However, the triplet DOS (Figure 4g,h) shows one important difference between the LC-BLYP and LVC results: whereas the LC-BLYP triplet states start appearing at energies around 1 eV, some triplet states in the LVC model can be found at lower energies up to −1 eV, i.e., even below the ground state. This is a severe problem because, in the excited-state dynamics, triplet energies below the ground state will favor some molecules that reach the S₀ ground state leaking to these lower-lying triplet states artificially. This difficulty is inherent to the approximate nature of the LVC model: because vibronic couplings are described only linearly, the further away the molecule is displaced from the FC geometry, the larger the differences of the approximated linear couplings become compared to the real couplings, resulting in errors in the excitation energies that, in the worst case, can lead to negative energies.

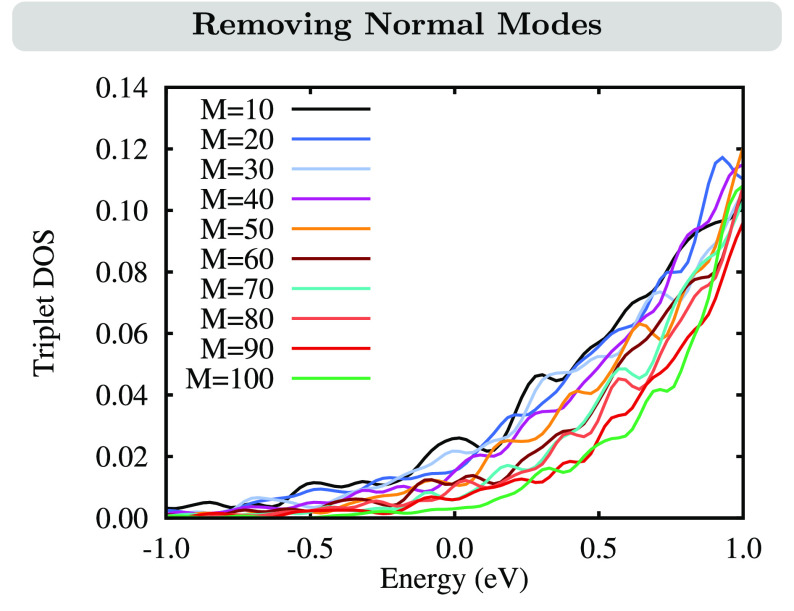
This problem can be alleviated by removing the modes responsible for the artificial lowering of the triplet-state energies. Spurious modes were identified by removing each normal mode of [Fe^II(tpy)(pyz-NHC)]²⁺ individually and calculating the DOS of the corresponding reduced LVC model. The DOSs were then sorted by the decrease of density below 0 eV that was achieved upon removal of the mode. Finally, we set up new LVC models by removing a number of M normal modes with the largest impact on the negative-energy triplet DOS. In Figure 5, we show the impact of eliminating M = 10–100 normal modes on the low-energy triplet DOS.

Figure 5.

Effect of removing normal modes on the triplet DOS for different numbers of modes M. The list of normal modes is in Table S5.

Removing an increasing number of normal modes gradually reduces the negative-energy triplet DOS, until it is nearly quenched at M = 100. However, as for the excited-state dynamics simulations it is desirable to include as many normal modes as possible, the compromise of excluding 80 normal modes from the LVC model was reached. We note here that the small remaining negative-energy triplet DOS still enforced some trajectories to undergo artificial ISC from S₀; however, because there were only a few, these trajectories could be safely excluded from the statistical analysis. The majority of the excluded normal modes (Table S5) are low-frequency vibrations with frequencies ω ≤ 500 cm^–1, e.g., corresponding to torsions in the alkyl groups or backbone vibrations of the whole molecule, which should have only negligible influence on the excited-state dynamics. Furthermore, because of their typical anharmonicity, such modes are only badly described in the harmonic LVC model. Thus, their exclusion appears justifiable. The resulting absorption spectrum, LVC(20,80), and its associated DOS still contain 244 normal modes, and as can be seen from Figure 4c,f,i, apart from the small amount of triplet DOS at low energies, there are no apparent differences between this and the full LVC(20,all) model.

Nonadiabatic Excited-State Dynamics Simulations

Using the LVC(20,80) model that considers 244 normal modes and 20 singlet and 20 triplet states, the excited-state dynamics of [Fe^II(tpy)(pyz-NHC)]²⁺ was simulated for 2 ps. The time evolution of the excited-state populations is shown in Figure 6 until 1.4 ps because it does not noticeably change afterward. The electronic states are represented in their spin-adiabatic basis, i.e., meaning that they are distinguished by their spin multiplicity (singlets and triplets) and energetic ordering.

Figure 6.

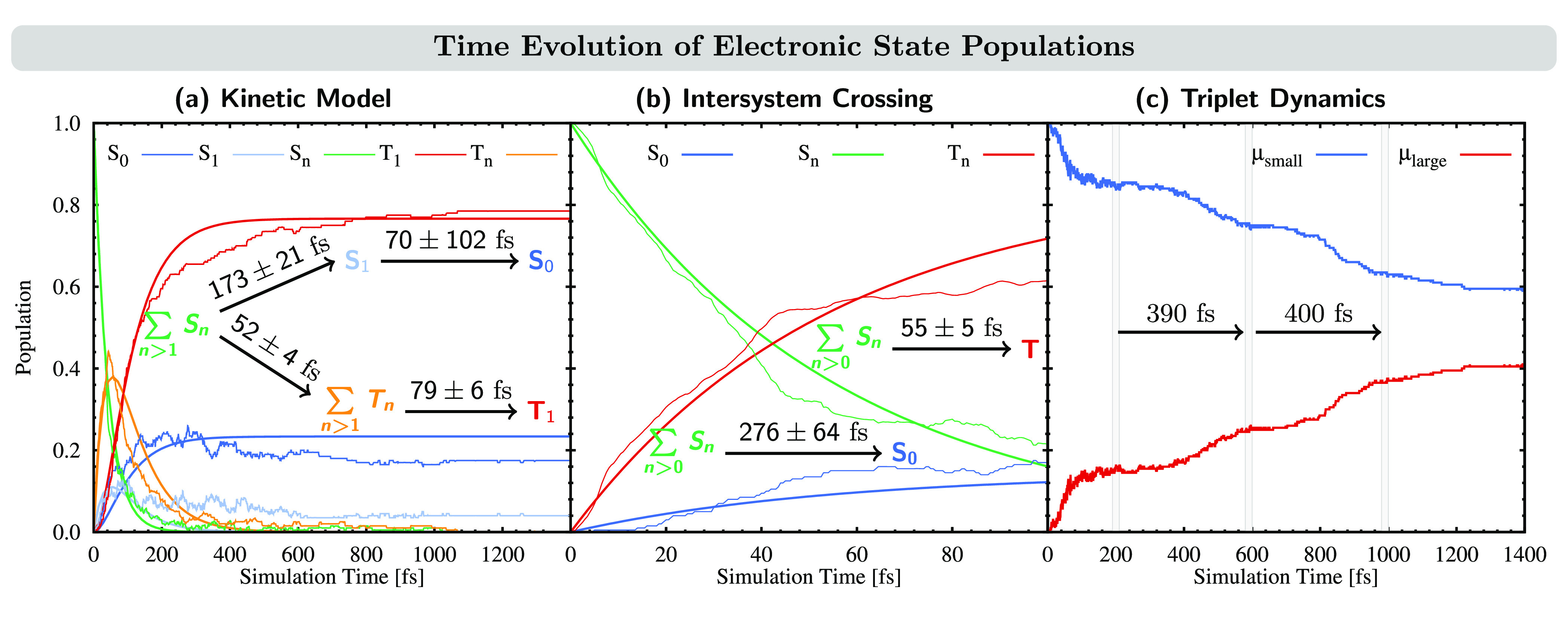
Time evolution of electronic state populations. Note the different time scales in the three panels. (a) Populations of spin-adiabatic electronic states. The populations of higher-lying singlet and triplet excited states S_n/T_n (n > 1) are combined into one line each. Thin lines represent the actual state populations, and thick lines represent fitted curves following the dynamic model shown in the figure. (b) Combined populations of singlet and triplet states, as indicated. (c) Populations of trajectories ending up in a triplet state with dipole moment μ < 0.5 D (μ_small) and μ > 0.5 D (μ_large). Gray bars separate the extent of the coherent oscillations observed between both populations.

Initially, all trajectories start in states higher than S₁, indicated by (green curve). Immediately, a major part of the population is transferred to high-lying triplet states (orange curve) via ISC, from where it relaxes to the T₁ state (red curve) in about 200 fs. A minor pathway is IC within the singlet manifold all the way down to S₁ (light-blue curve) before the electronic ground state S₀ (dark-blue curve) is recovered. The evolution suggests the simple kinetic model

4

5

according to which the population decay was fitted (thick lines in Figure 6a). The resulting time constants are all in the ultrafast domain, within 50–170 fs.

To analyze the ISC process closer, we combine the populations of all of the triplets and all of the singlets (excluding S₀) and perform a new fitting, obtaining an ISC time constant of 55 fs and a global IC time constant of 276 fs (Figure 6b). Because the ISC and IC time constants are very similar to those obtained using the kinetic model in eqs 4 and 5, i.e., τ = 52 fs for ISC and τ = 243 fs for the sum of both ICs within the singlet manifold, this simplified model seems reasonable to describe the main deactivation pathways. After 1 ps, most of the population has reached the T₁ state (78%), while the remaining population is in the S₀ and S₁ states (16% vs 4%). We note that in the similar complex [Fe^II(tpy)(py-NHC)]²⁺, which features a pyridine unit in place of the pyrazine unit in the NHC ligand, weak fluorescence has been observed.⁷⁵ This indicates that a small part of the population remains in the S₁ state, as is the case in our dynamics simulations. Further transient-absorption experiments²² revealed that, after photoexcitation to a ¹MLCT state, [Fe^II(tpy)(py-NHC)]²⁺ undergoes ISC to a ³MLCT state in less than 100 fs. This is followed by transfer to the MC manifold in less than 100 fs, before [Fe^II(tpy)(py-NHC)]²⁺ relaxes to the ground state with a time constant of 173 ps. In the present dynamics, [Fe^II(tpy)(pyz-NHC)]²⁺ also undergoes ISC in less than 100 fs. However, the molecule then stays in the triplet states of mainly MLCT character for the duration of the simulation time, in contrast to [Fe^II(tpy)(py-NHC)]²⁺.

Interestingly, upon analysis of all trajectories that end in the triplet manifold, we observed that the static dipole moments μ of nearly all triplet states fell into one of two narrow ranges: μ ≤ 0.005 D or μ = 1.48–1.51 D—only seven trajectories end in triplet states around the intermediate μ ∼ 1 D value at t = 1 ps. This indicates that the spin-adiabatic T₁ state corresponds to two different spin-diabatic triplet states. In contrast to spin-adiabatic triplet states, which are only characterized by their energetic ordering, spin-diabatic triplet states refer to triplet excited states described by different electronic configurations and which therefore can possess different electronic character, e.g., resulting in different static dipole moments. Accordingly, different spin-diabatic triplet states can correspond to the same spin-adiabatic triplet state at different places on the PES, such as in the present case, when for one set of trajectories, triplet states with small dipole moments become the lowest in energy, while for the other set of trajectories, triplet states with large dipole moments become the lowest in energy. For completeness, we mention here that all trajectories ending in a singlet state possess a similar dipole moment of μ ≤ 0.005 D.

Figure 6c shows the time evolution of the subset of trajectories that end in any triplet state (which ultimately will be the T₁) classified by their static dipole moments using the threshold μ = 0.5 D. As can be seen, all trajectories included in this analysis start with small static dipole moments (blue curve). However, during the initial ISC (t < 100 fs), ca. 15% of the trajectories increase their static dipole moments (red curve) before both sets of trajectories reach a short plateau (t = 100–200 fs). After t = 200 fs, another part of the population is transferred from triplet states with small dipole moments [T(μ_small)] to triplet states with large dipole moments [T(μ_large)], a process that is repeated once more. As indicated by the gray lines in Figure 6c, the period for this coherent stepwise population transfer from T(μ_small) to T(μ_large) is ca. 400 fs. We anticipate that such coherent oscillations could be observed experimentally, as a fingerprint of the existence of two different sets of nuclear configurations in the triplet manifold, which ultimately end in the lowest T₁ PES. Note that similar oscillations in the excited-state dynamics have been observed by X-ray absorption⁷⁶ and X-ray emission⁷⁷ experiments of [Fe^II(bpy)₃]²⁺ and [Fe^II(bmip)₃]²⁺ [bmip = 2,6-bis(3-methylimidazol-1-ylidene)pyridine], respectively—although in these cases, the oscillations were assigned to the dynamics in MC excited states and showed a larger number of repetitions than in the present case. After 1.3 ps, about 40% of the triplet population switches from states with small dipole moments to states with large dipole moments. Because after 1 ps the population in any triplet state different from T₁ state is negligible (recall Figure 6a, orange line), we can assume that two different T₁ configurations have been reached.

A transition-density analysis for the excited states involved during the dynamics has also been carried out. Parts a–c of Figure 7 illustrate the time evolution of the excitation character of all trajectories in the singlet manifold (a), the triplet manifold with a small dipole moment μ < 0.5 D (b), and the triplet manifold with a large dipole moment μ > 0.5 D (c). As a complementary analysis, we show the hole and electron populations of the three fragments M, L1, and L2 for the three sets of trajectories during the dynamics in Figure 7d–f. As can be seen, there are no noticeable changes for the trajectories in the singlet state, with the largest change being a reduction of the ML1CT character from 50% to 45%. However, this is different for the trajectories in the triplet states. For the trajectories with small μ, the excitation character evolves from ML1CT/ML2CT to MC, changing from the initial contributions 50/16/5% (ML1CT/ML2CT/MC) to 43/7/23%. Because in all of these excitations the hole is created in a metal orbital, the hole population of all three fragments does not show large fluctuation (Figure 7e); however, the electron population in the metal increases, while it decreases on both ligands. For trajectories in triplet states with large μ, a dramatic change in the MLCT character is observed. Initially, these states possess 50% ML1CT and 18% ML2CT character; at the end, their relative population is inverted, with 49% ML2CT and 10% ML1CT character. In addition, also the L2C character increases from 4% to 14%, while the interligand L2L1CT character decreases from 10% to 2%, thus further reducing the contribution from excitations involving L1. As in the triplet trajectories with small μ, the hole population remains rather constant, while the electron population decreases/increases on the tpy ligand/pyz-NHC ligand, respectively.

Figure 7.

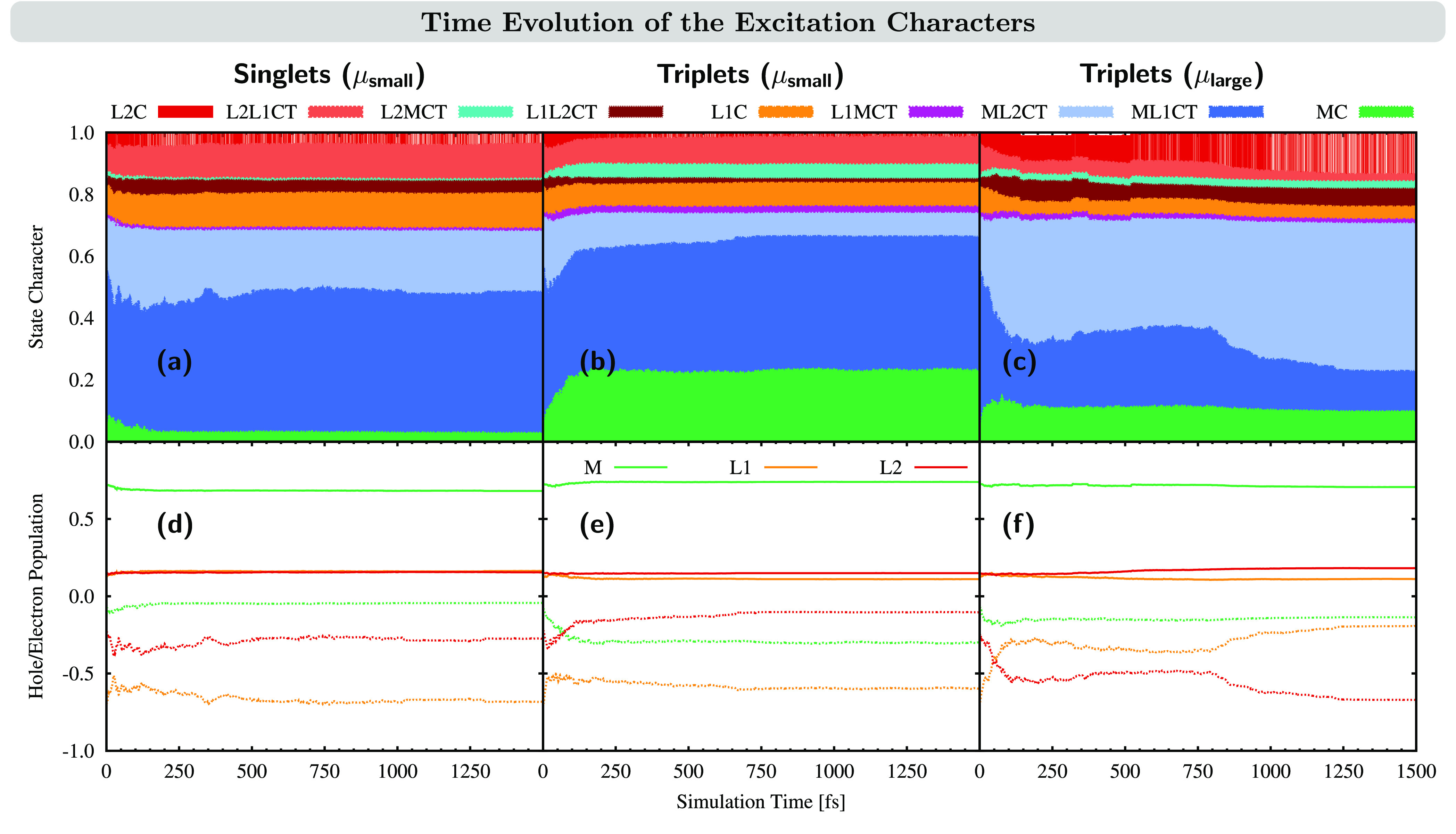
Time evolution of the excited-state character. (a–c) Analysis in terms of the excitation character as defined in Figure 3. (d–f) Hole (positive axis, solid line) and electron (negative axis, dotted line) populations on the three fragments during the dynamics. Left panel (a and d): Analysis for trajectories remaining in the singlet manifold. Middle panel (b and e): Analysis for trajectories ending up in the triplet manifold with small dipole moments μ < 0.5 D. Right panel (c and f): Analysis for trajectories ending up in the triplet manifold with large dipole moments μ > 0.5 D.

To conclude the analysis of the electronic states, we show in Figure 8 the atomic hole and electron populations as well as their difference populations for the three sets of trajectories. All populations are depicted as circles, whereby the area of the circle corresponds to the size of the population. Because the hole populations sum up to one at all times and so do the electron populations, the sum of the areas of their circles is constant for all time steps. The difference population represents the difference between the hole and electron populations for each atom (positive difference in blue and negative difference in red). For the difference population, the sums of the positive and negative contributions cancel; however, these sums can change during the dynamics, e.g., when the amount of local excitation character varies. As such, for CT, the sum of the positive and negative differences is maximum (big circles), and if the excitation is completely localized, then there are no differences; i.e., no circles is present. The atomic hole/electron/difference population analysis is an expansion of the previous analysis for the three fragments M, L1, and L2 (Figure 7d–f), where now every atom constitutes an independent fragment. Videos for the time evolution of the atomic hole/electron/difference populations are shown in the Supporting Information. Note that the hole and electron populations at each time step describe the change in the electron distribution with respect to the ground-state electron density; they are, in general, different from the atomic charges and, thus, not directly related to the size of the static dipole moment.

Figure 8.

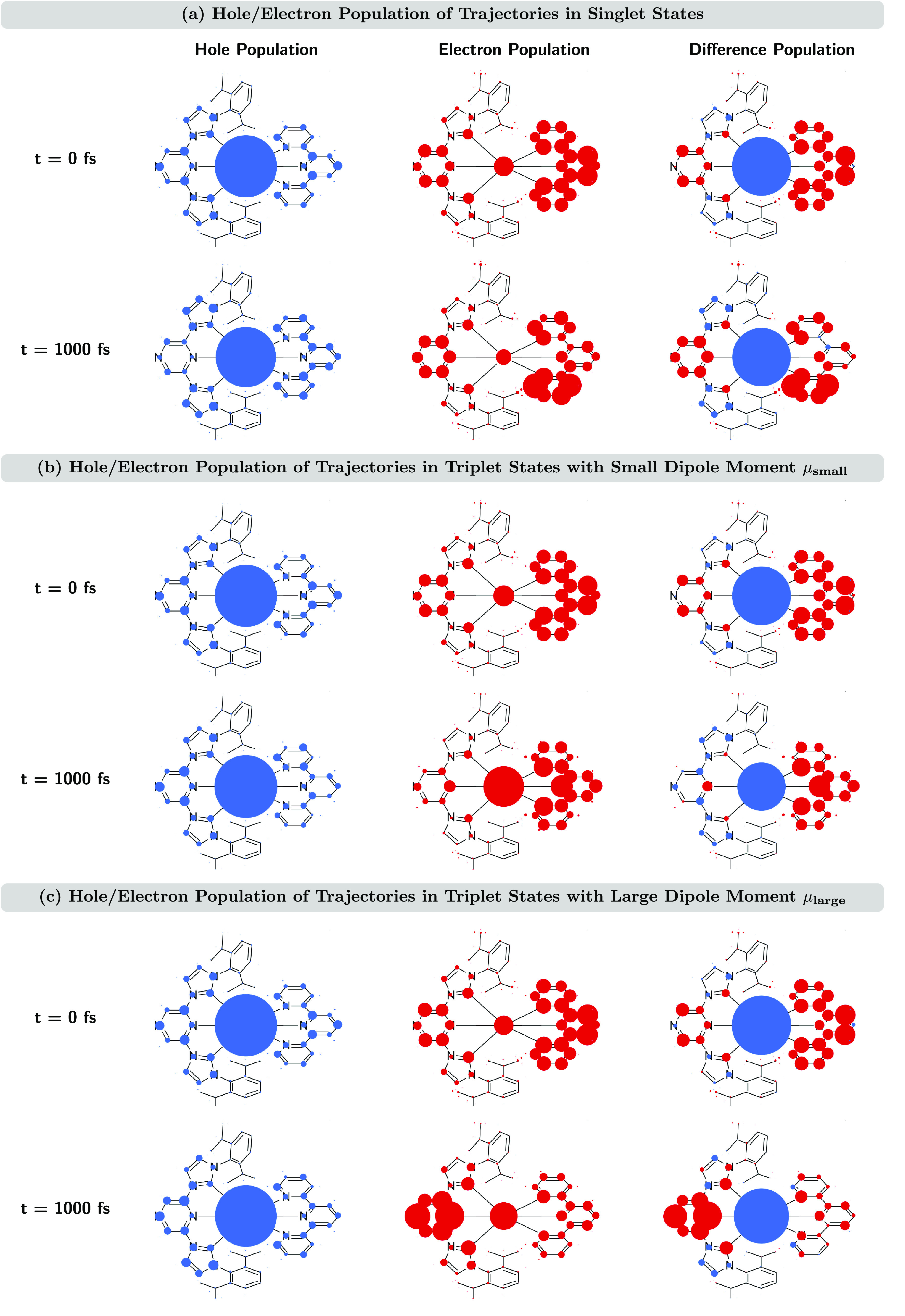
Atomic hole populations (left column), electron populations (middle column), and hole/electron difference populations (right column) for trajectories in singlet states (a), trajectories in triplet states with small static dipole moments μ_small (b), and trajectories in triplet states with large static dipole moments μ_large (c) at different simulation times t = 0 and 1000 fs. The areas of the circles correspond to the sizes of the populations. Positive (negative) hole/electron difference populations are shown as blue (red) circles.

The atomic hole/electron/difference populations illustrate the charge flow during the dynamics. For the singlet trajectories (Figure 8a), the charge flow is only small; i.e., there is a small growth in the hole population at the NHC units in ligand L2 (best seen in the difference population), while some of the electron population is redistributed within ligand L1. In contrast, for triplet trajectories, the charge flow is more pronounced. For trajectories with small static dipole moments (Figure 8b), the hole population remains rather constant during the dynamics; however, the electron population is shifted from the pyrazine unit in the pyz-NHC ligand L2 to the central metal atom, thus explaining the increase of MC excitation character and the decrease of ML2CT excitation character described above. This process is again accompanied by the redistribution of the electron population within ligand L1. For trajectories in triplet states with large static dipole moments (Figure 8c), the charge flow is the most dramatic. Here, large parts of the electron population are moved from all parts of ligand L1 to the pyrazine unit of ligand L2, thus explaining the shift from ML1CT to ML2CT excitation character.

Conclusion

In this work, we have investigated the excited-state dynamics of [Fe^II(tpy)(pyz-NHC)]²⁺ using a LVC model within the framework of trajectory SH. Upon excitation to the lowest-energy absorption band, the complex is excited to a mixture of singlet excited states of MLCT nature with contributions in both the tpy and pyz-NHC ligands, in a ratio of ca. 1:2.5. From this broad MLCT band, the majority of the population undergoes ultrafast ISC from the singlet to triplet manifold on a ∼50 fs time scale. The rest (20%) of the population converts internally all the way down to the electronic singlet ground state in about 300 fs. In the triplet manifold, there is also competing IC to the lowest T₁ PES. Interestingly, the population that is promoted to the triplet manifold bifurcates: 60% of the triplet trajectories stay in states with small static dipole moments, whereas 40% travel to states with large static dipole moments. The transfer from triplets with small dipole moments to triplets with large dipole moments shows coherent oscillations with a period of ca. 400 fs. During relaxation, the trajectories in the triplet states with small static dipole moments exhibit charge flow of the electron density from the tpy ligand to the metal center, thus increasing the MC character in the triplet state. In contrast, the triplet population with a large static dipole moment inverts its amount of MLCT character, resulting in a pronounced charge flow from the tpy ligand to the pyrazine site in the pyz-NHC ligand.

This work also illustrates that, although vibronic Hamiltonians can be very useful, severe complications might also exist when used in full dimensionality. The here-employed LVC model is capable of reproducing the absorption spectrum of its LC-BLYP reference at low excitation energies. However, for low-lying triplet states, the inclusion of all of the normal modes leads to erroneous prediction of excitation energies. Such errors have not been identified in the past, probably because the number of normal modes included in quantum-dynamical simulations that employ vibronic models has been very small and thus they have been very carefully chosen to strongly influence the dynamics. Here, because we start from a full-dimensional case, it was necessary to identify and thus exclude some normal modes responsible for this erroneous behavior. Out of the 324 vibrational degrees of freedom of [Fe^II(tpy)(pyz-NHC)]²⁺, we performed excited-state dynamics using 244 and were able to achieve qualitatively correct dynamics, thus hugely pushing the use of vibronic Hamiltonians in dynamical studies, with particular emphasis on iron(II) complexes. In future work, we expect to use this approach to further investigate iron(II) complexes with longer MLCT lifetimes.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c02147.

• Experimental data (¹H NMR, IR, optical absorption spectrum, X-ray; section S1), Cartesian coordinates of the FC geometry (section S2), DOS for the LC-BLYP/6-31G* calculations in terms of spin-adiabatic states (section S3), characterization of the excited states at the FC geometry (section S4), list of normal modes used in the LVC model (section S5), and charge flow during the dynamics (section S6) (PDF)

• Videos in gif format showing the charge flow during the dynamics (additional files) (ZIP)

Accession Codes

CCDC 2017341 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

The authors declare no competing financial interest.