COVID-19 in China: Risk Factors and R₀ Revisited

Abstract

The COVID-19 epidemic spread rapidly through China and subsequently proliferated globally leading to a pandemic situation around the globe. Human-to-human transmission, as well as asymptomatic transmission of the infection, have been confirmed. As of April 03, 2020, public health crisis in China due to COVID-19 was potentially under control. We compiled a daily dataset of case counts, mortality, recovery, temperature, population density, and demographic information for each prefecture during the period of January 11 to April 07, 2020. Understanding the characteristics of spatial clustering of the COVID-19 epidemic and R₀ is critical in effectively preventing and controlling the ongoing global pandemic. Considering this, the prefectures were grouped based on several relevant features using unsupervised machine learning techniques. Subsequently, we performed a computational analysis utilizing the reported cases in China to estimate the revised R₀ among different regions. Finally, our overall research indicates that the impact of temperature and demographic factors on virus transmission may be characterized using a stochastic transmission model. Such predictions will help in prevention planning in an ongoing global pandemic, prioritizing segments of a given community/region for action and providing a visual aid in designing prevention strategies for a specific geographic region. Furthermore, revised estimation and our methodology will aid in improving the human health consequences of COVID-19 elsewhere.

1. Introduction

The world is facing an unprecedented pandemic of a virus (COVID-19) that firstly identified in Wuhan, China. As such, the virus has been declared a global public health emergency by the World Health Organization (WHO). The virus is of the genus betacoronavirus which are zoonotically transmitted enveloped RNA viruses (Weiss and Leibowitz, 2011). Certain strains of Coronavirus are known to cause infections in humans and have led to previous epidemics, such as severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS) (Yin and Wunderink, 2018). A new strain of Coronavirus called the COVID-19 has led to a global epidemic since its emergence in Wuhan, China (Zhu et al., 2020). As of September 21, 2020, this disruptive pandemic has been spread among 180 countries and infected >31.03 million individuals and caused >0.96 million deaths since the onset of the epidemic. Nearly 0.09 million cases were diagnosed in mainland China (JHU, 2020; WHO, 2020a). The epidemic in China is now under control.

Initial efforts to stall transmission of the COVID-19 by the Chinese authorities included the closure of the Huanan Seafood Wholesale Market which was considered to be the focal point of the outbreak (Li et al., 2020a). However, in spite of such strong intervention attempts, the rapid spread of the virus could not be prevented. Apart from measures to prevent exposure to the source, diagnostic recognition of the virus is an essential part of prevention measures to prevent transmission. Diagnostic tests for COVID-19 were developed after isolation of the virus from lower respiratory tract specimens and blood serum (Huang et al., 2020). Scientists in China provided the genetic sequence of COVID-19 to the WHO, which had in turn, made Real-Time Polymerase Chain Reaction (RT-PCR) tests available globally (Huang et al., 2020). COVID-19 has a clinically milder presentation and lower case fatality ratio (CFR) when compared to SARS and MERS (Peeri et al., 2020) and hence, there seems to be an increased risk of asymptomatic or pre-clinically diagnosed individuals spreading the disease (Hui et al., 2020).

With the current state of globalization and increased interconnectedness of the world, the risk of infectious disease spread has increased. A revised estimation of R₀ based on some potential risk factors is one of the powerful tools for assessing an epidemic's ability to spread (Sanche et al., 2020; Zhao et al., 2020). This provides vital information regarding where resources for containment and treatment should be targeted.

There have been some interesting findings in the literature with respect to different risk factors in the context of COVID-19 as follows. Infection rate and mortality are higher among males as compared with females (Jin et al., 2020). The mortality rate is higher among the older age groups (Jin et al., 2020). Population density might be one of the potential risk factors in the spread of COVID-19 infections (Team, 2020). Control effort proved one of the keys to prevent and contain the spatial spread (Zhang et al., 2020a). The role of temperature in the spread of COVID-19 has been studied (He et al., 2020; Liu et al., 2020; Pawar, 2020; Qi et al., 2020; Shi et al., 2020; Sobral et al., 2020; Sun et al., 2020; Tobias and Molina, 2020; Yao et al., 2020) and debated among policymakers. Temperature may even have no role in transmission since winter is over and temperature started increasing and cases are increasing in warm areas. Control effort, health behavior, and social distance have a very big role in R₀ estimation and can inform public health officials and decision makers about where to improve the allocation of resources, testing sites; also, and where to implement stricter quarantines and travel bans (Battiston, 2020).

All these findings, albeit in isolation from each other, indicate that a revised estimation based on the geographic distribution of population density, age group, gender, temperature, morbidity, mortality, and recovery rate from COVID-19 in a contained epidemic country is necessary in order to accurately predict the spatial spread of the virus and identify the risk factors for targeted control. With the above backdrop, we are motivated to estimate R₀ following a new methodology where we leverage unsupervised machine learning techniques (i.e., clustering) to group China into regions and then apply the popular and simple SIR model (Kermack, 1927) to do the R₀ estimation at the regional level. Thus, our study models the spread of COVID-19 among three regions in China, where the regions are not clustered geographically; rather they are intelligently grouped based on several relevant features (mentioned above) through application of unsupervised machine learning techniques. Thus, it is expected to provide more accurate findings regarding where public health measures should be targeted.

2. Materials and Methods

2.1. Data Source

In this study, prefecture-level administrative areas in Mainland China were taken into consideration. The number of daily confirmed, cured, and death of COVID-19 cases were collected from the National Health Commission of the People's Republic of China (http://www.nhc.gov.cn/) and the provincial health commissions.

COVID-19 that started to spread from Wuhan in the mainland of China is a notifiable disease (Epidemiology Working Group for Ncip Epidemic Response and Prevention, 2020). Local health professionals (responsible for investigation and exposure information collection) tied to add the daily reported cases in China's Infectious Disease Information System (IDIS). IDIS recorded all cases with identification numbers to avoid data duplication. All data contained information about morbidity, mortality, and recovery from COVID-19 case records in the IDIS through the end of April 3, 2020, were extracted (excluding Wuhan from our analysis due to missing data). IDIS categorized all the confirmed cases as suspected, clinically diagnosed (Hubei Province only), or asymptomatic. Confirmed cases were diagnosed by testing the viral nucleic acid in throat swabs specimens (some samples tested retrospectively) (Epidemiology Working Group for Ncip Epidemic Response and Prevention, 2020). Suspected cases were diagnosed based on the clinical symptoms and exposure and were classified as clinically diagnosed cases. Clinically diagnosed cases include suspicious cases with lung imaging features consistent with coronavirus pneumonia. The positive viral nucleic acid test is used to diagnose asymptomatic cases (without any COVID19 symptoms, e.g., fever, dry cough) (Epidemiology Working Group for Ncip Epidemic Response and Prevention, 2020). The date of diagnosis, recovery, and mortality were used as an onset date of infection in the time series data (Epidemiology Working Group for Ncip Epidemic Response and Prevention, 2020).

2.2. Population

Demographic data for each city were obtained from the National Bureau of Statistics of China (http://www.stats.gov.cn/).

2.3. Temperature

The daily surface air temperature dataset from a joint project of National Centres for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) is obtained at the prefecture-level of China. The NCEP/NCAR reanalysis dataset is continuously available (1948 - present) at the global gridded dataset of earth atmosphere, incorporating the in-situ observations and numerical weather prediction (NWP) model output. The temporal resolution is 6-hour (0000, 0600, 1200, and 1800 UTC) with a spatial resolution of 2.5-degree.

Google earth engine platform was used to download the required data following a three-step process: selection of required data, extraction to geographical location, and export to google drive. Data selection parameters include, dataset identifier (NCEP_RE/surface_temp), geographical location (China prefecture level), and date (2019-12-01 – 2020-04-07). To get the temperature data for each prefecture, ee.Reducer.first() function is used to get the first (or only) value of temperature. Finally, the extracted dataset is exported to the google drive as a CSV file. The temperature dataset consists of four observations per day and is used to obtain minimum, maximum, and mean temperatures.

2.4. Computational Analysis

We divided China into three different regions applying a carefully designed clustering exercise as described below. The full analysis pipeline is illustrated in Figure S1. Initially, all the prefectures that reported zero cases were excluded from the analysis. Then we applied an unsupervised clustering algorithm, namely, K-means algorithm, based on several features (Table S1) and identified three separate regions within mainland China. Now, different sets of features (i.e., criteria used for clustering) may result in different outputs (i.e., different regional grouping). To analyse this, we applied our clustering algorithm on four different sets of features/criteria that include incidence, recovery rate, mortality rate, male-female ratio, age group ratio, minimum, mean and maximum temperature in each prefecture. Table 1 lists the criteria/features used for clustering (further details are provided in Table S1). Since each of the clustering schemes we has more than two features (i.e., for Clustering Schemes A, B, C and D we have 8, 7, 9 and 3 features, respectively), we use Principal Component Analysis (PCA) to reduce dimensions to two with a goal to visually inspect the results of the different clustering schemes (i.e., A ∼ D) and the contribution of the features therein (Figure S2 and S3). Please note that in the actual clustering PCA has not been used.

Table 1.

Five different sets of criteria/features for different clustering schemes. The features used are, Incidence (I), Recovery Rate (RR), Mortality Rate (MR), Male/Female Ratio (MFR), Age Group Ratio (AGR), and Temperature (T). More details can be found Table 1 (Supplement).

Clustering Scheme	Feature Set
A	I, RR, MR, MFR, AGR>64, Tmin, Tavg, Tmax
B	I, RR, MR, AGR>64, Tmin, Tavg, Tmax
C	I, RR, MR, AGR<15, AGR15-64, AGR>64, Tmin, Tavg, Tmax
D	Tmin, Tavg, Tmax

Incidence, mortality rate, and recovery rate are calculated as follows:

$$Incidence\left(per100,000population\right)=\left(\frac{Totalnumberofcases}{totalpopulation}\right)x100,000$$ (1)

$$Recoveryrate=\left(\frac{Totalnumberofrecoveredcases}{totalnumberofcases}\right)x100$$ (2)

$$Mortalityrate=\left(\frac{Totalnumberofdeath}{totalnumberofcases}\right)x100$$ (3)

The K-means clustering algorithm (with default parameters) was used to do the clustering (Hartigan, 1979; Lloyd, 1957; MacQueen, 1967). In our dataset, there are 302 prefectures with at least one incidence. However, population and temperature data were available, for 298 and 296 prefectures, respectively. That is why 298 prefectures were considered for Clustering Scheme B. On the other hand, 296 prefectures were considered for the remaining clustering schemes. Notably, Wuhan was excluded from the analysis, because data for early days of transmission for Wuhan is not available (Li et al., 2020b).

After dividing all the prefectures into three different regions, a stochastic transmission dynamic model to estimate R₀ for each region was fitted. The daily incidence, recovery, and mortality of each region were fitted in the model. For estimating R₀ of a region, we considered the daily confirmed incidences for all the prefectures of that region. The same procedure was applied for recovery and mortality.

We divided the population into three different compartments, namely, susceptible, infected and removed (SIR model (Kermack, 1927), i.e., isolated, recovered, dead, or otherwise no longer infectious). The rate of change from susceptible to infected is termed as the rate of transmission. Similarly, the rate of change from infected to removed is termed as the removal rate. Following the work of Kucharski et al. (Kucharski et al., 2020), in our model, we have assumed that the delay distribution from the onset to isolation follows the well-known Erlang distribution with a mean of 2.9 days and a standard deviation of 2.1 days (Jodra, 2012). So the removal rate is assumed to be 0.34 (1/2.9) ^{31, 32}. Transmission is modelled as a stochastic random walk process and sequential Monte Carlo simulation is used to infer the transmission rate over time, resulting number of cases, and the time varying basic reproduction number (R_t). Sequential Monte Carlo (i.e., particle filter) simulation (Kucharski et al., 2020) is run 100 times with bootstrap fits. R₀ is then estimated by taking the median of the first 14 days of R_t. For fitting the time series incidence, mortality, and recovery data, we tried to maximize the log-likelihood. More details about the model structure and model fitting with Sequential Monte Carlo method are provided in the supplement texts.

2.5. Model Validation

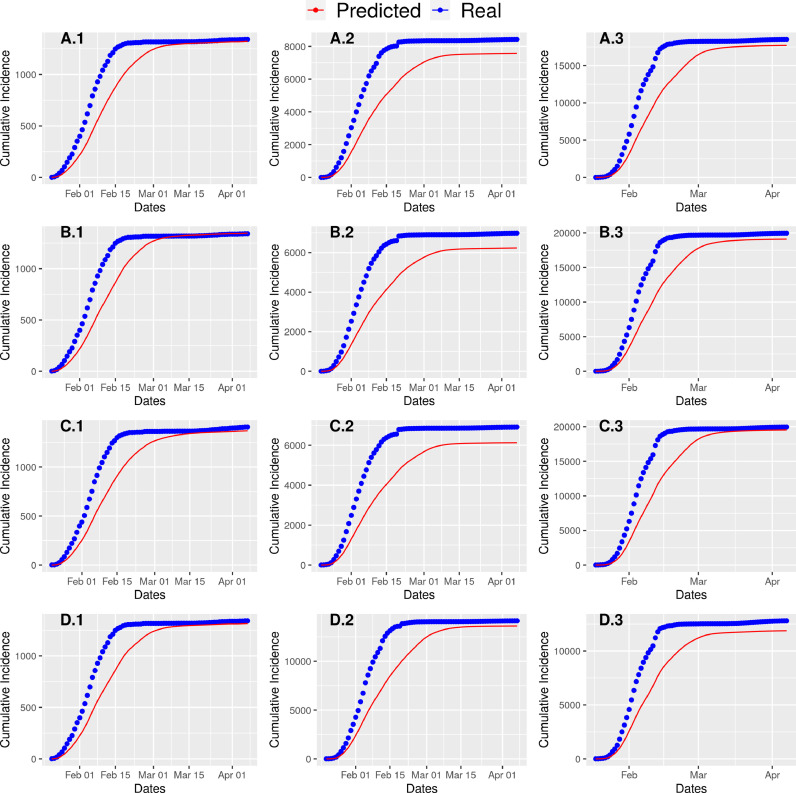
The primary validation of the model is done by visually inspecting the graph generated by plotting the model-inferred number of cases against the actual number of cases. Then we calculated the Root Mean Square Error (RMSE) values from the cumulative real and predicted incidences (Table S2). While calculating the RMSE value for a particular cluster (under a particular clustering scheme), we compared the cumulative true number of cases against the predicted one for each day.

All analysis was conducted using the R language (version 3.6.3). We adopted and modified the code provided by Kucharski et al. (Kucharski et al., 2020). For reading and manipulating data we used readxl, magrittr, tidyverse, tidyr, DMwr and plyr R packages in addition to pre-installed packages. For processing dates we used R package lubridate. We leveraged R package ggplot2, ggpubr, sf and RColorBrewer for plotting different figures including maps. R package factoextra was used for visualizing PCA. For parallelization, we used for each, doMC and mgcv. All data and code for simulation are available at the following link: https://github.com/rizvi23061998/estimate_chinese_r0.

3. Results

As of April 7, 2020, a total of 83,845 (including Wuhan) cases were reported in China. The average of daily mean temperature ranged from -25.06°C to 21.39°C.

3.1. Three regions in different clustering

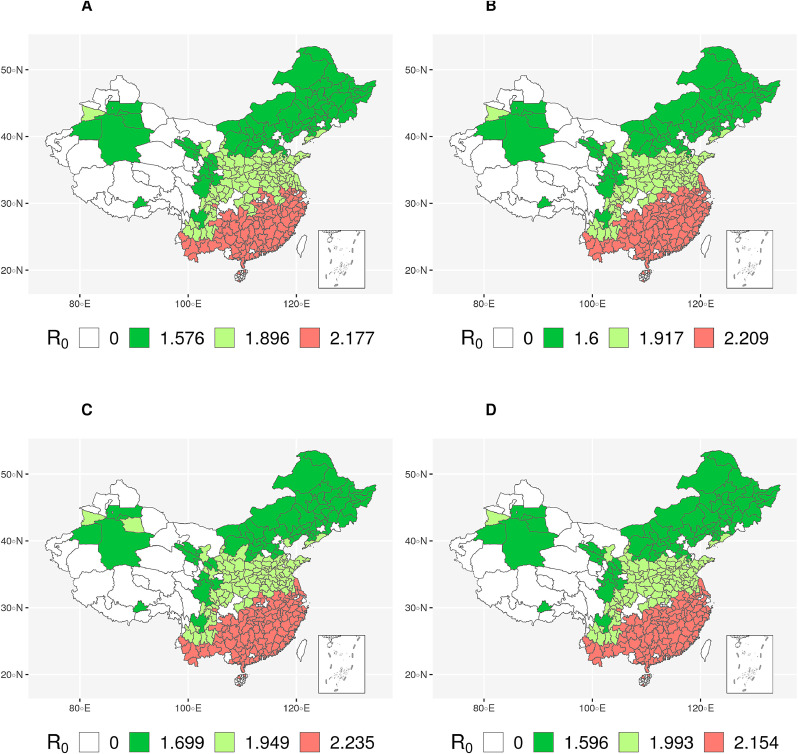
All four clustering schemes (Table 1) produced similar regions (Figure 1 ) and predicted similar R₀ values (Table 2 & Figure 2 ) increasing the confidence level of this analysis. In particular, the prefectures are in fact geographically grouped into regions automatically despite that, no direct geographical features have been used for clustering (Table 1 & Table S1). From the PCA analysis (Figure S2), it is evident that temperature profile played a significant role, and it is easily noticeable that the increase in temperature increases the R₀ value.

Fig. 1.

R0 values for different regions in China. A, B, C, and D indicates the clustering based on different sets of features. R0 value of 0 indicates no cases in that prefecture.

Table 2.

Different regional (Regions 1 ∼ 3) results for different clustering schemes (A ∼ D) are reported in this table. The ranges within brackets refer to 95% Confidence Interval (CI) of R₀.

		A	B	C	D
Regions	1	1.58 (1.25-1.99)	1.60 (1.30-1.93)	1.70 (1.39-2.12)	1.60 (1.29-2.00)
	2	1.90 (1.40-2.54)	1.92 (1.49-2.54)	1.95 (1.57-2.46)	1.99 (1.57-2.62)
	3	2.18 (1.81-2.85)	2.21 (1.74-2.63)	2.24 (1.84-2.71)	2.15 (1.76-2.54)

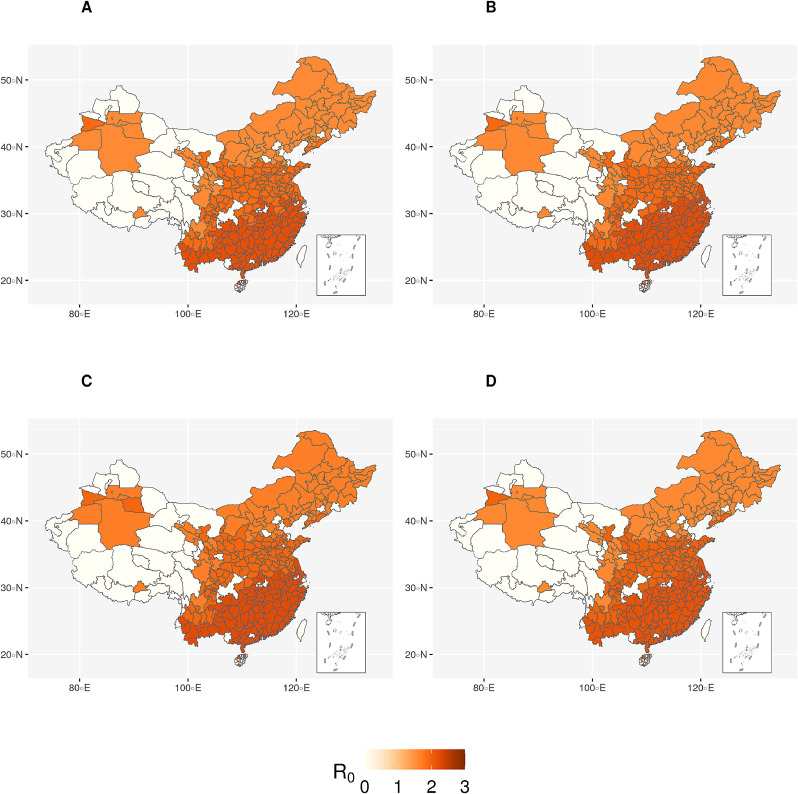
Fig. 2.

R0 values for different regions in China (scaled to 0-3). A, B, C, D indicates the clustering based on different sets of features. White colour indicates no cases in that prefecture. Darker shade of red corresponds to higher R0 and vice versa.

An interesting point can be noticed in Clustering Scheme D (Figure 1(d)) as follows. It exhibits two light green (medium R₀) prefectures (namely, Tangshan and Binzhou) in the eastern region, which is otherwise assigned green (low R₀) in other clustering schemes. The fact that Clustering Scheme D considers population profile in more detail than other clustering schemes, has played a role here. As it turns out, the ratio of aged population is markedly higher in these two prefectures which essentially put these into the immediate higher R₀ region. In the same context, we also notice another apparently anomalous prefecture (i.e., Turfan) at the north-western region, which is light green (medium R₀) in Clustering Scheme D as opposed to being green (low R₀) in Clustering Schemes A and C. The analysis shows that the aged population group is not prominent in Turfan; however, further analysis reveals that the sufficiently lower temperature therein has played its part and overshadowed the effect of the aged population (different age group percentage compared to the total population). Thus, it seems that we can give higher rank to temperatures in terms of contribution towards transmission than population age.

3.2. Regional Transmission Levels

Region 3 has been identified to be the highest transmission region (among the three) according to all four clustering schemes and the predicted R₀ for all clustering schemes remains at around 2.19 (2.18 ∼ 2.24). The low (medium) transmission region is Region 1 (2). In both cases, the predicted R₀ for all clustering schemes are quite similar, at around 1.62 (1.58 ∼ 1.70) for Region 1 and around 1.94 (1.90 ∼ 1.99) for Region 2.

Notably, due to the stochastic property of the Monte Carlo simulation, we can safely assume this range as acceptable (Figure 3 ).

Fig. 3.

Real cumulative cases of COVID-19 and predicted cumulative cases by our model are plotted together. A.* corresponds to Region * of Clustering scheme A.

4. Discussions

To the best of our knowledge, this is the first study to determine the impact of temperature and other potential risk factors through a clustering exercise and to estimate the revised R₀ of COVID-19 in different regions in China. We have applied the clustering algorithms using different combination of relevant features to ensure a confident and coherent analysis. Our results strongly indicated that R₀ may be affected (i.e., worsened) by higher temperature, and the prefectures having older population likely favoured its transmission.

Clustering Scheme E is based on temperature profile only and it clearly suggested that higher temperature produced higher R₀. This is a unique finding in itself as the role of temperature in the spread of COVID-19 has been studied (Liu et al., 2020; Pawar, 2020; Qi et al., 2020; Shi et al., 2020; Sobral et al., 2020; Sun et al., 2020; Tobias and Molina, 2020; Yao et al., 2020) and the predominant prediction was mostly the opposite; evidence from published studies documented negative associations between increasing temperature and COVID-19 transmission (Liu et al., 2020; Shi et al., 2020; Tobias and Molina, 2020).

Also, population turned out to be an important discriminant feature in clustering, and from the results it can be inferred that higher fraction of aged population is a risk factor and contributes to higher R₀. While identifying Region 3, temperature was the most contributing factor following the demographic factor. Region 3 (exhibiting the highest R₀) is the warm region where average of the daily mean temperature is around 8.57 °C whereas Region 1 and Region 2 has this value below 0 °C.

We estimated that the mean R₀ for the COVID-19 ranges from 1.58 to 2.24 (Table 2) and is significantly larger than 1 and is consistent with the other estimations for the human-to-human (direct) transmission ranged from 1.3 to 7.7 (Campos et al., 2020; Dropkin, 2020; Samui et al., 2020; Temime et al., 2020; Wei et al., 2020; WHO, 2020b; Yuan et al., 2020; Zhang et al., 2020b). On the other hand, most of the early predictions of mean R₀ in the literature range from 2 to 5, and are largely inconsistent with our results (Zhao et al., 2020). The reason might be that active surveillance, contact tracing, quarantine, and early strong social distancing efforts contributed to stop transmission of the virus and significantly decreased the effective reproduction number of COVID-19 in China (Sanche et al., 2020). Published studies also suggest that the first lockdown resulted in a 65% decrease of the reproduction factor, R ₀ and the second, stricter wave of measures eventually managed to bring it down to close to 0 (Prem et al., 2020).

Several factors can influence COVID-19 transmission, including environmental variables, population density, and strong public health infrastructures (Wang, 2020). The previous studies have seldom analyzed the effects of temperature on the development of COVID-19 in a large scale. However, the association between COVID-19 and temperature was not consistent and changes in temperature showed no significant correlation with cases transmitted, deaths or recovered (Pawar, 2020). Our findings at the prefecture level on the impact of temperature conditions over the transmission of COVID-19 are not consistent with other published studies (Prata et al., 2020; Wang, 2020). However, our results are consistent with several published studies (He et al., 2020; Luo, 2020; Rashed et al., 2020; Xie et al., 2020), which reported that the changes in temperature in spring and summer months might not lead to decline of confirmed case counts without the implementation of extensive public health interventions.

The most important environmental implication in our analysis proved temperature to be a critical factor for COVID-19 transmission, which also deserve to be better studied in other regions during this pandemic (Liu et al., 2020).

This study has several limitations, most notably the fact that these analyses were based on routinely collected data during pandemic with the potential for both over and under reporting of COVID-19 cases. Secular changes in reporting could have biased incidence estimates and errors could have been introduced as data were aggregated at higher levels of the health information system. Data accuracy and completeness were not systematically assessed. Some cases might be detected based on clinical signs and symptoms, with the potential for misclassification (Tsang et al., 2020). Testing systems have also limited sensitivity and specificity and are particularly likely to misclassify individuals. The observed associations between temperature, demographic factors and estimated R₀ were ecologic and not at the level of individuals.

4.1. Conclusion

R₀ is a rough estimate that depends on assumptions. It can increase or decrease when case numbers are low and do not capture the status of an epidemic. It is also an estimate on an average for a whole population and there can be local variations. Many countries across the globe that have recovered from the first wave of the pandemic are now experiencing the second wave thereof. It is crucial to watch for geographic clusters of cases and to set up comprehensive systems to test, trace their contacts, and isolate the infected individuals to control the pandemic. There were spatial heterogeneities in COVID-19 occurrence, which could be attributed to temperature. The reasons for the inconsistency in the impact of meteorological factors on COVID-19 among prefectures need further study. This research provides a novel methodology for the global health authorities. We also believe that our clustering approach can be replicated in other countries where the epidemic has subsided and depending on the quality and availability of the data, more complex models could replace our simple model with more realistic results.

Funding

UH was supported by the Research Council of Norway (grant # 281077). Wenyi Zhang was partly supported by grants from the Chinese Major grant for the Prevention and Control of Infectious Diseases (No. 2018ZX10733402-001-004, 2018ZX10713003). Yong Wang was partly supported by the National Natural Science Foundation of China (No. 12031010).

Author contributions

IMK, MSR, UH: Conceptualization, Methodology, Writing - original draft, Data analysis: IMK, MSR, UH. Data preparation: SJ, WZ, JH, and UH. Writing - review & editing, SZ, WZ, JL and JH. All authors read and approved the final version of the manuscript.

Data and materials availability

The datasets used and/or analysed during the current study are available (https://github.com/rizvi23061998/estimate_chinese_r0).

Declaration of Competiung Interest

None declared.