Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 26;142(42):18073–18085. doi: 10.1021/jacs.0c07392

Molecular versus Excitonic Disorder in Individual Artificial Light-Harvesting Systems

Björn Kriete †, Anna S Bondarenko †, Riccardo Alessandri †,‡, Ilias Patmanidis ‡, Victor V Krasnikov †, Thomas L C Jansen †, Siewert J Marrink †,‡, Jasper Knoester †,*, Maxim S Pshenichnikov †,*
PMCID: PMC7582617  PMID: 32985187

Abstract

graphic file with name ja0c07392_0006.jpg

Natural light-harvesting antennae employ a dense array of chromophores to optimize energy transport via the formation of delocalized excited states (excitons), which are critically sensitive to spatio-energetic variations of the molecular structure. Identifying the origin and impact of such variations is highly desirable for understanding and predicting functional properties yet hard to achieve due to averaging of many overlapping responses from individual systems. Here, we overcome this problem by measuring the heterogeneity of synthetic analogues of natural antennae–self-assembled molecular nanotubes–by two complementary approaches: single-nanotube photoluminescence spectroscopy and ultrafast 2D correlation. We demonstrate remarkable homogeneity of the nanotube ensemble and reveal that ultrafast (∼50 fs) modulation of the exciton frequencies governs spectral broadening. Using multiscale exciton modeling, we show that the dominance of homogeneous broadening at the exciton level results from exchange narrowing of strong static disorder found for individual molecules within the nanotube. The detailed characterization of static and dynamic disorder at the exciton as well as the molecular level presented here opens new avenues in analyzing and predicting dynamic exciton properties, such as excitation energy transport.

Introduction

Natural photosynthetic complexes employ a network of light-harvesting antennae that allows them to efficiently harness sunlight, even in light-depleted environments.1 To achieve this, antenna complexes typically accommodate thousands of individual chromophores that are arranged in ordered, well-defined supramolecular structures.2 At the core of their functionality are delocalized excited states (Frenkel excitons) that are collectively shared by many molecules, which is possible only due to strong intermolecular resonance interactions.3 Hence, the excitonic properties of such structures depend critically on the packing of the constituting molecules and thus are dictated by the competing interplay between intermolecular interactions and various sources of disorder.4−6 The latter arise from nonideal molecular packing as well as (thermal) fluctuations of the system and its immediate environment, leading to time-dependent fluctuations of the molecular transition energies (molecular energy disorder) as well as the intermolecular interactions (interaction disorder). The deviations from the “ideal” situation tend to localize the excitonic wave function on short segments, thereby potentially impeding efficient energy transport.7−9 Such deviations directly translate to the system’s excitonic (optical) properties, allowing spectroscopic observables (e.g., absorption or photoluminescence peak positions, line shape and broadening, etc.) to become highly sensitive reporters of the underlying molecular-scale order and dynamics in multichromophoric systems.10,11

Unraveling the origin of the excitonic line shape in terms of underlying intermolecular interactions and various molecular-scale sources of static and dynamic disorder is of great interest in gaining a better understanding of excited-state dynamics in such complex systems yet is difficult to attain. One of the main obstacles is averaging over many systems that is inherent to conventional spectroscopy, where the information for a single system is masked by the overlapping responses from all other slightly different systems. Such systems might differ by random variations of their sizes, molecular packing motifs, and rolling angles inherited from the self-assembling process. The limitation of such averaging can be overcome by employing single-molecule (or single-system) spectroscopy.12 In this case, the distribution of (spectral) parameters is constructed by measuring one system at a time, which grants access to information that would otherwise remain concealed under broad features of the ensemble response. Since the first successful demonstration of single-molecule spectroscopy,13,14 the technique has been further developed and applied to numerous natural photosynthetic complexes,15−17 artificial light-harvesting complexes,18,19 molecular aggregates,20−22 and conjugated polymers.23,24 Complementary to this approach, ultrafast 2D correlation spectroscopy has been extensively used to gain access to the magnitudes and time scales of the dynamical fluctuations of the exciton frequencies that eventually govern the optical spectra.4,25,26 The interpretation of these experiments, which provide increasingly detailed information, has also triggered the development of new theoretical and computational approaches that are able to model the exciton energetics and dynamics of large molecular assemblies in interaction with a complex and fluctuating embedding matrix (such as a solvent or a protein scaffold).27−29

To ease the interpretation of the optical spectra, the complexity of natural light-harvesting systems can be reduced by using artificial light-harvesting complexes. These synthetic analogues closely mimic the supramolecular structure of their natural counterparts but offer better controllability via chemical engineering of individual building blocks paired with a high degree of structural homogeneity of the final supramolecular structure.30 In this regard, molecular double-walled nanotubes based on amphiphilic cyanine chromophores have sparked particular interest.10,11 These nanotubes combine a large spectral red shift upon self-assembly with remarkable narrowing of the spectral lines in both absorption and photoluminescence as compared to dissolved monomers (as is typical for J-aggregates), which implies a low degree of disorder and strongly delocalized excitons.31,32 Indeed, previous cryogenic transmission electron microscopy (cryo-TEM) studies have revealed a high degree of structural homogeneity along different segments of an individual nanotube as well as between different nanotubes.11,33 To date, cryo-TEM cannot resolve the local molecular packing of the nanotubes and is still limited by the fact that possible dynamic fluctuations of the structures are frozen at cryogenic temperatures that otherwise might have a profound impact on the optical and functional properties.10,11,34

In this article, we use a combination of single-nanotube photoluminescence spectroscopy, ultrafast 2D correlation spectroscopy, and multiscale modeling to obtain a detailed picture of the line-broadening mechanisms of the exciton transitions and the underlying molecular-scale fluctuations in artificial light-harvesting nanotubes. Measurement of the photoluminescence spectrum from short (∼480 nm) segments of individual nanotubes demonstrates a high degree of homogeneity among the nanotubes. We further corroborate this conclusion by 2D spectroscopy by retrieving ultrafast (∼50 fs) dynamics of the line broadening. Multiscale calculations confirm this time scale and further reveal that the homogeneity at the exciton level results from strong exchange narrowing of considerable static disorder that exists at the level of individual molecules in the nanotubes.

Results and Discussion

Bulk Absorption and Photoluminescence (PL)

The double-walled nanotubes with diameters of ∼6 nm (inner wall) and ∼13 nm (outer wall) and lengths of several micrometers were formed via the self-assembly of C8S3 monomers (molecular structure in Figure 1a) in water10,11 (Figure 1b–d). The self-assembly is accompanied by a strong spectral red shift of ∼2400 cm–1 and the simultaneous formation of several narrow absorption peaks (Figure 1e). For the nanotubes, the most prominent peaks at ∼590 nm (∼17 000 cm–1) and ∼600 nm (∼16 700 cm–1) originate from absorption of the excitons located at the outer and inner walls, respectively, of the double-walled nanotubes.10,34

Figure 1.

Figure 1

Open in a new tab

Structural and optical properties of the double-walled nanotubes. (a) Chemical structure of the C8S3 molecule. (b) Schematic of the double-walled structure of the nanotubes with the inner and outer walls marked in red and gray, respectively, with their diameters indicated. (c) Cryo-TEM micrograph of highly homogeneous double-walled nanotubes. (d) Photograph of the cuvette containing H2O (bottom phase) and C8S3 dissolved in methanol (top phase). In the intermediate phase, the formation of nanotubes due to hydrophobic/hydrophilic interactions is evident from the spectral red shift. The solution colors were contrasted with white paper in the background. (e) Change in absorption (solid) and PL (dashed) spectra in solution upon formation of double-walled nanotubes (spectra in pink) from monomers (spectra in orange).

Optical absorption of the nanotubes at λexc = 561 nm excites higher-lying states in the exciton band, which is followed by ultrafast intraband relaxation on a sub-100-fs time scale to the bottom of the exciton bands from where PL occurs.35 In the nanotubes’ PL spectrum, the same assignment of peaks as in the absorption spectrum holds with virtually no Stokes shift between the corresponding peaks but with a reversed amplitude ratio. The inner-wall PL is significantly brighter than the outer-wall PL because the exciton populations of the weakly coupled inner and outer walls fully thermalize (i.e., reach thermal equilibrium on a subpicosecond time scale prior to emission as was shown by time-resolved PL36 and transient absorption37 experiments).

Single-Nanotube Spectroscopy

For single-nanotube spectroscopy (see the detailed description of the setup in Supporting Information Section 1), we immobilized the nanotubes in a glassy sugar matrix where their tubular structure is preserved,38 which was verified by bulk absorption and PL spectroscopy (Supporting Information Section 2). An example image of an optically thin (submicrometer thickness of the sugar film) sample in which the nanotubes are spatially well separated is shown in Figure 2a. The lateral size of the nanotube images (i.e., the PL intensity profile across) corresponds to the diffraction-limited point-spread function of the microscope (PSF; Supporting Information Section 3), while their length typically extends to several micrometers. Intensity variations of the PL signal along a single nanotube are likely caused by the finite thickness of the sugar matrix in which parts of the nanotube are out of focus and therefore appear blurred in the image. For spectral acquisition, we first located a nanotube using wide-field excitation and then positioned the sample such that the individual nanotube is excited by a (tightly) focused excitation spot with a diameter of ∼330 nm (at full width at half-maximum level, Supporting Information Section 4).

Figure 2.

Figure 2

Open in a new tab

Microspectroscopy of the individual double-walled nanotubes immobilized in a glassy sugar matrix. (a) Wide-field PL image recorded at room temperature. The PL intensity was normalized to the maximum amplitude in the image and is depicted on a linear color scale of between 0 and 1. The green circle (dashed) highlights the wide-field illumination area. The position of the focused excitation spot is schematically indicated by a white circle (not to scale). The excitation wavelength was λexc = 561 nm. (b) PL spectrum of a single nanotube (left) and the corresponding fit of the data with two Lorentzian line shapes for the inner wall (red) and the outer wall (gray) following focused excitation. For comparison, the PL spectrum of an ensemble of nanotubes is shown in the background in the left panel (purple shade).

An example PL spectrum of an individual nanotube at room temperature following focused excitation is shown in Figure 2b. Note that under the experimental conditions used in this study we observed very minor photobleaching that affects both inner and outer walls to a similar extent (Supporting Information Section 5). This allowed the acquisition and subsequent averaging of several spectra over a total time of 30 s in order to enhance the signal-to-noise ratio. In total, we recorded PL spectra for 50 individual spots (i.e., segments of different nanotubes).

In order to extract the spectral properties of a nanotube segment, we fit its PL spectrum to a sum of two Lorentzian line shapes (Supporting Information Section 6)

graphic file with name ja0c07392_m001.jpg 1

representing the spectra of the inner and outer walls with amplitude A, spectral width γ (the half width at half-maximum, HWHM), and spectral position ν0 (Figure 2b). Hereby, we treat the inner and outer walls as two independent excitonic subsystems.10,11 The underlying reasons for the Lorentzian rather than Gaussian line shapes follow from the fast–intermediate modulation regime as will be established by 2D spectroscopy and substantiated in the theory section (vide infra).

Repeating this procedure for each individual nanotube spectrum, we obtained statistical distributions of the spectral positions ν0 (Figure 3) and spectral widths γ (Figure 3, insets) of the PL spectra for the inner and outer walls.

Figure 3.

Figure 3

Open in a new tab

Statistical analysis of the PL spectra of the individual double-walled nanotubes. Histograms for the peak position (main panel) and the peak widths (inset) of the PL of the inner wall (red) and outer wall (gray). The black line represents the averaged PL spectra from individual nanotubes, with the error bars indicating the standard error of the mean. For the histograms, the binning size was set to 5 cm–1 for both the spectral position and the spectral width. Vertical dashed lines in the insets mark the spectral widths of the PL spectrum of an ensemble of nanotubes (purple shade in the main panel) obtained by averaging the PL spectra collected from 20 different sample areas using wide-field excitation. The small but noticeable shoulder at ∼605 nm (∼16 540 cm–1) originates from nanotube bundles (Supporting Information Section 7).

A comparison of the peak position distributions (Figure 3, red and gray) to the PL spectrum of an ensemble of nanotubes (Figure 3, purple and black) reveals that for both walls the spread of the peak positions is much narrower than the width of the corresponding peaks in the averaged spectra centered at around 16 660 ± 1 and 16 967 ± 2 cm–1 (mean value ± standard error of the mean). The mean peak position of the outer wall is in excellent agreement with the peak position in the PL spectrum of the nanotube. The slight deviation (by 6 cm–1) of the mean peak position of the inner wall from that for the nanotube ensemble is likely caused by an additional spectrally red-shifted and partially overlapping peak (centered at 16 544 ± 1 cm–1; Supporting Information Section 7) originating from bundled nanotubes.39 For the bundled nanotubes, the outer wall PL is strongly diminished, which explains why the outer wall peak in the bulk PL spectrum is not affected whereas the inner wall peak is. The contribution of bundles can readily be discriminated in single-nanotube spectroscopy but is unavoidable in bulk measurements.

The spectral width from short segments already accounts for 80–90% of the spectral width of the nanotube ensemble spectrum: ⟨γinner⟩ = 46 ± 1 cm–1 versus γensemble = 55 cm–1 for the inner wall and ⟨γouter⟩ = 84 ± 1 cm–1 versus γensemble = 93 cm–1 for the outer wall (Figure 3 inset and Table 1). The spectral widths of the ensemble agree reasonably well with previously published values.38,40 Similar behavior was observed at low temperature (77 K), where the mean spectral widths of the inner and outer walls decrease to ⟨γinner⟩ = 32 ± 1 cm–1 and ⟨γouter⟩ = 69 ± 4 cm–1, respectively, but the standard deviation widths of the distributions of the spectral positions remain unchanged (Supporting Information Section 8). This implies that the causes of spectral broadening are inherent in segments of the nanotubes that are as short as ∼480 nm, for which we will address the underlying reasons in the following section.

Table 1. Summary of the Spectral Parametersa.

  peak position, ν0 spectral width, γ
individual nanotubes ⟨ν0,inner⟩ = (16 660 ± 1) cm–1 ⟨γinner⟩ = (46 ± 1) cm–1
SDν0,inner = 9 cm–1 SDγ,inner = 4 cm–1
⟨ν0,outer⟩ = (16 967 ± 2) cm–1 ⟨γouter⟩ = (84 ± 1) cm–1
SDν0,outer = 13 cm–1 SDγ,outer = 8 cm–1
ensemble of nanotubes ν0,inner = 16 654 cm–1 γinner = 55 cm–1
ν0,outer = 16 966 cm–1 γouter = 93 cm–1
Open in a new tab
a

Peak positions and spectral widths for the inner and outer walls of the C8S3 nanotubes are obtained from single-nanotube spectroscopy in comparison to that of the nanotube ensemble spectrum. ⟨···⟩ denotes the average over individual nanotube spectra with the error margins referring to the standard error of the mean. The width of the respective parameter distribution is specified as its standard deviation (SD).

To end this section, we note that the distributions of the spectral position and the spectral width are broader for the outer wall than for the inner wall, which may originate from a combination of several reasons. First, the inherently lower signal amplitude of the outer wall as compared to that of the inner wall (as a consequence of weaker PL) introduces a larger uncertainty in fitting the outer wall’s spectral contribution. Second, the outer wall PL peak is broadened by its finite lifetime due to a fast population transfer time of τ ≈ 300 fs from the outer wall to the inner wall.35,41 This contribution can be estimated to be γ ≈ ℏ(2τ)−1 ≈ 10 cm–1, with the factor of 2 originating from the fact that γ is defined as the HWHM (eq 1). Third, PL from the first higher-lying state in the exciton band of the inner wall (blue shifted by ∼500 cm–1) that is partially overlapped with the outer wall PL might cause additional broadening. Nonetheless, at 77 K, where thermally activated PL is strongly reduced, the outer tube peak is still broader than the inner tube peak (Supporting Information Section 8).

Two-Dimensional Correlation Spectroscopy

Having established that the PL peak positions of individual nanotube spectra cluster together while their spectral widths already account for almost the whole width of the nanotube ensemble spectrum, we can perform 2D correlation spectroscopy (see Methods and Supporting Information Section 9) on bulk samples, which is capable of discerning the dynamics of the spectral broadening.4,25,26 The central quantity here is the frequency–frequency correlation function C(t) = ⟨(ω(t) – ⟨ω⟩)(ω(0) – ⟨ω⟩)⟩, where ω(t) indicates the exciton transition frequency at time t and ⟨···⟩ denotes the ensemble average of many nanotubes. C(t) reveals the pace at which the memory of the initially excited frequency ω(0) is lost in a particular time interval t (also known as dephasing) and the magnitude of static and dynamic disorder components.

Figure 4a depicts representative 2D spectra recorded at two different waiting times, with the low- and high-frequency pair of peaks corresponding to the inner and outer walls, respectively.10,25,39 Each tube gives rise to a negative ground-state bleach/stimulated emission (GSB/SE) signal and a positive excited-state absorption (ESA) signal. The latter is spectrally blue-shifted with respect to the GSB/SE signal, as is typical for molecular J-type aggregates.41−43 As a metric for the memory loss of the initial excitation frequency, we obtained ellipticity function M(T) ≅ C(t)/C(0)44,45 for the outer and inner walls of the nanotubes from the analysis of the peak shape (Supporting Information Section 10) of the GSB/SE signal in the 2D spectra at different waiting times T (Figure 4b). At early times, the inhomogeneous and homogeneous widths are balanced, which is reflected in the values of the ellipticity functions close to ∼0.5. Thereafter, both functions decay on an ∼ 50 fs time scale before leveling off at ∼0.1.

Figure 4.

Figure 4

Open in a new tab

Two-dimensional correlation spectroscopy on double-walled nanotubes. (a) Representative absorptive 2D spectra for waiting times of T = 0 and 150 fs with the excitation (ω1) and detection (ω3) axes in the horizontal and vertical directions, respectively. The signal amplitude is shown as ΔOD in which negative signals arise from ground-state bleach/stimulated emission (GSB/SE) and positive signals arise from excited-state absorption (ESA). The spectra were normalized to their respective maximum absolute amplitude and are displayed on a color scale of between −1 and +1 with color increments in steps of 0.1. Diagonal lines (dashed gray) are drawn for ω1 = ω3. The contour lines drawn at signal increments of 0.1 depict fits of the data using pairs of Gaussian peaks (one for GSB/SE and ESA) for each wall. The spectral regions used for fitting are marked as dashed red for the inner wall and dashed black for the outer wall. The arrows in the left panel (orange) showcase the ellipticity of the detected outer wall peak, with a and b denoting the widths along the long and short axes. (b) Ellipticity function M(T) for the inner (red dots) and outer (black dots) tube obtained from experiment. Solid lines depict the ellipticity functions retrieved from modeled 2D spectra in the framework of the Brownian oscillator model. The inset shows the normalized frequency–frequency correlation functions C(t)/C(0) which served as input for the calculation of the 2D spectra. A reference line (dashed gray) was drawn to emphasize the fact that C(t)/C(0) does not decay to zero.

The experimental values of the ellipticities were modeled in the framework of the Brownian oscillator model46 (Supporting Information Section 11), as for the example used in ref (25). Assuming that we can effectively treat GSB/SE of the exciton transitions as separate two-level transitions, we use the following exponential correlation function as input (Figure 4b, inset)

graphic file with name ja0c07392_m002.jpg 2

where Δinh and Δh are the amplitudes of frequency fluctuations of static (inhomogeneous) and dynamic (homogeneous) contributions, respectively, and τc is the correlation time. The experimentally measured ellipticity functions were well reproduced using Δinh = 20 cm–1, Δh = 75 cm–1, and τc = 45 fs for the inner wall and Δinh = 25 cm–1, Δh = 120 cm–1, and τc = 40 fs for the outer wall (Supporting Information Section 11) as input parameters for calculating the 2D spectra from nonlinear response theory (from which the ellipticity was subsequently determined). The correlation times are also similar to the 100 fs value obtained from 2D spectroscopy on chlorosomes from green sulfur bacteria.26

Given the combination of correlation times and frequency-fluctuation amplitudes, we find that at the exciton level the fast-intermediate regime of spectral broadening is realized,46 since 2πΔhτc ≈ 0.6 (inner wall) and 0.9 (outer wall) (Supporting Information Section 12). It is this fast-intermediate regime that is responsible for the predominantly Lorentzian line shape of the PL spectrum (Supporting Information Section 13). In this case, the spectral width of the linear spectra is a good approximation given by the dephasing rate Γ = 2πΔh2τc (HWHM), for which we find 47 cm–1 (107 cm–1) for the inner (outer) wall, in good agreement with the single-nanotube results. The long tail of the correlation function indicates small residual inhomogeneity (∼10%); this value is in line with the spread of central frequencies obtained from single-nanotube spectroscopy (Figure 3). Finally, the correlation time of frequency fluctuations of ∼50 fs is much shorter than the outer-inner wall population transfer time of ∼300 fs which makes the energy transfer fully incoherent. Indeed, no sign of coherence was obtained in the cross-peak dynamics (Supporting Information Section 14), in agreement with earlier reports.25,35,41

Multiscale Modeling

To unravel the origin of molecular and excitonic disorder in the nanotubes, we performed multiscale simulations to retrieve the time-dependent exciton Hamiltonian that describes the collective optical excitations and their dynamics in each wall of the nanotube. We built on recent work where a combination of molecular dynamics (MD) simulations and quantum mechanical exciton modeling was used to calculate the structure and the linear absorption spectrum of the double-walled C8S3 nanotubes in interaction with the surrounding solvent.29 Using this model as a starting point, we ran an MD simulation to generate a time sequence of configurations of the entire nanotube and solvent at 10 fs intervals. From these configurations, we obtained the optical transition energies ωn(t) of individual C8S3 molecules as a function of time using microelectrostatic calculations as well as the intermolecular excitation transfer interactions Jnm(t) (n and m label the molecules in a particular wall of the nanotube) using the extended dipole model (Methods section). These quantities define the Hamiltonian for each wall at time t as ℏ = 1

graphic file with name ja0c07392_m003.jpg 3

Equation 3 accounts for disorder in the energies ωn(t) that arises from fluctuations in the electrostatic properties of the environment of each C8S3 molecule and disorder in the interactions Jnm(t) that arises from fluctuations in relative distances and orientations of molecules n and m. In this equation, |n⟩ denotes the state where molecule n is in its excited state and all other molecules are in their ground states.

The multiscale simulations allow us to distinguish between static and dynamic disorder. Thus, we separate the molecular transition energies into three parts

graphic file with name ja0c07392_m004.jpg 4

where ω0 is the ensemble average (i.e., the transition energy obtained when averaging over many molecules and long trajectories); δωn,s is the static disorder of molecule n (i.e., the deviation of the average of its transition energy over the entire trajectory from the ensemble average); and δωn,d(t) is the dynamic disorder in this energy, which describes the remaining fluctuations as a function of time.

Similarly, the interactions can be broken down into ensemble-averaged values, static disorder, and dynamic disorder. To characterize the disorder of all of the individual interactions Jnm(t) is neither practical nor very useful. It is important to realize that in the end our interest lies in the fluctuations that occur in the energies of the optically dominant exciton states as a result of the fluctuations in the interactions. For a single-walled homogeneous tubular nanotube with one molecule per unit cell, three superradiant transitions occur: the totally symmetric one |e⟩ = N−1/2Σn|n⟩ (with N being the total number of molecules), where all molecules oscillate in phase and which has a transition dipole parallel to the axis of the cylinder, and two degenerate ones, where the phase of the molecular excitation cycles over exactly 2π within each ring of the nanotube, with transition dipoles perpendicular to the axis.47 The totally symmetric state commonly has the lowest energy, as is also the case for the C8S3 nanotubes studied here.10,32 Superradiant states with perpendicular polarization also exist for this system (because the dipoles of the individual molecules have components both along and perpendicular to the axis10,29), but they are not visible in fluorescence due to their higher energy (and they lie outside the spectral window of the 2D correlation experiments). Thus, the two exciton bands that are relevant here are derived from the totally symmetric states of the inner and outer walls, respectively. We note that the notion of a particular symmetry in the exciton states is approximately valid even in the presence of disorder as long as the exciton delocalization length is at least on the order of the tube’s circumference.48 For tubular nanotubes, exciton localization by disorder is suppressed due the locally two-dimensional nature of the tube and the long-range dipole–dipole interactions32,49 implying that the approximate symmetries and optical selection rules indeed often persist under experimental conditions.

The totally symmetric state has an energy that is shifted relative to the molecular transition energy by an amount given by Sn(t) = Σm≠nJnm(t) (i.e., the sum of all transfer interactions between molecule n and all other molecules in the nanotube wall considered). For an ordered static tube, this quantity is constant and equal for all n (discarding boundary effects). In the presence of disorder, however, Sn(t) fluctuates from molecule to molecule, and it fluctuates in time. Given the above reasoning, the fluctuations in Sn(t) may be used as a measure of the fluctuations in the exciton energies of interest.50 Henceforth, we will be particularly interested in the stochastic properties of Sn(t). By analogy to eq 4, we may separate Sn(t) as

graphic file with name ja0c07392_m005.jpg 5

It is useful to define the correlation functions for ωn(t) and Sn(t) as

graphic file with name ja0c07392_m006.jpg 6

and

graphic file with name ja0c07392_m007.jpg 7

respectively, where, as before, ⟨···⟩ denotes the ensemble average, carried out as an average within each wall over many molecules (35 for the energies as highlighted in Figure 5a and all molecules for the interactions; see the Methods section). Both correlation functions are plotted in Figure 5b,c, respectively. They have been fitted to simple two-component functions with a static and a dynamic part

graphic file with name ja0c07392_m008.jpg 8
graphic file with name ja0c07392_m009.jpg 9

where σs, σd, and τmol denote the standard deviations of the static and dynamic disorder in the molecular transition energy and the correlation time of the dynamic fluctuations, respectively, and Σs, Σd, and τint are the analogous quantities for the exciton shift. Thus, a total of six parameters describe the static and dynamic disorder in each wall. Correlations between the dynamic fluctuations in the transition energies ωn(t) for different molecules were found to be small (Supporting Information Section 15). Henceforth, correlations between transition energies of different molecules will be ignored, as will be correlations between the exciton shifts of different molecules Sn(t) and possible cross-correlations between energies and exciton shifts.

Figure 5.

Figure 5

Open in a new tab

Correlation functions of the molecular energies and interactions from multiscale modeling. (a) Slab from the center of the inner wall with the representative molecules for which the excitation energies were followed in time, marked in red, and the slab of the double-walled nanotube with the molecules used for the energy calculations marked in red and blue for the inner and outer walls, respectively. For top views, see Supporting Information Section 15. (b) Correlation functions for the molecular excitation energies (eq 6) for the inner (red dots) and outer walls (black dots) averaged over the molecules highlighted in panel (a). Solid lines: fits to an exponential function (eq 8). (c) Correlation functions of the intermolecular interactions for the inner (red dots) and outer walls (black dots) as reflected in the exciton shift (eq 7). Solid lines: fits to an exponential function (eq 9).

For both walls, the disorder parameters obtained from our simulations are given in Table 2. The parameters for both walls are quite similar; the largest differences are found for the molecular energy disorder, whose static magnitude in the outer wall is about 10% larger than that in the inner wall, in line with the larger standard deviations in peak positions and line widths found in the single-nanotube PL experiments (Table 1). We will disregard this difference as not playing a significant role in our further considerations. The disorder strength in the molecular transition energies is seen to be about half the strength of the interaction disorder, and the static disorder strengths for all quantities are about 2.5 to 3 times the dynamic strengths. This latter observation is in stark contrast to the dominance of homogeneous broadening which we found in the above experimental studies. Furthermore, it is seen that the fluctuations in the transition energies are about 3 times faster than those in interactions. Interestingly, the dynamic energy disorder is in the fast-intermediate regime (2πσdτmol ≈ 0.8), while the dynamic interaction disorder is in the slow-modulation regime (2πΣdτint ≈ 4.9). Note that from 2D correlation spectroscopy we found that at the exciton level the dynamic disorder is primarily in the fast-intermediate regime. From the above, the question arises as to why the dominance of static disorder on the molecular scale and the slow nature of the dynamic disorder in the interactions do not lead to a stronger inhomogeneity of the excitonic transitions than was observed in experiment. We will see below how the apparent contradictions between theory and experiment can be reconciled in one united picture.

Table 2. Overview of Correlation Function Parametersa.

molecular energy disorder
 interaction disorder
  inner wall outer wall   inner wall outer wall
σs (cm–1) 208 232 Σs (cm–1) 460 467
σd (cm–1) 83 81 Σd (cm–1) 172 177
τmol (fs) 46 57 τint (fs) 145 156
Open in a new tab
a

Parameters characterizing correlation functions Cmol(t) and Cint(t) for the molecular transition energies and the intermolecular excitation transfer interactions reflected in the exciton shift for the inner and the outer walls as obtained from multiscale modeling.

Multiscale modeling allows us to resolve disorder at the molecular level and therefore to further explore the origin of the above parameters. For the transition energies of the C8S3 molecules, we have distinguished between contributions to the disorder arising from the solvent (water molecules and Na+ counterions) and the other (surrounding) C8S3 molecules (Supporting Information Section 16). The static molecular energy disorder is ∼10% larger for the outer wall than for the inner wall; however, interestingly enough, there are considerably larger differences in the relative contributions from different sources. In particular, we found that the relative contribution from the surrounding C8S3 molecules compared to the water is larger for the inner wall than for the outer wall. This originates from the inward curvature in the inner wall, which leads to a higher packing density of the charged sulfonate groups. The same holds for the Na+ counterions in the solvent, which also cause larger static disorder contributions in the inner wall than in the outer wall. Because the sulfonate groups and Na+ counterions have opposite charges, their electrostatic effects partially cancel each other. Similar observations can be made for the magnitudes of the dynamic disorder components (Supporting Information Section 16).

We further found that the solvent governs the time scale of the dynamic disorder; the fluctuations caused by the C8S3 molecules occur on a slower time scale. The difference in time scale between solvent and C8S3 molecules is particularly large for the outer wall, where the fluctuations caused by the C8S3 molecules are about 2 times slower than those caused by the solvent. In contrast, in the inner wall the fluctuations caused by the C8S3 molecules are only 1.3 times slower than those incurred by the solvent. We attribute this convergence of time scales to the fact that for the inner wall the charges of the C8S3 molecules and the solvent form relatively tightly bound clusters where both constituents move in unison. This stronger binding between C8S3 and solvent is caused by the fact that, as argued above, the densities of charges in the inner wall as well as in the solvent near the inner wall are larger than in the outer wall, leading to stronger electrostatic interactions.

The interaction disorder is caused by structural fluctuations, in particular, by relative displacements of molecules with respect to each other and relative rotations. We artificially froze these motions by calculating the intermolecular interaction while keeping the same position or orientation of the transition dipoles as in the initial frame throughout the trajectory. We established that both contributions are of the same order of magnitude and occur on a similar time scale (Supporting Information Section 17).

From Molecules to Excitons

Having characterized the disorder in the quantities that determine the exciton Hamiltonian, we now have a complete model from which the behavior of the excitons in the nanotubes and their optical response may be derived and compared to experiment. The most straightforward way to do this is to calculate the optical properties directly from the fluctuating exciton Hamiltonian, for instance, by using the surface hopping method or the numerical integration of the Schrödinger equation, among other methods.51,52 Given the size of the nanotubes considered and the fact that simulating the 2D spectra requires the inclusion of two-exciton states, this would be a formidable task which actually would not necessarily provide us with much insight. Therefore, we turn to a much simpler and more conceptual approach, which exploits the well-known effect of exchange narrowing of disorder.31 This is the effect that in systems with molecular-scale disorder, for instance, in the excitation energies of individual molecules, the optically dominant collective excitations (delocalized excitons) have an energy distribution that is narrower than the molecular disorder distribution. This results from the fact that delocalized states average over the independent disorder values of a number of molecules. This effect sometimes is also referred to as motional narrowing, by analogy to the narrowing of NMR line shapes due to rapid changes in the dynamic environment of a precessing spin. While at the formal level there is an analogy (one may look at the exciton as moving from molecule to molecule and thereby effectively averaging over a changing environment), we prefer to stick to the term “exchange narrowing” to stress the differences in physics and the types of interactions that play a role.

The exchange narrowing approach starts from assuming that the disorder is small enough to be treated in first-order perturbation theory. In this case, the effect on the optically dominant exciton is a time-dependent energy shift δωe(t) relative to the value obtained in the absence of disorder (Hamiltonian H0), given by

graphic file with name ja0c07392_m010.jpg 10

This simply is the mean of the disorder values on all molecules of the nanotube at time t, which has a correlation function that is directly derived from the correlation functions for the energies and the shifts (eqs 5 and 6) to be

graphic file with name ja0c07392_m011.jpg 11

The exciton energy correlation function thus follows from the parameters in Table 2 and the value of N, where the key effect is that the variances of the disorder, σs2, σd2, Σs2, and Σd2, are reduced by a factor N due to the fact that the delocalized exciton wave function is averaged over N uncorrelated realizations of the disorder in the molecular quantities (i.e., the disorder is typically reduced by √N).

Clearly, the double-walled nanotubes are much too large for a perturbative approach to apply. However, even in this case the above concept can still be used if one replaces the number of molecules N by an effective number that characterizes the relevant exciton states. This reasoning is commonly applied to the static disorder component, where one replaces N with the typical delocalization size Ndel of the exciton states in the optically dominant region caused by the static disorder.31,53 Here, the region of interest is the position of the lowest-energy J band, where our numerical calculations of the exciton states yield Ndel ≈ 450 (Methods section), leading to an effective standard deviation of the static disorder component in the exciton energy given by 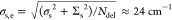Inline graphic for both walls. We note that this number is in excellent agreement with the effective static disorder Δinh values of 20 and 25 cm–1 for the inner and outer walls, respectively, that were obtained from 2D correlation spectroscopy.

The above strongly suggests that our multiscale simulations of the structure of the nanotube and surrounding solvent capture the essential sources of static disorder. Moreover, this reveals that the small amount of inhomogeneity found from both single-nanotube spectroscopy and 2D correlation spectroscopy does not necessarily imply that at the molecular scale the static disorder is small. In fact, as is evident from Table 2, for all molecular quantities, the static disorder is considerably larger than the dynamic disorder. The smallness of the static disorder at the exciton level is a direct consequence of exchange narrowing of the molecular-scale disorder over the many molecules that share the eigenstates of the exciton Hamiltonian with static disorder. This in turn is a consequence of the strong intermolecular excitation transfer interactions and the fact that tubular aggregates are not truly one-dimensional systems, leading to weak exciton localization.32,49

We next turn to the effects of the dynamic disorder components in the exciton Hamiltonian. As is seen from eq 11, at the exciton level, the dynamic disorder component is biexponential. For a simple characterization, we will treat both correlation times τmol and τint as equal and of the order of 100 fs and regard this as the correlation time τe of the exciton energies. This agrees in order of magnitude with the correlation times τc found from the 2D correlation experiments. The magnitude of the dynamic disorder at the level of the exciton transitions may be found by reasoning similar to that used above for the static disorder. In this case, however, one cannot use Ndel because this would only account for the reduction of the excursions of the exciton transition energies around their static values as a result of the dynamic disorder. Thereby, this approach would totally ignore the scattering of the static exciton states caused by the dynamic fluctuations. This scattering gives rise to transitions from one particular exciton state to others. The relevant length scale is then given by the scattering length or mean free path, Nscat = |J|/Γ, where Γ is the intraband scattering rate. Calculating Γ from the above Hamiltonian would involve a detailed analysis of the scattering process, which is beyond the scope of this article. However, assuming that intraband scattering dominates the exciton dephasing rate, we may identify Γ with the HWHM found in the single-nanotube experiments (Table 1). Using the average value Γ ≈ 60 cm–1 for both walls and J ≈ −1000 cm–1 (as obtained from the multiscale simulations), we arrive at Nscat ≈ 16. Using the numbers presented in Table 2, we obtain an estimate of the dynamic disorder strength at the exciton level given by 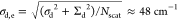Inline graphic. Given the handwaving nature of the above arguments, this number is in good agreement with the experimental values of Δh = 75 and 120 cm–1 for the inner and outer walls, respectively. We also note that through the narrowing effect, the effective dynamic disorder at the exciton level is brought from the slow-modulation regime to the fast-intermediate regime 2πσd,eτe ≈ 0.9. It is this fast-intermediate modulation regime that is responsible for the predominantly Lorentzian line shape of the PL spectrum, which therefore justifies our treatment of the single-nanotube PL data using eq 1 (Supporting Information Sections 12 and 13).

These findings also seem to imply an ∼16-fold acceleration of the radiative (superradiant) emission rate of nanotubes compared to that of monomers.54 In the experiment, however, the PL lifetime decreases only by approximately a factor of 3 upon nanotube formation,55 namely, from τmonomersPL ≈ 110 ps down to τnanotubes ≈ 40 ps. This discrepancy mainly arises from the fact that both monomers and nanotubes are subject to prominent nonradiative decay channels as concluded from low quantum yields (less than 5%) (Supporting Information Section 18 and refs (11) and (56)). A quantitative comparison of these rates, however, would require detailed knowledge of the nonradiative pathways, which is beyond the scope of this article. On the side of theory, a detailed analysis of the exciton scattering processes and nonradiative decay channels is required to obtain further insight into the predicted PL lifetime and make a comparison to experiment.

The theory above shows that the parameters that characterize static and dynamic disorder in the exciton energies, Δinh, Δh, and τc, as measured by 2D correlation spectroscopy, can be well understood from the microscopic disorder in the molecular transition energies and excitation transfer interactions as predicted by multiscale calculations of the nanotube. Taken together these lead to a detailed understanding in terms of exchange narrowing factors dictated by the exciton delocalization size imposed by static disorder and the exciton scattering length imposed by dynamic disorder.

Conclusions

By recording single-nanotube PL and 2D correlation spectra on artificial light-harvesting nanotubes, we have shown that the excitonic line width is dominated by dynamic disorder with an amplitude of ∼100 cm–1 and a correlation time of ∼50 fs, with only a minor contribution (∼20 cm–1) from inhomogeneous broadening. As a result, different (segments of) nanotubes have similar optical properties. The remarkable degree of homogeneity demonstrated herein makes it possible to assign the excitonic properties measured on bulk samples to individual systems.

Multiscale modeling allowed us to unravel the static and dynamic disorder components in the molecular excitation energies and the intermolecular excitation transfer interactions. The considerable static disorder of about 500 cm–1 at the molecular level (combined with the molecular transition energies and the transfer interactions) is mitigated at the exciton level due to the delocalized (over about 450 molecules) excitonic wave function leading to an exchange narrowing factor of ∼20. This is consistent with the fluctuations in the exciton peak positions as observed from single-nanotube PL spectroscopy, demonstrating the capability of this experiment to directly observe the exchange narrowing of static disorder. Similarly, the dynamic disorder of about 200 cm–1 is narrowed through the exciton scattering size of about 20 molecules imposed by intraband scattering. This narrowing brings the dynamic disorder from the slow modulation regime at the molecular level into the fast-to-intermediate modulation regime at the exciton level.

All in all, a molecular-level understanding of static and dynamic fluctuations in the collective excitations of a large self-assembled system has been attained at an unprecedented level of detail. Together with more sophisticated techniques, such as spatially resolved 2D spectroscopy57−59 and super-resolution microscopy,60 our results pave the way to a more detailed picture of how the delocalized excited states are spatially and temporally constrained and mobilized by static and dynamic disorder at the level of individual nanotubes, which is an important step toward formulating (structural) design rules for multichromophoric systems.

Methods

Sample Preparation

Dye 3,3′-bis(2-sulfopropyl)-5,5′,6,6′-tetrachloro-1,1′-dioctylbenzimidacarbocyanine (C8S3) was purchased from FEW Chemicals (Wolfen, Germany) and used as received. Molecular nanotubes were prepared via the alcohol route10,11 and used within 3 days after preparation; in order to obtain bundles, the sample solution was stored for ∼10 months in the dark. Nanotubes and bundles were immobilized in a sugar matrix following ref (38). To achieve optically thin films suited for microscopy, the method was modified and combined with a drop-flow technique.61 First, cover glass slides (22 × 22 mm2; thickness 170 μm) were cleaned by submerging them in a 1:1:2 mixture by volume of H2O2/NH4OH/H2O for ∼24 h. Before sample deposition, the substrates were rinsed with methanol and dried with compressed air. Next, equal volumes of the sample solution (10-fold diluted with Milli-Q water) and a saturated sugar solution in water (1:1 mixture of sucrose/trehalose by weight) were mixed. Then, 200 μL of the resulting solution was homogeneously applied at the top edge of the cover glass that was inclined 60° relative to the laboratory bench. The sample solution quickly flowed off, leaving a thin (in a submicrometer range) film on the cover glass surface, which was left in the dark to dry for ∼1 h.

Absorption and PL Spectra

Absorption spectra of the sample solutions (diluted with Milli-Q water by a factor of ∼3.5) were measured using a PerkinElmer Lambda 900 UV/vis/NIR spectrometery with a 1 mm cuvette. Solution PL spectra were recorded while pumping the sample (diluted with Milli-Q water by a factor of ∼6) through a 50-μm-thick cuvette that was placed on the same microscope as was used for single-nanotube experiments (vide infra) equipped with an M = 4× objective (NA = 0.1, achromat, Leica). Details regarding the microfluidic setup are given in ref (55).

Single-Nanotube Spectroscopy

Single-nanotube spectroscopy was carried out on a home-built optical microscopy setup constructed around a Carl Zeiss Observer D1 microscope equipped with an oil-immersion objective (Carl Zeiss Apochromat; 100× magnification, NA = 1.4). A CW laser (λ = 561 nm, Coherent Sapphire 561-100) served as an illumination source. Two beams for wide-field and focused excitation were projected by the microscope objective onto the sample mounted on a motorized translation stage. The excitation intensities for wide-field and focused excitation were set to ∼0.1 and ∼3.6 W cm–2 at the sample plane, respectively. The PL was directed to a CCD camera (Photometrics Coolsnap HQ2) through an image magnifier (1.6×) for imaging or coupled into a multimode optical fiber connected to a spectrometer (∼12 cm–1 spectral resolution) and equipped with an EMCCD camera (PhotonMax 512, Princeton Instruments). For a single nanotube, 30 sequential PL spectra were recorded with an exposure time of 1 s per frame and later averaged. A detailed schematic of the setup and the data processing protocol is given in Supporting Information Section 1.

Two-Dimensional Correlation Spectroscopy

Two-dimensional spectra were collected using a pulse-shaper-based setup operating at 1 kHz (Supporting Information Section 9); the design is similar to that in ref (62). The output of a noncollinear optical parametric amplifier (NOPA; centered at 16 950 cm–1, pulse duration ∼25 fs) was sent to an acousto-optic programmable dispersive filter (AOPDF; DAZZLER, fastlite) to generate the excitation pulse pair. The compressed output of a second NOPA served as the broad-band probe beam. The probe and pump beams were focused at a small angle (∼2°) into a microfluidic flow cell (micronit) containing the sample solution (peak optical density of 0.1–0.2). The polarizations of pump and probe pulses were both set parallel to the flow direction of the sample solution along which the nanotubes preferentially align.41 This allowed efficient excitation/probing of the pair of strongest transitions with their dipole moments directed along the nanotubes.63 After the sample, the probe pulse was spectrally dispersed in a spectrograph (Jobin Yvon HR320) and detected pulse-by-pulse by a NMOS linear image sensor (Hamamatsu, S3921-128Q), which provided the detection axis of the 2D spectra with a spectral resolution of 14 cm–1. For the collection of 2D spectra, the DAZZLER generated two phase-locked pulse replicas with a delay time τ that was scanned between 0 and 400.4 fs in steps of 0.7 fs. Fourier transformation along τ provided the excitation axis of the 2D spectra with a spectral resolution of 42 cm–1 given the scanning range of τ. Two-dimensional spectra were acquired using a two-step phase cycling scheme of the pump pulses applied by the DAZZLER and averaged for 50 spectra. The probe beam was delayed relative to the second pump pulse by waiting time T and split before the sample to provide a reference for pulse-to-pulse intensity normalization of the probe spectrum using a second NMOS linear image sensor.64 The pump and probe pulse energies were set to 100 pJ and 200 pJ, respectively, corresponding to ∼1 absorbed photon per 1200 monomers, which is low enough to avoid creation of or population at the two-exciton state.41 Measurements were conducted at room temperature.

Molecular Dynamics Simulations

We used a recently developed large-scale atomistic model of the C8S3 double-walled nanotube.29 The initial structures were obtained by constructing 2D lattices from a unit cell in which the C8S3 molecules were arranged in a herringbone formation. The lattices were then rolled into cylindrical shapes and put together to create double-walled structures that maintained their tubular formation. (For more details, see refs (29) and (65).) The nanotube model is 100 nm long, corresponding to 7024 C8S3 molecules, and solvated in water and Na+ counterions. This leads to a system with a total of approximately 4.2 × 106 atoms (placed in a simulation box with approximate dimensions of 20 × 20 × 130 nm3). The MD simulations were run with the GROMACS 2019 simulation package66 and employed a force field refined for C8S3 molecules29 based on the general AMBER force field (GAFF);67 the TIP3P water model was used,68 while Na+ was modeled with GAFF. Temperature (300 K) and pressure (1 bar) were maintained by using the v-rescale thermostat69 (coupling constant of 0.1 ps) and the Berendsen barostat70 (coupling constant of 1 ps; compressibility of 4.5 × 10–5 bar–1), respectively. The neighbor lists update was done according to the Verlet cutoff scheme, and a 1.4 nm cutoff for van der Waals (Lennard-Jones) and electrostatic (reaction-field) interactions was employed. Starting from a snapshot of an equilibrated structure taken after 20 ns of MD simulations, we ran 10 ps of MD and stored the atom positions every 10 fs. The resulting 1000 snapshots were used to explicitly compute the molecular energies and intermolecular excitation transfer interactions. We refer to ref (29) for further details on the model and its validation.

Molecular Energy Calculations

The effect of the surroundings on the C8S3 molecular transition energies ωn(t) was calculated as energy shifts relative to the gas-phase monomer excitation energy as obtained via atomistic microelectrostatic calculations.29,71,72 The essence of the method is to treat the effect of the environment at a polarizable molecular mechanics level. Hence, we computed the difference in interaction energies between the ground- and excited-state charge distributions (computed at the (time-dependent) density functional theory (TD)DFT level, see ref (29)) of a central molecule interacting with its molecular environment. When computing such interaction energies, both the central molecule and the surrounding ones were described by atomic charges and polarizabilities. The polarizable environment broadens the energy levels in both walls considerably.29 Because doing this for all molecules at all times is computationally too expensive, we have developed a stochastic model by performing these calculations for each of the 1000 MD snapshots for 35 molecules selected to be representative in each wall (Figure 5a) using the DRF90 software.73 The convergence of the energy distributions was tested against a simulation for a larger set of molecules (Supporting Information Section 19). More specifically, the energy shift of a particular C8S3 molecule relative to the gas-phase transition energy was obtained by separately calculating the energy shifts, ΔEg and ΔEe, of the molecular ground and excited states relative to their gas-phase values. This was done in two separate calculations, where a particular C8S3 molecule was modeled by either its excited state (for ΔEe) or its ground state (for ΔEg) point charge distribution in the presence of the ground-state point charges and isotropic polarizabilities of the surrounding C8S3 and solvent molecules within a radius of 3.0 nm from the center of the central C8S3 molecule. The total shift of the transition energy with respect to the gas-phase value was subsequently computed as the difference ΔEe – ΔEg. The ground- and excited-state charges for C8S3 were obtained using DFT and can be downloaded from ref (29). For water and Na+, the MD force field charges described above were used. We refer to ref (29) for further details on the DFT and microelectrostatic calculations.

Stochastic Model for the Site Energies

The frequency correlation functions (eq 6) were obtained for each wall by averaging over the 35 selected molecules. The frequencies were found to fluctuate with a slow (static) component and a fast one with an exponentially decaying correlation (eq 8). Consequently, to model the full nanotube (eq 3), trajectories for the time-dependent transition energies, ωn(t), for each C8S3 molecule were generated by adding to the ensemble-averaged transition energy a static random number from a Gaussian distribution with mean zero and standard deviation σs and a time-dependent random number constructed (using the procedure in ref (74)) to obey the correlation function σd2e–t/τmol.

Intermolecular Interaction Calculations

To calculate the intermolecular excitation transfer interactions in eq 3, we used the extended dipole model75 with the parameters taken from ref (34). We mapped the transition dipole of each C8S3 molecule on the polymethine bridge coordinates taken from the MD trajectory. The model allows us to treat all 7024 C8S3 molecules (2932 and 4092 for the inner and outer walls, respectively) of the MD model and was applied to obtain the intermolecular interactions for all 1000 snapshots.

Exciton Delocalization Calculations

To estimate Ndel, we computed the inverse participation ratio,76 defined as

graphic file with name ja0c07392_m014.jpg 12

where |q⟩ = Σnφqn|n⟩ is the qth eigenstate of the Hamiltonian (eq 3) and ρ(ω) is the exciton density of states. The exciton states were obtained by numerical diagonalization of the Hamiltonian. The reciprocal of the IPR(ω), also known as the participation ratio, PR(ω), is proportional to the number of molecules that participates in (shares) the collective excitations at energy ω (i.e., the exciton delocalization size). For a tubular aggregate, we use Ndel = (9/4)PR, where the prefactor is introduced to ensure that in the absence of disorder, the delocalization size equals the system size.77

Acknowledgments

C. van Hooff and S. Kosar are acknowledged for their contributions at an early stage of the project. T. Zijp is acknowledged for his contribution to some microscopy measurements. B.K. and M.S.P. thank F. de Haan for general laboratory assistance and R. M. Hildner for helpful discussions of the manuscript. We gratefully acknowledge numerous discussions with A. H. de Vries. The authors acknowledge funding by the Dieptestrategie Programme of the Zernike Institute for Advanced Materials (University of Groningen, The Netherlands). We thank the Center for Information Technology of the University of Groningen for providing access to the Peregrine High-Performance Computing Cluster and the National Computing Facilities Foundation of The Netherlands Foundation for Scientific Research (NWO) for providing computing time.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c07392.

  • Absorption and PL spectra of nanotubes in solution and films; layout and characterization of the setups for single-nanotube and 2D correlation spectroscopy; analysis of peak amplitudes in 2D spectra; quantum yield of monomers and nanotubes; characterization of photobleaching of the sample; signature of bundled nanotubes in single-object spectroscopy; low-temperature single-object spectroscopy of nanotubes and bundles; details of fitting and calculation of the nanotubes’ PL spectra, including quantification of the spectral broadening regime; details of the ellipticity analysis of experimental and calculated 2D spectra; details of the theoretical modeling including cross-correlations of molecular energy fluctuations and different contributions to the molecular energy and interaction disorders; and convergence of energy distributions for calculations with more molecules (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja0c07392_si_001.pdf (2.9MB, pdf)

References

  1. Mirkovic T.; Ostroumov E. E.; Anna J. M.; van Grondelle R.; Govindjee; Scholes G. D. Light Absorption and Energy Transfer in the Antenna Complexes of Photosynthetic Organisms. Chem. Rev. 2017, 117 (2), 249–293. 10.1021/acs.chemrev.6b00002. [DOI] [PubMed] [Google Scholar]
  2. McConnell I.; Li G.; Brudvig G. W. Energy Conversion in Natural and Artificial Photosynthesis. Chem. Biol. 2010, 17 (5), 434–447. 10.1016/j.chembiol.2010.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Scholes G. D.; Rumbles G. Excitons in Nanoscale Systems. Nat. Mater. 2006, 5 (9), 683–696. 10.1038/nmat1710. [DOI] [PubMed] [Google Scholar]
  4. Arias D. H.; Stone K. W.; Vlaming S. M.; Walker B. J.; Bawendi M. G.; Silbey R. J.; Bulović V.; Nelson K. A. Thermally-Limited Exciton Delocalization in Superradiant Molecular Aggregates. J. Phys. Chem. B 2013, 117 (16), 4553–4559. 10.1021/jp3086717. [DOI] [PubMed] [Google Scholar]
  5. Chmeliov J.; Trinkunas G.; van Amerongen H.; Valkunas L. Light Harvesting in a Fluctuating Antenna. J. Am. Chem. Soc. 2014, 136 (25), 8963–8972. 10.1021/ja5027858. [DOI] [PubMed] [Google Scholar]
  6. Wittmann B.; Wenzel F. A.; Wiesneth S.; Haedler A. T.; Drechsler M.; Kreger K.; Köhler J.; Meijer E. W.; Schmidt H.-W.; Hildner R. Enhancing Long-Range Energy Transport in Supramolecular Architectures by Tailoring Coherence Properties. J. Am. Chem. Soc. 2020, 142 (18), 8323–8330. 10.1021/jacs.0c01392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Malyshev A. V.; Malyshev V. A.; Domínguez-Adame F. On the Low-Temperature Diffusion of Localized Frenkel Excitons in Linear Molecular Aggregates. J. Phys. Chem. B 2003, 107, 4418–4425. 10.1021/jp0341218. [DOI] [Google Scholar]
  8. Dijkstra A. G.; Jansen T. L. C.; Knoester J. Localization and Coherent Dynamics of Excitons in the Two-Dimensional Optical Spectrum of Molecular J-Aggregates. J. Chem. Phys. 2008, 128, 164511. 10.1063/1.2897753. [DOI] [PubMed] [Google Scholar]
  9. Moix J. M.; Khasin M.; Cao J. Coherent Quantum Transport in Disordered Systems: I. The Influence of Dephasing on the Transport Properties and Absorption Spectra on One-Dimensional Systems. New J. Phys. 2013, 15 (8), 085010. 10.1088/1367-2630/15/8/085010. [DOI] [Google Scholar]
  10. Eisele D. M.; Cone C. W.; Bloemsma E. A.; Vlaming S. M.; van der Kwaak C. G. F.; Silbey R. J.; Bawendi M. G.; Knoester J.; Rabe J. P.; Vanden Bout D. A. Utilizing Redox-Chemistry to Elucidate the Nature of Exciton Transitions in Supramolecular Dye Nanotubes. Nat. Chem. 2012, 4 (8), 655–662. 10.1038/nchem.1380. [DOI] [PubMed] [Google Scholar]
  11. Kriete B.; Bondarenko A. S.; Jumde V. R.; Franken L. E.; Minnaard A. J.; Jansen T. L. C.; Knoester J.; Pshenichnikov M. S. Steering Self-Assembly of Amphiphilic Molecular Nanostructures via Halogen Exchange. J. Phys. Chem. Lett. 2017, 8, 2895–2901. 10.1021/acs.jpclett.7b00967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kondo T.; Chen W. J.; Schlau-Cohen G. S. Single-Molecule Fluorescence Spectroscopy of Photosynthetic Systems. Chem. Rev. 2017, 117 (2), 860–898. 10.1021/acs.chemrev.6b00195. [DOI] [PubMed] [Google Scholar]
  13. Moerner W. E.; Kador L. Optical Detection and Spectroscopy of Single Molecules in a Solid. Phys. Rev. Lett. 1989, 62 (21), 2535. 10.1103/PhysRevLett.62.2535. [DOI] [PubMed] [Google Scholar]
  14. Orrit M.; Bernard J. Single Pentacene Molecules Detected by Fluorescence Excitation in a P-Terphenyl Crystal. Phys. Rev. Lett. 1990, 65 (21), 2716. 10.1103/PhysRevLett.65.2716. [DOI] [PubMed] [Google Scholar]
  15. Bopp M. A.; Sytnik A.; Howard T. D.; Cogdell R. J.; Hochstrasser R. M. The Dynamics of Structural Deformations of Immobilized Single Light-Harvesting Complexes. Proc. Natl. Acad. Sci. U. S. A. 1999, 96 (20), 11271–11276. 10.1073/pnas.96.20.11271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Van Oijen A. M.; Ketelaars M.; Köhler J.; Aartsma T. J.; Schmidt J. Unraveling the Electronic Structure of Individual Photosynthetic Pigment-Protein Complexes. Science (Washington, DC, U. S.) 1999, 285 (5426), 400–402. 10.1126/science.285.5426.400. [DOI] [PubMed] [Google Scholar]
  17. Schlau-Cohen G. S.; Yang H.-Y.; Krüger T. P. J.; Xu P.; Gwizdala M.; van Grondelle R.; Croce R.; Moerner W. E. Single-Molecule Identification of Quenched and Unquenched States of LHCII. J. Phys. Chem. Lett. 2015, 6 (5), 860–867. 10.1021/acs.jpclett.5b00034. [DOI] [PubMed] [Google Scholar]
  18. Trofymchuk K.; Reisch A.; Didier P.; Fras F.; Gilliot P.; Mely Y.; Klymchenko A. S. Giant Light-Harvesting Nanoantenna for Single-Molecule Detection in Ambient Light. Nat. Photonics 2017, 11, 657–663. 10.1038/s41566-017-0001-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hinton D. A.; Ng J. D.; Sun J.; Lee S.; Saikin S. K.; Logsdon J.; White D. S.; Marquard A. N.; Cavell A. C.; Krasecki V. K.; Knapper K. A.; Lupo K. M.; Wasielewski M. R.; Aspuru-Guzik A.; Biteen J. S.; Gopalan P.; Goldsmith R. H. Mapping Forbidden Emission to Structure in Self-Assembled Organic Nanoparticles. J. Am. Chem. Soc. 2018, 140 (46), 15827–15841. 10.1021/jacs.8b09149. [DOI] [PubMed] [Google Scholar]
  20. Lang E.; Sorokin A.; Drechsler M.; Malyukin Y. V.; Köhler J. Optical Spectroscopy on Individual Amphi-PIC J-Aggregates. Nano Lett. 2005, 5 (12), 2635–2640. 10.1021/nl051132z. [DOI] [PubMed] [Google Scholar]
  21. Lin H.; Camacho R.; Tian Y.; Kaiser T. E.; Würthner F.; Scheblykin I. G. Collective Fluorescence Blinking in Linear J-Aggregates Assisted by Long-Distance Exciton Migration. Nano Lett. 2010, 10 (2), 620–626. 10.1021/nl9036559. [DOI] [PubMed] [Google Scholar]
  22. Wan Y.; Stradomska A.; Knoester J.; Huang L. Direct Imaging of Exciton Transport in Tubular Porphyrin Aggregates by Ultrafast Microscopy. J. Am. Chem. Soc. 2017, 139 (21), 7287–7293. 10.1021/jacs.7b01550. [DOI] [PubMed] [Google Scholar]
  23. Aggarwal A. V.; Thiessen A.; Idelson A.; Kalle D.; Würsch D.; Stangl T.; Steiner F.; Jester S. S.; Vogelsang J.; Höger S.; Lupton J. M. Fluctuating Exciton Localization in Giant π-Conjugated Spoked-Wheel Macrocycles. Nat. Chem. 2013, 5 (11), 964–970. 10.1038/nchem.1758. [DOI] [PubMed] [Google Scholar]
  24. Nakamura T.; Sharma D. K.; Hirata S.; Vacha M. Intrachain Aggregates as the Origin of Green Emission in Polyfluorene Studied on Ensemble and Single-Chain Level. J. Phys. Chem. C 2018, 122 (15), 8137–8146. 10.1021/acs.jpcc.8b01767. [DOI] [Google Scholar]
  25. Sperling J.; Nemeth A.; Hauer J.; Abramavicius D.; Mukamel S.; Kauffmann H. F.; Milota F. Excitons and Disorder in Molecular Nanotubes: A 2D Electronic Spectroscopy Study and First Comparison to a Microscopic Model. J. Phys. Chem. A 2010, 114 (32), 8179–8189. 10.1021/jp102173n. [DOI] [PubMed] [Google Scholar]
  26. Dostál J.; Mančal T.; Augulis R.; Vácha F.; Pšenčík J.; Zigmantas D. Two-Dimensional Electronic Spectroscopy Reveals Ultrafast Energy Diffusion in Chlorosomes. J. Am. Chem. Soc. 2012, 134 (28), 11611–11617. 10.1021/ja3025627. [DOI] [PubMed] [Google Scholar]
  27. Mennucci B.; Corni S. Multiscale Modelling of Photoinduced Processes in Composite Systems. Nat. Rev. Chem. 2019, 3 (5), 315–330. 10.1038/s41570-019-0092-4. [DOI] [Google Scholar]
  28. Li X.; Buda F.; de Groot H. J. M.; Sevink G. J. A. Dynamic Disorder Drives Exciton Transfer in Tubular Chlorosomal Assemblies. J. Phys. Chem. B 2020, 124 (20), 4026–4035. 10.1021/acs.jpcb.0c00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Bondarenko A. S.; Patmanidis I.; Alessandri R.; Souza P. C. T.; Jansen T. L. C.; de Vries A. H.; Marrink S.-J.; Knoester J. Multiscale Modeling of Molecular Structure and Optical Properties of Complex Supramolecular Aggregates. Chem. Sci. 2020, 1–11. 10.1039/D0SC03110K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Würthner F.; Kaiser T. E.; Saha-Möller C. R. J-Aggregates: From Serendipitous Discovery to Supramolecular Engineering of Functional Dye Materials. Angew. Chem., Int. Ed. 2011, 50 (15), 3376–3410. 10.1002/anie.201002307. [DOI] [PubMed] [Google Scholar]
  31. Knapp E. W. Lineshapes of Molecular Aggregates, Exchange Narrowing and Intersite Correlation. Chem. Phys. 1984, 85 (1), 73–82. 10.1016/S0301-0104(84)85174-5. [DOI] [Google Scholar]
  32. Bloemsma E. A.; Vlaming S. M.; Malyshev V. A.; Knoester J. Signature of Anomalous Exciton Localization in the Optical Response of Self-Assembled Organic Nanotubes. Phys. Rev. Lett. 2015, 114 (15), 156804. 10.1103/PhysRevLett.114.156804. [DOI] [PubMed] [Google Scholar]
  33. Berlepsch H. v.; Ludwig K.; Kirstein S.; Bottcher C. Mixtures of Achiral Amphiphilic Cyanine Dyes Form Helical Tubular J-Aggregates. Chem. Phys. 2011, 385 (1), 27–34. 10.1016/j.chemphys.2011.04.027. [DOI] [Google Scholar]
  34. Didraga C.; Pugžlys A.; Hania P. R.; von Berlepsch H.; Duppen K.; Knoester J. Structure, Spectroscopy, and Microscopic Model of Tubular Carbocyanine Dye Aggregates. J. Phys. Chem. B 2004, 108 (39), 14976–14985. 10.1021/jp048288s. [DOI] [Google Scholar]
  35. Pandya R.; Chen R.; Cheminal A.; Thomas T. H.; Thampi A.; Tanoh A.; Richter J. M.; Shivanna R.; Deschler F.; Schnedermann C.; Rao A. Observation of Vibronic Coupling Mediated Energy Transfer in Light-Harvesting Nanotubes Stabilized in a Solid-State Matrix. J. Phys. Chem. Lett. 2018, 9, 5604–5611. 10.1021/acs.jpclett.8b02325. [DOI] [PubMed] [Google Scholar]
  36. Pugžlys A.; Augulis R.; Van Loosdrecht P. H. M.; Didraga C.; Malyshev V. A.; Knoester J. Temperature-Dependent Relaxation of Excitons in Tubular Molecular Aggregates: Fluorescence Decay and Stokes Shift. J. Phys. Chem. B 2006, 110 (41), 20268–20276. 10.1021/jp062983d. [DOI] [PubMed] [Google Scholar]
  37. Augulis R.; Pugzlys A.; van Loosdrecht P. H. M. Exciton Dynamics in Molecular Aggregates. Phys. Status Solidi C 2006, 3 (10), 3400–3403. 10.1002/pssc.200672105. [DOI] [Google Scholar]
  38. Caram J. R.; Doria S.; Eisele D. M.; Freyria F. S.; Sinclair T. S.; Rebentrost P.; Lloyd S.; Bawendi M. G. Room-Temperature Micron-Scale Exciton Migration in a Stabilized Emissive Molecular Aggregate. Nano Lett. 2016, 16 (11), 6808–6815. 10.1021/acs.nanolett.6b02529. [DOI] [PubMed] [Google Scholar]
  39. Eisele D. M.; Arias D. H.; Fu X.; Bloemsma E. A.; Steiner C. P.; Jensen R. A.; Rebentrost P.; Eisele H.; Tokmakoff A.; Lloyd S.; Nelson K. A.; Nicastro D.; Knoester J.; Bawendi M. G. Robust Excitons Inhabit Soft Supramolecular Nanotubes. Proc. Natl. Acad. Sci. U. S. A. 2014, 111 (33), E3367–E3375. 10.1073/pnas.1408342111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Clark K. A.; Krueger E. L.; Vanden Bout D. A. Temperature-Dependent Exciton Properties of Two Cylindrical J-Aggregates. J. Phys. Chem. C 2014, 118 (42), 24325–24334. 10.1021/jp507791q. [DOI] [Google Scholar]
  41. Kriete B.; Lüttig J.; Kunsel T.; Malý P.; Jansen T. L. C.; Knoester J.; Brixner T.; Pshenichnikov M. S. Interplay between Structural Hierarchy and Exciton Diffusion in Artificial Light Harvesting. Nat. Commun. 2019, 10 (1), 4615. 10.1038/s41467-019-12345-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Juzeliunas G. Exciton Absorption Spectra of Optically Excited Linear Molecular Aggregates. Z. Phys. D: At., Mol. Clusters 1988, 8 (4), 379–384. 10.1007/BF01437105. [DOI] [Google Scholar]
  43. Fidder H.; Knoester J.; Wiersma D. A. Observation of the One-Exciton to Two-Exciton Transition in a J-Aggregate. J. Chem. Phys. 1993, 98 (8), 6564–6566. 10.1063/1.464797. [DOI] [Google Scholar]
  44. Okumura K.; Tokmakoff A.; Tanimura Y. Two-Dimensional Line-Shape Analysis of Photon-Echo Signal. Chem. Phys. Lett. 1999, 314 (5–6), 488–495. 10.1016/S0009-2614(99)01173-2. [DOI] [Google Scholar]
  45. Lazonder K.; Pshenichnikov M. S.; Wiersma D. A. Easy Interpretation of Optical Two-Dimensional Correlation Spectra. Opt. Lett. 2006, 31 (22), 3354. 10.1364/OL.31.003354. [DOI] [PubMed] [Google Scholar]
  46. Mukamel S.Principles of Nonlinear Optical Spectroscopy; Oxford University Press, Oxford, 1995. [Google Scholar]
  47. Didraga C.; Klugkist J. A.; Knoester J. Optical Properties of Helical Cylindrical Molecular Aggregates: The Homogeneous Limit. J. Phys. Chem. B 2002, 106, 11474–11486. 10.1021/jp026217s. [DOI] [Google Scholar]
  48. Vlaming S. M.; Bloemsma E. A.; Nietiadi M. L.; Knoester J. Disorder-Induced Exciton Localization and Violation of Optical Selection Rules in Supramolecular Nanotubes. J. Chem. Phys. 2011, 134 (11), 114507. 10.1063/1.3528993. [DOI] [PubMed] [Google Scholar]
  49. Bondarenko A. S.; Jansen T. L. C.; Knoester J. Exciton Localization in Tubular Molecular Aggregates: Size Effects and Optical Response. J. Chem. Phys. 2020, 152 (19), 194302. 10.1063/5.0008688. [DOI] [PubMed] [Google Scholar]
  50. Since the structure considered here actually has two molecules per unit cell in each wall, the proper eigenstates are slightly more complicated. It is to be expected, however, that the fluctuations in Sn(t) still yield good insight into the typical fluctuations in the excitonic energies caused by fluctuations in the interactions.
  51. Tully J. C. Molecular Dynamics with Electronic Transitions. J. Chem. Phys. 1990, 93 (2), 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
  52. Jansen T.; la C.; Knoester J. Nonadiabatic Effects in the Two-Dimensional Infrared Spectra of Peptides: Application to Alanine Dipeptide. J. Phys. Chem. B 2006, 110 (45), 22910–22916. 10.1021/jp064795t. [DOI] [PubMed] [Google Scholar]
  53. Malyshev V. A. Localization Length of a 1-D Exciton and Temperature Dependence of the Radiative Lifetime in Frozen Dye Solutions with J Aggregates. Opt. Spectrosc. 1991, 71 (6), 505–506. [Google Scholar]
  54. Spano F. C.; Mukamel S. Superradiance in Molecular Aggregates. J. Chem. Phys. 1989, 91 (2), 683–700. 10.1063/1.457174. [DOI] [Google Scholar]
  55. Kriete B.; Feenstra C. J.; Pshenichnikov M. S. Microfluidic Out-of-Equilibrium Control of Molecular Nanotubes. Phys. Chem. Chem. Phys. 2020, 22 (18), 10179–10188. 10.1039/D0CP01734E. [DOI] [PubMed] [Google Scholar]
  56. Pugžlys A.; Hania P. R.; Augulis R.; Duppen K.; Van Loosdrecht P. H. M. Cylindrical Aggregates of 5,5′,6,6′-Tetrachlorobenzimida-Carbocyanine Amphiphilic Derivatives: Structure-Related Optical Properties and Exciton Dynamics. Int. J. Photoenergy 2006, 2006, 029623. 10.1155/IJP/2006/29623. [DOI] [Google Scholar]
  57. Tiwari V.; Matutes Y. A.; Gardiner A. T.; Jansen T. L. C.; Cogdell R. J.; Ogilvie J. P. Spatially-Resolved Fluorescence-Detected Two-Dimensional Electronic Spectroscopy Probes Varying Excitonic Structure in Photosynthetic Bacteria. Nat. Commun. 2018, 9 (1), 4219. 10.1038/s41467-018-06619-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Goetz S.; Li D.; Kolb V.; Pflaum J.; Brixner T. Coherent Two-Dimensional Fluorescence Micro-Spectroscopy. Opt. Express 2018, 26 (4), 3915–3925. 10.1364/OE.26.003915. [DOI] [PubMed] [Google Scholar]
  59. Jones A. C.; Kearns N. M.; Ho J.-J.; Flach J. T.; Zanni M. T. Impact of Non-Equilibrium Molecular Packings on Singlet Fission in Microcrystals Observed Using 2D White-Light Microscopy. Nat. Chem. 2020, 12 (1), 40–47. 10.1038/s41557-019-0368-9. [DOI] [PubMed] [Google Scholar]
  60. Penwell S. B.; Ginsberg L. D. S.; Noriega R.; Ginsberg N. S. Resolving Ultrafast Exciton Migration in Organic Solids at the Nanoscale. Nat. Mater. 2017, 16 (11), 1136–1141. 10.1038/nmat4975. [DOI] [PubMed] [Google Scholar]
  61. Eisele D. M.; Knoester J.; Kirstein S.; Rabe J. P.; Vanden Bout D. A. Uniform Exciton Fluorescence from Individual Molecular Nanotubes Immobilized on Solid Substrates. Nat. Nanotechnol. 2009, 4 (10), 658–663. 10.1038/nnano.2009.227. [DOI] [PubMed] [Google Scholar]
  62. Myers J. A.; Lewis K. L.; Tekavec P. F.; Ogilvie J. P. Two-Color Two-Dimensional Fourier Transform Electronic Spectroscopy with a Pulse-Shaper. Opt. Express 2008, 16 (22), 17420–17428. 10.1364/OE.16.017420. [DOI] [PubMed] [Google Scholar]
  63. Clark K. A.; Cone C. W.; Vanden Bout D. A. Quantifying the Polarization of Exciton Transitions in Double-Walled Nanotubular J-Aggregates. J. Phys. Chem. C 2013, 117 (50), 26473–26481. 10.1021/jp409573h. [DOI] [Google Scholar]
  64. Bizimana L. A.; Brazard J.; Carbery W. P.; Gellen T.; Turner D. B. Resolving Molecular Vibronic Structure Using High-Sensitivity Two-Dimensional Electronic Spectroscopy. J. Chem. Phys. 2015, 143 (16), 164203. 10.1063/1.4934717. [DOI] [PubMed] [Google Scholar]
  65. Patmanidis I.; de Vries A. H.; Wassenaar T. A.; Wang W.; Portale G.; Marrink S.-J. Structural Characterization of Supramolecular Hollow Nanotubes with Atomistic Simulations and SAXS. Phys. Chem. Chem. Phys. 2020, 22, 21083. 10.1039/D0CP03282D. [DOI] [PubMed] [Google Scholar]
  66. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindah E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  67. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25 (9), 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  68. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79 (2), 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  69. Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126 (1), 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  70. Berendsen H. J. C.; Postma J. P. M.; Van Gunsteren W. F.; Dinola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81 (8), 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  71. D’Avino G.; Muccioli L.; Zannoni C.; Beljonne D.; Soos Z. G. Electronic Polarization in Organic Crystals: A Comparative Study of Induced Dipoles and Intramolecular Charge Redistribution Schemes. J. Chem. Theory Comput. 2014, 10 (11), 4959–4971. 10.1021/ct500618w. [DOI] [PubMed] [Google Scholar]
  72. Alessandri R.; Sami S.; Barnoud J.; de Vries A. H.; Marrink S. J.; Havenith R. W. A. Resolving Donor-Acceptor Interfaces and Charge Carrier Energy Levels of Organic Semiconductors with Polar Side Chains. Adv. Funct. Mater. 2020, 2004799. 10.1002/adfm.202004799. [DOI] [Google Scholar]
  73. Swart M.; van Duijnen P. T. DRF90: A Polarizable Force Field. Mol. Simul. 2006, 32 (6), 471–484. 10.1080/08927020600631270. [DOI] [Google Scholar]
  74. Cringus D.; Jansen T. L. C.; Pshenichnikov M. S.; Wiersma D. A. Ultrafast Anisotropy Dynamics of Water Molecules Dissolved in Acetonitrile. J. Chem. Phys. 2007, 127 (8), 084507. 10.1063/1.2771178. [DOI] [PubMed] [Google Scholar]
  75. Czikkely V.; Försterling H. D.; Kuhn H. Light Absorption and Structure of Aggregates of Dye Molecules. Chem. Phys. Lett. 1970, 6 (1), 11–14. 10.1016/0009-2614(70)80062-8. [DOI] [Google Scholar]
  76. Thouless D. J. Electrons in Disordered Systems and the Theory of Localization. Phys. Rep. 1974, 13 (3), 93–142. 10.1016/0370-1573(74)90029-5. [DOI] [Google Scholar]
  77. Didraga C.; Knoester J. Optical Spectra and Localization of Excitons in Inhomogeneous Helical Cylindrical Aggregates. J. Chem. Phys. 2004, 121 (21), 10687–10698. 10.1063/1.1807825. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja0c07392_si_001.pdf (2.9MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES