Language-Related Longitudinal Predictors of Arithmetic Word Problem Solving: A Structural Equation Modeling Approach

Abstract

We investigated the longitudinal relations between cognitive skills, specifically language-related skills, and word-problem solving in 340 children (6.10 to 9.02 years). We used structural equation modeling to examine whether word-problem solving, computation skill, working memory, nonverbal reasoning, oral language, and word reading fluency measured at second grade were associated with performance on measures of word-problem solving in fourth grade. Results indicated that prior word-problem solving, computation skill, nonverbal reasoning, and oral language were significantly associated with children’s later word-problem solving. Multi-group modeling suggested that these relations were not significantly different for boys versus girls. Implications of these findings are discussed.

Longitudinal Associations between Language-Related Skills and Arithmetic Word-Problem Solving: A Structural Equation Modeling Approach

By the end of fourth grade, only 40% of students in the United States are scoring at or above proficiency in mathematics (NCES, 2017). This is problematic because early mathematics skills are associated with academic and life outcomes (Claessens, Duncan, & Engel, 2009; Magnuson, Duncan, Lee, & Metzger, 2016; Rivera-Batiz, 1992). Given this, we investigated the longitudinal relations between early cognitive skills and later arithmetic word-problem solving. We focused on word-problem solving because the ability to solve word problems is significantly associated with later life outcomes (Murnane, Willett, Braatz, & Duhaldeborde, 2009) and are emphasized within key educational initiatives (e.g., Common Core State Standards, the National Mathematics Advisory Panel, and statewide high-stakes assessments; Cohen, Gregg, Deng, 2005; Common Core State Standards Initiative, 2010; National Mathematics Advisory Panel, 2008).

Word problems are “verbal descriptions of problem situations wherein one or more questions … can be [answered] … by application of mathematical operations to numerical data available in the problem statement” (Verschaffel, Greer, & de Corte 2000, p. ix). For example, “John has nine balloons. He gave away three balloons to his friend, Mark. How many balloons does John have now?” In this instance, the problem solver needs to identify relevant linguistic and numerical information (nine and three) and the appropriate operands indicated in the narrative (gave away) to solve the problem (six balloons). Thus, it is not surprising that word-problem solving requires the consolidation of a variety of cognitive skills, including non-mathematical processes such as working memory, reasoning ability, and oral language (Andersson, 2007; Fuchs et al., 2006, 2008a; Jordan, Levine, & Huttenlocher, 1995).

The complexity of word problems, and subsequent recruitment of multiple cognitive processes, may explain why word problems tend to be more difficult for children to solve than de-contextualized numerical problems (Cummins, Kintsch, Reusser, & Weimer, 1988; Daroczy, Wolska, Meurers, & Nuerk, 2015). That is, solving the mathematical problem 9 – 3 = ___ (the numerical equivalent of the above word problem) is easier than a word problem including the same numerical information but presented verbally. This increased difficulty may explain why some children who struggle to solve word problems perform adequately on other measures of mathematic skill (e.g., Swanson, Jerman, & Zheng, 2008). Further, although arithmetic skills are foundational to word-problem solving, a unique set of cognitive skills is associated with word-problem solving separate from arithmetic or calculations (Fuchs et al., 2006, 2010b; Swanson & Beebe-Frankenberger, 2004).

Because word-problem solving ability appears to be a discrete skill (e.g., Fuchs et al., 2006) strongly associated with mathematical competence (Cohen et al., 2005) and life outcomes (Murnane et al., 2009), we aimed to investigate the association between early (second grade) word-problem solving, arithmetic skill, nonverbal reasoning, working memory, oral language, and word reading fluency and later (fourth grade) word-problem solving. Below, we review several relevant theoretical frameworks of word-problem solving. Next, we provide empirical and theoretical rationale for the inclusion of the chosen cognitive variables. Following this, we discuss the importance of examining sex differences in word-problem solving. Finally, we provide a brief description of prior studies focused on sex differences in word-problem solving and a rationale for the present study.

Theoretical Frameworks of Word-Problem Solving

Given the multifaceted nature of the word-problem solving process, several theoretical frameworks have been proposed. In their comprehensive report, the Mathematics Learning Study Committee and National Research Council (MLSC/NRC, 2001) outlined five foundational skills, referred to a strands, thought to be critical to the development of mathematics proficiency. These include mathematical knowledge (conceptual understanding) as well as the ability to carry out mathematical operations (procedural fluency), apply appropriate problem-solving strategies (strategic competence), and think critically and logically (adaptive reasoning); individuals additionally need to believe that mathematics is a useful skill (productive disposition; see also Mayer, 2013).

Although this framework describes the development of mathematical proficiency in broad terms, each of these skills are important for word-problem solving competency more specifically. For instance, word problems often include descriptions of real-world situations (Staub & Reusser, 1995; productive disposition) and require an individual to understand the nature of the word problem (mathematical knowledge; Seh Bae, Chiang, & Hickson, 2015), apply necessary computational skills (procedural fluency; Muth, 1984) and strategies (strategic competence; de Corte & Verschaffel, 1987), and make logical inferences (adaptive reasoning; Tajika, Nakatsu, Nozaku, Neumann, & Maruno, 2007) in order to successfully derive a solution. Several of these strands are also embedded within word-problem-specific theoretical frameworks, which we describe in greater detail below.

Kintsch and Greeno’s (1985) dual representation model asserts that, given the format of word problems, an individual’s text comprehension skill impacts the ability to solve word problems. Further, individuals’ experience(s) with similar texts and information allows them to build a situation model that subsequently facilitates comprehension of the text (see van Dijk & Kintsch, 1983) and likely aids word-problem solving. Therefore, linguistic knowledge is identified as a key component of comprehending the text and subsequently solving the word problem; exposure to the text provides an opportunity for the individual to create a mental representation of the information (situation model) and merge this with prior knowledge to identify a problem model (Kintsch & Greeno, 1985).

Thus, successful word-problem solvers integrate their knowledge of mathematical problem solving (e.g., rules related to sums and minuends and conceptual understanding; MLSC/NRC, 2001) and corresponding verbal information contained in the problem statement (e.g., activating verbal knowledge for words/phases such as have altogether and less than and their corresponding operands and procedural fluency; MLSC/NRC, 2001; Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009; Thevenot, Devidal, Barrouillet, & Fayol, 2007). As such, word-problem solving additionally relies on cognitive processes beyond those required for text comprehension (e.g., word-problem-specific language comprehension; Fuchs, Fuchs, Compton, Hamlett, & Wang, 2015).

Hegarty and colleagues (1995) also proposed a more linguistic-based model. In their model, reading the word problem prompts an individual to create or update their semantic situation model via a direct translation approach (i.e., identify and integrate some semantic and corresponding mathematical information) or the problem model approach (i.e., create or update the problem or situation model to adequately fit with the word problem as opposed to relying on a subset of features). With either approach, the individual then creates a plan to solve the word problem. Individuals who take the direct route are more likely to encounter word-problem solving difficulties because they have an incomplete situation model due to their reliance on a subset of the words/numbers. Individuals who take the problem model approach experience greater success because they have a more comprehensive understanding of the problem (Hegarty et al., 1995). These frameworks are supported by studies showing that word problems with simpler language are easier to comprehend and solve than those with more complex language (e.g., Cummins et al., 1988) and that word-problem features, such as words or operands, affect word-problem solution accuracy (Daroczy et al., 2015; Koedinger & Nation, 2004).

Cognitive Skills Associated with Word-Problem Solving

Previous research has identified several relatively robust cognitive skills that are associated with word-problem solving, including arithmetic competence, nonverbal reasoning, working memory, oral language, and word reading fluency. Based on the previously discussed theoretical frameworks of word-problem solving, arithmetic competence and nonverbal reasoning would facilitate the development of situation and problem models (e.g., Kintsch & Greeno, 1985; Hegarty et al., 1995) and the application of logical inference-making and strategies (MLSC/NRC, 2001). Working memory would facilitate the activation of situation models, text comprehension, and formation of the problem model, while enabling individuals to hold and manipulate representations in memory. Oral language would facilitate an understanding of verbal information in the word problem and the creation a situation and problem model. We next discuss empirical evidence for the relations between word-problem solving and each of these cognitive skills.

Arithmetic skill.

Arithmetic skill, defined as the ability to solve single-digit calculation problems (Fuchs et al., 2006), is distinct from word-problem solving skill (Fuchs et al., 2008a; Seethaler, Fuchs, Fuchs, & Compton, 2012). However, arithmetic is robustly associated with word-problem solving (Fuchs et al., 2008a; Kail & Hall, 1999; Wang et al., 2016). For example, children with mathematical disabilities (MD) tend to perform worse on word-problem solving than children without MD (e.g., Fuchs & Fuchs, 2002). These relations likely exist because word problems require the application of mathematical knowledge (Verschaffel et al., 2000) while also tapping pre-algebraic knowledge in some instances (Fuchs et al., 2010b).

Nonverbal reasoning.

Nonverbal reasoning, the ability to engage in visual problem solving (Kroger et al., 2002), is associated with word-problem solving both concurrently and longitudinally (Fuchs et al., 2005, 2006; Tolar et al., 2012). Reasoning skills are often uniquely related to word-problem solving over and above other well-established cognitive skills (e.g., number line estimation, number sets, language, attention, working memory, and processing speed; Fuchs et al., 2010a), likely because mathematical reasoning underlies the development of the problem model (Quilici & Mayer, 1996). Reasoning may also affect an individual’s application of strategies and the understanding of whether a correct solution is obtained (e.g., Xin et al., 2005).

Working memory.

Working memory, or the ability to maintain and process information (Baddeley, 1992), is related to word-problem solving outcomes (e.g., Andersson, 2007; Cummins et al., 1988; Passolunghi & Siegel, 2001; Zheng, Swanson, & Marcoulides, 2011). For instance, children with problem solving difficulties often have associated weaknesses in working memory (e.g., Andersson & Lyxell, 2007; Passolunghi & Mammarella, 2010; Swanson & Beebe-Frankenberger, 2004). Working memory also often explains variance in word-problem solving over and above a variety of other cognitive skills (e.g., phonological processing, IQ, reading comprehension, and calculation skill; Swanson, 2004).

Oral language.

Oral language is a broad term used to describe various language-based skills, including vocabulary knowledge, listening comprehension, and syntactic knowledge among others. Numerous studies demonstrate that oral language plays a strong role in both text and language comprehension (e.g., Hoover & Gough, 1990; Kendeou, Van den Broek, White, & Lynch, 2009; Marchman & Fernald, 2008; Roth, Speece, & Cooper, 2002) and that these same variables are related to word-problem solving (Fuchs et al., 2006, 2015; Fuchs, Gilbert, Fuchs, Seethaler, & Martin, 2018; Kintsch & Greeno, 1985; Pina, Fuentes, Castillo, & Diamantopoulou, 2014; Wang et al., 2016). In fact, children with word-problem solving difficulties tend to exhibit corresponding language deficits (e.g., Fuchs et al., 2008a). This association may occur because language deficits are often associated with general arithmetic difficulties (Donlan, Cowan, Newton, Llyod, 2007) and because oral language potentially facilitates development of mathematical skill (Fletcher, Lyon, Fuchs, & Barnes, 2007; Purpura, Hume, Sims, & Lonigan, 2011).

Word reading fluency.

Word reading fluency, or the ability to read words quickly and accurately, is associated with both text comprehension (Klauda & Guthrie, 2008; Petscher & Kim, 2011) and word-problem solving (Fuchs et al., 2006). Children with poor reading fluency often have word-problem solving deficits. For instance, Fuchs and Fuchs (2002) examined word-problem solving performance for children categorized as having MD (scoring below 1.5 standard deviations [SD] on computational fluency), combined MD and reading disability (scoring below 1.5 SD on computational fluency and reading fluency), and as being typically developing. Children with MD and reading disability performed lower on complex word problems and real-world problem solving relative to typically developing children and children with MD only.

Sex Differences

Although research suggests that the prevalence of MD is similar across males and females (Lewis & Fisher, 2016), empirical evidence indicates that males tend to outperform females on arithmetic and word-problem solving (e.g., Hedges & Nowell, 1995; Jogi & Kikas, 2016; Low & Over, 1993). However, findings on sex differences in math are often mixed (see for example, Vilenius-Tuohimaa et al., 2008). This may occur because word-problem solving is potentially affected by a variety of other factors, such as language competencies that tend to favor females (e.g., Cole, 1997; Loveless, 2015; Voyer & Voyer, 2014), psychological characteristics, such as math anxiety and/or strategy use (e.g., Davis & Carr, 2002; Devine, Fawcett, Szucs, & Dowker, 2012), and methodological features of math assessments (e.g., Berberoglu, 1995). Therefore, it remains important to investigate whether relations between cognitive correlates of word-problem solving skills differ for boys versus girls.

The Present Study

The aim of present study was to extend previous findings in several important ways. First, although multiple studies have examined sex differences in mathematical performance (e.g., Carr & Jessup, 1997; Geary et al., 2000; Marshall & Smith, 1987; Royer, Tronsky, Chang, Jackson, & Marchant, 1999) and word-problem solving (Chipman, Marshall, Scott, 1991; Quinn & Spencer, 2001; Walsh, Hickey, & Duffy, 1999), few have examined sex differences in longitudinal word-problem-solving outcomes (see Jogi & Kikas, 2016, Kyttala & Bjorn, 2014, and Bjorn, Aunola, & Nurmi, 2016). Third, despite prior investigations of associations between cognitive skills and word-problem solving, several relied on single-time point data (e.g., Kyttala & Bjorn, 2013), included sex as the independent variable (e.g., Jogi & Kikas, 2016; Vilenius-Tuohimaa et al., 2008), or did not examine sex differences at all (e.g., Fuchs et al., 2015; Wang et al., 2016).

Jogi and Kikas (2016) examined word-problem solving outcomes in 864 children from first to third grade who were assessed on calculation skill, word-problem solving, nonverbal IQ, language, executive function, and task persistence assessed in first and third grades. All variables, including sex, explained unique variance in third-grade word-problem solving. Bjorn and colleagues (2016) examined longitudinal relations among fluency, reading comprehension, calculations, and word-problem solving in a sample of 224 fourth graders, who were also assessed in seventh and ninth grade. Fourth-grade reading comprehension was associated with word-problem solving in in seventh and ninth grades for boys and girls, respectively. Similarly, in a sample of 99 eighth graders, Kyttala and Bjorn (2014) found that reading comprehension was significantly associated with word-problem solving for boys while technical reading was related to word-problem solving for girls. None of these previous studies, however, examined the contributions of prior word-problem solving, reasoning skills, working memory, oral language, and word reading fluency within a single model while considering sex differences. Thus, previous findings are capable of identifying whether boys and girls may perform differently on a specific outcome measure but reveal little about how individual differences in the development of word-problem solving occur and potential sex differences in relations between other variables of interest. Further, in the few instances when researchers have examined boys and girls separately, those studies did not include measures of language or working memory in their models (e.g., Bjorn et al., 2016; Kyttala & Bjorn, 2014).

We therefore extended previous work by bringing together the methods of (a) studies that did not examine sex differences but included a rich cognitive battery (e.g., Fuchs et al., 2015; Wang et al., 2016) with (b) studies that examined sex differences but with a more limited set of assessments. We also sought to extend previous findings on the relations between cognitive processes and word-problem solving (Andersson, 2007; Fuchs et al., 2008a; Nordtvedt, 2008; Swanson & Beebe-Frankenberger, 2004; Tolar et al., 2012) by examining associative relations across second to fourth grade, when children are building foundational skills related to word-problem solving competency (Wilson, 2009) and by considering how findings support theoretical models of word-problem processing.

We were also interested in the whether our findings would support text comprehension models of word-problem solving (e.g., dual representation model; Kintsch & Greeno, 1985) by examining the extent to which foundation reading comprehension-related skills (word reading and oral language; Hoover & Gough, 1990) were also related to word-problem solving longitudinally. Further, we aimed to extend the findings of three studies by Fuchs and colleagues who across studies, investigated the longitudinal cognitive correlates of text comprehension versus word-problem solving (Fuchs et al., 2015, 2018) and pre-algebraic knowledge versus word-problem solving (Fuchs et al., 2016). The present study builds on these previous studies by examining similar variables over a wider developmental span (Fuchs et al., 2015, 2018) and assessing whether the pattern of effects is similar for boys and girls within a latent variable framework (Fuchs et al., 2016). Thus, findings of the present study add in important ways to the present literature and to theoretical frameworks of word-problem solving.

Materials and Methods

Participants were four cohorts of second graders, ages 6.10 to 9.02 years (M = 7.63, SD = 0.43) near the start of the study, who were part of a larger longitudinal intervention study (Fuchs et al., 2014) conducted in the Southeastern United States. Study approval was granted by the Vanderbilt University Institutional Review Board prior to conducting the study (IRB # 130999). In the present analysis, we only included children who did not receive intervention as part of the parent study, because intervention was designed to alter the natural course of development. The sample included 341 children from 39 classrooms, with complete data on the second and fourth-grade variables used in the analysis. Participants were identified as 41.3% African American, 25.8% white non-Hispanic, 25.8% white Hispanic, 2.9% Kurdish, and 4.2% other (9.1% did not specify). The sample was 56.5% female (9.1% did not specify).

Measures

Start-of-second-grade variables.

The variables in our models were word-problem solving, computation skill, nonverbal reasoning, working memory, oral language, and word reading fluency (see Table 1).

Table 1.

Measures in the Current Study

Measure	Skill(s) Assessed	Assessment Features
Story Problemsa	Word-problem solving	Solve up to 14 orally-presented word problems (change, combine, compare, equalize) with sums less than 10
Addition 0–12a	Arithmetic fluency	Solve up to 25 single-digit addition problems with sums ranging from 6–12
Addition 0–18a	Arithmetic fluency	Solve up to 25 single-digit addition problems with sums ranging from 5–18
DD Additiona	Computation fluency	Solve up to 20 double-digit addition problems with and without regrouping
Subtraction 0–12a	Arithmetic fluency	Solve up to 25 single-digit subtraction problems with minuends ranging from 6–12
Subtraction 0–18a	Computation fluency	Solve up to 25 single-digit subtraction problems with minuends ranging from 5–18
DD Subtractiona	Calculation fluency	Solve up to 20 double-digit subtraction problems with and without regrouping
WASI MR	Nonverbal reasoning	Complete a missing portion of a matrix; multiple-choice
WJ-III CF	Rule/concept understanding	Identify rules for concepts based on previously presented exemplars
WMTB-C LR	Working memory	Recall numerals of counted sets for up to 6 visually-presented cards across multiple spans
WMTB-C CR	Working memory	Recall the last word for up to 6 orally-presented sentences across multiple spans
WASI Vocabulary	Vocabulary	Provide definitions for up to 42 presented pictures/orally-presented words
WDRB LC	Language comprehension	Provide a missing word for up to 38 orally-presented sentence/passages
WIF-Ba	Word reading fluency	Read a list of words
WIF-Na	Word reading fluency	Read a list of words
ITBS9b	Word-problem solving	Solve up to 24 orally-presented word problems based on information presented in graphs/tables; multiple-choice
ITBS10b	Word-problem solving	Solve up to 24 orally-presented word problems based on information presented in graphs/tables; multiple-choice
VSPb	Word-problem solving	Solve up to 18 orally-presented word problems (total, difference, change) both with and without irrelevant information and with and without graphs

Note.

^aTimed;

^bOutcome;

DD = Double digit; WASI = Wechsler Abbreviated Scale of Intelligence; MR = Matrix Reasoning; WJ=III = Woodcock-Johnson, Third Edition; CF = Concept Formation; WMTB-C = Working Memory Test Battery for Children; LR = Listening recall; CR = Counting recall; WDRB = Woodcock Diagnostic Reading Battery; LC = Listening comprehension; WIF-B/N = Word identification fluency form B/N; VSP = Vanderbilt Story Problems; ITBS9/10 = Iowa Test of Basic Skills level 9/10.

With Story Problems (Jordan & Hanich, 2000), students solve word problems with sums and minuends less than 10. This assessment contains four word-problem types (change, combine, compare, equalize) with a total of 14 items. Items are read aloud, while students see the text; they have 30 sec to respond. Answers are scored for correct numerical answers. On the full sample, α was .83 to .92.

Four subtests from Math Fact Fluency (Fuchs, Hamlett, & Powell, 2003) and two subtests from the Double-Digit Addition and Subtraction Tests (Fuchs et al., 2003) were used to assess addition and subtraction fluency in second grade. With Math Fact Fluency, students solve single-digit addition and subtraction problems with sums and minuends from 6 to 12 for the first group of items and 5 to 18 for the second group of items (up to 25 items per subtest). Students have 1 min for each subtest. Test-retest reliability is .87 (Fuchs et al., 2016). With Double-Digit Addition and Subtraction, students solve double-digit addition and subtraction problems (up to 20 items in each subtest) within 5 min per subtest. As per Fuchs et al. (2013), α = .94 and .92 for Double-Digit Addition and Subtraction, respectively.

With Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999) - Matrix Reasoning, students are presented with a matrix that has a portion missing and are given five options to complete the matrix. Answers are generated verbally or by pointing to an option. Reliability for this subtest is .94 (Wechsler, 1999).

With Woodcock-Johnson Tests of Achievement-Concept Formation (3^rd ed. WJ-III; Woodcock, McGrew, & Mather, 2001), students identify rules for concepts based on previously presented exemplars. Reliability for this assessment is .94 (Shrank, McGrew, & Woodcock, 2014).

With Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) - Counting Recall and Listening Recall, students recall a series of items. Each subtest has six items at span levels 1–6 to 1–9. Passing four items at a level moves the child to the next, increasing the number of items to be remembered by one. Failing three items within a level terminates the subtest. The score is trials correct. For Counting Recall (working memory-numerals), children count 4, 5, 6, or 7 dots on a series of cards; then they recall the numerals of the counted sets. At second grade, subtest stability is .83–.85. For Listening Recall (working memory-words), children determine if each sentence in a series is true; then they recall the last word of each sentence.

With WASI (Wechsler, 1999) - Vocabulary, the tester presents up to 42 pictures or oral words; students provide definitions. Answers are awarded a score of 0, 1 or 2 depending on the definition’s quality. Testing stops after five consecutive errors. Split-half reliability is .86 – .87 (Zhu, 1999).

With Woodcock Diagnostic Reading Battery - Listening Comprehension (WDRB; Woodcock, 1997), the tester presents up to 38 sentences or passages of varying difficulty (e.g., verbal analogies, discerning implications); for each, students restore a missing word. Testing stops after six consecutive errors. Reliability is .80 (Woodcock, 1997).

With Word Identification Fluency (WIF; Fuchs, Fuchs, & Compton, 2004), students have 1 min to read a list of words. When students hesitate more than three sec, the tester moves them to the next word. The score is the average words read across two lists. Alternate-form reliability is .88 to .97 (Fuchs et al., 2004).

Fourth-grade outcome measures.

Word-problem solving was measured using Vanderbilt Story Problems (VSP; Fuchs & Seethaller, 2008) and two versions (Levels 9 and 10) of the Iowa Test of Basic Skills (ITBS; Hoover, Hieronymous, Dunbar, & Frisbie, 1993; see Table 1). Items are read aloud; students see the text. VSP measures the ability to solve combine, compare, and change word problems of varying degrees of complexity (with and without irrelevant information; with and without graphs) across 18 items. One point is awarded each for math answer (i.e., arithmetic computation) and one point for the label (i.e., word-problem processing). The score is the sum of correct math answers and labels. As per Fuchs et al. (2009), α = .86.

With ITBS, students solve up to 24 multiple-choice word problems of varying difficulty (e.g., single- and multi-step calculation; determining sums and differences). Items are read aloud, while students see the text. Kuder-Richardson 20 internal consistency values range from .84 to .92 for the mathematics portion of the ITBS Levels 9 and 10 (Dunbar et al., 2015).

Procedure

Students were assessed in September-October of second grade. Math Fact Fluency and Double-Digit Addition and Subtraction were administered in whole-class format; WASI, WMTB-C, WJ-III, WDRB, and WIF were administered individually. Students were assessed on the outcomes in April of fourth grade in small-group format. All directions were provided orally. Trained research assistants administered all assessments, and data collection was standardized using written directions. Individual assessments were audio recorded, with 20% scored for procedural accuracy (> 97%).

Analyses

We used confirmatory factor analysis (CFA) modeling and structural equation modeling (SEM) to examine the associations between start-of-second-grade variables and fourth-grade outcomes. We began by specifying CFA models in order to create latent variables for all proposed constructs. Next, we specified several SEMs that included paths from age and start-of-second-grade cognitive skills to fourth-grade word-problem solving outcomes. Across models, we included all variables and allowed the second-grade variables to correlate given the likelihood of anticipated associations across measures. We used a step-by-step model-testing approach to systematically remove paths (i.e., fixed these paths to zero within the model) that were nonsignificant (aside from age, which we retained as a control variable across models). We then compared these nested models using chi-square difference testing in order to identify the best-fitting and most parsimonious model (e.g., Bentler & Mooijaart, 1989; Muliak et al., 1989). Across CFA and SEM models, we began by fitting models to the full sample followed by modeling girls and boys separately. Following this, we ran multi-group models to identify whether relations among skills differed across boys and girls.

Model fit was determined using several common indices, including the chi-square statistic (χ²), comparative fit index (CFI), Tucker-Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR). CFI and TLI values greater than .95, RMSEA values at or below .08, and SRMR values at or below .05 are indicative of good model fit (Hu & Bentler, 1999; MacCallum, Browne, & Sugawara, 1996); CFI and TLI values greater than .90, RMSEA values at or below .10, and SRMR values at or below .08 are indicative of adequate model fit (Hu & Bentler, 1999; Kline, 2015; MacCallum et al., 1996).

Results

Preliminary Analyses

Data were analyzed using SPSS software (Version 25.0; IBM Corp., 2017) and Mplus software (Version 7.11; Muthen & Muthen, 2013). Prior to SEM, we examined the full sample data for univariate and bivariate outliers, skewness and kurtosis, and missingness. Outliers were identified using the median plus or minus two interquartile ranges criterion. Based on this criterion, outliers accounted for 0.78% of the total data. The addition 0–18 subtest of the Math Fact Fluency also exhibited a kurtosis value (2.12) outside the acceptable range of plus or minus 2. Given these patterns in the data, we replaced outlier values with values at the highest or lowest end of the outlier range. We then identified one multivariate outlier using Mahalanobis distance across the 18 measures of interest (p < .001); this participant was removed from all subsequent analyses.

All variables demonstrated adequate variability and had skewness and kurtosis values within the acceptable range of plus or minus 2 (see Table 2 for descriptive statistics for the full sample; see Table A.1 in the appendix for descriptive statistics for boys and girls separately). We used Little’s MCAR test to determine if the data were missing completely at random. Based on expectation-maximization statistics (means and correlations) for the measures of interest, including age and gender (as a categorical variable), the data were missing completely at random, χ² = 150.506 (145), p = .360 (see Table 3 for correlations for the full sample; see Table B.1 in the appendix for correlations for boys and girls separately). Thus, we used maximum likelihood estimation in all subsequent SEMs. Students whose teachers did not specify the child’s sex (N = 31) were excluded from single- (i.e., boys only and girls only models) and multi-group analyses examining sex differences.

Table 2.

Descriptive Statistics Across the Full Sample

Measure	N	Min.	Max.	Mean	SD	Skew	Kurtosis
Age	338	6.10	9.02	7.630	0.434	0.231	0.522
Sex	309	1	2	1.437	0.497	0.256	−1.947
Story Problemsa	339	0	14	6.501	3.417	0.298	−0.697
Addition 0–12a	338	1	22	8.411	4.644	0.738	0.067
Addition 0–18a	338	0	16	6.056	3.481	0.534	−0.066
DD Additiona	335	0	12	3.260	3.049	0.771	−0.232
Subtraction 0–12a	338	0	12	4.320	2.608	0.665	0.200
Subtraction 0–18a	338	0	11	3.033	2.375	0.925	0.763
DD Subtractiona	335	0	9	2.290	2.659	0.985	−0.042
WASI –MR	340	2	28	11.374	5.771	0.654	−0.546
WJ-III CF	335	1	27	11.272	5.589	0.577	−0.019
WMTB-C LR	338	0	16	7.092	3.766	−0.091	−0.420
WMTB-C CR	338	2	26	14.192	4.436	0.104	−0.146
WASI Vocabulary	340	5	37	21.853	6.535	−0.010	−0.049
WDRB LC	340	5	29	16.500	4.715	−0.401	−0.076
WIF-B	338	0	111	41.794	24.811	0.382	−0.630
WIF-N	337	1	120	55.941	22.377	−0.116	−0.319
ITBS9b	283	1	17	10.131	3.684	−0.193	−0.621
ITBS10b	283	1	11	5.452	2.167	0.334	−0.445
VSPb	283	0	29	11.004	6.627	0.596	0.021

Note. Raw scores reported.

^aTimed;

^bOutcome;

SD = Standard deviation; Min. = Minimum; Max. = Maximum; Age = Age in second grade; DD = Double digit; WASI = Wechsler Abbreviated Scale of Intelligence; MR = Matrix Reasoning; WJ=III = Woodcock-Johnson, Third Edition; CF = Concept Formation; WMTB-C = Working Memory Test Battery for Children; LR = Listening recall; CR = Counting recall; Vocab. = Vocabulary; WDRB = Woodcock Diagnostic Reading Battery; LC = Listening comprehension; WIF-B/N = Word identification fluency form B/N; VSP = Vanderbilt Story Problems; ITBS9/10 = Iowa Test of Basic Skills level 9/10.

Table 3.

Correlations Across the Full Sample

Variables	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
1. Age	--
2. Sex	.110	--
3. Story Problems	.030	.126*	--
4. Addition 0–12	.045	.043	.362**	--
5. Addition 0–18	.018	.029	376**	. .760**	--
6. DD Addition	−.011	−.007	.277**	.527**	.479**	--
7. Subtraction 0–12	.074	.129*	.384**	.561**	.531**	.336**	--
8. Subtraction 0–18	.083	.100	.343**	.520**	.461**	.327**	.750**	--
9. DD Subtraction	−.054	−.058	.239**	.460**	.420**	.718**	.261**	.305**	--
10.WASI MR	−.025	.063	.278**	.178**	.249**	.076	.187**	.160**	.104	--
11. WJ-III CF	−.011	.020	.471**	.239**	.266**	.158**	.232**	.227**	.129*	.326**	--
12. WMTB-C LR	−.004	.012	392**	187**	147**	.138*	147**	.140**	.052	.285**	.309**	--
13. WMTB-C CR	.020	.040	.282**	.271**	.216**	.274**	.214**	.224**	.229**	.272**	.260**	.391**	--
14. WASI Vocabulary	.015	−.018	.368**	.084	.076	−.007	−.027	−.031	−.059	.175**	.377**	.321**	.198**	--
15. WDRB LC	.029	.089	.401**	.140*	.140**	.040	.132*	.131*	−.005	.183**	.393**	.412**	.206**	.603**	--
16. WIF-B	−.052	.005	.425**	.404**	.369**	.316**	.374**	.347**	.218**	.196**	.298**	.351**	.237**	.249**	.330**	--
17. WIF-N	−.063	−.018	.407**	.462**	.426**	.342**	.415**	.395**	.278**	.190**	.271**	.362**	.236**	.224**	.322**	.892**	--
18. ITBS9	−.066	.127*	.610**	.390**	.400**	.284**	.381**	.325**	.195**	.459**	.446**	.391**	.330**	.403**	.414**	.430**	.422**	--
19. ITBS10	−.067	.096	.539**	.364**	.356**	.246**	.316**	.221**	174**	.383**	.386**	.259**	.271**	.352**	.365**	.311**	.322**	.561**	--
20. VSP	−.047	−.002	.541**	.430**	.404**	.236**	.364**	.272**	.158**	.397**	.461**	.402**	.347**	.271**	.344**	.448**	.429**	.602**	.512**

Note. Across correlations, N range 267–340. Age = Age in second grade; DD = Double digit; WASI = Wechsler Abbreviated Scale of Intelligence; MR = Matrix Reasoning; WJ=III = Woodcock-Johnson, Third Edition; CF = Concept Formation; WMTB-C = Working Memory Test Battery for Children; LR = Listening recall; CR = Counting recall; WDRB = Woodcock Diagnostic Reading Battery; LC = Listening comprehension; WIF-B/N = Word identification fluency form B/N; VSP = Vanderbilt Story Problems; ITBS9/10 = Iowa Test of Basic Skills 9/10.

^**p < .01

^*p < .05

CFA and SEM

For the full sample, we initially specified a CFA model that included all proposed constructs as latent variables (see Table C.1 in the appendix for factor loadings for all CFA models). Further, students’ single- and double-digit addition and subtraction were specified as comprising a higher-order latent factor of Computation Skill (see Figure 1). The variance of this factor was fixed to one in order to obtain factor loadings for all three factors. This model provided an excellent fit to the data (Model F1), suggesting that all the observed indicators were adequately represented by their respective latent variables. Initially, we specified the observed indicators of WASI Matrix Reasoning and WJ-III Concept Formation as comprising a single latent factor (Reasoning); however, there was a linear dependency between this factor and the fourth-grade Word-Problem Solving factor for the full sample (r = .969) and for boys (r = 1.015); correlations between these factors were strong for girls as well (r = .928). Therefore, these variables were instead included as observed variables across all models for consistency.

Figure 1.

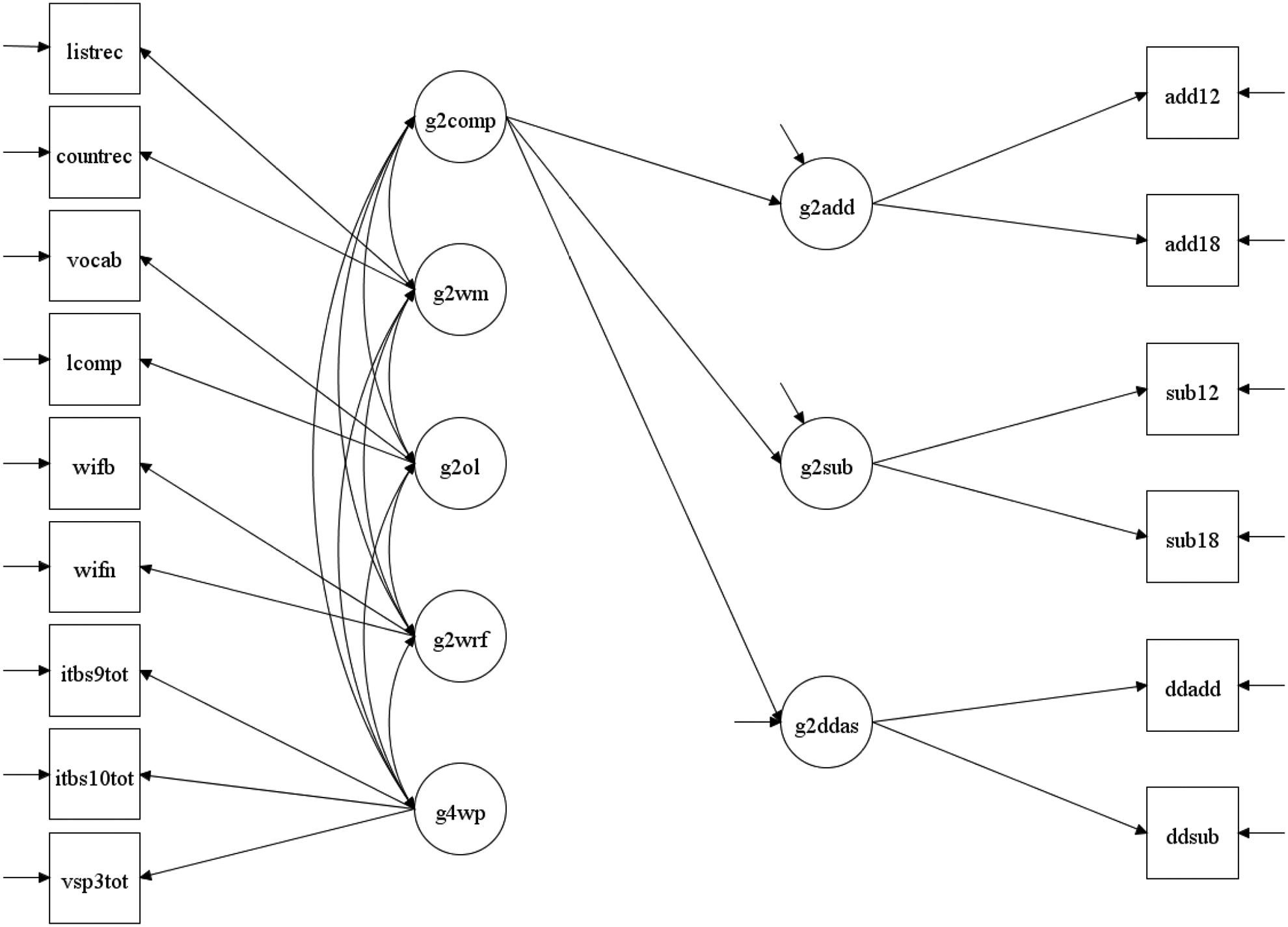
Confirmatory factor analysis model for single- and multi-group modeling. Note. G2/4 = Grade 2/4; comp = Computation skill; wm = Working memory; ol = Oral language; wrf = Word reading fluency; wp = Word-problem solving; add = Addition; sub = Subtraction; ddas = Double-digit addition and subtraction; listrec = Listening recall; countrec = Counting recall; vocab = Vocabulary; lcomp = Listening comprehension; wifb/n = Word identification fluency; itbs9/10tot = Iowa Test of Basic Skills 9/10; vsp3tot = Vanderbilt Story Problems.

In our initial SEM (Model F2), we specified associations between all variables (age, start-of-second-grade word-problem solving, computation skill, matrix reasoning, concept formation, working memory, oral language, and word reading fluency) and fourth-grade word-problem solving (see Figure 2a). This model provided an excellent fit to the data (see Table 4). The weakest parameters included working memory (β = 0.062, p = .518 in Model F2), word reading fluency (β = 0.055, p = .375 in Model F3), and concept formation (β = 0.056, p = .279 in Model F4). Each of these were paths were removed when specifying Models F3, F4, and F5, respectively (see Table D.1 in the appendix for parameter estimates across Models F2, F3, and F4). Chi-square difference testing indicated nonsignificant differences between Models F2 and F3, Models F3 and F4, and Models F5 and F4, suggesting that the most parsimonious model (Model F5) was the preferred model (see Table 4). This final model provided an excellent fit to the data (χ² = 162.537 (120), p = .006, CFI = .985, TLI = .979, RMSEA = .032, 90% confidence interval [0.018, 0.044], p-close = .994; SRMR = .038). In this final model, students’ age (β = −0.107, p < .05) and prior performance on oral language (β = 0.351, p < .001), word-problem solving (β = 0.304, p < .001), computation skill (β = 0.386, p < .001), and matrix reasoning (β = 0.276, p < .001) were all significantly associated with word-problem solving in fourth grade (see Table 5 and Figure 2b). These variables accounted for 85.1% variance in children’s fourth-grade word-problem solving.

Figure 2.

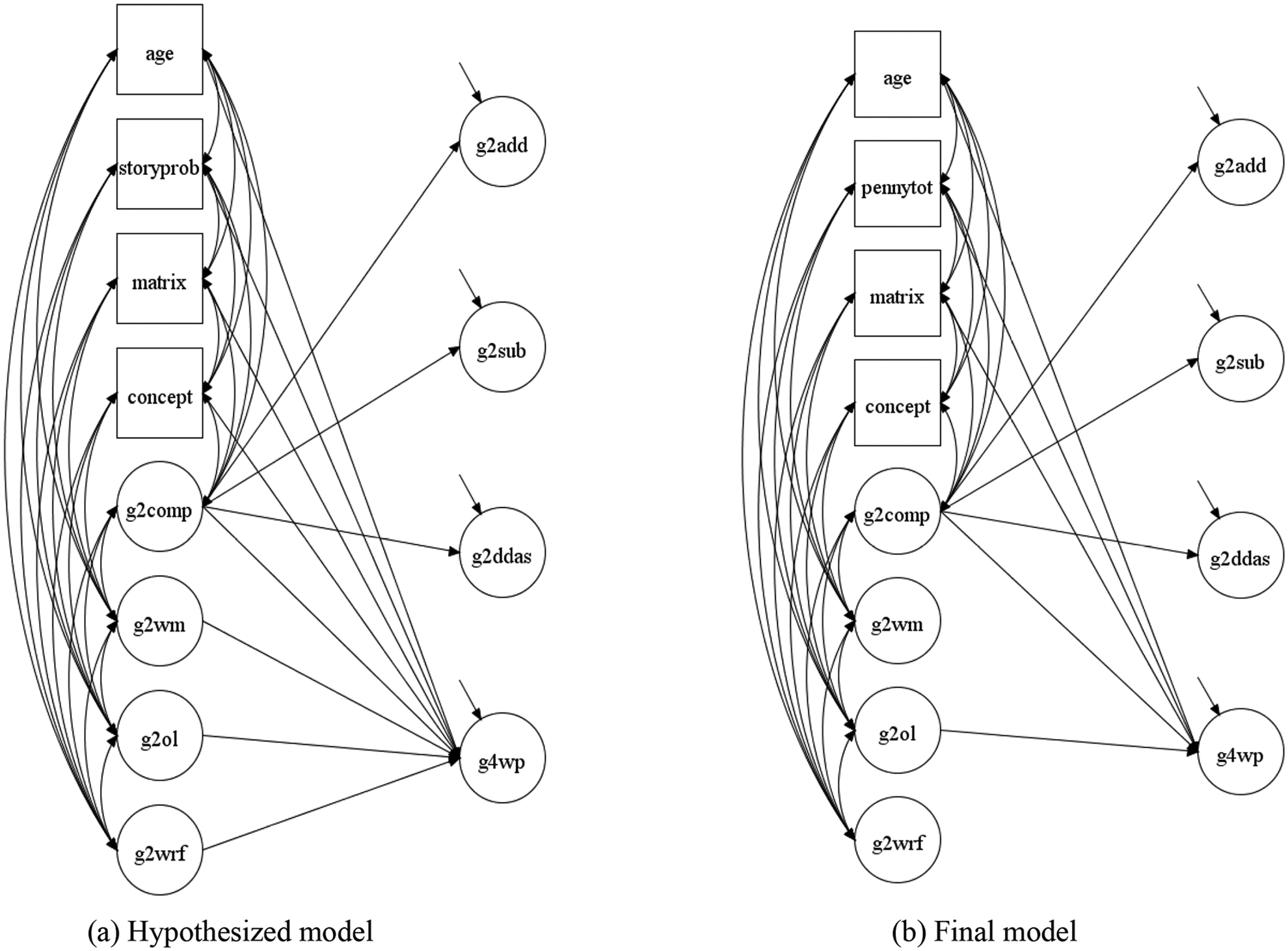
Hypothesized structural equation model (a) and final model (b) for single- and multi-group modeling. Note. Observed indicators are omitted. storyprob = Story Problems; matrix = Matrix Reasoning; concept = Concept formation; G2/4 = Grade 2/4; comp = Computation skill; wm = Working memory; ol = Oral language; wrf = Word reading fluency; wp = Word-problem solving; add = Addition; sub = Subtraction; ddas = Double-digit addition and subtraction.

Table 4.

Model Comparisons for Single- and Multi-Group Analyses

			Model Fit Statistics							Model Comparisons
Analysis	Sample	Model	χ2	df	p	CFI	TLI	RMSEA	SRMR	Comparison	Δχ2	Δdf
Single-Group
	Full Sample
		F1	112.781	77	.005	.986	.981	.037	.042	--	--	--
		F2	160.190	117	.005	.985	.978	.033	.037	--	--	--
		F3	160.610	118	.006	.985	.979	.033	.037	F2 vs. F3	0.420	1
		F4	161.378	119	.006	.985	.979	.032	.037	F3 vs. F4	0.768	1
		F5	162.537	120	.006	.985	.979	.032	.038	F4 vs. F5	1.159	1
	Girls
		G1	115.388	77	.003	.969	.958	.054	.057	--		--
		G2	179.815	117	< .001	.956	.938	.056	.051	--	--	--
		G3	179.869	118	< .001	.957	.939	.055	.051	G2 vs. G3	0.054	1
		G4	180.270	119	< .001	.957	.940	.054	.051	G3 vs. G4	0.401	1
		G5	182.665	120	< .001	.956	.940	.055	.052	G4 vs. G5	2.395	1
	Boys
		B1	101.318	77	.033	.978	.970	.048	.052	--	--	--
		B2	144.455	117	.043	.978	.969	.042	.048	--	--	--
		B3	144.830	118	.047	.979	.970	.041	.048	B2 vs. B3	0.375	1
		B4	145.831	119	.048	.979	.970	.041	.049	B3 vs. B4	1.001	1
		B5	146.870	120	.048	.979	.971	.041	.049	B4 vs. B5	1.039	1
Multi-Group
	Girls/Boys
		MGa1	187.557	138	.003	.979	.968	.048	.046	--	--	--
		MGa2	201.999	146	.002	.976	.966	.050	.051	MG1a vs. MG2a	. 14.442	8
		MGa3	214.984	154	.001	.974	.965	.051	.052	MG2a vs. MG3a	. 12.985	8
		MGb1	246.363	170	< .001	.968	.960	.054	.060	--	--	--
		MGb2	247.726	172	< .001	.968	.961	.053	.061	MGb1 vs. MG2b	1.363	2
		MGb3	258.686	179	< .001	.966	.961	.054	.064	MGb3 vs. MGb2	10.960	7
		MGc1	366.476	265	< .001	.962	.953	.050	.057	--	--	--
		MGc2	374.556	269	< .001	.961	.952	.050	.059	MGc1 vs. MGc2	8.080	4
		MGd1	374.583	270	< .001	.961	.952	.050	.059	--	--	--
		MGd2	375.229	271	< .001	.961	.953	.050	.059	MGd1 vs. MGd2	0.646	1
		MGd3	377.444	272	< .001	.961	.952	.050	.061	MGd2 vs. MdG3	2.215	1
		MGd4	378.550	273	< .001	.961	.952	.050	.061	MGd3 vs. MGd4	1.106	1
		MGd5	378.563	274	< .001	.961	.953	.050	.061	MGd4 vs. MGd5	0.013	1

Note. F = Full sample; G = Girls; B = Boys; Models F/G/B1 are confirmatory factor analysis (CFA) models; F/B/G2–5 are structural equation models (SEM); MG = Multigroup; a = Testing first-order CFA factors; b = Testing second-order CFA factors; c = Testing SEM means for observed variables; d = Testing SEM path constraints; χ2 = Chi-square; df = Degrees of freedom; CFI = Comparative fit index; TLI = Tucker-Lewis index; RMSEA = Root mean square error of approximation; SRMR = Standardized root mean square residual.

Table 5.

Parameter Estimates for Best-Fitting Models of Fourth-Grade Word-Problem Solving

Sample	Model	Variables	Estimate	SE
Full Sample
	F5
		Age	−0.107*	0.042
		Story Problems	0.304**	0.061
		Computation Skill	0.386**	0.056
		Matrix Reasoning	0.276**	0.045
		Oral Language	0.351**	0.056
Girls
	G5
		Age	−0.090	0.061
		Story Problems	0.337**	0.081
		Computation Skill	0.421**	0.082
		Matrix Reasoning	0.228**	0.065
		Oral Language	0.308**	0.080
Boys
	B5
		Age	−0.158*	0.063
		Story Problems	0.230*	0.102
		Computation Skill	0.381**	0.091
		Matrix Reasoning	0.301**	0.067
		Oral Language	0.424**	0.089

Note. Estimates are standardized. F = Full sample (N = 340); G = Girls (N = 174); B = Boys (N = 135); SE = Standard error.

^*p < .05;

^**p < .001

For girls, we began by specifying a CFA model identical to the model specified for the full sample (see Figure 1 and Table C.1). Similar to the full group analysis, this model (Model G1) provided an excellent fit to the data and thus provided the base model for SEM (see Table 4 and Figure 2a). We initially specified a model that included all variables, which provided a good fit to the data (Model G2; see Tables 4 and 5 for model fit statistics and parameter estimates, respectively). Similar to the full sample, we specified new models after removing the weakest parameters (see Table D.1), which included word reading fluency (β = 0.022, p = .816 in Model G2), concept formation (β = 0.049, p = .525 in Model G3), and working memory (β = 0.200, p = .140 in Model G4). Differences between Models G2 and G3, Models G3 and G4, and Models G4 and G5 were nonsignficant (see Table 4). This final model (Model G5; see Figure 2b) continued to provide adequate fit to the data (χ² = 182.665 (120), p < .001, CFI = .956, TLI = .940, RMSEA = .055, 90% confidence interval [0.038, 0.070], p-close = .300; SRMR = .052). Girls’ prior oral language (β = 0.308, p < .001), word-problem solving (β = 0.337, p < .001), computation (β = 0.421, p < .001), and matrix reasoning skills (β = 0.228, p < .001) were all significantly related to word-problem solving in fourth grade; age was not (β = −0.090, p = .139). This model accounted for 85.1% of the variance in fourth-grade word-problem solving performance.

For boys, the CFA model (Model B1) provided an excellent fit (see Figure 1 and Tables 4 and C.1). Thus, we proceeded to test SEMs using these previously specified latent variables. In the initial SEM, we included all variables and allowed them to correlate (see Figure 2a). This model (Model B2) provided an excellent fit to the data (see Table 4). As done previously, we removed nonsignificant variables from subsequent models (see Table D.1). These included working memory (β = −0.099, p = .555 in Model B2), concept formation (β = 0.075, p = .316 in Model B3), and word reading fluency (β = 0.093, p = .300 in Model B4). Nonsignificant chi-square differences resulted for all comparisons: Model B2 vs. B3, Model B3 vs. B4, and Model B4 vs. B5 (see Table 4). Thus, we retained the most parsimonious model (Model B5), which provided excellent fit (χ² = 146.870 (120), p = .048, CFI = .979, TLI = .971, RMSEA = .041, 90% confidence interval [0.004, 0.062], p-close = .745; SRMR = .049). In this final model, boys’ age (β = −0.158, p < .05) and prior oral language (β = 0.424, p < .001), word-problem solving (β = 0.230, p < .05), computation skill (β = 0.381, p < .001), and matrix reasoning (β = 0.301, p < .001) were all significantly associated with fourth-grade word-problem solving (see Table 5 and Figure 2b). Similar to previous models, these variables accounted for 85.3% variance in fourth-grade word-problem solving.

We also ran multi-group models to examine these same relations while permitting comparison between boys and girls (see Appendix E for a description of invariance testing for the CFA model). Based on previous modeling, we specified a model that included all constructs as correlated skills, and included only age, word-problem solving, computation skill, matrix reasoning, and oral language as being related to fourth grade word-problem solving. Prior to testing the equivalence of the parameter estimates across the two groups, we first needed to establish equivalence of the means for the observed variables that were not included in the CFA model (age, story problems, matrix reasoning, and concept formation). The unconstrained means model provided a good fit to the data (Model MGc1; see Table 4). A comparison of this model to a model in which the means were constrained to equality (Model MGc2) did not result in a significant chi-square difference, Δχ2 = 8.080 with 4 df, p = .089. Therefore, we were able to test for equality for the parameter estimates of the variables across boys and girls.

Constraining the parameter estimates of age (Model MGd1), word-problem solving (Model MGd2), computation skill (Model MGd3), matrix reasoning (Model MGd4), and oral language (Model MGd5) to equality to did not result in significant chi-square differences (see Table 4). Further, the difference between the fully unconstrained (Model MGc2) and the fully constrained model (Model MGd5) was not significant, Δχ2 = 4.007 with 5 df, p = .548. This suggests that these skills and cognitive processes were not differentially associated for boys versus girls.

Discussion

In the present study, we examined the longitudinal relations between word-problem solving, computation skill, working memory, nonverbal reasoning, oral language, and word reading fluency in second grade and word-problem solving in fourth grade. As anticipated, foundational word-problem solving and computation skill as well as reasoning ability were significantly associated with later word-problem solving performance in the full sample. Each SD increase in second grade word-problem solving, computation skill, and reasoning was associated with a .304, .386, and .276 SD increase, respectively, in fourth grade word-problem solving. Moreover, oral language accounted for unique variance in word-problem solving over and above earlier word-problem solving, computation skill, and nonverbal reasoning. For each SD increase in oral language, students scored .351 SD higher on word-problem solving. This indicates that oral language was more strongly related to future word-problem solving than beginning word-problem solving performance.

These results are in line with previous findings showing that foundational skills and oral language ability account for variance in concurrent and longitudinal word-problem solving performance (Fuchs et al., 2006, 2010b; Tolar et al., 2012; Vilenius-Tuohimaa et al., 2008; Wang et al., 2016; Zheng et al., 2011). Although nonsignificant relations between oral language and word-problem solving have been observed (e.g., Seethaler et al., 2012), the present findings are in line with a larger body of work showing that oral language does provide a platform for development word-problem solving (Fuchs et al., 2006, 2008a, 2015; Wang et al., 2016).

Surprisingly, however, working memory was not significantly related to word-problem solving in any of the models. This stands in contrast to previous studies (e.g., Pina et al., 2014; Wang et al., 2016) and may be due to a few differences between prior investigations and the present study. First, we modeled multiple constructs using a latent variable framework, whereas several studies included only single measures or composite constructs (e.g., Fuchs et al., 2008a, 2015; Pina et al., 2014). Second, several investigations showing effects for working memory on word-problem solving were concurrent (Fuchs et al., 2008a; Pina et al., 2014) or, if longitudinal designs were used, the gap between assessment periods was shorter than in the present study (Fuchs et al., 2015, 2018; Wang et al., 2016). Third, our working memory latent variable was created using at least one measure that may have tapped language skills (listening recall), and this may be in part why this factor did not account for unique variance over and above oral language.

Further, the present sample likely included at least some children who were relatively proficient problem solvers, and the role of working memory in word-problem solving may diminish in proficient problem solvers. Evidence in fact suggests that fluency in mathematical problem solving impacts the extent to which individuals rely on working memory (e.g., Imbo & Vandierendonck, 2007). Thus, given the potentially complex associations between working memory and mathematical problem solving, future investigations should examine potential interactions between mathematical proficiency/automaticity and working memory as well as between language proficiency and working memory and later word-problem solving performance.

When relations were examined for boys and girls separately, we found that these same variables were associated with word-problem solving across both groups. Prior word-problem solving and computation skill appeared to be stronger for girls than for boys (0.337 vs. 0.230 and 0.421 vs. 0.381 for word-problem and computation skill, respectively), while matrix reasoning and oral language seemed to be stronger for boys than for girls (0.301 vs. 0.228 and 0.424 vs. 0.308). However, multigroup modeling indicated these differences were not significant, and although these skills accounted for more variance in word-problem solving for boys than girls, this difference was negligible (ΔR² = .002). Overall, this pattern suggests that boys and girls do not depend on different sets of cognitive processes and foundational skills to support word-problem solving development.

In terms of theoretical implications, results provide support for the NRC and dual representation models and the problem-model strategy framework of word-problem solving (Hegarty et al., 1995; Kintsch & Greeno, 1985; MLSC/NRC, 2001). Finding that early word-problem solving and computation skills is related to later word-problem solving lends support to the assertion that prior knowledge, word-problem solving experience(s), and strategies affect the ability to discern the structure of and successfully solve word-problems (e.g., Kintsch & Greeno, 1985; MLSC/NRC, 2001). The association between nonverbal reasoning and word-problem solving also provides support to problem models, in which the ability to solve word problems involves creating a mental problem model and thus requires reasoning ability (Hagerty et al., 1995). The importance of reasoning is well established for mathematics broadly (e.g., mathematical reasoning and logical inference; Geary, 1994; MLSC/NRC, 2001) and word-problem solving (Mercer, 1997 cited in Steele, 2002; Rourke, 1993). These relations likely exist because reasoning affects strategy use in mathematics (Case, Lombardi, Pollock, Fineman, & Pezaris, 2017; Laski et al., 2013) and because the application of strategies impacts word-problem solving (Koedinger & Tabachneck, 1994).

The importance of oral language to word-problem solving is additionally emphasized in both models of word-problem solving (Hegarty et al., 1995; Kintsch & Greeno, 1985). These models assert that when presented with a word problem, individuals construct a text base that facilitates an understanding of the text, thus leading to development of the problem model. That is, the ability to understand the text is supported by an understanding of individual words (e.g., Hoover & Gough, 1990) in addition to the language structure. Further, the strength of the relation between oral language and word-problem solving, in the context of a rich model with many competing foundational skills and cognitive abilities, lends additional credence to Kintsch and colleagues’ (1985) hypothesis that word-problem solving is at least, in part, a form of text comprehension.

In terms of practical implications, the present findings are in line with previous investigations showing that children who have difficulty with word-problem solving, computation, nonverbal reasoning, and oral language in second grade likely endure difficulty in solving word problems over time. Given this, interventions that aim to build these foundational skills in addition to building reasoning and language processes in the context of word-problem solving instruction are needed to remediate word-problem solving difficulties early in school (Fuchs & Fuchs, 2002; Fuchs et al., 2008b; Kong & Orosco, 2015; Passolunghi & Siegel, 2001; Traf & Samuelsson, 2013).

Although the present study suggests that researchers may not need to be sensitive to sex differences when selecting measures for identifying students for such services, further research on this topic is needed because the absence of significant differences between boys and girls may be partly due to insufficient power. With larger samples, researchers may detect some of the differences suggested in the observed magnitudes in relations for boys versus girls (Δβ were 0.107 and 0.040 in foundational word-problem solving and computation, respectively, favoring girls; Δβ were 0.073 and 0.116 for matrix reasoning and oral language, respectively, favoring boys).

Before closing, we note four study limitations. First, we remind readers that the present set of analyses, although prospectively longitudinal, are correlational. Therefore, causal inferences are not possible based on present findings. Second, our sample includes the full distribution children. As a result, we cannot draw conclusions specifically for children with learning disabilities or other disorders. Third, although we included measures of various cognitive processes, we did not include some potentially associative constructs (e.g., attention and reading comprehension; Bjorn et al., 2016; Fuchs et al., 2006). It is possible that inclusion of these variables within a single model may change the observed pattern of results. Fourth, findings apply only to students in the early elementary grades. In the later grades, the cognitive demands of more complex word-problem solving may alter the nature of associations. Nonetheless, the present investigation adds to our understanding of the developmental relations between children’s early cognitive skills and later word-problem solving.

Conclusions

Findings suggest that early language-related skills, such as vocabulary and language comprehension, are significantly associated with children’s later word-problem solving outcomes over and above prior word-problem solving, computational abilities, and nonverbal reasoning. Because the observed role of oral language in word-problem solving aligns with several theoretical frameworks of word-problem solving, such as the dual representation model, it is necessary to consider language skills in conjunction with children’s reasoning and mathematical abilities when designing intervention programs for remediating poor word-problem solving outcomes. Results also indicate similar associations across boys and girls, although additional research is warranted. In sum, this investigation adds important information about individual differences in word-problem solving development and suggests that language skills should be considered within word-problem solving interventions.

Highlights.

• Word problems are more challenging for children to solve than numerical problems.

• We examined predictors of word-problem solving in 340 children followed from second to fourth grade.

• Word-problem solving, computation skill, nonverbal reasoning, and oral language measured in second grade were significant predictors of children’s fourth-grade word-problem solving.

• Relations were similar for boys and girls.

Table A.1.

Descriptive Statistics for Girls and Boys

		Girls							Boys
Variable	Measure	N	Min.	Max.	Mean	SD	Skew	Kurtosis	N	Min.	Max.	Mean	SD	Skew	Kurtosis
Controls
	Age	174	6.10	8.81	7.585	0.425	0.007	1.107	135	6.69	9.02	7.681	0.441	0.431	−0.067
	Story Problems	174	0	14	6.138	3.309	0.280	−0.599	134	1	14	7.007	3.534	0.337	−0.841
	Addition 0–12	174	2	22	8.316	4.565	0.820	0.299	133	1	22	8.722	4.887	0.615	−0.201
	Addition 0–18	174	0	16	6.017	3.547	0.548	−0.122	133	0	16	6.226	3.513	0.494	0.060
	DD Addition	173	0	12	3.254	3.024	0.726	−0.356	132	0	12	3.212	3.111	0.908	0.062
	Subtraction 0–12	174	0	12	4.052	2.499	0.633	0.002	133	0	12	4.744	2.811	0.586	0.165
	Subtraction 0–18	174	0	10	2.885	2.229	0.805	0.101	133	0	11	3.368	2.610	0.975	0.874
	DD Subtraction	173	0	9	2.358	2.597	0.992	0.166	132	0	9	2.053	2.662	1.093	0.079
	WASI MR	174	2	26	11.270	5.686	0.727	−0.582	135	3	28	12.000	5.869	0.591	−0.518
	WJ-CF	174	3	27	11.253	5.492	0.333	−0.597	135	1	27	11.489	6.028	0.767	0.226
	WMTB-C LR	174	0	16	7.121	3.838	−0.010	−0.538	135	0	16	7.215	3.724	−0.244	−0.236
	WMTB-C CR	174	4	24	13.977	4.394	0.053	−0.390	135	2	26	14.341	4.678	0.175	0.031
Predictors
	WASI Vocabulary	174	7	37	22.149	5.938	0.126	0.188	135	5	37	21.919	7.089	−0.037	−0.368
	WDRB LC	174	5	29	16.172	4.495	−0.382	0.097	135	5	26	17.015	4.985	−0.441	−0.236
	WIF-B	174	0	111	41.667	24.485	0.387	−0.594	135	2	111	41.935	24.836	0.385	−0.505
	WIF-N	173	1	120	56.543	22.107	−0.171	0.046	135	7	105	55.733	22.687	−0.070	−0.612
Outcomes
	ITBS9 b	152	1	17	9.711	3.816	−0.121	−0.730	115	2	17	10.670	3.573	−0.270	−0.496
	ITBS10 b	152	1	11	5.257	2.073	0.315	−0.363	115	1	11	5.678	2.308	0.332	−0.588
	VSP b	152	0	29	11.066	6.756	0.541	−0.199	115	0	29	11.043	6.719	0.684	0.246

Note. Raw scores reported; SD = Standard deviation; Min. = Minimum; Max. = Maximum; Age = Age in 2^nd grade; DD = Double digit; WASI = Wechsler Abbreviated Scale of Intelligence; MR = Matrix Reasoning; WJ=III = Woodcock-Johnson; CF = Concept Formation; WMTB-C = Working Memory Test Battery for Children; L/CR = Listening/counting recall; WDRB = Woodcock Diagnostic Reading Battery; LC = Listening comprehension; WIF-B/N = Word identification fluency form B/N; VSP = Vanderbilt Story Problems; ITBS9/10 = Iowa Test of Basic Skills level 9/10.

Table B.1.

Correlations Across Girls and Boys

Group	Measure	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
Girls
	1. Age	--
	2. Story Problems	.070	--
	3. Addition 0–12	.178*	.268**	--
	4. Addition 0–18	.086	.264**	.754**	--
	5. DD Addition	.074	.240**	.522**	.492**	--
	6. Subtraction 0–12	.149	.363**	.502**	.549**	.290**	--
	7. Subtraction 0–18	.193*	.330**	.427**	.399**	.264**	.740**	--
	8. DD Subtraction	−.087	.262**	.465**	.415**	.730**	.153*	.206**	--
	9. WASI MR	.005	.361**	.206**	.311**	.217**	.224**	.183*	.243**	--
	10. WJ-III CF	.012	.463**	.239**	.241**	.242**	.222**	.227**	.228**	.358**	--
	11. WMTB-C LR	.059	.425**	.157*	.171*	.190*	.158*	.171*	.205**	.326**	.392**	--
	12. WMTB-C CR	.069	.249**	.220**	.221**	.283**	.123	.138	.317**	.273**	.300**	.408**	--
	13. WASI Vocabulary	.011	.353**	.072	.132	.004	−.027	−.038	.021	.191*	.385**	.366**	.221**	--
	14. WDRB LC	.071	.397**	.135	.163*	.086	.173*	.169*	.125	.189*	.443**	474**	.111	.578**	--
	15. WIF-B	.079	.427**	.340**	.338**	.265**	.410**	.376**	199**	.259**	.254**	.398**	.274**	.242**	.291**	--
	16. WIF-N	−.003	.406**	.404**	.398**	.314**	.475**	441**	.286**	.258**	.251**	.406**	.277**	.232**	.333**	.883**	--
	17. ITBS9	.009	.583**	.405**	.400**	.317**	.354**	.308**	.267**	.454**	.418**	447**	.253**	.376**	.376**	.394**	.403**	--
	18. ITBS10	−.040	.489**	.372**	.331**	.292**	.301**	.246**	.268**	.346**	.343**	.260**	.232**	.312**	.350**	.272**	.321**	.480**	--
	19. VSP	.038	.536**	.311**	.298**	.197*	.278**	.198*	.125	.368**	.437**	.443**	.292**	.258**	.360**	.450**	.447**	.589**	.440**	--
Boys
	1. Age	--
	2. Story Problems	−.077	--
	3. Addition 0–12	−.066	.478**	--
	4. Addition 0–18	−.085	.516**	.801**	--
	5. DD Addition	−.110	.319**	.518**	.494**	--
	6. Subtraction 0–12	−.001	.398**	.649**	.543**	.399**	--
	7. Subtraction 0–18	−.039	.347**	.653**	.576**	.409**	.754**	--
	8. DD Subtraction	−.011	.223*	.478**	.463**	.704**	.348**	.425**	--
	9. WASI MR	−.023	.199*	.119	.167	−.057	.165	.129	.011	--
	10. WJ-III CF	−.011	494**	.254**	.301**	.096	.254**	.229**	.045	.279**	--
	11. WMTB-C LR	−.086	.417**	.257**	.172*	.180*	.165	.126	−.020	.236**	.234**	--
	12. WMTB-C CR	−.031	.341**	.354**	.266**	.290**	.311**	.314**	.161	.313**	.254**	.405**	--
	13. WASI Vocabulary	.061	.440**	.071	.022	.040	−.024	−.026	−.073	.161	.365**	.243**	.231**	--
	14. WDRB LC	.002	.410**	.105	.088	.018	.046	.070	−.133	.177*	.372**	.338**	.329**	.652**	--
	15. WIF-B	−.176*	.391**	.445**	.402**	.382**	.335**	.305**	.232**	.057	.346**	.308**	.189*	.217*	.317**	--
	16. WIF-N	−.116	.383**	.515**	.434**	.403**	.356**	.350**	.280**	.057	.291**	.341**	.200*	.177*	.255**	.900**	--
	17. ITBS9	−.189*	.640**	.397**	.418**	.287**	.416**	.352**	.166	444**	.509**	.309**	.412**	.478**	.452**	.492**	.482**	--
	18. ITBS10	−.078	.584**	.366**	.399**	.217*	.330**	.216*	.129	.430**	.436**	.269**	.321**	.413**	.409**	.366**	.346**	.665**	--
	19. VSP	−.128	.551**	.562**	.552**	.291**	.486**	.384**	.227*	.416**	.504**	.359**	411**	.293**	.354**	.437**	.408**	.633**	.606**	--

Note. Across correlations, N ranges 151–174 and 112–135 for girls and boys, respectively. Age = Age in second grade; DD = Double digit; WASI = Wechsler Abbreviated Scale of Intelligence; MR = Matrix Reasoning; WJ=III = Woodcock-Johnson, Third Edition; CF = Concept Formation; WMTB-C = Working Memory Test Battery for Children; LR = Listening recall; CR = Counting recall; Vocab. = Vocabulary; WDRB = Woodcock Diagnostic Reading Battery; LC = Listening comprehension; WIF-B/N = Word identification fluency form B/N; VSP = Vanderbilt Story Problems; ITBS9/10 = Iowa Test of Basic Skills level 9/10.

^**p < .01

^*p < .05

Table C.1.

Factor Loadings for Confirmatory Factor Analysis Models for the Full Sample (N = 340), Girls Only (N = 174), and Boys Only (N = 135)

		Factor Loading
Latent Variable	Indicators	Full Sample	Girls	Boys
G2 Addition
	Addition 0–12	0.906	0.875	0.945
	Addition 0–18	0.839	0.862	0.849
G2 Subtraction
	Subtraction 0–12	0.909	0.945	0.871
	Subtraction 0–18	0.825	0.783	0.868
G2 DD Addition/Subtraction
	DD Addition	0.920	0.946	0.887
	DD Subtraction	0.781	0.772	0.794
G2 Computation Skill
	G2 Addition	0.933	0.911	0.949
	G2 Subtraction	0.738	0.695	0.827
	G2 DD Addition/Subtraction	0.654	0.633	0.673
G2 Working Memory
	WMTB-C LR	0.745	0.868	0.595
	WMTB-C CR	0.525	0.470	0.681
G2 Word Reading Fluency
	WIF-B	0.915	0.894	0.929
	WIF-N	0.974	0.988	0.969
G2 Oral Language
	WASI Vocabulary	0.724	0.684	0.788
	WDRB LC	0.833	0.846	0.828
G4 Word Problem Solving
	ITBS9	0.810	0.806	0.837
	ITBS10	0.686	0.625	0.760
	VSP	0.755	0.732	0.782

Note. Factor loadings are standardized estimates. G2/4 = Grade 2/4; DD = Double-digit; WMTB-C = Working Memory Test Battery for Children; WIF-B/N = Word identification fluency Form B/N; WASI = Wechsler Abbreviated Scale of Intelligence; WDRB = Woodcock Diagnostic Reading Battery; LC = Listening comprehension; ITBS9/10 = Iowa Test of Basic Skills level 9/10; VSP = Vanderbilt Story Problems. All loadings are significant at p < .001.

Table D.1.

Parameter Estimates Across All Models Predicting Fourth-Grade Word-Problem Solving

Sample	Model	Variable	Estimate	SE
Full Sample
	F2
		Age	−0.095*	0.043
		Story Problems	0.300***	0.060
		Computation Skill	0.325***	0.072
		Matrix Reasoning	0.259***	0.049
		Concept Formation	0.067	0.052
		Working Memory	0.062	0.096
		Oral Language	0.262**	0.082
		Word Reading Fluency	0.046	0.064
	F3
		Age	−0.095*	0.043
		Story Problems	0.307***	0.059
		Computation Skill	0.334***	0.072
		Matrix Reasoning	0.272***	0.045
		Concept Formation	0.066	0.052
		Oral Language	0.292***	0.069
		Word Reading Fluency	0.055	0.062
	F4
		Age	−0.103*	0.042
		Story Problems	0.300***	0.060
		Computation Skill	0.375***	0.057
		Matrix Reasoning	0.271***	0.045
		Concept Formation	0.056	0.052
		Oral Language	0.321***	0.062
Girls
	G2
		Age	−0.078	0.062
		Story Problems	0.328***	0.079
		Computation Skill	0.356**	0.107
		Matrix Reasoning	0.192**	0.069
		Concept Formation	0.055	0.081
		Working Memory	0.181	0.136
		Oral Language	0.156	0.117
		Word Reading Fluency	0.022	0.095
	G3
		Age	−0.082	0.060
		Story Problems	0.326***	0.079
		Computation Skill	0.372***	0.085
		Matrix Reasoning	0.190**	0.068
		Working Memory	0.193	0.131
		Concept Formation	0.049	0.077
		Oral Language	0.161	0.116
	G4
		Age	−0.086	0.060
		Story Problems	0.326***	0.079
		Computation Skill	0.380***	0.085
		Working Memory	0.200	0.136
		Matrix Reasoning	0.195**	0.069
		Oral Language	0.186	0.112
Boys
	B2
		Age	−0.146*	0.066
		Story Problems	0.251*	0.105
		Computation Skill	0.341*	0.133
		Matrix Reasoning	0.328***	0.081
		Concept Formation	0.064	0.078
		Working Memory	−0.099	0.167
		Oral Language	0.397**	0.134
		Word Reading Fluency	0.094	0.091
	B3
		Age	−0.140*	0.064
		Story Problems	0.239*	0.100
		Computation Skill	0.300**	0.107
		Matrix Reasoning	0.301***	0.066
		Concept Formation	0.075	0.075
		Oral Language	0.348***	0.100
		Word Reading Fluency	0.095	0.089
	B4
		Age	−0.143*	0.064
		Story Problems	0.254*	0.101
		Computation Skill	0.314**	0.108
		Matrix Reasoning	0.308***	0.066
		Oral Language	0.379***	0.097
		Word Reading Fluency	0.093	0.090

Note. Estimates are standardized. SE = Standard error;

^*p < .05;

^**p < .01;

^***p < .001

Appendix E. Invariance Testing for Multi-Group Confirmatory Factor Analysis (CFA) Modeling

Although we previously established that the latent constructs were adequately represented by their observed indicators, the multi-group CFA models allowed for a test of whether the means and factor loadings were similar or dissimilar across the two groups. To test this, we specified three different models: a configural model, a metric model, and a scalar model. In the configural model, the observed variable means and the factor loadings are allowed to vary; essentially, we are testing whether the factor structure is equivalent across boys and girls. In the metric model, we imposed constraints on the factor loadings; however, the means are allowed to vary across the two groups. Finally, in the scalar model, we constrained the means and factor loadings to equality across groups. Invariance across both means and factor loadings is necessary to meaningfully compare the two groups. Given that we included a higher-order factor within our CFA models, we first tested invariance for the first-order factors and then followed-up with invariance testing for the higher-order factor separately.

The configural model (Model MGa1) provided an excellent fit to the data (see Table 4), indicating the factor structure was appropriately represented for the first-order factors for boys and girls. Following this, we tested for metric invariance. Because the configural model was nested within the metric model (Model MGa2), we used chi-square difference testing to determine whether adding equality constraints led to a significant worsening of model fit. When compared to the configural model, imposing equality constraints on the factor loadings did not result in a significantly worse fitting model, Δχ2 = 14.442 with 8 df, p = .071, suggesting the factor loadings were similar across the two groups. Thus, the more parsimonious metric model was retained. Comparing the metric model to the scalar model (Model MGa3), while imposing additional equality constraints on the means across the two groups, did not result in significantly worse fit, Δχ2 = 12.985 with 8 df, p = .112. So the scalar model was the most parsimonious and preferred model. Thus, we established that the mean structure and factor loadings were equivalent for the first-order factors across boys and girls.

Because we were able to establish invariance for the first-order factors, we tested for metric invariance for the second-order factor (i.e., whether the loadings for the subtraction and addition factors were similar across the two groups). For the multi-group models, we fixed the unstandardized path from the computation factor to one of the first order factors to 1 given that standardization is inappropriate in multi-group analyses (see Kline, 2011). First, we specified a configural model for the factor structure of the second-order factor only (MGb1). Following this, we constrained the factor loadings to equality across boys and girls (MGb2). A comparison of this model to the configural model resulted in a nonsignificant chi-square difference, Δχ2 = 1.363 with 2 df, p = .506. Scalar invariance was tested by constraining the latent factor means to equality (i.e., fixed to zero across groups; Model MGb3). This did not lead to a significant degradation in model fit compared to the metric model, Δχ2 = 10.960 with 7 df, p = .140. Because we established invariance for the full CFA model, we proceeded by testing equivalence of the estimates for the best-fitting SEMs for boys and girls (across Models B5 and G5).