Abstract
Deep neural networks have achieved remarkable success in various challenging tasks. However, the black-box nature of such networks is not acceptable to critical applications, such as healthcare. In particular, the existence of adversarial examples and their overgeneralization to irrelevant, out-of-distribution inputs with high confidence makes it difficult, if not impossible, to explain decisions by such networks. In this paper, we analyze the underlying mechanism of generalization of deep neural networks and propose an (n, k) consensus algorithm which is insensitive to adversarial examples and can reliably reject out-of-distribution samples. Furthermore, the consensus algorithm is able to improve classification accuracy by using multiple trained deep neural networks. To handle the complexity of deep neural networks, we cluster linear approximations of individual models and identify highly correlated clusters among different models to capture feature importance robustly, resulting in improved interpretability. Motivated by the importance of building accurate and interpretable prediction models for healthcare, our experimental results on an ICU dataset show the effectiveness of our algorithm in enhancing both the prediction accuracy and the interpretability of deep neural network models on one-year patient mortality prediction. In particular, while the proposed method maintains similar interpretability as conventional shallow models such as logistic regression, it improves the prediction accuracy significantly.
I. Introduction
Cardiovascular diseases (CVDs) cause severe economic and healthcare related burdens not only in the United States but worldwide [1]. Acute myocardial infarction (AMI) is a type of CVD which is defined as “myocardial necrosis in a clinical setting consistent with myocardial ischemia”, or heart attack in simple words [2]. AMI is the leading cause of death worldwide [3]. Identifying risky patients in Intensive Care Unit (ICU) and preparing for their health needs are crucial to appropriately managing AMI and employing timely interventions to reduce mortality [4].These facts motivate recent efforts on building mortality prediction models for ICU patients with AMI [5]. Electronic health records (EHRs) with rich data of patient encounters present unprecedented opportunities for critical clinical applications such as outcome prediction [6]. However, medical data are typically heterogeneous and building machine learning models using this type of data is more challenging than using homogeneous data like images. The necessity of dealing with heterogeneous data is not limited to medical applications, but it is shared among many other applications of machine learning [7].
Unlike traditional machine learning approaches, deep learning methods do not require feature engineering [8]. Such networks have demonstrated significant successes in many challenging tasks and applications [9]. Even though they have been employed in numerous real-world applications to enhance the user experience, their adoption in healthcare and clinical practice has been slow. Among the inherent difficulties, the complexity of these models remains a huge challenge [10] as it is not clear how they arrive at their predictions [11]. In medical practice, it is unacceptable to only rely on predictions made by a black-box model to guide decision-making for patients. Any incorrect prediction such as erroneous diagnosis may lead to serious medical errors, which is currently the third leading cause of death in the United States [12]. This issue has been raised and the necessity of interpretable deep learning models has been identified [13]. However, it is not clear how to improve the interpretability and at the same time retain the accuracy of deep neural networks. Deep neural networks have improved application performance by capturing complex latent relationships among input variables. To make the matter worse, these models are typically overparameterized, i.e., they have more parameters than the number of training samples [14]. Overparametrization simplifies the optimization problem for finding good solutions [15]; however, the resulting solutions are even more complex and more difficult to interpret. Consequently, interpretability enhancement techniques would be difficult without handling the complexity of deep neural networks.
Recognizing that commonly-used activation functions (ReLU, sigmoid, tanh, and so on) are piece-wise linear or can be well approximated by a piece-wise linear function, such neural networks partition the input space into (approximately) linear regions. In addition, gradient-based optimization results in similar linear regions for similar inputs as their gradient tends to be similar. By clustering the linear regions, we can reduce the number of distinctive linear regions and at the same time improve robustness. To further improve the performance, we train multiple models and use consensus among the models to reduce their sensitivity to adversarial examples with small perturbations and also reduce overgeneralization to irrelevant inputs of individual models. We demonstrate the effectiveness of deep neural network models and the proposed algorithms on one-year mortality prediction in patients diagnosed with AMI or post myocardial infarction (PMI) in MIMIC-III database. The workflow of this study is depicted in Fig. 1. Furthermore, the experimental results show that the proposed method improves the performance as well as the interpretability.
Fig. 1.
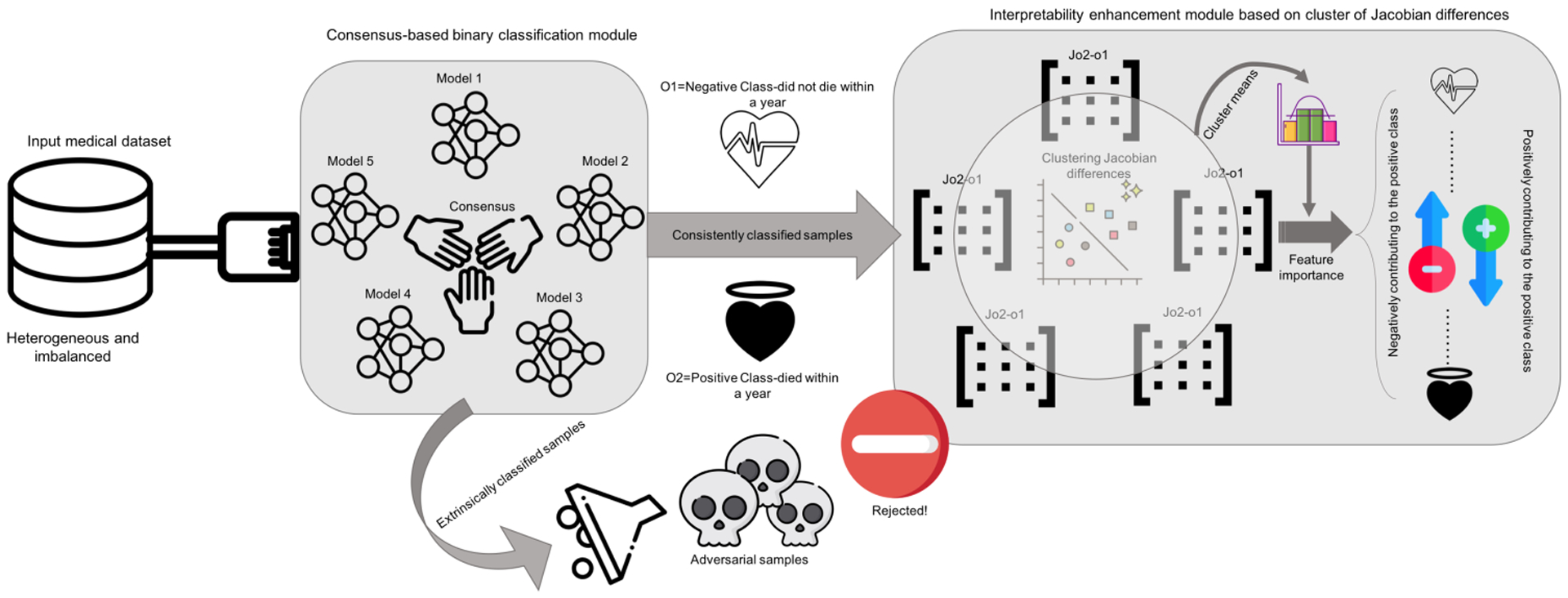
The workflow of the study (Icons made by https://www.flaticon.com).
The paper is organized as follows. In the next section, we present generalization and overgeneralization in the context of deep neural networks and the proposed deep (n, k) consensus-based classification algorithm. After that, we describe a consensus-based interpretability method. Then, we illustrate the effectiveness of the proposed algorithms in enhancing one-year mortality predictions via experiments. Finally, we review recent studies that are closely related to our work and conclude the paper with a brief summary and plan for future work.
II. Generalization and Overgeneralization in Deep Neural Networks
Fundamentally, a neural network approximates the underlying unknown function using f (x; θ), where x is the input, and θ is a vector that includes all the parameters (weights and biases). Given a deep learning model and a training dataset, there are two fundamental problems to be solved: optimization and generalization. The optimization problem deals with finding the parameters θ by minimizing a loss function on the training set. Overparametrization [16] in deep neural networks makes the problem easier to solve by increasing the number of good solutions exponentially [17].
Since there are numerous good solutions, understanding their differences and commonalities is essential to developing more effective multiple-model based methods. Toward a systematic understanding of deep neural network models in the input space, one must consider the behavior of these models in case of typical, irrelevant and adversarial inputs (the inputs that are “computed” intentionally to degrade the system performance) [18]. As a representative example, we have trained five different deep neural networks on the MNIST dataset [19] and used images from the CIFAR-10 dataset [20] as irrelevant images since they do not contain valid handwritten digits; we have cropped the images and converted them to the same input format of MNIST. Fig. 2(left) shows how the five models agree on irrelevant samples by showing the maximum number of models that agree with each other over the same classification label for samples. It shows that the models respond (almost) randomly to such irrelevant inputs.
Fig. 2.
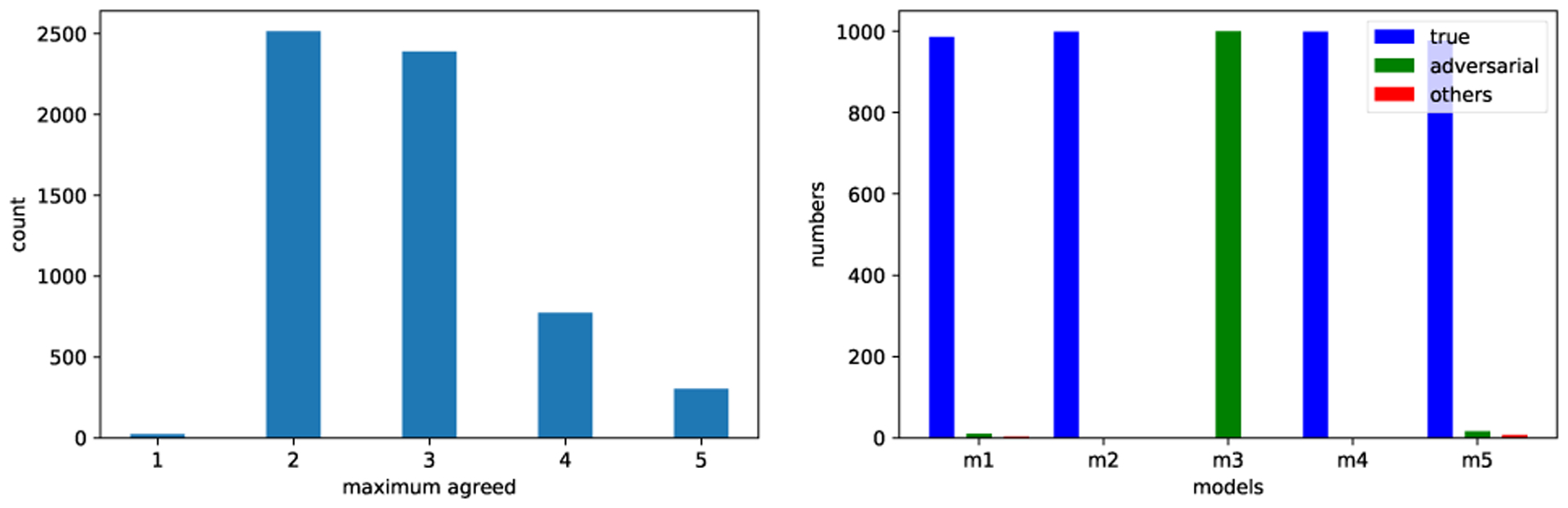
Left: Bar plot that shows how the five models trained on the MNIST dataset agree on the overgeneralized samples (e.g., dog samples of the CIFAR-10 dataset). Right: Bar plot that shows how the five models classify the adversarial examples generated by one of the models (m3); the bars denote the classification of the samples to true labels, adversarial labels and other labels, respectively.
We have also generated adversarial examples using the fast sign algorithm [18] as the direction to find the minimum step size required to change the class label to another class. By perturbing the inputs using one of the models (m3), we investigate how the other models respond to those perturbed inputs, i.e., adversarial examples. Fig. 2(right) shows the classification results of the five models on the adversarial images which are generated by m3. Clearly, the other four models recognize the adversarial examples correctly for most of the perturbed examples.
A. Deep (n, k) Consensus Algorithm
As all the models classify training samples accurately, they generate similar linear regions and should behave similarly at training samples. In Fig. 3, the models (trained on the one-year patient mortality prediction dataset) generalize perfectly along the path of the same class even though they differ in details. We find this is a representative behavior, the main reason why multiple DNN models mostly agree with each other to meaningful inputs and can filter out adversarial and irrelevant samples. While individual approximations are sensitive to adversarial examples, consensus can be used to capture the underlying common structures in training data, not accidental features. Similar to Fig. 3, Fig. 4 shows that along the path to other class, all models behave similarly in that the decision boundaries occur around 0.5 and there is no significant oscillation between class 0 and 1 samples. Therefore, consensus between the models makes sense.
Fig. 3.

Outputs from the penultimate layer for model 1, 2, 3, 4 and 5 respectively centered at a training sample of the one-year patient mortality prediction dataset, along the direction to another sample in the same class.
Fig. 4.

Outputs from the penultimate layer for model 1, 2, 3, 4 and 5 respectively centered at a training sample of the one-year patient mortality prediction dataset, along the direction to another sample in the other class.
We propose to use consensus among different models to differentiate extrinsically classified samples from intrinsically/consistently classified samples (CCS). Samples are considered to be consistently classified if they are classified by multiple models with a high probability in the same class. In contrast, extrinsic factors such as randomness of weight initialization or oversensitiveness to accidental features are responsible for the classification of extrinsic samples. As such random factors cannot happen consistently in multiple models, we can reduce them exponentially by using more models.
To tolerate accidental oversensitiveness of a small number of models, we propose deep (n, k) consensus algorithm1, which is given in Algorithm 1. Note that Pmin is a vector with one value for each class as it is computed class-wise. Essentially, the algorithm requires consensus among k out of n trained models in order for a sample to be classified; pt, a threshold parameter, is used to decide if the prediction probability of a model is sufficiently high.
To illustrate the effectiveness of the proposed algorithm, Fig. 5 shows the results on the irrelevant samples, generated using randomized values. Majority of the irrelevant samples are rejected using a (5, 5) consensus algorithm as shown in Fig. 5; note that a (5,4) algorithm would also be effective even though it could not reject the ones where four models agree accidentally.
Fig. 5.
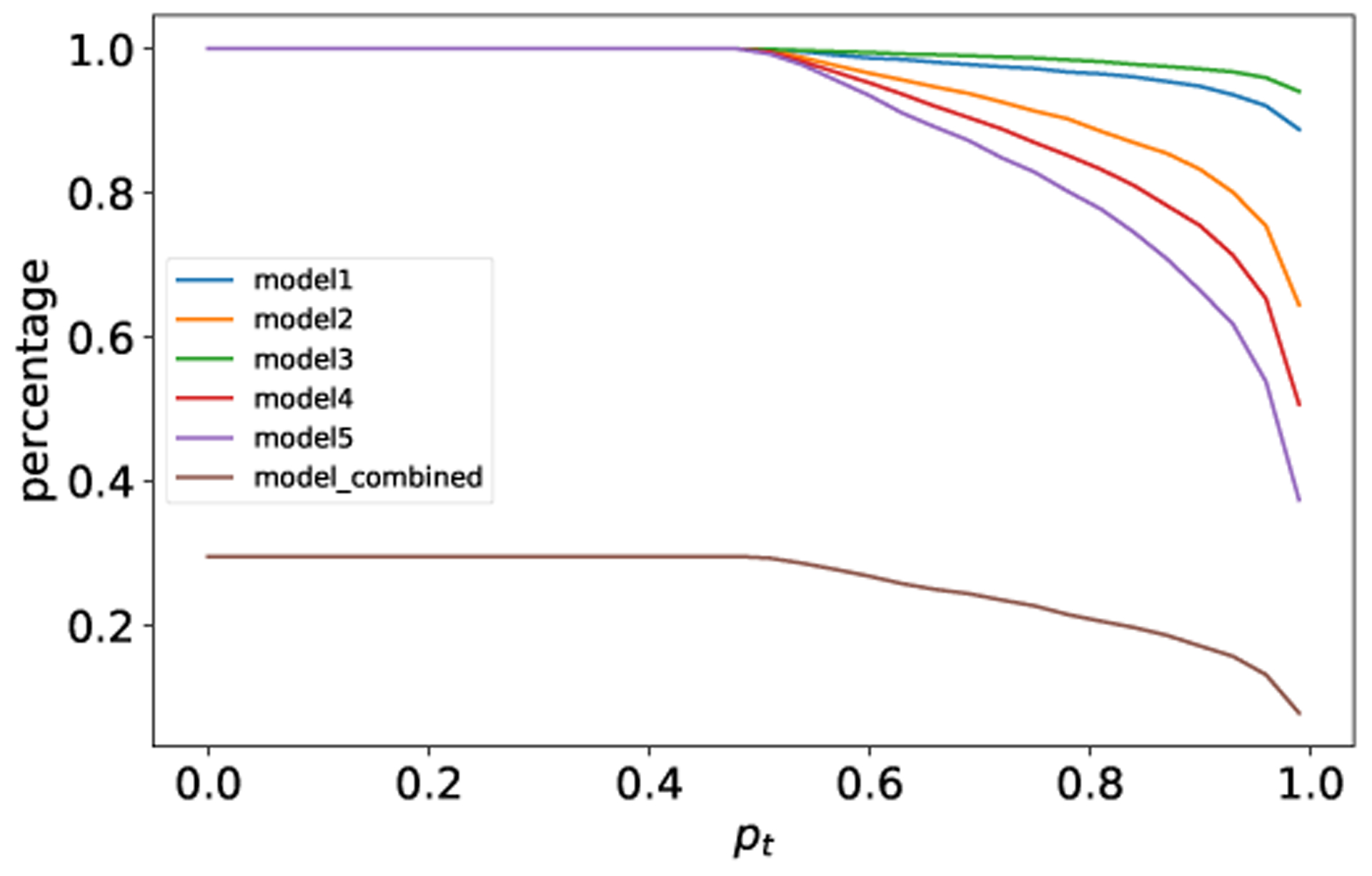
Percentage of classified overgeneralized samples with (5,5) consensus. The samples are out-of-distribution inputs for the one-year patient mortality prediction dataset.

As a whole, the deep network models generalize in a similar way for the intrinsic features. These models behave consistently for the samples that are supported by the training set, however, their behavior can differ in terms of the exact direction that leads to adversarial examples. Therefore, consensus among the models should also be able to reduce adversarial examples. We have conducted systematic experiments to illustrate that with MNIST dataset, where after generating adversarial examples using one model, most of the other models are able to reject them. Fig. 8 shows that by using a (5,4) consensus algorithm we can classify most of the adversarial examples correctly; the only ones are rejected due to that model m5 misclassified several samples. Clearly, as model m3 is oversensitive to the adversarial examples, a (5, 5) algorithm will reject all the adversarial images.
Fig. 8.

Change of accuracy and percentage with deep (n, k) consensus when adversarial examples created by model-3 on the MNIST dataset. (a) Accuracy of the models with (5,5) consensus. (b) Percentage of the classified samples with (5,5) consensus. (c) Accuracy of the models with (5,4) consensus. (d) Percentage of the classified samples with (5,4) consensus.
The proposed algorithm is different from ensemble methods [22], which are used to improve the performance of multiple models via voting. The proposed consensus algorithm is based on the distinctive behaviors of deep learning models demonstrated in Fig. 3 and Fig. 4. Since they are trained on the same data, intrinsically they will behave similarly as they generalize to new samples in a similar manner. Ensemble methods, while using multiple (deep learning) models, assume different models behave differently and the results based on votes will be more accurate. In other words, the consensus method is possible only because deep learning models use the same underlying mechanism for generalization while ensemble methods can be applied to any multiple models; since there is no general underlying mechanism, agreements among the models cannot be attributed to underlying reasons. Similarly, in applications (such as data mining) where a set of samples need to be classified by possibly multiple classifiers at the same time, correlations between different classes can be utilized to create multiple labels for similar objects by maximizing agreements among the assigned labels to the objects (e.g., [23]). However, these methods can not recognize and reject adversarial and out-of-distribution samples, while our algorithm is designed to handle those samples via inherent consensus of the multiple deep neural network models. In addition, the proposed consensus-based algorithm is not trying to force or maximize the consensus among the models for the classification task, rather because the consensus exists naturally in deep networks for the samples they can generalize.
III. A Consensus-Based Interpretability Method
With a robust way to handle irrelevant and adversarial inputs, we propose a novel method to interpret decisions by trained deep neural networks, based on that such networks behave linearly locally and linear regions form clusters due to weight symmetry.
The linear approximation reveals rich deep neural network model behavior in the neighborhood of a sample. Interesting characteristics of the model can be uncovered by walking along certain directions from that sample. For example, adversarial examples are evident along the direction shown in Fig. 4, where the classification changes quickly outside ϵ = 0 (where the given training sample is). On the other hand, Fig. 3 shows robust classification along this particular direction.
More formally, under the assumption that the last layer in a neural network is a softmax layer, we can analyze the outputs from the penultimate layer (i.e., the layer before the softmax layer). Using the notations introduced earlier, the outputs can be written as the following:
| (1) |
where O is the vector-valued function. Since the model is locally close to linear, if we perturb an input (e.g., x0) by a small value Δx (i.e., x = x0 + Δx), then the Equation 1 can be approximated using the first order Taylor expansion around input x0.
| (2) |
Here, J is the Jacobian matrix of function O, defined as . Note that the gradient or the Jacobian matrix, in general, has been used in a number of methods to enhance interpretability (e.g., [24], [25]).
However, the Jacobian matrix only reflects the changes for each output individually. As classification is inherently a discriminative task, the difference between the two largest outputs is locally important. In the binary case, we can write the difference of the two outputs as:
| (3) |
where J0,: and J1,: are the first and second row of J. In general, for multiple class cases, we need to analyze the difference between the top two outputs locally. For example, we can focus on the difference between the top 2 classes, even though there are 10 classes in case of MNIST dataset [19]. In general, we can apply pairwise difference analysis; however, most pairs will be irrelevant locally. The differences between bottom classes are likely due to noisy.
The Jacobian difference vector essentially determines the contributions of changes in the features, i.e., the feature importance locally. This allows us to explain why the deep neural network model behaves in a particular way in the neighborhood of a sample. Note that the first part of Equation 3, i.e., f2(x0, θ)− f1(x0, θ) is important to achieve high accuracy. However, the local Jacobian matrices, while important, are not robust. To increase the robustness of interpretation and at the same time reduce the complexity, we propose to cluster the difference vectors of Jacobian matrices.
The Jacobian difference vectors can be clustered using K-means or any other clustering algorithm. In this paper, we identify consistent clusters using the correlation coefficients of the Jacobian difference vectors of the training samples. To create a cluster, we first identify the pair that has the highest correlation. Then, we expand the cluster by adding the sample with the highest correlation with all the samples in the cluster already. This can be done efficiently by computing the minimum correlations to the ones in the cluster already for each remaining sample and then choosing the one with the maximum. We add samples iteratively until the maximum correlation is below a certain threshold. To avoid small clusters, we also impose a minimum cluster size. We repeat the clustering process to identify more clusters. Due to the equivalence of local linear models, the number of clusters is expected to be small. Our experimental results support this. Note that neural networks still have different biases at different samples, enabling them to classify samples with high accuracy with a small number of linear models.
We do clustering for each of the models first. The clusters from different models can support each other with strong correlations between their means and can also complement each other by capturing different aspects of the data. Therefore, we group highly correlated clusters to get more robust interpretations. Note that different subsets of clusters have different interpretations based on the correlations among the clusters.
Given a new sample (e.g., validation sample), we need to check if that sample can be classified correctly by the models at first. If the sample is rejected by the deep (n, k) consensus algorithm, we do not interpret such sample for which models are not confident. In contrast, if the sample can be classified, we estimate the Jacobian difference for each of the models and then compare that with the cluster means (by consensus of multiple models) to identify the clusters that provide the strongest support. This allows us to check that the new sample is not only classified correctly but also its interpretation is consistent with the interpretation for training samples.
IV. Experimental Results on One-year Mortality Prediction
A. Dataset
The Medical Information Mart for Intensive Care III (MIMIC-III) database is a large database of de-identified and comprehensive clinical data which is publicly available. This database includes fine-grained clinical data of more than forty thousand patients who stayed in critical care units of the Beth Israel Deaconess Medical Center between 2001 and 2012. It contains data that are associated with 53,432 admissions for patients aged 16 years or above in the critical care units [26].
In this study, only those admissions with International Classification of Diseases, Ninth Revision (ICD-9) code of 410.0–411.0 (AMI, PMI) or 412.0 (old myocardial infarction) are considered. These criteria return 5436 records. We use structured data to train the deep neural network models. Structured data includes admission-level information about admission, demographic, treatment, laboratory and chart values, and comorbidities. More details on the features used in this work can be found in a recent work [27].
B. Results from Individual Models
Five different deep neural network models are trained for the purpose of this work. Each of these models consists of three dense layers and a softmax layer for classification. Table I provides implementation details of these models.
Table I.
Implementation Detail of Five Individual Models.
| Specification | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|---|
| Neurons | 200 | 200 | 250 | 250 | 300 |
| Activation | relu | tanh | relu | tanh | tanh |
| Optimization | SGD | Adamax | Adadelta | Adamax | Adagrad |
| Bias | zeros | ones | costant | ones | random normal |
| Weights | random uniform | random uniform | random normal | random uniform | random normal |
The five models are trained using the same 90% of the records in the dataset that were randomly selected and evaluated on the remaining 10%. All the values are normalized to between 0 and 1. The evaluation results of the five models are provided in Table II. The overall accuracy, while varying from model to model, is in general agreement with other methods.
Table II.
Evaluation Result of Five Individual Models.
| Model | Accuracy | ROC | Precision | Recall | F-ineasure |
|---|---|---|---|---|---|
| 1 | 0.7421 | 0.6906 | 0.5849 | 0.5568 | 0.5705 |
| 2 | 0.7679 | 0.7259 | 0.6242 | 0.6167 | 0.6204 |
| 3 | 0.7348 | 0.6953 | 0.5657 | 0.5928 | 0.5789 |
| 4 | 0.7513 | 0.7006 | 0.6012 | 0.5846 | 0.5846 |
| 5 | 0.7495 | 0.6993 | 0.5974 | 0.5688 | 0.5828 |
C. Results from the deep (n, k) Consensus Algorithm
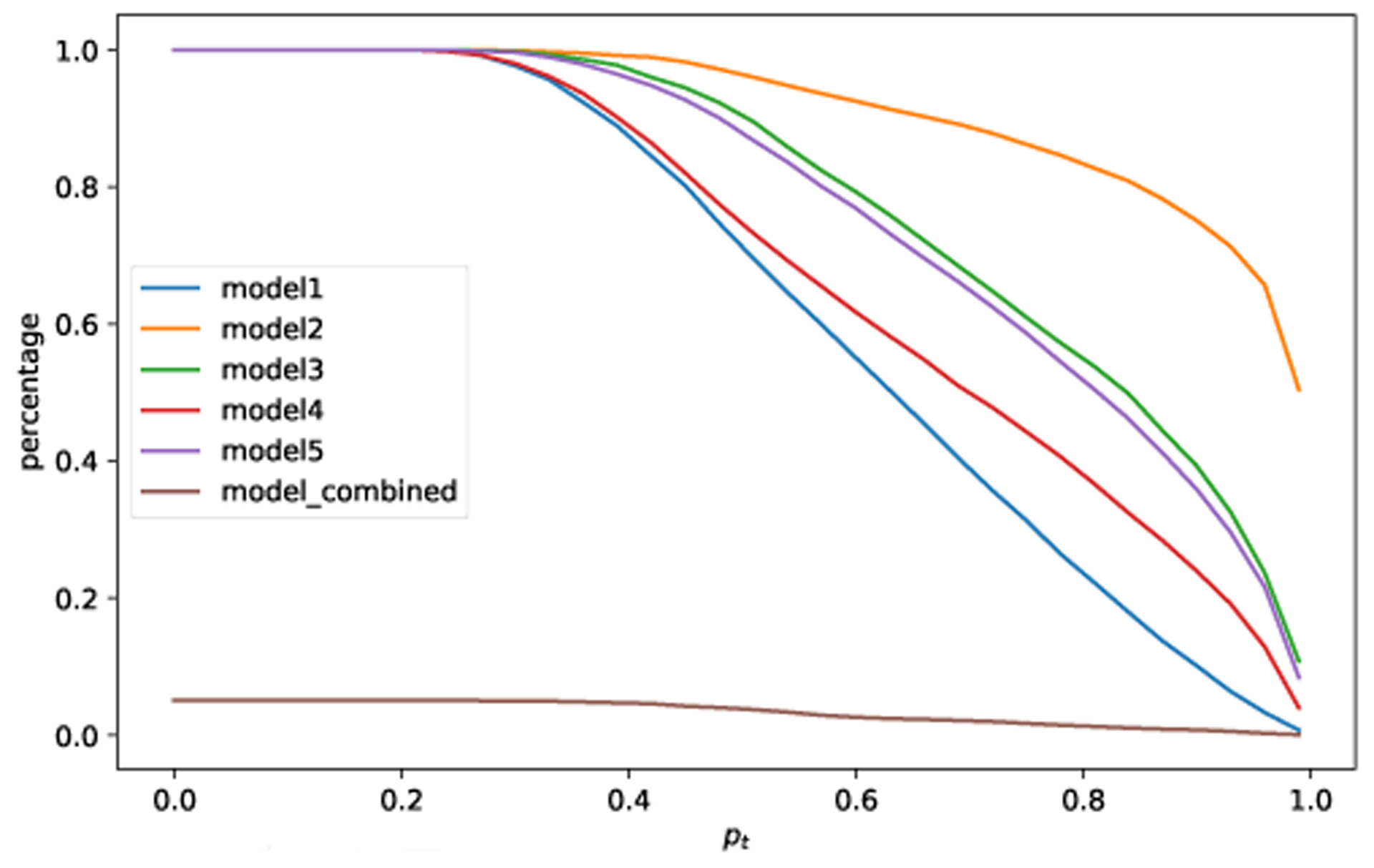
Here we illustrate the results using the proposed deep (n, k) consensus algorithm. Fig. 6 illustrates its effectiveness on one-year mortality prediction task. It depicts the comparison between the results from individual models and the consensus of the models. Fig. 6(a) and 6(b) show that when the threshold is low (e.g., pt < 0.5), (5,5) consensus achieves around 86% accuracy which is substantially higher than any single model, with around 67% of the test samples classified. We also check the effect of the (5,4) and (5,3) versions on the same dataset and observe that (5,4) consensus (i.e., Fig. 6(c) and 6(d)) works well also for this one-year mortality prediction dataset. For pt < 0.5, it provides around 81% accuracy with around 88% of the test samples classified. In all the (n, k) cases, we observe that the number of correctly classified samples among all the consistently classified ones increases with the threshold.
Fig. 6.

Change of accuracy and percentage of CCS samples with deep (n, k) consensus on the one-year patient mortality prediction dataset. (a) shows the increase of intrinsic accuracy while (5,5) consensus. (b) shows the percentage of CCS samples while (5,5) consensus. (c) shows the increase of intrinsic accuracy while (5,4) consensus. (d) shows the percentage of CCS samples while (5,4) consensus.
For DNN models, as they generalize similarly, the result is not sensitive to the choice to k (in most cases, n-1 or n should work well). In general, for DNNs, k should be close to n and pt should be 0.5 or higher. Different values of the parameters do allow one to fine-tune the trade-off between accuracy and percentage of classified samples. One can choose these two parameters based on how much one would like to emphasize more: accuracy or robustness. What percentage of samples should be retained, that should be as large as possible, while the accuracy should be as large as possible.
D. Interpretability Models
To systematically examine the proposed method, we first compute the Jacobian of the training samples and then compute the pairwise correlations. As described in section III, we group highly correlated clusters to achieve more robust interpretations. On this dataset, we have considered two subsets of highly correlated clusters among 8 representative clusters by our clustering algorithm. Fig. 7 depicts the averages of these subsets along with individual cluster averages. The higher values (i.e., extreme values - leftmost negative or rightmost positive ones) of the average vector correspond to the most relevant and important features. Since they are highly correlated, we notice similar behavior to the average on the subset for each of the clusters. Based on the sorted average of the first subset, we observe that leftmost features in the list have negative impact and rightmost features have positive impact on the positive class (“died within a year”). For the second subset, we notice almost identical features with the positive and negative impact on the positive class. To interpret validation samples, we look at the correlations with each subset. As a result, we have found that a specific set of features contributes positively to the “died within a year” class while some other set of features contributes positively to the “did not die within a year” class. Also, some features show neutral behavior to the classification task, which are placed in the middle of the spectrum with slight tendencies towards either positive or negative ends of the spectrum. Due to space limitations, we illustrate the contributions of only selected features. We have excluded ethnicity and religion-related features since most of them show neutral effect on the prediction outcome. Table III shows some examples of the most positive, negative features contributing to the positive class.
Fig. 7.
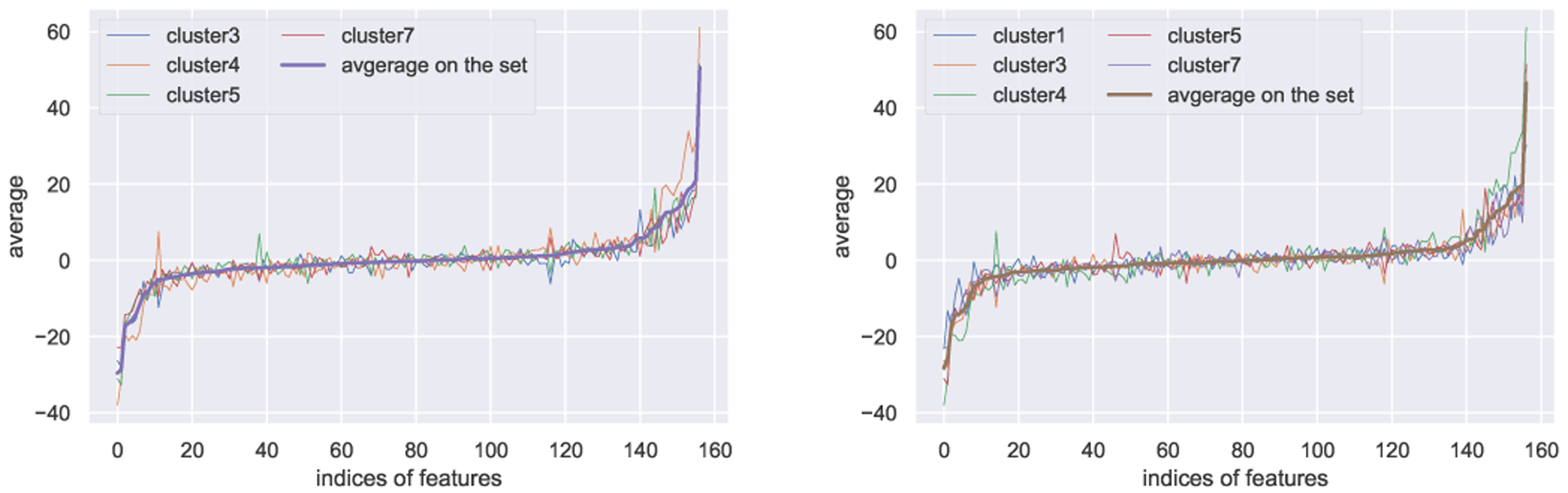
Average of the Jacobian difference vector of highly correlated cluster set. The thicker smooth curve depicts the average on the whole set. The other curves show the average on each cluster of that particular set. Left: First cluster subset. Right: Second cluster subset.
Table III.
Some Examples of Positively and Negatively Contributing Lab Features to Positive Class.
| Feature | Level of Contribution | Stand dev | Mean | Median | Minimum | Maximum |
|---|---|---|---|---|---|---|
| sodium | 46.54 | 3.32 | 138.63 | 138.73 | 97 | 160.27 |
| glucose | 19.74 | 43.6023 | 141.4247 | 130.47 | 51 | 543 |
| bicarbonate | −25.60 | 3.61 | 24.82 | 25 | 7 | 47.57 |
| chloride | −28.29 | 4.29 | 103.81 | 103.91 | 80.42 | 125.61 |
Note that the proposed algorithm is inherently scalable. Computing Jacobian is done implicitly by backpropagation; as such, the Jacobian difference vectors can be computed similarly to training the models for one epoch using mini batches. Furthermore, datasets of billion vectors can be clustered efficiently using product and residual vector quantization techniques (e.g., [28]).
E. Interpretability Evaluation
Any interpretability enhancement method for black-box models has to be rigorously evaluated. Measuring interpretability is not a straightforward process as there is no agreed-upon definition of interpretability in machine learning yet [29]. We base our evaluation of interpretability on the work of Yang et al. [30], considering three criteria: generalizability, fidelity, and persuasiveness. Also, we compare the interpretability of our model with two conventional machine learning models, i.e., support vector machine (SVM) and logistic regression (LR), as the baseline methods.
1). Evaluation On Generalizability:
The proposed interpretability method in this paper is based on the intrinsic characteristics of the activation functions used in each individual deep model (either ReLU or tanh). These activation functions either show locally linear or approximately linear behavior. Thus we consider this model to be semi-intrinsically interpretable. Yang et al. [30] define the generalizability evaluation of intrinsic interpretability task to be equivalent to the model evaluation using performance evaluation metrics such as accuracy, precision, and recall. According to the aforementioned results, the proposed consensus-based model significantly outperforms shallow models as well as the 5 individual deep-learning-based models.
2). Evaluation On Fidelity:
In a previous section, we demonstrate how the proposed consensus-based algorithm can effectively reject irrelevant samples. To further examine this capability of the proposed algorithm, similar experiments are conducted on the MNIST image dataset. The proposed algorithm can successfully reject adversarial (e.g., Fig. 8) and irrelevant samples (e.g., Fig. 9) in the case of image dataset too.
Fig. 9.
Percentage of classified overgeneralized samples with (5,5) consensus. The samples are from the CIFAR-10 dataset, i.e., out-of-distribution inputs for the MNIST dataset.
3). Evaluation On Persuasiveness:
The validity of the interpretability method in this paper is evaluated by a medical expert in a real-world setting. These evaluations show that if a patient has issues with other organ systems, he/she is at higher risk for developing a positive outcome (“die within a year”) with the exception of infection and endocrinology. In general, this indicates that a patient with issues with other organs is more susceptible to complications (i.e., comorbidities) along with AMI. Anemia diagnosed by hematocrit seems to significantly increase the risk of one-year mortality (positive outcome). Anemia defined by hemoglobin seems to be weakly predictive of one-year mortality. Liver and kidney dysfunction seem to be indicative of significant increased risk of one-year mortality, which is consistent with the fact that the patient is generally sicker and has more critical conditions. Also, a cluster of procedures performed on patients decreases the risk of one-year mortality. This suggests that invasive procedures can decrease such a risk. An observation to note is that some of the features that are strongly indicative of higher risk of one-year mortality seem to have an average within the normal range across the population. However, a closer look at their distribution profile in each class suggests that a slight deviation from the normal range associated with these features can enhance the risk for one-year mortality.
4). Comparisons with Baseline Evaluations:
Linear SVM and LR are considered to have intrinsic interpretability [31] and are quite popular for health data analysis [32]. We also try the clusters of SVM (CSVM) by Gu and Han [33] to check if this ensemble method improves the performance of the shallow learner for this particular classification task. We set the number of clusters to 10 and observe that increasing it does not significantly enhance the model performance. Table V includes a comparison of the performance of LR, SVM, CSVM, and the proposed consensus-based algorithm. To compare the feature-importance list as a result of interpretability enhancement of the consensus-based model to that of baseline models, we group features into top-n-features from n=10 to n=100 with step-size=10 and then calculate the percentage of similarity (♯ features ranked with same priority by both models/n). The detailed comparison is provided in Table IV. On average, the proposed consensus-based model shows 0.73 agreement with LR and 0.74 agreement with SVM on the feature-importance. These results confirm the fact that the proposed model shows linear behavior in local regions.
Table V.
Comparing the Performance of LR, SVM, and CSVM With Consesnsus-based Model.
| Model | Accuracy | ROC | Precision | Recall | F-measure |
|---|---|---|---|---|---|
| LR | 0.7845 | 0.7162 | 0.6923 | 0.5389 | 0.6060 |
| SVM | 0.7826 | 0.7066 | 0.7024 | 0.5089 | 0.5902 |
| CSVM | 0.7794 | 0.7257 | 0.6577 | 0.5868 | 0.6202 |
| Consensus | 0.8623 | 0.87 | 0.7631 | 0.6516 | 0.7030 |
Table IV.
Comparison of the Similarity of Resulting Feature-importance List From Intrinsically Interpretable Models and Proposed Consensus-based Deep Model.
| n-features (top n/2 pos, top n/2 neg) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| SVM | 0.8 | 0.7 | 0.8 | 0.725 | 0.68 | 0.683 | 0.728 | 0.762 | 0.777 | 0.8 |
| LR | 0.9 | 0.7 | 0.766 | 0.675 | 0.62 | 0.683 | 0.7 | 0.762 | 0.766 | 0.78 |
V. Related Work
The lack of interpretability of deep neural networks is a limiting factor of their adoption by healthcare and clinical practices. Existing interpretability enhancement methods can be categorized into integrated and post-hoc approaches [13]. The integrated methods utilize intrinsically interpretable models [34] but they usually suffer from lower performance compared to deep models. In contrast, the post-hoc interpretation methods attempt to provide explanations on an uninterpretable black-box model [35]. Such techniques can be further grouped into local and global interpretation categories. The local interpretation methods (e.g., LIME [36] and SHAP [37]) determine the importance of features regarding a specific instance. This is different from the global interpretability approach (e.g., this paper), which provides a certain level of transparency on the model considering the whole data [38]. Our method relies on the local Jacobian difference vector to capture the importance of input features. At the same time, clusters of the difference vectors capture robust model behavior supported by multiple training samples, reducing the complexity while retaining high accuracy.
VI. Conclusion and Future Work
In this paper, we have proposed an interpretability method by clustering local linear models of multiple models, capturing feature importance compactly using cluster means. Using consensus of multiple models allows us to improve classification accuracy and interpretation robustness. Furthermore, the proposed deep (n, k) consensus algorithm overcomes overgeneralization to irrelevant inputs and oversensitivity to adversarial examples, which is necessary to be able to have meaningful interpretations. For critical applications such as healthcare, it would be essential if causal relationships between features and the outcomes can be identified and verified using existing medical knowledge. This is being further investigated.
Acknowledgment
This study was partially supported by the National Institute on Aging of the National Institutes of Health (NIH) under Award R21AG061431 and FSU-UF Clinical and Translational Science Award UL1TR001427. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Footnotes
While a preliminary version of the algorithm was introduced in [21], no justification was provided.
References
- [1].Benjamin EJ, Virani SS, Callaway et al. , “Heart disease and stroke statistics-2018 update: a report from the american heart association.” Circulation, vol. 137, no. 12, p. e67, 2018. [DOI] [PubMed] [Google Scholar]
- [2].Members AF, Steg PG, James et al. , “ESC Guidelines for the management of acute myocardial infarction in patients presenting with ST-segment elevation: The Task Force on the management of ST-segment elevation acute myocardial infarction of the European Society of Cardiology (ESC),” European Heart Journal, vol. 33, no. 20, pp. 2569–2619, 08 2012. [DOI] [PubMed] [Google Scholar]
- [3].Reed GW, Rossi JE, and Cannon CP, “Acute myocardial infarction,” The Lancet, vol. 389, no. 10065, pp. 197–210, 2017. [DOI] [PubMed] [Google Scholar]
- [4].McNamara RL, Kennedy KF, Cohen DJ, Diercks DB, Moscucci M, Ramee S, Wang TY, Connolly T, and Spertus JA, “Predicting in-hospital mortality in patients with acute myocardial infarction,” Journal of the American College of Cardiology, vol. 68, no. 6, pp. 626–635, 2016. [DOI] [PubMed] [Google Scholar]
- [5].Kawaguchi K, Benigo Y, Verma V, and Pack Kaelbling L, “Towards understanding generalization via analytical learning theory,” 10 2018. [Google Scholar]
- [6].Shickel B, Tighe PJ, Bihorac A, and Rashidi P, “Deep ehr: a survey of recent advances in deep learning techniques for electronic health record (ehr) analysis,” IEEE journal of biomedical and health informatics, vol. 22, no. 5, pp. 1589–1604, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].L’heureux A, Grolinger K, Elyamany HF, and Capretz MA, “Machine learning with big data: Challenges and approaches,” IEEE Access, vol. 5, pp. 7776–7797, 2017. [Google Scholar]
- [8].Steele AJ, Denaxas SC, Shah AD, Hemingway H, and Luscombe NM, “Machine learning models in electronic health records can outperform conventional survival models for predicting patient mortality in coronary artery disease,” PloS one, vol. 13, no. 8, p. e0202344, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].LeCun Y, Bengio Y, and Hinton G, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, May 2015. [DOI] [PubMed] [Google Scholar]
- [10].Ahmad MA, Eckert C, and Teredesai A, “Interpretable machine learning in healthcare,” in Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics. ACM, 2018, pp. 559–560. [Google Scholar]
- [11].Zhang Q, Nian Wu Y, and Zhu S-C, “Interpretable convolutional neural networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 8827–8836. [Google Scholar]
- [12].Makary MA and Daniel M, “Medical error—the third leading cause of death in the us,” Bmj, vol. 353, p. i2139, 2016. [DOI] [PubMed] [Google Scholar]
- [13].Adadi A and Berrada M, “Peeking inside the black-box: A survey on explainable artificial intelligence (xai),” IEEE Access, vol. 6, pp. 52 138–52 160, 2018. [Google Scholar]
- [14].Zhang C, Bengio S, Hardt M, Recht B, and Vinyals O, “Understanding deep learning requires rethinking generalization,” CoRR, vol. abs/161103530, 2016. [Google Scholar]
- [15].Allen-Zhu Z, Li Y, and Liang Y, “Learning and generalization in overparameterized neural networks, going beyond two layers,” CoRR, vol. abs/181104918, 2018. [Google Scholar]
- [16].Neyshabur B, Li Z, Bhojanapalli S, LeCun Y, and Srebro N, “Towards understanding the role of over-parametrization in generalization of neural networks,” CoRR, 2018. [Google Scholar]
- [17].Wu L, Zhu Z, and Weinan E, “Towards understanding generalization of deep learning: Perspective of loss landscapes,” CoRR, vol. abs/170610239, 2017. [Google Scholar]
- [18].Goodfellow IJ, Shlens J, and Szegedy C, “Explaining and harnessing adversarial examples,” arXiv preprint arXiv:14126572, 2014. [Google Scholar]
- [19].Lecun Y, Bottou L, Bengio Y, and Haffner P, “Gradient-based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, November 1998. [Google Scholar]
- [20].Krizhevsky A, “Learning multiple layers of features from tiny images,” Tech. Rep, 2009. [Google Scholar]
- [21].Salman S and Liu X, “Overfitting mechanism and avoidance in deep neural networks,” CoRR, vol. abs/190106566, 2019. [Google Scholar]
- [22].Ju C, Bibaut A, and van der Laan MJ, “The Relative Performance of Ensemble Methods with Deep Convolutional Neural Networks for Image Classification,” arXiv e-prints, p. arXiv:170401664, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Xie S, Kong X, Gao J, Fan W, and Yu PS, “Multilabel consensus classification,” in 2013 IEEE 13th International Conference on Data Mining, 2013, pp. 1241–1246. [Google Scholar]
- [24].Simonyan K, Vedaldi A, and Zisserman A, “Deep inside convolutional networks: Visualising image classification models and saliency maps,” arXiv preprint arXiv:13126034, 2013. [Google Scholar]
- [25].Sundararajan M, Taly A, and Yan Q, “Axiomatic attribution for deep networks,” in Proceedings of the 34th International Conference on Machine Learning. PMLR, 2017, pp. 3319–3328. [Google Scholar]
- [26].Johnson AE, Pollard TJ, Shen L, Li-wei HL, Feng M, Ghas-semi M, Moody B, Szolovits P, Celi LA, and Mark RG, “Mimic-iii, a freely accessible critical care database,” Scientific data, vol. 3, p. 160035, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Barrett LA, Payrovnaziri SN, Bian J, and He Z, “Building computational models to predict one-year mortality in icu patients with acute myocardial infarction and post myocardial infarction syndrome,” AMIA Summits on Translational Science Proceedings, vol. 2019, p. 407, 2019. [PMC free article] [PubMed] [Google Scholar]
- [28].Matsui Y, Ogaki K, Yamasaki T, and Aizawa K, “Pqk-means: Billion-scale clustering for product-quantized codes,” CoRR, 2017. [Google Scholar]
- [29].Doshi-Velez F and Kim B, “Towards a rigorous science of interpretable machine learning,” arXiv preprint arXiv:170208608, 2017. [Google Scholar]
- [30].Yang F, Du M, and Hu X, “Evaluating explanation without ground truth in interpretable machine learning,” arXiv preprint arXiv:190706831, 2019. [Google Scholar]
- [31].Friedler SA, Roy CD, Scheidegger C, and Slack D, “Assessing the local interpretability of machine learning models,” arXiv preprint arXiv:190203501, 2019. [Google Scholar]
- [32].Wang J, Li L, Yang P, Chen Y, Zhu Y, Tong M, Hao Z, and Li X, “Identification of cervical cancer using laser-induced breakdown spectroscopy coupled with principal component analysis and support vector machine,” Lasers in medical science, vol. 33, no. 6, pp. 1381–1386, 2018. [DOI] [PubMed] [Google Scholar]
- [33].Gu Q and Han J, “Clustered support vector machines,” in Artificial Intelligence and Statistics, 2013, pp. 307–315. [Google Scholar]
- [34].Melis DA and Jaakkola T, “Towards robust interpretability with self-explaining neural networks,” in Advances in Neural Information Processing Systems, 2018, pp. 7786–7795. [Google Scholar]
- [35].Koh PW and Liang P, “Understanding black-box predictions via influence functions,” in Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017, pp. 1885–1894. [Google Scholar]
- [36].Ribeiro MT, Singh S, and Guestrin C, “Why should i trust you?: Explaining the predictions of any classifier,” in Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. ACM, 2016, pp. 1135–1144. [Google Scholar]
- [37].Lundberg SM and Lee S-I, “A unified approach to interpreting model predictions,” in Advances in neural information processing systems, 2017, pp. 4765–4774. [Google Scholar]
- [38].Du M, Liu N, and Hu X, “Techniques for interpretable machine learning,” arXiv preprint arXiv:180800033, 2018. [Google Scholar]


