A Novel Computational Model of the Rabbit Atrial Cardiomyocyte With Spatial Calcium Dynamics

Abstract

Models of cardiac electrophysiology are widely used to supplement experimental results and to provide insight into mechanisms of cardiac function and pathology. The rabbit has been a particularly important animal model for studying mechanisms of atrial pathophysiology and atrial fibrillation, which has motivated the development of models for the rabbit atrial cardiomyocyte electrophysiology. Previously developed models include detailed representations of membrane currents and intracellular ionic concentrations, but these so-called “common-pool” models lack a spatially distributed description of the calcium handling system, which reflects the detailed ultrastructure likely found in cells in vivo. Because of the less well-developed T-tubular system in atrial compared to ventricular cardiomyocytes, spatial gradients in intracellular calcium concentrations may play a more significant role in atrial cardiomyocyte pathophysiology, rendering common-pool models less suitable for investigating underlying electrophysiological mechanisms. In this study, we developed a novel computational model of the rabbit atrial cardiomyocyte incorporating detailed compartmentalization of intracellular calcium dynamics, in addition to a description of membrane currents and intracellular processes. The spatial representation of calcium was based on dividing the intracellular space into eighteen different compartments in the transversal direction, each with separate systems for internal calcium storage and release, and tracking ionic fluxes between compartments in addition to the dynamics driven by membrane currents and calcium release. The model was parameterized employing a population-of-models approach using experimental data from different sources. The parameterization of this novel model resulted in a reduced population of models with inherent variability in calcium dynamics and electrophysiological properties, all of which fall within the range of observed experimental values. As such, the population of models may represent natural variability in cardiomyocyte electrophysiology or inherent uncertainty in the underlying experimental data. The ionic model population was also able to reproduce the U-shaped waveform observed in line-scans of triggered calcium waves in atrial cardiomyocytes, characteristic of the absence of T-tubules, resulting in a centripetal calcium wave due to subcellular calcium diffusion. This novel spatial model of the rabbit atrial cardiomyocyte can be used to integrate experimental findings, offering the potential to enhance our understanding of the pathophysiological role of calcium-handling abnormalities under diseased conditions, such as atrial fibrillation.

1. Introduction

Mathematical models of cardiac electrophysiology (EP) have advanced significantly over the past decades, and are valuable tools for gaining physiological insight from the expanding pool of experimental data (Heijman et al., 2016; Vagos et al., 2018). While animal models remain the primary source of experimental data on ion channels and electrical activity in the heart, computational models of different animal species constitute an important tool for knowledge extraction and translation between species. The rabbit has been a particularly useful animal model to study different aspects of cardiac electrophysiology and arrhythmia, given the similarities of their electrophysiological properties to the human (Ravelli and Allessie, 1997; Eijsbouts et al., 2003; Rouge et al., 2006; Greiser et al., 2014; Li et al., 2014; Wang et al., 2017; Frommeyer et al., 2019). The wide application of the experimental rabbit model has motivated the development of rabbit-specific mathematical models of cardiomyocyte (CM) electrophysiology (see e.g., Hilgemann and Noble, 1987; Demir et al., 1994, 1999; Lindblad et al., 1996; Kurata et al., 2002; Shannon et al., 2004; Mahajan et al., 2008; Aslanidi et al., 2009; Maltsev and Lakatta, 2009), which incorporate rabbit-specific formulations of ionic currents.

One important characteristic of rabbit atrial CMs is the lack of a well-developed T-tubule (TT) system (Tidball et al., 1991; Blatter, 2017), which leads to a characteristic U-shaped wave front in line scans of intracellular calcium, indicating asynchronous Ca²⁺ release (Smyrnias et al., 2010; Greiser et al., 2014). This shape results from the “fire-diffuse-fire” response (Coombes and Timofeeva, 2003), in which a Ca²⁺ wave is initiated by L-type Ca²⁺ channels (LTCC) at the cell periphery and subsequently propagates toward the center of the cell in a saltatory manner through diffusion and Ca²⁺-induced Ca²⁺ release (Bootman et al., 2002, 2011). Similar U-shaped Ca²⁺ propagation patterns have been observed in atrial CMs of other small animal species, such as cat (Hüser et al., 1996; Blatter et al., 2003), and rat (Mackenzie et al., 2004; Bootman et al., 2011). However, it has also been observed in rat atrial CMs that Ca²⁺ signals originating at the cell periphery typically did not fully propagate to the center (Bootman et al., 2011). This effective truncation of the Ca²⁺ wave was due to the lack of TTs, increased Ca²⁺ buffering capacity, and the so-called “diffusion barrier” of the mitochondria and Serca2a in these cells. This lack of regeneration of the Ca²⁺ signal results in a progressive damping of the centripetal Ca²⁺ wave with a peak amplitude and rate of Ca²⁺ rise significantly lower at central regions as compared to the periphery (Mackenzie et al., 2004; Trafford et al., 2013). These observations have also been replicated in a model of Ca²⁺ propagation in a CM without TTs, demonstrating that Ca²⁺ propagation or lack thereof results from a complex interplay between different effectors of the Ca²⁺ handling system (Thul et al., 2012). The reduced systolic Ca²⁺ levels and delayed Ca²⁺ signals in central regions associated with the lack of TTs in some atrial CMs, as well as remodeling-induced detubulation, can thus have a profound effect on electrophysiological changes driven by ionic current remodeling or β-adrenergic stimulation (Trafford et al., 2013).

Despite the important role that spatial intracellular Ca²⁺ dynamics can play in the generation and maintenance of aberrant electrical activity in atrial cells and tissues, previously developed mathematical models of the rabbit atrial CM do not incorporate spatial description of Ca²⁺ movement within the cell. Therefore, although useful in reproducing whole-cell characteristics of rabbit EP, these models are not able to assess the sub-cellular mechanisms of altered Ca²⁺ propagation and their role in arrhythmic activity. In contrast, models with spatial Ca²⁺ description would permit assessment of the effect of sub-cellular structures on intracellular Ca²⁺ dynamics and Ca²⁺ wave propagation, but such models have not been developed for rabbit atrial physiology.

In this paper, we describe the development of a novel model of the rabbit atrial CM with spatial description of ionic species and the Ca²⁺ handling system. The structure of the model allows simulation of the spatial distribution of Ca²⁺, as well as the propagation of intracellular Ca²⁺ over time. We parameterized the maximum conductances in the model using a “population of models” approach to reproduce the normal electrophysiological properties of the rabbit, as supported by experimental data reported in the literature. The result is a population of models that all closely approximate the experimental data, but with differences in the models that appropriately reflect individual variability or inherent uncertainty in the data. We shall henceforth refer to this selected population as “control population.” We are aware that the dynamics of Ca²⁺ wave propagation are most directly affected by parameters that modulate the SR content, and Ca²⁺ release and uptake kinetics. However, the aim of the present study was not to focus on the role of these parameters in modulating Ca²⁺ wave propagation, but instead to parameterize the maximum conductances of ionic currents and asses their effect on intracellular Ca²⁺ dynamics Thus, the motivation to create a spatial model was to study the model's behavior in terms of this radial Ca²⁺ flux as we changed the maximum conductances of ion currents, and our primary hypothesis was that variations in ion-channel expression and function (in particular of Ca²⁺ currents) may contribute to alterations in radial Ca²⁺ flux. We then used the control population to (1) assess if changes in current conductances have an effect on Ca²⁺ propagation dynamics; (2) to quantify possible correlations between Ca²⁺ properties at the membrane and at the center of cell; and (3) to query the underlying mechanisms of the differences observed in the Ca²⁺ propagation patterns across the control population.

2. Methods

2.1. Model Development

The rabbit atrial CM model was developed based on the previously published human atrial CM model by Voigt & Heijman (Voigt et al., 2014), which is a spatial model with the calcium handling system divided into discrete domains. We modified this model to incorporate ion current formulations from the non-spatial rabbit atrial CM model by Lindblad et al. (1996) and Aslanidi et al. (2009) to reflect the rabbit electrophysiology.

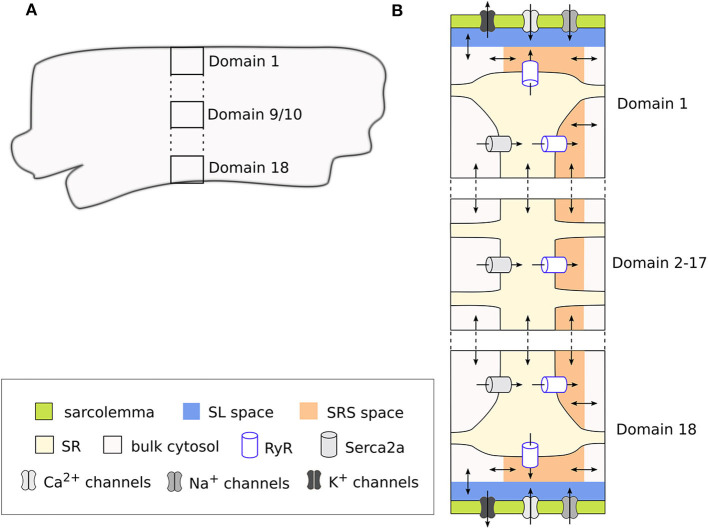
The model is structured into discrete segments in the longitudinal direction of the CM, and each segment is further divided into discrete domains in the radial (or transversal) direction. This architecture allows simulating the radial flux of Ca²⁺ from the membrane toward the center of the CM (i.e., centripetal diffusion) through an implementation of Ca²⁺ diffusion terms. Thus, a total of 18 domains represent a one-dimensional cross-section of the cell, where the two outermost domains (1 and 18) correspond to the region close to the cell membrane. These domains therefore include the sarcolemmal currents, Ca²⁺ release units (CRU), and Ca²⁺ buffers. In contrast, the inner domains (2–17) are not in direct contact with the cell membrane and contain only the CRUs and Ca²⁺ buffers. The inner domains contain a cytosolic space, the sarcoplasmic reticulum (SR), and a sub-SR space (SRS), while the membrane domains also include a subsarcolemmal (SL) space. In domains 1 and 18 the SRS represents a junctional space in which LTCC and the ryanodine receptors (RyR) interact, which is indicated with “junc.” This corresponds to the dyadic space in other CM models. We used a cell volume of 16 pL based on an estimated cell length of 130 μm (Lindblad et al., 1996) and a radius of 6.3 μm (Greiser et al., 2014). This volume is divided equally across the 18 domains, that the cytosolic, SR and SRS compartments make up 65, 3.5, and 0.1% of each domain, respectively, and that in addition the SL space takes up 2% of the cell volume. The domains and compartments, as well as the ionic fluxes between them, are schematically illustrated in Figure 1.

Figure 1.

Schematic representation of a segment of the rabbit CM model showing the discrete cell domains and different intracellular compartments. A single segment corresponds to the cross section of the CM (A), and is composed of 18 domains. Here only 3 domains are represented for simplicity, with the vertical dots representing the omitted domains. The membrane domains (1 and 18) contain the sarcolemmal currents and Ca²⁺ handling system, while the inner domains (2–17) contain only the Ca²⁺ handling system (B). Each membrane domain contains five different compartments: cytosolic space, sarcoplasmic reticulum (SR), sub-SR (SRS) space, and subsarcolemmal (SL) spaces, which together constitute the cleft space. Ca²⁺ diffuses between the different compartments in the model, and between adjacent domains and segments. Because we use a deterministic RyR formulation, the model is symmetrical around the two central domains.

Because in this model Ca²⁺ enters the cell only through the membrane domains, CaTs in the inner domains are dependent on diffusion from the periphery. Thus, the model allows to reproduce radial gradients and possible heterogeneities in CaTs arising from local control mechanisms. The model also includes implementations of both deterministic and a stochastic RyR models. However, for the sake of simplicity, we have employed the deterministic formulation of the RyR, and thus in our simulations only one segment was simulated, since segments are identical when using the deterministic model.

The membrane model includes Ca²⁺ currents I_CaL and I_CaT; the fast Na⁺ current I_Na; repolarizing K⁺ currents I_to1, I_Kr, I_Ks, and I_K1, as well as three background currents I_Cab, I_Nab, and I_Clb. Additionally, the model includes the ionic currents of the Na⁺-Ca²⁺ exchanger (I_NCX); the Na⁺-K⁺ pump (I_NaK); and the plasmalemmal Ca²⁺ pump (I_CaP). The total membrane current in the model is the sum of all these currents:

$$\begin{array}{l}{I}_{\text{C}{\text{a}}_{\text{tot}}}=(I_{\text{Ca}{\text{L}}_{\text{junc}}}+I_{\text{Ca}{\text{L}}_{\text{SL}}})+(I_{\text{Ca}{\text{T}}_{\text{junc}}}+I_{\text{Ca}{\text{T}}_{\text{SL}}})+(I_{\text{Ca}{\text{P}}_{\text{junc}}}+I_{\text{Ca}{\text{P}}_{\text{SL}}})+\\ +(I_{\text{Ca}{\text{b}}_{\text{junc}}}+I_{\text{Ca}{\text{b}}_{\text{SL}}})-2(I_{\text{NC}{\text{X}}_{\text{junc}}}+I_{\text{NC}{\text{X}}_{\text{SL}}}).\end{array}$$

$$\begin{array}{l}{I}_{\text{N}{\text{a}}_{\text{tot}}}=(I_{\text{N}{\text{a}}_{\text{junc}}}+I_{\text{N}{\text{a}}_{\text{SL}}})+3(I_{\text{NC}{\text{X}}_{\text{junc}}}+I_{\text{NC}{\text{X}}_{\text{SL}}})-3\times (I_{\text{Na}{\text{K}}_{\text{junc}}}+I_{\text{Na}{\text{K}}_{\text{SL}}})+\\ +(I_{\text{Na}{\text{b}}_{\text{junc}}}+I_{\text{Na}{\text{b}}_{\text{SL}}}).\end{array}$$

$$\begin{array}{l}{I}_{{\text{K}}_{\text{tot}}}=I_{\text{to}}+I_{\text{Kr}}+I_{\text{Ks}}+I_{\text{K}1}-2\times (I_{\text{Na}{\text{K}}_{\text{junc}}}+I_{\text{Na}{\text{K}}_{\text{SL}}})+I_{\text{stim}}.\end{array}$$

$$\begin{array}{l}{I}_{\text{tot}}=I_{\text{C}{\text{a}}_{\text{tot}}}+I_{\text{N}{\text{a}}_{\text{tot}}}+I_{{\text{K}}_{\text{tot}}}+I_{\text{Clb}}\end{array}$$

$$\begin{array}{l}\frac{dV}{dt}=-\frac{1}{C_{\mathrm{\text{m}}}}{I}_{\mathrm{\text{tot}}}\end{array}$$

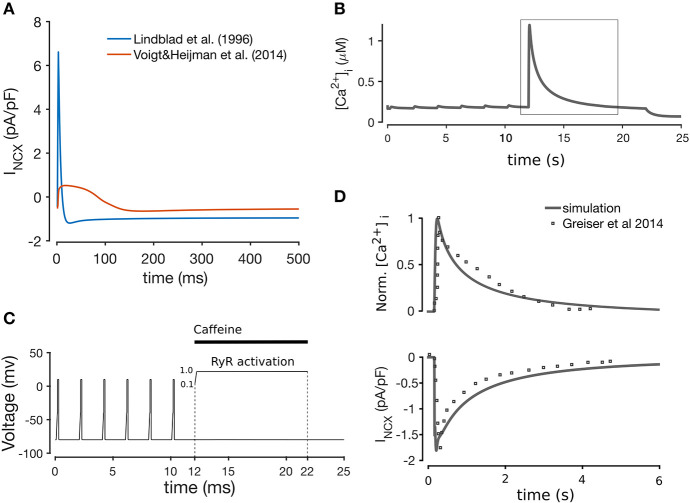
Most of the formulations were adopted from Aslanidi et al. (2009), which in turn are modifications of the formulations in Lindblad et al. (1996). We included the background chloride current (I_Clb) from the Lindblad et al. model, since a chloride current has been reported in rabbit atrial CMs (Kanaporis and Blatter, 2016). The formulation of I_NCX was taken from Voigt et al. (2014) (equations provided in the Supplementary Material), originally described in Weber et al. (2001), since we found this current to replicate more realistically the forward and reverse modes of the Na⁺-Ca²⁺ exchanger observed in the rabbit Bers (2002), as shown in Figure 2A. We tested this model component specifically by simulating a caffeine-induced Ca²⁺ release protocol to assess Ca²⁺ extrusion rate through the NCX, shown in Figure 2B. The caffeine-induced Ca²⁺ release protocol used was as follows: the model was paced at 0.5 Hz (after being paced to steady state) for 12 s (6 beats), and then caffeine application was simulated by increasing RyR2 activation to 1.0 over the course of 10 ms, and keeping the channels fully open for another 10 s. The effect of the caffeine was then removed by unclamping the RyR activation for 3 s. This protocol is illustrated in Figure 2C. As illustrated in Figure 2D, the normalized CaT and decay time of I_NCX closely matched experimental data in Greiser et al. (2014).

Figure 2.

(A) Comparison between the Lindblad et al. (1996) and Voigt et al. (2014) models of the Na⁺-K⁺ exchanger, showing that the latter is closer to the I_NCX shape observed experimentally (Bers, 2002). Simulation of caffeine-induced Ca²⁺ release (B) using the voltage clamp protocol shown in (C), whereby application of caffeine is simulated through the instant opening of the RyRs for 10 s with subsequent closing. (D) Comparison of I_NCX and normalized CaT with experimental data from Greiser et al. (2014), after pacing at 0.5 Hz for 12 s, and a 10 s quiescent period.

The model's spatial description of Ca²⁺ and Na⁺ allows for these ionic species to vary between domains. Specifically, Ca²⁺ concentrations in the bulk cytosolic, SL, SR, and SRS spaces are updated independently in each compartment and in each model domain. Similarly, Na⁺ concentrations are updated separately in the SL, junc (SRS), and bulk cytosolic spaces, but the cytosolic Na⁺ trace is common to all domains, so that only this is updated in the inner domains. The concentrations and fluxes of Ca²⁺ and Na⁺ across the different model compartments in a membrane domain are schematically shown in Supplementary Figure 1. The mass balance equations for Ca²⁺ can be found in the supplementary material of Voigt et al. (2014), and the equations for Na⁺ are provided in the Supplementary Material.

The rabbit atrial CM model was implemented in C++, and the state equations were solved using a forward Euler scheme. All simulations were performed on the Abel computer cluster from the University of Oslo, running the Linux Operating system (64 bit CentOS 6). The source code of the model is available at https://github.com/marciavagos/Rabbit_model.git.

2.2. Parameterization of Ionic Currents

We initially implemented the model using the original published parameters from Aslanidi et al., which resulted in an action potential (AP) that was morphologically similar to experimentally measured APs, but did not match in terms of quantifiable metrics. The action potential duration at 90% repolarization (APD₉₀) was 143 ms, which is longer than the reported 120 ms, and the resting membrane potential (RMP) was around −74 mV as compared to the −80 mV reported in literature. Additionally, the CaT amplitude (CaT-A) in the baseline model was only about 0.09 μM, compared to the ~1.0 μM amplitude in simulated CaTs by Lindblad et al. (1996), and Aslanidi et al. (2009). The model also showed a suppression of the Ca²⁺ signal at the center of cell. Ca²⁺ measurements of rabbit atrial CMs in Blatter (2017) show a partial suppression of the central CaT compared to the peripheral CaT. In contrast, measurements from Greiser et al. (2014) show a fully regenerative CaT in control rabbit atrial CMs. These differing findings seem to suggest a natural variability in the intracellular regeneration of the Ca²⁺ signal in rabbit atrial CMs. However, as far we know there is no evidence that complete absence of Ca²⁺ release in central regions is present in rabbit atrial CMs in the absence of disease-related remodeling, thus we considered this to represent an unphysiological behavior.

In order to adjust the model parameters to match reported experimental CaT and AP data (Qi et al., 1994; Muraki et al., 1995; Wang et al., 1995; Lindblad et al., 1996; Aslanidi et al., 2009; Greiser et al., 2014; Kanaporis and Blatter, 2016; Hou et al., 2018), we employed a population-of-models approach to scale the maximum conductances of the 13 ionic currents in the model. This approach is useful to perform parameter fitting, while at the same time allowing uncertainty and natural variability to be incorporated into the models (Amrita et al., 2012; Sánchez et al., 2014). We note that the populations-of-models approach is used in this work in a somewhat different context than done in previous works. While this approach has more commonly been used to incorporate variability into a “calibrated” model to either test hypotheses, or perform parameter sensitivity analysis (as done in e.g., Sarkar and Sobie, 2010; Amrita et al., 2012; Sánchez et al., 2014; Chang et al., 2015; Johnstone et al., 2016; Morotti and Grandi, 2017), here we have applied the method to parameterize the model in regard to uncertain parameters, in this case the maximum conductances. A population is constructed by randomly sampling the model parameters from specified probability distributions, thereby generating a population of several “baseline” models. For the present population, the 13 maximum conductances were varied over a range between 25 and 400% of their published values, and resampled from uniform distributions using Latin Hypercube sampling. Such a large degree of variation was chosen to incorporate as much variability as possible, allowing for the population to capture the natural variability and uncertainty in the data. The initial population consisted of 3,000 models, which were all paced at 2 Hz pacing for 2 min to ensure approximation to steady state, and then the last five beats were recorded for analysis. The varied maximum conductances and their respective nominal (published) values are listed in Table 1, and the initial ionic concentrations are listed in Supplementary Table 2.

Table 1.

List of the maximum conductances of the ionic currents in the model and their nominal values.

Parameter	Nominal value	Description
GCaL	0.144 nS/pF	Maximum conductance of the L-type Ca2+ channel
GCaT	0.120 nS/pF	Maximum conductance of the T-type Ca2+ channel
${\text{I}}_{\mathrm{\text{NCX}}}^{max}$	4.41 pA/pF	Maximum flux of the Ca2+-Na+ exchanger
${\text{I}}_{\mathrm{\text{NaK}}}^{max}$	1.288 × 10−3 nA/pF	Maximum flux of the Na+-K+ pump
${\text{I}}_{\mathrm{\text{CaP}}}^{max}$	0.190 nS/pF	Maximum flux of the plasmalemmal Ca2+ ATPase
GNa	0.028 × 10−3 µL/(spF)	Maximum conductance of the fast Na+ channel
Gto	0.200 nS/pF	Maximum conductance of the transient outward K+ channel
GKr	0.070 nS/pF	Maximum conductance of the rapidly activating delayed rectifier K+ channel
GKs	0.050 nS/pF	Maximum conductance of the slowly activating delayed rectifier K+ channel
GK1	0.203 nS/pF	Maximum conductance of the inward rectifier K+ channel
GCab	0.4 × 10−3 nS/pF	Maximum conductance of the background Ca2+ channels
GNab	0.4 × 10−3 nS/pF	Maximum conductance of the background Na+ channels
GClb	2.4 × 10−3 nS/pF	Maximum conductance of the background K+ channels

Models in the population were then selected against experimental data from measurements of rabbit APs and CaTs to select models whose APs and CaTs represent typical rabbit-like morphology (Qi et al., 1994; Muraki et al., 1995; Wang et al., 1995; Lindblad et al., 1996; Aslanidi et al., 2009; Greiser et al., 2014; Kanaporis and Blatter, 2016; Hou et al., 2018).

Finally, uncertainties of output measures of APs and CaTs were defined through the mean and standard deviation (std).

2.3. Model Selection

Since we allowed a large degree of variation in the model parameters, the initial population included a number of non-physiological models. The second step of the population-of-models approach was to select a subset of models that matched previous experimental recordings, to create a control population. Experimentally measured APs of rabbit atrial CMs reported in literature are rather inconsistent. For instance, Muraki et al. (1995), and Wang et al. (1995) recorded APs with APD₉₀ values of 93 and 103 ms, respectively, while Yamashita et al. (1995) reported 70 ms. Lindblad et al. (1996) reported a similar APD₉₀ of 80 ms at 2 Hz, while more recent studies have reported higher values. Greiser et al. (2014) measured APD₉₀ in rabbit CMs paced at 2 Hz between 100 and 140 ms, in agreement with the 130 ms Hou et al. (2018) at 1 Hz. APD₅₀ measured in Wang et al. (1995) and Hou et al. (2018) was 44 (at 2 Hz) and 55 ms (at 1 Hz), respectively, while in Yamashita et al. (1995) this was about 18 ms in the crista terminalis, and 38 ms in pectinate muscle CMs. Additionally, APD₄₀ in Qi et al. (1994) was 30 ms in left atrium, and 51 ms in right atrium at 1 Hz. APD₂₀ in Hou et al. (2018) was also between 13 to 17 ms. Given this wide range of reported APD₅₀ and APD₄₀ values, we required APD₄₀ to be between of 20 and 60 ms.

AP amplitude (APA) has been reported at around 100 mV (Qi et al., 1994; Muraki et al., 1995; Aslanidi et al., 2009; Hou et al., 2018), and 120 mV (Lindblad et al., 1996; Kanaporis and Blatter, 2016). Reported values of RMP are more consistent across sources, with most reporting around -80 mV (Qi et al., 1994; Muraki et al., 1995; Yamashita et al., 1995; Aslanidi et al., 2009; Greiser et al., 2014; Hou et al., 2018), although Lindblad et al. reported an RMP of -71 mV (Lindblad et al., 1996). Given this heterogeneity of measured electrophysiological properties of CMs, there is no single generic model of an atrial cell, which motivated our choice of a population-of-models approach to parameterize the model.

To our knowledge, absolute values of intracellular Ca²⁺ levels have only been reported by Kettlewell et al. (2019), who measured an average diastolic and systolic [Ca²⁺]_i, and CaT amplitude of about 0.07, 0.57, and 0.51 μM, respectively. Additionally, Lindblad et al. (1996) assumed a resting Ca²⁺ of 50 nM, and peak Ca²⁺ levels in their model simulations were within ~0.1 and ~1.0 μM. CaTs measured from fluorescence imaging of rat (Mackenzie et al., 2001, 2004) and human (Voigt et al., 2012, 2014) atrial CMs also show amplitude values in this range. Therefore, we excluded models whose whole-cell CaT amplitude was outside this range. The rise time of the CaT was also constrained to be no larger than 100 ms at 2 Hz pacing (Greiser et al., 2014). Additionally, [Na⁺]_i was constrained to be between 6.5 and 12.5 mM, which corresponds to reported values in rabbit atrial cells (Hilgemann and Noble, 1987; Greiser et al., 2014). Finally, models showing early after-depolarizations (EAD) and alternans were also manually excluded.

These experimental metrics are compiled in Table 2 for convenience, and the output properties and corresponding value ranges considered in the selection of the models are listed in Table 3. These properties were determined as the average of the values calculated for the five recorded beats.

Table 2.

Experimental values of electrophysiological parameters obtained from literature.

Source	APD90 (ms)	APD50 (ms)	APD40 (ms)	APD20 (ms)	APA (mV)	RMP (mV)	CaT amp. (µM)	[Na+]i (mM)
Muraki et al. (1995)	93	–	–	–	~100	–	–	–
Wang et al. (1995)	103	44 (2 Hz)	–	–	–	–	–	–
Yamashita et al. (1995)	70	18 (CT) 38 (PM)	–	–	–	–	–	–
Lindblad et al. (1996)	80 (2 Hz) 55 (1 Hz)	–	–	–	–	−71	–	–
Qi et al. (1994)	–	–	30 (LA), 51 (RA) (1 Hz)	–	~100	–80	–	–
Aslanidi et al. (2009)	–	–	–	–	~100	−80	–	–
Voigt et al. (2012) (human)	–	–	–	–	–	–	[0.1–1]	–
Greiser et al. (2014)	[100–140] (2 Hz)				–	−80	–	[6.5–12.5]
Kanaporis and Blatter (2016)	–	–	–	–	~120	–	–	–
Hou et al. (2018)	~130	55 (1 Hz)	–	13–17	~100	−80	–	–
Kettlewell et al. (2019)	–	–	–	–	–	–	[0.1–1]	–
Mackenzie et al. (2004) (rat)	–	–	–	–	–	–	[0.1–1]	–
Hilgemann and Noble (1987)	–	–	–	–	–	–	–	[6.5–12.5]

Table 3.

Values of electrophysiological parameters used for selecting models in the control population.

Metric	Calibration criteria	All 3000 models		Calibrated
		Mean	Std	Mean	Std
APD90 (ms)	80–120	165	126	96	13
APD40 (ms)	20–60	98	91	57	6
APA (mV)	90–140	102	31	121	7
RMP (mV)	< −75	−57	37	−78	2
CaT-A (μM)	0.1–1.0	1.0	2.9	0.30	0.05
[Na+]i (mM)	8–12	11.7	6.4	9.5	2.0
CaT rise time	<100 ms	89	60	97	11
EAD	Absent	38%		Absent
Alternans	Absent	18%		Absent

(Values were based on experimental data in Table 2), and corresponding mean and standard deviation (std) values of the original and control populations.

2.4. Analysis of Calcium Wave Propagation

The primary focus of this paper is on Ca²⁺ dynamics, and the Ca²⁺ signal and wave dynamics were subject to a more extensive analysis than the other output variables. Spatio-temporal plots of Ca²⁺ dynamics, resembling line-scan plots of Ca²⁺ fluorescence, were created to asses the radial propagation of Ca²⁺. More detailed analysis of spatial variations in Ca²⁺ signal morphology was done by comparing plots of the cytosolic CaTs (Ca_i) in the membrane domains (domains #1 and #18), and in the central domains (domains #9 and #10). The membrane and central CaTs are denoted as CaT_m and CaT_c, respectively. When using deterministic RyR formulations, the model is symmetric about the cell center, resulting in identical CaTs in domains 1 and 18, as well as in domains 9 and 10. Whole-cell CaTs were also obtained as the mean bulk cytosolic CaTs of the 18 domains.

Additionally, we extracted and analyzed a number of relevant metrics that characterize CaT_m and CaT_c traces at steady state (20 min pacing). Specifically, we analyzed the rise time (measured from onset of the CaT to peak), duration at 50% decay (CD50), and amplitude, in addition to the time difference between peaks of CaT_c and CaT_m, as measured from AP onset (CaT_delay), represented schematically in Figure 3. The Ca²⁺ metrics presented were again determined as the average of the values calculated for the last 5 beats.

Figure 3.

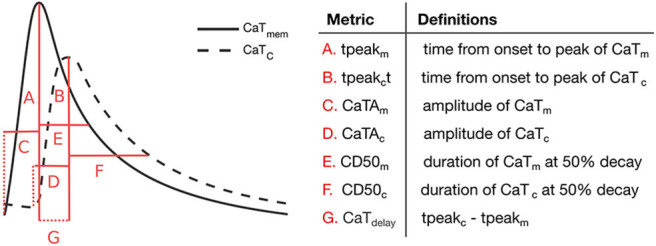
Ca²⁺ transient metrics defined to compare peripheral and central CaT traces, and corresponding descriptions.

We additionally extracted Ca_SR and [Na⁺]_i traces to analyse in relation to the other CaT metrics. In our analyses, we determined Ca_SR and [Na⁺]_i as the mean value during each beat, with Ca_SR corresponding to the average over all cell domains.

Finally, we performed correlation analysis to identify significant correlations between selected model parameters and output variables. We analyzed the correlations between the maximum ion channel conductances and the Ca²⁺ metrics defined above, as well as correlations between the Ca²⁺ metrics in the membrane domains and in the central domains, and between Ca_SR and [Na⁺]_i and the central Ca²⁺ metrics. The correlations were determined using Kendall's tau (τ), since the variables followed discrete distributions. Significance was determined with 95% confidence, and all data analyses were performed in Matlab R2017a employing custom routines.

3. Results

3.1. Population of Models

Varying the maximum conductances between 25 and 400% resulted in an initial population of 3,000 models with a large degree of variation in AP and CaT properties. Calibration of the population by constraining output values to the ranges in Table 3 resulted in the selection of 16 out of 3,000 models. Restricting values of APD₉₀, APD₄₀, and CaT-A was responsible for excluding the majority of models, with 175 models satisfying the requirements for these three parameters. Mean and standard deviation of APD₉₀, APD₄₀, APA, RMP, CaT-A, [Na⁺]_i, and CaT rise time for the original and control populations are shown in Table 3. EAD and alternans in the entire population are shown as % of occurrence.

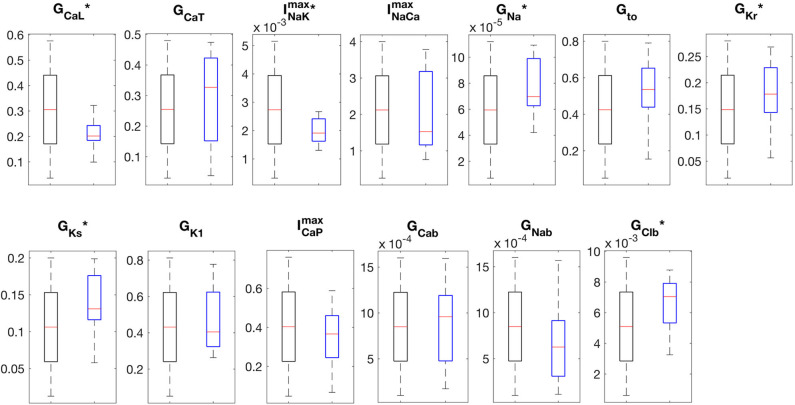
The APs and CaTs of the control population are shown in Figures 4A,B. Although the model selection step obviously reduced the variability in APs and CaTs, the maximum values of the ionic conductances retained a relatively large range of variation. Only six of the thirteen varied maximum conductances showed significantly reduced variation in the control as compared to the whole population (G_CaL, ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$, G_Na, G_Kr, G_Ks, and G_Clb). The reduced variability in these six parameters was found to be significant (two-sample Kolmogorov-Smirnov test, α = 0.05), and the distributions are illustrated in Figure 5. This indicates that these ion currents affect the rabbit AP and CaT morphology to a larger extent than the other conductances, and also that these parameters are easier to constrain and identify using the considered metrics.

Figure 4.

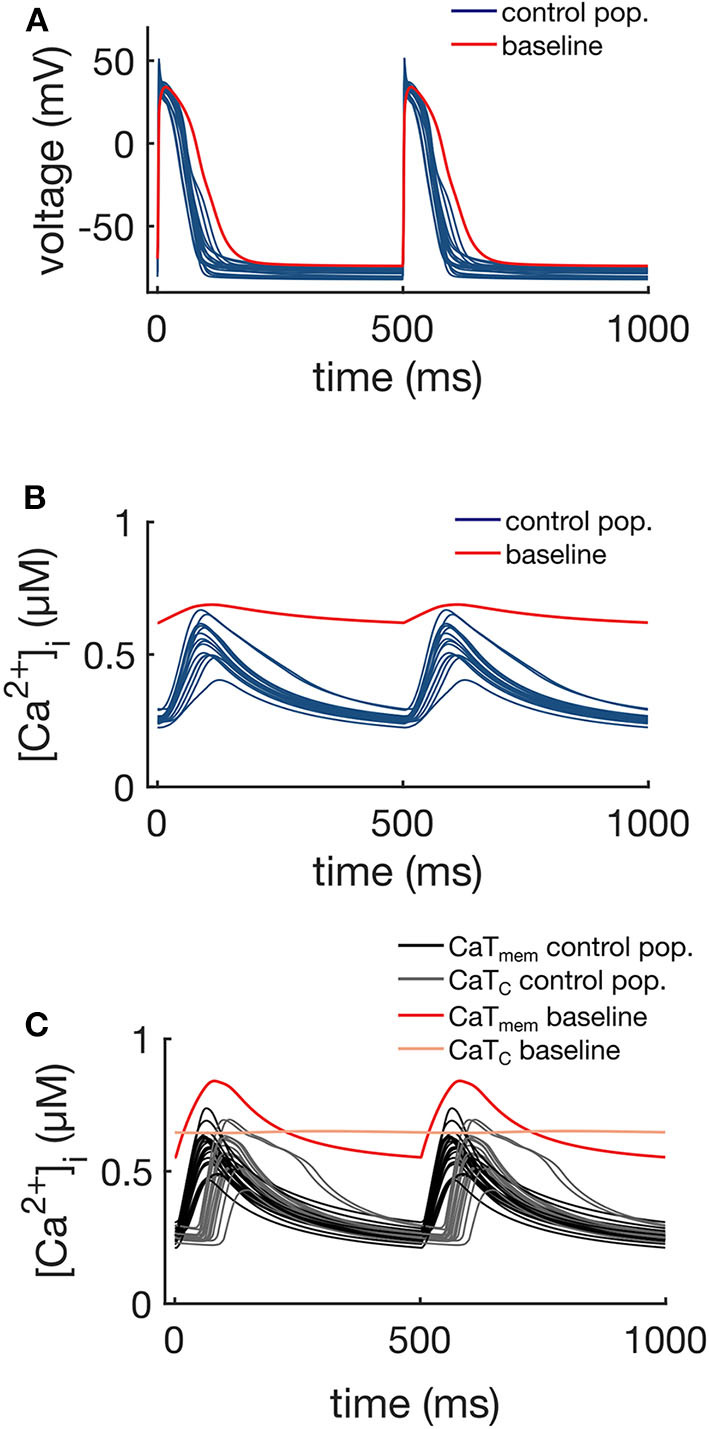
APs (A), whole-cell CaTs (B), and membrane (CaT_m) and center of cell (CaT_c) CaTs (C) of the control population (16 models), at 2 Hz steady pacing. The red traces represent the baseline model with the original maximum conductances shown in Table 1.

Figure 5.

Boxplots of the distributions of maximum conductances. The “*” indicates distributions that were significantly different between the original (black boxes, n = 3000) and control populations (blue boxes, n = 16) (Kolmogorov-Smirnov test, p-val < 0.05).

Figure 4C shows the CaT_m and CaT_c traces of the control population. As expected, the Ca²⁺ signals at these two different locations showed differences in morphology, resulting from the differences in the underlying mechanisms driving the signal. The membrane signal CaT_m results from a combination of Ca²⁺ entering the cell via I_CaL and Ca²⁺ released from junctional CRUs, while the central signal CaT_c is the Ca²⁺ released from non-junctional CRUs via CICR as a result of Ca²⁺ diffusing from neighboring domains. The CaT_c is therefore initiated with a time delay in comparison to CaT_m, which corresponds to the diffusion time of Ca²⁺ from the periphery to the central regions of the cell.

3.2. Calcium Dynamics and Wave Propagation

The values of the Ca²⁺ metrics for 16 models are shown in Table 4. Both the rise time and CD50 were significantly different between the CaT_m and CaT_c traces (two-sample Kolmogorov-Smirnov test, α = 0.05), with no significant differences in the amplitudes of CaT_m and CaT_c, which is consistent with findings in control atrial CMs (Greiser et al., 2014). The CaT_c showed a shorter tpeak (time to peak from central AP onset) and a longer CD50 than CaT_m. Furthermore, CaT_delay in the population was 42 ± 12 ms, which matches the 52 ms time delay measured from line scans of rabbit atrial CMs (Greiser et al., 2014). While Ca_SR was fairly consistent across the 16 models (0.30 μM), [Na⁺]_i showed a large degree of variation among models.

Table 4.

Values of the Ca²⁺ metrics obtained from the control population.

Model	tpeakm (ms)	tpeakc (ms)	CaTdelay (ms)	CaTAm (μM)	CaTAc (μM)	CD50m (ms)	CD50c (ms)	[Na+]i	CaSR (μM)
1	74	67	47	0.29	0.28	92	96	7.8	0.29
2	88	67	40	0.24	0.28	110	96	7.8	0.29
3	74	61	34	0.32	0.37	103	99	7.5	0.31
4	60	62	41	0.37	0.34	84	98	12.5	0.30
5	72	63	38	0.35	0.32	92	98	6.9	0.30
6	78	62	34	0.27	0.41	133	166	10.6	0.32
7	63	67	51	0.39	0.27	71	96	10.9	0.29
8	71	61	31	0.35	0.37	99	99	10.5	0.31
9	72	67	50	0.29	0.28	86	96	8.9	0.29
10	70	64	38	0.30	0.31	95	98	8.2	0.30
11	67	63	38	0.39	0.32	85	99	11.1	0.30
12	65	61	36	0.50	0.36	73	99	10.4	0.31
13	89	67	48	0.25	0.27	108	96	7.6	0.28
14	70	74	79	0.25	0.21	95	94	7.1	0.26
15	65	63	36	0.41	0.41	99	192	12.3	0.32
16	68	61	31	0.39	0.37	84	99	12.5	0.31
Mean	72	64	42	0.33	0.32	94	109	9.5	0.30
Std	8	4	12	0.07	0.06	15	28	2.0	0.02

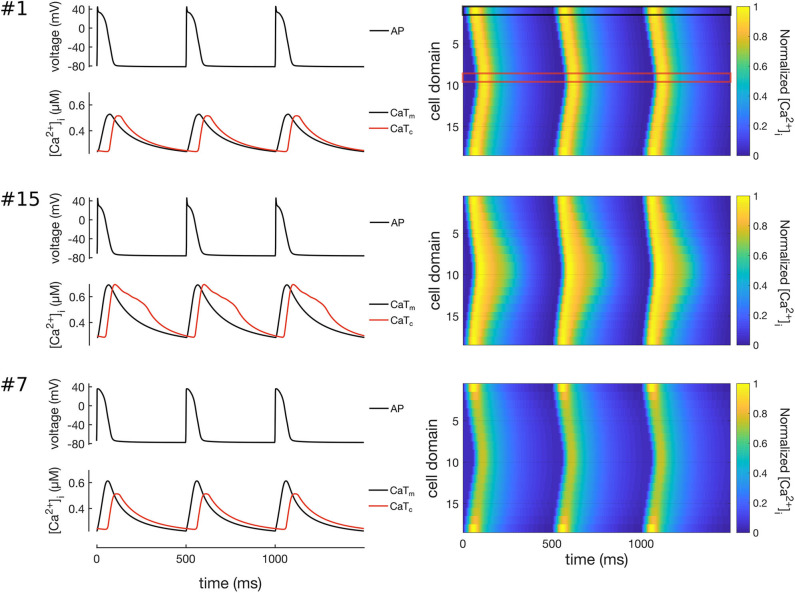
All 16 models of the control population showed similar Ca²⁺ wave propagation patterns with physiological characteristics under normal conditions, including full regenerative propagation, delayed CaT_c, and steady CaTs over time. However, despite the similarities there were also measurable differences in the propagation patterns, as characterized by the Ca²⁺ metrics defined above and by plots of the spatio-temporal Ca²⁺ dynamics. Three representative Ca²⁺ wave propagation patterns (models 1, 15, and 7 in Table 4) are also shown in Figure 6. Model #1 corresponds to a CaT_delay very close to the average, and with similar CaTA_m and CaTA_c; model #15 shows a shorter CaT_delay, and slowed CaT_c decay; and model #7, in turn, showed a slightly longer CaT_delay, but a damping of CaT_c.

Figure 6.

Simulation of Ca²⁺ waves in three representative models of the control population (models #1, #7, and #15). Traces on left hand-side show the APs (top), CaTs (bottom) at the membrane (CaT_m, black lines) and centre of cell (CaT_c, red lines). The right hand-side of the Figure shows line scans of propagating Ca²⁺ waves in 3 simulated beats at 2 Hz pacing. The black and red boxes on the top-right panel show the domains corresponding to the CaT_m and CaT_c traces. Model #1 shows a propagating Ca²⁺ wave where CaT_m and CaT_c have rather similar morphologies; model #15 shows a Ca²⁺ wave with slightly larger CaT_delay; and model #7 shows a wave patterns with decreased CaTA_c as compared to CaTA_m.

We also noted that models #6 and #15 showed a biphasic CaT_c decay, with a distinct Ca²⁺-wave pattern as compared to all the other models in the control population. The most likely candidate mechanism is a reduced Ca²⁺-extrusion rate, which causes cytosolic Ca²⁺ to accumulate in the inner domains.To investigate this mechanism we first compared the maximum conductances of I_CaL, I_CaP, I_NCX, and I_NaK in the two models. We noticed that the models corresponded to two distinct combinations of the maximum conductances of these four ionic currents, which suggests that the mechanisms underlying the prolonged CaT_c might be different.

Model #6 showed a combination of reduced peak magnitude of I_CaL, I_NaK, I_NCX, and slightly reduced peak I_CaP (despite a large ${\text{I}}_{\mathrm{\text{CaP}}}^{max}$). In contrast, model #15 showed reduced peak I_NaK and I_CaP, only slightly reduced I_NCX, and increased I_CaL. Thus, the common characteristic in the two models was a low I_NaK magnitude. An interesting observation is that in model #6 the magnitude of I_NCX was reduced, yet to a lesser extent than ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$, which means that in this model the increased [Ca²⁺]_i still resulted in an enhancement of I_NCX. A possible mechanism in model #6 may be simply the reduced ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$ which resulted in [Ca²⁺]_i accumulation and the observed prolongation of CaT_c. In model #15, however, the mechanism seems to be different, possibly the reduced I_NaK resulted in an accumulation of [Na⁺]_i, which further reduced the activity of I_NCX, and consequently increased [Ca²⁺]_i prolonging CaT_c. This was paralleled by a smaller extrusion via I_CaP.

In order to investigate the role of I_NaK and I_NCX in the decay of CaT_c, we gradually increased the values of ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ and ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$ individually. The results of these simulations are shown in Figures 7, 8. As can been seen from these results, increasing either ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ or ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$ decreased the CaT_c decay time, abolishing the biphasic decay behavior, although at different thresholds for each of the models. In model #6 the threshold for transition from biphasic to monotonic decay occurred at 80% increase of ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ and 120% increase of ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$, whereas in model #15 the transition occurred at 82 and 54% increase of ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ and ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$, respectively. Although these results do not allow to discern the relative contribution of I_NCX and I_NaK to the prolongation and biphasic behavior of CaT_c decay due to the small number of observations, they do seem to indicate that these two currents play a major part in determining the decay of CaT_c, as is expected given their role in regulating [Ca²⁺]_i.

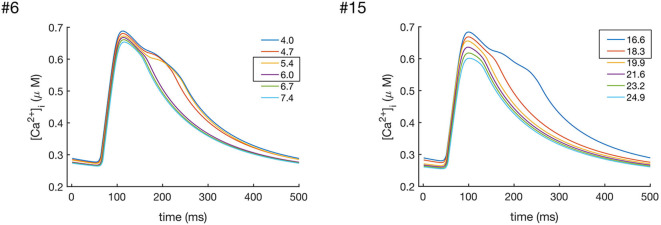
Figure 7.

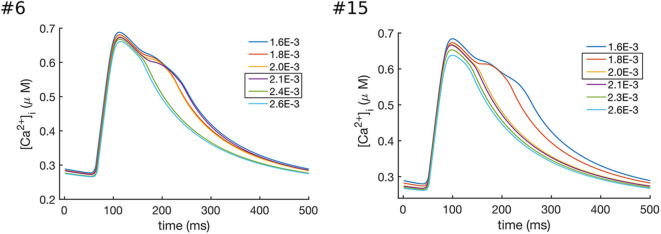
Effects of increasing the values of ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ in models #6 and #15, which resulted in the enhanced Ca²⁺ extrusion and a faster CaT_c decay. In model #6 the transition between the biphasic and smooth CaT profile occurred at values of ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ between 2.1 × 10⁻³ and 2.4 × 10⁻³ ns/pF, while in model #15 the transition occurred at values between 1.8 × 10⁻³ and 2.0 × 10⁻³ ns/pF.

Figure 8.

Effects of increasing the values of ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$ in models #6 and #15, which resulted in the enhanced Ca²⁺ extrusion and a faster CaT_c decay. In model #6 the transition between the biphasic and smooth CaT profile occurredat values of ${\text{I}}_{\mathrm{\text{NCX}}}^{max}$ between 5.4 and 6.0 nS/pF, while in model #15 the transition occurred at values between 16.6 and 18.3 nS/pF.

3.3. Correlation Analysis

We next analyzed the correlations between the maximum conductances of individual currents and the Ca²⁺ metrics defined in Figure 3. The results are summarized in Table 5, where significant correlation coefficients (p-value < 0.05) are highlighted in bold. Our analyses reveal that the Ca²⁺ wave properties of these 16 models were primarily sensitive to G_CaL, ${\text{I}}_{\mathbf{\text{NCX}}}^{max}$, and ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$. The L-type Ca²⁺ channel conductance G_CaL showed a negative correlation with CD50_m, but not with CaTA_m and CaTA_c. ${\text{I}}_{\mathbf{\text{NCX}}}^{max}$ was negatively correlated with tpeak_m and CD50_m, which is the expected given role of I_NCX in Ca²⁺ extrusion. ${\text{I}}_{\mathbf{\text{NCX}}}^{max}$ was also positively correlated with CaTA_m, possibly because larger CaTs increase NCX activity. However, ${\text{I}}_{\mathbf{\text{NCX}}}^{max}$ did not affect CaT_delay. Finally, we found ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ to be negatively correlated with CaTA_c and CD50_c, indicating that a larger I_NaK current resulted in a smaller CaT_c signal.

Table 5.

Kendall's τ and corresponding p-values of the correlations between maximum conductances and CaT_m and CaT_c properties.

Param.	tpeakm		tpeakc		CaTdelay		CaTAm		CaTAc		CD50m		CD50c
	τ	p-val	τ	p-val	τ	p-val	τ	p-val	τ	p-val	τ	p-val	τ	p-val
GCaL	−0.33	0.086	0.13	0.52	0.31	0.11	0.30	0.12	−0.23	0.23	−0.51	0.0076	−0.21	0.31
GCaT	0.093	0.65	0.13	0.52	0.10	0.62	−0.25	0.19	−0.18	0.35	0.10	0.62	−0.25	0.23
${\text{I}}_{\mathrm{\text{NaK}}}^{max}$	0.14	0.47	0.27	0.17	0.31	0.11	−0.20	0.31	−0.43	0.020	−0.14	0.50	−0.54	0.007
${\text{I}}_{\mathbf{\text{NCX}}}^{max}$	−0.72	0.0001	−0.079	0.71	0.10	0.62	0.45	0.015	−0.050	0.82	−0.75	0.0001	−0.045	0.85
GNa	−0.19	0.32	−0.044	0.85	−0.051	0.82	0.22	0.27	0.017	0.97	−0.15	0.44	0.082	0.71
Gto	−0.11	0.59	0.13	0.52	0.10	0.62	0.10	0.63	−0.13	0.51	−0.12	0.56	−0.082	0.71
GKr	−0.16	0.42	−0.11	0.58	0.017	0.96	0.13	0.51	−0.033	0.89	−0.22	0.26	−0.064	0.78
GKs	−0.21	0.28	0.13	0.52	0.19	0.34	0.0	1.0	−0.033	0.89	−0.17	0.39	−0.064	0.78
GK1	−0.36	0.058	0.062	0.78	0.17	0.39	0.15	0.45	−0.083	0.69	−0.27	0.16	−0.12	0.58
GCaP	0.30	0.12	−0.027	0.93	−0.068	0.75	−0.30	0.12	0.067	0.76	0.27	0.16	−0.10	0.64
GCab	−0.13	0.53	−0.22	0.27	−0.14	0.50	0.10	0.63	0.10	0.63	−0.24	0.22	0.064	0.78
GNab	0.093	0.65	−0.34	0.082	−0.31	0.11	−0.083	0.69	0.15	0.45	−0.017	0.96	0.12	0.58
GClb	−0.30	0.12	0.20	0.31	0.29	0.13	0.10	0.63	−0.20	0.31	−0.085	0.68	−0.17	0.40

The correlation among the seven Ca²⁺ metrics, [Na⁺]_i, and Ca_SR are compiled in Table 6, with significant correlation coefficients (p-value < 0.05) highlighted in bold. We observe that CaT_delay which was not sensitive to any of the ion current conductances, was strongly correlated with Ca_SR. We also found [Na⁺]_i to be correlated with tpeak_m, CaTA_m, and CD50_c. Furthermore, we observe that the individual Ca²⁺ metrics related to CaT_m and CaT_c were in general not correlated, except for CaTA_m which was correlated with tpeak_c, and CD50_c, while CaT_delay was strongly correlated with all CaT_c properties, tpeak_c, CaTA_c, and CD50_c. The three Ca²⁺ metrics t_rise, CD50, and amplitude, were correlated for both CaT_m and CaT_c, as expected (data not shown).

Table 6.

Kendall's τ and corresponding p-values of the correlations between CaT_m and CaT_c properties, [Na⁺]_i, and Ca_SR.

Parameters	tpeakc		CaTAc		CD50c		CaTdelay		[Na+]i		CaSR
	τ	p-val	τ	p-val	τ	p-val	τ	p-val	τ	p-val	τ	p-val
tpeakm	0.18	0.38	−0.093	0.65	−0.15	0.49	0.0	1.0	−0.44	0.019	−0.093	0.65
CaTAm	−0.41	0.035	0.33	0.08	0.43	0.03	−0.27	0.16	0.40	0.033	0.33	0.079
CD50m	0.081	0.71	0.10	0.62	0.10	0.64	−0.16	0.44	−0.25	0.19	0.10	0.62
CaTdelay	0.79	0.0001	−0.77	0.0001	−0.77	0.0001	1	0	−0.26	0.19	−0.77	0.0001
[Na+]i	−0.34	0.082	0.37	0.052	0.41	0.041	−0.26	0.19	1	0	0.37	0.052
CaSR	−0.79	0.0001	1.0	0.0	0.88	0.00	−0.77	0.0001	0.37	0.052	1	0

4. Discussion

We have developed a model of a healthy atrial CM with rabbit-specific EP and spatially distributed Ca²⁺ dynamics. The central motivation for developing the model was to be able to describe radial diffusion of calcium, which is important for the investigation of the effects of asynchronous Ca²⁺ release on arrhythmic activity in atrial CMs lacking TTs. We used a population-of-models approach to parameterize the maximum conductances of sarcolemmal ion currents to produce a pool of models that matched reported experimental data from the rabbit atria. The result was a population of 16 models that were all consistent with observed experimental values, but still recapitulated observed variability in Ca²⁺ wave characteristics.

The small number of models selected by the experimental data shows that imposing a sufficiently large number of constraints in model outputs (in this case, eight parameters) can reduce the parameter space to discrete sets of parameterizations, each following a unique trajectory. This shows that rather different parameter combinations can result in models with very similar behaviors (see Figure 4 and Supplementary Table 3, highlighting the non-uniqueness of CM models, a consequence of the compensatory effects of ionic currents (Sarkar and Sobie, 2010; Zaniboni, 2011; Muszkiewicz et al., 2018). Nonetheless, the model selection step significantly reduced the variability in six of the maximum conductances, as seen in Figure 5, indicating that the electrophysiology and Ca²⁺ metrics used in the model selection step were, in general, sensitive to these maximum conductances.

It is worth noting that the data used here to constrain the model were obtained from a large assortment of published experimental data. Therefore, the 16 models of the control population reflect not only the natural variability observed within different atrial regions, but also experimental uncertainties inherent to methodologies used by different research groups. The population-of-models-based approach we used here contrasts with the more standard approach, wherein a computational model is fitted to a small set of experimental observations, often obtained from a single atrial region, to yield a single model parameterization that captures the average behavior in the experimental data. Although useful for assessing the mechanisms underlying general characteristic behaviors of the model, the single-parameter approach lacks the ability to reproduce experimental observations from a range of data. In contrast, incorporating variability into the model via the population-of-models-based approach employed here allows a generalization of model results to a wider set of conditions and phenotypes.

4.1. Correlations Analysis

The seven extracted Ca²⁺ metrics from CaT_m and CaT_c quantify differences in the Ca²⁺ wave properties across the 16 models. Correlation analysis showed that G_CaL and ${\text{I}}_{\mathbf{\text{NCX}}}^{max}$ and ${\text{I}}_{\mathrm{\text{NaK}}}^{max}$ were the only maximum conductances significantly affecting Ca²⁺ wave propagation in the model. This result is consistent with the known role of these ionic currents in intracellular Ca²⁺ regulation. For instance, experimental observations have shown the role of increased sarcolemmal Ca²⁺ in modulating the regenerative propagation of the Ca²⁺ signal toward the inner locations of the cell (Mackenzie et al., 2004).

The strong correlation between ${\text{I}}_{\mathbf{\text{NCX}}}^{max}$ and CaT_m metrics indicates a strong modulating effect of I_NCX on Ca²⁺ dynamics at the cell membrane. The importance of the role of I_NCX on modulation of Ca²⁺ dynamics during the AP is well-documented both experimentally, and through computational simulations (Hilgemann et al., 1992; Sher et al., 2008; Xie et al., 2015). Furthermore, since I_NaK affects [Na⁺]_i homeostasis, which in turn affects I_NCX function, it is not surprising that I_NaK was correlated with CaTA_c and CD50_c. However, it is somewhat unexpected that I_NaK was more strongly correlated to the CaT_c than to CaT_m properties.

The observed correlations between CaTA_m and tpeak_c and CD50_c indicates that the rate of Ca²⁺ release and uptake in the CRUs is modulated to some extent by the amount of Ca²⁺ that enters the membrane and initiates CICR. We also observed that CaT_delay was correlated to tpeak_c, CaTA_c, and CD50_c, which indicates that the velocity of Ca²⁺ wave propagation was mostly modulated by the dynamics of the regenerative propagation of the Ca²⁺ signal along CRUs, and not by the amount of Ca²⁺ entering via the cell membrane. CaT_delay measures the time for the Ca²⁺ wave to propagate to the innermost cell domains which depends on the strength and rate of the regenerative CICR. This also determines the shape of the local CaTs in each inner domains. Therefore, it is expected that CaT_delay co-varies with the CaT_c properties, but not with the CaT_m properties.

The observation that CaT_delay strongly correlated with Ca_SR is not unexpected, since a higher SR Ca²⁺ load would naturally promote a faster rise of the CaT at inner domains (smaller tpeak_c), and thus reduce CaT_delay, while simultaneously promoting a longer CaT duration (larger CD50_c). The observed correlation between Ca²⁺ metrics and [Na⁺]_i is also expected since [Na⁺]_i plays a significant role in the modulation of NCX function, and therefore in the regulation of the sub-sarcolemmal Ca²⁺ signal (Hilgemann et al., 1992; Sher et al., 2008; Xie et al., 2015).

Overall the results of the correlation analyses presented here are in good agreement with our understanding of Ca²⁺ handling dynamics in atrial CMs, and provide additional insight into the mechanisms driving Ca²⁺ wave propagation in the newly developed model taking into account population variability.

4.2. Limitations and Future Directions

It is important to note that the conclusions derived from the analyses presented here are limited by the experimental data that was used in the model selection step. In particular, the lack of quantitative measurements of intracellular Ca²⁺ makes it difficult to validate the model predictions of the spatial characteristics of the Ca²⁺ dynamics. The correlation analysis used in this paper also has its own limitations and assumptions. For instance, simultaneously varying parameters to build the population can lead to interaction effects, which can mask the individual contributions of each varied parameter. The analyses presented here can be extended by, for example, determining multivariate correlations. This would require increasing the sample size to allow for a more robust regression analysis of the parameters. A way to achieve this would be by constructing new models by perturbing the parameters around the values that originated the 16 models. Alternatively, partial correlations can be determined by removing the effect of collinearity of variables.

Furthermore, the developed pool of normal rabbit atrial CM models can be used to study the effects of altered Ca²⁺ handling parameters, such as Ca²⁺ release and uptake from the SR, and Ca²⁺ buffering strength on Ca²⁺ wave propagation dynamics. Variability in these parameters will likely have a stronger modulating effect on the Ca²⁺ wave metrics studied here than the ionic currents, and thus constitute a natural extension of the present work.

Another relevant model limitation is the use of a deterministic RyR model, which implicitly assumes homogeneous distribution and behavior of CRUs. Therefore, this simplification does not include stochastic Ca²⁺ release events and subcellular fluctuations in calcium-handling proteins, which may influence the results (Sutanto et al., 2018) and limit the applicability of the model to describe pathological conditions. Using a stochastic formulation would allow the incorporation of spatial heterogeneity in Ca²⁺ release, which constitutes an important trigger for spontaneous Ca²⁺ waves, and consequently for abnormal Ca²⁺-wave propagation patterns. The current model implementation has limited ability to describe these events, but it can easily be extended to a stochastic RyR model to address the role of Ca²⁺ release stochasticity in Ca²⁺ wave dynamics. Additionally, the model can easily be extended to incorporate additional layers of intra- and inter-cellular variability, including TT structures.

We also recognize that the Ca²⁺-handling model from the Voigt et al. (2014) has the intrinsic limitations of not being specific to spatial Ca²⁺ distribution in rabbit atrial CMs. Previously developed atrial CM models with rabbit-specific Ca²⁺ handling include the models from Hilgemann and Noble (1987) and from Lindblad et al. (1996). Hilgemann and Noble (1987) proposed a 4-state model of the Serca pump with a component dependent on SR Ca²⁺ to incorporate Serca regulation by luminal Ca²⁺. Lindblad et al. (1996) modified this formulation to take into account additional experimental observations, Ca²⁺ buffering, and to adjust graded Ca²⁺ release and CICR in the model. The Shannon rabbit ventricular CM model (and our model), in turn, uses a bi-directional Hill equation with affinity for cytosolic and SR Ca²⁺, although the formulation used here (from the Voigt & Heijman model) had been adjusted to human atrial CM data. Additionally, Ca²⁺-release in Hilgemann and Noble (1987) is modeled as a simple function of SR Ca²⁺ concentration, while in Lindblad et al. (1996) this formulation was modified to also take into account cytosolic Ca²⁺. On the other hand, the Shannon model and our model use a 4-state Markov Model that allows to simulate local control of Ca²⁺ release. Hilgemann and Noble (1987) and Lindblad et al. (1996) used essentially the same formulation for the Na⁺-Ca²⁺ exchanger, while both the Shannon and our model use a similar formulation for I_NCX with additional terms to reflect Na⁺ and Ca²⁺ dependence. Thus, given the differences in Ca²⁺ handling formulations in the various models, it is fair to say that there is considerable uncertainty regarding which model structure is the most appropriate, especially also because of the limited amount of data on Ca²⁺ handling in rabbit atrial CMs. Future work should investigate how these different Ca²⁺ models reflect overall Ca²⁺ dynamics in rabbit atrial CMs by comparing Ca²⁺ wave propagation patterns. We note that, to the best of our knowledge, this study is the first attempt at providing a systematic approach for analyzing intracellular Ca²⁺ wave propagation in a rabbit atrial cardiomyocyte model with spatial Ca²⁺ handling.

We also note that RyR density in the model should be adjusted to reflect the smaller size of rabbit as compared to human atrial CMs. The model assumes a transversal spacing of 0.7 μm, which is smaller than the 1 μm spacing assumed in the original Voigt & Heijman model. This is an important consideration since the number of RyR has a direct impact on the amplitude of the cytosolic Ca²⁺ signal and on Ca²⁺ diffusion, and consequently on Ca²⁺ wave propagation dynamics. An overestimation of these parameters may result in exacerbated Ca²⁺ propagation which does not necessarily reflect physiological Ca²⁺ diffusion. Nevertheless, the model can also be simulated with fewer domains. Thus, further developments of the model should address this by adjusting RyR density and Ca²⁺ diffusion parameters, and Ca²⁺ diffusion properties should be validated against rabbit data, for example as done in Sutanto et al. (2018).

Another important consideration is the effect of TTs on atrial CM Ca²⁺ cycling. Although a general absence of significant TT networks has been reported in rabbit atrial CMs (Tidball et al., 1991; Blatter, 2017), a large regional variability in TT density across the atria, as well as the presence of axial TTs has been observed in various species, with corresponding variability in Ca²⁺ release synchrony profiles (Richards et al., 2011; Frisk et al., 2014; Brandenburg et al., 2018). Thus, the implications of considering TT networks in atrial myocytes should be discussed in more detail here. Several computational studies have explored the role of TTs in modulating intracellular Ca²⁺ propagation and disturbances. For example, Nivala et al. (2015) studied the effects of spatial heterogeneity in LTCC distribution and [Na⁺]_i on Ca²⁺ alternans propensity in a model with three-dimensional diffusion. Their results showed that TT disruption did not cause Ca²⁺ alternans by itself but promoted their occurrence and lowered the onset threshold when acting in concert with increased [Na⁺]_i (which increased Ca²⁺ load), and down-regulation of Serca (together with increased [Na⁺]_i), with alternans amplitude increasing with increasing percentage of TT disruption or [Na⁺]_i. This study emphasized not only the role of the spatial distribution of LTCCs in the generation of alternans, and thus the importance of considering spatial heterogeneity of Ca²⁺ cycling, but also the role of regulating [Na⁺]_i on abnormal intracellular Ca²⁺ propagation.

Colman et al. (2017) performed a similar study on a model with 3D spatial Ca²⁺ cycling with variable TT density, showing that decreased TT density correlated with increased propensity for Ca²⁺ alternans. Their simulations with patchy TTs also showed observable spatial Ca²⁺ gradients leading to the formation of intracellular Ca²⁺ waves at the sites with no TTs and of delayed after depolarizations. In a similar study, Song et al. (2018) also presented a 3D spatial model of Ca²⁺ incorporating different TT architectures, which showed an increased incidence of Ca²⁺ alternans and intracellular Ca²⁺ wave formation in non-uniform random TT networks, as compared to uniform networks.

Marchena and Echebarria (2018) also developed a model of intracellular spatial Ca²⁺ distribution, but using a different framework based on a submicron resolution grid of points, allowing for a more refined description of CM subcellular structure with transverse TTs at the z-lines. At the membrane level, RyR and LTCC clusters are distributed at regular intervals, whereas inside the CM the RyR clusters follow a Gaussian distribution centered at the z-line, with only some of the grid points containing CRUs. Furthermore, they defined cytosolic, SR, and buffer-bound Ca²⁺ concentrations for each grid. Interestingly, their simulations showed an almost complete absence of Ca²⁺ signal at the center despite their model accounting for TTs. A later study by the same authors (Marchena and Echebarria, 2020) where the same model was used but incorporating variable lengths and distributions of both transverse and axial tubules emphasized the role of these structures on spatial Ca²⁺ propagation, showing a progressive enhancement and synchronization of the Ca²⁺ signal at the cell center with increasing TT density.

Biophysically detailed models of CM ultrastructure with spatially-realistic RyR distribution are also important for understanding structure-function relationships in Ca²⁺ handling. Rajagopal et al. (2015) and Ladd et al. (2019) developed such a model for the rat ventricular CM integrating spatial information from high-resolution imaging that included RyR, myofibrils, and mitochondria, and examined the role of these structures on Ca²⁺ dynamics in a CM cross-section. They showed that incorporating spatially-realistic distribution of RyRs in the model captured the spatial Ca²⁺ heterogeneities observed in line scans. Their simulations also suggest that modeling mitochondria as passive barriers to Ca²⁺ diffusion also introduces heterogeneity in the local CaTs, although to a lesser extent than RyR. These findings further suggest that local distribution of Ca²⁺ re-uptake may also have important consequences for the spatial Ca²⁺ handling, and highlight the importance of considering CM ultrastructure in studying Ca²⁺ diffusion properties.

The effect of adding axial TTs to the Voigt & Heijman human CM model was also studied by Sutanto et al. (2018). Their simulations with variable axial TT density and distribution shows a progressive synchronization of the intracellular Ca²⁺ release in the radial direction. Additionally, their results suggested an increased incidence of spontaneous Ca²⁺ release events when incorporating axial TTs, with the events originating primarily at the RyR clusters adjacent to the axial TTs. Holmes et al. (2018) also presented a model of the rabbit atrial CM implementing the Aslanidi et al. (2009) AP model and the three-dimensional stochastic Ca²⁺ handling model with Ca²⁺ diffusion terms developed by Colman et al. (2017). The latter was based on real geometries and intracellular ultrastructures extracted from sheep ventricular CMs, but otherwise implements a very similar Ca²⁺ handling model as ours and other models. The Holmes et al. (2018) model allowed to simulate the effects of TTs and intracellular Ca²⁺ heterogeneities in spontaneous Ca²⁺ waves. Of note, in their simulations with the fully detubulated model, the CaT morphology was similar to the whole-cell CaT produced by our model, although with a lower diastolic Ca²⁺ level. The CaT delay between the periphery and the center is about 75 ms, ca. 20 ms longer than in our simulations. Although an important result, showing that increased detubulation indeed results in a slowed Ca²⁺ wave propagation, which is in agreement to experimental data, the model was not adjusted to match rabbit specific cellular ultrastructure and intracellular Ca²⁺ diffusion. However, their work does point out the influence of Ca²⁺ dynamics stochasticity on AP shape, although it is not clear from their study how introducing stochasticity in the Ca²⁺ model affected wave propagation. Together these results show that TTs, and in particular axial TTs in atrial CMs, have great importance in modulating intracellular Ca²⁺ propagation and potentially play a role in Ca²⁺ alternans and triggered activity. As such, computational models of atrial CM with spatial Ca²⁺ handling are an essential tool to improve our understanding of Ca²⁺-handling abnormalities in atrial pathophysiology.

Given the wide range of variation of the maximum conductances in the control population (see Figure 5), and the fact that the models were selected entirely based on AP and CaT characteristics, it is natural to ask whether individual ionic currents of the models are in physiological ranges. We have compared simulated I-V curves of I_CaL, I_Na, I_to, I_K1, and I_Kr for the 16 models against experimental data reported by Aslanidi et al. (2009), and Muraki et al. (1995), as well as dynamic current traces from our model population with the Aslanidi model (at steady state at 2 Hz pacing). I-V curves and dynamic current traces are also shown in Supplementary Figures 2, 3, while peak current values are reported in Supplementary Table 4. We observe that the I-V curves are qualitatively similar to the experimental data. Although the range of variation is large, the magnitudes of _CaL (−13.9 to −4.3 pA/pF) and _to (3.4 to 16.6 pA/pF) are approximately within ±50% of the experimental values (I_CaL: −7 to −8 pA/pF, I_to: 8 to 13 pA/pF, Aslanidi et al., 2009). Reported experimental values of peak I_K1 are between 4 and 5 pA/pF (Aslanidi et al., 2009), whereas the largest peak I_K1 in our population of 0.6 pA/pF, which is similar to the peak I_K1 observed in the Aslanidi model, at 0.66 pA/pF. I_Na, however, was considerably higher in our population (between −737 and −291 pA/pF) as compared to the experimentally reported value of −70 pA/pF. We note, however, that peak dynamic I_Na we obtained from the Aslanidi model was −120 pA/pF. Peak I_Kr values (0.45–2.1 pA/pF) in our population were also in general considerably larger than the reported experimental value of 0.7 pA/pF (Muraki et al., 1995), assuming a cell capacitance of 50 pF). Peak I_Kr in the Aslanidi model was 0.43 pA/pF, which is close to the experimental value.

We also note that variability in experimental recordings of ion currents is typically very large, and ideally this should have been taken into account in the validation of the population. Nevertheless, there are observable discrepancies between peak currents in our control population and in experiments, which are limitations of the model, and we recognize that these should be further investigated. Future iterations in the development of the control population should include fine-tuning of the maximum conductances of the 16 models in order to produce a control population that better matches experimental data.

Finally, a relevant model improvement would be to include the calcium-dependent component of the chloride current, which has been shown to be involved in APD alternans in rabbit atria (Kanaporis and Blatter, 2016), and could therefore potentially affect Ca²⁺ wave propagation dynamics. Future work could also address the effects of AF-induced remodeling on Ca²⁺ wave propagation, and in particular look at the role of RyRs and Serca2a parameters in abnormal behaviors, such as failed Ca²⁺ propagation, Ca²⁺ alternans, and afterdepolarizations.

5. Conclusions

This paper presented a novel model of the rabbit atrial CMs, and provides a framework for analysing cardiac cell models based on correlation analysis. We have shown that the model is able to reproduce experimentally observed physiological Ca²⁺ wave propagation patterns. These differences were directly linked to two Ca²⁺ currents, I_CaL, and I_NCX. However, the study also showed the Ca²⁺ wave patterns to be a complex interplay among different components, including Ca_SR and [Na⁺]_i.

The spatial Ca²⁺ description in the model, along with the methodology presented here can be used as a tool to study sub-cellular mechanisms, and their implication in the arrhythmogenesis in diseased condition, such as atrial fibrillation. This work can therefore be extended to assess such mechanisms under altered conditions, such as electrical remodeling. In particular, the framework can be useful for querying the drivers of arrhythmogenic Ca²⁺ cycling, such as Ca²⁺ alternans, and to formulate hypothesis on new targets to restore normal cell function. In conclusion, the study provides a population of spatial models of the rabbit atrial cardiomyocyte that can serve as a starting point for future studies employing the commonly used experimental model.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MV, JH, and US conceived the study. MV performed the computational simulations and data analysis, and drafted the manuscript. HA, JS, and JH provided the critical revision to the manuscript. All authors approved the final version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2020.556156/full#supplementary-material