ARIMA models for predicting the end of COVID-19 pandemic and the risk of second rebound

Abstract

Globally, many research works are going on to study the infectious nature of COVID-19 and every day we learn something new about it through the flooding of the huge data that are accumulating hourly rather than daily which instantly opens hot research avenues for artificial intelligence researchers. However, the public’s concern by now is to find answers for two questions; (1) When this COVID-19 pandemic will be over? and (2) After coming to its end, will COVID-19 return again in what is known as a second rebound of the pandemic? In this work, we developed a predictive model that can estimate the expected period that the virus can be stopped and the risk of the second rebound of COVID-19 pandemic. Therefore, we have considered the SARIMA model to predict the spread of the virus on several selected countries and used it for predicting the COVID-19 pandemic life cycle and its end. The study can be applied to predict the same for other countries as the nature of the virus is the same everywhere. The proposed model investigates the statistical estimation of the slowdown period of the pandemic which is extracted based on the concept of normal distribution. The advantages of this study are that it can help governments to act and make sound decisions and plan for future so that the anxiety of the people can be minimized and prepare the mentality of people for the next phases of the pandemic. Based on the experimental results and simulation, the most striking finding is that the proposed algorithm shows the expected COVID-19 infections for the top countries of the highest number of confirmed cases will be manifested between Dec-2020 and  Apr-2021. Moreover, our study forecasts that there may be a second rebound of the pandemic in a year time if the currently taken precautions are eased completely. We have to consider the uncertain nature of the current COVID-19 pandemic and the growing inter-connected and complex world, that are ultimately demanding flexibility, robustness and resilience to cope with the unexpected future events and scenarios.

Introduction

On 08-Dec-2019, a novel coronavirus disease (COVID-19), a member of the family of the severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2), started to infect people in the city of Wuhan, China [1]. COVID-19 was declared as pandemic by the World Health Organization (WHO) on 11-Mar-2020, and since then it invaded almost all countries of the world [2].

Essentially, COVID-19 is an infectious viral disease that is transmitted from human-to-human through droplets whether direct; during coughing, sneezing of the patient or the carrier of the disease or indirect; through getting in contact with the patient’s saliva on close contact, shaking hands, using his personal articles or touching surfaces soaked with his droplets containing the virus. The virus finds its way into the human body through the mucus membranes of the mouth, nose and eyes [2–4].

Clinical picture of the COVID-19 infected patients varies significantly, from being asymptomatic to having severe form of the disease. In most cases, high fever, cough, sore throat, general weakness, fatigue and muscular pain are manifested in many patients. In the severe cases, pneumonia, acute respiratory distress syndrome, micro-coagulopathies, sepsis and septic shock are highly manifested, and in many instances, it could lead to death. Reports show that clinical deterioration occurs rapidly, often during the second week of the course of the disease [5, 6]. Patients with underlying medical conditions such as cardiovascular disease, diabetes, chronic respiratory disease, cancer and old-aged people are more likely to experience serious illness [7].

Since it has been first reported, the COVID-19 invaded 210 countries and territories around the world [8]. As for 10-Aug-2020, in more or less seven months, a total of 20,173,775 confirmed cases of COVID-19 were reported and its death toll showed about 736,300 deaths.

Many research works are going on to study the infectious nature of COVID-19, and every day we learn something new about it through the flooding of the huge data that are accumulating hourly rather than daily [9]. However, currently, some information is known about COVID-19; its full characteristics are still unclear. One of the COVID-19 features is that due to its accelerated genetic mutations, it changes its behaviour very quickly. Therefore, scientists are continuously performing observational studies just to establish facts about COVID-19 that will help in ending its pandemic. However, the viral genetic mutations increase the likelihood of having a second wave of the pandemic in future [9].

After recognizing the high rates of spread of COVID-19, the severity of cases and its related high death rates, governments followed the advice of the WHO and took decisions of lock-down cities, banning local and international flights, restricting movements of millions and suspending schools, universities and business operations. Such decisions made the people feel stressed, depressed and/or anxious, with variable degrees of psychological impacts. Moreover, with the long stay at home, the people are getting anxious and looking forward to returning to their normal life, work and activities [10, 11].

The ARIMA and SARIMA models are widely used statistical approaches for time-series analysis and forecasting. The non-seasonal ARIMA $(p,d,q)$ method is employed to build the pure seasonal SARIMA $(p,d,q)\times {(P,D,Q)}_s$ model. Currently, the public’s concern is to find answers for two questions; (1) When this COVID-19 pandemic will be over? and (2) After coming to its end, will COVID-19 return again in what is known as a second rebound of the pandemic? In this work, we have used the SARIMA statistical model to answer both questions on the scientific basis of algorithmic modelling.

The main contributions of our research work include:

• Finding the best prediction models for daily confirmed cases in countries with the highest number of COVID-19 cases in the world to have more readiness in health care systems to forecast of the confirmed cases.

• Analysis the risk of second rebound of COVID-19 pandemic

• Estimating the pandemic life cycle and selecting the optimal parameter of the model using the grid search method. The proposed method outcomes matched the updated daily data.

• Significant results are achieved when compared with the state-of-the-art models. Hence, the proposed SARIMA model can be extended and used to predict other countries as it is giving an acceptable performance when observed its accuracy.

• Mathematical model presents the statistical estimation of the slowdown period of the pandemic which is extracted based on the concept normal distribution.

This paper is organized as follows: Sect. 2 presents the related works. Section 3 presents dataset description with current statistics. Section 4 introduces the proposed methodology. Section 5 presents the experimental observations and detailed discussion. Finally, the conclusions and possible future works are introduced in Sect. 6.

Related work

Lai et al. [12] studied the epidemic nature of COVID-19 incidence in terms of daily cumulative index, mortality rate and associative status of the countries health care resources and economy. With the catastrophic outbreak of COVID-19 globally, a huge volume of data is generated instantly and opens a hot research avenue for machine learning and artificial intelligence researchers.

Luo [13] provided a simple figure for each country to show the estimated pandemic life cycle together with the actual data to date and reveals the rate of spread of the infection and ending phase. The predictions were started purely driven by personal curiosity regarding when COVID-19 will end. However, this work needs more update with more analyses and cases, as well as sharing of learning and reflections from this exercise, and they did not use any mathematical model to show the predictive model’s behaviour.

Dandekar and Barbastathis [14] proposed a method to capture the current infected curve growth and predict a halting of infection spread by 20-Apr-2020. This method has shown that reversing quarantine measures right at this time can lead to an exponential explosion in the infected case count, thus annulling the part played by all measures implemented in the USA since 15-Mar-2020. However, the model used data of one-month period following the current US policy, that implies it has lack of sufficient data to make strong predicts.

The Institute for Health Metrics and Evaluation (IHME) COVID-19 health service utilization forecasting team, Christopher [15] peaked daily deaths varies from 30-Mar-2020 through 12-May-2020 by state in the USA and 27-Mar-2020 through 04-May-2020 by countries in the European Economic Area (EEA). They have estimated that through the end of July, there will be 60,308 deaths from COVID-19 in the USA and 143,088 deaths in the EEA. Deaths from COVID-19 are estimated to drop below 0.3 per million between 04-May-2020 and 29-Jun-2020 by state in the USA and between 04-May-2020 and 13-Jul-2020 by country in the EEA. Timing of the peak required for hospital resources highly varies across states in the USA and regions of Europe.

According to the WHO report on guidelines to protect COVID-19 [16], it infects humans by entering the body via different parts such as eyes, nose and/or mouth. It shall be noted that to avoid this infection, the guideline by WHO suggests not to touch the face with unwashed hands. Proper washing of hands with detergents such as soap and water for at least 20 s or cleaning hands thoroughly with alcohol-based solutions is recommended in all settings. It is also recommended to stay one meter or more away from one another to reduce the risk of infection through respiratory droplets. COVID-19 spreads rapidly in droplets and somehow surfaces.

Lutfi and Burcu [17] performed Auto-Regressive Integrated Moving Average (ARIMA) model on the European Centre for Disease Prevention and Control (ECDC) COVID-19 data to predict the number of confirmed cases and deaths of COVID-19. The limitation of this particular study is that a limited number of countries were considered. However, Tandon et al. [18] developed a model to use for forecasting future COVID-19 cases in India. The study indicates an ascending trend for the cases in the coming days.

Previous researchers were focused on developing methods to achieve an accurate and time-efficient model for prediction of the spread of COVID-19. The main drawbacks of the previous research works were less accurate prediction in most cases. In reference to the related work on COVID-19, there were great ideas to improve and indicate an ascending trend for the cases in the future. Generally, previous works lack promising features that could enable us to predict the spread of COVID-19 with better accuracy and manifest the time when it will slow down.

Dataset description

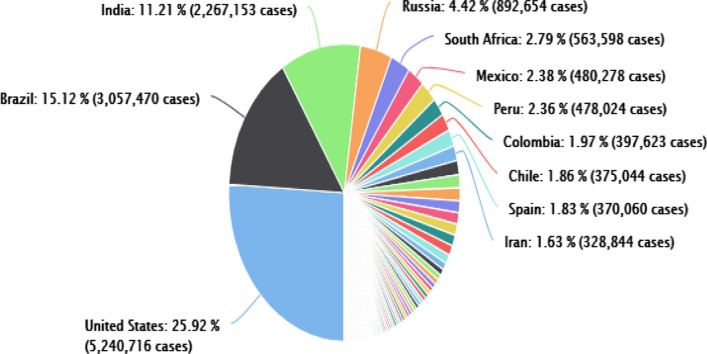
To validate our work, we used the records of COVID-19 data from WHO and Johns Hopkins university official websites [8]. The data shows confirmed cases, daily recovery and death rates. In our work, we have considered COVID-19 datasets for 20 countries that have a maximum spread of the pandemic as shown in Table 1 that indicates the updated data as of 10-Aug-2020, and the pie chart in Fig. 1 shows the distribution of confirmed cases whereby the top 11 countries confirmed cases are presented in percentage. The remaining countries show a small number of confirmed cases; hence, we do not present them in percentage. Table 2 describes the currently active and closed cases where out of the total infected cases, 99% of the patients are in mild condition and 1% are in critical condition. In the cases of closed cases, 95% of the patients have been recovered and 5% of them have died.

Table 1.

The top 20 countries sorted by the number of confirmed cases as of 10-Aug-2020 [8]

Country, other	Total cases	New cases	Total deaths	New deaths	Total recovered	Active cases	Serious, critical	Tot cases/1M pop	Deaths/1M pop	Total tests	Tests/1M pop
World	20,173,775	+146,944	736,300	+2748	12,996,871	6,440,604	64,740	2588	94.5
USA	5,231,737	+32,293	165,949	+332	2,679,401	2,386,387	17,795	15,796	501	66,007,623	199,290
Brazil	3,039,349	+3767	101,269	+133	2,118,460	819,620	8318	14,288	476	13,231,548	62,201
India	2,266,954	+52,817	45,352	+886	1,580,269	641,333	8944	1641	33	24,583,558	17,795
Russia	892,654	+5118	15,001	+70	696,681	180,972	2300	6117	103	30,800,000	211,044
South Africa	559,859		10,408		411,474	137,977	539	9427	175	3,250,583	54,735
Mexico	480,278	+4376	52,298	+292	322,465	105,515	3708	3721	405	1,091,695	8458
Peru	478,024		21,072		324,020	132,932	1488	14,477	638	2,573,691	77,943
Colombia	387,481		12,842		212,688	161,951	1493	7607	252	1,909,111	37,477
Chile	375,044	+1988	10,139	+62	347,342	17,563	1276	19,601	530	1,867,367	97,595
Spain	370,060	+2873	28,576	+73	N/A	N/A	617	7915	611	7,472,031	159,806
Iran	328,844	+2132	18,616	+189	286,642	23,586	3992	3910	221	2,711,817	32,243
UK	311,641	+816	46,526	+21	N/A	N/A	67	4588	685	18,349,668	270,146
Saudi Arabia	289,947	+1257	3199	+32	253,478	33,270	1824	8315	92	3,872,599	111,057
Pakistan	284,660	+539	6097	+15	260,764	17,799	776	1286	28	2,147,584	9703
Bangladesh	260,507	+2907	3438	+39	150,437	106,632		1580	21	1,273,168	7722
Italy	250,825	+259	35,209	+4	202,248	13,368	46	4149	582	7,276,276	120,365
Argentina	246,499		4634	+28	108,242	133,623	1565	5449	102	856,055	18,922
Turkey	241,997	+1193	5858	+14	224,970	11,169	603	2866	69	5,326,035	63,078
Germany	218,353	+1072	9263	+3	197,900	11,190	236	2605	111	8,586,648	102,450
France	202,775	+785	30,340	+14	82,836	89,599	383	3106	465	4,279,588	65,548

Fig. 1.

Distribution of cases as of 10-Aug-2020 for top 11 countries [8]

Table 2.

A sample of the top countries sorted by the number of confirmed cases in 10-Aug-2020 [8]

Active cases		Closed cases
Currently infected patients	6,440,604	Cases which had an outcome:	13,733,171
In mild condition	6,375,864 (99%)	Recovered/discharged	12,996,871 (95%)
Serious or critical	64,740 (1%)	Deaths	736,300 (5%)

Current statistics

The age factor and death rate due to COVID-19: Table 3 presents the collected data from New York City (NYC) Health as of 14-Apr-2020 and 13-May-2020, [8, 19]. All data in this report are preliminary and are subject to change as cases continue to be investigated. These data include cases in NYC residents and foreign residents treated in NYC facilities. This table shows only confirmed deaths. A death is considered confirmed when a person dies after positive COVID-19 laboratory test has been confirmed. The main underlying illnesses that lead to high risk of death if one has got infected by COVID-19 include diabetes, lung disease, cancer, immunodeficiency, heart disease, hypertension, asthma, kidney disease and liver disease. The death rate is computed as shown in Eq. 1.

$$\begin{array}{cc}\hfill \text{Death Rate}=& \text{number of deaths}/\text{number of cases}\hfill \\ \hfill =& \text{probability of dying if infected by the virus (\%)}.\hfill \end{array}$$ 1

Preexisting medical conditions (comorbidities) put patients at higher risk of death from COVID-19 pandemic. Patients who have no preexisting (comorbidities) medical conditions are having a fatality rate of 0.9%. Table 3 depicts the rate of death due to COVID-19 for various age range in New York City. For people in the age range from 0 to 17 years old, the rate of death is insignificant if the patients do not have an underlying health condition. In the case of elderly people whose age is 75+ years old, the rate of death rate reaches 14.3%. Generally, as the age increases and if the patient has an underlying health condition, there is a high risk of death due to the COVID-19.

Table 3.

The age factor and death rate due to COVID-19 in New York city health on 13-May-2020 [8]

Age	Number of deaths	Share of deaths	With underlying conditions	Without underlying conditions	Unknown if with underlying cond.	Share of deaths of unknown + w/o cond.
0–17 years old	9	0.06%	6	3	0	0.02%
18–44 years old	601	3.9%	476	17	108	0.8%
45–64 years old	3413	22.4%	2851	72	490	3.7%
65–74 years old	3788	24.9%	2801	5	982	6.5%
75+ years old	7419	48.7%	5236	2	2181	14.3%
Total	15,230	100%	11,370 (75%)	99 (0.7%)	1551 (24.7%)	25.3%

Moreover, the data depicts men are highly susceptible to death compared to that of women. Out of the total death rates, 61.8% men and 38.2% women die due to COVID-19 in New York City as of 13-May-2020 as shown in Table 4.

Table 4.

Sex ratio of death rate due to COVID-19 in New York city health on 13-May-2020 [8]

Sex	Deaths	Share of deaths	With underlying conditions	Share within this category	Without underlying conditions	Share within this category	Unknown if with cond.	Share within this category
Male	4095	61.8%	3087	62.2%	96	72.2%	912	59.5%
Female	2530	38.2%	1.873	37.8%	37	27.8%	620	40.5%

Table 5 shows the COVID-19 fatality rate by age in China. The fatality rate varies depending on the age group. The percentages shown do not have to add up to 100%, as they do not represent the share of deaths by age group. It presents the risk of dying if one is infected with COVID-19 for a person in a given age group. In general, relatively few fatality cases are seen among children [19].

Table 5.

Death rate in China due to COVID-19 by age group [19]

Age	Death rate confirmed cases (%)	Death rate all cases (%)
80+ years old	21.9	14.8
70–79 years old		8.0
60–69 years old		3.6
50–59 years old		1.3
40–49 years old		0.4
30–39 years old		0.2
20–29 years old		0.2
10–19 years old		0.2
0–9 years old		No fatalities

Table 6 shows the fatality rate in China in terms of sex ratio. Like the cases in other countries, the probability of fatality rate by sex ratio in China varies. When reading these numbers, it must be taken into account that smoking in China is much more prevalent among males. Smoking increases the risks of respiratory complications. Hence, males are highly susceptible to death when compared to females which are evidenced empirically as 4.7% and 2.8%, respectively.

Table 6.

Sex ratio of death rate due to COVID-19 in China on 13-May-2020 [8]

Sex	Death rate confirmed cases (%)	Death rate all cases (%)
Male	4.7	2.8
Female	2.8	1.7

Table 7 shows COVID-19 fatality rate by comorbidity in China. This probability differs depending on the preexisting condition. The percentage shown in the table does not represent in any way the share of deaths by a preexisting condition. Rather, it represents, for a patient with a given preexisting condition, the risk of dying if infected by COVID-19.

Table 7.

Fatality rate by comorbidity in China [8]

Preexisting condition	Death rate confirmed cases (%)	Death rate all cases (%)
Cardiovascular disease	13.2	10.5
Diabetes	9.2	7.3
Chronic respiratory disease	8.0	6.3
Hypertension	8.4	6.0
Cancer	7.6	5.6
No preexisting conditions		0.9

Methodology

In the subsequent subsections, the proposed Auto-Regressive Integrated Moving Average (ARIMA) have been described. The ARIMA is a statistical and econometric model applicable in time-series analysis-related problems mainly to understand the data or to predict future points in the series [20].

The ARIMA models

A time-series $Y_t$ is described as a series of independent variables based on time, where $t$ is a time step [21]. A deterministic time-series is expressed by the function, $Y_t=f(t)$. While the stochastic time series is expressed by $Y_t=X(t)$, where $X$ is a random variable. The ARMA model developed by Box et al. [22] has been used for the forecasting process in the stationary time series. Box-Jenkins (ARMA) forecasting model is very popular as it has high prediction efficiency in the stationary time series analysis [23]. An autoregression AR $(p)$ is a known time series method used to predict the future value by using observations from previous $p$-time steps as inputs to the regression equation multiplied by the appropriate coefficients $\varphi$ of AR [24, 25]. Besides, the sum is extended by adding the mean of the series $\mu$ and white noise $\omega$ that is a random error. The AR  $(p)$ model is given in the form shown in Eq. 2.

$$\begin{array}{c}\hfill AR(p):y_t=\mu +\sum _{i=1}^p({\varphi }_i{y}_{t-i})+{\omega }_t\end{array}$$ 2

The polynomial function of the Moving Average MA $(q)$ method is not included for any variable from a time-series [26]. It consists of three parts that include: the first part is the mean of the series $\mu$, the second part is the summation of the multiplication of a finite number of MA coefficients, $\theta$, and model residuals $\omega$, and the third part is the white noise ${\omega }_t$. The MA $(q)$ model is given in Eq. 3.

$$\begin{array}{c}\hfill MA(q):y_t=\mu +\sum _{i=1}^q({\theta }_i{\omega }_{t-i})+{\omega }_t\end{array}$$ 3

The ARMA $(p,q)$ model composes of two main polynomials which are AR $(p)$ and MA $(q)$ [27]. Mathematically it is represented as shown in Eq. 4.

$$\begin{array}{c}\hfill y_t=\mu +\sum _{i=1}^p({\varphi }_i{y}_{t-i})+\sum _{j=1}^q({\theta }_j{\omega }_{t-j})+{\omega }_t\end{array}$$ 4

or

$$\begin{array}{c}\hfill \varphi (B)y_t=\mu +\theta (B){\omega }_t\end{array}$$ 5

The notation ARMA $(p,q)$ represents the order of an ARMA method, described as follows:

• $y_t$ stands for predicted value at time $t$,

• $p$: is the order of AR polynomial indicating number of autoregressive lags,

• $q$: stands for the order of MA model presenting the number of moving average model lags,

• ${\varphi }_i$: The AR $(p)$ coefficients has to estimate $(i=1,2,\dots ,p)$,

• ${\theta }_j$: MA $(q)$ coefficients (parameters) that need to estimate, $(j=0,1,2,\dots ,q)$,

• $\mu$: represents the mean value of the time series data,

• $d$: represents the number of differences and is calculated based on the equation $\mathrm{\Delta }{y}_t=y_t-y_{t-1}$

• ${\omega }_t$: represents the white noise of the time-series at time t.

The ARIMA $(p,d,q)$ model is a widely used statistical method used in stationary time-series analysis such as forecasting [28]. To build such a model, the primary step is to investigate whether the statistical stationery of a time-series can be satisfied or not. Then, the next phase is estimating the numerical values of $p$ and $q$ parameters for AR and MA models. Thus, the essential idea of the ARIMA model is based on the assumption that the predicted value of the variable $y_t$ is generated from a linear equation of several previous observations with random errors [29]. A process $X_t$ is an ARIMA $(p,d,q)$ when it satisfies the form in Eq. 6.

$$\begin{array}{c}\hfill {\mathrm{\nabla }}^d{X}_t={(1-B)}^d{X}_t\end{array}$$ 6

In other words, the process $X_t$ should be stationary after differencing a non-seasonal process d times. During the training step of the ARIMA model using the available dataset, the values of p, d, and q are continually changing until the end and the last values are considered for the forecasting of the future values. The mathematical description of the model is presented as shown in Eq. 7.

$$\begin{array}{c}\hfill {\varphi }_p(B){(1-B)}^d{X}_t=\mu +\theta (B){\omega }_t\end{array}$$ 7

Seasonal ARIMA model

The non-seasonal ARIMA model (p, d, q) is vital in building pure seasonal SARIMA$(p,d,q)\times {(P,D,Q)}_s$ model, whereby the term (p, d, q) presents the non-seasonal part of the model and ${(P,D,Q)}_s$ describes the seasonal part of the model [30, 31]. The mathematical description of the model is presented as shown in Eq. 8.

$$\begin{array}{c}\hfill {\varphi }_p(B){\mathrm{\Phi }}_P(B^s)W_t={\theta }_q(B){\mathrm{\Theta }}_Q(B^s){\omega }_t\end{array}$$ 8

The notation of Eq. 8 is described as follows: p, d  and q are represented in the previous Eq. 4, P presents the order of seasonal AR model, D indicates the number of seasonal differencing, Q refers to the order of seasonal MA, and s is the length of the season (periodicity). Besides, the ${\omega }_t$ and B are the white noise value at period t, and the backward shift operator, respectively.

Equation 8 presents the seasonal components of SARIMA which can be expanded mathematically after substituting the value of $W_t={\mathrm{\nabla }}^d(B){\mathrm{\nabla }}_s^D(B)X_t$.

$$\begin{array}{c}\hfill {\varphi }_p(B){\mathrm{\Phi }}_P(B^s){(1-B)}^d{(1-B^s)}^D{X}_t={\theta }_q(B){\mathrm{\Theta }}_Q(B^s){\omega }_t\end{array}$$ 9

The components of seasonal SARIMA can be written as:

• non-seasonal AR:${\varphi }_p(B)=1-{\varphi }_{1}B-{\varphi }_2{B}^2-{\varphi }_3{B}^3-\cdots -{\varphi }_p{B}^p,$

• non-seasonal MA: ${\theta }_q(B)=1-{\theta }_{1}B-{\theta }_2{B}^2-{\theta }_3{B}^3-\cdots -{\theta }_q{B}^q,$

• seasonal AR: ${\mathrm{\Phi }}_P(B^s)=1-{\mathrm{\Phi }}_1{B}^s-{\mathrm{\Phi }}_2{B}^{2s}-{\mathrm{\Phi }}_3{B}^{3s}-\cdots -{\mathrm{\Phi }}_p{B}^{\mathit{ps}},$

• seasonal MA: ${\mathrm{\Theta }}_Q(B^s)=1-{\mathrm{\Theta }}_1{B}^s-{\mathrm{\Theta }}_2{B}^{2s}-{\mathrm{\Theta }}_3{B}^{3s}-\cdots -{\mathrm{\Theta }}_Q{B}^{\mathit{Qs}}$

and

• $B^s{X}_t=X_{t-s}$,

• ${\mathrm{\nabla }}_s{X}_t={\mathrm{\nabla }}_s(B)X_t=(1-B^s)X_t=X_t-B^s{X}_t=X_t-X_{t-s},$

• ${\mathrm{\nabla }}^d(B)X_t={(1-B)}^d{X}_t,$

• ${\mathrm{\nabla }}_s^D(B)X_t={(1-B^s)}^D{X}_t$

Considering the relationship within the data, SARIMA$(p,d,q)\times {(P,D,Q)}_s$ model is successfully applied to different time-series because of the order of SARIMA is a relatively small number. The period value of time-series s (seasonality) is based on the dataset. For instance, $s=$7,30,365 for weekly, monthly and yearly data respectively. The d and D indicate the order of the non-seasonal and seasonal differencing and its values are not more than 1 and 2 total of seasonal difference, respectively (i.e., $0\le d,D\le 1$).

Model selection

There are three steps in ARIMA model creation namely identification, parameter estimation, and diagnostic checking [32]. The identification process of the model deals with determining proper differencing to get stationary time-series, the order of the model desired and the autocorrelation (ACF) and partial autocorrelation (PACF) functions that are used to recognize the temporal correlation structure of the transformed data. ACF is a statistical metric of the correlation that is used to check if previous values in the time-series analysis have a certain relationship with the latest values or not. For all low order lags, PACF represents the value of the correlation coefficient between the variable and its time lag [33].

The two main methods commonly used to select appropriate models are Akaike’s Information Criterion (AIC) and the Bayesian Information Criterion (BIC) of Schwarz which are presented in Eqs. 10 and 11 for AIC and BIC, respectively [34, 35].

$$\begin{array}{cc}\hfill AIC=& -2log(L)+2k=-2log(L)\hfill \\ \hfill & +2(p+q+P+Q)\hfill \end{array}$$ 10

$$\begin{array}{cc}\hfill BIC=& -2log(L)+kln(n)=-2log(L)\hfill \\ \hfill & +(p+q+P+Q)ln(n)\hfill \end{array}$$ 11

In this regard, n refers to the size of the series, and k presents the number of the parameters of the ARIMA method. It is experimentally proved that our model becomes efficient when the value of AIC is smaller. According to [22], an optimal forecasting model is selected based on the best fitting that has the minimum AIC value of the group.

Data normalization

In this work, data normalization using the min-max scalar function which is available in the scikit-learn library has been applied. Scaling data is a vital task to stabilize the value of variance. Generally, data normalization enhances performance and minimal computational complexity. Equation 12 is used to normalize all datasets before starting to train the model where $Y_i$ presents the scaled datasets, $x_i$ refers to the actual data, and the terms $min(x_i)$ and $max(x_i)$ presents the minimum and maximum values of the actual dataset, respectively.

$$\begin{array}{c}\hfill Y_i=\frac{x_i-min(x_i)}{max(x_i)-min(x_i)}\end{array}$$ 12

Experimental results and evaluation

In the subsequent subsections, the experimental results of the proposed method are presented. The experimental results are presented in terms of simulated results and tabular form and comparative study with state-of-the art methods also are carried out.

Experimental results

To carry out the experiments, the following machine learning libraries such as scikit-learn and Stat are used. The experimentations are executed on the Kaggle environment that provides the required packages. The COVID-19 dataset is collected starting from 22-Jan-2020 to the present time from official websites and data repositories such as WHO and world meter [3, 8]. To attain the best prediction, different parameters of the proposed model are tuned using a grid search technique. The values of parameters have been selected based on the collected data from the corresponding countries. For each country, the best parameters of the SARIMA model are identified and used to forecast for the next 60 days.

The SARIMA model can predict the current time and forecasts the future. In this study, the model is used to forecast the number of confirmed in the next few weeks. It can estimate the full pandemic life cycle and visualize its corresponding curves. The model is fitted with the training data set followed by validation using the test set. After estimating the full life cycle curve for each country, it determines the peak point in the bell-shaped curve to show when the pandemic will stop. For each model, the initial phase creates a set of parameters and initializes them with a bunch of values. Then, the grid search is applied to find out the optimal model that has minimum values of AIC. Next, the model selects the best combination of parameters that can provide minimum error (AIC) and assigned to the best model.

The proposed method is used to estimate the pandemic life cycle. To select the best parameter of the model, the grid search method is applied to each country’s data. The proposed method updates the daily data with the newest version. Table 8 presents the experimental results of the proposed method for the diagnostics test on the global dataset. Moreover, Table 9 shows the experimental results of the diagnostic test using the SARIMA model for the global data that have p-values $\le 0.05$, that indicates minimum values of the AIC of each model.

Table 8.

The experimental results of the diagnostics test on the global COVID-19 data using the proposed SARIMA model

(p, d, q)	(P, D, Q, s)	AIC	MAPE	MAE	MPE	MSE	RMSE	Corr	MinMax
(9, 0, 8)	(0, 0, 0, 3)	−2199.02	14.5343	1.57071	−0.00496	2.48513	1.57643	0.99759	0.887658
(9, 0, 8)	(0, 0, 0, 7)	−2199.02	14.5343	1.57071	−0.00496	2.48513	1.57643	0.99759	0.887658
(9, 0, 8)	(0, 0, 0, 12)	−2199.02	14.5343	1.57071	−0.00496	2.48513	1.57643	0.99759	0.88765
(6, 0, 8)	(0, 0, 0, 3)	−2185.95	14.7139	1.61634	0.07944	2.64173	1.62534	0.99858	0.89227

Table 9.

Experimental results of the diagnostics test for SARIMA models that have p-values less than 0.05 for Global

(p, d, q)	(P, D, Q, s)	AIC	MAPE	MAE	MPE	MSE	RMSE	Corr	MinMax
(9, 0, 0)	(0, 0, 2, 3)	−2159.78	14.7057	1.61697	0.0855918	2.64438	1.62616	0.99866	0.892429
(9, 0, 0)	(0, 0, 1, 7)	−2158.26	14.7219	1.61975	0.0898155	2.65398	1.6291	0.998662	0.892665
(9, 0, 1)	(0, 0, 1, 7)	−2117.39	14.6918	1.61123	0.0802179	2.62402	1.61988	0.998488	0.891833
(9, 0, 0)	(0, 0, 1, 12)	−2114.51	14.6787	1.61202	0.0774122	2.62729	1.62089	0.998648	0.891992
(9, 0, 1)	(0, 0, 2, 3)	−2104.37	14.712	1.61476	0.0857744	2.63616	1.62362	0.998492	0.89214

In this work, we have experimentally proved that the model parameters vary from country to country as the data for each country substantially differs. Considering the relationship within the data, the SARIMA model $(p,d,q)\times {(P,D,Q)}_s$ is successfully applied to different time-series data. The period value of time-series s (seasonality) is considered based on the dataset. Since the daily data for a few months have been used, the value of s is assigned to be 3,7,12. The best forecasting SARIMA model parameters are selected based on the minimum values of AIC, and P-values that are less than 0.05. Table 8 presents the AIC values of different forecasting models. The following SARIMA$(9,0,8)\times (0,0,0,3)$ model has the lowest AIC values as shown in Table 9. The best combination of the parameters $(9,0,8)\times (0,0,0,3)$ is considered to be the best for the corresponding model.

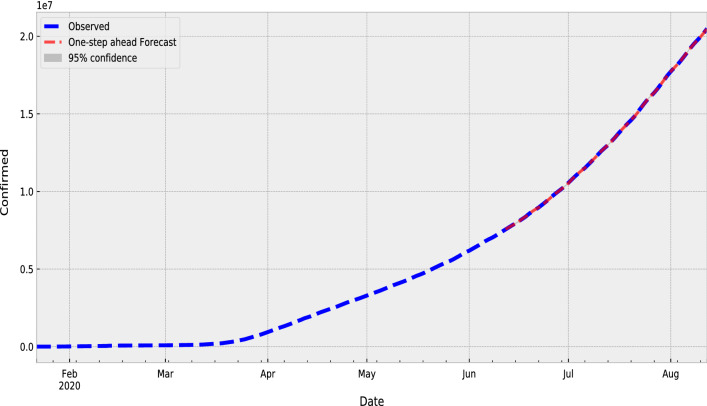
To train and validate the proposed SARIMA model, We have split the COVID-19 data into training and testing dataset on the basis of 70% and 30% ratio for training and validation for testing for each country. The training set comprises data from 22-Jan-2020 to  15-Jun-2020 and the testing set is from 15-Jun-2020 to current day. Table 10 presents the forecasting values with lower and upper confidence limits that are calculated using the proposed model for the period from 15-Jun-2020 to current day. Figure  2 shows the observed (marked in blue line) or training set from 22-Jan-2020 to 15-Jun-2020 and the testing set from 15-Jun-2020 to present-day and values for one step ahead forecasting is presented by the red line. In Fig.  3, the forecasted values marked in the red line, actual values marked in blue line and grey shading area are used for the confidence intervals with lower and upper confidence limits.

Table 10.

Experimental results for the proposed SARIMA$(9,0,8)\times (0,0,0,3)$ Model (from  14-Jul-2020 until  12-Aug-2020) with 95% CI

Date	Actual	Predict	Lower	Upper	Date	Actual	Predict	Lower	Upper
14-Jul-2020	13215902	13210010	13194410	13225600	29-Jul-2020	16907684	16902060	16886470	16917660
15-Jul-2020	13446597	13453240	13437640	13468830	30-Jul-2020	17187933	17203880	17188290	17219480
16-Jul-2020	13698747	13692050	13676450	13707640	31-Jul-2020	17477354	17471090	17455500	17486690
17-Jul-2020	13940201	13944210	13928610	13959800	01-Aug-2020	17727758	17733930	17718340	17749530
18-Jul-2020	14177487	14166590	14151000	14182190	02-Aug-2020	17956551	17955820	17940220	17971410
19-Jul-2020	14391785	14386690	14371090	14402280	03-Aug-2020	18158766	18184260	18168670	18199860
20-Jul-2020	14597751	14605150	14589550	14620740	04-Aug-2020	18416559	18410800	18395200	18426390
21-Jul-2020	14830792	14826130	14810530	14841720	05-Aug-2020	18687247	18701040	18685440	18716630
22-Jul-2020	15110912	15087820	15072220	15103420	06-Aug-2020	18971993	18978590	18963000	18994190
23-Jul-2020	15393012	15386550	15370960	15402150	07-Aug-2020	19252210	19247700	19232100	19263290
24-Jul-2020	15673428	15663950	15648360	15679550	08-Aug-2020	19511342	19503500	19487900	19519090
25-Jul-2020	15928573	15933060	15917470	15948660	09-Aug-2020	19735209	19727920	19712320	19743510
26-Jul-2020	16141458	16167220	16151630	16182820	10-Aug-2020	19962254	19954320	19938720	19969920
27-Jul-2020	16367174	16367310	16351710	16382900	11-Aug-2020	20216340	20216720	20201130	20232320
28-Jul-2020	16619072	16623080	16607480	16638680	12-Aug-2020	20492606	20504110	20488510	20519700

Fig. 2.

Comparison between the observed and predicted values (one-step ahead result) for SARIMA model on COVID-19 dataset

Fig. 3.

The forecasted values for the COVID-19 new cases over the globe until 15-Nov-2020

The proposed model predicts the number of the confirmed cases of the next few days or months using the previously observed data as shown in Table 11 with lower and upper confidence limits. Although the increasing trend is visible, the proposed model has better performance for the testing set. Generally, the forecast performance is acceptable when the MSE and RMSE values for the testing set from  15-Jun-2020 to present day are 2.48513 and 1.57643, respectively.

Table 11.

The forecasted values of daily confirmed cases for 60 days using SARIMA$(9,0,8)\times (0,0,0,3)$ model with 95% CI

Date	Predicted	Lower	Upper	Date	Predicted	Lower	Upper
13-Aug-2020	20792367	20776772	20807963	12-Sep-2020	29188539	28260321	30116756
14-Aug-2020	21084923	21058525	21111321	13-Sep-2020	29435471	28457387	30413554
15-Aug-2020	21345577	21309105	21382049	14-Sep-2020	29678949	28650726	30707172
16-Aug-2020	21574054	21526767	21621341	15-Sep-2020	29957835	28878513	31037158
17-Aug-2020	21802821	21742548	21863094	16-Sep-2020	30285328	29153157	31417500
18-Aug-2020	22058307	21984681	22131933	17-Sep-2020	30638542	29451469	31825615
19-Aug-2020	22348910	22259069	22438751	18-Sep-2020	30975118	29731554	32218682
20-Aug-2020	22659604	22549663	22769545	19-Sep-2020	31264945	29964175	32565716
21-Aug-2020	22960884	22828738	23093030	20-Sep-2020	31513451	30155353	32871548
22-Aug-2020	23227743	23073035	23382450	21-Sep-2020	31758282	30342636	33173927
23-Aug-2020	23462762	23284968	23640556	22-Sep-2020	32041177	30567071	33515284
24-Aug-2020	23695762	23493979	23897545	23-Sep-2020	32376197	30841935	33910459
25-Aug-2020	23957641	23730778	24184504	24-Sep-2020	32738483	31142078	34334888
26-Aug-2020	24258265	24004081	24512448	25-Sep-2020	33082355	31422266	34742443
27-Aug-2020	24580351	24295972	24864730	26-Sep-2020	33375605	31651144	35100067
28-Aug-2020	24890891	24574346	25207436	27-Sep-2020	33624359	31835435	35413283
29-Aug-2020	25164510	24815110	25513910	28-Sep-2020	33869239	32015671	35722807
30-Aug-2020	25404653	25022092	25787213	29-Sep-2020	34155078	32235989	36074167
31-Aug-2020	25641999	25225753	26058245	30-Sep-2020	34496799	32510528	36483071
01-Sep-2020	25910170	25459144	26361195	01-Oct-2020	34867421	32812015	36922826
02-Sep-2020	26220390	25732602	26708178	02-Oct-2020	35217714	33091666	37343763
03-Sep-2020	26553448	26026491	27080405	03-Oct-2020	35513214	33315859	37710568
04-Sep-2020	26873196	26305281	27441112	04-Oct-2020	35760795	33492077	38029512
05-Sep-2020	27153072	26543451	27762693	05-Oct-2020	36004315	33664089	38344542
06-Sep-2020	27397194	26745661	28048727	06-Oct-2020	36291935	33879352	38704519
07-Sep-2020	27638128	26944324	28331931	07-Oct-2020	36639469	34152887	39126052
08-Sep-2020	27912053	27174956	28649151	08-Oct-2020	37017636	34455122	39580151
09-Sep-2020	28231258	27449030	29013487	09-Oct-2020	37373405	34733470	40013339
10-Sep-2020	28574713	27745179	29404247	10-Oct-2020	37669881	34951892	40387871
11-Sep-2020	28903208	28024702	29781714	11-Oct-2020	37914764	35118699	40710830

The risk of second rebound of COVID-19 pandemic

Epidemiologically, the history of the deadly pandemic viral infection demonstrates that after getting to the end, they are usually followed by waves of significant spread and deaths. For instance, the Spanish flu first appeared in the USA and then transmitted to Europe via World War I participant soldiers in early Mar-1918. It had all the hallmarks of the seasonal flu, that is highly contagious and infectious strains. Yet the first wave of the virus did not appear to be particularly deadly, with symptoms like high fever and malaise usually lasting only three days. There was hope at the beginning that the virus had finalized its course. However, somewhere in Europe, a mutated strain of the Spanish flu virus had emerged. This mutated virus got spread by the end of wartime troop movements from England to France, Africa and the USA causing the fatal severity of the Spanish flu’s “second rebound” [36, 37].

Another example was the H7N9 pandemic. Since its emergence in Mar-2013, novel avian influenza A H7N9 virus has triggered five epidemics of human infections in China. This raises concerns about the pandemic threat of this quickly evolving H7N9 subtype for humans [38–41].

The worrying thing is that many countries are preparing to ease their lockdowns while planning to continuously monitor potential new cases to prevent a second deadly outbreak. The uneven progress of countries’ efforts to control the virus has led health researchers to warn that nations will have to monitor closely for new infections and adjust the measures in place until the availability of vaccine. China’s aggressive control over the daily life have nearly brought the first wave of COVID-19 to an end; however, the danger of a second wave remains uncertain [3, 4].

While these control measures appear to have reduced the number of infections to some extent, without herd immunity against COVID-19, cases could easily resurge as businesses, factory operations and schools gradually resume and increase social mixing, particularly given the increased risk of imported cases from overseas as COVID-19 continues to spread globally. World leaders and health officials are warning that hard-won gains must not be risked by people relaxing physical distancing measures [42, 43].

From the outset of this worldwide pandemic, multiple models have been developed by different organizations and research institutions. Generally, models present the worst-case and best-case scenarios, under different sets of circumstances. With each model, the timing, height, and width of the peak of confirmed COVID-19 cases and deaths rates are uncertain. This is due to complexity and randomness in the dynamics of virus transmission and uncertainty in key epidemiological parameters [44].

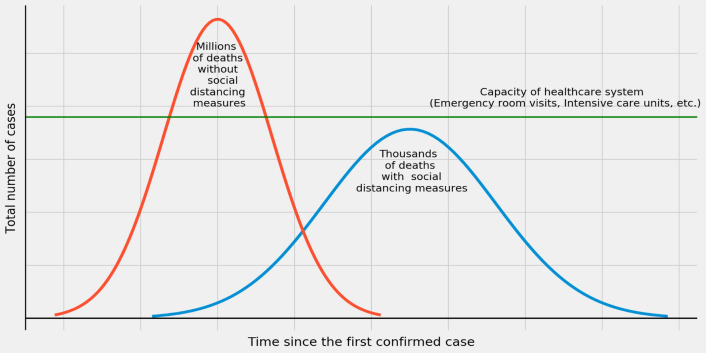
As presented in Fig. 4, the green line depicts the health care system capacity. The part of the red line of the bell curve above the ideal green line shows that if social distancing is not respected, millions of people may die due to the pandemic. On the other hand, if the social distancing measures are strictly followed, only thousands of people may die before the end of the pandemic (as depicted by the blue coloured bell-shaped line). Besides lowering the morbidity and mortality indices, social distancing measures aim to ensure there is less burden to the health care system [44, 45].

Fig. 4.

Death flatten curve

With due acknowledgement to the uncertain nature of the ongoing COVID-19 pandemic and our growing inter-connected and complex world, what is eventually and fundamentally required are the flexibility, robustness and resilience to deal with unexpected future events and scenarios.

Moreover, the proposed model forecasts that there is a chance of the second rebound of the pandemic in a year time if the prevention guidelines and precautions are not followed. We have to consider the uncertain nature of the current COVID-19 pandemic and the growing inter-connected and complex world, that are ultimately demanding flexibility, robustness and resilience to cope with the unexpected future events and scenarios. Our study shows the pandemic rebound is in line with the current scenario in some countries such as India, Brazil and the USA as their social distancing and related measures are relaxed (See Tables 12 and 14).

Table 12.

Expected deadline for some countries in the first and second rebounds

Country	First confirmed case	Estimation without forecasting					Estimation with Forecasting
		Peak point	Start date 95%	End date 99%	Start value	End value	Peak point	Start date 95%	End date 99%	Start value	End value
The first rebound
USA	22-Jan-2020	06-May-2020	06-Jul-2020	06-Aug-2020	402	11	30-May-2020	23-Aug-2020	01-Oct-2020	13747	11
Spain	01-Feb-2020	06-May-2020	21-Jun-2020	18-Jul-2020	2277	2	09-Jun-2020	07-Aug-2020	12-Sep-2020	49515	2
Italy	31-Jan-2020	06-May-2020	22-Jun-2020	20-Jul-2020	12462	3	08-Jun-2020	09-Aug-2020	14-Sep-2020	69176	3
France	24-Jan-2020	06-May-2020	03-Jul-2020	02-Aug-2020	1136	6	01-Jun-2020	20-Aug-2020	27-Sep-2020	12758	11
United Kingdom	31-Jan-2020	06-May-2020	22-Jun-2020	20-Jul-2020	459	9	08-Jun-2020	09-Aug-2020	14-Sep-2020	8164	9
Germany	27-Jan-2020	06-May-2020	29-Jun-2020	28-Jul-2020	1176	14	04-Jun-2020	15-Aug-2020	22-Sep-2020	24873	16
Russia	31-Jan-2020	06-May-2020	22-Jun-2020	20-Jul-2020	28	2	08-Jun-2020	09-Aug-2020	14-Sep-2020	495	2
The second rebound
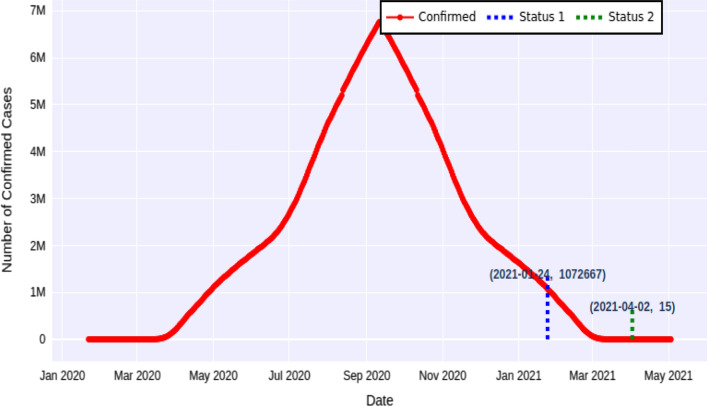
US	22-Jan-2020	12-Aug-2020	08-Dec-2020	05-Feb-2020	701996	13	12-Sep-2020	24-Jan-2021	02-Apr-2021	1072667	15
Brazil	26-Feb-2020	12-Aug-2020	14-Oct-2020	01-Dec-2020	135773	793	12-Sep-2020	30-Nov-2020	26-Jan-2021	291579	2247
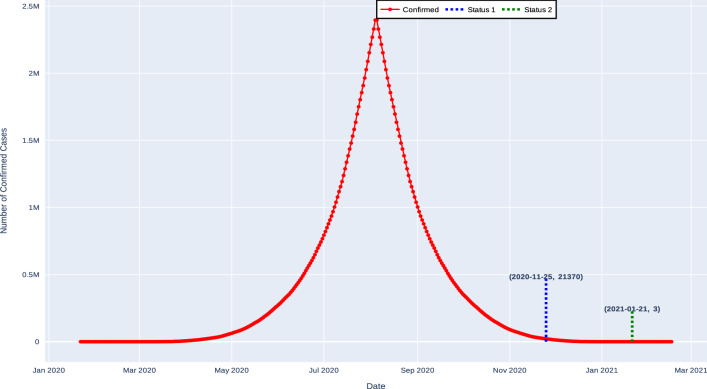
India	30-Jan-2020	12-Aug-2020	25-Nov-2020	21-Jan-2021	21370	3	12-Sep-2020	12-Jan-2021	18-Mar-2021	46437	3
Spain	01-Feb-2020	12-Aug-2020	22-Nov-2020	17-Jan-2021	213024	15	12-Sep-2020	09-Jan-2021	14-Mar-2021	219329	120
Italy	31-Jan-2020	12-Aug-2020	24-Nov-2020	19-Jan-2021	187327	453	12-Sep-2020	10-Jan-2021	16-Mar-2021	213013	1694
France	24-Jan-2020	12-Aug-2020	05-Dec-2020	01-Feb-2021	148086	12	12-Sep-2020	21-Jan-2021	29-Mar-2021	167305	12
United Kingdom	31-Jan-2020	12-Aug-2020	24-Nov-2020	19-Jan-2021	141540	37	12-Sep-2020	10-Jan-2021	16-Mar-2021	196780	94
Germany	27-Jan-2020	12-Aug-2020	30-Nov-2020	26-Jan-2021	147065	16	12-Sep-2020	16-Jan-2021	23-Mar-2021	165664	46
Russia	31-Jan-2020	12-Aug-2020	24-Nov-2020	19-Jan-2021	57999	2	12-Sep-2020	10-Jan-2021	16-Mar-2021	155370	2

Table 14.

Comparison of the proposed model with the state-of-the-art method on the first rebound

Countries	The state-of-the-art models [13]			The proposed model (the first wave)
	Turning Date	End 99%	End 100%	Turning date	End 99%	End 100%
France	3-Apr-2020	18-May-2020	5-Aug-2020	01-Jan-2020	27-Sep-2020	13-Oct-2020
Italy	29-Mar-2020	21-May-2020	25-Aug-2020	08-Jan-2020	14-Sep-2020	01-Oct-2020
US	10-Apr-2020	24-May-2020	27-Aug-2020	30-May-2020	01-Oct-2020	15-Oct-2020
Russia	24-Apr-2020	28-May-2020	20-Jul-2020	08-Jan-2020	14-Sep-2020	01-Oct-2020
United Kingdom	12-Apr-2020	27-May-2020	14-Aug-2020	08-Jan-2020	14-Sep-2020	01-Oct-2020

Estimation of slowdown of COVID-19

The COVID-19 is similar to other pandemics in terms of life cycle pattern which includes the outbreak, slowdown, stoppage phases and infection peak point. Based on the various phases of the life cycles of COVID-19 at a specific point in time, each country has a different starting date of the first phase based on the first confirmed case. For example, the first confirmed cases in the USA and Italy is on 15-Jan-2020, and on 31-Jan-2020, respectively [8].

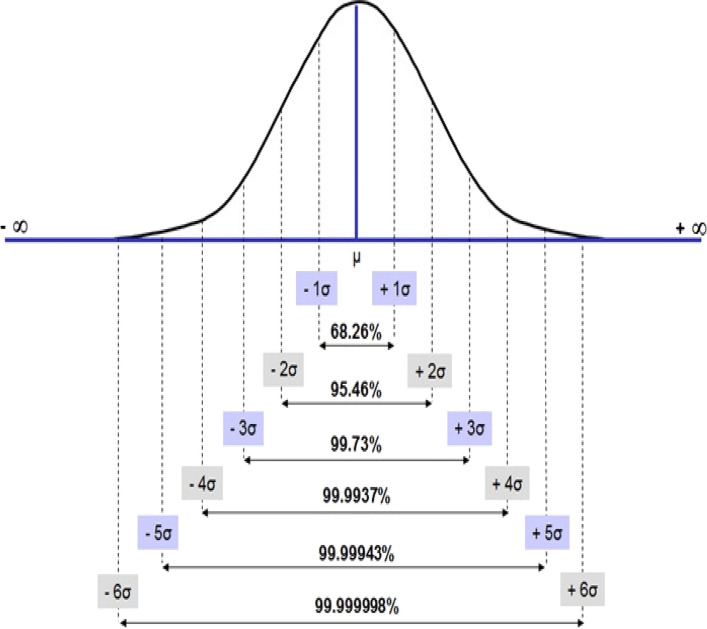
The basic idea of our assessment is based on the assumption that the data follows the concept of normal distribution. The proposed predictive model enables to estimate the expected period that the virus can be slowed down and ultimately stopped. The inflection’s peak point is specified as it appears like the peak point in the bell-shaped curve that depicts a possible slowdown and stoppage of the pandemic based on the normal distribution as shown in Fig. 5. However, estimating the ending date varies based on different considerations such as the first confirmed case and protective measures. Theoretically, one can define the end date as the one with the last predicted case in the pandemic life cycle curve, and others may consider an early date as the end date from businesses, schools or governments when most of the predicted infections (indicated by the regressed pandemic life cycle curve) have been actualized and only a small portion of the total predicted epidemic population is left.

Fig. 5.

A normal distribution within 1 standard deviation ($\sigma$) from the mean ($\mu$) using SARIMA

The following mathematical Equations present the statistical estimation of the slow down period of the pandemic which is extracted based on the concept of normal distribution. It explains how to calculate the area under the curve between $\mu +2\sigma$ and $\mu +3\sigma$ corresponding to the period that the pandemic can stop.

$$\begin{array}{cc}\hfill p(\mu +2\sigma <X<\mu +3\sigma )=& p(\frac{\mu +2\sigma -\mu }{\sigma }\hfill \\ \hfill <& Z<\frac{\mu +3\sigma -\mu }{\sigma })\hfill \\ \hfill =& p(\frac{2\sigma }{\sigma }<Z<\frac{3\sigma }{\sigma })\hfill \\ \hfill =& p(2<Z<3)=2.1\%\hfill \end{array}$$

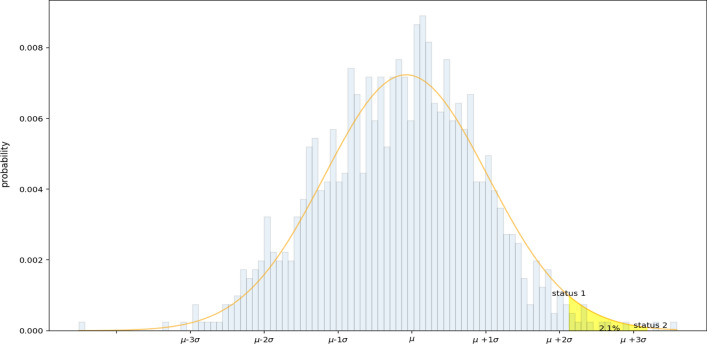
Figure 6 shows the confidence intervals (CI) for the expected total cases that have been identified and calculated as follows:

$$\begin{array}{c}\hfill p(\mu -2\sigma <Z<\mu +2\sigma )=95.46\%\\ \hfill p(\mu -3\sigma <Z<\mu +3\sigma )=99.73\%\end{array}$$

The final predictions of the proposed model provide the following three estimates of end dates: (1) The estimated period from $\mu +2\sigma$ to $\mu +3\sigma$ with probability 2.1% presents the last expected cases have identified. (2) The estimated period from $\mu -2\sigma$ to $\mu +2\sigma$ presents 95.46% of the expected total cases that have been identified. (3) The estimated period from $\mu -3\sigma$ to $\mu +3\sigma$ presents the date when 99.73% of the expected cases have been identified as shown in Fig. 6.

Fig. 6.

A normal distribution within 1 standard deviation ($\sigma$) from the mean ($\mu$)

Table 12 presents the experimental results of the proposed model that shows the expected deadline of specified countries. The topmost affected countries in the first are the USA, Spain, Italy, France, the UK, Germany and Russia. In the second rebound of the pandemic, the model generates the countries namely the US, Brazil, India, Spain, Italy, France, the UK, Germany and Russia. Table 12 presents estimation without forecasting or with forecasting (for one month ahead) in the first rebound. Similarly, in the second rebound, the model generates estimation without forecasting or with forecasting (for one month ahead). The table has the names of the attributes such as country, date of the first confirmed case, the peak point (top of the bell-shaped graph), the start date is the first expected date with a confidence interval of 95%, the end date which is the last expected date with a confidence interval of 99%, start value (the corresponding value of the start date) and the end value is the corresponding value of the end date.

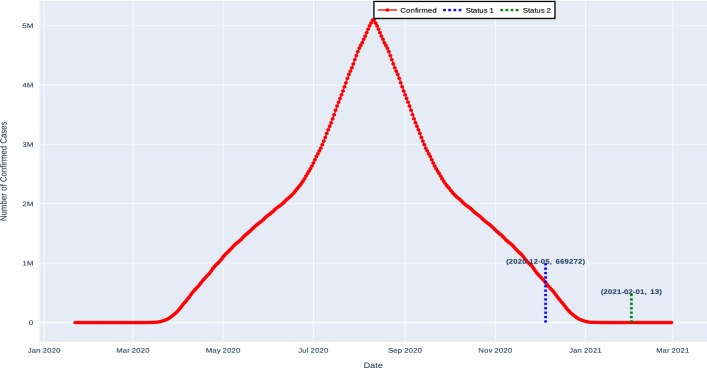
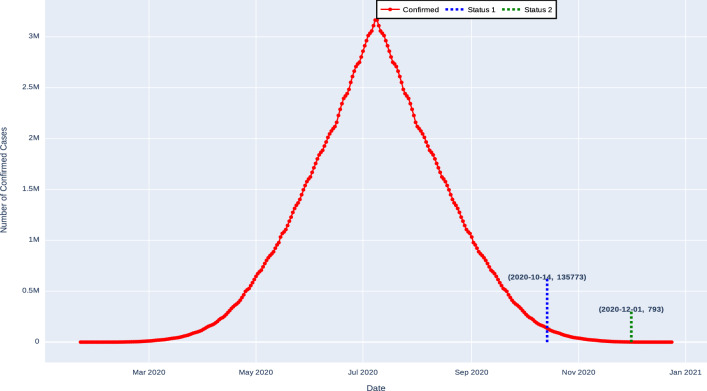
The proposed method exhibits different forecasting results for the first and second rebounds of the pandemic for various countries. To make the forecasted results more updated and in line with reality, we are describing the second rebound cases. Table 12 shows the estimated time for the USA by applying forecasting approach. The expected number of confirmed cases for the USA will be 701996 on  08-Dec-2020, and after one and a half month that is on  05-Feb-2020, the number of confirmed cases will decrease to 13 as shown in Fig. 7. Moreover, for the second rebound when forecasting approach is applied, the expected number of confirmed cases will be 1072667 on  24-Jan-2020, and after three months that is on  02-Apr-2020, the number of confirmed cases will decrease to 15 as shown in Fig. 8.

Fig. 7.

Expected dead line for the USA without forecasting

Fig. 8.

Expected deadline for the USA in the second rebound with forecasting

Table 12 presents the estimated values of the end date of the pandemic in India. When forecasting approach is applied, the proposed method exhibited different results. Hence, the expected number of confirmed cases will be 21370 on  25-Nov-2020, and after two months, that is on  21-Jan-2021, the number of confirmed cases will decrease to 3 as shown in Fig. 9

Fig. 9.

Expected deadline for the India in the second rebound without forecasting

As presented in Table 12, for the case of Brazil, when forecasting approach is applied, the proposed method exhibits various results. The expected number of confirmed cases will be 135773 on  14-Oct-2020, and after two months, that is on  01-Dec-2020, the number of confirmed cases will decrease to 793 as shown in Fig. 10.

Fig. 10.

Expected deadline for the Brazil in the second rebound without forecasting

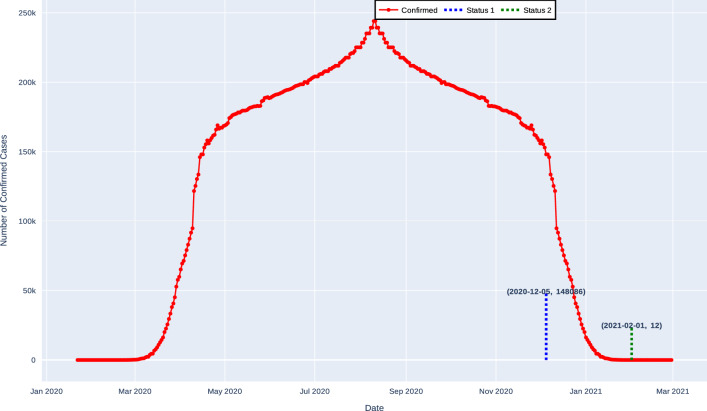
Table 12 shows the prediction of the deadline to end the pandemic for France using the real data, and the results showed that expected number of confirmed cases will be 148084 on  02-Dec-2020, and after two months that is on  28-Jan-2021, the number of confirmed cases will decrease to 12 without applying forecasting approach. When forecasting approach is applied, the proposed method exhibits different results. The expected number of confirmed cases will be 12758 on  20-Aug-2020, and after a month that is on  27-Sep-2020, the number of confirmed cases will decrease to 11 as shown in Fig. 11.

Fig. 11.

Expected deadline for the France in the second rebound without forecasting

China was successful in halting the COVID-19 epidemic as the government applied early quarantine strategy. The confirmed cases trend in China becomes stable and frequently remains between zero and one. This fact indicates that quarantine worked well to reduce human exposure and succeeded to control the epidemic. Moreover, the study shows Brazil and India had unstable trends. Finally, the expected confirmed cases for the top countries will be manifested between Dec-2020 to Apr-2020 as shown in Table 12. Moreover, these predictions may vary based on many factors such as the lockdown period or developing an effective vaccine against COVID-19.

Comparison with state-of-the-art models

In our work, we have carried out a comparative study with state-of-the-art methods as presented in Table 13. The comparative study is carried in the following models namely ARIMA, Machine learning (Random Forest) and deep learning model (LSTM). The performance of each model is evaluated using various metrics such as root-mean-square error (RMSE) and mean absolute error (MAE) on the test dataset. Based on the experimental results of the proposed SARIMA model, it is indicated that significant results are achieved when compared with the state-of-the-art models. Hence, the proposed SARIMA model can be extended and used to predict other countries as it is giving an acceptable performance when observed its accuracy.

Table 13.

A comparative study of the proposed method with the state-of-the-art models in terms of confirmed cases

	The state-of-the-art models			The proposed model (SARIMA)
	Country	Metrics (RMSE/MAE)	Value	Country	Metrics (RMSE/MAE)	Value
ARIMA [17]	Spain	RMSE	379.89	Spain	RMSE	0.68588
ARIMA [20]	India	MAE	47.42	India	MAE	4.06187
Machine learning (Random Forest) [46]	worldwide	MAE	368.821	worldwide	MAE	1.61697
Deep learning (LSTM) [47]	worldwide	RMSE	30758	worldwide	RMSE	1.57643
Deep learning (LSTM) [48]	US	RMSE	324.61	US	RMSE	1.25634

Table 14 presents the comparison with the state-of-the-art model for the top countries on the first rebound. The estimation of COVID-19 end dates for top countries with forecasting approach as of  Oct-2020 is 99.73% percentage. For example, the end date based on a the-state-of-art method for the USA is 27-Aug-2020 [13] while our model’s prediction date is on 15-Oct-2020 which is statistically more accurate. In any case, prediction and specifying an end date is arbitrary. Alternatively, estimation as a range of dates might make sense for such uncertain predictions. The estimated date range is expected to become narrower as the countries continually evolve along the pandemic life cycle curve to its end date.

In any prediction tasks, more data are needed to achieve better performance from the models underuse. The best predictive models can help in predicting future confirmed cases if the spread of the virus does not change radically. It is known that the pandemic COVID-19 virus is novel and can be transmitted easily. This can affect all the predictions, but to the best of our knowledge and in the time of writing, our proposed model is best compared to the state-of-the-art methods.

Conclusion

This research work investigates the answer to the most important questions raised today: when will the COVID-19 pandemic end and is there a possibility for the second rebound in case of returning to daily routine life. Despite accelerated virus mutation and the nature of the dataset based on time and date, the work done tried to reduce the variability of the data by taking only the dataset from WHO and John Hopkins University. The proposed model provides a statistical estimate of the slowing down of the pandemic, which is derived based on the normal distribution principle. The work done helped in estimating the life cycle of the pandemic and selecting the optimal model parameter using the grid search method. The experimental results of the proposed method match with the daily data to show the realistic nature of the proposed model.

The results pointed out to the likelihood that there will be a second rebound of the pandemic in a year time if the currently taken precautions are eased completely. This study will have a significant benefit in helping governments in making decisions and planning for the future to reduces anxiety and prepare the minds of people for the next phases of the pandemic. The proposed work has some limitations. Hence, we believe that it could lead to the next research avenue on COVID-19 pandemic and can be a good starting point considering the uncertain nature of the pandemic and our growing inter-connected and complex world. What is eventually and fundamentally needed is the flexibility, robustness and resilience to deal with unexpected future events and scenarios. The future work of this research will focus on improving the performance of our model by using a huge data and applying the proposed model to more countries. Moreover, we plan to update this study with more analyses and cases, by fine-tuning the prediction and visualization methodology.

Compliance with ethical standards

Conflict of interest

The authors declare that there is no conflict of interest.