Interference patterns in subject-verb agreement and reflexives revisited: A large-sample study

Abstract

Cue-based retrieval theories in sentence processing predict two classes of interference effect: (i) Inhibitory interference is predicted when multiple items match a retrieval cue: cue-overloading leads to an overall slowdown in reading time; and (ii) Facilitatory interference arises when a retrieval target as well as a distractor only partially match the retrieval cues; this partial matching leads to an overall speedup in retrieval time. Inhibitory interference effects are widely observed, but facilitatory interference apparently has an exception: reflexives have been claimed to show no facilitatory interference effects. Because the claim is based on underpowered studies, we conducted a large-sample experiment that investigated both facilitatory and inhibitory interference. In contrast to previous studies, we find facilitatory interference effects in reflexives. We also present a quantitative evaluation of the cue-based retrieval model of Engelmann et al. (2019), with respect to the reflexives data. Data and code are available from: https://osf.io/reavs/.

Introduction

What are the constraints on linguistic dependency formation in online sentence comprehension? This has been a central theoretical question in psycholinguistics. Inspired by research in cognitive psychology, constraints on working memory have been invoked to explain how the human sentence parsing system works out who did what to whom. For example, when a verb is read or heard, what mechanism does the parsing system use to identify the subject and object of the verb? A widely accepted view (Lewis, Vasishth, & Van Dyke, 2006; McElree, 2003; Van Dyke & Lewis, 2003) is that a cue-based retrieval mechanism drives this dependency completion process. When a dependency needs to be completed, the cue-based retrieval account assumes that certain features (retrieval cues) are used to retrieve the co-dependent item, the retrieval target, from memory. An important consequence of such a cue-based retrieval mechanism is that whenever other items, called distractors, also match some or all of the retrieval cues, similarity-based interference can arise.

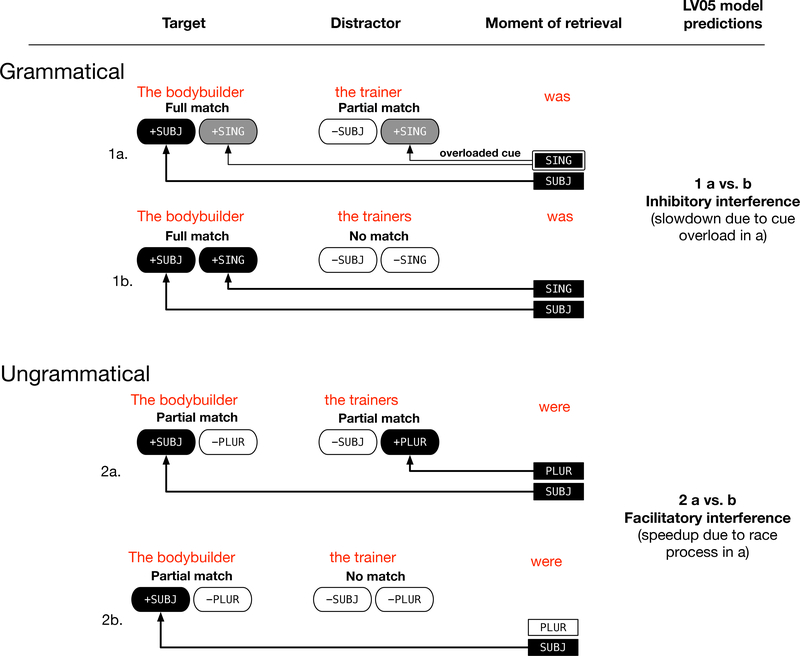
As an example of similarity-based interference, consider the subject-verb dependency shown below in 1. This set of sentences is taken from Dillon, Mishler, Sloggett, and Phillips (2013). Following the convention in Engelmann, Jäger, and Vasishth (2019), we show retrieval cues in curly braces, and binary-valued features on nouns that match or mismatch the retrieval cues.

$$\begin{array}{l}\text{a}.\mathit{Agreement};\mathit{grammatical};\mathit{interference}\\ \text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{+singular}\text{who}\text{worked}\text{with}\text{the}\text{personal}\\ {\text{trainer}}_{-localsubject}^{\text{+}singular}\text{amazingly}\text{was}\left\{\begin{array}{l}singular\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\\ \text{b}.\mathit{Agreement};\mathit{grammatical};\mathit{no}\mathit{interference}\\ \text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{+singular}\text{who}\text{worked}\text{with}\text{the}\text{personal}\\ {\text{trainers}}_{-localsubject}^{-singular}\text{amazingly}\text{was}\left\{\begin{array}{l}singular\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\end{array}$$ (1)

In these sentences, the dependency of interest is the one between the main clause verb was and its subject the amateur bodybuilder. Consistent with evidence suggesting that focal attention is highly limited (e.g., McElree, 2006), the distal subject must be retrieved from memory when the verb is encountered. Simplifying somewhat, we assume that the verb uses two cues, number and local-subject status, to search for the retrieval target (i.e., the subject). Because of the perfect match between the retrieval cues and the target, the sentences are grammatical.

In 1a, one of these retrieval cues, the singular number feature, matches not only with the main-clause singular subject but also with the distractor, the singular noun inside the relative clause, the personal trainer. By contrast, in 1b, this distractor noun is plural-marked (the personal trainers) and so does not match the number retrieval cue. The situation in 1a, where both the target and the distractor noun (partially) match the retrieval cues, is referred to as cue overload. This cue overload leads to interference, which is expressed as a slowdown at the verb (where the subject must be retrieved) in reading time in self-paced reading and eyetracking experiments (Van Dyke, 2007; Van Dyke & Lewis, 2003; Van Dyke & McElree, 2011). Following Dillon (2011), we will refer to this slowdown as inhibitory interference.

Interference due to cue-overload is a key prediction of cue-based retrieval models of sentence processing (Lewis & Vasishth, 2005; McElree, 2000; Van Dyke, 2007; Van Dyke & Lewis, 2003; Van Dyke & McElree, 2011). A computationally implemented model that predicts such inhibitory interference effects is the cue-based retrieval model of Lewis and Vasishth (2005) (henceforth LV05).¹ This model was developed within the general cognitive architecture, Adaptive Control of Thought-Rational (ACT-R, Anderson et al. 2004). Cue-based retrieval models can explain interference effects (Dillon et al., 2013; Jäger, Engelmann, & Vasishth, 2015; Kush & Phillips, 2014; Nicenboim, Logačev, Gattei, & Vasishth, 2016; Nicenboim, Vasishth, Engelmann, & Suckow, 2018; Parker & Phillips, 2016,1; Patil, Vasishth, & Lewis, 2016; Vasishth, Bruessow, Lewis, & Drenhaus, 2008), but they have also been invoked in connection with a range of other issues in sentence processing: the interaction between predictive processing and memory (Boston, Hale, Vasishth, & Kliegl, 2011), impairments in individuals with aphasia (Mätzig, Vasishth, Engelmann, Caplan, & Burchert, 2018; Patil, Hanne, Burchert, Bleser, & Vasishth, 2016), the interaction between oculomotor control and sentence comprehension (Dotlačil, 2018; Engelmann, Vasishth, Engbert, & Kliegl, 2013), the processing of ellipsis (Martin & McElree, 2009; Parker, 2018), the effect of working memory capacity differences on underspecification and “good-enough” processing (Engelmann, 2016; von der Malsburg & Vasishth, 2013), and the interaction between discourse/semantic processes and cognition (Brasoveanu & Dotlačil, 2019). The source code of the model used in this paper is available from https://github.com/felixengelmann/inter-act; and quantitative predictions can be derived graphically using the Shiny App available from https://engelmann.shinyapps.io/inter-act/.

Inhibitory interference arises in the LV05 model as a consequence of the spreading activation assumption inherent in the ACT-R architecture: multiple items (e.g., the target noun and the distractor noun in 1a above) match a retrieval cue, leading to an activation penalty on each item, increasing average retrieval time. The linguistic context that leads to inhibitory interference is illustrated schematically in the upper part of Figure 1.

Figure 1.

A schematic figure illustrating inhibitory and facilitatory interference in the Lewis & Vasishth (2005) cue-based retrieval model. Inhibitory interference refers to a slowdown in reading time and facilitatory interference to a speedup in reading time due to the presence of a partially matching distractor. The figure is adapted from Engelmann, Jäger, & Vasishth (2019).

In addition to inhibitory interference, cue-based retrieval also predicts a so-called facilitatory interference effect in specific situations: when no retrieval candidate fully matches the retrieval cues, and a distractor is present that partially matches the retrieval cues, an overall speedup is observed in reading time (Engelmann et al., 2019; Logačev & Vasishth, 2016). Here, the word “facilitatory” only refers to the observed speedup, and not to a facilitation in comprehension or parsing. Facilitatory interference arises in ACT-R through the following mechanism: when a retrieval attempt is initiated, all partial matches become candidates for retrieval, and the item which happens to have a higher activation in a particular trial gets retrieved. When multiple items are candidates for retrieval, a so-called race situation arises. If such a race holds, average reading times will be as fast or faster compared to when no race condition occurs. When the mean finishing times of both processes are similar, the average finishing time will be faster; and when one process has a much faster finishing time than the other, the average finishing time will follow the distribution of the faster process. This is illustrated in Figure 2. Also see Logačev and Vasishth (2016) for a detailed exposition.

Figure 2.

An illustration of a race process involving two distributions. When the two distributions have similar means (left-hand side figure), the distribution of the values from a race process will lead to an overall facilitation. When one distribution has a much smaller mean (right-hand side figure), the distribution of the race process will have the same distribution as the distribution with the smaller mean.

There is considerable evidence for this kind of facilitatory interference effect in sentence processing. For example, Dillon et al. (2013) showed that in sentences like 2a vs. 2b, mean reading time at the main clause verb were was faster by −119 ms (95% confidence interval of [−205, −33] ms). These sentences are ungrammatical because the subject does not match the matrix verb’s number marking; under ACT-R assumptions, the race situation arises in 2a because a distractor noun phrase matches the number marking on the verb.²

$$\begin{array}{l}\text{a}.\mathit{Agreement};\mathit{grammatical};\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}\\ {\text{trainers}}_{-localsubject}^{+plural}\text{amazingly}\text{were}\left\{\begin{array}{l}plural\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\\ \text{b}.\mathit{Agreement};\mathit{ungrammatical};\mathit{no}\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}\\ {\text{trainer}}_{-localsubject}^{-plural}\text{amazingly}were\left\{\begin{array}{l}plural\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\end{array}$$ (2)

Such facilitatory effects (i.e., speedups) have been found in self-paced reading studies on subject-verb number agreement; for English, see Wagers et al. (2009), and for Spanish, see Lago et al. (2015). In eyetracking data, semantic plausibility manipulations (Cunnings & Sturt, 2018) also show a speedup in total fixation time (i.e., the sum of all fixation durations on a region) that can be explained in terms of a race process.

Although the bulk of research in the cue-based retrieval tradition supports the predictions of inhibitory and faciltatory interference, there is one apparent counterexample. Consider the sentences shown in 3a vs. 3b. The sentence 3a has the same characteristics as the ungrammatical subject-verb construction 2a discussed earlier: the subject (the amateur bodybuilder) matches only some of the retrieval cues on the reflexive; it does not match the number cue. In dependencies such as subject-verb agreement, non-structural cues like number are assumed to be used in addition to syntactic cues. Consequently, the phrase the personal trainers is a distractor and will be retrieved in some proportion of trials, leading to a race condition, according to the LV05 model. However, as we discuss below in detail, Dillon et al. (2013) found facilitatory interference only in subject-verb dependencies; they did not find evidence for facilitatory interference in antecedent-reflexive constructions. Their explanation for this asymmetry between the two dependency types is based on a proposal by Sturt (2003) according to which, in reflexives, Principle A of the binding theory (Chomsky, 1981) is used exclusively for seeking out the antecedent. Thus, Principle A acts as a filter that allows the parser to unerringly identify the antecedent even if distractors are present. In the original proposal by Sturt (2003), a distinction was made between early and late processes: the privileged role of the grammatical constraint was assumed to apply only in early measures in eyetracking data. However, this early-late distinction seems to have been abandoned in subsequent work on reflexives. We return to this point in the General Discussion.

$$\begin{array}{l}\text{a}.\mathit{Reflexive};\mathit{ungrammatical};\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+c-com}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}{\text{trainers}}_{-c-com}^{+pular}\\ \text{amazingly}\text{injured}\text{themselves}\left\{\begin{array}{l}plural\hfill \\ c-com\hfill \end{array}\right\}\text{on}\text{the}\text{lightest}\text{weights}.\\ \text{b}.\mathit{Reflexive};\mathit{ungrammatical};\mathit{no}\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+c-com}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}{\text{trainer}}_{-c-com}^{-plural}\\ \text{amazingly}\text{injured}\text{themselves}\left\{\begin{array}{l}plural\hfill \\ c-com\hfill \end{array}\right\}\text{on}\text{the}\text{lightest}\text{weights}.\\ \end{array}$$ (3)

Dillon et al. (2013)’s conclusion that there is an asymmetry between subject-verb dependencies and antecedent-reflexive dependencies has important theoretical consequences: it implies that fundamentally different memory operations may be associated with particular linguistic contexts. Dillon et al. (2013)’s argument is that in reflexives, non-structural cues play no role at all in the retrieval of antecedents; this is clear from Table A.4 of Dillon (2011, p. 322), which reports the modeling in more detail than in the published paper. Kush (2013) and Cunnings and Sturt (2014) take a more intermediate position, that structural cues are merely weighted higher than non-structural cues in reflexive-antecedent dependencies (thus, Dillon and colleagues’ claim amounts to assuming that non-structural cues have weight 0). A related finding was made by Van Dyke and McElree (2011), who observed that in (non-agreement) subject-verb dependencies as well, structural cues such as subjecthood are weighted higher than semantic cues. Dillon et al. (2013)’s Experiment 1 is unique in that it is the only within-participants sentence comprehension study that directly compares the two dependency types by varying a single feature match/mismatch with a retrieval cue.

Because of this theoretical significance of Dillon et al. (2013)’s conclusions, we felt that it is important to establish a strong empirical basis for the associated claims. The total fixation time results from Experiment 1 of Dillon et al. (2013) had a number of statistical issues, which we explain next. These issues motivated us to attempt a direct replication of their study.

The first issue was the possibly low statistical power in Dillon et al.’s Experiment 1. Taking the quantitative predictions of the LV05 cue-based retrieval model as a guide, we see that the original study had relatively low prospective power (see Appendix A). Low power has two adverse consequences: as discussed in Hoenig and Heisey (2001) and Gelman and Carlin (2014), null results will be found in repeated runs of the experiment even when the null hypothesis is false, and statistically significant results will have exaggerated estimates (so-called Type M error) or even have the wrong sign (so-called Type S error). As discussed in Jäger, Engelmann, and Vasishth (2017), low power has been a common problem in previous studies on interference. It would therefore be valuable and informative to run as high-powered a replication attempt as logistically feasible of Dillon et al.’s Experiment 1. A second worry in the total fixation time results of Dillon and colleagues is that, within ungrammatical configurations, a dependency × interference interaction must be shown in order to argue for a difference between the two dependency types. Statistically, it is not sufficient to show that a significant facilitatory interference effect is seen in subject-verb dependencies and no significant facilitatory interference effect (i.e., a null result) is seen in reflexive conditions. Dillon et al. (2013) tested for a three-way interaction between grammaticalty, dependency type and interference. This interaction was significant by subjects (F₁(1, 39) = 8, p < 0.01) and not significant by items (F₂(1, 47) = 4, p < 0.055), and the MinF′ statistic, which computes the significance across by-subjects and by-items analyses, showed a non-significant p-value of 0.11 (see also Section Bayesian re-analysis of the Dillon et al. data below). This issue—not establishing that an interaction exists—is apparently a common problem in published work in psychology and psycholinguistics. One example is Vasishth and Lewis (2006); they found a significant interference effect in one experiment but not in a subsequent one, and argued incorrectly that this difference between the two experiments was meaningful. That this is a pervasive problem is clear from Nieuwenhuis, Forstmann, and Wagenmakers (2011); they reviewed 513 neuroscience articles published in top-ranking journals and showed that the authors of more than half of these studies argued for a difference between two pairs of conditions without demonstrating that an interaction holds. Given these concerns, in order to evaluate the predictions of cue-based retrieval theory and to obtain accurate estimates of facilitatory interference effects (if any) in subject-verb dependencies vs. antecedent-reflexive dependencies, it seems vitally important to conduct a higher-power direct replication attempt of the central claims in the Dillon et al. (2013) paper.

We had two related goals in this paper. First, we wanted to establish whether in ungrammatical configurations, a difference between reflexives and agreement can be observed in total fixation times such that agreement shows the predicted facilitation whereas reflexives show no sensitivity to the interference manipulation, as was claimed by Dillon et al. (2013). Second, we were interested in comparing cue-based retrieval theory’s predictions with the total fixation time data in Dillon et al. (2013)’s original study and in our replication attempt. We were specifically interested in comparing the model predictions to the observed interference patterns in grammatical and ungrammatical conditions.

Towards this end, we begin by presenting quantitative predictions of the Lewis and Vasishth (2005) model. Then, we explain how these predictions will be evaluated against data. Finally, we re-analyze the original data of Dillon et al. (2013)’s Experiment 1 as well as our large-sample replication data to obtain quantitative estimates of interference effects and their interaction with dependency type.³

Deriving quantitative predictions from the Lewis and Vasishth (2005) model

We computed quantitative predictions of the LV05 cue-based retrieval model using the simplified version of the model presented in Engelmann et al. (2019). This simplified model computes retrieval time and accuracy for the grammatical and ungrammatical configurations shown in Figure 1, by abstracting away from any incremental parse steps taken in the original Lisp-based parser presented in Lewis and Vasishth (2005).⁴

Computing quantitative predictions from the LV05 model

In the Engelmann et al. (2019) paper, all parameters were fixed except the latency factor, which is a free scaling parameter in ACT-R. This was also the approach taken by Lewis and Vasishth (2005). The reason for limiting the number of free parameters in the 2005 paper was to reduce the degrees of freedom in the model (Roberts & Pashler, 2000). Generally speaking, the larger the number of free parameters in a model, the easier it is to fit, indeed overfit, the data. At least when modeling a relatively homogeneous unimpaired adult population of native speakers, it is important to restrict parametric variation in the model. Lewis and Vasishth (2005) explain this point as follows:

“As with any ACT-R model, there are two kinds of degrees of freedom: quantitative parameters, and the contents of production rules and declarative memory. The quantitative parameters, such as the decay rate, associative strength, and so on, are the easiest to map onto the traditional concept of degrees of freedom in statistical modeling. With respect to these parameters, our response is straightforward: We believe we have come as close as possible to zero-parameter predictions by adjusting only the scaling factor, adopting all other values from the ACT-R defaults and literature, and using the same parameter settings across multiple simulations.”

Focusing only on the latency parameter then, we present two kinds of predictions from the model: prior and posterior predictive distributions.

Computing prior predictive distributions

Taking a Bayesian perspective, we define a prior distribution on the parameter θ (here, latency factor) of the model $\mathcal{M}$. This prior distribution reflects our knowledge or belief about the a priori plausible values of the parameter. Given such a model $\mathcal{M}\left(\theta \right)$, we can derive the prior predictive distribution of reading times and of the interference effects of interest. The prior predictive distribution involves no data; it reflects the predictions that the model makes as a function of the prior. Since the prior can have different degrees of informativity (Gelman et al., 2014), the prior predictive distribution will of course depend on the prior adopted and should therefore never be seen as an invariant gold standard prediction. Later in this paper, we will use the prior predictive distribution for evaluating model predictions against data.

Figure 3 shows the prior predictive distribution of reading times when we set a Beta(2,6) prior on the latency factor parameter. Such a prior implies that we believe that the mean latency is approximately 0.25, with a 95% probability of lying between 0.04 and 0.6. The figure shows that the reading time distribution generated by the model is reasonable given typical reading data. Figure 4 shows the prior predictive interference effect in grammatical and ungrammatical conditions.

Figure 3.

The left-hand side histogram shows the Beta(2,6) prior distribution defined on the latency factor parameter. The histogram on the right shows the prior predictive distribution of reading times from the LV05 model generated using the Beta(2,6) prior on the latency factor, holding all other parameters fixed at the defaults used in Engelmann, Jäger, and Vasishth (2019).

Figure 4.

Prior predictive distributions from the LV05 model of the interference effect in grammatical and ungrammatical conditions. The latency factor has a Beta(2,6) prior, and all other parameters are fixed at the defaults used in Engelmann, Jäger, and Vasishth (2019).

Computing posterior predictive distributions

The second kind of prediction one can derive from a model is the posterior predictive distribution of retrieval times. Given a vector of data y and the model $\mathcal{M}\left(y|\theta \right)$ which has priors (θ) defined on the parameters, one can use Bayes’ rule to derive the posterior distribution of the parameters, conditional on having seen the data. Bayes’ rule states that the posterior distribution of the parameters given data, (θ | y), is proportional to the model (usually, the likelihood), $\mathcal{M}\left(y|\theta \right)$, multiplied by the priors (θ). Posterior distributions can be derived through Markov Chain Monte Carlo methods. When the model cannot be expressed as a likelihood, then Approximate Bayesian Computation (ABC) is an option for deriving the posteriors of the parameters (Palestro, Sederberg, Osth, Van Zandt, & Turner, 2018; Sisson, Fan, & Beaumont, 2018). Because the cue-based retrieval model cannot be easily expressed in terms of a likelihood function, we use ABC for deriving the posteriors. For details, see the accompanying MethodsX article (Vasishth, 2019).

Once the posterior distribution of the parameter (conditioned on the data) has been computed, we can use this posterior distribution to generate a so-called posterior predictive distribution of the data. This distribution represents predicted future data from the model, conditioned on the observed data. Posterior predictive distributions should be seen as a sanity check to determine whether the model can generate data that is approximately similar to the data that the parameters were conditioned on; they should not be regarded as a way to evaluate the quality of model fit to the data that were used to estimate the posterior distributions of the parameters. Using posterior predictive distributions as a way to evaluate model fit would lead to a classic overfitting problem, whereby a model is unfairly evaluated by testing its performance on the same data that it was trained on. A further potential use of posterior predictive distributions is that they could be used as informative priors on a future replication attempt. For extensive discussion of prior and posterior predictive distributions for model evaluation in the context of cognitive science applications, see Schad, Betancourt, and Vasishth (2019).

In order to obtain the posterior distribution of the latency factor parameter, we used Approximate Bayesian Computation (ABC) with rejection sampling (Palestro et al., 2018; Sisson et al., 2018). The posterior distribution was computed using the Dillon et al. (2013) data-set. Previous papers using the LV05 model (most recently, Engelmann et al., 2019) have used grid search to obtain point value estimates of parameters when fitting the model to data. ABC represents a superior approach (Kangasraasio, Jokinen, Oulasvirta, Howes, & Kaski, 2019) because we can obtain a posterior distribution of the parameter (or of multiple parameters) of interest. The posterior distribution of the parameter allows us to incorporate uncertainty about the true value of the parameter in our model predictions, instead of using estimated point values for the parameter.⁵

To summarize the steps taken to obtain posterior predictive distributions of the interference effects in grammatical and ungrammatical conditions:

1. Using the Dillon et al. (2013) data and the LV05 model, the ABC rejection sampling method was used to obtain the posterior distribution of the latency factor parameter for the primary conditions of interest: the ungrammatical agreement and reflexives conditions.

2. Then, the posterior distribution of the latency factor parameter was used in the LV05 model to generate posterior predicted interference effects (predicted data given the posterior distribution and the model) for both grammatical and ungrammatical conditions.

Figure 5 summarizes the results of these simulations, which use the posterior distribution of the latency factor computed using the Dillon et al. (2013) data. The histograms show that inhibitory interference is predicted in grammatical conditions, and facilitatory interference in ungrammatical conditions. In ungrammatical conditions, the facilitatory interference effect is smaller in reflexives than in agreement, but this is because the posterior distribution is based on the Dillon et al. (2013) data, which showed a similar pattern (this is discussed below in detail).

Figure 5.

Posterior predictive distributions from the Lewis & Vasishth (2005) ACT-R cue-based retrieval model for interference effects caused by a cue-matching distractor in sentences with a fully matching target (i.e., grammatical sentences) as in conditions a,b of Example 1, and an only partially cue-matching target (i.e., ungrammatical sentences) as in conditions a,b of Example 2. The histograms show the distributions of the model’s posterior predicted interference effects in grammatical vs. ungrammatical conditions, for agreement and reflexive conditions. We used the total fixation time data from Dillon et al., 2013 to estimate the latency factor parameter from the LV05 model. See the accompanying MethodsX article for details on how the latency factor parameter was estimated (Vasishth, 2019).

The model predictions for grammatical agreement conditions lie within the 95% range [22,59] ms; and for grammatical reflexives the range is [3,38] ms. The predictions for ungrammatical agreement conditions are [−72,−25] ms, and for ungrammatical reflexives conditions, [−46,−4] ms.

How can we evaluate this range of model predictions against empirical data? We turn to this question below.

Model evaluation

We adopt the so-called region of practical equivalence (ROPE) approach for model evaluation (Freedman, Lowe, & Macaskill, 1984; Hobbs & Carlin, 2008; Kruschke, 2015; Spiegelhalter, Freedman, & Parmar, 1994). The ROPE approach has the advantage that it places the focus on the uncertainty of the data against the uncertainty of the model’s predictions. This is one way to implement the proposal in the classic article by Roberts and Pashler (2000) on model evaluation, which points out that both model and data uncertainty should be considered when assessing the quality of a model fit.

In the ROPE approach, a range of effect sizes that is predicted by the theory is defined. Such a range can be obtained by generating a prior predictive distribution from the model. As mentioned earlier, the prior predictive distribution is conditional on the prior(s) defined for the model parameter(s), and therefore should not be taken as an invariant prediction of the model. Future evaluations should revise the ROPE region conditional on the available data; such a ROPE will necessarily be tighter than ours.

Once the ROPE is defined, the data are collected with as much precision as is logistically and financially feasible; the goal is to obtain a Bayesian 95% credible interval of the effect of interest such that it is either smaller than or as small as the width of the predicted range from the model. The 95% credible interval demarcates the range over which we can be 95% certain that the true value of the parameter of interest lies, given the data and the statistical model. This is very different from the interpretation of the frequentist confidence interval (Hoekstra, Morey, Rouder, & Wagenmakers, 2014).

The data will be interpreted as consistent with the theory whenever the 95% credible interval of the effect of interest falls within the bounds of the range of predicted effects. This is illustrated in scenario E in Figure 6. By contrast, the data will be interpreted as falsifying the theory whenever the credible interval lies completely outside of the range of model predictions; these are scenarios A and B in Figure 6. The intermediate outcomes occur when the credible interval and the range of model predictions overlap; these will be interpreted as equivocal evidence; see scenarios C and D in Figure 6. Scenario F represents a situation where the credible interval from the data is wider than the predicted range from the model; in this case, more data should be collected before any conclusions can be drawn.

Figure 6.

Possible outcomes when interpreting the empirical data against predictions of the Lewis and Vasishth (2005) cue-based retrieval model. Panel (a) shows the prior predicted interference effect in grammatical conditions, and panel (b) shows the effect in ungrammatical conditions; the range of ACT-R predictions are shown at the bottom of each panel (see Section Deriving quantitative predictions from the Lewis and Vasishth (2005) model for details). A-F represent the 95% credible intervals of hypothetical posterior distributions of the interference effects as estimated from the data. Outcomes A and B falsify the model, outcomes C and D are equivocal outcomes, and E would be strong support for the model. Outcome F is uninformative and can only occur when the data does not have sufficient precision given the range of model predictions. The figure is adapted from Spiegelhalter et al. (1994, p. 369).

This method can also be used to evaluate whether an effect is essentially zero or not; here, it is necessary to define the range that counts as no effect. An example using this approach is presented in Vasishth, Mertzen, Jäger, and Gelman (2018). A related method has been proposed by Matthews (2019) as a replacement for null hypothesis significance testing.

Since our model evaluation procedure depends on conducting Bayesian analyses, we explain our data analysis methodology next.

Bayesian parameter estimation

In order to use the region-of-practical-equivalence approach for model evaluation, we need the marginal posterior distribution of the interference effect, computed using the data and a hierarchical linear model (linear mixed model) specification. A posterior distribution is a probability distribution over possible effect estimates given the data and the statistical model. The posterior distribution thus displays plausible values of the effect given the data and model. Bayes’ rule allows this computation: Given a vector y containing data, a joint prior probability density function p(θ) on the parameters θ, and a likelihood function p(y | θ), we can compute, using Markov chain Monte Carlo methods, the joint posterior conditional density of the parameters given the data, p(θ | y). The computation uses the fact that we can approximate the posterior density up to proportionality via Bayes’ rule. From this joint posterior distribution of the parameters θ, the marginal distribution of each parameter can easily be computed. Introductions to Bayesian statistics are provided by Kruschke (2015), McElreath (2016), and Lambert (2018).

Because psycholinguistics generally uses repeated measures factorial designs, the likelihood function is a complex hierarchical linear model with many variance components. The prior distributions for the parameters are typically chosen so that they have a regularizing effect on the posterior distributions to avoid overfitting (these are sometimes referred to as mildly informative priors). In the analyses presented in this paper, we limit ourselves to such regularizing priors. These priors have the effect that the so-called maximal linear mixed model (Barr, Levy, Scheepers, & Tily, 2013) will always converge even when data are relatively sparse; when there is insufficient data, the posterior estimate of each parameter will be determined largely by the regularizing prior. By contrast, maximal models in the frequentist paradigm will fail to converge when there is insufficient data; even if it appears that the maximal model converged, the parameter estimates of the variance components can be very unrealistic and/or can lead to degenerate variance-covariance matrices (Bates, Kliegl, Vasishth, & Baayen, 2015; Vasishth, Nicenboim, Beckman, Li, & Kong, 2018). Fitting maximal models using Bayesian methods gives the most conservative estimates of the effects, and allows us to take all potential sources of variance into account, as Barr et al. (2013) recommend.

The Bayesian approach is also more informative than the frequentist one as it is not limited to merely falsifying a point null hypothesis (although this can be done with Bayes factors, Jeffreys 1939/1998), but rather provides direct information about the plausibility of different effect estimates given the data and the model. For an extended discussion of this point in the context of psycholinguistics, see Nicenboim and Vasishth (2016). Based on the posterior distributions, it is possible to make quantitative statements about the probability that an effect lies within a certain range. Thus, we can calculate the 95% credible interval for plausible values of an effect.⁶

Next, we carry out a Bayesian data analysis of the Dillon et al. (2013) study, and of our large-sample replication attempt. We begin by reanalyzing the original data of Dillon et al. (2013)’s Experiment 1; this allows us to directly compare the original results with our replication attempt.

Reanalysis of the Dillon et al. 2013 Experiment 1 data

Recall that Dillon et al. (2013) concluded that the processing of the different syntactic dependencies differs with respect to whether all available retrieval cues are weighted equally and are used for retrieval, or whether structural cues are used exclusively. Specifically, they argue that in the processing of subject-verb agreement, morphosyntactic cues such as the number feature are used, whereas in reflexives, which are subject to Principle A of the binding theory (Chomsky, 1981), only structural cues are deployed to access the antecedent. This claim is based on their Experiment 1, which directly compared interference effects in subject-verb agreement and in reflexives. The main finding was that in total fixation times, facilitatory interference is seen only in ungrammatical subject-verb agreement sentences but not in ungrammatical reflexive conditions.

In the following, we will first summarize the method and materials used by Dillon et al. (2013) in their Experiment 1, and then present a Bayesian analysis of their data.

Method and materials of Dillon et al. 2013

In a reading experiment using eyetracking, Dillon et al. collected data from 40 native speakers of American English in the USA who were presented with 48 experimental items. There were eight experimental conditions (shown in Example 4), which were presented in a Latin square design, interspersed with 128 fillers and 24 items from a different experiment. The grammatical-to-ungrammatical ratio was 4.6 to 1. Items a-d relate to the subject-verb agreement conditions, and e-h to the reflexives.

$$\begin{array}{l}\text{a}.\mathit{Agreement};\mathit{grammatical};\mathit{interference}\\ \text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{+singular}\text{who}\text{worked}\text{with}\text{the}\text{personal}{\text{trainer}}_{-localsubject}^{\text{+}singular}\text{amazingly}\text{was}\left\{\begin{array}{l}singular\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\\ \text{b}.\mathit{Agreement};\mathit{grammatical};\mathit{no}\mathit{interference}\\ \text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{+singular}\text{who}\text{worked}\text{with}\text{the}\text{personal}{\text{trainers}}_{-localsubject}^{\text{+}singular}\text{amazingly}\text{was}\left\{\begin{array}{l}singular\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\\ \text{c.}\mathit{Agreement};\mathit{ungrammatical};\mathit{no}\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}{\text{trainer}}_{-localsubject}^{-plural}\text{amazingly}\text{were}\left\{\begin{array}{l}plural\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\\ \text{d}.\mathit{Agreement};\mathit{ungrammatical};\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+localsubject}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}{\text{trainers}}_{-localsubject}^{+plural}\text{amazingly}\text{were}\left\{\begin{array}{l}plural\hfill \\ localsubject\hfill \end{array}\right\}\text{competitive}\text{for}\text{the}\text{gold}\text{medal}.\\ \text{e}.\mathit{Reflexive};\mathit{grammatical};\mathit{interference}\\ \text{The}\text{amateur}{\text{bodybuilder}}_{+c-com}^{+singular}\text{who}\text{worked}\text{with}\text{the}\text{personal}traine{r}_{-c-com}^{+singular}\text{amazingly}\text{injured}himself\left\{\begin{array}{c}singular\\ c-com\end{array}\right\}\text{on}\text{the}\text{lightest}\text{weights}.\\ \text{f}.\\ \mathit{Reflexive};\mathit{grammatical};\mathit{no}\mathit{interference}\\ \text{The}\text{amateur}{\text{bodybuilder}}_{+c-com}^{+singular}\text{who}\text{worked}\text{with}\text{the}\text{personal}trainer{s}_{-c-com}^{-singular}\text{amazingly}\text{injured}himself\left\{\begin{array}{c}singular\\ c-com\end{array}\right\}\text{on}\text{the}\text{lightest}\text{weights}.\\ \text{g}.\mathit{Reflexive};\mathit{ungrammatical};\mathit{no}\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+c-com}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}traine{r}_{-c-com}^{-plural}\text{amazingly}\text{injured}themselves\left\{\begin{array}{c}plural\\ c-com\end{array}\right\}\text{on}\text{the}\text{lightest}\text{weights}.\\ \text{h}.\mathit{Reflexive};\mathit{ungrammatical};\mathit{interference}\\ *\text{The}\text{amateur}{\text{bodybuilder}}_{+c-com}^{-plural}\text{who}\text{worked}\text{with}\text{the}\text{personal}trainer{s}_{-c-com}^{+plural}\text{amazingly}\text{injured}themselves\left\{\begin{array}{c}plural\\ c-com\end{array}\right\}\text{on}\text{the}\text{lightest}\text{weights}.\end{array}$$ (4)

All eight conditions in one set of items started with the same singular subject noun phrase (NP), which was the target for retrieval (The amateur bodybuilder in Example 4). This target NP was modified by a subject-relative clause containing a distractor NP (the personal trainer/s in Example 1) whose match with the number feature on the matrix verb (agreement conditions a-d) or the reflexive (conditions e-h) was manipulated; we refer to the number manipulation on the distractor NP as the interference factor.

For agreement conditions, the matrix clause verb (was/were in Example 4) that triggered the critical retrieval was followed by an adjective. For reflexive conditions, the antecedent of the reflexive (himself/themselves in Example 4) was the sentence-initial noun phrase. The grammaticality of the sentences was manipulated by having the number feature of the reflexive or the matrix verb match or mismatch the singular target NP. Hence, conditions with a plural matrix verb or a plural reflexive were ungrammatical.

Bayesian re-analysis of the Dillon et al. data

Our primary analysis focused on total fixation times (i.e., the sum of all fixation durations on a region), in both the re-analysis of the original data as well as in the confirmatory analysis of the replication experiment. This is because the conclusions of Dillon et al. (2013) were based on total fixation time.

Dillon et al. (2013, p. 92) report a difference between the interference patterns in the two dependency types; they observed a three-way dependency × grammaticality × interference interaction that was significant by participants (F₁(1, 39) = 8, p < 0.01) and marginally significant by items (F₂(1, 47) = 4, p < 0.055). They also reported a minF′ statistic, which was not significant, minF′(1, 81) = 2.66, p = 0.11). An important note here is that in the published analysis, the contrast coding for the interference vs. baseline conditions had the opposite signs in grammatical vs. ungrammatical conditions (see Appendix B, Acknowledgements). For evaluating the predictions of the cue-based retrieval model, the contrast coding for the interference vs. baseline condition needs to be set to have the same sign in both grammatical and ungrammatical conditions. If we adopt this latter contrast coding, the estimated mean of the three-way interaction is centered around zero. The other measures Dillon et al. (2013) report (first-pass regressions out of the critical region, and first-pass reading time) did not show any evidence for an interaction.

We used the same critical region as Dillon et al. (2013): in agreement conditions, the critical region was the main clause verb and the following adjective, and in the reflexive conditions, it was the reflexive and the following preposition. We only analyzed the critical region as Dillon and colleagues’ conclusions were based on this region.

All data analyses were carried out in the R programming environment, version 3.5.1 (R Core Team, 2016). The Bayesian hierarchical models were fit using Stan (Carpenter et al., 2017), via the R package RStan, version 2.18.1 (Stan Development Team, 2017a). For calculating Bayes factors, we used the R package brms, version 2.8.0 (Bürkner, 2017).

We fit two hierarchical linear models in order to unpack the main effects and interactions, and the nested effects of interest. Model 1 tests for an interaction between dependency and interference separately within ungrammatical and grammatical conditions. If dependency type does not matter, no interactions involving dependency type are expected. Model 2 investigates interference effects separately in agreement and reflexive constructions; these interference effects are nested within the grammatical and ungrammatical conditions. Both models include main effects of dependency, grammaticality, and the interaction between grammaticality and dependency in order to fully account for the factorial structure of the experiment. The contrast coding of all comparisons included in the models is summarized in Table 1.

Table 1.

Contrast coding of the independent variables. For the analysis of total fixation times of the original Dillon et al. (2013, Experiment 1) data as well as of the replication data, two models were fit, as described in the main text. Here, gram refers to grammatical, ungram refers to ungrammatical, and int refers to interference.

		Experimental condition
		Agreement				Reflexives
		gram		ungram		gram		ungram
		int	no int	int	no int	int	no int	int	no int
Models 1, 2	Dependency	0.5	0.5	0.5	0.5	−0.5	−0.5	−0.5	−0.5
	Grammaticality	−0.5	−0.5	0.5	0.5	−0.5	−0.5	0.5	0.5
	Dependency×Grammaticality	−0.5	−0.5	0.5	0.5	0.5	0.5	−0.5	−0.5
Model 1	Interference [grammatical]	0.5	−0.5	0	0	0.5	−0.5	0	0
	Interference [ungrammatical]	0	0	0.5	−0.5	0	0	0.5	−0.5
	Dependency×Interference [grammatical]	0.5	−0.5	0	0	−0.5	0.5	0	0
	Dependency×Interference [ungrammatical]	0	0	0.5	−0.5	0	0	−0.5	0.5
Model 2	Interference [grammatical] [reflexives]	0	0	0	0	0.5	−0.5	0	0
	Interference [grammatical] [agreement]	0.5	−0.5	0	0	0	0	0	0
	Interference [ungrammatical] [reflexives]	0	0	0	0	0	0	0.5	−0.5
	Interference [ungrammatical] [agreement]	0	0	0.5	−0.5	0	0	0	0

All interference effects were coded such that a positive coefficient means inhibitory interference, i.e., a slowdown in reading times in the interference conditions. A positive coefficient for the main effect of grammaticality means that the ungrammatical conditions are read more slowly and a positive coefficient for the effect of dependency means that agreement conditions take longer to read than reflexive conditions. All contrasts were coded as ±0.5, such that the estimated model parameters would reflect the predicted effect, i.e., the difference between the relevant condition means (Schad, Hohenstein, Vasishth, & Kliegl, 2019).

Our first research goal was to establish whether there is a difference between the dependency types with respect to the interference effect in ungrammatical conditions as claimed by Dillon et al. (2013). Here, the relevant comparison is the two-way interaction between dependency and interference within ungrammatical sentences in Model 1.

Our second research goal was to conduct a quantitative evaluation of the predictions of cue-based retrieval theory. Here, the relevant comparisons are the interference effects within grammatical and ungrammatical conditions of Model 1. From the model’s perspective, the overall effect collapsed over the two dependency types is the relevant effect; however, in order to account for the possibility of a difference between the dependency types, we will also evaluate the model against each of the grammatical and ungrammatical interference effects nested within dependency type, which are included in Model 2. None of the other fixed effects are of theoretical interest to our research goals and are only included to reflect the factorial design of the experiment.

We used a hierarchical LogNormal likelihood function to model the raw values in milliseconds (ms); this is equivalent to fitting a hierarchical linear model with a Normal likelihood on log-transformed values. All models assumed correlated varying intercepts and slopes for items and for subjects, for all predictors. As prior distributions, we used a standard normal distribution N(0, 1) for all fixed effects (except the intercept, which had a N(0, 10) prior), and a standard normal distribution truncated at 0 for the standard deviation parameters. These are so-called uninformative priors (Gelman et al., 2014). Within the variance-covariance matrices of the by-subject and by-items random effects, priors were defined for the correlation matrices using a so-called LKJ prior (Lewandowski, Kurowicka, & Joe, 2009). This prior has a parameter, η; setting the parameter to 2.0 has a regularizing effect of strongly disfavoring extreme values near ±1 for the correlations (Stan Development Team, 2017b). This regularization is desirable because, when data are sparse, the correlations will be severely mis-estimated (Bates et al., 2015). The other priors are vague and allow the likelihood to dominate in determining the posterior; in other words, the posterior estimates of the fixed effects parameters and of the standard deviations are not unduly influenced by the priors.

For each of the models, we sampled from the joint posterior distribution by running four Monte Carlo Markov Chains at 2000 iterations each. The first half of the samples was discarded as warm-up samples. Convergence was checked using the R-hat convergence diagnostic and by visual inspection of the chains (Gelman et al., 2014).

Results

The results of our Bayesian analysis of the original data from Dillon et al. (2013)’s Experiment 1 are summarized in Table 2, which shows the mean of the posterior distribution of each parameter of interest (backtransformed to ms), together with a 95% credible interval (CrI), i.e., a range of plausible values of the effect given the data and the model. A detailed comparison of our analysis with the original one performed by Dillon et al. (2013) is provided in Appendix B.

Table 2.

Bayesian analysis of Dillon et al. (2013)’s Experiment 1. The table shows the mean of all fixed effects’ posterior distributions together with 95% Bayesian credible intervals of total fixation times at the critical region. Both models were fit on the log-scale; all numbers in this table are back-transformed to ms for easier interpretability. For more details about the model specification and the contrast coding of the fixed effects, see Section Bayesian re-analysis of the Dillon et al. data.

	Effect	Posterior mean and 95% Credible Interval (ms)
Models 1, 2	Dependency	119 [71, 169]
	Grammaticality	100 [69, 134]
	Dependency×Grammaticality	9 [−18, 36]
Model 1	Interference [grammatical]	−16 [−52, 20]
	Interference [ungrammatical]	−38 [−79, 1]
	Dependency×Interference [grammatical]	−17 [−56, 19]
	Dependency×Interference [ungrammatical]	−21 [−56, 12]
Model 2	Interference [grammatical] [reflexives]	2 [−57, 60]
	Interference [grammatical] [agreement]	−34 [−85, 15]
	Interference [ungrammatical] [reflexives]	−18 [−72, 36]
	Interference [ungrammatical] [agreement]	−60 [−112, −5]

We will present the results focusing on the two research questions we set out to answer: (i) is there a principled difference between the facilitation profiles observed in ungrammatical subject-verb agreement and reflexives, as claimed by Dillon et al. (2013), and (ii) are the predictions of cue-based retrieval theory consistent with the empirical data?

The interference effect in ungrammatical conditions across dependency types

Model 1 investigates the two-way interaction between dependency and interference within ungrammatical sentences, and does not show any evidence for a difference between the dependency types: the mean of the posterior is −21 ms with CrI [−56, 12] ms.

Model 2 reveals that the interference effect in ungrammatical conditions is numerically much larger in subject-verb agreement than in reflexives. In fact, given the reading (eyetracking and self-paced reading) literature on interference effects (for an overview, see Jäger et al., 2017), the mean of the posterior distribution of the interference effect in ungrammatical agreement conditions is surprisingly large: −60 ms, CrI [−112, −5] ms (cf. the Jäger et al. (2017) meta-analysis estimate of −22 ms, CrI [−36, −9]). In reflexives, the mean of the posterior is much smaller: −18 ms, CrI [−72, 36] ms.

Comparison of the empirical estimates with model predictions

Figure 7 compares the range of effect sizes predicted by the LV05 cue-based retrieval model with the empirical estimates obtained from Dillon et al. (2013)’s Experiment 1 total fixation time data. The figure shows the estimated interference effects observed in total fixation times within each level of grammaticality for the two dependency types separately (i.e., the estimates obtained from Model 2), and collapsed over the two dependency types (Model 1).

Figure 7.

Evaluation of the ACT-R predictions (see Section Deriving quantitative predictions from the Lewis and Vasishth (2005) model for details) against the corresponding estimates (posterior means and 95% credible intervals) obtained from total fixation times of the empirical data of Dillon et al. (2013).

In the grammatical conditions, for agreement the credible interval of the interference effect is [−85, 15] ms, and for reflexives it is [−57, 60] ms. When collapsing the two dependencies, the credible interval of the overall interference effect is [−52, 20] ms. When comparing these estimates for the grammatical conditions with the model predictions (see Figure 7), we see that the range of model predictions for agreement overlap only slightly with the observed data (analogous to scenario C of panel (a) in Figure 6), and the model predictions for reflexives fall within the 95% credible interval of the observed data, analogous to scenario F of panel (a) in Figure 6.

In the ungrammatical conditions, for agreement the credible interval of the interference effect is [−112, −5] ms, and for reflexives [−72, 36] ms. The credible interval of the overall interference effect across the two dependencies is [−79, 1] ms. Figure 7 shows that for agreement we are in scenario C in panel (b) of Figure 6, and for reflexives we are in scenario F. The credible intervals in both agreement and reflexives are very wide, leading us to conclude that these data are uninformative for a quantitative evaluation of the Lewis and Vasishth (2005) cue-based retrieval model. A higher-power study is necessary to adequately evaluate these predictions; for detailed discussion on power estimation see Cohen (1988) and Gelman and Carlin (2014).

Additional analysis

Dillon et al. (2013) conducted between-experiment partial replications of their Experiment 1. Their Experiment 2 tested the same four reflexives conditions as Experiment 1. Consistent with their Experiment 1, they found no evidence for facilitatory interference effects in reflexives. In a post-hoc analysis, we combined these data in order to increase statistical power of the analysis. The posterior mean of the overall dependency × interference interaction within ungrammatical sentences is 3 ms with a 95% credible interval of [−29, 34] ms. A nested analysis for each dependency type within ungrammatical sentences shows that for agreement, the posterior mean with 95% credible interval of the interference effect is −59[−113, −7] ms, and for reflexives it is 0[−33, 33] ms. Moreover, Dillon (2011) partially replicated Experiment 1 for agreement conditions only. Since this experiment has not been published yet, we did not include it in any analysis. The code and data associated with these analyses are in the repository for this paper: https://osf.io/reavs/.

Discussion

The results of our analysis of Dillon et al. (2013)’s Experiment 1 show that it is difficult to argue for a dependency × interference interaction (within grammatical or within ungrammatical conditions). In particular, the data do not support the claim that agreement conditions show facilitatory interference effects in ungrammatical sentences but reflexives do not; the large uncertainty associated with the interference effect in reflexives does not allow any conclusions about the absence or presence of an effect. However, our additional analysis, in which we combined the data of Dillon et al. (2013)’s Experiment 1 with the data from their Experiment 2, suggests that the critical interaction might indeed exist.

We now turn to the larger-sample replication attempt.

Replication experiment

Due to concerns about the statistical power of Dillon et al. (2013)’s Experiment 1, we carried out a direct replication attempt with a larger participant sample. The relatively low power of the Dillon et al. study can be established by a prospective power analysis, which is discussed in detail in Appendix A. Here, we briefly summarize the methodology adopted for the power analysis. Because the goal is to evaluate the predictions of the Lewis and Vasishth 2005 model specifically for the ungrammatical conditions, as estimates of the effect, we used the first quartile, the median, and the third quartile of the posterior predictive distributions representing the facilitatory interference in agreement and reflexives. These posterior predictive distributions were computed using the Dillon et al. data and the simplified Lewis and Vasishth 2005 model as implemented by Engelmann et al. (2019). For agreement, the first quartile, the median, and the third quartile were −48, −39, and −32 ms; and for reflexives, they were −32, −23, and −14 ms.

A future study looking for a facilitatory interference effect in reflexives with 40 participants (as in the original experiment) would have power between 5 and 25%, with the power estimate for the median effect being 13%. By contrast, a sample size of 184 participants would have prospective power between 25% and 69%, with power for the median effect being 42%. The lower bounds on the estimates of power represent the situation where the true effect is very small. If the true effect really is small, even our larger-sample study’s sample size would not be sufficient to achieve high power.

Method

Participants

Eye-movement data of 190 native speakers of American English aged 16 to 24 were collected at Haskins Laboratories (New Haven, CT). All participants had normal or corrected-to-normal vision, no previous diagnoses of reading or language disability and a full scale IQ of at least 75 according to the WASI II Subtests Matrix Reasoning and Vocabulary. For their participation, each participant received 20USD. Data from nine poorly calibrated participants whose recorded scanpath did not overlap with the experimental stimulus for a majority of trials were deleted. The data were collected over four years (2014–2018).

Materials

We followed the experiment design by Dillon et al. (2013) and used the same 48 experimental items as the original Experiment 1 (see Example 1). For more details about the experimental stimuli see Section Method and materials of Dillon et al. 2013. We used the same 128 filler items as Dillon et al. (2013), but did not use the additional 24 items from a different experiment that had been included in the original data collection of Dillon et al. (2013). This additional experiment involved the negative polarity item ever, in the presence or absence of negation. As in the original experiment, half of all experimental and filler items were followed by a yes/no comprehension question which targeted different parts of the sentences.

Because of the change in the number and type of fillers in our experiment, strictly speaking, our experiment cannot be seen as an exact replication of the original experiment. A true direct replication would be conducted in the same laboratory under all the same conditions as in the original study, but with new participants. However, we are assuming here that the effect of interest (the asymmetry between agreement and reflexives that Dillon and colleagues found) should not be affected in any important manner by the number and type of fillers used, and by the fact that the experiment was conducted in a different laboratory.

Procedure

The 48 experimental items were presented in a Latin Square design. Experimental and filler items were randomized within each Latin Square list. Sentences were presented in one line on the screen in Times New Roman font (size 20). For some very long sentences, the non-critical end of the sentence was displayed in a second line. A 21-inch monitor with a resolution of 1680×1050 pixels was used to display the sentences. The eye-to-screen distance was 98 cm, resulting in approximately 3.8 characters subtended by one degree of visual angle.

After giving informed consent, participants were seated in front of the display monitor. A chin rest and forehead rest were used to avoid head movements. An Eyelink 1000 eye-tracker with a desktop-mounted camera was used for monocular tracking at a sampling rate of 1000 Hz.

After setting up the camera, a 9-point calibration was performed. An average calibration error of less than 0.5° and a maximum error of below 1° were tolerated. Testing began after a short practice session of 4 trials. Comprehension questions were answered by pressing a button on a gamepad. A break was offered to participants halfway through the session, and additional breaks were given when necessary. Re-calibrations were performed after the break, and whenever deemed necessary.

The collection of eye-movement data, including setup, calibrations, re-calibrations and breaks, took approximately 45 minutes.

Results

Question response accuracies

Overall response accuracy on experimental trials followed by a comprehension question was 88%. Mean accuracies for each experimental condition are provided in Table 3. Accuracy on filler items was 91%.

Table 3.

Mean response accuracies of the trials followed by a comprehension question for each experimental condition (int refers to the interference conditions, and no int to the no-interference conditions).

	Agreement				Reflexives
	grammatical		ungrammatical		grammatical		ungrammatical
	int	no int	int	no int	int	no int	int	no int
Accuracy (%)	88	88	89	89	86	87	90	89

Primary analysis based on total fixation time

Following the Dillon et al. (2013) analysis, we collapsed the main clause verb or the reflexive with the subsequent word to form the critical region. Recall that Dillon et al. (2013) only found an effect in total fixation time; first-pass regressions and first-pass reading time showed no evidence for differing interference profiles in the two dependency types. Accordingly, we restricted our primary analysis to total fixation time, and we fit the same two Bayesian hierarchical models discussed in the section entitled Bayesian re-analysis of the Dillon et al. data.

The total fixation time results are summarized in Table 4, which shows the posterior mean of each fixed effect together with a 95% credible interval. Overall, the posterior distributions of the parameters obtained from the replication experiment have a much higher precision (i.e., tighter credible intervals) than the posteriors computed from the original data, as was expected given the much larger sample size.

Table 4.

Bayesian analysis of total fixation time in the replication experiment. The table shows the posterior means of the fixed effects together with 95% Bayesian credible intervals of total fixation times at the critical region. Both models were fit on the log-scale; all numbers in this table are back-transformed to milliseconds for easier interpretability. For more details about the model specification and the contrast coding of the fixed effects, see Section Bayesian re-analysis of the Dillon et al. data and Table 1.

	Effect	Posterior mean and 95% Credible Interval (ms)
Models 1, 2	Dependency	141 [100, 184]
	Grammaticality	121 [100, 141]
	Dependency×Grammaticality	−17 [−30, −5]
Model 1	Interference [grammatical]	9 [−9, 28]
	Interference [ungrammatical]	−23 [−41, −5]
	Dependency×Interference [grammatical]	−4 [−21, 13]
	Dependency×Interference [ungrammatical]	1 [−17, 18]
Model 2	Interference [grammatical] [reflexives]	12 [−16, 43]
	Interference [grammatical] [agreement]	5 [−18, 28]
	Interference [ungrammatical] [reflexives]	−23 [−48, 2]
	Interference [ungrammatical] [agreement]	−22 [−46, 3]

Similar to the presentation of the results of the Bayesian analysis of the original data, we will focus on the effects that are relevant for evaluating (i) the Dillon et al. (2013) claim that in ungrammatical sentences, interference from the number feature affects only subject-verb agreement but not reflexives, and (ii) the quantitative predictions of the Lewis and Vasishth (2005) cue-based retrieval model.

The interference effect in ungrammatical conditions across dependency types

The two-way interaction between dependency and interference within ungrammatical conditions (Model 1) is effectively centered around zero (1 [−17, 18] ms). Hence, from the replication data, it is difficult to argue for a difference between the dependency types in ungrammatical conditions as claimed by Dillon et al. (2013).

Comparison of the empirical estimates with model predictions

Figure 8 shows the range of model predictions from the Lewis and Vasishth (2005) cue-based ACT-R model of sentence processing (see Section Deriving quantitative predictions from the Lewis and Vasishth (2005) model) together with the empirical estimates obtained from the replication experiment. The figure shows the estimated interference effects observed in total fixation times within each level of grammaticality for the two dependency types separately (i.e., the estimates obtained from Model 2), as well as the overall interference effect across the two dependency types (Model 1).

Figure 8.

Evaluation of the ACT-R predictions (see Section Deriving quantitative predictions from the Lewis and Vasishth (2005) model for details) against the corresponding estimates (posterior means and 95% credible intervals) obtained from total fixation times of the replication experiment.

In the grammatical conditions, for agreement the credible interval of the interference effect is [−18, 28] ms, and for reflexives it is [−16, 43] ms. The overall interference effect across dependency types (Model 1) has the credible intervals [−9, 28] ms. As shown in Figure 8, for both agreement and reflexives, the range of model predictions and the empirical estimates overlap partly, resulting in the theoretical scenario C in panel (a) of Figure 6. Under this scenario, the evidence is equivocal.

In the ungrammatical conditions, the credible intervals of the interference effects for agreement and for reflexives are strikingly similar: for agreement, they are [−46, 3] ms, and for reflexives, [−48, 2] ms. The overall interference effect across dependency types has the credible interval [−41, −5] ms. As shown in Figure 8, there is a much larger overlap of the model predictions and the empirical data — but still the estimates’ credible intervals do not completely fall inside the range of model predictions, resulting in the theoretical scenario D in panel (b) of Figure 6.

Secondary analysis based on first-pass regressions from the critical region

As mentioned earlier, our primary, confirmatory analysis of total fixation times was based on the fact that Dillon et al. (2013) found effects (facilitatory interference in subject-verb agreement but not in reflexives) only in this dependent measure in their Experiment 1. In first-pass reading times and first-pass regressions from the critical region, they found no evidence for the dependency × interference interaction. Dillon et al. (2013, p. 88) expected slower reading times or a lower proportion of regressions in ungrammatical interference manipulations in both agreement and reflexive constructions. This is not a very focused prediction: it subsumes all eyetracking dependent measures. One common problem that eyetracking researchers face is that often a predicted effect cannot a priori be attributed to a specific reading measure or a limited set of measures. As a consequence, a frequently used procedure is to analyze several measures (often at multiple regions, such as the critical and post-critical region).⁷ These multiple comparisons, however, lead to a greatly inflated Type I error probability in eyetracking data (von der Malsburg & Angele, 2017). Because of this multiple testing problem, it is possible that the original Dillon et al. pattern found in total fixation time is indeed a false positive. A further issue is that such exploratory analyses of the data render hypothesis testing—including significance testing in the frequentist framework—invalid (De Groot, 1956/2014; Nicenboim et al., 2018).

Despite these issues, it can be useful to conduct exploratory analyses to generate new hypotheses that can be tested in future experiments. Hence, we additionally analyzed two further dependent measures: first-pass reading times and first-pass regressions from the critical region (these are sometimes referred to as first-pass regressions out). Should the effect of interest be observed in (either of) these two measures, it will be necessary to validate such an exploratory finding in a future confirmatory study.

First-pass reading times did not show any indication of contrasting interference profiles in our data; no interference effects were found at all in this measure in subject-verb agreement dependencies nor in antecedent-reflexive dependencies. We therefore don’t discuss this measure any further.

The patterns seen in first-pass regressions are more interesting. In grammatical conditions, agreement shows no interference, but reflexives show some indication of the predicted inhibitory interference effect.⁸ The posterior mean of the interaction between dependency type and interference is −2.3%, with a 95% credible interval of [−4.7, 0.1]%. By contrast, in ungrammatical conditions, agreement conditions show a clear indication of the predicted facilitation, whereas reflexives do not show any interference. The posterior distribution of the dependency × interference interaction has a mean of −2.4%, and a credible interval of [−4.7, 0.0]%. Figure 9 shows the interference effects in first-pass regressions estimated from the replication data together with the ones obtained from the original data of Dillon et al. (2013). Quantitative predictions of the cue-based retrieval model are not shown because there is no obvious linking function that quantitatively maps retrieval time in cue-based retrieval theory to first-pass regressions.

Figure 9.

Analysis of first-pass regressions out of the critical region. Interference effects in grammatical (panel a) and ungrammatical conditions (panel b). The figure shows the posterior means together with 95% credible intervals of the interference effects in the percentage of first-pass regressions. These estimates were obtained from the Bayesian analysis of the original data of Dillon et al. (2013), and from our replication data. Separate effect estimates for each dependency type as well as the overall effect obtained when collapsing over dependencies are presented. Quantitative predictions of the cue-based retrieval model are not shown alongside the regression probabilities because there is no obvious linking function that quantitatively maps retrieval time in cue-based retrieval theory to first-pass regressions.

Discussion

As in the total fixation time analysis of the original data, total fixation time in the replication data do not show any indication for a difference between the interference profiles of the two dependency types. Indeed, we find almost identical estimates for the speedup in ungrammatical sentences involving subject-verb agreement and reflexive dependencies. This is not consistent with the idea, suggested by Dillon and colleagues, that there are contrasting interference profiles for agreement vs. reflexives. Furthermore, the estimated facilitation in the agreement conditions is much smaller for our larger-sample replication attempt than the estimate obtained from the original data. The smaller estimates in our replication data, along with their much tighter credible intervals relative to the original study, suggest that the effect estimate for agreement conditions in the original data may be an overestimate, a so-called Type M(agnitude) error (Gelman & Carlin, 2014). Type M errors can occur when statistical power is low (for a discussion of Type M errors in psycholinguistics, see Vasishth, Mertzen, et al. 2018).

Turning next to the analysis of first-pass regressions from the critical region, in grammatical conditions, reflexives show inhibitory interference. This is an uncontroversial finding as it is predicted by cue-based retrieval theories in terms of cue-overload. By contrast, the subject-verb agreement dependency appears to be insensitive to the interference manipulation. The absence of an inhibitory interference effect in grammatical subject-verb agreement conditions is consistent with previous studies’ findings, as summarized in the literature review by Jäger et al. (2017). As Nicenboim et al. (2018) suggest, it may be difficult to detect this effect even in large sample-size studies due to a small effect size in grammatical subject-verb agreement configurations. An alternative explanation for the absence of the effect is suggested by Wagers et al. (2009): cue-based retrieval is only triggered in ungrammatical subject-verb agreement constructions, where a mismatch is detected between the subject and verb’s number feature, or, as Avetisyan, Lago, and Vasishth (2019) put it, between the number feature of the verb phrase that has been predicted by the subject and the number feature of the encountered verb. If no retrieval occurs in grammatical subject-verb agreement constructions, no interference would occur. Thus, the absence of inhibitory interference effects in grammatical conditions could have several alternative explanations.

By contrast, in ungrammatical conditions we see a contrasting interference profile in subject-verb agreement vs. reflexives, a pattern consistent with the Dillon et al. (2013) proposal. Here, agreement conditions show facilitation, whereas reflexives seem to be immune to interference. The reflexives result is also consistent with the original Sturt (2003) proposal, which stated that reflexives are immune to interference only in the early moments of processing. If first-pass regressions index early processing, then our finding would be consistent with Sturt’s original account.

It is difficult to draw a strong conclusion from first-pass regressions in the ungrammatical conditions without a fresh confirmatory analysis with a large sample of data. There are several reasons for being skeptical. First, the original study by Dillon and colleagues—the only published study that investigated that the dependency × interference interaction—does not show any evidence at all for interference effects in first-pass regressions; crucially, the study does not even show the uncontroversial facilitatory interference effect in subject-verb dependencies. This total absence of any interference effect in first-pass regressions in Dillon and colleagues’ study could simply be due to low power; but it may also be that the observed interference in our replication data is an accidental outcome. Second, very few reading studies show interference effects in first-pass regressions: the literature review in Jäger et al. (2017) shows that only 4 out of 22 comparisons found significant interference effects in first-pass regressions, whereas 12 had total fixation time as the dependent measure (see Appendix A of Jäger et al. 2017). Open-access data from studies published more recently, such as Cunnings and Sturt (2018) or Parker and Phillips (2017), which investigate facilitatory interference effects, do not show interference effects in first-pass regressions (we discuss the Parker & Phillips, 2017 data below in more detail). Third, there is only weak evidence for this dependency × interference interaction effect in our replication data. Evidence for or against an effect being present requires a hypothesis test, which can be carried out using Bayes factors.⁹ Comparing the full model which contains all the contrasts with a null model that does not have the relevant interaction term in it (i.e., when the null hypothesis is that the interaction term is 0) shows that in first-pass regressions, the evidence for a dependency × interference interaction is between 0.6 and 2 in grammatical conditions and between 1.5 and 5 in ungrammatical conditions. A Bayes factor of larger than 10 in favor of the full model is generally considered to be strong evidence for an effect being present (Jeffreys, 1939/1998). Thus, the evidence from first-pass regressions for an interaction is quite weak. The results of the Bayes factor analyses are shown in Table 5.

Table 5.

Bayes factor analysis of first-pass regressions from the critical region in our replication data of the dependency × interference interaction, in grammatical and ungrammatical conditions. Shown are increasingly informative priors on the parameter representing the interaction term in the model; for example, Normal(0,1) means a normal distribution with mean 0 and standard deviation 1. We consider a range of priors here because of the well-known sensitivity of the Bayes factor to prior specification. The Bayes factor analysis shows the evidence in favor of the interaction term being present in the model; a value smaller than 1 favors the null model, and a value larger than 1 favors the full model including the interaction term. A value of larger than 10 is generally considered to be strong evidence for the effect of interest being present (Jeffreys, 1939/1998).

Grammatical conditions
	Prior on Dep × Int effect	Bayes factor in favor of alternative
1	Normal(0,1)	0.57
2	Normal(0,0.8)	0.71
3	Normal(0,0.6)	0.95
4	Normal(0,0.4)	1.36
5	Normal(0,0.2)	1.94
Ungrammatical conditions
	Prior on Dep × Int effect	Bayes factor in favor of alternative
1	Normal(0,1)	1.54
2	Normal(0,0.8)	1.97
3	Normal(0,0.6)	2.54
4	Normal(0,0.4)	3.54
5	Normal(0,0.2)	5.31

Nevertheless, it is possible that the first-pass regression patterns we observed are replicable and robust; if this turns out to be the case, this would be a strong validation of the Sturt (2003) and Dillon et al. (2013) proposal. For this reason, a very informative future line of research would be to conduct a new larger-sample replication attempt, i.e., a confirmatory study, that investigates the effect in first-pass regressions, as well as in total fixation times. If the same pattern as in our replication can be found, that would validate the original Sturt (2003) proposal that reflexives should be immune to interference in only early measures (in the Sturt paper, this was first-pass reading time); in late measures (for Sturt, this was re-reading time), interference effects should be observed. The patterns we found could be consistent with this proposal, provided that two sets of effects from first-pass regressions and total fixation times can be replicated.

Returning to the confirmatory analysis involving total fixation times, we can conclude the following. The total fixation times show nearly identical facilitatory interference effects in both dependency types, suggesting a similar retrieval mechanism. Our conclusion that different dependencies might have a similar retrieval mechanism is also supported by a recent paper by Cunnings and Sturt (2018), which found facilitatory interference effects in total fixation time in non-agreement subject-verb dependencies. Of course, larger-scale replication attempts should be made to replicate the findings that we report here; in that sense, our conclusions should be regarded as conditional on the effects replicating in future work.

With respect to the predictions of the cue-based retrieval model, and assuming equal cue-weighting, in ungrammatical conditions, the replication data are consistent with the quantitative model predictions. However, the data also suggest that the facilitatory effect in ungrammatical sentences might be even smaller than the model’s predicted range of effects. By contrast, in grammatical conditions, the data really are equivocal: they neither falsify nor validate the model. Here, too, the data indicate that the true interference effect might be smaller than the model’s predictions.

General Discussion

In this work, we had two related goals. First, we wanted to establish with a larger-sample replication experiment whether, in ungrammatical configurations, reflexive-antecedent and subject-verb agreement dependencies differ in their sensitivity to an interference manipulation, as has been claimed by Dillon et al. (2013). This relates to an important open theoretical question originally raised by Sturt (2003): do configurational cues, such as those triggered by Principle A of the binding theory, serve as a filter for memory search in sentence processing? Such a proposal could mean that certain cues may have a higher weighting than others. An absence of facilitatory interference effects in antecedent-reflexive conditions could imply that Principle A renders this dependency type immune to interference effects.

Second, we were interested in comparing the estimates from the higher-powered replication attempt with the quantitative predictions of cue-based retrieval theory, under the assumption that equal weighting is given to all cues.

The results of our investigations of the total fixation time data are summarized in Figure 10, which also shows the estimates from the data in the original study by Dillon and colleagues. The figure shows the interference effects for reflexives and subject-verb agreement separately, and the overall interference effect computed across both dependency types (recall that the relevant effect from the model’s perspective is the overall effect collapsed over the two dependency types). The quantitative predictions of the Lewis and Vasishth (2005) ACT-R cue-based retrieval model are also shown in the figure. These predictions are generated with the assumption that syntactic cues do not have a privileged position when resolving dependencies of either type.

Figure 10.

Interference effects in grammatical (a) and ungrammatical conditions (b). The figure shows the posterior means together with 95% credible intervals of the interference effects in total fixation times. These estimates were obtained from the Bayesian analysis of the original data of Dillon et al. (2013), and from our replication data. Separate effect estimates for each dependency type as well as the overall effect obtained when collapsing over dependencies are presented. The left-most line of each plot shows the range of predictions of the Lewis and Vasishth (2005) ACT-R cue-based retrieval model (see Section Deriving quantitative predictions from the Lewis and Vasishth (2005) model for details).

Regarding the difference in the interference profiles in ungrammatical agreement and reflexive conditions, our data analyses of total fixation times using mildly informative priors show that neither the original data collected by Dillon et al. (2013) nor the replication data provide any indication for a difference between the two dependency types. A comparison of the quantitative model predictions with the replication estimates shows that the model’s predictions for ungrammatical sentences are consistent with the observed estimates in the replication data. Thus, the mean effects in the replication data are consistent with the view that tree-configurational and non-configurational cues have equal weight. Interestingly, our findings in this replication attempt conflict with those of our recent meta-analysis, where we found facilitatory interference only in ungrammatical configurations of subject-verb agreement, but not in reflexives (Jäger et al., 2017). However, the meta-analysis results need to be treated with caution since any statistical or methodological issues present in the reviewed data cannot be overcome by the meta-analysis without extensive bias modeling (Turner, Spiegelhalter, Smith, & Thompson, 2008). Since there are several statistical and methodological issues (e.g., low power, and confounds in the experimental materials), we consider the contribution of the meta-analysis to be limited to summarizing the published literature in a quantitative manner.

Regarding the evaluation of the model predictions, for the grammatical conditions the conclusion based on the larger-sample replication attempt is equivocal: there is some overlap between the range of predicted values from the model and the 95% credible intervals from the data. For the ungrammatical conditions, the estimates from the replication data seem to be consistent with the LV05 model: the credible intervals from the data largely overlap with the range of values predicted by the model. Of course, it would be very informative to carry out an even larger sample-size study than ours to obtain tighter credible intervals; a strong validation of the LV05 prediction would require that the credible intervals from the data fall entirely within the predicted range. We leave such a larger study for future work.

Arguments in favor of a privileged position for configurational cues

The broader theoretical question relates to whether there is a privileged position for configurational cues. There are in fact good a priori reasons to assume that syntactic cues in general may have some priority. For example, by manipulating syntactic and semantic cues in inhibitory interference settings, Van Dyke (2007), Tan, Martin, and Van Dyke (2017), and Glaser, Martin, Van Dyke, Hamilton, and Tan (2013) have shown that syntactic interference effects were observed earlier than semantic interference effects.

In the specific case of reflexives, Sturt (2003) has proposed that Principle A could play a dominant role in the earliest moments of processing. Sturt’s argument for an early immunity of reflexives to interference was based on the absence of interference effects in first fixation durations. Thus, the fact that our replication study shows facilitatory interference effects in reflexives in the late measure total fixation time may still be consistent with Sturt’s original proposal of the priority of configurational syntax.

However, one would then expect to see facilitatory interference effects in ungrammatical subject-verb agreement constructions in early measures, and specifically in first-pass reading times; this is because in agreement dependencies, no immunity from interference is assumed in the early stages (Dillon et al., 2013). We do not see any interference effects at all in first-pass reading times in the original data from Dillon et al. (2013) or in our replication data. First-pass regressions from the critical region also didn’t show any interference effects in the original Dillon et al. (2013) data. However, in our replication data, we do see some evidence for the Sturt proposal in our exploratory analysis of first-pass regressions: in ungrammatical conditions, subject-verb agreement shows indications of facilitatory interference but reflexives do not. To our knowledge, ours is the first study to find such a dependency × interference interaction in first-pass regressions. If this effect can be robustly replicated in future studies, this would indicate that the original Sturt proposal, which made a distinction between early and late processes, was on the right track: contrasting interference profiles would be expected in the first-pass regressions but not in total fixation time. One problem that would remain for the Sturt account is the fact that in our data, in grammatical conditions first-pass regressions showed indications of an inhibitory interference effect in reflexives. If reflexives are immune to interference but subject-verb agreement configurations are not, then the prediction is that inhibitory interference should not occur in reflexives—this is not consistent with our finding. Future research should investigate this mismatch between the Sturt account and our data.

Here, it is worth mentioning that an intermediate position is also tenable: it is possible that the configurational cues do not render reflexives completely immune to interference (even in the early moments of processing), but are weighted higher than non-configurational cues. This proposal was investigated by Parker and Phillips (2017) empirically and with computational modeling. They derived quantitative predictions using an implementation of the Lewis and Vasishth (2005) model to show that configurational cues have a higher weight than non-configurational ones (they refer to these cues as structural vs. morphological), but that the weighting of non-configurational cues is not zero. This proposal seems quite reasonable: Parker and Phillips found evidence showing larger facilitatory interference effects in eyetracking reading data as a consequence of increasing the number of feature mismatches (one vs. two mismatches) in ungrammatical subject-verb agreement and antecedent-reflexive conditions. They did not report first-pass regressions or total fixation time results; however, the authors shared their data with us, which allowed us to evaluate the evidence in these measures for their claim. First-pass regressions showed no effects at all in two out of their three experiments; in their Experiment 3, there were fewer first-pass regressions when there was a two-feature match with the distractor.¹⁰ By contrast, total fixation times show evidence supporting their conclusion in all of their three experiments. Our reanalyses are available from https://osf.io/reavs/. Thus, Parker and Phillips’ total fixation time data furnish good evidence in favor of such an intermediate position as a possible resolution to the theoretical question. Incidentally, because their first-pass regressions don’t show clear evidence for facilitatory interference, this further reduces our confidence in the dependency × interference interaction we found in our replication data.

In sum, there are good reasons to assume that syntactic cues more generally, and configurational cues in particular, may have a higher weighting compared to other cues. Dillon and colleagues adopted an extreme version of this hypothesis: that configurational cues have all the weighting, leading to complete immunity in reflexive constructions. However, both our current data and the data from Parker and Phillips cast doubt on this extreme position. We have demonstrated that our total fixation time data are consistent with an implementation of cue-based retrieval that assumes equal weighting for all cues.

Stepping back from the details of this particular experiment and the theoretical issues we have addressed, this work also contributes to the rapidly expanding body of work that re-examines claims in psycholinguistics by conducting higher-powered studies (Nicenboim et al., 2018,1; Nieuwland et al., 2018; Vasishth, Mertzen, et al., 2018). In the early days of psycholinguistics, studies on phenomena like garden-path effects needed relatively small sample sizes to robustly demonstrate that an effect can be observed. But when researchers investigate relatively subtle effects, relying on conventional sample sizes of 30–40 participants will lead to either a high proportion of null results, or exaggerated estimates (due to Type M error) that cannot be replicated (Vasishth, Mertzen, et al., 2018). This implies that higher power studies and direct replications are necessary when investigating subtle effects. Prospective power analyses as shown in Appendix A should be carried out routinely before starting a study to ensure that estimates are accurate and have higher precision.

Highlights.

• Large-sample eyetracking-while-reading experiment.

• Investigation of interference effects in subject-verb agreement and reflexives.

• Facilitatory interference is observed in both, subject-verb agreement and reflexives.

• Quantitative evaluation of a cue-based retrieval model of sentence processing.

Appendix A

Prospective power analysis of Experiment 1 in Dillon et al., 2013 and of our replication experiment Given theoretical quantitative estimates of an effect size, we can obtain estimates of power for a particular experimental design such as Experiment 1 of Dillon et al. (2013) by generating simulated data repeatedly to determine true discovery rate, i.e., the proportion of cases where the absolute t-value of the effect of interest exceeds 2.

We carried out this true discovery rate or power analysis focusing only on the ungrammatical conditions as follows. Reproducible code and the associated data are available from https://osf.io/reavs/. We focused on the facilitatory interference effect in ungrammatical subject-verb agreement, and the corresponding effect in ungrammatical reflexives, as these are the important data points for the present paper.

The method for calculating power is as follows:

1. For a given experimental design and given an existing data-set, a maximal linear mixed model with full variance-covariance matrices for subjects and items (without correlation parameters in the variance-covariance matrices) is fit using lme4 to compute estimates of all parameters. The estimates from this model are stored.

2. Then, fake data are generated repeatedly 100 times. For data generation, parameter estimates are taken from the preceding step above; the exception is the parameter estimates for ungrammatical agreement and reflexives conditions, which are taken from the respective posterior predictive distributions computed from the model (using Approximate Bayesian Computation) and the Dillon et al. Experiment 1 data-set. As estimates of the interference effect in ungrammatical reflexives and in agreement, we take the first quartile, the median, and the third quartile; this range of values allows us to get an estimate of the uncertainty in the power estimate as a function of effect size.¹¹ Each fake data-set is analyzed using a maximal linear mixed model (without correlation coefficients). Convergence failures (which were below 3% in the present case) are discarded.

3. True discovery rates are computed for agreement and reflexives in ungrammatical conditions by computing the proportion of cases where the absolute t-value of the effect of interest is greater than 2.

Table A1 summarizes the power analyses using this method. The power analyses shown are for the sample size in the original Dillon et al. (2013) Experiment 1 and for the sample size in our replication attempt.

Table A1.

Prospective power analysis of Experiment 1 of Dillon et al. (2013), and of our larger-sample replication attempt (ungrammatical conditions only). Shown are a range of effect sizes derived from the posterior predictive distributions of the cue-based retrieval model of Lewis & Vasishth (2005), using the Dillon et al. (2013) data. The corresponding power estimates (the probability of correctly detecting the effect under repeated sampling, expressed as a percentage) for the two experiments are shown. The number of items was 48 in both experiments.

Agreement
	1st quartile	Median	3rd quartile
Posterior predicted effects (in ms)	−48	−39	−32
Power estimate for Dillon et al., 2013 (in %)	40	31	20
Power estimate for our replication (in %)	97	84	70
Reflexives
	1st quartile	Median	3rd quartile
Posterior predicted effects (in ms)	−32	−23	−14
Power estimate for Dillon et al., 2013 (in %)	25	13	5
Power estimate for our replication (in %)	69	42	25

Appendix B

Comparison of our analysis with the original analysis by Dillon et al. 2013 In addition to using the Bayesian paradigm for our analysis, there are several other important differences between our analysis and the original analysis conducted by Dillon et al. (2013). First, Dillon and colleagues used repeated measures ANOVAs rather than linear mixed models to analyze total fixation times. To use ANOVA, one has to aggregate over items or participants, which artificially eliminates one source of variance in the data. Using repeated measures ANOVA will generally lead to artificially low p-values in the F1 (by subjects) and F2 (by items) ANOVA because the variance components due to subjects and items are not taken into account simultaneously, as is the case in hierarchical linear models with crossed random subjects and items.

Second, the contrast coding of the interference effect in Dillon et al. (2013) differs from ours. In our contrast coding, within grammatical and ungrammatical conditions alike, a positive interference effect means a slowdown (inhibitory interference) due to a distractor that matches the retrieval cue under manipulation. By contrast, in Dillon et al., the interference effect is coded in opposite directions within grammatical and ungrammatical conditions: In ungrammatical conditions, the interference effect is coded identically to our contrast; in grammatical conditions, however, the interference effect is coded such that a positive sign of the effect means a speedup (facilitatory interference) due to a retrieval cue-matching distractor (see Table B1 for an overview). In other words, a positive main effect of interference in Dillon et al. (2013)’s coding would mean that there is inhibitory interference in ungrammatical conditions and facilitatory interference in grammatical conditions, whereas in our coding, a positive main effect of interference would mean that there is inhibitory interference independent of grammaticality (see Dillon et al. 2013, p. 92).¹² The difference in the contrast coding affects the three-way interaction between dependency type, grammaticality and interference. Specifically, this difference in the contrast coding is the reason why Dillon et al. report a three-way interaction different from zero whereas in our re-analysis of their data, the dependency type × grammaticality × interference interaction is centered around zero.

Table B1.

Comparison of the contrast coding of the interference effect applied by Dillon et al. (2013) and this paper.

	Dillon et al. (2013)				This paper
Experimental condition	gram		ungram		gram		ungram
	int	no int	int	no int	int	no int	int	no int
Interference	−0.5	0.5	0.5	−0.5	0.5	−0.5	0.5	−0.5
Interference [grammatical]	−0.5	0.5	0	0	0.5	−0.5	0	0
Interference [ungrammatical]	0	0	0.5	−0.5	0	0	0.5	−0.5

From a quantitative perspective, our results differ substantially from those presented by Dillon et al.; see Table B2 for an overview. Most importantly, the interference effect within ungrammatical agreement conditions has been estimated to be −119 ms with a confidence interval of [−205, −33] ms by Dillon et al. (2013), whereas the mean of the posterior distribution obtained from our analysis is −60 ms with a credible interval of [−112, −5] ms. This considerable difference in the estimated effect size is due to the logarithmic transformation we applied to the total fixation times which reduced the impact of extremely large values. By contrast, in ungrammatical conditions of reflexives, we get a larger effect size (−18 ms with a credible interval of [−72, 36] ms) compared to the original analysis (−8 ms [−67, 51] ms, see Dillon et al. 2013, p. 92). In the grammatical conditions, the estimates are also different, albeit less substantially. Whereas Dillon reports an interference effect of −43 ms [−106, 20] ms for agreement and 10 ms [−48, 68] ms for reflexives (see Dillon et al. 2013, p. 92), the mean and credible intervals of the posterior distribution obtained in our analysis are −34 ms [−85, 15] ms and 2 ms [−57, 60] ms, respectively. All of these differences are explained by the log-transformation we have applied and, to a much smaller extent, to the random effects structure of our models: whereas Dillon et al. report by-subject estimates aggregated over items, the hierarchical models we have used account for both between-items and between-subjects variance simultaneously. This is more conservative than aggregating over subjects and over items.

Table B2.

Comparison of our Bayesian estimates of the interference effects nested within grammaticality and dependency type computed from log-transformed data with the estimates reported by Dillon et al. (2013, p. 92) which were computed from untransformed data. For the Bayesian estimates, we show the posterior mean and 95% credible interval, backtransformed to the ms scale; the estimates taken from Dillon et al. (2013) represent means and 95% confidence intervals. We have adjusted the sign of Dillon et al.’s estimates to match our contrast coding.

		Dillon et al., 2013 (ms)	Our reanalysis (ms)
Grammatical	Reflexives	10[−48, 68]	2 [−57, 60]
	Agreement	−43[−106, 20]	−34 [−85, 15]
Ungrammatical	Reflexives	−8[−67, 51]	−18 [−72, 36]
	Agreement	−119[−205, −33]	−60 [−112, −5]