Word predictability effects are linear, not logarithmic: Implications for probabilistic models of sentence comprehension

Abstract

During language comprehension, we routinely use information from the prior context to help identify the meaning of individual words. While measures of online processing difficulty, such as reading times, are strongly influenced by contextual predictability, there is disagreement about the mechanisms underlying this lexical predictability effect, with different models predicting different linking functions – linear (Reichle, Rayner & Pollatsek, 2003) or logarithmic (Levy, 2008). To help resolve this debate, we conducted two highly-powered experiments (self-paced reading, N = 216; cross-modal picture naming, N = 36), and a meta-analysis of prior eye-tracking while reading studies (total N = 218). We observed a robust linear relationship between lexical predictability and word processing times across all three studies. Beyond their methodological implications, these findings also place important constraints on predictive processing models of language comprehension. In particular, these results directly contradict the empirical predictions of surprisal theory, while supporting a proportional pre-activation account of lexical prediction effects in comprehension.

General Introduction

Across multiple cognitive domains, efficient perception and decision making depend on our ability to exploit statistical regularities in the surrounding environment. During language comprehension, the role of context is particularly important, as comprehenders must rapidly extract meaning from signals that are often ambiguous and noisy. Indeed, a large body of evidence suggests that a word’s contextual predictability is one of the strongest predictors of how quickly and accurately that word will be recognized (see Kuperberg & Jaeger, 2016; Staub, 2015, for reviews).

While all contemporary models of language comprehension acknowledge the important role of prior context, there are disagreements about the cognitive mechanisms linking contextual predictability and word processing difficulty. In the present study, we focus on two classes of models that make divergent predictions about the precise linking function between predictability and word processing time – whether it is linear or logarithmic. After providing an overview of these models, we present data from two behavioral experiments, and a meta-analysis of the prior literature to help resolve this debate.

Linear accounts

A nearly universal assumption in models of language comprehension is that congruent sentence contexts facilitate word processing, with predictable words being recognized more quickly and accurately than unpredictable words (The boat passed under the bridge vs. The artist was painting the bridge; Balota, Pollatsek & Rayner, 1985; Rayner & Well, 1996; Stanovich & West, 1979; see Staub, 2015 for a review). These facilitation effects are usually attributed to the degree of match between the incoming word’s lexical features and features that have been predicted based on the prior linguistic context. Here we will use the terms prediction and pre-activation to refer to any contextually-driven activation of linguistic features (e.g. semantic, syntactic, orthographic) before they become available in the bottom-up input.

Theoretically, these predictions could be generated by a serial guessing mechanism in which comprehenders select and pre-activate a single likely continuation at each point in a sentence (Kleinman, Runnqvist & Ferreira, 2015, Smith & Levy, 2013; Van Petten & Luka, 2012). According to this account, whenever a correctly predicted word appears in the bottom-up input, it receives a fixed amount of facilitation (F), resulting in faster recognition times. So long as words are selected according to a probability matching strategy (Vulkan, 2000), this serial guessing mechanism would produce a linear reduction in processing difficulty as lexical predictability increases.

Similar facilitation effects would also be produced by a parallel model. According to this account, readers can predict multiple word candidates, assigning pre-activation in proportion to each word’s estimated probability of occurrence. Because the features of multiple words are activated in parallel, any word with a non-zero probability (P) will receive some facilitation (F × P) if/when it appears in the bottom-up input. Similar to the serial guessing mechanism described above, so long as comprehenders’ probability estimates reflect the average statistics of the language environment, the time required for word recognition should decrease linearly as lexical predictability increases. Here, we refer to this as a proportional pre-activation account.

A linear facilitation mechanism of this kind is currently implemented in the E-Z Reader model of eye-movement control (Reichle, Rayner & Pollatsek, 2003), and mechanisms similar to this account have been endorsed, at least implicitly, in many theories of anticipatory processing in language comprehension (Delong et al., 2005; Federmeier, 2007; Schwanenflugel & LaCount, 1988; Staub, 2015; Staub, Grant, Astheimer, & Cohen, 2015).

Logarithmic accounts

A different conception of the link between contextual predictability and processing difficulty comes from surprisal theory, which was first formulated as a theory of syntactic parsing (Hale, 2001; Levy, 2008). According to this theory, comprehenders assign probabilities to all possible syntactic parses of the current sentence, and this probability distribution is updated incrementally after each incoming lexical item. Assuming a deterministic relationship between higher-level syntactic parses and lower-level lexical inputs, Levy (2008) showed that the magnitude of the probability shift over syntactic parses, before and after encountering a word (the Kullback-Leibler divergence), is formally equivalent to the surprisal of that word — its negative log probability, given the prior context, −logP(W|C). Hale and Levy further demonstrated that increases in lexical surprisal could correctly predict localized increases in processing difficulty for several classes of syntactically complex sentences (see also Boston, Hale, Kliegl, Patil & Vasishth, 2008; Demberg & Keller, 2008). Based on these findings, the authors proposed that surprisal may provide a key linking function between the mechanisms underlying incremental sentence comprehension and behavioral measures of processing difficulty.

This theory of syntactic parsing has also been extended into a more general theory of processing difficulty during language comprehension (Levy, 2008; Smith & Levy, 2013). The assumption here is that comprehenders assign probabilities, not just to syntactic parses, but to all possible message-level interpretations of a sentence. Again, assuming an equivalence between the shift in message-level probabilities and the log-probability of each incoming word, the authors hypothesized that all word-by-word variation in processing difficulty could be explained by variability in lexical surprisal.

Surprisal theory has had an important influence on the field of sentence processing. While it shares some principles in common with the proportional pre-activation account described above, it can be distinguished in two main respects. First, because this theory predicts a logarithmic relationship between processing difficulty and word probability, surprisal theory implies that comprehenders must pre-activate a large number of low probability words, including continuations that are unlikely to ever appear in the bottom-up input. In Smith and Levy (2013), a non-anticipatory version of surprisal theory was briefly considered (pp. 309-312), but the authors ultimately rejected this possibility in favor of an anticipatory mechanism that preactivates “large portions of the lexicon” in a non-linear fashion.

The second major assumption of surprisal theory is that it equates the difficulty of accessing lexical features with the difficulty of fully integrating this information into the prior context. This assumption is again derived from the formal equivalence between lexical surprisal and the full shift in probability distributions over message-level interpretations. In this sense, by collapsing multiple aspects of language processing difficulty into a single mechanism, surprisal theory takes the principles of incrementality and interactivity to their extreme. Under this account, reading time differences due to word frequency (Inhoff & Rayner, 1986), semantic constraints (Rayner & Well, 1996), and syntactic misanalysis (Frazier & Rayner, 1982) are all generated via a single computational mechanism, reflected in the log-probability of individual lexical items.

Another reason to posit a non-linear mapping between predictability and processing difficulty comes from extensions of the Bayesian Reader model. Although originally formulated as an account of isolated word recognition (Norris, 2006, 2009), Bayesian Reader has also been adapted to explain eye-movement behavior during sentence comprehension (Bicknell & Levy, 2010). Within this framework, comprehenders continually sample information from a noisy perceptual environment in order to reach a desired level of certainty about the identity of the currently attended word. According to this theory, comprehenders use a process equivalent to Bayes Rule to optimally combine their prior beliefs about a word’s identity with the bottom-up perceptual input. When applied iteratively, this process of Bayesian updating results in an approximately logarithmic relationship between processing time and a word’s prior probability in context.

Behavioral evidence

In summary, certain models like the proportional pre-activation account predict a linear relationship between predictability and processing difficulty, while others, like surprisal theory predict a logarithmic relationship. Despite the large number of studies showing a graded relationship between lexical predictability and processing time, the precise mathematical function linking these two variables remains unclear.

Some of the earliest behavioral evidence for a graded relationship comes from Rayner and Well (1996), who measured reading times for high, medium, and low predictability words during reading comprehension. In this study, the authors operationalized word probability using cloze probability, which is the proportion of participants providing a word in an offline sentence continuation task (Taylor, 1953). In addition to showing faster reading times to more predictable words, the authors saw some evidence that context effects were larger at the low end of the probability scale (Low > Medium = High), consistent with the predictions of logarithmic accounts. However, a later eye-tracking study using the same sentence materials produced the opposite pattern of results (Rayner, Reichle, Stroud, Williams & Pollatsek, 2006), with reading time benefits observed only on highly predictable words (Low = Medium > High). In addition to these reading time studies, there are a number of word naming and picture naming studies that have manipulated contextual probability across a wide range of values. Generally, these studies have reported a roughly linear relationship between contextual probability and naming times (Griffin & Bock, 1998; McClelland & O’Regan, 1981; Traxler & Foss, 2000), although these tasks clearly differ in many respects from normal reading comprehension.

There are several issues that prevent these previous studies from clearly distinguishing the predictions of linear and logarithmic accounts. First, these studies typically included only a small number of items and participants, resulting in relatively low statistical power. Second, most of these studies contained only a small number of items in the low probability range (0%-20% cloze). This is important because this low probability range is precisely where the linear and logarithmic accounts make the most divergent predictions. Specifically, while a linear account would predict very small differences in processing difficulty when moving from a 10% probability word to a 1% probability word, logarithmic accounts would predict relatively large differences in processing difficulty over this range.

Smith & Levy, 2013

To address these issues in the prior literature, a study was conducted by Smith and Levy (2013) to help clarify the linking function between lexical predictability and reading times. The authors analyzed reading times from two naturalistic corpora, which included eye-tracking data from the Dundee corpus (N = 10; Kennedy & Pynte, 2005) and a newly collected self-paced reading dataset based on passages from the Brown corpus (N = 32). The authors estimated conditional probabilities at each word using trigram co-occurrence measures. They then used a mixed-effects regression approach to examine the association between predictability and reading times over a wide range of probability values (10⁻¹ to 10⁻⁶). The authors observed a logarithmic relationship between trigram probability and reading times in both eye-tracking and self-paced reading measures, and, based on these findings, they suggested that very small differences in word probability can have a large impact on reading behavior, particularly when they occur at the low end of the probability scale.

These findings by Smith and Levy (2013) have been interpreted as strong evidence in support of surprisal theory, and logarithmic predictability effects more generally. However, it is important to consider some potential methodological limitations of this study. First, there are inherent limits to the “naturalistic”, corpus-based approach they adopted. In a typical experimental design, items are randomly assigned to different levels of lexical predictability while other potentially confounding variables are held constant. In contrast, in a “corpus-based” design, no experimental control is exerted. Instead, participants are presented with texts that vary, word-by-word, in both the predictor of interest (e.g. predictability) and other confounding factors that may also influence reading times. In these designs, regression methods are often used to statistically adjust for confounding factors. But, even in the presence of statistical controls, it can be difficult to establish direct inferences in these designs due to measurement error (Shear & Zumbo, 2013; Westfall & Yarkoni, 2016), collinearity (Friedman & Wall, 2005), and the presence of unmeasured confounds (Christenfeld, Sloan, Carroll & Greenland, 2004).

Because contextual predictability was not experimentally manipulated in Smith and Levy (2013), it is possible that the observed relationship between trigram probability and reading times was distorted by inadequately controlled lexical or contextual confounds (Greenland, Robins & Pearl, 1999; Shear & Zumbo, 2013). For example, in natural texts, trigram measures have been shown to correlate very strongly with unigram word frequency (r = .8, Ong & Kliegl, 2011; Moers, Meyer & Janse, 2017; Smith & Levy, 2011), which is another variable that strongly influences word identification times. Given that the relationship between word frequency and processing difficulty is known to be logarithmic (Carpenter & Just, 1983; White, Drieghe, Liversedge & Staub, 2018), it is possible, in the presence of measurement error, that trigram probabilities may “mimic” the effects of subjective word frequency, simply due to shared variance (Ong & Kliegl, 2011; Westfall & Yarkoni, 2016).

The second methodological limitation in Smith and Levy (2013) was the use of trigram co-occurrence as an estimate of readers’ subjective lexical probabilities. This corpus-derived measure of lexical predictability has the advantage of being calculated quickly and efficiently. However, this measure only takes into account the immediately preceding two words of context, while human readers are sensitive to much broader contextual constraints (Fitzsimmons & Drieghe, 2013, Brothers, Wlotko, Warnke & Kuperberg, 2020). For this reason, offline sentence completions from human readers (cloze completions, Taylor, 1953) have often been considered the gold standard for estimating subjective lexical probabilities. In fact, conditional co-occurrence measures such as trigram have been shown to be only weakly to moderately correlated with such cloze measures (r = .5, Ong & Kliegl, 2011; Smith & Levy, 2011), and to provide worse fits for human reading time data (Frisson, Rayner & Pickering, 2005; Smith & Levy, 2011). While ideally this type of estimation error would only add noise to the model, there is also the possibility of systematic bias. For example, the relationship between subjective probability and trigram probability may, itself, be non-linear, which would necessarily distort the estimated relationship between trigram probability and reading times.

The current study

Given the methodological limitations of Smith and Levy (2013), and the important theoretical claims put forward by the authors, we thought that it was important to re-examine the relationship between word probability and processing difficulty using 1) a more tightly controlled experimental design, and 2) a more direct estimate of lexical probability obtained from skilled adult readers (cloze). In this way, we hoped to provide a more stringent empirical test for distinguishing linear and logarithmic accounts.

For the present experiments, we generated a carefully controlled set of sentences in which cloze probability was parametrically manipulated across a wide range (High: 91%, Moderate: 20%, Low: 1%). To increase the statistical power of our design, we included a large number of items and participants, as well as sentence materials that sampled heavily at the low end of the cloze probability scale (where the predictions of linear and logarithmic accounts are the most distinct). Most simply, if the function linking contextual probability and word processing time is linear, we should see greater facilitation when comparing high and moderate-cloze words (91% vs. 20%) than when comparing moderate and low-cloze words (20% vs. 1%). In contrast, a logarithmic account would predict the opposite pattern, with greater processing time differences at the low end of the probability scale (log₁₀ units, High vs. Moderate: −0.04 vs −0.73; Moderate vs. Low −0.73 vs −2.00).

In Experiment 1, participants read single sentences for comprehension at their own pace, and reading times were measured at each word. In Experiment 2, a subset of these items was used in a cross-modal picture naming task, in which participants listened to sentence contexts and then named pictures with varying degrees of predictability. This paradigm allowed us to test the robustness of our results, using a different presentation modality (auditory sentence contexts) and a different measure of processing difficulty (naming latency). The large context effects in this task also allowed us to estimate the shape of the word probability function at the level of individual participants. Finally, we carried out a combined meta-analysis of eight previously published eye-tracking while reading studies that also included parametric cloze manipulations (total N = 218).

To preview our results, in all three datasets we observed a robust linear relationship between word probability and lexical processing difficulty, contrary to the findings of Smith and Levy (2013). Based on these results, we argue that the relationship between word probability and processing difficulty is, in fact, linear, and that prior evidence supporting a logarithmic relationship was likely the result of statistical artifact.

Experiment 1: Self-paced reading

In Experiment 1, we examined the linking relationship between lexical predictability and reading times using the same self-paced reading task employed by Smith and Levy (2013). In addition to predicting a reduction in reading times with increasing levels of lexical predictability (Brothers, Swaab & Traxler, 2017; Smith & Levy, 2013), this study was designed to directly test whether this reduction in reading times would follow a linear or logarithmic function.

Methods

Materials

We selected 216 critical words (nouns, verbs, and adjectives), which we used to construct sentences with three levels of semantic constraint. Across these three sentence frames, the same critical word was either high-cloze (91%, STD = 7%), moderate-cloze (20%, STD = 7%), or low-cloze (1%, STD = 1%), as verified using an offline cloze norming study.

High: Her vision is terrible and she has to wear glasses in class.

Mod: She looks very different when she has to wear glasses in class.

Low: Her mother was adamant that she has to wear glasses in class.

The position of the critical word was always the same within each triplet (average = 10 words, STD = 1.4), and one to five words prior to the critical word were held constant (two words on average). Two to five additional words were added after the critical word (e.g. “in class”). These words were always identical within each triplet, and there were no differences, across conditions, in the mean semantic similarity between words in the spillover region and words in the prior context (F < 1; word2vec cosine similarity; Mikolov, Sutskever, Chen, Corrado, & Dean, 2013).

Cloze norming was carried out by participants recruited from the online crowd-sourcing platform, Mechanical Turk. In this, and all subsequent experiments, protocols were approved by Tufts University Social, Behavioral, and Educational Research Institutional Review Board, and all participants provided informed consent. Participants was asked to read one sentence frame from each triplet (“The web was spun by the…”) and to provide the first continuation that came to mind. On average, 90 participants provided a completion for each frame (range: 88 - 93). Any spelling errors were corrected, and singular and plural completions were scored as the same word. The final set of items fell into three, non-overlapping groups of cloze probability (high: 100%-65%, moderate: 50%-7%, or low: 5%-0%). For a complete set of sentences, see Supplementary Materials, https://osf.io/b9kns/.

Procedure

In Experiment 1, we recruited 240 participants from Amazon Mechanical Turk, none of whom participated in the previous cloze norming study. These participants were asked to complete the self-paced reading task through a web-based platform (Ibex Farm; http://spellout/ibexfarm.nef). Stimuli were presented in a counterbalanced Latin square design, with each participant randomly assigned to one of three experimental lists. This ensured that each critical word appeared equally often across conditions and that no participants saw the same critical word more than once. Each participant read 216 experimental sentences and 96 filler sentences, presented in a unique random order. They progressed through each sentence word-byword, using a moving window self-paced reading paradigm. (Just, Carpenter & Wooley, 1982). Reading times were recorded as the time elapsed between button presses when a word was visible on the screen. Spaces between words were unmasked, similar to natural reading, and, following 25% of sentences, participants answered a comprehension question:

S: “The athlete loved lifting weights in the gym in the evening.”

Q: “Which workout time does he prefer?” (early / late)

S: “Everett lit the campfire while I pitched the tent near the woods.”

Q: “ Were they going to sleep in a hotel?” (yes / no).

Twenty-four participants were excluded because of comprehension accuracies below 75%. In the final sample (N = 216), average comprehension accuracy was 95% (SD = 5%). This suggests that, even with remote data collection, participants were attending carefully to the sentence materials throughout the experiment (for similar reading and comprehension rates in an undergraduate sample, see Brothers, Swaab and Traxler, 2017). A similar pattern of reading time results was also observed when using a more stringent accuracy cut-off (>90%)

Data analysis

Before calculating log-transformed cloze probability, one half of a response was added to items with an observed cloze probability of zero (15% of items; Lowder, Choi, Ferreira & Henderson, 2018). Linear and log-transformed cloze probability were defined at the item-level, and these predictors were mean-centered prior to analysis. We used general additive mixed models (GAMMs) with the mgcv packkage (version 1.8-23; Wood, 2004; Wood 2006) to estimate penalized cubic spline functions modeling the effects of linear and log-transformed word predictability on single-trial reading times. We also used linear mixed effects models (lme4, version 1.1-17) to directly compare the fits of linear and logarithmic functions. All of these models were fit using maximum likelihood estimation with random slopes and intercepts for both subjects and items. Reported p-values were estimated using the Satterthwaite approximation (ImerTest). For original data and analysis scripts, see https://osf.io/b9kns/.

To capture spill-over effects (Brothers, Swaab & Traxler, 2017; Smith & Levy, 2013), we combined reading times for the critical word and the two subsequent words. Within items, this three-word critical region was always identical across conditions. Reading times that were three standard deviations above a participant’s condition mean (2.7% of trials), or with critical region reading times of less than 300ms (0.4% of trials), were replaced with these cutoff values.

Results

Self-paced reading times in the three-word critical region were faster for sentences with high-cloze words (933ms) than for sentences with moderate-cloze (953ms) or low-cloze words (957ms; see Table 2). The relationship between cloze probability and reading time was clearly linear, with larger reading time differences between high-cloze and moderate-cloze words (High vs. Moderate: 20ms ± 7) than for moderate-cloze and low-cloze words (Moderate vs. Low: 4ms ± 7). Recall that logarithmic models predicted the opposite pattern of results, with larger cloze effects at the low end of the probability scale. This dissociation (20ms vs. 4ms) was reliable across both subjects and items, t₁(215) = 2.66, p = .008; t₂(215) = 2.47, p = .01.¹

Table 2.

Experiment 1 reading times (and within-subject SDs) for critical word (N) and the two subsequent spillover words

	Low-cloze 1%	Moderate-cloze 20%	High-cloze 90%
Word N	299 (13)	301 (12)	295 (13)
Word N+1	312 (14)	308 (12)	302 (15)
Word N+2	346 (20)	342 (21)	336 (21)

When single-trial reading times were fit with GAMMs, using raw cloze probability as a continuous predictor, there was a clear linear relationship between word predictability and reading time (see Figure 1). In contrast, when this analysis was performed using log-transformed cloze values as the predictor, the GAMM produced a non-linear pattern with stronger reading time differences at the high end of the probability scale.

Figure 1.

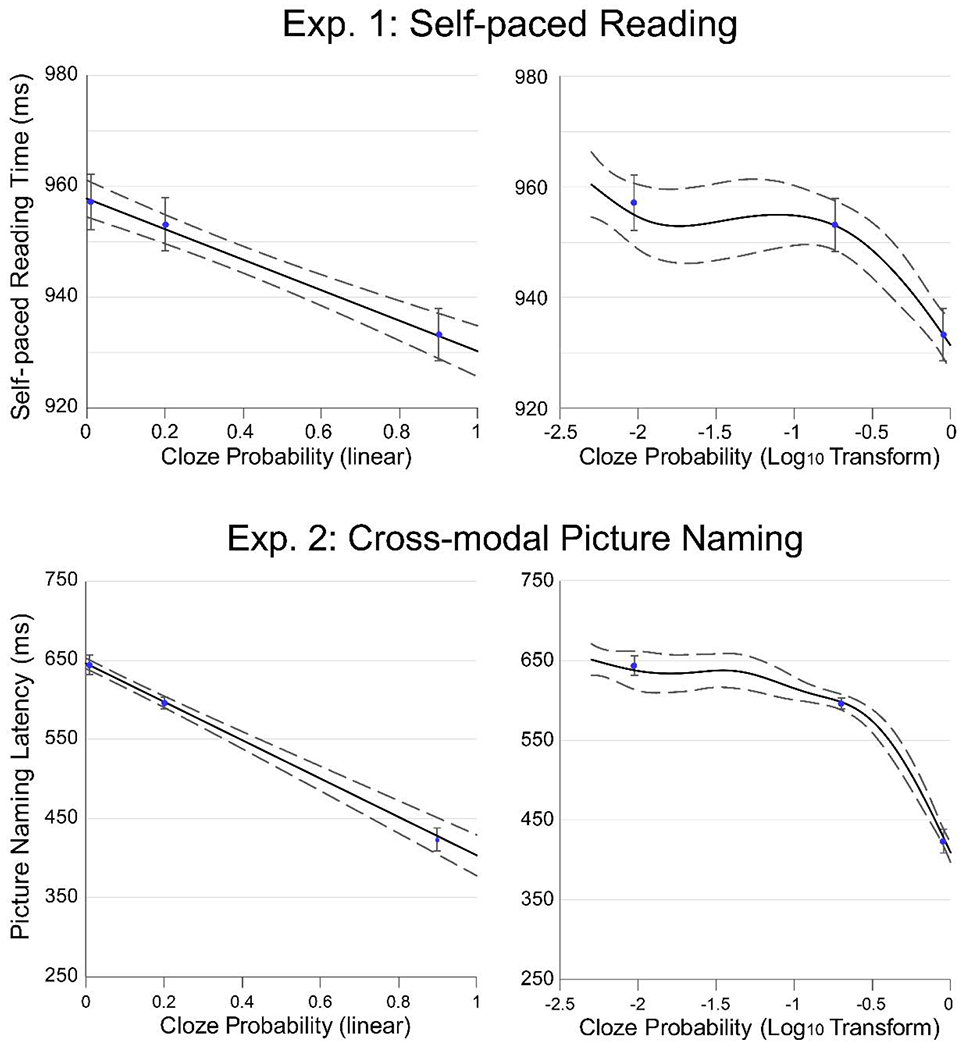
The upper panel shows the relationship between self-paced reading times (three-word region) and the predictability of the critical word in Experiment 1. The lower panel shows picture naming times in Experiment 2. Black lines represent penalized GAM smooth splines fitted to the continuous data, with dashed 95% Bayesian credible intervals. Blue dots represent mean RTs for low, moderate, and high-cloze items, with error bars representing 95%, within-subject confidence intervals. Note the linear relationship between cloze probability and processing time across both experiments (left). When cloze was log-transformed, the predictability-RT relationship became strongly non-linear (right).

To further compare linear and logarithmic accounts, we fit two separate linear mixed effects models to the data, one with linear cloze probability and one with log-transformed cloze probability as a predictor. Both models significantly predicted reading time (linear: b = −27ms, t = −6.92, p < .001; logarithmic: b = −11ms, t = −6.06, p < .001), but the linear model showed a much better fit, as indicated by Log Likelihood (linear, −322224, logarithmic. −322243). When quadratic terms were added to two models (cloze², log cloze²), this significantly improved the fit of the logarithmic model (b = −9.2, t = −3.53, p < .001), but did not improve the fit of the linear model (b = −12.0, t = −0.60, p = .55), consistent with the GAMM results.

An issue of restricted range?

These findings provide strong evidence for a linear, rather than a logarithmic relationship between lexical probability and reading time. Specifically, we saw greater facilitation in reading times at the high end of the cloze probability scale (91% vs 20%), and linear measures of cloze probability provided a more accurate model of single-trial RTs.

Before considering the theoretical implications of these findings, we considered a potential limitation of our approach. Because cloze probability values are based on the responses of individual readers, the precision of this estimate depends on the number of cloze responses obtained. Even with a relatively large number of responses (N = 90), it is difficult to estimate probability differences at the low end of the scale (e.g. 1% to 0.0001%), which is precisely where surprisal predicts the largest reading time differences. It could therefore be argued, under a logarithmic account, that cloze probability measures are simply less effective at capturing reading time variability at the low end of the probability scale.

For example, consider these two sentences used in Experiment 1:

“Over at the loading dock they needed a long hose…”

“My uncle is installing solar panels on his farm…”

While the critical words hose and farm both have cloze probabilities of zero in these contexts, these words also have conditional trigram probabilities of 0.2% and 0.0008% according to the British National Corpus (−2.7 log₁₀ vs. −5.1 log₁₀). Based on this difference in log-probability, surprisal theory predicts larger reading time differences for these two critical words than for the High versus Low probability contrast examined in the current experiment (91% vs. 1%).

To test this prediction directly, we extracted trigram probabilities for each critical word, employing the same methods used in Smith and Levy, 2013 (Knesser-Ney smoothed language model trained on the British National Corpus). As expected, there was clear variability in trigram probabilities across items (log10 mean = −3.57, range = −7.3 to −0.1), but trigram probabilities were only weakly correlated with cloze (r = 0.15). This trigram measure also strongly underestimated lexical probabilities compared to human readers (trigrams: HC: 2.1%, MC: 0.5%, LC: 0.3%; cloze: HC: 91%, MC: 20%, LC: 1%).

If trigram probability can account for additional variance at the low end of the probability scale, then including trigram as a predictor should significantly improve model fit, beyond the effects of cloze. However, this was not what we found. In separate linear mixed effects models, we saw no significant effects of either raw (t = 1.48) or log-transformed (t = 0.31) trigram probability, while the effects of cloze probability remained highly significant (|t|s > 6). A similar pattern of results was obtained using a larger and more accurate language model (character CNN, LSTM model, Jozefowicz, et al., 2016). While this model’s probability estimates were somewhat closer to human readers’ (r = .36), LSTM model probabilities again accounted for no additional variability in reading times (|t|s < 1.5).

To summarize, in a self-paced reading task similar to Smith and Levy (2013), we observed shorter reading times in the three-word critical region with increasing levels of lexical predictability. Critically, this predictability effect was clearly linear, with the majority of the cloze effect being driven by high predictability words. Finally, trigram probability had no independent effect on reading times, which suggests that our results were not driven by imprecision in our cloze probability measure or by undetected reading time differences for very low probability continuations (<1%).

Experiment 2: Cross-modal picture naming

While the results of Experiment 1 are highly suggestive, they were obtained in a single language comprehension task (self-paced reading), which showed a relatively modest effect of lexical predictability (24ms, d_z = 0.46). In Experiment 2, we employed a different paradigm – picture naming, which is also sensitive to differences in lexical processing difficulty (Levelt, 2001). Although cross-modal picture naming differs in many respects from normal word-byword reading, we thought this experiment would provide an informative conceptual replication (Munafo & Smith, 2018), allowing us to test whether this this same linear relationship is observed across different input modalities (text vs. speech comprehension) and measures of processing difficulty (reading vs. naming latencies).

In addition, because the sentence context effects observed in picture naming tasks are extremely robust (Griffin & Bock, 1998) this paradigm can provide an even more precise empirical test by allowing us to compare the fits of linear and logarithmic models at the level of individual participants.

Methods

Materials

In Experiment 2, we selected a subset of 84 items from the larger stimulus set used in Experiment 1. For these sentence triplets, the critical word was always a concrete noun that could be depicted easily in an image (cloze: High = 92%, Moderate = 20%, Low = 1%). Spoken versions of each sentence frame were recorded by a male speaker with the critical word and remainder of the sentence omitted (“The web was spun by the…”). Sentence frame durations ranged from 2.5 seconds to 5.8 seconds and did not differ across conditions (F < 1, High: 3971ms, Moderate: 4022ms, Low: 3985ms).

Procedure

Thirty-six Tufts University undergraduates participated in this study for course credit. On each trial, participants heard a high, moderate or low constraint sentence frame, and after a 250ms delay, they saw a color image of the critical noun presented on a computer monitor. Participants were instructed to name each image as quickly and accurately as possible using a single word.

Over the course of the experiment, participants heard 168 critical sentences, randomly intermixed with 24 fillers. Each critical picture was presented twice in two different sentence contexts – once in the first half of the experiment and once in the second. Sentence frames were never repeated. In total there were six experimental lists, counterbalancing level of constraint and order of presentation across participants (e.g. List 1: HC-MC, 2: HC-LC, 3: LC-MC, 4: MC-HC, 5: LC-HC, 6: MC-LC).

The entire experiment lasted approximately 25 minutes. Immediately afterward, participants performed an old/new recognition memory task to confirm they were attending to the sentence frames. On average, participants correctly identified 93% of the old sentence frames and misidentified only 1% of the new items. Picture naming responses were recorded using a desk-mounted microphone, and speech onset latencies and naming errors were scored manually by raters who were blind to condition.

Data analysis

Statistical analyses were exactly the same as in Experiment 1. We excluded trials with non-responses, naming errors, or naming latencies greater than 3 standard deviations (3.5% of trials). Because naming accuracy was close to ceiling (97%), naming errors were not analyzed further.

Results

In Experiment 2, participants were faster to name high-cloze pictures (424ms), relative to moderate-cloze (597ms) and low-cloze pictures (644ms). Similar to the self-paced reading data, the relationship between cloze probability and naming latency was almost perfectly linear (see Figure 2), with larger differences between high-cloze and moderate-cloze words (High vs. Moderate: 173ms ± 16) than between moderate-cloze and low-cloze words (Moderate vs. Low: 47ms ± 11). Again, this dissociation (173ms vs. 47ms) was highly reliable, t₁(35) = 14.08, p < .0001; t₂(83) = 9.55, p < .0001.

Figure 2.

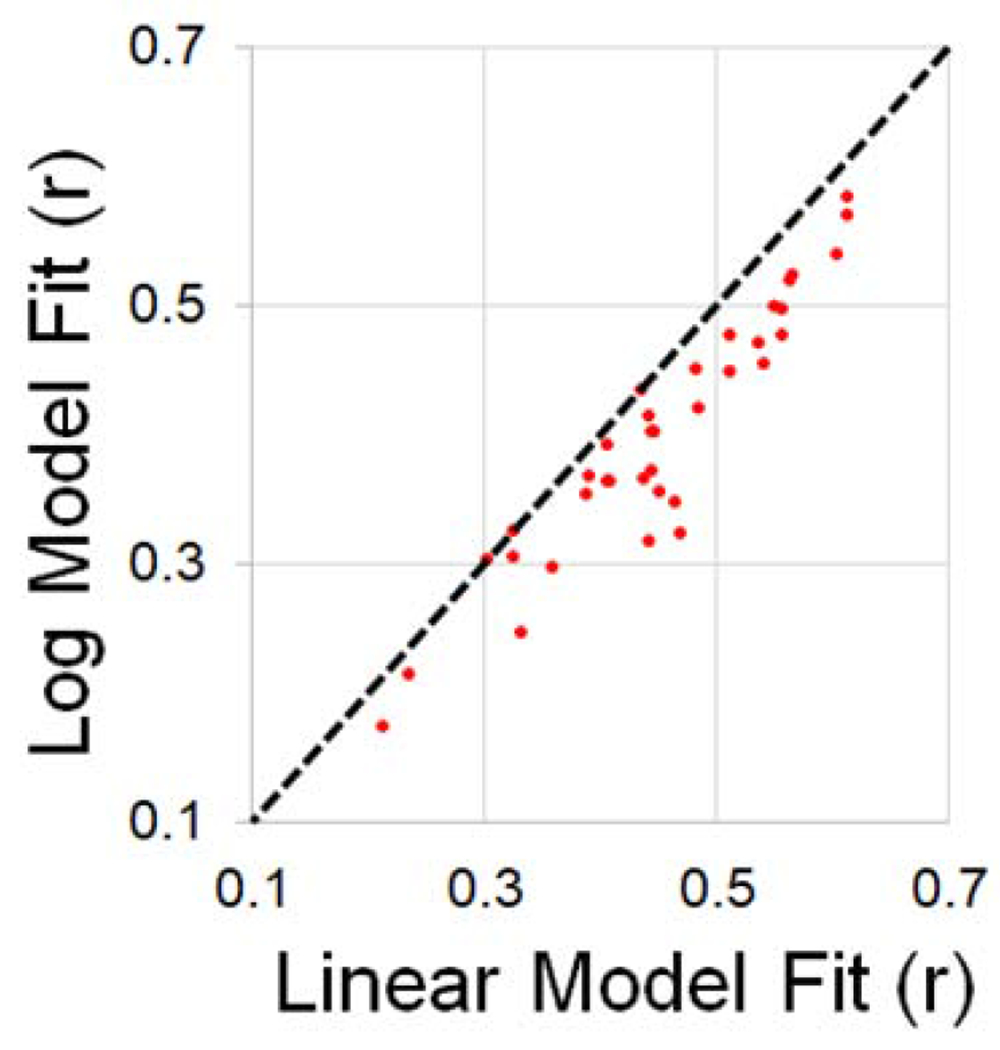
Model fit comparisons for individual participants in Experiment 2 (picture naming). All 36 participants fall below the line of unity, indicating better fits for the linear model.

In separate models, we saw significant effects of both linear (b = −240.5, t = −17.7, p < .0001) and log-transformed cloze probability (b = −105.2, t = −15.0, p < .0001), but again, the linear model showed a much higher Log Likelihood (linear: −38137, logarithmic: −38340). Only the log-transformed model was significantly improved by the addition of a quadratic term (b = −97.1, t = −12.8, p < .0001), with no improvement for the linear cloze model (b = 5.9, t = 0.12, p = .90). This result is consistent with the GAMM plots (see Figure 2), which showed a linear relationship between cloze probability and naming time, and a strong non-linear relationship in log-probability space.

As expected, the sentence context effect was much larger in the picture naming task (d_z = 3.4), allowing us to investigate the shape of predictability-RT functions for individual participants. At the single-trial level, behavioral responses for all thirty-six participants (36/36) were better fit by a linear function (mean r = −.435) than by a logarithmic function (mean r = −.399), t(35) = −9.64, p < .0001 (see Figure 2). This finding is particularly important and demonstrates 1) that the linear linking function is not a byproduct of multi-subject averaging (Tauber, Navarro, Perfors & Steyvers, 2017), and 2) that this linear relationship is robust and replicable across individuals.

As in Experiment 1, when both cloze probability and trigram probability were included in a linear mixed effects model, trigram estimates failed to account for any additional variance in naming times (linear trigram: t = −1.60; log trigram: t = −1.86), while the effect of cloze remained highly significant (|t| > 17).

Discussion

Consistent with the findings of Experiment 1, we observed robust linear effects of lexical predictability on naming latencies. Single-trial naming latencies were better explained by a linear, rather than logarithmic model, and these differences in model fit were observed consistently across all 36 participants.

To visualize this pattern of results across experiments, we calculated the relative size of the cloze effect at high and low ends of the probability range (91% vs. 20% and 20% vs. 1%), and then plotted these values alongside the predictions of a linear, logit (log(p/1-p)), and logarithmic model (see Figure 3). Again, the linear pattern was nearly identical across Experiments 1 and 2, despite differences in the comprehension task and behavioral measures used across experiments.

Figure 3.

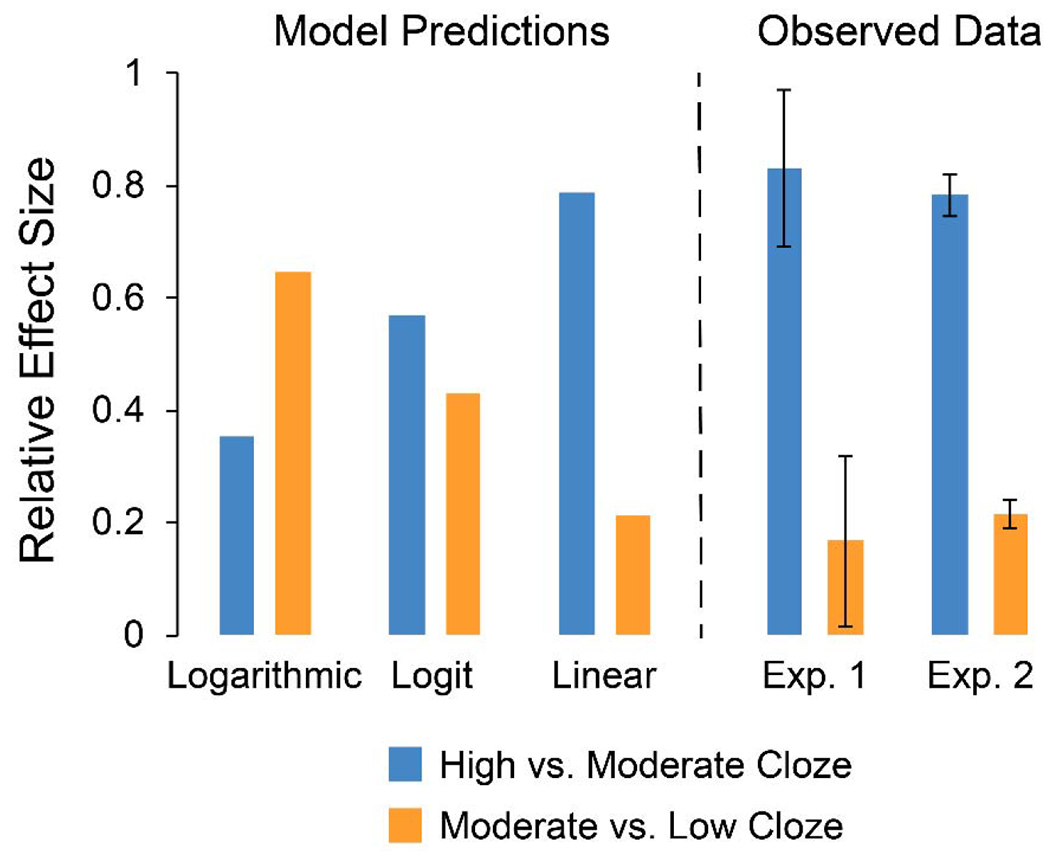
Relative size of the contextual predictability effect when comparing high-cloze vs. moderate-cloze words (91% vs. 20%) and moderate-cloze vs. low-cloze words (20% vs. 1%). Results predicted by logarithmic, logit, and linear models are plotted on the left. Observed data from Experiment 1 (self-paced reading) and Experiment 2 (picture naming) are plotted on the right. Error bars represent within-subject standard errors.

Study 3: Eye-tracking Meta-analysis

Introduction

In Experiments 1 and 2 the relationship between word probability and processing difficulty was distinctly linear, contrary to prior corpus-based findings, and contrary to the predictions of surprisal theory. It should be noted though that the behavioral tasks used in these experiments (self-paced reading and cross-modal picture naming) differ in many respects from everyday reading comprehension. In order to further test the generalizability of our findings we examined data from previously published eye-tracking while reading studies, which more closely approximate normal reading comprehension. While, individually, these studies did not have sufficient statistical power to estimate the shape of the word probability function, by combining data across studies we hoped to provide additional experimental evidence for adjudicating between log and linear accounts.

Methods

To identify relevant studies for this meta-analysis, we searched publicly available archives using combinations of the search terms “predictability”, “cloze”, “eye-tracking”, and “reading”. We included any experiments investigating eye-movement behavior during sentence comprehension that 1) were conducted in native, adult readers, and 2) included a factorial manipulation of cloze probability with at least three levels (e.g. high, medium, low), see Table 1. All of these experiments were conducted in English, except Rayner et al. (2005), which presented sentences in Mandarin. While critical words in these studies were not always counterbalanced across levels of cloze probability, these words were always matched in length and frequency across conditions. The meta-analysis included five studies with eight separate experiments (Paul, unpublished dissertation, Experiments 3 and 4; Rayner & Well, 1996; Rayner, Reichle, Stroud & Williams, 2006; Rayner Li Juhasz & Yan 2005; Sereno, Hand, Shahid, Yao & O’Donnell, 2018). To the best of our knowledge, no other studies meet the inclusion criteria, outlined above.

Table 1.

Summary of studies included in the eye-tracking meta-analysis

	#Subs	#Items	HC	MC	MC*	LC	Experiment Details
Rayner & Well, 1996	18	36	86%	41%		4%
Rayner, et al., 2005	16	36	85%	36%		4%	Native Mandarin readers
Rayner, et al., 2006 (younger)	16	36	86%	41%		4%	3x2: Pred. x Font difficulty
Rayner, et al., 2006 (older)	16	36	86%	41%		4%	3x2: Pred. x Font difficulty
Sereno, et al., 2018 - Exp. 1	40	150	97%	54%		1%	3x2: Pred. x Frequency
Sereno, et al., 2018 - Exp. 2	40	150	97%	54%		1%	Pred. x Freq.; invalid previews
Paul - Exp. 3 (unpublished)	32	32	91%	67%	37%	6%	*Two “med. cloze” conditions
Paul - Exp. 4 (unpublished)	40	48	90%	65%	35%	5%	50% invalid previews

All together, the meta-analysis included data from 218 participants and 16,680 experimental trials. In some studies, predictability was crossed with a second experimental factor ((font difficulty, Rayner, Reichle, Stroud & Williams, 2006; word frequency, Sereno, et al., 2018; preview validity, Paul, Exp. 4). For these experiments, we collapsed across this second factor by averaging reading time measures within each level of cloze. Additional methods and individual condition means are provided in Appendix A.

Because eye-tracking studies typically show minimal “spillover” effects in subsequent regions of the text, eye-movement measures in these studies were restricted to the critical word. All studies reported multiple measures of processing difficulty, including word fixation rate, first fixation duration, gaze duration (the sum of all first-pass fixations), and total time (summed reading time including re-fixations). For each experiment, we obtained the total number of participants, study-specific cloze probabilities, and the mean and within-subject standard error for each reading time measure in each condition. Because within-subjects standard errors were not always provided, these values were calculated using pooled standard deviations and an estimate of the within-subjects correlation coefficient for each dependent measure (range: r = .32 - .79; Brothers, Hoversten & Traxler, 2017; Morris & DeShon, 2002).

To visualize the relationship between cloze probability and processing difficulty, we combined cloze probabilities and reading time measures in each condition (high, medium, low), weighting each experiment mean by the inverse of its variance (see Figure 4). In this analysis, for studies with more than three levels of cloze, we collapsed reading time measures across the two intermediate conditions. The weighted cloze values across studies were: high-cloze = 95%, (range = 97% - 85%); medium-cloze = 52%, (range = 54% - 36%); low-cloze = 2%, (range = 6% 1%).

Figure 4.

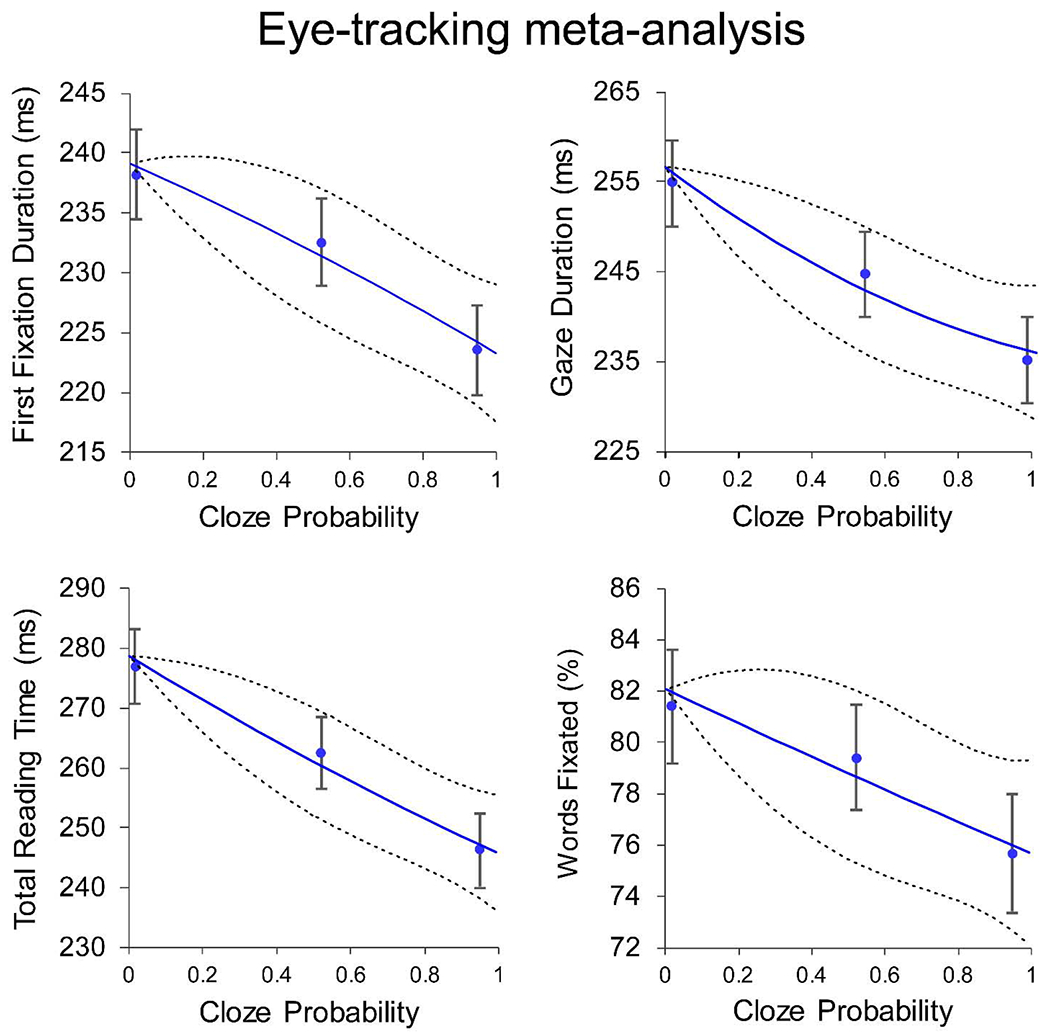
The relationship between reading behavior and word probability in a meta-analysis of 8 eye-tracking while reading experiments (total N = 218). Data points represent weighted eye-tracking measures for high, medium, and low predictability words (combined across studies) and their 95% confidence intervals. Lines represent quadratic best fits and 95% confidence intervals from the dose-response meta-analysis.

In addition, in order to capture variability in cloze values across experiments, we also conducted a series of a dose-response meta-analyses using the “mean difference” method (dosresmeta package; Crippa & Orsini, 2016; Shim & Lee, 2019). First, difference scores were calculated for each condition, relative to an implicit baseline (the low cloze condition). Regression coefficients for linear and quadratic effects were then calculated and pooled across experiments. In order to directly compare model fits, separate meta-analyses were conducted using linear and log-transformed measures of cloze probability.

Results

For all dose-response meta-analyses, measures of between-study heterogeneity were low (Q’s < 12, p’s > .10), indicating that the magnitude of cloze probability effects was relatively consistent across experiments. Contextual predictability influenced all four reading measures, with shorter reading times and fewer first-pass fixations as predictability increased (first-fixation: −15.9ms; z = −5.47; gaze duration: −21.4ms, z = −5.76; total time: −33.0ms, z = −6.94; fixation rate: −6.4%, z = −3.61). More importantly, for all four reading time measures the effects of word probability were clearly linear, with no consistent logarithmic trends (see Figure 4). Measures of chi-squared model improvement were higher for all four linear models (χ² diffs: 2.7 – 9.2). Moreover, when quadratic terms were added to each model, this did not improve the fit of any linear model (all |z|’s < 0.8), but it did improve fit for a majority of logarithmic models (first-fixation: z = −2.76; gaze duration: z = −2.09; total time: z = −3.76; fixation rate: z = −1.68). This finding indicates that a logarithmic function could not adequately account for the observed relationship between cloze probability and reading times.²

Although this meta-analysis contained only half as many observations as Experiment 1, these two datasets produced remarkably similar results. Our findings suggest that the time needed for word identification is a linear function of a word’s prior probability and that this linear relationship is remarkably consistent across a variety of comprehension tasks.³

General Discussion

In the present studies, our goal was to determine the empirical function linking contextual predictability and measures of word processing difficulty during sentence comprehension. Data were obtained from a large self-paced reading study (Experiment 1), a cross-modal picture naming study (Experiment 2), and a meta-analysis of prior eye-tracking while reading experiments. The results from all three datasets were clear and consistent, revealing a robust linear relationship between lexical predictability and processing time. In all three studies, we demonstrated that linear measures of cloze probability provided a superior fit to the behavioral data, and we observed no evidence of a non-linear trend, despite the considerable statistical power of the current experiments. Furthermore, small differences in lexical probability below 1% (as estimated by corpus co-occurrence) had little to no effect on reading behavior.

When considered in isolation, it may be possible to explain some of these results by appealing to idiosyncratic processing strategies, tied to a particular experimental paradigm (self-paced reading, picture naming, eye-tracking). When considered together, however, we believe the consistent linear linking function points to a more general processing principle {proportional pre-activation) which may apply across multiple language processing domains.

In the following sections, we first consider the discrepancy between these findings and those reported by Smith and Levy (2013), followed by a more general discussion of the methodological implications of our findings. We then discuss empirical and theoretical challenges to surprisal-based accounts of sentence comprehension, and we sketch out the principles of an alternative hierarchical generative framework that can accommodate the present results.

Discrepancy with Smith & Levy, 2013

Our findings directly conflict with the results of Smith and Levy (2013), who reported a logarithmic effect of conditional trigram probability on word-by-word reading times in a corpus reading study. We believe that this discrepancy can be explained by considering two methodological issues in this study, which may have distorted the observed relationship between predictability and reading times.

Corpus-based analyses with uncontrolled linguistic stimuli

First, rather than directly manipulating lexical predictability, Smith and Levy (2013) took a corpus-based approach, examining associations between reading times and text characteristics in two naturalistic corpora. As discussed in the Introduction, there are several issues which limit the interpretability of studies conducted using uncontrolled naturalistic datasets. Particularly important is the role of uncontrolled lexical and contextual confounds (see Rayner, Pollatsek, Drieghe, Slattery & Reichle, 2007 for a discussion). For example, in natural texts, words that are more predictable are also more likely to be short, highly-frequent, function words that are often repeated. While Smith and Levy (2013) attempted to statistically control for some of these confounding variables (e.g. length, frequency, sentence position), the observed relationship between lexical predictability and reading times can still be substantially distorted in the presence of measurement error, unmeasured confounders, or high levels of collinearity (Friedman & Wall, 2005; Johnston, Jones & Manley, 2018; Westfall & Yarkoni, 2016). It is for these reasons that non-experimental data, like those reported in Smith and Levy (2013), are often considered insufficient for making causal empirical claims (Greenland, 1990; Greenland, Robins & Pearl, 1999; Rutter, 2007).

To better understand these limitations, it is worth considering a set of results reported by Kennedy and Pynte (2005), who performed a corpus-based analysis of the same Dundee eye-tracking corpus used by Smith and Levy (2013). In this study, Kennedy and Pynte reported a strong association between the frequency of an upcoming word (N+1) and reading times on the currently fixated word (N), which had important theoretical implications for models of reading comprehension (Rayner, 2009). In fact, however, in carefully controlled experimental designs, this N+1 frequency effect disappears completely, suggesting that this initial finding was likely a statistical artifact, driven by uncontrolled lexical confounds within and between word positions (see Angele, et al., 2015; Brothers, Hoversten & Traxler, 2017; Drieghe, 2011 for addition discussion). We believe that similar confounds may account for the discrepancies between Smith and Levy (2013) and the current experimental results (see Appendix B for a detailed discussion).

Limitations of corpus-based metrics of predictability

A second methodological issue in Smith and Levy (2013) was the use of trigram co-occurrence to estimate lexical probability. Compared to human-based probability metrics like cloze, model-based metrics can be obtained relatively easily and can provide estimates for very low probability continuations. Nonetheless, the weak relationship observed between corpus probabilities and cloze (Ong & Kliegl, 2011; Smith & Levy, 2011) suggests that these alternatives are often far from ideal, and that language models and skilled human readers are often sensitive to different aspects of the prior linguistic context. Indeed, in the present experiments, trigram probability had no significant influence on reading times, after controlling for the effects of cloze (for similar results, see Frisson, Rayner & Pickering, 2005; Smith & Levy, 2011).

Methodological Implications

Taken together, these findings have important methodological implications. First, the discrepancy between our findings and those of Smith and Levy (2013) suggest that researchers should be cautious before placing too much confidence in results of corpus-based analyses conducted on “naturalistic” datasets – particularly those that analyze neural or behavioral responses for every word in a text. While, the use of longer, more naturalistic language materials is often beneficial, corpus-based studies also carry costs in terms of interpretability and limited causal inference. Therefore, while corpus studies of reading behavior may serve as useful exploratory tools for investigating new phenomena, we agree with Rayner and colleagues (2007), that new theoretical “claims made from regression analysis techniques should not be accepted until confirmed via controlled experimental techniques.”

Second, we suggest that, whenever possible, researchers should avoid using conditional co-occurrence probability or other model-based measures as a proxy for lexical predictability. While the accuracy of some language models is likely to improve in the coming years, cloze probability still remains the recommended gold standard for assessing contextual predictability effects in sentence comprehension. Indeed, the use of cloze in large-scale behavioral and neuroimaging studies has only become more efficient with the advent of online crowd sourcing platforms (Carter, Foster, Muncy & Luke, 2019; Lowder, Choi, Ferreria & Henderson, 2018). In the end, we are inclined to agree with Ong and Kliegl (2011) who stated, “It is somewhat disappointing that CCP [conditional co-occurrence probability] is so unsuitable to act as a replacement of predictability.”

Finally, based on the present findings, we believe that researchers should avoid logtransforming measures of lexical probability. Whether they are analyzing sentence context effects, matching lexical probabilities across conditions, or building computational models of human reading behavior, linear cloze measures are likely to provide better empirical fits to human reading time data and a more appropriate index of the underlying cognitive mechanisms of interest. Note that this recommendation is specific to context-based measures of lexical predictability. Log transformations may still be appropriate for other predictors (e.g. word frequency) or dependent measures (e.g. reaction times).

Theoretical Implications

Beyond their methodological implications, these findings also help constrain theories of predictive processing in language comprehension, while generating a clear challenge for some accounts of sentence context effects, including surprisal theory.

Challenges to surprisal theory

As noted in the Introduction, many theories of language comprehension assume that readers probabilistically predict features of upcoming words (with debates regarding exactly how, and at what levels of linguistic representation, these predictions are generated). By assuming a logarithmic relationship, surprisal theory makes a number of assumptions regarding the nature and function of these anticipatory mechanisms. Below we reconsider some of these assumptions in detail, challenging them on both theoretical and empirical grounds.

Assumption 1: The pre-activation of very low probability words

In order to produce a logarithmic linking function between lexical predictability and reading times, surprisal theory assumes that readers use prior contexts to pre-activate information non-proportionally across “large portions of the lexicon” (Smith & Levy, 2013). Therefore, this account implies that comprehenders devote relatively fewer resources to pre-activate high probability continuations and relatively more resources to pre-activate a large number of low probability continuations.

A non-proportional pre-activation mechanism of this kind may be effective in a comprehension system with unlimited processing resources. However, this is far from the case in human comprehension. Anticipatory processing requires the transmission of information between cortical areas, and it therefore taps into a limited store of metabolic and computational resources (Attwell & Laughlin, 2001; Laughlin, de Ruyter van Steveninck, & Anderson, 1998; see Kuperberg & Jaeger, 2016, for discussion). Thus, from a bounded rational perspective (Griffiths, Lieder, & Goodman, 2015; Howes, Lewis, & Vera, 2009), the pre-activation of a large number of low probability words could be viewed as remarkably inefficient and irrational, given that most of these low-probability words are unlikely to ever appear in the bottom-up input. In an ideal comprehension system, these resources would instead be allocated to higher probability linguistic information that is more likely to facilitate upcoming comprehension. Indeed, for a given allotment of pre-activation, a logarithmic scheme will always produce less efficient reading, on average, compared to a linear, probability-matching strategy.

Note that this bounded rationality argument applies differently to context-based predictability effects, which must be updated continually as a sentence unfolds, and word frequency effects, which are based on stored distributional knowledge of a word’s overall likelihood. While both of these effects are often interpreted probabilistically (high frequency words are, on average, more probable than low frequency words), only contextually-based information must be actively accessed and maintained. Word frequency effects, in contrast, could arise from structural biases in the word recognition system itself (Seidenberg, 2005; Plaut, 1997), incurring no additional metabolic costs. This functional distinction may explain why the effects of word frequency follow a logarithmic function (Carpenter & Just, 1983; White, et al., 2018) while context-based predictability effects appear to be linear (for further evidence distinguishing the effects of word frequency and contextual predictability, see Staub, 2015).

Assumption 2: Surprisal as a single “causal bottleneck ”

A second (and related) assumption of surprisal theory is that the difficulty of processing a word and the difficulty of inferring a new message-level interpretation are functionally identical, representing a single processing mechanism. This assumption stems from the mathematical equivalence between the information theoretic measure lexical surprisal (−log P(word | context)) and Bayesian surprise (the shift in higher message-level probabilities after receiving new input; see Levy, 2008). The former could be viewed as the costs of ‘lexical access”, and the latter could be viewed as the difficult of “integrating” a word into a new, high-level representation of meaning. In both surprisal theory (Levy, 2008) and extensions of Bayesian Reader (Bicknell & Levy, 2010), these processes are subsumed into a single “causal bottleneck”, with all differences in sentence processing difficulty ultimately arising from word-by-word variability in surprisal.

Currently, it is difficult to reconcile this “single-mechanism” account with the finding that different types of contextual constraints can produce qualitative differences in reading behavior. For example, manipulations of lexical predictability are known to influence early behavioral and neural responses (e.g. word skipping, Rayner et al., 1996, 2006; and N400 amplitudes, Kutas & Hillyard, 1984), while implausible or strongly syntactically dispreferred “garden path” continuations typically influence later measures associated with re-analysis (e.g. regressive eye movements, Clifton, Staub & Rayner, 2007; Rayner, 2009; and P600 responses, Osterhout & Holcomb, 1992). Similarly, when controlling for cloze, words that violate strong lexical constraints (Federmeier et al., 2007; Frisson, Harvey & Staub, 2017), or that are highly “informative” for re-interpreting the prior context (Brothers, Greene & Kuperberg, 2020) do not produce additional difficulty during lexical access (as indexed by reading times or N400 amplitudes). Instead these manipulations trigger distinct neural responses which may be linked to the updating of discourse-level information in working memory (for a discussion, see Kuperberg, Brothers, Wlotko, 2020; Brothers, Wlotko, Warnke & Kuperberg, 2020). If all forms of sentence processing difficulty exerted their effects through a single processing mechanism (surprisal), then these sorts of qualitative distinctions would not occur.

Proportional pre-activation during language comprehension

What sort of language processing architecture could account for these qualitative differences in lexical/post-lexical processing difficulty while also predicting a linear relationship between lexical predictability and reading times? We suggest that this linear relationship can be explained within a metabolically constrained, hierarchical generative framework (Kuperberg & Jaeger, 2016; Kuperberg, Brothers, Wlotko, 2020). Within this framework, passing predictions from higher to lower cortical levels consumes a limited pool of metabolic resources. In order to optimally allocate these resources, comprehenders pre-activate lexical features of upcoming inputs in proportion to their estimated likelihood. When words are encountered in the bottom-up input, processing costs are reduced as a function of the “match” between the bottom-up input and top down pre-activation, with greater levels of pre-activation producing greater levels of behavioral facilitation. To the extent that accessing new, unpredicted lexico-semantic features increases the time required for word recognition, a proportional pre-activation scheme of this type should produce a linear reduction in processing time as lexical probability increases.⁴

In this proportional pre-activation account, just as in surprisal theory, successful lexical access is sometimes functionally equivalent to successful ‘integration’. This is because, by accessing and passing up the relevant set of lexically-linked semantic and syntactic features, alternative hypotheses at the highest level of the generative model will be effectively ‘explained away’, and the most likely interpretation of the input will be successfully inferred. Critically, however, there will be other times in which new inputs cannot be explained at higher levels of the generative model. In such cases, this temporary failure in interpretation may recruit additional comprehension mechanisms (e.g. regressive eye-movements) in order to re-analyze or re-interpret the bottom-up input.

Conclusion

In sum, while surprisal theory provides a simple and compelling account of lexical probability effects during reading, we believe the empirical predictions of this model are incompatible with the available experimental evidence. In two behavioral experiments and a series of meta-analyses we have provided clear evidence for a linear relationship between lexical processing difficulty and a word’s prior probability in context. Our findings highlight the limitations of corpus-based analyses in uncontrolled “naturalistic” datasets, while demonstrating the utility of large experimental samples for establishing precise quantitative relationships between text characteristics and online reading behavior. We have argued that these results support a proportional pre-activation account of linguistic context effects in which comprehenders generate probabilistic predictions about the features of upcoming words in proportion to their estimated probability of occurrence.

Highlights.

• The quantitative function linking word predictability and processing time is unclear

• We investigated this question in two behavioral experiments and a meta-analysis

• Across all three datasets this relationship was linear, not logarithmic

• These findings contradict the predictions of surprlsal theory

• Instead, they support a proportional pre-activation account

Appendix A: Meta-analysis Methods

For most studies included in this meta-analysis, gaze durations were calculated as the sum of all first-pass fixations on the critical word of interest. In Paul (unpublished dissertation) Experiments 3 and 4, measurements of Oms were also included in the calculation of gaze duration whenever the critical word was skipped. In order to use a consistent definition across studies, gaze duration values in these two experiments were divided by the fixation rate in each condition

In Tables 3 and 4, we calculated the relative fit of linear and logarithmic models for each dataset by comparing correlation coefficients between study-specific cloze values and mean reading times across conditions. For simplicity, the two medium cloze conditions in Paul (unpublished dissertation) were combined in these tables, but all four conditions were included in these calculations and in the dose-response meta-analyses reported in the main text. Fixation rates were calculated as (1 – skipping rate). Fixation rate measures were not included from experiments or conditions with invalid parafoveal previews (Sereno, et al., Exp.2; Paul, Exp. 4, invalid condition).

Table 3.

Average first-fixation and gaze-duration measures for studies included in the meta-analysis, with check marks indicating whether each dataset better supports a linear or logarithmic model

	First fixation (ms)			linear	log	Gaze duration (ms)			linear	log
	HC	MC	LC			HC	MC	LC
1) Rayner & Well 1996	239	240	250		✓	261	261	281		✓
2) Rayner, et al., 2005	261	265	282		✓	282	288	330		✓
3) Rayner et al., 2006 (younger)	248	263	267	✓		264	274	295		✓
4) Rayner et al., 2006 (older)	291	316	310	✓		314	357	356	✓
5) Sereno, et al., 2018 - Exp. 1	198	203	213	✓		207	210	226		✓
6) Sereno, et al., 2018 - Exp. 2	235	248	248	✓		269	280	284	✓
7) Paul - Exp. 3 (unpublished)	228	237	249	✓		245	263	269	✓
8) Paul - Exp. 4 (unpublished)	278	276	291		✓	316	328	332	✓
Combined Data	223.6	232.6	238.3	✓		235.0	244.6	254.7	✓

Table 4.

Average total reading time and fixation rates for studies included in the meta-analysis, with check marks indicating whether each dataset better supports a linear or logarithmic model

	Total Time (ms)			linear	log	Fixation Rate (%)			linear	log
	HC	MC	LC			HC	MC	LC
1) Rayner & Well 1996	294	301	360		✓	78	88	90	✓
2) Rayner, et al., 2005	408	469	503	✓		75	79	88		✓
3) Rayner et al., 2006 (younger)	305	312	359		✓	75	80	83	✓
4) Rayner et al., 2006 (older)	366	437	433	✓		71	77	76	✓
5) Sereno, et al., 2018 - Exp. 1	218	230	245	✓		72	73	76		✓
6) Sereno, et al., 2018 - Exp. 2	304	319	328	✓		-	-	-	-	-
7) Paul - Exp. 3 (unpublished)	235	267	273	✓		85	90	90	✓
8) Paul - Exp. 4 (unpublished)	341	345	367	✓		86	88	88	✓
Combined Data	246.2	262.6	277.0	✓		75.7	79.4	81.4	✓

Appendix B: Spurious effects in corpus-based studies

It has been suggested that corpus-based reading time studies sometimes produce spurious effects (Drieghe, 2011; Rayner et al., 2007), which later fail to replicate in carefully controlled experiments (Brothers, Hoversten & Traxler, 2017; Angele et al., 2015). A potential reason for these discrepancies is that many corpus-based studies either 1) fail to control for potential lexical or contextual confounds altogether, or 2) fail to explicitly model the reliability of control measures in their analyses (Christenfeld, Sloane, Carroll & Greenland, 2004).

For example, consider the hypothetical relationship between daily ice-cream sales and the number of swimming pool deaths (see Westfall and Yarkoni, 2016). Ideally, this spurious (non-causal) relationship would disappear after including the relevant confounding variable (outdoor temperature) in our statistical model. Unfortunately, if outdoor temperature is measured imprecisely, the “effect” of ice-cream sales may remain significant, due to residual confounding. Indeed, a number of simulation studies have shown that, in the presence of measurement error, regression analyses can often produce spurious or biased effects (Fewell, Smith & Sterne, 2007; Shear & Zumbo, 2013), particularly when sample sizes are large (Westfall & Yarkoni, 2016).

Although many psycholinguistic variables (e.g. word frequency) serve as imperfect proxy measures for latent psychological constructs of interest (e.g. subjective familiarity), the influence of measurement error is rarely considered in corpus-based reading time studies. To examine whether residual confounding may have influenced the results of Smith and Levy (2013), we calculated unigram frequencies and smoothed trigram probabilities from the British National Corpus for all 648 experimental sentences presented in Experiment 1 (7,696 words in total). We then examined the marginal effects of word-by-word trigram predictability, controlling for the effects of unigram word frequency. Critically, rather than examining reading times, we used a different dependent measure that was causally unrelated to contextual predictability. Specifically, we replaced reading times at each word with the average lexical decision latency for that word, obtained from a large publicly-available database (English Lexicon Project; Balota et al., 2007).

Obviously, it is impossible that these lexical decision times could be influenced by the contextual predictability of words in this specific set of experimental sentences. After all, words in the English Lexicon Project were presented with no prior context, to a completely different group of participants more than a decade ago. Nonetheless, in a by-items multiple regression, we observed significant effects of both log BNC unigram frequency (b = −0.033, t = −9.74, p < 0.001) and log BNC trigram predictability (b = −0.009, t = −3.66, p < 0.001) on lexical decision times.

This finding demonstrates that, even with the inclusion of statistical controls, corpus-based analyses can still produce significant spurious effects. A simple explanation is that in naturalistic texts, many contextual factors contain non-specific variance that is difficult (or even impossible) to eliminate using statistical controls. Consistent with this suggestion, in another set of multiple regression analyses, log-transformed trigram predictabilities were also strongly associated with measures of orthographic neighborhood size (unigram: t = 19.31, p < 0.001; trigram: t = 5.89, p < .001), age-of-acquisition (unigram: t = −28.06, p < 0.001; trigram: t = −8.97, p < .001), and log-frequency counts obtained from a separate corpus: SUBTLEX-US (unigram: t = 132.47, p < 0.001; trigram: t = 18.11, p < .001).

These analyses highlight a serious limitation of corpus-based reading time studies, which limits their ability to identify direct relationships between text-characteristics and reading behavior. In the prior literature, inferences from corpus-based studies have often relied on unstated assumptions about the reliability of statistical controls. In fact, by combining 1) measurement error, 2) high levels of predictor collinearity, and 3) large sample sizes, corpus-based studies often present a “worst-case scenario” for generating spurious and biased effects (see Shear & Zumbo, 2013; Westfall & Yarkoni, 2016 for discussion). In order to improve the reliability and replicability of corpus-based studies, researchers may need to adopt alternative statistical methods, such as structural equation modelling, which would allow them to directly incorporate measures of uncertainty.