Bayesian Inference of Ancestral Host–Parasite Interactions under a Phylogenetic Model of Host Repertoire Evolution

Abstract

Intimate ecological interactions, such as those between parasites and their hosts, may persist over long time spans, coupling the evolutionary histories of the lineages involved. Most methods that reconstruct the coevolutionary history of such interactions make the simplifying assumption that parasites have a single host. Many methods also focus on congruence between host and parasite phylogenies, using cospeciation as the null model. However, there is an increasing body of evidence suggesting that the host ranges of parasites are more complex: that host ranges often include more than one host and evolve via gains and losses of hosts rather than through cospeciation alone. Here, we develop a Bayesian approach for inferring coevolutionary history based on a model accommodating these complexities. Specifically, a parasite is assumed to have a host repertoire, which includes both potential hosts and one or more actual hosts. Over time, potential hosts can be added or lost, and potential hosts can develop into actual hosts or vice versa. Thus, host colonization is modeled as a two-step process that may potentially be influenced by host relatedness. We first explore the statistical behavior of our model by simulating evolution of host–parasite interactions under a range of parameter values. We then use our approach, implemented in the program RevBayes, to infer the coevolutionary history between 34 Nymphalini butterfly species and 25 angiosperm families. Our analysis suggests that host relatedness among angiosperm families influences how easily Nymphalini lineages gain new hosts. [Ancestral hosts; coevolution; herbivorous insects; probabilistic modeling.]

Extant ecological interactions, such as those between parasites and hosts, are often the result of a long history of coevolution between the involved lineages (Elton 1946; Klassen 1992). Specialization is predominant among parasites, including parasitic herbivorous insects, which complete all their larval development on an individual host (Thompson 1994; Forister et al. 2015). But host–parasite interactions are not static, they continuously evolve over time via gains and losses of hosts (Janz and Nylin 2008; Nylin et al. 2018). The colonization of new hosts and loss of old hosts not only shape the evolutionary trajectories of the interacting lineages but can also have large effects at ecological timescales (Nosil 2002; Calatayud et al. 2016). These effects are evident, for example, with emerging infectious diseases and zoonotic diseases (Acha and Szyfres 2003), which involve the colonization of new hosts within and among groups of domesticated species (Subbarao et al. 1998), wildlife (Fisher et al. 2009), and humans (Hahn et al. 2000). Unraveling the processes that underlie changes in species interactions is thus key to understanding evolutionary and ecological phenomena at various timescales, such as the emergence of infectious diseases, community assembly, and parasite diversification (Hoberg and Brooks 2015).

Many methods developed to study historical associations focus on congruence between host and parasite phylogenies (Brooks 1979; Huelsenbeck et al. 1997; de Vienne et al. 2013). Such methods largely fall into two main classes of cophylogenetic approaches: 1) topology- and distance-based methods, which estimate the congruence between two phylogenies (Legendre et al. 2002) and 2) event-based methods, which map the parasite phylogeny onto the host phylogeny using evolutionary events (Ronquist 2003). Typically, cospeciation is the null hypothesis in these methods, where host shifts are invoked only to explain deviations from cospeciation (de Vienne et al. 2013). Moreover, most of these methods do not allow ancestral parasites to be associated with more than one host lineage, thus failing to account for a potentially important driver of parasite diversification (Janz and Nylin 2008).

An alternative approach to studying coevolving host–parasite interactions is to perform ancestral state reconstructions of individual host taxa onto the parasite phylogeny and combine the ancestral host states a posteriori into inferred host ranges (e.g., Nylin et al., 2014). Even though this approach allows ancestral parasites to have multiple hosts, it assumes that the interactions between the parasite and each host evolve independently. This has a number of serious drawbacks. For instance, ancestral parasites may be inferred to have an unrealistically high number of hosts, or no host at all. Furthermore, the more narrowly circumscribed the host taxa are, the more likely it is that ancestral parasite lineages are reconstructed as having no hosts. In addition, the independence assumption causes the phylogenetic relationships among hosts to be ignored, meaning that the model assigns equal rates to all colonizations of new hosts regardless of how closely related the new host is to the current hosts being used by the parasite.

A desirable model of host usage should therefore allow parasites to have multiple hosts, while also allowing for among-host (or context-dependent) effects to influence ancestral host use estimates and gain and loss rates in whatever manner explains the biological data best. One possible solution is to restate the problem of host–parasite coevolution in terms of historical biogeography. For instance, the Dispersal-Extirpation-Cladogenesis model of Ree et al. (2005) allows species ranges to stochastically evolve as a set of discrete areas over time through area gain events (dispersal), area loss events (extirpation), and cladogenetic events (range inheritance patterns that reflect speciational models). Although these methods are designed for biogeographic inference, a similar approach is clearly suitable for more realistic modeling of host–parasite coevolution dynamics, where colonization and loss of hosts (instead of discrete areas) is modeled as a continuous-time Markov process (e.g., Hardy, 2017). In biogeography, the colonization of a new area or the disappearance from a previously occupied area is modeled as a binary trait: the species is either present or absent in the area. While this binary view might be adequate in biogeography, it may be too simplistic for use in the coevolution between hosts and parasites. For instance, it is known that butterflies can utilize a range of plants that they do not regularly feed on in the wild, and it has been suggested that these potential hosts have played an important role in the evolution of host use in butterflies, by increasing the variability in host use through time and across clades (Janz et al. 2016; Braga et al. 2018). This hypothesis can only be directly tested, however, if we explicitly model the evolution of host use as a two-step process, which cannot be done with the binary methods that are used today to study host–parasite coevolution or biogeography.

Here, we propose a model where a parasite is assumed to have a host repertoire, defined as the set of all potential and actual hosts for that parasite. In this model, the colonization of a new host involves two steps: first, the parasite gains the ability to use the new host (it becomes a potential host), and then starts actually using it in nature (it becomes an actual host). These two steps can be interpreted as the inclusion of the new host into the fundamental host repertoire of the parasite, and then into the realized host repertoire of the parasite—analogous to the concepts of fundamental and realized niches (Nylin et al. 2018; Larose et al. 2019) and to the compatibility and encounter filters of Combes (2001). Similarly, the complete loss of a host from a parasite’s realized repertoire involves two steps. First, it changes from an actual to a potential host, and then it is lost completely from the host repertoire. For example, if the geographic range of a host contracted to become allopatric with respect to a parasite’s geographic range, the host would remain as part of the fundamental repertoire until the parasite completely lost the ability to use the host, in which case the host would be lost from the repertoire. Even when in sympatry, the evolution of a new defense mechanism by the host may prevent the parasite from using that host. However, since host use is a complex and multidimensional trait, it is unlikely that a parasite loses all the machinery necessary to use a host in one single event, and it may well retain some ability to survive on the host. Thus, a complete gain or loss of a host lineage requires at least two events, and three host–parasite interaction states are necessary for such a two-step model: the host is used (actual host), the parasite has some ability to use the host but does not use it in nature (potential host), and the parasite cannot use the host (nonhost).

In this article, we develop a Bayesian approach to coevolutionary inference based on such a model of host repertoire evolution, inspired by the previous work on similar biogeographic inference problems by Landis et al. (2013). The basic two-state biogeographic model, when applied to coevolution, accommodates both multiple ancestral hosts and changes in host configurations over time that correspond to evolutionary changes in host usage. We extend this model to also include a two-step host colonization process, such that the fundamental host repertoire can persist over time and affect the evolution of the realized repertoire. We have implemented the model in RevBayes (Höhna et al. 2016), allowing us to simulate data as well as perform Bayesian Markov chain Monte Carlo (MCMC) inference under the model. This Bayesian framework allows one to estimate the joint distribution of host gain and loss rates, the effect (if any) of phylogenetic distances among hosts upon host gain rates, and the historical sequences of evolving host repertoires among the parasites. Using simulations, we explore the statistical behavior of our approach and demonstrate its empirical application with an analysis of the coevolution between Nymphalini butterflies and their angiosperm hosts.

Methods

Model Description

We are interested in modeling the evolution of ecological interactions between M extant parasite taxa and N host taxa, where each parasite uses one or more hosts. Rooted and time-calibrated phylogenetic trees describe the evolutionary relationships among the M parasite taxa and among the N host taxa. In this study, the trees are considered to be known without error. In principle, it would be straightforward for the model to accommodate phylogenetic uncertainty in the host or parasite trees but MCMC inference may prove challenging under such conditions.

Each parasite taxon has a host repertoire, which is represented by a vector of length N that contains the information about which hosts the given parasite uses. The interaction between the mth parasite and the nth host is denoted 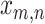. At any given time, each host taxon can assume one of three states with respect to a parasite lineage: 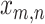is equal to 0 (nonhost), 1 (potential host), or 2 (actual host). Criteria for how to code nonhost, potential host, and actual host states will depend on the host–parasite system under study; below, we provide criteria for our Nymphalini data set that may act as guidelines. We allow all host repertoires in which the parasite has at least one actual host. Thus, the state space, , includes host repertoires for N hosts.

Here, we define the transition from state 0 to state 1 as the gain of the ability to use the host, and the transition from state 1 to state 2 as the time when the parasite actually starts to use the host in nature. If we assume that gains and losses of hosts occur according to a continuous-time Markov chain, the probability of a given coevolutionary history between a parasite clade and their hosts can be easily calculated (Ree and Smith 2008). This calculation is based on a matrix, Q, containing the instantaneous rates of change between all pairs of host repertoires, and thus describing the Markov chain. Based on the Q matrix, it is possible to calculate the transition probability of the observed host repertoires at the tips of the parasite tree by marginalizing over the infinite number of histories that could produce the observed host repertoires. Unfortunately, computing these transition probabilities becomes intractable as the number of host repertoire configurations, 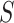, grows large. Modeling host repertoire evolution for host repertoire size requires an 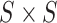rate matrix defined for 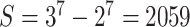, causing Q to be too large for efficient inference. In order to handle large host repertoires, we numerically integrate over possible histories along the parasite tree using data augmentation and MCMC rather than analytically computing the probabilities using matrix exponentiation. This data augmentation approach has been used to model sequence evolution for protein-coding genes (Robinson 2003) and historical biogeography (Landis et al. 2013; Quintero and Landis 2020), suggesting the framework may be useful to model host–parasite interactions as well. In this study, we assume that both daughter lineages identically inherit their host repertoires from their immediate ancestor at the time of cladogenesis. It is possible to extend the model to consider more complex speciation scenarios, such as daughter lineages dividing the host repertoire between them, but we leave the exploration of such model variants for future studies.

We define a model where the gain of a host (both 0 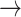1 and 1 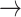2) depends on the phylogenetic distance between the available hosts and those currently used by a lineage. Figure 1 schematically illustrates the evolutionary dynamics of the model using 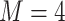parasite species and 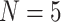host species, while assuming that host gain rates are independent (Fig. 1a,c) or dependent (Fig. 1b,d) of phylogenetic distances among hosts. To formalize these dynamics, let 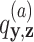be the rate of change from host repertoire y to repertoire z by changing the state of host 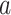. Also, let 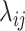be the rate at which an individual host changes from state 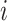to state 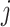, and 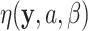be a phylogenetic-distance rate modifier. In practice, we constrain the host change rates such that 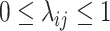, and estimate the parameter, 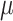, which we use to rescale all rates in 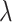. We refer to 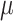as the maximum rate (or rate, for short) of host repertoire evolution, since 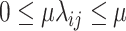. The phylogenetic-distance rate modifier function, 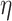, further rescales the rates of host gain to allow new hosts that are closely related to the parasite’s current hosts to be colonized at higher rates than distantly related hosts. Poulin (2010) reported a negative exponential relationship between host relatedness and parasite faunas they share, emulating the relationship between dispersal rates and the geographical distances among islands (MacArthur and Wilson 1967) by treating hosts as islands and host ancestry as space (Janzen 1968). Taking this as inspiration, we defined the phylogenetic-distance rate modifier function to impose a negative exponential relationship between the host gain rates and the phylogenetic distances of newly acquired hosts. We define the instantaneous rate of change as

and the phylogenetic-distance rate modifier function as

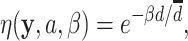(0.1)

where 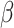controls the effect of 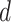, the average pairwise phylogenetic distance between the new host, 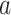, and the hosts currently occupied in y; and 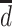is the average phylogenetic distance between all pairs of hosts. Pairwise phylogenetic distance is defined as the sum of branch lengths separating two leaf nodes. The difference between 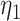and 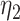is that for the first function, pairwise distances are calculated between the new host and all potential and actual hosts, while in the second only actual hosts are included. This allows for a model formulation where the effect of host distances on 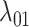and on 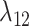are independent, while still allowing a formulation where they are equal. Regardless of its formulation, the effect of host distances depends on how it is scaled by 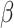. If , the gain rate of phylogenetically close hosts is higher than distant hosts. If 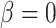, the gain rate of host 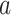is equal to the unmodified gain rate, 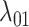or .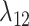

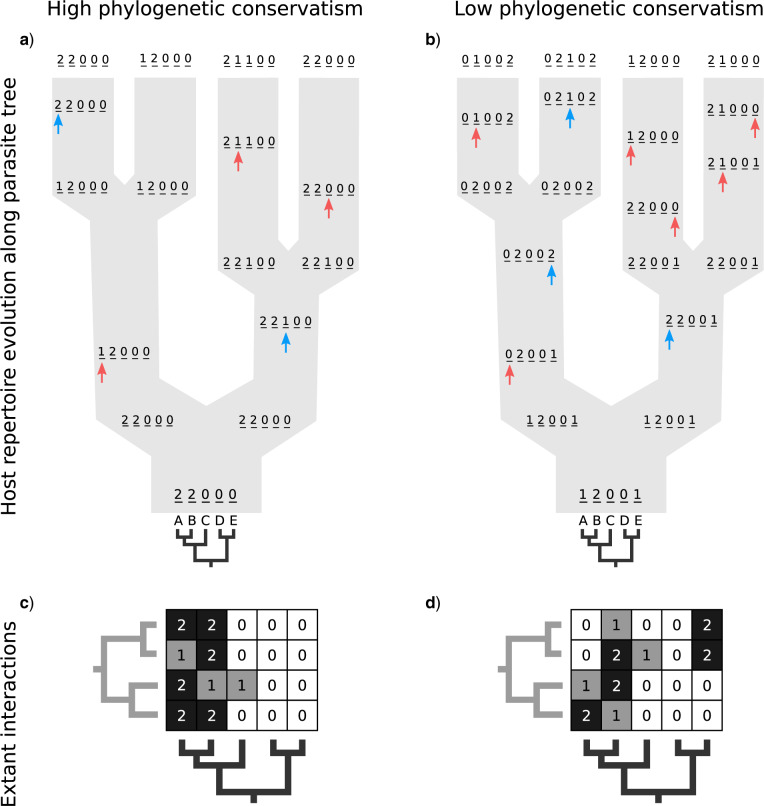
Figure 1.

Host repertoire evolution within a hypothetical parasite clade and resulting host-parasite interactions. Two examples of coevolutionary histories between four parasites and five hosts are shown to illustrate how the model works. Host repertoires evolve by gains (0 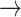1 and 1 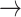2, blue arrows) and losses (1 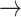0 and 2 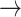1, red arrows). Coevolutionary histories in (a) and (b) produce the interactions in (c) and (d), respectively. In (c) and (d), each column represents one host, and each row represents the host repertoire of one parasite. High phylogenetic conservatism is produced when the rate of repertoire evolution, 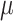, is low and the effect of the phylogenetic distance between hosts, 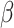, is high. Conversely, low phylogenetic conservatism is produced when 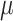is high and 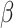is low.

The process of host repertoire evolution with different combinations of 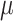and 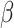will produce data sets with different levels of phylogenetic conservatism. When 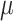is low, the host repertoire evolves slowly, resulting in similar repertoires between closely related butterflies, that is, high phylogenetic conservatism. We use phylogenetic distances between hosts as a proxy for differences in traits related to host use. Thus, 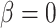is equivalent to fast trait evolution, where phylogenetic distance is not a good proxy for trait distance. On the other hand, when 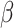is high, phylogenetic and trait distances match (high phylogenetic conservatism), hence closely related hosts are more similar then distantly related hosts.

We fit this model using the Bayesian data augmentation strategy described in Landis et al. (2013). The method estimates the joint posterior probability of model parameters, 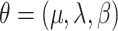, and data-augmented evolutionary histories, 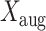, conditional on the observed host repertoire data, 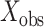, the rooted time-calibrated tree for the parasites, 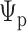, and rooted time-calibrated tree for the hosts, 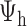, using MCMC. To sample values from the posterior, 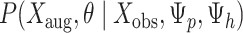, new parameter values for 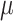, , 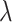and 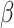are proposed using standard Metropolis–Hastings proposals for updating simple parameters (Hastings 1970). Analogously, our MCMC stochastically proposes and/or accepts new augmented host repertoire histories using the Metropolis–Hastings algorithm. Augmented histories are proposed using two types of MCMC moves: branch-specific moves and node-and-branch moves. Branch-specific moves propose a new augmented history by sampling a branch from the phylogeny uniformly at random, then proposing new histories for a subset of host characters using the rejection sampling method of Nielsen (2002) under the assumption that all host characters evolved under mutual independence (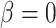); this assumption allows us to rapidly propose new augmented histories. Although augmented histories are proposed assuming host characters evolve independently, we compute the acceptance probability for the branch-specific move by considering the full-featured model probability that allows for nonindependent rates of character change when calculating the Metropolis–Hastings ratio. Thus, the augmented histories are sampled in proportion to their posterior probabilities under the full model. Node-and-branch moves involve sampling new host repertoire states for a node sampled uniformly at random within the parasite tree, along with the three branches incident to the node. Together, the branch-specific moves, the node-and-branch moves, and the parameter moves allow MCMC to estimate the posterior probability of combinations of host repertoire histories and evolutionary parameters. Further details are provided in Landis et al. (2013) and Quintero and Landis (2020).

Model Selection

When 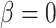, the phylogenetic-distance dependent model, becomes a mutual-independence model, , where the interaction between the parasite and each host evolves independently. These models are therefore nested (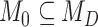), and we can compute Bayes factors for model 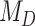over model 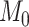using the Savage–Dickey ratio (Verdinelli and Wasserman 1995; Suchard et al. 2001; Marin et al. 2010), defined as

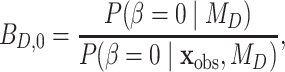(0.2)

where 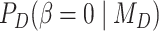is the prior probability and 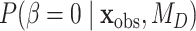is the posterior probability, both defined in terms of the phylogenetic-distance dependent model, , at the restriction point where and 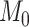are equivalent. In practice, we are careful to assign 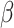a prior that is independent of other model parameters to satisfy the conditions of the “naïve” Savage–Dickey ratio (Heck 2019). While we could directly compute the prior probability of 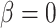, we approximated the posterior probability of 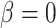using the kernel density estimator from the R package kdensity (Chen 2000) with a gamma function, which only takes positive values, with a bandwidth of 0.02. To interpret if and how Bayes factors favored the phylogenetic-distance dependent model, 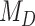, we followed the guidelines of Jeffreys (1961): model 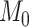is favored for Bayes factors with values less than 1, insubstantial support is awarded to model 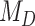for values between 1 and 3, substantial support for values between 3 and 10, strong support for values between 10 and 30, very strong support for values between 30 and 100, and decisive support for values greater than 100.

Data Analysis

Simulation study

We simulated 50 data sets for each of nine combinations of values for the rate of host repertoire evolution, 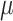(0.1, 0.5, and 1.0), and values of 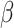(0, 1, and 4). These parameter combinations produce data sets with varying degrees of phylogenetic conservatism for both parasites and hosts: when 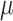is low, closely related butterflies have similar repertoires; and when 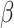is high, closely related hosts are used by the butterflies (Fig. 2). Each data set contained 34 insects and 25 hosts and was produced by simulating host repertoire evolution in the parasite tree used in the empirical study (see below). Host gain and loss rates were chosen to resemble the rates inferred from the empirical analysis. This simulation was designed to assess our statistical power to detect the effect of phylogenetic distance among hosts upon host gain rates given the size of our empirical data set and the type of variation we expected it to contain.

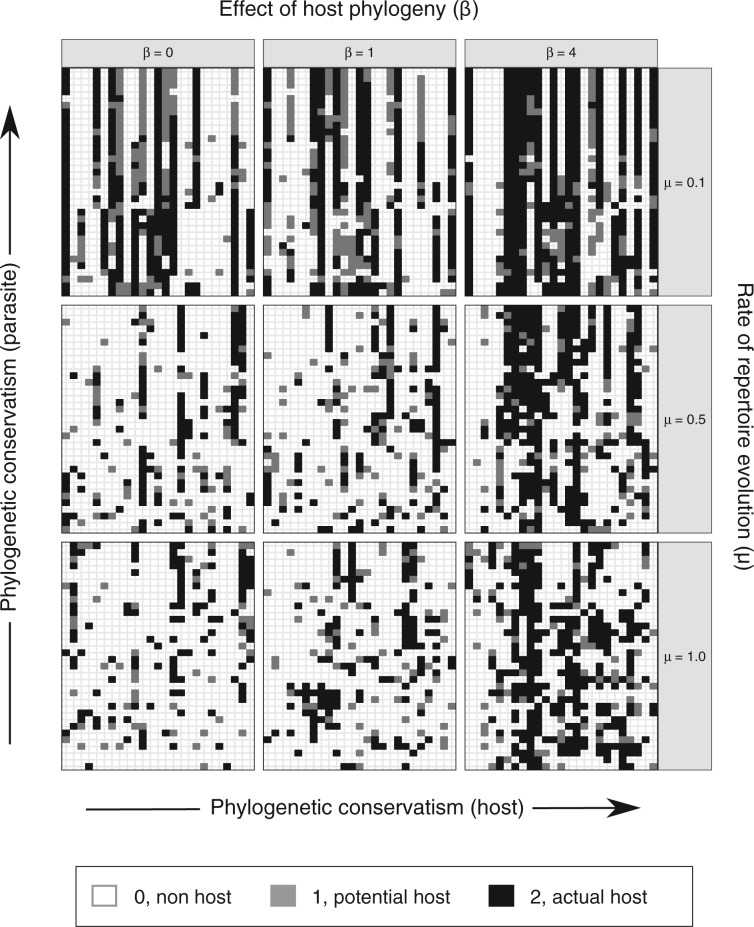
Figure 2.

Simulated data sets for nine parameter combinations. Interactions between Nymphalini butterflies and their host plants for one of 50 simulations with each parameter combination. In each of the nine data sets, each column represents one host in the repertoire and each row shows the host repertoire of one butterfly species. Rows and columns are ordered by butterfly and plant phylogeny, respectively. When phylogenetic conservatism in host–parasite interactions is low for both hosts and parasites, the interactions are more randomly spread (matrix at bottom-left corner). As phylogenetic conservatism among parasites increases, host repertoires (rows) become more similar (upper matrices). When there is phylogenetic conservatism among hosts, host repertoires include more closely related hosts (neighboring columns; matrices to the right).

We ran independent MCMC analyses for each set of 50 data sets, under the phylogenetic-distance dependent model. We then quantified how well the posterior probabilities of coevolutionary histories corresponded to the true history known from each simulation. Specifically, we first computed the posterior probability of interaction between each host and each internal node in the butterfly tree, for states 1 and 2 separately. Then, we compared the true coevolutionary history of each simulation to the corresponding posterior distribution of the sampled coevolutionary histories (observed probability). In order to estimate how much of the observed accuracy in ancestral state estimation should be expected by chance, we calculated, for each simulated coevolutionary history, the mean posterior probability for each true state across the 50 replicates with the same parameter combination (probability expected by chance). This shows what is the expected posterior probability for each true ancestral state when the data set used for inference has similar properties to the true data set, but not the same tip states.

Empirical study

In order to validate our method, we compiled data from the literature for butterflies from the tribe Nymphalini (Nymphalidae) and their host plants (see Supplementary Material available on Dryad at https://doi.org/10.5061/dryad.x95x69pdw for reference list). We chose this butterfly clade because we expect that a large fraction of the real potential hosts are known, as there have been systematic experimental studies of larval feeding ability. The data set included 34 butterflies species and plants from 16 angiosperm families (Supplementary Figs. S1 and S2 available on Dryad). For each butterfly species, host plants commonly used in nature were coded as “actual hosts” and plants never used were coded as “nonhosts.” Plants that are not commonly used in nature, but for which there is strong evidence (field observation or experiment) that the larvae can feed upon them, were coded as “potential hosts.”

Because we lack the information on potential hosts for most host–parasite systems (i.e., hosts are usually only classified as hosts or nonhosts), we tested whether our model is able to recover the same parameter estimates and coevolutionary histories when all the potential hosts are recoded as nonhosts. For that, we ran the same analysis as for the full data set, but replaced all the 1s from the empirical data set with 0s. Then, we compared the posterior probabilities inferred from the full data set and the recoded data set. To assess the similarities between the coevolutionary histories inferred using the different data sets, we calculated summary statistics for the absolute difference in probability of each interaction between hosts and internal nodes in the butterfly tree.

For both the simulation and empirical studies, we used the phylogenetic relationships between butterfly species in the Nymphalini tribe as proposed by Chazot et al. (2020, Supplementary Fig. S3 available on Dryad) and the phylogenetic relationships between angiosperm families proposed by Magallón et al. (2015). Although our framework allows the inclusion of a large number of hosts in the same analysis, computational time increases significantly with the size of the host repertoire. We therefore chose to include 25 plant families, which allows the inclusion of all the 16 host lineages used by any of the butterflies. For biologists interested in applying our method to their data sets, we found our data set of 34 parasite species and 25 host lineages took approximately 1 week to analyze, while a larger data set comprised of 66 parasite species and 50 host lineages took about 3 weeks to complete the same number of generations.

To ensure the inclusion of all plant lineages that might have been used as hosts in the past, we pruned the angiosperm phylogenetic tree so that all 16 families in the data set were included, and the remaining branches were collapsed to more ancestral nodes until only 25 tips were left. We then pruned all the branches leading up to the tips to the time of origin of the butterfly clade (approx. 22 Ma), and this pruned tree was then used to calculate phylogenetic distances between hosts. To simplify the analysis, we hold the phylogenetic distances between plant families constant through geological time, even though the distances would be expected to increase as evolution proceeds towards the recent. After preliminary analyses, however, we found that time-calibrated distances between host lineages (i.e., phylogenetic distance calculated as described above) have a weak effect on host gains. On the other hand, “cladogenetic” distances (calculated as the phylogenetic distance between host lineages after setting each branch length equal to 1) had a much stronger effect. Thus, we present the results using cladogenetic distances in the main paper and results using the untransformed “anagenetic” distances in the Supplementary Figs. S4–S6 available on Dryad).

We summarized inferred coevolutionary histories in two ways. First, we calculated the posterior probability for fundamental and realized host repertoires at internal nodes of the Nymphalini phylogeny based on the frequency with which states 1 and 2 were sampled for each host during MCMC. Second, in order to facilitate the visualization of ancestral state reconstructions, we reduced the dimensionality of the host repertoire by assigning hosts to modules based on extant butterfly–plant interactions (Supplementary Fig. S2 available on Dryad). Modules are groups of plants and butterflies that interact more with each other than with other taxa, thus host plants are assigned to the same module when they are used by the same butterflies. To identify the modules, we used a simulated annealing algorithm that maximizes the index of modularity. Specifically, we used Newman and Girvan’s metric (Newman and Girvan 2004) modified for bipartite networks (Barber 2007) as implemented in the software MODULAR (Marquitti et al. 2014).

Software configuration

All analyses were performed in RevBayes (Höhna et al. 2016). For the simulated data, we ran two independent MCMC analyses for 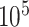cycles, sampling parameters and node histories every 50 cycles, and discarding the first 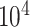cycles as burnin. For the empirical data, we ran three independent MCMC analyses, each set to run for 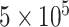cycles, sampling every 50 cycles, and discarding the first 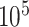cycles as burnin. To verify that MCMC analyses converged to the same posterior distribution, we applied the Gelman diagnostic (Gelman and Rubin 1992) provided through the R package coda (Plummer et al. 2006), and used a threshold of 1.1. For both simulated and empirical data sets, we used the following priors: 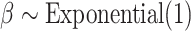, , 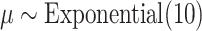and 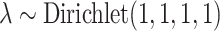. A RevBayes tutorial for the empirical analysis is available at https://revbayes.github.io/tutorials/host_rep/host_rep.html. Analysis scripts and data files are available in the Supplementary material available on Dryad.

Results

Simulation Study

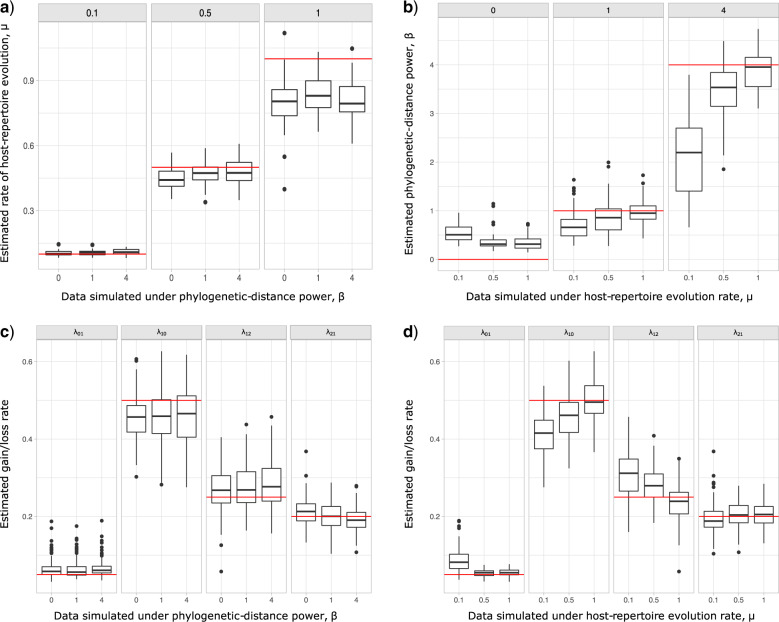
Posterior distributions of parameter values for the 9100 MCMC analyses are shown in Figure 3. Overall, the model was able to accurately recover the true simulation parameters. When estimating 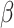, accuracy was lowest when 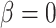, possibly because the density of the prior distribution of 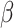is highest close to zero. Estimating 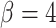was most difficult when 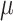was small, that is, when 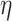produces the smallest host gain rate multipliers. Also, accuracy was lower when estimating the highest rate of host repertoire evolution, 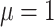, which is likely due to higher rates of evolution generating more uncertainty in ancestral state estimates.

Figure 3.

Posterior probabilities of parameters in the simulation study. a) and b) Faceted by true parameter values of 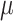and 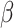, respectively. Fifty data sets were simulated for each combination of 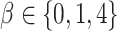and 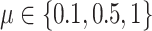, while , , 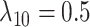, 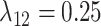and 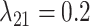were held constant. Boxplots show the distribution of mean estimated parameter values for each of the 50 data sets for each parameter combination. Medians are represented by thick black lines, boxes are delimited by first and third quartiles, black vertical lines extend at most 1.5 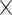IQR (i.e., the interquartile range), and dots show outliers. Red horizontal lines mark the true parameter value used in the simulations.

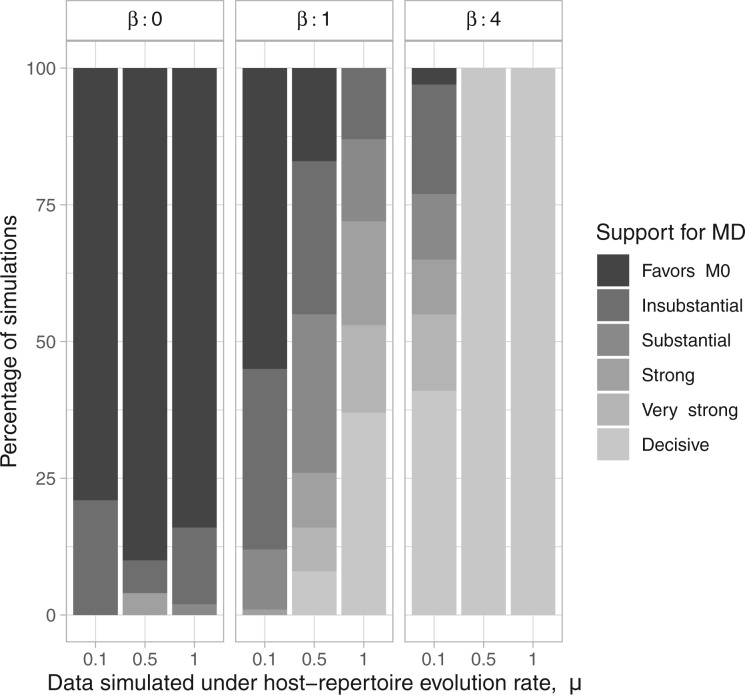
We performed model selection based on Bayes factors (Fig. 4). Considering that the prior distribution is 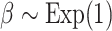, a high density for under 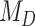is necessary to result in a Bayes factor 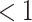and thus selection of 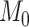. For simulations with 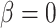, the correct model, 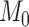, was selected in the majority of simulations. When 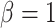, Bayes factors correctly selected 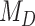in many cases, but strong support for 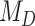was only achieved in simulations with high 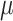. Finally, the large majority of simulations with 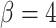supported .

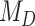Figure 4.

Distribution of Bayes factors for the simulation study. Each column corresponds to the strength of support per 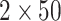MCMC analyses.

Figure 5 shows that accuracy in ancestral state estimation was affected by both 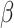and 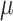, increasing with phylogenetic conservatism on both the butterfly (low 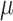) and the plant phylogenies (high 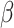). Overall, posterior probability was higher on the estimation of actual hosts (State 2) than potential hosts (State 1), but for both, the observed accuracy was higher than the accuracy expected by chance across all parameter combinations.

Figure 5.

Posterior probability of true ancestral states in the simulation study. Each boxplot shows the distribution of average posterior probability for the true state across all interactions between hosts and internal nodes in the butterfly tree for each batch of 50 simulated data sets. Each panel shows the observed and expected probabilities for States 1 and 2, for each combination of 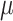and .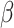

Empirical Study

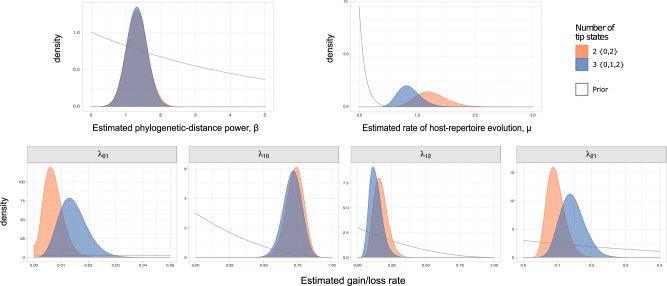
The estimated mean rate of host repertoire evolution for Nymphalini was 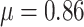, the mean phylogenetic-distance parameter value was 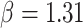, and the mean gain/loss rates were 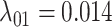, , 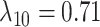, 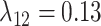and 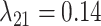(Fig. 6, blue). Our method recovered similar parameter estimates for the empirical data set when omitting the intermediate state at the tips—that is, recoding all potential hosts (State 1) as nonhosts (State 0): 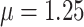, , 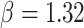, , 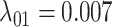, 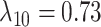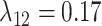and 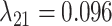(Fig. 6, orange). 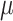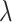Although the and estimates differ somewhat between the analyses, both analyses produced similar mean total numbers of events per unit time (1.35 and 1.17 events/Myr for the observed and recoded data sets, respectively). We note, however, that the rates into State 1 were underestimated, and the rates out of State 1 were overestimated when 1s were removed from the data set. For both the full data set and the recoded data set, Bayes factors (BF) selected the dependence model, 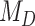(BF 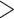100). For comparison, when using the time-calibrated tree for host plants, the independence model, 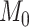was selected (BF 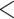1) for both full and recoded data sets.

Figure 6.

Marginal posterior densities for parameters in the Nymphalini-Angiosperms study for both the full data set (three states at tips) and the data set omitting the intermediate state (two states at tips). Gray lines correspond to the priors 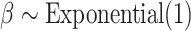, , 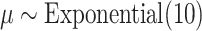and 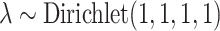, where elements of 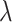follow the marginal distribution, .

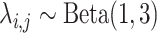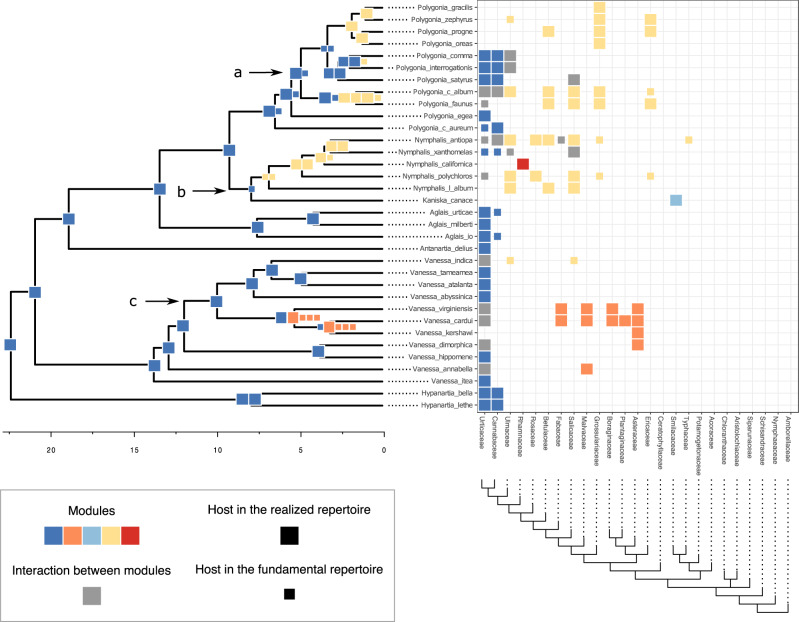
Finally, we reconstructed the fundamental and realized host repertoires at internal nodes of the Nymphalini phylogeny based on the sampled histories during MCMC. Coevolutionary histories inferred using the full and recoded data sets were very similar, as well as when using the branch-length-transformed (cladogenetic) host phylogeny and when using the time-calibrated (anagenetic) host phylogeny to measure phylogenetic distance. Thus, we only display the ancestral states inferred from the three-state data set and the cladogenetic host phylogeny (all branch lengths = 1) in the results (Fig. 7). Supplementary Figure S5 available on Dryad shows the posterior distribution of ancestral states for all the four model variants investigated in this study. To facilitate visualization of the ancestral state reconstruction, we grouped the 16 parasitized host families into five modules, as identified by the simulated annealing algorithm (Supplementary Fig. S2 available on Dryad). Eleven families (representing three modules) were inferred to be used by ancestral Nymphalini species with probability 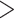0.9.

Figure 7.

Evolution of butterfly–plant interactions through time. Ancestral state estimates (left) of host repertoire across the Nymphalini phylogeny are shown for interactions with more than 90% posterior probability. The x-axis under shows time before present in millions of years. Extant species interactions (right) between Nymphalini and their host plants are presented as a raster, where each square represents one interaction between a butterfly species and a host family. Colors represent different modules, that is, groups of plants that are often hosts to the same butterflies at present time. Square size was used to differentiate between actual and potential hosts. Arrows indicate nodes shown in Figure 8.

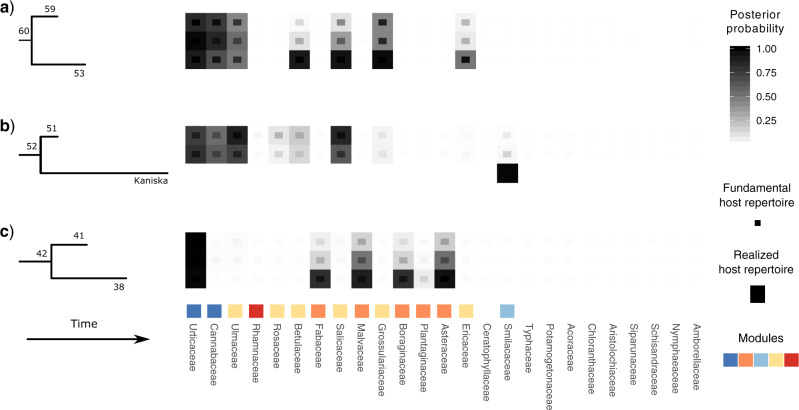
We found strong support for the interaction between the ancestor of all Nymphalini butterflies and Urticaceae hosts. All other host families have been colonized in the last 10 Myr, after the divergence of the two largest clades within Nymphalini, Vanessa, and Nymphalis + Polygonia. Most species within Vanessa, both extant and ancestral, are specialists on Urticaceae. Vanessa virginiensis and Vanessa cardui are the only extant species that use more than two host families, and these hosts have likely been colonized by their most recent common ancestor (node 38 in Fig. 8). On the other hand, the variation in host use in the Nymphalis + Polygonia clade seems to be the result of host colonizations by multiple species along the diversification of the clade. For example, in Figure 8 we can see the colonization of new hosts by the ancestor of Polygonia c-album and Polygonia faunus (node 53) as well as strong specialization on a new host by Kaniska canace and a less pronounced shift in host preference by its sister species (node 51).

Figure 8.

Host repertoires at selected nodes of the Nymphalini tree (arrows in Fig. 7). Numbers indicate the node index (compatible with Supplementary Fig. S3 available on Dryad). For the only terminal taxa depicted, Kaniska canace, the observed host repertoire is shown. For all other repertoires, the posterior probabilities for hosts being in the fundamental (States 1 or 2) and the realized (State 2) host repertoire are shown. Colors indicate module affiliation of each host family and are consistent with Figure 7.

Discussion

The method we develop here to infer the evolutionary history of ecological interactions has many advantages over previous approaches. First, it is based on stochastic models and on established principles of statistical inference, which means that it provides a robust framework for characterizing the evolutionary processes that shape ecological interaction networks and for selecting among alternative coevolutionary models. Second, our model introduces the concept of a host repertoire as the evolving trait, which we think is an important step forward. Besides accounting for the possibility of parasites having more than one host over time scales of macroevolutionary significance, we can now directly infer the influence of host relatedness on the process of gaining new hosts. Third, the stochastic model of host–parasite coevolution that we introduce here is, to our knowledge, the first that explicitly accounts for evolution of the fundamental host repertoire. By recognizing the fact that a parasite may have potential hosts in addition to its actual hosts, and that the set of potential hosts may persist over time, the dynamic of the model changes. What would otherwise have appeared as remarkable repeated patterns of colonization of the same host lineages can now be explained as the effect of frequent transitions between potential and actual hosts in an otherwise conserved host repertoire.

Our model can readily be extended in many interesting ways. The version we present here accounts for the effect of host phylogeny by allowing the rate of host gain to depend on host relatedness. For simplicity, we assumed that the number of available hosts and host relatedness remain constant over geological time. This would be appropriate for a group of parasites that radiated after the relevant host lineages had been formed, which is arguably the case for the empirical example we chose. However, it should be relatively straightforward to extend our framework to account for more complex dependencies on host phylogeny. For instance, the host configurations could be modeled as changing over time, reflecting host cladogenesis.

Another interesting direction for future research would be to modify the particular ways in which hosts and parasites coevolve. We note, for example, that Figure 7 shows that host repertoires of Vanessa species overlap very little with the host repertoires of Nymphalis + Polygonia species, but it is not immediately clear what drives this pattern. One could design a model that allows the rates of host gain and loss to be influenced by evolving host traits—like secondary metabolites, growth form, or phenology, to mention a few examples relevant for insect–host plant interactions—in addition to relatedness among hosts. Or, one might extend the model to allow closely related parasite lineages to competitively exclude one another from host usage, similar to how competing lineages might exclude one another from geographical regions (Quintero and Landis 2020). Finally, one might introduce a biogeographical component to the coevolutionary process, requiring parasites to be in sympatry with their actual hosts, while allowing parasites to be in sympatry or allopatry with their potential hosts. Statistically comparing such model variants will help illuminate drivers of host–parasite coevolution.

A potential concern with our approach is that already the basic version of the model is fairly parameter-rich. Given the type and amount of data that we can likely collect on host–parasite interaction, is there enough statistical power to select among the models of interest? And is it possible to infer the model parameters of interest with a reasonable degree of accuracy?

Overall, our results are encouraging in this respect. The simulations indicate that it is possible to infer the true parameter values of the basic model regardless of the level of phylogenetic conservatism in both parasites and hosts (Fig. 3). We were also able to distinguish between models with or without host relatedness effects using Bayes factors (Fig. 4). Further studies will have to show to what extent the sensitivity of the model test can be increased by selecting appropriate priors and improving the sampling of parameter space close to the boundary condition satisfying the restricted model. One option is to relax the assumption that 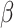is nonnegative, which would simplify the sampling of values close to 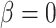. It will also be important to explore how data set sizes and tree shapes, for both hosts and parasites, influence our ability to distinguish the models when the effect of host phylogeny is small.

Importantly, the empirical analysis indicates that the method is able to model the evolution of fundamental and realized host repertoires even when the information about potential hosts is lacking. This significantly increases the applicability of our method, as information about fundamental host repertoires is missing for most host–parasite systems. Potential host data is difficult to collect, as it requires experimental testing of a large number of potential host–parasite pairs. A possible improvement of our method, which we did not explore here, would be to model uncertainty in the observations of nonhosts when data on potential hosts are missing. That is, if we had no information about a host species being used by a particular parasite, we would translate that to a certain probability 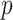of the species actually being a nonhost, and a complementary probability 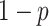of it being a potential host (Kuhner and McGill 2014). Modeling this observational uncertainty could help reduce the bias in parameter estimates that we observed when data on potential hosts were missing and all 0-valued states in the data set were inappropriately treated as true nonhosts. This extension would also allow us to make predictions about host use abilities in extant parasites that could then inform experiments that aim to characterize fundamental host repertoires.

We demonstrated the empirical application of our approach with a Bayesian inference of the coevolutionary history between 34 Nymphalini butterflies and 25 angiosperm families. We estimated the rate of host repertoire evolution along each branch of the butterfly tree as being 1.35 events per million years. Bayes factors favored the dependence model, 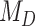, where the probability of gaining a given hosts is affected by the phylogenetic distance between hosts, thus highlighting the importance of accounting for shared evolutionary history among host lineages. It is also interesting to note that this effect was not large enough to support 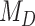when phylogenetic distances between host plants were proportional to divergence time (anagenetic distances). As expected, 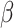tends to be lower and harder to infer in star-like host phylogenies, whose divergence times are clustered near its root node. Perhaps of greater interest, because the estimates of 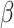were lower when estimated using anagenetic, rather than the cladogenetic, host distances, the result suggests those traits that determine how easily a plant family is colonized by Nymphalini originated close in time to the origins of the plant families themselves.

Estimates of gain and loss rates were not symmetric, and the rates also varied between states. According to our results, gain of the ability to use a host, 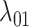, is very rare (0.8–2% of overall rate), whereas loss is common (59–83% of overall rate). On the other hand, transition rates between states 1 and 2 were more symmetric ( 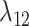between 5% and 22%; 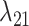between 8% and 21% of overall rate). These rate estimates support the idea that the use of the same host lineage by multiple, phylogenetically widespread butterfly lineages is more likely explained by recolonization of hosts that have been used in the past (recurrence homoplasy), that is, by transitions between actual and potential hosts, rather than by completely independent colonizations of the same host (Janz et al. 2001). Note that alternative scenarios that have been proposed in the literature to explain the evolution of Nymphalini host plant preferences, for instance by involving narrow ancestral host plant ranges and repeated independent colonization events (Hardy and Otto, 2014, e.g.), are also allowed by our model, but they are inferred to be much less likely than the conservative host repertoire scenario. Yet, because the potential host state is exited at the highest rate, the rate estimates also suggest that parasites do not retain their potential host relationships for prolonged periods of time. The moderate rates of transitions between potential and actual host states and the high departure rate from the potential host state together help explain why phylogenetic “pulses” of recurrent host acquisition manifest in some lineages but not others.

For example, the use of Grossulariaceae by two nonsister clades within Polygonia is best explained by a scenario where Grossulariaceae was a potential host for the ancestral species (node 60 in Fig. 8) and was subsequently gained as an actual host twice (at nodes 53 and 58, Fig. S5 available on Dryad). The ability to use Salicaceae host plants seems to be even older. Salicaceae was likely a potential host for the ancestor of Nymphalis + Polygonia and later became an actual host in three different parts of the clade. If potential hosts were not explicitly modeled here, these transitions would look like three independent colonizations of a plant group that is very distant from the ancestral host (Salicaceae and Urticaceae diverged about 90 Ma). Instead, we could show that what might appear as big and sudden host shifts are in fact the result of retention of ancestral host use abilities.

Understanding how ecological interactions change is crucial if we want to predict both short- and long-term consequences of global mixing of biota (Hoberg and Brooks 2015). Host–parasite interactions are of particular interest given the risk of emerging diseases, which can affect human populations directly and indirectly through their effects on crop species and wildlife (Brooks et al. 2014). Our method was designed to quantify changes in host–parasite interactions by modeling the process of gaining and losing hosts, thus allowing us to make predictions based on host–parasite history. We hope our approach will not only generate deeper insights into the evolutionary dynamics of host–parasite interactions but also help humankind mitigate some of the risks incurred by current environmental change.

Supplementary Material

Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.x95x69pdw.

Funding

The Swedish Research Council supported [2015-04218 to S.N.] and [2014-05901 to F.R.]; The Donnelley Fellowship through the Yale Institute of Biospheric Studies, with early work in this study supported by the NSF Postdoctoral Fellowship in Biology [DBI-1612153] to M.J.L.