Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 15;12(41):46212–46219. doi: 10.1021/acsami.0c13960

High Thermoelectric Performance in Two-Dimensional Janus Monolayer Material WS-X (X = Se and Te)

Abhishek Patel †, Deobrat Singh ‡,*, Yogesh Sonvane §, P B Thakor †,*, Rajeev Ahuja ‡,∥,*
PMCID: PMC7584335  PMID: 32931245

Abstract

graphic file with name am0c13960_0006.jpg

In the present work, Janus monolayers WSSe and WSTe are investigated by combining first-principles calculations and semiclassical Boltzmann transport theory. Janus WSSe and WSTe monolayers show a direct band gap of 1.72 and 1.84 eV at K-points, respectively. These layered materials have an extraordinary Seebeck coefficient and electrical conductivity. This combination of high Seebeck coefficient and high electrical conductivity leads to a significantly large power factor. In addition, the lattice thermal conductivity in the Janus monolayer is found to be relatively very low as compared to the WS2 monolayer. This leads to a high figure of merit (ZT) value of 2.56 at higher temperatures for the Janus WSTe monolayer. We propose that the Janus WSTe monolayer could be used as a potential thermoelectric material due to its high thermoelectric performance. The result suggests that the Janus monolayer is a better candidate for excellent thermoelectric conversion.

Keywords: 2D Janus monolayer, electronic properties, thermoelectric properties, lattice-thermal conductivity, Boltzmann transport equation

Introduction

The world’s energy demand is rapidly increasing due to factors like considerable growth in population, industrialization, development in technology, etc. Until recently, these energy needs were being fulfilled with fossil fuels and other nonrenewable resources;1 however, the massive consumption of such resources led to the unavailability of them. The burning process generates energy with waste heat, exhaust gases, pollution, and other harmful effects on the environment.2,3 The renewable resources have a small contribution in fulfilling these energy needs. The total replacement of fossil fuels is not possible at present.4 Hence, improved energy efficiency and reduced energy demand are the expected solutions to this problem.5 Thermoelectric materials have the ability to convert electricity from heat by the Seebeck effect, and they are also able to produce a cooling effect by the Peltier effect.6 Light-weight, cost-effective, and efficient thermoelectric materials can help in generating electric energy from waste heat. Development and identification of such materials with high thermoelectric conversion performance have remained a big challenge since the discovery of the thermoelectric concept.7,8 The ability of thermoelectric conversion of thermoelectric material is summarized by the thermoelectric figure of merit (ZT), which is expressed as ZT = S2σT/κ, where S, σ, and κ represent the Seebeck coefficient, electrical conductivity, and thermal conductivity, respectively.9−11 The thermal conductivity of the material is expressed as κ = κl + κe. The thermal conductivity (k) involves lattice thermal conductivity (κl) due to lattice vibrations and electronic contributions (κe) due to electronic motion.10,11 The best thermoelectric performance measured until now has ZT values ranging from 2.5 to 2.8.11−14 The new material (a thin layer of iron, vanadium, tungsten, and aluminum applied to a silicon crystal) developed by the scientists of TU Wien has shown that the high efficiency ZT value lies between 5 and 6.15

The new derivatives of two-dimensional (2D) materials, Janus 2D materials, have attracted considerable research attention due to their distinct properties. Their properties are quite different compared to the traditional 2D materials.16 The Janus 2D material possesses unique properties due to its mirror asymmetry in the structure.16,17 The Janus transition metal dichalcogenides (TMDs) belong to an important class of materials due to their structure, stability, electronic properties, and other properties.16 In 2013, the dynamical stability of MoSSe, WSSe, WSTe, and WSeTe was proved through a theoretical investigation by Cheng et al.18 Various methods, such as micromechanical exfoliation, liquid exfoliation, chemical vapor deposition (CVD), and hydrothermal synthesis, are used for the experimental synthesis of 2D materials. Janus 2D materials do not exist in nature. However, the Janus MoSSe monolayer from MoS2 was first successfully synthesized through CVD by Li and co-workers in 2017.16 The Janus monolayer MoSSe was also experimentally synthesized from MoSe2 in 2017.19 Among these previously reported materials, MoSSe provides a foundation for theoretical and experimental investigations on other Janus type materials.17 Recent theoretical studies suggest that the Janus monolayer has promising applications in various fields such as gas sensing,20 optoelectronics,21 photocatalysts,22,23 spintronics, and valleytronics.18,24,25 In addition, Gu and Yang found that the lattice thermal conductivity can be significantly reduced by the minimization of the frequency gap.26 It can also be reduced by changing its stoichiometry.27,28 Low lattice thermal conductivity can effectively increase the ZT.

Motivated by these exciting properties of the Janus monolayer, we have systematically investigated the structural properties, electronic properties, lattice thermal conductivity, and thermoelectric behavior of the Janus 2D material WS-X (where X = Se and Te). The structure of WSSe and WSTe can be prepared by the replacement of one S atom with Se and Te in the molecule of WS2.27,29,30. We have also reported a comparative study with its traditional disulfide form WS2. To effectively simulate their thermoelectric behavior, the Seebeck coefficient, electric conductivity, thermal conductivity, and ZT have been determined as a function of temperature. The results of this study show the enhancement in thermoelectric performance from WS2 toward WSSe and WSTe.

Computational Methods

In this work, first-principles simulations are performed using Vienna Ab initio Simulation Package (VASP) software.31,32 The density-functional theory calculations are performed by the generalized gradient approximation method with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation (XC) functional.33 For the monolayer WS-X system (X = S, Se, and Te), a projected augmented wave (PAW) with a default energy of 500 eV was used to describe the core and valence electron interactions.34 We also have the Heyd–Scuseria–Ernzerhof (HSE06) functional to obtain accurate electronic properties. For hybrid functional HSE06, we have used the exchange-correlation energy functional HSE06 with a mixing parameter (α) of 25% and a screening parameter of 0.2 Å–1. The thick vacuum of order 25 Å is inserted to prevent interactions between periodic layers along the normal direction (z-direction).35 The Monkhorst pack meshes of (19 × 19 × 1) are used for the k-point sampling.36 For these materials, the optimized structures are achieved by the conjugate gradient (CG) method within a converge criterion of 10–3 eV/Å for Hellmann–Feynman forces and 10–8 eV/cell for energy. In order to check dynamic stability, the phonon dispersions for these materials are calculated through the density functional perturbation theory (DPFT) method by creating supercells of 5 × 5 × 1 and using a k-point mesh of 3 × 3 × 1.37 Lattice thermal conductivity of these materials are determined by a relaxation time approximation (RTA) method through a Phono3py code.38 The second-order force constants (for harmonic phonons) for the 4 × 4 × 1 sized supercells of these materials and the third-order force (an-harmonic force constants) for the 3 × 3 × 1 sized supercells of these materials are computed by the finite-displacement method using a k-point mesh of for the 3 × 3 × 1 sized supercells of these materials.37 To calculate the lattice thermal conductivity, a q-mesh of 19 × 19 × 1 is used for sampling. The alternative 24 × 24 × 1 q mesh did not have a relevant effect on our conclusions. The deformation potential (DP) theory developed by Bardeen and Shockley is employed to calculate carriers’ mobility.39 The semiclassical Boltzmann theory, Boltzmann transport equation (BTE), and RTA methods have been employed to calculate the Seebeck coefficient and transport properties of these materials through the BoltzTrap2 code.40,41 We have used constant relaxation time approximation with t = 10–14 s for thermal and electrical conductivity calculations. Ab initio molecular dynamics (AIMD) simulations31,42 were performed in the canonical ensemble (fixed particle number, volume, and temperature, NVT) with a time step of 2 fs by keeping the temperature fixed at 1200 K to check the thermal stability. Vesta software was used for visualization of materials.43

Results and Discussions

Structural Properties of WS2, WSSe, and WSTe

The optimized stable structures of the monolayer WS2 and the Janus monolayer WSSe and WSTe are shown in Figure 1. These materials have hexagonal lattice symmetry in 2D space. Here, each unit cell of these material contains three atoms (one atom of W, one atom of S, and one atom of X = S, Se, or Te). Each tungsten (W) atom has four coordinates (4 W–X bonds; X = S, Se, and Te). While sulfur (S), selenium (Se), and tellurium (Te) atoms have two coordinates (2 W–X bonds; X = S, Se, or Te) in the structures. The optimized WS2 monolayer has lattice parameters a = 3.191 Å and b = 3.191 Å in x and y directions, respectively, as shown in Table 1. This value is agreed with previously reported values.44,45 A high vacuum of 25 Å is also present in the z-direction to prevent interactions between adjacent layers.

Figure 1.

Figure 1

Open in a new tab

Unit cell of full optimized structures of (a) WS2, (b) WSSe, and (c) WSTe. Top view of (d) WS2, (e) WSSe, and (f) WSTe, and also different orientations of the side view of (g) WS2, (h) WSSe, and (i) WSTe Janus materials.

Table 1. Calculated Lattice Parameters and Angles in Janus Materials.

materials lattice a (Å) b (Å) α β γ bonds
WS2 (monolayer) hexagonal 3.191 3.191 90° 90° 120° 2 W-S (2.422 Å)
WSSe (JTMDs) hexagonal 3.258 3.258 90° 90° 120° 1 W-S (2.546 Å)1 W-Se (2.429 Å)
WSTe (JTMDs) hexagonal 3.370 3.370 90° 90° 120° 1 W-S (2.445 Å)1 W-Te (2.729 Å)
Open in a new tab

The Janus monolayer structure for this two-dimensional WS2 monolayer can be achieved by the replacement of any one S atom with Se atom or Te atom in its structure. After optimization of the predicated Janus materials WSSe and WSTe, the WSSe has lattice constants a = 3.258 Å, and b = 3.258 Å in x and y directions, respectively, and the WSTe has lattice constants a = 3.370 Å and b = 3.370 Å (see Table 1). This optimized lattice parameter is very close to previous investigations.27 Both materials, WSSe and WSTe, have a hexagonal lattice arrangement in 2D space. There are two W–S bonds having a bond length of 2.42 Å, whereas the Janus monolayer WSSe has one W–S bond of 2.55 Å and another W–Se bond of 2.43 Å. In addition, Janus WSTe has one W–S bond of 2.44 Å and a W–Te bond of 2.73 Å as presented in Table 1. The W–S bonding is relatively weaker than that in the Janus TMDs, WSSe and WSTe. The W–Te bond in Janus WSTe is weaker than any other bonding among these materials. To check the dynamical stability of this monolayer, we have computed the phonon band structure as shown in Figure S1 (see Supporting Information). From the phonon band structures, we can see that there is no negative frequency. It means that the Janus monolayer is a dynamically stable structure. From ab initio molecular dynamics (AIMD) calculations, all these monolayers at 1200 K show thermal stability, which is shown in Figure S2 (see Supporting Information).

Electronic Properties of Monolayer WS2 and Janus WSSe and WSTe

To study the electronic properties of the 2D single materials WS2, WSSe, and WSTe, the PBE band structure and the hybrid band structure were computed along the symmetry path Γ-M-K-Γ. Here, Figure 2(a,c, and e) shows the PBE bandstructure of monolayers WS2, WSSe, and WSTe. The calculated band gap of WS2 is 1.84 eV, which is of direct nature. This value of the direct band gap for the monolayer WS2 is very close to the experimental value of the band gap in the previous investigation.46−50 Similarly, the calculated direct-gaps of WSSe and WSTe are 1.72 and 1.23 eV, which are also agreed with earlier reported values.51 The band gaps for the HSE06 functional (see Figure S3 in Supporting Information) are 2.15 eV for WSSe, which is very close to the previously reported values 2.07 and 1.71 eV for WSTe, which also agrees with the pristine value 1.56 eV.30,52 The Janus TMD monolayers WSSe and WSTe have a semiconductor nature as presented in Table 2.

Figure 2.

Figure 2

Open in a new tab

(a) Band structure of monolayer WS2, (b) PDOS of monolayer WS2, (c) band structure of Janus monolayer WSSe, (d) PDOS of Janus monolayer WSSe, (e) band structure of Janus monolayer WSTe, and (f) PDOS of monolayer WSTe.

Table 2. Direct Band Gap (eV) at the K-Point of Materials Using PBE and HSE06 Functionals.

materials material type structure Eg (using PBE) Eg (using HSE06)
WS2 monolayer hexagonal (2D) 1.83 2.78
WSSe Janus monolayer hexagonal (2D) 1.72 2.15
WSTe Janus monolayer hexagonal (2D) 1.23 1.71
Open in a new tab

For a better analysis of the electronic structure, the projected density of states (PDOS) for two-dimensional materials WS2, WSSe, and WSTe is determined as shown in Figure 2(b,d, and f). For these materials, the d-orbital of the W atom provides the main contribution to the formation of conduction bands. It also provides the main contribution in the valence band near the Fermi levels of these materials. The p-orbital of the S atom also provides small contributions over conduction bands. Similarly, p-orbitals of S, Se, and Te have contributed to the conduction band of WSSe and WSTe. The s-orbitals of W, S, Se, and Te have negligible contribution information of conduction and valence bands. Far from the Fermi level, the p-orbitals of S, Se, and Te have a more massive contribution in the valence band of Janus WSSe and WSTe. In the WS2 monolayer, this contribution has been provided by only the S atom. This indicates the stable replacement of the S atom by the Se and Te atom in Janus WSSe and WSTe, respectively.

Another significant contribution of d-orbitals of the W atom is found in the valence band of all of these materials. At many places, the d-orbitals of the W atom are overlapped with p-orbitals of S, Se, and Te atoms in the valence band far from the Fermi level. The flat band lines in these suggest a large effective mass for them, and the Seebeck coefficient directly depends on the effective mass (m*).53 According to that, the monolayers WS2, Janus WSSe, and WSTe have higher values of the Seebeck coefficient.

Carrier Mobility and Relaxation Time

Using the DP theory based on the effective mass of carriers presented by Bardeen and Shockley, the carrier mobility can be determined by the following expression: μ = Inline graphic where μ is carrier mobility, C is elastic modulus in the strain direction, m* is the effective mass of the carrier, kb is the Boltzmann constant, and E1 is the DP. 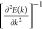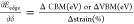Here, the effective mass m* = ℏ2Inline graphic is obtained by parabolic fitting of the band edge, where E(k) is the total energy and DP is defined as E1 = Inline graphic, where ΔCBM (eV) = ∂Eedge is the shift in the conduction band minimum and ΔVBM (eV) = ∂Eedge is the shift in the valence band minimum under the strain δ. E1 is determined by the linear fitting of the ΔCBM (eV) and ΔVBM (eV) values of Eedge with respect to strain d (ΔCBM for electrons and ΔVBM for holes).

The strain δ (%) is expressed as δ = 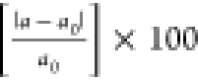Inline graphic. Here, a0 is the lattice constant without strain and a is the lattice constant after application of strain (see Figures S4–S6 in the Supporting Information).

Figure 3(a,b) shows the plot of electron mobility and hole mobility. The electronic mobility of WS2 is slightly bigger than WSSe and WSTe. The effective masses of carriers in WSTe are slightly more than WS2 and WSTe as presented in Table 3. For WS2 and WSSe, the hole’s effective mass is slightly larger than that of the electron in the case of WSTe as shown in Table 3, whereas the hole mobility of WSSe is slightly larger than WS2 and WSTe. The curve of carries’ mobility has shown a parabolic decrease with temperature. In addition, the values of carrier mobilities at room temperature for Janus materials are presented in Table 3. In these materials, the relaxation time of the electron and can be calculated through the formula τ =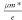Inline graphic. Therefore, the curve of relaxation time is also a parabolic function of temperature. The relaxation time of electronic collision is decreased with an increase in the temperature. The relaxation time of the carrier is the same for the WS2 monolayer and its Janus materials. Figure 3(c,d) shows the relaxation time of electrons and holes.

Figure 3.

Figure 3

Open in a new tab

(a) Electron mobility, (b) hole mobility, (c) relaxation time of electrons, and (d) relaxation time of holes.

Table 3. Calculated Deformation Potential (E1), Elastic Constant (C), the Effective Mass of the Electron (me*), the Effective Mass of the Hole (mh*), Electron Mobility (μe), and Hole Mobility (μh) at 300 K.

materials carriers E1 (eV) C (N/m) m*(m0) μ (cm2 V–1 s–1)
WS2 (monolayer) electron 14.22 235.46 me* = 0.43 μe = 90.97
hole 6.96 mh* = −0.52 μh = 262.36
WSSe (Janus) electron 13.21 229.31 me* = 0.48 μe = 81.50
hole 6.06 mh* = – 0.57 μh = 276.64
WSTe (Janus) electron 13.59 222.21 me* = 0.45 μe = 85.73
hole 8.99 mh* = −0.43 μh = 214.79
Open in a new tab

Thermoelectric Properties of Janus Monolayer Materials

The Seebeck coefficient, electric conductivity, thermal conductivity, and ZT are calculated as a function of temperature with a constant relaxation time (τ = 10–14 s) for the monolayer WS2 and the Janus monolayers WSSe and WSTe. Figure 4(a) shows the computed Seebeck coefficients of the material at a temperature range from 300to 1200 K. Initially, the Seebeck coefficient of a pure monolayer WS2 has a slightly higher value than both Janus monolayers at 300 K (see Table 4). For the materials WS2, WSSe, and WSTe, the Seebeck effect decreases as a parabolic function of temperature. In the Janus monolayers WSSe and WSTe, the value of Seebeck coefficients decreases more slowly than the pure monolayer WS2. The value of Janus WSSe Seebeck coefficients exceeds the values of WS2 near 400 K. Similarly, the curve of the Seebeck coefficient of WSTe crosses at a higher temperature at 800 K. At higher temperatures, both Janus materials WSSe and WSTe have shown more Seebeck effect.

Figure 4.

Figure 4

Open in a new tab

(a) Seebeck Coefficients, (b) electrical conductivity, (c) ZT values of monolayer WS2, Janus TMDs WSSe, and WSTe, (d) thermal conductivity of WS2, (e) thermal conductivity of WSSe, and (f) thermal conductivity of WSTe.

Table 4. Calculated Seebeck Coefficient (S) and Figure of Merit (ZT).

  S (μV/K) ZT
material 300 K 1200 K 300 K 1200 K
WS2 (monolayer) 328.15 206.08 0.006 0.238
WSSe (JTMDs) 322.26 218.66 0.013 0.355
WSTe (JTMDs) 322.15 219.44 0.742 2.562
Open in a new tab

Figure 4(b) shows the electrical conductivity of materials. The Janus monolayer WSTe has low electric conductivity than the monolayer WS2 and the Janus monolayer WSSe in the whole temperature range. The electric conductivity of all materials increases with temperature, but the electric conductivity of WSTe increases much slower than WS2 and WSSe. For higher temperatures, WS2 and WSSe have almost the same value. At low temperatures, the electric conductivity of WSSe shows a slightly higher value.

Thermal conductivities of the monolayer WS2 and the JTMD monolayers WSSe and WSTe are shown in Figure 4(d–f). The monolayer WS2 has higher thermal conductivity than the JTMD monolayers WSSe and WSTe. It is observed that the WSTe has ultralow thermal conductivity because both the electronic part and lattice contribution are very low; whereas, for the WS2 and WSSe, the lattice thermal conductivity is very high in comparison to the electronic thermal conductivity. Therefore, they too have a high thermal conductivity in comparison to WSTe. WSTe has ultralow thermal conductivity. Its value is almost 150 times smaller than that of WS2 and 100 times smaller than that of WSSe near room temperature. The thermal conductivity of the Janus WSTe monolayer is relatively very low as compared to other 2D materials.54−56 The ultralow value of thermal conductivity plays a significant role in the enhancement of the high ZT. Graphene has a high thermoelectric power factor (S2σ), but it has a very low ZT value of 0.55 × 10–3 at room temperature due to its ultrahigh thermal conductivity.57 Graphene oxide is a potential 2D thermoelectric material with a ZT value of 0.05–0.75 due to its thermopower factor of 127–287 μV K–1 (4–22 times of the graphene value) and very low lattice thermal conductivity of 15–22% of the graphene value.58 Therefore, lattice thermal conductivity plays an important role in the thermoelectric ZT.

The calculated ZT values for these materials are shown in Figure 4(c). WS2 and WSSe have low ZT values in the whole temperature range because both these materials have high thermal conductivity. The monolayer WS2 and the Janus monolayer WSSe report a ZT value of 0.006 and 0.012. Here, it is observed that the replacement of one S atom by a Se atom optimizes the ZT value. Predicated WSTe shows high thermoelectric conversion performance with a high ZT value. Initially, its ZT value is 0.75 at 300 K (near room temperature) as shown in Table 4. Its ZT increases with temperature. At higher temperatures (near 600 K temperature), it becomes constant with temperature. It shows ZT = 2.56 at a higher temperature (1200 K) as shown in Table 4. The single layers of GaS, GaSe, and GaTe have ZT values of 0.89, 0.90, and 0.85 at room temperature, respectively, and decrease with the increase in temperature.59 The single-layer MoS2 has reported ZT values of 0.04, 0.07, and 0.11 at 300 K, 400 K, and 500 K, respectively.60 The ZT of 0.52, 0.59, and 0.25 at room temperature are found in AlS, AlSe, and AlTe monolayers under moderate conditions.61 The anisotropic materials PdS2, PdSe2, and PdTe2 show larger thermoelectric conversion performance with ZT values of 0.85, 1.18, and 2.42, respectively, compared to the commercial thermoelectric material Bi2S3 (ZT = 0.80).55

Conclusions

In the present study, the structural, electronic, and thermoelectric properties of the 2D monolayer WS2 and Janus TMD materials WSSe and WSTe are calculated by first-principles calculations. From the phonon band structures and ab initio molecular dynamics calculations, the monolayer materials considered are dynamically and thermally stable. WS2, WSSe, and WSTe show a direct band gap of 1.32, 1.72, and 1.84 eV, respectively. The band through the HSE06 functional is found to be 2.15 eV for WSSe and 1.71 eV for WSTe. The carrier mobility of holes is relatively higher than the electrons. The values of the Seebeck coefficient (S) of WS2, WSSe, and WSTe are 328.15, 322.26, and 322.15 μV K–1, respectively. Replacement of one S atom by Se and Te in the WS2 structure significantly reduces the lattice thermal conductivity. This reduction in thermal conductivity results in an improvement in the ZT value. The Janus WSTe monolayer shows superior ZT values of 0.74 and 2.56 at 300 K and 1200 K, respectively, which is larger than most of the 2D materials, and it can be superior to the commercial TE material Bi2Te3. Among these materials, the Janus monolayer WSTe can be proposed with a ZT value of 2.56 at 1200 K for thermoelectric applications such as the production of electricity from waste heat and Peltier cooling.

Acknowledgments

A.P. is thankful to the Council of Scientific and Industrial Research (CSIR), India, for his Junior Research Fellowship (File No: 09/1008(0003)/2019-EMR-1) and financial supports. D.S. and R.A. thank Olle Engkvists stiftelse (198-0390), Carl Tryggers Stiftelse for Vetenskaplig Forskning (CTS: 18:4), and Swedish Research Council (VR-2016-06014) for financial support. HPC2N and SNIC are acknowledged for the high-performance computing (HPC) facilities.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.0c13960.

  • Electronic band structures using phonon dispersion spectra, ab initio molecular dynamics calculations (AIMD) at 1200 K, and HSE06 functional and strain–energy and VBM/CBM edge positions (PDF)

Author Contributions

The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

am0c13960_si_001.pdf (342.7KB, pdf)

References

  1. Yang L.; Chen Z. G.; Dargusch M. S.; Zou J. High Performance Thermoelectric Materials: Progress and Their Applications. Adv. Energy Mater. 2018, 8, 1701797. 10.1002/aenm.201701797. [DOI] [Google Scholar]
  2. Perera F. Pollution from Fossil-Fuel Combustion Is the Leading Environmental Threat to Global Pediatric Health and Equity: Solutions Exist. Int. J. Environ.Res. Public. Health 2018, 15, 16. 10.3390/ijerph15010016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Jiang X.; Zhu L.; Li B.; Yao K. Thermoelectric Properties of Monolayer α-Te: Low Lattice Thermal Conductivity and Extremely High Dimensionless Figure of Merit. Phys. Lett. Sect. A Gen. At. Solid State Phys 2020, 384, 126222. 10.1016/j.physleta.2019.126222. [DOI] [Google Scholar]
  4. Owusu P. A.; Asumadu-Sarkodie S. A Review of Renewable Energy Sources, Sustainability Issues and Climate Change Mitigation. Cogent Eng. 2016, 3, 1167990. 10.1080/23311916.2016.1167990. [DOI] [Google Scholar]
  5. Sorrell S. Reducing Energy Demand: A Review of Issues, Challenges and Approaches. Renew. Sustain. Energy Rev. 2015, 47, 74–82. 10.1016/j.rser.2015.03.002. [DOI] [Google Scholar]
  6. Zhang X.; Zhao L. D. Thermoelectric Materials: Energy Conversion between Heat and Electricity. J. Mater. 2015, 1, 92–105. 10.1016/j.jmat.2015.01.001. [DOI] [Google Scholar]
  7. Freer R.; Powell A. V. Realising the Potential of Thermoelectric Technology: A Roadmap. J. Mater. Chem. C 2020, 8, 441–463. 10.1039/C9TC05710B. [DOI] [Google Scholar]
  8. Liu W.; Jie Q.; Kim H. S.; Ren Z. Current Progress and Future Challenges in Thermoelectric Power Generation: From Materials to Devices. Acta Mater. 2015, 87, 357. 10.1016/j.actamat.2014.12.042. [DOI] [Google Scholar]
  9. Snyder G. J.; Snyder A. H. Figure of Merit ZT of a Thermoelectric Device Defined from Materials Properties. Energy Environ. Sci. 2017, 10, 2280–2283. 10.1039/C7EE02007D. [DOI] [Google Scholar]
  10. Mishra P.; Singh D.; Sonvane Y.; Ahuja R. Two-Dimensional Boron Monochalcogenide Monolayer for Thermoelectric Material. Sustain. Energy Fuels 2020, 4, 2363–2369. 10.1039/D0SE00004C. [DOI] [Google Scholar]
  11. Patel A.; Singh D.; Sonvane Y.; Thakor P. B.; Ahuja R. Bulk and Monolayer As2S3 as Promising Thermoelectric Material with High Conversion Performance. Comput. Mater. Sci. 2020, 183, 109913. 10.1016/j.commatsci.2020.109913. [DOI] [Google Scholar]
  12. Beretta D.; Neophytou N.; Hodges J. M.; Kanatzidis M. G.; Narducci D.; Martin-Gonzalez M.; Beekman M.; Balke B.; Cerretti G.; Tremel W.; et al. Thermoelectrics: From History, a Window to the Future. Mater. Sci. Eng. R Reports 2019, 138, 100501. 10.1016/j.mser.2018.09.001. [DOI] [Google Scholar]
  13. Nshimyimana E.; Hao S.; Su X.; Zhang C.; Liu W.; Yan Y.; Uher C.; Wolverton C.; Kanatzidis M. G.; Tang X. Discordant Nature of Cd in GeTe Enhances Phonon Scattering and Improves Band Convergence for High Thermoelectric Performance. J. Mater. Chem. A 2020, 8, 1193–1204. 10.1039/C9TA10436D. [DOI] [Google Scholar]
  14. Zhao L. D.; Lo S. H.; Zhang Y.; Sun H.; Tan G.; Uher C.; Wolverton C.; Dravid V. P.; Kanatzidis M. G. Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals. Nature 2014, 508, 373–377. 10.1038/nature13184. [DOI] [PubMed] [Google Scholar]
  15. Hinterleitner B.; Knapp I.; Poneder M.; Shi Y.; Müller H.; Eguchi G.; Eisenmenger-Sittner C.; Stöger-Pollach M.; Kakefuda Y.; Kawamoto N.; et al. Thermoelectric Performance of a Metastable Thin-Film Heusler Alloy. Nature 2019, 576, 85–90. 10.1038/s41586-019-1751-9. [DOI] [PubMed] [Google Scholar]
  16. Li R.; Cheng Y.; Huang W. Recent Progress of Janus 2D Transition Metal Chalcogenides: From Theory to Experiments. Small 2018, 14, 1802091. 10.1002/smll.201802091. [DOI] [PubMed] [Google Scholar]
  17. Lu A.-Y.; Zhu H.; Xiao J.; Chuu C.-P.; Han Y.; Chiu M.-H.; Cheng C.-C.; Yang C.-W.; Wei K.-H.; Yang Y.; et al. Janus Monolayers of Transition Metal Dichalcogenides. Nat. Nanotechnol. 2017, 12, 744–749. 10.1038/nnano.2017.100. [DOI] [PubMed] [Google Scholar]
  18. Cheng Y. C.; Zhu Z. Y.; Tahir M.; Schwingenschlögl U. Spin-Orbit–Induced Spin Splittings in Polar Transition Metal Dichalcogenide Monolayers. EPL (Europhysics Lett) 2013, 102, 57001. 10.1209/0295-5075/102/57001. [DOI] [Google Scholar]
  19. Zhang J.; Jia S.; Kholmanov I.; Dong L.; Er D.; Chen W.; Guo H.; Jin Z.; Shenoy V. B.; Shi L.; et al. Janus Monolayer Transition-Metal Dichalcogenides. ACS Nano 2017, 11, 8192–8198. 10.1021/acsnano.7b03186. [DOI] [PubMed] [Google Scholar]
  20. Yang X.; Singh D.; Xu Z.; Ahuja R. Sensing the Polar Molecules MH3 (M = N, P, or As) with a Janus NbTeSe Monolayer. New J. Chem. 2020, 44, 7932–7940. 10.1039/D0NJ01022G. [DOI] [Google Scholar]
  21. Yang X.; Singh D.; Xu Z.; Wang Z.; Ahuja R. An Emerging Janus MoSeTe Material for Potential Applications in Optoelectronic Devices. J. Mater. Chem. C 2019, 7, 12312–12320. 10.1039/C9TC03936H. [DOI] [Google Scholar]
  22. Yang X.; Banerjee A.; Ahuja R.. Structural Insight of the Frailty of 2D Janus NbSeTe as An Active Photocatalyst. ChemCatChem 2020, 10.1002/cctc.202000540. [DOI] [Google Scholar]
  23. Rawat A.; Mohanta M. K.; Jena N.; Dimple; Ahammed R.; De Sarkar A. Nanoscale Interfaces of Janus Monolayers of Transition Metal Dichalcogenides for 2D Photovoltaic and Piezoelectric Applications. J. Phys. Chem. C 2020, 124, 10385–10397. 10.1021/acs.jpcc.0c02199. [DOI] [Google Scholar]
  24. Yang J.; Wang A.; Zhang S.; Liu J.; Zhong Z.; Chen L. Coexistence of Piezoelectricity and Magnetism in Two-Dimensional Vanadium Dichalcogenides. Phys. Chem. Chem. Phys. 2019, 21, 132–136. 10.1039/C8CP06535G. [DOI] [PubMed] [Google Scholar]
  25. Ji Y.; Yang M.; Lin H.; Hou T.; Wang L.; Li Y.; Lee S.-T. Janus Structures of Transition Metal Dichalcogenides as the Heterojunction Photocatalysts for Water Splitting. J. Phys. Chem. C 2018, 122, 3123–3129. 10.1021/acs.jpcc.7b11584. [DOI] [Google Scholar]
  26. Gu X.; Yang R. Phonon Transport in Single-Layer Transition Metal Dichalcogenides: A First-Principles Study. Appl. Phys. Lett. 2014, 105, 131903. 10.1063/1.4896685. [DOI] [Google Scholar]
  27. Guo S.-D.; Dong J. Biaxial Strain Tuned Electronic Structures and Power Factor in Janus Transition Metal Dichalchogenide Monolayers. Semicond. Sci. Technol. 2018, 33, 85003. 10.1088/1361-6641/aacb11. [DOI] [Google Scholar]
  28. Tao W.-L.; Mu Y.; Hu C.-E.; Cheng Y.; Ji G.-F. Electronic Structure, Optical Properties, and Phonon Transport in Janus Monolayer PtSSe via First-Principles Study. Philos. Mag. 2019, 99, 1025–1040. 10.1080/14786435.2019.1572927. [DOI] [Google Scholar]
  29. Idrees M.; Din H. U.; Ali R.; Rehman G.; Hussain T.; Nguyen C. V.; Ahmad I.; Amin B. Optoelectronic and Solar Cell Applications of Janus Monolayers and Their van Der Waals Heterostructures. Phys. Chem. Chem. Phys. 2019, 21, 18612–18621. 10.1039/C9CP02648G. [DOI] [PubMed] [Google Scholar]
  30. Wang J.; Shu H.; Zhao T.; Liang P.; Wang N.; Cao D.; Chen X. Intriguing Electronic and Optical Properties of Two-Dimensional Janus Transition Metal Dichalcogenides. Phys. Chem. Chem. Phys. 2018, 20, 18571–18578. 10.1039/C8CP02612B. [DOI] [PubMed] [Google Scholar]
  31. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B - Condens. Matter Mater Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  32. Kresse G.; Furthmüller J.; Hafner J. Ab Initio Force Constant Approach to Phonon Dispersion Relations of Diamond and Graphite. Europhys. Lett. 1995, 32, 729–734. 10.1209/0295-5075/32/9/005. [DOI] [Google Scholar]
  33. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  34. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  35. Chaurasiya R.; Dixit A.; Pandey R. Strain-Mediated Stability and Electronic Properties of WS2, Janus WSSe and WSe2 Monolayers. Superlattices Microstruct. 2018, 122, 268–279. 10.1016/j.spmi.2018.07.039. [DOI] [Google Scholar]
  36. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  37. Togo A.; Tanaka I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  38. Mizokami K.; Togo A.; Tanaka I. Lattice Thermal Conductivities of Two SiO2 Polymorphs by First-Principles Calculations and the Phonon Boltzmann Transport Equation. Phys. Rev. B 2018, 97, 224306. 10.1103/PhysRevB.97.224306. [DOI] [Google Scholar]
  39. Bardeen J.; Shockley W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72–80. 10.1103/PhysRev.80.72. [DOI] [Google Scholar]
  40. Madsen G. K. H.; Carrete J.; Verstraete M. J. BoltzTraP2, a Program for Interpolating Band Structures and Calculating Semi-Classical Transport Coefficients. Comput. Phys. Commun. 2018, 231, 140–145. 10.1016/j.cpc.2018.05.010. [DOI] [Google Scholar]
  41. Madsen G. K. H.; Singh D. J. BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 2006, 175, 67–71. 10.1016/j.cpc.2006.03.007. [DOI] [Google Scholar]
  42. Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  43. Momma K.; Izumi F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
  44. Amin B.; Kaloni T. P.; Schwingenschlögl U. Strain Engineering of WS2, WSe2, and WTe2. RSC Adv. 2014, 4, 34561–34565. 10.1039/c4ra06378c. [DOI] [Google Scholar]
  45. Kang J.; Tongay S.; Zhou J.; Li J.; Wu J. Band Offsets and Heterostructures of Two-Dimensional Semiconductors. Appl. Phys. Lett. 2013, 102, 12111. 10.1063/1.4774090. [DOI] [Google Scholar]
  46. Gusakova J.; Wang X.; Shiau L. L.; Krivosheeva A.; Shaposhnikov V.; Borisenko V.; Gusakov V.; Tay B. K. Electronic Properties of Bulk and Monolayer TMDs: Theoretical Study Within DFT Framework (GVJ-2e Method). Phys. status solidi 2017, 214, 1700218. 10.1002/pssa.201700218. [DOI] [Google Scholar]
  47. Gutiérrez H. R.; Perea-López N.; Elías A. L.; Berkdemir A.; Wang B.; Lv R.; López-Urías F.; Crespi V. H.; Terrones H.; Terrones M. Extraordinary Room-Temperature Photoluminescence in Triangular WS2 Monolayers. Nano Lett. 2013, 13, 3447–3454. 10.1021/nl3026357. [DOI] [PubMed] [Google Scholar]
  48. Elías A. L.; Perea-López N.; Castro-Beltrán A.; Berkdemir A.; Lv R.; Feng S.; Long A. D.; Hayashi T.; Kim Y. A.; Endo M.; et al. Controlled Synthesis and Transfer of Large-Area WS2 Sheets: From Single Layer to Few Layers. ACS Nano 2013, 7, 5235–5242. 10.1021/nn400971k. [DOI] [PubMed] [Google Scholar]
  49. Zhao W.; Ghorannevis Z.; Chu L.; Toh M.; Kloc C.; Tan P.-H.; Eda G. Evolution of Electronic Structure in Atomically Thin Sheets of WS2 and WSe2. ACS Nano 2013, 7, 791–797. 10.1021/nn305275h. [DOI] [PubMed] [Google Scholar]
  50. Tongay S.; Fan W.; Kang J.; Park J.; Koldemir U.; Suh J.; Narang D. S.; Liu K.; Ji J.; Li J.; et al. Tuning Interlayer Coupling in Large-Area Heterostructures with CVD-Grown MoS2 and WS2 Monolayers. Nano Lett. 2014, 14, 3185–3190. 10.1021/nl500515q. [DOI] [PubMed] [Google Scholar]
  51. Liu H.; Huang Z.; He C.; Wu Y.; Xue L.; Tang C.; Qi X.; Zhong J. Strain Engineering the Structures and Electronic Properties of Janus Monolayer Transition-Metal Dichalcogenides. J. Appl. Phys. 2018, 125, 82516. 10.1063/1.5041486. [DOI] [Google Scholar]
  52. Idrees M.; Din H. U.; Rehman S. U.; Shafiq M.; Saeed Y.; Bui H. D.; Nguyen C. V.; Amin B. Electronic Properties and Enhanced Photocatalytic Performance of van Der Waals Heterostructures of ZnO and Janus Transition Metal Dichalcogenides. Phys. Chem. Chem. Phys. 2020, 22, 10351–10359. 10.1039/D0CP01264E. [DOI] [PubMed] [Google Scholar]
  53. Levin E. M. Charge Carrier Effective Mass and Concentration Derived from Combination of Seebeck Coefficient and 125Te NMR Measurements in Complex Tellurides. Phys. Rev. B 2016, 93, 245202. 10.1103/PhysRevB.93.245202. [DOI] [Google Scholar]
  54. Tao W.-L.; Lan J.-Q.; Hu C.-E.; Cheng Y.; Zhu J.; Geng H.-Y. Thermoelectric Properties of Janus MXY (M = Pd, Pt; X, Y = S, Se, Te) Transition-Metal Dichalcogenide Monolayers from First Principles. J. Appl. Phys. 2020, 127, 035101 10.1063/1.5130741. [DOI] [Google Scholar]
  55. Lan Y.-S.; Chen X.-R.; Hu C.-E.; Cheng Y.; Chen Q.-F. Penta-PdX2 (X = S, Se, Te) Monolayers: Promising Anisotropic Thermoelectric Materials. J. Mater. Chem. A 2019, 7, 11134–11142. 10.1039/C9TA02138H. [DOI] [Google Scholar]
  56. Zhou Y.; Zhao Y.-Q.; Zeng Z.-Y.; Chen X.-R.; Geng H.-Y. Anisotropic Thermoelectric Properties of Weyl Semimetal NbX (X = P and As): A Potential Thermoelectric Material. Phys. Chem. Chem. Phys. 2019, 21, 15167–15176. 10.1039/C9CP02020A. [DOI] [PubMed] [Google Scholar]
  57. Anno Y.; Imakita Y.; Takei K.; Akita S.; Arie T. Enhancement of Graphene Thermoelectric Performance through Defect Engineering. 2D Mater 2017, 4, 25019. 10.1088/2053-1583/aa57fc. [DOI] [Google Scholar]
  58. Zhou S.; Guo Y.; Zhao J. Enhanced Thermoelectric Properties of Graphene Oxide Patterned by Nanoroads. Phys. Chem. Chem. Phys. 2016, 18, 10607–10615. 10.1039/C6CP01012A. [DOI] [PubMed] [Google Scholar]
  59. Bahuguna B. P.; Saini L. K.; Sharma R. O.; Tiwari B. Hybrid Functional Calculations of Electronic and Thermoelectric Properties of GaS, GaSe, and GaTe Monolayers. Phys. Chem. Chem. Phys. 2018, 20, 28575–28582. 10.1039/C8CP04723E. [DOI] [PubMed] [Google Scholar]
  60. Jin Z.; Liao Q.; Fang H.; Liu Z.; Liu W.; Ding Z.; Luo T.; Yang N. A Revisit to High Thermoelectric Performance of Single-Layer MoS2. Sci. Rep. 2015, 5, 18342. 10.1038/srep18342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Chen X.; Huang Y.; Liu J.; Yuan H.; Chen H. Thermoelectric Performance of Two-Dimensional AlX (X = S, Se, Te): A First-Principles-Based Transport Study. ACS Omega 2019, 4, 17773–17781. 10.1021/acsomega.9b02235. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am0c13960_si_001.pdf (342.7KB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES