Abstract
The ability to accurately compute low-energy excited states of chlorophylls is critically important for understanding the vital roles they play in light harvesting, energy transfer, and photosynthetic charge separation. The challenge for quantum chemical methods arises both from the intrinsic complexity of the electronic structure problem and, in the case of biological models, from the need to account for protein–pigment interactions. In this work, we report electronic structure calculations of unprecedented accuracy for the low-energy excited states in the Q and B bands of chlorophyll a. This is achieved by using the newly developed domain-based local pair natural orbital (DLPNO) implementation of the similarity transformed equation of motion coupled cluster theory with single and double excitations (STEOM-CCSD) in combination with sufficiently large and flexible basis sets. The results of our DLPNO–STEOM-CCSD calculations are compared with more approximate approaches. The results demonstrate that, in contrast to time-dependent density functional theory, the DLPNO–STEOM-CCSD method provides a balanced performance for both absorption bands. In addition to vertical excitation energies, we have calculated the vibronic spectrum for the Q and B bands through a combination of DLPNO–STEOM-CCSD and ground-state density functional theory frequency calculations. These results serve as a basis for comparison with gas-phase experiments.
Introduction
Chlorophylls are photosynthetic pigments that play crucial roles in the absorption of sunlight, excitation energy transfer, and primary charge separation in photosynthetic organisms.1−4 Their low-energy electronic transitions comprise the Q band (including the Qy and Qx transitions) and the B band, also known as the Soret band. Vibrational overtones accompany each major peak in the absorption spectra. The Qy and Qx transitions (subscripts denote the idealized polarization direction within the macrocycle plane) are the most important for determining the biophysical properties of chlorophyll species in particular and chlorophyll-containing photosystems in general.5−12 The transitions are conventionally described by the four-orbital Gouterman model,13,14 which, however, has known limitations. These arise from the fact that the electronic nature of actual excitations is more complex than that suggested by the Gouterman model, particularly for the B band, and because of the possible mixing of transitions due to vibronic coupling.9,11,12,15−19
The accurate calculation of the low-energy spectrum of the chlorophyll excited states has been a long-standing target of quantum chemistry.20−22 A wide variety of computational investigations have been used for computing excitation energies and absorption profiles, ranging from time-dependent density functional theory (TD-DFT)23−30 and DFT/multireference configuration interaction (MRCI)31 to various wave function methods such as SAC-CI,32 CC2,33,34 and ADC(2).34 Advanced multireference approaches have so far been applied only to bacteriochlorophylls.35−37 TD-DFT remains a popular choice for photosynthetic chromophores because of its low computational cost and sometimes acceptable accuracy. However, questions have been raised about the performance of the approach for chlorophylls and similar systems.26 In addition, the inadequacy of TD-DFT to properly predict charge-transfer states, and hence be reliably applied in the context of photosynthetic charge separation, is well known.25,27,38 Wave function-based approaches are able to deliver systematically better results than DFT, albeit at increased computational cost; therefore, it is important to seek new ways for their practical usage.
In recent years, the domain-based local pair natural orbital (DLPNO) approach has been successfully applied to accelerate the methods of the coupled cluster (CC) hierarchy for ground-state calculations. Significant progress has also been made in the use of localization techniques for excited states. The first breakthrough in this regard was the implementation of the local CC variant of EOM-CCSD by Korona and Werner,39 which was soon followed by a local CC2 method making use of the density fitting40 and Laplace transform41 techniques. The concept of state-specific pair natural orbitals was proposed by Helmich and Hättig42 and was soon implemented for CC2 and ADC(2)43 as well as for EOM-CCSD.44 Excited-state approaches based on state-specific natural orbitals have also been proposed at the CC245 and ADC(2)46 levels by Mester et al. In contrast, Peng et al. rely on state-averaged PNOs in their EOM-CCSD implementation.47,48 Further details on this and other methods are provided in a recent review.24 Among these methods, our group49−51 has recently proposed a combination of ground-state DLPNOs52,53 with the similarity transformed equation of motion (STEOM) approach of Nooijen and Bartlett,54 which has the advantage that single excitations are decoupled from the doubles. This property allows for reducing the final diagonalization step to the size of the space of single (hole/particle) excitations. Thus, the final excitation space is similar to that of TD-DFT and other particle/hole theories. However, unlike TD-DFT, the effect of the doubles is retained, and a further implicit triple correction improves the description of charge-transfer states. This is the reason why frequently the results of STEOM-CCSD calculations surpass the accuracy of the EOM-CCSD method itself.54 We emphasize that the STEOM-CCSD method and its DLPNO variant do not rely on a perturbative approximation to EOM-CCSD, as the popular and more approximate CC2 and ADC(2) methods do. One caveat of the method is that STEOM-CCSD introduces an active space of occupied and virtual orbitals. However, this active space is not a complete active space in the sense of multiconfigurational approaches, but it serves to identify the orbitals that dominantly participate in the electron depopulation and repopulation processes that accompany electronic excitations. This active space is not practically restricted to about 14 orbitals (as would be the case for a complete active space approach). Fortunately, recent work has demonstrated that the selection of this active space can be automatized.55,56
In order to account for vibronic transitions, we followed the ideas outlined by Baiardi et al.57 in developing a time-dependent approach58−60 that relies on DLPNO-STEOM vertical excitation energies (VEEs), transition dipole moments (TDMs) (Franck–Condon approximation61−63), and their derivatives (Herzberg–Teller effects64), whereas the ground- and excited-state geometries as well as harmonic vibrational frequencies are calculated at the DFT/TD-DFT level. This approach essentially amounts to calculating Fermi’s golden rule by Fourier transforming it into the time domain and applying the path integral formula for the harmonic oscillator to evaluate the resulting time-correlation function. The resulting composite method has been used with success to characterize and interpret a variety of spectroscopic measurements.58−60,65−67 It is also worthwhile to mention a similar approach used by Barone and co-workers on a variety of chemical compounds.68−74
In this study, we apply the above DLPNO–STEOM-CCSD approach to all states that comprise the absorption spectrum of the chlorophyll a (Chl a) model (Figure 1). The results, which can be considered as reference values for lower-level coupled-cluster approximations and for DFT approaches, are compared with the results obtained by a variety of other methods and with the experimental gas-phase results75 on Chl a. Moreover, we demonstrate that treating vibronic coupling, including Herzberg–Teller effects,74,76 is, in fact, required in order to obtain an accurate representation of the linear absorption spectrum of Chl a.
Figure 1.

Structure of the gas-phase optimized Chl a model. The phytyl-carrying group at position 17 in the present calculations is replaced by a methyl group.
Methodology
All quantum chemical computations in this work were performed using the development version of the ORCA 4.2 program package.77 The initial molecular geometry of a Chl a molecule was extracted from the crystal structure of photosystem II (PDB ID: 3WU2).78 As a first step, we built different variants of Chl a with respect to the length of the group at position 17 of the chlorin ring, either with the phytyl chain terminated after the ester group (capped with a methyl group) or with the group replaced by a methyl group. Both models were fully optimized with the B3LYP hybrid functional.79 No variations in macrocyclic ring curvature were observed. VEEs (obtained with DLPNO–STEOM-CCSD, see Table S1) are invariant with respect to the phytyl chain length of the model. Based on these results, we chose the model with a minimal representation of the chain at position 17 of the chlorin ring that is capped with a methyl group (Figure 1). Final gas-phase geometry optimizations were performed using CAM-B3LYP80 along with def2-TZVP81−83 basis sets, with the inclusion of dispersion corrections via the D3(BJ) scheme.84,85 The choice of the functional was motivated by the observation that it provides better balance in the description of low- and high-energy states compared to other functionals, as well as in order to ensure the consistency of methods between geometry optimization and calculation of ground- and excited-state frequencies. In addition, a recent study86 demonstrated an improved performance of CAM-B3LYP over B3LYP for the prediction of the vibronic spectrum for both Chl a and Chl f. The RIJCOSX approximation87,88 was used to speed up the calculations. Tight thresholds were employed for the self-consistent field (SCF) and optimization (verytightscf and verytightopt keywords in ORCA nomenclature). The resulting geometries had no imaginary frequencies. TD-DFT VEEs were computed using range-separated CAM-B3LYP80 and ωB97X-D3(BJ),89−92 as well as hybrid functionals B3LYP,79 PBE0,93 and BHandHLYP,94 and the double-hybrid B2PLYP95,96 and ωB2PLYP.97 A total of 10 roots were computed. This number of roots was selected so as to ensure that all excitations that could possibly correspond to the B band are fully recovered. All results are reported in detail in the Supporting Information.
The DLPNO–STEOM-CCSD calculations were performed with the def2-TZVP basis set (total of 1464 basis functions). Calculations with larger basis sets and basis sets with diffuse functions could not be successfully completed for the present system. A total of 10 roots were requested depending on the requirement for a particular given case. No change in excitation energies was observed when a higher number of roots were computed; however, the cost of the calculation increases steeply beyond this point. The calculations were performed with the “TightPNO” setting, the TCutPNOsingles keyword set to 6.6 × 10–10 and the active space selection keywords “Othresh” and “Vthresh” set to 1.0 × 10–3. As an indication of computational cost, one such calculation for 10 roots took 5 days 7 h (wall clock time) on 8 cores of an Intel Xeon E5-2640 v3 CPU. Slightly lower thresholds in active space selection (“Othresh” and “Vthresh” set to 5.0 × 10–3) reduce the total computational time to 3 days 20 h with no change in the computed VEEs. Additionally, if the basis set is reduced to def2-SVP, the required time is reduced to less than 12 h with no noticeable loss in accuracy (see the Supporting Information). At this level, the cost is about 2 to 3 times that of TD-DFT calculations with double-hybrid functionals. Nevertheless, all the reported values in the present work utilize the more conservative thresholds and large basis sets stated above.
The vibronic spectrum of the excited states associated with both x- and y-polarized components of the Q and B states was computed using the excited-state dynamics (ESD) module of the ORCA package. One of the basic requirements for the computation of the vibronic spectrum using this methodology is the ground- and excited-state Hessians, which were computed using the CAM-B3LYP/def2-TZVP level of theory. The influence of the vibronic coupling on the absorption spectra was computed using the Herzberg–Teller effects. The temperature was set to 300 K during the calculations to match with the experimental conditions. We have used a Gaussian line shape to model the absorption spectra together with a computed linewidth equal to the experimental full width at half-maximum. The vibronic progression (sticks format) was computed using an intrinsic linewidth of 0.1 cm–1 (using the INLINEW keyword of the ORCA_ESD module).
A direct comparison of the computed vertical excitation or the 0–0 energies with the experimental band maximum is conceptually incorrect,98 as the experimental bands contain contributions from the vibrational levels and geometric relaxation in the excited states. In this study, we report an effort to derive “quasi-experimental” vertical excitation and 0–0 energies to allow for a direct comparison of the experimental results with the quantum chemical calculations (Table S2). Our approach is based on band shape calculations using the vertical gradient (VG) approach for the x- and y-polarized components of the Q and B states.
Results and Discussion
Experimental Gas-Phase Spectra and the Gouterman Model
Experimental data on the absorption spectra of chlorophylls and bacteriochlorophylls refer almost exclusively to the species in solution. Depending on the solvent, magnesium may coordinate either one or two solvent molecules axially, with a concomitant geometric distortion of the chlorin ring. Additionally, solvent molecules may directly interact with the ring substituents. Both effects result in the alterations of the electronic properties and hence of the absorption spectrum of the molecule. The treatment of the solvation effects represents a challenge to theoretical approaches as significant as the intrinsic electronic structure problem. Indeed, most theoretical studies of chlorophylls have dealt with solvated, or in general axially coordinated, systems.16,99−108 However, to disentangle the two problems and be able to focus on the electronic structure itself, it is useful to have experimental gas-phase values that can serve as reference for quantum chemical calculations. Such gas-phase spectra have been reported only recently and only for Chl a and Chl b using action spectroscopy (Figure 2).28,29,75,109 However, gas-phase experiments with neutral chlorophyll molecules are challenging to perform as these molecules decompose easily.28 Therefore, the experiments are generally performed using a charge tag approach, where a cationic species is used alongside the chlorophyll molecules. Variable sizes of charge tags are used to observe the influence on the chlorophyll absorption profiles. Interestingly, a study by Wellman and Jockusch109 demonstrated the influence of the alkali metal-tagged Chl a on the Soret region. The experimental data75 mentioned in the present study were obtained using tetramethylammonium cations.
Figure 2.

Gas-phase action spectra (at 300 K) of charge-tagged Chl a after one-photon absorption. The original data are from the study of Gruber et al.(75) Band maxima in the Q band are observed at 1.94, 2.07, 2.23, and 2.38 eV (the first and third are assigned to Qy and Qx), whereas B-band maxima are observed at 3.08 and 3.38 eV (assigned to Bx and By).
Before proceeding to the presentation and discussion of the computational results, it is useful to recall that absorption spectroscopy of porphyrin-like macrocyclic compounds is conventionally discussed in the context of the Gouterman model, which emphasizes excitations among the four frontier molecular orbitals HOMO – 1, HOMO, LUMO, and LUMO + 1, creating the Q and B bands (Figure 3). The Gouterman model originates from the description of the porphyrin ring, where these four orbitals transform as the accidentally degenerate pair a2u and a1u, plus the unoccupied eg degenerate pair (egx and egy) in the idealized D4h point group. As Chl a loses all of the formal symmetry elements of the parent porphyrin system, all degeneracies in the frontier MOs are lifted, leading to the splitting of transitions into distinct components. These are conventionally labeled as x and y according to the transition dipole orientation in the macrocyclic plane, although the situation is not as clear-cut in chlorophylls and bacteriochlorophylls as implied by the formal analogy of the labels with the porphyrin case. The y-labeled features are principally associated with HOMO → LUMO and HOMO – 1 → LUMO + 1 transitions, whereas the x-labeled features are mostly associated with HOMO – 1 → LUMO and HOMO → LUMO + 1 transitions.
Figure 3.

Chl a frontier molecular (Hartree–Fock) orbitals associated with the Q- and B-band transitions according to the Gouterman model. Although no symmetry elements or degeneracies are present, the orbitals resemble at least qualitatively those of the parent porphyrin system. In parentheses, the symmetry labels of the parent porphyrin (D4h point group) and chlorin (C2v point group) systems are provided for reference. The arrows show which orbital pairs contribute mostly to the corresponding excitations, with the labels adhering to the nomenclature originally defined for the parent porphyrin system to indicate the approximate polarization of individual transitions.
As we will discuss in more detail in a later section presenting the band shape calculations, we have attempted to back-correct the experimental data shown in Figure 2. This gives us a set of VEEs, 0–0 energies, and band maxima that we will refer to as “quasi-experimental” in the following. These energies will make it easy to compare the calculated VEEs from various quantum chemical approaches with the quasi-experimental energies. Table 1 presents the results of this analysis that are used as reference in the following.
Table 1. Quasi-Experimental 0–0 Energies and VEEs Associated with the Individual Excited States (All Values in eV).
| Qy | Qx | Bx | By | |
|---|---|---|---|---|
| band max | 1.94 | 2.23 | 3.08 | 3.38 |
| 0–0 energy | 1.93 | 2.22 | 3.07 | 3.37 |
| VEE | 1.99 | 2.30 | 3.12 | 3.38 |
Results of DLPNO–STEOM-CCSD Calculations
DLPNO–STEOM-CCSD calculations predict two excited states in the Q region, at 1.75 and 2.24 eV, which can be identified with Qy and Qx, respectively. Two higher energy transitions at 3.17 and 3.39 eV fall within the Soret region and are assigned to the Bx and By components, respectively. These assignments are straightforwardly based on the nature of the molecular orbitals involved (Figure 3), the computed configuration interaction coefficients for the excitations (Table 2), the corresponding natural transition orbitals (NTOs) (Figure 4), and the orientation of the TDM vector relative to the macrocyclic plane (Figure 5). The Qy transition mainly involves the HOMO → LUMO excitation, which largely conforms to the Gouterman model, whereas Qx is composed of a smaller contribution from the HOMO – 1 → LUMO excitation combined with the HOMO → LUMO + 1 transition. It is noted that both LUMO and LUMO + 1 have some contribution from the vinyl group at position 3 of the chlorin macrocycle. The calculated oscillator strengths are consistent with the above assignment, with Qy higher than Qx (fosc = 0.22 vs 0.04) and the Soret bands having significantly higher oscillator strengths of fosc = 1.30 and 1.23 for Bx and By, respectively. The relevant information of the higher lying excited states is provided in the Supporting Information (Table S3 and Figure S1).
Table 2. VEEs (E, in eV) of Gas-Phase Optimized Chl a Using DLPNO–STEOM-CCSDa.
| excited state | E (eV) | frontier molecular orbitals | % contribution | |μ| (Debye) |
|---|---|---|---|---|
| S1 (Qy) | 1.746 (0.219) | HOMO → LUMO, HOMO – 1 → LUMO + 1 | 0.69, 0.16 | 5.76 |
| S2 (Qx) | 2.240 (0.040) | HOMO – 1 → LUMO, HOMO → LUMO + 1 | 0.59, 0.28 | 2.15 |
| S3 (Bx) | 3.172 (1.304) | HOMO → LUMO + 1, HOMO – 1 → LUMO | 0.49, 0.22 | 10.34 |
| S4 (By) | 3.397 (1.231) | HOMO – 1 → LUMO + 1, HOMO → LUMO | 0.61, 0.15 | 9.79 |
Oscillator strengths are shown in parenthesis. The major contributions in the canonical basis associated with the first four electronic states are described. The magnitude of the TDM (μ, in Debye) associated with the excited state is also provided.
Figure 4.

NTOs associated with the first four electronic excited states computed by DLPNO–STEOM-CCSD. Isosurface maps are drawn with a cutoff value of ±0.3 au.
Figure 5.

Orientation of TDMs associated with the Q- and B-band transitions computed using DLPNO–STEOM-CCSD. The TDM vectors of Qy, Qx, Bx, and By deviate (with reference to the y-axis) by 10.1, 45.3, 71.3, and 6.4°, respectively.
Compared to the quasi-experimental VEEs, the computed excitation energy for the lowest excited state (Qy) appears to be red-shifted by 0.24 eV. This represents the largest deviation from the reference among the computed values. On the other hand, the second excited state (Qx) matches well with the quasi-experimental value of 2.30 eV. In the B-band region, the computed values for both the Bx and By bands agree very well with the quasi-experimental values. It is particularly encouraging that the new method delivers a balanced description of all relevant transitions. Only the apparent slight underestimation of the lowest energy excitation (i.e., Qy) seems to require further analysis given the importance of the lowest excited state in photosynthetic processes. A similar red shift has been observed in a STEOM-CCSD study110 of free base porphyrin. In addition to a possible yet-to-be determined methodological origin, one possible reason is the reference geometric structure used for the calculations. As discussed in greater detail below, the results for certain transitions can be highly sensitive to this choice. Another possible reason for the apparent divergence of the computed Qy from the quasi-experimental reference value could be related to the charge-tagged approach employed in the experiments: depending on the specificity of the binding of cationic species around Chl a, electrochromic shifts can be produced in the absorption spectra,109,111 and hence the low-energy part of the action spectrum may deviate from the net gas-phase spectrum of Chl a. However, such deviations are predicted to be small.30
Accurate determination of the TDM and its orientation associated with the low-energy excited states of the biological chromophores112 hold the key to model important energy-transfer processes. Based on our DLPNO–STEOM-CCSD calculations, the TDM associated with Qy slightly deviates from the xy plane and is not perfectly aligned to the y axis (Figure 5). Interestingly, similar results were obtained in the experimental study (polarization-resolved femtosecond visible pump–infrared probe spectroscopy) performed with d8-toluene as the solvent.113 In addition, we find the TDMs associated with Qy and Qx to be nonorthogonal,9,12 with an angle of 35° between them. Similarly, the TDMs associated with By and Bx were found to be nonorthogonal, with a mutual angle of 65°.
Comparison of DLPNO–STEOM-CCSD to the Literature Results
In comparison with other wave function methods, SAC-CI27,32 predicts two excitations each in the Q-band and B-band regions, whereas non-Gouterman-type excitations (N bands) were found nearly degenerate with the By component (0.01 eV above By), consistent with the present DLPNO–STEOM-CCSD results. The lowest excited state (Qy) obtained from the present DLPNO–STEOM-CCSD approach is within the range previously reported by SAC-CI,27,32 that is, from 1.75 to 1.81 eV, depending on the geometry used and the computational details.
Literature values for the first excited state obtained with other approximations to the CC theory, such as CC2 and ADC(2), range from 1.99 to 2.26 eV,34 but the performance of such approximate methods for higher excited states that comprise the complete spectrum remains to be evaluated. A collection of literature values is summarized in the Supporting Information (Table S4). It is important to note that most past studies that applied wave function methods to this problem have used diverse geometric models, in some cases obtained directly from a protein crystal structure without further optimization32 (a practice that is strongly discouraged114,115) and in other cases optimized at the levels of theory that perhaps would not have been used today. A direct comparison of correlated wavefunction-based methods may not be reliable in the absence of results obtained with a common high-quality geometric reference, converged technical settings, and full coverage of all excited states of interest.
Non-negligible variations in the VEEs were noticed with respect to the DFT functional employed for the ground-state geometry optimization. Two important structural differences can be observed: PBE-116 and B3LYP-optimized geometries produced more in-plane vinyl conformations; however, CAM-B3LYP preferentially rotates the vinyl group more out of the plane vinyl rotation (Figure S2). On the other hand, CAM-B3LYP geometries have slightly shorter Mg–N distances compared to PBE- and B3LYP-optimized geometries. Single-point DLPNO–STEOM-CCSD calculations on the CAM-B3LYP-optimized geometry produce more blue-shifted VEEs for both the Q and B bands (by 0.1–0.2 eV) compared to the B3LYP and PBE ground-state geometries. As noted earlier, the first non-Gouterman-type excitation lies 0.13 eV above By using the CAM-B3LYP geometry. However, this excitation is found to be nearly degenerate with the By excitation with the B3LYP-optimized geometry and falls in between Bx and By in case of the geometry optimized with the PBE functional (Table S5). Therefore, small variations in geometry lead to non-negligible changes in the energetics of the low-energy excitations and lowering of non-Gouterman-type excitations, which further complicate the B-band description; however, these changes do not alter the fundamental description of the spectrum.
To probe the effect of the vinyl group rotation on the structure–property correlations, we computed VEEs using DLPNO–STEOM-CCSD on structures with exactly the same macrocyclic geometry, where the dihedral angle associated with the vinyl group rotation is scanned from 0 to 90° in 15° steps (Table S6). We found that vinyl rotation does not impact the x- and y-polarized Q and B components but only affects the stabilization of a non-Gouterman state. Therefore, it is the variation produced by the various DFT functionals in the bond distances of the macrocyclic ring that produces the spectral shift in the Q and B bands. Beyond the implications for understanding the biophysical role of specific chlorophylls, this has consequences for the evaluation of theoretical methods used for excitation energies, as the choice of geometry becomes a critical parameter in assessing the quality of theoretical methods, affecting the perceived error of a given method for the calculation of excited states.
Comparison of DLPNO–STEOM-CCSD Calculations with DFT
Table 3 compares the DLPNO–STEOM-CCSD values with the excited-state energies predicted by seven diverse functionals using the same geometry for Chl a. All functionals predict two excitations in the Q region, and the overarching impression from the TD-DFT results is the tendency to produce blue-shifted values for Qy, and even more so for Qx, for which range-separated functionals perform surprisingly poorly.
Table 3. VEEs (in eV) Associated with the x- and y-Polarized Components of the Q and B Bands of Chl a Computed with DLPNO–STEOM-CCSD and TD-DFT, Compared to Quasi-Experimental Valuesa.
| method | Qy | Qx | Bx | By |
|---|---|---|---|---|
| DLPNO–STEOM-CCSD | 1.75 (0.219) [1] | 2.24 (0.040) [2] | 3.17 (1.304) [3] | 3.40 (1.231) [4] |
| PBE0 | 2.19 (0.248) [1] | 2.40 (0.020) [2] | 3.26 (0.509) [4] | 3.45 (0.786) [7] |
| B3LYP | 2.16 (0.237) [1] | 2.35 (0.019) [2] | 3.17 (0.481) [4] | 3.35 (0.731) [7] |
| BHandHLYP | 2.18 (0.269) [1] | 2.58 (0.021) [2] | 3.50 (0.966) [3] | 3.80 (0.899) [5] |
| CAM-B3LYP | 2.14 (0.239) [1] | 2.53 (0.029) [2] | 3.44 (0.885) [3] | 3.71 (0.895) [5] |
| ωB97X-D3(BJ) | 2.09 (0.222) [1] | 2.71 (0.047) [2] | 3.56 (1.058) [3] | 3.93 (0.730) [5] |
| B2PLYP | 2.12 (0.262) [1] | 2.23 (0.019) [2] | 3.17 (0.905) [3] | 3.27 (0.748) [4] |
| ωB2PLYP | 2.04 (0.233) [1] | 2.49 (0.048) [2] | 3.45 (1.158) [3] | 3.78 (0.704) [4] |
| quasi-exp. VEE | 1.99 | 2.30 | 3.12 | 3.38 |
Values in parenthesis indicate oscillator strengths. Numbers in brackets represent the rank of the root based on increasing excitation energies; DFT methods often predict additional spurious low-energy states (see the Supporting Information for complete data).
Unlike DLPNO–STEOM-CCSD, all DFT functionals that do not incorporate perturbational correlation contribution (double-hybrids) predict more than two excitations in the Soret region. Besides the predicted Bx and By, these additional non-Gouterman-type27 excitations have a charge-transfer character with diminishing oscillator strengths. Similar observations were reported earlier, and some of these excitations were labeled as N transitions.27 They might be considered as artifacts or “ghost states”, at least in the sense that they appear unphysically low in energy. We observe three categories of functionals giving distinct results. PBE0 and B3LYP predict three non-Gouterman-type excitations, one between Qx and Bx and two between Bx and By (Table S7). For CAM-B3LYP, ωB97X-D3(BJ), and BHandHLYP, the results are better as they predict the first non-Gouterman-type excitation situated right in between Bx and By (Table S8 and Figures S3–S5). In contrast, DLPNO–STEOM-CCSD predicts such excitations only above the B band (see Table S3). Double-hybrid functionals B2PLYP and ωB2PLYP provide a similar description of the ordering of excited states as that obtained by the DLPNO–STEOM-CCSD computations (Tables S9 and S10). However, both double-hybrid functionals predict the first N transitions to be nearly isoenergetic with the By band (a difference of 0.003 and 0.045 eV in the case of B2PLYP and ωB2PLYP, respectively). Overall, B2PLYP performs bests among the DFT functionals and provides results of practically equal quality to the DLPNO–STEOM-CCSD results. In contrast, CAM-B3LYP, ωB97X-D3(BJ), BHandHLYP, and ωB2PLYP functionals overestimate the B-band excitation energies and suffer from the presence of ghost states. Therefore, with the important exception of B2PLYP, no other DFT functional can provide a one-stop-solution, in the framework of TD-DFT, for all low-energy absorption features of Chl a. It is stressed that the lack of balance and the occurrence of ghost states are characteristic of TD-DFT and are by no means unique to the chlorophyll system.38,117,118
Band Shape Calculations
Understanding the features of the Q band of biochromophores is central for understanding various photophysical phenomena related to the protein–pigment interaction.119,120 In general, the Q-band regions of important chromophores such as bacteriochlorophyll a and pheophytin a are easier to interpret (in terms of Qy and Qx assignment) because of their large Qy–Qx energy gaps.9 The situation is more complicated for Chl a because of the small Qy–Qx energy gap and the difficulty in assigning the Qx origin. The most recent recommendations regarding the Qx origin by Reimers et al.(9) are based on a model which includes the vibronic picture to obtain satisfactory results. In addition, they report that Qy and Qx mix, influencing exciton transport and coherence. Qy and Qx mixing was reported to depend on the solvent, as solvent molecules can ligate axially,103 form peripheral hydrogen bonds, influence the macrocyclic ring curvature, and so forth. These structural perturbations collectively can influence the Q-band properties and the overall vibronic structure. Here, we present an intrinsic vibronic picture of the Q band of Chl a in vacuo for comparison against the experimental spectrum.
As part of this investigation, we have first used the comparison of the computed and experimental band shapes to estimate the shifts required to adjust the experimental band maxima to VEEs. On the basis of these data, we have determined the energy difference between the band maxima, the vertical excitation, and the corresponding 0–0 energy. We found that most band maxima are slightly red-shifted compared to the VEE for each excited state under consideration; however, the extent of the red shift is slightly different for each excited state (Table S2). Subsequently, we used these obtained shifts for each individual excited state and applied them to the band maxima of the experimental spectrum as a correction, which allows us to extract “quasi-experimental” VEEs and 0–0 energies that can be compared to the computed values (see Table 1).
In the following, we describe how we have employed band shape calculations in combination with the DLPNO–STEOM-CCSD energies to analyze the spectrum of Chl a. We have used two distinct approximations: the VG approach and the adiabatic Hessian after-step (AHAS) approach. Both methods require an optimized ground-state geometry, whereas the excited-state structure is approximated by a single augmented Hessian optimization step. The VG approach assumes that the ground-state Hessian adequately approximates the excited-state one, whereas AHAS relies on an explicitly computed Hessian for the excited state. For the present calculations, all Hessians were computed with CAM-B3LYP, and the VEEs and TDMs were those of DLPNO–STEOM-CCSD.
Both approaches show significant overlap between the vibronic progressions associated with the Qy and Qx excitations, and the overall spectrum is in very good agreement with the experimental spectrum. The main difference between the VG and AHAS results is that the AHAS approach produces an amplified shoulder in the region next to Qy (Figures S8 and S9). On the other hand, both approaches produce equivalent results for Qx and the respective vibronic progression. The shift results in an increased overlap, but even though there are vibrational modes that appear at the same region in the vibronic progression of Qy and Qx, there are no modes with high intensities among them. Overall, the VG result approximates better the experimental envelope and is to be preferred over the much more expensive AHAS scheme (Figures S6 and S7). It is also important to note here that previous studies121 using the VG approach in the context of the Chl a absorption spectra yielded satisfactory results.
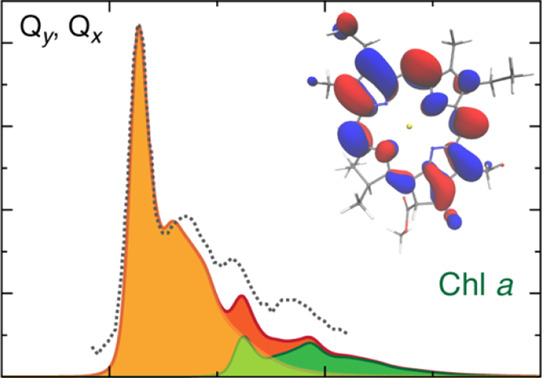
The complete vibronic progression associated with the Qy and Qx excitations using the VG approach compared to the experimental spectrum is shown in Figure 6. For simplicity, the spectral features observed in the experimental spectra are broken down into four regions (Pi, i = 1–4). The computed vibronic progression associated with the Qy excitation typically covers all four regions, with a higher contribution in the P1 and P2, whereas its tail spans regions P3 and P4. P1 corresponds to the 0–0 transition, with a minor contribution from the low-frequency out-of-plane chlorin deformation modes and substituent rotations, as well as low-energy in-plane bending modes. The P2 region corresponds to the vibronic progression, with the contribution from various in-plane stretching–bending modes, whereas the accompanying shoulder region corresponds to the in-plane chlorin deformations combining the C–C and C–N stretching and C–H bending modes. No fundamentals of the first excited state occur in the P3 region, which is associated with the Qx excitation. The P4 region encompasses modes of the second excited state ascribed to the P2 shoulder from the first excited state. Based on the present results, the Herzberg–Teller contribution has a noticeable effect on the overall form of the P3 and P4 regions (see Figures S10 and S11), whereas P1 and P2 can be adequately described in the Frank–Condon picture.
Figure 6.

Computed vibronic spectrum of the Q band using the VG approximation. The spectrum associated with the Qy excitation (i.e., S0 → S1) is shifted by 0.18 eV to align with the experimental band maximum. The “raw” band shape is depicted in Figure S5. Various absorption maxima observed in the experimental spectra are labeled accordingly.
Our calculations do not allow us to directly discuss the mixing of states, as we are operating in an adiabatic picture that excludes the effects of nonadiabatic coupling matrix elements. Although this is a limitation to be addressed in future developments, we observe that the experimental spectrum can be reproduced sufficiently well without explicitly accounting for the mixing of states. Therefore, we may suggest that mixing is not a dominant feature in the gas-phase absorption spectra of Chl a.
The vibronic spectrum associated with the Bx and By excited states of the B band is presented in Figure 7. The B band is significantly less well resolved experimentally compared to the Q band; therefore, we do not consider it feasible to delve into detailed assignments. However, it is important to stress that the overall shape of the spectrum is reproduced quite accurately by the present simulations. This includes not only the two principal features, whose separation is only slightly underestimated, but also the shoulders that are attributed to the vibrational progressions of Bx and By.
Figure 7.

Computed vibronic spectrum of the B band using the VG approximation.
The present study has focused strictly on gas-phase Chl a models. As a final note, we would therefore like to point out that the separation between the Qy and Qx band maxima, which Figure 6 indicates to be ca. 2500 cm–1 (ca. 0.3 eV), is suggested to decrease upon solvent coordination. For example, the vibronic model developed by Reimers et al.(9) predicted this energy gap to be 0.2 eV in ether, 0.12 eV in pyridine, 0.10 eV in MeOH/EtOH mixture. A recent study by Ogilvie and co-workers12 showed a significant overlap between the vibrational modes associated with the Qy side-band and Qx band for an axially isopropanol-coordinated Chl a (Qy–Qx gap of 0.14 eV). Based on their study, this overlap was evident as the excitation energy of S2 decreases as a result of the axial ligation due to HOMO – 1 destabilization. On the same principle, the heterogeneous protein environment can also modulate the Qy–Qx energy gap and other properties of the chromophores122 through axial ligation,78 hydrogen bonding,123,124 macrocyclic ring distortion,125,126 and electrostatic effects.119 The vibrational modes of Chl a are also fine-tuned in a protein matrix for efficient energy transfer and charge separation. The vibronic picture shown above can thus be considered as a reference point for gas-phase Chl a and as a guide for comparison with environmentally or chemically modulated forms of the system.
Conclusions
In conclusion, the present study demonstrates that the DLPNO–STEOM-CCSD approach is eminently useable for systems as large and complex as chlorophylls and provides accurate results in reasonable turnaround times and in a black box fashion. It is noted that in terms of cost, the method in the current implementation is only a few times more expensive than double-hybrid DFT. Importantly, DLPNO–STEOM-CCSD offers a balanced treatment of both the low-energy and high-energy regions of the spectrum, in contrast to any of the investigated DFT methods with the possible exception of B2PLYP. The study serves as a springboard for further large-scale applications that will use DLPNO–STEOM-CCSD to calculate the absorption features of photosynthetic pigments in solvents or within proteins. The treatment of the environment, axial ligation, ring deformation, and peripheral hydrogen bonding, among others, will all affect the excited-state profile of the chromophore. A reliable electronic structure method such as the one described here will be essential for ensuring that the fundamental physics of the system is correctly reproduced.
Acknowledgments
We thank Prof. Lars H. Andersen for kindly providing original experimental data from ref (75). Support by the Max Planck Society is gratefully acknowledged. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2033-390677874-RESOLV.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c05761.
Excitation energies computed with different methods; analysis and composition of excited states; and molecular orbitals, vibronic spectra, and Cartesian coordinates of optimized structures (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Blankenship R. E.Molecular Mechanisms of Photosynthesis, 2nd ed.; Wiley: Chichester, 2014; p 312. [Google Scholar]
- Senge M. O.; Ryan A. A.; Letchford K. A.; MacGowan S. A.; Mielke T. Chlorophylls, Symmetry, Chirality, and Photosynthesis. Symmetry 2014, 6, 781–843. 10.3390/sym6030781. [DOI] [Google Scholar]
- Croce R.; van Amerongen H. Natural strategies for photosynthetic light harvesting. Nat. Chem. Biol. 2014, 10, 492–501. 10.1038/nchembio.1555. [DOI] [PubMed] [Google Scholar]
- Müh F.; Zouni A. Structural basis of light-harvesting in the photosystem II core complex. Protein Sci. 2020, 29, 1090–1119. 10.1002/pro.3841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuller F. D.; Pan J.; Gelzinis A.; Butkus V.; Senlik S. S.; Wilcox D. E.; Yocum C. F.; Valkunas L.; Abramavicius D.; Ogilvie J. P. Vibronic coherence in oxygenic photosynthesis. Nat. Chem. 2014, 6, 706–711. 10.1038/nchem.2005. [DOI] [PubMed] [Google Scholar]
- Cardona T.; Sedoud A.; Cox N.; Rutherford A. W. Charge Separation in Photosystem II: A Comparative and Evolutionary Overview. Biochim. Biophys. Acta, Bioenerg. 2012, 1817, 26–43. 10.1016/j.bbabio.2011.07.012. [DOI] [PubMed] [Google Scholar]
- Krewald V.; Retegan M.; Pantazis D. A. Principles of Natural Photosynthesis. Top. Curr. Chem. 2016, 371, 23–48. 10.1007/128_2015_645. [DOI] [PubMed] [Google Scholar]
- Reimers J. R.; Biczysko M.; Bruce D.; Coker D. F.; Frankcombe T. J.; Hashimoto H.; Hauer J.; Jankowiak R.; Kramer T.; Linnanto J.; et al. Challenges facing an understanding of the nature of low-energy excited states in photosynthesis. Biochim. Biophys. Acta, Bioenerg. 2016, 1857, 1627–1640. 10.1016/j.bbabio.2016.06.010. [DOI] [PubMed] [Google Scholar]
- Reimers J. R.; Cai Z.-L.; Kobayashi R.; Rätsep M.; Freiberg A.; Krausz E. Assignment of the Q-Bands of the Chlorophylls: Coherence Loss via Qx–Qy Mixing. Sci. Rep. 2013, 3, 2761. 10.1038/srep02761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novoderezhkin V. I.; Romero E.; van Grondelle R. How exciton-vibrational coherences control charge separation in the photosystem II reaction center. Phys. Chem. Chem. Phys. 2015, 17, 30828–30841. 10.1039/c5cp00582e. [DOI] [PubMed] [Google Scholar]
- Romero E.; Augulis R.; Novoderezhkin V. I.; Ferretti M.; Thieme J.; Zigmantas D.; Van Grondelle R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676. 10.1038/nphys3017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y.; Schubert A.; Maret E.; Burdick R. K.; Dunietz B. D.; Geva E.; Ogilvie J. P. Vibronic structure of photosynthetic pigments probed by polarized two-dimensional electronic spectroscopy and ab initio calculations. Chem. Sci. 2019, 10, 8143–8153. 10.1039/c9sc02329a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceulemans A.; Oldenhof W.; Gorller-Walrand C.; Vanquickenborne L. G. Gouterman’s “four-orbital” model and the MCD spectra of high-symmetry metalloporphyrins. J. Am. Chem. Soc. 1986, 108, 1155–1163. 10.1021/ja00266a007. [DOI] [Google Scholar]
- Gouterman M. Spectra of porphyrins. J. Mol. Spectrosc. 1961, 6, 138–163. 10.1016/0022-2852(61)90236-3. [DOI] [Google Scholar]
- Hughes J. L.; Conlon B.; Wydrzynski T.; Krausz E. The assignment of Qy(1, 0) vibrational structure and Qx for chlorophyll a. Phys. Procedia 2010, 3, 1591–1599. 10.1016/j.phpro.2010.01.226. [DOI] [Google Scholar]
- Lewis N. H. C.; Fleming G. R. Two-dimensional electronic-vibrational spectroscopy of chlorophyll a and b. J. Phys. Chem. Lett. 2016, 7, 831–837. 10.1021/acs.jpclett.6b00037. [DOI] [PubMed] [Google Scholar]
- Rätsep M.; Linnanto J.; Freiberg A. Mirror symmetry and vibrational structure in optical spectra of chlorophyll a. J. Chem. Phys. 2009, 130, 194501. 10.1063/1.3125183. [DOI] [PubMed] [Google Scholar]
- Rätsep M.; Linnanto J. M.; Freiberg A. Higher Order Vibronic Sidebands of Chlorophyll a and Bacteriochlorophyll a for Enhanced Excitation Energy Transfer and Light Harvesting. J. Phys. Chem. B 2019, 123, 7149–7156. 10.1021/acs.jpcb.9b06843. [DOI] [PubMed] [Google Scholar]
- Engel G. S.; Calhoun T. R.; Read E. L.; Ahn T.-K.; Mančal T.; Cheng Y.-C.; Blankenship R. E.; Fleming G. R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782. 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
- Linnanto J.; Korppi-Tommola J. Quantum chemical simulation of excited states of chlorophylls, bacteriochlorophylls and their complexes. Phys. Chem. Chem. Phys. 2006, 8, 663–687. 10.1039/b513086g. [DOI] [PubMed] [Google Scholar]
- Dreuw A.; Head-Gordon M. Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. 10.1021/cr0505627. [DOI] [PubMed] [Google Scholar]
- König C.; Neugebauer J. Quantum Chemical Description of Absorption Properties and Excited-State Processes in Photosynthetic Systems. ChemPhysChem 2012, 13, 386–425. 10.1002/cphc.201100408. [DOI] [PubMed] [Google Scholar]
- Sundholm D. Density functional theory calculations of the visible spectrum of chlorophyll a. Chem. Phys. Lett. 1999, 302, 480–484. 10.1016/s0009-2614(99)00194-3. [DOI] [Google Scholar]
- Sundholm D. Comparison of the electronic excitation spectra of chlorophyll a and pheophytin a calculated at density functional theory level. Chem. Phys. Lett. 2000, 317, 545–552. 10.1016/s0009-2614(99)01428-1. [DOI] [Google Scholar]
- Cai Z.-L.; Sendt K.; Reimers J. R. Failure of density-functional theory and time-dependent density-functional theory for large extended π systems. J. Chem. Phys. 2002, 117, 5543–5549. 10.1063/1.1501131. [DOI] [Google Scholar]
- Dahlbom M.; Reimers J. Successes and failures of time-dependent density functional theory for the low-lying excited states of chlorophylls. Mol. Phys. 2005, 103, 1057–1065. 10.1080/00268970412331333528. [DOI] [Google Scholar]
- Cai Z.-L.; Crossley M. J.; Reimers J. R.; Kobayashi R.; Amos R. D. Density Functional Theory for Charge Transfer: The Nature of the N-Bands of Porphyrins and Chlorophylls Revealed through CAM-B3LYP, CASPT2, and SAC-CI Calculations. J. Phys. Chem. B 2006, 110, 15624–15632. 10.1021/jp063376t. [DOI] [PubMed] [Google Scholar]
- Milne B. F.; Toker Y.; Rubio A.; Nielsen S. B. Unraveling the Intrinsic Color of Chlorophyll. Angew. Chem., Int. Ed. 2015, 54, 2170–2173. 10.1002/anie.201410899. [DOI] [PubMed] [Google Scholar]
- Stockett M. H.; Musbat L.; Kjær C.; Houmøller J.; Toker Y.; Rubio A.; Milne B. F.; Brøndsted Nielsen S. The Soret absorption band of isolated chlorophyll a and b tagged with quaternary ammonium ions. Phys. Chem. Chem. Phys. 2015, 17, 25793–25798. 10.1039/c5cp01513h. [DOI] [PubMed] [Google Scholar]
- Preciado-Rivas M. R.; Mowbray D. J.; Lyon K.; Larsen A. H.; Milne B. F. Optical excitations of chlorophyll a and b monomers and dimers. J. Chem. Phys. 2019, 151, 174102. 10.1063/1.5121721. [DOI] [PubMed] [Google Scholar]
- Parusel A. B. J.; Grimme S. A Theoretical Study of the Excited States of Chlorophyll a and Pheophytin a. J. Phys. Chem. B 2000, 104, 5395–5398. 10.1021/jp000346w. [DOI] [Google Scholar]
- Hasegawa J.; Ozeki Y.; Ohkawa K.; Hada M.; Nakatsuji H. Theoretical Study of the Excited States of Chlorin, Bacteriochlorin, Pheophytin a, and Chlorophyll a by the SAC/SAC-CI Method. J. Phys. Chem. B 1998, 102, 1320–1326. 10.1021/jp972894o. [DOI] [Google Scholar]
- Winter N. O. C.; Hättig C. Scaled opposite-spin CC2 for ground and excited states with fourth order scaling computational costs. J. Chem. Phys. 2011, 134, 184101. 10.1063/1.3584177. [DOI] [PubMed] [Google Scholar]
- Suomivuori C.-M.; Winter N. O. C.; Hättig C.; Sundholm D.; Kaila V. R. I. Exploring the Light-Capturing Properties of Photosynthetic Chlorophyll Clusters Using Large-Scale Correlated Calculations. J. Chem. Theory Comput. 2016, 12, 2644–2651. 10.1021/acs.jctc.6b00237. [DOI] [PubMed] [Google Scholar]
- Anda A.; Hansen T.; De Vico L. Multireference Excitation Energies for Bacteriochlorophylls A within Light Harvesting System 2. J. Chem. Theory Comput. 2016, 12, 1305–1313. 10.1021/acs.jctc.5b01104. [DOI] [PubMed] [Google Scholar]
- Anda A.; De Vico L.; Hansen T. Intermolecular Modes between LH2 Bacteriochlorophylls and Protein Residues: The Effect on the Excitation Energies. J. Phys. Chem. B 2017, 121, 5499–5508. 10.1021/acs.jpcb.7b02071. [DOI] [PubMed] [Google Scholar]
- Anda A.; Hansen T.; De Vico L. Qy and Qx Absorption Bands for Bacteriochlorophyll a Molecules from LH2 and LH3. J. Phys. Chem. A 2019, 123, 5283–5292. 10.1021/acs.jpca.9b02877. [DOI] [PubMed] [Google Scholar]
- Dreuw A.; Head-Gordon M. Failure of time-dependent density functional theory for long-range charge-transfer excited states: the zincbacteriochlorin–bacteriochlorin and bacteriochlorophyll–spheroidene complexes. J. Am. Chem. Soc. 2004, 126, 4007–4016. 10.1021/ja039556n. [DOI] [PubMed] [Google Scholar]
- Korona T.; Werner H.-J. Local treatment of electron excitations in the EOM-CCSD method. J. Chem. Phys. 2003, 118, 3006–3019. 10.1063/1.1537718. [DOI] [Google Scholar]
- Kats D.; Korona T.; Schütz M. Local CC2 electronic excitation energies for large molecules with density fitting. J. Chem. Phys. 2006, 125, 104106. 10.1063/1.2339021. [DOI] [PubMed] [Google Scholar]
- Kats D.; Schütz M. A multistate local coupled cluster CC2 response method based on the Laplace transform. J. Chem. Phys. 2009, 131, 124117. 10.1063/1.3237134. [DOI] [PubMed] [Google Scholar]
- Helmich B.; Hättig C. Local pair natural orbitals for excited states. J. Chem. Phys. 2011, 135, 214106. 10.1063/1.3664902. [DOI] [PubMed] [Google Scholar]
- Helmich B.; Hättig C. A pair natural orbital implementation of the coupled cluster model CC2 for excitation energies. J. Chem. Phys. 2013, 139, 084114. 10.1063/1.4819071. [DOI] [PubMed] [Google Scholar]
- Frank M. S.; Hättig C. A pair natural orbital based implementation of CCSD excitation energies within the framework of linear response theory. J. Chem. Phys. 2018, 148, 134102. 10.1063/1.5018514. [DOI] [PubMed] [Google Scholar]
- Mester D.; Nagy P. R.; Kállay M. Reduced-cost linear-response CC2 method based on natural orbitals and natural auxiliary functions. J. Chem. Phys. 2017, 146, 194102. 10.1063/1.4983277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mester D.; Nagy P. R.; Kállay M. Reduced-cost second-order algebraic-diagrammatic construction method for excitation energies and transition moments. J. Chem. Phys. 2018, 148, 094111. 10.1063/1.5021832. [DOI] [Google Scholar]
- Peng C.; Clement M. C.; Valeev E. F. State-Averaged Pair Natural Orbitals for Excited States: A Route toward Efficient Equation of Motion Coupled-Cluster. J. Chem. Theory Comput. 2018, 14, 5597–5607. 10.1021/acs.jctc.8b00171. [DOI] [PubMed] [Google Scholar]
- Izsák R. Single-reference coupled cluster methods for computing excitation energies in large molecules: The efficiency and accuracy of approximations. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, 10, e1445 10.1002/wcms.1445. [DOI] [Google Scholar]
- Dutta A. K.; Neese F.; Izsák R. Towards a pair natural orbital coupled cluster method for excited states. J. Chem. Phys. 2016, 145, 034102. 10.1063/1.4958734. [DOI] [PubMed] [Google Scholar]
- Dutta A. K.; Saitow M.; Riplinger C.; Neese F.; Izsák R. A near-linear scaling equation of motion coupled cluster method for ionized states. J. Chem. Phys. 2018, 148, 244101. 10.1063/1.5029470. [DOI] [PubMed] [Google Scholar]
- Dutta A. K.; Saitow M.; Demoulin B.; Neese F.; Izsák R. A domain-based local pair natural orbital implementation of the equation of motion coupled cluster method for electron attached states. J. Chem. Phys. 2019, 150, 164123. 10.1063/1.5089637. [DOI] [PubMed] [Google Scholar]
- Riplinger C.; Neese F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. 10.1063/1.4773581. [DOI] [PubMed] [Google Scholar]
- Riplinger C.; Pinski P.; Becker U.; Valeev E. F.; Neese F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. 10.1063/1.4939030. [DOI] [PubMed] [Google Scholar]
- Nooijen M.; Bartlett R. J. Similarity transformed equation-of-motion coupled-cluster theory: Details, examples, and comparisons. J. Chem. Phys. 1997, 107, 6812–6830. 10.1063/1.474922. [DOI] [Google Scholar]
- Dutta A. K.; Nooijen M.; Neese F.; Izsák R. Automatic active space selection for the similarity transformed equations of motion coupled cluster method. J. Chem. Phys. 2017, 146, 074103. 10.1063/1.4976130. [DOI] [PubMed] [Google Scholar]
- Dutta A. K.; Nooijen M.; Neese F.; Izsák R. Exploring the Accuracy of a Low Scaling Similarity Transformed Equation of Motion Method for Vertical Excitation Energies. J. Chem. Theory Comput. 2018, 14, 72–91. 10.1021/acs.jctc.7b00802. [DOI] [PubMed] [Google Scholar]
- Baiardi A.; Bloino J.; Barone V. General Time Dependent Approach to Vibronic Spectroscopy Including Franck–Condon, Herzberg–Teller, and Duschinsky Effects. J. Chem. Theory Comput. 2013, 9, 4097–4115. 10.1021/ct400450k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Souza B.; Neese F.; Izsák R. On the theoretical prediction of fluorescence rates from first principles using the path integral approach. J. Chem. Phys. 2018, 148, 034104. 10.1063/1.5010895. [DOI] [PubMed] [Google Scholar]
- de Souza B.; Farias G.; Neese F.; Izsák R. Predicting Phosphorescence Rates of Light Organic Molecules Using Time-Dependent Density Functional Theory and the Path Integral Approach to Dynamics. J. Chem. Theory Comput. 2019, 15, 1896–1904. 10.1021/acs.jctc.8b00841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Souza B.; Farias G.; Neese F.; Izsák R. Efficient simulation of overtones and combination bands in resonant Raman spectra. J. Chem. Phys. 2019, 150, 214102. 10.1063/1.5099247. [DOI] [PubMed] [Google Scholar]
- Franck J.; Dymond E. G. Elementary processes of photochemical reactions. Trans. Faraday Soc. 1926, 21, 536–542. 10.1039/tf9262100536. [DOI] [Google Scholar]
- Condon E. Theory of Intensity Distribution in Band Systems. Phys. Rev. 1926, 28, 1182–1201. 10.1103/physrev.28.1182. [DOI] [Google Scholar]
- Condon E. U. Nuclear Motions Associated with Electron Transitions in Diatomic Molecules. Phys. Rev. 1928, 32, 858–872. 10.1103/physrev.32.858. [DOI] [Google Scholar]
- Herzberg G.; Teller E. Schwingungsstruktur der Elektronenübergänge bei mehratomigen Molekülen. Z. Phys. Chem., Abt. B 1933, 21, 410–446. 10.1515/zpch-1933-2136. [DOI] [Google Scholar]
- Salla C. A. M.; Teixeira dos Santos J.; Farias G.; Bortoluzi A. J.; Curcio S. F.; Cazati T.; Izsák R.; Neese F.; de Souza B.; Bechtold I. H. New Boron(III) Blue Emitters for All-Solution Processed OLEDs: Molecular Design Assisted by Theoretical Modeling. Eur. J. Inorg. Chem. 2019, 2247–2257. 10.1002/ejic.201900265. [DOI] [Google Scholar]
- Berraud-Pache R.; Neese F.; Bistoni G.; Izsák R. Computational Design of Near-Infrared Fluorescent Organic Dyes Using an Accurate New Wave Function Approach. J. Phys. Chem. Lett. 2019, 10, 4822–4828. 10.1021/acs.jpclett.9b02240. [DOI] [PubMed] [Google Scholar]
- Berraud-Pache R.; Neese F.; Bistoni G.; Izsák R. Unveiling the Photophysical Properties of Boron-dipyrromethene Dyes Using a New Accurate Excited State Coupled Cluster Method. J. Chem. Theory Comput. 2020, 16, 564–575. 10.1021/acs.jctc.9b00559. [DOI] [PubMed] [Google Scholar]
- Barone V.; Bloino J.; Biczysko M.; Santoro F. Fully Integrated Approach to Compute Vibrationally Resolved Optical Spectra: From Small Molecules to Macrosystems. J. Chem. Theory Comput. 2009, 5, 540–554. 10.1021/ct8004744. [DOI] [PubMed] [Google Scholar]
- Bloino J.; Biczysko M.; Santoro F.; Barone V. General Approach to Compute Vibrationally Resolved One-Photon Electronic Spectra. J. Chem. Theory Comput. 2010, 6, 1256–1274. 10.1021/ct9006772. [DOI] [PubMed] [Google Scholar]
- Santoro F.; Lami A.; Improta R.; Barone V. Effective method to compute vibrationally resolved optical spectra of large molecules at finite temperature in the gas phase and in solution. J. Chem. Phys. 2007, 126, 184102. 10.1063/1.2721539. [DOI] [PubMed] [Google Scholar]
- Santoro F.; Cappelli C.; Barone V. Effective Time-Independent Calculations of Vibrational Resonance Raman Spectra of Isolated and Solvated Molecules Including Duschinsky and Herzberg–Teller Effects. J. Chem. Theory Comput. 2011, 7, 1824–1839. 10.1021/ct200054w. [DOI] [PubMed] [Google Scholar]
- Lin N.; Santoro F.; Rizzo A.; Luo Y.; Zhao X.; Barone V. Theory for Vibrationally Resolved Two-Photon Circular Dichroism Spectra. Application to (R)-(+)-3-Methylcyclopentanone. J. Phys. Chem. A 2009, 113, 4198–4207. 10.1021/jp8105925. [DOI] [PubMed] [Google Scholar]
- Santoro F.; Barone V. Computational approach to the study of the lineshape of absorption and electronic circular dichroism spectra. Int. J. Quantum Chem. 2010, 110, 476–486. 10.1002/qua.22197. [DOI] [Google Scholar]
- Santoro F.; Lami A.; Improta R.; Bloino J.; Barone V. Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg–Teller effect: The Qx band of porphyrin as a case study. J. Chem. Phys. 2008, 128, 224311. 10.1063/1.2929846. [DOI] [PubMed] [Google Scholar]
- Gruber E.; Kjær C.; Nielsen S. B.; Andersen L. H. Intrinsic Photophysics of Light-harvesting Charge-tagged Chlorophyll a and b Pigments. Chem.—Eur. J. 2019, 25, 9153–9158. 10.1002/chem.201901786. [DOI] [PubMed] [Google Scholar]
- Yang P.; Qi D.; You G.; Shen W.; Li M.; He R. Influence of Duschinsky and Herzberg-Teller effects on S0→ S1 vibrationally resolved absorption spectra of several porphyrin-like compounds. J. Chem. Phys. 2014, 141, 124304. 10.1063/1.4895958. [DOI] [PubMed] [Google Scholar]
- Neese F.; Wennmohs F.; Becker U.; Riplinger C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. 10.1063/5.0004608. [DOI] [PubMed] [Google Scholar]
- Umena Y.; Kawakami K.; Shen J.-R.; Kamiya N. Crystal Structure of the Oxygen-Evolving Photosystem II at a Resolution of 1.9 Å. Nature 2011, 473, 55–60. 10.1038/nature09913. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Thermochemistry. III. The Role Of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Weigend F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- Hellweg A.; Hättig C.; Höfener S.; Klopper W. Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. 10.1007/s00214-007-0250-5. [DOI] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H–Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Zamzam N.; van Thor J. J. Excited State Frequencies of Chlorophyll f and Chlorophyll a and Evaluation of Displacement through Franck-Condon Progression Calculations. Molecules 2019, 24, 1326. 10.3390/molecules24071326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neese F.; Wennmohs F.; Hansen A.; Becker U. Efficient, Approximate and Parallel Hartree–Fock and Hybrid DFT Calculations. A “Chain-of-Spheres” Algorithm for the Hartree–Fock Exchange. Chem. Phys. 2009, 356, 98–109. 10.1016/j.chemphys.2008.10.036. [DOI] [Google Scholar]
- Izsák R.; Neese F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. 10.1063/1.3646921. [DOI] [PubMed] [Google Scholar]
- Chai J.-D.; Head-Gordon M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- Lin Y.-S.; Li G.-D.; Mao S.-P.; Chai J.-D. Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections. J. Chem. Theory Comput. 2013, 9, 263–272. 10.1021/ct300715s. [DOI] [PubMed] [Google Scholar]
- Najibi A.; Goerigk L. The Nonlocal Kernel in van der Waals Density Functionals as an Additive Correction: An Extensive Analysis with Special Emphasis on the B97M-V and ωB97M-V Approaches. J. Chem. Theory Comput. 2018, 14, 5725–5738. 10.1021/acs.jctc.8b00842. [DOI] [PubMed] [Google Scholar]
- Mardirossian N.; Head-Gordon M. ωB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Phys. Chem. Chem. Phys. 2014, 16, 9904–9924. 10.1039/c3cp54374a. [DOI] [PubMed] [Google Scholar]
- Adamo C.; Barone V. Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
- Becke A. D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. 10.1063/1.464304. [DOI] [Google Scholar]
- Grimme S.; Neese F. Double-hybrid density functional theory for excited electronic states of molecules. J. Chem. Phys. 2007, 127, 154116. 10.1063/1.2772854. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
- Casanova-Páez M.; Dardis M. B.; Goerigk L. ωB2PLYP and ωB2GPPLYP: The First Two Double-Hybrid Density Functionals with Long-Range Correction Optimized for Excitation Energies. J. Chem. Theory Comput. 2019, 15, 4735–4744. 10.1021/acs.jctc.9b00013. [DOI] [PubMed] [Google Scholar]
- Bai S.; Mansour R.; Stojanović L.; Toldo J. M.; Barbatti M. On the origin of the shift between vertical excitation and band maximum in molecular photoabsorption. J. Mol. Model. 2020, 26, 107. 10.1007/s00894-020-04355-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balaban T. S.; Braun P.; Hättig C.; Hellweg A.; Kern J.; Saenger W.; Zouni A. Preferential pathways for light-trapping involving β-ligated chlorophylls. Biochim. Biophys. Acta, Bioenerg. 2009, 1787, 1254–1265. 10.1016/j.bbabio.2009.05.010. [DOI] [PubMed] [Google Scholar]
- Li Y.; Cai Z.-L.; Chen M. Spectroscopic Properties of Chlorophyll f. J. Phys. Chem. B 2013, 117, 11309–11317. 10.1021/jp402413d. [DOI] [PubMed] [Google Scholar]
- Li Y.; Scales N.; Blankenship R. E.; Willows R. D.; Chen M. Extinction coefficient for red-shifted chlorophylls: chlorophyll d and chlorophyll f. Biochim. Biophys. Acta, Bioenerg. 2012, 1817, 1292–1298. 10.1016/j.bbabio.2012.02.026. [DOI] [PubMed] [Google Scholar]
- Sharma Yamijala S. R. K. C.S.; Periyasamy G.; Pati S. K. Computational Studies on Structural and Excited-State Properties of Modified Chlorophyll f with Various Axial Ligands. J. Phys. Chem. A 2011, 115, 12298–12306. 10.1021/jp2041235. [DOI] [PubMed] [Google Scholar]
- Heimdal J.; Jensen K. P.; Devarajan A.; Ryde U. The role of axial ligands for the structure and function of chlorophylls. J. Biol. Inorg Chem. 2007, 12, 49–61. 10.1007/s00775-006-0164-z. [DOI] [PubMed] [Google Scholar]
- Saito K.; Shen J.-R.; Ishikita H. Influence of the axial ligand on the cationic properties of the chlorophyll pair in photosystem II from Thermosynechococcus vulcanus. Biophys. J. 2012, 102, 2634–2640. 10.1016/j.bpj.2012.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito K.; Suzuki T.; Ishikita H. Absorption-energy calculations of chlorophyll a and b with an explicit solvent model. J. Photochem. Photobiol., A 2018, 358, 422–431. 10.1016/j.jphotochem.2017.10.003. [DOI] [Google Scholar]
- Kjær C.; Stockett M. H.; Pedersen B. M.; Nielsen S. B. Strong Impact of an Axial Ligand on the Absorption by Chlorophyll a and b Pigments Determined by Gas-Phase Ion Spectroscopy Experiments. J. Phys. Chem. B 2016, 120, 12105–12110. 10.1021/acs.jpcb.6b10547. [DOI] [PubMed] [Google Scholar]
- Sun Y.; Wang H.; Zhao F.; Sun J. The effect of axial Mg2+ ligation and peripheral hydrogen bonding on chlorophyll a. Chem. Phys. Lett. 2004, 387, 12–16. 10.1016/j.cplett.2004.01.103. [DOI] [Google Scholar]
- Suomivuori C.-M.; Fliegl H.; Starikov E. B.; Balaban T. S.; Kaila V. R. I.; Sundholm D. Absorption shifts of diastereotopically ligated chlorophyll dimers of photosystem I. Phys. Chem. Chem. Phys. 2019, 21, 6851–6858. 10.1039/c9cp00616h. [DOI] [PubMed] [Google Scholar]
- Wellman S. M. J.; Jockusch R. A. Tuning the intrinsic photophysical properties of chlorophyll a. Chem.—Eur. J. 2017, 23, 7728–7736. 10.1002/chem.201605167. [DOI] [PubMed] [Google Scholar]
- Gwaltney S. R.; Bartlett R. J. Coupled-cluster calculations of the electronic excitation spectrum of free base porphin in a polarized basis. J. Chem. Phys. 1998, 108, 6790–6798. 10.1063/1.476094. [DOI] [Google Scholar]
- Hanson L. K.; Fajer J.; Thompson M. A.; Zerner M. C. Electrochromic effects of charge separation in bacterial photosynthesis: theoretical models. J. Am. Chem. Soc. 1987, 109, 4728–4730. 10.1021/ja00249a050. [DOI] [Google Scholar]
- Oviedo M. B.; Sánchez C. G. Transition Dipole Moments of the Qy Band in Photosynthetic Pigments. J. Phys. Chem. A 2011, 115, 12280–12285. 10.1021/jp203826q. [DOI] [PubMed] [Google Scholar]
- Linke M.; Lauer A.; von Haimberger T.; Zacarias A.; Heyne K. Three-Dimensional Orientation of the Qy Electronic Transition Dipole Moment within the Chlorophyll a Molecule Determined by Femtosecond Polarization Resolved VIS Pump–IR Probe Spectroscopy. J. Am. Chem. Soc. 2008, 130, 14904–14905. 10.1021/ja804096s. [DOI] [PubMed] [Google Scholar]
- Dreuw A.; Harbach P. H. P.; Mewes J. M.; Wormit M. Quantum chemical excited state calculations on pigment–protein complexes require thorough geometry re-optimization of experimental crystal structures. Theor. Chem. Acc. 2010, 125, 419–426. 10.1007/s00214-009-0680-3. [DOI] [Google Scholar]
- Wanko M.; Hoffmann M.; Strodel P.; Koslowski A.; Thiel W.; Neese F.; Frauenheim T.; Elstner M. Calculating Absorption Shifts for Retinal Proteins: Computational Challenges. J. Phys. Chem. B 2005, 109, 3606–3615. 10.1021/jp0463060. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
- Neese F. Prediction of Molecular Properties and Molecular Spectroscopy with Density Functional Theory: From Fundamental Theory to Exchange-Coupling. Coord. Chem. Rev. 2009, 253, 526–563. 10.1016/j.ccr.2008.05.014. [DOI] [Google Scholar]
- Neese F. A critical evaluation of DFT, including time-dependent DFT, applied to bioinorganic chemistry. J. Biol. Inorg Chem. 2006, 11, 702–711. 10.1007/s00775-006-0138-1. [DOI] [PubMed] [Google Scholar]
- Curutchet C.; Mennucci B. Quantum Chemical Studies of Light Harvesting. Chem. Rev. 2017, 117, 294–343. 10.1021/acs.chemrev.5b00700. [DOI] [PubMed] [Google Scholar]
- Segatta F.; Cupellini L.; Garavelli M.; Mennucci B. Quantum Chemical Modeling of the Photoinduced Activity of Multichromophoric Biosystems: Focus Review. Chem. Rev. 2019, 119, 9361–9380. 10.1021/acs.chemrev.9b00135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barone V.; Biczysko M.; Borkowska-Panek M.; Bloino J. A Multifrequency Virtual Spectrometer for Complex Bio-Organic Systems: Vibronic and Environmental Effects on the UV/Vis Spectrum of Chlorophyll a. ChemPhysChem 2014, 15, 3355–3364. 10.1002/cphc.201402300. [DOI] [PubMed] [Google Scholar]
- Fresch E.; Meneghin E.; Agostini A.; Paulsen H.; Carbonera D.; Collini E. How the Protein Environment Can Tune the Energy, the Coupling, and the Ultrafast Dynamics of Interacting Chlorophylls: The Example of the Water-Soluble Chlorophyll Protein. J. Phys. Chem. Lett. 2020, 11, 1059–1067. 10.1021/acs.jpclett.9b03628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llansola-Portoles M. J.; Li F.; Xu P.; Streckaite S.; Ilioaia C.; Yang C.; Gall A.; Pascal A. A.; Croce R.; Robert B. Tuning antenna function through hydrogen bonds to chlorophyll a. Biochim. Biophys. Acta, Bioenerg. 2020, 1861, 148078. 10.1016/j.bbabio.2019.148078. [DOI] [PubMed] [Google Scholar]
- Agostini A.; Meneghin E.; Gewehr L.; Pedron D.; Palm D. M.; Carbonera D.; Paulsen H.; Jaenicke E.; Collini E. How water-mediated hydrogen bonds affect chlorophyll a/b selectivity in Water-Soluble Chlorophyll Protein. Sci. Rep. 2019, 9, 18255. 10.1038/s41598-019-54520-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednarczyk D.; Dym O.; Prabahar V.; Peleg Y.; Pike D. H.; Noy D. Fine Tuning of Chlorophyll Spectra by Protein-Induced Ring Deformation. Angew. Chem., Int. Ed. 2016, 55, 6901–6905. 10.1002/anie.201512001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucchelli G.; Brogioli D.; Casazza A. P.; Garlaschi F. M.; Jennings R. C. Chlorophyll Ring Deformation Modulates Qy Electronic Energy in Chlorophyll-Protein Complexes and Generates Spectral Forms. Biophys. J. 2007, 93, 2240–2254. 10.1529/biophysj.107.104554. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


