Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 15;11(19):8459–8469. doi: 10.1021/acs.jpclett.0c01259

The Bending Mode of Water: A Powerful Probe for Hydrogen Bond Structure of Aqueous Systems

Takakazu Seki †, Kuo-Yang Chiang †, Chun-Chieh Yu †, Xiaoqing Yu †, Masanari Okuno ‡, Johannes Hunger †, Yuki Nagata †,*, Mischa Bonn †,*
PMCID: PMC7584361  PMID: 32931284

Abstract

graphic file with name jz0c01259_0011.jpg

Insights into the microscopic structure and dynamics of the water’s hydrogen-bonded network are crucial to understand the role of water in biology, atmospheric and geochemical processes, and chemical reactions in aqueous systems. Vibrational spectroscopy of water has provided many such insights, in particular using the O–H stretch mode. In this Perspective, we summarize our recent studies that have revealed that the H–O–H bending mode can be an equally powerful reporter for the microscopic structure of water and provides more direct access to the hydrogen-bonded network than the conventionally studied O–H stretch mode. We discuss the fundamental vibrational properties of the water bending mode, such as the intermolecular vibrational coupling, and its effects on the spectral lineshapes and vibrational dynamics. Several examples of static and ultrafast bending mode spectroscopy illustrate how the water bending mode provides an excellent window on the microscopic structure of both bulk and interfacial water.

Water plays an important role in many biological and chemical processes. The hydration structure of proteins and lipids affects their biological functions, and the interaction of water with solid surfaces such as mineral and metal oxide surfaces determines surface chemistry and surface–catalytic reactions. In addition to these critical roles in natural and industrial processes, the fundamental physical properties of condensed phase (liquid- and solid-state bulk water) and interfacial water, e.g., anomalously high surface tension, high viscosity, high boiling point, and so forth, have also attracted a great deal of attention. Some of these unique features have been attributed to the cooperative hydrogen-bond network of multiple water molecules.1 Thus, to unveil the physics underlying the unique properties of water, a molecular-level understanding of the structure and dynamics of the hydrogen-bond network is essential.

Vibrational spectroscopy techniques have provided detailed information on the microscopic hydrogen-bond structure of water in aqueous solutions, primarily via the O–H stretch mode of water.2,3 The study of the O–H stretch mode is prompted by the strong correlation between the frequency of O–H stretch vibration and the individual hydrogen-bond strength (Figure 1a);4,5 a strong (weak) hydrogen bond leads to a red-shift (blue-shift) of the O–H stretch frequency. While the O–H stretch frequency is an excellent marker of the local hydrogen-bonding arrangement in neat water or very simple systems, complications quickly arise when other molecular moieties are present in the sample. The broad O–H stretch band of water then overlaps with other vibrational bands such as the O–H stretch mode of alcohols and biomolecules as well as their N–H stretch/amide A modes. Disentangling the different modes is a formidable challenge, which cannot be resolved, for instance, by H/D isotopic substitution, because of rapid proton exchange. Also, vibrational couplings such as energy splitting between the O–H stretch modes and Fermi resonance with bending overtone often complicate the interpretation of the O–H stretch mode spectra and dynamics.

Figure 1.

Figure 1

Open in a new tab

(a) Time averaged probability distribution of the O–H stretch frequency vs hydrogen bond strength. Reproduced from ref (5). (b) A scatter plot of the experimentally determined H–O–H bending frequency vs averaged O–H stretch frequency of water. The data points were experimentally obtained by measuring the frequencies of water in various media.6 The blue and red lines represent the relations of eqs 1 and 2, respectively.

Compared to the stretch mode, the H–O–H bending mode has several advantages. Because the bending mode of water is unique to water molecules, it is spectrally separated from the C–O–H and C–N–H bending modes of alcohols and biomolecules. Essentially, water has only one bending mode in a molecule, which means there is no intramolecular bending mode–bending mode vibrational coupling. In addition to these advantages, the bending frequency can provide information on the hydrogen-bond strength of water, in a manner very similar to the stretch mode frequency. For example, the bending mode frequency of the H–O–H increases from ∼1590 cm–1 in the gas phase to ∼1650 cm–1 in the liquid phase because of the formation of hydrogen bonds. More quantitatively, Falk proposed the linear relation of the O–H stretch mode frequency and H–O–H bending mode frequency (Figure 1b), which satisfies the stretch and bend frequencies in the gas phase (ωbendg = 1590.4 cm–1 and ωstr = 3706 cm–1). This reads6

graphic file with name jz0c01259_m001.jpg 1

A very similar coefficient of −1/0.259 was obtained from ab initio calculations.7 When the nonlinear term is included in eq 1, one can add the additional condition satisfying the stretch and bend frequencies in liquid water (ωbendl = 1650 cm–1 and ωstr = 3400 cm–1) to eq 1.8,9 This is given as10

graphic file with name jz0c01259_m002.jpg 2

These relations manifest that the higher H–O–H bending mode frequency indicates the lower O–H stretch mode frequency, thus indicative of a stronger intermolecular O··H hydrogen-bond.

The vibrational nature of the water bending mode, however, has been much less investigated than the stretch mode, presumably because of its weaker absorbance. In contrast to the O–H stretch mode, it has been unclear how isotopic dilution affects the spectral shape and the vibrational dynamics of the bending mode, i.e., bending mode–bending mode and bending mode–other vibrational mode couplings have not been fully elucidated.2 At the interface, it has been controversially discussed whether the bending mode signal in surface-specific vibrational spectra arises from the interfacial water molecules7,11,12 or from the bulk.13 As such, despite the potential advantage of using the bending mode probe to explore the hydrogen-bond network, fundamental knowledge on the vibrational nature of the bending mode is still lacking.

In this Perspective, recent spectroscopic advances on the water bending mode will be introduced, followed by a discussion of the fundamental vibrational properties of the bending mode in bulk liquid, the vibrational dynamics, and the surface specificity and coupling nature of the bending mode of the interfacial water. Subsequently, several examples of probing the bending mode of water are discussed. Finally, the key results are summarized.

First, we examined the static spectra of the water bending mode in pure bulk water through the comparison of the stretch and the bending modes. Figure 2a shows that the use of isotopically diluted water (HOD in D2O) changes the lineshapes of the O–H stretch mode in both the IR and Raman spectra of neat H2O.14,15 The shoulder at ∼3200 cm–1 diminishes while the ∼3400 cm–1 contribution persists upon isotopic dilution, resulting in an overall narrowing of the vibrational line shape. These spectral variations are well reproduced by simulations using the frequency-mapping technique (Figure 2b) and can be explained by intermolecular intramode (i.e., stretch mode–stretch mode) coupling as well as intramolecular intermode coupling mainly due to the Fermi resonance between the stretch and the overtone of the bending mode.16,17 The intra/intermolecular intra/inter-mode couplings for the O–H stretch mode and H–O–H bending mode are summarized in Tables 1 and 2, respectively.

Figure 2.

Figure 2

Open in a new tab

(a) Measured IR and Raman spectra of the O–H stretch vibration. The data are reproduced from refs (14 and 15), respectively. (b) Computed IR and Raman spectra of the O–H stretch vibration based on the frequency-mapping technique, with the intermolecular intramode coupling and Fermi resonance (H2O) and without any vibrational coupling (HOD in D2O). The data are reproduced from refs (16 and 17), respectively. (c) Measured IR and Raman spectra. The data are reproduced from ref (18). (d) Computed IR spectra of the H–O–H bending vibration based on the frequency-mapping technique, including the intermolecular intramode coupling (H2O) and without any vibrational couplings (dilute H2O in D2O). The data are reproduced from ref (7). All data are normalized to the peak maximum.

Table 1. Four Types of Vibrational Couplings of the O–H Stretch Vibration and the Impact of Isotope Dilution (in Red Font).

graphic file with name jz0c01259_0009.jpg

Open in a new tab

Table 2. Three Types of Vibrational Coupling of the H–O–H Bending Vibration and the Impact of Isotope Dilution (in Colored Font).

graphic file with name jz0c01259_0010.jpg

Open in a new tab

How does the lineshape of the bending mode change upon isotopic dilution of water? Recently, we compared the experimentally determined lineshapes of the H–O–H bending mode of neat H2O and isotopically diluted water by carefully subtracting the H–O–D bending mode contribution from the measured spectra, which is plotted in Figure 2c.18 The data show that the peak frequency is slightly shifted to higher frequencies (∼7 cm–1) upon isotopic dilution. At the same time, the full width at half-maximum (fwhm) of the bending mode is rather insensitive to the isotopic composition, in stark contrast to the stretch mode. Modeling and detailed analysis of bending mode spectra are, however, still largely unexplored. One of the pioneering works for the bending mode has been reported by Ni and Skinner.7Figure 2d displays the simulated bending mode IR spectra with and without the intermolecular intramode (bending mode–bending mode) coupling. Figure 2d shows a slight blue-shift (∼10 cm–1) of the uncoupled oscillators, relative to the coupled mode, in reasonable agreement with the experimental data.18 However, the simulation indicates a substantial narrowing of the H–O–H bending mode spectra upon isotopic dilution, in contrast to the experimental spectra in Figure 2c. As such, theoretical modeling of the IR bending mode spectra is challenging. Furthermore, a theoretical calculation of the Raman response of the bending mode is lacking.

Overall, the experimental lineshapes indicate that intermolecular intramode coupling of the bending mode causes only minimal distortion of the lineshape, and shifts the peak position of the bending mode spectra of water, but the shift is very tiny. This is in contrast with the stretch mode response, which is strongly affected by a complex interplay of intramolecular intermode and intermolecular intramode couplings. Thus, the water bending mode in bulk water is a more direct reporter of the hydrogen-bond network.

Next, we turn our attention to the vibrational dynamics of liquid water, which plays an important role in chemical processes occurring in aqueous media, for example, by facilitating energy dissipation during chemical reactions. Time-resolved spectroscopies, including pump–probe IR or two-dimensional IR (2D-IR) spectroscopy, have been used to quantify the time scales of the vibrational dynamics such as vibrational energy relaxation, orientational memory decay, and spectral diffusion.19,20 When vibrationally exciting the O–H stretch mode, the excess vibrational energy relaxes from the O–H stretch mode to lower-frequency modes (e.g., the H–O–H bending mode at 1650 cm–1, the librational mode at 600–800 cm–1, and the hydrogen-bond stretch mode at 180 cm–1), i.e., vibrational energy relaxation. Because the infrared excitation light is typically linearly polarized, it preferentially excites water molecules with transition dipole moments aligned along the field polarization. The decay of orientation memory, i.e., excitation anisotropy, has also been used to characterize how the orientation of the transition dipole of the O–H stretch mode is scrambled via thermally activated rotational diffusion as well as vibrational energy transfer.21 Spectral diffusion has been widely used to describe how quickly the O–H stretch mode loses its frequency memory, i.e., how fast the frequency of an excited oscillator is scrambled, because of the intermolecular interactions and vibrational energy transfer.22,23

Table 3 summarizes typical time scales for the dynamics of the O–H vibration in neat H2O and highly diluted HDO in D2O samples. One can see that the vibration dynamics of the O–H stretch mode is largely accelerated for neat H2O compared with that for HDO in D2O. For example, the anisotropy decay time in neat H2O is >10 times faster than that of HDO in D2O, because of the fast depolarization caused by energy transfer.21 This acceleration of the dynamics of the O–H stretch mode arises from two mechanisms.24 One is the vibrational energy transfer from one O–H stretch mode to other O–H stretch modes. Because the orientations of these O–H groups are rarely identical, this energy transfer will lead to depolarization of the excitation. The other mechanism is the delocalization of the O–H stretch mode in neat H2O. The vibrational excitation is delocalized over several neighboring O–H groups. This orientation of the transition dipole moment for the delocalized mode can be easily modulated by the conformational fluctuation of the neighboring water molecules.

Table 3. Vibrational Dynamics of the O–H Stretch Mode.

  vibrational lifetime (ps) anisotropy decay (ps) spectral diffusion (ps)
neat H2O 0.23 ± 0.0323,34,35 0.075,22,23 0.7,39 <0.321 <0.05,23 0.1822
HOD in D2O 0.72 ± 0.0336−38 0.7,15 2.4,8 <3.0–4.021,38,40 0.5–1.037,41−43
Open in a new tab

In comparison to the O–H stretch mode, the vibrational dynamics of the H–O–H bending mode have been much less investigated. In Table 4, we summarize the previously reported time scales for the bending mode dynamics of H2O in neat H2O and H2O in D2O. Multiple studies have identified a vibrational lifetime of 170–260 fs for the H–O–H bending mode in pure H2O.18,25−27 Noticeably, the time scale of the H–O–H bending mode energy relaxation is comparable with respect to the O–H stretch mode energy relaxation of pure water. The ultrafast energy relaxation of the O–H stretch (H–O–H bending mode) has been explained by the strong intramolecular coupling attributed to the vibrational frequency matching between the O–H stretch (H–O–H bending) mode and the overtone of the H–O–H bending (librational) mode. Because the bending mode frequency is reduced from 1650 to 1450 cm–1, going from H–O–H bending to H–O–D bending, increasing the frequency mismatch between the O–H stretch and the bend overtone results in weakening the intramolecular intermode coupling between O–H stretch and H–O–D bending modes. Hence, it is expected that, upon the isotopically dilution of water, the vibrational energy relaxation of the O–H stretch mode slows down because of this reduced coupling. Indeed, the vibrational relaxation of the O–H stretch mode is slower by a factor of 3 for HDO in D2O compared to pure H2O.

Table 4. Vibrational Dynamics of the H–O–H Bending Mode.

  vibrational lifetime (ps)
 anisotropy decay (ps)
 spectral diffusion (ps)
  exptl sim exptl sim exptl sim
neat H2O 0.17–0.26,25−27,30,33,44,45 0.218 0.12–0.2728,46,47 0.08–0.17,26,30 0.3118   0.15 ± 0.0333a, 0.24 ± 0.0833b ∼0.06 and ∼0.1232
H2O in D2O 0.17–0.2718   0.3–0.418      
Open in a new tab
a

Centerline slope method.

b

Integrated photon-echo peak shift.

In contrast, isotopic dilution of water has a smaller effect on the frequency mismatch between the H–O–H bending mode and the overtone of the librational mode, and this intramolecular intermode coupling remains largely unchanged. Hence, one can expect the vibrational energy relaxation of the H–O–H bending mode to be insensitive to the isotopic dilution. This is also borne out by experiment: we found that the vibrational lifetime of the H–O–H bending model is invariant to the isotopic composition, with a time scale of ∼200 fs.18 This fast vibrational energy relaxation of the bending mode arises from the ultrafast energy transfer of the bending mode to the higher-frequency side of the librational motion.28

To obtain the orientational memory dynamics, transient spectra at different polarization combinations are recorded to determine the anisotropy decay.2 The anisotropy decay traces of the H–O–H bending mode for various H2O/D2O concentration ratios are shown in Figure 3a. These results indicate that the anisotropy decay dynamics of the H–O–H bending mode are less sensitive to the H2O/D2O concentration. This is in sharp contrast to the anisotropy decay of the O–H stretch mode, which is >10 times faster in neat H2O compared to isotopically diluted water. Figure 3b summarizes these vastly different dynamics, showing the time scale of the anisotropy decay of the stretching and bending modes versus H2O concentration.

Figure 3.

Figure 3

Open in a new tab

(a) Anisotropy decay for various H2O/D2O mixture. The hot ground state was subtracted from the transient absorption signal. Traces are offset by increments of 0.4. Symbols show experimental data, and solid lines show fits using a single-exponential decay. (b) Comparison of the anisotropic decay times for the bending mode and the stretch mode as a function of H2O/O–H fraction. The stretch mode data were taken from ref (21). Both bending and stretching mode data are approximated by single exponentials. The lines serve to guide the eye. The bending mode data are reprinted from ref (18).

The orientation of the transition dipole moments associated with the bending and stretch modes are aligned, roughly, along the bisector axis of the H–O–H angle and the O–H axis, respectively. As such, for sufficiently low OH concentrations, for which energy transfer is negligible, the anisotropy decay of the two modes reflects the reorientational motion of water along those two molecular coordinates. From simulations and experiments, the decay of the rotational correlation function of the bisector axis and the O–H axis of water are known to be very similar, with a decay time of 1.5–2 ps.29 This time constant is similar to the time constant of the anisotropy decay when pumping and probing the O–H stretch mode of isolated HDO in D2O, while the anisotropy decay when pumping and probing the H–O–H bending mode is much faster than 1.5–2 ps. Currently, this is understood as the mixing of the bending mode and other vibrational modes; because of strong vibrational mixing,18,22,30,31 the orientation of the transition dipole moment is rapidly randomized. As such, the anisotropy decay of the bending mode is much faster than the actual molecular reorientation, even for isotopically diluted water.

Finally, we discuss the spectral diffusion of the bending mode. 2D-IR spectroscopy can provide the time scale of the spectral diffusion, reflecting the memory loss of the excitation frequency. So far, only a few studies have been done to understand the spectral diffusion of the bending vibration.30,32,33Figure 4 displays the 2D-IR spectra of the H–O–H bending mode in neat H2O obtained from experiments and simulation. The 2D spectra commonly show a positive ground-state bleach of the 1 → 0 transition at ω3 = ∼1630–1650 cm–1 and a negative excited-state absorption of the 1 → 2 transition at ∼1550–1600 cm–1. At the waiting time of 0.1 ps, all the 2D-IR spectra show a positive peak similarly elongated along the diagonal line, and the spectra become parallel to the probe axis at 0.4–0.5 ps. The time evolution of the central line slope (CLS) of the positive peak measures the memory loss of the pumping frequency. The simulation and experimental data are in good agreement, with time constants of 120 and 150 fs, respectively.32,33 Simulation have attributed this rapid spectral diffusion to a strong intramolecular intermode coupling of the bending mode to the O–H stretch mode and low-frequency mode.32

Figure 4.

Figure 4

Open in a new tab

2D-IR spectra in the H–O–H bending mode region as a function of waiting time for pure H2O. (a) Experimental data of Tokmakoff and co-workers (Reproduced with permission from ref.30 Copyright 2017 AIP Publishing), (b) experimental data of Kuroda and co-workers (Reproduced with permission from ref (33). Copyright 2014 the Royal Society of Chemistry.), and (c) simulation data of Saito and co-workers (Reproduced with permission from ref (32). Copyright 2013 AIP publishing.). The ω1 and ω3 indicates pump and probe frequencies, respectively.

A question here is to what extent the isotopic dilution impacts the spectral diffusion. Kuroda and co-workers have compared the spectral diffusion dynamics in the 2D-IR measurement for the H–O–H bending mode in neat H2O and the H–O–D bending mode in isotopically diluted water.33 They found that the H–O–D bending mode in isotopically diluted water and the H–O–H bending mode in neat H2O show similar peak shift dynamics of the 2D-IR spectra with the time constant of 0.3 ± 0.05 ps and 0.24 ± 0.08 ps, respectively. This indicates that the water bending mode is almost insensitive to the intermolecular intramode coupling.

The hydrogen-bond structure at the air–water interface has been studied by vibrational sum-frequency generation (VSFG) spectroscopy over the past two decades. Because of the optical selection rule of SFG, the SFG signal arises only from the interface where inversion symmetry is broken, i.e., not from isotropic bulk water. Because SFG signal is resonantly enhanced by interfacial vibrational transitions, it can provide vibrational and structural information on specifically interfacial water. This region is limited to the topmost few layers of water at the water–air interface.3

The first SFG intensity spectrum (the square of the effective surface nonlinear susceptibility, |χeff(2)|2) of the bending mode at the air–water interface was experimentally measured in 2012,48 and then the imaginary part of the SFG susceptibility, (Im(χbend)), was reported.13 This Im(χbend(2)) spectrum shows a positive band. In contrast, MD simulations show that the imaginary part of the bending mode SFG spectrum exhibits both positive and negative features.7,11,49 Tahara and co-workers attributed this discrepancy of the experimentally measured and simulated Im(χbend) to the bulk quadrupole contribution; the simulation had assumed that the SFG signal arises solely from the interface because the interfacial dipole contribution is stronger than the bulk quadrupole contribution (electric dipole approximation),50 while the experimental data may contain not only the leading contribution of the interfacial dipole but also contributions from the bulk quadrupole.51 If the bulk quadrupole indeed dominates the bending mode signal, there is no chance to extract the interfacial water contribution from the SFG bending mode signal.

To explore the origin of the water SFG bending signal, one can take advantage of the fact that the sign of the Im(χbend(2)) SFG signal will change if the transition dipole moment flips its orientation along with the interfacial water molecules themselves. On the other hand, if the bending mode signal is governed by the proposed bulk quadrupole contribution, the sign of the Im(χbend) will remain unchanged upon flipping the orientation of the interfacial water molecules.51 By identifying the negative/positive change of Im(χbend(2)) upon going from a positively to a negatively charged interface,52 one could elucidate whether Im(χbend) arises from interfacial water or from bulk water.

As the presence of surface charge will induce the formation of the electrical double layer (EDL), the obtained SFG signal, χeff(2), originates from two contributions: one arises from the water molecules interacting with surface molecules in the Stern layer, χstern, while the other originates from the water molecules which can flip their orientations in response to the surface electric field in diffuse layer, χDiffuse(2). Thus, extracting the χDiffuse contribution from the χeff(2) spectrum is needed in order to address the sign of the change of the Im(χstern). The χDiffuse(2) is strongly dependent on the degree of screening of the surface charge by electrolytes in solution and therefore depends on ion concentration c. The overall response can be approached by53−55

graphic file with name jz0c01259_m003.jpg 4

where Φ(c), κ(c), and Δkz denote the surface potential, the inverse of the Debye length, and the mismatch of the wave-vectors along the surface normal (z-axis) in the reflected SFG configuration, respectively.

We measured the SFG intensity (|χeff(2)|2) spectra by varying the ion concentrations, which are displayed in Figure 5a,b. Note that the spectral shape may be affected by beam geometries (Fresnel factors). The SFG spectra at the water-charged lipids interface showed a sharp C=O stretch peak at ∼1710 cm–1 and the bending mode peak at ∼1650 cm–1. These spectra show that the interference between the 1710 cm–1 C=O stretch peak and the 1650 cm–1 water bend peak is different for the positively and negatively charged interfaces. By obtaining complex χeff from a Lorentzian fit of the SFG intensity and subsequently disentangling Stern and diffuse layer contributions from χeff(2) via eq 4, one can obtain the Im(χbend) and Im(χbend(3)Φ (c)) spectra where 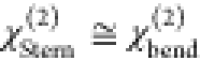Inline graphic in our notation and 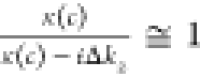Inline graphic. These spectra at the negatively and positively charged interfaces are displayed in Figure 5c,d. The opposite sign of the Im(χbend) response for the positively and negatively charged interfaces manifests that the bending mode contribution arises from the interfacial water molecules.

Figure 5.

Figure 5

Open in a new tab

(a, b) SFG spectra at the (a) negatively charged (H2O/DPPG) and (b) positively charged (H2O/DPTAP) interfaces with various ion concentrations at ssp polarization combination (s-, s-, and p-polarization for the SFG signal, visible pulse, and IR pulse, respectively). The black lines represent the fit. The pink and blue shaded regions indicate H–O–H bending mode and C=O stretch mode contributions, respectively. (c, d) The interfacial Im(χbend(2)) (black line) and the bulk Im(χbendΦ(c)) (colored lines) spectra obtained from the fit of the spectra for the (c) water/DPPG and (d) water/DPTAP interfaces. The data were reproduced with permission from ref (56). Copyright 2019 American Chemical Society.

Having established that the bending mode signal arises from interfacial water molecules, we further confirm that the vibrational spectral response Im(χbend(2)) is insensitive to the isotope composition, as established for the bending mode of bulk water. Figure 6a displays the variation of the SFG intensity spectra at the water–air interface by varying the H2O/D2O concentration. Even the pure D2O spectrum, which does not have any resonances in the displayed frequency region, has tilted features, which is the signature of the tail of the O–D stretch mode (∼2400 cm–1). The non-negligible contribution from the O–D stretch mode implies that the bending mode SFG signal is much weaker than the stretch mode SFG signal.

Figure 6.

Figure 6

Open in a new tab

(a) SFG intensity spectra of the H–O–H bending mode at the water–air interface with 1/0, 2/1, 1/1, 1/2, and 0/1 H2O/D2O mixtures at ssp polarization combination. Solid lines are fits to the data. The data are reprinted from ref (10) by permission of the PCCP Owner Societies. (b) Normalized Im(χbend(2)) spectra of neat H2O and H2O in D2O at the water–air interface. The data are constructed from the fits of the SFG intensity spectra in panel a. The dashed line data is obtained from [H2O] = 25%. The solid and striped shaded regions indicate the uncertainty of each measurement.10,56 (c) Normalized Im(χstr) spectra of neat H2O and HOD in D2O at the water–air interface. The data are reproduced from refs (57) (blue) and (59) (red). The dashed line data is obtained from an H2O/D2O mixture with [OH] = 25%.

By fitting the intensity spectra with a Lorentzian model, we obtain the Im(χbend(2)) response of the bending mode (Figure 6b).10 The spectra show that the isotopically diluted water and neat H2O data are similar within the error, which is in line with the bending mode of bulk water, discussed above. A relatively large deviation at ∼1600 cm–1 between refs (10 and 56) indicates that capturing the bending mode signal is still challenging. One can compare these bending mode SFG spectra with the O–H stretch mode SFG spectra. To have a coherent discussion about the bending mode of bulk water, we show the O–H stretch mode Im(χstr) spectra upon isotopic dilution in Figure 6c. The spectra differ slightly for reports from different groups.57−59 So far, a commonly observed feature in the Im(χstr(2)) spectra is the reduced low-frequency side of the negative peak around 3300 cm–1 and the 3600 cm–1 positive shoulder peak upon the isotope dilution. As a result, the isotopic dilution alters the lineshape of the O–H stretch SFG spectra, unlike the bending mode SFG spectra. This further demonstrates that the use of the bending mode is beneficial to identify the aqueous interfacial structure without isotopically diluting water.

Above, we have described the vibrational nature of the water bending mode in the IR, Raman, and SFG spectra, in comparison with the water stretch mode. We have shown that the bending mode is insensitive to the intermolecular intramode (bending mode–bending mode) vibrational coupling, allowing us to connect the vibrational spectra with the net water structure in the aqueous system, without isotope dilution. What have the recent studies clarified using the bending mode probe? Here, we pick two examples: a study of the microscopic structure of alcohol–water binary mixtures and a study of water at protein–water interfaces. Both examples make use of the fact that the H–O–H bending mode arises solely from water molecules with no interference from other modes, unlike the O–H stretch mode for which alcohol and biomolecules also contribute. Thus, the observation based on the bending mode can provide clear evidence of the water contribution for these samples.

First, we focus on the water–alcohol mixtures, a model system of hydrophobic hydration. Water molecules surrounding a hydrophobic moiety of a molecule have been proposed to form tetrahedral or cluster-like structures,60 which may explain the unique properties of water–alcohol mixtures, such as enhanced heat capacity. To clarify to what extent the water hydrogen-bond network in water–alcohol mixtures varies with changing the temperature, the IR spectra of the water bending mode have been measured for various water–alcohol mixtures.61

Figure 7 displays temperature-dependent IR spectra of the water bending mode in various water–alcohol mixtures. The data show that increasing temperature induces a red-shift of the H–O–H bending mode frequency. As is accounted for in Figure 1, the red-shift of the bending mode frequency means that the hydrogen-bond of water is weakened. As a result, the IR spectra show that the hydrogen-bond strength of water is weakened at elevated temperatures. The interesting point is that the red-shift of the bending mode peak frequency upon increasing temperature amounts to only 0.05 cm–1/°C for pure water, while it is 0.38 cm–1/°C on average for alcohol–water mixtures. Furthermore, alcohols with longer alkyl chains tend to induce a larger frequency shift, indicating a more substantial weakening induced by temperature for longer alkyl chains. The observation that the hydrogen-bond strength of water is stronger in the presence of alcohol than in the pure water is linked with the enhanced heat capacity of the water–alcohol mixture.62 Owing to the interference of the different O–H stretch modes of alcohols and water, this information cannot be obtained from the O–H stretch response. As such, the bending mode spectroscopy unraveled the variation of the hydrogen-bond network in the water–alcohol mixture.

Figure 7.

Figure 7

Open in a new tab

IR spectra in the water bending mode range of alcohol–water mixtures at various temperatures. These solutions have the same composition of 1/0.2 molar ratio (alcohol/water). The legend indicates the temperature of the system in units of °C. The data is reproduced with permission from ref (61). Copyright 2019 American Chemical Society.

The second example is the protein–water interface, where the O–H stretch mode of the protein side chain cannot be disentangled from the water O–H stretch mode contribution. Furthermore, the N–H stretch mode may complicate the interpretation of the O–H stretch mode spectra, because the N–H and O–H stretch frequencies overlap substantially. The H–O–H bending mode can circumvent the first problem, but the H–O–H bending mode may be masked by the very strong amide I mode at almost the same frequency. Instead, one can use the H–O–D bending mode (∼1460 cm–1)63 because the amide II mode (1480–1570 cm–1) only weakly contributes at this frequency region because of the small Raman cross section of the amide II mode.64

We extracted the net water contribution at the human serum albumin (HSA) protein–water interface using the H–O–D bending mode. The SFG intensity spectra are displayed in Figure 8a, while Figure 8b shows the Im(χbend(2)) spectra obtained through the Lorentzian model fit (black lines in panel a). The H–O–D bending mode contribution (see shaded region in Figure 8b) varies upon changing the isotope composition. The variation of the amplitude shows excellent agreement with the H–O–D concentration inferred from an equation of [HOD]2/[H2O][D2O] = 3.8665−67 (Figure 8c), confirming the peak assignment. The H–O–D bending mode contribution exhibits substantially higher peak frequency in the presence of HSA (∼1510 cm–1) than for bulk water (∼1460 cm–1). This indicates that interfacial water molecules near the HSA protein are more strongly hydrogen-bonded than water in the bulk. This observation seems to be linked with the fact that the HSA protein has a negatively charged site, which strongly modulates the hydrogen-bond strength of the interfacial water. As such, the water bending mode spectroscopy opens a path to extract information on water in bulk and at interfaces from the vibrational spectra of complex aqueous solutions.

Figure 8.

Figure 8

Open in a new tab

(a) The H–O–D bending mode spectra at HSA–water interface with various H2O/D2O mixture ratios. (b) The Im(χ(2)) spectra of HSA and water contributions from the fits (solid lines in panel a). Shaded regions in blue represent the H–O–D bending mode contributions of isotopically diluted water. (c) Amplitude of the H–O–D contribution vs H2O fraction. Theoretical prediction denoted by the black broken line is obtained from the equation of [HOD]2/[H2O][D2O] = 3.86.65−67 These data are reproduced from ref (10) by permission of the PCCP Owner Societies.

In summary, we have presented new insights into the nature of water’s bending mode and recent advancements in static and time-resolved water bending mode spectroscopy. We have demonstrated that the bending mode static spectral feature and also the vibrational dynamics can report directly on the hydrogen-bonded network, as the bending mode is sensitive to hydrogen bonding yet not obscured by intermolecular vibrational coupling effects. This makes the bending mode an excellent complement to the O–H stretch mode, which has been traditionally studied as a reporter of the microscopic structure and dynamics of water’s hydrogen-bond network, and for which intermolecular vibrational coupling effects do play a role.

Several fundamental properties of the bending mode remain unknown. The vibrational properties of the bending mode in ice are not well understood.68 Even though time-resolved vibrational spectroscopy in the bulk has revealed the vibrational dynamics to be insensitive to the local molecular environments for bulk liquid water, this observation may not apply to interfacial water. Time-resolved surface vibrational spectroscopy needs to be carried out to explore the energy transfer of bending mode excitation at the air–water (ice) interface to understand the energy flow at the interface. Bending mode spectroscopy can further provide a powerful way to (re)explore the microscopic hydrogen-bond network of various aqueous systems, which can be applied to further understand complicated phenomena such as liquid–liquid phase separation or hydrogen-evolution reactions at the surface of catalysts in situ/operando.

Acknowledgments

We thank Shumei Sun, Ellen Backus, Hiro-o Hamaguchi, Konrad Meister, and Tatsuhiko Ohto for fruitful discussions. We are grateful for financial support from the MaxWater initiative from the Max Planck Society and the DAAD project based personnel exchange program (#57526761).

Biographies

Takakazu Seki received his M.S. in chemistry at University of Tokyo, Japan in 2014 and his doctorate at Tokyo Institute of Technology, Japan in 2019. After that, he joined the Max Planck Institute for Polymer Research (MPI-P), Mainz, Germany as a postdoctoral fellow, and his current research focus is on interfacial water behaviors explored by SFG spectroscopy.

Kuo-Yang Chiang is a Ph.D. student at the MPI-P, Mainz, Germany. He received his Physics masters degree in 2016 from National Central University (NCU) and stayed at Academia Sinica, Taipei, Taiwan. He joined the MPI-P as a Ph.D. candidate in 2019. His research focuses on the structure and vibrational dynamics of interfacial water by SFG spectroscopy.

Chun-Chieh Yu obtained his M.S, in Molecular Science, Applied Chemistry at National Chiao Tung University, Taiwan in 2018. He is currently pursuing a Ph.D. degree at the MPI-P, Mainz, Germany. His research interests are focused on the nonlinear spectroscopy of water including SFG and hyper-Raman spectroscopy.

Xiaoqing Yu obtained her M.S. in Materials Science and Engineering at Beijing University of Chemical Technology, Beijing, China in 2018. She is currently a Ph.D. student at the MPI-P, Mainz, Germany. Her research interests are interfacial water structure at static and dynamic interfaces.

Masanari Okuno is an associate professor at the University of Tokyo, Tokyo, Japan. He received his Ph.D. in 2012 from the University of Tokyo. After postdoctoral research at MPI-P, he became an assistant professor at University of Tsukuba in 2013. He joined the University of Tokyo in 2019. His research focus is vibrational spectroscopy of the molecular structure and intermolecular interaction in liquids and solutions.

Johannes Hunger is a group leader at the MPI-P, Mainz, Germany. He received his Ph.D. in 2010 from the University of Regensburg, Germany. After his postdoctoral stay at the FOM Institute AMOLF, Netherlands, he joined the MPI-P in 2012. His research interests are centered around the dynamics of liquids with a focus on hydrogen-bonding and Coulombic interactions.

Yuki Nagata is a group leader at the MPI-P, Mainz, Germany. He received his Ph.D. in 2007 from Kyoto University. After his stay at BASF SE and the University of California, Irvine, he joined MPI-P in 2011. His research focus is on the theoretical modeling and experiment of vibrational spectroscopy.

Mischa Bonn is a director at MPI-P, Mainz, Germany. He received his Ph.D. in 1996 from the University of Eindhoven, The Netherlands. After postdoctoral research at the Fritz Haber Institute and Columbia University, he worked at Leiden University. In 2004 he became a group leader at AMOLF, Amsterdam, The Netherlands. In 2011 he joined MPI-P. His research interests are the structure and dynamics of molecules at interfaces and electron transfer across interfaces.

Author Contributions

# T.S. and K.-Y.C. contributed equally.

The authors declare no competing financial interest.

References

  1. Ball P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74–108. 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
  2. Bakker H. J.; Skinner J. L. Vibrational Spectroscopy as a Probe of Structure and Dynamics in Liquid Water. Chem. Rev. 2010, 110, 1498–1517. 10.1021/cr9001879. [DOI] [PubMed] [Google Scholar]
  3. Shen Y. R.; Ostroverkhov V. Sum-Frequency Vibrational Spectroscopy on Water Interfaces: Polar Orientation of Water Molecules at Interfaces. Chem. Rev. 2006, 106, 1140–1154. 10.1021/cr040377d. [DOI] [PubMed] [Google Scholar]
  4. Rey R.; Møller K. B.; Hynes J. T. Hydrogen Bond Dynamics in Water and Ultrafast Infrared Spectroscopy: A Theoretical Study. J. Phys. Chem. A 2002, 106, 11993–11996. 10.1021/jp026419o. [DOI] [Google Scholar]
  5. Ojha D.; Karhan K.; Kühne T. D. On the Hydrogen Bond Strength and Vibrational Spectroscopy of Liquid Water. Sci. Rep. 2018, 8, 16888. 10.1038/s41598-018-35357-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Falk M. The Frequency of the H-O-H Bending Fundamental in Solids and Liquids. Spectrochim. Acta 1984, 40, 43–48. 10.1016/0584-8539(84)80027-6. [DOI] [Google Scholar]
  7. Ni Y.; Skinner J. L. IR and SFG Vibrational Spectroscopy of the Water Bend in the Bulk Liquid and at the Liquid-Vapor Interface, Respectively. J. Chem. Phys. 2015, 143, 014502. 10.1063/1.4923462. [DOI] [PubMed] [Google Scholar]
  8. Perakis F.; De Marco L.; Shalit A.; Tang F.; Kann Z. R.; Kühne T. D.; Torre R.; Bonn M.; Nagata Y. Vibrational Spectroscopy and Dynamics of Water. Chem. Rev. 2016, 116, 7590–7607. 10.1021/acs.chemrev.5b00640. [DOI] [PubMed] [Google Scholar]
  9. Maréchal Y. IR Spectroscopy of an Exceptional H-Bonded Liquid: Water. J. Mol. Struct. 1994, 322, 105–111. 10.1016/0022-2860(94)87025-X. [DOI] [Google Scholar]
  10. Seki T.; Yu C.-C.; Yu X.; Ohto T.; Sun S.; Meister K.; Backus E. H. G.; Bonn M.; Nagata Y. Decoding the Molecular Water Structure at Complex Interfaces through Surface-Specific Spectroscopy of the Water Bending Mode. Phys. Chem. Chem. Phys. 2020, 22, 10934–10940. 10.1039/D0CP01269F. [DOI] [PubMed] [Google Scholar]
  11. Nagata Y.; Hsieh C.-S.; Hasegawa T.; Voll J.; Backus E. H. G.; Bonn M. Water Bending Mode at the Water-Vapor Interface Probed by Sum-Frequency Generation Spectroscopy: A Combined Molecular Dynamics Simulation and Experimental Study. J. Phys. Chem. Lett. 2013, 4, 1872–1877. 10.1021/jz400683v. [DOI] [PubMed] [Google Scholar]
  12. Dutta C.; Benderskii A. V. On the Assignment of the Vibrational Spectrum of the Water Bend at the Air/Water Interface. J. Phys. Chem. Lett. 2017, 8, 801–804. 10.1021/acs.jpclett.6b02678. [DOI] [PubMed] [Google Scholar]
  13. Kundu A.; Tanaka S.; Ishiyama T.; Ahmed M.; Inoue K.; Nihonyanagi S.; Sawai H.; Yamaguchi S.; Morita A.; Tahara T. Bend Vibration of Surface Water Investigated by Heterodyne-Detected Sum Frequency Generation and Theoretical Study: Dominant Role of Quadrupole. J. Phys. Chem. Lett. 2016, 7, 2597–2601. 10.1021/acs.jpclett.6b00657. [DOI] [PubMed] [Google Scholar]
  14. Ford T. A.; Falk M. Hydrogen Bonding in Water and Ice. Can. J. Chem. 1968, 46, 3579–3586. 10.1139/v68-591. [DOI] [Google Scholar]
  15. Hu Q.; Zhao H.; Ouyang S. Understanding Water Structure from Raman Spectra of Isotopic Substitution H2O/D2O up to 573 K. Phys. Chem. Chem. Phys. 2017, 19, 21540–21547. 10.1039/C7CP02065A. [DOI] [PubMed] [Google Scholar]
  16. Kananenka A. A.; Skinner J. L. Fermi Resonance in OH-Stretch Vibrational Spectroscopy of Liquid Water and the Water Hexamer. J. Chem. Phys. 2018, 148, 244107. 10.1063/1.5037113. [DOI] [PubMed] [Google Scholar]
  17. Auer B. M.; Skinner J. L. IR and Raman Spectra of Liquid Water: Theory and Interpretation. J. Chem. Phys. 2008, 128, 224511. 10.1063/1.2925258. [DOI] [PubMed] [Google Scholar]
  18. Yu C.-C.; Chiang K.-Y.; Masanari O.; Seki T.; Ohto T.; Yu X.; Zhong K.; Korepanov V.; Hamaguchi H.; Bonn M.; Hunger J.; Nagata Y.. Vibrational Couplings and Energy Transfer Pathways of Water’s Bending Mode. ChemRxiv 2020 10.26434/chemrxiv.12640760.v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mukamel S.Principles of Nonlinear Optical Spectroscopy; Oxford University Press, 1999. [Google Scholar]
  20. Laage D.; Stirnemann G.; Sterpone F.; Rey R.; Hynes J. T. Reorientation and Allied Dynamics in Water and Aqueous Solutions. Annu. Rev. Phys. Chem. 2011, 62, 395–416. 10.1146/annurev.physchem.012809.103503. [DOI] [PubMed] [Google Scholar]
  21. Woutersen S.; Bakker H. J. Resonant Intermolecular Transfer of Vibrational Energy in Liquid Water. Nature 1999, 402, 507–509. 10.1038/990058. [DOI] [Google Scholar]
  22. Ramasesha K.; De Marco L.; Mandal A.; Tokmakoff A. Water Vibrations Have Strongly Mixed Intra- and Intermolecular Character. Nat. Chem. 2013, 5, 935–940. 10.1038/nchem.1757. [DOI] [PubMed] [Google Scholar]
  23. Cowan M. L.; Bruner B. D.; Huse N.; Dwyer J. R.; Chugh B.; Nibbering E. T. J.; Elsaesser T.; Miller R. J. D. Ultrafast Memory Loss and Energy Redistribution in the Hydrogen Bond Network of Liquid H2O. Nature 2005, 434, 199–202. 10.1038/nature03383. [DOI] [PubMed] [Google Scholar]
  24. Nagata Y.; Yoshimune S.; Hsieh C.; Hunger J.; Bonn M. Ultrafast Vibrational Dynamics of Water Disentangled by Reverse Nonequilibrium Ab Initio Molecular Dynamics Simulations. Phys. Rev. X 2015, 5, 021002. 10.1103/PhysRevX.5.021002. [DOI] [Google Scholar]
  25. Lindner J.; Vöhringer P.; Pshenichnikov M. S.; Cringus D.; Wiersma D. A.; Mostovoy M. Vibrational Relaxation of Pure Liquid Water. Chem. Phys. Lett. 2006, 421, 329–333. 10.1016/j.cplett.2006.01.081. [DOI] [Google Scholar]
  26. Huse N.; Ashihara S.; Nibbering E. T. J.; Elsaesser T. Ultrafast Vibrational Relaxation of O-H Bending and Librational Excitations in Liquid H2O. Chem. Phys. Lett. 2005, 404, 389–393. 10.1016/j.cplett.2005.02.007. [DOI] [Google Scholar]
  27. Ashihara S.; Huse N.; Espagne A.; Nibbering E. T. J.; Elsaesser T. Vibrational Couplings and Ultrafast Relaxation of the O-H Bending Mode in Liquid H2O. Chem. Phys. Lett. 2006, 424, 66–70. 10.1016/j.cplett.2006.04.051. [DOI] [Google Scholar]
  28. Imoto S.; Xantheas S. S.; Saito S. Ultrafast Dynamics of Liquid Water: Energy Relaxation and Transfer Processes of the OH Stretch and the HOH Bend. J. Phys. Chem. B 2015, 119, 11068–11078. 10.1021/acs.jpcb.5b02589. [DOI] [PubMed] [Google Scholar]
  29. Wu Y.; Tepper H. L.; Voth G. A. Flexible Simple Point-Charge Water Model with Improved Liquid-State Properties. J. Chem. Phys. 2006, 124, 024503. 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
  30. Carpenter W. B.; Fournier J. A.; Biswas R.; Voth G. A.; Tokmakoff A. Delocalization and Stretch-Bend Mixing of the HOH Bend in Liquid Water. J. Chem. Phys. 2017, 147, 084503. 10.1063/1.4987153. [DOI] [PubMed] [Google Scholar]
  31. Rey R.; Ingrosso F.; Elsaesser T.; Hynes J. T. Pathways for H2O Bend Vibrational Relaxation in Liquid Water. J. Phys. Chem. A 2009, 113, 8949–8962. 10.1021/jp9036342. [DOI] [PubMed] [Google Scholar]
  32. Imoto S.; Xantheas S. S.; Saito S. Ultrafast Dynamics of Liquid Water: Frequency Fluctuations of the OH Stretch and the HOH Bend. J. Chem. Phys. 2013, 139, 044503. 10.1063/1.4813071. [DOI] [PubMed] [Google Scholar]
  33. Chuntonov L.; Kumar R.; Kuroda D. G. Non-Linear Infrared Spectroscopy of the Water Bending Mode: Direct Experimental Evidence of Hydration Shell Reorganization?. Phys. Chem. Chem. Phys. 2014, 16, 13172–13181. 10.1039/C4CP00643G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Kraemer D.; Cowan M. L.; Paarmann A.; Huse N.; Nibbering E. T. J.; Elsaesser T.; Miller R. J. D. Temperature Dependence of the Two-Dimensional Infrared Spectrum of Liquid H2O. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 437–442. 10.1073/pnas.0705792105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. van der Post S. T.; Hsieh C.-S.; Okuno M.; Nagata Y.; Bakker H. J.; Bonn M.; Hunger J. Strong Frequency Dependence of Vibrational Relaxation in Bulk and Surface Water Reveals Sub-Picosecond Structural Heterogeneity. Nat. Commun. 2015, 6, 8384. 10.1038/ncomms9384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. De Marco L.; Ramasesha K.; Tokmakoff A. Experimental Evidence of Fermi Resonances in Isotopically Dilute Water from Ultrafast Broadband IR Spectroscopy. J. Phys. Chem. B 2013, 117, 15319–15327. 10.1021/jp4034613. [DOI] [PubMed] [Google Scholar]
  37. Woutersen S.; Emmerichs U.; Nienhuys H. K.; Bakker H. J. Anomalous Temperature Dependence of Vibrational Lifetimes in Water and Ice. Phys. Rev. Lett. 1998, 81, 1106–1109. 10.1103/PhysRevLett.81.1106. [DOI] [Google Scholar]
  38. Fecko C. J.; Loparo J. J.; Roberts S. T.; Tokmakoff A. Local Hydrogen Bonding Dynamics and Collective Reorganization in Water: Ultrafast Infrared Spectroscopy of HOD/D2O. J. Chem. Phys. 2005, 122, 054506. 10.1063/1.1839179. [DOI] [PubMed] [Google Scholar]
  39. De Marco L.; Fournier J. A.; Thämer M.; Carpenter W.; Tokmakoff A. Anharmonic Exciton Dynamics and Energy Dissipation in Liquid Water from Two- Dimensional Infrared Spectroscopy Water from Two-Dimensional Infrared Spectroscopy. J. Chem. Phys. 2016, 145, 094501. 10.1063/1.4961752. [DOI] [PubMed] [Google Scholar]
  40. Nienhuys H.-K.; van Santen R. A.; Bakker H. J. Orientational Relaxation of Liquid Water Molecules as an Activated Process. J. Chem. Phys. 2000, 112, 8487–8494. 10.1063/1.481451. [DOI] [Google Scholar]
  41. Lascoux N.; Gallot G.; Hache F.; Gale G. M.; Bratos S.; Leicknam J. C. Femtosecond Dynamics of Hydrogen Bonds in Liquid Water: A Real Time Study. J. Chin. Chem. Soc. 2000, 47, 685–692. 10.1002/jccs.200000093. [DOI] [Google Scholar]
  42. Laenen R.; Rauscher C.; Laubereau A. Dynamics of Local Substructures in Water Observed by Ultrafast Infrared Hole Burning. Phys. Rev. Lett. 1998, 80, 2622–2625. 10.1103/PhysRevLett.80.2622. [DOI] [Google Scholar]
  43. Lawrence C. P.; Skinner J. L. Vibrational Spectroscopy of HOD in Liquid D2O. VI. Intramolecular and Intermolecular Vibrational Energy Flow. J. Chem. Phys. 2003, 119, 1623–1633. 10.1063/1.1582173. [DOI] [Google Scholar]
  44. Ashihara S.; Fujioka S.; Shibuya K. Temperature Dependence of Vibrational Relaxation of the OH Bending Excitation in Liquid H2O. Chem. Phys. Lett. 2011, 502, 57–62. 10.1016/j.cplett.2010.12.001. [DOI] [Google Scholar]
  45. Lindner J.; Cringus D.; Pshenichnikov M. S.; Vöhringer P. Anharmonic Bend-Stretch Coupling in Neat Liquid Water. Chem. Phys. 2007, 341, 326–335. 10.1016/j.chemphys.2007.07.051. [DOI] [Google Scholar]
  46. Bastida A.; Zúñiga J.; Requena A.; Miguel B. Hybrid Quantum/Classical Simulation of the Vibrational Relaxation of the Bend Fundamental in Liquid Water. J. Chem. Phys. 2009, 131, 204505. 10.1063/1.3266834. [DOI] [PubMed] [Google Scholar]
  47. Ingrosso F.; Rey R.; Elsaesser T.; Hynes J. T. Ultrafast Energy Transfer from the Intramolecular Bending Vibration to Librations in Liquid Water. J. Phys. Chem. A 2009, 113, 6657–6665. 10.1021/jp9022713. [DOI] [PubMed] [Google Scholar]
  48. Vinaykin M.; Benderskii A. V. Vibrational Sum-Frequency Spectrum of the Water Bend at the Air/Water Interface. J. Phys. Chem. Lett. 2012, 3, 3348–3352. 10.1021/jz3014776. [DOI] [Google Scholar]
  49. Moberg D. R.; Straight S. C.; Paesani F. Temperature Dependence of the Air/Water Interface Revealed by Polarization Sensitive Sum-Frequency Generation Spectroscopy. J. Phys. Chem. B 2018, 122, 4356–4365. 10.1021/acs.jpcb.8b01726. [DOI] [PubMed] [Google Scholar]
  50. Tang F.; Ohto T.; Sun S.; Rouxel J. R.; Imoto S.; Backus E. H. G.; Mukamel S.; Bonn M.; Nagata Y. Molecular Structure and Modeling of Water-Air and Ice-Air Interfaces Monitored by Sum-Frequency Generation. Chem. Rev. 2020, 120, 3633–3667. 10.1021/acs.chemrev.9b00512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Shen Y. R. Basic Theory of Surface Sum-Frequency Generation. J. Phys. Chem. C 2012, 116, 15505–15509. 10.1021/jp305539v. [DOI] [Google Scholar]
  52. Nihonyanagi S.; Yamaguchi S.; Tahara T. Direct Evidence for Orientational Flip-Flop of Water Molecules at Charged Interfaces: A Heterodyne-Detected Vibrational Sum Frequency Generation Study. J. Chem. Phys. 2009, 130, 204704. 10.1063/1.3135147. [DOI] [PubMed] [Google Scholar]
  53. Wen Y.-C.; Zha S.; Liu X.; Yang S.; Guo P.; Shi G.; Fang H.; Shen Y. R.; Tian C. Unveiling Microscopic Structures of Charged Water Interfaces by Surface-Specific Vibrational Spectroscopy. Phys. Rev. Lett. 2016, 116, 016101. 10.1103/PhysRevLett.116.016101. [DOI] [PubMed] [Google Scholar]
  54. Gonella G.; Lütgebaucks C.; De Beer A. G. F.; Roke S. Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces Is Modulated by Interference. J. Phys. Chem. C 2016, 120, 9165–9173. 10.1021/acs.jpcc.5b12453. [DOI] [Google Scholar]
  55. Ohno P. E.; Wang H.; Geiger F. M. Second-Order Spectral Lineshapes from Charged Interfaces. Nat. Commun. 2017, 8, 1032. 10.1038/s41467-017-01088-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Seki T.; Sun S.; Zhong K.; Yu C.; Machel K.; Dreier L. B.; Backus E. H. G.; Bonn M.; Nagata Y. Unveiling Heterogeneity of Interfacial Water through the Water Bending Mode. J. Phys. Chem. Lett. 2019, 10, 6936–6941. 10.1021/acs.jpclett.9b02748. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Nihonyanagi S.; Ishiyama T.; Lee T.-K.; Yamaguchi S.; Bonn M.; Morita A.; Tahara T. Unified Molecular View of the Air/Water Interface Based on Experimental and Theoretical χ□(2) Spectra of an Isotopically Diluted Water Surface. J. Am. Chem. Soc. 2011, 133, 16875–16880. 10.1021/ja2053754. [DOI] [PubMed] [Google Scholar]
  58. Xu X.; Shen Y. R.; Tian C. Phase-Sensitive Sum Frequency Vibrational Spectroscopic Study of Air/Water Interfaces: H2O, D2O, and Diluted Isotopic Mixtures. J. Chem. Phys. 2019, 150, 144701. 10.1063/1.5081135. [DOI] [PubMed] [Google Scholar]
  59. Smit W. J.; Versluis J.; Backus E. H. G.; Bonn M.; Bakker H. J. Reduced Near-Resonant Vibrational Coupling at the Surfaces of Liquid Water and Ice. J. Phys. Chem. Lett. 2018, 9, 1290–1294. 10.1021/acs.jpclett.7b03359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Cheng Y. K.; Rossky P. J. Surface Topography Dependence of Biomolecular Hydrophobic Hydration. Nature 1998, 392, 696–699. 10.1038/33653. [DOI] [PubMed] [Google Scholar]
  61. Deng G.-H.; Shen Y.; Chen H.; Chen Y.; Jiang B.; Wu G.; Yang X.; Yuan K.; Zheng J. Ordered-to-Disordered Transformation of Enhanced Water Structure on Hydrophobic Surfaces in Concentrated Alcohol-Water Solutions. J. Phys. Chem. Lett. 2019, 10, 7922–7928. 10.1021/acs.jpclett.9b03429. [DOI] [PubMed] [Google Scholar]
  62. Benson G. C.; D’Arcy P. J. Excess Isobaric Heat Capacities of Water-n-Alcohol Mixtures. J. Chem. Eng. Data 1982, 27, 439–442. 10.1021/je00030a021. [DOI] [Google Scholar]
  63. Falk M. Frequencies of H-O-H, H-O-D and D-O-D Bending Fundamentals in Liquid Water. J. Raman Spectrosc. 1990, 21, 563–567. 10.1002/jrs.1250210907. [DOI] [Google Scholar]
  64. Kurouski D.; Van Duyne R. P.; Lednev I. K. Exploring the Structure and Formation Mechanism of Amyloid Fibrils by Raman Spectroscopy: A Review. Analyst 2015, 140, 4967–4980. 10.1039/C5AN00342C. [DOI] [PubMed] [Google Scholar]
  65. Meija J.; Mester Z.; D’Ulivo A. Mass Spectrometric Separation and Quantitation of Overlapping Isotopologues. H2O/HOD/D2O and H2Se/HDSe/D2Se Mixtures. J. Am. Soc. Mass Spectrom. 2006, 17, 1028–1036. 10.1016/j.jasms.2006.02.008. [DOI] [PubMed] [Google Scholar]
  66. Duplan J. C.; Mahi L.; Brunet J. L. NMR Determination of the Equilibrium Constant for the Liquid H2O-D2O Mixture. Chem. Phys. Lett. 2005, 413, 400–403. 10.1016/j.cplett.2005.07.005. [DOI] [Google Scholar]
  67. Wolfsberg M.; Massa A. A.; Pyper J. W. Effect of Vibrational Anharmonicity on the Isotopic Self-Exchange Equilibria H 2 X+D 2 X = 2HDX. J. Chem. Phys. 1970, 53, 3138–3146. 10.1063/1.1674461. [DOI] [Google Scholar]
  68. Imoto S.; Xantheas S. S.; Saito S. Molecular Origin of the Difference in the HOH Bend of the IR Spectra between Liquid Water and Ice. J. Chem. Phys. 2013, 138, 054506. 10.1063/1.4789951. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES