Efficient Treatment of Correlation Energies at the Basis-Set Limit by Monte Carlo Summation of Continuum States

Abstract

The calculation of electron correlation is vital for the description of atomistic phenomena in physics, chemistry, and biology. However, accurate wavefunction-based methods exhibit steep scaling and often sluggish convergence with respect to the basis set at hand. Because of their delocalization and ease of extrapolation to the basis-set limit, plane waves would be ideally suited for the calculation of basis-set limit correlation energies. However, the routine use of correlated wavefunction approaches in a plane-wave basis set is hampered by prohibitive scaling due to a large number of virtual continuum states and has not been feasible for all but the smallest systems, even if substantial computational resources are available and methods with comparably beneficial scaling, such as the Møller–Plesset perturbation theory to second order (MP2), are used. Here, we introduce a stochastic sampling of the MP2 integrand based on Monte Carlo summation over continuum orbitals, which allows for speedups of up to a factor of 1000. Given a fixed number of sampling points, the resulting algorithm is dominated by a flat scaling of 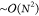. Absolute correlation energies are accurate to <0.1 kcal/mol with respect to conventional calculations for several hundreds of electrons. This allows for the calculation of unbiased basis-set limit correlation energies for systems containing hundreds of electrons with unprecedented efficiency gains based on a straightforward treatment of continuum contributions.

1. Introduction

Electron correlation lies at the heart of a wide range of fundamental physical and chemical phenomena, which range from the structural diversity and dynamics of water¹ over the dissociation of liquid hydrogen at high pressure² and the stability and mobility of point defects in semiconductors³ to the barrier height of chemical reactions. Wavefunction-based methods allow for a conceptually simple and convenient treatment of electron correlation⁴⁻⁶ and have found widespread and long-lasting use in theoretical chemistry. Correlated wavefunction methods have been widely applied as a benchmarking tool^7,8 in the development of computationally more expedient methods such as the Kohn–Sham density functional theory (KS-DFT).^9,10 More recently, their scope has been enlarged by rigorous hybridization schemes that combine KS-DFT with correlated wavefunction approaches,¹¹⁻¹⁵ giving rise to some of the most accurate density functional approximations available to date.^{12,13,16−19} In particular, while it has been pointed out that many recently developed density functional approximations fail to yield correct densities and energies at the same time,²⁰ double hybrid (DH) functionals have been shown to be able to overcome this fundamental problem.²¹ Recently, modern machine learning techniques have considerably increased timescales and system sizes that can be sampled on conventional infrastructure, but the generation of reliable input data for the training of such methods still relies on the computational feasibility of reference calculations of sufficient accuracy. In this perspective, the importance and scope of wavefunction-based first-principles techniques applied to condensed matter systems can therefore only be expected to grow further, both as a standalone method and in combination with DFT.

To this day, wavefunction-based correlation methods are hampered by a scaling that is polynomial at best and that is associated with a considerable prefactor. This implies that for larger systems, trade-offs have to be made between the accuracy of the basis set employed and the number of electrons that can be treated with reasonable computational resources. Moreover, correlated wavefunction approaches have only scarcely been applied in the condensed phase, which is due to additional difficulties encountered in periodic systems.²²⁻⁴⁰ These difficulties can be further exacerbated by the large basis sets needed to obtain basis-set limit reference energies.⁴¹ This precludes the routine use of wavefunction-based methods for large condensed phase systems; at the same time, benchmarking possibilities, for example, against newly developed density functionals, remain restricted to comparably few atoms and small supercells^{27,31,34,35,38} or have to be based on basis sets which are far from completeness. In benchmarking, this can be particularly problematic in combination with the erroneous convergence behavior of certain density functionals, which obfuscates any comparison that is not explicitly made at the complete basis-set limit.^42,43 The availability of basis-set limit results is therefore necessary not only for formal reasons, but is also of great importance for the assessment of the physical accuracy of existing models and approximations, representing an important guideline in the development of new techniques and approximations that are able to reach far beyond current system sizes and limitations.

In principle, plane wave (PW) basis sets would constitute an ideal choice for the calculation of basis-set limit correlation energies since they do not introduce any localization bias and allow for a controlled, simple, and well-defined extrapolation to the complete basis-set limit⁴⁴ without the linear dependency issues commonly encountered in large atom-centered bases.^28,35,45,46 In particular, since a single PW is the solution of the Schrödinger equation of a free electron, its use enables the description of continuum states, which have been shown to play a crucial role in the complete description of electron correlation.⁴⁷ In the following, we will refer to continuum states in finite systems as those virtual states that resemble a free electron; it is also this resemblance that lies at the heart of simple extrapolation to basis-set limit values.⁴⁴ By virtue of their very nature, conventional atom-centered bases such as Gaussian functions or combined Gaussian/PW (GPW)⁴⁸ bases are unable to describe such continuum states, which also account for the absence of physical models that would allow for a simple extrapolation to the basis-set limit. Instead, they usually rely on specifically constructed basis sets that allow for certain extrapolation models to be applied; this, however, does not commonly hold for density functionals.^42,49 PWs have not been reported to suffer from this drawback.⁴³ In addition, PWs are equally suitable for the treatment of both periodic and nonperiodic systems with either wavefunction-based methods, density functional techniques, or hybridizations thereof. These advantages, however, come at a price: The presence of a large number of continuum states in PW setups exacerbates the steep scaling of correlated wavefunction methods, making them computationally intractable for all but the smallest systems, which on their own will already require substantial resources on conventional high-performance compute clusters. In the following, we will show that PW-based correlated wavefunction calculations can be sped up by a factor of up to 1000 by stochastically sampling continuum state contributions via Monte Carlo summation. The error introduced by this stochastic approach remains below 0.01 kcal/mol per electron. This enables correlated wavefunction calculations in PWs for unprecedented system sizes on conventional computational infrastructure, making unbiased basis-set limit values routinely accessible for systems with up to hundreds of electrons. The same reflections hold for hybrid wavefunction/DFT methods, such as DH¹¹ density functionals.

1.1. Møller–Plesset Perturbation Theory

Among the correlated wavefunction methods, second-order Møller–Plesset perturbation theory (MP2)⁵⁰ exhibits a comparably flat scaling of with the number of electrons or basis functions N, making it one of the flattest scaling correlated, wavefunction-based approaches available, second only to the random phase approximation (RPA) and the direct RPA (dRPA), respectively.^51,52 In general, MP2 has been found to provide a good first estimate of the dynamic correlation energy.^6,53 Conceptually simple, the MP2 correlation energy E_c^MP2 is obtained by a perturbative treatment that includes up to doubly excited determinants and summation over pairs of all N_occ occupied and N_vir virtual orbitals. For the spin-restricted case,⁴

1

where i, j and a, b denote spatial occupied and virtual orbitals ψ, respectively, that are eigenstates of the Hartree–Fock operator with eigenvalues ε. The MP2 matrix element e̅(i,j,a,b) is expressed in terms of four-electron Coulomb energies, which can be cast into a positive-definite form

2

where ⟨ij|ab⟩ are two-electron matrix elements. In DH density functionals, the second-order integrals in eq 1 are evaluated using a ground-state KS determinant, rather than the Hartree–Fock solution,¹¹ and will only contribute to a fraction of the total correlation energy, the remainder being treated by pure density functional methods. If the advantages of DHs are to be made routinely available in condensed matter applications, they too require an efficient treatment of the terms in eq 1, and any improvements in the calculation of the MP2 term will directly benefit DH calculations.

Historically, E_c^MP2 has been evaluated using atom-centered basis sets or mixed GPW⁵⁴ implementations. In particular, in periodic setups, use of localized basis functions has been reported to be susceptible to basis-set convergence issues,^28,35,45,46 whereas problematic basis-set superposition effects and possible linear dependencies are absent in a PW representation. Applications in solid-state physics have also been scarce, which is in part due to the divergence of the MP2 integrand in zero-band gap systems, but a Thomas–Fermi screening of the MP2 amplitudes can resolve this issue.⁵⁵

The presence of continuum (or continuum-like) states allows for simple extrapolation to the complete basis-set limit: Alavi and co-workers have demonstrated that in a PW basis at large N_vir, E_c^MP2 decays as ∝ε_a^–3/2.⁴⁴ PW-based methods therefore offer the unique advantage of a simple evaluation of basis-set limit values in both periodic and isolated systems, making them a potentially invaluable tool for basis-set bias-free calculations. PW MP2 calculations are few and have only recently been reported.^34,35,56,57 This is in part due to their extensive memory requirements. The presence of a number of virtual states close to the number of PWs themselves (up to 10⁹) can further complicate the calculations. However, given sufficient memory, the integrals of eq 2 are easily evaluated in the reciprocal space: Exchange-like matrix elements are easily obtained by solving the Poisson equation for a set of pair densities ρ_ia(r) = ψ_i(r)ψ_a(r) in reciprocal space, where the Coulomb operator is diagonal. The real-space pair densities can simply be subjected to a fast Fourier transform (FFT), ρ_ia(G) = FFT[ρ_ia(r)]. Then, at the Γ-point, the reciprocal-space equivalent of a matrix element reads⁵⁸

3

where † stands for the complex conjugate and index permutation. Ω is the volume of the system, G are reciprocal-space vectors, and Φ(G) is a suitably generalized form of the reciprocal-space Coulomb potential.^59,60 Attempts to reduce the overall cost of the method have included mapping the virtual states onto a localized subspace,^37,61−65 the use of stochastic orbitals⁶⁶⁻⁶⁹ and (real-space^70,71 or graph-based^57,72) sampling approaches, respectively, as well as exploiting Laplace transforms^{53,56,73−76} to enhance parallel efficiency. In an alternative strategy, one seeks to accelerate convergence of the correlation energy by improving the description of the electron–electron cusp. To this end, explicitly correlated basis sets can be used. In an ansatz commonly referred to as the F12 theory,^77,78 the description of the electron–electron cusp is improved by combining a conventional, atom-centered Gaussian basis with a set of strongly orthogonal geminals. This approach has recently been extended to PWs.³⁶

However, localization procedures fail for continuum states; previously reported stochastic techniques either introduce system-dependent errors of up to 2 kcal/mol per occupied orbital⁶⁹ or carry a prefactor too large for practical applications,⁷⁰ and approaches based on the Laplace transform⁵⁶ require repeated calculations at different quadrature points, increasing the overall operation count for the sake of parallel efficiency, with modest reported speedups of around 4 to 5. A combined stochastic/Laplace-transform approach that results in appreciable computational speedups leads to errors of at least 20%.⁵⁷ Similarly, due to the presence of nonfactorizable many-electron integrals, the cost of evaluating the MP2 integrand in PW-F12 is higher than for a pure PW basis set,³⁶ and the efficiency of a graph-based approach⁷² was hindered by the absence of an optimized weighting scheme for graph generation. In a more general scope, a recent diagrammatic decomposition of the coupled cluster pair correlation function has allowed for the introduction of a basis-set correction in PWs that results in speedups of 2 orders of magnitude.⁷⁹ Alternatively, in the context of Full Configuration Interaction Quantum Monte Carlo calculations,⁸⁰ use of an effective, transcorrelated Hamiltonian⁸¹ has been shown to substantially improve convergence of the correlation energy of the uniform electron gas. In the GW theory,⁸² stochastic sampling schemes have successfully been applied with competitive accuracy and favorable timings with respect to deterministic calculations.⁸³

In the following, we shall demonstrate how the presence of continuum states can be exploited to drastically reduce the computational cost of MP2 calculations without impacting their accuracy. The approach is based on a simple stochastic sampling of the integrands of eq 1 and can be implemented with little effort, representing a sleek and clean approach to tackle the issues arising in the continuum. This opens the path to routine applications of PW MP2-based approaches in both isolated and periodic systems with up to hundreds of occupied orbitals, making it possible to obtain basis-set limit DH or MP2 correlation energies on conventional computational infrastructure within a reasonable time.

2. Distribution of Continuum States and Stochastic Sampling

The possibility of introducing stochastic sampling is rooted in the behavior of the integrand at large ε_a, where continuum states arise. In this regime, E_c^MP2 grows as ε_a^–3/2,⁴⁴ and the overlap elements ⟨ij|ab⟩ must therefore be of low magnitude. It is obvious from eq 3 that overlaps will only be non-negligible whenever the symmetries of the continuum states match, but explicit symmetry determination for all states would be prohibitively expensive. Instead, given two high-lying virtual states, the statistical distribution of non-negligible overlaps is expected to be similar between truncations of eq 1 at a and some subsequent a + δ with arbitrary δ. For a spatially infinite supercell at infinite PW cutoff, one can define a cutoff energy ε_c with orbital index c, from where on all orbitals a ≥ c are part of the continuum. Then, the correlation energy can be separated

4

with the continuum contribution η_c(a) accounting for the incremental change in correlation energy when adding an additional continuum orbital to the system:

5

where ∑_b′ is due to pairs of continuum (a) and noncontinuum (b′) virtual orbitals and we have used that, at the Γ-point, ψ_a = ψ_a^*. Note that the last term in eq 4 contains only one explicit sum over virtual orbitals N_vir, with the orbital pairs themselves being formed by the triple sum in eq 5.

The simplest possible stochastic treatment of eq 5 is given by a uniform sampling of the summand, but this calls for a regular distribution of the overlap values obtained over all tuples ijab, which are the arguments of η_c(a); that is, the high-lying virtual orbitals of a finite system at finite PW cutoff need to reasonably approximate free, continuum electrons. Figure 1 shows the distribution of these arguments for a finite periodic box with ε_c – ε_HOMO = 50 eV and a total of N_vir = 3000 virtual orbitals. With the positive-definite definition of e̅ adopted in eq 2, the resulting distribution is indeed regular and smooth, indicating that η_c(a) could be predestinated to be treated by uniform Monte Carlo sampling. This is the approach we will privilege in the following. Note that in the limit of an infinite system, this is equal to Monte Carlo integration over the continuum; such integration techniques have been used as early as 1957 to calculate the high-density correlation energy of the uniform electron gas.⁸⁴

Figure 1.

Figure showing the absolute occurrence P of orders of magnitude of the summand e̅(i,j,a,b) of η_c(a) of eq 5 from a = c to a = 3000 for ε_c – ε_HOMO = 50 eV. The order of magnitude of the matrix elements is small, and its distribution is smooth.

Let p_s ∈ [0, 1) be a predefined sampling probability (i.e., p_s is larger than or equal to zero but always smaller than 1). We define the function p as

6

Symmetry at the Γ-point, which gives rise to a factor of 2 in continuum/continuum and mixed continuum/noncontinuum terms of eq 5, can be accounted for by introducing a Kronecker delta. Then, the sums in η_c(a) can be simplified, and the stochastic expression for η_c(a) is

7

where x_ijab ∼ U([0, 1)) is a sequence of random numbers drawn from a uniform distribution U and b covers both b and b′ of eq 5. In the limit of a continuum, the error of the sampling is expected to decrease as , with N_MC being the number of tuples ijab that are explicitly sampled. The combination of eqs 4 and 7 amounts to a stochastic summation over all orbital pairs that contribute to an increase in E_c^MP2, once a continuum orbital a is added to a system already containing a – 1 virtual orbitals.

For any sampling probability p_s < 1, only elements of η_c(a) with p(x_ijab, p_s) = 1 have to be evaluated. In a finite cell with a finite PW cutoff and a sufficiently large number of virtual orbitals N_vir, estimates for η_c(a) are then obtained for every given continuum orbital a ∈ [c, N_vir] as follows: rather than randomly generating a tuple of indices for a predetermined number of Monte Carlo moves, a random number p(x_ijab, p_s) is drawn for every element of the summand in eq 7, determining whether a particular tuple ijab will enter into the estimator of η_c(a). p_s therefore defines a target value N_MC ∝ p_s of tuples that are expected to be sampled for every continuum orbital a. The advantages of such an algorithm are twofold: On the one hand, it avoids under- or oversampling of the subspace associated with orbital a; on the other hand, it enables efficient extrapolation to the basis-set limit in one single calculation, directly providing E_c^MP2 as a function of the highest virtual orbital included in eq 4.

In the following, we will adopt an orbital-dependent sampling probability p_s(a) = N_MC/N_card(a), where N_card(a) = (2a – 1)N_occ(N_occ + 1)/2 is the product of the cardinalities of the sums in eq 7. N_card(a) therefore explicitly depends on the virtual orbital a that is added to eq 4. With this choice of a continuum-orbital-dependent p_s(a), the density of the sampling decreases as a increases. This allows for N_MC to remain a fixed, system-independent input quantity. We shall later show that conservative estimates for N_MC and ε_c can be regarded as system-independent.

For orbitals that are part of the continuum, the resulting algorithm scales formally as 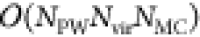, where N_PW is the number of PWs in the basis set. This follows from eqs 4 and 7 since the cost of evaluation of the triple sum over N_occ²N_vir in eq 7 is reduced to elements with p(x_ijab, p_s(a)) = 1, which in turn is proportionate to N_MC. For virtual orbitals with ε_a < ε_c, the conventional scaling applies (cf. eqs 1 and 3). Further on in the text, we will show that in practice, the number of terms due to eigenvalues ε_a < ε_c does not dominate scaling. Once N_MC can be made both independent of the orbital index a and the system at hand, the scaling of the resulting method reduces to 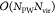integral evaluations for all orbitals with eigenvalue ε > ε_c.

3. Computational Methods

3.1. General Setup

Hard pseudopotentials of the Goedecker–Teter–Hutter (GTH) form⁸⁵ parametrized for Hartree–Fock calculations³¹ have been used for all calculations. PW MP2 and stochastic MPs2 energies were calculated using a modified version of the CPMD code.⁸⁶ The convergence threshold on the residual gradient on occupied orbitals was set to 10^–7 a.u., whereas a threshold of 10^–5 a.u. was used for the virtual space. For isolated systems, periodic images were decoupled using the Poisson solver by Martyna and Tuckerman.⁸⁷ The wavefunction cutoff energies E_cut^ψ were set to 150 Ry for all systems but for the ethylene crystal, where a value of 140 Ry was used. A density cutoff E_cut^ρ = 4E_cut^ψ was adopted for all systems, while cutoff energies for MP2 pair densities were set to E_cut^ψ without impacting accuracy. The calculation of the MP2 term is based on straightforward evaluation of eq 3 as in ref (58). Since no derivatives with respect to E_c have to be evaluated, reciprocal-space orbital pairs ρ_ia(G) are stored in memory, allowing for substantial speedups with respect to an on-the-fly evaluation of every pair density. The size of the periodic super- or unit-cells, the number of electronic states as well as molecular geometries, and PW energy cutoffs are given in the Supporting Information.

3.2. Extrapolation of Correlation Energies

Correlation energies are obtained from single-point extrapolation using the ε_Nvir^–3/2 dependency (equivalent to 1/N_vir) as described in ref (44). Such a leading-order approximation requires a sufficient number of high-energy orbitals in order to gather sufficient statistics and reliable extrapolated values. In this work, we adopt a fitting scheme with various windows (ranges of points to fit) moving along the curve. Those vary in size with respect to the number of orbitals included, with a shift of ∼200 orbitals between them. The maximum window size is taken as the one that retains a fitting error comparable to smaller windows when finishing fitted ranges at N_vir^max, the highest orbital available from a Davidson diagonalization. The smallest window is given by the smallest possible window size that provides a stable fit.

MP(s)2 curves are fitted according to

8

The series of α(N_vir), obtained from all windows along the curves that terminate at N_vir up to N_vir^max, converge to an estimate of the MP(s)2 energies at the basis-set limit, E_c(ε_Nvir → ∞) Averaging over different windows allows to account for sensitivity and variance of extrapolated values, which are given in the Supporting Information along with figures that illustrate the extrapolation procedure and error determination.

4. Results and Discussion

4.1. Accuracy of Stochastic Summation

Our stochastic sampling scheme was tested both on isolated systems as well as in periodic, condensed-phase setups. Test systems in the condensed phase include solid-state ethylene and benzene molecular crystals as well as a liquid consisting of a hydronium ion solvated in 32 water molecules. Isolated (gas-phase) systems are represented by a benzene monomer and a dimer in sandwich configuration. All calculations were carried out with a modified version of the CPMD code⁸⁶ using GTH pseudopotentials generated for Hartree–Fock calculations.^31,85

We first investigate the dependency of the accuracy of our stochastic sampling of eqs 4 and 7, called MPs2, on the number of orbitals in the occupied subspace and the choice of the continuum cutoff value ε_c^gap. This quantity is given with respect to the highest occupied molecular orbital (HOMO) in order to be independent of the system setup or reference frame: ε_c = ε_c – ε_HOMO. Figure 2 shows the absolute difference between MP2 and MPs2 calculations for a benzene crystal and a benzene monomer for ε_c^gap ranging from 20 to 180 eV. Differences rapidly decrease by increasing ε_c. Errors averaged over independent stochastic runs remain <0.01% for continuum cutoffs ≥120 eV. Reducing this value by half to 60 eV results in doubling of the relative error, which can still be acceptable. Further lowering of ε_c^gap, however, leads to rapidly increasing errors. The standard deviation of the sampling error depends much more strongly on ε_c than on N_occ. From ε_c^gap = 120 eV on, standard deviations become negligible and virtually identical for both systems. Notably, relative sampling errors are lower for the crystal at N_occ = 60 than for the monomer (graphs are provided in the Supporting Information). This strongly supports that accuracy is mainly influenced by ε_c, whereas at constant N_MC, the error is independent of the partitioning of occupied and virtual states in eq 7.

Figure 2.

Absolute differences between stochastic and nonstochastic MP2 correlation energies, ΔE_MPs2^MP2, as a function of the continuum cutoff energy ε_c for a benzene crystal (N_occ = 60, four molecules per unit cell) and a benzene monomer (N_occ = 15) at N_MC = 12,000. Error bars were obtained by averaging over six independent runs.

In the following and in line with the values of Figure 2, we will adopt N_MC = 12,000 and ε_c^gap = 120 eV to investigate the accuracy of stochastic sampling for different systems. Figure 3 shows the correlation energy as a function of the eigenvalue of the highest virtual orbital included (ε_Nvir) for two exemplary systems: one periodic (ethylene crystal) and one isolated (benzene monomer) setup, calculated both with a full summation according to eq 1 as well as with our stochastic sampling. The corresponding extrapolated basis-set limit values are shown in Table 1. The largest errors of the extrapolated, absolute MP2 correlation energies lie between 0.02 and 0.1 kcal/mol. Errors in the binding energy of the benzene sandwich are of comparable magnitude, which is far below chemical accuracy. Differences per electron, ΔE/e^–, do not exceed 0.1 meV. These values compare well to an expected stochastic error of ≤0.01%. Table 1 also shows the number of matrix element evaluations for all setups. With our system-independent choice of N_MC, stochastic sampling reduces this number by 1–2 orders of magnitude compared to conventional calculations.

Figure 3.

E_c^MP2 as a function of the highest eigenvalue ε_Nvir in the sum of eq 1 for both conventional and stochastic MP2 (MPs2) for an ethylene crystal (N_vir = 11,158) and an isolated benzene monomer (N_vir^max = 14,985). Domains without stochastic sampling are colored in gray. Differences between the curves, ΔE_MPs2, are plotted on a secondary y-axis. Extrapolated basis-set limit values for all systems described here are found in Table 1.

Table 1. MP2 Correlation Energies E_c^MP2 Obtained from a Conventional MP2 Calculation and the Stochastic Approach, MPs2^a.

system		EcMP2 [a.u.]	EcMPs2 [a.u.]	ΔEMPs2MP2 [a.u.]	ΔE/e– [a.u.]	Nijab	psNijab
ethylene	crystal	–0.78054	–0.78056	2 × 10–5	8 × 10–7	5.06 × 109	3.26 × 108
benzene	crystal	–4.69164	–4.69149	–1.5 × 10–4	–1 × 10–6	1.30 × 1011	3.50 × 109
	monomer	–1.05681	–1.05695	1.4 × 10–4	5 × 10–6	8.62 × 109	6.26 × 108
	dimer	–2.12780	–2.12777	–3 × 10–5	–5 × 10–7	3.33 × 1010	8.78 × 109
	binding	–0.01417	–0.01387	–3 × 10–4	–5 × 10–6

^aΔE_MPs2^MP2 and ΔE/e^– denote absolute and per-electron energy differences between stochastic sampling and conventional calculations, respectively. N_ijab denotes the number of matrix elements (ijab-tuples) sampled in a conventional calculation, and p_sN_ijab is the number of effectively sampled matrix elements in a stochastic MPs2 calculation, with both numbers rounded to three digits. The threshold for stochastic sampling expressed with respect to the HOMO was identical for all systems, ε_c = ε_c – ε_HOMO = 120 eV. The same holds for N_MC = 12,000, the number of terms sampled per virtual contribution η_c(a), as described in eq 7. For details on the systems used, cf. the Supporting Information.

For both absolute energies and energy differences, the observed deviations are several orders of magnitude lower than the reported error of other stochastic or Laplace transform-based schemes.^57,66−72 For comparison, values of correlation energies obtained with atom-centered all-electron⁸⁸ and GPW codes⁸⁹ are listed in the Supporting Information; all values are consistently higher than those reported for our PW calculations. In particular, we note that differences between different basis sets tend to be substantially larger than the stochastic sampling error, further confirming the viability of uniform, stochastic sampling of the continuum space.

4.2. Performance and Speedups

With the error of the stochastic sampling scheme being considerably lower than the errors documented for other PW implementations, effective speedups remain to be determined. Figure 4 shows the resulting cumulative execution times and speedups of the stochastic sampling compared to the direct implementation of eqs 1 and 3 for the ethylene crystal. Timings are reported as a function of the highest orbital index included in the expansion, N_vir. For the ethylene crystal, at N_vir = 10,000, speedups of up to 957 can be reached with stochastic summation, making the calculation about 3 orders of magnitude faster compared to a conventional implementation. All the while, the error introduced by uniform stochastic summation with respect to a full calculation is only about 10^–2 kcal/mol for this system (cf. Table 1). This has to be compared to maximum speedups of about 5 documented for Laplace transform-based schemes that allow for similar accuracy to be retained⁵⁶ and 20% errors in correlation energies for algorithms that allow for larger speedups⁵⁷ versus errors around 0.01% reported here. Figure 4 also includes a fit of the CPU time of our stochastic scheme to a function O(N_vir) = a₀ + a₁N_vir, demonstrating that the scaling is described well by , assuming that N_MC = cnst. 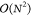constitutes a formal improvement over the scaling achieved with a stochastic graph-based approach in atom-centered basis sets,⁷² which was reported to be of .

Figure 4.

Cumulative execution times (left) and speedups (right) compared between conventional algorithm and stochastic sampling for an ethylene crystal as a function of the highest virtual orbital index, N_vir, included in eq 4. O(N_vir) = a₀ + a₁N_vir denotes a least-squares fit on N_vir ∈ [5000, 10,000] with a₀ = −4.76586 s, a₁ = 0.010515 s. For sufficiently large N_vir > 2000, formal and practical scaling show excellent agreement. At N_vir = 10,000, the stochastic approach with N_MC = 12,000 is 3 orders of magnitude faster. Timings were obtained by dividing the computational load over 5 OMP (Open Multi-Processing) threads and 24 MPI (Message Passing Interface) tasks.

Together with the high accuracy of the method, this considerable gain in efficiency allows for the treatment of systems that would be intractable when treated with conventional algorithms. One typical usage example of accurate wavefunction-based theories or computationally demanding high-quality DFT methods such as DH functionals lies in postprocessing of simulation data, for example, in a posteriori calculations of potential energy surfaces or reaction paths generated using lower-level methods in the context of molecular dynamics or Monte Carlo simulations. Recent developments have even made it possible to directly sample⁹⁰ high-quality potential energy surfaces by virtue of multiple time step (MTS) propagators,⁹¹ which allow for an important decrease in computational cost and substantial improvements in tractability by permitting less-frequent evaluation of the full, high-quality Hamiltonian during a first-principles molecular dynamics run.

A liquid constituted of 1 hydronium ion solvated in 32 water molecules (264 electrons) will serve as an example of the performance of stochastic sampling in a typical setup encountered in first-principles (MTS-)molecular dynamics. Using the stochastic summation scheme reported here, calculating the basis-set limit correlation energy of this system, shown in Figure 5, is feasible in about 15 h on 25 16-core compute nodes with 128 GB of RAM, using the same, conservative estimates for ε_c^gap reported in Table 1, which yielded accurate results for all test systems considered so far. Additionally, calculations using ε_c = 60 eV and ε_c^gap = 90 eV have been carried out for the sake of comparison. Already at ε_c = 90 eV, the execution time is almost halved to about 8 h and can be further reduced by using ε_c^gap = 60 eV, at which the basis-set limit correlation energy can be calculated in a mere 5 h. In particular, this drastic reduction in execution time is not accompanied by a considerable loss of accuracy. Extrapolated correlation energies are given in Table 2. It should be noted that postprocessing protocols can be applied when training machine learning algorithms with high-quality data, based on a coarse sampling of configuration space with a lower-level method (cf., e.g. ref (1)). Speedups in the calculation of correlation energies with MP2 or DH functionals will therefore be directly reflected in less time-consuming training procedures, thus considerably increasing throughput.

Figure 5.

Hydronium ion solvated in 32 water molecules (264 electrons explicitly accounted for). Calculation of E_c^MPs2 takes between 5 and 15 h on 25 16-core compute nodes. Molecules within the periodically repeated supercell are highlighted. Using ε_c = 120 eV and N_MC = 12,000 yields an extrapolated E_c^MPs2 = −10.22952 a.u.

Table 2. Stochastic MP2 Correlation Energies E_c^MPs2 for a Hydronium Ion Solvated in 32 Water Molecules Using Different Thresholds for Continuum Energies ε_c^a.

EcMPs2 [a.u.]	NMC	εcgap [eV]	t
–10.22771	12,000	60	4 h 55
–10.23190	12,000	90	8 h 10
–10.22952	12,000	120	15 h 25

^aTimings t, rounded to 5 min, are given for the execution time of the MP2 routine on 25 16-core nodes in a hybrid setup (50 MPI tasks, 8 OMP threads).

4.3. Generalization to RPA

The promising performance of the stochastic summation scheme described here also opens the possibility of its application to similar approaches in which continuum states can play a role. In DFT, the exact-exchange plus RPA approach has emerged as a promising method capable of more accurately predicting van der Waals binding energies, adsorption energies on surfaces, or lattice constants in molecular solids.^{44,54,92−94} Based on the similarity of the MP2 energy expression and the RPA, one can expect transferability of the stochastic sampling approach to the evaluation of the RPA. The reciprocal-space form of the RPA correlation energy E_c^RPA is^51,52

9

where χ̃_G,G′(q,iω) are elements of the full density response function, including the Coulomb interaction. At the Γ-point with q = 0, the diagonal elements in a stochastically sampled RPA scheme become

10

with

11

where the variables c, x_jb, and p_s are used analogously to eq 7. In this limit, we investigate the RPA integrand of eq 9 for an ethylene crystal at different values of ω. Figure 6 shows the values of E_c^RPA at varying iω for N_vir = 11,040 as well as an estimate of the overall RPA correlation energy based on trapezoidal integration. Stochastic sampling with p_s = 1/3 introduces a maximum error of about 1% in the integrand. Overall, the stochastic sampling introduces a final error of less than 0.03 kcal/mol, which is comparable to the error obtained in MP2 calculations for the same system. These results demonstrate that the stochastic sampling of continuum states can also be applied for methods other than MP2 that include a substantial continuum-state contribution.

Figure 6.

Value of the integrand of eq 9, abbreviated as Tr{···}, for an ethylene crystal at q = 0 and N_vir = 11,040 as a function of iω for both conventional and stochastic calculations. The difference between the curves, ΔTr{···}, rapidly decreases as iω is increased; differences are plotted on the secondary y-axis and do not exceed 1.5%. Simple trapezoidal integration leads to E_c^RPA = −0.03365 a.u. for a full calculation and E_c = −0.03360 a.u. for stochastic sampling.

5. Conclusions and Outlook

Continuum states have been shown to be an important contributor to the overall electron correlation energy.⁴⁷ Among the basis sets commonly used in solid-state physics, quantum chemical calculations, and first-principles molecular dynamics, PWs stand out as the only choice that can effectively account for continuum contributions, which are also the base of a simple basis-set limit extrapolation technique.⁴⁴ Here, we have introduced a uniform stochastic sampling approach to treat continuum states arising in correlation energy calculations, where contributions due to states with orbital eigenvalues beyond some threshold ε_c are added by stochastic summation. This algorithm has been applied to the calculation of second-order perturbation energies which occur in both MP2 and DH density functionals. We have shown that stochastic summation over the continuum orbitals allows for the calculation of MP2 correlation energies with speedups of up to 3 orders of magnitude at remarkably low errors. This significant increase in efficiency enables calculations with several hundreds of electrons at a relatively low computational cost, making it possible to standardly apply MP2 and DH methods in a PW basis, which has so far been intractably expensive even on high-performance compute clusters. Importantly, the results presented here also enable straightforward DH calculations in the condensed phase, thus extending the availability of one of the most accurate density functional methods available to date for condensed matter systems. We have also shown that stochastic sampling of the continuum orbitals can easily be extended to other approaches, demonstrating the generality of the ansatz employed here. Calculations carried out within a stochastic RPA suggest errors comparable to the stochastic MP2 scheme. The stochastic sampling scheme itself is straightforward, easy to implement, and based on simple physical concepts.

Stochastic sampling of continuum states permits to easily obtain basis-set limit values, be it for periodic or isolated systems, with maximum errors of only 0.1 meV per electron. This accuracy makes basis-set limit values for correlation energies available using reasonable computational resources and execution times. This will allow for thorough benchmarking of new computational methods without basis-set bias, for routine postprocessing of potential energy landscapes generated using lower-level methods, as well as on-the-fly generation of high-accuracy first-principles molecular dynamics trajectories using multiple time stepping schemes. This data, in turn, can be used to feed high-throughput methods based on artificial intelligence. Overall, the techniques presented in this text pave the road to routinely apply accurate MP2 and DH calculations at the basis-set limit in condensed matter systems, ultimately extending the use of a method well-established for isolated systems to the condensed phase.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00724.

• System setups, fitting errors for all basis-set limit values reported in this manuscript, graphs of E_c^MP(s)2(N_vir) for all systems, E_c obtained in Gaussian and Gaussian/PW basis sets for comparison, and relative sampling errors and their standard deviation as a function of ε_c^gap for the benzene monomer and crystal (PDF)

Author Contributions

^§ M.P.B. and J.V. contributed equally to this work.

The authors declare no competing financial interest.