Abstract

A recently popularized approach for the calculation of pseudocontact shifts (PCSs) based on first-principles quantum chemistry (QC) leads to different results than the classic “semiempirical” equation involving the susceptibility tensor. Studies that attempted a comparison of theory and experiment led to conflicting conclusions with respect to the preferred theoretical approach. In this Letter, we show that after inclusion of previously neglected terms in the full Hamiltonian, one can deduce the semiempirical equations from a rigorous QC-based treatment. It also turns out that in the long-distance limit, one can approximate the complete A tensor in terms of the g tensor. By means of Kohn–Sham density functional theory calculations, we numerically confirm the long-distance expression for the A tensor and the theoretically predicted scaling behavior of the different terms. Our derivation suggests a computational strategy in which one calculates the susceptibility tensor and inserts it into the classic equation for the PCS.
In this Letter, we study a paramagnetic center and a sufficiently far nucleus with magnetic moment MK. In an external magnetic field B, this nucleus experiences an NMR chemical shielding that is dipolar in origin. Thus, this shielding originates from an additional dipolar magnetic field that is created by the induced average magnetic moment of the paramagnetic center. Because of the dipolar origin, the resulting “pseudocontact shifts” (PCSs) have an inverse cubic dependence on the distance of the nucleus from the paramagnetic center. Consequently, their analysis provides a wealth of structural information that was heavily exploited during the last decades in chemistry1−6 and structural biology.7−15 PCSs are also gaining momentum in the characterization of the electronic structures of single ion magnets.6,16−18
In the following, we use Hartree atomic units (ℏ = me = e = 4πϵ0 = 1) throughout. Traditionally, PCSs are often interpreted by the “semiempirical” (SE) expression for the chemical shielding tensor σ:
| 1 |
where R is the distance vector between the nucleus and the paramagnetic center and χ is the paramagnetic susceptibility tensor. The PCS is then given by19,20
| 2 |
where Δχax = χzz −1/2(χxx + χyy) and Δχrh = χxx – χyy are the axial and rhombic susceptibility parameters and θ and ϕ are the polar and azimuthal angles of the direction of the nucleus in the principal axis system of the susceptibility tensor. Equation 2 was described by McConnell and Robertson21 and by Kurland and McGarvey22 in the spin Hamiltonian (SH) approximation.
In recent years, alternative treatments of PCSs in terms of rigorous first-principles quantum chemistry (QC) have been developed. A very general approach was given by Van den Heuvel and Soncini23 and leads to an expression for the chemical shielding tensor as a mixed second partial derivative of the electronic Helmholtz free energy F = −kBT ln Z (where Z = ∑ie–βEi):
 |
3 |
The different operators that appear in this expression are derivatives of the full electronic Hamiltonian H = H(B, MK) around B = 0 and MK = 0. The summations in eq 3 are over eigenstates |Ψnν(0)⟩ (with eigenvalues En) of the field-free Hamiltonian H0 = H(B = 0, MK = 0). The indices n, m, ... label energy levels, and μ, ν, ... are additional labels for degenerate states with the same energy. Z0 is the zeroth-order canonical partition function, and β = 1/kBT.
If all relevant states can be described by a SH of the form
| 4 |
| 5 |
where the “spin dyadic” ⟨SST⟩ is a matrix that depends on the zero-field splitting tensor D and the temperature:
| 6 |
The zeroth-order eigenfunctions and energies in eq 6 are derived from the zeroth-order Hamiltonian in the SH approximation, Hspin(0) = S·D·S. The analogous SH expression for the susceptibility tensor is28,29
| 7 |
In some previous studies on chemical shieldings based on eq 5,28,30−33 all of the contributions to the hyperfine coupling (HFC) tensor A except for the Fermi contact (FC) and spin-dipolar (SD) ones were neglected. Under this assumption, the chemical shift in the point-dipole approximation (PDA) turns out to be26,28,30,34
| 8 |
with the unsymmetrical tensor χ′ related to χ in eq 7 by χ = χ′·gT/ge. The appearance of this unsymmetrical tensor was considered a necessary consequence of the more rigorous QC treatment compared with the “semiempirical” eq 1.26,28,30 The two approaches are ostensibly different.26 Several recent papers prefer the use of eq 8 because it seemingly gives better agreement with the experimental data.28,32,33 Even recent and authoritative reviews29 indirectly contribute to endorsing the use of eq 8. Therefore, as the use of eq 8 is becoming increasingly attractive and the two equations can lead to significantly different results,26,35 it is important to establish as soon as possible and beyond doubt which of the two expressions should be used for the calculation of PCSs. Comparison between the calculations and the experimental data does not resolve the issue in full: paramagnetic NMR calculations from first principles involve the estimation of SH parameters (the g and D tensors), which are not directly accessible experimentally at room temperature in solution for most metal ions. Furthermore, the uncertainties in the calculation of these parameters can collectively be on the same order of magnitude as the expected difference between the two approaches. For this reason, a recent study34 has investigated the performance of the two equations for a copper(II) ion with S = 1/2 in an axial protein environment, where the results are expected to differ by a factor of roughly 2. This comparison is particularly strong, because it does not rely on calculations of the SH parameters but rather depends on the direct experimental measurement of the g anisotropy (with uncertainty smaller than 1%) under the same conditions in which the NMR data are also measured. It was found that the “semiempirical” equation performs much better for the prediction of the PCSs than the equation derived from first principles.34 To date, a QC-based explanation for this result is missing.
A first hint at possible problems with eq 8 comes from the insight that the same orbital currents, induced by spin–orbit coupling (SOC), are responsible for the orbital contributions to both the g tensor and the HFC tensor. Equation 8 incorporates this orbital contribution in the former but not the latter, i.e., in a very unsymmetrical way.20,26,35
Starting from these premises, in this Letter we go beyond the previous QC-based treatments in two important aspects: (1) we include in the molecular Hamiltonian the so-called gauge correction terms,36 which are necessary to preserve gauge invariance in the presence of SOC, and (2) we explicitly include all of the contributions (not only the SD one) to the magnetic hyperfine field and to the A tensor. With regard to the electronic Hamiltonian, we assume the usual nonrelativistic Hamiltonian with magnetic fields incorporated by adding the magnetic vector potential to the canonical momentum operator, supplemented with SOC in the effective nuclear charge approximation.37 We incorporate two contributions into the magnetic vector potential, one describing a homogeneous external magnetic field and the other describing the field created by a point magnetic dipole at the nucleus under consideration. In order to obtain gauge-invariant results, it is furthermore necessary to add gauge-correction terms36 to the Hamiltonian. The detailed expressions for the complete Hamiltonian and its derivatives are given in the Supporting Information.
We now assume that the paramagnetic part of the system is localized in one region of space and that the nucleus of interest is at a large distance from this region. Our analysis is similar to that of McConnell38 based on Ramsey’s expression for nondegenerate ground states.39,40RO is a position in the region where the paramagnetic center is located, and RK is the position of the nucleus. We use RO also as the gauge origin for the homogeneous external magnetic field. Furthermore, we define riO = ri – RO and riK = ri – RK, where ri is the position of electron i. We assume that the only relevant contributions to the chemical shift come from electrons located at the paramagnetic center. Then riO can be assumed to be small compared with R = RO – RK if the latter becomes large enough, i.e., riK = riO + R ≈ R. Following McConnell, inverse powers of riK can then be expanded in a Taylor series around the point riO = 0, which gives38
| 9 |
| 10 |
Inserting these expressions into the equations for the Hamiltonian derivatives occurring in eq 3 that depend on the nuclear position and neglecting all terms with inverse powers of R larger than 3 (PDA), one obtains
 |
11 |
and
| 12 |
In eq 11, ∂H/∂MKl contains FC, SD, paramagnetic spin–orbit (PSO), and gauge contributions, while ∂H/∂Bm contains spin, orbital, and gauge contributions. The commutator terms in eq 11 originate only from the PSO and gauge correction operators. One can observe that these expressions contain terms that scale like R–2, apparently violating the PDA, for which the terms with the slowest decay should scale like R–3. This problem can be resolved by noticing that the commutators with H0 in eq 11 lead to a cancellation with the energy difference in the denominator of the sum-over-states term (third term) of eq 3. The resulting R–2 term exactly cancels the corresponding term originating from eq 12, which has the same size but opposite sign. Such a cancellation of slowly decaying terms was already observed in the pioneering work by McConnell.38 A similar cancellation of R–2 terms that follows the same kind of reasoning was observed by Helgaker and co-workers in the long-distance limit of indirect nuclear spin–spin coupling constants.41 As a result, eqs 11 and 12 inserted into eq 3 exactly reproduce the “semiempirical” eq 1 with the susceptibility tensor defined via the equation
 |
13 |
This is a generalization of the well-known van Vleck equation first presented by Gerloch and McMeeking42 including a diamagnetic term that was missing in their treatment; also see the discussion by Van den Heuvel and Soncini.23 In summary, we have demonstrated that the use of rigorous first-principles quantum mechanics confirms eq 1, which was originally derived in a semiempirical way. Our derivation therefore demonstrates that eq 1 has a solid theoretical foundation. This is the main result of the current Letter. The alternative expression based on the unsymmetric tensor χ′ (eq 8) is flawed because of the neglect of contributions to the hyperfine field beyond the SD one, which, as our derivation demonstrates, is not justified. It is important to stress that we derived our result in a very general way using only relatively weak assumptions. Notably, we did not choose a particular electronic structure method. The only assumptions that went into our derivation are the validity of the equation for the chemical shielding given by Van den Heuvel and Soncini (eq 3), our particular choice of electronic Hamiltonian, and the PDA. We expect that it will be possible to derive eq 1 also for the more exact Dirac Hamiltonian or even without resorting to an explicit choice of Hamiltonian at all. This will be discussed in more detail in a forthcoming publication.
The validity of eq 1 that we just established, together with the SH expressions eq 5 and eq 7, suggests that in the long-distance limit one can approximate the HFC tensor as
| 14 |
The validity of this equation is well-established for the spin-only contributions to A and g.26 It was shown that within the LS coupling approximation, the orbital contributions to A and g also fulfill eq 14.26 Furthermore, a nonrigorous motivation for the validity of eq 14 for the full A and g tensors was given by Autschbach et al.43 The FC contribution to A vanishes in the long-distance limit, where there should be no spin density at the position of the nucleus. At the level of second-order degenerate perturbation theory (DPT2), the remaining contributions to g and A are36,44−46
| 15 |
| 16 |
| 17 |
 |
18 |
where the |ΨISS⟩ are the principal components (M = S) of the eigenstates of the nonrelativistic zeroth-order Hamiltonian H0 = H0 – HSOC with eigenvalues EI(0),nonrel. Equations 16 and 18 are the well-known orbital contributions to g and A, which make sizable contributions for transition metals, where SOC cannot be neglected. Equations 15 and 17 are the less well-known contributions due to gauge correction terms in the molecular Hamiltonian. While the gauge contribution to g has been investigated in a number of cases,47−53 the gauge contribution to A has only rarely been considered in the existing literature.54,55
Similar to eq 11, one can express the long-range limit of the PSO operator as
 |
19 |
Inserting this into eq 18 and noticing as before that the commutators with H0nonrel can be used to cancel the energy difference in the denominator, one obtains
 |
20 |
The second term (the expectation value of the commutator) prevents APSO/SOC and gorb/SOC from fulfilling eq 14. It can also be seen that one of the terms in the commutator scales again as R–2, in contrast to the expected R–3. However, when considering the long-range limit of the gauge contribution (eq 17), one notices that the same erroneous terms appear with opposite sign. Hence, these terms exactly cancel when the two contributions are added:
| 21 |
This concludes the proof of eq 14 for the complete A and g. A more in-depth theoretical discussion of the results derived in this Letter will be presented in a forthcoming publication.
In order to corroborate our theoretical results,
we investigated eq 21 numerically. We
performed calculations on the radicals H2O+,
CO+, H2CO+, and NF3+ and the transition metal complexes Cu(NO3)2, Ni(CO)3H, and TiF3. A proton serving
as a probe nucleus was placed at different distances from the paramagnetic
center. A “naked” proton was used for radicals and an
HF molecule for the metal complexes. The proton A and g tensors were then calculated with Kohn–Sham density
functional theory (KS-DFT) using the BP86 exchange–correlation
functional and correlation-consistent basis sets of different sizes.
GGA functionals are not expected to yield extremely accurate SH parameters
compared with the experiment. However, absolute accuracy is not our
concern here, since our comparison is not with the experiment but
entirely “internal”, i.e., we compare different quantities
calculated at the same level of theory. In order to provide a measure
of the “size” of the calculated tensors and their individual
contributions, we calculate the Frobenius norm defined as  . This allows for the definition of a “relative
deviation” Δrel as a measure of the difference
between some exact tensor and an approximation like the PDA:
. This allows for the definition of a “relative
deviation” Δrel as a measure of the difference
between some exact tensor and an approximation like the PDA:
| 22 |
When we compare the exact APSO/SOC with gorb/SOC inserted into eq 14, we denote the relative difference as ΔrelSOC; when we compare the two sides of eq 21, we denote it as Δrel.
Among all of the investigated systems, the gauge correction was found to be most important for the CO+ radical, for which we present results in Figure 1. We expect that with larger distance, where the PDA (eq 14) becomes better, the relative deviation Δrel should get smaller. This is also what we observe for ΔrelSOC+gauge according to eq 21, but only for the largest basis set (decontracted cc-pV6Z). For smaller basis sets, strong deviations from this expected behavior and slow basis set convergence can be observed, although for some systems, like TiF3, the convergence is much faster (see the Supporting Information). This suggests that eq 14 is only a valid long-distance approximation in the limit of a complete basis set, an issue that we will discuss further in a forthcoming publication. We note that the strong basis set dependence is solely due to the slow convergence of the A tensor, while the g tensor converges very quickly when the basis set size is increased. The observed basis set dependence is in contrast to the SD contribution to the A tensor, for which eq 14 holds irrespective of the basis set size. In contrast to Δrel, ΔrelSOCincreases with increasing distance for all basis set sizes. This indicates that eq 14 is not valid when only the orbital contribution is considered without the gauge contribution, as expected from eq 20. The presence of the R–2 scaling in the unphysical second term of this equation means that it will increasingly dominate APSO/SOC, which explains why the PDA for this contribution alone becomes increasingly worse.
Figure 1.
Comparison of the exact A tensor contributions to an approximation calculated with eq 14 for the CO+ radical. The presented numbers are the relative deviations (see eq 22) in %.
We now investigate how APSO/SOC, Agauge, and their sum scale with the distance R for the CO+ radical. According to our theoretical analysis, both APSO/SOC and Agauge have terms that scale as R–2, and these terms cancel each other out in the sum to give the physical R–3 scaling. In Figure 2 we show the norms of these tensors as functions of the distance in a log–log plot, where the slope corresponds to the exponent of R. In order to guide the eye and emphasize deviations from the ideal R–3 scaling behavior, we have also plotted in red color a straight line with slope −3 that passes through the last data point. For APSO/SOC, the data points proceed roughly parallel to the red line for small distances, indicating an approximately R–3 scaling. However, for larger distances, the slope is reduced, which indicates that the R–2 term that decays more slowly is gaining importance. For Agauge, the slope is already significantly different from −3 for small distances, indicating that here the R–2 term becomes important earlier. For APSO/SOC + Agauge, the slope is very close to −3 even at large distances, which confirms eq 21 that suggests that the unphysical terms cancel each other in the sum. The slopes of the different HFC tensor contributions in the beginning (small distance) and end (large distance) of the data series are summarized for all of the investigated systems in Table 1. It can be seen that CO+ is the only investigated system for which the R–2 term changes the scaling of APSO/SOC in the long-distance limit. For Agauge, the R–2 term shows up in several systems, including the metal complex Ni(CO)3H.
Figure 2.
Log–log plots of the norm of the A tensor contributions versus R, the distance of the probe nucleus from the center of the CO+ radical, with the decontracted cc-pV6Z basis set. The computed data are shown with diamond symbols for only the PSO/SOC part (top), only the gauge correction part (middle), and their sum (bottom). Shown in red are straight lines with slope = −3 passing through the last data points.
Table 1. Slopes of the Log–Log Plots (as in Figure 2 for CO+) at the Beginning and End of the Data Series for Different A Tensor Contributionsa.
| first two data points (small R) | last two data points (large R) | ||
|---|---|---|---|
| CO+ | APSO/SOC | –3.09 | –2.46 |
| Agauge | –2.16 | –2.02 | |
| APSO/SOC + Agauge | –3.17 | –3.02 | |
| H2CO+ | APSO/SOC | –3.08 | –3.00 |
| Agauge | –2.73 | –2.12 | |
| APSO/SOC + Agauge | –3.07 | –3.01 | |
| H2O+ | APSO/SOC | –3.02 | –3.02 |
| Agauge | –3.01 | –2.85 | |
| APSO/SOC + Agauge | –3.02 | –3.02 | |
| NF3+b | APSO/SOC | –2.98 | –3.00 |
| Agauge | –3.00 | –3.00 | |
| APSO/SOC + Agauge | –2.98 | –3.00 | |
| Cu(NO3)2 | APSO/SOC | –3.02 | –3.00 |
| Agauge | –2.82 | –3.00 | |
| APSO/SOC + Agauge | –3.02 | –3.00 | |
| Ni(CO)3H | APSO/SOC | –3.05 | –3.00 |
| Agauge | –3.01 | –2.18 | |
| APSO/SOC + Agauge | –3.05 | –3.00 | |
| TiF3 | APSO/SOC | –2.98 | –3.00 |
| Agauge | –2.98 | –3.00 | |
| APSO/SOC + Agauge | –2.98 | –3.00 |
The used basis sets were decontracted cc-pV5Z for transition metal complexes and decontracted cc-pV6Z for radicals.
For NF3+, the calculations for the first distance (5 Å) did not converge. Hence, the first two data points correspond to 7 and 9 Å.
In order to gain an idea of the importance of the gauge contribution, we plot the ratio of the norms of Agauge and APSO/SOC + Agauge in Figure 3. One can observe that the gauge contribution is more important for the radicals than for the transition metal complexes. One can also see that in cases where the gauge contribution has a sizable R–2 part (CO+, H2CO+, and Ni(CO)3H; see Table 1), its importance increases with increasing distance. These results indicate that while APSO/SOC has an unphysical part that scales as R–2 that will eventually dominate at large enough distances, the prefactor of this part might be so small that it is negligible at all distances of interest. However, the CO+ example shows that the gauge contribution can be essential for a correct description even for small distances, which is why one should never neglect this contribution. Although the gauge contribution seems to be less important for metal complexes, it is definitely needed for the Ni(CO)3H complex from our test set, as demonstrated in Figure 4 (the analogue of Figure 1 for CO+).
Figure 3.
Ratios of the norms of the gauge contribution to the A tensor and the sum of the PSO/SOC and gauge contributions. All of the values were calculated with the decontracted cc-pV6Z basis set for the radicals and with the decontracted cc-pV5Z basis set for the transition metal complexes.
Figure 4.
Comparison of the exact A tensor contributions to an approximation calculated with eq 14 for the Ni(CO)3H complex. The presented numbers are the relative deviations (see eq 22) in %.
Our results have important implications for the ab initio treatment of PCSs. In principle, one can evaluate the chemical shieldings directly from eq 3 (as already demonstrated by Gendron et al.56) or more commonly from the SH approximation (eq 5). Although such an approach would have the advantage of going beyond the PDA, the latter case has the disadvantage that a separate set of response equations has to be solved in order to obtain the A tensor for each individual nucleus. For systems with many nuclei, like proteins, the computational cost would quickly explode. This makes the use of the PDA attractive, as only a single electronic structure calculation is necessary to determine the PCSs for all of the nuclei in the system. In the context of the SH approximation, we have shown that eq 8 with the asymmetric χ′ tensor is fundamentally flawed because of the neglect of orbital and gauge correction contributions to A. The incorporation of these contributions shows that the correct equation to use is eq 1, which confirms the classic semiempirical treatments of PCSs. Importantly, this equation is not restricted to the SH approximation. The susceptibility tensor can also be directly calculated according to eq 13 using either ab initio or, for example, ligand field models. Such an approach has been followed already by some researchers.4,16,17,57 We expect that this can lead to more accurate predictions than the equations involving the g tensor, especially in situations where the conditions for applying the SH approximation are not fulfilled.
Computational Details
All of the calculations were performed with a development
version
of the ORCA electronic structure program.58A and g tensors were calculated using
KS-DFT50,59 with the BP8660,61 exchange–correlation
functional, grid5 integration grids, and without the resolution of
the identity (RI) approximation. A number of correlation-consistent
basis sets of increasing accuracy62−64 were used for the calculations.
For the radicals, we used cc-pVDZ, cc-pVQZ, cc-pV6Z, and for even
higher accuracy, the decontracted cc-pV6Z basis set. For transition
metals, cc-pV6Z is not defined, and we used cc-pV5Z and decontracted
cc-pV5Z instead. The integrals needed for the gauge correction to
the A tensor (see eq 17) diverge if nuclei K and A are identical. Therefore,
this contribution was omitted, as is common practice.54,65 For computational tests of the PDA behavior, we placed probe nuclei
(protons) at different distances from the center of the paramagnetic
molecule (RO) along the arbitrarily chosen
unit vector 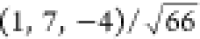 .
We chose distances between 5 and 45 Å
in steps of 2 Å. The centers were defined as O for H2O+, the midpoint between C and O for CO+, C
for H2CO+, N for NF3+,
and the metal atom for the transition metal complexes. For the radicals,
bare protons were used as probe nuclei. For the metal complexes, this
was not possible because of their smaller ionization energy. Therefore,
the probe nucleus was chosen to be the proton of a HF molecule. The
geometries were taken from an earlier g value study.50 More details can be found in the Supporting Information.
.
We chose distances between 5 and 45 Å
in steps of 2 Å. The centers were defined as O for H2O+, the midpoint between C and O for CO+, C
for H2CO+, N for NF3+,
and the metal atom for the transition metal complexes. For the radicals,
bare protons were used as probe nuclei. For the metal complexes, this
was not possible because of their smaller ionization energy. Therefore,
the probe nucleus was chosen to be the proton of a HF molecule. The
geometries were taken from an earlier g value study.50 More details can be found in the Supporting Information.
Acknowledgments
L.L. thanks Willem Van den Heuvel for fruitful discussions. We gratefully acknowledge financial support of this work by the Max Planck Society. This work was supported by the Fondazione Cassa di Risparmio di Firenze, MIUR Italy “Progetto Dipartimenti di Eccellenza 2018–2022” to the Department of Chemistry “Ugo Schiff” and PRIN 2017A2KEPL. We acknowledge the use of resources of the Centre CERM, Italy, of Instruct-ERIC, an ESFRI Landmark. This work was also supported by Instruct-ULTRA (Grant 731005), an EU H2020 project to further develop the services of Instruct-ERIC.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02462.
The authors declare no competing financial interest.
Supplementary Material
References
- Bleaney B.; Dobson C. M.; Levine B. A.; Martin R. B.; Williams R. J. P.; Xavier A. V. Origin of lanthanide nuclear magnetic resonance shifts and their uses. J. Chem. Soc., Chem. Commun. 1972, 13, 791b–793. 10.1039/c3972000791b. [DOI] [Google Scholar]
- Di Bari L.; Lelli M.; Salvadori P. Ligand Lability and Chirality Inversion in Yb Heterobimetallic Catalysts. Chem. - Eur. J. 2004, 10 (18), 4594–4598. 10.1002/chem.200400302. [DOI] [PubMed] [Google Scholar]
- Di Bari L.; Lelli M.; Pintacuda G.; Pescitelli G.; Marchetti F.; Salvadori P. Solution versus Solid-State Structure of Ytterbium Heterobimetallic Catalysts. J. Am. Chem. Soc. 2003, 125 (18), 5549–5558. 10.1021/ja0297640. [DOI] [PubMed] [Google Scholar]
- Vonci M.; Mason K.; Suturina E. A.; Frawley A. T.; Worswick S. G.; Kuprov I.; Parker D.; McInnes E. J. L.; Chilton N. F. Rationalization of Anomalous Pseudocontact Shifts and Their Solvent Dependence in a Series of C3-Symmetric Lanthanide Complexes. J. Am. Chem. Soc. 2017, 139 (40), 14166–14172. 10.1021/jacs.7b07094. [DOI] [PubMed] [Google Scholar]
- Peters J. A.; Djanashvili K.; Geraldes C. F. G. C.; Platas-Iglesias C. The chemical consequences of the gradual decrease of the ionic radius along the Ln-series. Coord. Chem. Rev. 2020, 406, 213146. 10.1016/j.ccr.2019.213146. [DOI] [Google Scholar]
- Parker D.; Suturina E. A.; Kuprov I.; Chilton N. F. How the Ligand Field in Lanthanide Coordination Complexes Determines Magnetic Susceptibility Anisotropy, Paramagnetic NMR Shift, and Relaxation Behavior. Acc. Chem. Res. 2020, 53 (8), 1520–1534. 10.1021/acs.accounts.0c00275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gochin M.; Roder H. Protein structure refinement based on paramagnetic NMR shifts: Applications to wild-type and mutant forms of cytochrome c. Protein Sci. 1995, 4 (2), 296–305. 10.1002/pro.5560040216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banci L.; Bertini I.; Bren K. L.; Cremonini M. A.; Gray H. B.; Luchinat C.; Turano P. The use of pseudocontact shifts to refine solution structures of paramagnetic metalloproteins: Met80Ala cyano-cytochrome c as an example. JBIC, J. Biol. Inorg. Chem. 1996, 1 (2), 117–126. 10.1007/s007750050030. [DOI] [Google Scholar]
- Schmitz C.; Bonvin A. M. J. J. Protein–protein HADDocking using exclusively pseudocontact shifts. J. Biomol. NMR 2011, 50 (3), 263–266. 10.1007/s10858-011-9514-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto K.; Dürr U. H. N.; Xu J.; Im S.-C.; Waskell L.; Ramamoorthy A. Dynamic Interaction Between Membrane-Bound Full-Length Cytochrome P450 and Cytochrome b5 Observed by Solid-State NMR Spectroscopy. Sci. Rep. 2013, 3 (1), 2538. 10.1038/srep02538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong L.; Wen X.; Rabinowitz T. M.; Russell B. S.; Karan E. F.; Bren K. L. Heme axial methionine fluxionality in Hydrogenobacter thermophilus cytochrome c552. Proc. Natl. Acad. Sci. U. S. A. 2004, 101 (23), 8637. 10.1073/pnas.0402033101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitsche C.; Otting G. Pseudocontact shifts in biomolecular NMR using paramagnetic metal tags. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 98–99, 20–49. 10.1016/j.pnmrs.2016.11.001. [DOI] [PubMed] [Google Scholar]
- Bertini I.; Luchinat C.; Parigi G.; Ravera E.. NMR of Paramagnetic Molecules: Applications to Metallobiomolecules and Models; Elsevier, 2016. [Google Scholar]
- Ravera E.; Carlon A.; Fragai M.; Parigi G.; Luchinat C. Paramagnetic NMR as a new tool in structural biology. Emerging Top. Life Sci. 2018, 2 (1), 19–28. 10.1042/ETLS20170084. [DOI] [PubMed] [Google Scholar]
- Keizers P. H. J.; Ubbink M. Paramagnetic tagging for protein structure and dynamics analysis. Prog. Nucl. Magn. Reson. Spectrosc. 2011, 58 (1), 88–96. 10.1016/j.pnmrs.2010.08.001. [DOI] [PubMed] [Google Scholar]
- Hiller M.; Sittel T.; Wadepohl H.; Enders M. A New Class of Lanthanide Complexes with Three Ligand Centered Radicals: NMR Evaluation of Ligand Field Energy Splitting and Magnetic Coupling. Chem. - Eur. J. 2019, 25 (45), 10668–10677. 10.1002/chem.201901388. [DOI] [PubMed] [Google Scholar]
- Hiller M.; Krieg S.; Ishikawa N.; Enders M. Ligand-Field Energy Splitting in Lanthanide-Based Single-Molecule Magnets by NMR Spectroscopy. Inorg. Chem. 2017, 56 (24), 15285–15294. 10.1021/acs.inorgchem.7b02704. [DOI] [PubMed] [Google Scholar]
- Novikov V. V.; Pavlov A. A.; Belov A. S.; Vologzhanina A. V.; Savitsky A.; Voloshin Y. Z. Transition Ion Strikes Back: Large Magnetic Susceptibility Anisotropy in Cobalt(II) Clathrochelates. J. Phys. Chem. Lett. 2014, 5 (21), 3799–3803. 10.1021/jz502011z. [DOI] [PubMed] [Google Scholar]
- Bertini I.; Luchinat C.; Parigi G. Magnetic susceptibility in paramagnetic NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2002, 40 (3), 249–273. 10.1016/S0079-6565(02)00002-X. [DOI] [Google Scholar]
- Parigi G.; Ravera E.; Luchinat C. Magnetic susceptibility and paramagnetism-based NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2019, 114–115, 211–236. 10.1016/j.pnmrs.2019.06.003. [DOI] [PubMed] [Google Scholar]
- McConnell H. M.; Robertson R. E. Isotropic Nuclear Resonance Shifts. J. Chem. Phys. 1958, 29 (6), 1361–1365. 10.1063/1.1744723. [DOI] [Google Scholar]
- Kurland R. J.; McGarvey B. R. Isotropic NMR shifts in transition metal complexes: The calculation of the fermi contact and pseudocontact terms. J. Magn. Reson. 1970, 2 (3), 286–301. 10.1016/0022-2364(70)90100-9. [DOI] [Google Scholar]
- Van den Heuvel W.; Soncini A. NMR chemical shift as analytical derivative of the Helmholtz free energy. J. Chem. Phys. 2013, 138 (5), 054113. 10.1063/1.4789398. [DOI] [PubMed] [Google Scholar]
- Soncini A.; Van den Heuvel W. Communication: Paramagnetic NMR chemical shift in a spin state subject to zero-field splitting. J. Chem. Phys. 2013, 138 (2), 021103. 10.1063/1.4775809. [DOI] [PubMed] [Google Scholar]
- Martin B.; Autschbach J. Temperature dependence of contact and dipolar NMR chemical shifts in paramagnetic molecules. J. Chem. Phys. 2015, 142 (5), 054108. 10.1063/1.4906318. [DOI] [PubMed] [Google Scholar]
- Parigi G.; Benda L.; Ravera E.; Romanelli M.; Luchinat C. Pseudocontact shifts and paramagnetic susceptibility in semiempirical and quantum chemistry theories. J. Chem. Phys. 2019, 150 (14), 144101. 10.1063/1.5037428. [DOI] [PubMed] [Google Scholar]
- Vaara J.; Rouf S. A.; Mareš J. Magnetic Couplings in the Chemical Shift of Paramagnetic NMR. J. Chem. Theory Comput. 2015, 11 (10), 4840–4849. 10.1021/acs.jctc.5b00656. [DOI] [PubMed] [Google Scholar]
- Mareš J.; Vaara J. Ab initio paramagnetic NMR shifts via point-dipole approximation in a large magnetic-anisotropy Co(II) complex. Phys. Chem. Chem. Phys. 2018, 20 (35), 22547–22555. 10.1039/C8CP04123G. [DOI] [PubMed] [Google Scholar]
- Pell A. J.; Pintacuda G.; Grey C. P. Paramagnetic NMR in solution and the solid state. Prog. Nucl. Magn. Reson. Spectrosc. 2019, 111, 1–271. 10.1016/j.pnmrs.2018.05.001. [DOI] [PubMed] [Google Scholar]
- Benda L.; Mareš J.; Ravera E.; Parigi G.; Luchinat C.; Kaupp M.; Vaara J. Pseudo-Contact NMR Shifts over the Paramagnetic Metalloprotein CoMMP-12 from First Principles. Angew. Chem., Int. Ed. 2016, 55 (47), 14713–14717. 10.1002/anie.201608829. [DOI] [PubMed] [Google Scholar]
- Mondal A.; Gaultois M. W.; Pell A. J.; Iannuzzi M.; Grey C. P.; Hutter J.; Kaupp M. Large-Scale Computation of Nuclear Magnetic Resonance Shifts for Paramagnetic Solids Using CP2K. J. Chem. Theory Comput. 2018, 14 (1), 377–394. 10.1021/acs.jctc.7b00991. [DOI] [PubMed] [Google Scholar]
- Srb P.; Svoboda M.; Benda L.; Lepšík M.; Tarábek J.; Šícha V.; Grüner B.; Grantz-Šašková K.; Brynda J.; Řezáčová P.; Konvalinka J.; Veverka V. Capturing a dynamically interacting inhibitor by paramagnetic NMR spectroscopy. Phys. Chem. Chem. Phys. 2019, 21 (10), 5661–5673. 10.1039/C9CP00416E. [DOI] [PubMed] [Google Scholar]
- Chyba J.; Novák M.; Munzarová P.; Novotný J.; Marek R. Through-Space Paramagnetic NMR Effects in Host–Guest Complexes: Potential Ruthenium(III) Metallodrugs with Macrocyclic Carriers. Inorg. Chem. 2018, 57 (15), 8735–8747. 10.1021/acs.inorgchem.7b03233. [DOI] [PubMed] [Google Scholar]
- Cerofolini L.; Silva J. M.; Ravera E.; Romanelli M.; Geraldes C. F. G. C.; Macedo A. L.; Fragai M.; Parigi G.; Luchinat C. How Do Nuclei Couple to the Magnetic Moment of a Paramagnetic Center? A New Theory at the Gauntlet of the Experiments. J. Phys. Chem. Lett. 2019, 10 (13), 3610–3614. 10.1021/acs.jpclett.9b01128. [DOI] [PubMed] [Google Scholar]
- Ravera E.; Parigi G.; Luchinat C. What are the methodological and theoretical prospects for paramagnetic NMR in structural biology? A glimpse into the crystal ball. J. Magn. Reson. 2019, 306, 173–179. 10.1016/j.jmr.2019.07.027. [DOI] [PubMed] [Google Scholar]
- Harriman J. E.Theoretical Foundations of Electron Spin Resonance; Academic Press: New York, 1978. [Google Scholar]
- Koseki S.; Gordon M. S.; Schmidt M. W.; Matsunaga N. Main Group Effective Nuclear Charges for Spin-Orbit Calculations. J. Phys. Chem. 1995, 99 (34), 12764–12772. 10.1021/j100034a013. [DOI] [Google Scholar]
- McConnell H. M. Theory of Nuclear Magnetic Shielding in Molecules. I. Long-Range Dipolar Shielding of Protons. J. Chem. Phys. 1957, 27 (1), 226–229. 10.1063/1.1743676. [DOI] [Google Scholar]
- Ramsey N. F. Magnetic Shielding of Nuclei in Molecules. Phys. Rev. 1950, 78 (6), 699–703. 10.1103/PhysRev.78.699. [DOI] [Google Scholar]
- Ramsey N. F. Chemical Effects in Nuclear Magnetic Resonance and in Diamagnetic Susceptibility. Phys. Rev. 1952, 86 (2), 243–246. 10.1103/PhysRev.86.243. [DOI] [Google Scholar]
- Watson M. A.; Sałek P.; Macak P.; Jaszuński M.; Helgaker T. The Calculation of Indirect Nuclear Spin–Spin Coupling Constants in Large Molecules. Chem. - Eur. J. 2004, 10 (18), 4627–4639. 10.1002/chem.200306065. [DOI] [PubMed] [Google Scholar]
- Gerloch M.; McMeeking R. F. Paramagnetic properties of unsymmetrical transition-metal complexes. J. Chem. Soc., Dalton Trans. 1975, (22), 2443–2451. 10.1039/dt9750002443. [DOI] [Google Scholar]
- Autschbach J.; Patchkovskii S.; Pritchard B. Calculation of Hyperfine Tensors and Paramagnetic NMR Shifts Using the Relativistic Zeroth-Order Regular Approximation and Density Functional Theory. J. Chem. Theory Comput. 2011, 7 (7), 2175–2188. 10.1021/ct200143w. [DOI] [PubMed] [Google Scholar]
- McWeeny R.Methods of Molecular Quantum Mechanics; Academic Press, 1992. [Google Scholar]
- Neese F.; Solomon E. I.. Interpretation and Calculation of Spin-Hamiltonian Parameters in Transition Metal Complexes. In Magnetism: Molecules to Materials IV; Miller J. S., Drillon M., Eds.; Wiley-VCH: Weinheim, Germany, 2003; pp 345–466. [Google Scholar]
- Neese F. Quantum Chemistry and EPR Parameters. eMagRes 2017, 6 (1), 1–22. 10.1002/9780470034590.emrstm1505. [DOI] [Google Scholar]
- Lushington G. H.; Bündgen P.; Grein F. Ab initio study of molecular g-tensors. Int. J. Quantum Chem. 1995, 55 (5), 377–392. 10.1002/qua.560550503. [DOI] [Google Scholar]
- Lushington G. H.; Grein F. Complete to second-order ab initio level calculations of electronic g-tensors. Theor. Chim. Acta 1996, 93 (5), 259–267. 10.1007/BF01127505. [DOI] [Google Scholar]
- Schreckenbach G.; Ziegler T. Calculation of the G-Tensor of Electron Paramagnetic Resonance Spectroscopy Using Gauge-Including Atomic Orbitals and Density Functional Theory. J. Phys. Chem. A 1997, 101 (18), 3388–3399. 10.1021/jp963060t. [DOI] [Google Scholar]
- Neese F. Prediction of electron paramagnetic resonance g values using coupled perturbed Hartree–Fock and Kohn–Sham theory. J. Chem. Phys. 2001, 115 (24), 11080–11096. 10.1063/1.1419058. [DOI] [Google Scholar]
- Kaupp M.; Reviakine R.; Malkina O. L.; Arbuznikov A.; Schimmelpfennig B.; Malkin V. G. Calculation of electronic g-tensors for transition metal complexes using hybrid density functionals and atomic meanfield spin-orbit operators. J. Comput. Chem. 2002, 23 (8), 794–803. 10.1002/jcc.10049. [DOI] [PubMed] [Google Scholar]
- Neese F. Correlated ab initio calculation of electronic g-tensors using a sum over states formulation. Chem. Phys. Lett. 2003, 380 (5), 721–728. 10.1016/j.cplett.2003.09.047. [DOI] [Google Scholar]
- Neese F. Analytic derivative calculation of electronic g-tensors based on multireference configuration interaction wavefunctions. Mol. Phys. 2007, 105 (19–22), 2507–2514. 10.1080/00268970701549389. [DOI] [Google Scholar]
- Arbuznikov A. V.; Vaara J.; Kaupp M. Relativistic spin-orbit effects on hyperfine coupling tensors by density-functional theory. J. Chem. Phys. 2004, 120 (5), 2127–2139. 10.1063/1.1636720. [DOI] [PubMed] [Google Scholar]
- Sandhoefer B.; Kossmann S.; Neese F. Derivation and assessment of relativistic hyperfine-coupling tensors on the basis of orbital-optimized second-order Møller–Plesset perturbation theory and the second-order Douglas–Kroll–Hess transformation. J. Chem. Phys. 2013, 138 (10), 104102. 10.1063/1.4792362. [DOI] [PubMed] [Google Scholar]
- Gendron F.; Sharkas K.; Autschbach J. Calculating NMR Chemical Shifts for Paramagnetic Metal Complexes from First-Principles. J. Phys. Chem. Lett. 2015, 6 (12), 2183–2188. 10.1021/acs.jpclett.5b00932. [DOI] [PubMed] [Google Scholar]
- Blackburn O. A.; Chilton N. F.; Keller K.; Tait C. E.; Myers W. K.; McInnes E. J. L.; Kenwright A. M.; Beer P. D.; Timmel C. R.; Faulkner S. Spectroscopic and Crystal Field Consequences of Fluoride Binding by [Yb·DTMA]3+ in Aqueous Solution. Angew. Chem., Int. Ed. 2015, 54 (37), 10783–10786. 10.1002/anie.201503421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neese F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8 (1), e1327 10.1002/wcms.1327. [DOI] [Google Scholar]
- Neese F. Metal and ligand hyperfine couplings in transition metal complexes: The effect of spin–orbit coupling as studied by coupled perturbed Kohn–Sham theory. J. Chem. Phys. 2003, 118 (9), 3939–3948. 10.1063/1.1540619. [DOI] [Google Scholar]
- Perdew J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 33 (12), 8822–8824. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38 (6), 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90 (2), 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Wilson A. K.; van Mourik T.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. VI. Sextuple zeta correlation consistent basis sets for boron through neon. J. Mol. Struct.: THEOCHEM 1996, 388, 339–349. 10.1016/S0166-1280(96)80048-0. [DOI] [Google Scholar]
- Balabanov N. B.; Peterson K. A. Systematically convergent basis sets for transition metals. I. All-electron correlation consistent basis sets for the 3d elements Sc–Zn. J. Chem. Phys. 2005, 123 (6), 064107. 10.1063/1.1998907. [DOI] [PubMed] [Google Scholar]
- Vaara J.; Ruud K.; Vahtras O. Correlated response calculations of the spin–orbit interaction contribution to nuclear spin–spin couplings. J. Comput. Chem. 1999, 20 (12), 1314–1327. . [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






