Abstract

Absorption and magnetic circular dichroism (MCD) spectra have been measured and theoretically simulated for a series of palladium octaethylporphyrins substituted at the meso positions with phenyl groups (n = 0–4). Analysis of the spectra included the perimeter model and time-dependent density functional theory (TDDFT) calculations. With the increasing number of phenyl substituents, the molecule is transformed from a positive hard (ΔHOMO > ΔLUMO) to a soft (ΔHOMO ≈ ΔLUMO) chromophore. This is manifested by a drastic decrease of the absorption intensity in the 0–0 region of the Q-band and by the strongly altered ratio of MCD intensities in the Q and Soret regions. Such behavior can be readily predicted using perimeter model, by analyzing frontier orbital shifts caused by various perturbations: alkyl and aryl substitution, insertion of a metal, and deviations from planarity. TDDFT calculations confirm the trends predicted by the perimeter model, but they fail in cases of less symmetrical derivatives to properly reproduce the MCD spectra in the Soret region. Our results confirm the power of the perimeter model in predicting absorption and MCD spectra of large organic molecules, porphyrins in particular. We also postulate, contrary to previous works, that the isolated porphyrin dianion is not a soft chromophore, but rather a strongly positive-hard one.
Introduction
Tetrapyrroles (mostly heme and chlorophyll derivatives) are ubiquitous in nature and function in a wide range of biological processes, including respiration, electron transfer, oxidation catalysis, and signaling in photosynthesis, among others.1 In addition to their basic macrocycle properties, i.e., coordination ability and the presence of specific functional groups, their conformation may have a significant relevance for the biological function.2 This is based on the hypothesis that fine-tuning of the macrocycle conformation by the protein scaffold is a way by which nature might control the physicochemical properties of the tetrapyrrole–protein complexes. It means that the structural organization of tetrapyrrole complexes in vivo, in which chromophore molecules are in nonplanar labile conformations, is a tool for subtle control of enzymatic and photocatalytic properties of natural porphyrins.2−7 The variations observed in spectral-luminescent properties, as well as in redox characteristics of interacting subunits, can be caused not only by purely electronic effects in natural nanoassemblies but also by changes in the spatial structure of the tetrapyrrole macrocycle itself.8
It has been demonstrated that several unique up-converting solid-state functional nanomaterials based on palladium 2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP) and Pd-meso-tetraphenyl-tetrabenzo[2,3]porphyrin with bulky side substituents are attractive for many applications, such as photocatalytic cells and photovoltaic devices.9−11 It cannot be excluded that possible steric hindrance effects should also be taken into account in order to optimize the functionality of such nanodevices or to improve photostability. In this respect, we recently succeeded in showing the manifestation of steric interactions in PdOEP derivatives with a sequential increase of the number of meso-phenyl substituents (n = 1–4) based on spectral, kinetic, pump–probe, and phosphorescence measurements in the temperature range of 80–293 K (solutions and glassy rigid matrices), as well as on quantum-chemical calculations.12 It was demonstrated that a sequential transition from a planar PdOEP molecule to the set of sterically hindered derivatives, that is, PdOEP → PdOEP1 → PdOEP2t → PdOEP2c → PdOEP3 → PdOEP4 (Figure 1), manifests itself in a noticeable shortening of triplet-state lifetimes (from 210 to 0.04 μs in degassed solutions at 293 K) and in the pronounced decrease of the efficiency of singlet oxygen generation (from 1.0 to 0.05 in non-deaerated toluene). On the basis of the whole set of experimental data and the analysis of Arrhenius plots of rate constants for the overall deactivation of triplet state, a detailed picture of steric interactions between bulky meso-phenyls and peripheral β-alkyl substituents of pyrrole ring has been obtained. These interactions were proposed as the main factor responsible for the essential shortening of the triplet state lifetime.
Figure 1.
Structures and acronyms for the investigated Pd-porphyrins. Palladium 2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP); palladium 5-phenyl-2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP1); palladium 5,15-diphenyl-2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP2t); palladium 5,10-diphenyl-2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP2c); palladium 5,10,15-triphenyl-2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP3); palladium 5,10,15,20-tetraphenyl-2,3,7,8,12,13,17,18-octaethylporphyrin (PdOEP4); palladium tetraphenylporphyrin (PdTPP), a reference compound with planar π-conjugated macrocycle having four meso-phenyl rings and no β-ethyl substituents on pyrrole rings.
In this work we measure, calculate, and analyze the spectral parameters of the singlet excited states of these palladium porphyrin derivatives with the help of magnetic circular dichroism (MCD) spectroscopy. MCD measures the difference in absorption of left- and right-circular-polarized light of a molecule under the influence of an external magnetic field pointing in the direction of light propagation. The MCD technique is complementary to UV–visible absorption spectroscopy. It can provide information on ground and excited state degeneracies; the analysis of the MCD spectrum is also crucial for understanding of the electronic structure of not only high-symmetry macrocycles but also low-symmetry derivatives. In many cases, MCD spectroscopy has provided key information for a successful assignment of the absorption bands of organic molecules, e.g., porphyrin or its constitutional isomers and their derivatives, which could not be derived from considerations based only on the electronic absorption spectrum or the results of quantum-chemical calculations.13−19 It should also be noted that even though modern ab initio or time-dependent density functional theory (TDDFT) calculations of MCD are now available,20−25 the analysis based on semiempirical approaches such as Gouterman’s four-orbital model26 and, in particular, Michl’s perimeter model27−30 should still be regarded as an essential starting point of any assignment of the optical spectra of compounds that can be derived from [n]annulenes containing (4N + 2) π-electrons. The perimeter model provides a simple and easy-to-grasp interpretation of the MCD and electronic absorption spectra based on the comparison of ΔHOMO and ΔLUMO, that is, the energy differences between the two highest occupied and two lowest unoccupied frontier π-orbitals. Molecules in which the ΔHOMO and ΔLUMO are significantly different are classified as “hard chromophores”, in the sense that their MCD and absorption characteristics are well-defined and difficult to alter. In contrast, chromophores with ΔHOMO ≈ ΔLUMO belong to the category of “soft chromophores”; their MCD signs and intensities as well as absorption coefficients can be readily modified, even by weak perturbations, e.g., methyl substitution. Porphyrins belong to this category. The power of the perimeter model for predicting their special properties has been demonstrated in numerous papers.14−19,24,31−42
While extremely useful, the perimeter model is rather limited to qualitative analysis. The development of reliable and fast computational techniques has now made it possible to check the perimeter model predictions quantitatively. This seems particularly challenging for molecules where several different types of perturbations are present. Such is the case of the porphyrins investigated in this work. Their formal derivation from an ideal perimeter involves bridging, metal insertion, multiple alkyl and aryl substitutions, and, finally, distortion of planarity. Our goal was to assess the role of each of these perturbations and to check whether they can be considered additive. For this purpose, we combine the analysis of experimental studies of absorption and MCD spectra with TDDFT calculations carried out for the full set of meso-phenyl substituted derivatives of PdOEP.
Experimental and Computational Details
Objects and Solvents
The formulas of the investigated set of Pd-porphyrins are presented in Figure 1 together with the corresponding acronyms. Octaethylporphyrin free bases with various numbers of meso-phenyl rings (n = 1–4) have been synthesized according to procedures described in refs (43) and (44). TPP was prepared using the method described in ref (45). Pd-complexes of the porphyrins under study have been obtained from the free-base analogues by the method described in ref (46), followed by purification and separation by chromatography. Structure of the compounds under study has been confirmed by mass-spectrometry (Shimadzu Axima Confidence, MALDI-TOF) and NMR 1H (Bruker 500) measurements. Solvents, tetrahydrofuran and 2-methyltetrahydrofuran (Aldrich, spectral-grade), were used without further purification.
Absorption and MCD Measurements
Absorption spectra were recorded using Shimadzu UV2700 spectrophotometer. MCD spectra were measured with an OLIS DSM17 spectropolarimeter equipped with a permanent magnet. The difference between the spectra recorded with the opposite directions of the magnetic field was used to minimize the baseline artifacts. Optical cuvettes (Hellma QS-111, path length = 1 cm) have been used. In most experiments, the porphyrin concentration was lower than 10–6 M–1 in order to exclude possible aggregation effects. All spectroscopic measurements have been done at ambient temperature and completed within a few hours after fresh sample preparation.
Quantum-Chemical Calculations
Optimizations of ground-state geometry were carried out with Gaussian 09 (A.01)47 software package, using the B3LYP functional48−50 and def2-SVP basis set. Whenever it was possible, geometries were optimized with symmetry restrictions. The Hessian matrix was checked for the absence of negative frequencies to ensure that the calculated structure corresponds to a real minimum. We also performed semiempirical INDO/S calculations of excited electronic states and Faraday B terms for the zinc porphyrin analogues. We used a modified version of DZDO program, kindly provided by Josef Michl and John Downing. The structures were initially optimized using DFT.
Absorption and MCD spectra have been simulated using TDDFT and magnetically perturbed TDDFT23 methodology, as implemented in version 2017 of the Amsterdam Density Functional (ADF) package.51 B3LYP (20% HF exchange52), CAM-B3LYP,53 and BP86D54−56 functionals and TZP basis set were used. In these calculations, ethyl substituents were replaced by methyl groups. For each functional, the geometry was separately optimized. Since palladium is a heavy atom, we checked for possible relativistic effects by comparing the results obtained with and without scalar relativistic ZORA (zero-order regular approximation) option. No significant differences were found. The values of Faraday A and B terms were calculated using two approaches: (a) sum of states (SOS) and (b) direct solution of the system of equations by the conjugate gradient procedure. The former is somewhat less accurate, but much faster. Moreover, slow convergence problems were encountered while using the direct approach. Therefore, the MCD simulations presented in this work are based on the results obtained by the SOS procedure, with 30 lowest excited states allowed to mix.
Results and Discussion
It has been well established that alkyl and aryl substituents can strongly affect absorption and, in particular, MCD spectra of porphyrins.13,31−34 Moreover, substituents of the same type (e.g., electron-donating) can act in different directions, depending on whether they are located at the meso or β positions. Another factor is the nature of the central atom. Finally, one has to take into account steric hindrance interactions of bulky peripheral substituents (β-ethyls and meso-phenyls) which can lead to nonplanarity. All these factors can contribute to the final form of electronic spectra.
The 4-fold symmetry of metalloporphyrins may not be exact for substituted molecules. For instance, each of the alkyl groups may be somewhat differently oriented with respect to the plane of the macrocycle. When the deviation from the ideal symmetry is small, the MCD spectra will exhibit an A term type shape (pseudo A term). It is practically impossible to distinguish between the case of real and pseudo A terms (two very close-lying states with opposite B terms). We believe the latter description is more realistic and use it below.
Absorption Spectra
Earlier we described in detail the spectral and kinetic properties of singlet and triplet states of meso-phenyl substituted (n = 1–4) octaalkyl derivatives, including free bases of octaethyl- and octamethylporphyrins,57,58 as well as metallocomplexes, PdOEPs.12 Here, we start by comparing the absorption spectra of PdOEP and PdTPP, two planar metalloporphyrins, differing by the number, type, and position of substituents. The spectra are depicted in Figure 2 and summarized in Table 1. Upon passing from PdOEP to PdTPP the short-wavelength B (Soret) and the long-wavelength Q(0,0) bands (almost degenerate L1 and L2 transitions) in the absorption spectra are bathochromicaly shifted by 1400 and 200 cm–1, respectively. The main difference is observed for the Q(0,0) band intensities: The absorption coefficient of PdOEP is about 40 times larger than that in PdTPP. At the same time, the intensities of the Q(0,1) vibronic components are comparable in the two molecules. As a result, the intensity ratio of the long-wavelength electronic Q(0,0) band to that of the vibronic one, Q(0,1), becomes much smaller in PdTPP, reflecting the diminishing of the oscillator strength of the (0–0) component of the S0 → S1 transition in this molecule.
Figure 2.
Left: experimental; right: simulated (B3LYP/TZP) absorption and MCD spectra of PdOEP (top) and PdTPP (bottom). A 500 cm–1 halfwidth was assumed in calculations.
Table 1. Experimentally Determined Absorption and MCD Characteristics.
Values are divided by (103 cm–1).
We now turn to the main changes observed at ambient temperature for the investigated series, characterized by the increasing degree of steric interactions of bulky side substituents (β-ethyl groups and meso-phenyl rings). The spectra are shown in Figures 3–6. It is evident that the successive introduction of meso-phenyl substituents into PdOEP leads to considerable transformations of the absorption (as well as fluorescence and phosphorescence)12 spectra. The increase of the number of meso-phenyl groups leads to bathochromic shifts in both Soret and Q(0,0) absorption bands. Similar behavior was also observed in fluorescence and phosphorescence spectra, accompanied by strong decrease of the lifetime of the excited T1 (more sensitive) and S1 states. We also observe regular changes in the pattern of vibronic activity in the absorption spectra along the series. Starting with PdOEP, a compound without phenyl substituents, an intense 0–0 band of the Q transition is followed by weaker vibronic components. This pattern gradually changes with the increasing number of phenyl substituents, reaching the minimum value for PdOEP4, which has four phenyl groups at the meso positions: Its absorption is characterized by a weak 0–0 transition and strong vibronic satellites. This behavior is well-represented by variable Q(0,0)/Q(0,1) intensity ratio, both in absorption and fluorescence spectra along the series. It should also be recalled that the Stokes shift between the absorption and fluorescence bands noticeably increases with the increase in the number of meso-phenyl rings.12
Figure 3.
Left: experimental; right: simulated (B3LYP/TZP) absorption and MCD spectra of PdOEP1.
Figure 6.
Left: experimental; right: simulated (B3LYP/TZP) absorption and MCD spectra of PdOEP4.
MCD Spectra
Two different MCD sign conventions have been used in the literature. Therefore, in order to avoid the confusion, it is better refer to the signs of the recorded MCDspectra, not to the signs of Faraday B terms. Figures 2-6 show that in all octaethyl metallocomplexes the same pattern of the MCD signs is observed, −, +, −, +, in ascending energy. The sequence of signs is also the same for PdTPP, which does not contain ethyl groups (for the Q region of PdTPP, this can be inferred from the Q(0,1) bands, as the Q(0,0) ones are too weak to be reliably detected). As already mentioned, it is interesting at the beginning to compare two molecules that were selected as reference compounds with planar geometry of the porphyrin macrocycle: PdTPP with four phenyls at the meso positions and PdOEP without phenyls, but with eight ethyl groups at the β positions (Figure 2). The L1 and L2 0–0 transitions (Q-band region) of PdTPP are extremely weak in absorption, practically undetectable in MCD, and about 100 times less intense than the Soret bands. This behavior is known as characteristic for porphyrins which exhibit almost equal splitting of frontier LUMO and HOMO orbitals, ΔLUMO and ΔHOMO (soft chromophores).28 In such molecules, the MCD signals corresponding to transitions to two lowest excited states are weak and dominated by vibronic bands. In contrast, the 0–0 transitions in the region of Q bands of PdOEP are very strong in MCD spectra and significantly higher than the signals of the transitions in the Soret bands region. In the absorption spectra, the 0–0 transitions to the first two electronic states are also relatively strong and dominant over vibronic transitions, but they are significantly weaker than the high-energy transitions in the Soret region. With the increasing number of phenyl substituents, the behavior of MCD spectra changes drastically, whereas the changes in the absorption spectra are not so spectacular. In the case of the compound with one phenyl group, PdOEP1, the MCD signal intensity of the Q bands is still much higher than those of the Soret bands (Figure 3). However, upon introducing more phenyl substituents at the meso positions, the relative ratio of MCD signals of Q versus Soret bands becomes smaller and smaller (Figures 4 and 5), leading to almost equal intensities for PdOEP4, the compound with four phenyls (Figure 6).
Figure 4.
Left: experimental; right: simulated (B3LYP/TZP) absorption and MCD spectra of PdOEP2t (top) and PdOEP2c (bottom).
Figure 5.
Left: experimental; right: simulated (B3LYP/TZP) absorption and MCD spectra of PdOEP3.
Structural Considerations
Before discussing the results of computational analysis, we take into account the following experimental findings. According to the experimental data,5,59 mono- and symmetrically (5,15Ph) di-meso-phenyl substituted β-alkylporphyrins (free bases) are planar, and correspondingly, the absorption and fluorescence properties are close to those characteristic of ordinary planar porphyrins.60 As was shown previously5,8,59,61,62 for free base β-alkyl-porphyrins, an increase in the number of bulky meso-phenyl substituents (n > 2), which experience steric interactions with closely located peripheral β-alkyl groups, leads to spatial distortions of the tetrapyrrole macrocycle, considerably changing its geometric structure not only in the T1 state but also in S0: Out-of-plane distortions of the π-conjugated tetrapyrrole macrocycle have been confirmed by NMR data. Computer modeling61,63 shows that out-of-plane deformations of the porphyrin macrocycle for molecules of OEP-Ph type manifest themselves in the rotation of pyrrolic rings (flanking the phenyl ring) around the Cα–Cα axis. As a result, the nitrogen atom and β-carbons of the pyrrolic ring are on the opposite sides relative to the porphyrin plane. Calculations also show that the nonplanarity of the π-conjugated porphyrin macrocycle is more pronounced in T1 than that in S0. These findings may be related to the decrease of the porphyrin skeleton rigidity in the excited T1 state, possibly due to the π-bonds alternation increase. However, the picture of out-of-plane deformations of the porphyrin macrocycle for meso-phenyl substituted PdOEP molecules may differ from that of free bases because of the higher rigidity of π-conjugated macrocycle for metallocomplexes.64 Finally, because of out-of-plane deformations of the porphyrin macrocycle, the manifestation of new electronic transitions cannot be excluded.63,65,66
Calculations
The focus of our attention is the analysis of the spectroscopic properties (absorption and MCD spectra) of meso-phenyl substituted PdOEP molecules using the obtained experimental data and the results of calculations. Figures S1–S6 show the calculated frontier molecular orbitals, their energies, as well as ΔHOMO and ΔLUMO values for differently substituted porphyrins, based on DFT (B3LYP/dev2-SVP) geometry optimizations. The optimized geometries of the palladium porphyrins under study are depicted in Figure 7. According to the calculations, deviation from the macrocycle planarity becomes noticeable starting from PdOEP2c and then increases with the number of meso-phenyl rings. Upon sequential increase of the number of meso-phenyl substituents, frontier orbital energies of LUMOs remain degenerate or almost-degenerate, i.e., ΔLUMO ≈ 0 in all cases. In contrast, ΔHOMO values systematically decrease upon going from planar PdOEP to highly distorted PdOEP4 (ΔHOMO ≈ 0 in the last case). According to the calculations and experiment,67,68 the tetrapyrrolic moiety of PdTPP is planar or nearly planar. ΔHOMO is slightly larger than ΔLUMO, but both splittings are very small, which is also characteristic for the free base analogue.
Figure 7.
Linear displays (cylindrical projection onto a cylinder tangent to the least-squares mean plane of 24 atoms of the porphyrin core) of the optimized ground-state structures, revealing deviations of the macrocycle from planarity in molecules containing two or more phenyl substituents (hydrogen atoms and ethyl substituents are omitted).
Figures 2–6 contain the comparison of the experimental absorption and MCD spectra with the simulated (B3LYP/TZP) ones. The agreement between calculated and measured absorption patterns is excellent. Even though the calculations overestimate the L and B transition energies (by less than 2000 cm–1), the energy gap between Q and Soret bands is perfectly reproduced, within 100–300 cm–1. The same applies to the predicted transition energy shifts that accompany substitution. The changes in the Q/Soret intensity ratios (oscillator strengths of Q(0,0) transitions becoming smaller with the increasing number of phenyl substituents) are also correctly simulated.
Regarding MCD, the situation is more complicated. The calculations properly simulate the MCD sign sequence and correctly reproduce the trend of decreasing the MCD intensity of Q transitions with subsequent addition of phenyl substituents. The relative MCD intensities in the Q and Soret regions agree well with experiments for PdOEP and PdTPP, the molecules are of approximately D4h symmetry. In contrast, for less symmetric and nonplanar porphyrins, the simulated MCD patterns are very different from the observed ones. The obvious reason is the presence of many allowed transitions in the Soret range. It is experimentally confirmed by the shape of MCD curves, revealing several bands (2–3) other than those corresponding to B transitions. The errors in the calculated positions of these states will propagate onto the simulated shape of MCD spectra. This phenomenon has been previously discussed in the context of comparison of experimental and theoretical MCD spectra of magnesium, calcium, zinc, and nickel porphyrins.69,70 It can be illustrated by analysis of the theoretical predictions for a specific porphyrin using various functionals. As an example, we compare the spectra simulated for PdOEP with B3LYP, CAM-B3LYP, and BP86D (Figure S7). The first two functionals yield practically the same absorption and MCD spectra, whereas for the third one, a different pattern of transitions in the Soret region is obtained. As a consequence, the simulated MCD spectrum looks completely different in this range, whereas for the Q region, all functionals lead to very similar and correct MCD patterns.
It should be recalled that these additional “intruder states” are not taken into account in Gouterman’s and Michl’s four-orbital models, since they involve other orbitals.
Discussion
The experimental findings can be analyzed using the Gouterman’s four-orbital26 or Michl’s perimeter model.30 The starting points for the analysis are somewhat different in the two approaches: porphyrin dianion in the former and a C20H202+ (4N + 2 =) 18-π-electron perimeter in the latter. Except for special cases,71 the two models lead to similar conclusions regarding the absorption and MCD intensities. The molecules under investigation can be derived from the perimeter by a combination of structural perturbations (Figure 8). Introduction of four N– bridges combined with the distortion of the C20H202+ perimeter produces the porphyrin dianion, which upon adding the central metal cation is converted into a metalloporphyrin. Further perturbations are due to substitution of aryl and alkyl groups at the meso and β positions, respectively. Finally, distortion of the planar structure caused by steric crowding should also be taken into account. Each of these factors can lead to shifts in orbital energies. The relative shifts can be easily predicted qualitatively by inspection of the nodal properties of the orbitals of the parent, unperturbed perimeter or by looking at the shapes of the frontier orbitals of porphyrin dianion. In order to obtain a quantitative picture of orbital splittings, quantum-chemical calculations are required. In this work, we used both qualitative and quantitative procedures, with the goal of separating and comparing the contributions to orbital shifts stemming from each of the above-mentioned effects.
Figure 8.
Bottom: formal derivation of PdOEP from an 18-π-electron perimeter, the [20]annulene dication (C20H202+) by bridging with N– (a), metal insertion (b), and ethyl substitution (c). Top left: perimeter orbitals in the real form, with indicated positions of nodal planes and bridging. Top right: DFT-calculated frontier orbitals of PdOEP.
We now recall the basics of the perimeter model. In general, a perturbation may lead to the splitting of the energies of HOMO and LUMO pairs, initially degenerate in the unperturbed perimeter, by an amount described by complex parameters a and b:
| 1 |
The degree of mixing of the L and B states (alternatively: Q and Soret transitions) can be described by two parameters, α and β. They determine the orientation of the nodes of the perturbed MOs with respect to the molecular framework, which can be written as
| 2 |
| 3 |
where E(B) – E(L) is the energy difference between the L and B states in the parent perimeter.
It can be shown that the values of transition dipole moments, as well as the values of MCD B terms can be expressed in terms of the strength of the structural perturbation (α and β parameters) and the electric (m) and magnetic (μ+ and μ–) dipole contributions. The quantity m, electric transition dipole contribution, is a simple function of N and of the perimeter size, n. Similarly, magnetic moments μ+ and μ– also depend on N and n. The former is proportional to the sum of the magnetic moments of the parent perimeter orbitals involved, μ+ = μN+1 + μN ,and is therefore much larger than the latter, which is proportional to their difference, μ– = μN+1 – μN. The μ– contribution is small and structure-insensitive, whereas the magnitude and sign of μ+ contribution depends on ΔHOMO – ΔLUMO. The ΔHOMO – ΔLUMO difference determines the sign of the B terms (and thus, of the MCD spectrum) of the L and B states of aromatic molecules. The negative difference is characterized by the MCD sign sequence +, −, −, + or +, −, +, −, in ascending energy for L1, L2, B1, and B2 transitions, respectively, depending on how strong the perturbation is. The compounds exhibiting such sequence of the MCD signs are classified as negative-hard chromophores. If the difference ΔHOMO – ΔLUMO is positive, the the MCD sign sequence is −, +, −, +, with no dependence on the strength of perturbation. The molecules characterized by this pattern are classified as positive-hard chromophores. The compounds with β close to zero (ΔHOMO ≈ ΔLUMO) belong to soft chromophores, which as confirmed experimentally, are most sensitive to perturbations. For such molecules, one should expect almost vanishing values of B terms, and thus very weak MCD intensity in the region of Q bands.
Analysis of Orbital Shifts Caused by Different Perturbations
In order to understand structure–spectra correlation for the compounds investigated in this work, we compare the effects of phenyl and ethyl substituents, as well as the influence of the central metal ion on the energy levels of four frontier molecular orbitals. The effect of nonplanarity, appearing due to interaction of bulky ethyl groups with phenyls, is another important factor to be discussed.
Figure 9 shows the DFT-calculated response of the frontier orbitals of the C20H202+ perimeter to different perturbations: bridging, substitutions of phenyl and ethyl groups, and introduction of the central metal ion in order to produce compounds of interest. The amount by which an orbital of the parent perimeter will be stabilized or destabilized depends on the values of LCAO coefficients at the position of substitution and the symmetry of the orbital, especially the positions of nodal planes. An alternative approach in the spirit of Gouterman’s model is to start with the orbitals of the dianion.
Figure 9.
DFT-calculated (B3LYP/def2-SVP) orbital responses to various types of perimeter perturbations.
The first considered perturbation is bridging by N– groups combined with in-plane deformation of the perimeter, which leads to porphyrin dianion (formally, it can be described as bridging by CH–, followed by aza replacement). Since the high, 4-fold symmetry is preserved, the two LUMO orbitals remain degenerate. This conclusion may also be reached by looking at the shape of the two LUMOs: each of them should be affected to the same degree. With respect to HOMO orbitals, only one of them (a2u assuming D4h symmetry) should be affected, but rather slightly, because of very small LCAO coefficients on the atoms connected by bridging. As expected, the DFT calculations yield ΔLUMO = 0, but the splitting of the HOMO pair is not that small: ΔHOMO = 0.605 eV. In the literature, the two HOMOs of the anion are referred to as accidentally nearly degenerate.28,30,31,33,35 This is based on very weak intensity of the absorption intensity of the Q(0–0) transition.33,72 We note, however, that the absorption spectra have been obtained for solutions containing very high concentration of sodium hydroxide. Under such conditions, it is appropriate to assume that the sodium atoms can be present in the vicinity of the dianion. We have optimized a structure consisting of a porphyrin dianion with two sodium atoms, one above and the other below the molecular plane (Figure S2). The calculated value of ΔHOMO was 0.170 eV, very close to that obtained for free base porphyrin (0.160 eV, Figure S3). We believe this result explains the apparent discrepancy between the experiment and the strong positive-hard character predicted for an isolated porphyrin dianion.
The perturbation effect due to the central metal ion can also be predicted by inspection of the frontier orbitals. It is best visualized when looking at the shape of the orbitals of the dianion (Figure 9). Insertion of a metal cation in the central position will strongly stabilize the a2u HOMO orbital, because it has large LCAO coefficients on the nitrogen atoms. The a1u orbital should not be affected, as the nitrogens are located on the nodal plane. Due to symmetry, both LUMOs should be stabilized to the same degree. One thus expects ΔHOMO ≠ 0 and ΔLUMO = 0. This is confirmed by calculations (Figure S4). The calculated ΔHOMO splitting is now much smaller than in the dianion, where the a2u orbital was higher in energy than a1u by 0.605 eV. Stabilization of this orbital by the metal cation decreases ΔHOMO to 0.014 eV. With that small HOMO splitting (and ΔLUMO = 0 by symmetry), unsubstituted palladium porphyrin is predicted to behave like a “double-soft “ chromophore.27
It has been previously shown that the degree of the orbital energy stabilization is related to the rising electronegativity of the central ion.73 The increase of the electronegativity of the central ion should lead to two consequences clearly observed in absorption spectra: (i) increase of the absorption intensity ratio A[Q(0,0)]/A[Q(0,1)] for pure electronic Q(0,0) and vibronic Q(0,1) bands and (ii) hypsochromic shift of visible electronic transitions. The intensity ratio of pure electronic and vibronic bands is 4 (obtained in this work) and 1.833 for PdOEP and ZnOEP, respectively. The visible absorption bands maxima are 545 nm for PdOEP and 568 nm for ZnOEP, which confirms the more significant stabilization of the a2u orbital in the case of PdOEP compared to the Zn analogue. The calculated a2u orbital energies are −5.29 eV for the former and −5.16 eV for the latter. For the parent unsubstituted palladium and zinc porphyrins, we obtain −5.56 and −5.41 eV, respectively.
The alkyl groups donate electron density to the porphyrin ring and can be classified as weak −E substituents. Their symmetric positioning on the porphyrin ring leaves the relative positions of two LUMO orbitals unchanged and, according to the LCAO coefficients, it will preferentially destabilize the a1u orbital. Again, it is nicely visualized if the orbitals of the dianion are taken as a reference (Figure 9). Therefore, ΔHOMO > ΔLUMO is predicted for this type of perturbations, suggesting the positive-hard character of PdOEP. This result is in a good agreement with quantum-chemical calculations (Figure S5), which yield ΔHOMO = 0.188 eV > ΔLUMO = 0 eV.
One should note that adding the alkyl groups one by one may result in a nonmonotonous variation of ΔHOMO – ΔLUMO. In porphyrins of lower symmetry, the two LUMO orbitals will be destabilized to a different degree. The LUMO splitting, however, should be smaller than ΔHOMO, because the energy separation between the alkyl substituent orbital and those of HOMOs and LUMOs is larger for the latter. This is illustrated in Figure S6a.
The perturbation effect of the phenyl groups is also electron-donating,33,46 but now it is the a2u orbital which is preferentially destabilized. The LUMO orbitals shift by the same amount in the tetraphenyl derivative, but not when the number of phenyl substituents is lower. However, as was the case for alkyl substituents, the LUMO splittings are very small and can be neglected (the calculated splittings are of the order of 0.01 eV).
We note a completely different pattern of orbital energy shifts calculated for the situation when the phenyl groups are added to the porphyrin dianion (Figure S1). The phenyls act as electron acceptors, and the energies of all orbitals are stabilized upon adding consecutive substituents. However, the same positive-hard pattern is predicted as for uncharged species.
Since the alkyl substituents in the β position act in the same direction, but on a different HOMO orbital, the contributions to HOMO splitting from alkyl and aryl groups partially cancel each other. The effect will grow with the increasing number of phenyl substituents. One thus expects the decrease of positive-hard character in the PdOEP–PdOEP4 series. This is indeed observed (Figures 3–6) and confirmed by calculations (Figure S5). The ΔHOMO values decrease in the approximately linear fashion, from 0.188 eV in PdOEP to a very small value of 0.007 eV in PdOEP4. One should note that in the latter the obtained value implicitly includes the effects due to nonplanarity. It is therefore important to compare the values of orbital energy changes calculated for successive additions of phenyl groups to PdOEP. Calculations reveal gradual destabilization of the a2u orbital, which becomes larger upon introducing the third and fourth phenyl groups. For comparison, we also calculated changes upon gradually introducing phenyl groups into unsubstituted palladium porphyrin (Figure S4); in this case, the changes in the a2u orbital energy become smaller when the third and fourth phenyl groups are being added. This chromophore remains planar in all derivatives. The larger destabilization in the case of PdOEPs can be explained by their nonplanarity. It is interesting to note that adding phenyls to PdPr should lead to an opposite effect than in PdOEP: change from a soft to positive-hard chromophore. This is because in unsubstituted PdPr the two HOMO orbitals are nearly degenerate (ΔHOMO = 0.014), whereas they are spaced by 0.188 eV in PdOEP, in which the a2u orbital lies lower than a1u. Since the a2u orbital is destabilized more strongly upon meso-phenyl substitution, ΔHOMO will decrease with the increasing number of phenyl groups in PdOEPs. In contrast, ΔHOMO will increase in phenyl-substituted PdPrs.
The above analysis leaves no doubt about the positive-hard character of PdOEP (β > 0, eq 3). It also clearly indicates the direction of orbital shifts due to substitution by additional phenyl groups. This allows us to predict the sign and intensity of MCD as well as absorption bands ratios for compounds with different number of phenyl groups.
For a positive difference of ΔHOMO – ΔLUMO the expected sign sequence in the MCD spectrum is −, +, −, +. This is indeed observed for all compounds. With the increasing number of phenyl substituents the difference of ΔHOMO – ΔLUMO decreases, reaching an almost zero value for PdOEP4 (β ∼ 0, eq 3). The behavior of PdOEP4 should therefore exhibit an almost soft chromophore character. As expected, the MCD intensity corresponding to Q bands decreases along the series, while the intensity of in the Soret bands region remains similar. The perimeter model also allows predictions of the intensities of the individual bands in the absorption spectra. The absorption bands ratio is described in terms of orbital splitting by the following equation:16
| 4 |
where D is the transition
dipole strength. Indeed, the absorption band ratio 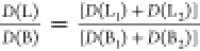 (the sum of absorption
bands is used because
they are strongly overlapping) decreases from 0.3 to 0.05 on going
from PdOEP to PdOEP4 and reflects the decrease of HOMO orbitals splitting
with the increasing number of phenyl substituents. TDDFT (B3LYP/TZP)
calculations confirm this trend, predicting the decrease of the L/B
absorption intensity ratio with the increasing number of phenyl substituents
from 0.042 (PdOEP) to 0.0017 (PdOEP4).
(the sum of absorption
bands is used because
they are strongly overlapping) decreases from 0.3 to 0.05 on going
from PdOEP to PdOEP4 and reflects the decrease of HOMO orbitals splitting
with the increasing number of phenyl substituents. TDDFT (B3LYP/TZP)
calculations confirm this trend, predicting the decrease of the L/B
absorption intensity ratio with the increasing number of phenyl substituents
from 0.042 (PdOEP) to 0.0017 (PdOEP4).
In order to verify the accuracy of description of the electronic structure by the perimeter model, we calculated, using INDO/S for the zinc porphyrin analogues, the values of the sum of squares of the four CI coefficients that describe the four configurations of the perimeter model. The CI basis included 196 singly excited configurations. The good description by the four-orbital model corresponds to the value approaching unity for a given electronic state. The results are presented in Table S1. On the basis of these results, we conclude that the Q transitions of all investigated compounds can be described by a perimeter model with excellent accuracy. Regarding the Soret region, the model still holds for molecules of approximately 4-fold symmetry, but it becomes questionable for less symmetrical chromophores, for which several allowed transitions are predicted to lie in this range.
Summary and Conclusions
The excited L and B states were assigned and described for the set of PdOEP derivatives with an increasing number of phenyl substituents at the meso position. The analysis of the MCD spectra confirms the ability of Gouterman’s four-orbital and Michl’s perimeter models to be used for studying the electronic structure of the investigated compounds, even in the case of significant nonplanarity. The character of the investigated compounds changes monotonically with the increasing number of aryl substituents, from positive-hard to soft chromophores. We have found that structural perturbations due to meso-phenyl substitution of the perimeter as well as the central metal ion play a role in determining the spectral behavior of the investigated compounds. The influence of nonplanarity on the absorption and MCD spectra was found to be minor and offset by orbital shifts caused by phenyl substitution. In the spirit of Gouterman’s and Michl’s model, substituent effects are additive.
Once more, the perimeter model proved to be an excellent and reliable tool for understanding the trends observed for a chromophore that is perturbed in several ways. Regarding the quantitative agreement of theoretical predictions with experiment, our results show that the TDDFT calculations work well in the case of two nearby states, well-isolated in energy from other transitions. This is the situation for the Q region in porphyrins. When several close-lying electronic states are present, there is no reason to expect a good agreement until the relative transition energies are well reproduced. We hope that this somewhat pessimistic statement (agreeing with conclusions of a recent study of phthalocyanines)25 can stimulate further theoretical efforts toward reproducing excited state energies as accurately as possible.
A result which, to the best of our knowledge, has not been discussed before is the large splitting of the HOMO orbitals in porphyrin dianion. The near degeneracy, postulated in literature, seems to be the result of the presence of counterions in solution. Under these conditions, the two HOMO orbitals do indeed come closer and the system behaves like a soft chromophore. Since the absorption and MCD spectra of soft chromophores are very sensitive even to minor perturbations, it would be very interesting to investigate possible spectral variations as a function of modifications such as (i) type, charge, and size of the counterion or (ii) switching from contact to solvent-separated ion pairs. Such experiments are planned in our laboratory.
Finally, we stress the relevance of perimeter model studies for guiding the rational design of novel dyes. In our opinion, the potential of this simple procedure for evaluating such crucial parameters as the intensity of electronic transitions has not been sufficiently exploited. Further efforts are required to make the perimeter model attractive to broader research communities.
Acknowledgments
This work was supported by the Polish National Science Centre (NCN) grant 2016/22/A/ST4/00029, the PL-Grid Infrastructure grant, the Horizon 2020 MSCA RISE grant 645628, the Polish Ministry of Science and Higher Education grant W77/H2020/2017, Belarussian State Program for Scientific Research “Convergence–2020 3.03, 2020 3.01”, and partly by a Grant of the President of Republic of Belarus in science (EZ, 2020).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c06669.
Plots of frontier molecular orbitals and their energies. Comparison of absorption and MCD spectra simulated using different functionals. Calculated (INDO/S) electronic states of Zn analogues of palladium porphyrins (PDF)
The authors declare no competing financial interest.
Author Status
# V.K.: deceased as of April 6, 2020.
Special Issue
Published as part of The Journal of Physical Chemistry virtual special issue “Josef Michl Festschrift”.
Supplementary Material
References
- Battersby A. R. Tetrapyrroles: The Pigments of Life. Nat. Prod. Rep. 2000, 17, 507–526. 10.1039/b002635m. [DOI] [PubMed] [Google Scholar]
- Shelnutt J. A.; Song X. Z.; Ma J. G.; Jia S. L.; Jentzen W.; Medforth C. J. Nonplanar Porphyrins and Their Significance in Proteins. Chem. Soc. Rev. 1998, 27, 31–41. 10.1039/a827031z. [DOI] [Google Scholar]
- Medforth C. J.; Berget P. E.; Fettinger J. C.; Smith K. M.; Shelnutt J. A. Determination of the Activation Energies for ND Tautomerism and Anion Exchange in a Porphyrin Monocation. J. Porphyrins Phthalocyanines 2016, 20, 307–317. 10.1142/S1088424616500103. [DOI] [Google Scholar]
- Rozas I.; Senge M. O. A Two-Pronged Attack on DNA: Targeting Guanine Quadruplexes with Nonplanar Porphyrins and DNA-Binding Small Molecules. Future Med. Chem. 2016, 8, 609–612. 10.4155/fmc-2016-0040. [DOI] [PubMed] [Google Scholar]
- Senge M. O.; Medforth C. J.; Forsyth T. P.; Lee D. A.; Olmstead M. M.; Jentzen W.; Pandey R. K.; Shelnutt J. A.; Smith K. M. Comparative Analysis of the Conformations of Symmetrically and Asymmetrically Deca- and Undecasubstituted Porphyrins Bearing Meso-Alkyl or -Aryl Groups. Inorg. Chem. 1997, 36, 1149–1163. 10.1021/ic961156w. [DOI] [PubMed] [Google Scholar]
- Roucan M.; Kielmann M.; Connon S. J.; Bernhard S. S. R.; Senge M. O. Conformational Control of Nonplanar Free Base Porphyrins: Towards Bifunctional Catalysts of Tunable Basicity. Chem. Commun. 2018, 54, 26–29. 10.1039/C7CC08099A. [DOI] [PubMed] [Google Scholar]
- Shi Z.; Franco R.; Haddad R.; Shelnutt J. A.; Ferreira G. C. The Conserved Active-Site Loop Residues of Ferrochelatase Induce Porphyrin Conformational Changes Necessary for Catalysis. Biochemistry 2006, 45, 2904–2912. 10.1021/bi051907i. [DOI] [PubMed] [Google Scholar]
- Medforth C. J.; Haddad R. E.; Muzzi C. M.; Dooley N. R.; Jaquinod L.; Shyr D. C.; Nurco D. J.; Olmstead M. M.; Smith K. M.; Ma J. G.; Shelnutt J. A. Unusual Aryl-Porphyrin Rotational Barriers in Peripherally Crowded Porphyrins. Inorg. Chem. 2003, 42, 2227–2241. 10.1021/ic010958a. [DOI] [PubMed] [Google Scholar]
- Pedrini J.; Monguzzi A. Recent Advances in the Application Triplet–Triplet Annihilation-Based Photon Upconversion Systems to Solar Technologies. J. Photonics Energy 2018, 8, 022005. 10.1117/1.JPE.8.022005. [DOI] [Google Scholar]
- Kwon O. S.; Kim J.-H.; Cho J. K.; Kim J.-H. Triplet–Triplet Annihilation Upconversion in Cds-Decorated Sio2 Nanocapsules for Sub-Bandgap Photocatalysis. ACS Appl. Mater. Interfaces 2015, 7, 318–325. 10.1021/am506233h. [DOI] [PubMed] [Google Scholar]
- Khnayzer R. S.; Blumhoff J.; Harrington J. A.; Haefele A.; Deng F.; Castellano F. N. Upconversion-Powered Photoelectrochemistry. Chem. Commun. 2012, 48, 209–211. 10.1039/C1CC16015J. [DOI] [PubMed] [Google Scholar]
- Gorski A.; Knyukshto V.; Zenkevich E.; Starukhin A.; Kijak M.; Solarski J.; Semeikin A.; Lyubimova T. Temperature Dependent Steric Hindrance Effects in Triplet State Relaxation of Meso-Phenyl-Substituted Pd-Octaethylporphyrins. J. Photochem. Photobiol., A 2018, 354, 101–111. 10.1016/j.jphotochem.2017.09.002. [DOI] [Google Scholar]
- Keegan J. D.; Bunnenberg E.; Djerassi C. Magnetic Circular-Dichroism Studies. 63. Sign Variation in the Magnetic Circular-Dichroism Spectra of Some Perimeter Symmetric Metallo Porphyrins. Spectrochim. Acta, Part A 1984, 40, 287–297. 10.1016/0584-8539(84)80051-3. [DOI] [Google Scholar]
- Mack J.; Stillman M. J.; Kobayashi N. Application of MCD Spectroscopy to Porphyrinoids. Coord. Chem. Rev. 2007, 251, 429–453. 10.1016/j.ccr.2006.05.011. [DOI] [Google Scholar]
- Kobayashi N.; Nakai K. Applications of Magnetic Circular Dichroism Spectroscopy to Porphyrins and Phthalocyanines. Chem. Commun. 2007, 4077–4092. 10.1039/b704991a. [DOI] [PubMed] [Google Scholar]
- Waluk J.; Müller M.; Swiderek P.; Köcher M.; Vogel E.; Hohlneicher G.; Michl J. Electronic States of Porphycenes. J. Am. Chem. Soc. 1991, 113, 5511–5527. 10.1021/ja00015a002. [DOI] [Google Scholar]
- Gorski A.; Lament B.; Davis J. M.; Sessler J.; Waluk J. Electronic States of a Novel Smaragdyrin Isomer: Polarized Spectroscopy and Theoretical Studies. J. Phys. Chem. A 2001, 105, 4992–4999. 10.1021/jp004255a. [DOI] [Google Scholar]
- Gorski A.; Vogel E.; Sessler J. L.; Waluk J. Magnetic Circular Dichroism of Octaethylcorrphycene and Its Doubly Protonated and Deprotonated Forms. J. Phys. Chem. A 2002, 106, 8139–8145. 10.1021/jp0201579. [DOI] [Google Scholar]
- Gorski A.; Vogel E.; Sessler J. L.; Waluk J. Magnetic Circular Dichroism of Neutral and Ionic Forms of Octaethylhemiporphycene. Chem. Phys. 2002, 282, 37–49. 10.1016/S0301-0104(02)00617-1. [DOI] [Google Scholar]
- Kjærgaard T.; Coriani S.; Ruud K. Ab Initio Calculation of Magnetic Circular Dichroism. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 443–455. 10.1002/wcms.1091. [DOI] [Google Scholar]
- Nørby M. S.; Coriani S.; Kongsted J. Modeling Magnetic Circular Dichroism within the Polarizable Embedding Approach. Theor. Chem. Acc. 2018, 137, 49. 10.1007/s00214-018-2220-5. [DOI] [Google Scholar]
- Khani S. K.; Faber R.; Santoro F.; Hättig C.; Coriani S. UV Absorption and Magnetic Circular Dichroism Spectra of Purine, Adenine, and Guanine: A Coupled Cluster Study in Vacuo and in Aqueous Solution. J. Chem. Theory Comput. 2019, 15, 1242–1254. 10.1021/acs.jctc.8b00930. [DOI] [PubMed] [Google Scholar]
- Seth M.; Ziegler T. Calculation of Magnetic Circular Dichroism Spectra with Time-Dependent Density Functional Theory. Adv. Inorg. Chem. 2010, 62, 41–109. 10.1016/S0898-8838(10)62002-8. [DOI] [Google Scholar]
- Mack J. Expanded, Contracted, and Isomeric Porphyrins: Theoretical Aspects. Chem. Rev. 2017, 117, 3444–3478. 10.1021/acs.chemrev.6b00568. [DOI] [PubMed] [Google Scholar]
- Belosludov R. V.; Nevonen D.; Rhoda H. M.; Sabin J. R.; Nemykin V. N. Simultaneous Prediction of the Energies of Qx and Qy Bands and Intramolecular Charge-Transfer Transitions in Benzoannulated and Non-Peripherally Substituted Metal-Free Phthalocyanines and Their Analogues: No Standard TDDFT Silver Bullet Yet. J. Phys. Chem. A 2019, 123, 132–152. 10.1021/acs.jpca.8b07647. [DOI] [PubMed] [Google Scholar]
- Gouterman M.; Wagnière G. H.; Snyder L. C. Spectra of Porphyrins. Part II. Four Orbital Model. J. Mol. Spectrosc. 1963, 11, 108–137. 10.1016/0022-2852(63)90011-0. [DOI] [Google Scholar]
- Michl J. Magnetic Circular-Dichroism of Cyclic π-Electron Systems. 1. Algebraic-Solution of Perimeter Model for A Terms and B Terms of High-Symmetry Systems with a (4N+2)-Electron[n] Annulene Perimeter. J. Am. Chem. Soc. 1978, 100, 6801–6811. 10.1021/ja00490a001. [DOI] [Google Scholar]
- Michl J. Magnetic Circular-Dichroism of Cyclic π-Electron Systems. 2. Algebraic-Solution of Perimeter Model for B Terms of Systems with a (4N+2)-Electron[n]Annulene Perimeter. J. Am. Chem. Soc. 1978, 100, 6812–6818. 10.1021/ja00490a002. [DOI] [Google Scholar]
- Michl J. Magnetic Circular-Dichroism of Cyclic π-Electron Systems. 3. Classification of Cyclic π-Chromophores with a (4N+2)-Electron [n]Annulene Perimeter and General Rules for Substituent Effects on MCD Spectra of Soft Chromophores. J. Am. Chem. Soc. 1978, 100, 6819–6824. 10.1021/ja00490a003. [DOI] [Google Scholar]
- Michl J. Magnetic Circular Dichroism of Aromatic Molecules. Tetrahedron 1984, 40, 3845–3934. 10.1016/S0040-4020(01)99999-5. [DOI] [Google Scholar]
- Keegan J. D.; Stolzenberg A. M.; Lu Y. C.; Linder R. E.; Barth G.; Bunnenberg E.; Djerassi C.; Moscowitz A. Magnetic Circular-Dichroism Studies. 59. Substituent-Induced Sign Variation in the Magnetic Circular-Dichroism Spectra of Chlorins. J. Am. Chem. Soc. 1981, 103, 3201–3203. 10.1021/ja00401a045. [DOI] [Google Scholar]
- Keegan J. D.; Stolzenberg A. M.; Lu Y. C.; Linder R. E.; Barth G.; Moscowitz A.; Bunnenberg E.; Djerassi C. Magnetic Circular-Dichroism Studies. 60. Substituent-Induced Sign Variation in the Magnetic Circular-Dichroism Spectra of Reduced Porphyrins. 1. Spectra and Band Assignments. J. Am. Chem. Soc. 1982, 104, 4305–4317. 10.1021/ja00380a001. [DOI] [Google Scholar]
- Keegan J. D.; Stolzenberg A. M.; Lu Y. C.; Linder R. E.; Barth G.; Moscowitz A.; Bunnenberg E.; Djerassi C. Magnetic Circular-Dichroism Studies. 61. Substituent-Induced Sign Variation in the Magnetic Circular-Dichroism Spectra of Reduced Porphyrins. 2. Perturbed Molecular-Orbital Analysis. J. Am. Chem. Soc. 1982, 104, 4317–4329. 10.1021/ja00380a002. [DOI] [Google Scholar]
- Lu Y.; Waleh A.; Shu A. Y. L.; Goldbeck R. A.; Kehres L. A.; Crandell C. W.; Wee A. G. H.; Knierzinger A.; Gaete-Holmes R. Sign Variation in the Magnetic Circular-Dichroism Spectra of Free-Base Porphyrins Having a Single π-Acceptor Pyrrole Ring Substituent. Structure Implications. J. Am. Chem. Soc. 1984, 106, 4241–4258. 10.1021/ja00327a029. [DOI] [Google Scholar]
- Goldbeck R. A. Sign Variation in the Magnetic Circular Dichroism Spectra of π-Substituted Porphyrins. Acc. Chem. Res. 1988, 21, 95–101. 10.1021/ar00147a001. [DOI] [Google Scholar]
- Mack J.; Asano Y.; Kobayashi N.; Stillman M. J. Application of MCD Spectroscopy and TD-DFT to a Highly Non-Planar Porphyrinoid Ring System. New Insights on Red-Shifted Porphyrinoid Spectral Bands. J. Am. Chem. Soc. 2005, 127, 17697–17711. 10.1021/ja0540728. [DOI] [PubMed] [Google Scholar]
- Waluk J.; Michl J. The Perimeter Model and Magnetic Circular-Dichroism of Porphyrin Analogs. J. Org. Chem. 1991, 56, 2729–2735. 10.1021/jo00008a029. [DOI] [Google Scholar]
- Rhoda H. M.; Akhigbe J.; Ogikubo J.; Sabin J. R.; Ziegler C. J.; Bruckner C.; Nemykin V. N. Magnetic Circular Dichroism Spectroscopy of Meso-Tetraphenylporphyrin-Derived Hydroporphyrins and Pyrrole-Modified Porphyrins. J. Phys. Chem. A 2016, 120, 5805–5815. 10.1021/acs.jpca.6b04618. [DOI] [PubMed] [Google Scholar]
- Saegusa Y.; Ishizuka T.; Komamura K.; Shimizu S.; Kotani H.; Kobayashi N.; Kojima T. Ring-Fused Porphyrins: Extension of π-Conjugation Significantly Affects the Aromaticity and Optical Properties of the Porphyrin π-Systems and the Lewis Acidity of the Central Metal Ions. Phys. Chem. Chem. Phys. 2015, 17, 15001–15011. 10.1039/C5CP01420D. [DOI] [PubMed] [Google Scholar]
- Rhoda H. M.; Crandall L. A.; Geier G. R. III; Ziegler C. J.; Nemykin V. N. Combined MCD/DFT/TDDFT Study of the Electronic Structure of Axially Pyridine Coordinated Metallocorroles. Inorg. Chem. 2015, 54, 4652–4662. 10.1021/ic502946t. [DOI] [PubMed] [Google Scholar]
- Okujima T.; Mack J.; Nakamura J.; Kubheka G.; Nyokong T.; Zhu H.; Komobuchi N.; Ono N.; Yamada H.; Uno H.; Kobayashi N. Synthesis, Characterization, and Electronic Structures of Porphyrins Fused with Polycyclic Aromatic Ring Systems. Chem. - Eur. J. 2016, 22, 14730–14738. 10.1002/chem.201602213. [DOI] [PubMed] [Google Scholar]
- Yamamoto Y.; Hirata Y.; Kodama M.; Yamaguchi T.; Matsukawa S.; Akiba K. Y.; Hashizume D.; Iwasaki F.; Muranaka A.; Uchiyama M.; Chen P.; Kadish K. M.; Kobayashi N. Synthesis, Reactions, and Electronic Properties of 16 π-Electron Octaisobutyltetraphenylporphyrin. J. Am. Chem. Soc. 2010, 132, 12627–12638. 10.1021/ja102817a. [DOI] [PubMed] [Google Scholar]
- Shul'ga A. M.; Ponomarev G. V. Porphyrins. 18. Synthesis of Octapropylporphyrin by Monopyrrole Cyclotetramerization of 5-Carboxy-2-Methoxymethyl-3,4-Dipropylpyrrole - Investigation of the Thermolysis of meso-N-Methylformaldiminoctapropyl Porphyrin. Chem. Heterocycl. Compd. 1984, 20, 748–753. 10.1007/BF00506964. [DOI] [Google Scholar]; (translated from Russian).
- Syrbu S. A.; Lyubimova T. V.; Semeikin A. S. Phenyl-substituted Porphyrins. 1. Synthesis of Meso-Phenyl-substituted Porphyrins. Chem. Heterocycl. Compd. 2004, 40, 1262–1270. 10.1007/s10593-005-0050-6. [DOI] [Google Scholar]; (translated from Russian).
- Lindsey J. S.; Schreiman I. C.; Hsu H. C.; Kearney P. C.; Marguerettaz A. M. Rothemund and Adler-Longo Reactions Revisited - Synthesis of Tetraphenylporphyrins under Equilibrium Conditions. J. Org. Chem. 1987, 52, 827–836. 10.1021/jo00381a022. [DOI] [Google Scholar]
- Adler A. D.; Longo F. R.; Kampas F.; Kim J. On Preparation of Metalloporphyrins. J. Inorg. Nucl. Chem. 1970, 32, 2443–2445. 10.1016/0022-1902(70)80535-8. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, revision A.01; Gaussian, Inc.: Wallingford, CT, 2009.
- Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
- te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
- Yanai T.; Tew D.; Handy N. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 33, 8822–8824. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Erratum: Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 34, 7406–7406. 10.1103/PhysRevB.34.7406. [DOI] [PubMed] [Google Scholar]
- Knyukshto V. N.; Shul’ga A. M.; Sagun E. I.; Zen’kevich E. I. Formation of Intersystem Crossing Transitions in Pd(II) and Pt(II) Porphyrins: Nonplanar Distortions of the Macrocycle and Charge Transfer States. Opt. Spectrosc. 2006, 100, 590–601. 10.1134/S0030400X06040163. [DOI] [Google Scholar]
- Sagun E. I.; Zenkevich E. I.; Knyukshto V. N.; Panarin A. Y.; Semeikin A. S.; Lyubimova T. V. Relaxation Processes with Participation of Excited S1 and T1 States of Spatially Distorted Meso-Phenyl-Substituted Octamethylporphyrins. Opt. Spectrosc. 2012, 113, 388–400. 10.1134/S0030400X12070193. [DOI] [Google Scholar]
- Kadish K.; Smith K. M.; Guilard R.. The Porphyrin Handbook; Elsevier Science, 2000. [Google Scholar]
- Zenkevich E. I. Structural Dynamics and Relaxation Processes with Participation of Excited Singlet and Triplet States in Sterically Hindered Porphyrins and Their Chemical Dimers. Makrogeterotsikly 2014, 7, 103–121. 10.6060/mhc140597z. [DOI] [Google Scholar]
- Sagun E. I.; Zenkevich E. I. Comparative Analysis of the Influence of Bulky Beta-Alkyl Substituents on Fluorescent Properties of Some Series of Spatially Distorted Meso-Phenyl Substituted Porphyrins. Opt. Spectrosc. 2013, 115, 727–738. 10.1134/S0030400X13110210. [DOI] [Google Scholar]
- Roder B.; Buchner M.; Ruckmann I.; Senge M. O. Correlation of Photophysical Parameters with Macrocycle Distortion in Porphyrins with Graded Degree of Saddle Distortion. Photochem. Photobiol. Sci. 2010, 9, 1152–1158. 10.1039/c0pp00107d. [DOI] [PubMed] [Google Scholar]
- Avilov I. V.; Zenkevich E. I.; Sagun E. I.; Filatov I. V. Quantum-Chemical Investigation of the Conformational Dynamics of Mono-Meso-Phenyl-Substituted Octaalkylporphyrins in the Triplet Excited State. J. Phys. Chem. A 2004, 108, 5684–5691. 10.1021/jp048930i. [DOI] [Google Scholar]
- Scher H.; Katz J. J. In Porphyrins and Metalloporphyrins; Smith K. M., Ed.; Elsevier Scientific Publishing Company: New York, 1975; pp 399–524. [Google Scholar]
- Mandal A. K.; Taniguchi M.; Diers J. R.; Niedzwiedzki D. M.; Kirmaier C.; Lindsey J. S.; Bocian D. F.; Holten D. Photophysical Properties and Electronic Structure of Porphyrins Bearing Zero to Four Meso-Phenyl Substituents: New Insights into Seemingly Well Understood Tetrapyrroles. J. Phys. Chem. A 2016, 120, 9719–9731. 10.1021/acs.jpca.6b09483. [DOI] [PubMed] [Google Scholar]
- Chirvony V. S.; van Hoek A.; Galievsky V. A.; Sazanovich I. V.; Schaafsma T. J.; Holten D. Comparative Study of the Photophysical Properties of Nonplanar Tetraphenylporphyrin and Octaethylporphyrin Diacids. J. Phys. Chem. B 2000, 104, 9909–9917. 10.1021/jp001631i. [DOI] [Google Scholar]
- Fleischer E. B.; Webb L. E.; Miller C. K. Crystal Molecular Structures of Some Metal Tetraphenylporphines. J. Am. Chem. Soc. 1964, 86, 2342–2347. 10.1021/ja01066a009. [DOI] [Google Scholar]
- Milgrom L. R. H-1-NMR and C-13-Nmr Spectra of Palladium and Platinum Meso-Tetraphenylporphyrins. Polyhedron 1984, 3, 879–882. 10.1016/S0277-5387(00)84638-0. [DOI] [Google Scholar]
- Solheim H.; Ruud K.; Coriani S.; Norman P. The A and B Terms of Magnetic Circular Dichroism Revisited. J. Phys. Chem. A 2008, 112, 9615–9618. 10.1021/jp803135x. [DOI] [PubMed] [Google Scholar]
- Peralta G. A.; Seth M.; Ziegler T. Magnetic Circular Dichroism of Porphyrins Containing M = Ca, Ni, and Zn. A Computational Study Based on Time-Dependent Density Functional Theory. Inorg. Chem. 2007, 46, 9111–9125. 10.1021/ic7008545. [DOI] [PubMed] [Google Scholar]
- Ceulemans A.; Oldenhof W.; Gorllerwalrand C.; Vanquickenborne L. G. Gouterman 4-Orbital Model and the MCD Spectra of High-Symmetry Metalloporphyrins. J. Am. Chem. Soc. 1986, 108, 1155–1163. 10.1021/ja00266a007. [DOI] [Google Scholar]
- Barth G.; Linder R. E.; Bunnenberg E.; Djerassi C. Magnetic Circular-Dichroism Studies. 26. Magnetic Circular-Dichroism Spectra of Porphyrin Dianions. J. Chem. Soc., Perkin Trans. 2 1974, 696–699. 10.1039/p29740000696. [DOI] [Google Scholar]
- Gouterman M. Study of the Effects of Substitution on the Absorption Spectra of Porphin. J. Chem. Phys. 1959, 30, 1139–1161. 10.1063/1.1730148. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.












