Abstract
Automatic Non-rigid Histological Image Registration (ANHIR) challenge was organized to compare the performance of image registration algorithms on several kinds of microscopy histology images in a fair and independent manner. We have assembled 8 datasets, containing 355 images with 18 different stains, resulting in 481 image pairs to be registered. Registration accuracy was evaluated using manually placed landmarks. In total, 256 teams registered for the challenge, 10 submitted the results, and 6 participated in the workshop. Here, we present the results of 7 well-performing methods from the challenge together with 6 well-known existing methods. The best methods used coarse but robust initial alignment, followed by non-rigid registration, used multiresolution, and were carefully tuned for the data at hand. They outperformed off-the-shelf methods, mostly by being more robust. The best methods could successfully register over 98% of all landmarks and their mean landmark registration accuracy (TRE) was 0.44% of the image diagonal. The challenge remains open to submissions and all images are available for download.
Keywords: Image registration, Microscopy
I. Introduction
IMAGE registration is one of the key tasks in biomedical image analysis, aiming to find a geometrical transformation between two or more images, so that corresponding objects appear at the same position in both/all images. This research area has received a lot of attention over the last several decades and literally hundreds of different registration algorithms exist [1]-[8]. An unbiased comparison of the registration algorithms is essential to help users choose the most suitable method for a given task.
A. Goals
The goal of this study is to report the results of the Automatic Non-rigid Histological Image Registration challenge (ANHIR)1, at the IEEE International Symposium on Biomedical Imaging (ISBI) 2019. To the best of our knowledge, ANHIR was the first open comparison of image registration algorithms on microscopy images. Moreover, we describe the associated annotated dataset of histology images, which is freely available from the challenge website, and is one of very few microscopy image datasets suitable for testing registration algorithms.
B. Previous work on image registration evaluation
One of the earliest image registration comparisons was the Retrospective Image Registration Evaluation (RIRE) project [9], comparing rigid registration algorithms on computed tomography (CT), magnetic resonance (MRI), and positron emission tomography (PET) human brain data using fiducial landmarks. Later studies added more methods [10], non-linear transformations [11]-[13], and other organs, such as lung [14], or liver and prostate [15], as well as comparison on microscopy data [16]. Registration performance is usually measured using landmark distances [9], [13], [15]-[17] or segmentation overlap [11], [12], [18].
In some of the above mentioned studies, the comparison was done by the authors themselves by means of publicly available implementations [13], which is a good strategy to find the best out-of-the-box performing approach. In other cases [17], authors (re)implemented the methods themselves, eliminating the differences in the quality of the implementation.
C. Challenges
It can be argued that the authors of a method are the best equipped and motivated to implement, tune, and run their own methods. In a challenge, the organizers prepare the data and invite participants to apply their methods to provided data and submit the results, which are then evaluated by given criteria. It is widely believed that challenges have a very beneficial effect on the progress in a particular field by: (i) lowering the entry barrier by providing (usually large) annotated datasets, (ii) motivating participants to improve the performance of their methods, (iii) identifying the state-of-the-art approaches, and (iv) tracking the overall progress of the field.
In some of the previous image registration comparisons, only known authors of image registration methods were invited to participate. Other challenges were opened to all participants, including the following:
The RIRE project [9] used masked fiducial points on MRI, CT and PET images. It is now fully open.
The EMPIRE10 challenge [18] on pulmonary images.
The recent CurlOUS challenge2 on the registration between presurgical MRI and intra-operative ultrasound.
The MOCO challenge asking for motion correction of myocardial perfusion MRI [19].
The Continous Registration Challenge3, which uses eight different datasets including lung 4D CT and MRI brain images differs in requiring participants to integrate their code to a common platform.
As far as we know, ANHIR, described here, is the only registration challenge using microscopy images.
D. Histology image registration
Microscopy images in histology need to be registered for a number of reasons [20], most frequently to create a 3D reconstruction from scanned 2D thin slices [21]-[29]. Other applications include distortion compensation [30], creating a high resolution mosaic from small 2D tiles [31], fusing information from differently stained slices [32]-[35] or even from different modalities, such as histology and MRI [36]. Registration can assist in segmenting unknown stains using known stains [37], or to combine gene expression maps from multiple specimens [38].
Histology image registration is challenging because of the following aspects: (i) large sizes of some images, e.g. 80k × 60k pixels for the whole slide images (WSI), (ii) repetitive texture, making it hard to find globally unique landmarks, (iii) sometimes large non-linear elastic deformation, occlusions and missing sections due to sample preparation, (iv) differences in appearance due to different staining or acquisition methods, and (v) differences in local structure between slices. Registration methods developed for other modalities might therefore not work optimally and need to be modified for microscopy images. Changes in appearance can be handled by color normalization [39] or deconvolution [40], focusing on the parts or stains common to both images [33], segmentation [41], [42] or probabilistic segmentation [43], or using multimodal similarity features such as structural probability maps [29]. While most algorithms are intensity-based, some use keypoint features [44] or edge features [45], and some combine the two approaches [22]. The very large image size is often handled simply by working on downscaled images but better precision can be obtained by dividing the images into smaller parts (tiles), registering them separately, and combining the results [31], [46]. The availability of a large number of consecutive slices can be used to improve robustness by enforcing consistency between different pairs of slices [22].
There is a relative paucity of microscopy image datasets suitable for image registration evaluation. The exception are datasets for testing cell tracking and cell nuclei registration in fluorescence microscopy [47], [48], which differs significantly from histological images considered here. Evaluation has been performed on other datasets, which are however not publicly available, such as a comparison of histology and block-face optical images [49], and a 3D alignment of ssTEM slices [50].
This work can be regarded as a continuation of an earlier image registration evaluation [16], [51], which is significantly expanded here in terms of the number of methods, number of images and image types, image size and resolution, and the quality of annotations.
II. ANHIR Challenge
The ANHIR challenge focused on comparing the accuracy, robustness, and speed of fully automatic non-linear registration methods on microscopy histology images. The images to be registered are large and differ in appearance due to different staining.
A. Data
In total, we have assembled 8 datasets, please see Table I for an overview and Fig. 1 for examples. More details are available in Sections4 S.I and S.IV. The appearance differences due to staining are sometimes important (see Fig. S2). In each case, high-resolution (up to 40× magnification) whole slide images were acquired. The images are organized in sets such that any two images within a set could be meaningfully registered, as they come from spatially close slices. Different stains are used for each image in a set and the local structure often differs, see Fig. S3. In total, we obtained 49 sets with 3 to 9 images per set, the average size was 5 slides per set. There are 355 images in total with 18 different stains5. We generated 481 image pairs for registration (each pair within each set but dropping symmetric pairs) and split them into 230 training and 251 testing pairs. Note that the lung lesions and lung lobes datasets were used in [16] and were therefore already completely public. We have therefore decided to treat these datasets as training only and not use them for the evaluation, except when explicitly mentioned.
TABLE I.
Summary of the datasets and their properties. See the supplementary material for a more detailed description. (COAD=Colon Adenocarcinoma).
| Name | Scanner | Mag. |
μm/ pixel |
Avg. size [pixels] |
# sets |
#train pairs |
#test pairs |
|---|---|---|---|---|---|---|---|
| Lung lesions | Zeiss | 40× | 0.174 | 18k × 15k | 3 | 30 | 0 |
| Lung lobes | Zeiss | 10× | 1.274 | 11k × 6k | 4 | 40 | 0 |
| Mammary glands | Zeiss | 10× | 2.294 | 12k × 4k | 2 | 38 | 0 |
| Mouse kidney | Hamam. | 20× | 0.227 | 37k × 30k | 1 | 15 | 18 |
| COAD | 3DHistech | 10× | 0.468 | 60k × 50k | 20 | 84 | 153 |
| Gastric | Leica | 40× | 0.2528 | 60k × 75k | 9 | 13 | 40 |
| Human breast | Leica | 40× | 0.253 | 65k × 60k | 5 | 5 | 20 |
| Human kidney | Leica | 40× | 0.253 | 18k × 55k | 5 | 5 | 20 |
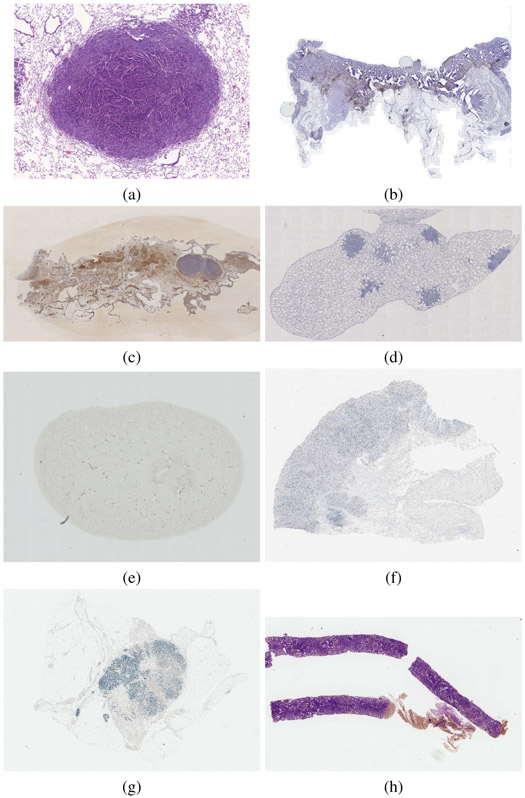
Fig. 1.
Example dataset images: (a) lung lesions, (b) COAD (colon adenocarcinoma), (c) mammary glands, (d) lung lobes, (e) mouse kidney, (f) gastric mucosa and adenocarcinoma, (g) human breast, (h) human kidney. Some images were cropped for visualization. Multiple stains exist for each tissue type.
Since the original images are very large, participants were suggested to register provided medium size images, chosen from a fixed set of scales so that their size is approximately 10k × 10k pixels. Most participants have themselves reduced the image size even further as part of the preprocessing. For convenience, we also provided small size images at 5% of the original size, around 2k × 2k pixels.
B. Landmarks
We have annotated significant structures in the images with landmarks spread over the tissue (see Figure 2 for an example). Each landmark position is known in all images from the same set. We have placed on the average 86 landmarks per image. There were 9 annotators. Annotating a set of images took around 2 hours on average, with 20 ~ 30% additional time for proofreading. In total, annotation and validation of the 355 images took about 250 hours. All images were annotated by at least two different people. The average distance between landmarks of the two annotators was 0.05% of the image diagonal (to be compared with the relative Target Registration Error, Section II-C). This corresponds to several pixels at the original resolution. Landmarks for some of the images were withheld by the organizers. Image pairs with landmarks for both images available to participants were used for training, while image pairs with landmarks for exactly one image known to the participants formed the set of testing pairs . See Section S.II in the Supplementary material for details.
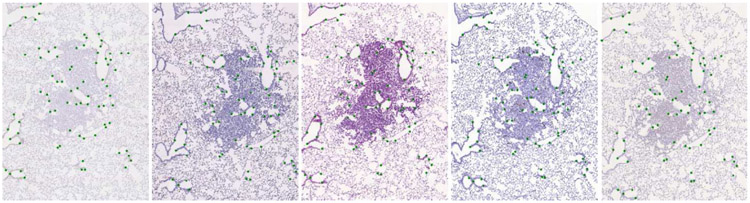
Fig. 2.
An example of a set of lung lesion tissue images using Cc10, CD31, H&E, Ki67 and proSPC stains (from left to right) with landmarks shown as green dots.
C. Evaluation measures
For each pair of images (i, j), we have determined the coordinates of corresponding landmarks , , where l ∈ Li, and Li is a set of landmarks, guaranteed to occur in both i and j. The participants were asked to submit the coordinates of landmark points in the coordinate system of image j corresponding to provided coordinates in the image i. We then define the relative Target Registration Error (rTRE) as the Euclidean distance between the submitted coordinates and the manually determined (ground truth) coordinates (withheld from participants)
| (1) |
normalized by the length of the image diagonal dj. Figure 3 shows an example of successful and unsuccessful registrations.
Fig. 3.
Examples of (a) successful and (b) unsuccessful registration. We are showing the warped image overlaid over the reference image, with the original positions and true displacements in green, estimated positions and estimated displacements in blue, target positions in magenta, and registration errors (TRE) in red.
Our main criterion to evaluate the registration algorithms is the average rank of median rTRE (ARMrTRE)
| (2) |
| (3) |
is the set of all test image pairs and is the set of all methods (a method corresponds to a single submission). In other words, we evaluate the rTRE (1) for all landmarks in an image and calculate the median of all rTRE values in an image. Aggregation by a median was chosen to eliminate outliers. We rank all methods according to this median. Ranking was chosen to compensate for differences in difficulty between datasets and images, which may influence the scale of the rTRE. Finally, we average the ranks over all test image pairs .
We also calculate other criteria aggregating the rTRE, namely average median rTRE (AMrTRE) and median of median rTRE (MMrTRE)
| (4) |
| (5) |
and similarly the average maximum rTRE (AMxrTRE)
| (6) |
and average rank maximum rTRE (ARMxrTRE)
| (7) |
To evaluate robustness, we compare individual rTREs for each landmark with the relative Initial Registration Error (rIRE) before registration
| (8) |
This is meaningful for our images, since the images i and j share the same or similar system of coordinates, i.e. is a reasonable initial approximation for . Let us call Ki,j ⊆ Li the set of successfully registered landmarks, i.e. those for which the registration error decreases, rTREl < rIREl. We define the robustness as the relative number of successfully registered landmarks,
| (9) |
and then, the average robustness over all test image pairs is
| (10) |
Finally, we asked the participants to report the registration times tij in minutes for each registration, including loading input images and writing the output files. We report the average registration time
| (11) |
The average registration time should only be considered as indicative, because it has not been independently validated. The times are approximately normalized with respect to participant computer performance by running an identical calibration program provided by the organizers.
D. Pairwise method comparison
For each pair of methods m and m′ from , we determine if a method m is significantly better than method m′. More specifically, we compare the median rTRE μ (3) on all test image pairs . Our null hypothesis is that μi,j (m) ≥ μi,j(m′). Clearly, the two μ values are dependent and not necessarily normally distributed, while the test image pairs are considered i.i.d. Hence, we employ the one-sided Wilcoxon signed-rank test and evaluate the p-value under the normal assumptions, since the number of samples is sufficiently large. For p < 0.01, we reject the null hypothesis and conclude that the method m indeed performs significantly better than method m′. The alternative would be permutation testing, as in [52], which is however much more computationally demanding.
E. Organization
The challenge was accepted to ISBI 2019 in October 2018 and officially announced in December 2018, after a website was set up and an evaluation system prepared. The lung lesions, lung lobes, and mammary glands data [16] with 9 training sets (108 image pairs with all landmark coordinates available) was immediately made accessible to enable the participants to start developing. In February 2019, we released the remaining images, training landmarks (122 image pairs) and a subset of the test landmarks (251 image pairs), and opened the web-based submission and evaluation system. The remaining test landmarks were released in the middle of March. The submission system was closed on March 31, 2019. Participants performed the registration on their own computers.
The challenge was widely advertised and totally open, anybody was free to participate. In total, 256 teams registered for the challenge and 10 submitted the results. For comparison, we also used two “internal submissions” corresponding to the bUnwarpJ and NiftyReg methods, see Section III. The teams were also asked to submit a description of their method. Seven teams complied and were invited to the workshop on April 11, during the ISBI 2019 conference, and to participate in writing this article. Winners were announced at this workshop. One of the teams (TUB) was unable to travel to the workshop, so only 6 teams presented there. The results announced at the workshop are given in Table III (column ‘rank’); the results shown here may be based on submissions updated later. Note also that the teams ranked 7, 9 and 11 chose not to provide a description of their methods.
TABLE III.
Quantitative result of all methods on the evaluation data. The first and second rows (‘average’, ‘median’ etc.) correspond to the aggregation method within each image pair and over all image pairs, respectively. The table is sorted by ARMrTRE (in bold). Rank corresponds to workshop results, missing numbers = insufficient information.
| method | rank | Average rTRE | Median rTRE | Max rTRE | Robustness | Median rTRE | Max rTRE |
Average time [min] |
||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average | Median | Average | Median | Average | Median | Average | Median | Average Rank | ||||
| (AArTRE) | (AMrTRE) | (AMxrTRE) | R | (ARMrTRE) | (ARMxrTRE) | |||||||
| initial | 0.1340 | 0.0684 | 0.1354 | 0.0665 | 0.2338 | 0.1157 | - | - | - | - | ||
| MEVIS | 1 | 0.0044 | 0.0027 | 0.0029 | 0.0018 | 0.0251 | 0.0188 | 0.9880 | 1.0000 | 2.84 | 5.04 | 0.17 |
| AGH | 3 | 0.0053 | 0.0032 | 0.0036 | 0.0019 | 0.0283 | 0.0225 | 0.9821 | 1.0000 | 3.42 | 6.00 | 6.55 |
| UPENN | 2 | 0.0042 | 0.0029 | 0.0029 | 0.0019 | 0.0239 | 0.0190 | 0.9898 | 1.0000 | 3.47 | 4.29 | 1.60 |
| CKVST | 4 | 0.0043 | 0.0032 | 0.0027 | 0.0023 | 0.0239 | 0.0189 | 0.9883 | 1.0000 | 4.41 | 5.27 | 7.80 |
| TUB | 5 | 0.0089 | 0.0029 | 0.0078 | 0.0021 | 0.0280 | 0.0178 | 0.9845 | 1.0000 | 4.53 | 3.81 | 0.02 |
| TUNI | 6 | 0.0064 | 0.0031 | 0.0048 | 0.0021 | 0.0287 | 0.0204 | 0.9823 | 1.0000 | 5.32 | 5.80 | 9.73 |
| DROP* | 0.0861 | 0.0042 | 0.0867 | 0.0028 | 0.1644 | 0.0273 | 0.8825 | 0.9892 | 7.06 | 7.43 | 3.99 | |
| ANTs* | 0.0991 | 0.0072 | 0.0992 | 0.0058 | 0.1861 | 0.0351 | 0.7889 | 0.9714 | 9.23 | 7.79 | 48.24 | |
| RVSS* | 0.0472 | 0.0063 | 0.0448 | 0.0046 | 0.1048 | 0.0275 | 0.8155 | 0.9928 | 9.65 | 8.42 | 5.25 | |
| bUnwarpJ* | 0.1097 | 0.0290 | 0.1105 | 0.0260 | 0.1995 | 0.0727 | 0.7899 | 0.9310 | 9.67 | 9.37 | 10.57 | |
| Elastix* | 0.0964 | 0.0074 | 0.0956 | 0.0054 | 0.1857 | 0.0353 | 0.8477 | 0.9722 | 10.04 | 8.88 | 3.50 | |
| UA | 10 | 0.0536 | 0.0100 | 0.0506 | 0.0082 | 0.1124 | 0.0353 | 0.8209 | 0.9853 | 10.28 | 8.83 | 1.70 |
| NiftyReg* | 0.1120 | 0.0372 | 0.1136 | 0.0355 | 0.2010 | 0.0714 | 0.7427 | 0.8519 | 11.08 | 10.08 | 0.14 | |
methods added by the organizers.
The challenge remains open to submissions and all images, as well as landmarks for the training image pairs, are available for download. The testing landmarks are kept confidential.
III. Registration methods
Let us briefly describe the evaluated registration methods. See also Table II for an overview. The participants were instructed to use the same settings for all test image pairs. Note, that the method names used here may differ from the team names found on the ANHIR webpage.
TABLE II.
Evaluated methods. NGF — normalized gradient field, NCC — normalized correlation coefficient, MI — mutual information, SSD — sum of squared differences, LM — Levenberg-Marquardt, L-BFGS — Limited memory Broyden–Fletcher–Goldfarb–Shanno, ASGD — Adaptive Stochastic Gradient Descent, CNN — convolutional neural network. Stars marks well-known methods added by the organizers.
| Method | Freely available |
Grayscale | Exhaustive search |
Affine/rigid prealignment |
Feature points |
Non-linear transformation |
Criterion | optimization/other |
|---|---|---|---|---|---|---|---|---|
| UA [54] | ✓ | ✓ | dense moving mesh | MI | gradient | |||
| TUNI [56] | ✓ | ✓ | ✓ | virtual springs | NCC | robust linear | ||
| CKVST | ✓ | ✓ | B-splines | NCC | L-BFGS | |||
| MEVIS [58] | ✓ | ✓ | ✓ | dense | NGF | L-BFGS | ||
| AGH | ✓ | ✓ | ✓ | ✓ | ✓ | various | various | various |
| UPENN [61] | ✓ | ✓ | ✓ | ✓ | dense | NCC | L-BFGS, gradient | |
| TUB [53] | ✓ | ✓ | dense | NCC | CNN | |||
| bUnwarpJ* [22] | ✓ | ✓ | B-splines | SSD | LM | |||
| RVSS* [22] | ✓ | ✓ | ✓ | ✓ | B-splines | SSD | LM | |
| NiftyReg* [69] | ✓ | ✓ | ✓ | B-splines | NCC, MI | conjugated-gradients | ||
| Elastix* [70] | ✓ | ✓ | ✓ | B-splines | NCC | ASGD | ||
| ANTs* [71] | ✓ | ✓ | ✓ | B-splines | MI, NCC | L-BFGS | ||
| DROP* [73] | ✓ | ✓ | B-splines | SSD | discrete optimization |
UA: (U. Alberta)6 The images are rescaled to 1/40 of their size and converted to grayscale. A translation and rotation is estimated first, followed by a non-rigid registration using a moving mesh framework [54], which alternates gradient descent on densely represented deformation and correction steps imposing incompressibility. Both steps use a mutual-information similarity criterion.
TUNI: (U. Tampere)7 The images are converted to grayscale and histogram equalized by Contrast Limited Adaptive Histogram Equalization (CLAHE) [55]. The registration is done by Elastic Stack Alignment (ESA) [56], which first finds a rigid transformation using Random Sample Consensus (RANSAC) from Scale-Invariant Feature Transform (SIFT) features. A non-linear registration follows using normalized correlation and virtual springs to keep the transformation close to a rigid one. Good parameters for the ESA algorithm were found by a parallel grid search on a computational cluster based on [57].
CKVST: (Chengdu)8 The images are decomposed into channels by a stain deconvolution procedure [40] and only the hematoxylin channel is used. A rigid transformation (including scaling) is estimated first on downsampled images. The transformation is further refined by evaluating the similarity on a set of selected high resolution patches. Finally, a non-rigid registration represented by B-splines is found locally. The normalized cross correlation is used for both rigid and non-rigid registration, with gradient descent and limited-memory Broyden-Fletcher-Goldfard-Shanno (L-BFGS) optimizers, respectively.
MEVIS: (Fraunhofer)9 Normalized gradient field (NGF) similarity [58]-[60] of grayscale versions of the images is used in a three-step approach. First, centers of mass are aligned and a number of different rotations are tried. Second, an affine transformation is found by a Gauss-Newton method. Third, a dense, non-rigid transformation is found using curvature regularization and L-BFGS optimization. The method is accelerated by optimizing memory access and by precalculation of reduced-size images.
AGH: (AGH UST)10 The images are converted to grayscale, downsampled and histogram equalized (for some of the procedures). The key feature of the AGH method is to apply several different approaches and then automatically select the best result based on a similarity criterion. An initial similarity or rigid transformation was determined by RANSAC from feature points detected by SIFT, ORB, or SURF. If it failed, the initial transformation was found by aligning binary tissue masks calculated from the images. Second, a non-rigid transformation was found using local affine registration, various versions of the demons algorithms, or a feature-point-based thinplate spline interpolation. For most of the cases, the most effective procedure was the MIND-based Demons algorithm.
UPENN: (U. Pennsylvania) [61]11 A stain deconvolution [40] is used to remove the DAB (diaminobenzidine) stain and make the appearance more uniform. The images are rescaled to 4% of the original size, converted to grayscale, and padded with a random noise. For robustness, 5000 random initial rigid transformations are evaluated. The registration itself is performed starting with an initial affine step using L-BFGS optimization, followed by the estimation of a detailed deformation field, using a fast multi-resolution version of the dense non-linear diffeomorphic registration with the Greedy tool [62] and a local NCC criterion.
TUB: (Tsinghua U.)12 A combined standard deviation of all color channels in a Gaussian neighborhood with σ = 1 pixel is used as a scalar feature for subsequent registration. Image size is reduced to about 512 × 512 pixels and padded to keep the aspect ratio. The registration is performed by a convolutional neural network similar to the Volume Tweening Network [63]. First a rigid and then a dense non-linear transformation is estimated. The network is first trained in an unsupervised manner, maximizing an image correlation coefficient, then finetuned using provided landmark positions on the training data.
The seven methods described come from the ANHIR challenge as described in Section II-E. For completeness, we have also included several well known, freely available and often used registration methods, which we already tested in [16], to enable a better comparison with the state of the art. These methods (marked by * in Tables II and III) were not part of the ANHIR competitions but were run by the organizers on the same data and evaluation protocols.
bUnwarpJ: The images are registered using the bUnwarpJ ImageJ plugin [22] which calculates a non-linear B-spline-based deformation in a multiresolution way, minimizing a sum of squares difference (SSD) criterion, generalizing earlier B-spline registration methods [64], [65]. The key feature of bUnwarpJ is to simultaneously calculate the deformation in both directions, enforcing invertibility by a consistency constraint and providing strong regularization. Additional regularization is possible by penalizing the deformation field divergence and curl.
RVSS: Register virtual stack slices is another ImageJ registration plugin which extends the bUnwarpJ method [22] by incorporating also SIFT [66] feature points in both images to add robustness. We start by estimating a rigid transformation, which we then refine using a B-spline transformation.
NiftyReg: The NiftyReg software is used to first perform an affine registration based on block matching [67], [68] and then a B-spline non-linear registration [69].
Elastix: Elastix [70] is a registration software providing a simple to use command-line interface to the Insight Segmentation and Registration Toolkit (ITK). We use a B-spline deformation and MI similarity criteria with the adaptive stochastic gradient descent optimizer.
ANTs: Advanced Normalization Tools [71] is another registration toolkit using ITK as a backend. We first perform an affine registration by MI maximization, followed by a dense symmetric diffeomorphic registration (SyN) using cross-correlation.
DROP: Similarly to many previously mentioned approaches, DROP [72], [73] represents the deformation using B-splines, minimizing a sum of absolute differences (SAD) (ℓ1) criterion. It differs by treating registration as a discrete optimization problem, solved efficiently in a multiresolution fashion using linear programming.
IV. Results
A. Relative target error comparison
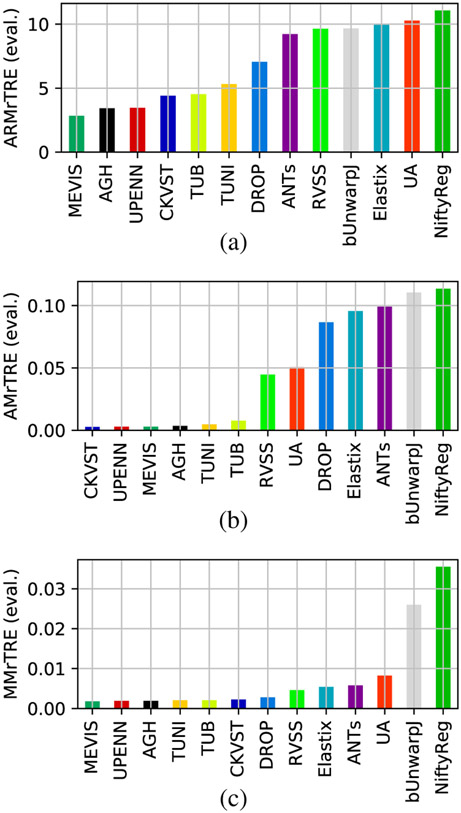
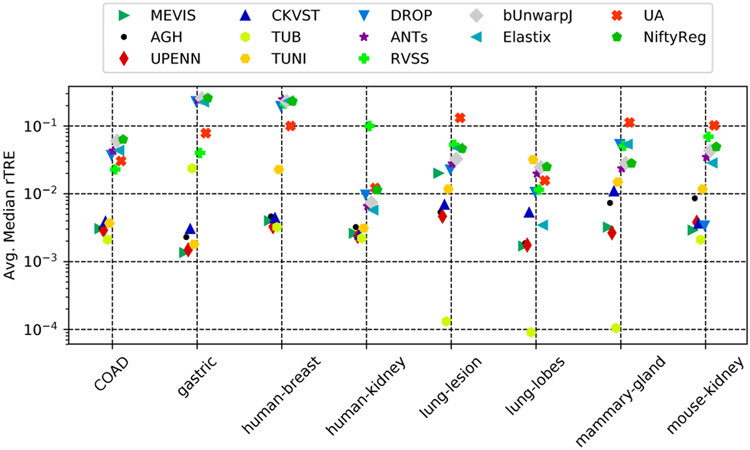
Our main evaluation criterion is ARMrTRE, average rank of median relative target registration error (see Section II-C, eq. 2). We show the values of ARMrTRE for all methods in Fig. 6, together with AMrTRE (4), and MMrTRE (5). We see that MEVIS is most often the best method, with AGH and UPENN within the top four, and TUB, TUNI, and CKVST more variable but close behind. On the other hand, the general methods (NiftyReg, bUnwarpJ, Elastix, DROP and ANTs), not optimized for microscopy images, are always in the second half of the ranking. It turns out that the results are almost the same when the other criteria from Section II-C are employed. A graphical comparison of those as well as other criteria based on of aggregating the relative landmark error rTRE can be found in Fig. S1 in the Supplementary material.
Fig. 6.
Average rank of median rTRE (a), average median rTRE (b), and median of median rTRE (c) per method on the test data.
For quantitative values on test data, see Table III. Since some datasets contain only training and no testing data, for completeness we also provide quantitative results on all data combined in Supplementary material Table SIII.
B. Pairwise method comparison
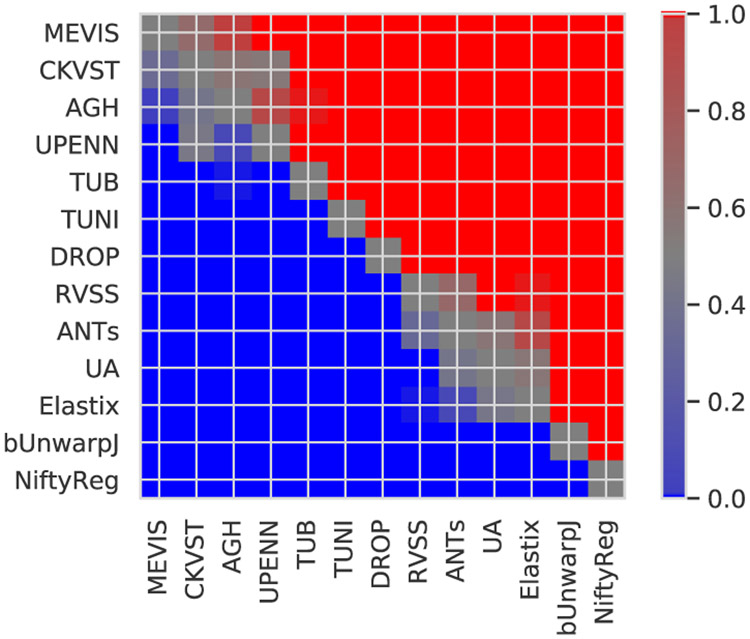
Fig. 7 shows the color coded p-values for pairwise comparison of the methods, as described in Section II-D. It turns out that we could (topologically) sort the methods by performance from the best methods at the top to the worst performers at the bottom. All differences between methods are significant with the following exceptions: There are no significant differences between the first three methods (MEVIS, CKVST, AGH), between CKVST, AGH, and UPENN, between ANTs and RVSS, and between UA, ANTs and Elastix methods.
Fig. 7.
Color coded p-values for pairwise comparison of methods over all test image pairs in terms of median rTRE, where the median is taken over all landmarks in an image. Red/blue indicates, that the method in the row performs statistically better/worse than the column method, respectively, according to the one-sided Wilcoxon signed-rank test at significance level p = 0.01. Gray and shades of gray indicate no significant differences. Methods are topologically sorted by performance from top to bottom.
C. Differences between datasets
We may ask whether some datasets are more difficult than others and whether some methods are particularly suited for specific datasets. It seems that the answer is yes to both questions. For example, according to Fig. 4, the (CNN based) TUB method outperforms all other methods by an order of magnitude in terms of AMrTRE on some datasets (lung lesions, lung lobes). However, this could be also due to overfitting, since for these datasets all landmark positions were available for training since the beginning and none of them are part of the testing set. Note that evaluation was done on the testing pairs for all datasets except lung lesions and lobes, and mammary glands, which contain only training pairs.
Fig. 4.
Relative performance of the methods on the different datasets in terms of AMrTRE.
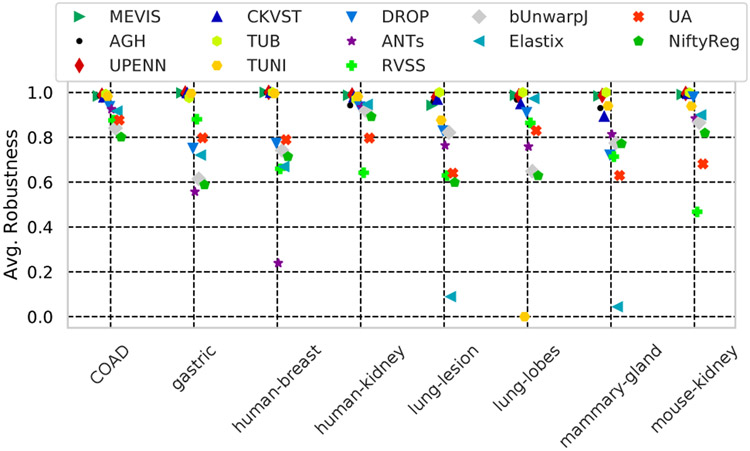
Fig. 5 compares the robustness (8) by datasets. We see that the best six methods have a very high robustness (> 98%), while others completely fail on some of the datasets (e.g. Elastix or TUNI). Fig. S4 in the Supplementary material compares the methods’ performance as a function of the combination of stains being registered.
Fig. 5.
Robustness (the relative number of landmarks which moved towards the ground truth location) of all methods on different tissues.
D. Training/testing
In Fig. S5, we compare the performance in terms of the distribution of the median rTRE and rank median rTRE between the training and testing data. For most methods, the distributions on training and testing data are rather similar. However, we note that TUB performs much better on training than on testing data, hinting again on possible overfitting. Interestingly, some methods, like MEVIS or CKVST, actually perform slightly better on the testing data.
V. Discussion and conclusions
Our experience with organizing the ANHIR challenge and a very positive reaction of the community, including a good attendance of the ANHIR workshop at ISBI 2019, confirmed that there is indeed a wide interest in such challenges.
However, organizing such a challenge requires a significant effort. The most time-consuming part was annotating the images with landmarks. Although the landmarks were sufficient to our purpose, there are sometimes large areas without salient corresponding structures, where very few landmarks can be identified. In the future, we would recommend that manually obtained landmarks are combined with other complementary means of evaluating the registration quality, such as measuring overlap using reference segmentations (as in NIREP [11]), or using synthetically generated (and therefore known) deformations [64]. We became aware that for the results to be meaningful, we must discourage the participants to overtrain on the provided datasets. Future challenges should also measure the speed of the algorithms more reliably, ideally by using a common hardware for all methods. Besides pairwise registration, we might consider other more advanced tasks such as 3D reconstruction by registering the histology slices, creating a large 2D mosaic from a set of smaller tile images, aligning 2D microscopy images with volumetric medical invivo images (e.g. MRI or ultrasound), or aligning standard histopathology with high-dimensional microscopy modalities such as MALDI [74]. For these applications, completely new evaluation approaches might be needed.
Perhaps surprisingly, most of the submitted methods (see Section III) used very similar and rather classical techniques. The best performing algorithms were originally developed for other modalities but were tuned for the data at hand. They consist of a carefully designed multi-step pipeline, which typically started with a coarse but robust prealignment, followed by a non-rigid registration step for fine tuning the results. Only one method (TUB) used the now ubiquitous CNNs; it was very fast and performed well, although not as well as the best performing methods and its generalization ability was limited. Interestingly, directly applying well-known off-the-shelf methods gave significantly worse results, although these methods contained very similar algorithmic ingredients as some of the best performing methods (e.g., MEVIS, CKVST, AGH). One explanation is that those general purpose methods were developed for other types of images, mostly 3D brain data, and possibly required more parameter tuning. Our observation is that the better performing methods often won not by being more accurate but by being more robust (see Table III), converging to the solution even from a far away initialization. The participants were clearly aware of this, since most submitted methods spend a significant effort to find a good initialization, for example by incorporating automatically detected landmarks (TUNI, AGH), trying many different starting points (MEVIS, UPENN), or even applying different methods in parallel (AGH). Another reason for the performance gap might be that the participants spent more time finding the optimal parameters for their own methods (even using a computing cluster in TUNI).
To summarize the evaluation, there was very little difference in terms of both robustness and accuracy between the first six methods (MEVIS, AGH, UPENN, CKVST, TUB, TUNI). Those six methods outperformed all others in all evaluation measures that we have tested.
On the other hand, there were large differences in the reported execution speed (Table III). With the exception of the extremely fast CNN method (TUB), the differences seem to be more due to the quality of engineering (implementation) and the choice of parameters, and not the choice of the key algorithms. While MEVIS and NiftyReg take on average a few seconds per registration, the majority of the methods need a few minutes, with the slowest method (ANTs) taking almost an hour. Note however that MEVIS uses precalculation extensively and NiftyReg might have taken advantage of the GPU.
No methods were developed explicitly for the ANHIR challenge or for this type of images. No evaluated method takes advantage of the full resolution or full color information. With a median landmark localization error measured in tens of pixels at the original resolution even for the best methods, none of the methods would be probably robust and accurate enough for routine, fully automatic use. However, these methods could certainly be used in a semi-supervised setting to substantially reduce the need for manual interaction in many tasks, such as fusing information from several differently stained images.
The above mentioned weaknesses will likely be addressed in future research, e.g. by creating algorithms capable of working on full resolution images or avoiding the overfitting in CNNs. We therefore believe that the need for objective performance evaluation will remain and that challenges such as ANHIR should be continued to stimulate and evaluate research in image registration.
Supplementary Material
Acknowledgements
The authors are grateful to Ben Glocker for his help with tuning the DROP parameters.
J. Kybic acknowledges the support of the OP VVV funded project CZ.02.1.01/0.0/0.0/16_019/0000765 Research Center for Informatics and the Czech Science Foundation project 17-15361S.
They acknowledge the support of the Russian Science Foundation grant 17-11-01279.
Their work was partly supported by the National Institutes of Health under grant award numbers NIH/NCI/ITCR:U24-CA189523, NIH/NIBIB:R01EB017255, NIH/NIA:R01AG056014, and NIH/NIA:P30AG010124.
His work is supported by Academy of Finland projects 313921 and 314558.
They acknowledge the support provided by WestGrid and Compute Canada.
Marek Wodzinski acknowledges the support of the Preludium project no. UMO-2018/29/N/ST6/00143 funded by the National Science Centre in Poland.
She acknowledges the support of the Spanish Ministry of Economy and Competitiveness (TEC2015-73064-EXP, TEC2016-78052-R and RTC-2017-6600-1) and a 2017 Leonardo Grant for Researchers and Cultural Creators, BBVA Foundation.
Footnotes
All references beginning with ‘S’ refer to the Supplementary material.
CD1a, CD31, CD4, CD68, CD8, Cc10, EBV, ER, HE, HER2, Ki67, MAS, PAS, PASM, PR, Pro-SPC, aSMA
N. Tahmasebi, M. Noga, K. Punithakumar
M. Valkonen. K. Kartasalo, L. Latonen, P. Ruusuvuori
Y. Xiang, Y. Yan, Y. Wang
J. Lotz, N. Weiss, S. Heldmann
M. Wodzinski, A. Skalski, https://github.com/lNefarin/ANHIR\_MW
L. Venet, S. Pati, P. Yushkevich, S. Bakas, https://github.com/CBICA/HistoReg
S. Zhao, Y. Xu, E. I-Chao Chang
Contributor Information
Jiří Borovec, Faculty of Electrical Engineering, Czech Technical University in Prague..
Jan Kybic, Faculty of Electrical Engineering, Czech Technical University in Prague..
Ignacio Arganda-Carreras, Ikerbasque, Basque Foundation for Science, Bilbao, University of the Basque Country and Donostia International Physics Center, Donostia-San Sebastian, Spain..
Dmitry V. Sorokin, Laboratory of Mathematical Methods of Image Processing, Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, Russia.
Gloria Bueno, VISILAB group and E.T.S. Ingenieros Industriales, Universidad de Castilla-La Mancha, Spain..
Alexander V. Khvostikov, Laboratory of Mathematical Methods of Image Processing, Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, Russia
Spyridon Bakas, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA..
Eric I-Chao Chang, Microsoft Research, Beijing, China.
Stefan Heldmann, Fraunhofer MEVIS, Lubeck, Germany.
Kimmo Kartasalo, Tampere University, Faculty of Medicine and Health Technology, Tampere, Finland.
Leena Latonen, University of Eastern Finland, Institute of Biomedicine, Kuopio, Finland..
Johannes Lotz, Fraunhofer MEVIS, Lubeck, Germany.
Michelle Noga, Department of Radiology & Diagnostic Imaging, University of Alberta, AB, Canada, and also with Servier Virtual Cardiac Centre, Mazankowski Alberta Heart Institute, AB, Canada..
Sarthak Pati, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA..
Kumaradevan Punithakumar, Department of Radiology & Diagnostic Imaging, University of Alberta, AB, Canada, and also with Servier Virtual Cardiac Centre, Mazankowski Alberta Heart Institute, AB, Canada..
Pekka Ruusuvuori, Tampere University, Faculty of Medicine and Health Technology, Tampere, Finland.; Institute of Biomedicine, University of Turku, Finland and with Faculty of Medicine and Health Technology, Tampere, Finland..
Andrzej Skalski, AGH University of Science and Technology, Department of Measurement and Electronics, Krakow, Poland..
Nazanin Tahmasebi, Department of Radiology & Diagnostic Imaging, University of Alberta, AB, Canada, and also with Servier Virtual Cardiac Centre, Mazankowski Alberta Heart Institute, AB, Canada..
Masi Valkonen, Tampere University, Faculty of Medicine and Health Technology, Tampere, Finland..
Ludovic Venet, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA..
Yizhe Wang, Chengdu Knowledge Vision Science and Technology Co., Ltd. Chengdu, China..
Nick Weiss, Fraunhofer MEVIS, Lubeck, Germany.
Marek Wodzinski, AGH University of Science and Technology, Department of Measurement and Electronics, Krakow, Poland..
Yu Xiang, Chengdu Knowledge Vision Science and Technology Co., Ltd. Chengdu, China..
Yan Xu, Microsoft Research, Beijing, China.; School of biological science and medical engineering and Beijing Advanced Innovation Center for Biomedical Engineering, Beihang University, Beijing.
Yan Yan, University of Electronic Science and Technology of China Chengdu, China..
Paul Yushkevic, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA..
Shengyu Zhao, Tsinghua University, Beijing, China..
Arrate Muñoz-Barrutia, Bioengineering and Aerospace Engineering Department, Universidad Carlos III de Madrid and Instituto de Investigation Sanitaria Gregorio Marañón, Madrid, Spain..
References
- [1].Zitová B and Flusser J, “Image registration methods: a survey,” Image and Vision Computing, no. 21, pp. 977–1000, 2003. [Google Scholar]
- [2].Brown L, “A survey of image registration techniques,” ACM Computing Surveys, vol. 24, no. 4, pp. 326–376, December 1992. [Google Scholar]
- [3].Maintz J and Viergever MA, “A survey of medical image registration,” Medical Image Analysis, vol. 2, no. 1, pp. 1–36, 1998. [DOI] [PubMed] [Google Scholar]
- [4].Lester H and Arridge SR, “A survey of hierarchical non-linear medical image registration,” Pattern Recognit, vol. 32, no. 1, pp. 129–149, 1999. [Google Scholar]
- [5].Pluim J, Maintz JBA, and Viergever MA, “Mutual-information-based registration of medical images: A survey,” IEEE Trans. Med. Imag, vol. 22, no. 8, pp. 986–1004, August 2003. [DOI] [PubMed] [Google Scholar]
- [6].Oliveira FPM and Tavares JMRS, “Medical image registration: a review,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 17, no. 2, pp. 1–21, 2012. [DOI] [PubMed] [Google Scholar]
- [7].Sotiras A, Davatzikos C, and Paragios N, “Deformable Medical Image Registration: A Survey,” IEEE Trans. Med. Imag, vol. 32, no. 7, pp. 1153–1190, July 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Zitova B, “Mathematical Approaches for Medical Image Registration,” in Reference Module in Biomedical Sciences, 2018. [Google Scholar]
- [9].West J, Fitzpatrick J, and Wang M, “Comparison and evaluation of retrospective intermodality brain image registration techniques,” Journal of Computer Assisted Tomography, vol. 21, no. 4, pp. 554–568, 1997. [DOI] [PubMed] [Google Scholar]
- [10].Hellier P et al. , “Retrospective evaluation of intersubject brain registration,” IEEE Trans. Med. Imag, vol. 22, no. 9, pp. 1120–1130, 2003. [DOI] [PubMed] [Google Scholar]
- [11].Christensen G et al. , “Introduction to the non-rigid image registration evaluation project (NIREP),” in Biomedical Image Registration. Springer, 2006, vol. 4057, pp. 128–135. [Google Scholar]
- [12].Klein A, Andersson J, Ardekani B et al. , “Evaluation of 14 nonlin-ear deformation algorithms applied to human brain MRI registration,” Neuroimage, vol. 46, no. 3, pp. 786–802, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ou Y, Akbari H, Bilello M, Da X, and Davatzikos C, “Comparative evaluation of registration algorithms in different brain databases with varying difficulty: Results and insights,” IEEE Trans. Med. Imag, vol. 33, no. 10, pp. 2039–2065, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Sarrut D, Delhay B, Villard P-F, Boldea V, Beuve M, and Clarysse P, “A Comparison Framework for Breathing Motion Estimation Methods From 4-D Imaging,” IEEE Trans. Med. Imag, vol. 26, pp. 1636–1648, 2007. [DOI] [PubMed] [Google Scholar]
- [15].Brock KK, “Results of a multi-institution deformable registration accuracy study (MIDRAS),” International Journal of Radiation Oncology • Biology • Physics, vol. 76, no. 2, pp. 583–596, 2010. [DOI] [PubMed] [Google Scholar]
- [16].Borovec J, Munoz-Barrutia A, and Kybic J, “Benchmarking of Image Registration Methods for Differently Stained Histological Slides,” in Proc. Int. Conf. Image Process, Athens, 2018, pp. 3368–3372. [Google Scholar]
- [17].Castillo R, Castillo E, Guerra R et al. , “A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets.” Phys. Med. Biol, vol. 54, no. 7, pp. 1849–1870, 2009. [DOI] [PubMed] [Google Scholar]
- [18].Murphy K, Van Ginneken B, Reinhardt J et al. , “Evaluation of registration methods on thoracic CT: The EMPIRE10 challenge,” IEEE Trans. Med. Imag, vol. 30, no. 11, pp. 1901–1920, 2011. [DOI] [PubMed] [Google Scholar]
- [19].Pontre B et al. , “An open benchmark challenge for motion correction of myocardial perfusion MRI.” IEEE J. Biomedical and Health Informatics, vol. 21, no. 5, pp. 1315–1326, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].McCann MT, Ozolek JA, Castro CA, Parvin B, and Kovacevic J, “Automated histology analysis: Opportunities for signal processing,” IEEE Signal Processing Magazine, vol. 32, no. 1, pp. 78–87, January 2015. [Google Scholar]
- [21].Pichat J, Iglesias JE, Yousry T, Ourselin S, and Modat M, “A survey of methods for 3D histology reconstruction.” Medical Image Analysis, vol. 46, pp. 73–105, 2018. [DOI] [PubMed] [Google Scholar]
- [22].Arganda-Carreras I et al. , “Consistent and elastic registration of histological sections using vector-spline regularization,” in Computer Vision Approaches to Medical Image Analysis, vol. 4241, 2006, pp. 85–95. [Google Scholar]
- [23].Feuerstein M, Heibel TH, Gardiazabal J, Navab N, and Groher M, “Reconstruction of 3-D histology images by simultaneous deformable registration.” in MICCAI, vol. 6892, 2011, pp. 582–589. [DOI] [PubMed] [Google Scholar]
- [24].Yushkevich PA et al. , “3D mouse brain reconstruction from histology using a coarse-to-fine approach.” in WBIR, vol. 4057, 2006, pp. 230–237. [Google Scholar]
- [25].Song Y, Treanor D, Bulpitt A et al. , “3D reconstruction of multiple stained histology images,” J. Path. Inf, vol. 4, no. 2, p. 7, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Tang M, “Automatic registration and fast volume reconstruction from serial histology sections.” Computer Vision and Image Understanding, vol. 115, no. 8, pp. 1112–1120, 2011. [Google Scholar]
- [27].Pichat J, Modat M, Yousry T, and Ourselin S, “A multi-path approach to histology volume reconstruction,” in Int. Symp. Biomed. Imag, April 2015, pp. 1280–1283. [Google Scholar]
- [28].Gibb M et al. , “Resolving the three-dimensional histology of the heart” in Comp. Meth. Syst. Biol, vol. 7605 Springer, 2012, pp. 2–16. [Google Scholar]
- [29].Mueller M, Yigitsoy M, Heibel H, and Navab N, “Deformable reconstruction of histology sections using structural probability maps,” in MICCAI, 2014. [DOI] [PubMed] [Google Scholar]
- [30].du Bois D’Aische A and Craene M, “Efficient multi-modal dense field non-rigid registration: alignment of histological and section images,” Medical Image Analysis, vol. 9, no. 6, pp. 538–546, 2005. [DOI] [PubMed] [Google Scholar]
- [31].Saalfeld S, Cardona A, Hartenstein V, and Tomancak P, “As-rigid-as-possible mosaicking and serial section registration of large sstem datasets,” Bioinformatics, vol. 26, no. 12, pp. −57, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Metzger GJ, Dankbar SC, Henriksen J et al. , “Development of multigene expression signature maps at the protein level from digitized immunohistochemistry slides.” PloS One, vol. 7, no. 3, p. e33520, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Obando D, Frafjord A, Oynebraten I et al. , “Multi-staining registration of large histology images,” in Int. Symp. Biomed. Imag, 2017, pp. 345–348. [Google Scholar]
- [34].Déniz O, Toomey D et al. , “Multi-stained whole slide image alignment in digital pathology,” in SPIE Med. Imag, vol. 9420, 2015, p. 94200Z. [Google Scholar]
- [35].Trahearn N, Epstein D, Cree I, Snead D, and Rajpoot N, “Hyperstain inspector: A framework for robust registration and localised coexpression analysis of multiple whole-slide images of serial histology sections,” Scientific Reports, vol. 7, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Ceritoglu C and Wang L, “Large deformation diffeomorphic metric mapping registration of reconstructed 3D histological section images and in vivo MR images,” Front. Hum. Neurosci, vol. 4, p. 43, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Gupta L, Klinkhammer BM, Boor P, Merhof D, and Gadermayr M, “Stain independent segmentation of whole slide images: A case study in renal histology,” in Int. Symp. Biomed. Imag, 2018, pp. 1360–1364. [Google Scholar]
- [38].Borovec J and Kybic J, “Binary pattern dictionary learning for gene expression representation in drosophila imaginal discs,” in Workshop Math. Comp. Meth. Biomed. Imag. Image Anal, 2017, pp. 555–569. [Google Scholar]
- [39].Wang C, Ka S, and Chen A, “Robust image registration of biological microscopic images,” Scientific Reports, vol. 4, no. 1, p. 6050, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Ruifrok AC and Johnston DA, “Quantification of histochemical staining by color deconvolution,” Anal. Quant. Cytol. Histol, vol. 23, no. 4, pp. 291–299, 2001. [PubMed] [Google Scholar]
- [41].Kybic J and Borovec J, “Automatic simultaneous segmentation and fast registration of histological images,” in Int. Symp. Biomed. Imag, 2014, pp. 774–777. [Google Scholar]
- [42].Borovec J, Kybic J, Bušta M, Ortiz-de Solorzano C, and Muñoz-Barrutia A, “Registration of multiple stained histological sections,” in Int. Symp. Biomed. Imag, San Francisco, 2013, pp. 1034–1037. [Google Scholar]
- [43].Song Y et al. , “Unsupervised content classification based nonrigid registration of differently stained histology images.” IEEE Trans. Biomed. Engineering, vol. 61, no. 1, pp. 96–108, 2014. [DOI] [PubMed] [Google Scholar]
- [44].Lobachev O, Ulrich C, Steiniger B, Wilhelmi V, Stachniss V, and Guthe M, “Feature-based multi-resolution registration of immunostained serial sections.” Medical Image Analysis, vol. 35, pp. 288–302, 2017. [DOI] [PubMed] [Google Scholar]
- [45].Kybic J, Dolejsi M, and Borovec J, “Fast registration of segmented images by normal sampling,” in Bio Image Computing (BIC) workshop at CVPR, 2015, pp. 11–19. [Google Scholar]
- [46].Solorzano L, Almeida G, Mesquita B, Martins D, Oliveira C, and Wählby C, “Whole slide image registration for the study of tumor heterogeneity,” in COMPAY: Comp. Pathol. workshop, 2018, pp. 95–102. [Google Scholar]
- [47].Sorokin DV, Peterlik I, Tektonidis M, Rohr K, and Matula P, “Non-rigid contour-based registration of cell nuclei in 2-D live cell microscopy images using a dynamic elasticity model,” IEEE Trans. Med. Imag, vol. 37, no. 1, pp. 173–184, 2017. [DOI] [PubMed] [Google Scholar]
- [48].Sorokin DV, Suchánková J, Bártová E, and Matula P, “Visualizing stable features in live cell nucleus for evaluation of the cell global motion compensation,” Folia biologica, vol. 60, no. Suppl. 1, pp. 45–49, 2014. [PubMed] [Google Scholar]
- [49].Shojaii R, Karavardanyan T, Yaffe MJ, and Martel AL, “Validation of histology image registration” in SPIE Med. Imag, vol. 7962 SPIE, 2011, p. 79621E. [Google Scholar]
- [50].Wang CW, Budiman Gosno E, and Li YS, “Fully automatic and robust 3D registration of serial-section microscopic images,” Scientific Reports, vol. 5, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Borovec J, “BIRL: Benchmark on image registration methods with landmark validation,” Czech Tech. Univ. in Prague, Tech. Rep, 2019. [Google Scholar]
- [52].Bakas S et al. , “Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge,” 11 2018, arXiv:1811.02629. [Google Scholar]
- [53].Lau TF, Luo J, Zhao S, Chang EI-C, and Xu Y, “Unsupervised 3D end-to-end medical image registration with volume tweening network.” CoRR, vol. abs/1902.05020, 2019. [DOI] [PubMed] [Google Scholar]
- [54].Punithakumar K, Boulanger P, and Noga M, “A GPU-accelerated deformable image registration algorithm with applications to right ventricular segmentation,” IEEE Access, vol. 5, pp. 20374–20 382, 2017. [Google Scholar]
- [55].Pizer SM et al. , “Adaptive histogram equalization and its variations,” Comput. Vision Graph. Image Process, vol. 39, no. 3, pp. 355–368, 1987. [Google Scholar]
- [56].Saalfeld S, Fetter R, Cardona A, and Tomancak P, “Elastic volume reconstruction from series of ultra-thin microscopy sections,” Nat. Meth, vol. 9, no. 7, pp. 717–720, July 2012. [DOI] [PubMed] [Google Scholar]
- [57].Kartasalo K, Latonen L, Vihinen J, Visakorpi T, Nykter M, and Ruusuvuori P, “Comparative analysis of tissue reconstruction algorithms for 3D histology.” Bioinformatics, vol. 34, no. 17, pp. 3013–3021, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Lotz J, Weiss N, and Heldmann S, “Robust, fast and accurate: a 3-step method for automatic histological image registration,” 2019. [Online]. Available: http://arxiv.org/abs/1903.12063 [Google Scholar]
- [59].Schmitt O, Modersitzki J, Heldmann S, Wirtz S, and Fischer B, “Image registration of sectioned brains,” Int. J. Comp. Vis, vol. 73, no. 1, pp. 5–39, September 2006. [Google Scholar]
- [60].Modersitzki J, FAIR: Flexible Algorithms for Image Registration. SIAM, 2009. [Google Scholar]
- [61].Venet L, Pati S, Yushkevich P, and Bakas S, “Accurate and robust alignment of variable-stained histologic images using a general-purpose greedy diffeomorphic registration tool,” 2019, arXiv:1904.11929. [Google Scholar]
- [62].Yushkevich PA, Pluta J, Wang H, Wisse LE, Das S, and Wolk D, “Fast automatic segmentation of hippocampal subfields and medial temporal lobe subregions in 3 Tesla and 7 Tesla T2-weighted MRI,” Alzheimer’s & Dementia, vol. 12, no. 7, Supp., pp. P126–P127, 2016. [Google Scholar]
- [63].Zhao S, Lau T, Luo J, Chang EI, and Xu Y, “Unsupervised 3D end-to-end medical image registration with volume tweening network,” IEEE J. Biomed. Health Informa, 2019. [DOI] [PubMed] [Google Scholar]
- [64].Kybic J and Unser M, “Fast parametric elastic image registration,” IEEE Trans. Imag. Proc, vol. 12, no. 11, pp. 1427–1442, 2003. [DOI] [PubMed] [Google Scholar]
- [65].Sánchez Sorzano C, Thévenaz P, and Unser M, “Elastic registration of biological images using vector-spline regularization,” IEEE Trans. Biomed. Eng, vol. 52, no. 4, pp. 652–663, April 2005. [DOI] [PubMed] [Google Scholar]
- [66].Lowe D, “Distinctive image features from scale-invariant keypoints,” Int. J. Comp. Vis, vol. 60, no. 2, pp. 91–110, 2004. [Google Scholar]
- [67].Ourselin S, Roche A, Subsol G, Pennec X, and Ayache N, “Reconstructing a 3D structure from serial histological sections,” Image Vision Comput., vol. 19, no. 1-2, pp. 25–31, 2001. [Google Scholar]
- [68].Modat M, Cash D, Daga P, Winston G, Duncan JS, and Ourselin S, “A symmetric block-matching framework for global registration,” in SPIE Med. Imag, vol. 9034, 03 2014, p. 90341D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, and Hawkes DJ, “Nonrigid registration using free-form deformations: application to breast MR images,” IEEE Trans. Med. Imag, vol. 18, no. 8, pp. 712–721, August 1999. [DOI] [PubMed] [Google Scholar]
- [70].Klein S, Staring M, and Murphy K, “Elastix: a toolbox for intensity-based medical image registration,” IEEE Trans. Med. Imag, vol. 29, no. 1, 2010. [DOI] [PubMed] [Google Scholar]
- [71].Avants B, Epstein C, Grossman M, and Gee JC, “Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain,” Medical Image Analysis, vol. 12, no. 1, pp. 26–41, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Glocker B, Komodakis N, Tziritas G, Navab N, and Paragios N, “Dense image registration through MRFs and efficient linear programming,” Medical Image Analysis, vol. 12, no. 6, pp. 731–741, 2008. [DOI] [PubMed] [Google Scholar]
- [73].Glocker B et al. , “Deformable medical image registration: Setting the state of the art with discrete methods,” Ann. Rev. Biomed. Eng, vol. 13, no. 1, pp. 219–244, 2011. [DOI] [PubMed] [Google Scholar]
- [74].Machálková M et al. , “Drug penetration analysis in 3D cell cultures using fiducial-based semiautomatic coregistration of MALDI MSI and immunofluorescence images,” Anal. Chem, vol. 91, no. 21, pp. 13 475–13 484, 2019. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.