Mapping the temperature-dependent and network site-specific onset of spectral diffusion at the surface of a water cluster cage

Significance

Water’s vibrational spectrum is dynamic: The OH oscillator frequency changes spontaneously within a diffuse envelope on an ultrafast timescale. Here, we explore the mechanics that drive this “spectral diffusion” at the molecular level by following the time-dependent frequency of single OH oscillators, each embedded in a cage of 20 deuterated water molecules, as a function of temperature. These cages are isolated in the gas phase and incorporate a single, isotopically labeled OH group that can occupy many spectroscopically distinct sites. The rates of spontaneous change in the OH frequency reflect the pathways for migration of the isotopic label among these sites, which occurs on a remarkably long (approximately millisecond) timescale at the onset of large-amplitude motion near 100 K.

Abstract

We explore the kinetic processes that sustain equilibrium in a microscopic, finite system. This is accomplished by monitoring the spontaneous, time-dependent frequency evolution (the frequency autocorrelation) of a single OH oscillator, embedded in a water cluster held in a temperature-controlled ion trap. The measurements are carried out by applying two-color, infrared-infrared photodissociation mass spectrometry to the D₃O⁺·(HDO)(D₂O)₁₉ isotopologue of the “magic number” protonated water cluster, H⁺·(H₂O)₂₁. The OH group can occupy any one of the five spectroscopically distinct sites in the distorted pentagonal dodecahedron cage structure. The OH frequency is observed to evolve over tens of milliseconds in the temperature range (90 to 120 K). Starting at 100 K, large “jumps” are observed between two OH frequencies separated by ∼300 cm⁻¹, indicating migration of the OH group from the bound OH site at 3,350 cm⁻¹ to the free position at 3,686 cm⁻¹. Increasing the temperature to 110 K leads to partial interconversion among many sites. All sites are observed to interconvert at 120 K such that the distribution of the unique OH group among them adopts the form one would expect for a canonical ensemble. The spectral dynamics displayed by the clusters thus offer an unprecedented view into the molecular-level processes that drive spectral diffusion in an extended network of water molecules.

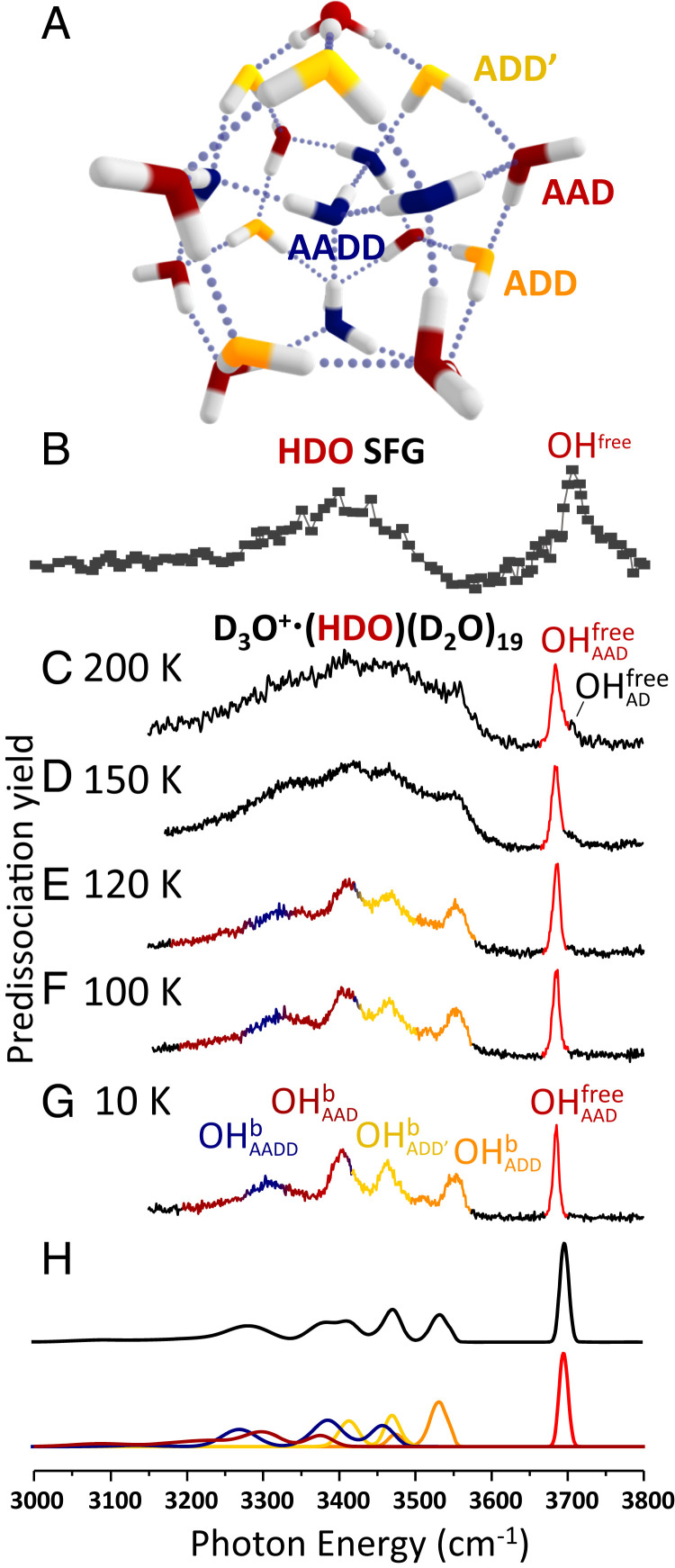
Chemical systems maintain equilibrium through kinetic processes that balance the populations of reactants and products. In solution, these processes involve energy exchange with the solvent, and simulations of chemical processes in solution often involve a hierarchy of methods. For example, local interactions involving the solute and first-shell solvent molecules might be treated with accurate quantum chemical methods, while the effects of the more distant solvent are included using simpler models (1, 2). In this report, we exploit temperature-controlled water clusters to provide a well-defined system in which to monitor the dynamic behavior of a simple reversible chemical process as a function of temperature. With the aid of theory, we identify the low-energy pathways that are associated with the onset of changes in the observed spectral patterns. Gas phase cluster ions are equilibrated through collisions with a low-pressure buffer gas and interaction with blackbody radiation in a radiofrequency ion trap, and hence can be viewed as being weakly coupled to a heat bath (3). We specifically consider the water cluster formed upon hydration of an “excess proton” by 21 water molecules, with a representative low-energy structure (4) shown in Fig. 1A. Note that its vibrational spectrum (Fig. 1C) strongly resembles that of the air–water interface (cf. Fig. 1B) (5).

Fig. 1.

Comparison of the isotope-diluted SFG spectrum of the air–water interface with vibrational predissociation spectra of D₃O⁺∙(HDO)(D₂O)₁₉ at temperatures in the range 10 to 200 K. (A) Representative low-energy structure of the H₃O⁺∙(H₂O)₂₀ cluster. The stick spectra of the clusters with the OH group in each of the possible sites of the cluster are included in SI Appendix, Fig. S2. (B) SFG spectrum of HDO at the air–water interface. Reprinted with permission from ref. 5. Copyright 2009 American Chemical Society. (C–G) Vibrational spectra of D₃O⁺∙(HDO)(D₂O)₁₉ from 200 to 10 K. OH^b and OH^free represent hydrogen-bonded OH and free OH. The A/D notation labels the number of hydrogen bond acceptors and donors on one water molecule. H displays the calculated spectrum based on 400 isotopomers of the 10 lowest energy structural isomers of the D₃O⁺∙(HDO)(D₂O)₁₉ cluster. The contribution from each type of water molecule (or site) to specific regions of the spectrum is colored to match the scheme in A.

Results and Discussion

The specific dynamical processes at play here are the temperature-dependent pathways for migration of a single H atom through the various distinct sites in an otherwise perdeuterated cage. This is accomplished by following how the frequency of the OH oscillator evolves in time as the temperature is systematically raised to enable large-amplitude motion of the water molecules. We specifically monitor the migration of the OH oscillator among the various spectroscopically distinct sites (labeled by different colors in the structure and spectra in Fig. 1) in the structure after a sudden disruption of the equilibrium population distribution. That is, the steady-state populations in the various network sites, constrained by the equilibrium constant (K_eq) in a thermal ensemble, are sustained through steady-state, site-to-site interconversion kinetics. We remark that these rearrangements are a cluster analog of those that drive ultrafast “spectral diffusion” in bulk and interfacial water (6–12).

Our experimental approach to measuring the spontaneous kinetic processes in clusters is motivated by the classic “T-jump” approach pioneered by Eigen in the 1950s, who demonstrated a way to determine the rates of the fast reactions that sustain a macroscopic equilibrium state. That method involved quickly displacing the system away from equilibrium and then observing the time response of the populations as a new equilibrium condition is established (13). Here, we employ a variation of this scheme in which we remove the population in one of the sites in an ensemble of clusters held at constant temperature and observe the system moving toward the new equilibrium population distribution.

The structure displayed in Fig. 1A is one of many distorted pentagonal dodecahedron (PD) arrangements with similar oxygen atom cages but different topologies of the extended H-bonding network (see the 10 low-lying isomers in SI Appendix, Fig. S1) (4, 14, 15). We introduce a single H atom into the perdeuterated isotopologue, which is isolated and studied using photofragmentation mass spectrometry as detailed in SI Appendix, Section I. These isotopologues occur in two classes according to whether the H isotope is sequestered in the hydronium ion or resides in the surrounding neutral water cage. We are here concerned with only the D₃O⁺·(HDO)(D₂O)₁₉ type (hereafter denoted PD_OH) because the OH stretches of the embedded hydronium are known to lie near 2,000 cm⁻¹ and do not contribute to the spectra in the OH stretching region (16). The PD_OH class occurs with many spectroscopically distinct isotopomers at low temperature according to the location of the unique OH group in the PD structure. This spectral variation occurs because the water molecule with the OH group is differentiated according to the number of H-bond donors (D) and acceptors (A) at play in each site, as well as the H-bonding topology of the more distant molecules in the network. We note that, because both intermolecular and intramolecular coupling are suppressed in the OH stretching spectra of the PD_OH isotopomers, the resulting bands are dramatically simplified compared to those displayed by the homogeneous H₃O⁺·(H₂O)₂₀ isotopologue (SI Appendix, Fig. S3) (16). There are five clearly distinct OH bands in the PD_OH spectrum that are color-coded in Fig. 1G (full spectrum in SI Appendix, Fig. S4) according to the specific sites that are calculated to yield fundamentals in the observed locations (SI Appendix, Fig. S2).

At low temperature, the spectrum of the mass-selected ion packet consists of a heterogeneous combination of the spectra of individual isotopomers, each of which can be isolated using isotopomer-selective vibrational spectroscopic methods as discussed at length in previous studies (17–20). Isotopomer selection is achieved by sequentially removing each isotopomer from the ion packet through infrared (IR) photodissociation at each of the five band positions with an initial IR laser with pulse width ∼8 ns (hereafter denoted the “bleach” laser). Features in the spectrum that are modulated by the bleach are revealed by interrogating the same ion packet with a second IR laser pulse (∼8 ns pulse width, hereafter denoted the “probe” laser) that follows the bleach pulse after a delay time, Δt. Site-specific spectra for the five sites were reported previously and are reproduced in SI Appendix, Fig. S3. The cold (T = 10 K) ensemble is static, such that photodestruction of an isotopomer permanently removes this species even when the ion packet is stored for long holding times (up to 1 s in the present study) in an ion trap. In this report, we explore the situation in which, as the temperature is elevated, the OH group is observed to spontaneously migrate from one site to another.

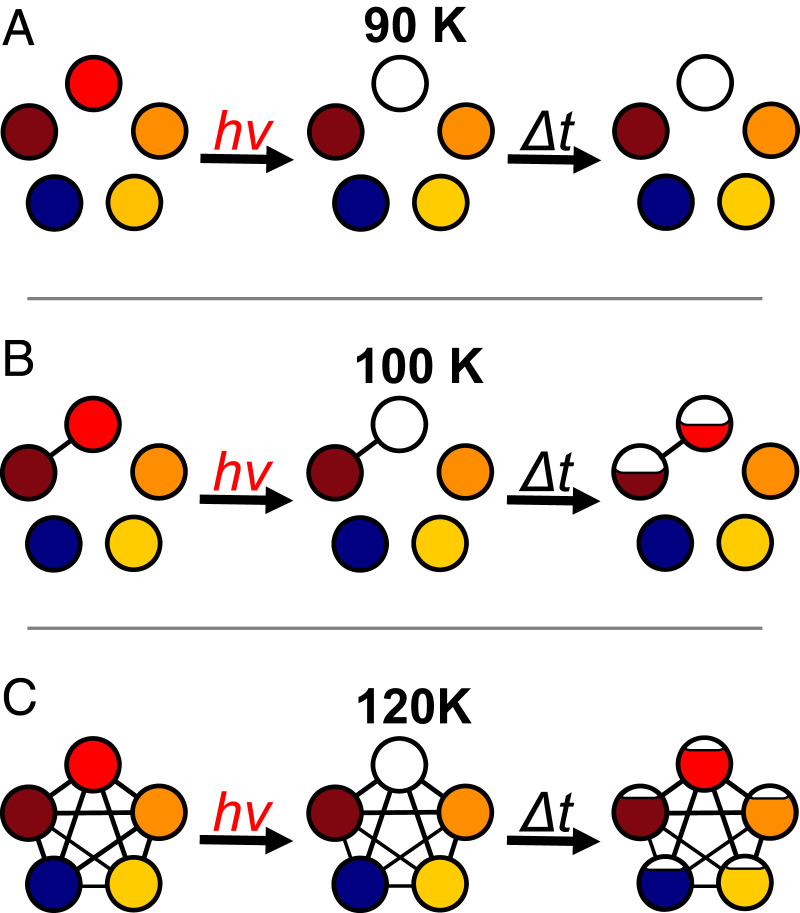
The strategy of our experimental approach was introduced in an earlier demonstration study of the I⁻·(HDO)·(D₂O) cluster (21–23), where the OH oscillator was found to migrate between all four positions when warmed to 150 K. That system is sufficiently small that it could be accurately treated with high-level theory (23). In this study, we explore the scenario presented by a larger water network in which the dynamics reflect different possible pathways for collective motions over a complex free energy landscape closer to that of condensed phase water. This scenario presents the possibility for sequential onsets of large-amplitude motions. Application to the present system involving five spectroscopically distinct sites is illustrated schematically in Fig. 2. Each circle represents the population in one of the sites with the appropriate color as defined in Fig. 1 A and G. The low-temperature case, which we exploited earlier to obtain the spectral signatures of OH in each site, is diagrammed in the top panel. Removal of population in the red sites by photodissociation leaves a static ensemble of the remaining ions. When the second laser probes the populations of the various other isomers at time Δt later, the four other features appear unaffected by the selective population removal by the first laser. As the temperature is increased, however, the OH group can migrate between sites. In the simplest case where only two sites interconvert (red and brown in Fig. 2B), and the bleach laser’s pulse width is short compared to the site-to-site exchange rate, the red population can be initially completely removed. This population partially recovers over time while the population in the brown state is reduced to achieve the ratio of populations in the two states dictated by the equilibrium constant. When steady state is restored at sufficiently long delay times, Δt, the populations of both red and brown sites will be reduced by half (assuming K_eq = 1), while those in the other three sites are unaffected. This site-specific population redistribution scenario is depicted by partial refilling of the bleached circle after a delay time Δt in Fig. 2B. The effect is observable in an experiment that monitors the modulations in the probe laser IR band intensities (and hence site populations) by the action of the bleach, which would yield diminution of the red and brown bands in the OH stretching region. The case where all sites interconvert at high temperature is diagrammed in Fig. 2C. The initially depleted red site is repopulated by site exchange with all other four sites, yielding strong initial depletion of the red band followed by nearly complete recovery. All other bands are reduced to a lesser extent over time. In this case, the IR spectrum for the ensemble would appear the same as that before the depletion laser, but with all bands attenuated by the fraction of total red site population removed at t = 0.

Fig. 2.

Scheme describing the onset of spectral diffusion by site exchange in a temperature-controlled cluster using selective photodissociation. The populations in the five spectroscopically distinct sites, color-coded to match those identified in Fig. 1 A and G, are indicated by the fractional filling of the circles. The panels correspond to three temperature regimes: (A) a low-temperature, static ensemble in which the red isotopomer is removed at t = 0, and subsequent interrogation of the ensemble after a delay time Δt reveals persistent removal of the red species from the ion packet; (B) an intermediate temperature where only two sites, red and brown, undergo interconversion on the timescale of the experiment. In this case, initial depletion of the red species, and hence its signature vibrational band, partially recovers after time Δt while the population of the brown isotopomer decreases to restore equilibrium with red; and (C) a sufficiently high temperature that all sites interconvert after initial depletion of red such that, after delay Δt, the red population is largely restored while those in the other four sites exhibit minor depletions upon returning to steady state.

The temperature-dependent measurements are carried out using a two-color, IR–IR photodissociation scheme. The experimental layout (SI Appendix, Fig. S5) and details of the experimental approach are included in SI Appendix. Because the PD cluster is relatively large, the unimolecular rates for laser-induced evaporation are on the order of several milliseconds. These rates dictate the time delay between bleach and probe such that the clusters excited by the bleach laser are efficiently removed from the ion packet before it is explored by the probe. In that case, when the scanning bleach laser excites any transition that modulates the population of the site interrogated by the probe, that change is registered as a depletion (or dip) in the probe signal. We note that because the evaporation rates and spectral dynamics are so slow, excitation by the bleach laser is carried out while the ions are held in the temperature-controlled, three-dimensional radiofrequency ion trap, which enables trapping for long periods without loss.

To apply the temperature-dependent IR–IR photobleaching method to the PD_OH clusters, it is important to first establish the temperature dependence of the linear IR spectrum, which is displayed in Fig. 1. At 10 K, the spectrum consists of a well-resolved grouping of five bands. These have been traced to the various classes of H-bonding arrangements color-coded with structural assignments in Fig. 1 (18). Interestingly, this five-band pattern persists up to 120 K before it recedes into a continuum envelope by 200 K, a temperature at which the clusters are unstable with respect to evaporation on the millisecond timescale of the mass spectrometer. For reference, the evaporation time (1/k_evap) is measured to be ∼17 ms at 200 K as described in detail in SI Appendix, Fig. S6. We note that the observed evolution of the spectra with temperature is consistent with nano-calorimetric measurements reported earlier (24) on H₃O⁺·(H₂O)₂₀. In that case, an inflection in the caloric curve near 135 K was interpreted to signal the cluster analog of a melting transition, which occurs below the onset of evaporation at around 150 K (24–28). We note also that recent molecular dynamics simulations of H₃O⁺·(H₂O)₂₀ by Korchagina et al. (29) indicate that the melting transition occurs over the 130 to 149 K range and that, although the PD structure dominates up to the melting region, cage structures containing four-membered rings begin to appear at 130 K. This is consistent with our temperature-dependent spectra, which display significant broadening of the bands as they are overcome by a diffuse background absorption between 120 and 150 K (Fig. 1 D and E). Additionally, a shoulder appears about 18 cm⁻¹ above the ${\text{OH}}_{\text{AAD}}^{free}$ feature at 150 K, which signals the presence of AD water molecules and the disruption of the PD cage motif (30). Meanwhile, the persistence of the telltale bands presented by the PD structure at 120 K establishes the integrity of this arrangement even when the clusters have substantial internal energy. For example, an estimate of the heat capacity at 120 K at the harmonic level (SI Appendix, Fig. S10) indicates that the average internal energy is ∼2,400 cm⁻¹, which corresponds to about two-thirds of the energy required to dissociate a water molecule from the cluster (3,742 cm⁻¹) (31, 32). We note that there is a rather broad expected distribution of energies (ΔE ∼ 1,200 cm⁻¹) in an ensemble of ions held at constant T = 120 K. It is likely that this temperature is maintained by collisions with the residual He buffer gas in the trap (33, 34), which we estimate to be on the order of 10⁻⁴ torr at 120 K.

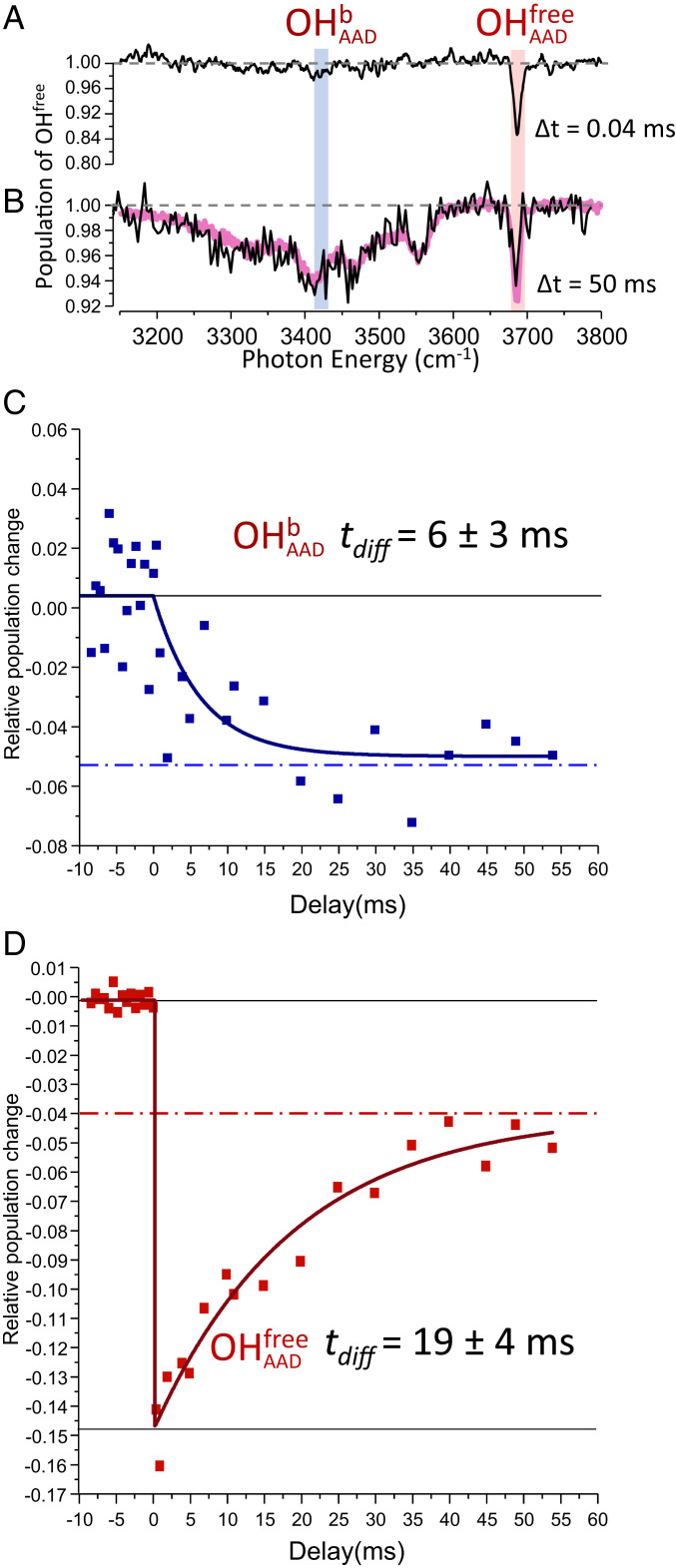
The Top panel in Fig. 3 presents the time dependence of the two color, IR–IR spectra of the PD_OH cluster at 120 K. The upper trace (Fig. 3A) displays the changes in the ${\text{OH}}_{\text{AAD}}^{free}$ site population, obtained by monitoring the probe laser fragment 40 μs after the bleach laser removes populations that have resonances at various energies along the course of the scan. The only dip feature occurs when the bleach laser excites the red (${\text{OH}}_{\text{AAD}}^{free}$) transition, which is the behavior expected for a static, heterogeneous ensemble. Under exactly the same conditions of excitation, however, the response of the probe laser fragment yield is dramatically different after a bleach to probe delay of 50 ms, with the result displayed in Fig. 3B. Indeed, depletion of red population is now obtained upon excitation of all five OH sites, with the result that the dip trace appears essentially the same as the linear spectrum of the entire ion isotopologue (purple lines through the points from the IR–IR scan in Fig. 3B, reproduced from Fig. 1E). This behavior is conclusive evidence that the spectrum associated with a single site at t = 0 evolves over time to encompass the contributions of all sites, which in turn establishes that the OH group migrates among all five locations. It is important to emphasize that this occurs while the overall spectrum retains the telltale bands of the PD cage. This implies that the migration is a rare event in the sense that the OH isotopic label almost always occupies a well-defined position in the cage. This general behavior was reported earlier in our initial study of temperature-dependent hole burning spectra of the much simpler I⁻⋅(H₂O)₂ system (21).

Fig. 3.

Time dependence of the PD_OH IR spectrum following photodepletion of the isotopomer with the isotopically labeled OH group in the nonbonded (red) site $\left(\mathbf{O}{\mathbf{H}}_{\mathbf{A}\mathbf{A}\mathbf{D}}^{\mathit{free}}\right)$ at T = 120 K. Double resonance spectra were obtained at bleach-probe delay times of (A) 0.04 ms and (B) 50 ms. The purple trace in B closely reproduces the single laser spectrum of the entire isotopologue (all sites occupied) from Fig. 1E. The time evolutions of the ${\text{OH}}_{\text{AAD}}^{free}$ population modulation by the bleach laser at two frequencies (${\text{OH}}_{\text{AAD}}^{\text{b}}$ and ${\text{OH}}_{\text{AAD}}^{free}$ in A) are presented in C and D, respectively. The time constants t_diff were extracted from exponential fits to the observed data. Negative delay times in C and D correspond to experiments with the bleach laser off.

The two Lower panels in Fig. 3 C and D present the time evolution of the depleted populations at two sites, one corresponding to the free OH (labeled ${\text{OH}}_{\text{AAD}}^{free}$), probed at 3,686 cm⁻¹, red, Fig. 3D) and the other associated with OH occupation at the bound AAD site (labeled ${\text{OH}}_{\text{AAD}}^{\text{b}}$, and probed at 3,407 cm⁻¹, blue, Fig. 3C). The different responses of these traces conform to the scenario outlined in Fig. 2. Specifically, the large depletion initially present in the population of the red ${\text{OH}}_{\text{AAD}}^{free}$ site (Fig. 3D) is gradually restored with a characteristic time constant of 19 ms, whereas a much smaller depletion in the population of site ${\text{OH}}_{\text{AAD}}^{\text{b}}$ occurs over similar time range (Fig. 3C) as these OH groups migrate to the free OH site. Note that, although we have focused on only two positions in this discussion, at T = 120 K all sites are interchanging with the red site, as evidenced by the extensive dip pattern in Fig. 3B. As such, the final fractional depletion in ${\text{OH}}_{\text{AAD}}^{free}$ (5%) is much smaller than the initial depletion (15%) since the other four sites contribute to compensate for the loss due to the bleach of the initial free OH site population.

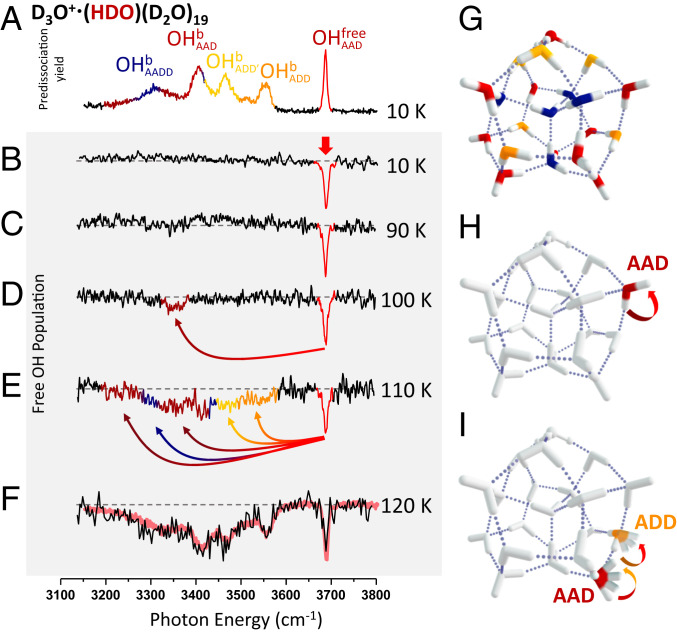
The spectral evolution at 120 K is well described in the scheme where slow migration of the OH groups reequilibrates the populations in the ion packet on the 50-ms timescale. This raises the question, however, of whether the pathways that are available for this migration depend on the temperature of the ensemble. This might be anticipated, for example, if the free energy barriers are different for the rearrangements necessary for the OH to migrate between the various sites. We therefore determined the temperature dependence of the IR–IR dip spectra. A summary of the results is presented in Fig. 4. At 90 K, the spectrum is dominated by a strong dip at the probe frequency, but by 100 K, there is a clear appearance of a weak, isolated second depletion feature near 3,350 cm⁻¹, about 300 cm⁻¹ from the red band. Interestingly, the heat capacity curve observed with nanocalorimetry on the same cluster has a minor inflection point around 90 K (24). This is consistent with the increase in phase space volume allowed by the onset of H-bond switching between the free OH and the bound OH on the same AAD water molecule that is implied here. Upon increasing the temperature to 110 K, it is clear that many more sites are exchanging with the probed red site, as the dip pattern (Fig. 4E) includes many of the most red-shifted OH groups. This behavior is significant because it emphasizes that the frequency of an OH oscillator does not gradually broaden with time about the original location, but instead abruptly changes to another, distant frequency. The experimental results, discussed above, are consistent with a low barrier isomerization process initiated at T ∼100 K, and higher barrier processes being engaged above T = 120 K. We examine the barriers for rotation of a HOD molecule in the various sites of a HDO(D₂O)₂₀ cluster composed of a hydrogen-bonding network mimicking that of the H₃O⁺·(H₂O)₂₀ cluster (35). We focus on the neutral rather than the protonated cluster because of the availability of highly accurate force fields for the former. The lowest barrier pathway for rotation of a water molecule involves an AAD water donating an H bond to an adjacent AAD molecule. The lowest barrier associated with the AAD–AAD pair is consistent with its classification as a “weak” hydrogen bond on the surface of polyhedral water clusters (36). As shown in SI Appendix, Fig. S14, this isomerization process is highly cooperative, involving the motion of several water molecules in the cluster. In addition, it proceeds through a stable intermediate with two four-membered and one three-membered ring, and a five-coordinated water molecule. The calculated vibrational frequencies of the HOD molecule in this site are in close agreement with those for the water molecule involved in the isomerization process that turns on at T = 100 K in the D₃O⁺·(HDO)(D₂O)₁₉ cluster. Note that the bound OH stretching band associated with AAD water molecules that donate to another AAD molecule were observed to be ∼3,350 cm⁻¹ in a previous study (17), which is indeed close to observed exchange feature that appears at 100 K (Fig. 4D). The barriers for rotating the other water molecules are >1.3 kcal/mol (450 cm⁻¹) higher in energy than the one for the low-energy pathway described above, a fact that is consistent with the more extensive isomerization observed experimentally at temperatures above 120 K as well as the ∼1.8 kcal/mol (∼630 cm⁻¹) difference in activation energy obtained experimentally (SI Appendix, Fig. S11).

Fig. 4.

Temperature-dependent evolution of the photobleaching spectra corresponding to a bleach-probe delay of 50 ms and fixing the probe laser to monitor population of the isotopomer with the isotopically labeled OH group in the nonbonded (red) site $\left({\mathbf{OH}}_{\mathbf{A}\mathbf{A}\mathbf{D}}^{\mathit{f}\mathit{r}\mathit{e}\mathit{e}}\right)$. (A) Vibrational spectrum of all isotopomers at 10 K and (B–F) hole burning spectra at 10 to 120 K. The red trace in F reproduces the single laser spectrum of the entire isotopologue (all sites occupied) from Fig. 1E. The vertical red arrow in B indicates the probe laser frequency, whereas the curved arrows in D and E indicate that the appearance of additional dips arise from OH migration from the ${\text{OH}}_{\text{AAD}}^{free}$ site to various other sites when their populations are depleted by the bleach laser, (G) a representative low-energy PD structure, (H) a possible pathway for OH migration at 100 K, and (I) schematic illustration of more complex pathways that likely operate at higher temperatures, where the ribbon arrows indicate the directions of OH group rotations.

Qualitatively, this large jump in frequencies at the onset of large-amplitude motion is reminiscent of models in which spectral diffusion reflects infrequent large-amplitude structural rearrangements rather than diffusive fluctuation about an initial configuration (6). We also emphasize that the 120 K dip spectrum, displayed in Fig. 4F, is effectively an inverted presentation of the linear spectrum of the entire ensemble at this temperature. The arrows in Fig. 4 indicate the direction of population transfer responsible for the diminution of absorption at the probe (red) frequency. In this way, we reveal the hierarchy of site-to-site interconversions that are accessible with increasing temperature. A particularly interesting feature in this regard involves the band associated with water molecules that are directly attached to the hydronium ion core (labeled as ADD′), which begin to undergo exchange with the free OH site at 110 K. This is significant because transfer of these OH sites to those associated with more remote locations in the cage requires migration of the hydronium ion. As such, we conclude that 110 K also marks the onset of charge translocation across the cluster surface.

In summary, we have measured the time- and temperature-dependent frequency of a single OH oscillator embedded in the surface of the water cage structure adopted by 20 water molecules upon accommodation of the hydronium ion. Although the telltale vibrational signature of the cluster remains intact up to 120 K, the frequency of the OH group is observed to change over time, revealing migration between spectroscopically distinct sites. The timescale of this motion is on the order of tens of milliseconds, indicating that the rearrangements occur as rare events. The onset for dynamics is ∼100 K, at which point the frequency changes between two local features separated by about 300 cm⁻¹. All sites are interchanged on this timescale by 120 K, a significantly lower temperature than that at which the well-defined cluster structure is lost. This ability to monitor kinetic processes that sustain dynamic equilibrium in increasingly complex clusters brings us closer to applications where thermally activated chemical transformations can be unraveled in the context of both solvent and solute contributions at the molecular level.

Methods

The experimental methods are described in detail in SI Appendix, Section I. Briefly, the D₃O⁺·(HDO)_m(D₂O)_n clusters were generated by electrospraying acidic HDO/D₂O solution and passing the product ions through several stages of differential pumping and into a temperature-controlled Paul trap. The absorption spectra of the water clusters so generated were obtained using a photofragmentation mass spectrometer as described previously (22). For isotopomer selective spectroscopy, the D₃O⁺·(HDO)(D₂O)₁₉ clusters were first mass isolated with secular frequency excitation and then irradiated with a tunable IR laser (denoted the “bleach”) in the temperature-controlled Paul trap. After an adjustable waiting time, the ion packet is extracted from the Paul trap and passed into the Time-of-Flight photofragmentation mass spectrometer, where a second laser (denoted the “probe”) is intersected with the mass-selected ion packet to monitor the population in a specific isotopomer.

Data Availability.

The authors declare that all data supporting the findings of this study are available within the paper and SI Appendix.