Signatures of a liquid–liquid transition in an ab initio deep neural network model for water

Significance

Water is central across much of the physical and biological sciences and exhibits physical properties that are qualitatively distinct from those of most other liquids. Understanding the microscopic basis of water’s peculiar properties remains an active area of research. One intriguing hypothesis is that liquid water can separate into metastable high- and low-density liquid phases at low temperatures and high pressures, and the existence of this liquid–liquid transition could explain many of water’s anomalous properties. We used state-of-the-art approaches in computational quantum chemistry, statistical mechanics, and machine learning and obtained evidence consistent with a liquid–liquid transition, supporting the argument for the existence of this phenomenon in real water.

Abstract

The possible existence of a metastable liquid–liquid transition (LLT) and a corresponding liquid–liquid critical point (LLCP) in supercooled liquid water remains a topic of much debate. An LLT has been rigorously proved in three empirically parametrized molecular models of water, and evidence consistent with an LLT has been reported for several other such models. In contrast, experimental proof of this phenomenon has been elusive due to rapid ice nucleation under deeply supercooled conditions. In this work, we combined density functional theory (DFT), machine learning, and molecular simulations to shed additional light on the possible existence of an LLT in water. We trained a deep neural network (DNN) model to represent the ab initio potential energy surface of water from DFT calculations using the Strongly Constrained and Appropriately Normed (SCAN) functional. We then used advanced sampling simulations in the multithermal–multibaric ensemble to efficiently explore the thermophysical properties of the DNN model. The simulation results are consistent with the existence of an LLCP, although they do not constitute a rigorous proof thereof. We fit the simulation data to a two-state equation of state to provide an estimate of the LLCP’s location. These combined results—obtained from a purely first-principles approach with no empirical parameters—are strongly suggestive of the existence of an LLT, bolstering the hypothesis that water can separate into two distinct liquid forms.

Water is ubiquitous in both the physical sciences and everyday life; as such, there is a very large body of literature characterizing its physical properties (1). This research has revealed that water exhibits a striking set of anomalies relative to most other liquids (2), including the fact that the liquid freezes into a less-dense solid phase at ambient and moderate pressures; liquid water’s observed density maximum; and the sharp increases in compressibility, heat capacity, and the magnitude of the thermal expansion coefficient of liquid water upon cooling (2–4). Several competing theories exist that provide thermodynamically consistent descriptions of these anomalies (2, 4), including the liquid–liquid transition (LLT) hypothesis (5), the stability-limit conjecture (6), and the singularity-free scenario (7). Much of the behavior discussed in these theories occurs under supercooled conditions (i.e., below the melting temperature of ice); experimental data in this region are challenging to obtain due to rapid crystallization (4, 8), which renders the liquid state short lived (9). Because of these challenges, the available experimental work has been fruitfully augmented by a large number of computational and theoretical studies aimed at illuminating the key phenomena and weighing the relative merits of these scenarios (2, 4, 8, 10–12). For example, recent simulation work illustrated that the stability-limit conjecture likely is not compatible with the shape of the thermodynamic extrema exhibited by the popular TIP4P/2005 water model (13) but that the LLT and singularity-free scenarios could still be potential candidates (14).

According to the LLT hypothesis (5, 10), under strongly supercooled conditions and high pressures, water undergoes a first-order phase separation into high-density liquid (HDL) and low-density liquid (LDL) states, which are metastable with respect to crystalline ice. In the pressure–temperature plane, this line of liquid–liquid coexistence terminates in a metastable liquid–liquid critical point (LLCP). Emanating from the LLCP toward higher temperatures and lower pressures is the so-called Widom line (11, 15), which is a locus of maximum correlation length in the fluid; maxima in other properties such as isothermal compressibility and constant-pressure heat capacity converge with the Widom line near the LLCP. There is some recent experimental evidence for a maximum in the isothermal compressibility upon cooling liquid water at ambient pressure (16). This result has elicited debate (17, 18), and analogous experiments at higher pressure have not been done to date.

In simulations, small system sizes serve to suppress homogenous nucleation of ice, and the timescales for nucleation and structural relaxation tend to be well separated in molecular models of water. These factors enable computational study of liquid water in the strongly supercooled regime across the full range of relevant temperatures and pressures. Rigorous evidence for the LLT has been obtained for three classical molecular models for water with simple pairwise interaction potentials: ST2 (19–24), TIP4P/2005 (13), and TIP4P/Ice (25, 26). There are also numerous studies presenting evidence consistent with an LLT but without a rigorous demonstration thereof (10, 27–29). However, it should be borne in mind that empirically parameterized models do not provide definitive proof of the presence or absence of an LLT in real water (10). In fact, other popular water models, such as the coarse-grained mW model (30, 31) and SPC/E (32–34), do not exhibit clear evidence of an LLT. There are also several more sophisticated models of water that explicitly represent many-body and/or polarizability effects and have been used to probe the supercooled liquid state, such as E3B3 (11, 27, 35), WAIL (28, 36), iAMOEBA (37, 38), RexPoN (39–41), MB-pol (42), and others (43). Some of these models are parameterized in order to reproduce experimental data (35), while others are fit to theoretical calculations (36, 41–43). Mixed approaches are also possible as is the case of the iAMOEBA model (38). These advanced models and methods have revealed significant insights about the structure and properties of liquid water (39, 40, 42) and in some cases, have even been suggestive of the existence of an LLT (10, 27, 28). However, in general these models are too computationally expensive to rigorously identify the LLT with current computational resources, especially in light of sluggish structural relaxation in the vicinity of the critical point.

Ab initio methods could also present an opportunity to evaluate many-body effects in supercooled liquid water. For instance, one could use ab initio molecular dynamics (AIMD), in which the forces that drive the simulation are obtained on the fly from electronic structure calculations (44). These types of simulations do not rely on empirically derived parameters or training data and thus, could provide truly predictive first-principles evidence of an LLT. Specifically in the case of water, the Strongly Constrained and Appropriately Normed (SCAN) (45) exchange correlation (XC) functional has been shown to be especially accurate among nonempirical XC functionals in predicting the properties of water (e.g., the increase in density upon melting ice 1-h) due to its accurate description of the balance of covalent, intermediate-range van der Waals and hydrogen bonding interactions (46). Thus, searching for evidence of an LLT in a SCAN-based description of water is appealing but hitherto impossible due to the timescales currently accessible with traditional AIMD (a few hundred picoseconds at most).

Augmenting traditional molecular simulations with machine learning provides a potential avenue by which these challenges in the computational study of supercooled liquid water might be addressed (47). In one class of machine learning-based simulation approaches, a neural network is trained to represent the potential energy surface (PES) of a system obtained from ab initio calculations (48–53). The trained neural network model translates the local environment of an atom to ab initio-level atomic energies and forces at a fraction of the computational cost, which can then be used to drive a molecular dynamics (MD) simulation. This scheme allows for the evolution of systems according to the underlying many-body ab initio PES but at simulation speeds orders of magnitude faster than (for example) density functional theory (DFT)-based AIMD (44). In the present context, such an approach now enables first-principles computational study of water commensurate with the system sizes and timescales necessary for studies of phase behavior in the deeply supercooled regime.

In this work, we used the Deep Potential Generator (DP-GEN) active learning procedure (54) to generate a deep neural network (DNN) model of water. We prepared the training data with DFT calculations using the SCAN functional (45), which has recently shown promise in accurately predicting the thermophysical properties of water (46). Via isothermal–isobaric Deep Potential Molecular Dynamics (DPMD) simulations (51, 55), we confirmed that the DNN model qualitatively reproduces key trends in the structural, bulk, and dynamic properties of supercooled liquid water. We then used DPMD simulations in the multithermal–multibaric (MTMB) ensemble (56–58) to efficiently obtain the thermophysical properties (e.g., density, internal energy, isothermal compressibility, heat capacity) of this model over a wide range of temperatures and pressures. The simulation data were consistent with the existence of an LLCP. We then used a phenomenological two-state equation of state (TSEOS) model (59–63), which represents water as an interconvertible mixture of high- and low-density structures, to describe the MTMB simulation data. The TSEOS closely matched the data and provided an estimate for the LLCP location in this DNN model. Overall, these results are consistent with the existence of an LLT in water, providing ab initio evidence for this phenomenon for a model free of empirical parameterizations.

Results and Discussion

DPMD Simulations with DNN Model.

We generated our DNN model using the DP-GEN active learning approach; refs. 54 and 64 have details. We performed DFT calculations using the Vienna ab initio simulation package (65, 66) within the SCAN functional approximation (45) on a total of 19,006 structures identified by the DP-GEN procedure, which covers temperature and pressure ranges of 0 to 600 K and 0 to 50 GPa, respectively. We then used the DeePMD-kit package (67) to train our DNN model to reproduce the ab initio-level atomic energies and forces from this DFT dataset. SI Appendix contains all details of the model training and validation procedures (SI Appendix, Fig. S1), as well as a comparison of the structure, thermophysical properties, and dynamics of the trained DNN model with available experimental data for supercooled liquid water (SI Appendix, Fig. S2). We also computed the ambient pressure ice 1-h melting point with this DNN model, which was in the vicinity of T = 312.5 K (SI Appendix, Fig. S4). The qualitative temperature and pressure dependence of water’s properties was well captured by the DNN model, including the density maximum and increase in isothermal compressibility upon cooling and the increase in diffusivity in supercooled liquid water at increased pressure. We note that our classical simulations with the DNN model predicted key properties of water (e.g., liquid water structure, ambient pressure density maximum, ice 1-h melting point) at temperatures ∼47-K higher than the equivalent temperature in experiments, which we attribute to a combination of nuclear quantum effects (68) and limitations in accuracy of the underlying SCAN functional (52, 69) (we discuss this in detail in SI Appendix). Acknowledging these factors, our DNN model nevertheless reproduced, at an ab initio level, qualitative trends in the available experimental data for structural, bulk, and dynamic properties of supercooled liquid water. Given this correspondence, we now turn to examine whether this DNN model demonstrates evidence for an LLCP.

Due to the DNN model’s high computational expense relative to classical atomistic models (albeit still much faster than AIMD at the DFT level), comprehensively exploring the thermophysical properties of this model in the deeply supercooled regime is not feasible using standard (unconstrained) MD simulations. To resolve this issue, we used advanced sampling simulations in the MTMB ensemble (58), which enabled us to sample a wide range of temperatures and pressures with a single simulation. Briefly, MTMB simulations bias the potential (i.e., configurational) energy and volume of a simulation to achieve a desired probability distribution that spans the full range that would be sampled in multiple unbiased simulations at different temperatures and pressures of interest. Then, the results from the biased simulation are reweighted as described in ref. 58 to calculate desired observables in the unbiased probability distribution at a given (T, P). Herein, we used two MTMB simulations to sample the range 240 K ≤ T ≤ 330 K and 1 bar ≤ P ≤ 3,000 bar [SI Appendix, Fig. S5 has an illustration of how this range of (T, P) corresponds with the experimental water phase diagram]. We obtained the thermophysical properties of this DNN model at ∼4,700 state points [i.e., individual (T, P)] within this range from just two simulations, at a total computational cost comparable with only ∼100 individual isothermal–isobaric simulations (Materials and Methods and SI Appendix have details). Additionally, we thus avoided having to run many separate slow to equilibrate simulations at the sluggish low-temperature state points of interest.

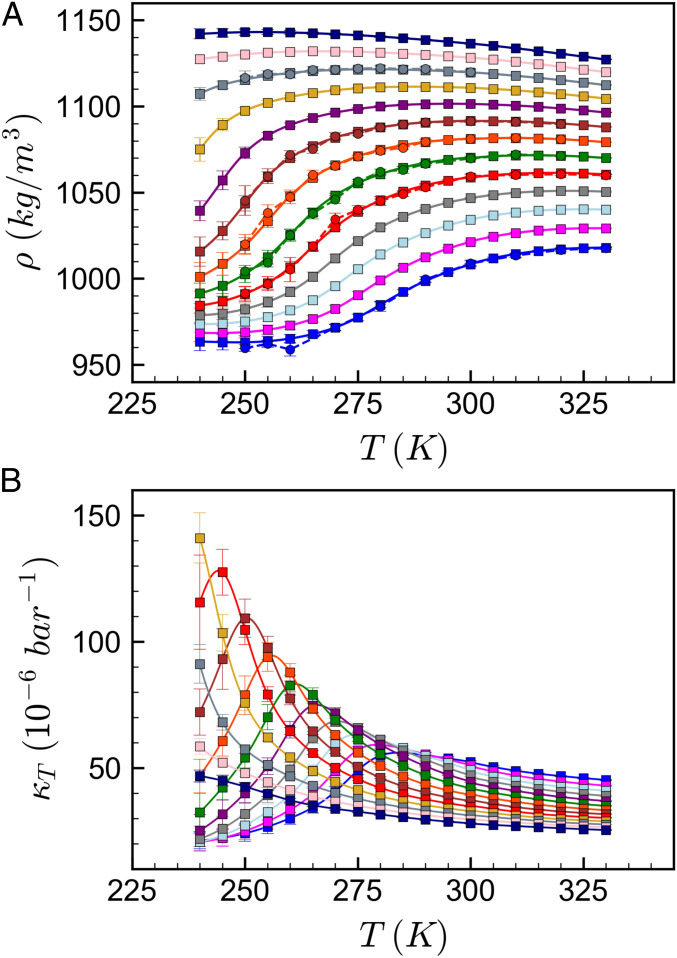
In Fig. 1A, we plot bulk mass density (ρ) along isobars obtained from MTMB simulations (squares and solid lines) and standard isothermal–isobaric (NPT) simulations (circles). The MTMB and NPT simulations agreed closely over the full range of T and P studied, and the uncertainty from the MTMB simulations (95% CIs obtained from a bootstrap analysis) (Materials and Methods) was significantly smaller than from NPT simulations. The isobars showed a strongly positive slope at low temperatures and intermediate pressures, reminiscent of the (ρ, T, P) behavior of other water models definitively shown to exhibit an LLCP [e.g., ST2 (59), TIP4P/2005 (60)]. Fig. 1B shows the isothermal compressibility (${\kappa }_T$), calculated via numerical evaluation of ${\kappa }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_T$ from the MTMB results. The ${\kappa }_T$ along isobars exhibited a maximum upon cooling, and the height of this maximum increased sharply with increasing pressure while shifting toward progressively lower temperatures, strongly suggestive of the existence of a Widom line terminating in an LLCP. In order to estimate the location of the LLCP predicted via this DNN model (if it exists), we fit the simulation data to a TSEOS.

Fig. 1.

MTMB and NPT simulation results along isobars. (A) Mass density, ρ, and (B) isothermal compressibility, ${\kappa }_T$, from NPT (circles and dashed lines) and MTMB (squares and solid lines) simulations using the DNN model. In both plots, the blue isobar is P = 1 bar, and the magenta to dark blue isobars range from P = 250 bar to P = 3,000 bar in steps of 250 bar. Note that the solid lines are MTMB results reweighted across the entire temperature range; squares are only included every 5 K for visual clarity.

Estimated LLCP Location and Thermodynamic Anomalies.

In order to explore the compatibility of the DNN simulation results with the existence of an LLCP, we fit the simulation data with a phenomenological TSEOS model (60). The TSEOS represents water as a binary mixture of interconvertible (high-entropy, high-density and low-entropy, low-density) local configurations and constructs the Gibbs free energy of the system as a function of (T, P) and the equilibrium low-density fraction (x_e) at any given state point. Then, relevant thermodynamic quantities, such as density, internal energy, heat capacity, isothermal compressibility, etc., can be calculated via the appropriate partial derivatives of the free energy. The TSEOS approach has been successfully shown to reproduce the thermodynamics of many popular models of water [including mW (70), ST2 (59), TIP4P/2005 (60, 61)] and also successfully describes a large set of available experimental data for liquid water (62, 63). Other versions of the two-state approach also successfully capture the anomalies of water and other tetrahedral liquids (71–73). Fig. 2 shows the predictions of our TSEOS model for the density and internal energy (configurational + kinetic energy), compared with the MTMB simulations. The correspondence between the simulation results and TSEOS predictions was excellent over the majority of the state points, with appreciable deviations only at the limits of the (T, P) range of interest. The liquid–liquid critical parameters obtained from the TSEOS were T_c = 224 ± 3 K, P_c = 2,687 ± 68 bar, and ρ_c = 1,072 ± 16 kg/m³. Uncertainties in the critical parameters were obtained by independently fitting the TSEOS to 200 block-bootstrap samples generated from the MTMB data, as described in Materials and Methods. Interestingly, the TSEOS fit to this DNN model predicts a relatively mild difference in the densities at coexistence between the LDL and HDL phases. For example, in this work ρ_HDL = 1,102 kg/m³ and ρ_LDL = 1,047 kg/m³ at a reduced temperature T/T_c = 0.965, whereas for the classical ST2 model, ρ_HDL = 1,150 kg/m³ and ρ_LDL = 900 kg/m³ at the same reduced temperature (19). This relatively subtle difference between the densities of the LDL and HDL states, combined with the small free energy barrier between them (19), may contribute to the difficulty in rigorously establishing the LLT in both simulations and experiments.

Fig. 2.

Fits of the TSEOS to the MTMB simulation data. (A) Mass density, ρ, and (B) internal energy, E, from MTMB simulations (squares) and TSEOS predictions (thick solid lines). In A, colors denote different isobars, with blue representing P = 1 bar and the magenta to dark blue isobars ranging from P = 250 bar to P = 3,000 bar in steps of 250 bar. In B, colors denote different isotherms, ranging from T = 240 K (lavender) to T = 330 K (dark blue) in steps of 5 K. The liquid–liquid binodal and LLCP location from the TSEOS are denoted by the thick black line and red circle, respectively.

Recalling SI Appendix, Fig. S2, in which we applied a −47 K temperature shift to the simulation data to achieve correspondence between the DNN and experimental results, the T_c near 224 K in this DNN model might correspond to an experimental temperature near 177 K, which is in the range of T_c values recently obtained for the popular and realistic classical TIP4P/2005 and TIP4P/Ice models (25). However, as seen in some other studies with advanced water models, the less sharp increase in compressibility at 1 bar compared with the experimental results (SI Appendix, Fig. S2C) suggests that the P_c predicted by this DNN model is somewhat higher than might be expected in experiments (11). We also note recent work that suggests an LLCP in AIMD simulations of water with the SCAN functional at small negative pressures (74); that work reported a van der Waals loop in a series of isothermal-isochoric simulations at only six state points and for a system much smaller than those considered here. Furthermore, their simulation timescales are two to four orders of magnitude smaller than those used in this work, which is likely not enough to reliably equilibrate the system in the deeply supercooled regime. Therefore, we consider our estimate for the location of the LLCP in this model to be within the range of estimates obtained from other models and approaches (10).

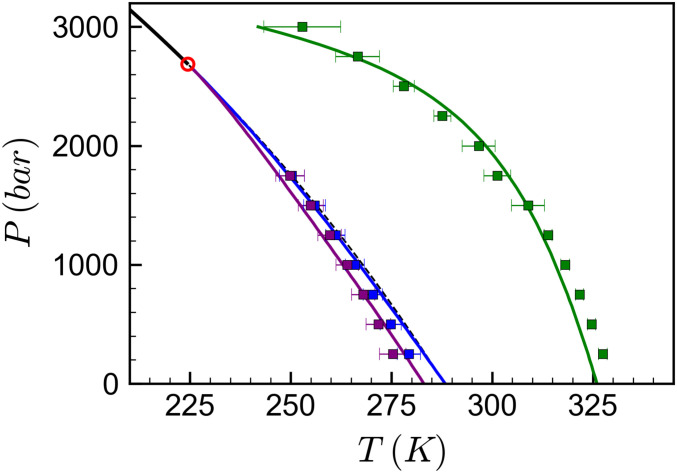
Fig. 3 shows water’s thermodynamic anomalies in the pressure–temperature plane from the MTMB simulations and the TSEOS. The TSEOS provides a good representation of the loci of maximum density, isothermal compressibility, and constant-pressure heat capacity calculated from our simulations with the DNN model. These data exhibit the expected trends, with the loci of maximum heat capacity and compressibility converging along the Widom line near the LLCP, as observed in other classical models for water (60, 61). The LLT transition line extends from the critical point to lower temperatures and higher pressures with slope and curvature given by the equality of Gibbs energy between the high- and low-density states (Materials and Methods). Overall, these results suggest that the thermophysical properties of this SCAN-based DNN model for water can be well described by the two-state picture. While as discussed in detail in previous TSEOS work (60), this analysis does not constitute definitive proof of an LLT or LLCP in the SCAN PES, the close agreement between simulation and TSEOS results and the qualitative shape of the density and compressibility isobars together provide strong evidence consistent with the existence of an LLCP. Furthermore, recent simulation and experimental scattering data provide evidence in support of the two-structure view of liquid water (75).

Fig. 3.

Thermodynamic anomalies from MTMB simulations and the TSEOS. The liquid–liquid coexistence line, the LLCP, and the Widom line predicted by the TSEOS (Materials and Methods) are plotted with the thick black line, red circle, and thin dashed black line, respectively. Green, blue, and purple symbols and lines denote the loci of maximum density, isothermal compressibility, and constant-pressure heat capacity, respectively, with squares representing MTMB simulation results and lines representing TSEOS predictions. Note that the ambient pressure ice 1-h melting temperature for this model is near T = 312.5 K (SI Appendix, Fig. S4).

Conclusions

We have combined state-of-the-art approaches in first-principles quantum chemistry, molecular simulation, statistical mechanics, and machine learning to explore the possibility of an LLT in the SCAN ab initio PES of water. We developed a DNN potential free of empirical parameters that captures the key features of experimental supercooled liquid water, at a computational cost orders of magnitude smaller than other comparable advanced models. We then connected this DNN model with MTMB sampling techniques to further extend the regimes of timescales and length scales accessible. Using this platform, we probed the properties of the SCAN description of water over a wide swath of the supercooled liquid water phase diagram. Our simulation results for density and compressibility along isobars were strongly suggestive of an LLCP, and we fit the simulation data to a TSEOS model. The trends in density and internal energy were compatible with the two-state picture, and the estimates for the critical parameters were within the ranges of other recent computational studies. Overall, the results reported herein strengthen the interpretation of supercooled liquid water as possessing two metastable liquid forms, providing first-principles evidence for this phenomenon free from empirical extrapolation.

In the future, we envision exploring in more detail the low-temperature phase behavior of this DNN model, including extending the lines of maximum density and ice 1-h melting point to negative pressures, as well as probing the effects of the choice of XC functional and the treatment of quantum fluctuations on water’s LLT. We note recent work that compared classical and path-integral simulations with a similar SCAN-based neural network model of water and found that the limitations of the SCAN XC functional may be the key contributor to discrepancies between simulation and experiment (69). It would be instructive to perform similar tests on the effect of nuclear quantum effects on the signatures of the LLT shown herein, perhaps by taking inspiration from prior work in which rigid models were used to estimate the effect of nuclear quantum effects with a more modest computational expense (76). One could also consider generating even more accurate DNN models from accurate but expensive quantum chemistry methods. Lastly, we envision using free energy techniques at state points predicted by the TSEOS in order to definitely establish liquid–liquid coexistence from first principles, further pushing the boundaries of problems accessible through this approach.

Materials and Methods

Simulation Methods.

We performed MD simulations with our SCAN-based DNN water model using the DPMD-augmented LAMMPS (77) software package [DeepMD-kit (64, 67) version 1.0 and LAMMPS version 9 Aug 2019]. We performed NPT simulations with 512 water molecules over a temperature range 250 K ≤ T ≤ 330 K and a pressure range 1 bar ≤ P ≤ 2,500 bar. We maintained temperature and pressure using the LAMMPS Nosé–Hoover-type thermostat and barostat, with relaxation times 50 and 500 fs, respectively. We equilibrated all NPT simulations at least two times longer than the structural relaxation time determined by the decay of the peak value of the self-intermediate scattering function F(k*,t) to a value of 1/e; most simulations were equilibrated 10 to 500 times longer than that. We computed thermodynamic averages over a sampling period of 4 to 32 ns depending on the state point. Because configurational properties obtained from classical simulations do not depend on the mass of the atoms, we used a hydrogen mass of 2 atomic mass units in the time integration to enable a time step size of 0.5 fs but used water’s average molar mass of 18.015 g/mol for analysis. In the NPT simulations, we calculated the isothermal compressibility via ${\kappa }_T=\left(⟨V^2⟩-{⟨V⟩}^2\right)/k_{B}T⟨V⟩$. Error bars in all quantities reported from the unconstrained simulations represent 95% CIs obtained from 10-block averages.

We performed the MTMB simulations (58) by patching the DPMD-LAMMPS implementation with the PLUMED software (78) using the Variationally Enhanced Sampling (VES) module (79). The MTMB approach is built upon the VES framework (80), in which a bias potential is added to the PES to achieve a desired marginal probability distribution of a chosen set of collective variables. In MTMB simulations, the potential energy (i.e., configurational energy) and volume are biased in order to sample a range of temperatures and pressures with a single simulation. In an initial stage, one first optimizes the functional form of the bias potential to achieve the MTMB probability distribution in potential energy and volume, and then in a sampling stage, one samples the MTMB distribution with a stationary (or nearly stationary) bias potential. Then, one can reweight the biased results to obtain a given observable $O\left(\mathit{R},V\right)$ that depends on the atomic coordinates R and the system volume V at a desired temperature (T′) and pressure (P′) via the following formula:

$$O{\left(\mathit{R},V\right)}_{T^{\text{'}},P^{\text{'}}}=\frac{{\langle O\left(\mathit{R},V\right)w\left(\mathit{R},V\right)\rangle }_{T,P,V}}{{\langle w\left(\mathit{R},V\right)\rangle }_{T,P,V}},$$ [1]

in which T and P are the nominal temperature and pressure of the MTMB simulation, respectively, and $w\left(\mathit{R},V\right)$ is a properly chosen weight for that configuration (SI Appendix). We refer the reader to ref. 58 for a full discussion of the MTMB method.

We performed two independent MTMB simulations with 192 water molecules to calculate the properties of the DNN model. We selected this smaller system size due to the large computational expense of the DNN simulations. In both MTMB simulations, we targeted the PLUMED TD_MULTITHERMAL_MULTIBARIC probability distribution in both energy and volume to a free energy threshold of 1 k_BT with a 10th-order Legendre polynomial bias potential in each dimension. We ran the first simulation at a nominal temperature and pressure of T = 270 K and P = 1,250 bar, respectively, and a second at T = 290 K and P = 1,250 bar, respectively. In the first simulation, the polynomials were defined in the potential energy range −1,567.71 kJ/mol ≤ U ≤ −1,557.29 kJ/mol and volume range 4.875 nm³ ≤ V ≤ 6.375 nm³, and in the second simulation, the ranges were −1,567.71 kJ/mol ≤ U ≤ −1,552.08 kJ/mol and 4.875 nm³ ≤ V ≤ 6.375 nm³ to cover the desired set of temperatures and pressures. We used the reweighted results of the first simulation to calculate all properties T ≤ 300 K and the second simulation to calculate properties in the temperature range 300 K < T ≤ 330 K, and both simulations spanned the pressure range 1 bar ≤ P ≤ 3,000 bar. For each MTMB simulation, we optimized the bias potential coefficients for ∼40 ns, followed by 150 ns of sampling with frozen coefficients for simulation 1 and 100 ns of sampling for simulation 2, with data saved every 0.25 ps. We used four independent walkers for each simulation to improve the efficiency of the sampling and the convergence of the bias potential. SI Appendix, Figs. S6 and S7 show the evolution of the MTMB bias potential coefficients, the form of the bias potential and statistical weights $w\left(\mathit{R},V\right)$ used in this work, and the potential energy-volume values visited by the MTMB and NPT simulations. Error bars for plots related to the MTMB simulations are 95% CIs obtained from sampling 200 block-bootstrap samples resampled from 40 blocks generated from the MTMB results.

In the lower-temperature simulation (T = 270 K), we observed that the system periodically entered a “sluggish” or “glassy” state, in which the molecules did not translate and the energy and volume of the system did not traverse the desired range (SI Appendix, Figs. S8–S10). Given that these configurations were highly correlated due to the lack of molecular motion, we excluded them from our MTMB reweighting. SI Appendix, Fig. S8 shows a quantification of the average molecular motion throughout the simulations, and SI Appendix, Figs. S9 and S10 show an illustration of how the sluggish state affected the energy and volume results. However, whether we included or excluded these points in the MTMB reweighting did not significantly affect our obtained results; including the sluggish state resulted in critical parameters less than 5% different from those reported herein (i.e., with the sluggish points excluded). We note that this sluggish state was not observed in the NPT simulations, so we conjecture it is a consequence of the large temperature range sampled via the MTMB algorithm.

Two-State Equation of State.

Following recent work, which used a TSEOS to describe the properties of the TIP4P/2005 (60, 61) and ST2 (59) models of water, we represent the molar Gibbs free energy of the system at a given state point by assuming that water is a mixture of two interconvertible states—high-density form A and low-density form B—with the fraction of molecules assuming local state B given by x:

$$G(T,P)=G^A+x{G}^{BA}+G^{mix}.$$ [2]

In Eq. 2, G^A is the Gibbs energy of pure structure A at a given (T, P), represented as a polynomial expansion of temperature and pressure:

$$G^A\left(T,P\right)=R{T}_c{\displaystyle \sum }_{m,n}{c}_{mn}\mathrm{\Delta }{\widehat{T}}^m\mathrm{\Delta }{\widehat{P}}^n.$$ [3]

In Eq. 3 and the following expressions, the temperature and pressure are nondimensionalized relative to the critical temperature T_c and critical pressure P_c by $\mathrm{\Delta }\widehat{T}=\frac{T-T_c}{T_c}$ and $\mathrm{\Delta }\widehat{P}=\frac{P-P_c}{P_c}$. G^BA is the difference in free energy between structure B and structure A, and we represent it with a simple nonlinear form:

$$G^{BA}\left(T,P\right)=RT\lambda \left(\mathrm{\Delta }\widehat{T}+a\mathrm{\Delta }\widehat{P}+b\mathrm{\Delta }\widehat{T}\mathrm{\Delta }\widehat{P}\right).$$ [4]

In the expression for G^BA, λ represents the entropy difference between states A and B. The set of temperatures and pressures that yield G^BA = 0 defines the LLT (for T < T_c) and Widom (for T > T_c) lines, in which a sets the slope of the LLT/Widom lines at the LLCP and b determines their curvature. The free energy of mixing between state A and state B is represented via a sum of ideal and nonideal terms:

$$G^{mix}\left(T,P\right)=RT\left[x\ln x+\left(1-x\right)\ln \left(1-x\right)+\frac{2+w_0\mathrm{\Delta }\widehat{P}}{T/T_c}x\left(1-x\right)\right].$$ [5]

The temperature and pressure dependence of the term $\frac{2+w_0\mathrm{\Delta }\widehat{P}}{T/T_c}$ is chosen to reproduce a “regular solution”-type nonideal enthalpy of mixing, which was previously shown to successfully capture the two-state thermodynamics of the ST2 and TIP4P/2005 models (59, 60).

In the above expressions, T_c, P_c, and the coefficients c_m,n, λ, a, b, and w₀ are fitting parameters that we optimized to match the predictions of the TSEOS to the MTMB simulation data. Our fitting procedure was as follows: first, we obtained the equilibrium low-density fraction (x_e) at a given (T, P) by solving ${\left(\frac{\partial G}{\partial x}\right)}_{T,P}=0$ numerically, followed by the evaluation of the molar density and internal energy as ${\rho }_m={\left[{\left(\frac{\partial G}{\partial P}\right)}_T\right]}^{-1}$ and $E=G+TS-PV=G-T{\left(\frac{\partial G}{\partial T}\right)}_P-P{\left(\frac{\partial G}{\partial P}\right)}_T$ via numerical differentiation of Eq. 2. We repeated this process for the desired range of (T, P) and then optimized the parameters of the TSEOS to minimize the total sum of squared error between the TSEOS predictions and MTMB simulation results. The optimized parameters are listed in Table 1. We obtained the critical density ρ_c by finding the temperature maximum of the binodal line defined by G^BA = 0 for T ≤ T_c. In order to provide an error estimate for the critical parameters, we fit an independent set of parameters to each of the 200 block-bootstrap samples of the MTMB results to obtain 95% CIs.

Table 1.

Optimized TSEOS parameters

Parameter	Value
Tc, K	224
Pc, bar	2,687
λ	1.660
a	0.3603
b	−0.2694
w0	0.1268
c00	−831.7
c01	2.091
c02	−0.01794
c11	0.2733
c20	−6.066
c12	−0.1736
c21	−0.1816
c30	−0.8471
c22	0.4378
c31	0.3749
c40	1.968
c23	0.1490
c32	−0.4847
c33	−0.1868

Data Availability.

All data related to this work, including software installation instructions, DP-GEN, LAMMPS, and PLUMED input files, trained DNN model, raw simulation trajectory data, and analysis scripts are publicly available for download at https://doi.org/10.34770/45m3-am91 (81).