Real-time observation of ligand-induced allosteric transitions in a PDZ domain

Significance

Allostery is a process in which a signal sensed upon ligand-binding at a distal site is transduced to the effector site, allowing for regulation of the activity of the latter. The propagation of an allosteric signal is a nonequilibrium process, but neither the nature of the signal is known on a molecular level (e.g., whether it is structural or dynamical properties that change) nor its speed. The real-time observation of such a signal requires the design of protein systems, in which one can synchronize ligand (un)binding events. Such a design is presented here, allowing us to investigate its allosteric transition in unprecedented detail.

Abstract

While allostery is of paramount importance for protein regulation, the underlying dynamical process of ligand (un)binding at one site, resulting time evolution of the protein structure, and change of the binding affinity at a remote site are not well understood. Here the ligand-induced conformational transition in a widely studied model system of allostery, the PDZ2 domain, is investigated by transient infrared spectroscopy accompanied by molecular dynamics simulations. To this end, an azobenzene-derived photoswitch is linked to a peptide ligand in a way that its binding affinity to the PDZ2 domain changes upon switching, thus initiating an allosteric transition in the PDZ2 domain protein. The subsequent response of the protein, covering four decades of time, ranging from $\sim$1 ns to $\sim$μs, can be rationalized by a remodeling of its rugged free-energy landscape, with very subtle shifts in the populations of a small number of structurally well-defined states. It is proposed that structurally and dynamically driven allostery, often discussed as limiting scenarios of allosteric communication, actually go hand-in-hand, allowing the protein to adapt its free-energy landscape to incoming signals.

Allostery represents the coupling of two sites in a protein or a protein complex, where the binding of a ligand to the distal site modifies the affinity at the active site (1). Since biological function is intimately related to protein structure, ligand-induced changes of the protein’s function (e.g., the transition from an inactive to an active state) are often associated with a change of the protein’s mean structure (2). On the other hand, ligand (un)binding may also alter the protein’s flexibility, which changes the variance of the structure and gives an entropic contribution to the free energy (3). Referring to the associated change of the structural fluctuations, the latter scenario, termed “dynamic allostery,” has been invoked to explain apparent absence of conformational change upon ligand (un)binding (3–10). Studying the effects of dynamic allostery has been mainly done by NMR spectroscopy (11–13), which, however, only accounts for equilibrium dynamics.

While both models, structural change vs. dynamic change, may appear plausible, the nature of the “allosteric signal” is not known. A stringent examination ultimately requires us to study the genesis of allostery. This includes three steps: 1) the (un)binding of a ligand (usually initiated by a change of its concentration) (14) causes 2) the atoms of the protein to undergo a nonequilibrium time evolution, which 3) eventually leads to a change of the binding affinity at a remote site of the protein. This so-called “allosteric transition” is a nonequilibrium process and has been observed directly only rarely, in part, because the smallness of the structural changes makes the transition pathways challenging to observe experimentally (15) and also because of the time-scale limitations of molecular dynamics (MD) simulations (16–18). In this work, we outline an approach to study the first two steps, i.e., the ligand-induced allosteric transition, employing a PDZ2 domain as model system.

Known for their modest conformational change upon ligand-binding, PDZ domains are considered prime examples of dynamic allostery (4, 6, 19). PDZ domain-mediated interactions play a pivotal role in many signal transduction complexes (20, 21). Allosteric information flow in PDZ domains is thought to be transduced via conserved allosteric networks in the protein (4, 22–25). The system considered here is the PDZ2 domain from hPTP1E (human tyrosine phosphatase 1E) and a RA-GEF-2 peptide derivative (Ras/Rap1 associating guanidine nucleotide exchange factor 2) (26) with an azobenzene moiety linked as photoswitch (27) (Fig. 1). It was recently reported for a very similar system that the phosphorylation of the serine (−2) residue, a common target in regulatory processes of PDZ domains (28), leads to an approximately five- to sevenfold difference in the affinity toward the PDZ2 domain (29). We will see that the binding affinity can be perturbed to the same extent (approximately fivefold) by introducing such a photoswitchable element on the ligand instead. Since the PDZ2 domain is not modified at all, this strategy leads to a much less artificial construct than obtained in our previous study (30, 31), where the photoswitch was covalently linked across the binding pocket of the PDZ2 domain. In addition, using the ligand as a trigger, one can apply this strategy to virtually any system.

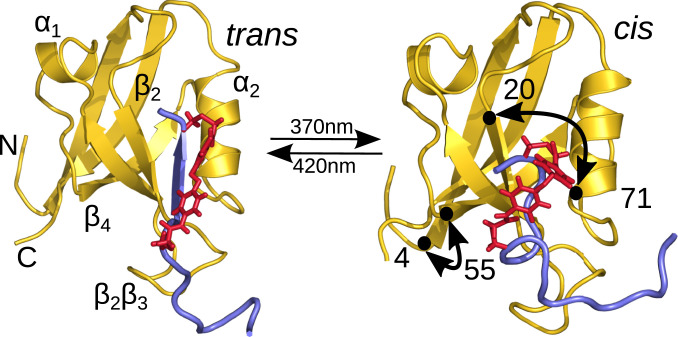
Fig. 1.

Ligand-switched PDZ2 domain. Main secondary structural elements and $C_{\alpha }$ distances $d_{\mathrm{20,71}}$ and $d_{\mathrm{4,55}}$ discussed below (Results, MD Simulations) are indicated. In the trans conformation of the photoswitch (red), the ligand (blue) fits well in the binding pocket, while it starts to move out when switching to cis.

By photoisomerizing the azobenzene moiety, we change the binding affinity of the ligand at a precisely defined point in time. We employ time-resolved vibrational spectroscopy in connection with an isotope labeling strategy to monitor the structural change of the protein in real time and perform extensive (more than 0.5 ms aggregate simulation time) all-atom nonequilibrium MD simulations combined with Markov modeling to interpret the experimental results in terms of the structural evolution of the system. We find that the mean structural change of the protein is rather small. However, in both experiment and MD simulations, the free-energy surface of the protein can be characterized by a small number of metastable conformational states. In agreement with the view of allostery as an interconversion between the relative population of metastable states, we see how the ligand-induced response of the PDZ2 domain is best described as remodeling of the free-energy landscape (32–36) and how the response is transduced from the ligand to the protein without introducing a significant structural change.

Results

Experimental.

To set the stage, we have investigated the influence of photoswitching of the ligand on its binding affinity. By choosing the spacing between the anchoring points of the azobenzene moiety, the peptide ligand was designed such that the longer trans conformation mimics the native extended $\beta$-strand conformation, while the cis configuration shortens the peptide and perturbs it from its extended form. To that end, the alanine residue at position −1 (the ligand is labeled by negative numbers) was chosen as the first anchoring spot for the photoswitch, since it has been shown that a mutation at this position does not significantly affect the binding, while residues that are crucial for binding [Val(0), Ser(−2) and Val(−3)] are preserved (37, 38). The second anchoring point chosen was Asp(−6) which allows the peptide to be maximally stretched in the trans configuration of the photoswitch. Protein and peptide have been expressed/synthesized using standard procedures (30, 39) (see Materials and Methods for details). The dissociation constants ($K_D$) in the two configurations of the photoswitchable peptide were determined by isothermal titration calorimetry (ITC), fluorescence, and circular dichroism (CD) spectroscopy (SI Appendix, Figs. S2 and S3) (40). The obtained values averaged for all methods ($K_{D,trans}=2.0\pm 0.6\hspace{0.17em}\mu$M, $K_{D,cis}=9.6\pm 0.5\hspace{0.17em}\mu$M; SI Appendix, Table S1) reveal an appreciable approximately fivefold difference in the binding affinity, with the cis state being the destabilized one, as anticipated.

Considering these binding affinities and the relatively high concentrations needed for the transient infrared (IR) experiment (1.25 mM for the peptide and 1.5 mM for the protein), it is clear that most of the ligands are bound in both states to a protein of the photoswitch (97% in cis and 99% in trans); hence, we will not observe many binding or unbinding events. Furthermore, as binding and unbinding in similar PDZ/ligand systems was observed to occur on 10- to 100-ms time scales (41), these processes are hardly within the time window of our experiment. Nevertheless, we will be able to observe the adaptation of the protein to a perturbed peptide conformation in the binding pocket and its transition to unspecific binding on the protein surface.

We investigate the ligand-induced conformational transition with the help of transient IR spectroscopy in the range of the amide I band (see Materials and Methods for details) (42–44). This band originates from mostly the C=O stretch vibration of the peptide/protein backbone and is known to be strongly structure-dependent (45). While one cannot invert the problem and determine the structure of a protein from the amide I band, any change in protein structure will cause small but distinct changes in this band (Fig. 2 A–C).

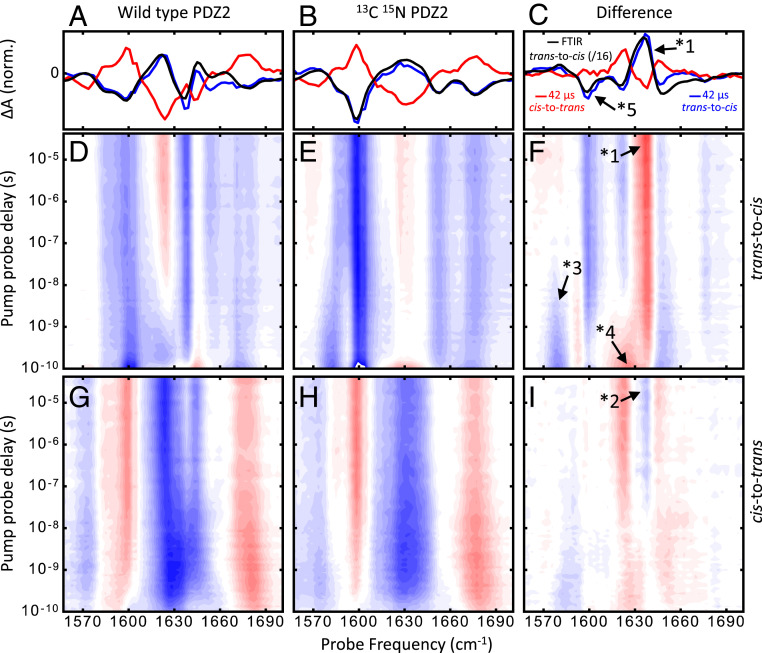
Fig. 2.

Transient IR spectra of PDZ2 in the region of the amide I band. A–C compare transient data at long pump–probe delay times (averaged from 20 μs to 42 μs to increase signal-to-noise) for trans-to-cis (blue) and cis-to-trans (red) switching, together with a properly scaled trans-to-cis FTIR difference spectrum (black). D–F show the complete transient data for trans-to-cis switching and G–I show that for cis-to-trans switching. The left graphs show the data for the WT protein, middle graphs show that for the sample with the protein ${}^{13}\mathrm{C}^{15}$N-labeled (the peptide ligand contains naturally abundant ${}^{12}\mathrm{C}^{14}$N), and right graphs show the ${}^{13}\mathrm{C}^{15}$N-WT difference data. Red colors in D–I indicate positive-absorbance changes, and blue colors indicate negative-absorbance changes. The relative scaling of the datasets and the labeled features are discussed in Experimental.

Fig. 2 shows the transient IR response in the spectral region of the amide I vibration after photoswitching in either the trans-to-cis (Fig. 2D–F) or the cis-to-trans direction (Fig. 2 G–I). To be directly comparable, the two datasets were scaled in a way that they refer to the same amount of isomerizing molecules and not the same amount of excited molecules. The scaling took into account the different pump-pulse energies used in the experiments (Materials and Methods), cross-sections (23,500 ${\mathrm{c}\mathrm{m}}^{-1}{\mathrm{M}}^{-1}$ for trans at 380 nm vs. 2,000 ${\mathrm{c}\mathrm{m}}^{-1}{\mathrm{M}}^{-1}$ for cis at 420 nm) (27), and isomerization quantum yields (8% for trans-to-cis switching and 62% for cis-to-trans switching) (46).

Selective isotope labeling can be used to disentangle the contribution of the peptide ligand from that of the protein. ${}^{13}\mathrm{C}^{15}$N-labeling of the protein backbone down-shifts the vibrational frequency of the amide I band by $\approx$25 ${\mathrm{c}\mathrm{m}}^{-1}$. By taking double-difference spectra between the sample with isotope-labeled protein vs. that with nonlabeled protein cancels out the contribution of the peptide ligand, which is not labeled in either case. By doing so, we implicitly assume that the spectra of protein and ligand are additive and that coupling between them can be neglected. This idea is utilized in Fig. 2, showing the response with the nonlabeled protein in the left graphs and that with the ${}^{13}\mathrm{C}^{15}$N-labeled protein in the middle graphs. The transient IR responses of both isotopologs look quite similar, as the signal is dominated by the photoswitchable peptide, which is perturbed directly by the azobenzene moiety. The double-difference spectra, removing the contribution of the photoswitchable peptide ligand, are shown in the right graphs of Fig. 2, with some of the more prominent features highlighted in Fig. 3 A–D. Great care was taken that protein and peptide concentrations were exactly the same in both experiments. Furthermore, both experiments were performed right after each other without changing any setting of the laser setup.

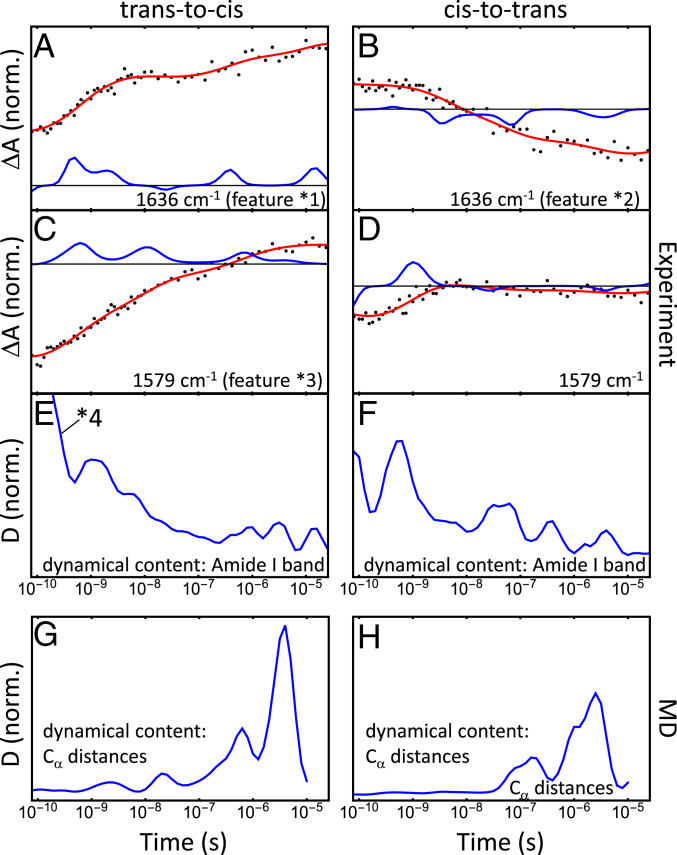
Fig. 3.

Transient ${}^{13}\mathrm{C}^{15}$N-WT difference data at 1,636 ${\mathrm{c}\mathrm{m}}^{-1}$ (A and B) and 1,579 ${\mathrm{c}\mathrm{m}}^{-1}$ (C and D) for trans-to-cis (Left) and cis-to-trans (Right) switching, highlighting features labeled as *1 to *3 in Fig. 2. Red lines are fits obtained from the time-scale analysis in Eq. 1, and blue lines represent the resulting time-scale spectra $a\left({\omega }_i,{\tau }_j\right)$. E and F show the corresponding dynamical content; the heat signal labeled as *4 is discussed in Experimental. G and H show the MD dynamical content, obtained from a time-scale analysis of the nonequilibrium time evolution of the mean ${\mathrm{C}}_{\alpha }$ distances (SI Appendix, Fig. S5).

Overall, the kinetics of these double-difference spectra are quite complex and cover many orders of magnitudes in time (47). Furthermore, the responses for trans-to-cis (Figs. 2F and 3 A and C) vs. cis-to-trans switching (Figs. 2I and 3 B and D) are not mirror images of each other, which one might expect if the protein would take the same pathway in the opposite direction. For example, the strongest band at 1,636 ${\mathrm{c}\mathrm{m}}^{-1}$ (marked as *1 in Figs. 2F and 3A) reveals the biggest step at around 1 ns in the trans-to-cis data, while the complementary feature in cis-to-trans data (marked as *2 in Figs. 2I and 3B) develops in a very stretched manner, from $\approx$3 ns to $\approx$3 $\mu$s. Worthwhile noting is also a transient band at 1,579 ${\mathrm{c}\mathrm{m}}^{-1}$ in the trans-to-cis data (marked as *3 in in Figs. 2F and 3C), existing up to $\approx$100 ns, that has no complementary counterpart in the cis-to-trans data (Figs. 2I and 3D).

The red lines in Fig. 3 A–D are fits revealed from a time-scale analysis of the signals using a maximum entropy method (48).

$$S\left({\omega }_i,t\right)=a_0\left({\omega }_i\right)-\sum _{k}a\left({\omega }_i,{\tau }_k\right)e^{-t/{\tau }_k}.$$ [1]

Here, ${\omega }_i$ denotes the probe frequency and $t$ the delay time of the signal, which is represented by a multiexponential function with time scales ${\tau }_k$. The time-scale spectra $a\left({\omega }_i,{\tau }_k\right)$ are shown in Fig. 3 A–D as blue lines. Each of the kinetic processes discussed above shows up as a peak in these time-scale spectra, and the pattern of peaks is different for all of the examples shown in Fig. 3 A–D. Nevertheless, the dynamical content (49),

$$D\left({\tau }_k\right)={\left[\sum _i{a}^2\left({\omega }_i,{\tau }_k\right)\right]}^{1/2},$$ [2]

which averages over the complete dataset shown in SI Appendix, Fig. S4, seems to indicate a relatively small number of discrete time scales (Fig. 3 E and F). We attribute the first peak around 100 ps (labeled as *4 in Figs. 2F and 3E) to a “heat signal” originating from the vibrational energy released by the photoisomerization of the azobenzene moiety, an effect that is seen universally in this type of experiments (50, 51).

The transient spectra at the latest pump–probe delay time that is accessible to our transient experiment (i.e., 42 $\mu$s) are shown in Fig. 2 A–C in blue for trans-to-cis switching and in red for cis-to-trans switching. They are compared with a properly scaled trans-to-cis Fourier-transform infrared spectroscopy (FTIR) difference spectrum (black), which represents the response at effectively infinite time after photoswitching. The counterpart of the negative band in the blue and black trans-to-cis spectra at 1,600 ${\mathrm{c}\mathrm{m}}^{-1}$ (marked as *5 in Fig. 2C) has not yet evolved in the red cis-to-trans spectrum. We conclude from this observation that the cis-to-trans transition is not completely finished after 42 $\mu$s.

MD Simulations.

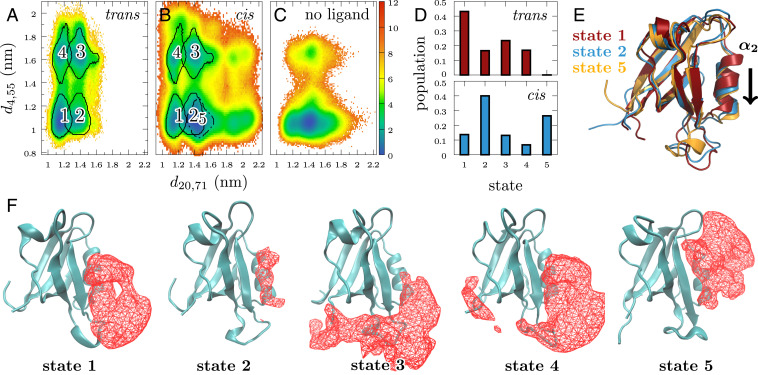
To aid the interpretation of the above experiments, we performed all-atom explicit-solvent MD simulations of the cis and trans equilibrium states as well as nonequilibrium MD simulations (52) of the ligand-induced conformational changes of PDZ2. Using the GROMACS v2016 software package (53) and the Amber99*ILDN force field (54–56), we collected in total $510\hspace{0.17em}\mu$s simulation time (Materials and Methods). For the structural characterization of the protein, we determined 56 ${\mathrm{C}}_{\alpha }$ distances $d_{i,j}$ between residues $i$ and $j$ that are not redundant (such as $d_{i,j}$ and $d_{i,j\pm 1}$) and whose ensemble average changes significantly ($⟨\mathrm{\Delta }{d}_{ij}⟩\ge 0.5$ Å) during the nonequilibrium simulations (SI Appendix, Fig. S5). To identify the essential coordinates of the system, we performed a principal component analysis (PCA) on the normalized distances of all simulation data (57), followed by robust density-based clustering (58) and a recently proposed machine-learning approach (59) (see Materials and Methods and SI Appendix, Fig. S6 for details). While we used six dimensions for the clustering, we find that two $C_{\alpha }$ distances suffice to qualitatively characterize the conformational distribution of PDZ2: $d_{\mathrm{20,71}}$ accounting for the width of the binding pocket located between ${\beta }_2$ and ${\alpha }_2$, as well as $d_{\mathrm{4,55}}$ representing the distance between the amino (N) terminus and ${\alpha }_1$-${\beta }_4$ loop, which reflects the compactness of the carboxy (C)- and N-terminal region (Fig. 1). Employing these coordinates, Fig. 4A shows the free-energy surface $\mathrm{\Delta }G=-k_{\mathrm{B}}T\ln P\left(d_{\mathrm{20,71}},d_{\mathrm{4,55}}\right)$, obtained from $5\hspace{0.17em}\times \hspace{0.17em}5\hspace{0.17em}\mu$s-long trans equilibrium simulations describing the ligand-bound state of PDZ2. The free-energy landscape reveals four well-defined local minima, indicating metastable conformational states of the system. Density-based clustering identifies state 1 as close to the crystal structure (60), while state 2 indicates an opening of the binding pocket. Both states are mirrored by states 3 and 4, which are shifted to larger values of coordinate $d_{\mathrm{4,55}}$.

Fig. 4.

Identification of metastable conformational states. Free-energy landscapes (in units of $k_{\mathrm{B}}T$) obtained from the trans (A), cis (B), and ligand-free (61) (C) equilibrium simulations of PDZ2, plotted as a function of two essential interresidue distances. The unlabeled state-like feature at the bottom right of B represents weakly populated ($\lesssim 1\%$) subregions of states 2 and 5. (D) Histogram of the state populations in trans and cis equilibrium, revealing the ligand-induced population shift of PDZ2. (E) Comparison of minimum-energy structures the of states 1, 2, and 5, revealing an increased opening of the ligand-binding pocket by a downward motion of ${\alpha }_2$. (F) Structures of states together with position densities of the ligand. The isosurface encloses a volume with a minimal probability of 0.4 to find a ligand atom within in all simulation snapshots belonging to a specific state. Fixed points for the comparison are the ${\mathrm{C}}_{\alpha }$ atoms of strands ${\beta }_4$ and ${\beta }_6$.

Upon switching the ligand from trans-to-cis configuration, PDZ2 undergoes a nonequilibrium time evolution until it relaxes within a few microseconds into its cis equilibrium state, describing the perturbed protein–ligand complex. Performing $25\hspace{0.17em}\times \hspace{0.17em}10\hspace{0.17em}\mu$s-long trans-to-cis nonequilibrium simulations, we took the last $7\hspace{0.17em}\mu$s of each trajectory to estimate the rather heterogeneous conformational distribution of the cis equilibrium state. When we compare the resulting free-energy landscapes of cis and trans, Fig. 4 A and B reveals that the accessible conformational space in cis is considerably increased, along with the occurrence of additional state 5 that reports on a further opening of the binding pocket. While states 2 and 5 largely overlap in this two-dimensional representation of the free energy, they are well separated when a third distance (e.g., $d_{\mathrm{27,69}}$) is invoked (SI Appendix, Fig. S6). Representing the populations of all states in trans and cis as a histogram, Fig. 4D demonstrates that the photoswitching of the ligand causes a notable ($\lesssim \hspace{0.17em}30\hspace{0.17em}\%$) shift of the state populations, mostly from state 1 to states 2 and 5.

To illustrate the conformational changes associated with these states, Fig. 4E displays an overlay of minimum-energy structures of states 1 and 2 as well as the cis-specific state 5. We find that the opening of the binding pocket described by $d_{\mathrm{20,71}}$ mainly reflects a shift of the ${\alpha }_2$ helix down and away from the protein core. Interestingly, the structural rearrangement between main states 1 and 2 results in an overall rms displacement of only $\lesssim \hspace{0.17em}1\hspace{0.17em}$ Å and causes only few ($\sim 5$) contacts to change (SI Appendix, Fig. S7). This is in striking contrast to the cross-linked photoswitchable PDZ2 studied by Buchli et al. (30), where 34 contact changes were found for the trans-to-cis reaction (61). Furthermore, in contrast to Fig. 4 A and B, the cis and trans free-energy landscapes hardly overlapped in the cross-linked photoswitchable PDZ2 domain (31, 49). These findings indicate that ligand-switching is considerably less invasive than a cross-linked photoswitch and therefore better mimics the natural unbiased system.

Is the above-discussed population shift as well as the very occurrence of states an inherent property of the protein’s rugged free-energy landscape (32, 33), or are these features rather induced by the ligand? Fig. 4C addresses this question by showing the free-energy landscape obtained from previously performed $6\hspace{0.17em}\times \hspace{0.17em}1\mu$s-long simulations of PDZ2 without a ligand (61). While the state separation along coordinate $d_{\mathrm{4,55}}$ still exists, we find that states 1, 2, and 5 merge into a single energy minimum. It is centered at the position of state 2, but is wide enough to cover a large part of states 1 and 5. Similarly states 3 and 4 form a weakly populated ($2\hspace{0.17em}\%$) single minimum. This indicates that ligand-free PDZ2 provides the flexibility to assess the entire free-energy landscape explored during binding and unbinding, while the interaction with the ligand appears to stabilize conformational states 1 and 4. Returning to the question at the beginning of the paragraph, we find that it is a bit of both, i.e., an inherent property of the protein’s rugged free energy that is modified to a certain extent by the ligand.

Showing protein structures of the main states together with position densities of the ligand, Fig. 4F illustrates these interactions (see also SI Appendix, Fig. S8). For one, we notice that the opening and closing of the binding pocket (described by $d_{\mathrm{20,71}}$) is associated with the conventional binding of the ligand’s C terminus in this pocket, which stabilizes closed state 1 in trans. In the open state 2, the probability to find the ligand in its binding mode is significantly decreased, pointing to a reduced ligand affinity of the protein. On the other hand, we find that the distinct conformations of the protein’s termini described by $d_{\mathrm{4,55}}$ are a consequence of the formation of contacts with the ligand’s N terminus in states 3 and 4, which are absent in states 1, 2, and 5. In particular, state 5 represents a situation where the hydrophobic photoswitch of the ligand forms a contact with a hydrophobic bulge at the protein surface around Ile20, which can be classified as unspecific binding of the ligand to the protein surface.

Adopting our trans-to-cis nonequilibrium simulations, we can describe the overall structural evolution of PDZ2 in terms of time-dependent expectation values of various observables. As an example, Fig. 5 A and B shows the time evolution of the two ${\mathrm{C}}_{\alpha }$ distances $d_{\mathrm{20,71}}$ and $d_{\mathrm{4,55}}$ introduced above. Following trans-to-cis ligand-switching, it takes about 100 ns until the sub-picosecond photoisomerization of the photoswitch affects the protein’s binding region (indicated by $d_{\mathrm{20,71}}$), which becomes wider as the ligand moves out. The flexible N-terminal region indicated by $d_{\mathrm{4,55}}$, on the other hand, undergoes conformational changes already within a few nanoseconds. The weak correlation between the two interresidue distances (i.e., $⟨d_{\mathrm{20,71}}{d}_{\mathrm{4,55}}⟩{\left(⟨d_{\mathrm{20,71}}^2⟩⟨d_{\mathrm{4,55}}^2⟩\right)}^{-1/2}\lesssim 0.02$ for all data), however, indicates that this early motion of the terminal region may be not directly related to the functional dynamics of PDZ2. Interestingly, the associated rmsd values of the two distances show quite similar behavior. Moreover, SI Appendix, Fig. S9 displays various ligand–protein distances and contact changes, which illustrate that the ligand leaves the binding pocket on time scales of 0.1–$1\hspace{0.17em}\mu$s. Similar to the experimental analysis (cf. Eq. 2), we also calculated the dynamical content associated with all considered intraprotein ${\mathrm{C}}_{\alpha }$ distances (Fig. 3 G and H). While MD and experimental results are seen to cover the same time scales, the peaks of the respective distributions differ clearly as they account for different physical observables. In principle, one would expect that the positions of the peaks coincide, even if the amplitudes are different due to the different physical observables, but that might be asking too much for the accuracy of the MD simulation.

Fig. 5.

Time evolution of various structural descriptors, following trans-to-cis ligand-switching of PDZ2. Shown are means (blue) and rmsd (orange) of ${\mathrm{C}}_{\alpha }$ distances $d_{\mathrm{20,71}}$ (A) and $d_{\mathrm{4,55}}$ (B), as well as populations of conformational states (C, D, and F). For easier representation, all MD data were smoothed. Starting at time $t\hspace{0.17em}=\hspace{0.17em}0$ almost completely in state 1, we compare results from the nonequilibrium MD simulations (C) with the corresponding predictions of an MSM (D). (E) Network representation of the MSM. The size of the states indicate their population, the thickness of the arrows and numbers indicate the transition times (in microseconds). For clarity, we discard transitions that take longer than 2.5 μs. (F) MSM simulations of the trans-to-cis transition, using trans equilibrium initial conditions.

It is instructive to consider the resulting time-dependent populations of the protein’s metastable states. Choosing initial conditions close to the crystal structure (60), Fig. 5C exhibits the trans-to-cis time evolution of the state populations. The system starts at time $t=0$ almost completely in state 1 and converts to the other states within microseconds. To rationalize these findings, we construct a Markov state model (MSM) (62, 63), which describes the conformational dynamics of PDZ2 via memoryless jumps between metastable states. To this end, we calculate a transition matrix $T$ containing the probabilities $T_{ij}$ that the system jumps from state $i$ to $j$ within lag time ${\tau }_{\text{lag}}$ and determine its eigenvectors ${\psi }_k$ and eigenvalues ${\lambda }_k$ (see Materials and Methods and SI Appendix, Fig. S10 for technical details). As a first impression, Fig. 5 C and D compares the state populations obtained from the nonequilibrium MD simulations and the corresponding MSM predictions (using ${\tau }_{\text{lag}}\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}$ns). We find excellent agreement for the first three decades of time but only qualitative agreement in the last decade, which reflects the bias of our nonequilibrium MD simulations toward shorter time scales ($75\hspace{0.17em}\times \hspace{0.17em}1\hspace{0.17em}\mu$s-long and $25\hspace{0.17em}\times \hspace{0.17em}10\hspace{0.17em}\mu$s-long data). Showing a network representation of the MSM, Fig. 5E illustrates the connectivity and transition times of the system. We see that the open–close transition of the binding pocket occurs on a time scale of $\sim \hspace{0.17em}1\hspace{0.17em}\mu$s, whereas transitions from states 1 and 2 to states 4 and 3 are a factor 4 faster with a back-rate that is even a factor 10 faster.

Assuming a time-scale separation between fast intrastate fluctuations and rarely occurring interstate transitions, MSM theory (62) states that the time-dependent expectation value of any dynamical observable can be written as a sum over exponential functions ${\mathrm{e}}^{-t/t_k}$ weighted by the projection of the observable onto the $k$th eigenvector of transition matrix $T$. The implied time scales $t_k\hspace{0.17em}=\hspace{0.17em}-{\tau }_{\text{lag}}/\ln {\lambda }_k$ of the MSM therefore govern the time evolution of such different observables as vibrational spectra and state populations (64). To facilitate a comparison of experimental and simulated time evolutions, we run an MSM simulation using trans equilibrium initial conditions, which is also the starting point of the trans-to-cis experiments. Comparing the simulation results (Fig. 5F) to the experimental time traces (Fig. 3), we find that both spectral and population evolutions appear to be completed on microsecond time scale. Moreover, the MSM populations exhibits various transient features on time scales of 10 to 100 ns, which are also present in the experimental time signals.

Discussion and Conclusions

Combining transient IR spectroscopy and nonequilibrium MD simulations, we have described the ligand-induced conformational transition in the PDZ2 domain, which is thought to be responsible for protein allosteric communication. We have found that the free-energy landscape of PDZ2 can be described in terms of a few metastable states with well-defined structure (Fig. 4), although the mean structural changes upon ligand-switching are rather small. That is, the secondary and tertiary structure of the protein are quite similar ($\lesssim \hspace{0.17em}1\hspace{0.17em}$-Å rms displacement) in the different states, and only modest ($\sim \hspace{0.17em}30\hspace{0.17em}$%) shifts of the state’s population are found (Fig. 4B). On average, the measurable structural change is therefore only in the order of 0.3 Å. This is a significantly smaller conformational change as reported in ref. 30, where the photoswitch was covalently linked directly to the binding groove of the protein, which resulted in an rmsd of 0.9 Å, as determined by NMR spectroscopy. In light of this result, it is remarkable that we can observe such minor structural changes by transient IR spectroscopy (Fig. 2), unpinning the extraordinary structural sensitivity of the method. We currently cannot exclude further conformational changes of the protein upon complete removal of the ligand. The study of these effects will require new concepts, both experimentally as well as computationally, as the expected time scales are very long (10 to 100 ms).

Using isotope labeling to discriminate the dynamics of protein and ligand, the resulting time-resolved double-difference IR spectra have revealed complex kinetics of the protein that cover many time scales (Fig. 2). The spectra for trans-to-cis and cis-to-trans ligand-switching are not mirror images of each other, and the trans-to-cis signals exhibit short-time transients that are not found for cis-to-trans. Moreover, the cis-to-trans transition does not seem to be finished within 42 $\mu$s (Fig. 2C). The overall slower response of the cis-to-trans transition reflects the general observation that enforced leaving of a well-defined (low entropy) ligand-binding structure (here trans) occurs faster than starting in a conformationally disordered (high-entropy) state (here cis) and trying to find stabilizing interactions to end in a more organized structure (65).

More specifically, the trans-to-cis nonequilibrium simulations reveal that the ligand remains bound with its C terminus to the protein-binding site between ${\beta }_2$ and ${\alpha }_2$ up to about 1 $\mu$s. In this way, it stabilizes the main bound-protein conformation (state 1). At longer times, it starts to move out from the binding pocket but remains nonspecifically bound to the protein surface. While diffusion on the surface may continue for long times after trans-to-cis switching, it only little affects the protein internal structure. Nevertheless, this diffusion will be the first rate-limiting step after cis-to-trans switching, which might be the reason that the ligand does not completely localize in the binding pocket within $42\hspace{0.17em}\mu$s.

The existence of well-defined metastable conformational states implies a time-scale separation between fast intrastate fluctuations and rarely occurring interstate transitions. This allowed us to construct a MSM, which illustrates the connectivity and transition times between the metastable states (Fig. 5D). In particular, the discrete time scales predicted by the MSM are directly reflected in the dynamical content calculated for experiments and MD simulations (Fig. 3 E–H), which both cover time scales from $\sim \hspace{0.17em}$1 ns to 10 $\mu$s. Reflecting different observables (transition dipole vs. ${\mathrm{C}}_{\alpha }$ distances, respectively), the weights of the various peaks are different.

While ligand-switching was shown to cause a conformational transition of PDZ2 in terms of the mean structure, at the same time, it may also effect a change of the protein’s fluctuations. Comparing the time evolution of the means of the distances and their rmsd, Fig. 5 A and B reveals that the two quantities correlate closely, a behavior that is found for all considered ${\mathrm{C}}_{\alpha }$ distances (SI Appendix, Fig. S5). This finding reflects the fact that the ${\mathrm{C}}_{\alpha }$-distance distributions pertaining to the individual states are in most cases well separated (SI Appendix, Fig. S11), such that a transition between two states affects both mean and variance. Accounting for an entropic contribution of the conformational transition, a change in variance is often referred to as “dynamic allostery” (3, 4, 6). The above findings indicate that allosteric transitions may involve both conformational and dynamic changes in the case of the PDZ2 domain (8). The answer to what is the dominant effect will greatly depend on the system under consideration and on the applied experimental method. While the overall structural change ($\lesssim \hspace{0.17em}0.3\hspace{0.17em}$-Å rms displacement) may be too small to be detected by structure analysis, NMR-relaxation methods can sensitively explore the structural flexibility of proteins. The IR spectrum of the amide I band, in contrast, is commonly thought of as a measure of structure (45), but dephasing due to fast fluctuation might also affect the IR line shape.

In conclusion, we have characterized the nonequilibrium allosteric transition in a joint experimental–theoretical approach. The protein per se was kept unmodified; hence, ligand-switching mimics very closely the naturally occurring allosteric perturbation caused by ligand (un)binding events. We employed a widely studied model system for this purpose, the PDZ2 domain, which is small enough to allow for a characterization of the process in atomistic detail by MD simulations, but we believe that the findings are of more general nature. That is, while the ligand-induced allosteric transition originates from a population shift between various metastable conformational states, the measurable mean structural change of the protein may be tiny and therefore difficult to observe (8). Moreover, we suggest that the separation between purely dynamically driven allostery and allostery upon a conformational change may not be as clear-cut as previously thought but rather that there may be an interplay between both that allows proteins to adapt their free-energy landscape to incoming signals. The photoswitching approach presented here is very versatile and allows us to shed light on the aspects of “time” and “speed” in allosteric communication.

Materials and Methods

Protein and Peptide Preparation.

Expression of the wild-type (WT) PDZ2 domain from human phosphatase 1E (26), isotope-labeled (${}^{13}\mathrm{C}^{15}$N) protein variant and synthesis of the photoswitchable peptide ligand was performed as described earlier (30, 39). The WT RA-GEF-2 sequence was modified in order to enable cross-linking the photoswitch, while preserving residues that are important for regulation and binding. That is, amino acids at positions (−1) and (−6) were chosen as anchoring points for the photoswitch and mutated into cysteine residues. Four N-terminal residues (RWAK) were added to the sequence in order to improve the water solubility and facilitate the concentration determination of the construct. The final sequence of the peptide was RWAKSEAKECEQVSCV. The purity of all samples was confirmed by mass spectrometry analysis (SI Appendix, Fig. S1). All samples were dialyzed against 50 mM borate, 150 mM NaCl buffer (pH 8.5). For transient infrared measurements, samples were lyophilized and resuspended in deuterated water (${\mathrm{D}}_2$O). Incubation of the samples in ${\mathrm{D}}_2$O overnight at room temperature before the measurements eliminated H/D exchange during experiments. The concentration of the samples was determined via the tyrosine absorption at 280 nm for the protein and 310 nm for the peptide and confirmed by amino acid analysis.

Determining the Binding Affinity.

Isothermal titration calorimetry (ITC) measurements were performed on a MicroCal ITC200 (Malvern). In order to ensure the obtained values for the cis and trans measurement were mutually comparable, the experiments were performed using the same stock solution of the peptide and protein for both measurements and under exactly the same experimental conditions. The experiment was performed in triplicate in order to ensure the reproducibility of the data. The sample cell was loaded with 250 $\mu$L of 80 $\mu$M PDZ2 domain solution, and the syringe was loaded with 40 $\mu$L of 800 $\mu$M photoswitchable peptide solution. For the trans measurement, the system was kept in the dark for the duration of the experiment, while for the cis measurement the syringe was constantly illuminated with a 370-nm continuous-wave (cw) laser (power $\approx$90 mW; CrystaLaser) (40). The results are shown in SI Appendix, Fig. S2.

As alternative method to determine the binding affinity, we also used CD spectroscopy as well as fluorescence quenching. Both spectroscopic signals change upon the formation of a protein–ligand complex; hence, when measuring them in dependence of peptide and protein concentration, the binding affinity can be fitted assuming a bimolecular equilibrium. CD measurements were done on a Jasco model J810 spectropolarimeter in a 0.1-cm quartz cuvette, as described previously (40). Intrinsic tryptophan fluorescence quenching experiment was done on Perkin-Elmer spectrofluorimeter, as described previously (40). In either case, the protein concentration was kept constant at 5 $\mu$M, respectively, while the peptide concentrations were varied. SI Appendix, Fig. S3 shows the results for the CD spectroscopy and tryptophan fluorescence quenching, while SI Appendix, Table S1 compares the binding affinities obtained from all different methods.

Transient IR Spectroscopy.

Transient visible pump–IR probe spectra were recorded using two electronically synchronized Ti:Sapphire laser systems (43) running at 2.5 kHz. The wavelength of the pump laser was tuned as to obtain 380-nm pump pulses (2.1 $\mu$J) for the trans-to-cis experiment and 420 nm (1.3 $\mu$J) for the cis-to-trans experiment, respectively, via second harmonic generation in a BBO crystal. The beam diameter of the pump pulse at the sample position was $\approx$180 $\mu$m, employing a pulse duration of $\approx$200 ps (by extracting the light directly after the regenerative amplifier and before the compressor) to minimize the sample degradation during the measurements. Mid-IR probe pulses centered at $\approx$1,630 ${\mathrm{c}\mathrm{m}}^{-1}$ (pulse duration: $\approx$100 fs; beam diameter on the sample: $\approx$150 $\mu$m) were obtained in a optical parametric amplifier (42), passed through a spectrograph and detected in a 2$\times$64 MCT array detector with a spectral resolution of $\approx$2 ${\mathrm{c}\mathrm{m}}^{-1}$ per pixel. Pump–probe spectra were acquired up to the maximum delay value of $\approx$42 $\mu$s with a time resolution of $\approx$200 ps. Normalization for noise suppression was performed as described in ref 44.

The samples ($\approx$700 $\mu$L) were pumped through a closed flow-cell system purged with ${\mathrm{N}}_2$. The system consisted of a sample cell with two ${\mathrm{C}\mathrm{a}\mathrm{F}}_2$ windows separated by a 50-$\mu$m Teflon spacer and a reservoir. The flow speed in the sample cell was optimized in order to minimize loss of sample at the largest pump–probe delay time ($\approx$42 $\mu$s), on the one hand, but to have the sample exchanged essentially completely for the subsequent laser shot after 400 $\mu$s on the other hand. The concentrations of the samples were set at 1.25 mM for the peptide and 1.5 mM for the protein. A slight excess of protein was needed to ensure that the peptide was fully saturated with the protein; in order to eliminate the response of free, photoswitchable peptide. As a reference, FTIR difference spectra have been taken in a Bruker Tensor 27 FTIR spectrometer, using the same sample conditions.

For the experiment with trans-to-cis switching, we relied on thermal cis-to-trans back reaction. By comparing its rate with the isomerization probability induced by the 380-nm pump light—determined by pump light power, total sample volume, absorption cross-sections (27), and isomerization quantum yield (46)—we estimated that the photoequilibrium in the total sample volume is 70/30% trans/cis during measurement. It furthermore helps that the absorption cross-section at 380 nm of the azobenzene moiety in the trans-state is $\approx$20 times larger than that of the cis state (27), which leads us to conclude that $>$97% of the molecules in the trans-to-cis experiment undergo the desired isomerization direction.

For the experiment with cis-to-trans switching, the sample could be actively switched back by illuminating the reservoir with an excess of light at 370 nm from a cw laser (150 mW; CrystaLaser).

MD Simulations.

All MD simulations of PDZ2 were performed using the GROMACS v2016 software package (53) and the Amber99*ILDN force field (54–56). Force-field parameters of the azobenzene photoswitch were taken from ref. 39. Protein–ligand structures were solvated with approximately 8,000 TIP3P water molecules (66) in a dodecahedron box with a minimal image distance of 7 nm; 16 Na⁺ and 16 Cl⁻ were added to yield a charge-neutral system with a salt concentration of 0.1 M. All bonds involving hydrogen atoms were constrained using the LINCS algorithm (67), allowing for a time step of 2 fs. Long-range electrostatic interactions were computed by the Particle Mesh Ewald method (68), whereas the short-range electrostatic interactions were treated explicitly with the Verlet cutoff scheme. The minimum cutoff distance for electrostatic and van der Waals interactions was set to 1.4 nm. A temperature of 300 K was maintained via the Bussi thermostat (69) (also known as velocity-rescale algorithm) with a coupling time constant of ${\tau }_T$ = 0.1 ps. A pressure $P=$1 bar was controlled using the pressure coupling method of Berendsen et al. (70) with a coupling time constant of ${\tau }_P$ = 0.1 ps.

The starting structure of the photoswitched ligand bound to PDZ2 was prepared previously (39) based on the crystal structure (Protein Data Bank ID code 3LNX) (60). Here, the azobenzene photoswitch was attached in $trans$ conformation to the ligand at positions (−6) and (−1), which had been mutated to cysteines as in experiment to provide covalent connection points. Residues missing at the N terminus of the ligand were added (Protein and Peptide Preparation). Following NPT equilibration of the system in $trans$ conformation for 10 ns, four statistically independent (i.e., with different initial velocity distributions) NVT runs of 100 ns each were performed. For one, we selected five randomly chosen snapshots from the end of these trajectories to perform $5\hspace{0.17em}\times \hspace{0.17em}5\mu$s-long $trans$ equilibrium simulations. Moreover, we selected 25 randomly chosen snapshots from each of the last 50 ns of these four NVT trajectories to perform trans-to-cis nonequilibrium simulations, yielding a total of 100 starting structures that consist mostly of metastable state 1 (for state definition, see Dimensionality Reduction and Clustering). Employing these initial conditions, trans-to-cis photoswitching was performed using a previously developed potential-energy surface-switching approach (52). All 100 trans-to-cis nonequilibrium simulations were run for $1\hspace{0.17em}\mu$s; 25 of them were extended to a length of 10 $\mu$s.

Upon switching the ligand from the trans to the cis configuration, PDZ2 undergoes a nonequilibrium time evolution until it relaxes within a few microseconds into its cis equilibrium state, describing the unbound protein–ligand complex. Performing $25\hspace{0.17em}\times \hspace{0.17em}10\hspace{0.17em}\mu$s-long trans-to-cis nonequilibrium simulations, we took the last $7\hspace{0.17em}\mu$s of each trajectory to estimate the rather heterogeneous conformational distribution of the cis equilibrium state. To generate initial structures for cis-to-trans photoswitching, we took from the 25 trans-to-cis trajectories 100 randomly chosen snapshot at a simulation time around 3.0$\mu$s. Following photoswitching, 100 cis-to-trans nonequilibrium trajectories were simulated for a trajectory length of 1 $\mu$s; 10 simulations were extended to a length of 8 $\mu$s.

Gromacs tools $gmx\hspace{0.17em}angle$ and $gmx\hspace{0.17em}mindist$ were employed to compute backbone dihedral angles, interresidue $C_{\alpha }$ distances, and the number of contacts between various segments of PDZ2. Time-dependent distributions and mean values of these observables were calculated via an ensemble average over 100 nonequilibrium trajectories.

Dimensionality Reduction and Clustering.

To choose suitable internal coordinates that account for the conformational transitions of the system (57), we determined 56 $C_{\alpha }$ distances $d_{i,j}$ between residues $i$ and $j$ that are not redundant (such as $d_{i,j}$ and $d_{i,j\pm 1}$) and whose ensemble average changes significantly ($⟨d_{ij}⟩\ge 0.5$ Å) during the first microsecond trans-to-cis nonequilibrium simulations (SI Appendix, Fig. S5). Moreover, we considered all backbone dihedral angles that show a change of $\gtrsim 10^{○}$ from their initial value during the trans-to-cis nonequilibrium simulations.

Since the interresidue $C_{\alpha }$ distances appear to provide more information, these coordinate are chosen for the subsequent PCA, which was performed on all data (57). For adequate relative weighting of short and long distances, the data were normalized (71). Diagonalizing the resulting covariance matrix, we obtain its eigenvectors (yielding the principal components [PCs]) and eigenvalues (reflecting the fluctuations of the PCs). The first two PCs cover 43% of the overall fluctuations, while six PCs yield about 65%. Calculating the free-energy profiles pertaining to the PCs, we find that in particular PCs 1 to 4, 6, and 7 show multistate behavior reflecting metastable states.

Including these six PCs, we performed robust density-based clustering (58), which first computes a local free-energy estimate for every structure in the trajectory by counting all other structures inside a six-dimensional hypersphere of fixed radius $R$. Normalization of these population counts yields densities or sampling probabilities $P$, which give the free-energy estimate $\mathrm{\Delta }G=-k_{\text{B}}T\ln P$. Thus, the more structures are close to the given one, the lower the free-energy estimate. By reordering all structures from low to high free energy, finally, the minima of the free-energy landscape can be identified. By iteratively increasing a threshold energy, all structures with a free energy below that threshold that are closer than a certain lumping radius will be assigned to the same cluster, until all clusters meet at their energy barriers. In this way, all data points are assigned to a cluster as one branch of the iteratively created tree. For PDZ2, we used a hypersphere $R=0.579$ that equaled the lumping radius employed in the last step.

SI Appendix, Fig. S6, Top shows the resulting total number of states obtained as a function of the minimal populations $P_{min}$ a state must contain. Here, we chose $P_{min}=50\hspace{0.17em}000$, resulting in a clustering into 12 states. According to visual inspection of the resulting free-energy landscapes (SI Appendix, Fig. S6, Middle), these states separate accurately all density maxima of the system. Since the five lowest-populated states cover less than 5% of the total population, we lumped them to main states 1 to 7 as follows: (1, 9)$\to$1, (2, 10)$\to$2, (4, 12)$\to$4, (5, 8, 11)$\to$5. This is justified due to their geometric vicinity in the free-energy landscape (SI Appendix, Fig. S6, Middle), as well as due to their kinetic vicinity in the transition matrix. Following the calculation of the time-dependent states populations, in a last step, we lumped states (4, 7)$\to$4 and states (5, 6)$\to$5 for the sake of easy interpretability.

Finally, we employed a recently proposed machine-learning approach (59) to identify the internal coordinates that allow to discuss the five main states of PDZ2 in a two-dimensional free-energy landscape. On the basis of the decision tree-based program XGBoost (72), we trained a model that determines the features of the molecular coordinates that are most important to discriminate given metastable states. Using an algorithm that exploits this feature importance via an iterative exclusion principle, we identified the essential internal coordinates, that is, the most important ${\mathrm{C}}_{\alpha }$ distances of PDZ2. SI Appendix, Fig. S6, Bottom shows that three distances, $d_{\mathrm{20,71}}$, $d_{\mathrm{4,55}}$, and $d_{\mathrm{27,69}}$, suffice to qualitatively distinguish the five main states of PDZ2. The XGBoost parameters are chosen as in ref. 59, including learning rate $\eta =0.3$, maximum tree depth of 6, 10 training rounds, and 70 and 30% of the data used for training and validation, respectively.

MSM.

On the basis of the above-defined seven metastable states, we constructed an MSM (62) of the trans-to-cis transition of PDZ2, using all ($75\hspace{0.17em}\times \hspace{0.17em}1\hspace{0.17em}\mu$s and $25\hspace{0.17em}\times \hspace{0.17em}10\hspace{0.17em}\mu$s) trans-to-cis nonequilibrium trajectories. A general problem with the definition of metastable states is that, due to the inevitable restriction to a low-dimensional space combined with insufficient sampling, we often obtain a misclassification of sampled points in the transition regions, which causes intrastate fluctuations to be mistaken as interstate transitions. As a simple but effective remedy, we use dynamical coring, which requires that a transition must a minimum time ${\tau }_{\mathrm{c}\mathrm{o}\mathrm{r}}$ in the new state for the transition to be counted (73, 74). A suitable quantity that reflects these spurious crossings is the probability $W_i\left(t\right)$ to stay in state $i$ for duration $t$ (without considering back-transitions). As shown in SI Appendix, Fig. S10, without coring, we observe a strong initial decay of $W_i\left(t\right)$ for all states, instead of a simple exponential decay we would expect for Markovian states. Applying coring with increasing coring times, this initial drop vanishes because fluctuations on time scales $t\lesssim {\tau }_{\text{cor}}$ are removed. Here, we determined ${\tau }_{\mathrm{c}\mathrm{o}\mathrm{r}}=1\hspace{0.17em}$ns as the shortest coring time, which removes the spurious interstate transitions.

SI Appendix, Fig. S10 shows the resulting implied time scales and eigenvectors of the model. Using a lag time of 1 ns, we moreover show the time evolution of the state populations, assuming that we start completely in a specific state.

Data Availability.

The experimental data used in this article have been deposited in Zenodo (https://zenodo.org: doi.org/10.5281/zenodo.3991616). MD data can be obtained from the authors upon request. MD data analysis tools including FastPCA, Robust Density-Based Clustering, and Essential Coordinates Learning are available at www.moldyn.uni-freiburg.de.