Revisited COVID-19 Mortality and Recovery Rates: Are we Missing Recovery Time Period?

How difficult time it is due to COVID-19 pandemic can be determined by its mortality and/or recovery rates. Predictive modeling can help us forecast how big the impact will be, especially for human lives? Prediction is one of the well-known studies that is entirely relying on machine learning based data analytics tools and techniques. In this study, we revisit mathematical models to measure severity levels of a COVID-19 pandemic.

A pandemic is an epidemic occurring on a scale that spreads rapidly across the world. The World Health Organization (WHO) considers epidemic diseases are Chikungunya, Cholera, Crimean – Congo hemorrhagic fever, Ebola Virus disease, Hendra virus infection, Influenza, Lassa fever, Plague, COVID-19, SARS, etc. In 2014, the United States Centre for Disease Control and Prevention (CDC) announced an equivalent framework to the WHO’s pandemic stages titled pandemic intervals framework [1–3], where two pre-pandemic and four pandemic intervals were reported. Investigation and recognition are pre-pandemic intervals. Initiation, acceleration of diseases, deceleration, and preparation are pandemic intervals. In a similar fashion, instead of using pandemic intervals, we take recovery time period into account. Recovery time period can be two days, a week, two weeks, a month, six months, a year or any finite number of days. For COVID-19, we consider an average recovery time period of 14 days [4].

In March 2020, Baud et al. [4] reported to take 14 days delay into account in order to compute right mortality rate during the COVID-19 pandemic. Their study suggested that the classical mortality rate undervalue the probable threat due to COVID-19 in symptomatic cases. Of all metrics, to measure an austerity of the COVID-19 pandemic, in addition to mortality rates, recovery rate is considered. Both, mortality and recovery rates are useful metrics only when recovery time period is considered. Practically, one cannot compute mortality and recovery rates without considering its recovery time period. Inspired from previous work [4], we revisit mathematical models for both mortality and recovery rates, where not recovered cases and recovery time period are discussed thoroughly with both synthetic and real datasets.

In the sequel, for any disease, mortality rate (MR) defines the probability of death, and can be expressed as, $\mathrm{MR}=\frac{\mathrm{D}}{\mathrm{N}}\times 100,$ where D and N refer to total number of deaths and infected people, respectively. While computing the MR, we consider the total number of an infected people till date, which will superfluously increase the denominator and hence decreases the MR. Therefore, practically, it is observed that the classical mathematical equation (to compute MR) may deviate from what it should be, since it does not take recovery time period into account. This primarily motivates us to revisit classical mathematical models.

Since recovery time periods vary a lot from person to person (of course, demography dependent, as reported in WHO [5]), it is important to define an average recovery time period (P_avg) as follows:

$${\mathrm{P}}_{avg}=\left\{\begin{array}{cl}0,& \mathrm{i}\mathrm{f}\mathrm{R}\mathrm{P}\approx 0,\mathrm{\infty }\\ \mathrm{A}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n},& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right)$$

where we do not practically consider recovery time period (RP) on the exact same day cases are tested positive and those who are not recovered for months/years.

While revisiting, since mortality rate changes over time during COVID-19 pandemic, we call it Progressive Mortality Rate (PMR). In general, for any case/pandemic, C with an average recovery time period of P_avg, PMR can be computed as,

$$\mathrm{PMR}=\frac{{\mathrm{D}}_{\mathrm{c}}}{{\mathrm{N}}_{{\mathrm{P}}_{\mathit{avg}}}}\times 100,$$

where D_c denotes the total number of death cases due to C disease and Np_avg refers to a total number of infections before average recovery time period P_avg.

Similarly, Recovery Rate (RR) used to follow classical mathematical equation, $\mathrm{RR}=\frac{\mathrm{R}}{\mathrm{N}}\times 100$, where R refers to total number of recovered cases. As before, when recovery time period is taken into account, Progressive Recovery Rate (PRR) is,

$$\mathrm{P}\mathrm{R}\mathrm{R}=\frac{{\mathrm{R}}_{\mathrm{C}}}{{\mathrm{N}}_{{\mathrm{P}}_{avg}}}\times 100,$$

where R_c refers to total number of recovered cases till date.

As a result, it is observed that we have notable differences between classical and revisited (progressive) rates. With ${\mathrm{N}}_{{\mathrm{P}}_{\mathit{avg}}}$, progressive rates, as compared to classical rates, vary a lot during the pandemic period. The primary reason behind that is, for any i^th day, progressive rates are calculated by taking data from (i-14)^th day plus those recovered and death cases into account, where for COVID-19, we consider P_avg = 14. Further, classical and progressive rates meet each other at the end i.e., (j + 14)^th day, where no new case is tested after j^th day. This means that mortality rates can only be determined by taking next average recovery time period from the day no new case(s) is(are) tested.

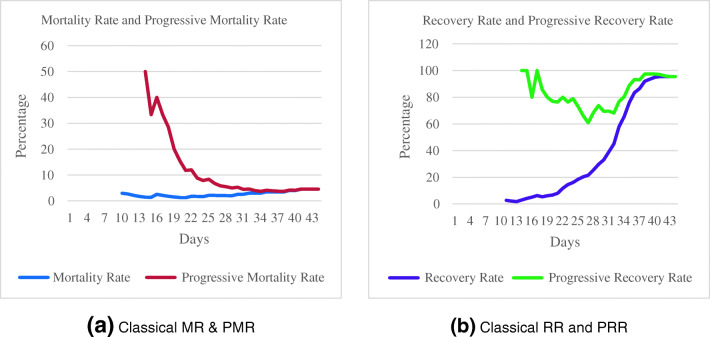
In previous correspondences [4, 6–8], the 14 days delay has been well discussed. However, since we do not have complete COVID-19 pandemic scenario, it is not trivial to get the real estimates from their models even though they look conceptually correct. To avoid possible confusions, we build a synthetic data, where we consider the first day having COVID-19 positive cases to the end of COVID-19 pandemic (see Table 2 in Appendix). Using our synthetic data, Fig. 1 shows how differences can happen when we take recovery time period into account. On 14th day, PMR and PRR are computed. Both classical and progressive rates meet each other when no new case is tested positive. As a result, these rates can be determined after 14 days from the day when no new case is tested positive. Interestingly, both classical and mathematical models hold exact same value at the end.

Table 2.

Computing PMR, PRR, MR, and RR of COVID-19 Pandemic using synthetic data

Days	No. of infections	No. of recovered cases	No. of death cases	MortalityRate (MR) (classical)	Progressive Mortality Rate (PMR)	Recovery Rate (RR) (classical)	ProgressiveRecovery Rate (PRR)	Progressive Total (PT)	% of cases (not recovered in P days, where P = 14 days)
1	2
2	3
3	5
4	6
5	7
6	10
7	13
8	17
9	25
10	34		1	2.94
11	38	1	1	2.63		2.63
12	48	1	1	2.08		2.08
13	59	1	1	1.69		1.69
14	69	2	1	1.45	50.00	2.90	100.00	150.00	−50.00
15	73	3	1	1.37	33.33	4.11	100.00	133.33	−33.33
16	80	4	2	2.50	40.00	5.00	80.00	120.00	−20.00
17	95	6	2	2.11	33.33	6.32	100.00	133.33	−33.33
18	112	6	2	1.79	28.57	5.36	85.71	114.29	−14.29
19	132	8	2	1.52	20.00	6.06	80.00	100.00	0.00
20	151	10	2	1.32	15.38	6.62	76.92	92.31	7.69
21	163	13	2	1.23	11.76	7.98	76.47	88.24	11.76
22	171	20	3	1.75	12.00	11.70	80.00	92.00	8.00
23	179	26	3	1.68	8.82	14.53	76.47	85.29	14.71
24	186	30	3	1.61	7.89	16.13	78.95	86.84	13.16
25	189	35	4	2.12	8.33	18.52	72.92	81.25	18.75
26	192	39	4	2.08	6.78	20.31	66.10	72.88	27.12
27	195	42	4	2.05	5.80	21.54	60.87	66.67	33.33
28	197	50	4	2.03	5.48	25.38	68.49	73.97	26.03
29	199	59	4	2.01	5.00	29.65	73.75	78.75	21.25
30	200	66	5	2.50	5.26	33.00	69.47	74.74	25.26
31	200	78	5	2.50	4.46	39.00	69.64	74.11	25.89
32	200	90	6	3.00	4.55	45.00	68.18	72.73	27.27
33	200	116	6	3.00	3.97	58.00	76.82	80.79	19.21
34	200	131	6	3.00	3.68	65.50	80.37	84.05	15.95
35	200	152	7	3.50	4.09	76.00	88.89	92.98	7.02
36	200	167	7	3.50	3.91	83.50	93.30	97.21	2.79
37	200	173	7	3.50	3.76	86.50	93.01	96.77	3.23
38	200	184	7	3.50	3.70	92.00	97.35	101.06	−1.06
39	200	187	8	4.00	4.17	93.50	97.40	101.56	−1.56
40	200	190	8	4.00	4.10	95.00	97.44	101.54	−1.54
41	200	191	9	4.50	4.57	95.50	96.95	101.52	−1.52
42	200	191	9	4.50	4.52	95.50	95.98	100.50	−0.50
43	200	191	9	4.50	4.50	95.50	95.50	100.00	0.00
44	200	191	9	4.50	4.50	95.50	95.50	100.00	0.00

Index:

a) $\mathrm{MR}=\frac{\mathrm{D}}{\mathrm{N}}\times 100$;

(b) $\mathrm{PMR}=\frac{{\mathrm{D}}_{\mathrm{C}}}{{\mathrm{N}}_{{\mathrm{P}}_{\mathit{avg}}}}\times 100;$

c)$\mathrm{RR}=\frac{\mathrm{R}}{\mathrm{N}}\times 100$;

d) $\mathrm{PRR}=\frac{{\mathrm{R}}_{\mathrm{C}}}{{\mathrm{N}}_{{\mathrm{P}}_{\mathit{avg}}}}\times 100$;

e) PT = PMR + PRR; and

f) NR = 100 – PT.

Fig. 1.

Relation between classical and progressive rates using synthetic data, where one can find a complete scenario from day 1 to day 30, where no new case is tested positive after 30th day

Mathematically speaking, PMR and PRR are disjoint sets. In other words, the set U is the union of PMR and PRR, and the percentage of the cases that are Not Recovered (NR) within P_avg. As a result, the cardinality of U is 100. Since recovery time period varies from person to person and is based on the severity level of infection [16], NR can be either positive, negative or zero:

$$\mathrm{N}\mathrm{R}=\left\{\begin{array}{ll}\le 0,& \mathrm{i}\mathrm{f}\mathrm{R}\mathrm{P}\le {\mathrm{P}}_{avg}\\ >0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right)$$

As before, PMR, PRR, and NR are disjoint sub-sets. As mentioned earlier, since recovery time period can be less than, equal to and more than P_avg, Progressive total (PT) can be computed as

$$\mathrm{P}\mathrm{T}=\left\{\begin{array}{ll}\le 100,& \mathrm{i}\mathrm{f}\mathrm{N}\mathrm{R}\ge 0\\ >100,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right)$$

where PT changes with NR. On the whole, PT = PMR + PRR.

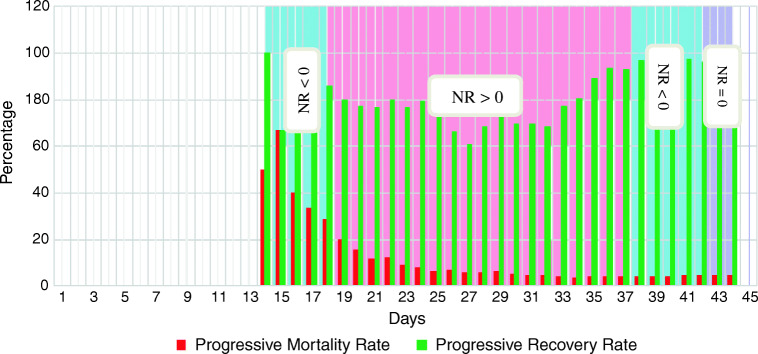
The selection of P_avg is crucial as it impacts progressive total, which is not the case when we compute classical MR and RR. In Fig. 2, using synthetic data (like in Fig. 1), we have a complete understanding of PRM and PRR from day 1 to day 44, where 30th day is the last day when no new COVID-19 positive is tested. Specifically, a) from day 14th to 18th and 38th to 42th, cases are recovered within P_avg and therefore, NR is negative; b) from day 19th to 37th, cases require more than 14 days to recover and therefore, NR is positive; and c) from 43rd to 45th, cases are recovered exactly on 14 days and therefore, NR is zero. In a nutshell, it is expected to have NR ≤ 0 for higher recovery rate. In other words, NR depends on PMR and PRR. With this note, PT reaches 100% when NR is zero. If NR < 0, PT crosses 100%. This means that when PT crosses 100%, infected cases are recovered in less than P_avg.

Fig. 2.

Different values of Not Recovered (NR) cases in accordance with RP and P_avg (data source: Table 2, appendix) in both PMR and PRR

For the exact same scenario (P_avg = 14 days), considering the real-world data (see Table 1), one can see reasonable differences between classical and progressive mortality/recovery rates. In Table 1, countries are ranked in accordance with the increasing order of the mortality rate. Let us summarize the observations so one can understand how PMR, PRR, and PT rely on NR, where P_avg is crucial. Two cases can be summarized as follows:

1. P_avg ≤ 14: For Canada and Brazil, since PT is close to 100% (100.26%, and 100.458%, respectively), an average recovery time period is 14 days i.e., P_avg ≈ 14. In other words, all infected cases take 14 days (on an average) to get recovered. While for India, Mexico, and Japan, since PT is 109.29%, 108.39% and 103.9% respectively, which is more than 100%, an average recovery time period is less than 14 days i.e., P_avg < 14.

2. P_avg > 14: For remaining countries (from Table 1), since PT is less than 100%, infected cases are taking more than 14 days to get recovered.

Table 1.

Computing MR, RR, PMR, PRR, and PT during the COVID-19 Pandemic

Country	Confirmed cases (July 5)	Confirmed cases (July 18)	Death cases	Recovered cases	Mortality Rate (classical)	Recovery Rate (classical)	Progressive Mortality Rate (PMR)	Progressive Recovery Rate (PRR)	Progressive Total (PT)
Singapore	53,051	55,747	27	51,953	0.05	93.19	0.05	97.93	97.98
New Zealand	1567	1631	22	1531	1.35	93.87	1.4	97.7	99.1
Russia	8,54,641	9,20,719	15,653	7,31,444	1.7	79.44	1.83	85.58	87.41
India	18,03,695	26,47,663	50,921	19,19,842	1.92	72.51	2.82	106.44	109.26
Japan	40,099	56,074	1103	40,560	1.97	72.33	2.75	101.15	103.9
United State	47,13,540	54,03,213	1,70,052	18,33,067	3.15	33.93	3.61	38.89	42.5
Brazil	27,50,318	33,40,197	1,07,852	26,55,017	3.23	79.49	3.92	96.53	100.45
Germany	2,12,111	2,25,007	9235	2,01,187	4.1	89.41	4.35	94.85	99.2
China	88,099	89,375	4703	83,200	5.26	93.09	5.34	94.44	99.78
Canada	1,18,973	1,24,004	9074	1,10,202	7.32	88.87	7.63	92.63	100.26
Mexico	4,43,813	5,22,162	56,757	4,24,298	10.87	81.26	12.79	95.6	108.39

On the whole, in this study, considering recovery time period, we are not just limited to provide mathematical models for progressive mortality and recovery rates but also analyze the importance of recovery time period during the pandemic. We have provided our analyses by using both synthetic as well as real-world data.

At this point, it is important to note that even though the recovery time periods vary from one case/pandemic to other, the exact same mathematical models can be used to compute mortality and recovery rates.

Appendix

In order to realize our revisited mathematical models for a complete COVID-19 pandemic scenario, we consider a city of 200 people. In our data, there are 2 COVID-19 positive cases on the first day, and 200 people get infected on 30th day. This means that after 30 days, no new cases are tested. Considering an average recovery time period of 14 days, we provide detailed information about classical and progressive rates for mortality and recovery rates (see Table below).

Compliance with ethical standards

Conflict of interest

Authors declared no conflict of interest.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors.