How Much Dispersion Energy Is Included in the Multiconfigurational Interaction Energy?

Abstract

We demonstrate how to quantify the amount of dispersion interaction recovered by supermolecular calculations with the multiconfigurational self-consistent field (MCSCF) wave functions. For this purpose, we present a rigorous derivation which connects the portion of dispersion interaction captured by the assumed wave function model—the residual dispersion interaction—with the size of the active space. Based on the obtained expression for the residual dispersion contribution, we propose a dispersion correction for the MCSCF that avoids correlation double counting. Numerical demonstration for model four-electron dimers in both ground and excited states described with the complete active space self-consistent field (CASSCF) reference serves as a proof-of-concept for the method. Accurate results, largely independent of the size of the active space, are obtained. For many-electron systems, routine CASSCF interaction energy calculations recover a tiny fraction of the full second-order dispersion energy. We found that the residual dispersion is non-negligible only for purely dispersion-bound complexes.

1. Introduction

Calculations of the intermolecular interaction energy typically involve the supermolecular approach. The perturbation theory is also a common choice and is often used to expose the nature of the interaction. In hybrid approaches, the supermolecular results are supplemented with energy contributions obtained in a perturbative manner, the most popular example being density functional theory (DFT) corrected for the dispersion energy.^1,2

A given wave function theory (WFT) approximation is useful in describing interactions either if it accounts for high-order components in the intermolecular interaction operator or when it is reasonably accurate in the lowest orders and it is known which higher-order components are missing. A representative example from the first group are the coupled cluster (CC) methods^3,4 which predict interaction energies with high accuracy when effects of single, double, and triple excitations are accounted for. The Hartree–Fock (HF) method belongs to the second group. The HF energy contains electrostatic, exchange, and induction interaction energy components and has been rigorously shown to miss the second-order dispersion component.⁵ In spite of this deficiency, the supermolecular HF result can be corrected for the dispersion energy which leads to a low-cost hybrid approach.⁶⁻⁸ The accuracy of the hybrid approach can be significantly improved by including intramonomer correlation effects in a perturbative manner which is known as the HFDc⁽¹⁾ method.^8,9

HF calculations assume a single-determinantal description of the interacting species. Although high-order single-reference CC methods may be applied to multireference systems,¹⁰ the cost of going to full triple or quadruple excitations is too high in practice. The multireference CC extensions^11,12 are expensive, and their applications to intermolecular interactions remain scarce (e.g., see refs (11), (13), (14)). Going beyond single-determinantal methods in the intermolecular interaction theory is a challenge. The multiconfigurational (MC) wave function methods are a good starting point and often the required one for open-shell systems, systems dominated by strong correlation, excited states, and transition-metal complexes. Although including multiple configurations guarantees proper representation of static correlation and partial recovery of the intramonomer correlation effects,^15,16 it is not a viable way to restore the remaining part of the dynamic correlation which in the case of intermolecular interactions manifests as dispersion. Notwithstanding significant progress in this field, none of the existing MC methods have yet achieved the levels of both accuracy and efficiency comparable to what is now within reach of black-box interaction-energy calculations for single-reference systems. Therefore, the search for new and improved MC approaches remains active.

The most popular strategies to capture dispersion forces in the MC framework are the configuration interaction (CI) expansion and the perturbation theory. Each of these approaches involves certain limitations both in terms of computational cost and in terms of accuracy. A significant problem of CI is the lack of size consistency. Although it can be ameliorated with approximate corrections,^17,18 the residual size inconsistency typically still has to be addressed. This is done by obtaining the asymptotic interaction energy limit in a dimer calculation with the monomers separated at a large distance and shifting the results with respect to this value.¹⁹ Note that in this scheme, the counterpoise correction (CP)²⁰ cannot be applied and the basis set superposition error (BSSE) is not removed. Additionally, because of the lack of triple excitations, multireference CI may underestimate the dispersion energy in van der Waals complexes by as much as 30%.^21,22

A common choice to account for dynamic correlation via the multireference perturbation theory are the complete active space (CAS) perturbation theory (CASPT2)^23,24 and n-electron valence state perturbation theory (NEVPT2)²⁵⁻²⁷ methods. Truncated at the second order, both require access to four-electron density matrices, which quickly becomes a computational bottleneck with respect to the size of the active space. Moreover, CASPT2 and multireference formulations of the Møller–Plesset theory^28,29 are plagued with intruder states³⁰ which have to be removed to guarantee a smooth potential energy surface. Various techniques that eliminate intruders exist, yet one should be cautious when choosing the optimal value of the shift parameter.³¹ The intruder-state problem is by design avoided in the NEVPT2 method. The accuracy of single-reference MP2 calculations is often insufficient for quantitative predictions. A major weakness is that MP2 restores the dispersion energy at the uncoupled level of theory³²⁻³⁴ which leads, for example, to the well-known overestimation of interaction energy in π–π complexes^35,36 or underestimation in the case of alkali-metal dimers.³⁷ This implies that the accuracy of the multireference second-order perturbation theory is seriously limited.

Several variants of the multiconfiguration DFT (MC DFT)^38,39 capable of treating dispersion forces have also been developed. In MC DFT, the connection between the DFT and wave function descriptions of the system is realized by partitioning of the Coulomb interaction operator into the short- and long-range components. The short-range (sr) electron–electron correlation effects are recovered by a density functional approximation, whereas the multiconfiguration wave function model acts in the long range. The usual strategy is to restrict the wave function to a few determinants, which is sufficient to recover the static correlation at a relatively low cost but not enough to capture the long-range dynamic correlation. This translates into the absence of the dispersion contribution in the interaction energy. As a remedy, Fromager and coauthors⁴⁰ proposed a long-range adaptation of the NEVPT2 approach. Recently, Hapka et al.⁴¹ introduced a less expensive alternative based on the multireference formulation of the adiabatic connection formalism⁴² which relies only on one- and two-electron reduced density matrices of the system. The cost-efficient route in which the complete active space self-consistent field (CASSCF) srPBE functional^43,44 is simply corrected with the semi-classical D3 dispersion correction of Grimme⁴⁵ has been advocated by Stein and Reiher.⁴⁶

The direct addition of the dispersion energy to the supermolecular CASSCF results, without correcting for the double counting, was attempted several times in the past. In the study of the Hg···Hg dimer, Kunz et al.¹⁵ used this approach to partially account for the dynamic correlation within the monomers—an effect that cannot be recovered in the simple “HF plus dispersion” model. Rajchel et al.⁴⁷ verified the performance of the “CAS plus dispersion” method against the RCCSD(T) results for the potential energy curves of the Sc···Cr complex in the ⁸Σ⁺, ⁸Π, and ⁸Δ states. The authors found that “CAS plus dispersion” consequently underestimated the magnitude of the interaction and predicted the location of the minima at ca. 0.2–0.3 bohr longer distances compared to the CC reference. The CAS-based approach was also applied to describe the unusually strong binding in the He···BeO(¹Σ⁺) dimer and showed excellent agreement with the MRCISD + Q potential.⁴⁸ In all of the mentioned examples, it was argued that the compact representation of the active space selected in CASSCF calculations is too small to recover the dispersion energy. Nevertheless, to the best of our knowledge, no systematic study of this claim has been presented to date and expressions for the residual dispersion energy recovered in the supermolecular CASSCF have not been derived.

In this work, we present how to rigorously extract the dispersion term in the interaction energy calculated with MC wave functions so that the double counting of the intermonomer correlation is avoided. As will be discussed, any wave function dissociating to MC wave functions for both monomers leads to recovering a small portion of the dispersion energy, denoted as E_DISP^MC. Being able to explicitly calculate the E_DISP contribution, we propose the “CAS plus dispersion” approach which strictly avoids the double counting of the dispersion contribution and recovers the total interaction energy as

1

where E_int^MC is the supermolecular interaction energy obtained within the assumed WFT and E_DISP is the full second-order dispersion energy. We present the results for wave functions of the CAS type and use the symmetry-adapted perturbation theory (SAPT)^49,50 to obtain the E_DISP⁽²⁾ energy contributions.

It is worth noticing that Stein and Reiher⁴⁶ raise the concern of dispersion double counting in the context of large active spaces available with the density-matrix renormalization group wave functions. They propose a procedure that could approximately remove the residual dispersion inherently captured by an MC function. This approach requires orbital localization, followed by the removal of configurations (determinants) corresponding to excitations of a dispersion-like character.⁵¹⁻⁵³ In contrast, our protocol for E_disp^MC evaluation avoids orbital localization and stems directly from the exact definition of the dispersion energy.

In the next section, we derive an exact expression for the dispersion energy recovered by supermolecular MC WFT calculation and discuss a method for its approximation. In Section 3, we present the details of the implementation and calculations. Section 4 provides numerical demonstration of the proposed “CAS plus dispersion” method on the example of model He···He and He···H₂ dimers as well as representative noncovalently bound, many-electron complexes. In Section 5, we summarize our findings.

2. Theory

2.1. Setting the Stage

For two weakly interacting electronic subsystems A and B forming a dimer AB, the interaction energy is defined as a difference of energies of the dimer E_AB and isolated monomers E_A and E_B

2

By definition, the interaction energy vanishes when subsystems are infinitely separated

3

where R_AB measures the distance between A and B. Let Ĥ_AB, Ĥ_A, and Ĥ_B denote the dimer Hamiltonian and the Hamiltonians of the isolated monomers, respectively. In the assumed WFT model, computation of the interaction energy in the supermolecular way requires finding wave functions for a dimer Ψ_AB and isolated monomers Ψ_A and Ψ_B, and making use of the pertinent Hamiltonians as follows

4

A primary condition which must be satisfied by a physically relevant WFT is size consistency, that is, vanishing of the supermolecular interaction energy in the infinite-separation limit, which can be written as

5

which in turn imposes the separability condition for the (antisymmetric) wave function Ψ_AB reading

6

where the antisymmetrization operator 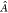is applied on the product Ψ_AΨ_B of monomer functions.

In the Rayleigh–Schrödinger (RS) perturbation theory applied to molecular interactions, a dimer N_AB-electron Hamiltonian is written as a sum of N_A- and N_B-electron Hamiltonians of the monomers (N_AB = N_A + N_B) and a remainder, which is the interaction operator V̂_int

7

A sum of Ĥ_A + Ĥ_B is taken as the zero-order Hamiltonian, V̂_int is taken as a perturbation, and the Ψ_AΨ_B product of monomer functions is the zero-order dimer eigenfunction. It is important to notice that the antisymmetrized wave function given in eq 6 is an eigenfunction of Ĥ_AB in the limit R_AB → ∞, but it is not an eigenfunction of the zero-order Hamiltonian Ĥ_A + Ĥ_B. As is well known, the interaction energy, eq 4, follows from perturbation theory as a sum of the first-, second-, and higher-order terms in the perturbation⁵⁴

8

where E_elst⁽¹⁾ denotes the electrostatic energy, while E_ind and E_disp⁽²⁾ denote the second-order induction and dispersion energy contributions, respectively. Each term is well defined and has a clear physical interpretation. In particular, the second-order dispersion energy is given by the expression

9

where i (j) refers to states Ψ_A,i (Ψ_B,j) of the energy E_A,i (E_B,j) corresponding to Ĥ_A (Ĥ_B) and a prime indicates that summation indices run through all states with the exception of the states of interest Ψ_A and Ψ_B for which the dispersion is computed. The leading term of the multipole expansion of the dispersion energy of molecular systems vanishes as R_AB^–6 and dominates in the asymptotic regime of the total interaction energy in van der Waals complexes.

The problem that we address in the next section is whether one can rigorously show to what extent a given wave function model accounts for the dispersion interaction in the supermolecular approach. The positive answer will be provided by singling out from the interaction energy expression terms of a dispersion character, which decay asymptotically in the same (R_AB^–6) fashion as the full dispersion energy, cf. eq 9, and which are equivalent to the latter if WFT corresponds to the full CI (FCI) description of a dimer.

2.2. Dispersion Interaction in the MC Wave Function Description of the Interaction Energy

In this section, we present the expression for the dispersion energy, E_disp^MC, which is included in the supermolecular interaction energy, obtained with the MC wave function description of a dimer. We begin by considering a general N-electron wave function which can be expressed as the antisymmetrized product of wave functions

10

where 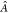is the antisymmetrization operator (including a normalization constant). Ψ_P is an N_P-electron antisymmetric wave function, and ∑_PN_P = N. In addition, it is assumed that the whole set of spin orbitals is partitioned into disjoint subsets and a given function Ψ_P is expanded in a set of Slater determinants built from spin orbitals belonging to a subset P. The assumed ansatz for Ψ is therefore a group product function.⁵⁵ We refer to Ψ_P as a group function, where P denotes a group, indexes a group function, and refers to a pertinent subset of spin orbitals. Ψ_P can be a single determinant or a combination of many determinants, for example, an MC wave function. MC self-consistent field (MCSCF) wave functions, which are in the focus of this work, conform to the ansatz given in eq 10. They can be written as an antisymmetrized product of the inactive part Ψ_inact and the active part Ψ_active

11

where Ψ_inact is a single Slater determinant built of one-electron groups, that is, spin orbitals φ_p

12

while Ψ_active is a combination of Slater determinants.

If Ψ of the form as in eq 10 is found variationally by minimizing the energy ⟨Ψ|Ĥ|Ψ⟩, where Ĥ is the electronic Hamiltonian, then, for each group wave function Ψ_P, one can form a group electronic Hamiltonian Ĥ_P reading

13

The intragroup Hamiltonian Ĥ_P,intra includes the kinetic energy operator, the interaction of N_P electrons, assigned to a group P, with all nuclei in the system (denoted as M_nuc), and the appropriate electron–electron interaction

14

The other part of the group Hamiltonian given in eq 13 describes the intergroup mean field interaction of electrons assigned to a group P with electrons in the other groups. It arises as a result of self-consistent field (SCF) optimization and depends on the self-consistently obtained group spin orbitals. The mean field intergroup interaction operator, Ĥ_P,SCF, is a sum of one-electron Coulomb and exchange operators pertaining to all groups except for P, namely

15

where r_1i = |r₁ − r_i|, x = (r,σ) stands for a combined spatial-spin coordinate, and the P̂_ij operator interchanges x_i with x_j; ρ_Q(x) = ⟨Ψ_Q|ρ^(x)|Ψ_Q⟩ and γ_Q(x,x′) = ⟨Ψ_Q|γ̂(x,x′)|Ψ_Q⟩ are, respectively, the density and one-electron reduced density matrix functions corresponding to Ψ_Q. A wave function Ψ_P is one of the eigenfunctions of Ĥ_P with the corresponding energy ε_P, that is, if we write the eigenproblem for the group Hamiltonian Ĥ_P

16

then, ∃iΨ_P = Ψ_P,i. Within the assumed wave function approximate model, Ψ_P,i is an MC wave function given as a combination of M_P Slater determinants Φ_P,K

17

and the Hamiltonian Ĥ_P is the diagonal in the M_P-dimensional space spanned by Φ_P,K functions.

It is straightforward to notice that the total electronic energy is given as a sum of group energies, ε_P = ⟨Ψ_P|Ĥ_P|Ψ_P⟩, with the intergroup Coulomb-exchange interaction energy subtracted to avoid its double counting

18

19

Now, consider a perturbed electronic Hamiltonian, linear in the perturbation parameter λ

20

A corresponding perturbed group Hamiltonian, cf. eqs 13 and 15, will include a direct perturbing term (linear in λ) and its SCF part will acquire a λ dependence because of the λ dependence of both the density and density matrices, namely

21

where

22

The total electronic energy, eq 18, expanded in terms of λ, is a sum of terms in different orders of the perturbation. Because our interest lies in the dispersion energy, which appears in the second order of the interaction operator, we only focus on the second-order term reading

23

where using the second Hellmann–Feynman theorem,⁵⁶ the second-order group energy is given as

24

Notice that we have assumed hermiticity of the perturbing operators and that wave functions are real-valued.

Let us now turn to the molecular interaction theory, where the interaction operator V̂_int, introduced in eq 7, is treated as a perturbation. The zero-order part is given as a sum of monomer Hamiltonians

25

and the explicit form of the perturbation, Ĥ⁽¹⁾ = V̂_int, reads

26

where the subscripts a and b label the nuclei and i and j denote the electrons of monomers A and B, respectively. A monomer X is composed of N_X electrons and M_nuc,X nuclei. Throughout the text, X will stand for either A or B.

When monomers are infinitely separated, the size-consistency condition given in eq 5 imposes that the total dimer wave function acquires the form of a product of monomer functions, as seen in eq 6. This can only be satisfied if each N_P-electron wave function Ψ_P dissociates into a product of monomer wave functions Ψ_PA and Ψ_PB, which are, respectively, N_PA- and N_PB-electron and N_P = N_PA + N_PB. Neglecting the electron exchange, the zero-order group function reads

27

In the R_AB → ∞ limit, the group density and the density matrix corresponding to Ψ_P separate into monomer group functions, namely

28

29

which is a consequence of vanishing overlap between Ψ_PA and Ψ_PB in the dissociation limit. Partitioning of the total electronic Hamiltonian assumed in eqs 25 and 26 results in the following decomposition of the group Hamiltonian Ĥ_P, cf. eq 21

30

where Ĥ_PA,intra collects intragroup operators for a group P in monomer A

31

analogously for Ĥ_PB,intra, and the interaction operator for a group P

32

includes the interaction of electrons in A assigned to a group P with nuclei in monomer B, the interaction of electrons in monomer B assigned to a group P with nuclei in monomer A, and the interaction among electrons in monomers A and B within a group P. At infinite intermonomer separation (the λ = 0 limit), the SCF part of the group Hamiltonian, eq 22, is partitioned as

33

34

where ρ_QX and γ_QX are the monomer group density and the density matrix, as seen in eqs 28 and 29, respectively. This allows one to write the group Hamiltonian, eq 30, as a sum of monomer group Hamiltonians

35

where

36

Our goal is to identify the dispersion terms in the second-order energy given in eq 23 corresponding to the intermolecular perturbation operator given in eq 26. First, one should notice that the last term in eq 23, which includes second-order perturbations of the Coulomb-exchange intergroup interactions, (E_Coul-Exch^PQ)⁽²⁾, cannot contribute to the dispersion energy. These terms describe the interactions of the perturbed one-electron density and density matrices. Next, let us consider the second-order group energy ε_P, presented in eq 24, where the group interaction operator Ĥ_P⁽¹⁾ = V̂_PAB is given in eq 32. The derivatives of Ĥ_P,SCF(λ) with respect to λ, involved in ε_P, are given by the pertinent derivatives of densities and density matrices

37

Thus, they are one-electron operators and as such cannot contribute to the dispersion interaction either. Therefore, the only term in eq 23 which may give rise to the dispersion interaction is the one involving the operator V̂_PAB. Retaining solely this term in E⁽²⁾ and denoting the resulting energy as E_d⁽²⁾, we write

38

To see under which condition dispersion terms emerge from E_d⁽²⁾, we need to find the first-order correction for group wave functions, Ψ_P. For this purpose, consider zero-order group functions, Ψ_P,i⁽⁰⁾, that are eigenfunctions of the Ĥ_P Hamiltonian, eq 35

39

describing a group P in the noninteracting, R_AB → ∞, limit. Let Ψ_PX,i denote monomer functions corresponding to a group monomer Hamiltonian Ĥ_PX given in eq 36

40

Then, any (N_P-electron) ith eigenfunction Ψ_P,i⁽⁰⁾ is a product of (N_PA- and N_PB-electron) monomer-group functions

41

with the corresponding energy

42

The index i, labeling ε_P⁽⁰⁾ and Ψ_P, is understood as a combined index (kl), where k and l label group states of A and B, respectively.

In the assumed multiconfiguration approximation, a monomer wave function can be written as

43

where {Φ_PX,K} is a set of single determinants built from spin orbitals belonging to a group P_X. In the multireference approximations considered in this work, orbital and configurational spaces are finite, and the wave functions are obtained with the optimal orbitals and configuration expansion coefficients. Having defined a group zero-order Hamiltonian, eq 35, with the corresponding eigenfunctions shown in eq 41, applying the standard perturbation theory to eq 16 using the first-order Hamiltonian V̂_PAB + Ĥ_P,SCF⁽¹⁾ as the perturbation (see eqs 30, 32 and 37) leads to obtaining first-order perturbation to an ith state of the group P, Ψ_P,i, which can be written in a general form as

44

The first term results from admitting state mixing and the sum runs over all unperturbed states of the Hamiltonian Ĥ_P⁽⁰⁾ orthogonal to Ψ_P,i. The second and third terms in eq 44 are due to orbital optimization, that is, allowing for mixing of orbitals between groups. If, for example, φ_p(x) is an unperturbed spin orbital belonging to a group P and assigned to monomer A, p ∈ P_A, then, its first-order perturbation φ_p⁽¹⁾ is expanded in the space of all spin orbitals except those belonging to P_A. Such first-order perturbations contribute to Ψ_P,i as combinations of singly excited determinants 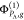and 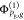. In other words, 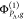denotes a determinant built of N_PA – 1 orbitals from a group P_A and one spin orbital from another group Q ≠ P_A (the same for monomer B). Assume from now on that the considered dimer is in its ground state, thus the indices i, l, and k in eq 44 will be set to 0. Notice, however, that the presented analysis is general, not limited to ground states. The explicit expression for C_P,0j coefficients in eq 44 reads

45

Coefficients {c_PX,0g} arising from orbital perturbations cannot be given explicitly. They follow as solutions of linear equations which are generalizations of the coupled-perturbed HF equations.^57,58 As in the case of the latter equations, c_PX,0g coefficients are linearly dependent on the elements 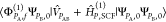, which allows us to write

46

similar for c_PB,0g, where the functions F_PX,gf depend on the energies ε_PX,0 and the matrix elements of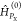

47

Let us return to the energy expression in eq 38 obtained after eliminating these terms from the second-order energy of the dimer, which cannot give rise to the dispersion energy. The C_P,0j coefficients (eq 45) which enter in the first term of eq 44 depend on the interaction operator V̂_PAB and a one-electron operator Ĥ_P,SCF⁽¹⁾. Only the former is retained because, as we discussed, the latter does not contribute to the dispersion interaction. The second and third terms in eq 44 (expression for Ψ_P,i), which arise from the orbital perturbation in SCF methods, cannot recover the dispersion interaction either. Their insertion into eq 38 leads to products of terms of the form 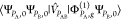, in which the interaction operator V̂_PAB does not connect the ground state with both-monomer-excited states. Such terms, corresponding to one monomer remaining in the ground state, contribute to the induction components of the interaction energy, not to dispersion.

Thus, out of all terms in E_d⁽²⁾, we retain only the ones involving C_P,0j and the operator V̂_PAB, cf. eq 45. After expressing both the zero-order energy and wave function in terms of its monomer counterparts, eqs 41 and 42, we arrive at the energy expression which is a part of the dimer energy and gives rise to the dispersion interaction. It reads

48

where ω_PX,i denotes a transition energy for a group P and a monomer X

49

and only the terms for which i ≠ 0 and j ≠ 0 have been kept (naturally, the terms for which i = 0 and j ≠ 0 and vice versa will be of the induction type; therefore, they have been excluded from eq 48).

A more convenient form of E_disp^MC follows after introducing transition density matrices. Notice that in the assumed wave function, eq 10, a set of occupied spin orbitals is divided into disjoint subsets P corresponding to group functions Ψ_P. In the dimer dissociation limit, each subset decomposes into sets P_A and P_B of the orbitals assigned to the pertinent monomers. A transition density matrix for a monomer X in the representation of the orbitals from P_X reads

50

which allows one to turn the expression in eq 48 into

51

where ⟨pa|qb⟩ are two-electron integrals in the 1212 convention. This is a central equation of this work.

E_disp^MC yields the amount of dispersion interaction energy recovered by the employed MC wave function model conforming to the ansatz in eq 10. Let us list the most relevant conclusions that the obtained result leads to

• (a)A given group P has nonzero contributions to the interaction energy of the dispersion type only if in the R_AB → ∞ limit, the wave function Ψ_P dissociates into a product Ψ_PAΨ_PB, where both Ψ_PA and Ψ_PB are MC functions. The reason is that only the states excited in the configurational space of the P_A and P_B groups enter E_disp^MC, which obviously implies that configurational spaces, cf. eq 43, must be at least two-dimensional.
• (b)The previous point immediately implies that E_disp^MC = 0 and no dispersion is recovered in supermolecular calculations in the case of the HF or CAS(2,2) description of a dimer or if upon dissociation, one monomer is described with a single determinant.
• (c)In a given wave function model, the inactive orbitals (doubly occupied in each Slater determinant) do not play a role in recovering the dispersion. A group of inactive orbitals forms a single determinant Ψ_inact, as seen in eq 11, which does not contribute to E_disp^MC.
• (d)Orbital optimization should not play a significant role, so CAS-CI and CASSCF at the same CAS(n,m) level are expected to reproduce the same amount of dispersion.

2.3. Dispersion Energy Recovered in the CAS Model

In this work, we focus our attention on the CAS model. A dimer wave function takes a product form, as shown in eq 11, where the active function Ψ_active is an n-electron full configuration function obtained from m orbitals called active. Such a function is denoted as CAS(n,m). The dispersion energy recovered by a dimer CAS function dissociating into CAS functions for monomers can be written as

52

pq (ab) are active orbitals of monomer A (B). Notice that in fact, eq 52 is more general and applies to any MCSCF model. By ω_activeX,i, we denote transition energies obtained by diagonalizing a Hamiltonian for the active group, cf. eqs 31, 34, and 36,

53

where N_active,X is the number of active electrons in monomer X, M_nuc,X denotes the number of nuclei in X, and ρ_inact,X and γ_inact,X are the density and the density matrix corresponding to inactive orbitals, respectively.

We have shown that the supermolecular CAS interaction energy recovers a portion of the second-order dispersion energy, quantified by eq 52, which directly relates to the size of the active space. In the extreme case, when all orbitals are active and the CAS turns into the FCI, the E_disp^CAS term becomes identical to the full second-order dispersion energy shown in eq 9. In other cases, the CAS supermolecular interaction energy can be corrected for the missing portion of the dispersion interaction by subtracting E_disp and adding the full dispersion energy recovered by a method of choice, which leads to the “CAS corrected for the dispersion” interaction energy method

54

When defining monomer CAS wave functions, which are dissociation products of the assumed CAS(n,m) dimer function, one should be cautious. It is clear that the number of active electrons in the monomers, n_A and n_B, should sum up to n to satisfy the size-consistency condition. However, if m = m_A + m_B active orbitals are considered, m_A of which are localized on A and m_B of which are localized on B, then in the limit R_AB → ∞, a product of CAS(n_A,m) and CAS(n_B,m) functions yields the same energy as a sum of monomer energies computed with the pertinent CAS(n_X,m_X) functions. Thus, the aforementioned product is a valid CAS zero-order wave function of a dimer, satisfying the size-consistency condition. In practical terms, this implies that in the supermolecular computation of the CAS interaction energy, the energy of monomers should be obtained with CAS(n_X,m) functions, where m includes m_X active orbitals on X and m – m_X orbitals on the other monomer. This problem is similar to, but not the same as, the counterpoise correction for the BSSE. We call it a counterpoise CAS-superposition error (CASSE) correction. It vanishes when the CAS function turns into the FCI and a complete basis set is used.

It should be noticed that the dispersion correction, E_disp^CAS, discussed in this section follows from the standard RS perturbation theory, which misses exchange contributions. If perturbation theory with symmetry forcing^59,60 were applied, it would reveal that the CAS interaction energy includes only a fraction of the second-order exchange-dispersion term, whose magnitude depends on the size of the active space. One would therefore arrive at the conclusion that the CAS must be corrected for the exchange-dispersion energy in a way similar to that for the dispersion energy, that is, in analogy to eq 54. In the next section, an approximate exchange-dispersion correction is proposed.

3. Computational Details

The second-order dispersion energies calculated in this work include both the polarization and exchange components. We use the E_DISP⁽²⁾ notation for the energy terms calculated directly within the SAPT^49,50 framework

55

Unlike E_disp^CAS, the second-order exchange-dispersion energy recovered in supermolecular CASSCF calculations, E_exch-disp, is not obtained directly but approximated by scaling of the full term

56

In analogy to eq 55, we use the

57

notation to represent the complete second-order dispersion energy recovered by the CAS (the E_disp^CAS term is given in eq 52). In other words, E_DISP denotes the dispersion energy which is accounted for in the supermolecular interaction energy, eq 2.

The “CAS corrected for dispersion” energy takes the form

58

For comparison, we also present the results obtained by taking the sum of the CASSCF interaction energy and the E_DISP⁽²⁾ term (the dispersion energy included in the CASSCF interaction energy is not removed), the approach which we denote as E_int. An analogous notation, E_int^HF+DISP, is used for the HF method supplemented with full dispersion.

Evaluation of the E_disp^CAS formula, eq 52, requires access to both transition energies and transition density matrices of the monomers corresponding to the active group Hamiltonian, eq 53. These may be obtained either by direct diagonalization of the Hamiltonian or from full linear response equations. In this work, we followed the latter approach for the model He···He and He···H₂ dimers using time-dependent linear response equations of ref (61). For these systems, therefore, E_disp is computed exactly, within a given basis set. For many-electron systems, we approximate the required response properties using solutions of extended random phase approximation^62,63 (ERPA) equations. The ERPA eigenproblem for each monomer is formulated for the Ĥ_actX Hamiltonian, as seen in, for example, eqs 6–9 in ref (16), which leads to a Hessian matrix of a simple form⁶⁴ (for details, see the Supporting Information). Both construction and diagonalization of the Hessian for a CAS wave function require steps which scale as M_act⁶, where M_act denotes the number of the active orbitals. Thus, the cost of computing E_disp in the ERPA approximation is small considering that regular CAS calculations employ an active space that is considerably smaller compared to the virtual space.

The CASSE introduced in the previous section was accounted for in E_disp^CAS energy calculations according to a three-step protocol. First, monomer CAS(n_A,m_A)SCF and CAS(n_B,m_B)SCF calculations were converged in the dimer-centered basis set. Next, a set containing inactive and active natural orbitals of a given monomer was extended with active orbitals from its interacting partner and orthonormalized according to the Schmidt procedure. The new sets containing m = m_A + m_B active orbitals for each monomer were completed by adding CASSCF secondary orbitals from monomer calculations. Finally, these orbital sets entered CAS-CI calculations.

The CAS wave function captures dynamic correlation effects only within the active space. This affects the quality of both the density and density matrices^16,65 and translates into a rather poor representation of the intramonomer correlation effects in the supermolecular CAS energy. To correct this deficiency, one may describe the first-order interaction energy terms, that is, the electrostatic and exchange energies, at the fully correlated level of theory instead of the CASSCF one. This may be realized in an approximate manner by subtracting the first-order terms calculated with CASSCF density matrices and replacing them with more accurate ones. When applied together with the discussed dispersion correction, this leads to

59

where the first term is given by eq 58. The first and second terms in square brackets represent corrections of electrostatic and exchange interaction components, respectively, where the E_elst⁽¹⁾ and E_exch terms account for intramonomer correlation effects. The E_elst⁽¹⁾(CAS) term is computed according to the known expression for electrostatic electron interaction, as seen in, for example, ref (49), with the electron density obtained from the pertinent CAS wave function. It is assumed that first-order exchange terms are calculated in the S² approximation (e.g., see eq 9 in ref (66)) which requires access only to one- and two-electron reduced density matrices of the monomers. The CASc + DispCAS approach can be interpreted as a multireference counterpart of the HFDc⁽¹⁾ method.⁶⁷

For the sake of convenience, acronyms and notations used in figures and tables throughout the article have been listed in Table 1.

Table 1. Notations Used for Dispersion Energy and Interaction Energy Expressions in This Work.

dispersion energy
Edisp(2)	second-order dispersion energy, eq 9
Eexch-disp(2)	second-order exchange-dispersion energy
EDISP(2)	sum of second-order dispersion and exchange-dispersion energies, eq 55
EdispCAS	residual CAS dispersion energy, eq 52
Eexch-dispCAS	residual CAS exchange-dispersion energy, eq 56
EDISPCAS	sum of residual CAS dispersion and exchange-dispersion energies, eq 57a

interaction energy
EintCASSCF	CAS: CASSCF supermolecular interaction energy
EintCAS+DISP	CAS + DISP: CASSCF supermolecular interaction energy with the EDISP(2) dispersion added (dispersion double counting present)
EintCAS+DispCAS	CAS + DispCAS: CASSCF supermolecular interaction corrected for the dispersion (dispersion double counting removed), eq 58
EintCASc+DispCAS	CASc + DispCAS: CASSCF supermolecular interaction corrected for both dispersion and first-order (electrostatic and exchange) energy, eq 59

^aE_DISP^CAS terms were corrected for CASSE in He···He and He···H₂ calculations (see the article).

Two model systems studied in this work are the He···He dimer and the He···H₂ dimer. The reference total interaction energy curve for He···He was taken from the work of Przybytek et al.⁶⁸ The benchmark interaction energies for excited states of the He···H₂ dimer were obtained at the FCI level of theory in the aug-cc-pVTZ basis set.⁶⁹ For many-electron systems from the A24 data set, the coupled-cluster single and double excitation and the perturbative triples/complete basis set [CCSD(T)/CBS] values from ref (70) served as a benchmark.

The E_disp^CAS energy calculations were performed in the in-house code. All necessary integrals and CASSCF one- and two-electron reduced density matrices were obtained from the Molpro⁷¹ program. The same software was used for supermolecular CASSCF calculations. The convergence threshold for SCF orbital optimization was set to 10^–10 in the gradient norm. All reported interaction energies were corrected for the BSSE using the CP scheme²⁰ of Boys and Bernardi. In contrast to E_disp, the supermolecular CASSCF results were not corrected for the CASSE.

CASSCF wave functions for systems from the A24 data set were obtained with MP2 natural orbitals employed as an initial guess for the CAS optimization. The supermolecular CAS interaction energy may suffer from the lack of size consistency if dimer active orbitals, obtained for the assumed CAS(n,m) model and yielding the lowest energy of a dimer in the dissociation limit, do not correspond to the optimal active orbitals of the monomers [it is assumed that monomers are described with CAS(n_X,m_X) functions such that n_A + n_B = n and m_A + m_B = m]. To eliminate the risk of size-consistency violation, for each dimer, the CASSCF energy was computed at an intermonomer distance of 200 bohr and it was checked that the dimer energy agrees with the sum of monomer energies within at least 10^–4 mHa.

For both the He···He and He···H₂ dimers, the reference values of SAPT energy components were calculated at the FCI level of theory in a house-developed code.^65,72 In the case of He···He, both dispersion and exchange-dispersion components were extrapolated to the CBS limit according to the aug-cc-pVQZ → aug-cc-pV5Z two-point scheme of Bak et al.⁷³ For He···H₂, all calculations employed the aug-cc-pVTZ basis and CBS extrapolation was not performed. For systems from the A24 data set, the SAPT energy components entering eqs 58 and 59 were obtained at the DFT-SAPT⁷⁴⁻⁷⁶ level of theory based on the asymptotically corrected⁷⁷ PBE0^78,79 functional using the dimer-centered basis for monomer calculations. The exchange energy components were calculated in the S² approximation. All DFT-SAPT calculations were performed in the Molpro⁷¹ program. The aug-cc-pVTZ basis set supplemented with (3s3p2d2f) midbond functions was used. Both midbond exponents and midbond location procedures were taken from ref (67).

4. Results

4.1. Model Systems: He···He and He···H₂

In this section, we examine the performance of the introduced “CAS plus dispersion” models for the interaction between two-electron monomers. As mentioned, in this case, we use accurate CAS transition density matrices which enter the E_disp^CAS expression. In calculations of the latter, the CASSE is removed according to the protocol described in the previous section. The second-order dispersion energy is obtained from SAPT calculations at the FCI level of theory.

As we have rigorously shown in Section 2.2, CASSCF recovers a portion of the dispersion energy, as seen in eq 52. Therefore, a simple addition of the dispersion component, cf. eq 55, to the supermolecular CASSCF interaction energy leads to double counting of intermonomer correlation effects, the magnitude of which depends on the size of the active space. This is illustrated in Figure 1 (see “CAS + DISP” curves) on the example of the He···He dimer in the ground state. While a small CAS(4,4) wave function of the dimer [dissociating to a product of CAS(2,2) monomer functions] supplemented with dispersion deviates from the benchmark only by 6.6% in the van der Waals minimum (R_eq = 5.6 bohr), going to the CAS(4,28) model leads to 72% overestimation of the interaction energy. Additionally, dispersion double counting shifts the minimum from the correct distance of 5.6 bohr for CAS(4,4) to 5.3 bohr for CAS(4,28). In the proposed CAS + DispCAS approach, we improve the CAS + DISP results by removing the partial dispersion contained in the supermolecular CASSCF energy, cf. eq 58. Consequently, the extension of the active space does not lead to overcorrelation and the errors in the He···He minimum region do not exceed 2% regardless of the active space size (Figure 1). The only exception is the CAS(4,4) + DispCAS curve where the error reaches 7%, which is mainly due to the poor representation of the first-order energy terms (see Figure S1 in the Supporting Information).

Figure 1.

He···He ground-state interaction energy curves. Left: E_int^CAS+DISP = E_int + E_DISP⁽²⁾; right: E_int (see eq 58). “Exact” refers to the benchmark nonrelativistic potential of ref (68). The basis set is aug-cc-pV5Z.

In the asymptotic regime the He···He interaction is dominated by the dispersion energy which decays with the inverse sixth power of the interatomic distance. Therefore, at large distances, the CASSCF interaction energy and the E_disp^CAS term calculated directly according to eq 52 should become identical. Indeed, in Figure 2 we demonstrate a perfect agreement on the example of CAS(4,10) and CAS(4,18) wave functions. Even in the larger active space, CASSCF recovers only approximately 50% of the C₆ coefficient, that is, 0.735 a.u. compared to the reference value of 1.461 a.u.⁸⁰ A closer comparison with the long-range behavior of the FCI curve reveals that neither CAS(4,10) nor CAS(4,18) recovers higher C_n coefficients. This is not surprising because only p orbitals are included in the active space.

Figure 2.

Comparison of the long-range behavior of the CASSCF interaction energy (E_int^CAS × R⁶) and the CASSCF dispersion energy (E_disp × R⁶) for the ground state of the He···He dimer based on the CAS(4,10) and CAS(4,18) references. “Exact” refers to the benchmark C₆ value of ref (80). The basis set is aug-cc-pVTZ.

A more challenging model system is the He···H₂ dimer in which the hydrogen molecule is in one of the two lowest excited states, that is, either the ¹Σ_u⁺ or the ¹Π_u state. Note that the dispersion corrections employed in “CAS plus dispersion” approaches may be applied to excited states provided that the zero-order wave function is nondegenerate. We present the results for the T-shaped geometry where we vary the distance R between the center of mass of H₂ and the He atom. The equilibrium bond lengths in the H₂ molecule are 2.443 bohr for the ¹Σ_u⁺ state and 1.951 bohr the ¹Π_u state. We begin by comparing the performance of the “CAS plus dispersion” models. In Figure 3, we show the results for the He···H₂(¹Π_u) complex obtained by choosing 2 active orbitals on the He atom and either 4 or 10 active orbitals on the H₂ molecule. Clearly, increasing the number of active orbitals leads to a severe overestimation of the interaction energy if the E_DISP⁽²⁾ term (eq 55) is directly added to the CASSCF interaction energy (cf. “CAS + DISP” curves in Figure 3). Because of the correlation double counting in the larger CAS space, the minimum is predicted at 2.8 bohr, while the smaller CAS + DISP model correctly locates it at 3.2 bohr. When the amount of the added dispersion is tailored to the employed multireference model, as proposed in the CAS + DispCAS approach, interaction energy curves greatly improve. For CAS(4,6), the error in the van der Waals minimum amounts to 2.3%. In CAS(4,12), it is larger and reaches 11%. Considering that the dispersion energy is calculated exactly, this should be attributed to the erroneous representation of the remaining energy components in the supermolecular CASSCF approach.

Figure 3.

He···H₂(¹Π_u) dimer interaction energy curve. The complex is kept in a T-shaped configuration. R denotes the distance between the He atom and the center of the H₂ molecule. The basis set is aug-cc-pVTZ.

Because applications of multireference methods to interacting excited systems are scarce, it is instructive to compare the performance of CAS + DispCAS with that of other approaches. In Figure 4, the results from CASPT2 and SAPT(FCI) calculations up to the second order in V̂_int (the latter denoted as E⁽¹⁾ + E⁽²⁾) are shown next to the CASSCF and “CAS plus dispersion” models. The He atom and H₂(¹Σ_u⁺) molecule were described with the CAS(2,5) and CAS(2,4) wave functions, respectively. In the He···H₂(¹Π_u) complex, we chose the CAS(2,2) active space for He and CAS(2,10) for H₂. The corresponding active spaces assumed for a dimer CASSCF calculation were (4,9) and (4,12) for the considered states. By confronting Figure 4, one observes a strikingly poor performance of the second-order SAPT energy (see “E⁽¹⁾ + E⁽²⁾” curves). Although the corresponding curves account for the second-order dispersion energy and in consequence show a correct asymptotic behavior, at intermediate- and short intermonomer distances second-order SAPT becomes even less accurate than CASSCF. This indicates that higher than second order induction terms, accounted for in CASSCF but missed in SAPT, are comparable in magnitude to the considered E⁽¹⁾ + E⁽²⁾ energy contributions. In the CASPT2 method the perturbation correction is added to the CASSCF energy, so the aforementioned higher-order terms are included. In spite of this, CASPT2 significantly underestimates the interaction energy for the ¹Σ_u⁺ state. In particular, the minimum is predicted at R = 4.1 bohr and 1.0 mE_h deep, which is too shallow compared to the FCI benchmark that is 1.7 mE_h deep and located at 3.7 bohr. For the ¹Π_u state, CASPT2 performs better and the curve has a correct shape. The interaction energy at the minimum (R = 3.2 bohr) is underestimated by 12.3%, which is similar in magnitude to the −11.0% overestimation from CAS + DispCAS calculations.

Figure 4.

He···H₂(¹Σ_u⁺) and He···H₂(¹Π_u) interaction energy curves. The complex is kept in the T-shaped geometry. R denotes the distance between the He atom and the center of the H₂ molecule. The basis set is aug-cc-pVTZ.

As already discussed, direct addition of the dispersion energy in the CAS + DISP approach leads to severe overcorrelation in both the He···H₂(¹Π_u) and He···H₂(¹Σ_u⁺) states (Figure 4). Contrary to this, CAS + DispCAS avoids dispersion double counting and performs well in both cases. The positions of van der Waals minima match the FCI benchmark and are predicted with −9.6 and −11.0% relative percent errors for the Σ_u⁺ and Π_u states, respectively. The improvement of the first-order interaction energy components according to the procedure proposed in eq 59, cf. the CASc + DispCAS curves, has a marginal effect on the CAS + DispCAS energies in the ¹Π_u state. For example, the error in the minimum is reduced from −11% to −8.6%. This points toward the inaccurate treatment of higher than second order terms. In the ¹Σ_u⁺ state, the difference is more pronounced—at the minimum geometry (R = 3.7 bohr) CASc + DispCAS deviates from the FCI by 2.2%, while CAS + DispCAS is off by – 9.6%.

4.2. Correcting Dispersion and First-Order Interaction Energy Components in the CAS Model for Many-Electron Systems

For model, few-electron systems discussed in Section 4.1, it is possible to employ large active spaces and restore a significant portion of the dispersion energy in size-consistent supermolecular CASSCF calculations. To verify what amount of the dispersion energy is captured by CASSCF for many-electron systems and examine the effect of correcting first-order interaction energy according to eq 59, in this section, we focus on a set of small, noncovalently bound dimers selected from the A24 database.⁷⁰ The analyzed complexes may be grouped according to the dominating interaction energy contributions into hydrogen-bonded dimers (H₂O···H₂O, HCN···HCN, and HF···HF), mixed electrostatic/dispersion dimers [HF···CH₄, HCOH···HCOH, C₂H₂···C₂H₂(1), and C₂H₄···C₂H₄(1)], and dispersion-dominated (van der Waals) dimers [Ar···CH₄, Ar···C₂H₄, C₂H₄···C₂H₂, C₂H₄···C₂H₄(2), and C₂H₂···C₂H₂(2)]. In Table 2, we report the interaction energy values following from “CAS plus dispersion” and “HF plus dispersion” calculations [CCSD(T)/CBS is taken as the reference]. Table 2 also contains error statistics in terms of the mean error Δ̅, the standard deviation σ, the mean absolute error Δ̅_abs, and the maximum absolute error Δ_max. We found that for the selected many-electron systems, the effect of the CASSE on the E_disp^CAS energy was negligible and the results presented in this section do not account for it (see Table S6 in the Supporting Information).

Table 2. Interaction Energies (kcal/mol) and Error Statistics (in Percent) for Selected Systems of the A24 Data Set^a.

					CAS		CASc
	HF	CAS	HF + DISP	HFc + DISP	+DISP	+DispCAS	+DISP	+DispCAS	ref.
H2O–H2O	–3.628	–2.710	–6.078	–4.859	–5.045	–5.012	–4.752	–4.719	–5.006
HCN–HCN	–4.100	–3.408	–5.866	–4.850	–5.108	–5.084	–4.695	–4.671	–4.745
HF–HF	–3.742	–2.741	–5.635	–4.294	–4.526	–4.505	–4.109	–4.088	–4.581
HF–CH4	–0.257	0.168	–1.839	–1.725	–1.347	–1.328	–1.628	–1.609	–1.654
HCOH–HCOH	–2.458	–0.656	–6.659	–4.743	–4.749	–4.718	–4.410	–4.379	–4.554
C2H2–C2H2(1)	–0.511	–0.254	–1.922	–1.724	–1.637	–1.637	–1.577	–1.577	–1.524
C2H4–C2H4(1)	0.902	0.801	–1.232	–1.280	–1.299	–1.281	–1.204	–1.186	–1.090
Ar–CH4	0.355	0.350	–0.494	–0.456	–0.470	–0.470	–0.425	–0.425	–0.405
Ar–C2H4	0.430	0.356	–0.348	–0.415	–0.409	–0.409	–0.390	–0.390	–0.364
C2H4–C2H2b	3.400	2.643	1.116	0.540	0.368	0.412	0.557	0.601	0.821
C2H4–C2H4(2)b	3.877	2.975	1.304	0.598	0.403	0.447	0.624	0.667	0.934
C2H2–C2H2(2)b	3.476	2.752	1.448	0.924	0.738	0.784	0.928	0.974	1.115
Δ̅	140	128	–6.4	–12.2	–16.2	–14.6	–7.3	–5.7
Δ̅abs	141	128	24.7	13.7	19.4	18.1	10.8	9.7
σ	112	71.5	27.7	13.1	22.5	20.8	13.9	12.2
Δmax	315	222	46.2	35.9	56.8	52.2	33.2	28.5

^aHFc and CASc denote supermolecular HF and CASSCF interaction energies, respectively, corrected for the first-order SAPT(PBE0AC) energy. “CAS plus dispersion” models include the dispersion energy obtained at the SAPT(PBE0AC) level of theory in the aug-cc-pVTZ + (3322) basis. For the “CAS + DispCAS” and “CASc + DispCAS” methods, see eqs 58 and 59, respectively. “Ref.” is the CCSD(T)/CBS benchmark of ref (70).

^bNonequilibrium geometry.

As expected for single-reference systems, both the CASSCF and HF methods not corrected for dispersion show similar, poor performance with mean errors that amount to 128% and 141%, respectively (Table 2). Addition of the E_DISP⁽²⁾ dispersion term from SAPT(DFT) calculations drastically improves the results (Δ̅_abs = 19% for CAS + DISP and Δ̅_abs = 25% for HF + DISP). Note that the CAS + DISP model clearly outperforms its HF counterpart for hydrogen-bonded dimers. In contrast, HF + DISP performs better for systems dominated by dispersion. The CAS-based approach may be corrected further by removing from CAS + DISP the dispersion energy recovered by CAS, that is, the E_DISP term, as done in the CAS + DispCAS model (see eq 58). This has a weak effect—the values of |E_DISP^CAS| are smaller than 0.05 kcal/mol for the investigated systems. The only notable error reduction in CAS + DispCAS with respect to CAS + DISP occurs for the van der Waals dimers and does not exceed 5% (see also Table S4 in the Supporting Information). We conclude that in many-electron systems described with moderate active spaces, the double counting of the dispersion energy does not play a significant role, with the only exception being van der Waals complexes where it introduces discernible errors.

Both HF and CASSCF clearly benefit when the first-order electrostatic and exchange interaction energy components are treated at the SAPT(DFT) level of theory. The resulting HFc and CASc models provide a nearly 2-fold reduction in terms of both mean errors and the standard deviation when compared with their uncorrected HF and CAS equivalents (Table 2). In particular, the CASc + DispCAS approach, as formulated in eq 59, performs the best in the group (Δ̅ = −5.7% and σ = 12.2%). Still, relatively large errors between 13 and 27% persist for dispersion-bounded dimers for which the interaction energy has a repulsive character.

5. Conclusions

We presented a way to quantify the amount of the dispersion energy recovered in the supermolecular interaction energy, the residual dispersion energy, calculated with MC wave functions. Applying the RS perturbation theory to a group product wave function, we arrived at a general expression that rigorously yields a portion of the dispersion energy in the MCSCF interaction energy (eq 51). It is different from 0 if a dimer wave function is such that it dissociates into monomer wave functions both of which are at least two-configurational. The dispersion-in-MCSCF energy increases upon active space expansion and reaches the full second-order dispersion limit when all orbitals are active.

By deriving the expression for the residual dispersion, we were able to rigorously address the problem of dispersion double counting which occurs when the dispersion energy is added directly to the supermolecular MCSCF interaction energy. We developed a dispersion correction for wave functions of the CAS type. The correction is tailored to the employed active space so that its addition to the CAS interaction energy, as shown in eq 54, accounts for exactly the amount of the second-order dispersion energy which is missed by the CAS. The resulting “CAS plus dispersion” method requires computing the E_disp^CAS energy, eq 52, either in an exact manner by diagonalization of the active Hamiltonians for the monomers or approximately, by solving ERPA equations formulated with the active Hamiltonian for each monomer. One should notice that the proposed route of avoiding dispersion double counting in supermolecular CAS calculations is rigorous and does not rely on orbital localization, contrary to the physically motivated scheme outlined in ref (46). In the latter approach, the degree to which double counting of dispersion is avoided will depend on how well orbitals are localized on fragments. The most expensive step of computing E_disp scales only with the sixth power of the number of active orbitals if ERPA equations are used, so it is modest comparing to the cost of CASSCF calculation. To assure the proper physical damping of the dispersion energy, we include exchange-dispersion terms approximated with second-order SAPT energy expressions, eqs 55–58. Therefore, in the CAS + DispCAS scheme proposed in this work, the CASSCF interaction energy is corrected for both dispersion and exchange-dispersion components.

On the example of the model He···He and He···H₂ systems in the ground and excited states, we demonstrated that the direct addition of the full second-order dispersion to the CAS interaction energy leads to overcorrelation which increases with the number of active orbitals. In contrast, the tailored dispersion correction applied in the CAS + DispCAS approach yields an accurate interaction energy regardless of the size of the active orbital set which validates the method. For the He···H₂(¹Σ_u⁺) and He···H₂(¹Π_u) complexes, CAS + DispCAS proved to be superior to CASPT2 and second-order SAPT. This shows that the method may be successfully applied to study excited-state interactions provided that an accurate representation of the dispersion energy is available.

To examine the extent of the dispersion double counting in CASSCF calculations for many-electron systems, we studied several representative dimers selected from the A24 data set. We found out that in small active spaces feasible for size-consistent calculations [up to CAS(12,12) for the dimer], CASSCF recovers only 2–3% of the true dispersion. The overcorrelation becomes relevant in van der Waals (dispersion-dominated) systems where it translates into interaction energy errors at the level of 4–5%. This effect may be larger in the case of systems in excited states, when a few active diffuse orbitals contribute significantly to the dispersion interaction. Taking into account the low cost of computing the residual dispersion (as shown in this work, it depends only on the number of active orbitals, which is always much lower than the total number of orbitals), it is advisable to remove it from the supermolecular energy, even when the employed active space is relatively small.

Applications of the proposed CAS + DispCAS method for truly multireference systems require an adequate representation of the dispersion energy. Currently, it is possible to calculate both the polarization and exchange components of the second-order dispersion energy for many-electron CAS wave functions within the ERPA formalism.^16,65 A substantial improvement of the CAS + DispCAS accuracy is achieved if both the electrostatic and exchange first-order components recovered by the CAS are corrected for intramonomer correlation effects, as shown in eq 59. This approach is analogous to the HF-based HFDc⁽¹⁾ method of ref (8). Improving the quality of 1-RDMs from CASSCF calculations to compensate for the missing intramonomer correlation is less straightforward compared to the single-reference HFDc⁽¹⁾ approach. The multiconfiguration DFT theory could be explored in this context. Works on further verification and improvement of the accuracy provided by the CAS + DispCAS method, particularly in complexes involving excited states, are being carried out in our group.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00681.

• ERPA equations for the active group Hamiltonian; second-order E_disp^CAS(n,m) energy values for the He···He interaction energy curve; CASSCF, CASPT2, SAPT, and “CAS plus dispersion” interaction energy curves for the He···H₂(¹Σ_u⁺, ¹Π_u) dimers; and absolute CASSCF energies and individual relative percent errors of “CAS plus dispersion” models for the systems from the A24 data set (PDF)

The authors declare no competing financial interest.